Skip to main content
SpringerLink
Log in

Nonlinear dynamics of traveling beam with longitudinally varying axial tension and variable velocity under parametric and internal resonances

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

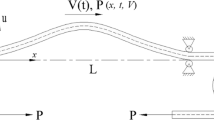
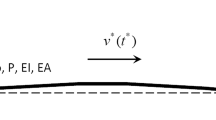
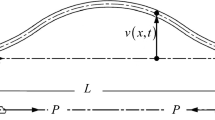
In this investigation, the nonlinear dynamics of an axially accelerating viscoelastic beam on a pully mounting system have been analyzed. The axial tension of the beam is modeled as a function of the traveling velocity, support stiffness parameter as well as spatial coordinate. Geometric cubic nonlinearity in the equation of motion is due to elongation in the neutral axis of the beam. The integro-partial differential equation of motion of the axially accelerating beam associated with the simply supported end conditions is solved analytically by adopting the direct perturbation method of multiple time scales. As a result, a set of complex variable modulation equations is generated, which governs the modulation of amplitude and phase. This set of modulated equations is numerically solved to explore the influence of the support stiffness parameter upon the stability and bifurcation of the beam which has not been addressed in the existing literature. Apart from this, the impact of fluctuating velocity component, viscoelastic coefficient, longitudinal stiffness parameter, internal and parametric frequency detuning parameters on the stability and bifurcation analysis is studied, revealing significant dynamic characteristics of the traveling system. The fourth-order Runge–Kutta method is applied is to find the dynamic solution of the system. The system displays stable periodic, quasi-periodic, and mixed-mode dynamic responses along with the unstable chaotic behavior for a specific set of system parameters. The results obtained through an analytical–numerical approach may help the design and operation of an axially moving beam.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

References

  1. Wickert, J.A.: Non-linear vibration of a traveling tensioned beam. Int. J. Non-Linear Mech. 27(3), 503–517 (1992)

    MATH  Google Scholar 

  2. Pakdemirli, M., Ozkaya, E.: Approximate boundary layer solution of a moving beam problem. Math. Comp. Appl. 3(2), 93–100 (1998)

    MATH  Google Scholar 

  3. Yang, X.D., Wu, H., Qian, Y.J., Zhang, W., Lim, C.W.: Nonlinear vibration analysis of axially moving strings based on gyroscopic modes decoupling. J. Sound Vib. 393, 308–320 (2017)

    Google Scholar 

  4. Oz, H.R.: On the vibrations of an axially travelling beam on fixed supports with variable velocity. J. Sound Vib. 239(3), 556–564 (2001)

    Google Scholar 

  5. Oz, H.R., Pakdemirli, M., Boyacı, H.: Non-linear vibrations and stability of an axially moving beam with time-dependent velocity. Int. J. Non-Linear Mech. 36(1), 107–115 (2001)

    MATH  Google Scholar 

  6. Pakdemirli, M., Oz, H.R.: Infinite mode analysis and truncation to resonant modes of axially accelerated beam vibrations. J. Sound Vib. 311, 1052–1074 (2008)

    Google Scholar 

  7. Pellicano, F., Vestroni, F.: Complex dynamics of high-speed axially moving systems. J. Sound Vib. 258(1), 31–44 (2002)

    Google Scholar 

  8. Marynowski, K., Kapitaniak, T.: Kelvin-Voigt versus Burgers internal damping in modeling of axially moving viscoelastic web. Int. J. Non-Linear Mech. 37(7), 1147–1161 (2002)

    MATH  Google Scholar 

  9. Marynowski, K.: Non-linear dynamic analysis of an axially moving viscoelastic beam. J. Theor. Appl. Mech. 40(2), 465–482 (2002)

    MATH  Google Scholar 

  10. Lv, H.W., Li, L., Li, Y.H.: Non-linearly parametric resonances of an axially moving viscoelastic sandwich beam with time-dependent velocity. Appl. Math. Model. 53, 83–105 (2018)

    MATH  Google Scholar 

  11. Saksa, T., Jeronen, J.: Dynamic analysis for axially moving viscoelastic Poynting–Thomson beams. Math. Model. Optim. Complex Struct. 40, 131–151 (2016)

    Google Scholar 

  12. Yao, G., Yimin, Z.: Reliability and sensitivity analysis of an axially moving beam. Meccanica 51(3), 491–499 (2016)

    MATH  Google Scholar 

  13. Chakraborty, G., Mallik, A.K.: Non-linear vibration of a travelling beam having an intermediate guide. Nonlinear Dyn. 20(3), 247–265 (1999)

    MATH  Google Scholar 

  14. Mao, X.Y., Ding, H., Chen, L.Q.: Parametric resonance of a translating beam with pulsating axial speed in the super-critical regime. Mech. Res. Commun. 76, 72–77 (2016)

    Google Scholar 

  15. Ding, H., Chen, L.: Nonlinear dynamics of axially accelerating viscoelastic beams based on differential quadrature. Acta Mech Solida Sin. 22(3), 267–275 (2009)

    Google Scholar 

  16. Ghayesh, M.H., Amabili, M., Farokhi, H.: Two-dimensional nonlinear dynamics of an axially moving viscoelastic beam with time-dependent axial speed. Chaos Solitons Fractals 52, 8–29 (2013)

    MATH  Google Scholar 

  17. Wang, Y., Ding, H., Chen, L.Q.: Nonlinear vibration of axially accelerating hyperelastic beams. Int. J. Non-Linear Mech. 99, 302–310 (2018)

    Google Scholar 

  18. Paidoussis, M.P., Moon, F.C.: Nonlinear and chaotic fluidelastic vibrations of a flexible pipe conveying fluid. J. Fluids Struct. 2(6), 567–591 (1988)

    Google Scholar 

  19. Czerwinski, A., Luczko, J.: Non-planar vibrations of slightly curved pipes conveying fluid in simple and combination parametric resonances. J. Sound Vib. 413, 270–290 (2018)

    Google Scholar 

  20. Chin, C.M., Nayfeh, A.H.: Three-to-one internal resonances in parametrically excited hinged-clamped beams. Nonlinear Dyn. 20(2), 131–158 (1999)

    MATH  Google Scholar 

  21. Huang, J.L., Su, R.K.L., Li, W.H., Chen, S.H.: Stability and bifurcation of an axially moving beam tuned to three-to-one internal resonances. J. Sound Vib. 330(3), 471–485 (2011)

    Google Scholar 

  22. Huang, J.L., Zhu, W.D.: A new incremental harmonic balance method with two-time scales for quasi-periodicmotions of an axially moving beam with internal resonanceunder single–tone external excitation. ASME J. Vib. Acoust. 139(2), 021010 (2017)

    Google Scholar 

  23. Ghayesh, M.H., Amabili, M.: Steady-state transverse response of an axially moving beam with time-dependent axial speed. Int. J. Non-Linear Mech. 49, 40–49 (2013)

    Google Scholar 

  24. Mao, X.Y., Ding, H., Chen, L.Q.: Internal resonance of a supercritically axially moving beam subjected to the pulsating speed. Nonlinear Dyn. 95(1), 631–651 (2019)

    Google Scholar 

  25. Ding, H., Huang, L., Mao, X., Chen, L.: Primary resonance of traveling viscoelastic beam under internal resonance. Appl. Math. Mech. 38(1), 1–14 (2017)

    MATH  Google Scholar 

  26. Ding, H., Li, Y., Chen, L.Q.: Effects of rotary inertia on sub-and super-critical free vibration of an axially moving beam. Meccanica 53(13), 3233–3249 (2018)

    Google Scholar 

  27. Ding, H., Lim, C.W., Chen, L.Q.: Nonlinear vibration of a traveling belt with non-homogeneous boundaries. J. Sound Vib. 424, 78–93 (2018)

    Google Scholar 

  28. Wang, Z., Ren, J., Li, M.: Two-to-one internal resonance of super-critically axially moving beams. Iran. J. Sci. Technol. Trans. Mech. Eng. 45(3), 639–653 (2019)

    Google Scholar 

  29. Wang, J., Yuda, H., Su, Y., Gong, L., Zhang, Q.: Magneto-elastic internal resonance of an axially moving conductive beam in the magnetic field. J. Theor. Appl. Mech. 57(1), 179–191 (2019)

    Google Scholar 

  30. Mote, C.D., Jr.: A study of band saw vibrations. J. Frankl. Inst. 279(6), 430–444 (1965)

    Google Scholar 

  31. Mockensturm, E.M., Guo, J.: Nonlinear vibration of parametrically excited, viscoelastic, axially moving strings. J. Appl. Mech. 72(3), 374–380 (2005)

    MATH  Google Scholar 

  32. Marynowski, K., Kapitaniak, T.: Zener internal damping in modelling of axially moving viscoelastic beam with time-dependent tension. Int. J. Non-Linear Mech. 42(1), 118–131 (2007)

    MATH  Google Scholar 

  33. Ma, L., Chen, J., Tang, W., Yin, Z.: Transverse vibration and instability of axially travelling web subjected to non-homogeneous tension. Int. J. Mech. Sci. 133, 752–758 (2017)

    Google Scholar 

  34. Wang, Y., Zhu, W.: Nonlinear transverse vibration of a hyperelastic beam under harmonic axial loading in the subcritical buckling regime. Appl. Math. Model. 94, 597–618 (2021)

    MATH  Google Scholar 

  35. Guo, Y., Zhu, B., Li, Y.: Nonlinear dynamics of fluid-conveying composite pipes subjected to time-varying axial tension in sub-and super-critical regimes. Appl. Math. Model. 101, 632–653 (2022)

    MATH  Google Scholar 

  36. Lenci, S., Clementi, F., Warminski, J.: Nonlinear free dynamics of a two-layer composite beam with different boundary conditions. Meccanica 50(3), 675–688 (2015)

    MATH  Google Scholar 

  37. Lenci, S., Clementi, F.: Natural frequencies and internal resonance of beams with arbitrarily distributed axial loads. J. Appl. Comput. Mech. 7(Special Issue), 1009–1019 (2021)

    Google Scholar 

  38. Lenci, S., Clementi, F., Rega, G.: Comparing nonlinear free vibrations of Timoshenko beams with mechanical or geometric curvature definition. Procedia IUTAM 20, 34–41 (2017)

    Google Scholar 

  39. Chen, L.Q., Tang, Y.Q.: Combination and principal parametric resonances of axially accelerating viscoelastic beams: recognition of longitudinally varying tensions. J. Sound Vib. 330(23), 5598–5614 (2011)

    Google Scholar 

  40. Tang, Y.Q., Zhang, D.B., Gao, J.M.: Parametric and internal resonance of axially accelerating viscoelastic beams with the recognition of longitudinally varying tensions. Nonlinear Dyn. 83(1), 401–418 (2016)

    MATH  Google Scholar 

  41. Tang, Y.Q., Zhou, Y., Liu, S., Jiang, S.Y.: Complex stability boundaries of axially moving beams with interdependent speed and tension. Appl. Math. Model. 89, 208–224 (2021)

    MATH  Google Scholar 

  42. Zhang, D.B., Tang, Y.Q., Liang, R.Q., Yang, L., Chen, L.Q.: Dynamic stability of an axially transporting beam with two-frequency parametric excitation and internal resonance. Eur. J. Mech. A/Solids 85, 104084 (2021)

    MATH  Google Scholar 

  43. Lv, H., Li, Y., Li, L., Liu, Q.: Transverse vibration of viscoelastic sandwich beam with time-dependent axial tension and axially varying moving velocity. Appl. Math. Model. 38, 2558–2585 (2014)

    MATH  Google Scholar 

  44. Liu, S., Tang, Y.Q., Chen, L.: Multi-scale analysis and Galerkin verification for dynamic stability of axially translating viscoelastic Timoshenko beams. Appl. Math. Model. 93, 885–897 (2021)

    MATH  Google Scholar 

  45. Yan, T., Yang, T., Chen, L.: Direct multiscale analysis of stability of an axially moving functionally graded beam with time-dependent velocity. Acta Mech Solida Sin. 33(2), 150–163 (2020)

    Google Scholar 

  46. Tang, Y.Q., Ma, Z.G.: Nonlinear vibration of axially moving beams with internal resonance, speed-dependent tension, and tension-dependent speed. Nonlinear Dyn. 98(4), 2475–2490 (2019)

    MATH  Google Scholar 

  47. Tang, Y.Q., Ma, Z.G., Liu, S., Zhang, L.Y.: Parametricvibration and numerical validation of axially moving viscoelastic beams with internalresonance, time and spatialdependent tension, and tension dependent speed. ASME J. Vib. Acoust. 141(6), 061011 (2019)

    Google Scholar 

  48. Nayfeh, A.H.: Introduction to Perturbation Techniques. Wiley, New York (1981)

    MATH  Google Scholar 

  49. Nayfeh, A.H., Balachandran, B.: Applied Nonlinear Dynamics. Wiley, New York (1995)

    MATH  Google Scholar 

Download references

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, IIIT, Bhubaneswar, 751003, India

    Sanjay Kumar Raj & Bamadev Sahoo

  2. Department of Physics, IIIT, Bhubaneswar, 751003, India

    Alok Ranjan Nayak

  3. Department of Mechanical Engineering, OUTR, Bhubaneswar, 751003, India

    L. N. Panda

Authors
  1. Sanjay Kumar Raj
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bamadev Sahoo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alok Ranjan Nayak
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. L. N. Panda
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bamadev Sahoo.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Data availability

All the data generated or analyzed during this study are included in this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

$$ \varsigma_{1} = \left[ { - 2(i\omega_{1} \phi_{1} + V_{0} \phi^{\prime } )A_{1}^{\prime } - 2i\alpha \omega_{1} A_{1} \phi_{1}^{\prime \prime \prime \prime } - 2i\mu \,\omega_{1} A_{1} \phi_{1} } \right] $$
$$ \varsigma_{2} = \overline{A}_{1} \,\left\{ {\,V_{1} \omega_{1} \overline{\phi }_{1}^{\prime } - \frac{{\,V_{1} \Omega }}{2}\,\overline{\phi }^{\prime}_{1} - \frac{{\,V_{1} \Omega }}{2}(1 - x)\overline{\phi }_{1}^{\prime \prime } + i\,kV_{0} V_{1} \overline{\phi }_{1}^{\prime \prime } } \right\} $$
$$ \varsigma_{3} = A_{2} \,\left\{ {\,V_{1} \omega_{2} \overline{\phi }_{2}^{\prime } - \frac{{v_{1} \Omega }}{2}\overline{\phi }_{2}^{\prime } - \frac{{V_{1} \Omega }}{2}(1 - x)\overline{\phi }_{2}^{\prime \prime } - ikV_{0} V_{1} \overline{\phi }_{2}^{\prime \prime } } \right\} $$
$$ \varsigma _{4} = \frac{1}{2}v_{l}^{2} \left\{ {A_{1}^{2} \bar{A}_{1} \left( {2\phi _{1}^{{\prime \prime }} \int\limits_{0}^{1} {\phi _{1}^{\prime } \,\bar{\phi }_{1}^{\prime } {\rm d}x + \bar{\phi }_{1}^{{\prime \prime }} } \int\limits_{0}^{1} {\phi _{1}^{{\prime 2}} {\rm d}x} } \right) + 2A_{1} A_{2} \bar{A}_{2} \left( {\bar{\phi }^{\prime\prime}_{2} \int\limits_{0}^{1} {\phi ^{\prime}_{1} \phi ^{\prime}_{2} {\rm d}x + 2A_{1} A_{2} \bar{A}_{2} \phi ^{\prime\prime}_{1} \int\limits_{0}^{1} {\phi ^{\prime}_{2} \bar{\phi }^{\prime}_{2} {\rm d}x} + 2A_{1} A_{2} \bar{A}_{2} \phi ^{\prime\prime}_{2} \int\limits_{0}^{1} {\phi ^{\prime}_{1} \bar{\phi }^{\prime}_{2} {\rm d}x} } } \right)} \right\} $$
$$ \varsigma_{5} = \frac{1}{2}v_{l}^{2} \left\{ {2\overline{A}_{1}^{2} A_{2} \overline{\phi }^{\prime\prime}_{1} \int\limits_{0}^{1} {\phi^{\prime}_{2} \overline{\phi }^{\prime}_{1} {\rm d}x} + \overline{A}_{1}^{2} A_{2} \phi^{\prime\prime}_{2} \int\limits_{0}^{1} {\overline{\phi^{\prime}}_{1}^{2} \,{\rm d}x} } \right\} $$
$$ \varsigma_{6} = \left[ { - 2\left( {i\omega_{2} \phi_{2} + V_{0} A^{\prime}_{2} \phi^{\prime}_{2} } \right)A^{\prime}_{2} \, - 2\alpha i\omega_{2} A_{2} \phi^{\prime\prime\prime\prime}_{2} - 2\mu \,i\omega_{2} A_{2} \phi_{2} } \right] $$
$$ \varsigma_{7} = A_{1} \left\{ { - \,V_{1} \omega_{1} \phi^{\prime}_{1} - \frac{{\,V_{1} \Omega }}{2}\phi^{\prime}_{1} - \frac{{\,V_{1} \Omega }}{2}\left( {1 - x} \right)\phi^{\prime\prime}_{1} + i\,kV_{0} V_{1} \phi^{\prime\prime}_{1} } \right\} $$
$$ \varsigma _{8} = \frac{1}{2}v_{l}^{2} \left\{ {A_{2}^{2} \bar{A}_{2} \left( {2\phi _{2}^{{\prime \prime }} \int\limits_{0}^{1} {\phi _{2}^{\prime } \bar{\phi }_{2}^{\prime } } {\text{d}}x + \bar{\phi }_{2}^{{\prime \prime }} \int\limits_{0}^{1} {\phi _{2}^{{\prime 2}} {\text{d}}x} } \right) + 2A_{1} \bar{A}_{1} A_{2} \left( {\phi _{1}^{{\prime \prime }} \int\limits_{0}^{1} {\phi _{2}^{\prime } \bar{\phi }_{1}^{\prime } {\text{d}}x} + \phi _{2}^{{\prime \prime }} \int\limits_{0}^{1} {\phi _{1}^{\prime } \bar{\phi }_{1}^{\prime } {\text{d}}x} + \bar{\phi }_{1}^{{\prime \prime }} \int\limits_{0}^{1} {\phi _{1}^{\prime } \phi _{2}^{\prime } {\text{d}}x} } \right)} \right\} $$
$$ \varsigma _{9} = \frac{1}{2}v_{l} ^{2} \left\{ {A_{1}^{3} \left( {\phi _{1}^{{\prime \prime }} \int\limits_{0}^{1} {\phi _{1}^{{\prime 2}} {\text{d}}x} } \right)} \right\} $$
$$ S_{1} = \frac{{\frac{1}{16}v_{l}^{2} \left\{ {2\int_{0}^{1} {\phi_{1}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1}^{\prime } {\text{d}}x} + \int_{0}^{1} {\overline{\phi }_{1}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} \int_{0}^{1} {\phi^{{\prime_{1}^{2} }} {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{1} \int_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}} $$
$$ S_{2} = \frac{{\frac{1}{8}v_{l}^{2} \left\{ {\int_{0}^{1} {\overline{\phi }_{2}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} \int_{0}^{1} {\phi_{1}^{\prime } \phi_{2}^{\prime } {\text{d}}x} + \int_{0}^{1} {\phi_{1}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2}^{\prime } {\text{d}}x} + \int_{0}^{1} {\phi_{2}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{2}^{\prime } {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{1} \int_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} + {\mkern 1mu} V_{0} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}} $$
$$ S_{3} = \frac{{\frac{1}{8}v_{l}^{2} \left\{ {\int_{0}^{1} {\phi_{2}^{\prime \prime } \overline{\phi }_{2} {\text{d}}x} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1}^{\prime } {\text{d}}x} + \int_{0}^{1} {\overline{\phi }_{1}^{\prime \prime } \overline{\phi }_{2} {\text{d}}x} \int_{0}^{1} {\phi_{1}^{\prime } \phi_{2}^{\prime } {\text{d}}x} + \int_{0}^{1} {\phi_{1}^{\prime \prime } \overline{\phi }_{2} {\text{d}}x} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{1}^{\prime } {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{2} \int_{0}^{1} {\phi_{2} \overline{\phi }_{2} {\text{d}}x} + {\mkern 1mu} V_{0} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2} {\text{d}}x} } \right\}}} $$
$$ S_{4} = \frac{{\frac{1}{16}v_{l}^{2} \left\{ {2\int_{0}^{1} {\phi_{2}^{\prime \prime } \overline{\phi }_{2} {\text{d}}x} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2}^{\prime } {\text{d}}x} + \int_{0}^{1} {\overline{\phi }_{2}^{\prime \prime } \overline{\phi }_{2} {\text{d}}x} \int_{0}^{1} {\phi^{{\prime_{2}^{2} }} {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{2} \int_{0}^{1} {\phi_{2} \overline{\phi }_{2} {\text{d}}x} + {\mkern 1mu} V_{0} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2} {\text{d}}x} } \right\}}} $$
$$ C_{1} = \frac{{ - i\omega_{1} \int_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} }}{{ - \left\{ {i\omega_{1} \int\limits_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} + {\mkern 1mu} V_{0} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}} $$
$$ C_{2} = \frac{{ - i\omega_{2} \int_{0}^{1} {\phi_{2} \overline{\phi }_{2} {\text{d}}x} }}{{ - \left\{ {i\omega_{2} \int_{0}^{1} {\phi_{2} \overline{\phi }_{2} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2} {\text{d}}x} } \right\}}} $$
$$ e_{1} = \frac{{ - i\omega_{1} \int_{0}^{1} {\phi_{1}^{\prime \prime \prime \prime } \overline{\phi }_{1} {\text{d}}x} }}{{ - \left\{ {i\omega_{1} \int_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}} $$
$$ e_{2} = \frac{{ - i\omega_{2} \int_{0}^{1} {\phi_{2}^{\prime \prime \prime \prime } \overline{\phi }_{2} {\text{d}}x} }}{{ - \left\{ {i\omega_{2} \int_{0}^{1} {\phi_{2} \overline{\phi }_{2} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2} {\text{d}}x} } \right\}}} $$
$$ g_{1} = \frac{{\frac{1}{16}v_{l}^{2} \left\{ {2\int_{0}^{1} {\overline{\phi }_{1}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{1}^{\prime } {\text{d}}x} + \int_{0}^{1} {\phi_{2}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} \int_{0}^{1} {\overline{\phi }^{{\prime_{1}^{2} }} {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{1} \int_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}} $$
$$ g_{2} = \frac{{\frac{1}{16}v_{l}^{2} \left\{ {\int_{0}^{1} {\phi_{1}^{\prime \prime } \overline{\phi }_{2} {\text{d}}x} \int_{0}^{1} {\phi^{{\prime_{1}^{2} }} {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{2} \int_{0}^{1} {\phi_{2} \overline{\phi }_{2} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2} {\text{d}}x} } \right\}}} $$
$$ K_{1} = \frac{{\frac{1}{2}\left\{ {V_{1} \omega_{1} \int_{0}^{1} {\overline{\phi }_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} - \frac{{V_{1} \Omega }}{2}\int_{0}^{1} {\overline{\phi }_{1}^{\prime } } \overline{\phi }_{1} {\text{d}}x - \frac{{V_{1} \Omega }}{2}\int_{0}^{1} {\left( {1 - x} \right)\overline{\phi }_{1}^{\prime \prime } } \overline{\phi }_{1} {\text{d}}x + i{\mkern 1mu} kV_{0} V_{1} \int_{0}^{1} {\overline{\phi }_{1}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{1} \int_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}} $$
$$ K_{2} = \frac{{\frac{1}{2}\left\{ {V_{1} \omega_{2} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{1} {\text{d}}x} - \frac{{v_{1} \Omega }}{2}\int_{0}^{1} {\phi_{2}^{\prime } } \overline{\phi }_{1} {\text{d}}x - \frac{{V_{1} \Omega }}{2}\int_{0}^{1} {\left( {1 - x} \right)\phi_{2}^{\prime \prime } } \overline{\phi }_{1} {\text{d}}x - ikV_{0} V_{1} \int_{0}^{1} {\phi_{2}^{\prime \prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{1} \int_{0}^{1} {\phi_{1} \overline{\phi }_{1} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{1} {\text{d}}x} } \right\}}} $$
$$ K_{3} = \frac{{\frac{1}{2}\left\{ { - V_{1} \omega_{1} \int_{0}^{1} {\phi_{1}^{\prime } \overline{\phi }_{2} {\text{d}}x} - \frac{{V_{1} \Omega }}{2}\int_{0}^{1} {\phi_{1}^{\prime } } \overline{\phi }{\text{d}}x - \frac{{V_{1} \Omega }}{2}\int_{0}^{1} {\left( {1 - x} \right)\phi_{1}^{\prime \prime } } \overline{\phi }_{2} {\text{d}}x + ikV_{0} V_{1} \int_{0}^{1} {\phi_{1}^{{\prime^{\prime } }} \overline{\phi }_{2} {\text{d}}x} } \right\}}}{{ - \left\{ {i\omega_{2} \int_{0}^{1} {\phi_{2} \overline{\phi }_{2} {\text{d}}x} + V_{0} \int_{0}^{1} {\phi_{2}^{\prime } \overline{\phi }_{2} {\text{d}}x} } \right\}}} $$

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Raj, S.K., Sahoo, B., Nayak, A.R. et al. Nonlinear dynamics of traveling beam with longitudinally varying axial tension and variable velocity under parametric and internal resonances. Nonlinear Dyn 111, 3113–3147 (2023). https://doi.org/10.1007/s11071-022-07948-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07948-9

Keywords

Search

Navigation