1 Introduction

Driven by increasing demands for higher system performance, the complexity of modern industrial systems is growing correspondingly, under which the constituents of control systems are more likely to experience unexpected faults. These faults could degrade system performance, increase system instability, and even result in a disaster [1, 2]. In consequence, the fault tolerant control (FTC) system design [3] plays a significant role in control domains to assure system functionalities with an acceptable performance in the presence of faults, especially when tighter requirements of system reliability, availability and safety have to be met in engineering practice, such as robotic systems, aircraft, underwater vehicles, and chemical process. In the existing literature, there are two main FTC techniques [4,5,6]: passive and active techniques. The passive FTC techniques adopt the unchanged control law to address both normal and faulty cases where prior knowledge of all possible faults is required. By contrast, the active FTC techniques can actively update the controller according to the fault effects imposed on the system, and utilize the online fault estimations to compensate for the effects of faults within the control plant. Consequently, the active FTC approaches reveal more preferable fault tolerant abilities. Note that most practical systems are nonlinear in nature and there are no unified FTC strategies to deal with the nonlinearity in different forms. Thereby, it is extremely worth investigating FTC strategies of nonlinear systems. Fortunately, the Takagi–Sugeno (T–S) fuzzy model [7] offers an effective approach to characterize nonlinear systems, which is comprised of a series of local linear systems combined through membership functions. Its favorable model structure motivates the development of system analysis and control synthesis of nonlinear systems and a large body of important results have been published, see, e.g., [8,9,10,11,12,13,14,15].

On the other hand, uncertainties quite frequently occur in practical applications and have an adverse effect on the control performance. As a consequence, taking uncertainties into account in the control design helps to guarantee the desired control performance and enhance robustness. However, although the type-1 fuzzy set is capable of characterizing nonlinearity of the control systems, it fails to address uncertainties directly through its crisp membership functions. To overcome this issue, the type-2 fuzzy set coined in [16] expands the type-1 fuzzy set theory with the capability to directly capture uncertainties. As a particular case of type-2 fuzzy sets, the interval type-2 (IT2) fuzzy set [17] comes out, which can not only cope with uncertainties efficiently but ease the computation burden with respect to general type-2 fuzzy sets. The research outputs in [18] manifest the merits of type-2 fuzzy model in handling uncertainties in contrast to the type-1 counterpart. In [19], an effective IT2 fuzzy modeling approach was provided to assist the design of IT2 fuzzy controller for nonlinear systems subject to parameter uncertainties. In [20], a seminal membership-function-dependent (MFD) control strategy was published where the information of membership functions is injected into the stability analysis with the imperfect premise matching (IPM) scheme adopted [21] which allows the fuzzy controller to freely choose the fuzzy rule number and membership functions not constrained to those of fuzzy model. Some recent works can be found in [22,23,24,25,26] on the basis of type-2 fuzzy model. In [27,28,29,30], the practical applications relevant to aerospace, robot control, and image processing are reported.

FTC strategies under the framework of IT2 fuzzy model have also arisen some attention in recent years. The works in [26, 31,32,33] focus on the passive FTC techniques which cannot be used in online system repair after fault occurrence. In [34], an active FTC method was studied where the IT2 fuzzy observer and controller are designed separately with the extremely strict assumption that they share totally the same membership functions with the IT2 fuzzy model, resulting in a rather limited application scope. To the authors’ best knowledge, there are limited efforts made on the IT2 fuzzy model-based active FTC design for nonlinear systems suffering from uncertainties, external disturbance and faults. Furthermore, the approaches in tackling these issues also have great room for improvement like conservatism reduction and flexibility enhancement. Considering the mismatched membership functions and estimation errors, there exist bidirectional robustness interactions [35] between observer and FTC modules, which make the separation principle inapplicable in the design of the observer-based FTC system. Thereby, it highlights the significance and necessity of the integrated design technique, that is, the observer and controller are designed together. However, the integrated design will increase the problem’s dimensions and result in the coupling problem between the observer and controller, which makes the analysis and design more complicated. Upon the discussion above, how to design the observer-based fault estimation (FE) and FTC for the IT2 fuzzy systems under the IPM mechanism as well as MFD approaches is a worthwhile and challenging research topic, which motivates the work.

In this paper, the IT2 fuzzy model-based FE and FTC are investigated for the highly nonlinear systems suffering from uncertainties, external disturbance and actuator faults. Firstly, the IT2 T-S fuzzy model is used to describe the nonlinear dynamics of the control system where uncertainties are captured by lower and upper membership functions. Then, resorting to Lyapunov stability theory, the stability conditions are achieved to guarantee that the augmented system is asymptotically stable under the predefined \(H_\infty \) performance index. By applying matrix inequality convexification techniques, the convex sufficient criteria for the existence of both the IT2 fuzzy observer and controller are obtained. Finally, two examples are provided to demonstrate the efficacy of the developed approach. The main contributions are concluded as follows:

  1. (1)

    In the analysis, the information of membership functions of each subdomain is taken into account along with some slack matrices injected to make the results not necessarily valid for all shapes of membership functions, leading to less conservative results, which is demonstrated by the simulation results.

  2. (2)

    In this work, the designs of FE and FTC are proposed for the complicated nonlinear systems subject to uncertainties, external disturbance and actuator faults under the IT2 fuzzy framework, in which the controller and observer gains are obtained simultaneously utilizing a single-step linear matrix inequality (LMI) formulation.

  3. (3)

    The IPM scheme is adopted to provide more design flexibility in the construction of the fuzzy fault tolerant controller. Furthermore, the computational complexity caused by the integrated design strategy can be alleviated via applying fewer fuzzy rules and relatively simple membership functions in the fuzzy controller design.

The remainder of this paper is organized as follows. The IT2 T-S fuzzy model, IT2 fuzzy observer and IT2 fuzzy fault tolerant controller are described in Sect. 2. The analysis process and main results are presented in Sect. 3. Section 4 shows the simulation examples to verify the validity of the proposed approach. The conclusion is summarized in Sect. 5.

Notation: The superscript “T” denotes matrix transposition; \(P>0 (\ge 0)\) stands for that P is a real symmetric and positive definite (semidefinite) matrix; I and 0 stand for the identity matrix and zero matrix with compatible dimensions, respectively; \(\Vert v(t) \Vert _2\) is defined by \(\Vert v(t) \Vert _2=\sqrt{\int _0^\infty v^T(t)v(t)dt}\); \(diag(\ldots )\) represents a block-diagonal matrix; \(\star \) is used to represent a symmetric term in a symmetric matrix.

2 Preliminaries

2.1 IT2 T–S fuzzy model

Consider a nonlinear system suffering from uncertainties, external disturbance and actuator faults characterized by the IT2 T-S fuzzy model with r rules as follows:

Rule i: IF \(\theta _{1}(\rho (t))\) is \(\tilde{M}_{1}^{i}\) and \(\theta _{2}(\rho (t))\) is \(\tilde{M}_{2}^{i}\) and \(\cdots \) and \(\theta _{\varPsi }(\rho (t))\) is \(\tilde{M}_{\varPsi }^{i}\), THEN

$$\begin{aligned} \left\{ \begin{array}{rll} {\dot{x}}(t) &{}= &{}A_{i}x(t) + B_i \big (u(t) + f(t) \big ) + D_iw(t), \\ y(t) &{} = &{} C x(t), \end{array} \right. \end{aligned}$$

where \(x(t)\in {{\mathbb {R}}}^{n}\) denotes the system state; \(u(t)\in {{\mathbb {R}}}^{m}\) denotes the control input; \(w(t)\in {\mathbb {R}}^{d}\) stands for the external disturbance belonging to \({\mathcal {L}}_2[0, \infty )\); \(y(t)\in {\mathbb {R}}^{p}\) represents the measurement output; \(f(t)\in {{\mathbb {R}}}^{m}\) signifies the additive actuator fault on the assumption of \({\dot{f}}(t)\) belonging to \({\mathcal {L}}_2[0, \infty )\); \(\rho (t)\in {{\mathbb {R}}}^{\vartheta }\) denotes the measurable vector; \(\theta _{\alpha }(\rho (t))\) and \(\tilde{M}_{\alpha }^{i}\), \(\alpha =1,2, \ldots , \varPsi \), \(i=1,2, \ldots , r\), signify the premise variable and IT2 fuzzy set, respectively; \(A_{i}\), \(B_{i}\), \(D_{i}\) and C are known system, input, disturbance and output matrices, respectively, in which C is constrained to full row rank. The firing strength of rule i is described by the following interval sets:

$$\begin{aligned} {\mathcal {W}}_{i}(\rho (t)) = [\underline{w}_i(\rho (t)),\ {\bar{w}}_i(\rho (t))], \ \ \ i=1,2,\ldots , r \end{aligned}$$

where \(\underline{w}_i(\rho (t))=\prod _{\alpha =1}^{\varPsi }\underline{\mu }_{\tilde{M}^i_\alpha }(\theta _\alpha (\rho (t)))\) and \({\bar{w}}_i(\rho (t))=\prod _{\alpha =1}^{\varPsi }{\bar{\mu }}_{\tilde{M}^i_\alpha }(\theta _\alpha (\rho (t)))\) stand for the lower and upper grades of membership, respectively. \(\underline{\mu }_{\tilde{M}^i_\alpha }(\theta _\alpha (\rho (t)))\) and \({\bar{\mu }}_{\tilde{M}^i_\alpha }(\theta _\alpha (\rho (t)))\) denote the lower and upper membership functions, respectively. From the definition of IT2 membership functions, it follows that \({\bar{\mu }}_{\tilde{M}^i_\alpha }(\theta _\alpha (\rho (t)))\ge \underline{\mu }_{\tilde{M}^i_\alpha }(\theta _\alpha (\rho (t)))\,\ge \,0 \), leading to \({\bar{w}}_i(\rho (t))\,\ge \, \underline{w}_i(\rho (t))\,\ge \, 0\) for all i. The overall IT2 fuzzy model is depicted as

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}(t) =& \sum \limits _{i=1}^r w_i(\rho (t)) \big [A_{i}x(t) + B_i\big (u(t) + f(t)\big ) + D_iw(t) \big ], \\ y(t) =&C x(t), \end{aligned} \right. \end{aligned}$$
(1)

where \(w_{i}(\rho (t)) = \underline{\lambda }_i(\rho (t))\underline{w}_i(\rho (t))+{\bar{\lambda }}_i(\rho (t)){\bar{w}}_i(\rho (t))\ge 0\) with the property of \(\sum _{i=1}^r w_{i}(\rho (t))=1\). \(\underline{\lambda }_i(\rho (t))\in [0, 1]\) and \({\bar{\lambda }}_i(\rho (t))\in [0, 1]\) are nonlinear weighting functions, not necessarily to be known but exist, with the property of \(\underline{\lambda }_i(\rho (t))+{\bar{\lambda }}_i(\rho (t))=1\) for all i. Assume that the IT2 fuzzy system in (1) is observable and controllable so that the existence of the observer and controller can be guaranteed to implement the observer-based FTC performance.

2.2 IT2 fuzzy observer

As IT2 membership functions of the model in (1) are unknown, they are unavailable in the design of fuzzy observer except for their lower and upper bounds. In this paper, the IT2 fuzzy observer is supposed to only share the same bounds of membership functions with the fuzzy model. The details of the IT2 fuzzy observer are as follows:

Rule j: IF \(\theta _{1}(\rho (t))\) is \(\tilde{M}_{1}^{j}\) and \(\theta _{2}(\rho (t))\) is \(\tilde{M}_{2}^{j}\) and \(\cdots \) and \(\theta _{\varPsi }(\rho (t))\) is \(\tilde{M}_{\varPsi }^{j}\), THEN

$$\begin{aligned} \left\{ \begin{array}{rll} \dot{\hat{x}}(t) &{} = &{} A_{j}\hat{x}(t)+B_{j}\big (u(t)+\hat{f}(t)\big ) + L_j\big (y(t)-\hat{y}(t)\big )\\ \dot{\hat{f}}(t) &{} = &{} F_{j}\big (y(t)-\hat{y}(t)\big )\\ \hat{y}(t) &{} = &{} C \hat{x}(t) \end{array} \right. \end{aligned}$$

where \(\hat{x}(t)\in {{\mathbb {R}}}^{n}\) denotes the observer state; \(\hat{f}(t)\in {{\mathbb {R}}}^{m}\) signifies the estimation of fault f(t); \(\hat{y}(t)\in {{\mathbb {R}}}^{p}\) stands for the observer output; \(L_{j}\) and \(F_{j}\) are the fuzzy observer gains to be determined. The overall IT2 fuzzy observer is depicted as

$$\begin{aligned} \left\{ \begin{aligned} \dot{\hat{x}}(t) =&\sum \limits _{j=1}^{r} \varphi _j(\rho (t)) \big [ A_{j}\hat{x}(t) + B_{j}\big (u(t) + \hat{f}(t)\big )\\&+ L_j\big (y(t)-\hat{y}(t)\big ) \big ]\\ \dot{\hat{f}}(t) =&\sum \limits _{j=1}^{r} \varphi _j(\rho (t)) \big [ F_{j} \big (y(t)-\hat{y}(t)\big ) \big ]\\ \hat{y}(t) =&C \hat{x}(t) \end{aligned} \right. \end{aligned}$$
(2)

where \(\varphi _j(\rho (t)) \,= \,\frac{\underline{\alpha }_j(\rho (t))\underline{w}_{j}(\rho (t))+{\bar{\alpha }}_j(\rho (t)){\bar{w}}_{j}(\rho (t))}{\sum _{k=1}^{r}\big (\underline{\alpha }_k(\rho (t))\underline{w}_{k}(\rho (t))+{\bar{\alpha }}_k(\rho (t)){\bar{w}}_{k}(\rho (t))\big )}\) and \(\sum _{j=1}^{r}\varphi _j(\rho (t))=1\). \( \underline{\alpha }_j(\rho (t)) \in [0, 1]\) and \({\bar{\alpha }}_j(\rho (t)) \in [0, 1]\) are nonlinear weighting functions with the property of \(\underline{\alpha }_j(\rho (t))+{\bar{\alpha }}_j(\rho (t))=1\) for all j, which can be chosen according to practical requirements [25].

2.3 IT2 fuzzy fault tolerant controller

On the basis of the information of system states and fault signal estimated by the fuzzy observer in (2), we design an IT2 fuzzy fault tolerant controller to stabilize the nonlinear systems subject to uncertainties, external disturbance and faults, which can be expressed by the IT2 fuzzy model in (1). In order to improve the design flexibility, the fuzzy fault tolerant controller is considered with c fuzzy rules, capable of selecting different rule number with respect to the fuzzy model. The lth rule of the IT2 fuzzy fault tolerant controller is depicted as follows:

Rule l: IF \(g_{1}(\rho (t))\) is \(\tilde{N}_{1}^{l}\) and \(g_{2}(\rho (t))\) is \(\tilde{N}_{2}^{l}\) and \(\cdots \) and \(g_{\varOmega }(\rho (t))\) is \(\tilde{N}_{\varOmega }^{l}\), THEN

$$\begin{aligned} u(t) =&K_l\hat{x}(t)-\hat{f}(t), \end{aligned}$$

where \(g_{k}(\rho (t))\) represents the premise variable and \(\tilde{N}_{k}^{l}\) signifies the IT2 fuzzy set, \(k=1,2, \ldots , \varOmega \), \(l=1,2, \ldots , c\). \(K_l\) is the fuzzy controller gain to be determined. The firing strength of rule l is described by the following interval sets:

$$\begin{aligned} {\mathcal {M}}_{l}(\rho (t)) = [\underline{m}_l(\rho (t)),\ {\bar{m}}_l(\rho (t))], \ \ \ l=1,2,\ldots , c \end{aligned}$$

where \(\underline{m}_l(\rho (t))=\prod _{\beta =1}^{\varOmega }\underline{\mu }_{\tilde{N}^l_\beta }(g_{\beta }(\rho (t))\) and \({\bar{m}}_l(\rho (t))=\prod _{\beta =1}^{\varOmega }{\bar{\mu }}_{\tilde{N}^l_\beta }(g_{\beta }(\rho (t))\) signify the lower and upper grades of membership, respectively. \(\underline{\mu }_{\tilde{N}^l_\beta }(g_\beta (\rho (t)))\) and \({\bar{\mu }}_{\tilde{N}^l_\beta }(g_\beta (\rho (t)))\) stand for the lower and upper membership functions, respectively. Upon the definition of IT2 membership functions, it follows that \({\bar{\mu }}_{\tilde{N}^l_\beta }(g_\beta (\rho (t)))\ge \underline{\mu }_{\tilde{N}^l_\beta }(g_\beta (\rho (t)))\ge 0 \), leading to \({\bar{m}}_l(\rho (t))\ge \underline{m}_l(\rho (t))\ge 0\) for all l. The overall IT2 fuzzy fault tolerant controller is inferred as

$$\begin{aligned} u(t) = \sum \limits _{l=1}^{c} m_l(\rho (t)) \big [K_l\hat{x}(t)-\hat{f}(t) \big ]. \end{aligned}$$
(3)

where \( m_l(\rho (t))=\frac{\underline{\beta }_l(\rho (t))\underline{m}_{l}(\rho (t))+{\bar{\beta }}_l(\rho (t)){\bar{m}}_{l}(\rho (t))}{\sum _{k=1}^{c}\big (\underline{\beta }_k(\rho (t))\underline{m}_{k}(\rho (t))+{\bar{\beta }}_l(\rho (t)){\bar{m}}_{k}(\rho (t))\big )}\) and \(\sum _{l=1}^{c}m_l(\rho (t))=1\). \( \underline{\beta }_l(\rho (t))\in [0, 1]\) and \({\bar{\beta }}_l(\rho (t))\in [0, 1]\) are nonlinear weighting functions with the property of \(\underline{\beta }_l(\rho (t))+{\bar{\beta }}_l(\rho (t))=1\) for all l.

Remark 1

Different from the existing work [34] in which the fuzzy observer and fault tolerant controller are designed separately by assuming that the IT2 membership functions of the fuzzy model are completely available, in this paper, the system membership functions are unknown except for their bounds, and with the IPM scheme employed, the fuzzy rule number and shapes of membership functions of the fault tolerant controller and fuzzy model can be different, which extends the application scope of the provided technique and offers more freedom in the control design. Besides, the proposed MFD approach utilizes a single-step LMI formulation to co-design the fuzzy observer as well as the fuzzy fault tolerant controller to achieve the required robust FTC performance.

3 Main results

In this section, the MFD stability criteria are provided to ensure the desired control performance for the IT2 fuzzy model-based FTC system. Upon the sufficient stability conditions obtained, the approach of co-designing the IT2 fuzzy observer and fault tolerant controller is carried out in the LMI forms.

3.1 MFD stability and performance analysis

In this paper, we define \(e_x(t)=x(t)-\hat{x}(t)\), \(e_f(t)=f(t)-\hat{f}(t)\), \(e(t)= [e_x^T (t)\ e_f^T(t)]^T\), and \(v(t)= [w^T (t)\ {\dot{f}}^T(t)]^T\). For simplicity, we remove the time t from symbols for the situation without ambiguity in the subsequent analysis. For instance, x(t) and \(\hat{x}(t)\) are represented as x and \(\hat{x}\), respectively. According to (1)-(3), we have

$$\begin{aligned} {\dot{x}} =&\sum \limits _{i=1}^r \sum \limits _{l=1}^c w_i(\rho )m_l(\rho ) \big [\big (A_{i}+B_iK_l\big )\hat{x} + A_ie_x + B_ie_f \nonumber \\&+ D_i w \big ], \end{aligned}$$
(4)
$$\begin{aligned} \dot{\hat{x}} =&\sum \limits _{j=1}^r \sum \limits _{l=1}^c \varphi _j(\rho )m_l(\rho ) \big [\big (A_j + B_jK_l\big )\hat{x} + L_jC e_x \big ], \end{aligned}$$
(5)
$$\begin{aligned} {\dot{e}} =&\sum \limits _{i=1}^r \sum \limits _{j=1}^r \sum \limits _{l=1}^c w_i(\rho )\varphi _j(\rho )m_l(\rho ) \big [{\bar{A}}_{ijl}^{21}\hat{x} + {\bar{A}}_{ij}^{22}e + {\bar{E}}_{i}^{21} v \big ], \end{aligned}$$
(6)

where

$$\begin{aligned}&{\bar{A}}_{ijl}^{21} = \left[ \begin{array}{cc} A_i-A_j+ \big (B_i-B_j\big )K_l \\ 0 \end{array} \right] , \\&{\bar{A}}_{ij}^{22}= \left[ \begin{array}{cc} A_i-L_jC &{} B_i \\ -F_jC &{} 0 \end{array} \right] , {\bar{E}}_{i}^{21}= \left[ \begin{array}{cc} D_i &{} 0 \\ 0 &{} I \end{array} \right] . \end{aligned}$$

Let \(\xi =[\hat{x}^T \ e^T ]^T\) and \(h_{ijl}(\rho ) = w_i(\rho )\varphi _j(\rho )m_l(\rho )\). The augmented system consisting of (5) and (6) can be described as follows:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{\xi }}&= \sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) \big [ {\bar{A}}_{ijl} \xi + {\bar{E}}_iv \big ],\\ z_p&= C_x \hat{x} + C_e e = {\bar{C}}\xi , \end{aligned} \right. \end{aligned}$$
(7)

where

$$\begin{aligned}&{\bar{A}}_{ijl}= \left[ \begin{array}{cc} {\bar{A}}_{jl}^{11} &{} {\bar{A}}_{j}^{12} \\ {\bar{A}}_{ijl}^{21} &{} {\bar{A}}_{ij}^{22} \end{array} \right] , \ \ \ {\bar{E}}_{i}= \left[ \begin{array}{cc} 0 \\ {\bar{E}}_{i}^{21} \end{array} \right] , \\&{\bar{A}}_{jl}^{11} = A_j+B_jK_l, \ \ \ {\bar{A}}_{j}^{12} = \left[ \begin{array}{cc} L_jC&0 \end{array} \right] , \end{aligned}$$

\({\bar{A}}_{ijl}^{21}\), \({\bar{A}}_{ij}^{22}\) and \({\bar{E}}_{i}^{21}\) have been defined below (6). \(z_p\in {\mathbb R}^{2n+m}\) is the performance output with a given weighting matrix \({\bar{C}}=[C_x \ C_e]\).

Remark 2

It follows from (4) and (6) that the control system is influenced by the estimation error e and disturbance w, and the error dynamics is also subject to the system state x, disturbance w and time derivative of the fault \({\dot{f}}\). There exist bidirectional robustness interactions between the observer and control system, which makes the separation principle inapplicable. Therefore, the technique of co-designing IT2 fuzzy observer and controller is put forward to realize the required robust FTC performance in this paper.

In order to bring more information into stability analysis, referring to [20], we divide the whole operation space of interest \(\varPhi \) into \({\mathcal {U}}\) connected substate spaces depicted by \(\varPhi _u\) (\(u=1,2, \ldots , {\mathcal {U}}\)) with \(\varPhi =\cup _{u=1}^{{\mathcal {U}}}\varPhi _u\). Define the lower and upper membership functions of \(h_{ijl}(\rho )\) as below

$$\begin{aligned} \underline{h}_{ijl}(\rho ) =&\sum \limits _{u=1}^{{\mathcal {U}}}\sum \limits _{i_1=1}^{2}\sum \limits _{i_2=1}^{2}\ldots \sum \limits _{i_\vartheta =1}^{2} \prod \limits _{g=1}^{\vartheta }\upsilon _{gi_gu}(\rho _g)\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u}, \end{aligned}$$
(8)
$$\begin{aligned} {\bar{h}}_{ijl}(\rho )=&\sum \limits _{u=1}^{{\mathcal {U}}}\sum \limits _{i_1=1}^{2}\sum \limits _{i_2=1}^{2}\ldots \sum \limits _{i_\vartheta =1}^{2} \prod \limits _{g=1}^{\vartheta }\upsilon _{gi_gu}(\rho _g){\bar{\delta }}_{ijli_1i_2\ldots i_{\vartheta } u}, \end{aligned}$$
(9)

where \(\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u}\) and \({\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}\) are constant scalars to be determined with \(0\le \underline{\delta }_{ijli_1i_2\ldots i_\vartheta u}\le {\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}\le 1 \), and \(\rho _g\) is the g-th element of the vector \(\rho \); \(0 \le \underline{h}_{ijl}(\rho ) \le {\bar{h}}_{ijl}(\rho ) \le 1\); for \(g=1, 2, \ldots , \vartheta \), \(i_g=1,2\), \(u=1, 2, \ldots , {\mathcal {U}}\), and \(\rho \in \varPsi _u\), \(0\le \upsilon _{gi_gu}(\rho _g)\le 1\) and \(\upsilon _{g1u}(\rho _g)+\upsilon _{g2u}(\rho _g)=1\); otherwise, \(\upsilon _{gi_gu}(\rho _g)=0\). Then, we have the property that \(\sum _{u=1}^{{\mathcal {U}}}\sum _{i_1=1}^{2}\sum _{i_2=1}^{2}\ldots \sum _{i_\vartheta =1}^{2} \prod _{g=1}^{\vartheta }\upsilon _{gi_gu}(\rho _g)=1\), which is useful in the following analysis.

Utilize the lower and upper membership functions expressed in (8) and (9) to reconstruct \(h_{ijl}(\rho )\) as

$$\begin{aligned} h_{ijl}(\rho )=\underline{\gamma }_{ijl}(\rho )\underline{h}_{ijl}(\rho )+{\bar{\gamma }}_{ijl}(\rho ){\bar{h}}_{ijl}(\rho ), \end{aligned}$$
(10)

where \( \underline{\gamma }_{ijl}(\rho )\in [0, 1]\) and \( {\bar{\gamma }}_{ijl}(\rho )\in [0, 1]\) are nonlinear weighting functions which are not necessarily to be known but exist with the property of \(\underline{\gamma }_{ijl}(\rho )+{\bar{\gamma }}_{ijl}(\rho )=1\) for all i, j and l.

The objective of this paper is to simultaneously design the IT2 fuzzy observer and fault tolerant controller to guarantee that the augmented system (7) is asymptotically stable and satisfies \(H_\infty \) performance \(\Vert z_p\Vert _2 \le \gamma \Vert v\Vert _2\) under zero initial condition after fault occurrence.

Theorem 1

Given a positive scalar \(\gamma \), predefined scalars \(\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u}\), \({\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}\), fuzzy controller gain \(K_l\in {\mathbb {R}}^{m\times n}\), and fuzzy observer gains \(L_j\in {\mathbb {R}}^{n\times p}\), \(F_j\in {\mathbb {R}}^{m\times p}\), the augmented system in (7) is asymptotically stable with the predefined \(H_\infty \) performance level \(\gamma \), if there exist matrices \(X_1\in {\mathbb {R}}^{n\times n}\), \(X_2\in {\mathbb {R}}^{(n+m)\times (n+m)}\), \(W_{ijl} \in \mathbb R^{(4n+3m+d)\times (4n+3m+d)}\), \(M=M^T \in \mathbb R^{(4n+3m+d)\times (4n+3m+d)}\) satisfying the following inequalities for \(i, j=1,2,\ldots , r\), \(l=1,2,\ldots , c\), \(u=1,2,\ldots , {\mathcal {U}}\), \(i_1, i_2, \ldots , i_\vartheta =1,2\):

$$\begin{aligned}&X_1 > 0, \end{aligned}$$
(11)
$$\begin{aligned}&X_2 > 0, \end{aligned}$$
(12)
$$\begin{aligned}&W_{ijl} \ge 0, \end{aligned}$$
(13)
$$\begin{aligned}&{\tilde{\varPsi }}_{ijl}+W_{ijl} + M > 0, \ \forall i, j, l \end{aligned}$$
(14)
$$\begin{aligned}&\sum \limits _{i=1}^{r} \sum \limits _{j=1}^{r} \sum \limits _{l=1}^{c} \big ({\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}{\tilde{\varPsi }}_{ijl} - (\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u} - {\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}) \nonumber \\&\times W_{ijl} +{\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}M \big ) - M < 0, \ \forall i_1, i_2, \ \ldots , i_\vartheta , u \end{aligned}$$
(15)

where

$$\begin{aligned} {\tilde{\varPsi }}_{ijl} =&\left[ \begin{array}{ccc} {\tilde{\varPsi }}_{ijl}^{11} + {\tilde{\varPsi }}_{ijl}^{{11} ^T} &{} {\bar{E}}_i &{} {\tilde{\varPsi }}^{13} \\ \star &{} -\gamma ^2I &{} 0 \\ \star &{} \star &{} -I \end{array} \right] ,\\ {\tilde{\varPsi }}_{ijl}^{11} =&\left[ \begin{array}{ccc} A_j X_1 +B_j K_l X_1 &{} \varPhi _j^{12} \\ (A_i - A_j)X_1 + (B_i - B_j)K_l X_1 &{} \varPhi _{ij}^{22} \\ 0 &{} \varPhi _{j}^{32} \end{array} \right] , \ \\ {\tilde{\varPsi }}^{13} =&\left[ \begin{array}{ccc} X_1C_x^T \\ X_2C_e^T\\ \end{array} \right] ,\ \ \varPhi _j^{12} = \left[ \begin{array}{ccc} L_j C&0 \end{array} \right] X_2, \\ \varPhi _{ij}^{22} =&\left[ \begin{array}{ccc} A_i-L_j C&B_i \end{array} \right] X_2, \ \ \varPhi _{j}^{32} = \left[ \begin{array}{ccc} -F_j C&0 \end{array} \right] X_2. \end{aligned}$$

Proof

To investigate the stability of the augmented system in (7), we define the Lyapunov functional candidate as

$$\begin{aligned} V(t) = \xi ^T P \xi \end{aligned}$$
(16)

where \(P=\left[ \ \begin{array}{cc} P_1 &{} 0 \\ 0 &{} P_2 \\ \end{array} \right] \), \(P_1>0\), \(P_2>0\) and thus \(P>0\). The derivative of V(t) with respect to time t can be deduced as below:

$$\begin{aligned} {\dot{V}}(t)=&{\dot{\xi }}^{T}P\xi +\xi ^{T}P{\dot{\xi }} \nonumber \\ =&\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) \big [ \xi ^T(P{\bar{A}}_{ijl} + {\bar{A}}_{ijl}^TP)\xi \nonumber \\&+ \xi ^T P{\bar{E}}_i v + v^T{\bar{E}}_i^T P\xi \big ], \end{aligned}$$
(17)

In order to build the \(H_\infty \) performance for the observer-based FTC system under the zero initial condition, we bring in the following induced index function:

$$\begin{aligned} H(t) =&\int _0^{\infty }\big (z_p^Tz_p -\gamma ^2 v^Tv)dt \nonumber \\ =&\int _0^\infty (z_p^Tz_p-\gamma ^2 v^Tv + {\dot{V}}(t))dt- \int _0^\infty {\dot{V}}(t) dt \nonumber \\ \le&\int _0^\infty (z_p^Tz_p-\gamma ^2 v^Tv + {\dot{V}}(t))dt. \end{aligned}$$
(18)

From (17), we have

$$\begin{aligned}&z_p^Tz_p-\gamma ^2 v^Tv + {\dot{V}}(t) = \sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) z^T\varPsi _{ijl}z, \end{aligned}$$
(19)

where

$$\begin{aligned} \varPsi _{ijl} =&\left[ \begin{array}{ccc} P{\bar{A}}_{ijl} + {\bar{A}}_{ijl}^T P + {\bar{C}}^T{\bar{C}} &{} P{\bar{E}}_i \\ \star &{} -\gamma ^2I \end{array} \right] , \\ z =&\left[ \begin{array}{ccc} \xi ^T&v^T \end{array} \right] ^T. \end{aligned}$$

Once the condition \(\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) \varPsi _{ijl} < 0\) holds, we can conclude that \(H(t)\le 0\) from (18) and (19), which implies that the \(H_\infty \) performance index is satisfied. Furthermore, when \(v=0\), considering (19), we can get \({\dot{V}}(t)<0\) excluding \( \xi = 0\), which implies the augmented system in (7) is asymptotically stability.

The aforesaid result is built on the basis of the satisfaction of inequality condition: \(\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) \varPsi _{ijl} < 0\). To avoid the simultaneous coupling between the observer, controller gain matrices and different Lyapunov matrices \(P_1\), \(P_2\) when co-designing the observer and fault tolerant controller in the next section, we perform the congruence transformation to \(\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) \varPsi _{ijl} < 0\) by premultiplying and postmultiplying \(diag\{X, I\}\) with the definition \(X= \left[ \begin{array}{ccc} X1 &{} 0 \\ 0 &{} X2 \end{array} \right] \), in which \(X_1=P_1^{-1}\) and \(X_2=P_2^{-1}\). Then, we can obtain

$$\begin{aligned} \sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) {\bar{\varPsi }}_{ijl} < 0, \end{aligned}$$
(20)

where

$$\begin{aligned} {\bar{\varPsi }}_{ijl} =&\left[ \begin{array}{ccc} {\bar{A}}_{ijl}X + X {\bar{A}}_{ijl}^T + X {\bar{C}}^T{\bar{C}} X &{} {\bar{E}}_i \\ \star &{} -\gamma ^2I \end{array} \right] . \end{aligned}$$

Applying Schur complement to (20) to address the nonconvex term \( X {\bar{C}}^T{\bar{C}} X \), one can get the following equivalent inequality:

$$\begin{aligned} \sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(x) {\tilde{\varPsi }}_{ijl} < 0, \end{aligned}$$
(21)

where

$$\begin{aligned} {\tilde{\varPsi }}_{ijl} =&\left[ \begin{array}{ccc} {\bar{A}}_{ijl}X + X {\bar{A}}_{ijl}^T &{} {\bar{E}}_i &{} X {\bar{C}}^T \\ \star &{} -\gamma ^2I &{} 0 \\ \star &{} \star &{} -I \end{array} \right] . \end{aligned}$$

Due to the intrinsic characteristics of IT2 membership functions and the utilization of IPM mechanism, the parallel distributed compensation (PDC)-based approaches cannot be applied in this stability analysis. To obtain less conservative results, the approach of MFD stability analysis is employed. The information of IT2 membership functions is introduced into the stability analysis with the injection of some slack matrices via the following expressions:

$$\begin{aligned}&\Big (\sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}\sum \limits _{l=1}^{c}\big (\underline{\gamma }_{ijl}(\rho )\underline{h}_{ijl}(\rho )+{\bar{\gamma }}_{ijl}(\rho ){\bar{h}}_{ijl}(\rho )\big ) -1 \Big ) M = 0, \end{aligned}$$
(22)
$$\begin{aligned}&-\sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}\sum \limits _{l=1}^{c}\big (1-\underline{\gamma }_{ijl}(\rho )\big )\big (\underline{h}_{ijl}(\rho )-{\bar{h}}_{ijl}(\rho )\big ) W_{ijl}\ge 0, \end{aligned}$$
(23)

where \(M=M^T\) and \(W_{ijl}=W^T_{ijl}\ge 0\) are the matrices with proper dimensions.

From (10), (21)–(23), we have

$$\begin{aligned}&\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(\rho ) {\tilde{\varPsi }}_{ijl} \nonumber \\&\quad \le \sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c} \left( \underline{\gamma }_{ijl}(\rho )\underline{h}_{ijl}(\rho )\right. \nonumber \\&\quad \left. + \big (1-\underline{\gamma }_{ijl}(\rho )\big ){\bar{h}}_{ijl}(\rho )\right) {\tilde{\varPsi }}_{ijl} \nonumber \\&\qquad +\Big (\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c} \big (\underline{\gamma }_{ijl}(\rho )\underline{h}_{ijl}(\rho )\nonumber \\&\qquad +\big (1-\underline{\gamma }_{ijl}(\rho )\big ){\bar{h}}_{ijl}(\rho )\big ) - 1 \Big ) M \nonumber \\&\qquad - \,\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c} \big (1-\underline{\gamma }_{ijl}(\rho )\big )\big (\underline{h}_{ijl}(\rho )-{\bar{h}}_{ijl}(\rho )\big ) W_{ijl} \nonumber \\&\quad =\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c} \underline{\gamma }_{ijl}(\rho )\big (\underline{h}_{ijl}(\rho )-{\bar{h}}_{ijl}(\rho )\big )\big ({\tilde{\varPsi }}_{ijl}+W_{ijl} \nonumber \\&\qquad + M) +\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c} \Big ({\bar{h}}_{ijl}(\rho ){\tilde{\varPsi }}_{ijl} -\big (\underline{h}_{ijl}(\rho ) \nonumber \\&\qquad -{\bar{h}}_{ijl}(\rho )\big )W_{ijl} +{\bar{h}}_{ijl}(\rho ) M\Big ) - M. \end{aligned}$$
(24)

Referring to (24) with the fact that \(\underline{\gamma }_{ijl}(\rho )(\underline{h}_{ijl}(\rho )-{\bar{h}}_{ijl}(\rho )) \le 0\), \(\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}h_{ijl}(x) {\tilde{\varPsi }}_{ijl} < 0\) is satisfied if the following inequalities hold:

$$\begin{aligned}&{\tilde{\varPsi }}_{ijl}+W_{ijl}+M>0, \ \forall i, j, l, \end{aligned}$$
(25)
$$\begin{aligned}&\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c} \Big ({\bar{h}}_{ijl}(\rho ){\tilde{\varPsi }}_{ijl} -(\underline{h}_{ijl}(\rho )-{\bar{h}}_{ijl}(\rho ))W_{ijl} \nonumber \\&+{\bar{h}}_{ijl}(\rho ) M \Big ) - M<0. \end{aligned}$$
(26)

The condition (26) cannot be numerically solved by the LMI optimization technique because of the existence of lower and upper membership functions \(\underline{h}_{ijl}(\rho )\) and \({\bar{h}}_{ijl}(\rho )\) represented by continuous nonlinear functions. By rewriting \(\underline{h}_{ijl}(\rho )\) and \({\bar{h}}_{ijl}(\rho )\) in terms of (8) and (9), which are depicted by constant scalars \(\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u}\) and \({\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}\), and recalling the fact that \(\sum _{u=1}^{{\mathcal {U}}}\sum _{i_1=1}^{2}\sum _{i_2=1}^{2}\ldots \sum _{i_\vartheta =1}^{2} \prod _{g=1}^{\vartheta }\upsilon _{gi_gu}(\rho _g)=1\), (26) is satisfied if the following equivalent inequality holds for all \(i_1, i_2, \ldots , i_\vartheta \), u:

$$\begin{aligned}&\sum _{i=1}^{r} \sum _{j=1}^{r} \sum _{l=1}^{c}\Big ({\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}{\tilde{\varPsi }}_{ijl} -(\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u} \nonumber \\&\quad -{\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}) W_{ijl} +{\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}M\Big )-M<0. \end{aligned}$$
(27)

Hence, once the conditions (11)–(15) in Theorem 1 are satisfied, it can be concluded that \(H(t)\le 0\), which implies that the augmented system in (7) is asymptotically stability under the \(H_\infty \) performance. This completes the proof. \(\square \)

3.2 Integrated design of IT2 fuzzy observer and fault tolerant controller

Theorem 1 conducts the stability analysis for the augmented system (7) with the given observer and fault tolerant controller gains. However, the gain matrices of the observer and fault-tolerant controller cannot be directly solved from Theorem 1 owing to nonconvex terms contained in the stability criteria. In this section, by virtue of the results obtained in Theorem 1, the singular value decomposition technique is exploited to convexify the stability conditions so that the IT2 fuzzy observer and fault tolerant controller can be gained via the LMI optimization technique in one step. The feasible design procedures are presented by the following theorem.

Theorem 2

Given a positive scalar \(\gamma \), predefined scalars \(\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u}\), \({\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}\), constant matrix \(J\in {\mathbb {R}}^{p\times m}\), the augmented system in (7) is asymptotically stable with the predefined \(H_\infty \) performance level \(\gamma \), if there exist matrices \(X_1\in {\mathbb {R}}^{n\times n}\), \(N_1\in {\mathbb {R}}^{p\times p}\), \(N_2 \in {\mathbb {R}}^{(n-p)\times (n-p)}\), \(N_3 \in \mathbb R^{(n-p)\times m}\), \(X_{22} \in {\mathbb {R}}^{m\times m}\), \(W_{ijl} \in {\mathbb {R}}^{(4n+3m+d)\times (4n+3m+d)}\), \(M=M^T \in \mathbb R^{(4n+3m+d)\times (4n+3m+d)}\), \({\mathcal {M}}_l \in \mathbb R^{m\times n}\), \({\mathcal {T}}_j \in {\mathbb {R}}^{n\times p}\), \({\mathcal {G}}_j \in {\mathbb {R}}^{m\times p}\) satisfying the following inequalities for \(i, j=1,2,\ldots , r\), \(l=1,2,\ldots , c\), \(u=1,2,\ldots , {\mathcal {U}}\), \(i_1, i_2, \ldots , i_\vartheta =1,2\):

$$\begin{aligned}&X_1 > 0, \end{aligned}$$
(28)
$$\begin{aligned}&\left[ \begin{array}{cc} X_{11} &{} X_{12} \\ \star &{} X_{22} \end{array} \right] > 0, \end{aligned}$$
(29)
$$\begin{aligned}&W_{ijl} \ge 0, \end{aligned}$$
(30)
$$\begin{aligned}&\varXi _{ijl}+W_{ijl} + M > 0, \ \forall i, j, l \end{aligned}$$
(31)
$$\begin{aligned}&\sum \limits _{i=1}^{r} \sum \limits _{j=1}^{r}\sum \limits _{l=1}^{c} \big ({\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}\varXi _{ijl} - (\underline{\delta }_{ijli_1i_2\ldots i_\vartheta u} - {\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}) \nonumber \\&\times W_{ijl} +{\bar{\delta }}_{ijli_1i_2\ldots i_\vartheta u}M\big ) - M < 0, \ \forall i_1, i_2, \ldots , i_\vartheta , u \end{aligned}$$
(32)

where

$$\begin{aligned} \varXi _{ijl} =&\left[ \begin{array}{ccc} \varXi _{ijl}^{11} &{} {\bar{E}}_i &{} X{\bar{C}}^T\\ \star &{} -\gamma ^2I &{} 0 \\ \star &{} \star &{} -I \end{array} \right] , \\ \varXi _{ijl}^{11} =&\left[ \begin{array}{ccc} \varOmega _{ijl}^{11} + {\varOmega _{ijl}^{11}}^T &{} \varOmega _{ijl}^{12} &{} t_{2j} \\ \star &{} \varOmega _{ij}^{22} + {\varOmega _{ij}^{22}}^T &{} \varOmega _{ij}^{23} \\ \star &{} \star &{} -g_{2j} - g_{2j}^T \end{array} \right] ,\\ \varOmega _{ijl}^{11} =&A_jX_1 + B_j {\mathcal {M}}_l,\\ \varOmega _{ijl}^{12} =&X_1(A_i-A_j)^T + {\mathcal {M}}_l^T(B_i-B_j)^T + t_{1j},\\ \varOmega _{ij}^{22} =&A_iX_{11} + B_i X_{12}^T - t_{1j},\\ \varOmega _{ij}^{23} =&A_iX_{12} + B_i X_{22} - t_{2j} - g_{1j}^T,\\ t_{1j} =&\left[ \begin{array}{cc} {\mathcal {T}}_{j}V_1V_2^{-1}&0_{n\times (n-p)} \end{array} \right] V_3^T, \ t_{2j} = {\mathcal {T}}_{j}J,\\ g_{1j} =&\left[ \begin{array}{cc} {\mathcal {G}}_{j}V_1V_2^{-1}&0_{m\times (n-p)} \end{array} \right] V_3^T, \ g_{2j} = {\mathcal {G}}_{j}J,\\ X_{11} =&V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1V_1V_2^{-1} &{} 0_{p\times (n-p)} \\ \star &{} N_2 \end{array} \right] V_3^T,\\ X_{12} =&V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1J \\ N_3 \end{array} \right] . \end{aligned}$$

\(V_1\), \(V_2\) and \(V_3\) are acquired through the singular value decomposition of the output matrix C, i.e., \(C=V_1[V_2\ 0]V_3^T\). The fuzzy observer gain matrices are given by \(L_j={\mathcal {T}}_jN_1^{-1}\), \(F_j={\mathcal {G}}_jN_1^{-1}\), and the fuzzy controller gain matrix is given by \(K_l={\mathcal {M}}_lX_1^{-1}\).

Proof

In Theorem 1, the coupling issues severely hinder solving of observer and controller gains. Hence, the main objective subsequently is to convexify the design conditions. As the output matrix C is of full row rank, the singular value decomposition of C can be presented as below

$$\begin{aligned} C = V_1 \left[ \begin{array}{cc} V_2&0_{p\times (n-p)} \end{array} \right] V_3^T, \end{aligned}$$
(33)

where \(V_1\in {\mathbb {R}}^{p\times p}\), \(V_2\in {\mathbb {R}}^{p\times p}\), and \(V_3\in {\mathbb {R}}^{n\times n}\) are all nonsingular matrices with \(V_1V_1^T=I\) and \(V_3V_3^T=I\). Then, for the convenience of design, we specify the positive definite matrix \(X_2\) in the form of

$$\begin{aligned} X_2 =&\left[ \begin{array}{cc} X_{11} &{} X_{12} \\ \star &{} X_{22} \end{array} \right] , \end{aligned}$$
(34)
$$\begin{aligned} X_{11} =&V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1V_1V_2^{-1} &{} 0_{p\times (n-p)} \\ \star &{} N_2 \end{array} \right] V_3^T, \end{aligned}$$
(35)
$$\begin{aligned} X_{12} =&V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1J \\ N_3 \end{array} \right] , \end{aligned}$$
(36)

where \(N_{1}\), \(N_{2}\), \(N_{3}\), \(X_{22}\) are unknown matrix variables to be determined, and J is the constant matrix determined by the user.

Then, upon (33)–(36), we can have

$$\begin{aligned} L_{j}CX_{11} =&\, L_{j} V_1 \left[ \begin{array}{cc} V_2&0 \end{array} \right] V_3^T \nonumber \\&\times V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1V_1V_2^{-1} &{} 0 \\ \star &{} N_2 \end{array} \right] V_3^T \nonumber \\ =&\left[ \begin{array}{cc} {\mathcal {T}}_{j}V_1V_2^{-1}&0 \end{array} \right] V_3^T \nonumber \\ :=&\, t_{1j}, \end{aligned}$$
(37)
$$\begin{aligned} L_{j}CX_{12} =&\, L_{j} V_1 \left[ \begin{array}{cc} V_2&0 \end{array} \right] V_3^T V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1J \\ N_3 \end{array} \right] \nonumber \\ =&{\mathcal {T}}_{j}J \nonumber \\ :=&\, t_{2j}. \end{aligned}$$
(38)

Similarly, we can also have

$$\begin{aligned} F_{j}CX_{11} =&\, F_{j} V_1 \left[ \begin{array}{cc} V_2&0 \end{array} \right] V_3^T \nonumber \\&\times V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1V_1V_2^{-1} &{} 0 \\ \star &{} N_2 \end{array} \right] V_3^T \nonumber \\ =&\left[ \begin{array}{cc} {\mathcal {G}}_{j}V_1V_2^{-1}&0 \end{array} \right] V_3^T \nonumber \\ :=&\, g_{1j}, \end{aligned}$$
(39)
$$\begin{aligned} F_{j}CX_{12} =&\, G_{j} V_1 \left[ \begin{array}{cc} V_2&0 \end{array} \right] V_3^T V_3 \left[ \begin{array}{cc} V_2^{-1}V_1^TN_1J \\ N_3 \end{array} \right] \nonumber \\ =&{\mathcal {G}}_{j}J \nonumber \\ :=&\, g_{2j}. \end{aligned}$$
(40)

Now, substituting the matrix variable \(X_2\) defined in (34)–(36) into (14) and (15) together with consideration of the matrices defined in (37)–(40), and \({\mathcal {M}}_l = K_lX_1\), the conditions (31) and (32) can be obtained. Thus, this completes the proof. \(\square \)

Remark 3

It is noted that the convexifying procedure reported in this paper is based on the singular value decomposition technique. Additionally, other approaches such as the matrix decoupling method [36] and completing squares [37], could also be adopted to separate decision variables. However, these methods would increase the number of stability conditions or the dimension of matrices together with some tuning parameters introduced which are required to be fixed beforehand, resulting in heavy computational burden especially when the MFD stability analysis approach is employed. In contrast, utilizing the singular value decomposition technique results in the stability conditions to be solved with much less computational complexity.

4 Simulation examples

In this section, two detailed simulation examples are provided to verify the validity of the proposed FTC technique.

4.1 Numerical example

Consider a nonlinear system subject to parameter uncertainties, which is described by the following three-rule IT2 T-S fuzzy model:

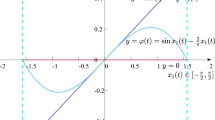
$$\begin{aligned} A_{1}= & {} \left[ \begin{array}{cc} 0.59 &{} -7.29 \\ 0.01 &{} -2.85 \end{array} \right] , A_{2}= \left[ \begin{array}{cc} 0.02 &{} -4.64 \\ 0.35 &{} -8.56 \end{array} \right] ,\\ A_{3}= & {} \left[ \begin{array}{cc} 0.73 &{} 8.45 \\ 0.26 &{} -15.43 \end{array} \right] , B_{1}=\left[ \begin{array}{cc} 1.0 \\ 0.3 \end{array} \right] ,\\ B_{2}= & {} \left[ \begin{array}{cc} 8.0&2.0 \end{array} \right] ^T,\ B_{3}=\left[ \begin{array}{cc} 4.0&0.8 \end{array} \right] ^T,\\ D_{1}= & {} D_{2} = D_{3} = \left[ \begin{array}{cc} 0&0.01 \end{array} \right] ^T, C= \left[ \begin{array}{cc} 1.0&0 \end{array} \right] , \end{aligned}$$

where the lower and upper membership functions of the IT2 fuzzy model are described as: \(\underline{w}_1(x_1)=1-1/(1+e^{(-x_1-3.5)})\), \(\underline{w}_3(x_1)=1/(1+e^{(-x_1+3.5)})\), \({\bar{w}}_2(x_1)=1-\underline{w}_1(x_1)-\underline{w}_3(x_1)\), \({\bar{w}}_1(x_1)=1-1/(1+e^{(-x_1-2.5)})\), \({\bar{w}}_3(x_1)=1/(1+e^{(-x_1+2.5)})\), \(\underline{w}_2(x_1)=1-{\bar{w}}_1(x_1)-{\bar{w}}_3(x_1)\). To demonstrate the design flexibility, a two-rule IT2 fuzzy fault tolerant controller is constructed to stabilize the faulty system with the lower and upper membership functions selected by: \(\underline{m}_1(x_1)=\{1\), when \(x_1<-5.2\); \((-x_1+4.8)/10\), when \(-5.2 \le x_1\le 4.8\); 0, when \(x_1>4.8\}\), \({\bar{m}}_1(x_1)=\{1\), when \(x_1<-4.8\); \((-x_1+5.2)/10\), when \(-4.8 \le x_1\le 5.2\); 0, when \(x_1>5.2\}\), \({\bar{m}}_2(x_1)=1-\underline{m}_1(x_1)\), \(\underline{m}_2(x_1)=1-{\bar{m}}_1(x_1)\).

Assume that the operating domain of \(x_1\) locates in the interval of \([-10, 10]\). In order to introduce more information of membership functions into the design process, we divide the whole operating domain \(x_1\) into 10 uniform subdomains where each interval is represented by \([-12+2u, -10+2u], \ u=1,2, \ldots , 10\). Through Theorem 2 with the prescribed \(H_\infty \) performance index \(\gamma =4.5\), the fuzzy observer and controller gains are obtained as follows: \(L_{1}=\left[ \begin{array}{cc} 220.4788 \\ 60.0927 \end{array} \right] \), \(L_{2}=\left[ \begin{array}{cc} 1168.4 \\ 295.5 \end{array} \right] \), \(L_{3}=\left[ \begin{array}{cc} 2022.9 \\ 432.1 \end{array} \right] \), \(F_{1}= 82.6389\), \(F_{2}= 367.1322\), \(F_{3}= 1997.8\), \(K_{1}=\left[ \begin{array}{cc} -184.0873&378.6501 \end{array} \right] \), \(K_{2}=\left[ \begin{array}{cc} -245.5332&502.1574 \end{array} \right] \).

To perform simulation, we choose the weighting functions \(\underline{\lambda }_1(x_1)=(\sin (5x_1)+1)/2\), \({\bar{\lambda }}_1(x_1)=1-\underline{\lambda }_1(x_1)\), \(\underline{\lambda }_3(x_1)=(\cos (5x_1)+1)/2\), \({\bar{\lambda }}_3(x_1)=1-\underline{\lambda }_3(x_1)\), from which we can obtain \(w_1(x_1)\) and \(w_3(x_1)\). \(\underline{\lambda }_2(x_1)\) and \({\bar{\lambda }}_2(x_1)\) are unnecessary to know as we can get \(w_2(x_1)\) from the relationship \(w_2(x_1)=1-w_1(x_1)-w_3(x_1)\). Additionally, the weighting functions of the IT2 fuzzy observer are chosen as \(\underline{\alpha }_j(x_1)={\bar{\alpha }}_j(x_1)=0.5\), \(j=1,2,3\). The weighting functions of the IT2 fuzzy fault tolerant controller are chosen as \(\underline{\beta }_l(x_1)={\bar{\beta }}_l(x_1)=0.5\), \(l=1,2\).

To investigate the FTC performance of the proposed approach, suppose that the fault f(t) is considered as

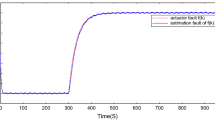
$$\begin{aligned} f(t)= \left\{ \begin{aligned}&2\sin (0.5t-5), \quad 5\le t \le 22.5 \\&0, \quad \quad \quad \quad \quad \quad \quad \quad otherwise \end{aligned} \right. \end{aligned}$$
(41)

and the external disturbance is characterized by \(\omega (t)=e^{-0.25t}\sin (0.29t)\). Under the initial condition \(x(0)=\hat{x}(0)=[0.1 \ 0.01]^T\), simulation results are displayed in Figs. 1, 2, 3, 4. Fig. 1 depicts the trajectories of actuator fault f(t) with its estimation \(\hat{f}(t)\), Figs. 2 and 3 depict the trajectories of system state x(t) with its estimation \(\hat{x}(t)\). Fig. 4 describes the control input signal u(t). From Figs. 1, 2, 3, it can be observed that the obtained IT2 fuzzy observer can offer effective estimations of the actuator fault and system states, contributing to the well construction of the fault compensation-based fault tolerant controller in the form of (3). Based on the simulation results, we can see that the designed two-rule IT2 fault tolerant controller can successfully stabilize the three-rule IT2 fuzzy system with the desired control performance in the presence of actuator fault and disturbance. By constructing the fuzzy controller with less rule number and simpler shapes of membership functions, it will be beneficial to the release of implementation cost and improvement of design flexibility.

Fig. 1
figure 1

Time response of actuator fault f(t) with its estimation \(\hat{f}(t)\)

Full size image
Fig. 2
figure 2

Time response of system state \(x_1(t)\) with its estimation \(\hat{x}_1(t)\)

Full size image
Fig. 3
figure 3

Time response of system state \(x_2(t)\) with its estimation \(\hat{x}_2(t)\)

Full size image
Fig. 4
figure 4

Time response of the control input signal u(t)

Full size image

Remark 4

To demonstrate the superiority of the MFD FTC strategy studied in this paper contrast with the membership-function-independent (MFI) one, we remove the terms relevant with the information of membership functions in Theorem 2. Then the sufficient criteria for the existence of the observer and fault tolerant controller become MFI which are summarized by (28), (29) and \(\varXi _{ijl}<0\), \(i,j =1,2,\ldots , r\), \(l=1,2,\ldots , c\). Under the same configuration aforesaid, no feasible solution can be found by the MFI approach. It reveals that our proposed approach incorporating the information of membership functions outperforms the MFI one with less conservativeness.

To further illustrate the performance of FTC affecting by the MFD approach proposed with different number of subdomains, we make comparison simulations under 3 cases where the whole state space of \(x_1\) is evenly divided into 7, 10 and 13 subdomains, respectively. The time responses of actuator fault estimation and system states are respectively displayed in Figs. 5, 6, 7 with all other settings being the same as above, from which we can see that better FE performance and superior transient response are obtained as the number of subdomains rises. It can be concluded that the studied fuzzy FTC strategy is furnished with more superior robustness along with more membership function information considered in the analysis. However, there is a tradeoff between the control performance and computational burden because the computational complexity will increase along with the number of subdomains growing.

Fig. 5
figure 5

Time response of actuator fault f(t) with its estimation \(\hat{f}(t)\) under different number of subdomains

Full size image
Fig. 6
figure 6

Time response of system state \(x_1(t)\) under different number of subdomains

Full size image
Fig. 7
figure 7

Time response of system state \(x_2(t)\) under different number of subdomains

Full size image

4.2 Nonlinear mass-spring-damper system

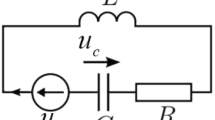
To further exemplify the effectiveness of the proposed FTC scheme, a nonlinear mass-spring-damper system suffering from the parameter uncertainty from [25] is considered. Its dynamics is described by

$$\begin{aligned} m\ddot{x}(t)+F_f+F_s=u(t) \end{aligned}$$

where x(t), m, \(F_f\), \(F_s\), and u(t) signify the displacement from a reference point, mass, the friction force, the restoring force of the spring, and the control input, respectively. Assume that \(F_f=c\dot{x}(t)\) and \(F_s=kx(t)+ka^2x^3(t)\) in which k is an uncertain parameter. Thereby, the following equation can be obtained:

$$\begin{aligned} m\ddot{x}(t)+c\dot{x}(t)+kx(t)+ka^2x^3(t)=u(t). \end{aligned}$$
(42)

Define \({{\textbf {x}}}(t)=[x_1(t)\ x_2(t)]^T=[x(t) \ \dot{x}(t)]^T\) and \(g(t)=\frac{-k-ka^2x_1^2(t)}{m}\), and suppose the operation domain \(x_1(t)\in [-1.5,\ 1.5]\). Let \(m=1kg\), \(c=1.5 N\cdot s/m\), \(a=0.2 m^{-1}\) and \(k\in [4,\ 6]N/m\). The maximum and minimum of g(t) are calculated as \(g_{max}=-4\) when \(x_1(t)=0\) and \(k=4\) and \(g_{min}=-6.54\) when \(x_1(t)=\pm 1.5\) and \(k=6\), respectively. Following the sector nonlinearity approach [38], the mass-spring-damper system (42) suffering from the parameter uncertainty, disturbance and actuator fault can be depicted by a two-rule IT2 T-S fuzzy model, where \(A_1= \left[ \begin{array}{cc} 0 &{} 1.0 \\ g_{min} &{} -\frac{c}{m} \end{array} \right] \), \(A_2= \left[ \begin{array}{cc} 0 &{} 1.0 \\ g_{max} &{} -\frac{c}{m} \end{array} \right] \), \(B_{1}=B_{2}= \left[ \begin{array}{cc} 0&\frac{1}{m} \end{array} \right] ^T\), \(D_{1}=D_{2}= \left[ \begin{array}{cc} 0&0.01 \end{array} \right] ^T\), \(C= \left[ \begin{array}{cc} 1.0&0 \end{array} \right] \). The lower and upper membership functions of the IT2 fuzzy model are computed as \(\underline{w}_1(x_1)=\frac{-g(t)+g_{max}}{g_{max}-g_{min}}\) with \(k=4\), \({\bar{w}}_1(x_1)=\frac{-g(t)+g_{max}}{g_{max}-g_{min}}\) with \(k=6\), \(\underline{w}_2(x_1)=\frac{g(t)-g_{min}}{g_{max}-g_{min}}\) with \(k=6\), and \({\bar{w}}_2(x_1)=\frac{g(t)-g_{min}}{g_{max}-g_{min}}\) with \(k=4\).

During the simulation, the uncertain parameter k is supposed as 5, and the number of subdomains is 15. The lower and upper membership functions of the designed IT2 fuzzy fault tolerant controller are selected as: \(\underline{m}_1(x_1)=1-1/(1+e^{\frac{-x_1-0.25}{2}})\), \({\bar{m}}_1(x_1)=1-1/(1+e^{\frac{-x_1+0.25}{2}})\), \(\underline{m}_2(x_1)=1-{\bar{m}}_1(x_1)\), and \({\bar{m}}_2(x_1)=1-\underline{m}_1(x_1)\). The weighting functions of the fuzzy observer and fault tolerant controller are chosen as: \(\underline{\alpha }_j(x_1)={\bar{\alpha }}_j(x_1)=0.5\), \(j=1,2\), and \(\underline{\beta }_l(x_1)={\bar{\beta }}_l(x_1)=0.5\), \(l=1,2\), respectively.

The initial conditions are given as \(x(0)=[0\ 0.1]^T\) and \(\hat{x}(0)=[0\ 0.05]^T\), and the injected fault is considered as follows:

$$\begin{aligned} f(t)= \left\{ \begin{array}{ll} 1, &{}10< t \le 20\\ 1.5 - 0.5e^{(-t+20)}, &{} 20< t \le 45 \\ 0.5 + \cos (0.1t-4.5 ), &{} 45 < t \le 129\\ 0, &{}otherwise \end{array}\right. \end{aligned}$$
(43)

The external disturbance is identical to that in Example 4.1. Applying Theorem 2 with the predefined \(H_\infty \) performance index \(\gamma =2.6\), the simulation results are presented in Figs. 8 and 9, which show the FE result and state response of the closed-loop system. As the figures display, the proposed approach can achieve effective FE and desired FTC performance for the nonlinear mass-spring-damper system in the presence of the parameter uncertainty, external disturbance and actuator fault, which verify the effectiveness of the proposed IT2 fuzzy model-based FTC strategy.

Fig. 8
figure 8

Time response of actuator fault f(t) with its estimation \(\hat{f}(t)\)

Full size image
Fig. 9
figure 9

Time response of system state \({{\textbf {x}}}(t)\) of the mass-spring-damper system

Full size image

5 Conclusion

In this paper, the problems of the observer-based FE and FTC for IT2 T-S fuzzy systems have been studied. In the proposed approach, an IT2 fuzzy observer is developed to estimate both the system states and actuator faults simultaneously. Upon these estimations obtained, a fuzzy fault tolerant controller is developed to offset the fault influences imposed on the control system and maintain the desired control performance of the closed-loop system. Based on Lyapunov stability theory, the IT2 fuzzy observer and fault tolerant controller are co-designed in a single step via the LMI formulation. The membership functions of the fuzzy fault tolerant controller proposed can be selected freely based on practical requirements, contributing to the enhancement of design flexibility. Moreover, to further relax the result conservativeness, the MFD technique is utilized by injecting the information of membership functions into the stability criteria. Finally, simulation examples have been presented to verify the effectiveness of the proposed IT2 fuzzy model-based FTC strategy. Considering the sampled-data problems frequently occur in practical control applications, the IT2 fuzzy model-based sampled-data FTC strategies will be investigated in the future. To expand applications, actuator faults and sensor faults could be considered at the same time. In addition, the fuzzy FTC strategies without differentiability restriction on the faults will be considered as well.