1 Introduction

Indeed, the Caudrey–Dodd–Gibbon–Kotera–Sawada equation (CDGKSE) and the generalized CDGKSE (gCDGKSE) describe two-layer fluid interaction. The gCDGKSE was currently considered in the literature. It is a higher-order generalization of the celebrated Kadomtsev–Petviashvili equation. In [1], a (2+1)-dimensional gCDGKS equation (2D-gCDGKSE) was studied by the Hirota bilinear method (HBM). A hierarchy of bilinear CDGKSE with a unified structure and a nonlinear superposition formula was proved under certain conditions [2]. Under the HBM, the specific expression for N-soliton solutions of 2D-gCDGKSE in fluid mechanics was given [3]. In [4], the 2D- CDGKS-like equation was investigated, based on bilinear neural network method, where novel solutions were derived. The N-soliton solutions were found by focusing on the nonlinear superposition between one lump and other types of localized waves of the2D-gCDGKSE [5]. By means of the HBM, lump-type solution and two types of interaction solutions of the 2D-Caudrey–Dodd–Gibbon–Kotera–Sawada equation were obtained [6]. The interaction phenomenon between the lump waves and stripe solitons in the 2D- CDGKSE, by making use of the HBM, was investigated [7]. The CDGKS hierarchy associated with a matrix spectral problem was suggested, based on Lenard recursion equations [8]. In [9], Bernoulli sub-equation function method was applied to obtain some new exact oscillating solutions. The CDGKSE was analytically investigated by using the HBM, where N-soliton solution was derived [10]. In [11], M-lump and interaction between lumps and kink solitons of the 2D- CDGKSE were studied based on HBM. Novel analytical and numerical solutions of the CDGKSE were established by means of Tanh method and order residual power series method [12]. The HBM was used to obtain some breather wave and lumps solutions to the CDGKSE that was converted into its potential version together with implementing of Cole–Hopf transformation [13]. The Lie symmetry analysis, exact solutions, and conservation laws to the time fractional CDGKSE with Riemann–Liouville derivative were investigated [14]. The solution of the third-order isospectral equation of the CDGKSE for soliton potential was obtained recursively from the Riccati equation via the auto-Backlund transformation [15]. The symmetry transformations of the 2D- CDGKSE with Lou’s direct method that based on Lax pairs were considered [16]. The Bäcklund transformation and Lax pair for a differential–difference CDGKSE were presented in [17]. The HBM of 2D- CDGSKE was used to obtain, a class of solutions, among them, lump, strip soliton, a pair of resonance solitons as well as the rogue wave [18]. A 2D- CDGKSE was investigated with the help of the HBM, where some singular soliton, shock-wave, breather-stripe soliton, and hybrid solutions were found [19]. In [20], the HBM combined with the simplified Hereman method was used to determine the N-soliton solutions for the fifth-order CDG equation. Some works related to the present work on CDGKSE with variable coefficients (VCs) have received the attention of many research works. The interaction between solitons and the cnoidal periodic waves of the2D- CDGKSE was explored via the consistent Tanh expansion [21].The Darboux transformation, associated with nonlocal symmetry of the 2D- CDGKSE, was localized by introducing four field quantities [22]. It is worthy to mention the CDGKSE with variable coefficients is modestly studied in the literature. In [23], soliton solutions of the 2D- VCs-CDGKSE were derived via a new velocity resonance condition. The (2+1)-dimensional variable-coefficient CDGKSE was studied, and N-th-order Pfaffian solutions were constructed [24]. In [25], the HBM was used to derive M-lump solution and N -soliton solution to the 2D- VCs-CDGKSE. Multi-waves and breathers solution of the 2D- VCs-CDGKSE, under the HBM, were obtained [26]. In [27], the bilinear form, bilinear Bäcklund transformation, and Lax pair of a 2D- VCs-CDGKSE were derived via Bell polynomials. The HBM was employed to study the 2D- VCs-CDGKSE [28].In these works, the studies focused on waves generated in a uniform fluid, while the notions of nonuniform fluid and the two-layer fluid interaction were not invoked there. In contrast with this, here, these characteristics are dealt with. The solitary wave ansatz method along with HBM and numerical simulations was used to study the CDGKSE and its bidirectional form [29, 30]. An algebraic method with symbolic computation was employed to construct a series of exact solutions of the 2D-CDGKSE [31]. Based on bilinear neural network method, the lump solutions were constructed by activation functions in the single hidden layer neural network model and the “3-2-2” neural network model [32]. The bilinear residual network method was proposed to solve the steady state CDGKSE, where rogue waves were shown [33]. After the graphs displayed in [33], they show peak waves and not rogue waves. We think that rogue waves are produced in a system, when it is in the unsteady state. Some relevant works were also carried in [34, 35].

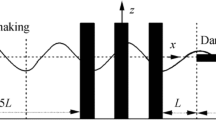
The NAUT- DGKSE ( with time-dependent coefficients) describes waves in nonuniform fluid, where the velocity is space dependent at a fixed time. It characterizes every fluid flows near a solid boundary. Thus, waterfall, water waves behind dams, and water flow in the network of canals during water release are non-uniform fluid flow. Here, a (2+1)-dimensional - NAUT-gCDGKSE is considered. So, we are concerned with inspecting waves in nonuniform flow. The exact solutions are found here via the extended unified method (EUM) [36,37,38,39,40]. Further papers on the neural network method were carried [41, 42]. Some works on rogue waves and dynamical fluid equations were presented [43,44,45,46,47,48,49,50].

The outlines of this paper are as follows. In Sect. 2, the model equation and a brief account of the EUM are presented. Section 3 is devoted to polynomial solutions, while rational solutions are given in Sect. 4. Section 5 is concerned with discussions, while some conclusions are given in Sect. 6

2 The model equation and outlines of EUM

2.1 The model equation

The (2 + 1)-dimensional gCDGKSE was considered in [1],

$$\begin{aligned} \begin{array}{l} 36u_{t}+(u_{xxxx}+15uu_{xx}+15u_{xxx})_{x}-\alpha \int u_{yy}dx\\ \quad -\gamma (u_{xxy}+3uu_{y}+3u_{x}\int u_{y}dx)=0, \end{array}\nonumber \\ \end{aligned}$$
(1)

where \(u=u(x,y,t)\) is the wave function ; \(\alpha \) and \(\gamma \) are real parameters. In (1), we put \(v=\int u_{y}dx\), so, (1) reduces to

$$\begin{aligned} \begin{array}{l} 36u_{t}+(u_{xxxx}+15uu_{xx}+15u_{xxx})_{x}-\alpha v_{y}\\ \quad -\gamma (u_{xxy}+3uu_{y}+3u_{x}v)=0,\\ v_{x}=u_{y}. \end{array} \end{aligned}$$
(2)

A more general CDGKSE is proposed, here, by

$$\begin{aligned} \begin{array}{l} \beta _{1}u_{t}+\nu \left( u_{xxxx}+\beta _{2}uu_{xx}+\beta _{2}u^{3}\right) _{x}\\ \quad -\alpha v_{y}-\gamma \left( u_{xxy}+\beta _{3}uu_{y}+\beta _{3}u_{x}v\right) =0,\\ v_{x}=u_{y}. \end{array} \end{aligned}$$
(3)

In (3), when \(\beta _{1}=36,\beta _{2}=15,\beta _{3}=3,\nu =1,\)then (3) reduces to (2). As, we are interested in studying non-autonomous gCDGKSE, we consider (3) with time-dependent coefficients

$$\begin{aligned} \begin{array}{l} \beta _{1}u_{t}+\nu (t)\left( u_{xxxx}+\beta _{2}uu_{xx}+\beta _{2}u^{3}\right) _{x}\\ \quad -\alpha (t)v_{y}-\gamma (t)\left( u_{xxy}+\beta _{3}uu_{y}+\beta _{3}u_{x}v\right) =0,\\ v_{x}=u_{y}. \end{array} \end{aligned}$$
(4)

Equation (4) suggests to introduce a stream function \(\psi (x,y,t)\) such that \(u=\psi _{x}\) and \(v=\psi _{y}\), and it reduces to the closed form

$$\begin{aligned}{} & {} -\alpha (t)\psi _{yy}+\beta _{1}\psi _{xt}-\gamma (t)\nonumber \\{} & {} \quad \left( \beta _{3}\left( \psi _{x}\psi _{xy}\left. +\psi _{y}\psi _{xx}\right) \left. +\psi _{xxxy}\right) \right. \right. \nonumber \\{} & {} \quad +\nu (t)\left( \beta _{2}\left( 3\psi _{x}^{2}\psi _{xx}+\left. \left. +\psi _{xx}\psi _{xxx}+\psi _{x}\psi _{xxxx}\right) \right. \right. \right. \nonumber \\{} & {} \quad +\left. \left. \left. \psi _{xxxxxx}\right) =0.\right. \right. \end{aligned}$$
(5)

In (5), we consider the similarity transformations \(\psi (x,y,t)=\varphi (z,t),z=\mu (t)x+\sigma (t)y,\) and \(t=t\), where z and t are independent variables. Thus, (5) becomes

$$\begin{aligned}{} & {} -\beta _{1}\mu (t)\varphi -\alpha (t)\sigma (t)^{2}\varphi _{zz}\nonumber \\{} & {} \quad -\gamma (t)\mu (t)^{2}\sigma (t)\left( 2\beta _{3}\varphi _{z}\varphi _{zz}+\mu (t)\varphi _{zzzz}\right) \nonumber \\{} & {} \quad +\nu (t)\left( \beta _{2}\mu (t)^{4}\left( 3\varphi _{z}^{2}\varphi _{zz}+\varphi _{zz}\varphi zzz+\mu (t)\varphi _{z}\varphi _{zzzz}\right) \right. \nonumber \\{} & {} \quad \left. +\mu (t)^{6}\varphi _{zzzzzz}=0.\right. \end{aligned}$$
(6)

The exact solutions of (6) are found, here, by using the EUM.

2.2 Outlines of the EUM

Consider the NLPDE’s , with explicit time-dependent

$$\begin{aligned} \begin{array}{c} f(t,u_{x},u_{y},u_{z}u_{t},v_{x},v_{y},v_{z}v_{t},u_{xx},....)=0.\end{array} \end{aligned}$$
(7)

We introduce the similarity transformations \(u(x,y,z,t)=U(z,t),\,z=\alpha (t)\,x+\beta (t)\,y,\) and \(t:=t;\)thus, (7) is rewritten as

$$\begin{aligned} \begin{array}{c} F(t,U_{t},U_{z},U_{tt},U_{zz},....)=0.\end{array} \end{aligned}$$
(8)

The EUM asserts that the solutions of (6) are expressed in polynomial and rational forms in an auxiliary function that satisfies suitable auxiliary equations. It is worthy to mention that the EUM can be considered as an alternative technique to the use of Lie group symmetries of NLPDEs. In the application, it is found that the use of the EUM is of lower time cost, in symbolic computations, than the Lie symmetry. So we think that it prevails the use of Lie symmetries as the later technique requires a long hierarchy of steps. On the other hand, it provides a wide class of solutions.

2.2.1 Polynomial solutions

The polynomial solutions of (6) are expressed in the form

$$\begin{aligned} \varphi (z,t)= & {} \sum _{j=0}^{j=n}a_{j}(t)\,g(z,t)^{j},\nonumber \\ (g_{z}(z,t))^{p}= & {} \mu \sum _{j=0}^{j=pk}c_{j}g(z,t)^{j},\nonumber \\ (g_{t}(\xi ,z,t))^{p}= & {} h(t)\sum _{j=0}^{j=pk}c_{j}g(z,t)^{j},p=1,2. \end{aligned}$$
(9)

The solutions in (9) exist if there exist integers n,  and k. Thus, our objective is to show that there exist integersn,  and k with relevance to (6). For achieving this, we use two conditions: the balance and consistency conditions. We consider the case when \(p=1.\) By inserting (9) into (7), we find that the balance condition gives rise to \(n=k-1.\) For the consistency condition, we need to calculate:

  1. (i)

    The number of equations that results from inserting Eq. (7) into Eq. (4) and by setting the coefficients of \(g(z,t)^{i},i=0,1,2,..\) etc. equals to zero; \(r(k)=7k-6\).

  2. (ii)

    The number of arbitrary functions and parameters in Eq. (7), namely \(c_{i},a_{i}(z,t),\) \(s(k)=2k+1.\)

Together with using the condition \(r(k)-s(k)\le q\), where q is the highest order derivative in (6) (\(q=6\)), the last conditions lead to \(1\le k\le 13/5.\)

When \(p=2,\)the same results hold. We mention that the solutions of Eq. (7) are hyperbolic functions when \(p=1.\), while, when \(p=2\), they are periodic or elliptic functions.

2.2.2 Rational forms

The rational solutions of Eq. (6) are expressed in the form

$$\begin{aligned}{} & {} U(z,t)=A(t)\frac{a_{1}g(z,t)+a_{0}}{s_{1}g(z,t)+s_{0}},\;\, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \begin{array}{l} \\ \;(g_{z}(z,t))^{p}=\sum _{j=0}^{j=pk}c_{j}g(z,t)^{j},\\ (g_{t}(z,t))^{p}=h(t)\sum _{j=0}^{j=pk}c_{j}g(z,t)^{j},p=1,2.\\ \\ \end{array} \end{aligned}$$
(11)

3 Polynomial solutions of (6)

3.1 When \(p=1\), \(k=2,\) \(n=1\)

In this case, we write

$$\begin{aligned} \varphi (z,t)=a_{1}(t)g(z,t)+a_{0}(t), \end{aligned}$$
(12)

and the auxiliary equations (AEs) are

$$\begin{aligned} \begin{array}{c} \;g_{z}(z,t)=c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0},\\ g_{t}(z,t)\text {:=}h(t)\left( c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}\right) . \end{array} \end{aligned}$$
(13)

Inserting (12) and (13) into (6) and by setting the coefficients of \(g(z,t)^{j}\),\(j=0,1,3,...\), equal to zero lead to

$$\begin{aligned}{} & {} \mu (t)=r,\;a_{1}(t)\nonumber \\{} & {} \quad =-\frac{c_{2}\left( \sqrt{\beta _{2}\left( \beta _{2}(2r+1)^{2}-120r^{2}\right) }+\beta _{2}(2r+1)\right) }{\beta _{2}},\nonumber \\{} & {} \quad \sigma (t)=\frac{1}{K}\left( r^{2}c_{1}^{2}-4c_{0}c_{2}\beta _{2}\left( \sqrt{\beta _{2}(\beta _{2}(2r+1)^{2}-120r^{2})}\right. \right. \nonumber \\{} & {} \quad \left. \left. +\beta _{2}\left( 2r^{2}+3r+1\right) \right. \right. \nonumber \\{} & {} \quad -60r^{2}\left. \left. +r\sqrt{\beta _{2}(\beta _{2}(2r+1)^{2}-120r^{2})}\right) \nu (t)\right) ,\nonumber \\{} & {} \quad K=2\left( \beta _{3}\sqrt{\beta _{2}(\beta _{2}(2r+1)^{2}-120r^{2})}\right. \nonumber \\{} & {} \quad \left. +\beta _{2}\left( \beta _{3}(2r+1)-6r\right) \right) \gamma (t),\nonumber \\{} & {} \quad h(t)=\frac{1}{M}(\sqrt{\beta _{2}(\beta _{2}(2r+1)^{2}-120r^{2})}(\left( c_{1}^{2}-4c_{0}c_{2}\right) {}^{2}\nonumber \\{} & {} \quad -r^{3}\nu (t) \left( -4\beta _{3}r^{2}\left( \beta _{3}(2r+1)+9r\right) \gamma (t)^{2}\right. \nonumber \\{} & {} \quad \left. +2\beta _{2}r(r+1)\right) ((\beta _{3}(2r+1)-3r)\gamma (t)^{2}-30r\alpha (t)\nu (t)\nonumber \\{} & {} \quad +\beta _{2}^{2}(r+1)^{2}(2r+1)\alpha (t)\nu (t)))-r^{3}\left( c_{1}^{2}-4c_{0}c_{2}\right) {}^{2}\nu (t)\nonumber \\{} & {} \quad \left( 240\beta _{3}^{2}r^{4}\gamma (t)^{2}+\beta _{2}^{3}(2r^{2}+3r+1)^{2}\alpha (t)\nu (t)\right. \nonumber \\{} & {} \quad -4\beta _{2}(r^{2}(-72r^{2}+3\beta _{3}(16r+13)r\nonumber \\{} & {} \quad +\beta _{3}^{2}(2r+1)^{2}))\gamma (t)^{2}-450r^{4}\alpha (t)\nu (t))\nonumber \\{} & {} \quad \left. +2\beta _{2}^{2}r(r+1)\left( (2r+1)\left( \beta _{3}(2r+1)\right. \right. \right. \nonumber \\{} & {} \quad \left. \left. \left. -3r\right) \gamma (t)^{2}-30r(3r+2)\alpha (t)\nu (t)\right) \right) ),\nonumber \\{} & {} \quad M=(8\beta _{1}\beta _{3}^{2}r\gamma (t)^{2}-24\beta _{1}\beta _{3}r\gamma (t)^{2}\nonumber \\{} & {} \quad +4\beta _{1}\beta _{3}^{2}\gamma (t)^{2})\sqrt{\beta _{2}(\beta _{2}(2r+1)^{2}-120r^{2})}\nonumber \\{} & {} \quad -240\beta _{1}\beta _{3}^{2}r^{2}\gamma (t)^{2} +16\beta _{1}\beta _{2}\beta _{3}^{2}r^{2}\gamma (t)^{2}\nonumber \\{} & {} \quad +72\beta _{1}\beta _{2}r^{2}\gamma (t)^{2}-48\beta _{1}\beta _{2}\beta _{3}r^{2}\gamma (t)^{2}\nonumber \\{} & {} \quad +16\beta _{1}\beta _{2}\beta _{3}^{2}r\gamma (t)^{2}-24\beta _{1}\beta _{2}\beta _{3}r\gamma (t)^{2}\nonumber \\{} & {} \quad +4\beta _{1}\beta _{2}\beta _{3}^{2}\gamma (t)^{2}. \end{aligned}$$
(14)

The solution of (5) (or (6)) is

$$\begin{aligned}{} & {} \psi (x,y,t){=}\frac{1}{2\beta _{2}}\sqrt{\beta _{2}(\beta _{2}(2r+1)^{2}-120r^{2})}\nonumber \\{} & {} \quad +\beta _{2}(2r+1)\left( \sqrt{c_{1}^{2}-4c_{0}c_{2}}\right. \nonumber \\{} & {} \quad +c_{1}\text {Tanh}\left[ \frac{1}{2M}\sqrt{c_{1}^{2}-4c_{0}c_{2}}\left( rx+B(t)\right. \right. \nonumber \\{} & {} \quad +\left( r^{2}yc_{1}^{2}-4c_{0}c_{2}\beta _{2}\left( -60r^{2}\right. \right. \nonumber \\{} & {} \quad +\beta _{2}\left( 2r^{2}+3r+1\right) \nonumber \\{} & {} \quad \left. \left. +\sqrt{\beta _{2}(\beta _{2}(2r+1)^{2}-120r^{2})(}r+1)\right) \nu (t)\right) ))+a_{0}(t),\nonumber \\{} & {} \quad M=\left. 2\left( \beta _{3}\sqrt{\beta _{2}\left( \beta _{2}(2r+1)^{2}-120r^{2}\right) }\right. \right. \nonumber \\{} & {} \quad \left. \left. +\beta _{2}\left( \beta _{3}(2r+1)-6r\right) \right) \gamma (t)\right) ,\nonumber \\{} & {} \quad B(t)=\int _{0}^{t}h(s)ds, \end{aligned}$$
(15)

where h(t) is given in (14).

The two-layer solutions are \(u=\psi _{x}\) and \(v=\psi _{y}\), and they are

$$\begin{aligned}{} & {} u(x,y,t)=\frac{1}{4\beta _{2}}r\text {Sech}\left[ \frac{1}{2M}\sqrt{c_{1}^{2}-4c_{0}c_{2}}\right. \left( rx+B(t)\right. \nonumber \\{} & {} \quad \left. +\left( \left( c_{1}^{2}-4c_{0}c_{2}\right) r^{2}y\right. \right. \beta _{2}\left( \sqrt{\beta _{2}\left( \beta _{2}(2r+1)^{2}-120r^{2}\right) }(r+1)\right. \nonumber \\{} & {} \quad \left. +\beta _{2}\left( 2r^{2}+3r+1\right) -60r^{2}\right) \nu (t))]^{2})\left( c_{1}^{2}-4c_{0}c_{2}\right) \nonumber \\{} & {} \quad \left( \sqrt{\beta _{2}\left( \beta _{2}(2r+1)^{2}-120r^{2}\right) }+\beta _{2}(2r+1)\right) , \end{aligned}$$
(16)
$$\begin{aligned}{} & {} v(x,y,t)=\frac{1}{4M}\left( r^{2}\text {Sech}\left[ \frac{1}{2M}\sqrt{c_{1}^{2}-4c_{0}c_{2}}\left( rx+B(t)\right. \right. \right. \nonumber \\{} & {} \quad +\left( r^{2}y(c_{1}^{2}-4c_{0}c_{2})\right. \beta _{2}\left( (r+1)\sqrt{\beta _{2}\left( \beta _{2}(2r+1)^{2}-120r^{2}\right) }\right. \nonumber \\{} & {} \quad \left. +\beta _{2}\left( 2r^{2}+3r+1\right) -60r^{2}\right) \nu (t))]^{2}\left( c_{1}^{2}\right. \nonumber \\{} & {} \quad \left. -4c_{0}c_{2}\right) {}^{2}\left( \sqrt{\beta _{2}\left( \beta _{2}(2r+1)^{2}-120r^{2}\right) }\right. \nonumber \\{} & {} \quad \left. +\beta _{2}(2r+1)\right) \left. \left( (r+1)\sqrt{\beta _{2}\left( \beta _{2}(2r+1)^{2}-120r^{2}\right) }\right. \right. \nonumber \\{} & {} \quad \left. \left. +\beta _{2}\left( 2r^{2}+3r+1\right) -60r^{2}\right) \nu (t)\right) . \end{aligned}$$
(17)

The solutions in (16) and (17) are displayed for the two-layer functions u and v in Figs. 1 (i)-(vi).

Fig. 1
figure 1

Figure 1 (i)–(vi). The 3D and contour plots of u and v are displayed against y and t for two values of x, in Figs.1(i)–(iii) and 1(v)–(vi), respectively. When \( \alpha (t)=3\sin (2(t-2)),\nu (t)=e^{-0.5t}\sin (2(t-5)) (\cos (2(t-2))+2), \gamma (t)=\sqrt{\cos (2(t-2))+2}, \beta _{2}=5,r=0.25,c_{1}=2.5,c_{0}=0.7, c_{2}=1.5,\beta _{3}=0.3,\beta _{1}=0.2.\)

Figure 1(i) shows double-U-shape internal (hollowed waves). Figure 1(ii) shows U-shape and S-shape bulge waves. Figure 1 (iii) shows the same waves.

Figure 1(iv) shows U-shape internal (hollowed wave) and S-shape bulge wave. Figure 1(v) and (vi) shows the same behavior.

Full size image

3.2 When \(p=1,\) \(k=3\) and \(n=2\)

The solution of (6) and the AEs are

$$\begin{aligned} \begin{array}{l} \varphi (z,t)=a_{2}(t)g(z,t)^{2}+a_{1}(t)g(z,t)+a_{0}(t),\\ g_{z}(z,t)=c_{3}g(z,t)^{3}+c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0},\\ g_{t}(z,t)\text {:=}h(t)\left( c_{3}g(z,t)^{3}+c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}\right) .\\ \\ \end{array}\nonumber \\ \end{aligned}$$
(18)

From (18) into (6), it gives rise to

$$\begin{aligned}{} & {} a_{2}(t)=-\frac{2\left( \sqrt{30}\sqrt{\beta _{2}}-30\right) c_{3}}{\beta _{2}-30},\nonumber \\{} & {} \quad a_{1}(t)=\frac{20\left( 27\sqrt{30}\beta _{2}^{3/2}{-}16\beta _{2}^{2} {+}450\beta _{2}{-}1410\sqrt{30}\sqrt{\beta _{2}}{+}18900\right) c_{2}}{\nonumber }\\{} & {} \quad {\left( \beta _{2}-30\right) \left( 8\sqrt{30}\beta _{2}^{3/2}-165\beta _{2}-390\sqrt{30}\sqrt{\beta _{2}}+9450\right) },\nonumber \\{} & {} \quad \mu (t)=\frac{\sqrt{30}\sqrt{\beta _{2}}-\beta _{2}}{2\left( \beta _{2}-30\right) },\nonumber \\{} & {} \quad c_{0}=\frac{9c_{1}c_{2}c_{3}-2c_{2}^{3}}{27c_{3}^{2}},\nonumber \\{} & {} \quad \sigma (t)=\frac{P}{Q},\quad P=\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}\beta _{2}^{2}\nonumber \\{} & {} \quad \left( -13020304500000\sqrt{30}\sqrt{\beta _{2}}\right. \nonumber \\{} & {} \quad +40312424250000\beta _{2}\nonumber \\{} & {} \quad +50634517500000543408750000\beta _{2}^{2}\nonumber \\{} & {} \quad -1919359800000\sqrt{30}\beta _{2}^{3/2}+72994770000\sqrt{30}\beta _{2}^{5/2}\nonumber \\{} & {} \quad +876582000\sqrt{30}\beta _{2}^{7/2}-100068615000\beta _{2}^{3}\nonumber \\{} & {} \quad -48431250\sqrt{30}\beta _{2}^{9/2}\nonumber \\{} & {} \quad +331560\sqrt{30}\beta _{2}^{11/2} +1024\sqrt{30}\beta _{2}^{13/2}\nonumber \\{} & {} \quad -186240\beta _{2}^{6}+7159725\beta _{2}^{5} +1561092750\beta _{2}^{4})\nu (t),\nonumber \\{} & {} \quad Q=18c_{3}^{2}\left( \beta _{2}-30\right) {}^{2}\left( 128\sqrt{30}\left( 16\beta _{3}-195\right) \beta _{2}^{11/2}\right. \nonumber \\{} & {} \quad +6144\beta _{2}^{6}+3375634500000\beta _{3}3061800000\beta _{2}\left( 421\beta _{3}\right. \nonumber \\{} & {} \quad \left. -630\right) -16074450000\sqrt{30}\sqrt{\beta _{2}}\left( 40\beta _{3}-21\right) \nonumber \\{} & {} \quad +105\sqrt{30}\left( 976\beta _{3}+26625\right) \beta _{2}^{9/2}-240\left( 1040\beta _{3}\right. \nonumber \\{} & {} \quad \left. -1281\right) \beta _{2}^{5}-378000\left( 947\beta _{3}-18714\right) \beta _{2}^{3}\nonumber \\{} & {} \quad -1620000\sqrt{30}\beta _{2}^{3/2}-12600\sqrt{30}\left( 3494\beta _{3}+2841\right) \beta _{2}^{7/2}\nonumber \\{} & {} \quad +3150\left( 8875\beta _{3}-41928\right) \beta _{2}^{4}+27000\sqrt{30} \left( 87332\beta _{3}\right. \nonumber \\{} & {} \quad \left. \left. -177483\right) \beta _{2}^{5/2} -810000\left( 59161\beta _{3}+76260\right) \beta _{2}^{2}\right. \nonumber \\{} & {} \quad \left. +\left( 12710\beta _{3}-79569\right) \right) \nonumber \\{} & {} \gamma (t), \end{aligned}$$
(19)

and there exists an equation for h(t), which is very lengthy to be produced here.

The solution of (5) is

$$\begin{aligned}{} & {} \psi (x,y,t)=\frac{1}{M}\left( 10c_{2}^{2}(e^{2c_{1}(B(t)+z)}\right. \nonumber \\{} & {} \quad +e^{\frac{2c_{2}^{2}(B(t)+z)}{3c_{3}}})(4e^{2c_{1}(B(t)+z)}-e^{\frac{2c_{2}^{2}(B(t)+z)}{3c_{3}}}\nonumber \\{} & {} \quad -2e^{2c_{1}(B(t)+z)})(27\sqrt{30}\beta _{2}^{3/2}-16\beta _{2}^{2}+450\beta _{2}\nonumber \\{} & {} \quad -1410\sqrt{30}\sqrt{\beta _{2}}+18900)-90c_{1}c_{3}(e^{4c_{1}(B(t)+z)}\nonumber \\{} & {} \quad +e^{\frac{2\left( c_{2}^{2}+3c_{1}c_{3}\right) (B(t)+z)}{3c_{3}}})(27\sqrt{30}\beta _{2}^{3/2}-16\beta _{2}^{2}\nonumber \\{} & {} \quad +450\beta _{2}-1410\sqrt{30}\sqrt{\beta _{2}}+18900)\nonumber \\{} & {} \quad +20c_{2}\left( e^{2c_{1}(B(t)+z)}-e^{2c_{1}(B(t)+z)}\right) \nonumber \\{} & {} \quad e^{c_{1}(B(t)+z)}\sqrt{(c_{2}^{2}-3c_{1}c_{3})(e^{2c_{1}(B(t)+z)}+e^{\frac{2c_{2}^{2}(B(t)+z)}{3c_{3}}})}\nonumber \\{} & {} \quad (-81\sqrt{10}\beta _{2}^{3/2}+16\sqrt{3}\beta _{2}^{2}-450\sqrt{3}\beta _{2}\nonumber \\{} & {} \quad +4230\sqrt{10}\sqrt{\beta _{2}}-18900\sqrt{3})\nonumber \\{} & {} \quad +3\left( e^{\frac{2c_{2}^{2}(B(t)+z)}{3c_{3}}}+e^{2c_{1}(B(t)+z)}\right) {}^{2}c_{3}\beta _{2}\nonumber \\{} & {} \quad -30\left( 9450-390\sqrt{30}\sqrt{\beta _{2}}\right. \nonumber \\{} & {} \quad \left. \left. 8\sqrt{30}\beta _{2}^{3/2}-165\beta _{2}\right) a_{0}(t)\right) ,\nonumber \\{} & {} \quad M=3\left( \beta _{2}-30\right) c_{3}(e^{\frac{2c_{2}^{2}(B(t)+z)}{3c_{3}}} +e^{2c_{1}(B(t)+z)}){}^{2},\nonumber \\{} & {} \quad z=y\sigma (t)+\frac{\left( \sqrt{30}\sqrt{\beta _{2}}-\beta _{2}\right) x}{2\left( \beta _{2}-30\right) },\nonumber \\{} & {} \quad B(t)=\int _{0}^{t}h(s)ds, \end{aligned}$$
(20)

where \(\sigma (t)\) and h(t) are given in (19). By bearing in mind that \(u=\psi _{x}\) and \(v=\psi _{y}\), it leads to

$$\begin{aligned}{} & {} u(x,y,t)=-\frac{1}{N}\left( 10\left( \exp (\frac{\left( 2c_{2}^{2}+3c_{1}c_{3}\right) \left( 2\left( \beta _{2}-30\right) B(t)-\beta _{2}(x-2y\sigma (t))-60y\sigma (t)+\sqrt{30}\sqrt{\beta _{2}}x\right) }{3\left( \beta _{2}-30\right) c_{3}})\right. \right. \nonumber \\{} & {} \quad \left. +\exp (\frac{\left( c_{2}^{2}+6c_{1}c_{3}\right) \left( 2\left( \beta _{2}-30\right) B(t)-\beta _{2}(x-2y\sigma (t))-60y\sigma (t)+\sqrt{30}\sqrt{\beta _{2}}x\right) }{3\left( \beta _{2}-30\right) c_{3}})\right) \nonumber \\{} & {} \quad \left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}\sqrt{30}-\sqrt{\beta _{2}}\sqrt{\beta _{2}}\left( 18900-1410\sqrt{30}\sqrt{\beta _{2}} 27\sqrt{30}\beta _{2}^{3/2}-16\beta _{2}^{2}++450\beta _{2}\right) ,\end{aligned}$$
(21)
$$\begin{aligned}{} & {} v(x,y,t)=-\frac{20(\beta _{2}-30)}{N}\left( \exp (\frac{\left( 2c_{2}^{2}+3c_{1}c_{3}\right) \left( 2\left( \beta _{2}-30\right) B(t)-\beta _{2}(x-2y\sigma (t))-60y\sigma (t)+\sqrt{30}\sqrt{\beta _{2}}x\right) }{3\left( \beta _{2}-30\right) c_{3}})\right. \nonumber \\{} & {} \quad \left. +\exp (\frac{\left( c_{2}^{2}+6c_{1}c_{3}\right) \left( 2\left( \beta _{2}-30\right) B(t)-\beta _{2}(x-2y\sigma (t))-60y\sigma (t)+\sqrt{30}\sqrt{\beta _{2}}x\right) }{3\left( \beta _{2}-30\right) c_{3}})\right) \nonumber \\{} & {} \quad \left( 27\sqrt{30}\beta _{2}^{3/2}-16\beta _{2}^{2}+450\beta _{2}-1410\sqrt{30}\sqrt{\beta _{2}}+18900\right) \left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}\sigma (t),\nonumber \\{} & {} \quad N=3(\exp (2c_{1}(B(t)+y\sigma (t)+\frac{\left( \sqrt{30}\sqrt{\beta _{2}}-\beta _{2}\right) x}{2\left( \beta _{2}-30\right) }))+\exp (\frac{2c_{2}^{2}\left( B(t)+y\sigma (t)+\frac{\left( \sqrt{30}\sqrt{\beta _{2}}-\beta _{2}\right) x}{2\left( \beta _{2}-30\right) }\right) }{3c_{3}})){}^{3}\nonumber \\{} & {} \quad \left( \beta _{2}-30\right) {}^{2}\left( 8\sqrt{30}\beta _{2}^{3/2}-165\beta _{2}\right. \left. -390\sqrt{30}\sqrt{\beta _{2}}+9450\right) c_{3}^{2}. \end{aligned}$$
(22)

The solutions in (21) and (22) are displayed for the two-layer functions u and v in Figs.2 (i)-(vii).

Fig. 2
figure 2

Figure 2 (i)-(vii). The 3D and contour plots of u and v are displayed against y and t for two values of x, in Fig. 2(i)-(iv) and (v)-(vii), respectively. When \( \nu (t)=2\sin (5(t-5)),\alpha (t)=3\sin (5(t-5)) +\cos (5(t-5)),\beta _{3}=5, \beta _{1}=0.2,\gamma (t)=3e^{-0.3t}, \beta _{2}=0.1,c_{1}=0.05,c_{3}=0.025,c_{2}=0.5.\)

Figure 2(i) and (ii) shows waterfalls. Figure 2(iii) shows the same behavior as in Fig. 2(i) and 2(ii). Figure 2(iv) shows doubly periodic waves.

Figure 2(iv) and (v) shows towering rogue wave and internal rogue wave ( in submarine). Figure 2(vii) shows cyclic waves.

Full size image

3.3 When \(p=2\), \(k=2\) and \(n=1\)

Case (i)

We consider (12) and the AEs

$$\begin{aligned} \begin{array}{c} g_{z}(z,t)=(m_{1}g(z,t)\\ +m_{0})\sqrt{c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}},\\ g_{t}(z,t)\text {:=}h(t)(m_{1}g(z,t)\\ +m_{0})\sqrt{c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}}. \end{array} \end{aligned}$$
(23)

From (12) and (18) into 6), we have

$$\begin{aligned} \begin{array}{c} \mu (t)=-\frac{1}{2},\;\sigma (t)\\ =\frac{\left( 4c_{2}^{2}m_{0}^{2}+3c_{1}^{2}m_{1}^{2}-4c_{2}m_{1}\left( c_{1}m_{0}+2c_{0}m_{1}\right) \right) \beta _{2}\nu [t]}{64c_{2}\beta _{3}\gamma [t]},\;\\ c_{0}=\frac{m_{0}\left( 5c_{2}m_{0}-2c_{1}m_{1}\right) }{m_{1}^{2}},\;m_{1}=-\frac{10c_{2}m_{0}}{c_{1}},\\ a_{1}(t)=\frac{10\text { }\sqrt{30}c_{2}^{3/2}m_{0}}{c_{1}\sqrt{-\beta _{2}}},\\ \beta _{2}=-10\beta _{3},\;h(t)=\frac{81c_{2}^{2}m_{0}^{4}\nu (t)\left( 4\gamma [t]^{2}+25\alpha (t)\nu (t)\right) }{2\beta _{1}\gamma [t]^{2}}. \end{array} \end{aligned}$$
(24)

The solution of (6) is

$$\begin{aligned}{} & {} \psi (x,y,t)=-\frac{5\sqrt{3}\left( -1+e^{6(-z+B(t))\sqrt{c_{2}}m_{0}}\right) \sqrt{c_{2}}m_{0}}{\left( 5+e^{6(-z+B(t))\sqrt{c_{2}}m_{0}}\right) \sqrt{\beta _{3}}}\nonumber \\{} & {} \quad +a_{0}(t),\;z=-\frac{x}{2}-\frac{45c_{2}m_{0}^{2}\nu (t)}{2\gamma (t)}y\nonumber \\{} & {} \quad B(t)=\int _{0}^{t}h(s)ds, \end{aligned}$$
(25)

where h(t)is given in (24).

The two functions (u and v) solutions are

$$\begin{aligned} \begin{array}{l} u(x,y,t)\\ \quad =-\frac{90\sqrt{3}e^{6\sqrt{c_{2}}m_{0}(B(t)+\frac{1}{2}(x+\frac{45yc_{2}m_{0}^{2}\nu (t)}{\gamma (t)}))}c_{2}m_{0}^{2}}{\left( 5+e^{6\sqrt{c_{2}}m_{0}(B(t)+\frac{1}{2}(x+\frac{45yc_{2}m_{0}^{2}\nu (t)}{\gamma (t)}))}\right) {}^{2}\sqrt{\beta _{3}}},\\ v(x,y,t)\\ \quad =-\frac{4050\sqrt{3}e^{6\sqrt{c_{2}}m_{0}(B(t)+\frac{1}{2}(x+\frac{45yc_{2}m_{0}^{2}\nu (t)}{\gamma (t)}))}c_{2}^{2}m_{0}^{4}\nu [t]}{\left( 5+e^{6\sqrt{c_{2}}m_{0}(B(t)+\frac{1}{2}(x+\frac{45yc_{2}m_{0}^{2}\nu (t)}{\gamma (t)}))}\right) {}^{2}\sqrt{\beta _{3}}\gamma [t]}. \end{array} \end{aligned}$$
(26)

The two-layer functions u and v, given in (26), are displayed in Fig. 3 (i)-(vi).

Fig. 3
figure 3

Figure 3 (i)-(vi). The 3D and contour plots of u and v are displayed against y and t for two values of x, in Figs. 3(i)-(iii) and (v)-(vi), respectively. When \( \nu (t)=e^{-0.5t}\sin (5(t-5))(\cos (5(t-5))+2), \gamma (t)=\sqrt{\cos (5(t-5))+2}, \alpha (t)=3\sin (5(t-5)),\beta _{2}=5,m_{0}=0.25, c_{1}=2.5,c_{2}=0.05,\beta _{3}=0.3,\beta _{1}==2. \)

Figure 3(i) and (ii) shows saddle ( Fan waves) with periodic waves tail. Figure (iii) shows saddle waves.

Figure 3(iv) and (v) shows periodic waves cascade. Figure 3(vi) shows the same behavior.

Full size image

Case(ii)

We consider (12) and the AEs

$$\begin{aligned} \begin{array}{c} g_{z}(z,t)=\sqrt{m_{2}g(z,t)^{2}+m_{1}g(z,t)+m_{0}}\\ \sqrt{c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}},\\ g_{t}(z,t)=h(t)\sqrt{m_{2}g(z,t)^{2}+m_{1}g(z,t)+m_{0}}\\ \sqrt{c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}}. \end{array} \end{aligned}$$
(27)

From (12) and (27) into (6), it yields

$$\begin{aligned} \begin{array}{c} \mu (t)=-\frac{1}{2},\\ \sigma (t)=\frac{\beta _{2}\left( c_{2}^{2}\left( 3m_{1}^{2}-8m_{0}m_{2}\right) -2c_{2}m_{2}\left( c_{1}m_{1}+4c_{0}m_{2}\right) +3c_{1}^{2}m_{2}^{2}\right) \nu (t)}{64\beta _{3}c_{2}m_{2}\gamma (t)},\\ m_{0}=\frac{m_{1}^{2}}{4m_{2}}-\frac{\left( c_{1}^{2}-4c_{0}c_{2}\right) m_{2}}{4c_{2}^{2}},\\ m_{2}=\frac{c_{2}m_{1}}{c_{1}},\quad a_{1}'(t)=0,\quad a_{1}(t)=\frac{\sqrt{30}c_{2}\sqrt{m_{1}}}{\sqrt{-\beta _{2}}\sqrt{c_{1}}},\\ \beta _{2}=-10\beta _{3},\\ h(t)=\frac{\left( c_{1}^{2}-4c_{0}c_{2}\right) {}^{2}m_{1}^{2}\nu (t)\left( 25\alpha (t)\nu (t)+4\gamma (t)^{2}\right) }{32\beta _{1}c_{1}^{2}\gamma (t)^{2}}. \end{array}\nonumber \\ \end{aligned}$$
(28)

The solution of (5) (or (6) ) is

$$\begin{aligned}{} & {} \psi (x,y,t)=a_{0}(t)-\frac{\sqrt{3}\sqrt{m_{1}}(c_{1}-\sqrt{c_{1}^{2}-4c_{0}c_{2}}\tanh (\frac{\sqrt{c_{1}^{2}-4c_{0}c_{2}}\sqrt{m_{1}}\left( B(t)-\frac{5\left( c_{1}^{2}-4c_{0}c_{2}\right) m_{1}y\nu (t)}{8c_{1}\gamma (t)}-\frac{x}{2}\right) }{2\sqrt{c_{1}}}))}{2\sqrt{\beta _{3}}\sqrt{c_{1}}},\nonumber \\{} & {} B(t)=\int _{0}^{t}h(s)ds, \end{aligned}$$
(29)

where h(t) is given in (28).

The solutions u and v are

$$\begin{aligned} u(x,y,t)= & {} -\frac{\sqrt{3}\left( c_{1}^{2}-4c_{0}c_{2}\right) m_{1}\text {sech}^{2}(\frac{\sqrt{c_{1}^{2}-4c_{0}c_{2}}\sqrt{m_{1}}\left( \_B(t)-\frac{5\left( c_{1}^{2}-4c_{0}c_{2}\right) m_{1}y\nu (t)}{8c_{1}\gamma (t)}-\frac{x}{2}\right) }{2\sqrt{c_{1}}})}{8\sqrt{\beta _{3}}c_{1}},\qquad \qquad \qquad \end{aligned}$$
(30)
$$\begin{aligned} v(x,y,t)= & {} -\frac{5\sqrt{3}\left( c_{1}^{2}-4c_{0}c_{2}\right) {}^{2}m_{1}^{2}\nu (t)\text {sech}^{2}(\frac{\sqrt{c_{1}^{2}-4c_{0}c_{2}}\sqrt{m_{1}}\left( \_B(t)-\frac{5\left( c_{1}^{2}-4c_{0}c_{2}\right) m_{1}y\nu (t)}{8c_{1}\gamma (t)}-\frac{x}{2}\right) }{2\sqrt{c_{1}}})}{32\sqrt{\beta _{3}}c_{1}^{2}\gamma (t)}.\qquad \qquad \qquad \end{aligned}$$
(31)

The two-layer functions u and v, given in (30) and (31), are displayed in Figs. 4 (i)-(vi).

Fig. 4
figure 4

Figure 4 (i)-(vi). The 3D and contour plots of u and v are displayed against y and t for two values of x, in Fig. 4(i)–(iii) and (v)–(vi), respectively. When \(\alpha (t)=0.3e^{-0.5t}\sin (5(t-5))\sin (5(t-5)), \nu (t)=\cos (5(t-5))+2,,\beta =0.2, \gamma (t)=\sqrt{\cos (5(t-5))+2},\beta _{2}=5,c_{1}=2.5,m_{1} =1.5,c_{0}=0.7,c_{2}=1.5,\beta _{3}=0.3. \)

Figure 4(i) and (ii) shows internal dromoions. Figure 4(iii) shows helix-shaped waves.

Figure 4(iv)–(vi) shows the same behavior as in Figs. 4(i)-(iii).

Full size image

4 Rational solutions of (6).

Here, we consider the solution in (10) together with the AEs in (11).

4.1 When \(p=1\) and k=2

The AEs take the form given in (13), and into (6) it gives

$$\begin{aligned}{} & {} \mu (t)=-\frac{\beta _{2}}{\beta _{2}-30},\quad A'(t)=0,\nonumber \\{} & {} \quad c_{0}=\frac{m\left( s_{0}\left( c_{1}s_{1}-c_{2}s_{0}\right) \right) }{s_{1}^{2}},\nonumber \\{} & {} \quad A(t)=-\frac{60(m-1)s_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) }{\nonumber }\\{} & {} \quad {\left( \beta _{2}-30\right) \left( a_{1}s_{0}-a_{0}s_{1}\right) },\nonumber \\{} & {} \quad \sigma (t)=-\frac{5\beta _{2}^{3}\nu (t)\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) }{\nonumber }\\{} & {} \quad {\left( \beta _{2}-30\right) {}^{2}\left( \beta _{2}-10\beta _{3}\right) s_{1}^{2}\gamma (t)},\nonumber \\{} & {} \quad h(t)=\frac{1}{K}\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) {}^{2}\beta _{2}^{5}\nu (t)\nonumber \\{} & {} \quad \left( -100\left( \beta _{3}^{2}\gamma (t)^{2}\right. \right. \nonumber \\{} & {} \quad -15\beta _{3}\gamma (t)^{2}-225\alpha (t)\nu (t))\nonumber \\{} & {} \quad +\beta _{2}^{2}\left( 25\alpha (t)\nu (t)+4\gamma (t)^{2}\right) \nonumber \\{} & {} \quad \left. -30\beta _{2}\left( 50\alpha (t)\nu (t)+\left( \beta _{3}+5\right) \gamma (t)^{2}\right) \right) ,\nonumber \\{} & {} \quad K=\beta _{1}\left( \beta _{2}-30\right) {}^{5}\left( \beta _{2}-10\beta _{3}\right) {}^{2}s_{1}^{4}\gamma (t)^{2}. \end{aligned}$$
(32)

The solution of (5) is

$$\begin{aligned}{} & {} \psi (x,y,t)=\frac{P}{Q},\quad P=-\left( 60(m-1)s_{0}(c_{2}s_{0}-c_{1}s_{1})\right. \nonumber \\{} & {} \quad \left. \left( a_{0}-\frac{1}{2c_{2}}a_{1}\left( c_{1}\right. \right. \right. +\sqrt{\frac{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) }{s_{1}^{2}}+c_{1}^{2}}\text {Tanh}\nonumber \\{} & {} \quad \left[ \frac{1}{2}\sqrt{\frac{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) }{s_{1}^{2}}+c_{1}^{2}}\right. \nonumber \\{} & {} \quad (B(t)-\frac{5\beta _{2}^{3}y\nu (t)\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) }{\left( \beta _{2}-30\right) {}^{2}\left( \beta _{2}-10\beta _{3}\right) s_{1}^{2}\gamma (t)}\nonumber \\{} & {} \quad \left. \left. \left. -\frac{\beta _{2}x}{\beta _{2}-30})\right] \right) \right) ,\nonumber \\{} & {} \quad Q=(a_{1}s_{0}-a_{0}s_{1})(\beta _{2}-30)(s_{0}-\frac{1}{2c_{2}}s_{1}(c_{1}+\nonumber \\{} & {} \quad \sqrt{\frac{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) }{s_{1}^{2}}+c_{1}^{2}}\text {Tanh}\nonumber \\{} & {} \quad \left[ \frac{1}{2}\sqrt{\frac{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) }{s_{1}^{2}}+c_{1}^{2}}\right. (B(t)\nonumber \\{} & {} \quad \left. -\frac{5\beta _{2}^{3}y\nu (t)\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) }{\left( \beta _{2}-30\right) {}^{2}\left( \beta _{2}-10\beta _{3}\right) s_{1}^{2}\gamma (t)}\right. \nonumber \\{} & {} \quad \left. -\frac{\beta _{2}x}{\beta _{2}-30})\right] )),\nonumber \\{} & {} \quad B(t)=\int _{0}^{t}h(s)ds, \end{aligned}$$
(33)

where h(t)is given in (32).

The waves functions u and v are

$$\begin{aligned}{} & {} u(x,y,t)=\frac{P_{1}}{Q_{1}},\nonumber \\{} & {} \quad P_{1}=-60(m-1)\text {Sech}\left[ \frac{\sqrt{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) +c_{1}^{2}s_{1}^{2}}}{2s_{1}}\right. \nonumber \\{} & {} \quad \left. (B(t)-\frac{5\beta _{2}^{3}y\nu (t)\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) }{\left( \beta _{2}-30\right) {}^{2}\left( \beta _{2}-10\beta _{3}\right) s_{1}^{2}\gamma (t)}\right. \nonumber \\{} & {} \quad \left. -\frac{\beta _{2}x}{\beta _{2}-30})\right] ^{2}\nonumber \\{} & {} \quad \beta _{2}c_{2}s_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) \left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) ,\nonumber \\{} & {} \quad Q_{1}=s_{1}^{2}\left( \beta _{2}-30\right) {}^{2}\left( -2c_{2}s_{0}+s_{1}\left( c_{1}\right. \right. \nonumber \\{} & {} \quad +\frac{1}{s_{1}}\sqrt{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) +c_{1}^{2}s_{1}^{2}}\nonumber \\{} & {} \quad \text {Tanh}\left[ \frac{\sqrt{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) +c_{1}^{2}s_{1}^{2}}}{2s_{1}}\right. \nonumber \\{} & {} \quad (B(t)-\frac{5\beta _{2}^{3}y\nu (t)\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) }{\left( \beta _{2}-30\right) {}^{2}\left( \beta _{2}-10\beta _{3}\right) s_{1}^{2}\gamma (t)}\nonumber \\{} & {} \quad \left. \left. \left. -\frac{\beta _{2}x}{\beta _{2}-30})\right] \right) \right) ^{2}, \end{aligned}$$
(34)
$$\begin{aligned}{} & {} v(x,y,t)=\frac{P_{2}}{\gamma (t)\left( \beta _{2}-30\right) s_{1}^{2}Q_{1}},\nonumber \\{} & {} \quad P_{2}=-300(m-1)\text {Sech}\left[ \frac{1}{2}\sqrt{\frac{4c_{2}ms_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) }{s_{1}^{2}}+c_{1}^{2}}\right. \nonumber \\{} & {} \quad \left. (B(t)-\frac{5\beta _{2}^{3}y\nu (t)\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) }{\left( \beta _{2}-30\right) {}^{2}\left( \beta _{2}-10\beta _{3}\right) s_{1}^{2}\gamma (t)}-\frac{\beta _{2}x}{\beta _{2}-30})\right] ^{2}\nonumber \\{} & {} \quad \beta _{2}^{3}c_{2}s_{0}\left( c_{2}s_{0}-c_{1}s_{1}\right) \nu (t)\left( 4c_{2}^{2}ms_{0}^{2}-4c_{1}c_{2}ms_{1}s_{0}+c_{1}^{2}s_{1}^{2}\right) {}^{2}. \end{aligned}$$
(35)

The functions u and v given in (34) and (35) are displayed in Fig. 5 (i)–(vi).

Fig. 5
figure 5

Figure 5 (i)–(vi). The 3D and contour plots of u and v are displayed against y and t for two values of x, in Fig. 5(i)–(iii) and (v)-(vi), respectively. When \( \nu (t)=2\sin (5(t-5))(\cos (5(t-5))+2.), \alpha (t)=3e^{-0.3t}\sin (5(t-5))+ \cos (5(t-5)),\beta _{1}=0.2, \gamma (t)=0.03\sqrt{\cos (5(t-5))+2},\beta _{2}=0.1, c_{1}=0.05,c_{2}=0.5, \beta _{3}=5,s_{1}=1.2,s_{0}=0.5,m=0.7.\)

Figure 5(i) and (ii) shows waves similar to those created behind and in front of dams. Figure 5 (iii) shows two sets of separated waves.

Figure 5(iv)–(vi) shows doubly periodic waves.

Full size image

4.2 When \(p=2\) and \(k=2\)

We consider (10) and the AEs

$$\begin{aligned}{} & {} g_{z}(z,t)=\sqrt{c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}}\nonumber \\{} & {} \quad \left( m_{1}g(z,t)+m_{0}\right) ,\nonumber \\{} & {} \quad g_{t}(z,t)=h(t)\sqrt{c_{2}g(z,t)^{2}+c_{1}g(z,t)+c_{0}}\nonumber \\{} & {} \quad \left( m_{1}g(z,t)+m_{0}\right) . \end{aligned}$$
(36)

From (10) and (36) into (6), it leads to

$$\begin{aligned}{} & {} A'(t)=0,\quad c_{0}=\frac{c_{1}^{2}}{4c_{2}},\nonumber \\{} & {} \quad \sigma (t)=-\frac{5\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)},\nonumber \\{} & {} \quad \mu (t)=-\frac{1}{2},A(t)\nonumber \\{} & {} \quad =\frac{\sqrt{3}\sqrt{-\beta _{3}}s_{1}^{2}\sqrt{2c_{2}m_{0}-c_{1}m_{1}}\sqrt{2c_{2}m_{0}-c_{1}m_{1}}\left( c_{1}m_{1}-2c_{2}m_{0}\right) }{4\beta _{3}\sqrt{c_{2}}s_{1}\left( 4a_{0}c_{2}m_{1}-a_{1}\left( 2c_{2}m_{0}+c_{1}m_{1}\right) \right) },\nonumber \\{} & {} \quad h(t)=\frac{\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{4}\nu (t)\left( 25\alpha (t)\nu (t)+4\gamma (t)^{2}\right) }{512\beta _{1}c_{2}^{2}\gamma (t)^{2}},\nonumber \\{} & {} \quad s_{0}=\frac{1}{4}s_{1}\left( \frac{c_{1}}{c_{2}}+\frac{2m_{0}}{m_{1}}\right) . \end{aligned}$$
(37)

The solution of (5) is

$$\begin{aligned}{} & {} \psi (x,y,t)=\frac{P}{Q},\;=\sqrt{3}\sqrt{c_{2}}m_{1}2c_{2}m_{0}-c_{1}m_{1}\nonumber \\{} & {} \quad \left( a_{1}(m_{0}\exp (\frac{1}{2}\sqrt{c_{2}}m_{0}(B(t)\right. \nonumber \\{} & {} \quad -\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2})\nonumber \\{} & {} \quad -c_{1}\exp (\frac{c_{1}m_{1}(B(t)-\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2})}{2\sqrt{c_{2}}}))\nonumber \\{} & {} \quad +a_{0}(2c_{2}\exp (\frac{c_{1}m_{1}(B(t)-\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2})}{2\sqrt{c_{2}}})\nonumber \\{} & {} \quad \left. -m_{1}\exp \left( \frac{1}{2}\sqrt{c_{2}}m_{0}(B(t)\right. \right. \nonumber \\{} & {} \quad \left. \left. -\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2})\right) )\right) ,\nonumber \\{} & {} \quad Q=2c_{2}\exp (\frac{c_{1}m_{1}(B(t)-\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2})}{2\sqrt{c_{2}}})\nonumber \\{} & {} \quad +m_{1}\exp \left( \frac{1}{2}\sqrt{c_{2}}m_{0}(B(t)-\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2})\right) \nonumber \\{} & {} \quad \sqrt{-\beta _{3}}\left( 4a_{0}c_{2}m_{1}-a_{1}\left( 2c_{2}m_{0}+c_{1}m_{1}\right) \right) ,B(t)=\int _{0}^{t}h(s)ds, \end{aligned}$$
(38)

where h(t) is given in (37).

The two wave functions u and v are

$$\begin{aligned}{} & {} u(x,y,t)=\frac{P_{1}}{Q_{1}},\;P_{1}=\sqrt{3}m_{1}\left( c_{1}m_{1}-2c_{2}m_{0}\right) \left( c_{1}m_{1}-c_{2}m_{0}\right) \nonumber \\{} & {} \quad \exp \left( -\frac{\left( c_{2}m_{0}+c_{1}m_{1}\right) \left( 4c_{2}\left( 4\gamma (t)(x-2B(t))-5c_{1}m_{0}m_{1}y\nu (t)\right) +20c_{2}^{2}m_{0}^{2}y\nu (t)+5c_{1}^{2}m_{1}^{2}y\nu (t)\right) }{64c_{2}^{3/2}\gamma (t)}\right) ,\nonumber \\{} & {} \quad Q_{1}=4\sqrt{-\beta _{3}}(2c_{2}\exp \left( \frac{c_{1}m_{1}(B(t)-\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2})}{2\sqrt{c_{2}}}\right) +\nonumber \\{} & {} \quad m_{1}\exp (\frac{1}{2}\sqrt{c_{2}}m_{0}(B(t)-\frac{5y\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{2}\nu (t)}{32c_{2}\gamma (t)}-\frac{x}{2}))){}^{2},\qquad \qquad \quad \end{aligned}$$
(39)
$$\begin{aligned}{} & {} v(x,y,t)=\frac{P_{2}}{16c_{2}\gamma (t)Q_{1}}, P_{2}=5\sqrt{3}m_{1}\left( c_{1}m_{1}-2c_{2}m_{0}\right) {}^{3}\left( c_{1}m_{1}-c_{2}m_{0}\right) \nu (t)\nonumber \\{} & {} \quad \exp \left( -\frac{\left( c_{2}m_{0}+c_{1}m_{1}\right) \left( 4c_{2}\left( 4\gamma (t)(x-2B(t))-5c_{1}m_{0}m_{1}y\nu (t)\right) +20c_{2}^{2}m_{0}^{2}y\nu (t)+5c_{1}^{2}m_{1}^{2}y\nu (t)\right) }{64c_{2}^{3/2}\gamma (t)}\right) .\qquad \qquad \quad \end{aligned}$$
(40)

By using (39) and (4), the functions u and v are displayed in Fig. 6 (i)–(vi).

Fig. 6
figure 6

Figure 6 (i)–(vi). The 3D and contour plots of u and v are displayed against y and t for two values of x, in Fig. 6(i)–(iii) and (v)-(vi), respectively. When \( \nu (t)=0.2\sin (5(t-5))(\cos (5(t-5))+2.), \alpha (t)=0.3e^{-0.3t}\sin (5(t-5))+\cos (5(t-5)), \beta _{2}=0.1,c_{2}=1.5,\beta _{3}=-1.5s_{1}=1.6, s_{0}=1.3,m_{1}=1.2,m_{0}=-1.3, \gamma (t)=3\sqrt{\cos (5(t-5))+2},\beta _{1}=1.3,c_{1}=-1.6. \)

Figure 6(i) and (ii) shows wave breaking which may occur near barriers, near rocky ocean shores, or near boat sailing. Figure 5 (iii) shows separated waves.

Figure 6(iv)–(vi) shows doubly periodic waves.

Full size image

4.3 Double-wave solutions

In this case, two different AEs are used. We write

$$\begin{aligned} \begin{array}{c} \varphi (z,t)=\frac{A(t)\left( a_{1}g_{1}(z,t)+a_{2}g_{2}(z,t)+a_{0}\right) }{s_{1}g_{1}(z,t)+s_{2}g_{2}(z,t)+s_{0}},\\ \\ g_{1z}(z,t)=c_{1}g_{1}(z,t)+c_{2}g_{2}(z,t),\\ g_{1t}(z,t)=h(t)\left( c_{1}g_{1}(z,t)+c_{2}g_{2}(z,t)\right) ,\\ g_{2z}(z,t)=d_{1}g_{1}(z,t)+d_{2}g_{2}(z,t),\\ g_{2t}(z,t)=h(t)\left( d_{1}g_{1}(z,t)+d_{2}g_{2}(z,t)\right) . \end{array} \end{aligned}$$
(41)

From (41) into (6), we get

$$\begin{aligned}{} & {} A(t)=\frac{1}{\beta _{3}\left( a_{2}s_{0}-a_{0}s_{2}\right) {}^{2}}(2a_{2}\beta _{3}s_{0}^{2}\left( c_{1}s_{2}-c_{2}s_{1}\right) +2a_{0}\beta _{3}s_{2}s_{0}\left( c_{2}s_{1}-c_{1}s_{2}\right) \nonumber \\{} & {} \quad -\sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }s_{0}\left( a_{2}s_{0}-a_{0}s_{2}\right) \left( c_{2}s_{1}-c_{1}s_{2}\right) ),\nonumber \\{} & {} \quad \sigma (t)=-\frac{15\left( \sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+2\beta _{3}\right) {}^{2}\left( \sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+4\beta _{3}\right) {}^{2}\left( c_{2}s_{1}-c_{1}s_{2}\right) {}^{2}\nu (t)}{8\beta _{3}^{2}\left( 2\sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+4\beta _{3}-3\right) {}^{2}s_{2}^{2}\gamma (t)},\nonumber \\{} & {} \quad \mu (t)=-\frac{3}{2},\;d_{2}=-\frac{c_{2}s_{1}}{s_{2}}+c_{1}+\frac{d_{1}s_{2}}{s_{1}}, d_{1}=\frac{c_{2}s_{1}^{2}-2c_{1}s_{1}s_{2}}{s_{2}^{2}},\;\beta _{2}=30\beta _{3},\nonumber \\{} & {} \quad h(t)=\frac{P}{Q},\;P=-\left( 243(2\sqrt{\beta _{3}(4\beta _{3}-9)}+4\beta _{3}-3){}^{3}s_{0}^{5}(a_{2}s_{0}-a_{0}s_{2}){}^{5}\right. \nonumber \\{} & {} \quad (c_{1}s_{2}-c_{2}s_{1}){}^{9}(32\beta _{3}^{2}+9 +4\left( 4\sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }-15\right) \beta _{3}\nonumber \\{} & {} \quad -12\sqrt{\beta _{3}\left( 4\beta _{3}-9\right) })\left. \nu (t)\left( 25\alpha (t)\nu (t)+4\gamma (t)^{2}\right) \right) ,\nonumber \\{} & {} \quad Q=32s_{2}^{4}\beta _{1}\left( 2s_{0}(a_{2}s_{0}-a_{0}s_{2})(c_{2}s_{1}-c_{1}s_{2})\sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }\right. +a_{2}(4\beta _{3}-3)s_{0}^{2}(c_{2}s_{1}-c_{1}s_{2})\nonumber \\{} & {} \quad +\left. a_{0}(4\beta _{3}-3)s_{0}s_{2}(c_{1}s_{2}-c_{2}s_{1})\right) ^{5}\left. \gamma (t)^{2}\right) . \end{aligned}$$
(42)
$$\begin{aligned} \begin{array}{c} \psi (x,y,t)=\frac{\left( \sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+2\beta _{3}\right) s_{0}\left( c_{1}s_{2}-c_{2}s_{1}\right) (a_{2}B(t)\left( k_{1}s_{1}+k_{2}s_{2}\right) e^{\frac{c_{2}s_{1}z}{s_{2}}}+a_{0}s_{2}e^{c_{1}z})}{\beta _{3}s_{2}\left( a_{2}s_{0}-a_{0}s_{2}\right) (B(t)\left( k_{1}s_{1}+k_{2}s_{2}\right) e^{\frac{c_{2}s_{1}z}{s_{2}}}+s_{0}e^{c_{1}z})},\\ \\ z=-\frac{y\left( 15\left( \sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+2\beta _{3}\right) {}^{2}\left( \sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+4\beta _{3}\right) {}^{2}\left( c_{2}s_{1}-c_{1}s_{2}\right) {}^{2}\nu (t)\right) }{8\beta _{3}^{2}\left( 2\sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+4\beta _{3}-3\right) {}^{2}s_{2}^{2}\gamma (t)}-\frac{3x}{2},\\ B(t)=\int _{0}^{t}h(s)ds, \end{array} \end{aligned}$$
(43)

where h(t)is given in (42).

The wave functions u andv are

$$\begin{aligned}{} & {} u(x,y,t)=\frac{P_{1}}{Q_{1}},\;P_{1}=3\exp (\frac{1}{8s_{2}^{3}\gamma (t)}3(c_{2}s_{1}+c_{1}s_{2})(s_{2}^{2}(45c_{1}^{2}y\nu (t)+4x\gamma (t))\nonumber \\{} & {} \quad +45c_{2}^{2}s_{1}^{2}y\nu (t)-90c_{1}c_{2}s_{2}s_{1}y\nu (t))) \left( \sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+2\beta _{3}\right) s_{0}B(t)\left( c_{2}s_{1}-c_{1}s_{2}\right) {}^{2}\nonumber \\{} & {} \quad \left( k_{1}s_{1}+k_{2}s_{2}\right) ,Q_{1}=2\beta _{3}s_{2}^{2}\left( s_{0}\exp (\frac{3c_{2}s_{1}\left( s_{2}^{2}\left( 45c_{1}^{2}y\nu (t)+4x\gamma (t)\right) +45c_{2}^{2}s_{1}^{2}y\nu (t)-90c_{1}c_{2}s_{2}s_{1}y\nu (t)\right) }{8s_{2}^{3}\gamma (t)})\right. \nonumber \\{} & {} \quad \left. B(t)\left( k_{1}s_{1}+k_{2}s_{2}\right) \right. \left. +\exp (\frac{3c_{1}\left( s_{2}^{2}\left( 45c_{1}^{2}y\nu (t)+4x\gamma (t)\right) +45c_{2}^{2}s_{1}^{2}y\nu (t)-90c_{1}c_{2}s_{2}s_{1}y\nu (t)\right) }{8s_{2}^{2}\gamma (t)})\right) ^{2}, \end{aligned}$$
(44)
$$\begin{aligned}{} & {} v(x,y,t)=\frac{P_{2}}{4s_{2}^{2}\beta _{3}^{2}\left( 2\sqrt{\beta _{3}\left( 4\beta _{3}-9\right) }+4\beta _{3}-3\right) {}^{2}\gamma (t)Q_{1}}, P_{2}=15\exp (\frac{1}{8s_{2}^{3}\gamma (t)}3(c_{2}s_{1}+c_{1}s_{2})\nonumber \\{} & {} \quad (s_{2}^{2}(45c_{1}^{2}y\nu (t)+4x\gamma (t)) +45c_{2}^{2}s_{1}^{2}y\nu (t)-90c_{1}c_{2}s_{2}s_{1}y\nu (t)))s_{0}B(t)\nonumber \\{} & {} \quad \left( c_{2}s_{1}-c_{1}s_{2}\right) {}^{4}\left( k_{1}s_{1}+k_{2}s_{2}\right) \left( \sqrt{\beta _{3}(4\beta _{3}-9)}+2\beta _{3}\right) {}^{3}\left( \sqrt{\beta _{3}(4\beta _{3}-9)}+4\beta _{3}\right) {}^{2}\nu (t). \end{aligned}$$
(45)
Fig. 7
figure 7

Figure 7 (i)–(iv). The 3D plots of u and v are displayed against y and t for two values of x, in Figs. 7(i) and (ii) and 6 (iii) and (iv), respectively. When \( \nu (t)=2\cos (25(t-5)),\alpha (t)=5\sin (15(t-5)) +\cos (15(t-5)), s_{1}=0.6,s_{0}=0.5,\beta _{1}=3,c_{1}=0.6,c_{0}=0.4, a_{0}=2.5,a_{1}=0.5,a_{2}=2.5, \gamma (t)=3e^{0.5t},\beta _{2}=0.1,c_{2}=0.5,\beta _{3}=3, s_{2}=3,k_{1}=1,k_{2}=2. \)

Figure 7(i) shows different waterfall structures, while 7(ii) shows bulge and internal waves similar to those created by near a barrier (island).

Figure 7(iii) and (iv) shows waves similar to those created near a thin barrier.

Full size image

Equations (44) and (45) are used to display u and v in Fig. 7(i)–(iv).

5 Discussions

In the present work, multiple different waves structures were found. Attention is focused to simulate these waves to those created in a nonuniform fluid, that is, to waves created near a solid boundary.

(a) Figure 1(i) shows double-U-shape internal (hollowed waves). Figure 1(ii) shows U-shape and S-shape bulge waves.

Figure 1(iv) shows U-shape internal (hollowed wave) and S-shape bulge wave.

(b) Figure 2(i) and (ii) shows waterfalls. Figure 2(iv) shows doubly periodic waves.

Figure 2(iv) and (v) shows towering rogue wave and internal rogue wave ( near submarine).

(c) Figure 3(i) and (ii) shows saddle ( Fan waves) with periodic waves tail. Figure (iii) shows saddle waves.

Figure 3(iv) and (v) shows periodic waves cascade.

(d) Figure 4(i) and (ii) shows internal dromoions. Figure 4(iii) shows helix-shape waves.

(e) Figure 5(i) and (ii) shows waves similar to those created behind and in front of dams.

(f) Figure 7(i) shows different waterfall structures, while 7(ii) shows bulge and internal waves similar to those created by near a barrier (island).

An experimental work shows rogue wave formation a water tank (which is of solid boundary). This consolidates the results in Fig. 2. Sea also [51].

6 Conclusions

The Caudrey–Dodd–Gibbon–Kotera–Sawada equation is an integro-differential equation that describes two-layer fluid interaction. It was currently studied in the literature when it is with constant coefficients, while, in the non-autonomous version, it was rarely studied. Such equation is of time-dependent coefficients. In the works carried in the literature, in this area, the concepts of two-layer fluid interaction and the notion of nonuniform-fluid were not invoked. Here, these characteristics are taken into consideration. It is shown that the time-dependent coefficients play a crucial role in determining the waves geometry. Here, the later equation version is considered, which describes waves induced by two-layer nonuniform fluid. In this fluid, the velocity is space dependent at a fixed time. It stands for waves created near solid surfaces, boats, dams, networks of ( under ground) canals, and submarine. The exact solution of the of the later equation version is found by using the extended unified method, which is a more efficient method when compared with those used in the present case, as it is of lower time cost in symbolic computation. A class of exact solutions are obtained and they are represented graphically. A variety of waves structures are revealed, waves similar to those created, behind and in front of dams, near boat sailing, water fall, and internal waves near submarine. The results found in this paper can be utilized to explain some complex phenomena in oceans and seas. In future works, the extended unified method will be used to investigate waves generated in inhomogeneous or heterogeneous (inhomogeneous-non-uniform) fluids.