1 Introduction

Parkinson’s disease (PD) is a degenerative neurological disease. According to [42], approximately 1% of the population over the age of 60 is affected by PD. It impairs the lower and upper limb movements and causes several cognitive deficits. Freezing of gait (FoG) is a highly debilitating symptom among people with Parkinson’s disease. FoG is typically observed in the advanced stages of the disease [22]. It is defined as a sudden involuntary stoppage of the forward progression of gait. While there is no complete cure for PD and implicitly FoG, many non-invasive disease management options exist. These options focused on providing sensory and auditory cues and augmented feedback [30, 55, 57] to manage FoG. There is vast literature based on mathematical modelling to understand the effect of sensory feedback on normal gait [4, 72, 73]. However, to the best of our knowledge, comparatively, the research, from a mathematical modelling perspective, on how FOG is related to the feedback is somewhat limited. Provision of a physiologically relevant explanation for the intermittent transitions occurring to PD gait from walking to freezing and back to walking is essential.

There have been attempts to understand PD gait using modelling techniques. Muralidharan et.al’s [52] PD gait model captures the neuronal dynamics of FoG; however, they do not focus on the kinetic aspects of the PD gait. Moghadam et al. [51] combine the chaotic region of the Lorentz system with a passive dynamic walker and generate high variability observed in PD. Even though mechanical aspects of gait are captured in their model, the addition of chaos externally limits its biophysical meaning. Moreover, Modgam et al.’s model does not capture the FoG. Our earlier work [60] has demonstrated some aspects of PD gait, such as freezing and variability. The model uses an inverted pendulum with ankle push-off forces. However, there is still a need to delineate the effect of feedback and transitioning of gait from freezing to walking. Sarbaz et al. [69] provide a discrete map-based model to capture variability in PD. A ‘sine circle map’ is used in their discrete model; this model, even though very simple to be used with the data, its biophysical meaning is difficult to ascertain. Hence, one finds it necessary to develop a model that can explain FoG in PD gait addressing the mechanical and neuronal aspects of physiology.

CPG-based walking: Central pattern generators (CPG), typically argued to be fundamental to most rhythmic behaviours, are a group of neurons with interconnections that generates a fictive motor pattern when appropriately activated. CPG is used to drive the mechanical systems in several models of human locomotion. This approach assumes that the CPG receives feedback (perturbations) from the sensory system (or indirectly gets modulated by the brain) such that the overall system is synchronised [80]. Yamasaki et al. in [80] take a control systems-based approach to the problem using a simple model for the CPG. Their model also uses an IDM (inverse dynamics model) module, the physiological correlates of which is assumed or speculated to be in the cerebellum. Aoi et al. in [2] have made the model more physiologically relevant using the experimental findings from [37]. There are two difficulties associated with using these models for understanding freezing, (1) a large number of parameters, (2) the use of dimensionality reduction-based approximations. While Aoi et al.’s model is an excellent candidate for understanding normal walking, it is challenging to use it to understand FoG. This difficulty is because of too many tuned-parameters and the difficulty of judging which component’s failure caused FoG. Also, the muscle synergy and factor analysis-based approximations may not be valid in a pathological scenario. Sensory feedback to the brain and CPG is another crucial aspect of gait addressed in the modelling literature over the years [4, 72, 73]; however, current literature does not address how FoG is related to feedback. Moreover, how PD gait changes from walking to freezing and back also need a physiologically relevant explanation.

Link to robotics: While studying gait, it is impossible to ignore the robotics literature. The passive gait links the robotic literature with the biophysical models as the fundamental difference between the robotic models and the biophysical models lies in the control aspect. McGeer et al.’s early work in passive gait models [48] shows the stability and effect of external inputs on passive gait. Several others have also studied the passive gait models and their bifurcations [10, 16, 17, 23, 35, 44, 46, 66, 81]. The fully actuated bipedal robots are in the other end of the spectrum where typically feedback linearisation is used to nullify the ‘natural’ dynamics of the robot [26]. On the other hand, underactuated robots use the ‘natural’ dynamics of the rigid body system while simultaneously providing some actuation [26]. However, these models cannot directly explain PD pathology due to the lack of actuation or actuation’s biological nature.

Dealing with neuromuscular over-actuation: The neuromechanical system is over-actuated with redundancies as it contains less degree of freedom than the number of actuators. Optimal-control formalism addresses this issue to some extent and forms an alternative approach to modelling motor control. This approach assumes a cost functional, which is minimised during motor action. This is very suitable for robotic applications [36, 63]. Inverse optimal control can be used to circumvent the assumption of the cost functional by inferring it from the data. Nevertheless, this necessitates formulating the problem in such a way that there is a cost function that is minimised during a motor action [50, 61, 65]. In a pathological scenario such as PD gait, such an assumption need not be valid. Muscle synergy-based approaches also address the issue of redundancies. However, muscle synergy-based models assume co-activation of muscles as motor primitives to address the redundancy [3, 73]. Some authors still question the idea of muscle synergy [76]. However, an elegant description of the necessity of the synergy of muscles in terms ‘uncontrolled manifold’ hypothesis is presented in [41], where muscles that achieve targeted action are considered ‘good’ region of variability and that do not achieve targeted action are considered ‘bad’ regions of variability. Moreover, the equilibrium point hypothesis [15, 18], which suggests movements are the result of active changes in the motor system’s equilibrium state, has natural links to the muscle synergies [40]. One needs the determination of invariant characteristics [67] (e. g. torque–length characteristics [18]) for confirming equilibrium point hypothesis. However, achieving this in practice by advising the subjects to ‘not to intervene’ [18, 67] is debatable due to the possibility of involuntary responses.

Hybrid systems point of view: Walking involves the interaction of continuous differential dynamics generated by the limbs and their neural control and discrete dynamics due to the leg’s impact on the ground. Naturally, this results in a hybrid dynamic system. The hybrid systems theory becomes highly relevant to model the gait for studying the orbital stability of the limit cycle. A non-singular Jacobian is essential to the contraction analysis of the system, which is based on variational methods of the differential dynamics [43, 74]. However, biologically relevant gait models with event-driven feedback can have singular Jacobian. Therefore, this case requires adapting the Poincare section-based methodologies such as the one given by [23] for the study.

Time series analysis: Gait and FOG have also been studied using the time series data gathered during locomotion. Much of these studies involve signal processing and machine learning-based techniques to study the human gait and to understand freezing. The analysis study of publicly available locomotion data (MIT Gait database) reported in [64] makes use of the nonlinear time series analysis (such as mutual information, false nearest neighbour and Lyapunov exponent). Specifically, FoG time series has also been studied using nonlinear signal processing techniques to reveal the underlying mechanics of freezing. Moreover, the works on critical transitions [53] which lie in the intersection of dynamical systems theory and nonlinear signal processing is applicable in the area of FoG. Furthermore, studies reported in [47] [59] [62] apply machine learning techniques to time series stepping data for predicting freezing.

Summarising the problem: In summary, there is a need for a mathematical model that describes the FoG and the variability in PD gait, focusing on limb mechanics and event-driven feedback to CPG relevant to PD. As freezing is an intermittent behaviour, the model’s transient and long-term behaviours need to be studied. Moreover, event-dependent feedback on the synchronisation property of the CPG is studied to understand the effect of the augmented feedback on CPG.

How we address these problems: In this work, we combine a CPG model and a limb mechanics model. The limb model focuses on the ankle push-off forces [60] making it relevant to PD. A state dependant, event-driven feedback is provided to account for the impulse signal occurring at the heel strike. The mathematical description of such a system becomes a nonlinear-hybrid-dynamical system. The orbital stability of gait in this model is studied using a Poincare-based approach, since the Jacobian associated with the model is singular. The effect of the feedback on gait and its variability is studied from the perspective of the neuromechanical system and the synchronisation properties of the CPG. The intermittent transition of the gait from walking to freezing and back has been demonstrated.

2 Preliminaries

2.1 Introduction to hybrid system

Hybrid systems are a class of dynamical systems, which exhibit both continuous and discrete mode dynamics and their mutual influence, often associated with events such as resets or jumps, and switching. A system of ordinary differential equations typically governs the continuous behaviour, and a vector-valued function governs the discrete part. The dynamics in this work is governed by the general hybrid dynamical system of the form,

$$\begin{aligned}&\dot{z}(t) = \mathcal {F}(z(t),\lambda ),~z(t)^{-} \notin \mathcal {S}~, \end{aligned}$$
(1)
$$\begin{aligned}&z(t)^{+} = \varDelta (z(t)^{-},\lambda ),~z(t)^{-} \in \mathcal {S},~ \end{aligned}$$
(2)

where \(z \in \mathcal {Z}\) represents the state variables and \(\mathcal {Z} \subset \mathbb {R}^n\) is the state manifold. In (1), \(\mathcal {F}(z(t), \lambda ): \mathcal {Z} \times \varLambda \rightarrow \mathbb {R}^n\) is continuous vector-valued function, which is strictly forward invariant under \(\mathcal {F}\). Further, \(\lambda \in \varLambda \subset \mathbb {R}^m\) represents a vector of adjustable constant parameters of the system and \(\varLambda \) characterises a set of admissible parameter values. In this case, \(\mathcal {F}(z(t), \lambda ): \mathcal {Z} \times \varLambda \rightarrow \mathbb {T\mathcal {Z}}\) is \(\mathcal {C}^\infty \) vector field, in which \(\mathbb {T\mathcal {Z}}\) is the tangent bundle of state manifold \(\mathcal {Z}\). The solution curve of the system is denoted as \(\zeta (t,z_0,\lambda )\), such that \(z(t) = \zeta (t,z_0,\lambda )\) is the solution at time \(t >0\) of the system with an initial state \(z(0) = z_0\) at time \(t=0\).

In hybrid systems, the state can instantaneously reset to a discrete time part according to a \(\mathcal {C}^\infty \) reset map \(\varDelta (z(t)^{-},\lambda ) : \mathcal {Z} \times \varLambda \rightarrow \mathcal {Z}\) in Eq. 2. The switching surface is defined as

$$\begin{aligned} \mathcal {S}:=\{~z(t)\in \mathcal {Z} ~\big |~g_{r}(z(t)) =0~\}~, \end{aligned}$$
(3)

where \(g_{r}(z(t)) : \mathcal {Z} \rightarrow \mathbb {R}\) is a \(\mathcal {C}^\infty \) real valued switching function, satisfying the condition \(\frac{\partial {g_{r}}}{\partial z}(z) \ne 0\). The system with the reset, or so-called impulse effect, brings forth the possibility of the state’s jumping (also known as ‘resets’) when certain boundaries are crossed. In general, these boundaries are subsets of the space, \(\mathcal {S} \subset \mathcal {Z}\). The difference between a smooth system and a hybrid one lies in the fact that when the flow \(\zeta (t,~z_0,\lambda )\) reaches the switching surface Eq. 3, a reset map in Eq. 2 is applied.

Fig. 1
figure 1

Illustration of the trajectory in the hybrid system. The dashed line corresponds to the discrete mode dynamics, whereas the solid line corresponds to the continuous part of the hybrid system

Full size image

The time to reset function is then defined as \(T : \mathcal {Z} \times \varLambda \rightarrow \mathbb {R}_{+}\) as the first time at which the continuous part solution \(\zeta (t,z_0,\lambda )\) intersects the switching manifold \(\mathcal {S}\):

$$\begin{aligned} T(z_0, \lambda ) := \inf \{~t > 0~ |~\zeta (t,z_0,\lambda ) \in \mathcal {S}~ \}~. \end{aligned}$$
(4)

A Poincaré map, which describes the motion of the point of intersection of a differential dynamical system with a planar section traverse to the flow, \(P: \mathcal {Z} \times \varLambda \rightarrow \mathcal {Z}\), is defined by

$$\begin{aligned} P(z, \lambda ) := \zeta ( T(\varDelta (z,\lambda ),\lambda ),~\varDelta (z, \lambda ),~\lambda )~, \end{aligned}$$
(5)

and describes the evolution of the hybrid model in Eqs. 1–2 on the switching surface, \(\mathcal {S}\), which is considered as the Poincaré section (indicated in Fig. 1) according to a discrete time dynamics

$$\begin{aligned} z[k+1] = P(z[k], \lambda ),~~k=0,1,2,\cdots \end{aligned}$$
(6)

Typically a periodic orbit is transversal, i.e. not tangent, to the switching manifold \(\mathcal {S}\). Consequently, the invariant fixed point for the Poincaré map in Eq. 5 is

$$\begin{aligned} P(z^*,~\lambda ) = z^*,~\forall \lambda \in \varLambda . \end{aligned}$$
(7)

In the hybrid walking system described here, a Poincare map may be constructed by choosing the switching surface \(\mathcal {S}\) as the Poincare section [1, 78]. The discrete dynamics on the Poincaré section is defined as follows:

$$\begin{aligned} \mathcal {P}: z[k+1] = P(z[k],~\lambda ). \end{aligned}$$
(8)

One could note that the variable z when used as an argument to the Poincare map it is indicated with square braces to indicate the discrete nature of the map.

One gait cycle constitutes two steps since the left and right leg acts as a stance leg. Henceforth, a gait cycle is the composition of \(\mathcal {F}_R \circ \varDelta _{L\rightarrow R} \circ \mathcal {F}_L \circ \varDelta _{R \rightarrow L}\) where \(\mathcal {F}_L\) and \(\mathcal {F}_R\) denotes the flow corresponding to the left and right leg as the stance legs, respectively, and ‘\(\circ \)’ represents the composition. Symbols \(\varDelta _{L\rightarrow R}\) and \(\varDelta _{R\rightarrow L}\) represents the reset corresponding to the left leg to the right leg and vice versa. Consequently, it is convenient to study the composition of the Poincare map with itself (\({P}({P(.)}):=\tilde{{P}}(.)\)) for understanding the stability properties of the gait cycle. The stability of this map is numerically studied. The Jacobian that corresponds to the vector field and the Poincaré map is denoted by \( D \mathcal {F}\), and \( D {P}\), respectively. A non-singular \( D \mathcal {F}\) is essential to the contraction analysis of the system based on variational methods of analysis of the differential dynamics [43, 74]. A lack thereof leaves out the possibility of only Poincare-based analysis of P or its iterates.

Fig. 2
figure 2

The physiology and the associated modelling assumptions are depicted here. The brain (basal ganglia, cortical and subcortical areas) control the spinal cord which in turn control gait. CPG is modelled as coupled oscillators (representing neurons). The walking dynamics is represented by a simple pendulum model

Full size image

2.2 Physiology

The relevant physiology is briefed here. Central pattern generators (CPG) are neuronal circuits in the spinal cord that can generate oscillatory activity without being forced rhythmically [31]. There is evidence in the literature for the presence of CPG in quadrupeds [12, 25] and indirect evidence [12, 75] for its existence in humans. Brain modulates the CPG dynamics in the spinal cord [12, 70] which in turn coordinates the leg-muscles using feedback inputs from the brain[6, 49]. Simplified physiology of gait and the corresponding modelling aspects are depicted in Fig. 2.

A bursting dynamical state of a neuron is associated with the excitation of a group/bursts of action potentials in succession. The spinal CPG neurons are known to elicit bursting behaviour [24, 39] which control the torque generated by the muscles. While there are multiple spikes in a burst, the torque produced can be assumed to be resulting from the ‘equivalent membrane potential’ [20, 38] of the bursting dynamics. The torques are generated during the bursting region of the dynamics. Almost very low, or zero, torque is generated during the non-bursting region [8, 9, 29]. Consequently, the neuromechanical dynamics is controlled by the equivalent voltage of the motor neuron bursts [24, 39] rather than individual spikes.

The role of sensory feedback inputs through afferent nerves in walking rhythm generation is now well recognised [7, 12, 77]. Transmission of these signals requires a finite amount of time to reach the destination. Hence, it occurs with a delay. However, this delay is known to be negligibly small (< 50 ms) [45] when compared with the stepping times [5]. Hence, the feedback is modelled and studied as event-driven instantaneous inputs to the neuronal system. A defective utilisation of these afferent feedback inputs has been suggested in PD in [13] resulting in defective electromyogram (EMG) traces [13, 56] making feedback relevant in the study of PD gait.

3 Mathematical modelling

The dynamics of the neuromechanical system governing PD physiology is explained in this section. The section starts with the complete equations of motion, the underlying assumptions and the description of the subsystems successively follow.

Fig. 3
figure 3

A block diagram showing the feedback interaction between the neural and mechanical components of the system. While the neuronal states \(y_1\) and \(y_2\) become the inputs to the limbs, the proprioceptive feedback modelled as state \(\varXi \) modulates the CPG. The term I(t) represents other external inputs received by the CPG. This external input, in turn, phenomenologically models the cues given to the PD patients

Full size image

3.1 Equations of motion

A hybrid system formulation of the equations of motion (EoM), as in Eqs. 1 and 2, has three components: (1) continuous dynamics (\(\mathcal {F}(z(t),~\lambda )\)), (2) a discrete part (\(\varDelta (z(t)^{-},\lambda )\)) and (3) a definition for the switching surface (\(\mathcal {S}\)). In this study, the continuous part of the dynamics (\(\mathcal {F}(z(t),~\lambda )\)) comprises two interacting subsystems, of which, one is a neuronal CPG part (\(\varSigma _{n_i}\)), modelled as two coupled oscillators and the other corresponds to mechanical dynamics (\(\varSigma _m\)). Figure 3 shows the interaction between the neuronal and mechanical systems and the external input received by the CPG.

The overall system is described using Eqs. 1 and 2 with the following characterisation:

$$\begin{aligned}&z = \left[ \begin{matrix}y_1,~x_1,~y_2,~x_2,~ {\theta },~ \omega ,~\varXi \end{matrix}\right] ^T~, \end{aligned}$$
(9)
$$\begin{aligned}&\mathcal {F}(z,\lambda ):=\big [\begin{array}{c|c} \varSigma _{n_{1}}^T~ \varSigma _{n_{2}}^T~&~ \varSigma _m^T \end{array}\big ]^T~, \end{aligned}$$
(10)
$$\begin{aligned}&g_{r}\left( z\right) =\theta -\theta _\mathrm{reset}~, \end{aligned}$$
(11)
$$\begin{aligned}&\varDelta \left( z^-,\lambda \right) =\left[ \begin{matrix}y_1,~x_1,~y_2,~x_2, {-\theta },~ \omega \cos (\theta _h),~-\varXi \end{matrix}\right] . \end{aligned}$$
(12)

The dependency on time in the equations is absent for brevity. The variables \(x_i\) and \(y_i\) represent the states of the neuronal CPG, with \(y_i\) indicating the activity of the ith neuron. In Eq. 10, the dynamics of the neuronal CPG is written as follows:

$$\begin{aligned} \varSigma _{n_{i}}&:= \left[ \begin{array}{c}\frac{1}{\tau }\bigg (\overbrace{\frac{-\alpha y_i \left( x_i^2+y_i^2-e\right) }{e}-x_i}^{\text {Intrinsic CPG Dynamics}} +{\underbrace{\varXi \varPhi _i}_{\text {{Feedback}}}}\\ \quad {+\underbrace{\sum _{j=1}^{2} {w}_{i,j} y_j}_{\text {Neuronal Coupling}}}-\underbrace{a I_i(t)}_{\text {Ext. Input}}\bigg ) \\ \frac{y_i}{\tau }\\ \end{array}\right] ,~i=1,2. \end{aligned}$$
(13)

where

$$\begin{aligned} \varPhi:= & {} [-f_{b},~f_{b}]^T, \end{aligned}$$
(14)
$$\begin{aligned} w:= & {} \begin{bmatrix} 0 &{} S_t\\ S_t &{} 0 \end{bmatrix}. \end{aligned}$$
(15)

The term \(w_{i,j}\), which controls the mutual inhibition through the synaptic strength \(S_t\) is element of matrix \(w \in \mathbb {R}^{2\times 2}\). The neurons modelled are assumed to be mutually inhibiting (one inhibiting the other) and not directly influencing its own activity (\(w_{1,1} = w_{2,2} = 0\)). The element \(\varPhi _i\) of the vector \(\varPhi \in \mathbb {R}^2\) represents the positive or negative feedback strength (\(f_{b}\)). The term \(\varXi \) corresponds to the proprioceptive feedback from the limbs modulating the CPG dynamics. The constants \(e,~\alpha \) and \(\tau \) govern the intrinsic CPG oscillator dynamics [32] and discussed more in sequel.

In Eq. 13, the effect of periodic auditory/sensory cues [7, 12, 77] is represented as a scaled periodic external input \(aI_i(t)\) where

$$\begin{aligned} I(t)&:=\big [-u_{s}(t),~ u_s(t)\big ]^T~, \end{aligned}$$
(16)

and

$$\begin{aligned} u_s(t) = {\left\{ \begin{array}{ll} +1,~ \sin (2 \pi \varOmega _f t)\ge 0~,\\ -1,~\sin (2 \pi \varOmega _f t)<0~. \end{array}\right. } \end{aligned}$$
(17)

The variable a scales the amplitude of the external input, when present, and \(\varOmega _f\) represents the frequency of the input.

In Eq. 9, the states \(\theta ,~\omega \) and \(\varXi \) represent the angle subtended w.r.t. the horizontal, angular velocity and ‘proprioceptive feedback’, respectively. The ‘proprioceptive feedback’ state \(\varXi \in \{-1,~+1\}\) indicates which leg is on the ground at time t to generate an event-driven-feedback signal. In this formulation, the proprioceptive feedback is sent from the limbs to the neural system. In Eq. 10, the mechanics of the limbs (\(\varSigma _m\)) are described using the following set of equations,

$$\begin{aligned} \varSigma _m&=\left[ \begin{matrix}\omega \\ \frac{1}{\theta }\bigg (\varXi \max (0,~\theta ) \big (\frac{p(\theta ,~-\varXi )\tau _l\max (0,~y_1)}{l^2 m}\\ \qquad - \frac{p(\theta ,~\varXi )\tau _r\max (0,~y_2)}{l^2 m}\big )\bigg )+\frac{g \theta }{l}-q(\theta ) \\ 0 \end{matrix}\right] ~, \end{aligned}$$
(18)

where

$$\begin{aligned} p(\theta ,~\varXi )&:={\left\{ \begin{array}{ll} l\sin (2\theta ) ~&{}\text {when}~\varXi =+1~,\\ 1~ &{}\text {when} ~\varXi =-1~,\\ \end{array}\right. } \end{aligned}$$
(19)
$$\begin{aligned} q(\theta )&:= {\left\{ \begin{array}{ll} 0~ &{}\text{ if } ~~~\theta <-\theta _\mathrm{reset}+\epsilon ~,\\ K\theta ~~~ &{}\text{ if } ~\theta \ge -\theta _\mathrm{reset}+\epsilon ~,\\ \end{array}\right. } \end{aligned}$$
(20)

and l,  m,  g,  and K are length, mass, acceleration due to gravity and the stiffness constant of the trailing leg, respectively. The parameters \(\tau _l\) and \(\tau _r\) scales the neuronal activity signals \(y_1\) and \(y_2\) . The stiffness of the trailing leg (K) models the measure of the angular stiffness, and small positive scalar \(\epsilon \) is a design freedom. The hip angle (\(\theta _h\)) in Eq. 12 is considered as twice the reset angle \(\theta _\mathrm{reset}\) since the step angle is assumed constant in every step. The step length is defined to be equal to \(|\theta _\mathrm{reset}|\) where |.| denotes the absolute value.

3.2 Neuronal dynamics as locomotion control

The CPG is assumed to control the movement of the limb dynamics [14] while simultaneously affected by feedback with a negligible delay [45]. The ‘equivalent membrane potential’ [38] of the bursting dynamics is assumed to control the torques generated in the muscles. Moreover, the activity of those neurons is directly proportional to the torques generated in the muscles.

In this work, the CPG is modelled as two interconnected oscillators (matching the number of lower limbs in humans) effectively modelling the ‘equivalent membrane potential’. The intrinsic CPG dynamics part in Eq. 13 is inspired from [32] and in the absence of the external inputs and the feedback signal, the CPG exhibits limit cycle. Plantar flexors innervated by the neurons from the CPG supply the necessary torques to the limbs. The activation of CPG occurs only for the positive neuronal activity, i.e. when \(y_1>0\), or \(y_2>0\). Hence, this representation effectively models muscle contraction.

The parameter e in the intrinsic CPG dynamics in Eq. 13 increases the amplitude of the limit cycle. An increase in the amplitude of the limit cycle models the increased neuronal activity. The positive constants e and \(\tau >0\) together control the total energy in every stepping cycle. While the system is on the limit cycle, the term \(x_i^2+y_i^2\) is e, and thus there is no influence for the parameter \(\alpha \). Henceforth, the positive parameter \(\alpha \) can be interpreted as a scaling of the perturbation from the limit cycle. The feedback \(\varXi \varPhi _i\), the neuronal coupling \(\sum _{j=1}^{2} \text {w}_{i,j}y_j\) and the external input I(t) in Eq. 13 can apparently change the phase of the oscillator. The perturbations to the phase of the oscillator have influence on the synchronisation [38].

3.3 Mechanical model and definition of freezing

It has been shown in [60] that an inverted pendulum-based model adequately represents the freezing and irregular walking motion of the centre of mass of the body having PD. The torque generated due to the plantar flexors’ activity alone provides the ankle push-off forces to propel the leg forward. Inspired by this, the lower limb mechanics is modelled here as a hybrid inverted pendulum (inverted pendulum with a reset). The reset map and the differential part of the dynamics (Eqs. 12 and 18–20) are derived by balancing the torques and the angular momentum, respectively. The stiffness of the trailing leg is triggered when the angular displacement \(\theta \) increases beyond \(-\theta _\mathrm{reset}+\epsilon \) in the counter direction to walking. In this study, \(\epsilon \) is fixed at 0.02 (chosen arbitrarily, do not affect the dynamics qualitatively). The negative sign associated with the term \(\theta _\mathrm{reset}\) represents this convention. The stiffness term in Eq. 20 takes into account the opposing force exerted by the trailing leg preventing a fall; at this moment, the subject is assumed to freeze. This opposing stiffness force is necessary to model the shift from freezing to walking. The impulsive mechanics at ‘heel strike’ (when the swing leg hits the ground) is modelled using a reset, effectively making the dynamics belong to the class of hybrid system. At every instance the flow of the dynamics reaches the switching surface \(\mathcal {S}\) in Eq. 3, the reset map given in Eq. 12 is applied. The function \(g_r(z)\) in Eq. 11 defined the identity of the switching surface. The state representing the proprioceptive feedback \(\varXi \) is reset at every step accounting for the change in the stance leg loaded with the weight of body. The angular velocity is also reset to account for the conservation of angular momentum. Furthermore, the angle (\(\theta \)) is reset to account for the alternation between limbs as given in [60].

By convention, a negative angular velocity indicates limbs moving forward. At every point in the phase space, a finite amount of energy is necessary to keep the direction of the angular velocity negative (\(\omega <0\)). During a freezing episode, the limbs receive insufficient net torque to move forward. Consequently, the angular velocity \(\omega \) becomes positive, which leads to the following definition.

Definition 1

Let \(z_{t_0} \in \mathcal {S}\) be the state at time \(t_0\) and \(t_s - t_0\) be the time to impact (or reset). Freezing trajectory is defined as the set \(\mathcal {C}:=\{\zeta (t,~z_{t_0})~|~z_{t_0} \in \mathcal {S},~ \omega (t) > 0 ~\text{ for } \text{ some }~t \in ~(t_0,~t_s) \}\) .

The freezing fraction for a discrete simulation is determined by finding the fraction of time points where \(\omega (t)>0\) and satisfies Def. 1. The finite time simulation results are sampled uniformly, and the number of data points with \(\omega (t)>0\) is divided by the total number of points in the simulation to compute freezing fraction. From a physiological perspective, whenever the premature activation prevails upon the normal activation, the stance leg momentarily moves backwards, resulting in \(\omega >0\). Consequently, freezing fraction gauges the effect of premature activation of the muscles in the stance leg. According to [56] premature activation of plantar flexors is a characteristic of PD making freezing fraction very relevant for PD.

Table 1 The values of different parameters of the model and initial conditions
Full size table

4 Simulation results

The overall model described using Eqs. 1 and 2 with the characterisation given in Eqs. 9–12 is simulated. Unless specified otherwise, values of the parameters and initial conditions used in the model are listed in Table 1. While Table 1 specifies a particular set of parameters to reproduce the results, a larger set of parameter variations, for which the results are valid, are explored in sequel. The evolution of the states for a short duration of time is shown in Fig. 4. In simulations, high and low values of the feedback strength (\(f_b\)) are considered.

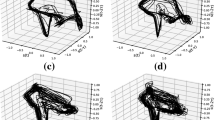
(i) Normal gait: In this simulation, no external input I(t) is considered. Figure 4a, b shows the states of the CPG dynamics and the mechanical system during normal walking. The value of the feedback gain (\(f_b\)) used in the simulation is 1.

(ii) Freezing of gait: The states of the neural and the mechanical system are indicated in Fig. 4c, d, respectively. When compared with the results of normal gait, the freezing of gait is obtained by decreasing the value of the single parameter, the feedback gain (\(f_b\)), to a lower value of 0.1 from 1.

Fig. 4
figure 4

a The states of the neural system (\(y_1,~y_2,~x_1,~x_2\)) at high value of feedback strength (\(f_b = 1\)). b States of the mechanical system (\(\theta ,~\omega ,~\varXi \)) at high value of feedback strength (\(f_b = 1\)). c The states of the neural system at a low value of feedback strength (\(f_b = 0.1\)) d States of the mechanical system at a low value of feedback strength (\(f_b = 0.1\)). Phases of Walking and Freezing, single step and one reset point are indicated. A freezing episode (Freeze) starts from one heel strike and lasts until the end of the heel strike, which is in accordance with the definition of the freezing trajectory. This depiction is relevant physiologically because it is relatively easier to determine a freezing trajectory between two heel strikes. The figure contains more than one walking and freezing regions, but only one is labelled here

Full size image

The oscillations in the four neuronal state variables of the CPG can be noticed in Fig. 4c. Among the states, the signals \(y_1\) and \(y_2\) control the mechanical part of the system. In this simulation, the chosen low value of feedback strength (\(f_b=0.1\)) is insufficient to synchronise the neural (\(\varSigma _{n_i}\)) and mechanical (\(\varSigma _m\)) systems. This aspect is evident from the resultant intermittent walking and freezing behaviour observed in Fig. 4d. The proprioceptive feedback state \(\varXi \), indicating which leg is on the ground, changes the sign on reset as indicated in Fig. 4d, since \(\varXi \in \{1,+1\}\) and \(\dot{\varXi } = 0\). From Fig. 4d, it can also be observed that at the reset point, the state \(\theta \) is reset to \(-\theta \) as well.

The trajectory from an initial condition till the reset is defined to be a ‘step’. A ‘freeze’ as defined in Def. 1 is indicated in Fig. 4d where \(\omega \) crosses zero and reaches a positive value generating a longer ‘pause’ in walking. Multiple steps without an intermediate freeze are indicated as walking. One could note that, from the hybrid systems point of view, the ‘pause’ in walking owes to the relatively higher time to reset.

The sharp changes in angular velocity owe to two aspects of the model: (i) the reset accounting for the conservation of angular momentum and (ii) the effect of the piecewise linear characteristics of \(q(\theta )\) in Eq. 20 as the angle \(\theta \) crosses the condition \(-\theta _\mathrm{reset}+0.02 = 0.12~\). The latter aspect contributes to the rapid changes to the angular velocity during the freezing episode shown in Fig. 4d.

Figure 5a shows the time series of states \(\theta \) and \(\omega \) from 20 s of simulation. In the simulation, the feedback gain is fixed at 0.1. The regions where freezing occurs are indicated in red colour. The intermittent episodes of walking and freezing can be observed. A plot of the trajectories in the \(\theta \)–\(\omega \) phase plane is shown in Fig. 5b. In the phase plot, the segment of trajectories in the first quadrant shown in red colour reflects freezing behaviour, since angular velocity is positive.

(iii) In presence of external input: An external input I(t) as in Eq. 16 is applied to the model (\(f_b = 0.1\)) which exhibited the intermittent freezing behaviour as shown in Fig. 4c, d. The frequency of the external input \(\varOmega _f\) is 1.2 and the parameter a equals 2.5. Figure 6 shows the effect of the external input, which converts an otherwise freezing gait into a normal gait.

The external input is shown to influence the neuromechanical system resulting in a gait without freezing. While Fig. 6 shows the dynamics with one particular external input, distinct effects of external inputs over a larger parameter range are explored in sequel in Sect. 6.2. In addition, short-time Fourier transform (STFT) of the filtered angular acceleration signal (\(\dot{\omega }(t)\)) is computed. A Gaussian filter of kernel radius ten is utilised for filtering the (\(\dot{\omega }(t)\)) signal. A window size of 0.32 sec and a sampling rate of 100Hz is adopted for the STFT calculation[33]. The STFT analysis indicated that the frequency content of the signal increases in the model during a freeze, which is in line with the experimental evidence [5, 68].

Fig. 5
figure 5

a Time series of \(\theta (t)\) with respect to time is provided for a low value of feedback gain (\(f_b = 0.1\)). The angular velocity \(\omega (t) = \dot{\theta }\) is shown in blur background. b \(\theta \)–\(\omega \) phase plane diagram; The regions in red colour show part of the data exhibiting freezing behaviour where \(\omega \) is positive. (Color figure online)

Full size image
Fig. 6
figure 6

Recovery of normal gait for a low value of feedback gain (\(f_b = 0.1\)) in the presence of an external input I(t). The results given here are for an example external input parameter set, \(a=2.5,~\varOmega _f = 1.2\). Physiologically this represents a scenario of external cueing-based FoG alleviation

Full size image

5 Stability analysis of periodic walking region

Fig. 7
figure 7

The value of \(\varXi \) as it changes between \(\mathcal {S}\) and \(\tilde{\mathcal {S}}\) has been shown. The dashed lines represent the discrete dynamics governed by \(\varDelta (.)\) and the solid lines represent the smooth dynamics governed by \(\mathcal {F}(.)\). The map \(\tilde{P}(.)\) formed by iterating P(.) two times, is also indicated

Full size image

Human locomotion is generally stable in the presence of certain class of perturbations [34]. The stability of the overall model in Eqs. 1 and 2 with the characterisation as given in Eqs. 9–12 is analysed in this section. The CPG model considered in this work is phenomenological. Three parameters of the CPG model—constant e governing the intrinsic CPG oscillator dynamics, the feedback gain \(f_b\) and the synaptic strength \(S_t\)—are of physiological significance [32]. For the purpose of stability analysis, the perturbation to these parameters is assumed to occur within the range \(e \in (0.1,~ 1), S_t \in (0,~ 6),\) and \(f_b \in (0,~2)\) where relevant walking and freezing behaviours are exhibited. Demonstration of orbital stability of the hybrid walking model in the presence of the perturbations is vital.

For stability analysis, the surface defined by the set \(\mathcal {S}\) is considered for constructing the Poincare section. The discrete map \(\varDelta (.)\) maps the points from \(\mathcal {S}\) to \(\tilde{\mathcal {S}}\) which is again mapped back to \(\mathcal {S}\) by the differential dynamics. The Poincare map P is defined as a composition of these maps taking a point \(z[k] \in \mathcal {S}\) to \(z[k+1]\in \mathcal {S}\). Since proprioceptive feedback state \(\varXi \) switches in every reset (as shown in Fig. 7), the map \(\tilde{P}\) is formed by iterating P twice, which is considered for the stability analysis.

Out of the seven state variables, only five (excluding \(\theta \) and \(\varXi \) as they remain constant during the evolution due to the differential part of the dynamics) are considered for the computation of the Jacobian. This results in the definition of a new map, denoted by \(\tilde{P}_c\), where the parameters \(\theta \) and \(\varXi \) remains constant. Hence, the map \(\tilde{P}_c\) is defined as follows,

$$\begin{aligned} \tilde{z}[{k+2}] = \tilde{P}_c(\tilde{z}[k])~, \end{aligned}$$
(21)

where \(\tilde{z}[k] := z[k] \setminus \{\theta [k],~\varXi [k] \} \in \mathbb {R}^{5}\) is the state vector of the overall system excluding \(\theta ,~\varXi \) at the kth step. The Jacobian associated with this system is denoted by \(D\tilde{P}_c \in \mathbb {R}^{5 \times 5}\).

A Taylor series-based methodology, adapted from [23], is used for the computation of the Jacobian matrix of the map \(\tilde{P}_c\). The eigenvalues of the Jacobian matrix \(\mathcal {D}\tilde{P}_c\) determine the stability of the system [11]. Following the approach in [23], at the periodic point \(\tilde{z}^*\) of the map \(\tilde{P}_c\), the perturbation vectors \(\delta \tilde{z}_i^*\)s are applied. The vector \(\delta \tilde{z}_i^*\) has only one small nonzero term (\(=10^{-3}\)), such that, the perturbations are applied to each state independently. Hence, a diagonal matrix \(\varvec{\gamma }\in \mathbb {R}^{5 \times 5}\) is defined constituting the perturbation vectors \(\delta \tilde{z}_i^*\) associated with each states as its columns. For the perturbation vector \(\delta \tilde{z}_i^*\) associated with each individual state, the corresponding \((\tilde{P}_c(\tilde{z}^*+\delta \tilde{z}_i^*)-\tilde{z}^*) \in \mathbb {R}^{1 \times 5}\) is computed, yielding the matrix \(\varvec{\varOmega } \in \mathbb {R}^{5 \times 5}\). Since \(\varvec{\gamma }\) is diagonal matrix and \(\varvec{\varOmega }\) is determined as described above using the map \(\tilde{P}_c\), it is possible to write the Jacobian of \(\tilde{P}_c\) as:

$$\begin{aligned} D \tilde{P}_c = \varvec{\varOmega }\varvec{\gamma }^{-1}. \end{aligned}$$
(22)

The sequence \(\{\tilde{z}_n\}\) is obtained by iterating the map \(\tilde{P}_c\) in Eq. 21 starting from an initial condition \(\tilde{z}_0 := (y_{1_{0}}, y_{2_{0}}, x_{1_{0}}, x_{2_{0}}, \theta _0, \omega _0)^T\) \(= (0.29, -0.29, 5.53, -5.53,\) \(0.1, -0.7)^T\). Fifty iterations of the map \(\tilde{P}_c\) are computed. The Jacobian matrix \(D\tilde{P}_c\) is determined using the last iterate. The maximum absolute value of the eigenvalues (MAE) of the Jacobian matrix \(D\tilde{P}_c\) determines the stability, and the system is stable whenever this value is less than 1. The condition (MAE \(< 1\)) can also include possible, stable, intermittent freezing behaviour of the dynamics. Normal gait responses are associated with the Period-1 orbits. Hence, in addition to the MAE condition, an additional term based on the return map information is made use to identify the Period-1 orbits. The additional metric introduced ensures the convergence to Period-1 orbit over a finite period of simulation time.

Fig. 8
figure 8

Results of the 1000-point Monte Carlo simulation showing stable periodic region and the rest. The region with MAE < 1 and \(\Vert \mathcal {C}_p\Vert _2<10^{-4}\) is shown in green. The rest of the region is indicated in red. The figure shows the ability of the model to elicit stable (under the perturbation of initial conditions as mentioned in Sect. 5) normal walking for a range of e and \(f_b\) values. (Color figure online)

Full size image

The convergence of the orbits to a limit cycle during a finite time simulation is tested by generating a vector \(\mathcal {C}_p\). The vector \(\mathcal {C}_p\) is generated by computing the norm of the differences between consecutive iterates of states for the last 20 iterations in the following way,

$$\begin{aligned} \mathcal {C}_p:=\{~\Vert (\tilde{z}[r] - \tilde{z}[r-1])\Vert _2~,~\forall r \in \{N-n,~N\}\}~. \end{aligned}$$
(23)

Here, N (= 50) is the total number of iterations simulated, n (= 20) is the number of consecutive iterations used for convergence estimation and r is the iteration number. The \(l_2\) norm of the resulting vector \(\mathcal {C}_p\) is computed as a measure of convergence. When \(\Vert \mathcal {C}_p\Vert _2 < 10^{-4}\) the orbit is assumed to converge to a limit cycle.

The procedure described addresses the Period-1 orbits (stability of normal walking) of the map \(\tilde{P}_c\). Period-1 orbit of the map \(\tilde{P}_c\) which in turn is formed by the iteration of the map P twice as explained in Fig. 7, hence when \(N=50\) a total of 100 steps are simulated.

A Monte Carlo stability analysis was performed. For this, the system in Eqs. 9–12 is simulated using 1000 randomly initiated \((e,~ S_t,~ f_b)\) parameter vectors. For each \((e,~ S_t,~ f_b)\) parameter vector, the procedure discussed above is followed, and the MAE and \(\Vert \mathcal {C}_p\Vert _2\) are computed to classify the stability of the walking regime of the system. Figure 8 shows the results of the Monte Carlo simulation. Here the green points indicate the stable Period-1 orbit, i.e. MAE < 1 and \(\Vert \mathcal {C}_p\Vert _2 \le 10^{-4}\). The analysis reveals the existence of stable periodic orbits for a subset of the parameter space considered. As evident in Fig. 8 while a higher value of e and \(s_t\) are beneficial for walking, the key distinguishing factor is \(f_b\). A higher value of \(f_b\) is necessary for the system to be in a stable periodic orbit. The median and standard deviation (given in brackets) of the parameter \(f_b,~e\) and \(S_t\) in the stable periodic region (green) is found to be 1.34 (± 0.37), 0.64 (\(\pm 0.23\)) and 3.5 (\(\pm 1.57\)), respectively. The distribution of the parameters \(f_b,~e\) and \(S_t\) in the stable region are significantly different (\(p<10^{-6}\) Mann–Whitney test) from that in the rest (red region).

Further analysis of the freezing fraction and coefficient of variation is aimed to study the possibility of a possible freezing episode during the iterations of the map.

6 Effect of external input in the absence of proprioceptive feedback

This section details the effect of periodic sensory signals such as auditory inputs and STN stimulation given to PD patients for alleviating FoG. The external input I(t) shown in Fig. 3 alters the phase and thereby influences the synchronisation as discussed in Sect. 3.2. In this section, the effects of varying the amplitude and the frequency of the external input I(t) on states defining the neuronal activity (\(y_1(t), y_2(t)\)) and the angular velocity state of the limbs (\(\varSigma _m\)) in the absence of the proprioceptive feedback \(\varXi (t)\) in Fig. 3 are studied. This helps to understand qualitative differences in the region of synchronous behaviour of CPG and the non-freezing regime under the action of external periodic input for the overall system in the absence of proprioceptive feedback. The analysis is done in two sub-sections as follows:

6.1 Effect of external input on neuronal activity

The system in Eqs. 9–12 under the influence of external input, with \(a \ne 0\) and \(f_b=0\), possibly resulting from sensory or auditory cues [7, 12, 77], is studied. By forcing the feedback term to zero, the effect of external input on the CPG neural part of the system only is considered here. The amplitude scaling parameter a and the frequency \(\varOmega _f\) of the external input in Eq. 13 are varied from 0 to 3 in steps of 0.1 and from 0 to 2 in steps of 0.025, respectively. The frequency range is chosen to be a representative range of the walking frequencies [27]. The effect of variations on the CPG is quantified in the following manner.

Fig. 9
figure 9

The \(l_2\) norm of the difference trajectories, \(\Vert \mathcal {E}\Vert _2\), for different values of frequency \(\varOmega _f\) in Eq. 17 and for different values of amplitude scaling parameter in \(\varSigma _{n_i}\) (with 0.1–0.025 grid). \(\Vert \mathcal {E}\Vert _2\) calculated for time duration from \(t_1=27 \text {~to~} t_2=30s\) with initial conditions a \(y_{10}=1\) and b \(y_{10}=2\). The highly synchronised regions are in blue with low value for the norm. This illustrates the ability of the external inputs to synchronise the CPG behaviour for a subset of frequency and amplitudes. (Color figure online)

Full size image

The system in Eqs. 9–12 are simulated for 30 s using two sets of initial conditions—(a) Nominal initial conditions as given in Table 1 and (b) Perturbed initial conditions with \(y_{10} = 2\) instead \(y_{10} = 1\) and the remaining as listed in Table 1. The perturbation to state \(y_1\) alone causes desynchronisation. The chosen perturbed initial condition corresponds to a point chosen outside the limit cycle of the oscillator. Suppose the subscripts ‘a’ and ‘b’ in sequel correspond to the two cases of initial conditions for the 30 s finite time simulation of the system as described above. Let \(\mathcal {Y}_a^{[t_1,~t_2]}\) and \(\mathcal {Y}_b^{[t_1,~t_2]}\) represent the CPG neuronal activity state vectors \((y_1(t), y_2(t))\) during the time period \([t_1,~t_2]\). While synchronisation is achieved, \(\mathcal {Y}_a^{[t_1,~t_2]}\) and \(\mathcal {Y}_b^{[t_1,~t_2]}\) must be close in both phase and amplitude, in a non-trivial manner. Further, let \(\Vert \mathcal {E}\Vert _2 := \Vert \mathcal {Y}_a^{[t_1,~t_2]} - \mathcal {Y}_b^{[t_1,~t_2]}\Vert _2\) be the \(l_2\) norm of the difference between the neuronal activity trajectories from \(t_1=27 \text {~to~} t_2=30s\). When two trajectories \(\mathcal {Y}_a^{[t_1,~t_2]}\) and \(\mathcal {Y}_b^{[t_1,~t_2]}\) are close in both phase and amplitude the \(\Vert \mathcal {E}\Vert _2\) reaches a very small value (\(\Vert \mathcal {E}\Vert _2<=10^{-4}\)) indicating here synchronisation of neuronal states. The term \(\Vert \mathcal {E}\Vert _2\) for different values of frequency \(\varOmega _f\) in Eq. 17 and for different values of scaling of amplitude a in \(\varSigma _{n_i}\) is plotted in Fig. 9.

External cueing is a highly relevant treatment option for PD [21, 54, 71, 79]. Moreover, orbitally stable walking requires synchronised neuronal activity at the level of CPG. In Fig. 9, a region of synchronised behaviour (blue region) can be observed for a higher amplitude of external input.

Even though one could see synchronised neural activity at a low amplitude of external input, synchronised neural behaviour is observed for a relatively broad range of frequencies at a higher amplitude of external input.

6.2 Effect of external input on the Freezing Fraction

The neuromechanical system described in Eqs. 9–12 under the influence of external input (with \(a \ne 0\) and \(f_b=0\)) is studied in this section for its effect on freezing fraction defined in Sect. 3.3. The parameters a and \(\varOmega _f\) of the state-independent exogenous input term aI(t) in Eq. 13 are varied. The frequency \(\varOmega _f\) and the amplitude a of the external input are plotted against the freezing fraction in Fig. 10. The simulation is executed for 30 s, and the fraction of freezing events is computed from the simulated data. The result is plotted in Fig. 10 where the blue and red region indicates the region of the low and high number of freezing episodes, respectively. A blue region is observed with a low freezing fraction when the external input frequency (\(\varOmega _f\)) is between 1 and 1.5 Hz. In this region, the neural and mechanical systems synchronise to generate a normal gait pattern. Figure 6a, b demonstrates the effect of external input on otherwise freezing neuromechanical model with a very low feedback (\(f_b=0.1\)), as fully evident from the present analysis in Fig. 10.

Fig. 10
figure 10

The effect of external input I(t) on a system with no feedback (\(f_b=0\)) is studied here. The amplitude of the input a and the frequency of stimulation \(\varOmega _f\) are plotted against the freezing fraction. The simulations are done for 30 s and the corresponding fraction of freezing events is computed. The blue region has a low, and the red region has a high fraction of freezing events. For the parameter set chosen, the appropriate frequency to achieve walking is between 1 and 1.5 Hz. This illustrates, even in the absence of feedback, the external input (plausibly resulting from cueing) reduces FoG, resulting in synchronised walking for a subset of the frequencies and amplitudes. The range of frequencies for which the system is synchronous increases for higher amplitudes. (Color figure online)

Full size image

7 Effect of feedback on the overall system

The sensitivity of the parameters \(f_b\) and e in CPG dynamics has been studied to understand gait variability. The coefficient of variation (CV) [58] is used as the metric for this study. The coefficient of variation is calculated as the ratio of the standard deviation to the mean of the angular velocity \(\omega \) in simulations. The static parameters \(f_b\) and e are varied, and the hybrid walking model is simulated for a duration of 30 s. The CV of the \(\omega \) is presented as a function of the parameters e and \(f_b\) in Fig. 11a. Lower \(f_b\) generates high variability. A very low value of e results in a lower energy supply to the mechanical system and results in higher variability. A region of appropriate \(f_b\) and e (the red region in Fig. 11a) results in low variability and low freezing. The freezing fraction also has a qualitatively identical pattern as that of Fig. 11a (see Fig. 11b). This helps to explain the higher variability seen in PD patients. [28].

Fig. 11
figure 11

The parameters \(e,~f_b,~\alpha ,~\tau ,~K,~S_t\) are studied here to understand its effect on the freezing fraction. The effect e and \(f_b\) on CV is also provided. While freezing depends on every parameter in the model, its dependence on \(S_t\), \(\tau \) and e, are qualitatively different from \(\alpha \) and K when simultaneously varied with \(f_b\). The effect of \(f_b\) on synchronisation is not altered by the other parameters, and an increase in \(\tau \) results in freezing even at high \(f_b\). From a physiological perspective, a higher feedback benefits to counter freezing. Increased \(\tau \) results in higher variability irrespective of feedback a CV of a 30 s. simulation while varying e and \(f_b\) has been plotted. A low value of \(f_b\) and e result in a higher absolute value of CV and vice versa. b Freezing fraction in 30 s. simulation; while varying e and \(f_b\) has been plotted. A low value of \(f_b\) and e result in higher freezing fraction and vice versa. c The effect of \(S_t\) and \(f_b\) on the freezing fraction is indicated d The effect of \(\tau \) and \(f_b\) on the freezing fraction is considered. e The effect of K and \(f_b\) on the freezing fraction is studied. f The effect of \(\alpha \) and \(f_b\) on the freezing fraction is plotted

Full size image

7.1 Parameters \(\alpha ,~\tau ,~K,~S_t\)

A set of figures are provided here which study the effect of parameters \(\alpha ,~\tau ,~K,~S_t\). The parameters are explored while varying simultaneously with \(f_b\). The parameters \(\alpha ,~\tau ,~K,~\text {and}~S_t\) (Fig. 11) are also studied to understand its effect on the freezing fraction while varied simultaneously with the parameter \(f_b\). Increasing \(\alpha \) and K from 0 to 1 and 10 to 60, respectively, showed qualitative changes in behaviour only at lower \(f_b\) (\(f_b<1\)). Increasing \(\tau \) resulted in higher freezing fractions even at higher \(f_b\) values. Varying \(S_t\) with \(f_b\) showed different regions of walking and freezing behaviour is higher \(f_b\) resulting in lower freezing fractions.

8 Discussion

A mathematical model has been developed, taking into account the CPG-based control, state-dependent proprioceptive feedback and limb mechanics. The proposed model exhibits normal gait with orbital stability, Freezing of gait (FoG) and transitions between the walking and freezing behaviour. The proposed model explains freezing from the perspective of proprioceptive feedback (Sect. 7) and has relatively lower dimensional complexity than existing detailed biophysical models such as the one by [3, 72]. The analysis of the multiple parameters of the model together with feedback strength \(f_b\) revealed the importance of individual parameters on the freezing fraction. A more detailed study of the variations in the oscillator’s time period, its stochastic nature and the variations in the phase responses of the neural system is future work.

The effect of sensory feedback on normal gait has been studied previously by several authors [4, 72, 73]. It is also hypothesised that subjects with PD show a lack of adequate feedback [21, 71]. The results in Sect. 7 articulates the role of feedback in freezing, primarily how the reduced feedback generates a lack of synchrony and consequently the FoG. The synchronisation of nonlinear systems using external inputs is well established [39]. This study, specifically the results in Sect. 6.2, reveals how the synchronisation gets induced in PD gait to avoid FoG. The results indicate that external input (I(t)) help to reduce the freezing incidences in this case for inputs of a range of frequencies (1–1.5 Hz) and amplitudes (greater than 1.2). Hence, there is potential for the use in real-life scenario with appropriate personalised adaptation of the model.

The external input models the auditory/sensory cueing in a phenomenological way, the frequency of which is vital [79]. Cueing at low and very high frequency are not considered appropriate for managing FoG [54, 79]. Moreover, an STN stimulation study by Fischer et al. [19] also shows entrainment in stepping in place for PD patients. Results in Sects. 6.1 and 6.2 indicate the plausible physiological mechanism underlying this frequency-dependent behaviour in PD. The ‘region of synchrony’ of oscillators shown in Fig. 9 is larger than the non-freezing areas shown in Fig. 10. Therefore, synchrony in CPG does not necessarily imply normal walking, and walking in humans is essentially a result of synergistic neuromechanical interaction of the limbs and CPG.