Predicting impact scenarios of a rimless wheel: a geometrical approach

Abstract

The 2D motion of a rigid rimless wheel on an inclined plane has been widely studied as a first simple case of passive walker. Usually, it is modelled as a hybrid dynamical system alternating continuous smooth phases and discrete impact ones. As in other bipedal walkers, the related research is often devoted to the analysis of cyclic motions and assumes that the spoke-ground collision is a single-point one. This work focuses exclusively on the impact problem and explores the possibility of different transitions within the impact interval (single-point to double-point collisions, dynamic jamb, stick-slide transitions and sliding reversal) as a function of the spokes angular aperture, the wheel inertia, the wheel-ground friction coefficient, and the initial conditions. This analysis is done through an innovative geometrical approach based on the Percussion Centre.

1 Introduction

The rimless wheel (RW) is probably the simplest passive walker. It has attracted the interest of many authors who have treated different realizations of it: from the simple case of the 2D motion of a rigid wheel [1, 2] or combined rigid wheels [3, 4], to the case of the 3D motion of a rigid wheel in [5, 6] or a wheel with elastoplastic legs [7, 8]. Because it is a bipedal walker, it has been used often as a toy model to study the stability and control of biped-gait in robotics and biomechanics [9,10,11,12].

From the impact point of view, the rimless wheel is equivalent to a rocking block with concave surface: both systems may exhibit single-point or double-point collisions with the ground [13,14,15,16].

The RW dynamics is hybrid: it contains continuous (non-percussive) phases (downward motion of the swing foot) and discrete (percussive) ones (collisions between feet and ground). Most researchers are mainly concerned about possible stable cyclic motions. Hence, both kinds of phases are taken into account in their studies.

During the discrete phases, the number of Degrees of Freedom (DoF) of the system may change, as the unilateral constraints between the spokes and the ground may be activated or deactivated as a result of the system dynamics.

In single-point impacts, a simple approach to study the discrete phase is the percussive one. Though deformations may play a fundamental role in such problems, there is a significant number of situations that can be treated through rigid body dynamics successfully. In that case, the configuration of the system is assumed to be constant. Within that formulation, the equations of movement become linear algebraic equations (instead of ordinary differential equations) leading to a linear algebraic solution.

Algebraic formulations exist also for multiple-point impacts [17, 18]. However, they usually imply some simplifications that may yield very unrealistic outcomes. These problems are better dealt with compliant models [19, 20].

Most studies on rimless wheels [21,22,23,24,25,26] assume that there is no sliding (sticking contact) and that the spoke-ground collision is a single-point perfectly plastic impact (as there is neither sliding nor bouncing in normal gait patterns). The forward spoke is a pivot point throughout the impact phase: the trailing spoke (backward spoke) loses ground contact at the same time instant as the forward spoke collides with the ground, and the normal velocity of that spoke just after collision $\left( {v_{{{\text{nf}}}}^{e} } \right)$ is zero (Fig. 1).

Fig. 1

Usual assumptions in wheel-ground impact: $v_{t}^{0} = v_{t}^{e} = 0,\;v_{{{\text{nb}}}}^{0} = 0,\;v_{{{\text{nf}}}}^{e} = 0$

Under those hypotheses, the solution is usually expressed through a transition equation:

$$ \left\{ {\dot{q}^{e} } \right\} = \left[ {{\text{TM}}} \right]\left\{ {\dot{q}^{0} } \right\} $$

(1.1)

where $\left\{ {\dot{q}^{0} } \right\}$ and $\left\{ {\dot{q}^{e} } \right\}$ are the vectors of initial (just before the impact) and end (just after the impact) velocities, respectively, and $\left[ {{\text{TM}}} \right]$ is the transition matrix (whose elements are constant).

However, sticking contact is not always guaranteed as it depends on the friction characteristics between the spokes and the ground. During the impact, slippage may stop or change its direction (from backward to forward) when it is initially nonzero $\left( {v_{t}^{0} \ne 0} \right)$, or may appear if it is initially zero $\left( {v_{t}^{0} = 0} \right)$. Hence, the formulation through a constant transition matrix is not always possible.

A few authors [27] do consider the possibility of slipping impacts $\left( {v_{t}^{0} > 0} \right)$ in a rimless wheel, and their evolution is treated in a straightforward way through a tangential coefficient of restitution $\left( {v_{t}^{e} = e_{t} v_{t}^{0} } \right)$ which may not always be energetically consistent.

A very complete and interesting study of the rimless wheel with 2D motion is that of Gamus and Or [28]. They cover all possible scenarios for the non-percussive phase (sticking, slipping and stick–slip transitions), and give the critical values of the ground-wheel interaction parameters leading to those behaviours. As for the impact phase (which they assume to be a single-point collision), they do consider the possibility of slipping or sticking (but not transitions between those two situations). They formulate the impact law through coefficients of restitution (CoR) and assume that both normal and tangential collisions are plastic (the Chatterjee and Ruina tangential CoR $e_{t}$ [23] is taken to be zero: the collision is totally plastic in both directions).

Among the simplifying hypotheses usually found in the literature on bipedal motion, maybe the most daring one is that of single-point collisions. Double-point collisions do happen, and treating them through restitution coefficients or simply transforming them into a sequence of single-point ones may yield erroneous results. So detecting transitions from single-point (SP) to double-point (DP) collisions is essential in order to deal with the latter properly.

For purely SP-collisions, the possible scenarios are definitely more complicated than those considered in [23]. Even if there is no initial slippage, it may appear immediately if the friction coefficient is lower than a critical value. If initial slippage is backwards, there may be sliding-reversal or a final sticking phase. If it is forwards, the slipping phase may be followed by a final sticking impact phase. In general, then, the impact may consist of more than one phase with constant dynamic characteristics (permanent sticking, permanent forward sliding, permanent backward sliding).

The main goal of this article is to predict the sequence of possible permanent-sliding-characteristics phases (PSLC phases from now on) that may occur in the percussive phase of the rimless wheel problem from the initial conditions $\left( {v_{{{\text{nb}}}}^{0} = 0,v_{{{\text{nf}}}}^{0} < 0,\;v_{t}^{0} = {\text{any}}\;{\text{value}}} \right)$ as a function of three parameters: the wheel mass distribution ($I_{G} = \lambda mL^{2}$, where m is the wheel mass, L is the spokes length and $\lambda > 0$), the angle $2\beta$ between consecutive spokes and the friction coefficient $\mu$ between ground and spokes. The material’s tangential compliance is assumed to be zero. However, if we detect the beginning of a double-point collision, the prediction does not go further, as that situation calls for a constitutive model.

The $\left( {\lambda ,\beta ,\mu } \right)$ parameters can be substituted by a different set including, for instance, the kinetic angle (related to the slenderness ratio of the object, [16]) instead of $\beta$.

We determine the critical values of parameters $\left( {\lambda ,\beta ,\mu } \right)$ marking the transitions from one behaviour to another, and draw a complete map of the $\left( {\lambda ,\mu } \right)$ plane (for a given $\beta$) that allows to follow the different possible transitions that may appear during the impact:

• single-point collision (SP) turning immediately to double-point (DP) collision: the backward spoke (that is not initially colliding with the ground as $v_{{{\text{nb}}}}^{0} = 0$) acquires an approaching normal velocity towards the ground $\left( {v_{{{\text{nb}}}} = \downarrow } \right)$.

• single-point collision (SP) phase followed by a double-point (DP) collision: the backward spoke (that is not initially colliding with the ground as $v_{{{\text{nb}}}}^{0} = 0$) acquires first a separating normal velocity $\left( {v_{{{\text{nb}}}} = \uparrow } \right)$ and then an approaching normal velocity $\left( {v_{{{\text{nb}}}} = \downarrow } \right)$ towards the ground until that spoke collides with the ground.

• dynamic jamb: the colliding spoke undergoes an increase of its normal approaching velocity; any nonzero initial tangential velocity disappears and the wheel tangential motion is blocked.

• slide-stick: an initial nonzero sliding velocity becomes zero before the collision end and never restarts.

• sliding reversal: for an initial backward sliding motion (which is not frequent but may arise as a consequence of a previous continuous phase), sliding stops and restarts in opposite direction.

We do not address the issue of the impact end: it depends on the particular values of the initial conditions. Our focus is on what possible scenarios may be visited before the impact is over according to the geometry, inertia and friction parameters. We do not solve the problem, we just explore which outcomes are possible and which will never appear.

This analysis is done through an original geometrical approach based on the dynamic concept of Percussion Centre (PC). The approach has proved to be very powerful: it has allowed us to map the complete $\left( {\lambda ,\mu } \right)$ space in terms of PSLC phases for a particular $\beta$ angle, and find the border leading to DP collisions. This map constitutes a synthetic presentation of an information that would be very laborious and cumbersome to obtain through analytical procedures.

If we detect a double-point collision, our analysis does not go further as treating that kind of problem calls for a constitutive model of the wheel-ground interaction [19, 29].

The non-percussive phase of the RW motion will not be considered at all, so nothing will be said about possible cyclic motions and their stability. Experimental validation of our predictions is also out of scope. Usual measurements in impact problems concern the initial and the end conditions. In order to validate our results, it would be necessary to measure the different PSLC phases that may appear between those two-time instants.

Instead of an experimental validation, we may compare our predictions with the results of numerical implementations of the problem. As mentioned earlier, the simulations of a rocking block in [15,16,17] could be a possibility. However, those studies on the rocking block do not cover the same range of independent parameters $\left( {\lambda ,\beta } \right)$ as the RW (as explained in Sect. 3). For that reason, we will implement a simple compliant model and integrate the dynamical equations of the RW to validate our predictions. Further comparisons with existing literature are left as future work.

The paper is organized as follows:

• Section 2 presents a complete kinematical description of the rimless wheel.

• Section 3 introduces the basic tool used in our geometrical approach: the PC half-plane, which is the half-plane where the wheel Percussion Centre evolves through the different collision phases.

• Section 4 analyses the possible transitions of the PC in that half-plane; this analysis allows to predict the conditions under which the collision is (from the very beginning) or becomes (before the impact is over) a double-point one, or those leading to dynamic jamb or to sliding transitions.

• Section 5 analyses a particular zone of the PC half-plane and illustrates that the predictions that can be drawn from that plane coincide with the results of a numerical integration (through a simple constitutive model).

• Section 6 proposes a practical guide for the use of the PC mapping.

• Section 7 concludes and proposes future work.

As a side complement, the study of the RW dynamics through the percussive version of Lagrange’s equations (which are widely used in this context) is outlined in “Appendix A”. “Appendix B” applies those equations to determine the equation of an interesting border in the PC mapping.

2 Kinematical description

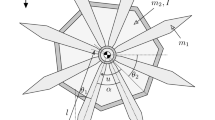
Figure 2 shows two spokes of a rimless wheel on an inclined plane. The general RW 2D motion is described by three Degrees of Freedom (DoF): the two components of the velocity of its centre of mass G $\left( {v_{x} ,v_{y} } \right)$, and the wheel angular velocity $\dot{\theta }$, all relative to the Ground Reference Frame (E). The front and the back contact points are denoted as ${\mathbf{Q}}_{{\text{f}}}$ and ${\mathbf{Q}}_{{\text{b}}}$, respectively.

Fig. 2

Kinematical description of a rimless wheel on an inclined plane (only the two spokes in contact with the ground have been represented for the sake of simplicity)

The wheel geometry is totally defined by the spokes length L and the angle $2\beta$ between consecutive spokes. If we restrict our study to single wheels with N evenly spaced spokes (so that $2\beta = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } N}} \right. \kern-\nulldelimiterspace} N}$), the maximum allowed value for $2\beta$ would be 180°, which corresponds to the two-spoked wheel (a rod colliding just through its two endpoints). In order to enlarge the study, one can consider wheels with spokes located in different parallel planes (as in [6]). In that case, $2\beta$ is not anymore the angle between neighbour spokes but between two subsequent colliding spokes.

Our study will be restricted to collisions starting with the kinematical initial conditions defined in Fig. 3$\left( {v_{{{\text{nb}}}}^{0} = 0,\;v_{{{\text{nf}}}}^{0} < 0,\;v_{t}^{0} = {\text{any}}\;{\text{value}}} \right)$. The tangential velocity $v_{t}^{0}$ may be either positive (forward sliding), negative (backward sliding) or zero. Backward sliding has been taken into account for the sake of completeness and because it does correspond to a possible (though not frequent) situation in real passive walkers. In the percussive problem (that is, during collision), the gravity force does not play any role and thus the surface inclination is irrelevant and can be considered horizontal.

Fig. 3

Initial kinematic conditions of the problem under study (a) and immediate evolution of the normal velocities $\left( {v_{{{\text{nb}}}} ,v_{{{\text{nf}}}} } \right)$ (b). Whether those four scenarios are possible has to be explored through the dynamic study of the RW

According to the system dynamic parameters (wheel-ground friction coefficient, wheel inertia and spokes aperture), different transitions may take place at the very beginning of the collision (Fig. 3):

• ${\text{d}}v_{{{\text{nb}}}} < 0$: transition to a double-point (DP) collision;

• ${\text{d}}v_{{{\text{nf}}}} < 0$: transition to dynamic jamb.

Though included in Fig. 3 (for the sake of completeness), having ${\text{d}}v_{{{\text{nb}}}}^{0} < 0$ and ${\text{d}}v_{{{\text{nf}}}}^{0} < 0$ simultaneously will be proved to be impossible in Sect. 4.

Concerning the evolution of $v_{t}^{0}$, there are many possibilities according to the signs of $v_{t}^{0}$ and ${\text{d}}v_{t}$. They will be studied in Sect. 4.

As will be proved further on, two PSLC phases (called simply “collision phases” from now on) may concatenate before the impact end in single-point (SP) collisions.

In the SP case and for each PSLC phase, let’s define the reference frame $W^{ - }$ whose motion (relative to the ground reference frame E) is that of the RW at the beginning of that phase (this is the meaning of the ‘-’script). If that initial motion is a pure translational motion relative to the ground, during the whole phase the $W^{ - }$ frame will have that translational motion even though the RW motion may start rotating during that phase. That is, the frame $W^{ - }$ and the RW are not the same: the RW motion relative to E changes during a PSLC phase, but that of the reference frame $W^{ - }$ relative to E does not (note that the superscript ‘−’ coincides with the superscript ‘0’ only for the first phase; in general, it denotes the initial condition of any PSLC phase. Similarly, ‘+’ coincides with ‘e’ for the last phase).

If we describe the kinematics of the wheel relative to $W^{ - }$, the initial velocities of the RW points are zero $\left( {v_{{W^{ - } }}^{ - } \left( {\mathbf{Q}} \right) = 0} \right)$, and their final values coincide with the incremental ones relative to E $\left( {\overline{v}_{{W^{ - } }}^{ + } \left( {\mathbf{Q}} \right) = \Delta \overline{v}_{E} \left( {\mathbf{Q}} \right)} \right)$ (Fig. 4). Those increments are the consequence of the wheel percussive dynamics.

Fig. 4

Reference frame $W^{ - }$ (where the incremental motion is a rotation about the PC) for initial conditions SP and nonzero sliding (a) and location of the PC from the incremental velocities (b)

The dynamic concept “Percussion Centre” (PC) is the key to our geometrical approach [30]. It is the wheel point J whose velocity remains unchanged throughout a single-point collision phase (or whose incremental velocity is zero). Consequently, it constitutes a permanent instantaneous centre of rotation (ICR) relative to $W^{ - }$ for each PSLC phase: the incremental motion relative to E of any wheel point Q is the consequence of the incremental rotation $\Delta \dot{\theta }$ about J:

$$ \Delta \overline{v}_{E} \left( {\mathbf{Q}} \right) = \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JQ}}}} \, {.} $$

(2.1)

In order to know the precise PC position for each PSLC phase, the wheel dynamics have to be solved, as the incremental velocities depend on the ground-wheel interaction forces during that phase.

3 The PC half-plane: the basic tool for the geometrical approach

The impulse of the percussive forces associated with the wheel-ground interaction for the case of a SP collision phase is described in Fig. 5. $P_{{\text{t}}}$ stands for the tangential percussion (or impulse) at the contact points. In a sliding phase, $\left| {P_{{\text{t}}} } \right| = \mu P_{{{\text{nf}}}}$; in non-sliding phases, $\left| {P_{{\text{t}}} } \right| < \mu P_{{{\text{nf}}}}$ (we have assumed that the kinetic and the static friction coefficients are identical as the main focus in this study is the original geometrical approach).

Fig. 5

Impulse of the percussive forces associated with the wheel-ground interaction in a single-point PSLC phase

As ${\mathbf{Q}}_{{\text{b}}}$ has an initial zero normal velocity relative to the ground in the first PSLC phase, an initial downward differential normal motion $\left( {{\text{d}}v_{{{\text{nb}}}}^{0} < 0} \right)$ will be indicative of the beginning of a DP collision. In that case, a normal percussion $P_{{{\text{nf}}}}$ should be added at point ${\mathbf{Q}}_{{\text{b}}}$. However, as our study will not include the resolution of DP collisions but just their detection, the dynamical scheme in Fig. 5 (with no percussion at ${\mathbf{Q}}_{{\text{b}}}$) is the one to be retained from now on.

The wheel dynamics may be described through the Linear Momentum Theorem (LMT) and Angular Momentum Theorem (AMT). Their integrated versions in the present case state:

$$ \begin{aligned} & {\text{LMT:}}\quad m\Delta \overline{v}_{E} \left( {\mathbf{G}} \right) = \overline{P}_{{{\text{nf}}}} + \overline{P}_{{\text{t}}} \equiv \overline{P}, \\ & {\text{AMT:}}\quad I_{G} \Delta \overline{\dot{\theta }} = \overline{{{\mathbf{GQ}}}}_{{\text{f}}} \times \overline{P}, \\ \end{aligned} $$

(3.1)

where m is the wheel mass, and $I_{G}$ is the wheel inertia moment about G (assuming that the wheel axis is a central axis of inertia). Note that $\overline{P}$ may have any value, but its direction has to lie within the friction cone.

Let’s consider that those incremental motions correspond to just one PSLC phase. Combining Eq. (3.1), we obtain:

$$ I_{G} \Delta \overline{\dot{\theta }} = m\overline{{{\mathbf{GQ}}}}_{{\text{f}}} \times \Delta \overline{v}_{E} \left( {\mathbf{G}} \right). $$

(3.2)

Using rigid body kinematics (Eq. (2.1)), Eq. (3.2) becomes:

$$ I_{G} \Delta \overline{\dot{\theta }} = m\overline{{{\mathbf{GQ}}}}_{{\text{f}}} \times \left( {\Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JG}}}} } \right). $$

(3.3)

As $\Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JG}}}}$ is perpendicular to $\Delta \overline{\dot{\theta }}$ (which in turn is perpendicular to the plane of motion) and to $\overline{{{\mathbf{JG}}}}$, the result of this cross product is contained in the plane of motion. In general, it will have two components, one parallel to $\overline{{{\mathbf{GQ}}}}_{{\text{f}}}$ (that is, to the forward spoke) and one perpendicular to it:

$$ \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JG}}}} = \left. {\Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JG}}}} } \right]_{{\parallel \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} + \left. {\Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JG}}}} } \right]_{{ \bot \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} $$

(3.4)

Only the latter is relevant in the double cross product in Eq. (3.3). Projecting $\overline{{{\mathbf{JG}}}}$ on those two directions, it is clear that only the projection of $\overline{{{\mathbf{JG}}}}$ on the direction of the forward spoke has to be taken in Eq. (3.3):

$$ \left. {\Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JG}}}} } \right]_{{ \bot \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} = \left. {\Delta \overline{\dot{\theta }} \times \left( {\left. {\overline{{{\mathbf{JG}}}} } \right]_{{\parallel \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} + \left. {\overline{{{\mathbf{JG}}}} } \right]_{{ \bot \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} } \right)} \right]_{{ \bot \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} = \Delta \overline{\dot{\theta }} \times \left( {\left. {\overline{{{\mathbf{JG}}}} } \right]_{{\parallel \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} } \right). $$

(3.5)

Hence:

$$ I_{G} \Delta \overline{\dot{\theta }} = m\overline{{{\mathbf{GQ}}}}_{{\text{f}}} \times \left( {\Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JG}}}} } \right]_{{\parallel \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} } \right) \Rightarrow \left| {\left. {\overline{{{\mathbf{JG}}}} } \right]_{{\parallel \overline{{{\mathbf{GQ}}}}_{{\text{f}}} }} } \right| = \frac{{I_{G} }}{{mL^{2} }}L \equiv \lambda L,\;{\text{to}}\;{\text{the}}\;{\text{left}}\;{\text{from}}\;{\mathbf{G}}. $$

(3.6)

Hence, J has to be located on a line perpendicular to $\overline{{{\mathbf{GQ}}}}_{{\text{f}}}$ at a distance $\lambda L$ from G (opposite to ${\mathbf{Q}}_{{\text{f}}}$). This line will be called $\lambda$-line from now on (Fig. 6). Note that, for a same $\lambda$ value, decreasing the $\beta$ value would generate a clockwise rotation of the $\lambda$-line (and a counterclockwise rotation of the backward spoke $\overline{{{\mathbf{GQ}}}}_{{\text{b}}}$).

Fig. 6

Possible PC locations (λ-line) for a given value of $\beta$ (particular case $\beta = 60^{ \circ }$) and any value and direction of the total percussion (provided it lies within the friction cone)

Figure 7 shows a set of $\lambda$-lines for a given $\beta$. As the minimum value of $\lambda$ is 0, the PC location is constrained to the grey-shadowed plane: the PC half-plane. The dimensionless inertia ratio $\lambda$ may have any non-negative value. The minimum value $\lambda = 0$ corresponds to the case where the wheel mass is concentrated at G (massless spokes), and $\lambda = 1$ corresponds to that where the wheel mass is concentrated at the spokes endpoints (for wheels contained in a circle with radius L). Cases with $\lambda > 1$ could be obtained by adding longer spokes in parallel planes in such a way that they never collide with the ground.

Fig. 7

$\lambda$-lines defining the PC half-plane for a given $\beta$. The red line corresponds to a homogeneous rocking block

This wide range of $\lambda$ values is not found in the rocking block studies, where the block is assumed to be a homogeneous rectangular plate (Fig. 8). This implies that, once its dimensions have been fixed (length of the two sides: 2a and 2b), the moment of inertia $I_{G}$ normalized to $mL^{2}$ (where L is the distance from G to the block vertices, something like the “equivalent spoke length”) is always ${1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$ (that is, our $\lambda$ parameter is ${1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$). This highly narrows the analysis of the possible behaviours. The rimless wheel may have any $\lambda$ value, independent from L and $\beta$.

Fig. 8

Equivalence between the rocking block parameters and the RW parameters

The precise position J of the PC on the $\lambda$-line can be known from the direction of the total percussion $\overline{P}$ at ${\mathbf{Q}}_{{\text{f}}}$. As $m\Delta \overline{v}_{E} \left( {\mathbf{G}} \right) = m\left( {\overline{{{\mathbf{JG}}}} \times \Delta \overline{\dot{\theta }}} \right) = \overline{P}$, the $\overline{{{\mathbf{JG}}}}$ line is perpendicular to $\overline{P}$. When the PSLC phase is a sliding one, the direction of $\overline{P}$ is well known: $\overline{P} = \overline{P}_{{{\text{nf}}}} + \overline{P}_{{\text{t}}} = \overline{P}_{{{\text{nf}}}} - \mu \left| {\overline{P}_{{{\text{nf}}}} } \right|\;{\text{sign}}\;\left( {v_{t}^{ - } } \right)$. For a given $\mu$ value, the forward sliding and the backward sliding define two lines fulfilling that condition; they will be called $\mu$-lines (Fig. 9).

Fig. 9

Possible PC locations (µ-lines) for a given value of $\mu$ (particular case $\beta = 60^{ \circ }$) for the forward (a) and backward (b) sliding cases

The information shown in Figs. 6 and 9 is gathered in Fig. 10.

Fig. 10

PC location (associated with a sliding phase) from the intersection of the corresponding $\mu$- and $\lambda$-lines. Particular case $\beta = 60^{ \circ }$

The $\lambda$-lines and the $\mu$-lines for a given $\beta$ are shown in Fig. 11. Note that, in forward-sliding phases (Fig. 11a), there are two sectors of $\mu$-lines ($\left[ {0 \le \mu \le \tan \beta } \right]$ and $\left[ {\tan \beta \le \mu \le \infty } \right]$) whereas there is a single sector $\left( {\left[ {0 \le \mu \le \infty } \right]} \right)$ in backward-sliding phases (Fig. 11b).

Fig. 11

The $\mu$-lines: possible PC locations (particular case $\beta = 60^{ \circ }$)

The case $v_{t}^{ - } = 0$, that seems to have been disregarded in the previous analysis, deserves a special treatment. The PC location is not as straightforward as in the sliding cases, and it will be analysed in the next section.

4 Analysis of the wheel dynamics through the PC half-plane

A few simple dynamical considerations lead to an interesting mapping of the PC half-plane. More precisely, we will be able to split that plane into domains according to the sign of the four incremental motions $\Delta \dot{\theta }, \, \Delta v_{t} , \, \Delta v_{{{\text{nb}}}}$ and $\Delta v_{{{\text{nf}}}}$ (in one single PSLC phase). Everything that is proved here is based on simple rigid body kinematics, relating the incremental velocity $\Delta \overline{v}$ of any wheel point S to the incremental rotation $\Delta \overline{\dot{\theta }}$ about the percussion center J: $\Delta \overline{v}\left( {\mathbf{S}} \right) = \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JS}}}}$.

4.1 Incremental rotation

The sign of $\Delta \dot{\theta }$ according to the particular PC location can be deduced from a simple dynamical consideration. As the normal percussion at a colliding point is always upwards, the incremental normal velocity of point G is always positive $\left( {\Delta v_{n} \left( G \right) > 0} \right)$, and its value is proportional to $\left| {\Delta \dot{\theta }} \right|$ through the PC distance $\left| {\rho_{G} } \right|$ to the “vertical” G-line (line orthogonal to the ground and going through G; though it is not a vertical line—it is not parallel to the Earth gravitational attraction, it will be called “vertical” line because the ground inclination can be disregarded during the impact phase): $\Delta \overline{v}_{n} \left( {\mathbf{G}} \right) = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JS}}}} } \right]_{{{\text{horiz}}}} \equiv \Delta \overline{\dot{\theta }} \times \overline{\rho }_{G}$. Consequently, if the PC is at the right-hand side of that line, the incremental $\Delta \dot{\theta }$ will be clockwise $\left( {\Delta \dot{\theta } > 0} \right)$. Conversely, $\Delta \dot{\theta }$ will be counter-clockwise $\left( {\Delta \dot{\theta } < 0} \right)$ whenever the PC is at the left-hand side of that line. A proper sign convention for $\rho_{G}$ can be defined so that $\Delta v_{n} \left( G \right) = - \rho_{G} \Delta \dot{\theta }$ (Fig. 12a).

Fig. 12

Analysis of incremental motions $\left( {\Delta \dot{\theta },\Delta v_{t} ,\Delta v_{{{\text{nb}}}} ,\Delta v_{{{\text{nf}}}} } \right)$ in the PC half-plane for SP collisions

4.2 Incremental tangential motion

Once the sign of $\Delta \dot{\theta }$ is known, the qualitative assessment of $\Delta v_{t}$ is straightforward, as it is a consequence of the rotation of the PC. Its sign depends on the $\Delta \dot{\theta }$ sign and that of the vertical coordinate y of the PC ($y > 0$ above the ground line, $y < 0$ otherwise): $\Delta \overline{v}_{t} \left( {\mathbf{G}} \right) = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JS}}}} } \right]_{{{\text{vert}}}} \equiv \Delta \overline{\dot{\theta }} \times \overline{y}$. The following analysis is done according to the information gathered in Figs. 7, 8 and 12a.

When the incremental rotation $\Delta \dot{\theta }$ is clockwise (so only the shaded area of the PC half-plane at the right-hand side of the vertical G-line can be taken into account, which corresponds just to forward sliding), the PC has to be located above the horizontal G-line; $\Delta v_{t}$ is backwards $\left( {\Delta v_{t} < 0} \right)$ and the forward sliding $\left( {v_{t}^{ - } > 0} \right)$ decreases:

$$ \Delta \overline{v}_{t} = \left. {\Delta \overline{v}\left( {{\mathbf{Q}}_{f,b} } \right)} \right]_{{{\text{horiz}}}} = \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JQ}}_{{{\text{f}},{\text{b}}}} }} = - \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{Q}}_{{{\text{f}},{\text{b}}}} {\mathbf{J}}}} = - \left( { \otimes \Delta \dot{\theta }} \right) \times \left( { \uparrow y} \right) = \leftarrow \Delta v_{t} , $$

where the arrows $\left( { \uparrow , \leftarrow } \right)$ indicate the upward vertical direction and the backward tangential direction, respectively.

When the incremental rotation $\Delta \dot{\theta }$ is counter-clockwise (shaded area of the PC half-plane at the left-hand side of the vertical G-line, which corresponds to backward sliding above the horizontal G-line, and to backward sliding otherwise):

$$ \Delta \overline{v}_{t} = \left. {\Delta \overline{v}\left( {{\mathbf{Q}}_{{{\text{f}},{\text{b}}}} } \right)} \right]_{{{\text{horiz}}}} = \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JQ}}_{{{\text{f}},{\text{b}}}} }} = - \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{Q}}_{{{\text{f}},{\text{b}}}} {\mathbf{J}}}} = - \left( { \odot \Delta \dot{\theta }} \right) \times \left( { \uparrow y} \right) = \left\{ {\begin{array}{*{20}l} {\left( { \to \Delta v_{t} } \right)} \hfill & {{\text{if}}\;y > 0} \hfill \\ {\left( { \leftarrow \Delta v_{t} } \right)} \hfill & {{\text{if}}\;y < 0} \hfill \\ \end{array} } \right. $$

Taking into account the direction of $\Delta \overline{v}_{t}$ and that of the initial sliding velocity $\overline{v}_{t}$ (backward or forward), the following conclusions can be proved:

• If the PC is located above the horizontal G-line, $\Delta v_{t}$ is forwards $\left( {\Delta v_{t} > 0} \right)$ and the backward sliding $\left( {v_{t}^{ - } < 0} \right)$ decreases (“horizontal” stands for “parallel to the ground”);

• if the PC is located between the horizontal G-line and the ground line, $\Delta v_{t} > 0$ and the forward sliding $\left( {v_{t}^{ - } > 0} \right)$ increases;

• if the PC is located under the ground line, $\Delta v_{t}$ is backwards $\left( {\Delta v_{t} < 0} \right)$ and the forward sliding $\left( {v_{t}^{ - } > 0} \right)$ decreases.

All this information is gathered in Fig. 12b. Note that a PC on the ground line implies necessarily $\Delta v_{t} = 0$ (constant $v_{t}^{ - }$). As the $\mu$-lines for the backward sliding phases never intersect the ground (Fig. 9), there will never be constant backward-sliding phases. If $v_{t}^{ - } \ne 0$, that PC on the ground is the intersection of the corresponding $\lambda$-line and $\mu$-line.

4.3 Normal incremental motion

The sign of $\Delta v_{{{\text{nb}}}}$ and $\Delta v_{{{\text{nf}}}}$ is obtained in a similar way through rigid body kinematics:

$$ \Delta \overline{v}\left( {{\mathbf{Q}}_{{{\text{f}},{\text{b}}}} } \right) = \Delta \overline{\dot{\theta }} \times \overline{{{\mathbf{JQ}}_{{{\text{f}},{\text{b}}}} }} \Rightarrow \Delta \overline{v}_{{{\text{nf}},{\text{nb}}}} = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JQ}}_{{{\text{f}},{\text{b}}}} }} } \right]_{{{\text{horiz}}}} . $$

Let’s introduce a coordinate $\overline{\rho }_{{{\text{f}},{\text{b}}}} \equiv \left. {\overline{{{\mathbf{JQ}}_{{{\text{f}},{\text{b}}}} }} } \right]_{{{\text{horiz}}}}$ with the following sign criterion: $\rho_{f,b} > 0$ whenever the percussion center J is located at the left-hand side of the corresponding contact point ${\mathbf{Q}}_{{{\text{f}},{\text{b}}}}$, $\rho_{f,b} < 0$ otherwise.

The evolution of the ${\mathbf{Q}}_{{\text{f}}}$ normal velocity depends both on the rotation sign and that of the $\rho_{f}$ coordinate:

• If the PC is located between the vertical G-line and the vertical ${\mathbf{Q}}_{{\text{f}}}$-line $\left( {\rho_{f} > 0} \right)$, the incremental rotation is always clockwise and $\Delta v_{{{\text{nf}}}}$ is downwards: $\Delta \overline{v}_{{{\text{nf}}}} = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JQ}}_{{\text{f}}} }} } \right]_{{{\text{horiz}}}} = \left( { \otimes \dot{\theta }} \right) \times \left( { \to \rho_{f} } \right) = \downarrow \Delta v_{{{\text{nf}}}}$. The wheel undergoes dynamic jamb.

• If the PC is located on the right-hand side the vertical ${\mathbf{Q}}_{{\text{f}}}$-line $\left( {\rho_{f} < 0} \right)$, the incremental rotation is also clockwise and $\Delta v_{{{\text{nf}}}}$ is upwards: $\Delta \overline{v}_{{{\text{nf}}}} = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JQ}}_{{\text{f}}} }} } \right]_{{{\text{horiz}}}} = \left( { \otimes \dot{\theta }} \right) \times \left( { \leftarrow \rho_{f} } \right) = \uparrow \Delta v_{{{\text{nf}}}}$.

• If the PC is located on the left-hand side the vertical G-line $\left( {\rho_{f} < 0} \right)$, the incremental rotation is counterclockwise and $\Delta v_{{{\text{nf}}}}$ is also upwards: $\Delta \overline{v}_{{{\text{nf}}}} = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JQ}}_{{\text{f}}} }} } \right]_{{{\text{horiz}}}} = \left( { \odot \dot{\theta }} \right) \times \left( { \to \rho_{f} } \right) = \uparrow \Delta v_{{{\text{nf}}}}$.

These conclusions are gathered in Fig. 12c.

The evolution of the ${\mathbf{Q}}_{{\text{b}}}$ normal velocity is shown in Fig. 12d, and can be obtained in a similar way:

• If the PC is located between the vertical G-line and the vertical ${\mathbf{Q}}_{{\text{b}}}$-line $\left( {\rho_{b} < 0} \right)$, the incremental rotation is always counterclockwise and $\Delta v_{{{\text{nb}}}}$ is downwards: $\Delta \overline{v}_{{{\text{nb}}}} = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JQ}}_{{\text{b}}} }} } \right]_{{{\text{horiz}}}} = \left( { \odot \dot{\theta }} \right) \times \left( { \leftarrow \rho_{b} } \right) = \downarrow \Delta v_{{{\text{nb}}}}$. If that PC corresponds to the first collision phase $\left( {v_{{{\text{nb}}}}^{0} = 0} \right)$, that phase is a DP one.

• If the PC is located at the left-hand side the vertical ${\mathbf{Q}}_{{\text{b}}}$-line $\left( {\rho_{b} > 0} \right)$, the incremental rotation is also counterclockwise and $\Delta v_{{{\text{nf}}}}$ is upwards: $\Delta \overline{v}_{{{\text{nb}}}} = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JQ}}_{{\text{b}}} }} } \right]_{{{\text{horiz}}}} = \left( { \odot \dot{\theta }} \right) \times \left( { \to \rho_{f} } \right) = \uparrow \Delta v_{{{\text{nb}}}}$.

• If the PC is located at the right-hand side the vertical G-line $\left( {\rho_{b} < 0} \right)$, the incremental rotation is clockwise and $\Delta v_{{{\text{nb}}}}$ is also upwards: $\Delta \overline{v}_{{{\text{nb}}}} = \Delta \overline{\dot{\theta }} \times \left. {\overline{{{\mathbf{JQ}}_{{\text{b}}} }} } \right]_{{{\text{horiz}}}} = \left( { \otimes \dot{\theta }} \right) \times \left( { \leftarrow \rho_{b} } \right) = \uparrow \Delta v_{{{\text{nb}}}}$.

4.4 Critical friction coefficient

From the PC location, we can also deduce the existence of a critical value of the friction coefficient $\mu_{{\text{c}}}$ (in SP collisions) guaranteeing that an initial forward sliding $\left( {v_{t}^{ - } > 0} \right)$ is kept constant throughout the collision phase (that is, $\Delta v_{t} = 0$). According to the previous analysis of the PC half-plane, this calls for a PC on the ground level: it is the intersection point J between the ground line and the $\lambda$-line corresponding to the particular wheel under study.

That critical value $\mu_{{\text{c}}}$ can be obtained analytically (see “Appendix A”), but it can be fully determined through geometric considerations from Fig. 13:

$$ \mu_{{\text{c}}} = \frac{\sin \beta \cos \beta }{{\lambda + \cos^{2} \beta }} \, {.} $$

(4.1)

Fig. 13

Geometrical determination of $\mu_{c}$ from the location of the PC that corresponds to $\Delta v_{t} = 0$

4.5 Predicting collision phases from the PC half-plane mapping

The exploration of the PC half-plane allows to predict whether there will be just one collision phase or two, and their characteristics from the initial conditions $\left( {v_{{{\text{nb}}}}^{0} = 0,\;v_{{{\text{nf}}}}^{0} < 0,\;v_{t}^{0} \ne 0} \right)$ according to the PC location. For a SP collision and a given $\left( {\lambda ,\beta } \right)$ pair, Figs. 14, 15 and 16 present the PC possible transitions for $\mu = \mu_{{\text{c}}} ,\;\mu < \mu_{{\text{c}}}$ and $\mu > \mu_{{\text{c}}}$, respectively. The analysis of each case is based on the incremental motions presented in Fig. 12 (where no particular $\mu$ value was assumed).

Fig. 14

Analysis of the PC transition for $\mu = \mu_{c}$

Fig. 15

Analysis of the PC transition for $\mu < \mu_{c}$

Fig. 16

Analysis of the PC transition for $\mu > \mu_{c}$

For $\mu = \mu_{{\text{c}}}$, if the initial sliding velocity is forwards, ($v_{t}^{0} > 0$, Fig. 14a), as the PC of the first phase $\left( {\left. {{\text{PC}}} \right]_{{1{\text{st}}}} } \right)$ is located on the ground line, the sliding velocity is constant, and the collision has just one phase. That PC is called critical PC $- {\text{PC}}_{{\text{c}}} -$ from now on. However, if the initial sliding velocity is backwards $\left( {v_{t}^{0} < 0} \right)$, as the first PC (called conjugated critical PC $- {\text{PC}}_{{\text{c}}}^{\prime } -$ from now on) lies above the level of G in a domain where $\Delta v_{t}$ is forwards $\left( {\Delta v_{t} > 0} \right)$, $v_{t}^{0}$ decreases (Fig. 14b). If the collision is over before sliding stops (which may happen for low $v_{{{\text{nf}}}}^{0}$ values), it is a one-phase collision. Otherwise, the PC jumps along the $\lambda$-line to the ground line and a non-sliding second phase follows.

For the cases shown in Fig. 15a, b $\left( {\mu < \mu_{{\text{c}}} } \right)$, the friction cone is narrower than the critical one. If the initial sliding is forwards ($v_{t}^{0} > 0$, Fig. 15a), as the PC lies between the ground line and the level of G, in a domain where $\Delta v_{t}$ is forwards $\left( {\Delta v_{t} > 0} \right)$, the sliding will increase permanently until the end of the collision, and the collision will have just one phase. If it is backwards ($v_{t}^{0} < 0$, Fig. 15b), as the PC lies above the level of G in a domain where $\Delta v_{t}$ is also forwards $\left( {\Delta v_{t} > 0} \right)$, the sliding decreases. If the collision is over before sliding stops (which may happen for low $v_{{{\text{nf}}}}^{0}$ values), it is a one-phase collision. Otherwise, the PC jumps along the $\lambda$-line to a new position in a domain where $\Delta v_{t}$ is still forwards $\left( {\Delta v_{t} > 0} \right)$ (Fig. 15b), and sliding restarts in the opposite direction (“sliding reversal”, $\left. {v_{t}^{ + } } \right]_{{{\text{1st}}\;{\text{phase}}}} = \left. {v_{t}^{ - } } \right]_{{{\text{2nd}}\;{\text{phase}}}} > 0$).

Finally, the case $\mu > \mu_{{\text{c}}}$ (for both forward and backward initial sliding velocity $v_{t}^{0}$) is shown in Fig. 16a, b, respectively. The friction cone is larger than the critical one, and thus the initial sliding $v_{t}^{0}$ will decrease throughout the collision $\left( {{\text{sign}}\left( {\Delta v_{t} } \right) = - {\text{sign}}\left( {v_{t}^{0} } \right)} \right)$. If it reaches the zero value within the collision interval, sliding will not restart as the required percussion to keep that value lies within the cone. The collision may be a one-phase collision (if it is over before zero sliding is attained) or a two-phase collision. For $\mu > \tan \beta$, if the PC lies in the jamb area, sliding stops necessarily before the collision end $\left( {\left. {v_{t}^{ + } } \right]_{{{\text{1st}}\;{\text{phase}}}} = \left. {v_{t}^{ - } } \right]_{{{\text{2nd}}\;{\text{phase}}}} = 0} \right)$, and a non-sliding second phase follows. If it does not lie in the jamb area, there may be one or two collision phases.

The particular case $v_{t}^{0} = 0$ is analysed in Fig. 17. As for the smooth case $\left( {\mu = 0} \right)$ there is only normal percussion at ${\mathbf{Q}}_{{\text{f}}}$, the $\mu$-line is the horizontal G-line (Fig. 17a), and the PC is at the left-hand side of the G-vertical-line. Hence, the immediate evolution of the rotation $\left( {{\text{d}}\dot{\theta }} \right)$ is counterclockwise, thus generating an immediate forward sliding $\left( {{\text{d}}v_{t} > 0} \right)$.

Fig. 17

Analysis of the PC immediate evolution when $v_{t}^{0} = 0$

For $0 < \mu < \mu_{{\text{c}}}$ (Fig. 17b), the tendency of ${\mathbf{Q}}_{{\text{f}}}$ to forward sliding originates a backward tangential percussion ${\text{d}}P_{{\text{t}}}$ at ${\mathbf{Q}}_{f}$. However, as $\mu < \mu_{{\text{c}}}$, the maximum possible value ${\text{d}}P_{{\text{t}}} = \mu {\text{d}}P_{n}$ is not enough to stop that tendency (as seen in Fig. 15), and sliding starts. As the PC is now between the horizontal G-line and the ground, the ${{{\text{d}}v_{t} } \mathord{\left/ {\vphantom {{{\text{d}}v_{t} } {{\text{d}}P_{{{\text{nf}}}} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}P_{{{\text{nf}}}} }}$ rate is lower than that corresponding to $\mu = 0$.

If $\mu = \mu_{{\text{c}}}$, the PC reaches the ground line, the sliding tendency at ${\mathbf{Q}}_{{\text{f}}}$ disappears $\left( {{\text{d}}v_{t} = 0} \right)$: sliding does not start (sticking phase).

If $\mu > \mu_{{\text{c}}}$, as the value of the required backward tangential percussion at ${\mathbf{Q}}_{{\text{f}}}$ to prevent sliding is ${\text{d}}P_{{\text{t}}} = \mu_{{\text{c}}} {\text{d}}P_{n}$ and it is lower than $\mu {\text{d}}P_{n}$ (that is, the total percussion at ${\mathbf{Q}}_{{\text{f}}}$ lies within the friction cone), the PC is located on the ground line, and sliding does not start.

In all cases, the collision has just one phase.

All the preceding analyses are summarized in Fig. 18. Only PCs located between the critical one (${\text{PC}}_{{\text{c}}}$, on the ground line) and the conjugated one (${\text{PC}}_{{\text{c}}}^{\prime }$, above the horizontal G-line) may yield sliding reversal. As proved in “Appendix B”, the “horizontal” and “vertical” coordinates $\left( {x_{c}^{\prime } ,y_{c}^{\prime } } \right)$ of those ${\text{PC}}_{{\text{c}}}^{\prime }$ (where the coordinates origin is the wheel center of inertia G) fulfil the equation:

$$ y_{c}^{\prime 2} - y_{c}^{\prime } x_{c}^{\prime } \tan \beta + L\left( {y_{c}^{\prime } \cos \beta + x_{c}^{\prime } \sin \beta } \right) = 0. $$

(4.2)

Fig. 18

Hyperbola containing the conjugated critical PCs for different $\lambda$ values

That is, the line containing the critical ${\text{PC}}_{{\text{c}}}^{\prime }$ for different $\lambda$ values (and a same spokes aperture $2\beta$) is a hyperbola with a horizontal asymptote located at a distance $\left( {L\cos \beta } \right)$ above the horizontal G-line.

PCs located in the area between the hyperbola and the horizontal G-line may yield sliding reversal, and PCs located between the horizontal G-line and the ground yield a one-phase collision with increasing forward sliding. For PCs outside those areas, if sliding stops it does not restart, and a non-sliding second phase follows. PCs located in the DP area have been omitted (if they correspond to the first phase, they correspond to DP collisions; if they correspond to the second phase, the collision could evolve to a DP one, as will be analysed in Sect. 5).

5 The particular case of SP collisions evolving to a DP phase

A complete mapping of the PC half-plane for $\beta = 60^{ \circ } ,45^{ \circ } ,30^{ \circ }$ is shown in Fig. 19. All the previous conclusions regarding SP/DP collision and dynamic jamb (Fig. 12c,d), evolution of the sliding velocity (Fig. 12b) and hyperbola of conjugated critical PCs (Fig. 18) have been gathered in that figure. Any location of the $\left. {{\text{PC}}} \right]_{{1{\text{st}}}}$ (excluding the DP area) indicates an initial SP collision phase whose evolution depends on the specific PC location.

Fig. 19

The complete mapping of the PC half-plane and definition of the SP-DP area: a $\beta = 60^{ \circ }$ (with SP-DP area); b $\beta = 45^{ \circ }$(threshold); c $\beta = 30^{ \circ }$ (no SP-DP area)

Interesting new information in Fig. 19a concerns the possible scenarios if the $\left. {{\text{PC}}} \right]_{{1{\text{st}}}}$ lies in the area between the $\lambda$-line through G (which corresponds to $\lambda = 0$) and the $\lambda$-line through ${\mathbf{Q}}_{{\text{b}}}$ (${\mathbf{Q}}_{{\text{b}}} - \lambda$-line), but excluding the DP zone (SP-DP area from now on). Note that the existence of the SP-DP area depends on the $\beta$ value. Figure 19b shows the limiting case $\beta = 45^{ \circ }$: the ${\mathbf{Q}}_{{\text{b}}} - \lambda$-line coincides with the $\left( {\lambda = 0} \right)$-line. For values $\beta < 45^{o}$ (Fig. 19c), there is no ${\mathbf{Q}}_{{\text{b}}} - \lambda$-line as the $\left( {\lambda = 0} \right)$-line intersects the ground at the left-hand side of ${\mathbf{Q}}_{{\text{b}}}$. If we are dealing with wheels with evenly distributed spokes, the cases where DP phases never happen (after a first SP phase) correspond to wheels with no less than 4 spokes. To our knowledge, all studies on RW found in the literature correspond to $\beta \le 45^{ \circ }$, hence the hypothesis of an initial SP phase not followed by a DP phase is always right.

If the $\left. {{\text{PC}}} \right]_{{1{\text{st}}}}$ is outside the DP and the SP-DP areas, the collision (which may have one or two phases, but no more than two) is a SP one until the end (as $\Delta v_{{{\text{nb}}}} \ge 0$).

If the $\left. {{\text{PC}}} \right]_{{1{\text{st}}}}$ is in the SP-DP area, there are two possible situations (Fig. 20):

• $\left. {{\text{PC}}} \right]_{{1{\text{st}}}}$ in the jamb area (as point B in Fig. 20a): initially $\Delta v_{{{\text{nf}}}} < 0$, and the sliding will necessarily stop before the collision end. The second SP phase may evolve into a DP one as $\Delta v_{{{\text{nb}}}} < 0$ from its very beginning.

• $\left. {{\text{PC}}} \right]_{{1{\text{st}}}}$ outside the jamb area (as point A in Fig. 20a): in this case, $\Delta v_{{{\text{nf}}}} > 0$ and the sliding may or may not stop before the collision end. If the collision is over when $v_{t} \ne 0$, it is a one-phase SP collision. However, if $v_{t} = 0$ before the collision end (as for the previous case, where the PC was located in the jamb area), the collision may evolve to a DP one in the second phase because $\Delta v_{{{\text{nb}}}} < 0$.

Fig. 20

PC evolution when initially located in the SP-DP area

Shifting to a constitutive model to study a DP collision implies taking into account the infinitesimal normal displacements of the colliding points $\left( {\delta_{{{\text{nf}}}} ,\delta_{{{\text{nb}}}} } \right)$. For an initial SP collision with $\Delta v_{{{\text{nb}}}} > 0$, the ${\mathbf{Q}}_{{\text{b}}}$ normal displacement during the first phase is upwards $\left( {\delta_{{{\text{nb}}}} > 0} \right)$, so that point will not be touching the ground when the initial sliding stops. Consequently, the second phase will still be a SP one until that displacement becomes zero. If the collision is over before this happens, the whole problem will be a two-phase SP collision. However, if $\delta_{{{\text{nb}}}} = 0$ before the collision end, there will be a DP phase.

We have implemented a simple constitutive model (for the behaviour in the normal direction) to corroborate the previous analysis. The results of the integration have been compared to the qualitative predictions done from the PC half-plane.

The constitutive model is a linear bi-stiffness one (with no permanent indentation), which is a simple and frequently used dissipative model [19].

The interaction between the colliding surfaces is formulated through a parallel association of a spring—whose repulsion force $F_{{{\text{spring}}}}$ is proportional to the normal deformation $\delta_{n}$–, and a dry-friction damper whose force is proportional to $F_{{{\text{spring}}}}$ through a friction coefficient $\mu_{n} < 1$: $\left| {F_{{{\text{fric}}}} } \right| = \mu_{n} F_{{{\text{spring}}}}$ (Fig. 21). Hence, the normal repulsion force is defined by two stiffness functions:

$$ \begin{aligned} & {\text{compression}}\;{\text{phase:}}\quad F_{n}^{{{\text{comp}}}} = k\left( {1 + \mu_{n} } \right)\delta_{n} { ,} \\ & {\text{expansion}}\;{\text{phase:}}\quad F_{n}^{{{\text{exp}}}} = k\left( {1 - \mu_{n} } \right)\delta_{n} \, {.} \\ \end{aligned} $$

(5.1)

Fig. 21

Linear bi-stiffness model

In the application example, the wheel parameters are $\lambda = 0.25,\;\beta = 60^{ \circ }$, the value of the tangential friction coefficient $\mu$ has been set to 2.9, and the parameters of the bi-stiffness model are $k = 1\;{\text{kN}}/{\text{m,}}\;\mu_{n} = 0.2$. The initial conditions are $v_{t}^{0} = 0.5\;{\text{m}}/{\text{s}}$(initial forward sliding) and $\delta_{{{\text{nb}}}}^{0} = \delta_{{{\text{nf}}}}^{0} = 0{, }v_{{{\text{nb}}}}^{0} = 0{, }v_{{{\text{nf}}}}^{0} = - 1\;{\text{m}}/{\text{s}}$. Thus, the $\left. {{\text{PC}}} \right]_{{1{\text{st}}}}$ location is qualitatively as that of point B in Fig. 19. According to what has been said for that initial PC, we should have jamb in the first phase (that is, $\Delta v_{{{\text{nf}}}} < 0$), and the sliding would have to stop before the collision end. Moreover, the second SP phase might evolve into a DP one as $\Delta v_{{{\text{nb}}}} < 0$.

The results are shown in Fig. 22. There is a first phase with $\Delta v_{t} < 0, \, \Delta v_{{{\text{nf}}}} < 0, \, \Delta v_{{{\text{nb}}}} > 0$: SP collision with decreasing sliding and jamb at point ${\mathbf{Q}}_{{\text{f}}}$ while point ${\mathbf{Q}}_{{\text{b}}}$ separates from the ground (orange-shadowed zone, $\delta_{{{\text{nb}}}} > 0$). When sliding stops, a second phase appears with $\Delta v_{{{\text{nf}}}} > 0,\;\Delta v_{{{\text{nb}}}} < 0$. Initially, there is compression at ${\mathbf{Q}}_{{\text{f}}}$, but then expansion at that point starts while ${\mathbf{Q}}_{{\text{b}}}$ moves towards the ground. When the latter reaches the ground $\left( {\delta_{{{\text{nb}}}} = 0} \right)$, the expansion at ${\mathbf{Q}}_{{\text{f}}}$ is still going on, and DP phase starts (grey-shadowed zone). The constitutive model allows us to go further and discover that the end of that DP phase is associated with the loss of ground contact at ${\mathbf{Q}}_{{\text{f}}}$ (though not at ${\mathbf{Q}}_{{\text{b}}}$). All this is exactly what has been predicted through the PC plane.

Fig. 22

Time evolution of velocities (left) and normal deformations (right) from the integration of the linear bi-stiffness model. The grey-shadowed zone corresponds to a DP phase

6 Prediction through the PC mapping: a synthesis

As mentioned earlier, backward sliding is not a usual initial condition (though it is possible) when studying passive walkers. Therefore, the PC mapping may be simplified in general by eliminating the upper left quadrant (which includes the sliding-reversal region). Actually, just a few lines have to be drawn in order to predict the possible phases during the impact:

• the horizontal and the vertical G-lines;

• the vertical lines through ${\mathbf{Q}}_{{\text{b}}}$ and ${\mathbf{Q}}_{{\text{f}}}$, which define the boundaries of the DP and the jamb domains;

• the $\left( {\lambda = 0} \right)$-line (perpendicular to the front spoke and going through G);

• the $\left( {\lambda = 1} \right)$-line (perpendicular to the front spoke and at a distance L from G);

• the $\lambda$-line corresponding to the particular RW under study (perpendicular to the front spoke and at a distance $\lambda L$ from G; the PC may evolve exclusively on that line).

• the $\mu_{{\text{c}}}$-line corresponding to the particular lambda value of the RW under study.

The intersection between the $\lambda$-line and the forward $\mu$-line (for $0 < \mu < \mu_{{\text{c}}}$), or between the $\lambda$-line and the ground line (when $\mu > \mu_{c}$ and $v_{t}^{0} = 0$), gives the PC location of the first collision phase, and from that one can proceed to the prediction of possible collision phases.

The simplified PC mapping for $\beta = 60^{ \circ }$ and $\lambda = 0.625$ is shown in Fig. 23. According to the particular $\mu$ value, the possible evolutions of the initial forward-sliding phase can be inferred from that figure.

• $0 < \mu < \mu_{{{\text{DP}}}} \left( { = 0.3} \right)$: the PC is located in the DP domain, between points A and B, and a constitutive law is needed from the very beginning;

• $\mu_{{{\text{DP}}}} < \mu < \mu_{{\text{c}}} \left( { = 0.49} \right)$: the PC is located in the SP subdomain between points B and ${\text{PC}}_{{\text{c}}}$ where sliding increases, so it will be a one-phase collision;

• $\mu = \mu_{{\text{c}}}$: the PC coincides with the critical one $\left( {{\text{PC}}_{{\text{c}}} } \right)$, and sliding is constant throughout the phase;

• $\mu_{{\text{c}}} < \mu < \tan \beta \left( { = 1.73} \right)$: the PC location is below the ground (as point C, for instance), and sliding decreases; if it stops before the collision is over, the PC jumps to ${\text{PC}}_{{\text{c}}}$, and the second collision phase is a non-sliding one;

• $\mu = \tan \beta$: the PC is located at $\infty$ on the blue line and sliding decreases; as just mentioned, it may be a two-phase collision with a second PC located at ${\text{PC}}_{{\text{c}}}$;

• $\tan \beta < \mu < \mu_{j} \left( { = 3.18} \right)$: the PC location is on the right-hand side of the vertical line through ${\mathbf{Q}}_{{\text{f}}}$ (as point D, for instance), and sliding decreases; again, possible two-phase collision with a second PC located at ${\text{PC}}_{{\text{c}}}$;

• $\mu_{j} < \mu < \infty$: the PC is located in the jamb domain, between points E and F; sliding will necessarily stop, the PC will jump to ${\text{PC}}_{{\text{c}}}$ and the second collision phase will be a non-sliding one.

Fig. 23

Simplified PC mapping for $\beta = 60^{ \circ }$ and $\lambda = 0.625$

If the initial sliding velocity is zero, the preceding statements hold whenever $\mu < \mu_{{\text{c}}}$. However, if $\mu \ge \mu_{{\text{c}}}$, there is only one sticking phase.

For $\beta = 60^{ \circ }$, the collision process is extremely sensitive to small perturbations of the $\lambda$ value around 0.5. For the present case, $\lambda$ is slightly above 0.5, therefore ${\text{PC}}_{{\text{c}}}$ is in the SP domain.

As mentioned in Sect. 3, decreasing the $\beta$ value generates a counterclockwise rotation of the ${\mathbf{GQ}}_{{\text{b}}}$ spoke and a clockwise rotation of the $\lambda$-lines, and consequently an initial narrowing of the AB segment shown in Fig. 23 (which contains all the initial PC leading to a DP phase). For any given $\lambda$ value, there exists a critical $\beta_{DP}$ for which the AB segment has zero length: the $\lambda$-line goes through the intersection of the vertical ${\mathbf{Q}}_{{\text{b}}}$-line with the horizontal G-line. For $\beta < \beta_{{{\text{DP}}}}$ no DP phase may exist (if the initial sliding is zero or downwards).

The critical $\beta_{{{\text{DP}}}}$ can be obtained geometrically from the simplified PC mapping by imposing that the intersection between the $\lambda$-line and the horizontal G-line (point A) lies on the left border of the DP zone.

In a rimless wheel with evenly-distributed spokes, the spokes aperture is $2\beta = 360^{ \circ } /n$ (with $n = 1,2,3 \ldots$), and $\beta_{{{\text{DP}}}}$ may not correspond to a possible $\beta$ value. However, this is not the case in rocking blocks: $\beta$ is related to the slenderness ratio $\left( {{a \mathord{\left/ {\vphantom {a b}} \right. \kern-\nulldelimiterspace} b}} \right)$, hence it may take any value between 0 and $90^{ \circ }$.

The simplified PC mapping for a rocking block ($\lambda = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$) is shown in Fig. 24. The preceding analysis has been applied to determine the critical $\beta$ value: $\beta_{{{\text{DP}}}} = 35.26^{ \circ }$, hence $\left( {{a \mathord{\left/ {\vphantom {a b}} \right. \kern-\nulldelimiterspace} b}} \right)_{{{\text{DP}}}} = {1 \mathord{\left/ {\vphantom {1 {\tan \beta_{{{\text{DP}}}} }}} \right. \kern-\nulldelimiterspace} {\tan \beta_{{{\text{DP}}}} }} = \sqrt 2$.

Fig. 24

Simplified PC mapping for a rocking block $\left( {\lambda = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}} \right)$ with $\beta_{{{\text{DP}}}} = 35.26^{ \circ }$

7 Conclusions

We have developed a thorough analysis of the possible evolutions of the impact phases of a rimless wheel with 2D motion. The wheel dynamics have been treated through a geometrical approach based on the concept of Percussion Centre (PC). The main tool has been the PC half-plane, which has been totally parameterized according to two dynamic parameters (related to the wheel inertia and to the ground-wheel friction).

For purely SP collisions, the geometrical approach has allowed to predict the possible different collision phases (where phase stands for permanent sliding characteristics: no sliding, forward sliding or backward sliding). We have proved that there is a variety of situations that can be encountered when the front spoke strikes the ground: dynamic jamb (self-locking process), slide-stick transition, sliding reversal, initial double-point (DP) collisions, and single-point (SP) collisions turning to DP ones.

For cases where a DP phase is detected (either as first phase or developing after one or two SP phases), our geometrical analysis cannot go further unless a constitutive model of the wheel-ground interaction is used.

We have implemented a bi-stiffness constitutive model (for the behaviour in the normal direction) to corroborate the qualitative predictions done from the PC half-plane. The results have been totally consistent.

Future work will deal with the comparison of our predicted scenarios with existing literature on bouncing dimers and rocking blocks, and the search for cyclic motion of the rimless wheel in the wider scenario considered in this paper, including the study of the DP collisions.

Appendices

Appendix A: Analysis of the wheel dynamics through Lagrange’s equations

For every phase in the collision process, Lagrange’s equations (in percussive version) yield the relationship between the percussions associated to the contact forces and the incremental values of the DoF. For a SP-collision phase, those equations are:

$$ \left[ M \right]\left\{ {\Delta \dot{q}} \right\} = \left[ {A^{{{\text{nf}}}} } \right]^{T} P_{{{\text{nf}}}} - \left[ {A^{t} } \right]^{T} P_{{\text{t}}} {,} $$

(A.1)

where matrices $\left[ {A^{{{\text{nf}}}} } \right]\;{\text{and}}\;\left[ {A^{t} } \right]$ are the first and last row of the Jacobian matrix [J]:

$$ \left\{ {\begin{array}{*{20}c} {v_{{{\text{nf}}}} } \\ {v_{{{\text{nb}}}} } \\ {v_{t} } \\ \end{array} } \right\} = \left[ J \right]\left\{ {\begin{array}{*{20}c} {v_{x} } \\ {v_{y} } \\ {\dot{\theta }} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 1 & { - L\sin \beta } \\ 0 & 1 & { + L\sin \beta } \\ 1 & 0 & { - L\cos \beta } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {v_{x} } \\ {v_{y} } \\ {\dot{\theta }} \\ \end{array} } \right\} \equiv \left[ {\begin{array}{*{20}c} {A^{{{\text{nf}}}} } \\ {A^{{{\text{nb}}}} } \\ {A^{t} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {v_{x} } \\ {v_{y} } \\ {\dot{\theta }} \\ \end{array} } \right\}{ ,} $$

(A.2)

and $\left[ M \right]$ is the mass matrix:

$$ \left[ M \right] = \left[ {\begin{array}{*{20}c} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & {I_{G} } \\ \end{array} } \right], $$

(A.3)

where m is the wheel mass and $I_{G} \left( { \equiv \lambda mL^{2} } \right)$ is its inertia momentum about its centre of mass G.

The relationship between $\left( {\Delta v_{{{\text{nf}}}} , \, \Delta v_{{{\text{nb}}}} , \, \Delta v_{t} } \right)$ and the percussions of the impulsive forces can be obtained combining Eqs. (A.1) and (A.2):

$$ \begin{aligned} & \left( {\text{a}} \right)\quad \frac{{\lambda m\Delta v_{{{\text{nf}}}} }}{{P_{{{\text{nf}}}} }} = \lambda + \sin^{2} \beta + \kappa \sin \beta \cos \beta {,} \\ & \left( {\text{b}} \right)\quad \frac{{\lambda m\Delta v_{{{\text{nb}}}} }}{{P_{{{\text{nf}}}} }} = \lambda - \sin^{2} \beta - \kappa \sin \beta \cos \beta {,} \\ & \left( {\text{c}} \right)\quad \frac{{\lambda m\Delta v_{t} }}{{P_{{{\text{nf}}}} }} = \sin \beta \cos \beta + \kappa \left( {\lambda + \cos^{2} \beta } \right){,} \\ \end{aligned} $$

(A.4)

where $\kappa = - P_{{\text{t}}} /P_{{{\text{nf}}}}$.

Equation (A.4) hold for every SP phase, and allow a full exploration of the $\left( {\lambda ,\kappa } \right)$ parameters yielding the different possible outcomes of the first collision phase.

For a given $\beta$ value and a nonzero sliding velocity (so $\kappa = \pm \mu$), the condition on the $\left( {\lambda ,\mu } \right)$ parameters to have an initial DP phase (which corresponds to $\Delta v_{{{\text{nb}}}} < 0$) are readily obtained from Eq. (A.4b):

• initial forward sliding: DP collision if $\lambda < \left( {1 - \left( {{\mu \mathord{\left/ {\vphantom {\mu {\tan \beta }}} \right. \kern-\nulldelimiterspace} {\tan \beta }}} \right)} \right)\sin^{2} \beta$ and $\mu < \tan \beta$ (as $\lambda$ has to be positive),

• initial backward sliding: DP collision if $\lambda < \left( {1 + \left( {{\mu \mathord{\left/ {\vphantom {\mu {\tan \beta }}} \right. \kern-\nulldelimiterspace} {\tan \beta }}} \right)} \right)\sin^{2} \beta$ (for any $\mu$ value).

The evolution of $v_{t}$ from $v_{t}^{0}$ can be studied through Eq. (A.4c). As $\left( {0 < \beta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)$, $\Delta v_{t} > 0$ whenever the initial phase is a backward-sliding one $\left( {v_{t}^{0} < 0, \, \kappa = \mu } \right)$. However, the evolution is not unique for a forward-sliding initial phase $\left( {v_{t}^{0} > 0, \, \kappa = - \mu } \right)$: for every particular value of $\lambda$, there is a critical value of $\mu$ over which the sliding decreases $\left( {\Delta v_{t} < 0} \right)$, and under which it increases $\left( {\Delta v_{t} > 0} \right)$:

$$ \mu_{{\text{c}}} = \frac{\sin \beta \cos \beta }{{\lambda + \cos^{2} \beta }} \Rightarrow \left\{ \begin{gathered} \mu > \mu_{{\text{c}}} \Rightarrow \Delta v_{t} < 0 \hfill \\ \mu < \mu_{{\text{c}}} \Rightarrow \Delta v_{t} \ge 0 \hfill \\ \end{gathered} \right.. $$

(A.5)

For $\mu = \mu_{{\text{c}}}$, forward sliding remains constant.

Imposing $\Delta v_{{{\text{nf}}}} = 0$ on Eq. (A.4a), we obtain a threshold value of $\mu$ over which jamb appears for the case of initial forward sliding:

$$ \mu > \frac{{\lambda + \sin^{2} \beta }}{\sin \beta \cos \beta } \, {.} $$

(A.6)

Combining those results to obtain the conditions on $\left( {\lambda ,\mu } \right)$ leading to different initial phases (as SP with $\Delta v_{t} > 0$, or SP with $\Delta v_{t} = 0$, or DP with $\Delta v_{t} < 0$) for any sliding initial condition is not difficult but is a laborious matter and far from being intuitive.

Appendix B: Equation of the hyperbola of conjugated critical PCs in the PC half-plane

The coordinates $\left( {x,y} \right)$ (tangential and perpendicular to the inclined surface and with origin at G) of the percussion centre J can be expressed as a function of the incremental DoF $\left( {\Delta v_{x} ,\Delta v_{y} ,\Delta \dot{\theta }} \right)$ applying RBK to relate $\overline{v}_{E} \left( {\mathbf{J}} \right)$ to $\overline{v}_{E} \left( {\mathbf{G}} \right)$, and imposing that the percussion center does not change its velocity $\left( {\Delta \overline{v}_{E} \left( {\mathbf{J}} \right) = \overline{0}} \right)$:

$$ \begin{gathered} \overline{v}_{E} \left( {\mathbf{J}} \right) = \overline{v}_{E} \left( {\mathbf{G}} \right) + \overline{\dot{\theta }} \times \overline{{{\mathbf{GJ}}}} \, \Rightarrow \, \left[ \begin{gathered} \left. {\overline{v}_{E} \left( {\mathbf{J}} \right)} \right]_{x} = \left. {\overline{v}_{E} \left( {\mathbf{G}} \right)} \right]_{x} + y\left( {\mathbf{J}} \right)\dot{\theta } \equiv v_{x} + y\left( {\mathbf{J}} \right)\dot{\theta } \hfill \\ \left. {\overline{v}_{E} \left( {\mathbf{J}} \right)} \right]_{y} = \left. {\overline{v}_{E} \left( {\mathbf{G}} \right)} \right]_{y} - x\left( {\mathbf{J}} \right)\dot{\theta } \equiv v_{y} - x\left( {\mathbf{J}} \right)\dot{\theta } \hfill \\ \end{gathered} \right. \hfill \\ \Delta \overline{v}_{E} \left( {\mathbf{J}} \right) = \overline{0} \, \Rightarrow \, \left\{ {\begin{array}{*{20}c} {x\left( {\mathbf{J}} \right)} \\ {y\left( {\mathbf{J}} \right)} \\ \end{array} } \right\} = \frac{1}{{\Delta \dot{\theta }}}\left\{ {\begin{array}{*{20}c} {\Delta v_{y} } \\ { - \Delta v_{x} } \\ \end{array} } \right\}. \hfill \\ \end{gathered} $$

(B.1)

The values of the coordinates $\left( {x\left( {\mathbf{J}} \right),y\left( {\mathbf{J}} \right)} \right)$ for the particular case of the conjugated critical PC $\left( {{\mathbf{J}}_{c}^{\prime } } \right)$ calls for the particularization of the ratios $\left( {{{\Delta v_{x} } \mathord{\left/ {\vphantom {{\Delta v_{x} } {\Delta \dot{\theta }}}} \right. \kern-\nulldelimiterspace} {\Delta \dot{\theta }}}{ , }{{\Delta v_{y} } \mathord{\left/ {\vphantom {{\Delta v_{y} } {\Delta \dot{\theta }}}} \right. \kern-\nulldelimiterspace} {\Delta \dot{\theta }}}} \right)$ for the case of backward sliding and critical friction coefficient $\left( {\mu_{{\text{c}}} } \right)$. Those ratios can be obtained from the percussive version of Eq. (A.1) with $P_{{\text{t}}} = \mu_{{\text{c}}} P_{{{\text{nf}}}}$:

$$ \left\{ {\begin{array}{*{20}c} {\Delta v_{x} } \\ {\Delta v_{y} } \\ {\Delta \dot{\theta }} \\ \end{array} } \right\} = \left[ M \right]^{ - 1} \left( {\left[ {A^{{{\text{nf}}}} } \right]^{T} + \mu_{{\text{c}}} \left[ {A^{t} } \right]^{T} } \right)P_{{{\text{nf}}}} = \left\{ {\begin{array}{*{20}c} {\mu_{{\text{c}}} /m} \\ {1/m} \\ {{{ - L\left( {\sin \beta + \mu_{{\text{c}}} \cos \beta } \right)} \mathord{\left/ {\vphantom {{ - L\left( {\sin \beta + \mu_{{\text{c}}} \cos \beta } \right)} {I_{G} }}} \right. \kern-\nulldelimiterspace} {I_{G} }}} \\ \end{array} } \right\}P_{{{\text{nf}}}} . $$

(B.2)

Substituting Eq. (B.2) into Eq. (B.1) yields

$$ \left\{ {\begin{array}{*{20}c} {x\left( {{\mathbf{J}}_{c}^{\prime } } \right)} \\ {y\left( {{\mathbf{J}}_{c}^{\prime } } \right)} \\ \end{array} } \right\} \equiv \left\{ {\begin{array}{*{20}c} {x_{c}^{\prime } } \\ {y_{c}^{\prime } } \\ \end{array} } \right\} = \frac{1}{{\Delta \dot{\theta }}}\left\{ {\begin{array}{*{20}c} {\Delta v_{y} } \\ { - \Delta v_{x} } \\ \end{array} } \right\} = - \frac{\lambda L}{{\sin \beta + \mu_{{\text{c}}} \cos \beta }}\left\{ {\begin{array}{*{20}c} 1 \\ {\mu_{{\text{c}}} } \\ \end{array} } \right\} \, \Rightarrow \, \left\{ \begin{gathered} \lambda = \frac{1}{L}\left[ {y_{c}^{\prime } \cos \beta - x_{c}^{\prime } \sin \beta } \right] \hfill \\ \mu_{{\text{c}}} = - \frac{{y_{c}^{\prime } }}{{x_{c}^{\prime } }} \hfill \\ \end{gathered} \right. $$

(B.3)

The hyperbola of critical PCs is obtained eliminating $\lambda$ and combining both equations:

$$ \left. \begin{gathered} \lambda = \frac{1}{L}\left( {y_{c}^{\prime } \cos \beta - x_{c}^{\prime } \sin \beta } \right) \hfill \\ \mu_{{\text{c}}} = - \frac{{y_{c}^{\prime } }}{{x_{c}^{\prime } }} = \frac{\sin \beta \cos \beta }{{\lambda + \cos^{2} \beta }} \hfill \\ \end{gathered} \right\} \Rightarrow y_{c}^{\prime 2} - y_{c}^{\prime } x_{c}^{\prime } \tan \beta + L\left( {y_{c}^{\prime } \cos \beta + x_{c}^{\prime } \sin \beta } \right) = 0. $$

(B.4)

The horizontal line $y = L\cos \beta$ is one of the asymptotes of that hyperbola.