Singularity analysis on the periodic response of a symmetrical MEMS gyroscope

Abstract

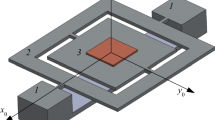
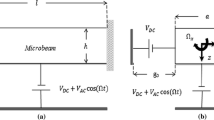
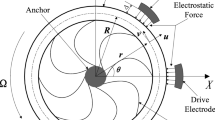
The singularity analysis on the periodic response of a symmetric comb driving and sensing MEMS gyroscope is carried out in this paper. Considering the nonlinear stiffness of the elastic beams and the nonlinear electrostatic forces of the driving and sensing combs, the dynamic equations are established by using the Lagrangian equation. The analytical solution of the periodic motion is obtained based on the method of averaging and the residue theorem. The transition sets on the finger spacing-comb separation plane and the DC–AC voltage plane, which divides the parameter planes into 6 regions, are acquired by the singularity theory. The topological structure of the corresponding bifurcation diagrams and the jump phenomenon with the change of the driving frequency are analyzed. Combined with the condition that no multiple solutions appear in the 3 dB bandwidth of the amplitude–frequency curve of the sensing direction, the available parameter regions that meet the working requirements of the gyroscope are given. The influence of the parameters on the mechanical sensitivity and the nonlinearity of the response are analyzed in the available regions.

Appendices

Appendix A

The residue theorem is used to solve the integral of the following equation.

$$\begin{aligned} {f_{X1}}\mathrm{{ = }} - \frac{\varepsilon }{{2\pi \Omega }}\int _{ - \pi }^\pi {{f_{EX}}\sin {\phi _1}{\mathrm{d}}\phi } \end{aligned}$$

(A.1)

By setting $z = \exp (i{\phi _1})$, where ${\phi _1} = \Omega \tau + {\theta _1}$, then we have

$$\begin{aligned} \cos {\phi _1} = {} \frac{{{z^2} + 1}}{{2z}}\sin {\phi _1} = \frac{{{z^2} - 1}}{{2iz}} \end{aligned}$$

(A.2)

Substituting (A.2) into (A.1), and according to the residue theorem, we have

$$\begin{aligned} {f_{X1}}= & {} - \frac{\varepsilon }{{2\pi \Omega }}\int _0^{2\pi } \frac{{\rho E{} {{(1 - \beta {} \cos \Omega \tau )}^2}}}{{{{(1 - X)}^2}}} \nonumber \\&- \frac{{\rho E{{(1 + \beta {} \cos \Omega \tau )}^2}}}{{{{(1 + X)}^2}}}\sin {\phi _1} {\mathrm{d}}{\phi _1}\nonumber \\= & {} - \frac{\varepsilon }{{2\pi \Omega }}\oint \limits _{|z| = 1} {f(z){\mathrm{d}}z} \nonumber \\= & {} - \frac{{i\varepsilon }}{\Omega }\sum {\mathrm{{Res}}[f(z),{z_k}]} \end{aligned}$$

(A.3)

where

$$\begin{aligned} f(z) = \frac{{4({z^2} - 1){} \left( \begin{array}{l} i\beta ({A^2}{z^6} - {A^2}{z^2} + {A^2}{} {z^4} - {A^2} + 4{} {z^4} - 4{} {} {z^2})\sin \theta \\ - \beta ({A^2}{} {z^6} + 3{A^2}{} {z^4} + 3{A^2}{} {z^2} + 4{z^4} + {A^2} + 4{z^2})\cos \theta \\ - A{\beta ^2}({z^6} + {z^4} + {z^2} + 1)\cos 2\theta + iA{\beta ^2}({z^6} + {z^4} - 1 - {z^2})\sin 2\theta \\ - (2{} {\beta ^2}{z^2} + 2{} {\beta ^2} + 4{} {z^2} + 4{} )A{z^2} \end{array} \right) }}{{z{{(A{z^2} + A + 2{} z)}^2}{{(A{z^2} + A - 2{} z)}^2}}} \end{aligned}$$

where ${z_k}$ is the isolated singularity of f(z) contained in the unit circle. Note that there are 3 poles in the unit circle, which are

$$\begin{aligned} {z_1}= & {} - \frac{{ - 1 + \sqrt{ - {A^2} + 1} }}{A},\nonumber \\ \mathrm{{ }}{z_2}= & {} \frac{{ - 1 + \sqrt{ - {A^2} + 1} }}{A},\mathrm{{ }}{z_3} = 0 \end{aligned}$$

(A.4)

where ${z_1},{z_2}$ are poles of order 2, and ${z_3}$ is a simple pole, then

$$\begin{aligned}&\mathrm{{Res}}[f(z),{z_k}] = \sum \limits _{k = 1,2} {\mathop {\lim }\limits _{z \rightarrow {z_k}} \frac{{\mathrm{d}}}{{{\mathrm{d}}z}}\{ (z - {z_k})f({z_k})\} } \nonumber \\&\quad + \mathop {\lim }\limits _{z \rightarrow 0} zf(0) \end{aligned}$$

(A.5)

Substituting (A.5) into (A.3) leads to

$$\begin{aligned} {f_{X1}} = - \frac{{4\beta \mathrm{{\{ }}[({A^2} - 2{} )\sqrt{1 - {A^2}} - 2{A^2} + 2{} ]\beta \cos \theta + (A - {A^3} - 4\sqrt{1 - {A^2}} )\mathrm{{\} }}\sin \theta }}{{{A^3}\Omega {} ({A^2} - 1)}} \end{aligned}$$

(A.6)

In the same way, it yields

$$\begin{aligned} \begin{array}{l} {f_{X2}} = - \frac{{\left( \begin{array}{l} [8{(1 - {A^2})^2} + 2(6{A^2} - 4 - {A^4})\sqrt{1 - {A^2}} {} ]{\beta ^2}{\cos ^2}\theta \\ + 4A[{(1 - {A^2})^2} + ({A^2} - 1)\sqrt{1 - {A^2}} ]\beta \cos \theta - 4{} {\beta ^2}{(1 - {A^2})^2}\\ + 2({A^4}{\beta ^2} - 3{A^2}{\beta ^2} + {A^4} + 2{\beta ^2})\sqrt{1 - {A^2}} \end{array} \right) }}{{{A^3}\Omega {} {{\left( {1 - {A^2}} \right) }^2}}}\\ {f_{Y1}} = 0\\ {f_{Y2}} = - \frac{{2A\sqrt{1 - {A^2}} }}{{\Omega {} {{\left( {1 - {A^2}} \right) }^2}}} \end{array} \end{aligned}$$

Appendix B

It can be solved from the first equation of Eq. 24 that

$$\begin{aligned} \sin \theta = \frac{{{C_3}}}{{{C_1} + {C_2}\cos \theta }} \end{aligned}$$

(B.1)

where

$$\begin{aligned} \begin{array}{l} {C_1} = E\beta {} {A_1}{} ({A_1}^4 - 8{A_1}^2\rho - {A_1}^2 - 8\rho \sqrt{1 - {A_1}^2} + 8\rho ),\\ {C_2} = 8E{\beta ^2}\rho {} ({A_1}^2\sqrt{1 - {A_1}^2} - 2\sqrt{1 - {A_1}^2} - 2{A_1}^2 + 2),\\ {C_3} = \xi {} A{1^4}\Omega {} (1 - {A_1}^2) \end{array} \end{aligned}$$

Then we have

$$\begin{aligned} {\cos ^2}\theta + {\sin ^2}\theta = {\cos ^2}\theta + \frac{{{C_3}^2}}{{{{({C_1} + {C_2}\cos \theta )}^2}}} = 1 \end{aligned}$$

(B.2)

The numerator of (B.2) can be given as

$$\begin{aligned} {f_1} = (1 - {\cos ^2}\theta ){({C_1} + {C_2}\cos \theta )^2} - {C_3}^2 = 0 \end{aligned}$$

(B.3)

Take the numerator of the second equation of Eq. 24 and arrange it to have

$$\begin{aligned} {B_1}{\cos ^2}\theta + {B_2}\cos \theta + {B_3} = 0 \end{aligned}$$

(B.4)

where

$$\begin{aligned}&{B_1} = 16{} E{\beta ^2}\rho [({A_1}^4 - 6{} {A_1}^2 + 4)\sqrt{1 - {A_1}^2} \\&\quad - 4{} {(1 - {A_1}^2)^2}]{},\\&{B_2} = - 4{} {A_1}{} E\beta {} [({A_1}^2 + 8{} \rho ){(1 - {A_1}^2)^2} \\&\quad + 8{} \rho (2{A_1}^2 - 1)\sqrt{1 - {A_1}^2} ],\\&{B_3} = {A_1}^4(3{} {A_1}^2\gamma - 4{} {\Omega ^2} + 4{} ){(1 - {A_1}^2)^2} \\&\quad + 16E[(3{A_1}^2 - {A_1}^4 - 2)\sqrt{1 - {A_1}^2} \\&\quad + 2{(1 - {A_1}^2)^2}]{\beta ^2}\rho \\&\quad - 16{} E\rho {} {A_1}^4\sqrt{ - A{1^2} + 1} \end{aligned}$$

According to (B.4), it can be solved

$$\begin{aligned} {\cos ^2}\theta = - \frac{{{B_2}\cos \theta + {B_3}}}{{{B_1}}} \end{aligned}$$

(B.5)

Note that by substituting (B.5) into (B.3), the power of $\cos \theta$ in (B.3) can be reduced until the expression of $\cos \theta$ is obtained. Substituting it into Eq. (B.4) can find the expression of the bifurcation equation.