Enhancing vibration mitigation in a Jeffcott rotor with active magnetic bearings through parametric excitation

Abstract

In previous studies of linear rotary systems with active magnetic bearings, parametric excitation was introduced as an open-loop control strategy. The parametric excitation was realized by a periodic, in-phase variation of the bearing stiffness. At the difference between two of the eigenfrequencies of the system, a stabilizing effect, called anti-resonance, was found numerically and validated in experiments. In this work, preliminary results of further exploration of the parametric excitation are shared. A Jeffcott rotor with two active magnetic bearings and a disk is investigated. Using Floquet theory, a deeper insight into the dynamic behavior of the system is obtained. Aiming at a further increase of stability, a phase difference between excitation terms is introduced.

1 Introduction

Time-periodic coefficients in equations of motion of mechanical systems, in contrast to forced excitation called parametric excitation, have been studied for a long time. The first occurrence of parametric excitation can be found in Mathieu and Hill equations, formulated in the nineteenth century. Initially, research concentrated mainly on undesirable destabilization from resonances caused by parametric excitation. It was as late as the 1970s that a phenomenon resulting in the stabilization of the trivial solution was discovered by Tondl [11]. Later this was named anti-resonance and understood as an energy transfer from a mode with lower damping to one with higher damping, causing an increase in effective damping of vibrations [4]. With the discovery of anti-resonance, increasing vibration mitigation via a deliberate introduction of parametric excitation became possible. This was proven to be feasible in real systems through various simulations and experiments as described in [4].

Another field of study on parametric excitation emerged from Cesari’s examination of asynchronous excitation through a phase shift between the excitation terms [2]. This was first seen as an undesired property, leading to the so-called total instability. Asynchronous excitation in combination with non-uniform damping was first studied by Schmieg [10]. In his work, he also introduced the use of Lyapunov characteristic exponents (LCEs), which allow for an analysis of destabilizing and stabilizing effects at the same time. From his results, a stabilizing effect in the case of non-uniform damping can already be deducted. However, because anti-resonance was not known at that time, Schmieg focused on instability only. In [4], the stabilizing effect depicted by the LCEs, also called equivalent damping, was studied for the cases of in-phase and anti-phase excitation. Later, in [8], a systematic investigation of combination resonance effects in parametrically excited, two-dimensional systems with a general phase shift as well as circulatory and gyroscopic terms was conducted. The largest LCE, sufficient for exploring all considered effects, was derived both numerically with Floquet method and through semi-analytical approximation with the method of normal forms. The results of [3] were confirmed that asynchronous excitation with a phase shift of $\pi$ in the coupling terms of bimodal systems may lead to swapping of the frequencies at which resonance and anti-resonance occur.

Active magnetic bearings (AMBs) are a broad research topic in recent years and due to their lack of mechanical friction especially interesting for application in high-speed rotors. Most research concentrates on stability boundaries and resonant system response for different stator configurations using nonlinear models. For an overview of the literature, see [9] and references. In [13], the influence of parametric excitation by time-periodic stiffness variation on resonances in a nonlinear model was investigated, using a semi-analytical perturbation approach. In [5], the effect of anti-resonance in a rotor with linearly modeled AMBs was found in numerical simulation and experiment. However, anti-resonance effects in AMBs are yet to be investigated in a more systematic way. In preparation for the analysis with semi-analytical approaches, it has to be shown that the anti-resonance is reflected in the LCEs, which are used as indicators for stability when applying approximation methods.

It is common practice to refer to the largest LCE for stability analysis (e.g., [4, 8]). Approaches, where all characteristic multipliers are utilized, can be found in the literature (e.g., [1]), but not with application to parametric excitation. However, this work will show that in order to gain insight into anti-resonance effects in multi-dimensional, coupled systems with parametric excitation, an analysis of only the largest LCE is not sufficient and a new, extended approach is needed. As an example that illustrates the necessity to consider all LCEs, the Jeffcott rotor described in [5, 12] will be analyzed. The focus of the investigation via all LCEs will be the effects of asynchronous excitation and coupling through parametric excitation, aiming at an enhancement of vibration mitigation caused by anti-resonance. The investigated effects and methods are, however, not limited to this example, but can be expected to be applicable to more general systems as well.

2 Stability of parametrically excited systems

Since parametric excitation can have a profound effect on the stability of the trivial solution, stability analysis is the main objective when analyzing systems with time-periodic coefficients. Unlike for differential equations with constant coefficients, an analytical derivation of solutions is generally not possible. Instead, either semi-analytical or numerical methods are employed to assess stability. Semi-analytical methods, such as normal forms or multiple scales, are ideal for generating deep insight into the underlying effects of phenomena in systems with few degrees of freedom (DoF) but become impractical when system complexity rises. Numerical methods, on the other hand, are better suited for the analysis of complex, multi-dimensional systems, albeit being constrained to initial conditions that need to be defined in advance. In the scope of this contribution, the Floquet method, which is described in detail in [7], will be applied. Numerical integration for a complete set of linear independent initial conditions over one period of the parametric excitation results in the monodromy matrix. The eigenvalues of the monodromy matrix, also called Floquet multipliers $\rho _{i}$, are indicators of the stability of the system. For every $\rho _{i}$, with the index i running from 1 to the number of DoF, the LCE $\lambda _{i}$ is defined as:

$$\begin{aligned} \lambda _{i} = \frac{1}{T}\ln {| \rho _{i} |} \end{aligned}$$

(1)

When all $\lambda _{i} \le 0$, the trivial solution is stable in the sense of Lyapunov, and $\lambda _{i} < 0$ assures asymptotic stability. It is a common approach to observe the change in the largest LCE $\varLambda = \text {max}( \lambda _{i})$ under variation of system parameters. Often, only the zero-crossing $\varLambda =0$ is of interest, to divide the range of varied parameters into stable $( \varLambda \le 0)$ and unstable $(\varLambda >0)$ areas, resulting in so-called stability maps. Stability maps, however, are not apt for analyzing anti-resonance when positive damping is present. Anti-resonance is characterized by a local minimum in the LCEs. When positive damping is present, the system without parametric excitation is already stable. Likewise, the system with parametric excitation is stable when not excited with a resonance frequency, resulting in $\varLambda <0$. Therefore, a further reduction of $\varLambda$, as caused locally by an anti-resonance, is not visible when viewing only the zero-crossing of $\varLambda$. Consequently, when examining anti-resonances, often the magnitude of $\varLambda$ is used instead. Apart from denoting stability, $\varLambda$ indicates the speed of decay as well, therefore also being called equivalent damping. This property will be used in the following to evaluate stabilization caused by parametric excitation.

3 System under consideration

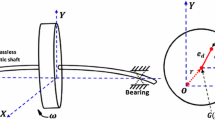
For the following analysis, the Jeffcott rotor shown in Fig. 1 will be used as an example. A detailed description of the rotor can be found in [5] and [12]. It consists of an elastic shaft, supported by two AMBs, holding a stiff disk and being driven by a motor. The AMBs are controlled by a PID controller, operating separately in two orthogonal directions y and z, which form an orthogonal coordinate system with the axis x along the shaft.

Fig. 1

Jeffcott rotor with two active magnetic bearings, studied in [5]

In accordance with [12], the system is modeled with three finite elements. The derived equations of motion are linear with time-periodic stiffness and formulated in dimensional form. Parameter values are given in [5]. As the focus of this work lies in the exploration of effects resulting from parametric excitation, nonlinearities, which are often found in models of AMBs in literature, are not considered. The resulting equations of motion are

$$\begin{aligned}&\begin{bmatrix} \mathbf {M}_{y}&{}0\\ 0&{} \mathbf {M}_{z} \end{bmatrix}^{16\times 16} \begin{bmatrix} \ddot{\mathbf {y}}\\ \ddot{\mathbf {z}} \end{bmatrix} +\ldots \nonumber \\ \ldots +&\begin{bmatrix} -\mathbf {P}_{L}^{T}k_{\textit{if}}k_{d} \mathbf {P}_{L}&{} -\mathbf {G} \varOmega _{r} \\ \mathbf {G} \varOmega _{r} &{} - \mathbf {P}_{L}^{T}k_{\textit{if}}k_{d} \mathbf {P}_{L} \end{bmatrix} \begin{bmatrix} \dot{\mathbf {y}}\\ \dot{\mathbf {z}} \end{bmatrix} + \ldots \nonumber \\ \ldots +&\begin{bmatrix} \mathbf {P}_{L}^{T} k_{\textit{if}}k_{p}\left( 1+ \varepsilon \mathbf {C}\right) \mathbf {P}_{L}+\mathbf {K}_{y}\,&{} 0 \\ 0 &{} \,\mathbf {P}_{L}^{T} k_{\textit{if}}k_{p}\left( 1+ \varepsilon \mathbf {C}\right) \mathbf {P}_{L}+\mathbf {K}_{z} \end{bmatrix}\nonumber \\&\quad \begin{bmatrix} \mathbf {y}\\ \mathbf {z} \end{bmatrix} = 0,\\ \mathbf {C} =&\begin{bmatrix} \cos \left( \varOmega t\right) &{} 0 \\ 0 &{} \cos \left( \varOmega t+ \varphi \right) \\ \end{bmatrix}^{2\times 2}, \nonumber \\&\quad \quad \mathbf {P}_{L} = \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \nonumber \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \end{bmatrix}. \end{aligned}$$

(2)

The matrices $\mathbf {M}_{i}$ and $\mathbf {K}_{i}$ denote the mass and stiffness. The matrix $\mathbf {G}$ contains gyroscopic terms, which are small compared to the other coefficients of the system. The vectors $\mathbf {y}$ and $\mathbf {z}$ consist of displacements and angles in y- and z-direction of all four knots of the three finite elements. The matrix $\mathbf {P}_{L}$ is used to transform the four knots’ DoF $\mathbf {y}$ and $\mathbf {z}$ to the DoF $(y_1,y_2)^{T}= \mathbf {P}_{L}\mathbf {y}$ and $(z_1,z_2)^{T}= \mathbf {P}_{L}\mathbf {z}$. The PID controller operates in $y_{1},z_{1}$ (AMB 1) and $y_{2},z_{2}$ (AMB 2). All damping of the system is introduced by the differential path of the PID controller with gain $k_{d}$. The constant $k_{\textit{if}}$ describes the proportionality between current and force in the AMBs. Parametric excitation is introduced into the system by the addition of a matrix $\mathbf {C}$, containing periodic terms, to the proportional path with gain $k_{p}$. The excitation with circular frequency $\varOmega$ is independent from the rotors’ angular velocity $\varOmega _{r}$ and scaled by a (small) parameter $\varepsilon$. Additionally, a phase shift between the parametric excitation terms of both bearings, $\varphi$, is added. Since the controller allows for a free choice of damping terms as well as manipulation of the stiffness, the system is well suited for exploring the effects of parametric excitation. Numerical simulation shows that the integral path of the PID controller has no significant effect on the results, so it was neglected for the sake of brevity.

4 Stability analysis of the system under consideration

As in [5], the stability of the Jeffcott rotor is explored in a MATLAB/Simulink model that is integrated over time. As initial condition, the whole shaft is displaced by $1\,\text {mm}$ in z-direction. The phase shift between parametric excitation terms is $\varphi =0$. To assess the systems’ response to the perturbation, the mean square of radial shaft deflections over time t and excitation frequency $\varOmega$ is analyzed (see Fig. 2). As mean deflections fall below a certain threshold, they are considered negligibly small and omitted from the plot. The time needed until the threshold is reached is used as a measurement for vibration decay. For most of the frequency spectrum, the parametric excitation has a slight influence only. Thus, the time after which the threshold is reached does not significantly differ from the unexcited system, which is indicated by a densely dashed line. At the fundamental resonance frequencies $2\omega _{1} \approx 330\frac{\hbox {rad}}{\hbox {s}}$ and $2 \omega _{2} \approx 545\frac{\hbox {rad}}{\hbox {s}}$, as well as the combination frequency $\varSigma _{31} = \omega _{3}+ \omega _{1} \approx 500\frac{\hbox {rad}}{\hbox {s}}$, the trivial solution is unstable and the deflections increase over time. However, at $\varDelta _{31} \approx 170\frac{\hbox {rad}}{\hbox {s}}$, the deflections decrease much faster compared to the unexcited system, hinting at the existence of an anti-resonance. This anti-resonance was also found and validated in experiments in [5].

Fig. 2

Contour plot of mean radial shaft deflections over time t and excitation frequency $\varOmega$. Deflections are given relative to a uniform perturbation in z-direction at $t=0$, with lighter shade indicating larger deflections. Sum and difference frequencies of $\omega _{i}$ and $\omega _{j}$ are denoted with $\varSigma _{ij}$ and $\varDelta _{ij}$, respectively. Deflections at the anti-resonance at $\varDelta _{31} \approx 170\frac{\hbox {rad}}{s}$ fall below threshold after $0.68\,\text {s}$, indicated by loosely dashed line

. Reference time for unexcited system shown with densely dashed line

For stability analysis without the limitation of being bound to a certain initial condition, in previous work on bimodal systems (e.g., [8]), the largest LCE $\varLambda$ was derived, revealing not only stable and unstable regions but resonance and anti-resonance phenomena as well. In this contribution, LCEs are computed numerically with Floquet analysis in a custom Python code. Floquet theory applied to the investigated equations of motion in Eq. (2) with a variation of the excitation frequency $\varOmega$ reveals $\varLambda$ as shown with a dotted line in Fig. 3. The fundamental resonances at $2 \omega _{1}$ and $2 \omega _{3}$ as well as the sum resonance at $\varSigma _{31} = \omega _{3} + \omega _{1}$ are visible. The effect of the anti-resonance at $\varDelta _{31} = \omega _{3} - \omega _{1}$, however, cannot be observed in the largest LCE. Instead, $\varLambda$ is just below 0 for all frequencies where the destabilizing resonances have no effect. This does not match with both the results from the numerical simulation in Fig. 2 and the observations in experiments conducted in [5].

The assumption previous work on parametric excitation was based on that the largest LCE $\varLambda$ is sufficient to show all resonance effects obviously cannot be generalized to multi-dimensional systems such as Eq. (2). Therefore, an extended perspective is proposed in this contribution to obtain deeper insight into the system’s dynamic response behavior. Instead of only the largest LCE $\varLambda$, all LCEs $\lambda _{i}$ are examined. For the given system, the LCEs are shown with solid lines in Fig. 3. A tracking algorithm based on the magnitude and phase of the complex Floquet multipliers is implemented to connect the LCEs across $\varOmega$, using the assumption that for the continuous change of an LCE the real and imaginary parts of the corresponding Floquet multiplier do not include any discontinuities.

Fig. 3

LCEs $\lambda _{i}$ of system in Eq. (2) over excitation frequency $\varOmega$ from 40 to $800\frac{\hbox {rad}}{s}$, $\varepsilon =0.15$, largest LCE $\varLambda$ shown with dotted line

Using this new approach to consider all LCEs, it becomes apparent that there are multiple LCEs indicating resonance phenomena that are obscured when evaluating only the largest LCE. The anti-resonance expected at the difference frequency $\varDelta _{31}$ is located in LCEs with lower magnitudes. Additionally, in these LCEs, all other fundamental and combination resonances are revealed near their expected frequencies. At fundamental as well as combination resonances, pairs of LCEs split up symmetrically, with one decreasing equally to the other increasing in magnitude. For fundamental resonances, the pairs are formed by adjacent LCEs, which are observed to differ slightly if gyroscopic terms $\mathbf {G}\ne \mathbf {0}$ are present. These pairs are colored with similar color shades in Fig. 3 with fundamental resonances of first $(2 \omega _{1})$, second $(2 \omega _{2})$, and third order $( \omega _{3})$ clearly visible. At combination resonances, i.e., at $\varSigma _{31}$, LCEs which are not in close vicinity to each other form pairs. This holds true also for the anti-resonance, around which the LCEs do not split up but move toward each other, crossing at $\varDelta _{31}$.

From the observations made, it could be conjectured to draw a connection between the three pairs of LCEs involved in the resonance phenomena and the first three modes of the unexcited system in both directions y and z. When $\varepsilon \rightarrow 0$ for $\varOmega$ beyond fundamental resonances, the LCEs in question indeed approach the real parts of the first modes’ eigenvalues. A direct connection between modes and LCEs ,however, cannot be made. It would contradict with the order the fundamental resonances appear in the LCEs. Considering the nth eigenfrequency, the mth-order resonance at $\varOmega =\frac{m \omega _{n}}{2}$ appears in the nth smallest LCE. This even holds true when the LCEs swap places at anti-resonances, as can be seen in the higher-order resonances of the first eigenfrequency in Fig. 3. The fundamental resonance at $2 \omega _{1}$ appears in the orange-colored LCEs but second and third order at $\omega _{1}$ and $\frac{3}{2} \omega _{1}$ in the LCEs with a red shade.

5 Modification of the system to increase vibration mitigation

If $\varOmega$ is far away from fundamental or combination resonances, the value of the ith-smallest LCE is $-\frac{\delta _{i}}{2}$ with $\delta _{i}$ being the ith-largest damping coefficient of the modes of the unexcited system. If the damping $\delta _{i}$ of the modes coupled by parametric excitation differs, anti-resonance emerges for $\varepsilon >0$. Whether it appears at the sum and/or difference of the modes’ eigenfrequencies depends on the phase shift between excitation terms and if the excitation is displacement- or velocity-proportional. At the anti-resonance frequency, the distance between the corresponding LCEs decreases as $\varepsilon$ increases, strengthening the stabilizing effect. When a certain $\varepsilon _{\text {crit}}$ is reached, the LCEs cross each other. The value of LCEs at the crossing point is found to be $-\frac{ \delta _{i}+ \delta _{j}}{4}$ in [4], exactly between the LCEs unaffected by resonances. Amplitudes $\varepsilon > \varepsilon _{\text {crit}}$ of the parametric excitation do not lead to further amplification of the anti-resonance. Thus, as the LCEs cross, the point of highest stabilization is reached. Further enhancement of damping properties at the point of highest stabilization can only be achieved by modifying either the system’s parameters or the structure of parametric excitation.

Fig. 4

All LCEs $\lambda _{i}$ of the system in Eq. (2) over $\varOmega$, $\varepsilon =0.15$, $\varphi = \frac{\pi }{2}$ (a) and $\varphi = \pi$ (b)

Apart from the intensity of the stabilizing effect, the width of an anti-resonance is another aspect of interest for vibration mitigation. The wider the frequency range where the influence of anti-resonance is noticeable, the more robust against variations in excitation frequency $\varOmega$ it is. In search of an increase in stability and robustness, the effects of a phase shift $\varphi$ on anti-resonance will be explored next.

In [3, 8], a phase shift $\varphi$ between parametric excitation terms on the main diagonal of a bimodal system showed not to affect combination resonance phenomena, as long as there is no coupling through the underlying systems’ matrices. Only between the coupling, off-diagonal terms of the parametric excitation will a phase shift influence resonances and anti-resonances. Viewing all LCEs (Fig. 4), it can be observed that this property found in two-dimensional systems cannot be applied to the multi-dimensional system in Eq. (2). Despite the absence of coupling between the excited DoF, a phase shift on the main diagonal of $\mathbf {C}$ affects the occurrence of resonances and anti-resonances. The combination resonances at $\varSigma _{31}$ and $\varDelta _{31}$ disappear for $\varphi = \pi$; instead new resonances at the combinations of $\omega _{1}$ and $\omega _{2}$ as well as $\omega _2$ and $\omega _3$ emerge. Fundamental resonances are far less pronounced, which is favorable for the enhancement of equivalent damping, considering that they may only lead to destabilization. In comparison with the anti-resonance for $\varphi =0$, the two newly found anti-resonances seem to be slightly advantageous regarding vibration mitigation: The LCEs at the crossing points are reduced, as now other LCEs with larger mean damping are coupling. Furthermore, the width of the anti-resonance effect is increased due to the two anti-resonances being in close vicinity to each other. Along with the two new anti-resonances, two resonances emerge at the corresponding frequencies. This, however, does not pose a problem regarding vibration mitigation, as $\varOmega$ can be set arbitrarily, e.g., to $\varDelta _{21}$, allowing for maximum stabilization at all operating points of the Jeffcott rotor.

Fig. 5

All LCEs $\lambda _{i}$ of system in Eq. (2) over $\varOmega$, coupling between bearings $\varepsilon =0.15$, $\varphi = \pi$

As the parameters of the PID controller in the system in Eq. (2) are fully accessible for modification, other forms of parametric excitations are possible as well. In [8], it was found that a phase shift between the DoF coupled through parametric excitation leads to swapping of the resonance phenomena at $\varSigma _{ij}$ and $\varDelta _{ij}$. To replicate the effect in the investigated system, the parametric excitation is modified to be

$$\begin{aligned} \mathbf {C} = \begin{bmatrix} 0 &{} \cos \left( \varOmega t \right) \\ \cos \left( \varOmega t + \varphi \right) &{} 0 \end{bmatrix}, \end{aligned}$$

(3)

keeping the phase shift and introducing coupling between the AMBs. The LCEs for this configuration are shown in Fig. 5. As expected, resonance and anti-resonance swap frequencies. The resonances lie at $\varDelta _{21}$ and $\varDelta _{32}$, whereas the anti-resonances are at $\varSigma _{21}$ and $\varSigma _{32}$. At $\varSigma _{21}$, both the width and stabilization effect of the anti-resonance are increased compared to the system without coupling. Whether the second anti-resonance at $\varSigma _{32}$ possesses any meaningful effect, which can be utilized for enhancing vibration mitigation, is not apparent from Fig. 5, as the exact relation of all LCEs at resonance phenomena and equivalent damping is yet to be fully understood.

Fig. 6

Contour plot of mean radial shaft deflections over time t and frequency $\varOmega$ after uniform perturbation of shaft in z-direction, $\varepsilon =0.15$. Amplitudes at anti-resonance get negligible small after $0.55\,\text {s}$, indicated by dashed line

To verify the discussed effects of parametric excitation with coupling and phase shift between the AMBs, shown in Fig. 5, numerical simulation of the deflections over time is used. The results are illustrated in Fig. 6. At $\varSigma _{21}$, the anti-resonance is observable. Comparing with uncoupled excitation without phase shift (Fig. 2), the increased stabilization becomes apparent, with $t=0.55\,\text {s}$ instead of $t=0.68\,\text {s}$ needed for the deflections to decay below the threshold. The second anti-resonance at $\varSigma _{32}$ is also visible, albeit only barely. This shows the approach to derive all LCEs from Floquet analysis can indeed be used to locate parameter configurations that lead to anti-resonance, providing a simple but insightful tool to gain deep insight into parametrically excited systems.

For the described approach to be applicable, all relevant eigenvalues of the monodromy matrix have to be identified and calculated. This might limit the application when studying very large systems as they occur in large finite element models. Further limitations to the feasibility of the presented results might stem from the model in Eq. 2 being linear. To gain a better understanding of if nonlinearities cause substantial changes to the anti-resonances found, either further experiments to validate the anti-resonances as done in [5] could be conducted, or Eq. 2 could be extended to include nonlinear terms. In the case of the latter, however, the proposed approach of using Floquet theory to calculate all LCEs is still applicable, so the general methodology would not change.

Another interesting subject for deeper exploration is to use the understanding obtained in this contribution to further optimize vibration mitigation. For instance, the existence of two adjacent anti-resonances as shown in Fig. 5 leads to the question of whether their location can be influenced by changing parameters of the parametric excitation, possibly even combining them to further increase the stabilizing effect. To depict the effect of parameter variation, it is practical to employ semi-analytical methods like normal forms or multiple scales, as they lead to analytical expressions that directly show each parameter’s influence. The method of normal forms was successfully applied to two-dimensional parametrically excited systems in [8]. It will have to be extended by calculation of all LCEs in future work to utilize the presented results.

6 Conclusion

Floquet analysis of a 16-DoF model of a Jeffcott rotor showed that examination of all LCEs, instead of only the largest, is necessary to investigate anti-resonance phenomena caused by parametric excitation in multi-dimensional systems. With this in mind, the effects of modifications to the parametric excitation were analyzed. A phase shift between AMBs produced two new anti-resonances, which were swapped with the corresponding resonances by coupling the bearings through parametric excitation. Both robustness and the stabilizing effect are increased at the newly found anti-resonances. The observations were verified in a simulation of the system’s amplitudes after an initial displacement. The investigation of all LCEs proves to give deep insight into stabilizing effects of parametric excitation in multi-dimensional systems, which is a powerful tool for precise enhancement of vibration mitigation.