Nonlinear aeroelastic analysis of a damped elastica-aerofoil system

Abstract

This work formulates a comprehensive model of a nonlinear aeroelastic system developed for the analysis of complex aeroelastic phenomena related to structural and aerodynamic nonlinearities. The system is formulated as a two-dimensional cantilevered elastica with a rigid airfoil section firmly attached at its tip undergoing large displacements in the crosswind conditions. The system can demonstrate a wide range of domain specific as well as coupled nonlinear phenomena. The structural model is developed by means of the Rayleigh–Ritz approach, with shape functions discretizing both vertical and horizontal displacements and Lagrangian multipliers enforcing inextensibility. Damping is modeled based on a non-local strain-based mechanism in the Kelvin–Voigt arrangement. The resulting structural model is examined through studying the behavior under a follower load and with a tip-attached tendon under tension to study the shape convergence properties and the alignment of the results with known characteristics in the literature. The ONERA dynamic stall model is used to model the aerodynamics of the problem to accurately capture post-stall behavior at large deformations. The LCO responses of the aeroelastic problem are evaluated through time-marched simulations, and the combined airspeed–damping interactions are studied in this manner.

1 Introduction

The study of nonlinear aeroelasticity is an area of research that continues to receive increasing attention, particularly in fields such as aerospace. Owing to its multi-disciplinary nature, the study of aeroelasticity invites a wide range of nonlinearities. Modeling of such systems requires careful modeling that ensures that the physics behind coupled nonlinear effects are captured accurately. This is of great importance in fully grasping the coupled aeroelastic behavior of modern aircraft systems with combined structural and aerodynamic nonlinearities [1]. In this context, an important historical milestone was the classical work of Theodorsen [2], which subsequently inspired extensive fundamental research in linear dynamic aeroelasticity. Following from this, the motivation behind the present research is the development of a low-order aeroelastic model with closely interacting geometric structural and aerodynamic nonlinear effects. The insights built through the analysis of the resulting model will be helpful in deepening the understanding of the dynamics of modern aerospace platforms such as highly flexible aircraft and high aspect-ratio (AR) wings.

Whilst high AR wings promise a reduction in drag and improved overall efficiency, their slender nature creates challenging aero-structural nonlinear effects and interactions with flight dynamics [3, 4]. An extensive range of research has been reported in the literature that surrounds the modeling of these wings [3, 5] as well as experimental work [6]. The source of structural nonlinearity is primarily a result of significant bending curvatures arising from large wing deflections. In addition to the altered modal properties due to the stiffening effects at large deflections [1, 3] and motion with flap–torsion–washout coupling [7], the response at large deflections can induce nonlinear hysteresis due to post-stall aerodynamics [6]. Damping effects too have significant influences on the post-critical responses in contrast to the linear flutter conditions [5]. The importance of these aero-structural nonlinearities equally applies to the static equilibrium states [8, 9].

The analysis of a typical rigid wing section and other simple configurations with the lumped mechanical parameters in the study of linear and nonlinear aeroelasticity is one that runs back decades [2] with more recent work reflected in [10,11,12,13,14,15]. Nonlinear response often gives rise to limit cycle oscillations (LCOs) that may be described as bounded periodic motions [1]. The thresholds of instabilities across which such responses emerge, known as Hopf bifurcations, can be evaluated through linear models, which, in many cases, are reasonable approximations for pre-instability conditions. However, certain nonlinearities such as free-play [10] can give rise to the LCOs below the linear flutter speed, whilst the speed itself is independent of free-play [11]. Post-critical responses, on the other hand, tend to be sensitive to nonlinearities such as the geometrical stiffening and post-stall aerodynamics and are responsible for the bounded character of the LCOs [1, 10]. Furthermore, galloping-like flutter mechanisms, particularly under the interactions of geometrical nonlinearities, has also shown sensitivity to damping and thus deviations from the known airspeed-based trends [12].

The Hopf bifurcation discussed above is one example among many bifurcation types that may be observed in nonlinear aerospace systems [13], across which periodic, quasi-periodic and chaotic behavior may be also experienced [1]. In the context of slender wings, detailed analysis of the LCO trajectories under parameter variations becomes critical to identify phenomena such as subcritical LCO responses [7]. Whilst methods such as time linearization [1] may indicate the onset of the initiation of such solutions to a certain extent, approaches such as harmonic balance, time-marched simulations and numerical continuation are required to evaluate limit cycle responses [13,14,15].

Another related area where relevant research has been carried out is in modeling general slender structures with geometrical nonlinearities [16,17,18]. Luongo [16] investigated bifurcations of the Beck’s problem with a variety of the stability boundary altering lumped viscoelastic configurations. This work utilized a cantilever formulation in the form of an integrodifferential equation, and bifurcation analysis was carried out after a bi-modal discretization. Dowell and McHugh, in [17] and [18], developed a model of an inextensible beam undergoing large displacements whilst discretizing both transversal and longitudinal displacements individually, whereby the inextensibility constraint was directly embedded in the resulting equations of motion posed as a system of nonlinear ordinary differential equations. This model was then used to study the Beck’s problem in time domain. As mentioned in [16], damping is another important aspect that continues to receive significant attention [19,20,21,22]. For instance, the Kelvin–Voigt (KV) model has been applied extensively, e.g., [20,21,22]. The effects of the nonlinear KV damping terms have been studied in [20].

Therefore, based on the needs arising from the modern highly nonlinear aircraft configurations, this research aims to develop a new analytically well-defined model, which can be used to study the stability questions specific to the systems with interacting nonlinear structural and aerodynamic sources. As with high AR wings, it is intended that the link between the structural geometry and the aerodynamics allows analysis of the phenomena such as dynamic stall, stall-flutter induced limit cycle behavior and their sensitivity to certain control or stability-enhancing parameters. This work develops the model that will enable further stability studies in the complex aero-structural context and their dependence on the structural shape, stiffness variations and the role of damping in stability augmentation.

The model comprises of a damped, two-dimensional slender cantilevered beam undergoing large deformations featuring geometric stiffening combined with an attached aerodynamic surface, which is the source of complex post-stall aerodynamics. The beam is modeled as a classical inextensible elastica [23, 24]. The specific numerical formulation is an extended form based on the model developed in [18]. The aerodynamics is represented by the ONERA model [25]. Owing to its intended modular architecture, the model uses an expandable set of orthogonal polynomial trial functions, geometrically exact KV model and exact combined transversal and spanwise beam deflection discretization.

The focus of this work is on the detailed model development posed as a system of nonlinear ordinary differential equations. The beam model is checked against the available classical in vacuo results. Initially, the model is verified by studying the Beck’s problem in its pre- and post-critical regime [16, 18]. Then, the model is further evaluated under the influence of the tendon-induced compressive loads [26]. Owing to the availability of the experimentally validated linear tendon-loaded beam model [27], the second case study continues the partial validation and extended the analysis of the post-critically tendon-loaded beam with additional look at the influence of the finite stiffness tendon on the beam stability. In addition to the aspect of validation in the context of this paper, this could be seen as a preliminary study towards understanding compressively loaded structures in aeroelastic settings. This has been discussed by previous researchers in the context of lowering flutter boundaries, including in experimental settings [28]. The final aeroelastic case study in the present paper evaluates a specific configuration aiming to demonstrate the varied and rich nonlinear responses and to systematically assess the damping and airspeed influence on the emerging nonlinear response regimes.

The paper is arranged as follows: In Sect. 2 the derivation of the structural model is presented followed by the two test cases in Sect. 3. This is presented to both demonstrate the dynamics of the mentioned problems and the convergence aspects of the model along with its links to classical results. Following this, Sect. 4.1 introduces the aerodynamic model. The time-marched results of the aeroelastic problem are discussed in Sect. 4.3 where emphasis is made on mapping the effects of structural damping and airspeed on the nature of the flutter responses.

2 Nonlinear model

2.1 Problem statement and energy integrals

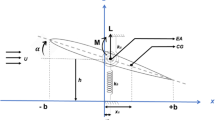
The aeroelastic configuration in question consists of a slender cantilevered beam with a flap section firmly attached at its tip, with the leading edge facing away from the root. The primary characteristic of this configuration is the innate link between the large geometrical deformations undergone by the structure and the resulting aerofoil geometry relative to the flow.

This configuration is inspired by the work on aeroelastic energy harvesters, which exploits the flow-induced LCOs for energy extraction [12, 29, 30]. Various arrangements have been studied for these mechanisms, with some versions consisting of a bluff body attached at the end of a cantilever to create galloping-like flutter mechanisms [12, 31, 32], which contrasts to later developments with hinged aerodynamic surfaces that showed the emergence of modal convergence-like flutter mechanisms [33]. The present model behaves in a similar fashion to the galloping-flutter mechanism, owing to its reduced degree of freedom due to the lack of a pitch hinge [12, 29]. This gives it stall flutter characteristics, which are triggered by periodic vortex shedding whilst undergoing larger heaving motions. This model is used to elaborate the combined characteristics of geometrical stiffening and aerodynamic stall.

Considering the sensitivity of the system to its geometrical attributes, the structural model is developed with emphasis on capturing these details. A geometrically exact, inextensible structural model is formulated in a similar fashion too [17]. This formulation discretizes both the vertical and horizontal displacements using the Rayleigh–Ritz approach with Lagrangian multipliers enforcing the inextensibility condition. Higher-order terms resulting from the horizontal displacement coordinates are retained to maintain detailed geometrical links between the geometry and stiffness. The aerodynamic model is developed with the use of the ONERA dynamic stall model [25] to capture the aforementioned stall-flutter behavior, including the stall delay and dynamic stall. A distributed Kelvin–Voigt strain-based damping model is used to study the combined airspeed–damping effects (Fig. 1).

Fig. 1

Investigated nonlinear aeroelastic configuration

As shown in Fig. 2, the formulation uses two coordinate systems, one situated along the arc length of the beam’s centroid locus and the other fixed at the root.

Fig. 2

Coordinate systems: a the root-fixed coordinate system with the arc-length measure $x$, b beam cross-section with the arc-length measure defined along the centroid locus

The vertical and the horizontal positions of a point $P$ situated at an arc-length position $x$ at a time $t$ are given by $\phi (x,t)$ and $u(x,t)$, respectively. With the described arc-length-based parametrization, the inextensibility constraint can be written as [34]:

$$ \phi ^{{\prime 2}} + u^{{\prime 2}} - 1 = 0 $$

(1)

where $\left( \circ \right)^{\prime }$ describes the derivative with respect to the arc-length $x$. It can be verified by the results of analytical geometry [35] that under the inextensibility constraint (i.e. the arc-length parameterization), the signed local curvature can be given as:

$$ \frac{1}{R} = \phi^{\prime \prime } u^{\prime } - \phi^{\prime } u^{\prime \prime } $$

(2)

which can be related to the bending strain energy of the beam:

$$ U = \frac{1}{2}\int_{0}^{L} {EI\frac{1}{{R^{{^{2} }} }}dx} = \frac{1}{2}\int_{0}^{L} {EI(\phi^{\prime \prime } u^{\prime } - \phi^{\prime } u^{\prime \prime } )^{2} dx} $$

(3)

The horizontal displacement $\gamma (x,t)$ is utilized rather than the horizontal position $u(x,t)$ for the model implementation. For the initially straight elastica under consideration, these two quantities may be related to each other as follows:

$$ u(x,t) = x + \gamma (x,t) $$

(4)

The inextensibility condition in (1) and the strain energy in (3) take then the forms:

$$ \phi^{\prime 2} + 2\gamma^{\prime } + \gamma^{\prime 2} = 0 $$

(5)

$$ U = \frac{1}{2}\int_{0}^{L} {EI(\phi^{\prime \prime 2} (1 + \phi^{\prime 2} ) + \phi^{\prime 2} \gamma^{\prime \prime 2} } )dx $$

(6)

Comparing with the relations developed in [17], the above equations only differ in terms of the presence of the higher-order terms in the arc-length derivatives of the horizontal displacements. These aspects are retained to maintain the geometrical exactness of the model considered herewith to account for large displacements.

Kinetic energy is derived considering a thin elastica, and hence, the contributions due to the warping of local sections and rotations are ignored. It is thus assumed that the sectional motion at the arc-length position $x$ is defined by the vertical and horizontal velocities $\dot{\phi }(x,t),\dot{\gamma }(x,t)$, where the over-dot represents the derivative with respect to time. The total kinetic energy of the elastica takes the form:

$$ T = \frac{1}{2}\int_{0}^{L} {\rho (\dot{\phi }^{2} } + \dot{\gamma }^{2} )dx $$

(7)

2.2 Model discretization and nonlinear geometry

Chebyshev polynomials of the first kind are used in the present work, with the application of a shifting and a scaling as discussed in [37]. Whilst the selection of the shape functions remains general, the appeal toward the mentioned choice in the present work is a result of the applicability of simple polynomial coefficient-based scaling functions to enforce the geometric boundary conditions and the adaptability of the resulting shape functions for problems with varied mechanical boundary conditions studied in Sect. 3. The choice of the scaling functions remains general, subject to the fact that they should be positive-definite to retain orthogonality. The functions, as described in [37], are generated through an iterative process defined by:

$$ \begin{gathered} s = - 2\left( \frac{x}{L} \right) + 1, \hfill \\ Y_{1} (x) = 1,\quad Y_{2} (x) = s \hfill \\ Y_{n} (x) = 2sY_{n - 1} (x) - Y_{n - 2} (x) \hfill \\ \end{gathered} $$

(8)

The shape functions defining the vertical displacement coordinates are defined by:

$$ Y_{{\phi_{n} }} (x) = x^{2} Y_{n} (x) $$

(9)

for $n \in \{ 1, \cdots ,N\}$ where the scaling function $x^{2}$ is applied to enforce the cantilever geometric conditions $\phi (0,t) = 0$ and $\phi^{\prime } (0,t) = 0$. Similarly, again for $n \in \{ 1, \cdots ,N\}$, the shape functions

$$ Y_{{\gamma_{n} }} = xY_{n} (x) $$

(10)

are allocated where the scaling function $x$ is applied to enforce the condition $\gamma (0,t) = 0$. The Lagrangian multiplier used to enforce the condition in (5) is discretized by:

$$ Y_{{\lambda_{k} }} = Y_{k} (x) $$

(11)

for $k = \{ 1, \cdots ,N_{C} \}$, where $N_{C} \le N$ to avoid over-constraining the problem. The displacements and the Lagrangian multiplier can then be described as products between the above-defined shape functions and the set of generalized coordinates ${\mathbf{q}}_{\phi } ,{\mathbf{q}}_{\gamma } \in {\mathbb{R}}^{N} ,\;{\mathbf{q}}_{\lambda } \in {\mathbb{R}}^{{N_{C} }}$ as:

$$ \phi (x,t) = {\mathbf{Y}}_{\phi }^{{\text{T}}} {\mathbf{q}}_{\phi } ,\quad \quad \gamma (x,t) = {\mathbf{Y}}_{\gamma }^{{\text{T}}} {\mathbf{q}}_{\gamma } ,\quad \quad \lambda (x,t) = {\mathbf{Y}}_{\lambda }^{{\text{T}}} {\mathbf{q}}_{\lambda } $$

(12)

where the allocated shape functions are arranged in the column vectors, ${\mathbf{Y}}_{\phi } ,{\mathbf{Y}}_{\gamma } \in {\mathbb{R}}^{N}$, ${\mathbf{Y}}_{\lambda } \in {\mathbb{R}}^{{N_{C} }}$ as:

$$ \begin{gathered} {\mathbf{Y}}_{\phi } (x) = \left[ {Y_{{\phi_{1} }} (x) \cdots Y_{{\phi_{N} }} (x)} \right]^{\text{T}} ,\quad {\mathbf{Y}}_{\gamma } (x) = \left[ {Y_{{\gamma_{1} }} (x) \cdots Y_{{\gamma_{N} }} (x)} \right]^{\text{T}} \hfill \\ {\mathbf{Y}}_{\lambda } (x) = \left[ {Y_{{\lambda_{1} }} (x) \cdots Y_{{\lambda_{{N_{C} }} }} (x)} \right]^{\text{T}} \hfill \\ \end{gathered} $$

(13)

The square brackets $[ \circ ]$ are used to identify the matrix terms in the equations from other terms. A vector of length $2N$ with the generalized displacement coordinates is also defined in the form ${\mathbf{q}} = \left[ {q_{1} \; \ldots \;q_{2N} } \right]^{{\text{T}}} = \left[ {{\mathbf{q}}_{\phi }^{{\text{T}}} \;,\;{\mathbf{q}}_{\gamma }^{{\text{T}}} } \right]^{{\text{T}}}$.

The rotation angles and the associated quantities are developed next. These results will be used in the extensions of the model to include the aerofoil. Owing to the inextensibility condition, the rate of change of the angular rotation of a local segment of the elastica with respect to the horizontal axis obeys:

$$ \frac{d\theta }{{dx}} = \frac{1}{R} = \phi^{\prime \prime } \left( {1 + \gamma^{\prime } } \right) - \phi^{\prime } \gamma^{\prime \prime } $$

(14)

The above can be integrated with respect to the arc-length to express the local angle as:

$$ \theta = {\mathbf{Y}}_{\phi }^{\prime {\text{T}}} {\mathbf{q}}_{\phi } + {\mathbf{q}}_{\gamma }^{\text{T}} \left[ {{\mathbf{Y}}_{\theta } (x)} \right]{\mathbf{q}}_{\phi } $$

(15)

of which the matrix ${\mathbf{Y}}_{\theta } (x) \in {\mathbb{R}}^{N,N}$ is defined by:

$$ {\mathbf{Y}}_{\theta } (x) = \int\limits_{0}^{x} {\left( {{\mathbf{Y}}_{\gamma }^{\prime } \otimes {\mathbf{Y}}_{\phi }^{\prime \prime } } \right) - \left( {{\mathbf{Y}}_{\gamma }^{\prime \prime } \otimes {\mathbf{Y}}_{\phi }^{\prime } } \right)} de $$

(16)

where $\otimes$ symbolizes the outer product.

Let $\nabla ( \circ ) = \left[ {\begin{array}{*{20}c} {\frac{\partial ( \circ )}{{\partial q_{1} }}} & \cdots & {\frac{\partial ( \circ )}{{\partial q_{2N} }}} \\ \end{array} } \right]^{{\text{T}}}$, which yields the derivatives of a quantity with respect to the generalized coordinates in a column vector of size $2N$. This operator when defining the generalized force terms. Applying this operator to the localized angular variable yields the coordinate derivatives of the rotation angles:

$$ \nabla \theta = \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{\phi }^{\prime } } \\ {{\mathbf{0}}_{N} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{N,N} } & {{\varvec{Y}}_{\theta }^{T} } \\ {{\mathbf{Y}}_{\theta } } & {{\mathbf{0}}_{N,N} } \\ \end{array} } \right]{\mathbf{q}} $$

(17)

The time derivatives of the angular rotation can be shown to be equivalent to:

$$ \dot{\theta } = \left( {\nabla \theta } \right)^{{\text{T}}} {\dot{\mathbf{q}}} $$

(18)

$$ \ddot{\theta } = \left( {\nabla \theta } \right)^{{\text{T}}}\, {\ddot{\mathbf{q}}} + 2{\dot{\mathbf{q}}}_{\gamma }^{{\text{T}}} {\mathbf{Y}}_{\theta } {\dot{\mathbf{q}}}_{\phi } $$

(19)

The trigonometric functions of the angular rotations are given by:

$$ \sin \theta = \phi^{\prime } = {\mathbf{Y}}_{\phi }^{\prime {\text{T}}} {\mathbf{q}}_{\phi } ,\;\;\;\;\;\cos \theta = 1 + \gamma^{\prime } = 1 + {\mathbf{Y}}_{\gamma }^{\prime {\text{T}}} {\mathbf{q}}_{\gamma } $$

(20)

2.3 Elastica equation of motion

Using the energy formulations and the constraint terms developed in the previous sections, the augmented Lagrangian including the constraint multiplier can be constructed as [36]:

$$ {\text{L}} = T - U + {\text{I}} $$

(21)

where ${\text{I}}$ is the contribution of the Lagrangian multipliers enforcing the inextensibility condition (5):

$$ I = \int_{0}^{L} {\lambda (\gamma^{\prime 2} + \phi^{\prime 2} + 2\gamma^{\prime } )dx} $$

(22)

The above Lagrangian is applied to the Lagrange equation of the second kind:

$$ \frac{d}{dt}\left( {\frac{{\partial {\text{L}}}}{{\partial \dot{r}_{j} }}} \right) = \frac{{\partial {\text{L}}}}{{\partial r_{j} }} + \sum\limits_{f} {Q_{j}^{f} } $$

(23)

where $\sum\nolimits_{f} {Q_{j}^{f} }$ is a set of the generalized forces which corresponds to the j-th generalized degree of freedom. Further, $r_{i} = q_{i}$ for $i \in \{ 1, \cdots ,2N\}$ and $r_{2N + k} = q_{{\lambda_{k} }}$ for $k \in \{ 1, \cdots N_{c} \}$.

The above yields the differential equations of motion for $j = 1, \cdots ,2N$:

$$ {\mathbf{M}}\ddot{\mathbf{q}} = - \left[ {{\mathbf{K}}({\mathbf{q}})} \right]{\mathbf{q}} + 2[{\mathbf{A}}({\mathbf{q}})]{\mathbf{q}}_{\lambda } + \sum\limits_{f} {{\mathbf{Q}}^{f} } $$

(24)

where the mass, stiffness and the constraint matrices, ${\mathbf{M}},{\mathbf{K}}({\mathbf{q}}) \in {\mathbb{R}}^{2N,2N}$, ${\mathbf{A}}({\mathbf{q}}) \in {\mathbb{R}}^{{2N,N_{C} }}$ are obtained such that:

$$ \begin{aligned} \left[ {{\mathbf{K}}\left( {\mathbf{q}} \right)} \right]{\mathbf{q}} & = \left[ {\frac{\partial U}{{\partial q_{1} }} \cdots \frac{\partial U}{{\partial q_{2N} }}} \right] \\ & = \left[ {\begin{array}{*{20}l} {\int_{0}^{L} {EI\left( {{\mathbf{Y}}_{\phi }^{\prime \prime } \phi^{\prime \prime } + \left( {{\mathbf{Y}}_{\phi }^{\prime } \phi^{\prime \prime } + {\mathbf{Y}}_{\phi }^{\prime \prime } \phi^{\prime } } \right)\phi^{\prime \prime } \phi^{\prime } + \left( {{\mathbf{Y}}_{\phi }^{\prime } \gamma^{\prime \prime } } \right)\gamma^{\prime \prime } \phi^{\prime } } \right)dx} } \\ {\int_{0}^{L} {EI\left( {{\mathbf{Y}}_{\gamma }^{\prime \prime } \phi^{\prime } } \right)\gamma^{\prime \prime } \phi^{\prime } dx} } \\ \end{array} } \right] \\ \end{aligned} $$

(25)

$$ 2[{\mathbf{A}}({\mathbf{q}})]{\mathbf{q}}_{\lambda } = \left[ {\begin{array}{*{20}l} {\frac{{\partial {\text{I}}}}{{\partial q_{1} }}} & \ldots & {\frac{{\partial {\text{I}}}}{{\partial q_{2N} }}} \\ \end{array} } \right]^{{\text{T}}} = 2\left[ {\begin{array}{*{20}l} {\int_{0}^{L} {\lambda \phi^{\prime}({\mathbf{Y^{\prime}}}_{\phi } )dx} } \\ {\int_{0}^{L} {\lambda \gamma^{\prime}({\mathbf{Y^{\prime}}}_{\gamma } ) + \lambda ({\mathbf{Y^{\prime}}}_{\gamma } )dx} } \\ \end{array} } \right] $$

(26)

$$ {\mathbf{M}}\ddot{\mathbf{q}} = \frac{\partial }{\partial t}\left[ {\begin{array}{*{20}l} {\frac{\partial T}{{\partial \dot{q}_{1} }}} & \cdots & {\frac{\partial T}{{\partial \dot{q}_{2N} }}} \\ \end{array} } \right]^{{\text{T}}} = \left[ {\begin{array}{*{20}l} {\int_{0}^{L} {\rho \left( {\ddot{\phi }{\mathbf{Y}}_{\phi } } \right)} dx} \\ {\int_{0}^{L} {\rho \left( {\ddot{\gamma }{\mathbf{Y}}_{\gamma } } \right)} dx} \\ \end{array} } \right] $$

(27)

These expressions can be further written in the following compact form:

$$ \begin{gathered} {\mathbf{M}} = \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{\phi } } & {{\mathbf{0}}_{N,N} } \\ {{\mathbf{0}}_{N,N} } & {{\mathbf{M}}_{\gamma } } \\ \end{array} } \right], \hfill \\ {\mathbf{A}}({\mathbf{q}}) = \left[ {\begin{array}{*{20}l} {{\mathbf{A}}_{\phi } ({\mathbf{q}})} \\ {{\mathbf{A}}_{{\gamma_{NL} }} \left( {\mathbf{q}} \right) + {\mathbf{A}}_{{\gamma_{lin} }} } \\ \end{array} } \right],\;\;{\mathbf{K}}\left( {\mathbf{q}} \right) = \left[ {\begin{array}{*{20}l} {{\mathbf{K}}_{{\phi_{lin} }} + {\mathbf{K}}_{\phi ,\phi } \left( {\mathbf{q}} \right)} & {{\mathbf{K}}_{\phi ,\gamma } \left( {\mathbf{q}} \right)} \\ {{\mathbf{K}}_{\phi ,\gamma } \left( {\mathbf{q}} \right)^{T} } & {{\mathbf{0}}_{N,N} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(28)

of which the details are given in Appendix B. The algebraic system of constraint equations can be derived from (23) and (22) for $j = 2N + 1, \cdots ,2N + N_{c}$:

$$ {\mathbf{0}} = \int_{0}^{L} {{\mathbf{Y}}_{\lambda } } \left( {\left( {{\mathbf{q}}_{\phi }^{{\text{T}}} {\mathbf{Y^{\prime}}}_{\phi } } \right)^{2} + \left( {{\mathbf{q}}_{\gamma }^{{\text{T}}} {\mathbf{Y^{\prime}}}_{\gamma } } \right)^{2} + 2\left( {{\mathbf{q}}_{\gamma }^{{\text{T}}} {\mathbf{Y^{\prime}}}_{\gamma } } \right)} \right)dx $$

(29)

which can be shown to be equivalent to:

$$ {\mathbf{0}} = \left[ {\begin{array}{*{20}l} {{\mathbf{A}}_{\phi } ({\mathbf{q}})^{{\text{T}}} } & {\left( {2{\mathbf{A}}_{{\gamma_{lin} }}^{{\text{T}}} + {\mathbf{A}}_{{\gamma_{NL} }} ({\mathbf{q}})^{{\text{T}}} } \right)} \\ \end{array} } \right]{\mathbf{q}} $$

(30)

Note that the matrix blocks in Eq. (30) are derived from those defined for ${\mathbf{A}}({\mathbf{q}})$ in (28), all of which are of size $N_{C} \times N$.

The elastica motion is governed by the family of ordinary differential equations in (24) and the algebraic system of equations in (30). Whilst the static equilibrium conditions may be obtained by solving these two families of equations with the time derivatives ignored, the implementation of explicit time-marching schemes requires additional manipulations as described in the next section.

2.4 Constraint embedding

Equations (24) and (30) represent the differential algebraic equations (DAEs) of index 2. To enable the use of conventional numerical time-marching methods, the algebraic equations are differentiated and combined with the original differential equations and the resulting system uses initial conditions that are consistent with the inextensibility constraint. Differentiating Eq. (29) once yields:

$$ {\mathbf{0}} = \int_{0}^{L} {{\mathbf{Y}}_{\lambda } ({\mathbf{Y^{\prime}}}_{\phi }^{{\text{T}}} {\mathbf{q}}_{\phi } )({\mathbf{Y^{\prime}}}_{\phi }^{{\text{T}}} {\dot{\mathbf{q}}}_{\phi } )dx} + \int_{0}^{L} {{\mathbf{Y}}_{\lambda } (1 + {\mathbf{Y^{\prime}}}_{\gamma }^{{\text{T}}} {\mathbf{q}}_{\gamma } )({\mathbf{Y^{\prime}}}_{\gamma }^{{\text{T}}} {\dot{\mathbf{q}}}_{\gamma } )dx} $$

(31)

and once more yields:

$$ \begin{aligned} {\mathbf{0}} & = \int_{0}^{L} {{\mathbf{Y}}_{\lambda } \left( {\left( {{\mathbf{Y}}_{\phi }^{{\prime {\text{T}}}} \mathop {\mathbf{q}}\limits^{.} _{\phi } } \right)^{2} + \left( {{\mathbf{Y}}_{\gamma }^{{\prime {\text{T}}}} \mathop {\mathbf{q}}\limits^{.} _{\gamma } } \right)^{2} } \right)dx} + \int_{0}^{L} {{\mathbf{Y}}_{\lambda } \left( {{\mathbf{Y}}_{\phi }^{{\prime {\text{T}}}} {\mathbf{q}}_{\phi } } \right)\left( {{\mathbf{Y}}_{\phi }^{{\prime {\text{T}}}} {\ddot{\mathbf{q}}}_{\phi } } \right)\,dx} \\ & \quad + \int_{0}^{L} {{\mathbf{Y}}_{\lambda } \left( {1 + {\mathbf{Y}}_{\gamma }^{{\prime {\text{T}}}} {\mathbf{q}}_{\gamma } } \right)\left( {{\mathbf{Y}}_{\gamma }^{{\prime {\text{T}}}} {\ddot{\mathbf{q}}}_{\gamma } } \right)\,dx} \\ \end{aligned} $$

(32)

which may be written as:

$$ {\mathbf{0}} = \alpha ({\mathbf{q}}) + [{\mathbf{A}}({\mathbf{q}})]^{{\text{T}}}\, {\ddot{\mathbf{q}}} $$

(33)

where the $k$-th element of the column vector $\alpha ({\mathbf{q}}) \in {\mathbb{R}}^{{N_{C} }}$ is given by:

$$ \left[ {\alpha ({\mathbf{q}})} \right]_{k} = {\dot{\mathbf{q}}}_{\phi }^{{\text{T}}} \left( {\int_{0}^{L} {Y_{{\lambda_{k} }} ({\mathbf{Y^{\prime}}}_{\phi } \otimes {\mathbf{Y^{\prime}}}_{\phi } )dx} } \right){\dot{\mathbf{q}}}_{\phi } + {\dot{\mathbf{q}}}_{\gamma }^{{\text{T}}} \left( {\int_{0}^{L} {Y_{{\lambda_{k} }} ({\mathbf{Y^{\prime}}}_{\gamma } \otimes {\mathbf{Y^{\prime}}}_{\gamma } )dx} } \right){\dot{\mathbf{q}}}_{\gamma } $$

(34)

for $k = \{ 1, \cdots ,N_{c} \}$. Inverting Eq. (24) with respect to the mass matrix and substituting in (33) in lieu of the acceleration terms yield:

$$ {\mathbf{0}} = \alpha ({\mathbf{q}}) + 2[{\mathbf{P}}({\mathbf{q}})]{\mathbf{q}}_{\lambda } + [\beta ({\mathbf{q}})]\left( { - \left[ {{\mathbf{K}}({\mathbf{q}})} \right]{\mathbf{q}} + \sum\limits_{f} {{\mathbf{Q}}^{f} } } \right) $$

(35)

where

$$ {\mathbf{P}}({\mathbf{q}}) = \left[ {{\mathbf{A}}\left( {{\mathbf{q}})} \right)} \right]^{{\text{T}}} \left[ {{\mathbf{M}}^{ - 1} } \right]\left[ {{\mathbf{A}}({\mathbf{q}})} \right] $$

(36)

$$ \beta ({\mathbf{q}}) = \left[ {{\mathbf{A}}({\mathbf{q}})} \right]^{{\text{T}}} \left[ {{\mathbf{M}}^{ - 1} } \right] $$

(37)

Equation (35) is re-arranged and substituted in (24) to eliminate ${\mathbf{q}}_{\lambda }$, yielding the ODEs of interest:

$$ {\mathbf{M}}\ddot{\mathbf{q}} = \left[ {{\mathbf{O}}_{\alpha } ({\mathbf{q}})} \right]\alpha ({\mathbf{q}}) + \left[ {{\mathbf{O}}({\mathbf{q}})} \right]\left( { - \left[ {{\mathbf{K}}({\mathbf{q}})} \right]{\mathbf{q}} + \sum\limits_{f} {{\mathbf{Q}}^{f} } } \right) $$

(38)

where

$$ \left[ {{\mathbf{O}}_{\alpha } ({\mathbf{q}})} \right] = - \left[ {{\mathbf{A}}({\mathbf{q}})} \right]\left[ {{\mathbf{P}}({\mathbf{q}})^{ - 1} } \right] $$

(39)

$$ \left[ {{\mathbf{O}}({\mathbf{q}})} \right] = {\mathbf{I}}_{2N,2N} - \left[ {{\mathbf{A}}({\mathbf{q}})} \right]\left[ {{\mathbf{P}}({\mathbf{q}})^{ - 1} } \right]\left[ {\beta \left( {{\mathbf{q}})} \right)} \right] $$

(40)

of which ${\mathbf{I}}_{2N,2N}$ is the $2N \times 2N$ identity matrix. Thus, the system of equation in (38) is employed in the study of the time-marched solutions. It is important that with this approach Eqs. (29) and (31) satisfy the initial conditions. This is achieved by considering the initial conditions where the elastica is undeformed and stationary, and the motion is triggered by a shear impulse applied at its tip.

It should be noted that whilst the present investigation does not delve into this matter, differentiated algebraic systems as employed herewith can pose challenges in the implementation of time-marching schemes [38]. These should be recognized in the context of wider applications of the presented model, particularly owing to its highly nonlinear character.

2.5 Additional model components

2.5.1 Generalized force formulation

The influence of the additional model components is introduced based on the principle of virtual work. Consider a force ${\mathbf{f}}$ acting on a point of the system with the position vector ${\mathbf{r}}$. Subject to a virtual displacement $\delta {\mathbf{r}}$, the virtual work imparted on the system is $\delta w = {\mathbf{f}} \cdot \delta {\mathbf{r}}$. Expanding out the displacement variation, this expression takes the form

$$ \delta w = {\mathbf{f}} \cdot \left( {\frac{{\partial {\mathbf{r}}}}{{\partial q_{1} }}\delta q_{1} + \frac{{\partial {\mathbf{r}}}}{{\partial q_{2} }}\delta q_{2} + \ldots + \frac{{\partial {\mathbf{r}}}}{{\partial q_{2N} }}\delta q_{2N} } \right) $$

(41)

The definition of the generalized force ${\mathbf{Q}}$ employed in application to the Lagrangian equations of motion discussed in Sect. 2.3 allows the above expression to be written as $\delta w = {\mathbf{Q}} \cdot \delta {\mathbf{q}}$, where the element ${\mathbf{Q}}_{j}$ corresponding to the j-th generalized degree of freedom is defined by:

$$ {\mathbf{Q}}_{j} = {\mathbf{f}} \cdot \frac{{\partial {\mathbf{r}}}}{{\partial q_{j} }} $$

(42)

The expressions and operations in (41) and (42) can be conveniently rearranged with the help of previously introduced differential (also known as del) operator. For instance,$\delta w = f_{\phi } \delta \phi + f_{\gamma } \delta \gamma + M\delta \theta$, where $f_{\phi } ,f_{\gamma }$, and $M$ are the force components along the respective directions and the moment. The virtual displacements in this expression can be written as $\delta \phi = \left( {\nabla \phi } \right) \cdot \delta {\mathbf{q}}$ and similarly for the others. Then, from Sect. 2.2, the corresponding generalized force is ${\mathbf{Q}} = f_{\phi } \left( {\nabla \phi } \right) + f_{\gamma } \left( {\nabla \gamma } \right) + M\left( {\nabla \theta } \right)$.

2.5.2 Structural damping

The damping model is developed based on the Kelvin–Voigt viscoelastic formulation [20, 21] where the damping induces stresses in proportion to the strain rate at each local cross-sectional position. The internal bending moment due to the strain rate is thus [21] (note that, as in the referred work, the term $CI$ is often written in terms of a scaled bending rigidity, $CI = EI\,t_{d}$):

$$ M_{\zeta } = CI\dot{\theta^{\prime}} = CI\frac{{\partial^{2} \theta }}{\partial x\,\partial t} $$

(43)

where $C$ is the constant of proportionality between the strain rate and damping stress and $I$ is the second moment of area about the cross-section centroid. Here, the substituted term $d_{\zeta } = CI$ is used.

The sum of the internal bending moments due to strain rate on a section of the arc length $\delta x$ is given by $M_{\zeta }^{\prime } \delta x$. During an infinitesimal rotation $\delta \theta$ of this element, the infinitesimal work done by the damping stresses on the element is $M_{\zeta }^{\prime } \delta x\delta \theta$. Integration of this expression throughout the length of the beam yields the total work done by the dissipative internal moment:

$$ \delta w^{\zeta } = \int_{0}^{L} {M^{\prime}_{\zeta } \left( {\delta \theta } \right)dx} $$

(44)

Thus, using the process highlighted in Sect. 2.5.1, the generalized force due to the internal damping stresses can be compiled as:

$$ {\mathbf{Q}}^{\zeta } = \int_{0}^{L} {M^{\prime}_{\zeta } \left( {\nabla \theta } \right)dx} = \int_{0}^{L} {d_{\zeta } \dot{\theta^{\prime\prime}}\left( {\nabla \theta } \right)dx} $$

(45)

The damping term is described in terms of a nonlinear damping matrix in the form:

$$ {\mathbf{Q}}^{\zeta } = - \left[ {{\mathbf{D}}\left( {\mathbf{q}} \right)} \right]{\dot{\mathbf{q}}},\;\;{\mathbf{D}}\left( {\mathbf{q}} \right) \in {\mathbb{R}}^{2N,2N} $$

(46)

The geometrically exact damping matrix ${\mathbf{D}}\left( {\mathbf{q}} \right)$ above is a superposition of a linear damping matrix, ${\mathbf{D}}_{1}$, a second-order nonlinear damping matrix given by ${\mathbf{D}}_{2,1} \left( {\mathbf{q}} \right) + {\mathbf{D}}_{2,2} \left( {\mathbf{q}} \right)$ and a third-order nonlinear damping matrix ${\mathbf{D}}_{3} \left( {\mathbf{q}} \right)$. The contents of these matrices are defined in Appendix C.

It is worth highlighting that the linear damping matrix may be directly visualized with the small angle approximation $\theta \approx \phi^{\prime }$ applied to (45), as defined in Appendix C. The relatability between the exact form in (43) and the implementation of the same strain-based formulations in other works such as [20, 22] may be conveniently understood when compared with this approximation.

2.5.3 Generalized load due to tendon compression

The configuration discussed in this context is the cantilevered beam with a light, elastic tendon (that is, an axially elastic tendon with no inertial contribution) attached between a fixed position along the horizontal axis and the tip of the beam as shown in Fig. 3. Note that the structure of this configuration does not include the rigid flap section and comprises purely of the cantilevered beam.

Fig. 3

The beam-tendon configuration: a the static deformed configuration with a static tension, b axially elastic tendon with geometry-dependent tension

The induced load variations are defined such that under static equilibrium (Fig. 3a) the tendon supports an axial tension $F_{{T_{0} }}$ whilst having an overall length $l_{{T_{0} }}$. During motion about this equilibrium (Fig. 3b), due the finite axial stiffness $K$, the overall length $\tilde{l}_{T}$ is time varying, and so is the axial tension $\tilde{F}_{T}$.

The generalized force term arising from the tension in the tendon can be written as (the subscript $L$ implies the function is evaluated at $x = L$):

$$ {\mathbf{Q}}^{Tendon} = \frac{{ - \tilde{F}_{T} ({\mathbf{q}})}}{{l_{T} ({\mathbf{q}})}}\left( {\phi_{L} \left( {\nabla \phi_{L} } \right) + \left( {L(1 - \Delta ) + \gamma_{L} } \right)\left( {\nabla \gamma_{L} } \right)} \right) $$

(47)

Note that in the above expression, the load in the tendon is essentially projected to the vertical and horizontal directions using the vertical and the horizontal vector components between the ends of the tendon, normalized by the length of the strained tendon, which is given by:

$$ l_{T} ({\mathbf{q}}) = \sqrt {\left( {L(1 - \Delta ) + {\mathbf{Y}}_{{\gamma_{L} }}^{{\text{T}}} {\mathbf{q}}_{\gamma } } \right)^{2} + \left( {{\mathbf{Y}}_{{\phi_{L} }}^{{\text{T}}} {\mathbf{q}}_{\phi } } \right)^{2} } $$

(48)

Considering the coordinates describing the static deformed shape as ${\mathbf{q}}_{0}$, it is evident that $F_{{T_{0} }} = \tilde{F}_{T} ({\mathbf{q}}_{0} )$ and $l_{{T_{0} }} = l_{T} ({\mathbf{q}}_{0} )$. Thus, the following expression is used to calculate the total tendon force

$$ \tilde{F}_{T} ({\mathbf{q}}) = K\left( {l_{T} ({\mathbf{q}}) - l_{{T_{0} }} } \right) + F_{{T_{0} }} $$

(49)

It should be recognized that the case $K = 0$ represents the case where the tendon tension is independent of the extension. Nonzero values of stiffness represent a physically relevant situation where the tension is dependent on the extension, and as $K \to \infty$, the condition of a rigid bar is attained.

2.5.4 Generalized loads due to follower forces and aerodynamics

Because of their general familiarity [18, 19] and applicability in the context of large deformation aeroelasticity, the effects caused by the follower force are used to verify the validity of the baseline elastica formulation. Then, a general system of the aerodynamic loads arising exclusively from the aerofoil part of the modeled system is also introduced in this section. The first arrangement consists of the cantilevered elastica with a compressive axial force directed along the beam tip as shown in Fig. 4. Further attributes presented in this section then characterize the aeroelastic configuration used in this paper. Figure 4 also illustrates the geometrical definitions of the attachment of the rigid flap section.

Fig. 4

Geometrical details of the modeled tip: a aerofoil-beam attachment geometry, b follower tip force and aerodynamic loads

The work done by infinitesimal displacements under the follower force takes the form $\delta w^{Fol} = - F_{Fol} \left( {\delta \phi_{L} \sin \theta_{L} + \delta \gamma_{L} \cos \theta_{L} } \right)$, and accordingly the generalized force term (as described in Sect. 2.5.1) can be written as:

$$ {\mathbf{Q}}^{Fol} = - F_{Fol} \left( {\left( {\nabla \phi_{L} } \right)\sin \theta_{L} + \left( {\nabla \gamma_{L} } \right)\cos \theta_{L} } \right) $$

(50)

where the trigonometric functions of the rotation angle used to define the load projections can be implemented using the geometrical results presented in (20).

The loads originating from aerodynamic effects are defined at the quarter-chord position and are given as lift l, drag d and moment m. Note that the orientation of these aerodynamic loads remains fixed, with the lift and drag being projected along $\phi$ and $- u$, respectively, and the moment about the quarter chord being defined positive in the anti-clockwise sense as illustrated in Fig. 4b. They can be related to the force coefficients, and this aspect is further developed in Sect. 4.1.

Linking the aerodynamic loads with the corresponding displacements described above, the generalized force terms can be developed:

$$ {\mathbf{Q}}^{aero} = l\left( {\nabla \phi_{L} } \right) - d\left( {\nabla \gamma_{L} } \right) + \left( {m + b\left( {a + \frac{1}{2}} \right)\left( {l\cos \theta_{L} + d\sin \theta_{L} } \right)} \right)\left( {\nabla \theta_{L} } \right) $$

(51)

2.5.5 Rigid flap inertial effects

The flap section is modeled as a rigid plate attached at the tip of the elastica, which takes the same angle as at the tip of the elastica $\theta (L,t)$. The influence of the flap’s inertia is expressed in the form of the Cartesian accelerations of the flap’s material particles distributed across the flap’s geometrical domain. In this way, both translational and rotational contributions of the flap to the overall kinetic energy of the system are accounted for.

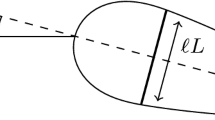
The vertical and the horizontal displacements of a point $- b(1 - a) \le h \le b(a + 1)$ on the plate is given by:

$$ \begin{gathered} \phi_{flap} (h,t) = \phi_{L} + h\sin \theta_{L} = {\mathbf{Y}}_{{\phi_{L} }}^{{\text{T}}} {\mathbf{q}}_{{\phi_{L} }} + h{\mathbf{Y^{\prime}}}_{{\phi_{L} }}^{{\text{T}}} {\mathbf{q}}_{{\phi_{L} }} \hfill \\ u_{flap} (h,t) = L + \gamma_{L} + h\cos \theta_{L} = L + {\mathbf{Y}}_{{\gamma_{L} }}^{{\text{T}}} {\mathbf{q}}_{{\gamma_{L} }} + h{\mathbf{Y^{\prime}}}_{{\gamma_{L} }}^{{\text{T}}} {\mathbf{q}}_{{\gamma_{L} }} \hfill \\ \end{gathered} $$

(52)

This constitutes the sum of the elastica’s displacement at the tip and a projected component of the chordwise flap coordinate relative to its attachment point. The expressions for the trigonometric functions of the tip rotations are readily available in terms of the coordinates through the expressions shown in (20). Noting that the additional kinetic energy due to the flap is:

$$ T_{flap} = \frac{1}{2}\int_{ - b(1 - a)}^{b(a + 1)} {\rho_{flap} } \left( {\dot{u}_{flap}^{2} + \dot{\phi }_{flap}^{2} } \right)dh $$

(53)

the mass matrix of the combined elastica-flat plate flap system can be written as follows:

$$ \begin{gathered} {\mathbf{M}}_{\phi } = \int_{ - b(1 - a)}^{b(a + 1)} {\rho_{flap} \left( {\left( {h{\mathbf{Y^{\prime}}}_{{\phi_{L} }} + {\mathbf{Y}}_{{\phi_{L} }} } \right) \otimes \left( {h{\mathbf{Y^{\prime}}}_{{\phi_{L} }} + {\mathbf{Y}}_{{\phi_{L} }} } \right)} \right)dh} + \int_{0}^{L} {\rho \left( {{\mathbf{Y}}_{\phi } \otimes {\mathbf{Y}}_{\phi } } \right)dx} \hfill \\ {\mathbf{M}}_{\gamma } = \int_{ - b(1 - a)}^{b(a + 1)} {\rho_{flap} \left( {\left( {h{\mathbf{Y^{\prime}}}_{{\gamma_{L} }} + {\mathbf{Y}}_{{\gamma_{L} }} } \right) \otimes \left( {h{\mathbf{Y^{\prime}}}_{{\gamma_{L} }} + {\mathbf{Y}}_{{\gamma_{L} }} } \right)} \right)dh} + \int_{0}^{L} {\rho \left( {{\mathbf{Y}}_{\gamma } \otimes {\mathbf{Y}}_{\gamma } } \right)dx} \hfill \\ \end{gathered} $$

(54)

3 Study 1: In vacuo model validation

3.1 Case A: stability of the model with the compressive follower force

This section presents a study of the Beck’s problem (in vacuo) with the formulated structural model that excludes the inertial effects from the flap. The mechanical attributes pertaining to this problem are presented in Sect. 2.5.4. This analysis is presented as a mean of validating the presented structural model against the existing results from the literature. The Beck’s problem is chosen owing to its nonlinear characteristics in the post critical regime and the range of work found in literature that demonstrates the resulting behavior.

An important aspect of this problem that can be conveniently compared against the existing work is the stability threshold driven by the applied follower load. To obtain this, the linearized eigenvalue problem is formulated adopting the standard approach which is elaborated in more detail later in Sect. 3.2. Figure 5 illustrates the resulting first two eigenvalue loci. To enrich this initial study further and to contrast the follower and tendon-based configurations, the tendon case ($K_{0} = 0$) is also included for comparison in the imaginary components in Fig. 5. The non-dimensional definition of the eigenvalues and the dimensionless follower force:

$$ \xi_{0} = \xi L^{2} \sqrt {\frac{\rho }{EI}} $$

(55)

$$ \mu_{Fol} = \frac{{L^{2} F_{Fol} }}{2EI} $$

(56)

are used to present the results, where $EI$ and $L$ are the bending rigidity and the beam length from Appendix A and $F_{Fol}$ is the applied follower force. Moreover, the eigenvalues are expressed as a.

Fig. 5

Eigenvalue loci for the follower elastica (Case I indicating its critical scenario) and the tendon-loaded configuration (Case II indicating its critical scenario): a imaginary components, b real components

Note that the eigenvalue loci produced above are for the undamped scenarios. The sample time-domain responses, however, were calculated with a small amount of damping applied to ensure that initial transients are damped out. The critical follower force has been recognized to reduce with the increased damping [16, 18], and the relationship between the dimensionless damping coefficient and the critical load is depended on the form of damping introduced (e.g., torsional/displacement/strain).

As demonstrated, the varied boundary conditions between the two cases produce a significant and qualitative difference in the behavior of the natural frequencies. The follower force scenario attains a modal convergence-like flutter mechanism (labelled II), unlike the tendon case where a buckling instability (formally, a pitch-fork bifurcation, at the point labelled I) is observed as demonstrated by the collapsing natural frequency prior to the emergence of new equilibrium solutions. Furthermore, the critical follower force predicted by the present model $\mu_{Fol} \approx 10$ is consistent with the value recognized in literature $\mu_{Fol} = 10.025$, e.g. [16]. Following the flutter point (or, formally, the Hopf bifurcation), the follower loaded elastica undergoes growing oscillations until a limit cycle is attained.

3.2 Case B: Tendon-controlled elastica configuration

To offer further means of validation whilst providing a brief insight into the mechanics of the problem, excluding the inertial flap effects, this section presents a focused study of a tendon-loaded system as discussed in Sect. 2.5.3. This section is also used to demonstrate the convergence of the calculated static deformed geometries with the increasing number of the generalized coordinates. The present case can be related to the other studies where experimental developments were already presented. In this context, eigenvalue analysis is used to show the effects of both pre- and post-buckled configurations and their relationship to the previous work [27]. The underlying mechanics associated with this configuration is discussed in the setup with the varying axial stiffness of the tendon.

In this work, the scenario with the tip-attached tendon fixed to the midpoint of the horizontal axis is considered (i.e., $\Delta = 0.5$). The convergence of the static solutions with the increasing number of the shape functions is demonstrated, and the eigenvalue loci are included again using a numerical linearization approach to show the effect of the applied tendon and its stiffness.

Initially, the static solutions ${\mathbf{q}}_{0}$ are found for the instances of increasing tendon tension. This is done considering a zero (dynamic) stiffness tendon. The induced static preload force can be treated as a vector of constant magnitude that points towards the fixed end of the tendon. An initial estimate for the static solution is obtained from a time-evolved solution with a significant amount of damping applied. This estimate is then used to calculate the exact static equilibrium using the fsolve function in MATLAB’s Optimization Toolbox [39]. The solutions are found for the varied tendon tensions using a numerical continuation-like approach.

Figure 6 illustrates the solutions obtained for different numbers of shape functions. The initial load in the tendon at the static position is expressed non-dimensionally as:

$$ \mu_{T} = \frac{{L^{2} F_{{T_{0} }} }}{2EI} $$

(57)

Fig. 6

Elastica convergence studies: a tip displacements with the varied numbers of shape functions, b deformation patterns with the converged number of the shape functions

Figure 6a illustrates the convergence of the solution obtained using this approach. The complexity of the resulting geometry can be observed by the large numbers of shape functions required to obtain acceptable convergence. Consequently, the proceeding work presented regarding this problem is calculated using $N = N_{C} = 13$ shape functions.

Subsequently, the equations of motions are linearized numerically about these converged static solutions for each of the tendon tension individually. Considering small perturbations ${\hat{\mathbf{q}}}$ in the form ${\mathbf{q}} = {\mathbf{q}}_{0} + {\hat{\mathbf{q}}}$, the resulting eigenvalue problem can be formulated in the form:

$$ \xi^{2} {{\overline{M}\hat{q}}} + \left[ {{\overline{\mathbf{K}}}(K)} \right]{\hat{{{\bf q}}}} = {{\overline{A} \hat{{q}}}}_{\lambda } $$

(58)

$${B}{\hat{ \mathbf{q}}} = 0 $$

(59)

where $\xi$ are square roots of the eigenvalues and the overall combined stiffness matrix is compiled as a function of the tendon stiffness. Note that (58) represents Eq (24), while (59) represents Eq. (30), when numerically linearized about the calculated static equilibrium solutions. The reduced ODE system (38) is not used for this purpose due to the influence of the constraint differentiation on the eigenvalues of interest [38].

These two equations are then rearranged to eliminate the terms in ${\hat{\mathbf{q}}}_{\lambda }$, and the resulting eigenvalue problem is solved. It should be noted that due to the constraint Eq. (59), $N_{C}$ additional eigenvalues are produced following this procedure. These do not hold significance for the presentation purposes, and the $2N - N_{C}$ eigenvalues of interest can be easily identified because the additional set is orders of magnitudes smaller.

The results are presented based on the non-dimensional eigenvalues as per (55), and the stiffness is given by:

$$ K_{0} = K\left( {\frac{{L^{3} }}{EI}} \right) $$

(60)

where $EI$, $\rho$, and $L$ are the bending rigidity, mass per unit length and length of the beam length from Appendix A, $K$ is the axial stiffness of the tendon, and $\xi$ is the square root of the eigenvalue.

Figure 7 illustrates the trajectories of the imaginary components of the eigenvalues against the tendon tension. Buckling instability is observed in the locus of the first mode, as the natural frequency drops to zero at approximately $\mu_{T} \approx 9.1$. This is also illustrated in Fig. 6, at the point where the non-trivial equilibrium solutions emerge. The value predicted by the present model is consistent with the previously calculated value for this scenario, $\mu_{T} = 9.138$ reported in [27]. As expected, the value of the critical loading point is insensitive to the tendon axial stiffness. The tendon stiffness changes the character of the post-critical behavior and intermodal coupling. It generally tends to raise the post-critical natural frequencies of the first two modes, with the variation of the natural frequencies being less sensitive at the higher stiffnesses where the tendon approaches the condition of an inextensible link. The tendon tension has a similar effect on the post-critical natural frequencies, with the first two frequencies rapidly rising just after the point of buckling as the tension is increased.

Fig. 7

Eigenvalue loci of the first two modes at varied nondimensional axial tendon stiffnesses

4 Study 2: Aeroelastic case study

4.1 Aerodynamic loads and ONERA model

The aerodynamic loads in the problem at hand are modeled by the ONERA dynamic stall model [25], which relates the force coefficients to multiple aerodynamic states. The primary driver to employ this model was its potential in capturing dynamic stall effects at large angles of attack and the ability to include effects such as stall delay. The latter is introduced by adding a delay term in the respective aerodynamic states.

The lift, drag, and the moment about the quarter chord position (as described in Fig. 4b) are expressed in terms of the corresponding forcing coefficients as follows:

$$ \begin{gathered} l = \rho_{\infty } U^{2} bSC_{l} \hfill \\ d = \rho_{\infty } U^{2} bSC_{d} \hfill \\ m = 2\rho_{\infty } U^{2} b^{2} SC_{m} \hfill \\ \end{gathered} $$

(61)

where $\rho_{\infty }$ is the air density, $U$ is the airspeed and $S$ is the flap span.

In the present work, the ONERA model is employed as laid out in [40]. Accordingly, the aerodynamic forcing coefficients in (61) are related to a total of 7 aerodynamic states by:

$$ \begin{gathered} C_{l} = s_{l} \left( \frac{b}{U} \right)\dot{W}_{0} + k_{l} \left( \frac{b}{U} \right)\dot{W}_{1} + X_{{l_{1} }} + X_{{l_{2} }} \hfill \\ C_{m} = C_{m}^{lin} + \overline{\sigma }_{m} \left( \frac{b}{U} \right)\dot{W}_{0} + s_{m} \left( \frac{b}{U} \right)\dot{W}_{1} + \sigma_{m} W_{1} + X_{{m_{2} }} \hfill \\ C_{d} = C_{{d_{0} }} + \sigma_{d} \left( \frac{b}{U} \right)\dot{W}_{0} + X_{{d_{1} }} \hfill \\ \end{gathered} $$

(62)

The aerodynamic states are modeled by the following system of seven first-order ODEs,

$$ \begin{aligned} \left( \frac{b}{U} \right)\mathop {\mathbf{X}}\limits^{.}_{l} & = \left[ {\begin{array}{*{20}c} { - \lambda } & 0 & 0 \\ 0 & 0 & {\Delta_{t} (t)} \\ 0 & { - r_{l} } & { - a_{l} } \\ \end{array} } \right]{\mathbf{X}}_{l} + \left[ {\begin{array}{*{20}c} {\lambda \left( {C_{l}^{lin} + \sigma_{l} W_{1} } \right)} \\ 0 \\ { - r_{l} \left( {\Delta C_{l} } \right)} \\ \end{array} } \right] \\ & + \left[ {\begin{array}{*{20}c} {\left( {m_{l} a_{{0_{l} }} + d_{l} } \right)\frac{b}{U}\mathop W\limits^{.}_{0} + \sigma_{l} m_{l} \frac{b}{U}\mathop W\limits^{.}_{1} } \\ 0 \\ { - e_{l} \frac{b}{U}\mathop W\limits^{.}_{0} } \\ \end{array} } \right] \\ \left( \frac{b}{U} \right)\mathop {\mathbf{X}}\limits^{.}_{m} = \left[ {\begin{array}{*{20}c} 0 & {\Delta_{t} (t)} \\ { - r_{m} } & { - a_{m} } \\ \end{array} } \right]{\mathbf{X}}_{m} + \left[ {\begin{array}{*{20}c} 0 \\ { - r_{m} \left( {\Delta C_{m} } \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ { - e_{m} \frac{b}{U}\mathop W\limits^{.}_{0} } \\ \end{array} } \right] \\ \left( \frac{b}{U} \right)\mathop {\mathbf{X}}\limits^{.}_{d} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - r_{d} } & { - a_{d} } \\ \end{array} } \right]{\mathbf{X}}_{d} + \left[ {\begin{array}{*{20}c} 0 \\ { - r_{d} \left( {\Delta C_{d} } \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ { - e_{d} \frac{b}{U}\mathop W\limits^{.}_{0} } \\ \end{array} } \right] \\ \end{aligned} $$

(63)

where ${\mathbf{X}}_{l} = \left[ {\begin{array}{*{20}c} {X_{{l_{1} }} } & {X_{{l_{2} }} } & {X_{{l_{3} }} } \\ \end{array} } \right]^{{\text{T}}}$, ${\mathbf{X}}_{m} = \left[ {\begin{array}{*{20}c} {X_{{m_{1} }} } & {X_{{m_{2} }} } \\ \end{array} } \right]^{{\text{T}}}$ and ${\mathbf{X}}_{d} = \left[ {\begin{array}{*{20}c} {X_{{d_{1} }} } & {X_{{d_{2} }} } \\ \end{array} } \right]^{{\text{T}}}$.

The induced geometric angles are given by:

$$ \begin{gathered} W_{0} = \sin \alpha \approx \frac{1}{U}\left( { - \dot{\phi }_{L} \cos \theta_{L} + U\sin \theta_{L} - b\left( {a + \frac{1}{2}} \right)\dot{\theta }_{L} } \right) \hfill \\ W_{1} = \left( \frac{b}{U} \right)\dot{\theta }_{L} \hfill \\ \end{gathered} $$

(64)

where $\alpha$ is the angle of attack and the relative airspeed is corrected to account for the horizontal motion of the flap through:

$$ U = U_{0} + \dot{\gamma }_{L} $$

(65)

For the purpose of this investigation, hypothetical static aerodynamic force coefficients were developed using the expressions laid out in [41]. These, along with the remaining terms in Eq. (63), are described in Appendix D. In the above system, the stall delay phenomenon is modeled by applying a Heaviside step function in time:

$$ \Delta_{t} (t) = {\text{H}}\left( {t - t_{s} - b(\vartriangle \tau )/U_{0} } \right) $$

(66)

These functions delay the effects of the driving terms $X_{{l_{3} }}$ and $X_{{m_{2} }}$, as proposed in [25]. The stall time occasion, $t_{s}$, is identified through the event detection feature included in the ODE time-marching process. Varied ranges of the non-dimensional time delays have been used in the applications of the ONERA model, including occasions where the delay effect was not enforced at all. In the present work, $\Delta \tau = 8$ is used.

The above aerodynamic coefficients are implemented in the aerodynamic loads as discussed in Sect. 2.5.5, and the pertaining generalized forces for this problem are compiled as $\sum\limits_{f} {{\mathbf{Q}}^{f} } = {\mathbf{Q}}^{\zeta } + {\mathbf{Q}}^{aero}$. Following this, the equations of motion are rearranged to the usual first-order ODE form to allow time marching to be employed efficiently using a fourth-order Runge–Kutta scheme.

4.2 Convergence analysis

To evaluate the convergence behavior, Fig. 8 illustrates the time-marched solutions achieved with the varied numbers of the shape functions. As shown, the primary discrepancy is noted in the period, which appears to reduce rapidly as the number of the shape functions is increased. The amplitudes on the other hand reached a reasonable agreement much faster, as illustrated in the phase portraits in Fig. 9. Note that the initial conditions used to generate these results were chosen to be an undeformed, stationary elastica triggered by a shear impulse at the tip.

Fig. 8

Time domain responses of the elastica-flap system, generated with the varied numbers of the shape functions

Fig. 9

Phase portraits of the time-domain responses with the varied numbers of the shape functions

It is also notable that for this case, the numbers of shape functions required to obtain a reasonable consistency are comparatively lower than in the case of the static deformations studied in 3.2. It may be stipulated that this is a result of the more complex shapes which the elastica attains in the tendon-loaded case as opposed to the problem studies in the above figures where the shape may be described as a pronounced and slightly distorted first cantilever beam mode.

4.3 Aeroelastic analysis

The system in question undergoes a range of behaviors, including the LCOs following an airspeed of just over 5 m/s and post-critical stationary responses. To establish a basic map of the distinct stable response types, Fig. 10 shows these within the space of the airspeed $U_{0}$ and the structural damping $d_{\zeta }$ parameters. Further, to monitor the characteristic attributes of this behavior, a tip displacement amplitude measure $Z_{\phi } = \left( {\max (\phi_{L} ) - \min (\phi_{L} )} \right)/L$ is used, which is expressed as a fraction of the beam length as a dimensionless quantity: this is indicated by the color map in the figure below. The measure of amplitude in this context is defined as the difference between the maximum and minimum heaving displacements as illustrated in Fig. 11. In contrast to some formal methods of numerical continuation in 2D, the time-marched solutions are used to traverse across the selected parameter space to form the boundaries of the various characteristic regions only approximately.

Fig. 10

A mapping of the heaving amplitude responses relative to airspeed and damping: the color intensity indicates the LCO amplitudes $Z_{\phi }$

Fig. 11

Stroboscopic views of the motion illustrating the LCOs and the definition of the amplitude

The studied domain is subdivided into the region $R_{1}$ characterized by the large symmetric LCOs, region $R_{2}$ which indicates the smaller asymmetric LCOs and region $R_{3}$ in the top-right dark region, which corresponds to the stationary post-critical responses following a sharp drop of the LCO amplitudes. The responses are highly depended on both parameters within the $U_{0} - d_{\zeta }$ parameter space. The boundary of the region $R_{1}$ is determined by the conditions where the two smaller LCOs from the region $R_{2}$ come into mutual contact. For this system, this occurs when the LCOs from $R_{2}$ reach the nominal undeformed position of the elastica. The resulting LCOs in $R_{1}$ take a ‘bow-tie’-like character.

Figure 12 offers further insights into the response characteristics of the system. Figure 12a relates the amplitude response map with the underlying aerodynamic performance, while Fig. 12b gives a range of example configurations in the $R_{3}$ region under the influence of varying airspeed.

Fig. 12

Response characteristics: a parameter space with the contours of the maximum LCO angles of attack superposed, b static equilibrium positions at the selected airspeeds (excluding symmetric solutions)

The extent of the induced aerodynamic responses in Fig. 12b is highlighted by including the contour lines of constant maximum angle of attack. Compared to the airspeed parameter, the damping has only marginal effect up to the conditions where the oscillatory responses cease to exist, and stationary solutions emerge. The gradient of the variations of the extreme angles of attack contours in Fig. 12a provides an insight into types of bifurcations at the boundaries to the regions with LCOs. As the airspeed is increased across the lower boundary where the LCO responses emerge, a smaller gradient is observed suggesting a gentle growth of the oscillatory responses, which is a characteristic of a Hopf bifurcation. The angle of attack contours decays sharply/coalesce toward the upper boundary suggesting a bifurcation where LCO responses simply cease to exist without undergoing a gentle decay, suggesting the possibility of a fold bifurcation in the LCO. Following this boundary that initiates the region $R_{3}$, the amplitudes drop rapidly and the system returns to a stationary state where it attains non-trivial, post-critical (deformed) equilibrium geometry as indicated in Fig. 12b. Thus, the non-stationary responses of the elastica–airfoil system are subtended by this stability threshold identified by the boundary to region $R_{3}$ and the lower limit dictated by a Hopf bifurcation that initiates the $R_{2}$ region.

It must, however, be emphasized that these observations could be influenced by the aerodynamic model implemented, namely the ONERA dynamic stall model in the present case: this could particularly be of concern in regions where deep stall behavior is observed. This specially applies to situations where the lift coefficient could be affected where the tendency of inaccuracies such as premature stall and underestimated lift coefficients are recognized [40].

These characteristics summarized above are further elaborated by studying the cut-through planes AA′ and BB′ demonstrated in Figs. 13, 14 and 15. The former slice passes through the region $R_{1}$ briefly and the latter only consists of the responses in $R_{2}$ and $R_{3}$. Note that the two cutting planes have two different levels of damping, with AA′ having the lower value.

Fig. 13

Bifurcation diagram across the slice AA' with example time responses from the selected points

Fig. 14

Bifurcation diagram across the slice BB' with example time responses from the selected points

Fig. 15

Amplitudes across the defined slices in the parameter space

Figures 13 and 14 show that the static divergence conditions occur just above 5 m/s, after which the non-trivial equilibria remain stable for a brief range of airspeeds. Following this, a small amplitude—cyclic responses (LCO) emerge. Observing Fig. 15, the slice AA′ then passes through the ‘bow-tie’ LCO region where it shows a rapid jump in the amplitude (at the $R_{1} - R_{2}$ boundary), whilst the slice BB′ shows a smooth growth of the amplitude across the corresponding range of airspeeds. The mechanism that encourages this transition at the $R_{1} - R_{2}$ boundary in AA′ is demonstrated by observing the extreme displacements of the symmetric limit cycles in Fig. 13, which illustrates that the symmetric ‘detached’ limit cycles approach each other/the trivial equilibrium prior to the bifurcation: this suggests a homoclinic bifurcation where the LCO comes into contact with an equilibrium and cease to exist. It can also be seen that all amplitudes grow smoothly following an airspeed of approximately 5.3 m/s as opposed to the rapid decay at the boundary to the region $R_{3}$ which again elaborates the Hopf and fold bifurcation characteristics discussed previously. It can be seen in Fig. 15 that while the airspeed has strong effect on the emergence of the non-stationary LCO behavior, the damping in the system is particularly influential in limiting or entirely suppressing the large-scale oscillatory behavior. It may be stipulated that the behavior surrounding the attainment of the stationarity at the corresponding equilibria is driven by the increasing geometrical stiffening effects caused by the considerably deformed elastica.

To conclude the study, Fig. 16 illustrates the nature of the LCOs observed at selected points indicated in the parameter space in Fig. 10 where the red and blue curves indicate the LCO in $R_{1}$ and $R_{2}$, respectively.

Fig. 16

LCO responses at selected points in the parameter space

The extent of the variation of the lift coefficient with time along with the demonstrated aerodynamic hysteresis phenomenon suggests deep-stall behavior. The mechanism of the dynamic instability following the divergence airspeed in this system may be the result of the negative static lift curve slope observed after the stall limit. This then induces a reversed damping effect during the flapping motion. The resulting low-frequency, large-amplitude motions is often identified as a characteristic of the stall flutter.

Overall, the illustrated time-marched studies revealed the extent of rich characteristics observed with the aeroelastic mechanism in question. More importantly, the illustrated responses and the suggested bifurcations highlight combined roles of the structural nonlinearities and the aerodynamic nonlinearities, particularly owing to the stall-flutter-driven oscillations and the emergence of post-critical equilibria.

5 Conclusions

A new small-scale nonlinear aeroelastic model is proposed in this work. This model consists of newly formulated geometrically exact model of the cantilevered elastica combined with the rigidly attached flap section and the advanced ONERA dynamic stall model. The resulting model is used to characterize the nonlinear aeroelastic behavior of the system, including that at large deflections and post-stall behaviors, and highlight the coupled aero-structural response characteristics potentially significant for future highly flexible wing configurations.

The structural model was constructed using the Rayleigh–Ritz approach, with the shape function discretization applied for both heaving and horizontal displacements with an inextensibility constraint applied based on the method of the Lagrangian multipliers. A strain-based nonlinear Kelvin–Voigt damping model was incorporated using the geometrically exact formulations constructed for the structural model. The resulting differential algebraic equations were modified to express the system in the form of the explicit ordinary differential equations. The aerodynamic loads were modeled with the ONERA dynamic stall model with the inclusion of a step function in the aerodynamic states to model stall delay. The responses were then studied through the time-marched simulations utilizing a fourth-order Runge–Kutta scheme.

The resulting model was verified and evaluated against the set of the test cases with the principal one involving the full-scale aeroelastic investigation under the influence of the chosen operational (airspeed) and design (damping) parameters. The system underwent stable LCO responses within a confined region in the damping–airspeed parameter space with the lower limit being strongly dictated by airspeed. The deep stall governed the oscillatory responses with the amplitudes that grew gradually following the emergence limit and decayed rapidly following an upper damping-sensitive limit, after which the mechanism attained a deformed stationary state. A region was also identified, where the system underwent comparatively large-amplitude LCOs at relatively low frequencies.

These studies highlight the significance of the focused aeroelastic investigations with the combined sources of nonlinearity, which can lead to complex aerostructural interactions. The proposed model allows investigations of the parameters that are influential when altering potentially undesirable aeroelastic response modes. The model also holds the potential to act as a “testing laboratory” to investigate certain nonlinear aspects of highly flexible wings that revolve around nonlinear aero-structural interactions such as the influence of geometric nonlinearities on the equilibria and initiation of unstable responses and the impact of unsteady aerodynamics on the instability thresholds.

Appendix

1.1 A. Mechanical and geometric parameters

The mechanical properties, particularly the beam length and the bending rigidity, are selected so as to deliberately allow for large deformations that are of interest in the present investigation (Table 1):

Table 1 Mechanical parameters used for the study

1.2 B. Structural stiffness and mass matrices

The mass matrices for a system comprising only of the beam can be written as:

$$ {\mathbf{M}}_{\phi } = \int_{0}^{L} {\rho ({\mathbf{Y}}_{\phi } \otimes {\mathbf{Y}}_{\phi } )dx} $$

(67)

$$ {\mathbf{M}}_{\gamma } = \int_{0}^{L} {\rho ({\mathbf{Y}}_{\gamma } } \otimes {\mathbf{Y}}_{\gamma } )dx $$

(68)

where $\otimes$ is the outer product. The subcomponents of the stiffness matrices, as indicated in the main text, can be written as:

$$ \left[ {{\mathbf{K}}_{{\phi_{lin} }} } \right] = \int_{0}^{L} {EI\left( {{\mathbf{Y}}_{\phi }^{\prime } \otimes {\mathbf{Y}}_{\phi }^{\prime \prime } } \right)} \;dx $$

(69)

$$ \begin{aligned} \left[ {{\mathbf{K}}_{\phi ,\phi } } \right]_{m,n} & = \int_{0}^{L} {EI\left( {Y_{\phi n}^{\prime \prime } Y_{\phi m}^{\prime } + Y_{\phi n}^{\prime } Y_{\phi m}^{\prime \prime } } \right)\phi^{\prime } \phi^{\prime \prime } dx} \\ & =\, {\mathbf{q}}_{\phi }^{\text{T}} \left( {\int_{0}^{L} {EI\left( {Y_{\phi n}^{\prime \prime } Y_{\phi m}^{\prime } + Y_{\phi n}^{\prime } Y_{\phi m}^{\prime \prime } } \right)\left( {{\mathbf{Y}}_{\phi }^{\prime \prime } \otimes {\mathbf{Y}}_{\phi }^{\prime } } \right)dx} } \right){\mathbf{q}}_{\phi } \\ \end{aligned} $$

(70)

$$ \begin{aligned} [{\mathbf{K}}_{\phi ,\gamma } ]_{m,n} & = \int_{0}^{L} {EI\left( {Y_{\gamma n}^{\prime \prime } Y_{\phi m}^{\prime } } \right)\gamma^{\prime \prime } } \phi^{\prime } dx \\ & & = {\mathbf{q}}_{\gamma }^{T} \left( {\int_{0}^{L} {EI\left( {Y_{\gamma n}^{\prime \prime } Y_{\phi m}^{\prime } } \right)\left( {{\mathbf{Y}}_{\gamma }^{\prime \prime } \otimes {\mathbf{Y}}_{\phi }^{\prime } } \right)dx} } \right){\mathbf{q}}_{\phi } \\ \end{aligned} $$

(71)

for $m,n \in \left\{ {1, \cdots ,N} \right\}$. Similarly, the components of the sub-matrices of the constraint terms can be laid out as:

$$ \left[ {{\mathbf{A}}_{\phi } ({\mathbf{q}})} \right]_{m,k} = \int_{0}^{L} {\left( {Y_{\phi m}^{\prime } Y_{{\lambda_{k} }} } \right)\phi^{\prime } } dx = {\mathbf{q}}_{\phi }^{\text{T}} \int_{0}^{L} {Y_{\phi m}^{\prime } Y_{{\lambda_{k} }} Y_{\phi }^{\prime } dx} $$

(72)

$$ \left[ {{\mathbf{A}}_{{\gamma_{NL} }} ({\mathbf{q}})} \right]_{m,k} = \int_{0}^{L} {\left( {Y_{\gamma m}^{\prime } Y_{{\lambda_{k} }} } \right)\gamma^{\prime } } dx = {\mathbf{q}}_{\gamma }^{\text{T}} \int_{0}^{L} {Y_{\gamma m}^{\prime } Y_{{\lambda_{k} }} \left( {{\mathbf{Y}}_{\gamma }^{\prime } } \right)dx} $$

(73)

$$ \left[ {{\mathbf{A}}_{{\gamma_{lin} }} } \right] = \int_{0}^{L} {\left( {{\mathbf{Y}}_{\gamma }^{\prime } \otimes {\mathbf{Y}}_{\lambda } } \right)} dx $$

(74)

For $m \in \left\{ {1, \cdots ,N} \right\}$, $k \in \left\{ {1, \cdots ,N_{c} } \right\}$.

1.3 C. Structural damping matrix

The damping matrix can be decomposed as:

$$ \left[ {{\mathbf{D}}({\mathbf{q}})} \right] = \left[ {{\mathbf{D}}_{1} } \right] + \left[ {{\mathbf{D}}_{2,1} ({\mathbf{q}})} \right] + \left[ {{\mathbf{D}}_{2,2} ({\mathbf{q}})} \right] + \left[ {{\mathbf{D}}_{3} ({\mathbf{q}})} \right] $$

(75)

where ${\mathbf{D}}_{1}$ is the linear component, ${\mathbf{D}}_{2,1} ,{\mathbf{D}}_{2,2}$ are second-order components and ${\mathbf{D}}_{3}$ contains the third-order components. Following from the results in Sect. 2.2, the following results may be deduced:

$$ \begin{gathered} \nabla \theta = \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{\phi }^{\prime } } \\ {{\mathbf{0}}_{N} } \\ \end{array} } \right] + f_{\theta } {\mathbf{q}} \hfill \\ \nabla \theta^{\prime \prime } = \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{\phi }^{\prime \prime \prime } } \\ {{\mathbf{0}}_{N} } \\ \end{array} } \right] + f_{\theta \prime } {\mathbf{q}} \hfill \\ \end{gathered} $$

(76)

where the matrices ${\mathbf{f}}_{\theta } ,{\mathbf{f}}_{{\theta^{\prime\prime}}} \in {\mathbb{R}}^{2N,2N}$ are given by:

$$ \begin{gathered} {\mathbf{f}}_{\theta } (x) = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{N,N} } & {{\mathbf{Y}}_{\theta } (x)^{\text{T}} } \\ {{\mathbf{Y}}_{\theta } (x)} & {{\mathbf{0}}_{N,N} } \\ \end{array} } \right] \hfill \\ {\mathbf{f}}_{\theta \prime \prime } (x) = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{N,N} } & {{\mathbf{Y}}_{\theta \prime \prime } (x)^{\text{T}} } \\ {{\mathbf{Y}}_{\theta \prime \prime } (x)} & {{\mathbf{0}}_{N,N} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(77)

of which:

$$ \begin{gathered} {\mathbf{Y}}_{\theta } (x) = \int_{0}^{x} {\left( {{\mathbf{Y}}_{\gamma }^{\prime } \otimes Y_{\phi }^{\prime \prime } } \right) - \left( {{\mathbf{Y}}_{\gamma }^{\prime \prime } \otimes {\mathbf{Y}}_{\phi }^{\prime } } \right)de} \hfill \\ {\mathbf{Y}}_{{\theta^{\prime\prime}}} (x) = \left( {{\mathbf{Y}}_{\gamma }^{\prime } \otimes {\mathbf{Y}}_{\phi }^{\prime \prime \prime } } \right) - \left( {{\mathbf{Y}}_{\gamma }^{\prime \prime \prime } \otimes {\mathbf{Y}}_{\phi }^{\prime } } \right) \hfill \\ \end{gathered} $$

(78)

The above formulations may be verified algebraically by the same procedures presented in Sect. 2.2 in the main text. It can also be shown that:

$$ \dot{\theta }^{\prime \prime } = \left( {\nabla \theta^{\prime \prime } } \right)^{\text{T}} \mathop {\mathbf{q}}\limits^{.} $$

(79)

Recalling (45) and applying the above, the elements of the decomposed damping components may be defined as:

$$ \left[ {{\mathbf{D}}_{1} } \right] = - \int_{0}^{L} {d_{\zeta } \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{\phi }^{\prime } } \\ {{\mathbf{0}}_{N} } \\ \end{array} } \right] \otimes \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{\phi }^{\prime \prime \prime } } \\ {{\mathbf{0}}_{N} } \\ \end{array} } \right]dx} $$

(80)

$$ \left[ {{\mathbf{D}}_{{2,1}} ({\mathbf{q}})} \right]_{{j,:}} = \left\{ {\begin{array}{*{20}l} { - {\mathbf{q}}^{\text{T}} \int_{0}^{L} {\left( {d_{\zeta } Y_{{\phi j}}^{\prime } } \right){\mathbf{f}}_{{\theta \prime \prime }}^{\text{T}} dx,} } & {j = 1, \ldots ,N} \\ {{\mathbf{0}}_{{1,N}} ,} & {j = N + 1, \ldots ,2N} \\ \end{array} } \right. $$

(81)

$$ \left[ {{\mathbf{D}}_{{2,2}} ({\mathbf{q}})} \right]_{{:,j}} = \left\{ {\begin{array}{*{20}l} { - \left( {\int_{0}^{L} {\left( {d_{\zeta } Y_{{\phi j}}^{{\prime \prime \prime }} } \right){\mathbf{f}}_{\theta } dx} } \right){\mathbf{q}},} & {j = 1, \ldots ,N} \\ {{\mathbf{0}}_{{N,1}} ,} & {j = N + 1, \ldots ,2N} \\ \end{array} } \right. $$

(82)

$$ \left[ {{\mathbf{D}}_{3} ({\mathbf{q}})} \right]_{i,j} = - {\mathbf{q}}^{\text{T}} \left( {\int_{0}^{L} {d_{\zeta } } \left[ {{\mathbf{f}}_{\theta } } \right]_{:,i} \otimes \left[ {{\mathbf{f}}_{\theta \prime \prime } } \right]_{:,j} dx} \right){\mathbf{q}}, \quad i,j \in \left\{ {1, \cdots ,2N} \right\} $$

(83)

1.4 D. Aerodynamic model formulation

1.4.1 Static aerodynamic force coefficients

The post-stall static aerodynamic curves for lift and drag forces are developed according to [41], with classical linear aerodynamics for a symmetric cross-section applied in the pre-stall regions:

$$ C_{{l_{s} }} = \left\{ {\begin{array}{*{20}l} {2\pi \alpha ,} & {\left| \alpha \right| \le \alpha _{s} } \\ {A_{1} \sin \left( {2\alpha } \right) + A_{2} \frac{{\cos ^{2} \left( \alpha \right)}}{{\sin \left( \alpha \right)}},} & {\left| \alpha \right| > \alpha _{s} } \\ \end{array} } \right. $$

(84)

$$ C_{{d_{s} }} = \left\{ {\begin{array}{*{20}l} {C_{{d_{0} }} + (C_{{d_{{stall}} }} - C_{{d_{0} }} )\left| {\frac{\alpha }{{\alpha _{s} }}} \right|^{2} ,} & {\left| \alpha \right| \le \alpha _{s} } \\ {B_{1} \sin ^{2} \left( \alpha \right) + B_{2} \cos \left( \alpha \right),} & {\left| \alpha \right| > \alpha _{s} } \\ \end{array} } \right. $$

(85)

where

$$ \begin{gathered} A_{1} = \frac{1}{2}C_{{d_{\max } }} \hfill \\ A_{2} = \left( {2\pi \alpha_{s} - C_{{d_{\max } }} \sin \left( {\alpha_{s} } \right)\cos \left( {\alpha_{s} } \right)} \right)\frac{{\sin \left( {\alpha_{s} } \right)}}{{\cos^{2} \left( {\alpha_{s} } \right)}} \hfill \\ B_{1} = C_{{d_{\max } }} \hfill \\ B_{2} = C_{{d_{stall} }} - \frac{{C_{{d_{\max } }} \sin^{2} \left( {\alpha_{s} } \right)}}{{\cos \left( {\alpha_{s} } \right)}} \hfill \\ \end{gathered} $$

(86)

The static moment is constructed assuming zero moment prior to stall, following which a growing pitching down moment is produced:

$$C_{{m_{s} }} = \left\{ {\begin{array}{*{20}l} {0,} & {\left| \alpha \right| \le \alpha _{s} } \\ {C_{{m_{\infty } }} \left( {1 - \exp \left( { - f\left( {\left| \alpha \right| - \alpha _{s} } \right)} \right)} \right),} & {\left| \alpha \right| > \alpha _{s} } \\ \end{array} } \right. $$

(87)

The parameters used in the above definitions are laid out in Table 2, and the resulting static force coefficients can be illustrated as in Fig. 

Fig. 17

Static aerodynamic force coefficients

17.

Table 2 Parameters defining the static force coefficients

1.5 ONERA coefficients

The coefficient in Eqs. (62) and (63) can be developed as follows (according to [40]):

$$ \begin{gathered} \left. {\begin{array}{*{20}c} {\Delta C_{Z} = C_{Z}^{linr} - C_{{Z_{s} }} } \\ {a_{Z} = a_{0} + a_{2} \left( {\Delta C_{Z} } \right)^{2} } \\ {r_{Z} = \left( {r_{0} + r_{2} \left( {\Delta C_{Z} } \right)^{2} } \right)^{2} } \\ {e_{Z} = e_{2} \left( {\Delta C_{Z} } \right)^{2} } \\ \end{array} } \right\}Z \in \left\{ {l,d,m} \right\} \hfill \\ d_{l} = d_{1} \left| {\Delta C_{l} } \right| \hfill \\ \sigma_{d} = \sigma_{0} W_{0} + \sigma_{1} \left| {\Delta C_{l} } \right| \hfill \\ \end{gathered} $$

(88)

where $Z$ represents the lift, moments, and the drag forces, and the terms $C_{Z}^{linr}$ are the linear static coefficients at the pre-stall angles of attack. The numerical values suggested in the same reference, [40], are used in this work:

See Table 3and the remaining terms are: $\lambda = 0.17$, $\Delta \tau = 8$, $m_{l} = 0.53$, $s_{l} = 2\pi$, $k_{l} = \pi /2$, $\sigma_{l} = 2\pi$, $\sigma_{0} = 9.8484$, $\sigma_{1} = - 2.2918$, $\sigma_{m} = - \pi /2$, $\overline{\sigma }_{m} = - \pi /4$ and $s_{m} = - 0.5879$.

Table 3 ONERA coefficients