Study of COVID-19 epidemiological evolution in India with a multi-wave SIR model

Abstract

The global pandemic due to the outbreak of COVID-19 ravages the whole world for more than two years in which all the countries are suffering a lot since December 2019. In this article characteristics of a multi-wave SIR model have been studied which successfully explains the features of this pandemic waves in India. Origin of the multi-wave pattern in the solution of this model is explained. Stability of this model has been studied by identifying the equilibrium points as well as by finding the eigenvalues of the corresponding Jacobian matrices. In this model, a finite probability of the recovered people for becoming susceptible again is introduced which is found crucial for obtaining the oscillatory solution in other words. Which on the other hand incorporates the effect of new variants, like delta, omicron, etc in addition to the SARS-CoV-2 virus. The set of differential equations has been solved numerically in order to obtain the variation of susceptible, infected and removed populations with time. In this phenomenological study, some specific sets of parameters are chosen in order to explain the nonperiodic variation of infected population which is found necessary to capture the feature of epidemiological wave prevailing in India. The numerical estimations are compared with the actual cases along with the analytic results.

1 Introduction

The outbreak of COVID-19 in December 2019, due to the spreading of infectious coronavirus named SARS-CoV-2 finally triggered to a global pandemic in which all the countries are suffering a lot till to date. This highly contagious disease has been transmitted to millions of people globally where a fraction of infected people is succumbed to it eventually. Most of the countries witnessed multiple peaks of epidemiological infections in its evolution which is counted as number of waves. Among the most affected countries, for example, countries in European union (CEU), USA, Russia and Canada experienced five successive epidemiological waves while the third wave is going on in India, Indonesia and Brazil. Which means that five peaks of the epidemiological infections are found in CEU, USA, Russia and Canada, while three distinct peaks are noted in India, Indonesia and Brazil. However, peaks of epidemiological infections in India are sharper than those found in Brazil. So, it is obvious that characteristics of these epidemiological waves found in different countries are not similar. Widths and heights of the peaks are different as well as the separation between them are not equal. It is observed that the same individual gets infected multiple times during this pandemic in all countries. This is due to fact that new variants of SARS-CoV-2 virus emerge in due course.

In order to study the dynamics of the pandemic in a deterministic approach, several models have been proposed based on the classic SIR model introduced by Kermack and Mckendrick in 1927 [1]. This model yields only a single peak for infection in its evolution, so, henceforth it is referred to as the single-wave SIR (SWSIR) model. Most of the previously studied models are mainly formulated to explain the characteristics of the solitary wave of the pandemic. Those are known as SEIR, SIQR and their hybrids which are all derived from the SWSIR model [2,3,4,5,6]. In those attempts, effects of quarantine, isolation, latent time of infection and other factors are taken into account where several predictions and forecasts are available [7, 8]. Nonetheless, periodic outbreak of disease in terms of SIR, SIQR, and SEIQR models are studied analytically in great details [9,10,11]. Evolution of the COVID-19 pandemic for different countries have been studied with the help of those models where origin of differences in its features are explained. Case studies on few countries are available [12,13,14,15,16,17,18,19,20,21]. However, generation of multi-wave pattern in the COVID-19 pandemic evolution in a deterministic approach through a single model is not reported before.

Hence, a multi-wave SIR (MWSIR) model is formulated by modifying the SWSIR model in order to explain the dynamics of epidemiological infections including the origin of multiple waves found in the infection pattern. This is a fact that the same individual has been infected repeatedly during this pandemic period. So in this model, probability of the same individual for getting infected multiple times after curing is taken into account [22]. Time delay between successive infections of the same individual is introduced in the MWSIR model. In this work, periodic outbreak of COVID-19 in India will be studied, and so, the daily new cases in terms of seven-day moving average in India during January 30, 2020 to March 14, 2022 (775 days) are shown in Fig. 1. It reveals that the duration of those waves are different, so, it is not at all periodic. The approximate duration of first and second waves are $T_1=370$ and $T_2=300$ days, respectively, while the third wave crosses 105 days ($T_3=105$). Hence, separation between adjacent peaks are different, and in addition, width and height of the peaks are unequal.

Fig. 1

Daily new COVID-19 cases in terms of seven-day moving average in India during January 30, 2020 to March 14, 2022 (775 days). The regions for first, second and third waves are demarcated by different colors

In Sect. 2 a MWSIR model is considered which gives rise to almost periodic epidemiological oscillation. The stability of this model is studied in Sect. 3 analytically while its periodic feature is studied numerically in Sect. 4. In order to produce nonperiodic oscillation, this model has been modified further. The epidemiological oscillation produced in this study is compared with the daily new COVID-19 cases in India. A discussion based on those results is available in Sect. 5.

2 Multi-wave SIR model

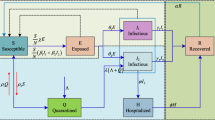
In order to explain the epidemiological waves of infection due to the spreading of COVID-19 in India, a MWSIR model is formulated where the total population is divided into three dynamic sub-populations, those are known as susceptible, infected and removed. Susceptible population is constituted by the individuals those are otherwise healthy but have a probability for having infected at any time in future. The intermediate stage is comprised of infected population where the individual is instantaneously contagious. In the terminal stage individuals are either recovered or succumbed to the disease, however, they jointly referred to as removed population. As the ongoing COVID-19 pandemic exhibits periodic outbreak of the disease globally, a modified version of SWSIR model is necessary to study the dynamics of this pandemic.

Therefore, in order to understand the nature of periodic outbreak, a MWSIR model has been formulated by modifying the primitive version of SIR model as described below. In this model the recovered population has a nonzero probability for getting infected again. As a result, the susceptible population gets enriched with time which is measured in terms of infected population with a time delay, $\tau$. Thus, the MWSIR model is defined by a set of coupled first-order nonlinear differential Eq. (1):

$$\begin{aligned} \frac{d { S}}{dt}&=\mu N-\alpha \, { S(t)}\,{ I(t)} +\gamma \,I(t\!-\!\tau )-\mu S(t), \end{aligned}$$

(1a)

$$\begin{aligned} \! \frac{d {I}}{dt}&=\alpha \, { S(t)}\,{ I(t)}-\beta \, { I(t)}-\mu I(t) , \end{aligned}$$

(1b)

$$\begin{aligned} \! \frac{d { R}}{dt}&=\beta \,{ I(t)}- \gamma \, I(t\!-\!\tau )-\mu R(t), \end{aligned}$$

(1c)

where S(t), I(t), and R(t) are the number of susceptible, infected and removed people at time t. The positive constants $\mu , \alpha , \beta$ and $\gamma$ are the rates of birth, transmission (or infection) per individual, removed and resusceptibility, respectively. The model incorporates the fact that the recovered people become susceptible again after the mean period $\tau$ [22]. However, $I(t-\tau )=0$, when $t<\tau$. The SWSIR model will be restored when $\mu =0$, and $\gamma =0$. The system in this formulation is closed in a sense that the total population, $N=S(t)+I(t)+R(t)$, does not change with time, which means the rate at which individual suffers natural mortality is also given by the parameter $\mu$. In other words, mean lifespan of individual turns out to be $1/\mu$. In the same way, $1/\beta$ can be regarded as the mean recovery time for the infected individual. The flowchart of this model is shown in Fig. 2.

Fig. 2

Flowchart for the MWSIR model

Now it is pertinent to explain how does this MWSIR model yield multiple peaks in its evolution. However, looking back on to the SWSIR model ($\mu =0,\gamma =0$), Eq. (1a) leads to the fact that $\dot{S}<0$ for all t. It means the number of susceptible individuals is always decreasing irrespective of the initial value, S(0). S(t) is monotone and positive which corresponds to $\lim _{t\rightarrow \infty }S(t)=S_{\infty }$. On the other hand, Eq. (1c) corresponds to $\dot{R}>0$ for all t, which means the number of removed individuals is always increasing. Although R(t) possesses monotonic behaviour irrespective of the initial conditions but it is bounded by total population N, which corresponds to $\lim _{t\rightarrow \infty }R(t)=R_{\infty }$.

Equation (1b) reveals that the number of infected individuals increases monotonically as long as $\beta <\alpha S(t)$ up to some maximum value and decreases to zero since the opposite condition, $\beta >\alpha S(t)$, is being satisfied beyond a certain time and thereafter. So, the epidemic dies out finally as $\lim _{t\rightarrow \infty }I(t)=I_\infty \rightarrow 0$. Thus it yields a solitary broad peak in the evolution for the number of infected individuals. Equation (1b) further predicts when this maximum will be attained as it can be determined by the condition $\dot{I}=0$, which corresponds to the relation, $S(t)=\beta /\alpha$. Further it can be shown that the value of the maximum can be expressed as [5],

$$\begin{aligned} I_{\mathrm{max}}=S(0)+I(0)-\beta (\ln {S(0)}-\ln {(\beta /\alpha )}+1)/\alpha . \end{aligned}$$

(2)

On the other hand, for the MWSIR model ($\mu =0,\gamma \ne 0$), different picture is observed since Eq. (1a) could be decomposed along the time domain as

$$\begin{aligned} \dot{S}< 0,&\; \mathrm{when}\; \gamma \,I(t\!-\!\tau )<\alpha \, { S(t)}\,{ I(t)}, \;{\mathrm{and}}, \end{aligned}$$

(3a)

$$\begin{aligned} \dot{S}> 0,&\;\mathrm{when} \; \gamma \,I(t\!-\!\tau )>\alpha \, { S(t)}\,{ I(t)}, \end{aligned}$$

(3b)

where the two opposite conditions are successively satisfied with the increase of time. To understand this point, let us start from $t=0$. As in the beginning $I(t-\tau )=0$, for $0<t<\tau$, Eq. (3a) is satisfied, so, $\dot{S} < 0$. Hence, the number of susceptible individuals decreases monotonically up to some minimum value. Obviously $\dot{S} > 0$ after some time since $I(t-\tau )>0$ when $t>\tau$, so, Eq. (3b) is fulfilled and as a consequence, S(t) increases afterwards. However, Eq. (3a) reveals that there is a possibility for the condition, $\dot{S} < 0$, to be satisfied again at a certain time when S(t) becomes very large. Thus the conditions, $\dot{S} < 0$ and $\dot{S} > 0$, are found to be valid alternately with the time leading to oscillations in its evolution. As a result, number of infected and removed individuals also show oscillatory behavior maintaining some phase difference between themselves. So eventually the populations altogether exhibit multiple peaks in their respective evolution which is shown Fig. 3. Positions of the extrema for the infected population could be determined easily by using Eq. (1b), as this one remains the same both for the SWSIR and MWSIR models. Therefore, positions of the extrema for the infected population could be determined using the same relation, $S(t)=\beta /\alpha$, also in this case. So, on the other hand, value of $\alpha$ can be found by locating the position of the peak for the infected population by plotting both the variations of S(t) and I(t) in the same scale and this geometrical method will be described later while confirming the value of $\alpha$. In addition, value of the first peak has been determined using Eq. (2).

The basic reproduction number, $R_0$ plays an important role in epidemiology, which is defined as average number of new infections per infected individual. So, in this three-compartment system, it is equal to the transmission rate multiplied by the infectious period, $R_0=\alpha /(\beta +\mu )$ [4, 11]. The value of $R_0$ is crucial to have an idea about how does the disease flow in the whole population and at the same time it provides clue to control its spreading.

3 Stability analysis of multi-wave SIR model

Theorem: Every solution of the MWSIR model along with its initial conditions is a subset in the interval [0,$\infty$) and $\{S(t),I(t),R(t) \}\ge 0$ for all values $0\le t <\infty$. In order to prove this, Eq. (1a),

$$\begin{aligned} \frac{d { S}}{dt}=\mu N-\alpha \, { S(t)}\,{ I(t)} +\gamma \,I(t\!-\!\tau )-\mu S(t), \end{aligned}$$

has been expressed as

$$\begin{aligned}&\frac{d}{dt}\!\left[ Se^{\left( \mu t +\alpha \int _0^t I(t') dt'\right) } \right] \\&\quad = (\mu N+\gamma \,I(t\!-\!\tau ))\,e^{\left( \mu t +\alpha \int _0^t I(t') dt'\right) } . \end{aligned}$$

Hence, upon integrating

$$\begin{aligned}&S(t)e^{\left( \mu t +\alpha \int _0^{t} I(t') dt'\right) } -S(0)\\&\quad =\int _0^{t} (\mu N+\gamma \,I(x\!-\!\tau ))\,e^{\left( \mu x +\alpha \int _0^x I(t') dt'\right) }dx . \end{aligned}$$

As $S(0)>0$,

$$\begin{aligned}&S(t)e^{\left( \mu t +\alpha \int _0^{t} I(t') dt'\right) } \\&\quad \ge \int _0^{t} (\mu N+\gamma \,I(x\!-\!\tau ))\,e^{\left( \mu x +\alpha \int _0^x I(t') dt'\right) }dx . \end{aligned}$$

Thus,

$$\begin{aligned} S(t)\ge & {} e^{-\left( \mu t +\alpha \int _0^{t} I(t') dt'\right) }\\&\int _0^{t} (\mu N+\gamma \,I(x\!-\!\tau ))\,e^{\left( \mu x +\alpha \int _0^x I(t') dt'\right) }dx >0. \end{aligned}$$

As a result, $S(t)>0$ at any time. Similarly, it can be shown that $I(t)>0$, and $R(t)>0$, which complete the proof.

In order to determine the stable equilibrium points, the rate of change of S(t), I(t) and R(t) with time are made zero. The trivial solution leads to $I(t)=0$ at any time, which corresponds to disease-free equilibrium (DFE). Mathematically, this point is expressed as $(S^*,I^*,R^*)_{\mathrm{tr}}=(N,0,0)$, where the entire population becomes susceptible but no infected individual. This is true for both $t<\tau$ and $t\ge \tau$. Anyway, this DFE is insignificant as it does not correspond to dynamics of epidemic by any means.

The nontrivial solution leads to $I(t)\ne 0$, at finite time, but, $I(t\rightarrow \infty )\rightarrow 0$, which corresponds to endemic equilibrium and that is observed in SWSIR model. However, in this MWSIR model, nontrivial solutions mean $I(t)> 0$, at any time. So these dynamic equilibrium points appear periodically with time without showing any signature of ending if there is no damping. These equilibrium points are marked by $(S^*,I^*,R^*)_\mathrm{ntr}=\left( \frac{\beta +\mu }{\alpha }, \frac{\mu N}{\beta +\mu }-\frac{\mu }{\alpha }, \frac{\beta N}{\beta +\mu }-\frac{\beta +\mu }{\alpha } +\frac{\mu }{\alpha }\right)$, when $t<\tau$, however, for $t\ge \tau$, $(S^*,I^*(t),R^*(t))_\mathrm{ntr}=\!\left( \frac{\beta +\mu }{\alpha }, \frac{\mu N}{\beta +\mu }\!+\!\frac{\gamma I(t\!-\!\tau )}{\beta +\mu }\!-\!\frac{\mu }{\alpha }, \frac{\beta N}{\beta +\mu }\!-\!\frac{\beta +\mu }{\alpha } \!-\!\frac{\gamma I(t\!-\!\tau )}{\beta +\mu }+\frac{\mu }{\alpha }\right)$. Hence, equilibrium points are static when $t<\tau$, but dynamic when $t\ge \tau$.

Fig. 3

Four successive waves are shown here those are generated numerically by solving MWSIR model (Eq 1). Values of the parameters: $S(0)=10,\,I(0)=1,\,R(0)=0,\,N=11,\,\alpha =0.5,\, \beta = 1,\, \gamma =1, \, \tau = 10,\,\mu =0.$ Time period of oscillation is marked by T

In order to understand the dynamics close to the equilibria, Jacobian matrix (J) is constructed which can be expressed at the respective equilibrium points. Jacobian matrix has the form

$$\begin{aligned} J= \left[ \begin{array}{ccc} -(\alpha I^*+\mu ) &{} -\alpha S^* &{}0 \\ \alpha I^* &{}\alpha S^* -\beta -\mu &{}0 \\ 0&{}\beta &{} -\mu \end{array}\right] . \end{aligned}$$

(4)

The eigenvalues of Jacobian matrix ($\lambda _0,\lambda _\pm$) can be given as

$$\begin{aligned} \left\{ \begin{array}{l}\!\lambda _0=-\mu , \\ \! \lambda _\pm =-\frac{\alpha (I^*-S^*)+\beta +2\mu }{2}\pm \frac{\sqrt{\alpha ^2 (I^*-S^*)^2+\beta ^2-2\alpha \beta (S^*+I^*)}}{2}. \end{array}\right. \end{aligned}$$

(5)

For the DFE, $(S^*,I^*,R^*)_{\mathrm{tr}}=(N,0,0)$, the eigenvalues are

$$\begin{aligned} \left\{ \begin{array}{l}\lambda _0=-\mu , \\ \lambda _+=\alpha N -\beta -\mu , \\ \lambda _-=-\mu . \end{array}\right. \end{aligned}$$

(6)

As a result, it will behave like a stable point when $\alpha <(\beta +\mu )/N$, which is similar to the SWSIR model. It is obvious that the eigenvalues will be complex for the general case when

$$\begin{aligned} \alpha \beta >\frac{\alpha ^2 (I^*-S^*)^2+\beta ^2}{2(S^*+I^*)}. \end{aligned}$$

It is expected that variations of S(t), I(t), and R(t) will be oscillatory around these points [4]. The solutions for S(t), I(t), and R(t) in this linearized model could be found in terms of the eigenvalues and eigenvectors of J, however, they are not necessary at this moment.

4 Numerical results

As the values of S(t), I(t), and R(t) cannot be determined analytically by solving the set of Eqs. (1), they have been solved numerically. The oscillations of S(t), I(t), and R(t) are noted for long time and it is observed that all are oscillating with almost constant amplitude. Four successive waves are shown in Fig. 3, where it is observed that the mean time period of oscillations, T, is always greater than $\tau$. The reason behind this oscillation can be understood in terms of Eqs. (3) which was explained before. As no damping factor is introduced here, amplitudes of the respective waves for S(t), I(t), and R(t) do not decay with time.

The time period of oscillations for S(t), I(t), and R(t) are obviously the same, although it decreases with the number of cycles. However the difference, $T\!-\!\tau$ vanishes with the increase of $\tau$. This feature is shown in Fig. 4 where variations of time period T along with relative difference between T and $\tau$ or $(T\!-\!\tau )/\tau$ with $\tau$ are plotted.

Fig. 4

Variation of T and $(T\!-\!\tau )/\tau$ with $\tau$, in the MWSIR model for $S(0)=10,\,I(0)=1,\,R(0)=0,\,N=11,\,\alpha =0.5,\, \beta = 1,\, \gamma =1, \, \mu =0$

Fig. 5

Variation of T with $\alpha$ and $\beta$, when $\tau =10$, in the MWSIR model for $S(0)=10,\,I(0)=1,\,R(0)=0,\,N=11,\, \gamma =1, \, \mu =0$

The variation of T with $\alpha$ and $\beta$ for fixed value of $\tau$ is shown in Fig. 5. It clearly indicates that $T>\tau$, for any values of $\alpha$ and $\beta$. Moreover, the difference, $T\!-\!\tau$ steadily decreases with $\alpha$ but increases gradually with $\beta$.

Fig. 6

Daily new COVID-19 cases in terms of seven-day moving average in India during January 30, 2020 to March 14, 2022 (775 days) is compared with the numerical results obtained by the MWSIR model. Values of the populations when $t=0$ are $S(0)=8.8\times 10^{5},\,\,I(0)=1,\,R(0)=0$

Features of the ongoing COVID-19 epidemiological waves observed in India are shown in Fig. 1. It reveals that the duration of successive waves are decreasing as $T_1>T_2>T_3$. On the other hand, amplitude of the second wave is the maximum while that of the first wave is the smallest. These features suggest that the prevailing pandemic wave is not periodic. Hence, the MWSIR model is further modified in order to explain its nonperiodic behavior. One can remember that transformation of SWSIR to MWSIR is accomplished by introducing two parameters $\gamma$ and $\tau$, where $\gamma$ is the rate at which the recovered people become susceptible again, while $\tau$ is the time delay introduced during the estimation of susceptible population in terms of infected population.

In order to capture this specific nonperiodic feature in the most simple way, the value of $\tau$, $\alpha$ and $\gamma$ have been split up in the MWSIR model as shown below,

$$\begin{aligned} \tau= & {} \left\{ \begin{array}{l}\tau _1,\\ \tau _2,\\ \tau _3, \end{array}\right. \end{aligned}$$

(7)

$$\begin{aligned} \alpha= & {} \left\{ \begin{array}{ll}\alpha _1,&{}0< t<\tau _2, \\ \alpha _2,&{} t\ge \tau _2, \end{array}\right. \end{aligned}$$

(8)

$$\begin{aligned} \gamma= & {} \left\{ \begin{array}{ll}0,&{} 0<t<\tau _1, \\ \gamma _1,&{} \tau _1 \le t< \tau _2, \\ \gamma _2,&{} t\ge \tau _2, \end{array}\right. \end{aligned}$$

(9)

where $\tau _1=173$, $\tau _2=440$, $\tau _3=457$, $\alpha _1=1.48\times 10^{-7}$, $\alpha _2=8.7\times 10^{-7}$, $\gamma _1=0.055$, and $\gamma _2=0.08$. The value of recovery rate, $\beta =1/14$ per day, is kept fixed as it corresponds to the mean recovery period of COVID-19 infection or $1/\beta =14$ days. Values of those constants are estimated with respect to the single infected people, $I(0)=1$. The numerical data obtained by solving the MWSIR model is drawn in red dashed line and compared with the daily new COVID-19 cases (seven-day moving average) in India drawn in blue sold line, which is shown in Fig. 6. A very good agreement is found besides the fact that height of the first peak is higher and the width of the second peak is narrow in this estimation with respect to the actual values. The relation, $\alpha _2>\alpha _1$ may attribute to the fact that transmission rate of new variants, like delta and omicron is higher than the primitive SARS-CoV-2 virus.

In order to confirm the values of $\alpha _1$ and $\alpha _2$ geometrically both S(t) and I(t) are drawn in Fig. 7. As the positions of peak of I(t) could be identified by the relation, $S(t)=\beta /\alpha$, the crossing point of S(t) and the horizontal line $\beta /\alpha _1=1/(14\times 1.48\times 10^{-7})=4.82625\times 10^{5}$, appears over the first peak of I(t) in other words. Similarly, crossing points of S(t) and the horizontal line $\beta /\alpha _2=1/(14\times 8.7\times 10^{-7})=8.21018\times 10^{4}$, must appear below the second and third peaks of I(t). Hence, the MWSIR model accurately identified the dates of first, second and third peaks of the infected population which occurred on Sep 16, 2020, May 8, 2021 and January 25, 2022, respectively. Height of the first peak of I(t) can be estimated approximately by using Eq. (2), with $\alpha _1=1.48\times 10^{-7},\,\beta =1/14,\, S(0)=8.8\times 10^{5},\,I(0)=1,$ which gives $I^{(1)}_{\mathrm{max}}=1.07471\times 10^{5}$. This value is 13.35% higher than the actual one. Similarly, heights of second and third peaks given by Eq. (2) are $I^{(2)}_{\mathrm{max}}=3.88941\times 10^{5}$ and $I^{(3)}_{\mathrm{max}}=2.57270\times 10^{5}$, respectively. Those are lower than actual observation by 0.58% and 17.52%, respectively. However, the numerical estimation is much better.

Fig. 7

Variation of S(t), I(t), R(t) obtained in MWSIR model along with the horizontal lines $\beta /\alpha _1=4.82625\times 10^{5}$ and $\beta /\alpha _2=8.21018\times 10^{4}$, are shown. It reveals that all the populations, S(t), I(t) and R(t) are always positive in the parameter regime in accordance to the theorem

This phenomenological study predicts that 5.5% of individuals infected during January 30, 2020 to April 14, 2021 become susceptible again for another infection. Similarly, 8.0% of individuals infected during later period become susceptible again for the next infection. These predictions are made in accordance to the estimated values of $\gamma _1=0.055$, and $\gamma _2=0.08$ in the different time domain. The difference, $\gamma _1 \ne \gamma _2$, may account the effects of quarantine, isolation, vaccination and other preventive measures along with the presence of new variants like delta and omicron those are regarded as more infectious. However, as the solutions of the nonlinear equations are highly sensitive to the initial conditions, like $S(0),\,I(0)$, and R(0), estimated values of the parameters, $\alpha ,\,\gamma$, and $\tau$ are likely to change accordingly with the change of initial values. Which on the other hand will change the predictions for obvious reason.

5 Discussion

In order to study the behaviour of ongoing pandemic of COVID-19 in India mathematically, a modified version of SWSIR model termed as MWSIR model is proposed here which is found successful to reproduce the emergence of the multiple peaks in epidemiological wave prevailed in this country. The model is deigned in such a fashion that it is able to yield periodic as well as nonperiodic epidemiological waves with varying widths and heights by tuning its parameters. Equation 1a reveals that the sign of $\dot{S}$ is determined by the factor $\alpha \, { S(t)}\,{ I(t)} -\gamma \,I(t\!-\!\tau )$, when $\mu =0$. So it depends on the values of both S(t) and I(t) and as a result the opposite relations, $\dot{S} < 0$ and $\dot{S} > 0$ are being satisfied alternately with the increase of time. This property ultimately leads to oscillatory solutions.

As the SARS-CoV-2 virus responsible for the COVID-19 is highly infectious, the spreading of this disease cannot be controlled easily by means of simple preventive measures like quarantine, isolation, lock-down and even vaccination. In addition, emergence of super-spreading new variants, for example, delta and omicron makes the situation worse at later time. As a result, in due course, a sizable fraction of recovered people gets infected multiple times leading to multiple waves of the epidemiological infection. In order to explain this particular feature, the SIR model has been modified where a finite probability of the recovered people for becoming susceptible again after their recovery is taken into account. The waves of epidemiological evolution witnessed in India during January 30, 2020 to March 14, 2022 (775 days) have been reproduced satisfactorily in this formulation. SARS-CoV-2 virus was transmitted into India by a number of COVID-19 patients who entered this country mainly via air-travel mode through different airports of India continuously by the end of January 2020. Testing facility of COVID-19 infection was not adequate at that time. So the true number of infected individual for that time is not available. Therefore, this study is carried out with respect to the minimum number of infected individual, which means $I(0)=1$. Estimated values of the parameters obtained in this study might be useful for imposing restrictions to control the pandemic in future. It will become helpful even for making accurate forecast and prediction.

However, in this simple model no time delay for the incubation period of the pathogens within the human body is considered, and the effect of quarantine, isolation, vaccination and other macroscopic measures are not take into account. So, it is expected that more accurate prediction can be made with the help of this model by accommodating the effect of quarantine, isolation, vaccination, lock-down and other factors in its modified version. Which means that the discrepancy between theoretical estimation and actual daily new cases can be removed further by formulating multi-wave SEIR, SIQR, SEIQR and other hybrid models. Obviously, this model can be employed for examining the characteristics of epidemiological waves found in other countries as well.