Bistability and delayed acceleration feedback control analytical study of collocated and non-collocated cases

Abstract

Stability and bifurcation analysis of a non-rigid robotic arm controlled with a time-delayed acceleration feedback loop is addressed in this work. The study aims at revealing the dynamical mechanisms leading to the appearance of limit cycle oscillations existing in the stable region of the trivial solution of the system, which is related to the combined dynamics of the robot control and its structural nonlinearities. An analytical study of the bifurcations occurring at the loss of stability illustrates that, in general, hardening structural nonlinearities at the joint promote a subcritical character of the bifurcations. Consequently, limit cycle oscillations are generated within the stable region of the trivial solution. A nonlinear control force is then developed to enforce the supercriticality of the bifurcations. Results illustrate that this strategy enables to partially eliminate limit cycle oscillations coexisting with the stable trivial solution. The mechanical system is analysed in a collocated and a non-collocated configuration, depending on the position of the sensor.

1 Introduction

Robots were originally developed for pick-and-place operations [25], for which extreme geometrical accuracy is not a particular need. Later, industrial robots were also used as a milling platform, first for prototype manufacturing of clay [38, 39] mostly for industrial design cases. The repeatability of positioning is more important for machining than for pick-and-place operations, which was enough for the mentioned clay prototype sculpture manufacturing. By the time, geometrical accuracy has increased by a factor of 10 from mm to tenth of mm by applying better sensors and proportional-derivative feedback control. Prototype manufacturing is slowly taken over by plastic 3D rapid prototyping [26, 44]; however, for some cases, clay still serves as cheap and durable solution to test design issues of e.g. sculpture-like car chassis prototypes. Indeed, the most common open kinematical chain robots are excellent to manufacture sculpture-like surfaces [9,10,11] due to their workspace, but this versatile configuration lacks rigidity.

Machine tools are created to perform machining on metal parts; their superstructure is designed to serve stiffness and rigidity [29], required to provide the necessary geometrical accuracy. This leads to a design very different with respect to robots, resulting in heavy, large, sturdy and consequently expensive superstructures for machine tools.

Machining of metal parts usually requires high shape accuracy; at first, the reflected stiffness must overcome the corresponding so-called cutting stiffness [43] ensuring the minimum requirement for a stable operation. This is still very much a must even for roughing operations, where accuracy is not an important factor, because of the great forces transmitted during cutting. This requirement is especially hard to achieve by industrial robots, which are generally slender and not particularly stiff [31, 32, 42]. There are stiffer geometric arrangements of open kinematic chains of robotic arms; however, they generally provide a drastically reduced utilisable workspace, if the cutting is possible at all.

Theoretically, an online control solution is possible to upgrade the robot dynamic performance by built-in velocity and acceleration feedback controllers. On the one hand, robot manufacturers are not taking the risk to open their control development kit to that level. On the other hand, possible factory level deployment of upgraded industrial robots can be accepted by owners either using off-line techniques or utilising a certified built-in control.

Since industrial robot users are also hesitant to accept mounted passive and semi-active embedded solutions to increase the dynamic reflected stiffness of the end-effector, another relatively cheap solution could be using simply feedback sensor signals in the built-in position control of stock industrial robots. This might sound impossible, but stable manufacturing might be achieved with careful parameter management, especially with the synchronisation of delays in the built-in and new feedback loop, most probably using acceleration signals.

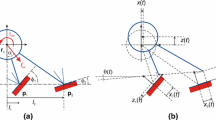
Usually, a proportional-derivative control scheme is used in the inner controller of the robot [47] to decrease the positioning error. An additional acceleration feedback controller, which is fed through the conventional inner controller of the robot, is sometimes utilised to mitigate the vibrations arising from the machining processes [7, 18, 34, 48, 49] or to compensate for the flexibility of the arm [12, 19]. Acceleration feedback is particularly appealing for industrial applications thanks to its reasonable price, compared to position and velocity measurement devices required to measure the state of the robot’s end-effector [14, 15]. Typically, sensors measure only the state of the motor’s rotor, while only relatively recently, sensors for directly (or indirectly) measuring the position of the arm have been proposed [3, 36]. Because of the flexibility of the robotic arm, especially at the joints [1], the correct positioning of the accelerometer can have a significant effect on the stability and effectiveness of the control scheme [13]. The system is named collocated if the sensors are positioned near the actuator and non-collocated if they are positioned far from the actuator [2, 22]. The two cases are illustrated in Fig. 1.

Fig. 1

Collocated (left) and non-collocated (right) robotic arms

Feedback controllers usually introduce time delays in the system [41], which is another element potentially having a substantial effect on the stability and effectiveness of the controller, even if it is relatively small [17, 23]. Nevertheless, its effect is not necessarily detrimental; indeed, several studies exploit time delay to enhance the stability performance of a controller [5]. For instance, in [4] and [45] time delay is purposely included in the system in order to enhance damping because of the phase shift it generates between the acceleration and the control force. A similar study is performed on a non-collocated system in [37], where the damping properties of the delayed acceleration feedback controller are evaluated.

A usual common experience on slender open kinematic chain robots is that they often encounter structural nonlinearities that could induce unstable limit cycles even in case of achieved stable stationary cutting domain. Especially the joints and the drive of the robotic arm can introduce nonlinearities to the stiffness characteristic, which is another feature relevant for the system dynamics often neglected [31, 40]. This aspect was partially studied, for instance, in [8], where a lumped mass model with a cubic nonlinearity controlled by a delayed acceleration feedback signal was investigated; the implications of 1:1 resonances and 1/3 subharmonic resonances on stability were analysed. It should be emphasised that the nonlinearity might limit the robustness of the equilibrium position to external perturbations even if the equilibrium is stable [21].

This study was motivated by the industrial experience on appearing structural nonlinearities and the possible solution to use an acceleration feedback control scheme in the built-in robot controller. The main objective of this work is to analyse the influence of the nonlinear behaviour at the joint of the robotic arm on its dynamics. In particular, we aim at unveiling how it affects the bifurcation characteristic at the loss of stability and to which extent this can be controlled.

We attempted to create the simplest possible equivalent model that is able to produce nonlinear behaviour and mimic the robot position control. However, it should be noted that it is far from the real-life behaviour of robotic arms. A two-degree-of-freedom (DoF) lumped model of a linear robotic arm, subject to an acceleration feedback control, is considered. Two configurations are studied, namely a collocated and a non-collocated one, depending on the position of the accelerometer. First, the stability of both configurations is analytically studied, and then, the effect of the various system parameters on the stability is analysed. The stability of the delayed and non-delayed systems is compared, which highlights the importance of considering time delay in such systems. Later, exploiting a multiple-scale perturbation technique [35], the bifurcations occurring at the loss of stability are analytically studied, providing a partial understanding of the global dynamics of the system. Finally, a nonlinear term is included in the control loop to modify the character of the bifurcation in the case of subcritical bifurcations, with the objective of improving the robustness of the stable solution. Limitations and advantages of the various configurations and control laws considered are carefully analysed.

2 Mechanical model

The adopted two-DoF mechanical system is shown in Fig. 2.

The model consists of two lumped masses $m_1$ and $m_2$ connected by a nonlinear spring k and a linear damping c. The prescribed reference trajectory $u_{\mathrm {d}}$ is programmed, such that in ideal circumstances an identical constrained motion $u_{\mathrm {r}}$ is imposed to the mass $m_1$ via a linear spring $k_1$ with time delay $\tau _{\mathrm {r}}$. This gives the dynamical system governed by the following equations of motion

$$\begin{aligned} \begin{aligned}&m_1u''_1+c\left( u'_1-u'_2\right) +k(\varDelta u)\left( u_1-u_2\right) \\&\quad +k_1u_1=k_1u_{\mathrm {r}},\\&m_2u''_2+c\left( u'_2-u'_1\right) +k(\varDelta u)\left( u_2-u_1\right) =0, \end{aligned} \end{aligned}$$

(1)

Fig. 2

Two-DoF model of the robotic arm

where $u_1$ and $u_2$ are the displacements of the lumped masses. Prime $(')$ indicates derivation with respect to time t. Furthermore, $\varDelta u:=u_2-u_1$ and the nonlinear spring is considered with a second-order nonlinearity in the stiffness characteristic $k(\varDelta u)=k_2+k_{\mathrm {nl}}\left( \varDelta u\right) ^2$, which will lead to cubic nonlinearities in the system. Apart from the prescribed reference trajectory $u_{\mathrm {d}}$, an additional feedback signal $u_{\mathrm {f}}$, with third-order nonlinear acceleration signal is fed back with time delay $\tau _{\mathrm {f}}$ and summarised with ideal constrained motion $u_{\mathrm {r}}$. This gives a final constrained motion $u_{\mathrm {r}}(t)=u_{\mathrm {d}}(t-\tau _{\mathrm {r}})+a_1u''_1(t-\tau )+a_{\mathrm {nl},1}u^{\prime \prime 3}_1(t-\tau )+a_2u''_2(t-\tau )+a_{\mathrm {nl},2}u^{\prime \prime 3}_2(t-\tau )$, where $\tau =\tau _{\mathrm {r}}+\tau _{\mathrm {f}}$ is the sum of the delays. The linear and nonlinear acceleration control gains are $a_1$, $a_2$, $a_{\text {nl},1}$ and $a_{\text {nl},2}$, respectively. The values $m_1$, $m_2$, c, $k_1$ and $k_2$ are assumed to be positive real numbers, while $k_{\text {nl}}$, $a_1$, $a_2$, $a_{\text {nl},1}$ and $a_{\text {nl},2}$ are generic real numbers. Generally, the control force is calculated based on the value of the acceleration of a specific point; therefore, we assume that either $a_1=0$ and $a_{\text {nl},1}=0$ or $a_2=0$ and $a_{\text {nl},2}=0$. These two cases correspond to a non-collocated or collocated controller, respectively. With these considerations, the equations of motion can be written as

$$\begin{aligned}&m_1u''_1+c\left( u'_1-u'_2\right) +k_2\left( u_1-u_2\right) +k_1u_1\nonumber \\&\quad +k_{\mathrm {nl}}\left( u_1-u_2\right) ^3=k_1\big (u_{\mathrm {d}\tau _{\mathrm {r}}}+a_1u''_{1\tau }+a_{\mathrm {nl},1}u^{\prime \prime 3}_{1\tau }\nonumber \\&\quad +a_2u''_{2\tau }+a_{\mathrm {nl},2}u^{\prime \prime 3}_{2\tau }\big ),\nonumber \\&m_2u''_2+c\left( u'_2-u'_1\right) +k_2\left( u_2-u_1\right) \nonumber \\&\quad +k_{\mathrm {nl}}\left( u_2-u_1\right) ^3=0, \end{aligned}$$

(2)

where $u_{\mathrm {d}\tau \mathrm {r}}=u_{\mathrm {d}}(t-\tau _{\mathrm {r}}),\;u''_{1\tau }=u''_1(t-\tau ),\;u''_{2\tau }=u''_2(t-\tau )$. In order to focus on the instabilities induced by the acceleration feedback controller, constant prescribed reference trajectory is assumed $u_{\mathrm {d}}(t)\equiv u_{\mathrm {d}}$. The equilibrium results in $({\overline{u}}_1,\;{\overline{u}}_2)=(u_{\mathrm {d}},\;u_{\mathrm {d}})$. With the introduction of perturbations $u_1={\overline{u}}_1+x_1$ and $u_2={\overline{u}}_2+x_2$, the equations of motion can be written as

$$\begin{aligned} \begin{aligned}&m_1x''_1+c\left( x'_1-x'_2\right) +k_2\left( x_1-x_2\right) +k_1{\tilde{x}}_1\\&\qquad +k_{\text {nl}}\left( x_1-x_2\right) ^3\\&\quad =k_1\left( a_1x''_{1\tau }+a_{\text {nl},1}x^{\prime \prime 3}_{1\tau }+a_2x''_{2\tau }+a_{\text {nl},2}x^{\prime \prime 3}_{2\tau }\right) ,\\&m_2x''_2+c\left( x'_2-x'_1\right) +k_2\left( x_2-{\tilde{x}}_1\right) \\&\quad +k_{\text {nl}}\left( x_2-x_1\right) ^3=0. \end{aligned} \end{aligned}$$

(3)

In order to reduce the number of parameters, we divide both equations by $m_1$; we introduce the dimensionless time $t\omega _1\rightarrow t$ and displacements $x_1\sqrt{|k_{\text {nl}}|/(rk_1)}\rightarrow x_1$ and $x_2\sqrt{|k_{\text {nl}}|/(rk_1)}\rightarrow x_2$, where $\omega _1^2:=k_1/m_1$ and $r:=m_2/m_1$. We thus reduce the system to

$$\begin{aligned} \begin{aligned}&\ddot{x}_1+2\chi r\gamma \left( \dot{x}_1-\dot{x}_2\right) +\gamma ^2 r\left( x_1-x_2\right) +x_1\\&\quad +\mu r\left( x_1-x_2\right) ^3-\big (\kappa _1\ddot{x}_{1\tau }+\kappa _{\text {nl},1}\ddot{x}_{1\tau }^3+\kappa _2\ddot{x}_{2\tau }\\&\quad +\kappa _{\text {nl},2}\ddot{x}_{2\tau }^3\big )=0\\&\ddot{x}_2+2\chi \gamma \left( \dot{x}_2-\dot{x}_1\right) +\gamma ^2\left( x_2-x_1\right) \\&\quad +\mu \left( x_2-x_1\right) ^3=0, \end{aligned} \end{aligned}$$

(4)

where over-dot ( $\dot{}$ ) indicates derivation with respect to the new, rescaled dimensionless time t, while $\ddot{x}_{1\tau }=\ddot{x}_1\left( t-\tau \right) ,\;\ddot{x}_{2\tau }=\ddot{x}_2\left( t-\tau \right)$, with the dimensionless time delay $\tau \omega _1\rightarrow \tau$. Besides, the dimensionless standalone natural frequency ratio $\gamma :=\omega _2/\omega _1$, the standalone damping ratio $\chi :=c/(2m_2\omega _2)$, with $\omega _2^2:=k_2/m_2$, the rescaled control parameters $\kappa _1:=\omega _1^2a_1$, $\kappa _2:=\omega _1^2a_2$, the rescaled nonlinear control parameters $\kappa _{\text {nl},1}:=\omega _1^6a_{\text {nl},1}rk_1/|k_{\text {nl}}|$, $\kappa _{\text {nl},2}:=\omega _1^6a_{\text {nl},2}rk_1/|k_{\text {nl}}|$ and $\mu :=\text {sign}(k_{\text {nl}})$ are introduced.

3 Stability analysis

In this section, we investigate the linear stability of the system’s trivial solution. Firstly, we study the system with a traditional approach, neglecting the time delay. Then, we analyse the delayed system and perform a parametric analysis to evaluate the sensitivity of the stable region to the parameter values.

3.1 Non-delayed case

In order to analyse the importance of considering the time delay of the control force, in this section, we study the stability of the collocated and non-collocated systems neglecting the time delay. Imposing $\tau =0$, regarded to the ideal non-delayed control, the system in Eq. (4) is reduced to

$$\begin{aligned} \begin{aligned}&\ddot{x}_1+2\chi r\gamma \left( \dot{x}_1-\dot{x}_2\right) \\&\quad +\gamma ^2 r\left( x_1-x_2\right) +x_1+\mu r\left( x_1-x_2\right) ^3\\&\quad -\left( \kappa _1\ddot{x}_1+\kappa _{\mathrm {nl},1}\ddot{x}_1^3+\kappa _2\ddot{x}_2+\kappa _{\mathrm {nl},2}\ddot{x}_2^3\right) =0,\\&\ddot{x}_2+2\chi \gamma \left( \dot{x}_2-\dot{x}_1\right) \\&\quad +\gamma ^2\left( x_2-x_1\right) +\mu \left( x_2-x_1\right) ^3=0. \end{aligned} \end{aligned}$$

(5)

This means that the control actions affect the inertia, while $\kappa _{\mathrm {nl},1}$ and $\kappa _{\mathrm {nl},2}$ introduces conventional nonlinear terms. By solving the system with respect to $\ddot{x}_1$ and $\ddot{x}_2$ and linearising it around its trivial equilibrium, we obtain the linear system

$$\begin{aligned} \dot{\mathbf {x}}={\mathbf {A}}{\mathbf {x}}, \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned}&{\mathbf {A}}= \begin{bmatrix} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ \frac{\gamma ^2\left( r-\kappa _2\right) +1}{\kappa _1-1} &{} \frac{\gamma ^2 (\kappa _2-r)}{\kappa _1-1} &{} \frac{2 \gamma \chi (r-\kappa _2)}{\kappa _1-1} &{} \frac{2 \gamma \chi (\kappa _2-r)}{\kappa _1-1} \\ \gamma ^2 &{} -\gamma ^2 &{} 2 \gamma \chi &{} -2 \gamma \chi \\ \end{bmatrix},\\&{\mathbf {x}}= \begin{bmatrix} x_1\\ x_2\\ {\dot{x}}_1\\ {\dot{x}}_2 \end{bmatrix}. \end{aligned} \end{aligned}$$

(7)

The stability of this system can be investigated with the Routh–Hurwitz criterion [46]. For this purpose, we calculate the characteristic equation

$$\begin{aligned} \begin{aligned}&\left| \lambda {\mathbf {I}}-{\mathbf {A}}\right| =\lambda ^4+\frac{2 \gamma \chi \left( \kappa _1+\kappa _2-1-r\right) }{\kappa _1-1}\lambda ^3\\&\quad +\frac{\gamma ^2 \left( \kappa _1+\kappa _2-1-r \right) -1}{\kappa _1-1}\lambda ^2\\&\quad -\frac{2 \gamma \chi }{{\kappa 1}-1}\lambda -\frac{\gamma ^2}{{\kappa 1}-1}=0, \end{aligned} \end{aligned}$$

(8)

which can be rewritten as

$$\begin{aligned} \left| \lambda {\mathbf {I}}-{\mathbf {A}}\right| =\lambda ^4+b_1\lambda ^3+b_2\lambda ^2+b_3\lambda +b_4=0, \end{aligned}$$

(9)

where ${\mathbf {I}}$ is the identity matrix. Considering the following Hurwitz matrix

$$\begin{aligned} {\mathbf {H}}= \begin{bmatrix} b_1 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ b_3 &{} \quad b_2 &{}\quad b_1 &{}\quad 1\\ 0 &{}\quad b_4 &{}\quad b_3 &{}\quad b_2\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad b_4 \end{bmatrix}, \end{aligned}$$

(10)

the system is stable if all the leading principal minors of ${\mathbf {H}}$ are positive. Conditions providing stability of the trivial solution for the collocated and non-collocated cases are discussed below.

3.1.1 Collocated case

If $\kappa _2=0$, then the four conditions from the Hurwitz matrix are

$$\begin{aligned} \begin{aligned}&\frac{-\gamma ^2}{\kappa _1-1}>0,\quad -\frac{4 \gamma ^2 \chi ^2 r}{(\kappa _1-1)^3}>0,\quad \frac{4 \gamma ^4 \chi ^2 r}{(\kappa _1-1)^4}>0,\\&\frac{2 \gamma \chi \left( \gamma ^2 (\kappa _1-1)^2\!+\!\gamma ^2 r^2\!-\!2 \gamma ^2 (\kappa _1-1) r\!+\!r\right) }{(\kappa _1-1)^2}\!>\!0. \end{aligned} \end{aligned}$$

(11)

These conditions can be reduced to two sets of conditions

$$\begin{aligned}&\gamma<0,\;\chi<0,\;r>0,\;\kappa _1<1.\nonumber \\&\gamma>0,\;\chi>0,\;r>0,\;\kappa _1<1. \end{aligned}$$

(12)

The frequency ratio $\gamma$ and mass ratio r have to be positive real values. Therefore, the following conditions must be fulfilled for the trivial solution to be stable:

$$\begin{aligned} \chi >0,\;\kappa _1<1. \end{aligned}$$

(13)

This result seems in disagreement with respect to what obtained regarding the stability analysis for the delayed case, illustrated in the following section (Fig. 3(i)). This discrepancy is discussed in Sect. 3.2.

3.1.2 Non-collocated case

If $\kappa _1=0$, then the four conditions from the Hurwitz matrix are

$$\begin{aligned} \begin{aligned}&\gamma ^2>0,\\&2 \gamma \chi \left( \gamma ^2 (\kappa _2-1)^2-\kappa _2\!+\!\gamma ^2 r^2\!-\!2 \gamma ^2 (\kappa _2-1) r+r\right)>0,\\&4 \gamma ^2 \chi ^2 (r-\kappa _2)>0,\\&4 \gamma ^4 \chi ^2 (r-\kappa _2)>0. \end{aligned} \end{aligned}$$

(14)

These conditions can be reduced to two sets of inequalities:

$$\begin{aligned}&\gamma<0,\;\chi<0,\;r\in {\mathbb {R}},\;\kappa _2<r.\nonumber \\&\gamma>0,\;\chi >0,\;r\in {\mathbb {R}},\;\kappa _2<r. \end{aligned}$$

(15)

Since the frequency and mass ratio must be positive real numbers, these conditions are reduced to

$$\begin{aligned} \chi >0,\;\kappa _2<r. \end{aligned}$$

(16)

This result is fully confirmed by the stability charts plotted in Fig. 3(ii). In fact, for all investigated cases, as $\tau \rightarrow 0$ the system is stable if $\kappa _2\in \left( -\infty ,r\right)$.

3.2 Delayed case

In order to study the stability of the trivial solution of the system, we temporarily neglect nonlinear terms and we consider the trial solution $x_1=\xi _1\mathrm {e}^{\lambda t}$ and $x_2=\xi _2\mathrm {e}^{\lambda t}$, obtaining

$$\begin{aligned} \begin{aligned}&\lambda ^2\xi _1+2 \chi r \gamma \lambda \left( \xi _1 -\xi _2 \right) +r \gamma ^2 \left( \xi _1-\xi _2\right) +\xi _1\\&\quad -\left( \kappa _1 \lambda ^2 \xi _1+\kappa _2 \lambda ^2 \xi _2\right) \mathrm {e}^{-\lambda \tau }=0\\&\lambda ^2\xi _2+2 \chi \gamma \lambda \left( \xi _2 -\xi _1 \right) +\gamma ^2 \left( \xi _2-\xi _1\right) =0, \end{aligned} \end{aligned}$$

(17)

By applying the D-subdivision method, when $\lambda =\mathrm {i}\omega$, the characteristic function has the following form

$$\begin{aligned} \begin{aligned}&\left( 1-\kappa _1\mathrm {e}^{-\mathrm {i}\tau \omega }\right) \omega ^4+\big (2 \mathrm {i} \chi \left( \kappa _1+\kappa _2\right) \gamma \mathrm {e}^{-\mathrm {i} \tau \omega }-2 \mathrm {i} \chi r \gamma \\&\quad -2 \mathrm {i} \chi \gamma \big )\omega ^3+\left( \left( \kappa _1+\kappa _2\right) \gamma ^2 \mathrm {e}^{-\mathrm {i} \tau \omega }-\left( r+1\right) \gamma ^2-1\right) \omega ^2\\&\quad +2 \mathrm {i} \chi \gamma \omega +\gamma ^2=0, \end{aligned} \end{aligned}$$

(18)

whose solution provides boundaries which separate regions of the parameter space in which the system has different number of eigenvalues having positive real part. Some of these boundaries mark the stable region of the system.

Separating real and imaginary parts of Eq. (18), we obtain

$$\begin{aligned} \begin{aligned}&\text {Re}:\; 2 \chi \left( \kappa _1+\kappa _2\right) \omega ^3 \gamma \sin \tau \omega +\big (\left( \kappa _1+\kappa _2\right) \omega ^2 \gamma ^2\\&\quad ,-\kappa _1\omega ^4\big ) \cos \tau \omega =\omega ^2 \left( (r+1) \gamma ^2+1\right) -\omega ^4\\&\quad -\gamma ^2,\\&\text {Im}:\; 2 \chi \left( \kappa _1+\kappa _2\right) \omega ^3 \gamma \cos \tau \omega -\big (\left( \kappa _1+\kappa _2\right) \omega ^2 \gamma ^2\\&\quad -\kappa _1\omega ^4\big )\sin \tau \omega =2 \chi \omega \gamma \left( (r+1) \omega ^2-1\right) . \end{aligned} \end{aligned}$$

(19)

Summing up the squares of these two equations leads to

$$\begin{aligned} \begin{aligned}&4 \chi ^2 \left( \kappa _1+\kappa _2\right) ^2 \omega ^6 \gamma ^2+\left( \left( \kappa _1+\kappa _2\right) \omega ^2 \gamma ^2-\kappa _1\omega ^4\right) ^2\\&\quad -\left( \omega ^2 \left( (r+1) \gamma ^2+1\right) -\omega ^4-\gamma ^2\right) ^2\\&\quad -\left( 2 \chi \omega \gamma \left( (r+1) \omega ^2-1\right) \right) ^2=0. \end{aligned} \end{aligned}$$

(20)

Equation (20) can be directly solved with respect to $\kappa _1$ or $\kappa _2$. In particular, we first impose $\kappa _2=0$, which refers to the case of a collocated controller, obtaining

$$\begin{aligned} \begin{aligned}&\kappa _1(\omega )=\pm \Big (\big (2 \gamma ^2 \omega ^2 \left( (r\!+\!1) \omega ^2-1\right) \big (2 \chi ^2 \left( (r\!+\!1) \omega ^2\!-\!1\right) \\&\quad -\omega ^2+1\big )+\gamma ^4 \left( (r+1) \omega ^2-1\right) ^2+\omega ^4 \left( \omega ^2-1\right) ^2\big )\Big /\\&\qquad \big (\omega ^4 \left( 2 \left( 2 \chi ^2-1\right) \gamma ^2 \omega ^2+\gamma ^4+\omega ^4\right) \big )\Big )^{1/2}.\end{aligned} \end{aligned}$$

(21)

Instead, imposing $\kappa _1=0$ and therefore referring to the case of a non-collocated controller, we have

$$\begin{aligned}&\kappa _1(\omega )=\pm \Big (\big (2 \gamma ^2 \omega ^2 \left( (r\!+\!1) \omega ^2-1\right) \big (2 \chi ^2 \left( (r\!+\!1) \omega ^2-1\right) \nonumber \\&\quad -\omega ^2+1\big )+\gamma ^4 \left( (r+1) \omega ^2-1\right) ^2+\omega ^4 \left( \omega ^2-1\right) ^2\big )\Big /\nonumber \\&\qquad \big (\gamma ^2 \omega ^4 \left( 4 \chi ^2 \omega ^2+\gamma ^2\right) \big )\Big )^{1/2}. \end{aligned}$$

(22)

Equations (21) and (22) will be directly used for defining the stability boundary in the $\tau ,\kappa _1$ and $\tau ,\kappa _2$ spaces for the collocated and non-collocated cases, respectively. Solving Eq. (19) with respect to $\sin \tau \omega$ and $\cos \tau \omega$, we obtain

$$\begin{aligned} \begin{aligned}&s(\omega ):=\sin \tau \omega \\&=\frac{2 \chi \gamma \omega \left( \kappa _1 r \omega ^2-\kappa _2 \omega ^2+\kappa _2\right) }{d(\omega )},\\&c(\omega ):=\cos \tau \omega \\&=\frac{1}{\omega ^2d(\omega )}\Big (\gamma ^2 \omega ^2 \big (\kappa _1 \big (4 \chi ^2 \left( (r+1) \omega ^2-1\right) \\&\qquad -(r+2) \omega ^2+2\big )\\&\qquad +\kappa _2 \left( 4 \chi ^2 \left( (r+1) \omega ^2-1\right) -\omega ^2+1\right) \big )\\&\qquad +\gamma ^4 (\kappa _1+\kappa _2) \left( (r+1) \omega ^2-1\right) +\kappa _1 \omega ^4 \left( \omega ^2-1\right) \Big ), \end{aligned} \end{aligned}$$

(23)

where

$$\begin{aligned}&d(\omega ):=2 \gamma ^2 \omega ^2 (\kappa _1+\kappa _2) \left( \left( 2 \chi ^2-1\right) \kappa _1+2 \chi ^2 \kappa _2\right) \nonumber \\&\quad +\gamma ^4 (\kappa _1+\kappa _2)^2+\kappa _1^2 \omega ^4. \end{aligned}$$

(24)

From Eq. (23), we can directly obtain the value of $\tau$ as a function of $\omega$, i.e.

$$\begin{aligned} \tau _n(\omega )=\frac{1}{\omega }\left( \arctan _2\left( s(\omega ),c(\omega )\right) +n2\pi \right) ,\qquad n\in {\mathbb {Z}}. \end{aligned}$$

(25)

Equations (21), (22) and (25) enable us to plot the stability diagram in the ($\tau ,\kappa _1$) and ($\tau ,\kappa _2$) spaces. The diagrams, illustrated in Fig. 3, are obtained spanning a large range of $\omega$ values adopting various n values in Eq. (25). The effect of parameter values on stability is discussed in Sect. 3.3.

Fig. 3

Stability charts for the collocated (i) and non-collocated (ii) cases with the investigated parameters: mass ratio r (a), standalone natural frequency ratio $\gamma$ (b) and the standalone damping factor $\chi$ (c). In the collocated case $\kappa _2=0$ and in the non-collocated case $\kappa _1=0$. The non-investigated parameters are $r=1,\;\gamma =1,\;\chi =0.1$. The shaded area shows the stable region. The light green line shows the case, where the largest characteristic root has minimum $\mathrm {Re}\lambda _{\mathrm {min}}$, which represents the best performance case. The parameters for this case are $r=1,\;\gamma =1,\;\chi =0.1$. (Color figure online)

Fig. 4

(a, b) Eigenvalues of the collocated system for $r=1,\;\gamma =1,\;\chi =0.1,\;\tau =10^{-5}$, $\kappa _1=-0.9999$ (a) and $\kappa _1=-1.0001$ (b); the insets show four eigenvalues of the spectra, which coincide with the eigenvalues of the non-delayed system. c, d Numerical simulations of the system dynamics for the same parameter values; c non-delayed case ($\tau =0$), d delayed case ($\tau =10^{-5}$); $\kappa _1$ as indicated in the figure

Figure 3(i) suggests that a necessary condition to have stability is that $-1<\kappa _1<1$, for the collocated case. This condition can be obtained analytically considering the limit of $\kappa _1$ for $\omega \rightarrow \infty$ in Eq. (21), which gives $\pm 1$. This result is typical for neutral delay differential equations as discussed, for instance, in [30]. Interestingly, this conclusion implies a discontinuity with respect to the non-delayed case for $\tau \approx 0$ and $\kappa _1<-1$. In fact, as demonstrated in Sect. 3.1, the trivial solution of the collocated system is stable for $\chi >0$ and $\kappa _1<1$, therefore, also for $\kappa _1<-1$. Figure 3(i) clearly shows that for $\tau \rightarrow 0$ the system is unstable if $\kappa _1<-1$.

Let us investigate the eigenvalues of the system in correspondence with the discontinuity. Figure 4a, b depicts some of the eigenvalues of the system for a very small time delay ($\tau =10^{-5}$), for $\kappa _1=-0.9999$ and $\kappa _1=-1.0001$, respectively. The four eigenvalues in the insets of the two plots exist for both the delayed and the non-delayed cases. In both cases, they remain in the left part of the complex plane, which suggests that the instability is not related to their perturbations. The two figures show other eigenvalues having the absolute value of their real part approximately 10. However, while for $\kappa _1=-0.9999$ (Fig. 4a) the real part is negative, for $\kappa _1=-1.0001$ (Fig. 4b) it is positive, which confirms the stable and unstable behaviour of the two cases, respectively. Nevertheless, since these eigenvalues are far apart despite having very similar parameter values, they confirm the discontinuity of the spectrum also for $\kappa _1=-1$ and $\tau \ne 0$. We speculate that the eigenvalues might move from the left to the right side of the complex plane through $\pm \infty$ of the imaginary axis, which is consistent with the limit of $\kappa _1$ for $\omega \rightarrow \infty$ in Eq. (21), and with the large value of their imaginary part. Indeed, a similar scenario might be responsible for the spectral discontinuity occurring at $\tau =0$ and $\kappa _1<-1$.

Previous studies [24, 27, 28, 33, 50] illustrate that similar discontinuities in the spectrum are rather common for systems governed by neutral delayed differential equations. For instance, in [28, 50], analogous discontinuities are encountered in the delayed control of an elastic beam, both for $\tau =0$ and for $\tau \ne 0$. The possible existence of such discontinuities was mathematically proven in [24]. Additionally, Insperger et al. [27] encountered a similar discontinuity for advanced delay differential equations as well.

Figure 4c, d provides time series of the system dynamics in correspondence of the discontinuity. Figure 4c shows that, for the non-delayed case, the system is stable and has practically unvaried behaviour for $\kappa _1$ slightly larger or smaller than $-1$. On the contrary, Fig. 4d illustrates that, for the delayed case ($\tau =10^{-5}$), if $\kappa _1<-1$, the system rapidly experiences instabilities that cause high-frequency oscillations of increasing amplitude.

3.3 Parameter analysis

In this section, we investigate the sensitivity and behaviour of the stable region with changing parameters. The stable region is studied in the plane of the time delay $\tau$ and control parameters $\kappa _1,\;\kappa _2$. Generally, one would think that lower time delays would be beneficial for stability. However, the control of the robot and the acceleration feedback controller can introduce relatively large time delays in the system, so the stable region for larger $\tau$ values has to be studied. Although the actuator’s saturation is neglected in this study, it should be noted that technological constraints limit the value of the control parameters $\kappa _1$ and $\kappa _2$; therefore, they cannot have arbitrarily large values. The parameter analysis of the system is illustrated in Fig. 3.

The light green line in Fig. 3 shows the controller with the best performance, i.e. where the largest characteristic root is minimum for one particular parameter set. It should be noted that this is very close to the boundary of stability; therefore, when one wants to operate the controller close to this line, the effect of the nonlinear terms can be particularly relevant for the system dynamics.

3.3.1 Variations of the mass ratio r

Stability charts for the collocated and non-collocated cases for various mass ratio r values, with the other parameters kept constant $\gamma =1,\;\chi =0.1$, are displayed in Fig. 3a. Regarding the collocated case (Fig. 3a, (i), the stable region is not very sensitive to variations of the mass ratio r. The positive stable region shrinks with increasing $\tau$ values. On the contrary, the negative stable region undergoes only a slight contraction for all the considered $\tau$ range. This feature, for the collocated case, will also be confirmed for other parameter values investigated below.

Conversely, the non-collocated system is much more sensitive to variations of r. In general, the stable region enlarges with r, particularly for small $\tau$ values. This effect is valid for both positive and negative ranges of $\kappa _2$. We notice that for $\tau \rightarrow 0$, the upper stability boundary tends to r, as calculated for the non-delayed system in Sect. 3.1.2. Therefore, this parameter is important because it defines the largest positive stable value of $\kappa _2$. In the negative region, as $\tau$ tends to zero, the stable values of $\kappa _2$ tend to negative infinity. With increasing time delay, the positive stable region shrinks much faster than the stable negative region, and it gets very small with large delays, for all considered r parameters. Interestingly, in the non-collocated case, the stable region is larger for $\kappa _2<0$ than for $\kappa _2>0$, being even unbounded for small $\tau$ values. On the contrary, for the collocated case, the stable region is generally smaller and bounded for any $\tau$ value.

3.3.2 Variations of the standalone frequency ratio $\gamma$

Stability charts for the collocated and non-collocated cases for various $\gamma$ values, with the other parameters kept constant $r=1,\;\chi =0.1$, are represented in Fig. 3b. For both collocated and non-collocated cases, the stable region is larger for smaller $\gamma$ values. However, in the non-collocated case, the system is much more sensitive to variations of $\gamma$. Regarding the collocated case, with larger $\gamma$ values, the positive stable region abruptly shrinks for relatively small $\tau$ values. Considering the non-collocated case, we notice that for relatively small $\gamma$ values (in Fig. 3b (ii), $\gamma =0.5$ and $\gamma =0.75$), a sort of peak can be given for the maximum positive value of $\kappa _2$. Smaller $\gamma$ values mean that the system is tuned for larger $\omega _1$ values than $\omega _2$ values, so the robot is stiffer close to the actuator. As expected, results illustrate that the stable region is larger in this case.

3.3.3 Variations of the standalone damping factor $\chi$

Stability charts for the collocated and non-collocated cases for various standalone damping factor $\chi$ values, with the other parameters kept constant $r=1,\;\gamma =1$, are displayed in Fig. 3c. As expected, the stable region becomes smaller for decreasing $\chi$ values in both cases. The shrinkage is more pronounced for larger values of time delay $\tau$. Considering the collocated case, we notice that for sufficiently large $\chi$ values, the destabilising effect of the time delay becomes negligible, and the maximum and minimum values of $\kappa _1$ which guarantee stability are constant with respect to $\tau$ for a large range (see, for instance, the blue curve in Fig. 3c (i)). Furthermore, the negative region does not seem to be particularly affected by small values of $\chi$; for instance, reducing $\chi$ from 0.1 to 0.01 practically leaves the negative stable region of the collocated case unchanged. Regarding the non-collocated case, the destabilising effect of small values of $\chi$ is relevant for both positive and negative half-plane of the stability diagram. However, the positive critical value of $\kappa _2$ for $\tau \rightarrow 0$ is unaffected by variations of $\chi$, which means that in the non-collocated case the stable region is much larger than in the collocated case as $\tau \rightarrow 0$. Nevertheless, even relatively small nonzero $\tau$ values shrink the stable region more significantly in the non-collocated case than in the collocated one.

We remark that, although the stable region significantly shrinks in some cases, the system is always stable for zero control force. This means that we cannot talk about a “more stable” configuration. Conversely, we can state that the system is more sensitive to large control gains in some cases. For instance, let us consider the case of $\tau \rightarrow 0$ and large mass ratio ($m_2\gg m_1$), which makes the non-collocated configuration stable for very large $\kappa _2$ values. This result does not mean that the system is very stable but that a control force applied on the first mass—which is relatively small—proportional to the acceleration of the second mass, has a negligible effect on the system stability, which indeed sounds physically reasonable.

4 Bifurcation analysis

We now aim at analysing the Andronov–Hopf bifurcations, identified by the D-curves, occurring at the loss of stability, and the effect of the sign of the system nonlinearity on it. In particular, a subcritical bifurcation might limit the robustness of the stable trivial solution in the proximity of the stability boundary, which can cause the onset of self-excited vibrations within the stable region. The method of multiple scales for time-delayed systems is adopted for such analysis [20, 35].

First, we transform the system in Eq. (4) into first-order form, i.e.

$$\begin{aligned} \dot{{\mathbf {y}}}=\mathbf {Ly}-\kappa _1{\mathbf {R}}_1\dot{{\mathbf {y}}}_\tau +{\mathbf {f}}_1 \end{aligned}$$

(26)

in the case of a collocated controller, or

$$\begin{aligned} \dot{{\mathbf {y}}}=\mathbf {Ly}-\kappa _2{\mathbf {R}}_2\dot{{\mathbf {y}}}_\tau +{\mathbf {f}}_2 \end{aligned}$$

(27)

for a non-collocated one, where

$$\begin{aligned} \begin{aligned} {\mathbf {y}}&:=\left[ \begin{array}{c}y_1\\ y_2\\ y_3\\ y_4 \end{array}\right] =\left[ \begin{array}{c}x_1\\ x_2\\ \dot{x}_1\\ \dot{x}_2 \end{array}\right] ,\, {\mathbf {y}}_\tau :={\mathbf {y}}(t-\tau ),\\ {\mathbf {L}}&:=\left[ \begin{array}{cccc}0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ -\gamma ^2 r-1&{}\quad \gamma ^2 r&{}\quad -2\chi r\gamma &{}\quad 2\chi r\gamma \\ \gamma ^2&{}\quad -\gamma ^2&{}\quad 2\chi \gamma &{}\quad -2\chi \gamma \end{array}\right] ,\\ {\mathbf {R}}_1&:=\left[ \begin{array}{cccc}0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\end{array}\right] ,\,\\ {\mathbf {f}}_1&:=\left[ \begin{array}{c}0\\ 0\\ -\mu r(y_1-y_2)^3+\kappa _{\text {nl},1}\dot{y}_{3\tau }^3\\ -\mu (y_2-y_1)^3\end{array}\right] ,\\ {\mathbf {R}}_2&:=\left[ \begin{array}{cccc}0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -1\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\end{array}\right] ,\,\\ {\mathbf {f}}_2&:=\left[ \begin{array}{c}0\\ 0\\ -\mu r(y_1-y_2)^3+\kappa _{\text {nl},2}\dot{y}_{4\tau }^3\\ -\mu (y_2-y_1)^3\end{array}\right] . \end{aligned} \end{aligned}$$

(28)

The adopted bifurcation parameters are the rescaled control parameters $\kappa _1$ and $\kappa _2$.

Next, in order to eventually obtain a convergent solution, we expand the solution of Eq. (26) (or Eq. (27)) as

$$\begin{aligned} {\mathbf {y}}(t;\varepsilon )=\varepsilon ^{1/2}{\mathbf {y}}_1\left( T_0,T_1\right) +\varepsilon ^{3/2}{\mathbf {y}}_2\left( T_0,T_1\right) +\cdots \end{aligned}$$

(29)

where $T_0=t$, $T_1=\varepsilon t$ and $\varepsilon$ is a small bookkeeping parameter. The derivative with respect to t is transformed into

$$\begin{aligned} \frac{\text{ d }}{\text{ d } t}=\frac{\partial }{\partial T_0}+\varepsilon \frac{\partial }{\partial T_1}=D_0+\varepsilon D_1\;, \end{aligned}$$

(30)

while delayed terms are expressed as

$$\begin{aligned} \begin{aligned}&{\mathbf {y}}(t-\tau ;\varepsilon )=\varepsilon ^{1/2}{\mathbf {y}}_1\left( T_0-\tau ,T_1-\varepsilon \tau \right) \\&\quad +\varepsilon ^{3/2}{\mathbf {y}}_2\left( T_0-\tau ,T_1-\varepsilon \tau \right) +\cdots , \end{aligned} \end{aligned}$$

(31)

which upon expansion for small $\varepsilon$ becomes

$$\begin{aligned} \begin{aligned}&{\mathbf {y}}(t-\tau ;\varepsilon )=\varepsilon ^{1/2}{\mathbf {y}}_1\left( T_0-\tau ,T_1\right) \\&\quad +\varepsilon ^{3/2}{\mathbf {y}}_2\left( T_0-\tau ,T_1\right) -\varepsilon ^{3/2}\tau D_1{\mathbf {y}}_1\\&\quad \left( T_0-\tau ,T_1\right) +\cdots . \end{aligned} \end{aligned}$$

(32)

The bifurcation parameters $\kappa _1$ and $\kappa _2$ are rewritten as $\kappa _1=\kappa _{1,\text {cr}}+\varepsilon \delta _1$ and $\kappa _2=\kappa _{2,\text {cr}}+\varepsilon \delta _2$, respectively, where $\kappa _{1,\text {cr}}$ and $\kappa _{2,\text {cr}}$ correspond to the $\kappa _1$ and $\kappa _2$ values at the loss of stability, while $\delta _1$ indicates the closeness of $\kappa _1$ to $\kappa _{1,\text {cr}}$, $\delta _2$ has an analogous meaning. As explained later, this expansion enables us to have a non-hyperbolic fixed point for order $\varepsilon ^{1/2}$ and secular terms generated for order $\varepsilon ^{3/2}$. Indeed, this choice of the order of $\varepsilon$ is suitable for systems having only cubic nonlinearities, like the one under study. For a more comprehensive explanation of the formalism adopted, we address the interested reader to [35].

Substituting Eqs. (29)–(32) into Eq. (26), we obtain

$$\begin{aligned} \begin{aligned}&\left( D_0+\varepsilon D_1\right) \left( \varepsilon ^{1/2}{\mathbf {y}}_1+\varepsilon ^{3/2}{\mathbf {y}}_2\right) -{\mathbf {L}}\left( \varepsilon ^{1/2}{\mathbf {y}}_1+\varepsilon ^{3/2}{\mathbf {y}}_2\right) \\&\quad +\left( \kappa _{1,\text {cr}}+\varepsilon \delta _1\right) {\mathbf {R}}_1\left( D_0+\varepsilon D_1\right) \\&\quad \left( \varepsilon ^{1/2}{\mathbf {y}}_{1\tau }+\varepsilon ^{3/2}{\mathbf {y}}_{2\tau }-\varepsilon ^{3/2}\tau D_1{\mathbf {y}}_1\right) =\varepsilon ^{3/2}\tilde{{\mathbf {f}}}_1+\text {h.o.t.}, \end{aligned} \end{aligned}$$

(33)

where h.o.t. indicates terms with values of $\varepsilon$ higher than order 3/2, ${\mathbf {y}}_{1\tau }={\mathbf {y}}_1\left( T_0-\tau ,T_1\right)$, ${\mathbf {y}}_{2\tau }={\mathbf {y}}_2\left( T_0-\tau ,T_1\right)$,

$$\begin{aligned} \tilde{{\mathbf {f}}}_1=\left[ \begin{array}{c}0\\ 0\\ -\mu \, r\left( y_{11}-y_{21}\right) ^3+\kappa _{\text {nl},1}\left( D_0y_{31\tau }\right) ^3\\ \mu \left( y_{11}-y_{21}\right) ^3 \end{array} \right] ,\\ \tilde{{\mathbf {f}}}_2=\left[ \begin{array}{c}0\\ 0\\ -\mu \, r\left( y_{11}-y_{21}\right) ^3+\kappa _{\text {nl},2}\left( D_0y_{41\tau }\right) ^3\\ \mu \left( y_{11}-y_{21}\right) ^3\end{array} \right] , \end{aligned}$$

$y_{11}$, $y_{21}$, $y_{31}$ and $y_{41}$ are the elements of vector ${\mathbf {y}}_1$. In the non-collocated case, $\kappa _{1,\text {cr}}$, $\delta _1$, ${\mathbf {R}}_1$ and $\tilde{{\mathbf {f}}}_1$ should be substituted with $\kappa _{2,\text {cr}}$, $\delta _2$, ${\mathbf {R}}_2$ and $\tilde{{\mathbf {f}}}_2$. For the sake of brevity, in the following, equations related to the non-collocated case will be omitted unless necessary.

Separating terms of different order of $\varepsilon$, we obtain

$$\begin{aligned}&\varepsilon ^{1/2}:D_0{\mathbf {y}}_1-\mathbf {Ly}_1+\kappa _{1,\text {cr}}{\mathbf {R}}_1D_0{\mathbf {y}}_{1\tau }={\mathbf {0}}. \end{aligned}$$

(34)

$$\begin{aligned}&\varepsilon ^{3/2}:D_0{\mathbf {y}}_2-\mathbf {Ly}_2+\kappa _{1,\text {cr}}{\mathbf {R}}_1D_0{\mathbf {y}}_{2\tau }=-D_1{\mathbf {y}}_1\nonumber \\&\quad -\kappa _{1,\text {cr}}{\mathbf {R}}_1D_1{\mathbf {y}}_{1\tau }-\delta _1{\mathbf {R}}_1D_0{\mathbf {y}}_{1\tau }\nonumber \\&\quad +\kappa _{1,\text {cr}}{\mathbf {R}}_1D_0D_1{\mathbf {y}}_1\tau +\varepsilon ^{3/2}\tilde{{\mathbf {f}}}_1. \end{aligned}$$

(35)

Order $\varepsilon ^{1/2}$

Equation (34) consists of the linearised system of equation for a critical value of the bifurcation parameter $\kappa _1$ (or $\kappa _2$). Therefore, its trivial solution is a centre and its general steady state solution is

$$\begin{aligned} {\mathbf {y}}_1(T_0,T_1)=A(T_1){\mathbf {c}}\mathrm {e}^{\mathrm {i}\omega T_0}+{\bar{A}}(T_1)\bar{{\mathbf {c}}}\mathrm {e}^{-\mathrm {i}\omega T_0}, \end{aligned}$$

(36)

where the overbar indicates complex conjugate and $\omega$ is given by Eq. (25) for a specific $\tau$ value and for $\kappa _1=\kappa _{1,\text {cr}}$ (or $\kappa _2=\kappa _{2,\text {cr}}$). ${\mathbf {c}}=\left[ 1\quad c_2\quad c_3\quad c_4\right] ^\intercal$ is obtained by the linear homogeneous system of equation

$$\begin{aligned} \left( \mathrm {i}\omega {\mathbf {I}}-{\mathbf {L}}+\kappa _{1,\text {cr}}{\mathbf {R}}_1\mathrm {i}\omega \mathrm {e}^{-\mathrm {i}\omega \tau }\right) {\mathbf {c}}={\mathbf {0}}, \end{aligned}$$

(37)

where ${\mathbf {I}}$ is the identity matrix, which gives

$$\begin{aligned} {\mathbf {c}}=\left[ \begin{array}{c}c_1\\ c_2\\ c_3\\ c_4\end{array}\right] =\left[ \begin{array}{c}1\\ \frac{\omega ^2 \left( -1+\kappa _{1,\text {cr}} \mathrm {e}^{-\mathrm {i} \tau \omega }\right) +\gamma r (\gamma +2 \mathrm {i} \chi \omega )+1}{\gamma r (\gamma +2 \mathrm {i} \chi \omega )}\\ \mathrm {i}\omega \\ \frac{\mathrm {i} \omega \left( \omega ^2 \left( -1+\kappa _{1,\text {cr}} \mathrm {e}^{-\mathrm {i} \tau \omega }\right) +\gamma r (\gamma +2 \mathrm {i} \chi \omega )+1\right) }{\gamma r (\gamma +2 \mathrm {i} \chi \omega )}\end{array}\right] \end{aligned}$$

(38)

and

$$\begin{aligned} {\mathbf {c}}=\left[ \begin{array}{c}c_1\\ c_2\\ c_3\\ c_4\end{array}\right] =\left[ \begin{array}{c}1\\ \frac{\mathrm {e}^{\mathrm {i} \tau \omega } \left( -\gamma r (\gamma +2 \mathrm {i} \chi \omega )+\omega ^2-1\right) }{\kappa _{2,\text {cr}} \omega ^2-\gamma r \mathrm {e}^{\mathrm {i} \tau \omega } (\gamma +2 \mathrm {i} \chi \omega )}\\ \mathrm {i}\omega \\ -\frac{\omega \mathrm {e}^{\mathrm {i} \tau \omega } \left( -\gamma r (\gamma +2 \mathrm {i} \chi \omega )+\omega ^2-1\right) }{\mathrm {i} \kappa _{2,\text {cr}} \omega ^2+\gamma r \mathrm {e}^{\mathrm {i} \tau \omega } (2 \chi \omega -\mathrm {i} \gamma )} \end{array}\right] \end{aligned}$$

(39)

for the collocated and non-collocated cases, respectively.

Order $\varepsilon ^{3/2}$

Substituting Eq. (36) into Eq. (35), we obtain

$$\begin{aligned} \begin{aligned}&D_0{\mathbf {y}}_2-\mathbf {Ly}_2+\kappa _{1,\text {cr}}{\mathbf {R}}_1D_0{\mathbf {y}}_{2\tau }=\Big [-\Big [{\mathbf {I}}+\kappa _{1,\text {cr}}{\mathbf {R}}_1\\&\quad \left( \mathrm {e}^{-\mathrm {i}\omega \tau }-\tau \, \mathrm {i}\omega \right) \Big ]{\mathbf {c}}\,A'-\delta _1\,{\mathbf {R}}_1A\,{\mathbf {c}}\,\mathrm i\omega \, \mathrm {e}^{-\mathrm {i}\omega \tau }\\&\quad +3A^2{\bar{A}}\,\tilde{\tilde{{\mathbf {f}}}}_1\Big ]\mathrm {e}^{\mathrm i\omega T_0}+\text {c.c.}+\text {n.s.t.} \end{aligned} \end{aligned}$$

(40)

where

$$\begin{aligned} \tilde{\tilde{{\mathbf {f}}}}_1=\left[ \begin{array}{c}0\\ 0\\ \mu \,r\left( 1-c_2\right) ^2\left( {\bar{c}}_2-1\right) +\mathrm {i}\,c_3^2{\bar{c}}_3\kappa _{\text {nl},1}\omega ^3\mathrm {e}^{-\mathrm {i}\omega \tau }\\ -\mu \left( 1-c_2\right) ^2\left( {\bar{c}}_2-1\right) \end{array}\right] ,\\\left( \tilde{\tilde{{\mathbf {f}}}}_2=\left[ \begin{array}{c}0\\ 0\\ \mu r\left( 1-c_2\right) ^2\left( {\bar{c}}_2-1\right) +\mathrm {i}c_4^2{\bar{c}}_4\kappa _{\text {nl},2}\omega ^3\mathrm {e}^{-\mathrm {i}\omega \tau }\\ -\mu \left( 1-c_2\right) ^2\left( {\bar{c}}_2-1\right) \end{array}\right] \right) , \end{aligned}$$

prime ($'$) stands for derivation with respect to $T_0$, c.c. and n.s.t. stand for “complex conjugate” and for “non secular terms”, respectively.

Because the homogeneous part of Eq. (40) has nontrivial solutions, the non-homogeneous equation has a solution only if a solvability condition is satisfied. To determine this solvability condition, we assume a particular solution of the form

$$\begin{aligned} {\mathbf {y}}_2(T_0,T_1)=\phi (T_1)\mathrm {e}^{\mathrm {i}\omega T_0}, \end{aligned}$$

(41)

and obtain

$$\begin{aligned} \begin{aligned}&\left[ {\mathbf {L}}-\kappa _{1,\text {cr}}{\mathbf {R}}_1\mathrm {i}\omega \mathrm {e}^{-\mathrm {i}\omega \tau }-\mathrm {i}\omega {\mathbf {I}}\right] \phi =\big [{\mathbf {I}}+\kappa _{1,\text {cr}}{\mathbf {R}}_1\\&\quad \left( \mathrm {e}^{-\mathrm {i}\omega \tau }-\tau \mathrm {i}\omega \right) \big ]{\mathbf {c}}\,A'+\delta _1{\mathbf {R}}_1A\,{\mathbf {c}}\,\mathrm {i}\omega \mathrm {e}^{-\mathrm {i}\omega \tau }-3A^2{\bar{A}}\,\tilde{\tilde{{\mathbf {f}}}}_1. \end{aligned} \end{aligned}$$

(42)

The solvability condition demands that the right-hand side of Eq. (42) is orthogonal to every solution of the adjoint homogeneous problem. The adjoint problem is governed by

$$\begin{aligned} \left[ {\mathbf {L}}^{\textsf {H}}+\kappa _{1,\text {cr}}{\mathbf {R}}_1^{\textsf {H}}\mathrm {i}\omega \mathrm {e}^{\mathrm {i}\omega \tau }+\mathrm {i}\omega {\mathbf {I}}\right] {\mathbf {b}}={\mathbf {0}}, \end{aligned}$$

(43)

where $^{\textsf {H}}$ indicates the conjugate transpose. To make ${\mathbf {b}}$ unique, we impose the condition

$$\begin{aligned} {\mathbf {b}}^{\textsf {H}}{\mathbf {c}}=1 \end{aligned}$$

(44)

and obtain

$$\begin{aligned} {\mathbf {b}}=\left[ \begin{array}{c}1\\ -\frac{\gamma ^2 r \omega ^2}{-\gamma ^2+2 \mathrm {i} \gamma \chi \omega +\gamma ^2 r \omega ^2+\omega ^2}\\ \frac{\mathrm {i} \omega \left( -\gamma ^2+2 \mathrm {i} \gamma \chi \omega +\omega ^2\right) }{-\gamma ^2+2 \mathrm {i} \gamma \chi \omega +\gamma ^2 r \omega ^2+\omega ^2}\\ -\frac{\mathrm {i} \gamma r \omega (\gamma -2 \mathrm {i} \chi \omega )}{-\gamma ^2+2 \mathrm {i} \gamma \chi \omega +\gamma ^2 r \omega ^2+\omega ^2} \end{array}\right] \end{aligned}$$

(45)

and

$$\begin{aligned} {\mathbf {b}}=\left[ \begin{array}{c}1\\ -\frac{\gamma \left( \omega ^2-1\right) }{\omega (\gamma \omega -2 \mathrm {i} \chi )}\\ \frac{2 \chi \omega +\mathrm {i} \gamma }{\gamma \omega -2 \mathrm {i} \chi }\\ \frac{\gamma r (2 \chi \omega +\mathrm {i} \gamma )-\mathrm {i} \left( \omega ^2-1\right) }{\gamma (\gamma \omega -2 \mathrm {i} \chi )} \end{array}\right] , \end{aligned}$$

(46)

for the collocated and non-collocated cases, respectively. We take the inner product of ${\mathbf {b}}^{\textsf {H}}$ with the right-hand side of Eq. (42), i.e.

$$\begin{aligned} \begin{aligned}&{\mathbf {b}}^{\textsf {H}}\Big (\left[ {\mathbf {I}}+\kappa _{1,\text {cr}}{\mathbf {R}}_1\left( \mathrm {e}^{-\mathrm {i}\omega \tau }-\tau \mathrm {i}\omega \right) \right] {\mathbf {c}}\,A'\\&\quad +\delta _1{\mathbf {R}}_1A\,{\mathbf {c}}\,\mathrm {i}\omega \mathrm {e}^{-\mathrm {i}\omega \tau }\\&\quad -3A^2{\bar{A}}\,\tilde{\tilde{{\mathbf {f}}}}_1\Big )=0, \end{aligned} \end{aligned}$$

(47)

from which we get the expression

$$\begin{aligned} A'=\varLambda _1\delta _1A+\varLambda _2A^2{\bar{A}}. \end{aligned}$$

(48)

4.1 Normal form

We introduce the polar form

$$\begin{aligned} A=\frac{1}{2}\,a\,\mathrm {e}^{\mathrm i\beta }, \end{aligned}$$

(49)

where a and $\beta$ are real functions of $T_1$. Substituting Eq. (49) into (48) and separating real and imaginary parts, we get

$$\begin{aligned}&\text {Re:}\,a'=\delta _1\varLambda _{1\mathrm {R}}a+\frac{1}{4}a^3\varLambda _{2\mathrm {R}} \end{aligned}$$

(50)

$$\begin{aligned}&\text {Im:}\,a\,\beta '=\delta _1\varLambda _{1\mathrm {I}}a+\frac{1}{4}a^3 \varLambda _{2\mathrm {I}}, \end{aligned}$$

(51)

where $\varLambda _{1\mathrm {R}}$, $\varLambda _{2\mathrm {R}}$, $\varLambda _{1\mathrm {I}}$ and $\varLambda _{2\mathrm {I}}$ are the real and imaginary parts of $\varLambda _1$ and $\varLambda _2$, respectively.

Equation (50) provides information about the oscillation amplitude of the system in the vicinity of the bifurcation. In order to identify periodic solutions, we impose $a'=0$ and obtain the solutions

$$\begin{aligned} a_0=0\quad \text {and}\quad a_1=2\sqrt{-\frac{\delta _1}{\varDelta }}, \end{aligned}$$

(52)

where

$$\begin{aligned} \begin{aligned}&\varDelta =\varLambda _{2\mathrm {R}}/\varLambda _{1\mathrm {R}}\\&=\frac{3 \text {Re}\left( \frac{\mu (c_2-1)^2 ({\bar{c}}_2-1)({\bar{b}}_4-{\bar{b}}_3 r)-\mathrm {i}{\bar{b}}_3c_3^2{\bar{c}}_3\kappa _{\text {nl},1}\omega ^3\mathrm {e}^{-\mathrm {i}\tau \omega }}{{\bar{b}}_1+{\bar{b}}_2 c_2-{\bar{b}}_3 c_3 \kappa _{1,\text {cr}} \mathrm {e}^{-\mathrm {i} \tau \omega }+\mathrm {i} {\bar{b}}_3 c_3 \kappa _{1,\text {cr}} \tau \omega +{\bar{b}}_3 c_3+{\bar{b}}_4 c_4}\right) }{\text {Im}\left( \frac{{\bar{b}}_3 c_3 \omega \mathrm {e}^{-\mathrm {i} \tau \omega }}{{\bar{b}}_1+{\bar{b}}_2 c_2-{\bar{b}}_3 c_3 \kappa _{1,\text {cr}} \mathrm {e}^{-\mathrm {i} \tau \omega }+\mathrm {i} {\bar{b}}_3 c_3 \kappa _{1,\text {cr}} \tau \omega +{\bar{b}}_3 c_3+{\bar{b}}_4 c_4}\right) } \end{aligned} \end{aligned}$$

(53)

for the collocated case and

$$\begin{aligned} \varDelta =\frac{3 \text {Re}\left( \frac{\mu (c_2-1)^2 ({\bar{c}}_2-1)({\bar{b}}_4-{\bar{b}}_3 r)-\mathrm {i}{\bar{b}}_3c_4^2{\bar{c}}_4\kappa _{\text {nl},2}\omega ^3\mathrm {e}^{-\mathrm {i}\tau \omega }}{{\bar{b}}_1+{\bar{b}}_2 c_2+{\bar{b}}_3 c_3-{\bar{b}}_3 c_4 \kappa _{2,\text {cr}} \mathrm {e}^{-\mathrm {i} \tau \omega }+\mathrm {i} {\bar{b}}_3 c_4 \kappa _{2,\text {cr}} \tau \omega +{\bar{b}}_4 c_4}\right) }{\text {Im}\left( \frac{{\bar{b}}_3 c_4 \omega \mathrm {e}^{-\mathrm {i} \tau \omega }}{{\bar{b}}_1+{\bar{b}}_2 c_2+{\bar{b}}_3 c_3-{\bar{b}}_3 c_4 \kappa _{2,\text {cr}} \mathrm {e}^{-\mathrm {i} \tau \omega }+\mathrm {i} {\bar{b}}_3 c_4 \kappa _{2,\text {cr}} \tau \omega +{\bar{b}}_4 c_4}\right) } \end{aligned}$$

(54)

for the non-collocated case.

Recalling Eqs. (29), (36), (49), (52) and that $\kappa _1=\kappa _{1,\text {cr}}+\varepsilon \delta _1$, we have that the amplitude of the LCOs in the vicinity of the bifurcation is approximated by

$$\begin{aligned} \begin{array}{l} y_1=\varphi _0\cos (\omega t+\beta ),\\ y_2=c_2\varphi _0\cos (\omega t+\beta ),\quad \varphi _0=2\sqrt{\frac{\kappa _{1,\text {cr}}-\kappa _1}{\varDelta }}. \end{array} \end{aligned}$$

(55)

Since $\delta _1$ represents small variations of $\kappa _1$ with respect to its critical value $\kappa _{1,\text {cr}}$, $a_1$ is real for $\delta _1>0$ ($<0$) if $\varDelta <0$ ($>0$). For the system under study, in most cases we have that for $\kappa _{1,\text {cr}}$ either positive or negative, the system is stable if $|\kappa _1|<|\kappa _{1,\text {cr}}|$. Therefore, for $\kappa _{1,\text {cr}}>0$, the Andronov–Hopf bifurcation is supercritical (subcritical) for $\varDelta <0$ ($\varDelta >0$) and the opposite for $\kappa _{1,\text {cr}}<0$. It means that when the signs of $\kappa _{1\mathrm {cr}}$ and $\varDelta$ are the same, the Andronov–Hopf bifurcation is subcritical, and when the signs are opposite, it is supercritical. The same scenario is verified for the non-collocated case.

5 Bifurcation diagrams

In this section, we analyse the results obtained through the bifurcation analysis performed with the multiple scales method in the previous section. These analytical results are compared with direct numerical integrations and with bifurcation diagrams obtained through the NDDE-Cont continuation software for neutral differential equations [6], which is based on the continuation toolbox DDE-BIFTOOL for MATLAB [16]. Initially, results obtained with a classical linear controller ($\kappa _{\text {nl},1}=0$ or $\kappa _{\text {nl},2}=0$) are presented. Later, possible improvements in the bifurcation behaviour related to introducing a nonlinear term in the controller are studied. For the sake of brevity, the values of $\chi$, r and $\gamma$ are fixed at 0.05, 1 and 1, respectively, throughout the whole analysis performed in this section. Nevertheless, extending the obtained results to other parameter values is a relatively simple task left for the interested reader.

5.1 Linear control: collocated system

Equation (53) enables us to characterise the types of bifurcations occurring at the loss of stability. At this stage, we assume that the controller is purely linear ($\kappa _{\text {nl},1}=0$). Based on the calculated value of $\varDelta$, Fig. 5a illustrates that for $\mu =1$, which corresponds to a hardening nonlinearity of the stiffness, bifurcations are always subcritical in the analysed parameter range. Indeed, in Fig. 5b it can be recognised that, for the stability boundary corresponding to $\kappa _{1,\text {cr}}>1$ ($\kappa _{1,\text {cr}}<1$), $\varDelta$ is positive (negative), which indicates that all corresponding Andronov–Hopf bifurcations are subcritical. The practical consequence of a subcritical bifurcation is that a branch of unstable periodic solutions exists within the stable region of the trivial solution. Generally, this limits the robustness of the stable trivial solution, causing the system to undergo large oscillations if subject to sufficiently large perturbations, even within the stable region of the trivial solution.

It can be noticed that the sign of $\varDelta$ directly depends on the sign of $\mu$. Therefore, considering a softening stiffness nonlinearity of the system ($\mu =-1$), we expect to have supercritical bifurcations instead of subcritical. This is confirmed in Fig. 5c, d, which shows exactly the same features of Fig. 5a, b, but with reversed sign of $\varDelta$, which indicates that all bifurcations are supercritical. This feature could be easily predicted by looking at Eq. (53) for $\kappa _{\text {nl},1}=0$.

Fig. 5

a, c Stability charts of the collocated system for the parameter values $\chi =0.05$, $r=1$ and $\gamma =1$; $\mu =1$ a and $\mu =-1$ (c); dashed lines: subcritical bifurcations, solid lines: supercritical bifurcations. b, d Corresponding values of $\varDelta$ for $\mu =1$ and $\mu =-1$

In Fig. 6, bifurcation diagrams obtained analytically (black lines) overlap with bifurcation diagrams obtained through the NDDE-Cont continuation software (blue and orange lines). The two procedures provide practically identical results at low amplitudes, which confirms the validity of the analytical procedure and that a softening nonlinearity produces subcritical bifurcations.

Fig. 6

Bifurcation diagrams for the collocated system; parameter values: $r=1$, $\gamma =1$, $\chi =0.05$, $\tau =0.1$ a, c and $\tau =0.8$ b, d, in (e) $\kappa _1=-0.87$, $\mu$ is indicated in the figures. Solid lines: stable branches, dashed lines: unstable branches, orange lines: hardening case, blue lines: softening case, black lines: analytical results. a and b are enlargements of (c) and (d) centred at the Andronov–Hopf bifurcations. (Color figure online)

Since the analytical procedure neglects terms of order higher than $\varepsilon ^{3/2}$, it provides a bifurcation curve that is restricted to a parabola, making it impossible to detect any other trend of the branches of periodic solutions arising at the loss of stability. However, more complicated shapes of the branches can be easily tracked by extending the numerical continuation to higher values.

Figure 6c illustrates that also in the case of softening nonlinearity (blue line), the branch of stable periodic solutions encounters a fold point at $\kappa _1\approx 0.5$, losing stability and turning back towards the stable region. This behaviour generates unstable periodic solutions within the stable region of the trivial solution, even in the case of supercritical Andronov–Hopf bifurcations. Nevertheless, this unstable branch has a very high amplitude, especially if compared with the red curve in Fig. 6c referring to the hardening case. This scenario suggests that the trivial solution, although not globally stable, is probably much more robust in the case of softening rather than hardening nonlinearity.

In this respect, Fig. 7 illustrates that, for fixed parameter values belonging to the stable region of the trivial solution, the system can either converge towards the trivial solution or not, depending on the initial conditions. In the case of hardening nonlinearity ($\mu =1$), Fig. 7a shows that selecting initial conditions ${\mathbf {y}}(t)=[0.735,\,0,\,0,\,0]^\intercal$ or ${\mathbf {y}}(t)=[0.740,\,0,\,0,\,0]^\intercal$ with $t\in \left( -\tau ,0\right]$, the system either converges towards the trivial solution or towards a much larger attractor (seemingly quasiperiodic). A somehow similar scenario occurs in the case of softening nonlinearity ($\mu =-1$), as depicted in Fig. 7b for the same parameter values (except $\mu$, of course). However, in this case, the system still converges towards the trivial solution for a significantly larger initial condition of $x_1$. Additionally, the non-convergent time series is not attracted to any bounded solution, but it diverges unboundedly. This behaviour is probably related to a statistical loss of stability due to the softening stiffness, which becomes negative for excessively large $|x_1-x_2|$ values and not to the unstable periodic solution detected by the numerical continuation. Clearly, for such large $|x_1-x_2|$ values, the mathematical model adopted fails to describe the mechanical system under study. Indeed, the unstable periodic solution encompasses points such that $\left( x_1-x_2\right) ^2>\gamma ^2$, for which the stiffness is negative, being therefore out of the region of validity of the mathematical model. Although rigorously proving that for hardening nonlinearity the trivial solution is less robust than for softening nonlinearity is very demanding because the system is infinite-dimensional, the performed analysis hints that a similar conclusion is plausible.

An interesting feature of the bifurcation diagram in Fig. 6c, for $\mu =1$, is that the branch of unstable periodic solutions reaches values of $\kappa _1$ close to zero (the fold occurs at $\kappa _1=0.023$), meaning that large amplitude vibrations might unexpectedly occur also for $\kappa _1$ far from the stability boundary.

Fig. 7

Time series obtained from direct numerical simulations of the collocated system for the parameter values $\chi =0.05$, $r=1$, $\gamma =1$, $\tau =0.1$, $\kappa _1=0.4$, $\mu =1$ (a) and $\mu =-1$ (b). Blue and red lines mark time series converging and not converging towards the trivial solution, respectively. Initial conditions are indicated in the figure. (Color figure online)

From the stability analysis of Sect. 3, we deduce that for $\kappa _1<-1$ an infinite number of eigenvalues has positive real parts. This occurrence makes it very hard for the numerical solver to track a periodic solution and perform a continuation in the vicinity of this boundary. For this reason, bifurcation diagrams for negative $\kappa _1$ values are depicted in Fig. 6b, d for $\tau =0.8$, where $\kappa _{1,\text {cr}}$ is equal to $-0.87$ and relatively far from $-1$ (see, for instance, Fig. 5a). Apart from confirming the analytical results, i.e. that the bifurcations are subcritical for hardening stiffness and supercritical for softening, the bifurcation diagram of Fig. 6d illustrates that the branch of unstable periodic solution exists for a wide range of $\kappa _1$ negative values (up to $\kappa _1<-0.07$). This observation implies that also for $\kappa _1<0$, unexpected large amplitude oscillations might occur for almost any $\kappa _1$ value in the case of hardening stiffness.

Figure 6e illustrates the bifurcation diagram for the same bifurcation point of Fig. 6d, but adopting the time delay $\tau$ as bifurcation parameter. For the hardening case ($\mu =1$), the figure shows that the branch of unstable periodic solutions is very steep, rapidly reaching high values. This suggests that in this case, for low values of time delay $\tau$, although the basin of attraction of the trivial solution is probably bounded, the trivial solution might still be globally stable limiting initial conditions to states of the mechanical system compatible with a physical system. The steep trend of the branch of periodic solutions for negative $\kappa _1$ could be already predicted by analysing the absolute value of $\varDelta$ in Fig. 5b, d, which is tiny for small $\tau$ values. In fact, Eq. (55) clearly shows that the smaller the absolute value of $\varDelta$, the steeper the branch of periodic solutions arising at the bifurcation.

5.2 Linear control: non-collocated system

We now consider the non-collocated system and repeat the analysis performed in the previous section for the collocated system. Analysing the value of $\varDelta$ from Eq. (54), the Andronov–Hopf bifurcations occurring at the loss of stability are characterised. Figure 8a, c illustrates that, similarly to the collocated case, also for the non-collocated system, the bifurcations are subcritical in the case of hardening stiffness and supercritical in the case of softening stiffness.

Fig. 8

a, c Stability charts of the non-collocated system for the parameter values $\chi =0.05$, $r=1$ and $\gamma =1$; $\mu =1$ (a) and $\mu =-1$ (c); dashed lines: subcritical bifurcations, solid lines: supercritical bifurcations. b, d Corresponding values of $\varDelta$ for $\mu =1$ and $\mu =-1$

Fixing the time delay $\tau$ at 0.15, bifurcation diagrams are depicted in Fig. 9. Also in this case, the good matching between analytical and numerical results exhibited in Fig. 9a, b validates the analytical procedure. Figure 9c, d provides a wider view of the bifurcation diagrams, which enables us to draw some conclusions about the effects of the bifurcations on the global system dynamics. In Fig. 9c, it can be noticed that both branches, for $\mu =1$ and $\mu =-1$, increase their amplitude very slowly, if compared with the bifurcation diagrams in Fig. 6b. This observation could be deduced by the analytical procedure by looking at the absolute value of $\varDelta$ in Fig. 8b, d. For $\kappa _{2,\text {cr}}<0$ and decreasing $\tau$, the absolute value of $\varDelta$ rapidly increases, such that $\lim _{\tau \rightarrow 0}{\varDelta }=\infty$. This is exactly the opposite trend of $\varDelta$ in the collocated case for $\kappa _{1,\text {cr}}<0$, where $\varDelta$ tends to 0 with a horizontal tangent for $\tau \rightarrow 0$ (Fig. 5b). Such a large $\varDelta$ value, in the case of a supercritical bifurcation, makes arising periodic solutions have a relatively small amplitude (see blue curve in Fig. 9c), which is a desirable feature from an engineering point of view in many applications. On the contrary, if the bifurcation is subcritical, a low branch of unstable periodic solutions is generated, which might significantly reduce the robustness of the stable trivial solution.

Fig. 9

Bifurcation diagrams for the non-collocated system; parameter values: $r=1$, $\gamma =1$, $\chi =0.05$, $\tau =0.15$, $\mu$ as indicated in the figures. Solid lines: stable branches, dashed lines: unstable branches, black lines: analytical results, blue and orange lines: numerical results. (Color figure online)

In Fig. 10a, time series obtained from direct numerical simulations illustrate the phenomenon. For $\mu =1$, $\kappa _2=-3$ and $\tau =0.15$, therefore inside the stable region, a small perturbation of the value of $x_1$ ($x_1(0)=0.27$ in the figure) is sufficient to make the system diverge from the trivial solution causing unbounded vibrations. For the same parameter values but with a softening stiffness ($\mu =-1$), the system converges to the trivial solution even for much larger initial displacement $x_1$, as shown in Fig. 10b.

Considering bifurcations occurring at the positive stability boundary ($\kappa _{1,\text {cr}}>0$), bifurcation diagrams for $\tau =0.15$ are illustrated in Fig. 9d. For the softening case ($\mu =-1$), the branch has a fold, similarly to the bifurcation diagram encountered in the collocated case (Fig. 6a). However, in this case, the fold is very far from the stability boundary and does not seem to endanger the robustness of the trivial solution inside its stable region. Conversely, for a hardening stiffness ($\mu =1$), the branch of unstable periodic solutions is rather steep and does not enter very deeply in the stable region (excluding the part of the branch having huge amplitude), meaning that the region of limited robustness of the trivial solution might be not very large.

The time series in Fig. 10c proves that, in the vicinity of the stability boundary ($\kappa _2=0.3$, $\tau =0.15$) and for softening nonlinearity, the system is bistable. Namely, depending on the initial conditions, the system’s dynamics either converges to the trivial solution (blue curve) or to a larger periodic solution (red curve), although the existence of other attractors cannot be excluded. We also remark that the amplitude of the large attractor ($x_{1\text {max}}=1.6$) and of the unstable periodic solution on which the system initially lies ($x_{1\text {max}}\approx 0.52$) in Fig. 10c agree with the results provided by the numerical continuation illustrated in Fig. 9d.

Fig. 10

Time series obtained from direct numerical simulations of the non-collocated system for the parameter values $\chi =0.05$, $r=1$, $\gamma =1$, $\tau =0.15$, $\kappa _2=-3$ (a, b), $\kappa _2=0.3$ (c), $\mu =1$ (a, c) and $\mu =-1$ (b). Blue and red lines mark time series converging and not converging towards the trivial solution, respectively. Initial conditions are indicated in the figure. (Color figure online)

5.3 Bifurcation manipulation via nonlinear control

All bifurcation diagrams illustrated in the previous sections refer to the case of a linear controller, i.e. with $\kappa _{\text {nl},1}=0$ (and $\kappa _{\text {nl},2}=0$). However, Eq. (53) suggests that a proper choice of $\kappa _{\text {nl},1}$ might change the sign of $\varDelta$ and switch the bifurcation characteristic from subcritical to supercritical or the other way around.

$\varDelta$ is linear with respect to $\kappa _{\text {nl},1}$, therefore values of $\kappa _{\text {nl},1}$ such that $\varDelta$ is either positive or negative generally exist. Furthermore, the value of $\kappa _{\text {nl},1}$ causing the transition from subcritical to supercritical behaviour (i.e. such that $\varDelta =0$) can be easily found analytically. Value of $\kappa _{\text {nl},1}$ and $\kappa _{\text {nl},2}$ at the bifurcation transition from subcritical to supercritical are illustrated in Fig. 11a, b for the collocated and non-collocated cases, respectively. Since bifurcations are already supercritical for softening stiffness, only the case of hardening stiffness ($\mu =1$) is considered, where forcing subcritical bifurcations to be supercritical might be beneficial.

Fig. 11

Values of $\kappa _{\text {nl},1}$ and $\kappa _{\text {nl},2}$ such that $\varDelta =0$ for the collocated (a) and non-collocated (b) cases; black lines refer to the upper stability boundary, while red lines refer to the lower stability boundary. Parameter values: $\chi =0.05$, $r=1$, $\gamma =1$ and $\mu =1$. (Color figure online)

The black curve in Fig. 11a refers to the upper stability boundary, while the red curve to the lower one. Interestingly, we notice that for the upper stability boundary a negative value of $\kappa _{\text {nl},1}$ is required, while for the lower one, a positive value. From an engineering point of view, this is not a desired feature, since, for instance, a positive value of $\kappa _{\text {nl},1}$ might be beneficial from the point of view of the global stability for $\kappa _1>0$, but it will be detrimental for $\kappa _1<0$. Another aspect highlighted by Fig. 11a is that just a very small value of $\kappa _{\text {nl},1}$ is required to change the character of the bifurcation of the lower stability boundary, while for negative values of $\kappa _1$ larger absolute values of $\kappa _{\text {nl},1}$ are required. This is directly related to the $\varDelta$ value depicted in Fig. 5b.

Regarding the collocated case, Fig. 12 illustrates the effect of the additional nonlinearity in the control law on the bifurcation diagram. Figure 12a refers to the upper stability boundary for $\tau =0.1$. According to Fig. 11a, the transition from subcritical to supercritical behaviour occurs at $\kappa _{\text {nl},1}=-0.0093$. Figure 12a confirms this prediction, showing that for $\kappa _{\text {nl},1}=5\times 10^{-5},\,0,\,-5\times 10^{-5},\,-5\times 10^{-4},\,-0.005$ the bifurcation is always subcritical, while it becomes supercritical for $\kappa _{\text {nl},1}=-0.01$. The different bifurcation diagrams in the figure illustrate that negative values of $\kappa _{\text {nl},1}$, in absolute value even smaller than 0.0093, generally reduce the extent of the bistable region, making the stable trivial solution more robust. Conversely, if $\kappa _{\text {nl},1}$ is positive, the bifurcation branch moves to the left. This effect most probably reduces the robustness of the stable region.

Figure 12b depicts bifurcation diagrams occurring at the lower stability boundary, for $\kappa _1<0$ and $\tau =0.8$. According to Fig. 11a, the transition of the bifurcation from subcritical to supercritical should occur at $\kappa _{\text {nl},1}=0.00033$. This prediction is also confirmed numerically in the figure, where the bifurcation diagram for $\kappa _{\text {nl},1}=0.0004$ presents a supercritical characteristic. In this case, although the analytical procedure can correctly predict the type of bifurcation, branches of unstable periodic solutions exist within the stable region also in the case of supercritical bifurcations (as for $\kappa _{\text {nl},1}=0.0004$). Nevertheless, further increasing $\kappa _{\text {nl},1}$ ($\kappa _{\text {nl},1}=0.001$) these branches seem so disappear.

From Fig. 12a, b, it can be noticed that bifurcation branches can move from negative to positive ranges of $\kappa _1$ and vice-versa. This feature, which was not observed in the case of a linear control force, implies that the tuning of $\kappa _{\text {nl},1}$ should be done with particular care. In fact, if the linear control parameters are such that the system is, for instance, close to the upper stability boundary and we aim at enforcing supercritical bifurcation to grant robustness to the system, we need to tune $\kappa _{\text {nl},1}$ to a negative value. However, this will cause the bifurcation branch arising at the lower stability boundary to bend to the right, reaching parameter spaces where $\kappa _1$ is positive, potentially mining the system’s robustness in the point of interest. This feature is better illustrated below for the non-collocated case.

Figure 11b, referring to the non-collocated system, depicts the values of $\kappa _{\text {nl},2}$ such that the bifurcations occurring at the loss of stability undergo a transition from subcritical to supercritical. Comparing Fig. 11a, b, we notice that, for both the collocated and non-collocated cases, a positive nonlinear coefficient is required to force bifurcations at the lower stability to be supercritical (except for $\tau <0.045$) and a negative one for the bifurcations at the upper stability boundary. However, in the non-collocated case, much larger controller nonlinearity values are required, particularly for small $\tau$ values. This peculiarity is related to $\varDelta$, which reaches very large values for $\kappa _{\text {nl},2}=0$, as visible in Fig. 8b.

In Fig. 13, bifurcation diagrams with various values of $\kappa _{\text {nl},2}$ are represented for the non-collocated case. In the figure, $\tau$ is fixed at 0.15. According to the analytical prediction, the transition of the bifurcations from subcritical to supercritical should occur at $\kappa _{\text {nl},2}=9.3$ at the lower boundary and $\kappa _{\text {nl},2}=-0.69$ at the upper boundary. This prediction is confirmed by the bifurcation diagrams in Fig. 13.

Fig. 12

Bifurcation diagrams for the collocated system; parameter values: $r=1$, $\gamma =1$, $\chi =0.05$, $\mu =1$, $\tau =0.1$ (a) and $\tau =0.8$ (b), $\kappa _{\text {nl},1}$ as indicated in the figures. Solid lines: stable branches, dashed lines: unstable branches; all curves refer to results obtained through numerical continuation

Fig. 13

Bifurcation diagrams for the non-collocated system; parameter values: $r=1$, $\gamma =1$, $\chi =0.05$, $\mu =1$ and $\tau =0.15$, $\kappa _{\text {nl},2}$ as indicated in the figures. Solid lines: stable branches, dashed lines: unstable branches; red curves in b indicate bifurcation branches arising at the lower stability boundary; all curves refer to results obtained through numerical continuation. (Color figure online)

Apart from correctly estimating the bifurcation transition, Fig. 13a also shows that, in general, positive values of $\kappa _{\text {nl},2}$ move the branch of periodic solutions to the left, probably increasing the robustness of the trivial solution, even if $\kappa _{\text {nl},2}$ is smaller than the critical value 9.3. On the contrary, in the upper stable region ($\kappa _2>0$), because of the shape of the branch of periodic solutions, characterised by multiple folds, it is arguable if the additional nonlinearity produces any beneficial effect in terms of robustness.

In Fig. 13b, red curves depict bifurcation branches arising at the lower stability boundary but reaching a region of positive $\kappa _2$. Interestingly, these curves lie below the bifurcation branches arising at the upper stability boundary for the same $\kappa _{\text {nl},2}$ values, mining the robustness of the trivial solution. This result highlights that introducing an additional nonlinearity in the control force must be done with particular care and considering the system’s global behaviour. This phenomenon is particularly relevant in the non-collocated case, where large nonlinearities are required to control bifurcations. Indeed, it is well known that systems encompassing large nonlinearities might present dynamical phenomena hardly predictable. We remark that bifurcation branches crossing the border of $\kappa _1=0$ (or $\kappa _2=0$) are present also in the other cases studied in this section but are not represented for clarity of illustration of the figures.

Fig. 14

Time series obtained from direct numerical simulations of the collocated (a) and non-collocated (b) systems for the parameter values $\chi =0.05$, $r=1$, $\gamma =1$, $\mu =1$; a $\tau =0.1$, $\kappa _1=0.4$; b $\tau =0.15$, $\kappa _2=0.3$. Values of $\kappa _{\text {nl},1}$ and $\kappa _{\text {nl},2}$ and initial conditions are indicated in the plot. Blue and red lines mark time series not converging towards the trivial solution, while black lines mark time series converging towards it

In order to directly illustrate the potentiality and limitations of utilising a nonlinear control force for enhancing robustness, Fig. 14 depicts time series obtained from direct numerical simulations. Figure 14a refers to the collocated system and parameter values close to the upper boundary (same parameter values as in Fig. 7a). If $\kappa _{\text {nl},1}=0$ and the initial displacement $x_1$ is too large, the system converges towards a large quasiperiodic attractor (red curve). However, including a small negative nonlinearity in the control force ($\kappa _{\text {nl},1}=-0.005$), for even larger initial conditions, the system still converges to the trivial solution. This result clearly suggests that the trivial solution is more robust thanks to the additional nonlinearity.

Referring to the non-collocated case, Fig. 14b shows time series for parameter values close to the upper stability boundary (same parameter values as in Fig. 10c). In this case, for certain initial conditions, the system either converges towards a large periodic attractor or towards the trivial solution, depending on the value of $\kappa _{\text {nl},2}$ (red and black curves in the figure, respectively, the large periodic attractor is visible in Fig. 10c). However, if the initial $x_1$ displacement is slightly increased, the system diverges unboundedly (blue curve) in the case of a nonlinear controller. This example directly shows that, although a nonlinear control force can increase robustness, it might also generate undesired and unexpected phenomena.

6 Conclusions

This study investigated the stability and bifurcation behaviour of a two-DoF system subject to delayed acceleration control. Two configurations of the same systems were considered, namely a collocated and a non-collocated one. The stability analysis illustrated the importance of considering the time delay of the control force, especially for the collocated case, where even an infinitesimal time delay can cause instabilities. Additionally, time delay seems particularly critical for both the collocated and non-collocated cases if damping is small.

The bifurcation analysis showed an interesting and unexpected feature about the global dynamics of the system. For both configurations studied, if the system encompasses a hardening stiffness nonlinearity, bifurcations at the loss of stability are subcritical, while they are supercritical in the case of softening nonlinearity. This behaviour has important consequences on the robustness of the stability of the trivial solution. In fact, particularly in the case of hardening nonlinearity, the system can experience large oscillations even within the stable region of the trivial solution if subject to a sufficiently large perturbation.

By adding a nonlinear term in the control force, a strategy to increase the robustness of the trivial solution was developed. Our analysis illustrates that, for a collocated controller, even a small nonlinearity can change the character of the bifurcations, improving the robustness of the trivial solution, even in the case of hardening nonlinearity. However, this approach seems to have significant limitations in the non-collocated case, where strong additional nonlinearities would be required to control bifurcations; these strong nonlinearities typically generate other undesired dynamical phenomena, hardly predictable.

The bifurcation analysis was performed for a given set of parameter values. The effect of the various parameters on the system’s nonlinear behaviour might illustrate other dynamical mechanisms not disclosed in this study. Other relevant aspects omitted in this work are the saturation of the control force and external excitations. These two elements might have an essential effect on the global dynamics of the system and will be analysed in future studies.