1 Introduction

The position and trajectory control of mechanical systems have been investigated extensively in the literature [27]. There are two basic approaches: the feed forward and the feedback methods. In the feed forward case, the effect of a command is estimated by means of a mechanical model, and the actuation is chosen in a way that the dynamic system performs the desired motion. Input shaping is a widely used feed forward control strategy that was first published in the 50s by Smith [29], and is still a research topic of control strategies [2, 6, 19, 20]. In contrast, the feedback control approach measures the actual states of the system and acts based on the measured states. However, using a feedback loop can be time- and resource-consuming; therefore, the feed forward and feedback approaches are occasionally combined [3].

The control strategies are often designed without the inclusion of time delay [4, 14, 25, 34]. However, due to the finite time of data processing, data transmission and the delayed response of the actuators, a certain amount of time delay always occurs, which may influence the stability properties. This is even more relevant in case of human operated machines with human sensing and actuation [22].

Mathematical modelling of delayed control of mechanical systems has two essential ways. In case of digital control, the states of the system are measured with a given sampling frequency, and the corresponding mathematical model leads to a discrete time system [9, 13]. However, when the sampling time is small compared to the data processing and transmission time, continuous time delay description can be applied, which leads to delay differential equations (DDE) [21, 32]. Similar DDE models are used in case of human-controlled machines [12].

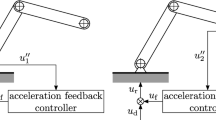
In many robotic applications, the effectors (like cameras, electrode holders of welding machines or polishers) are located at the end of an arm, the position of which is prescribed by the given technological process. If the corresponding robotic arm is not perfectly rigid, the end effector may oscillate before it reaches its desired position in space since the arm is actuated at its other end as shown in Fig. 1.

There are several solutions for this vibration problem. It is possible to use feedback control in a way that the applied actuator force is determined by the actual state of the end effector. This is called non-collocated control since the sensor of the state of the end effector is at a different location where the actuator is. There are a couple of practical problems with this solution: apart from the increased costs of sensing the position and velocity of the end effector in space, the non-collocated control may be sensitive for stability issues even if the time delays are negligible in the control loop.

The current practical solution is to use collocated position control, where the state of the arm at the actuator is sensed and used in the feedback loop. This way, the position of the end effector is only estimated but the stability of the system can easily be guaranteed for delay-free systems. However, if the delay of the actuation is not negligible, the collocated position control may also become unstable even for quite rigid arms and relatively small time delays. The present study discusses the corresponding conditions of stability and the possibly arising nonlinear vibrations.

Fig. 1
figure 1

Alternative position sensor configurations of an elastic robotic arm

Full size image

Although the delayed PD control and the destabilizing effect of the so-called unmodelled high-frequency dynamics is well-known in the theory of robot control [3], the resolution of the corresponding stability issues and vibration problems is usually left for the experimental gain tuning procedure in practice. An essential nonlinear vibration issue is whether the bifurcations at the stability boundaries are super- or subcritical. In case of delayed control, these boundaries are often subcritical [15, 16, 18, 33], while the saturation of the control force tends to cause stable vibrations around unstable equilibria [8]. The exploration of these phenomena can actually guide the above mentioned gain-tuning procedure.

In the present case, the delay-induced self-excited vibrations are investigated in collocated position control of an elastic arm with an aim to support, for example, the design of controlled worktables of machine tools carrying elastic workpieces [26] or elastic robotic arms subjected to heavy end effectors [17].

The outline of this paper is as follows. In Sect. 2, the simplified mechanical model is constructed in the presence of collocated feedback control with delay and saturation. The stability of the linearized system is examined and stability charts are constructed in Sect. 3. This is followed by the Hopf bifurcation calculation to characterize the emerging self-excited vibrations at loss of stability. The conclusions are summarized in Sect. 5.

2 Mechanical model

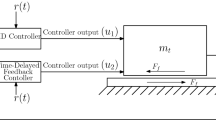
The mechanical model presented in Fig. 2 is a low degree of freedom approximation of the collocated control of the elastic arm in Fig. 1. Two blocks slide along a smooth horizontal straight path, which are connected with a linear spring of stiffness k that represents the elasticity of the arm in Fig. 1. The displacements of the blocks of masses \(m_1\) and \(m_2\) are \(x_1\) and \(x_2\), respectively. The generalized coordinates are chosen in a way that the spring is relaxed when \(x_1=x_2\). Between the block \(m_1\) and the ground, dry friction is considered, which models the friction that always occurs in the drive chain of the actuator.

In accordance with the collocated control strategy, the position and velocity of mass \(m_1\) are measured and fed back with a proportional-derivative controller. The control force F acting on the mass \(m_1\) is subjected to constant time delay \(\tau \) and saturates at \(\pm Q\), where Q is the maximal force which can be applied by the actuator in case of large input signals.

Fig. 2
figure 2

Collocated position control model

Full size image

Denoting the time derivative by dot, the governing equation of the above described system assumes the form

$$\begin{aligned} \begin{bmatrix} m_1 &{} 0\\ 0 &{} m_2 \end{bmatrix} \begin{bmatrix} \ddot{x}_1\\ \ddot{x}_2 \end{bmatrix} + \begin{bmatrix} k &{} -k\\ -k &{} k \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} F-F_{\mathrm {C}}\\ 0 \end{bmatrix}, \end{aligned}$$
(1)

where

$$\begin{aligned} F_{\mathrm {C}}\left\{ \begin{array}{ll} =C{\mathrm {sgn}}({\dot{x}}_1) &{}\quad \mathrm {if}\;{\dot{x}}_1\ne 0\\ \in [-C,C] &{}\quad \mathrm {if}\;{\dot{x}}_1=0 \end{array}\right. \end{aligned}$$
(2)

is the simplest model of Coulomb friction force, the maximal absolute value of which is C.

Considering also the saturation as a nonlinearity, the expression of the delayed control force takes the form

$$\begin{aligned} F(t) = Q\tanh \left( \frac{-K_{\mathrm {p}}x_1(t-\tau )-K_{\mathrm {d}}{\dot{x}}_1(t-\tau )}{Q}\right) , \end{aligned}$$
(3)

with the proportional and derivative control gains \(K_{\mathrm {p}}\) and \(K_{\mathrm {d}}\), respectively.

In the close neighbourhood of the desired zero position, the control force is assumed to be linear, which leads to an upper estimate of the static position error

$$\begin{aligned} \delta =\frac{C}{K_{\mathrm {p}}}. \end{aligned}$$
(4)

This error occurs when the system stops at \(x_2\approx x_1\in [-\delta ,\delta ],\) and consequently, the absolute value of the control force |F| becomes less than the Coulomb friction C and the block \(m_1\) sticks to the ground there. This means that the final position error \(\delta \) is inversely proportional to the gain \(K_{\mathrm {p}}\) after the control task is completed. Accordingly, the proportional gain should be maximized while keeping the system stable. This is challenging because the presence of time delay always leads to dynamic loss of stability as the proportional gain is increased.

Since the dry friction has a negative power, it has a stabilizing effect on the system [1]. Consequently, when the dry friction is neglected in the following stability and bifurcation analysis, a conservative estimate is applied from engineering viewpoint, while the maximization of the proportional gain still remains an essential goal.

To reduce the number of parameters, let us introduce the dimensionless time \({\tilde{t}} =t/\tau \) and the new dimensionless parameters:

$$\begin{aligned} \mu = \frac{m_2}{m_1}, \quad k_{\mathrm {p}} = \frac{K_{\mathrm {p}}\tau ^2}{m_1}, \quad k_{\mathrm {d}} = \frac{K_{\mathrm {d}}\tau }{m_1}, \quad \alpha = \tau \sqrt{\frac{k}{m_2}},\nonumber \\ \end{aligned}$$
(5)

which are the mass ratio \(\mu \), the dimensionless proportional gain \(k_{\mathrm {p}}\), the dimensionless differential gain \(k_{\mathrm {d}}\). The parameter \(\alpha \) can be considered either as a dimensionless delay or as a dimensionless natural frequency of the uncontrolled mechanical system when the block of mass \(m_1\) is fixed. We also introduce a new saturation parameter

$$\begin{aligned} q=\frac{Q\tau ^2}{m_1}. \end{aligned}$$
(6)

Let us calculate the Taylor series of the governing equation up to third order around the equilibrium position \(x_1=x_2=0\), where both blocks are at rest, the spring is relaxed, and the control force is zero. Dropping the tilde, the nonlinear DDE assumes the form:

$$\begin{aligned} \dot{{\mathbf {y}}}(t) = {\mathbf {L}}{\mathbf {y}}(t)+{\mathbf {R}}{\mathbf {y}}(t-1)+{\mathbf {F}}({\mathbf {y}}(t-1))\,, \end{aligned}$$
(7)

with \({\mathbf {y}} = \mathtt {col}[x_1\ {\dot{x}}_1\ x_2\ {\dot{x}}_2]\), dot referring to derivative with respect to the dimensionless time,

$$\begin{aligned} {\mathbf {L}}=\begin{bmatrix} 0&{}1&{}0&{}0\\ -\mu \alpha ^2&{} 0&{} \mu \alpha ^2&{} 0\\ 0&{}0&{}0&{}1\\ \alpha ^2&{} 0&{} -\alpha ^2&{}0 \end{bmatrix},\quad {\mathbf {R}}=\left[ \begin{array}{cccc} 0&{}0&{} 0&{} 0\\ -k_{\mathrm {p}}&{} -k_{\mathrm {d}}&{} 0&{} 0\\ 0&{}0&{} 0&{}0\\ 0&{} 0&{} 0&{}0 \end{array}\right] ,\nonumber \\ \end{aligned}$$
(8)

and

$$\begin{aligned} {\mathbf {F}}({\mathbf {y}}(t-1)) = \begin{bmatrix} 0\\ \frac{1}{q^2}f({\mathbf {y}}(t-1))\\ 0\\ 0 \end{bmatrix}, \end{aligned}$$
(9)

where

$$\begin{aligned} \begin{aligned} f({\mathbf {y}}(t-1))&= \frac{1}{3}k_{\mathrm {p}}^3y_1^3(t-1)\\&\quad +k_{\mathrm {p}}^2k_{\mathrm {d}}y_1^2(t-1)y_2(t-1)\\&\quad +k_{\mathrm {p}}k_{\mathrm {d}}^2y_1(t-1)y_2^2(t-1)\\&\quad +\frac{1}{3}k_{\mathrm {d}}^3y_2^3(t-1). \end{aligned} \end{aligned}$$
(10)

3 Linear stability analysis

First, let us examine the linear part of the governing equations. With respect to the dimensionless characteristic exponent \(\lambda \), the corresponding characteristic function

$$\begin{aligned} D(\lambda )=\det (\lambda {\mathbf {I}}-{\mathbf {L}}-{\mathbf {R}}\mathrm {e}^{-\lambda }) \end{aligned}$$
(11)

yields the quasi-polynomial characteristic equation:

$$\begin{aligned}&\lambda ^4+ \alpha ^2(1+\mu )\lambda ^2\nonumber \\&\quad +(k_{\mathrm {d}}\lambda ^3+k_{\mathrm {p}}\lambda ^2+\alpha ^2k_{\mathrm {d}}\lambda +\alpha ^2k_{\mathrm {p}})\mathrm {e}^{-\lambda } = 0, \end{aligned}$$
(12)

which has got infinitely many roots. These characteristic roots determine the stability of the system: it is exponentially stable if and only if all the roots have negative real parts.

For the construction of the stability chart, the characteristic roots are checked whether a root crosses the imaginary axis through the origin or a pair of complex conjugate roots enters the right-hand side of the complex plane.

The substitution of \(\lambda =0\) into the characteristic equation yields the static section of the D-curves (called static D-curve), where saddle-node bifurcation may occur; this is at \(k_{\mathrm {p}}=0\), along the \(k_{\mathrm {d}}\) axis in the \((k_{\mathrm {p}},k_{\mathrm {d}})\) parameter plane (see Fig. 3).

Fig. 3
figure 3

Stability chart for position control when \(\alpha = 0.5\) and \(\mu = 1\). The numbers represent the number of unstable characteristic roots in the disjunct parameter regions

Full size image
Fig. 4
figure 4

Stability charts for different values of \(\alpha \) when \(\mu = 1\). Stable regions are shaded. The saddle-node and Hopf bifurcations of the system are plotted with black and blue lines, respectively. The red dashed lines refer to the Hopf bifurcation boundary of the PD position control in case of a single degree of freedom (1 DoF) system with mass \(m=m_1+m_2\)

Full size image

The so-called dynamic D-curves related to possible Hopf bifurcations can be determined by substituting \(\lambda = \mathrm {i}\omega \) into Eq. (12) where \(\omega \ne 0\) is the dimensionless angular frequency of the emerging self-excited vibrations. Following the steps of the so-called D-subdivision method [11], the separation of the real and imaginary parts of the complex characteristic equation can be rearranged with respect to the critical control gains as a function of the parameter \(\omega \):

$$\begin{aligned} k_{\mathrm {p}}(\omega )&= \left( 1-\frac{\mu \alpha ^2}{\omega ^2-\alpha ^2}\right) \omega ^2\cos \omega , \end{aligned}$$
(13)
$$\begin{aligned} k_{\mathrm {d}}(\omega )&= \left( 1-\frac{\mu \alpha ^2}{\omega ^2-\alpha ^2}\right) \omega \sin \omega . \end{aligned}$$
(14)

Such D-curves are also shown in Fig.  3. Expressions (13) and (14) are singular at \(\omega =\alpha \), and for \(\alpha <\pi /2\), the left-hand side and right-hand side limits are plus and minus infinity, respectively.

The dynamic D-curve shown in Fig. 3 starts from the origin of the \((k_{\mathrm {p}},k_{\mathrm {d}})\) parameter plane, crosses the origin again at \(\omega =\alpha \sqrt{1+\mu }\), and spirals outwards counter clockwise.

The next important property of the system is the so-called root tendency, that is, in which direction the characteristic roots cross the imaginary axis as parameters vary. This can be determined with the help of implicit differentiation of the characteristic Eq. (12) with respect to the gain \(k_{\mathrm {p}}\) where the characteristic exponent is considered as a function \(\lambda (k_{\mathrm {p}})\) of this parameter:

$$\begin{aligned} \mathrm {Re}\frac{\mathrm {d}\lambda }{\mathrm {d}k_{\mathrm {p}}}=\mathrm {Re}\lambda '= \frac{b(\omega )\sin \omega -a(\omega )\cos \omega }{2\omega (a^2(\omega )+b^2(\omega ))}, \end{aligned}$$
(15)

where prime denotes the derivative with respect to \(k_{\mathrm {p}}\), and

$$\begin{aligned}&a(\omega )=\frac{1}{2}\left( 1-\frac{\mu \alpha ^2}{\omega ^2-\alpha ^2}\right) \left( \frac{1}{2}\sin (2\omega )-\omega \right) , \end{aligned}$$
(16)
$$\begin{aligned}&b(\omega )=1+\frac{\mu \alpha ^4}{\left( \omega ^2-\alpha ^2\right) ^2}-\frac{1}{2}\left( 1-\frac{\mu \alpha ^2}{\omega ^2-\alpha ^2}\right) \sin ^2{\omega }\,. \end{aligned}$$
(17)

The denominator of Eq. (15) is positive for \(\omega >0\) and \(\omega \ne \alpha \). Thus, the numerator of (15) specifies the sign, and so the direction of the root tendency as the dimensionless control gain \(k_{\mathrm {p}}\) increases. With the help of this, the number of the unstable characteristic roots can be determined in the disjunct parameter domains of the stability chart (see Fig. 3), which are defined by the stability boundaries.

Fig. 5
figure 5

Stable domains of the system when \(\mu =1\). The upper figure shows the slope of the Hopf bifurcation curve as a function of \(\alpha \), when it goes through the origin at \(\omega =\alpha \sqrt{1+\mu }\). The green and red line segments correspond to \(\alpha \) values at which there are parameter combinations which can stabilize the system, or there are not, respectively. The bottom figure shows the stable regions of the \((\alpha ,k_{\mathrm {d}})\) parameter plane at different values of the control parameter \(k_{\mathrm {p}}\)

Full size image

Figure 3 presents a D-shaped stable region. The system may loss its stability in a static way through the saddle-node bifurcation or in a dynamic way through the Hopf bifurcation where the emerging self-excited vibration has the dimensionless angular frequency \(\omega \in [\alpha \sqrt{1+\mu },~\pi /2]\). The stable area shrinks as the dimensionless delay \(\alpha \) increases, and it disappears at:

$$\begin{aligned} \alpha _{\mathrm {cr},1}=\frac{\pi }{2\sqrt{1+\mu }}; \end{aligned}$$
(18)

it is a critical value for \(\alpha \), that is, for the time delay of the system. However, it is not an absolute maximal delay where the system is still stabilizable. If we increase \(\alpha \) further, there will be further intervals for \(\alpha \) where the system can be stabilized again (see Fig. 4) with appropriate control parameters. In this context, the linear system with fixed parameters will be called not stabilizable if no proportional and derivative control gains exist to stabilize it.

The existence of the stable region is related to the slope of the dynamic D-curve at the origin. The initial slope of this boundary at \(\omega =0\) is independent of the dimensionless delay \(\alpha \):

$$\begin{aligned} \left. k_{\mathrm {d}}'\right| _{\omega =0} = \left. \frac{\tan \omega }{\omega }\right| _{\omega =0}= 1. \end{aligned}$$
(19)

However, when this boundary curve crosses the origin again at \(\omega =\alpha \sqrt{1+\mu }\), the same derivative is

$$\begin{aligned} \left. k_{\mathrm {d}}'\right| _{\omega =\alpha \sqrt{1+\mu }} = \frac{\tan \left( \alpha \sqrt{1+\mu }\right) }{\alpha \sqrt{1+\mu }}, \end{aligned}$$
(20)

which already depends on \(\alpha \). Clearly, a critical value of \(\alpha \) occurs when this derivative changes sign, while it tends to \(\pm \infty \). The first such critical value is at \(\alpha _{\mathrm {cr},1}\) as given in (18).

As the delay increases further, that is, \(\alpha >\alpha _{\mathrm {cr},1}\), the first branch of the dynamic D-curve for \(\omega \in [0,\alpha )\) bends to the left, and in the same time, the second branch for \(\omega \in (\alpha ,\infty )\) has a tangent line at \(\omega =\alpha \sqrt{1+\mu }\) that rotates counter clockwise according to Eq. (20). Thus, the second branch of the dynamic D-curve intersects the D-shaped region defined by the first branch for \(\omega \in [0,\pi /2]\) as a “windscreen wiper” turning it again and again to stable and unstable as the dimensionless delay \(\alpha \) increases through \(\alpha _{\mathrm {cr},2},\, \alpha _{\mathrm {cr},3},\ldots \) (see Fig. 4, also Fig. 5).

It is interesting to compare these stability charts to the ones of the PD-controlled single degree of freedom (DoF) system, where \(k\rightarrow \infty \) and \(m=m_1+m_2\). The corresponding dynamic D-curves are presented with the red dashed lines in Fig. 4. As \(\alpha \) increases, the first branch of the dynamic D-curve of the original system tends to this Hopf-type stability boundary of the single DoF system, which yields that the reappearing D-shaped stable region approximates the stable domain of the single DoF system (see for example the panel of Fig. 4 with \(\alpha =6\)). This agrees with our intuition, since, by definition, \(\alpha ^2\) is directly proportional to the stiffness of the spring, thus, the connection between the blocks becomes rigid as \(\alpha \rightarrow \infty \). Note that while these curves practically coincide for \(\alpha >6\), they are not necessarily stability boundaries of the two DoF system due to the above described periodic “windscreen wiper effect” caused by the rotating tail of the second branch of the dynamic D-curve for \(\omega \in (\alpha ,\infty )\).

The lower panel of Fig. 5 presents the stability boundaries in the dimensionless parameter plane \((\alpha ,k_{\mathrm {d}})\) at fixed values of the dimensionless control gain \(k_{\mathrm {p}}\). One can observe that increasing \(\alpha \) from 0, the stable domain shrinks, disappears and when it appears again, it is even larger than in the case of \(\alpha =0\). Note, however, that this phenomenon occurs only in the plane of the dimensionless control parameters. If one transforms them back to \(K_{\mathrm {p}}\) and \(K_{\mathrm {d}}\), then at \(\alpha =0\), that is at \(\tau =0\), the whole positive quadrant of the \((K_{\mathrm {p}},K_{\mathrm {d}})\) parameter plane is stable, while above \(\alpha _{\mathrm {cr},2}\), the reappearing stable domain is bounded and its size is smaller.

A practically relevant consequence of the dynamic analysis is related to the calculation of the possible maximal proportional control gains \(K_{\mathrm {p,max}}\) that ensures the smallest possible static position error \(\delta _{\mathrm {min}}=C/K_{\mathrm {p,max}}\) in (4). Panel (a) of Fig. 6 presents the maximal dimensionless proportional gains \(k_{\mathrm {p,max}}\) against the dimensionless delay \(\alpha \), which are determined by means of the rightmost parameter points of the stable domains (if exist) in the stability charts of Fig. 4. It can be observed that \(k_{\mathrm {p},\mathrm {max}}\) is even larger in the second domain of stability than in the first. However, the dimensional proportional gain \(K_{\mathrm {p,max}}=k_{\mathrm {p,max}}m_1/\tau ^2\) may have very large values in the first stable domain as a function of the delay \(\tau \) (see panel (b) of Fig. 6) because \(\tau \rightarrow 0\) yields \(K_{\mathrm {p,max}}\rightarrow \infty \).

In the meantime, since the dimensionless parameter \(\alpha \) also includes the spring stiffness k (see (5)), one can calculate \(K_{\mathrm {p,max}}\) also as a function of the spring stiffness [see the parameter point P in panel (c) of Fig. 6]. This results in the overall smallest static position error in the second stable domain at

$$\begin{aligned} k=12.4\frac{m_2}{\tau ^2}, \, K_{\mathrm {p}}=1.16\frac{m_1}{\tau ^2} \Rightarrow \delta _{\mathrm {min}}=0.86\frac{C}{m_1}\tau ^2. \end{aligned}$$
(21)

It clearly shows that decreasing the time delay improves the positional accuracy substantially.

Fig. 6
figure 6

Panel (a) presents the maximal dimensionless proportional gain \(k_{\mathrm {p,max}}\) against the dimensionless delay \(\alpha \) when \(m_1=m_2\). Panel (b) shows the maximal proportional gain \(K_{\mathrm {p,max}}\) as a function of the delay \(\tau \) at the fixed parameter values: \(m_1=1\,{\mathrm {kg}}\), \(m_2=1\,{\mathrm {kg}}\), \(k=10\,{\mathrm {kN/m}}\). Panel (c) presents \(K_{\mathrm {p,max}}\) against the spring stiffness k for \(m_1=1\,{\mathrm {kg}}\), \(m_2=1\,{\mathrm {kg}}\), \(\tau = 0.01\,{\mathrm {s}}\). The stabilizable regions are shaded

Full size image

4 Hopf bifurcation calculation

As a parameter point leaves the stable region of the \((k_{\mathrm {p}},k_{\mathrm {d}})\) plane at the stability boundary presented by the dynamic D-curves, a limit cycle may emerge, the amplitude of which can be approximated with the help of the Hopf bifurcation analysis. Its first step is to carry out the so-called centre manifold reduction, that is, to project the system from the infinite-dimensional state space of the DDE onto the two-dimensional invariant subspace that is tangent to the plane spanned by the critical eigenvectors [11, 24].

Introduce the function \({\mathbf {x}}_t:{\mathbb {R}} \rightarrow {\mathbb {X}}_{{\mathbb {R}}^4}\) with the shift \({\mathbf {x}}_t(\vartheta )={\mathbf {x}}(t+\vartheta )\), with \(\vartheta \in [-1,0]\), where the minimum of \(\vartheta \) corresponds to the length of the delay, which is 1 in the dimensionless form, and \({\mathbb {X}}_{{\mathbb {R}}^4}\) is the space of continuous functions mapping the interval \([-1,0]\) into \({{\mathbb {R}}^4}\). Furthermore, one can formulate the delay-differential equation (7) as an operator-differential equation (OpDE) [10]:

$$\begin{aligned} \dot{{\mathbf {x}}}_t = {\mathcal {A}}{\mathbf {x}}_t + {\mathcal {F}}({\mathbf {x}}_t), \end{aligned}$$
(22)

where the operators are defined as

$$\begin{aligned} \mathcal {A}\mathbf {\phi }(\vartheta )&= \left\{ \begin{array}{ll} \frac{\mathrm {d}}{\mathrm {d}\vartheta }\mathbf {\phi }(\vartheta ) &{}\quad \mathrm {if}\; -1\le \vartheta <0\\ \mathbf {L}\mathbf {\phi }(0) +\mathbf {R}\mathbf {\phi }(-1) &{}\quad \mathrm {if}\; \vartheta = 0 , \end{array} \right. \end{aligned}$$
(23)
$$\begin{aligned} \mathcal {F}(\mathbf {\phi })(\vartheta )&= \left\{ \begin{array}{ll} \mathbf {0} &{}\quad \mathrm {if}\;-1\le \vartheta <0\\ \mathbf {F}(\mathbf {\phi }(-1)) &{}\quad \mathrm {if}\; \vartheta = 0. \end{array} \right. \end{aligned}$$
(24)

Here, \({\mathbf {L}}\) and \({\mathbf {R}}\) are the coefficient matrices of the non-delayed and delayed state vectors in Eq. (7), respectively. The characteristic exponents of the linear part of (7) are the same as those of the linear operator \({\mathcal {A}}\) [11].

For the centre manifold reduction, we need the right eigenvectors of \({\mathcal {A}}\) corresponding to the critical eigenvalues \(\lambda _{\mathrm {cr}} = \pm \mathrm {i}\omega \). Then, the real eigenvectors \({\mathbf {s}}_{1,2}\in {\mathbb {X}}_{{\mathbb {R}}^4}\) satisfy (see [30]):

$$\begin{aligned} {\mathcal {A}}{\mathbf {s}}_1 = -\omega {\mathbf {s}}_2, \quad {\mathcal {A}} {\mathbf {s}}_2 = \omega {\mathbf {s}}_1, \end{aligned}$$
(25)

which is a boundary value problem for \({\mathbf {s}}_{1,2}(\vartheta )\) according to the definition of the linear operator \({\mathcal {A}}\) in Eq. (23). The solution assumes the form

$$\begin{aligned} \begin{aligned}&{\mathbf {s}}_1(\vartheta ) = {\mathbf {S}}_1\cos (\omega \vartheta )-{\mathbf {S}}_2\sin (\omega \vartheta ), \\&{\mathbf {s}}_2(\vartheta ) = {\mathbf {S}}_2\cos (\omega \vartheta )+{\mathbf {S}}_1\sin (\omega \vartheta ), \end{aligned} \end{aligned}$$
(26)

where \({\mathbf {S}}_{1,2}\in {\mathbb {R}}^4\) satisfy the linear homogeneous algebraic equation

$$\begin{aligned} \begin{bmatrix} {\mathbf {L}}+{\mathbf {R}}\cos {\omega } &{} \omega {\mathbf {I}} + {\mathbf {R}}\sin {\omega }\\ -\left( \omega {\mathbf {I}} + {\mathbf {R}}\sin {\omega }\right) &{} {\mathbf {L}}+{\mathbf {R}}\cos {\omega } \end{bmatrix} \begin{bmatrix} {\mathbf {S}}_1 \\ {\mathbf {S}}_2 \end{bmatrix} = \begin{bmatrix} {\mathbf {0}} \\ {\mathbf {0}} \end{bmatrix} \end{aligned}$$
(27)

as it follows from the corresponding boundary conditions. Let us choose the first components of \({\mathbf {S}}_1\) and \({\mathbf {S}}_2\) to be 1 and 0, respectively; then, (27) yields

$$\begin{aligned} {\mathbf {S}}_1 = \begin{bmatrix} 1\\ 0\\ \frac{\alpha ^2}{\alpha ^2-\omega ^2}\\ 0 \end{bmatrix}, \quad {\mathbf {S}}_2 = \begin{bmatrix} 0\\ \omega \\ 0\\ \frac{\omega \alpha ^2}{\alpha ^2-\omega ^2} \end{bmatrix}. \end{aligned}$$
(28)

In order to project the system onto the plane spanned by the eigenvectors \({\mathbf {s}}_1\) and \({\mathbf {s}}_2\), one needs the left eigenvectors \({\mathbf {n}}_{1,2}\) of the linear operator \({\mathcal {A}}\) associated with the critical eigenvalues \({\mp } \mathrm {i}\omega \).

Introduce the adjoint operator of \({\mathcal {A}}\) by

$$\begin{aligned} {\mathcal {A}}^\star {\psi }(\sigma ) = \left\{ \begin{array}{ll} -\frac{\mathrm {d}}{\mathrm {d}\sigma }{\psi }(\sigma ) &{}\quad \mathrm {if}\; 0<\sigma \le 1\\ {\mathbf {L}}^\star {\psi }(0)+{\mathbf {R}}^\star {\psi }(1) &{}\quad \mathrm {if}\; \sigma = 0, \end{array} \right. \end{aligned}$$
(29)

where \(^\star \) denotes the transposed conjugate matrix and also the adjoint operator.

The real eigenvectors \({\mathbf {n}}_{1,2}\in {\mathbb {X}}^\star _{{\mathbb {R}}^4}\) satisfy

$$\begin{aligned} {\mathcal {A}}^\star {\mathbf {n}}_1 = \omega {\mathbf {n}}_2, \quad {\mathcal {A}}^\star {\mathbf {n}}_2 = -\omega {\mathbf {n}}_1. \end{aligned}$$
(30)

From which

$$\begin{aligned} \begin{aligned} {\mathbf {n}}_1(\sigma )&= {\mathbf {N}}_1\cos (\omega \sigma )-{\mathbf {N}}_2\sin (\omega \sigma ), \\ {\mathbf {n}}_2(\sigma )&= {\mathbf {N}}_2\cos (\omega \sigma )+{\mathbf {N}}_1\sin (\omega \sigma ), \end{aligned} \end{aligned}$$
(31)

with \({\mathbf {N}}_{1,2}\in {\mathbb {R}}^4\) satisfying

$$\begin{aligned} \begin{bmatrix} {\mathbf {L}}^\star +{\mathbf {R}}^\star \cos {\omega } &{} -\left( \omega {\mathbf {I}} + {\mathbf {R}}^\star \sin {\omega }\right) \\ \omega {\mathbf {I}} + {\mathbf {R}}^\star \sin {\omega } &{} {\mathbf {L}}^\star +{\mathbf {R}}^\star \cos {\omega } \end{bmatrix} \begin{bmatrix} {\mathbf {N}}_1 \\ {\mathbf {N}}_2 \end{bmatrix}= \begin{bmatrix} {\mathbf {0}} \\ {\mathbf {0}} \end{bmatrix}.\nonumber \\ \end{aligned}$$
(32)

The solutions

$$\begin{aligned}&{\mathbf {N}}_1 \nonumber \\&\quad = \begin{bmatrix} \omega \left( 1+\frac{\mu \alpha ^2}{\alpha ^2-\omega ^2}\right) (N_{12}\frac{\sin (2\omega )}{2}-N_{22}\sin ^2\omega )+N_{22}\omega \\ N_{12}\\ \frac{\mu \omega \alpha ^2}{\alpha ^2-\omega ^2} N_{22}\\ \frac{\mu \alpha ^2}{\alpha ^2-\omega ^2} N_{12} \end{bmatrix},\end{aligned}$$
(33)
$$\begin{aligned}&{\mathbf {N}}_2 \nonumber \\&\quad =\begin{bmatrix} \omega \left( 1+\frac{\mu \alpha ^2}{\alpha ^2-\omega ^2} \right) (N_{22}\frac{\sin (2\omega )}{2} +N_{12}\sin ^2\omega )-N_{12}\omega \\ N_{22}\\ -\frac{\mu \omega \alpha ^2}{\alpha ^2-\omega ^2} N_{12}\\ \frac{\mu \alpha ^2}{\alpha ^2-\omega ^2} N_{22} \end{bmatrix} \end{aligned}$$
(34)

include the two free parameters \(N_{12}\) and \(N_{22}\) that are determined by means of the orthonormality conditions

$$\begin{aligned} \langle {\mathbf {n}}_1, {\mathbf {s}}_1 \rangle = 1, \quad \langle {\mathbf {n}}_1, {\mathbf {s}}_2 \rangle = 0, \end{aligned}$$
(35)

where \(\langle .,.\rangle \) denotes the inner product. With the definition of the inner product (see “Appendix A”), (35) can be expanded as

$$\begin{aligned}&\langle {\mathbf {n}}_1,{\mathbf {s}}_1\rangle = {\mathbf {N}}_1^\star {\mathbf {S}}_1 + \int _{\xi = -1}^{0}{\mathbf {n}}_1^\star (\xi +1){\mathbf {R}}{\mathbf {s}}_1(\xi )\mathrm {d}\xi = 1, \end{aligned}$$
(36)
$$\begin{aligned}&\langle {\mathbf {n}}_1,{\mathbf {s}}_2\rangle = {\mathbf {N}}_1^\star {\mathbf {S}}_2 + \int _{\xi = -1}^{0}{\mathbf {n}}_1^\star (\xi +1){\mathbf {R}}{\mathbf {s}}_2(\xi )\mathrm {d}\xi = 0, \end{aligned}$$
(37)

which yields

$$\begin{aligned} N_{12} = \frac{a}{a^2+b^2}, \quad N_{22} = \frac{b}{a^2+b^2}. \end{aligned}$$
(38)

Here, a and b are expressed in (16) and (17), respectively, which also appear in the root tendency Eq. (15).

In order to restrict the dynamics to the invariant centre manifold, the infinite-dimensional state \({\mathbf {x}}_t\) is projected to the right eigenvectors \({\mathbf {s}}_1\) and \({\mathbf {s}}_2\) by means of the corresponding inner product between the left eigenvectors \({\mathbf {n}}_{1,2}\) and \({\mathbf {x}}_t\). The infinite-dimensional part \({\mathbf {w}}\) of the state \({\mathbf {x}}_t\) is calculated by simple subtraction. Accordingly, the new scalar coordinates \(z_{1,2}\) on the centre manifold are introduced by

$$\begin{aligned} z_1&= \langle {\mathbf {n}}_1, {\mathbf {x}}_t \rangle , \end{aligned}$$
(39)
$$\begin{aligned} z_2&= \langle {\mathbf {n}}_2, {\mathbf {x}}_t \rangle , \end{aligned}$$
(40)

and

$$\begin{aligned} {\mathbf {w}} = {\mathbf {x}}_t-z_1{\mathbf {s}}_1-z_2{\mathbf {s}}_2. \end{aligned}$$
(41)

With these new variables, the operator differential Eq. (22) can be reformulated as

(42)

where is a zero operator, \({\mathcal {O}} : {\mathbb {X}}_{{\mathbb {R}}^4}\rightarrow {\mathbb {R}} \) is a zero functional; for details, see “Appendix B”.

In order to get the first Fourier term of the oscillation in the centre manifold, the first two rows of Eq. (42) should be calculated up to third order:

$$\begin{aligned} \begin{aligned} {\dot{z}}_1&= \omega z_2 + \sum _{ k+l = 3}f_{kl}z_1^k z_2^l +{\mathcal {O}}(z_{1,2}^5), \\ {\dot{z}}_2&= -\omega z_1 + \sum _{ k+l = 3}g_{kl}z_1^k z_2^l +{\mathcal {O}}(z_{1,2}^5), \end{aligned} \end{aligned}$$
(43)

where the indices k and l are nonnegative integers. Due to the symmetry of the nonlinearity, the nonlinear operator \({\mathcal {F}}\) does not have second-order terms, which implies that \({\mathbf {w}}\) is at least \({\mathcal {O}}(y_{1,2}^3)\), and so it effects only the fifth- and higher-order terms in (43).

The so-called Poincaré–Lyapunov coefficient \(\varDelta \) can be calculated with the help of the Bautin formula (see “Appendix C”). Since one obtains \(f_{12}=g_{21}=g_{03}=0\),

$$\begin{aligned} \varDelta = \frac{3}{8}f_{30} = \frac{\omega ^5\left( \sin (2\omega )-2\omega \right) }{32q^2(a^2+b^2)}\left( 1-\frac{\mu \alpha ^2}{\omega ^2-\alpha ^2}\right) ^4\,.\nonumber \\ \end{aligned}$$
(44)

This is always negative, that is, the Hopf bifurcation is always supercritical along the dynamic D-curves of Fig. 4.

In the centre manifold, the oscillation close to the Hopf bifurcation boundary can be approximated as

$$\begin{aligned} \begin{bmatrix} z_1(t)\\ z_2(t) \end{bmatrix} = A\begin{bmatrix} \cos (\omega t)\\ -\sin (\omega t) \end{bmatrix}, \end{aligned}$$
(45)

where the amplitude A can be expressed as

$$\begin{aligned} A = \sqrt{-\frac{\mathrm {Re}\lambda '}{\varDelta }(k_{\mathrm {p}}-k_{\mathrm {p},\mathrm {cr}})}. \end{aligned}$$
(46)

This yields that for proportional gain \(k_{\mathrm {p}}\) close enough to its critical value \(k_{\mathrm {p},\mathrm {cr}}\), the self-excited vibration can be approximated as

$$\begin{aligned} \begin{aligned} {\mathbf {x}}(t)&={\mathbf {x}}_t(0) \approx z_1(t){\mathbf {s}}_1(0)+z_2(t){\mathbf {s}}_2(0)\\&= A({\mathbf {S}}_1\cos (\omega t)-{\mathbf {S}}_2\sin (\omega t)), \end{aligned} \end{aligned}$$
(47)

where \({\mathbf {S}}_{1,2}\) are given in (28). This way, the substitution of (15) and (44) into (46) leads to the closed-form expressions of the vibration amplitudes \(A_1\) and \(A_2\) of the blocks \(m_1\) and \(m_2\), respectively:

$$\begin{aligned}&A_{1} =\frac{2q(\omega ^2-\alpha ^2)^2}{\omega ^3(\omega ^2-(1+\mu )\alpha ^2)^2} \sqrt{k_{\mathrm {p}}-k_\mathrm {p,cr}}\nonumber \\&\quad \times \sqrt{\frac{\sin \omega \left( 1+\mu \frac{\omega ^2\alpha ^2+\alpha ^4}{(\omega ^2-\alpha ^2)^2}\right) +\omega \cos \omega \left( 1-\mu \frac{\alpha ^2}{\omega ^2-\alpha ^2}\right) }{\omega -\frac{1}{2}\sin (2\omega )}} \end{aligned}$$
(48)

and

$$\begin{aligned} A_{2} =\frac{\alpha ^2}{\alpha ^2-\omega ^2}A_1. \end{aligned}$$
(49)

These algebraic expressions fit well to the amplitudes created with DDE-BIFTOOL [5, 28] for the original nonlinear system given in (7)–(10) (see Fig. 7). Clearly, the higher-order nonlinear terms result in an increasing deviation between the analytical and numerical results for \(k_{\mathrm {p}}>1.1\,k_\mathrm {p,cr}\).

Fig. 7
figure 7

Comparison of the analytical bifurcation diagram to the one created with DDE-BIFTOOL (\(\mu =1\), \(\alpha = 0.5\), \(k_{\mathrm {d}}=1\) and \(q=0.2\)). Green and red lines refer to the stable and unstable branches, respectively

Full size image

5 Conclusion

The delayed position control of two blocks connected through a linear spring was investigated as a simplified model of an elastic arm. A collocated proportional-derivative control force was considered with saturation nonlinearity. The linear stability analysis shows that the stable region in the plane of the dimensionless control parameters \((k_{\mathrm {p}},k_{\mathrm {d}})\) shrinks and disappears as the time delay increases. Further increase in the delay results in the reappearance of the stable parameter domain, which then disappears and reappears periodically. Note that these stable regions become negligible for the original control gains \(K_{\mathrm {p}}\), \(K_{\mathrm {d}}\) as it follows from the definitions of the dimensionless parameters in (5) for large delays.

However, the interpretation of the same dimensionless stability charts is different from the viewpoint of the stiffness of the linear spring. The increase in this stiffness also increases the dimensionless parameter \(\alpha \) [see (5)], which means that in case of a fixed time delay \(\tau \), the phenomenon of the periodic appearance/disappearance of the stable control parameter regions is also present as the stiffness parameter varies. These stable domains have about the same size for the original control parameters \(K_{\mathrm {p}}\), \(K_{\mathrm {d}}\) when the delay \(\tau \) is fixed, and they get close to the D-shaped stable domain of the PD-controlled single DoF system, where \(k\rightarrow \infty \) and \(m=m_1+m_2\).

Also in case of fixed delay \(\tau \), the static positional accuracy can be optimized with the help of (21) by tuning the system and control parameters accordingly.

If the stability chart of only the single DoF model is used in the tuning procedure of the control parameters, unexpected instabilities may occur even for relatively large spring stiffness values [see also panel (c) of Fig. 6] where a corresponding robotic arm might be assumed to be practically rigid (see Fig. 1).

The Hopf bifurcation calculation was executed after an infinite-dimensional centre manifold reduction. The Hopf bifurcation is supercritical all along the dynamic stability boundaries. The closed form algebraic expressions for the amplitudes of the arising self-excited oscillations are also checked by the freely available MATLAB software DDE-BIFTOOL. The comparison of the calculated and measured vibration amplitudes may help to estimate how far the stability boundaries are, in which direction the control parameter tuning procedure should be continued.

At the boundary of the stable area, the dynamic D-curve can intersect itself, which may correspond to codimension-2 Hopf bifurcation, where two pairs of complex-conjugate characteristic exponents cross the imaginary axis. At this parameter setting, the self-excited vibrations of the system may become quasiperiodic oscillations containing two distinct frequencies. See, for example, the lower left panel of Fig. 4 with \(\alpha =3.5\); here, the Hopf-Hopf point is denoted with \(\mathrm {H}^2\), and the two independent dimensionless angular frequencies are \(\omega _1=1.029\) and \(\omega _2 = 4.578\). The codimension-2 Hopf bifurcations can be analysed with the algorithm presented in [23, 31]. The existence of quasiperiodic oscillations is expected from the topological structure of the \(\mathrm {H}^2\) bifurcations [7], while its rigorous proof needs further work similarly to the analysis of higher DoF models. Note that the occurrence of quasiperiodic oscillations during the experimental tuning of the control parameters may provide an essential validation of the time-delayed mechanical model used in this study.

The methodology presented here can be generalized for multi-degree of freedom robotic arms, but due to the mathematical complexity, no analytical results are expected. In the meantime, the arising nonlinear vibrations will be qualitatively analogous to the ones observed in the low-dimensional case; its justification is part of a future research.