An asymmetric mode-localized mass sensor based on the electrostatic coupling of different structural modes with distributed electrodes

Abstract

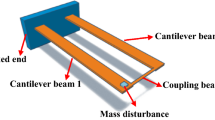
Mode-localized sensor with amplitude ratio as output metric has shown excellent potential in the field of micromass detection. In this paper, an asymmetric mode-localized mass sensor with a pair of electrostatically coupled resonators of different thicknesses is proposed. Partially distributed electrodes are introduced to ensure the asymmetric mode coupling of second- and third-order modes while actuating the thinner resonator by the distributed electrode. The analytical dynamic model is established by Euler–Bernoulli theory and solved by harmonic balance method (HBM) combined with asymptotic numerical method (ANM). Detailed investigations on the linear and nonlinear behavior, critical amplitude as well as the sensitivity of the sensor are performed. The sensitivity of the proposed sensor can be enhanced by about 20 times compared to first-order mode-localized mass sensors. By exploiting the nonlinearities while driving the device beyond the critical amplitude for the in-phase mode, the sensor performs a great improvement in sensitivity up to 1.78 times compared to linear case. The influence of the coupling voltage on the sensor performance is studied, which gives a good reference to avoid mode aliasing. Moreover, the effect of the length of driving electrode on sensitivity is investigated.

Appendices

Appendix A: Coefficients and forcing terms of the method of multiple scales

The parameters in Eq. (22) are defined as:

$$ \begin{gathered} k_{11} = \sqrt {\lambda_{1,3}^{4} - N_{1} \mathop \int \limits_{0}^{1} w^{\prime\prime}_{s1} \left( x \right)\phi_{1,j} dx - 2\alpha_{2} V_{dc}^{2} \mathop \int \limits_{0}^{1} \left( {\phi_{1,3}^{2} H_{1} \left( x \right)\left( {1 + 3w_{s1} (x) + 6w_{s1}^{2} (x)} \right)} \right)dx - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {q_{1,3} \phi^{\prime\prime}_{1,3} } \right)\phi_{1,3} \mathop \int \limits_{0}^{1} \left( {w^{\prime}_{s1} \left( x \right)^{2} } \right)dxdx - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {w^{\prime\prime}_{s1} \left( x \right)} \right)\phi_{1,3} \mathop \int \limits_{0}^{1} \left( {2q_{1,3} \phi^{\prime}_{1,3} w^{\prime}_{s1} \left( x \right)} \right)dxdx} \, \hfill \\ k_{12} = - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {q_{1,3} \phi^{\prime\prime}_{1,3} } \right)\phi_{1,3} \mathop \int \limits_{0}^{1} \left( { + 2q_{1,3} \phi^{\prime}_{1,3} w^{\prime}_{s1} \left( x \right)} \right)dxdx \hfill \\ \quad \quad - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {w^{\prime\prime}_{s1} \left( x \right)} \right)\phi_{1,3} \mathop \int \limits_{0}^{1} \left( {q_{1,3}^{2} \phi_{1,3}^{^{\prime}2} } \right)dxdx \hfill \\ \, \quad - 3\alpha_{2} V_{dc}^{2} q_{1,3}^{2} \mathop \int \limits_{0}^{1} (\phi_{1,3}^{3} H_{1} (x)(1 + 4w_{s1} (x)))dx \hfill \\ k_{13} = - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {q_{1,3} \phi^{\prime\prime}_{1,3} } \right)\phi_{1,3} \mathop \int \limits_{0}^{1} \left( {q_{1,3}^{2} \phi_{1,3}^{^{\prime}2} } \right)dxdx \hfill \\ \quad \quad - 4\alpha_{2} V_{dc}^{2} \mathop \int \limits_{0}^{1} (\phi_{1,3}^{4} H_{1} (x))dx \hfill \\ k_{c1} = - \frac{{2V_{c}^{2} \alpha_{2} }}{{R^{3} }}\mathop \int \limits_{0}^{1} q_{1,3} \phi_{1,3} \phi_{1,3} H_{2} \left( x \right)dx \hfill \\ k_{c2} = \frac{{2V_{c}^{2} \alpha_{2} }}{{R^{3} }}\mathop \int \limits_{0}^{1} q_{2,2} \phi_{2,2} \phi_{1,3} H_{2} \left( x \right)dx \hfill \\ f_{1} = - 2\alpha_{2} V_{dc} V_{ac} \cos \left( {\Omega t} \right)\mathop \int \limits_{0}^{1} \left( {\phi_{1,3} H_{1} \left( x \right)\left. {\left( {1 + 2w_{s1} \left( x \right) + 3w_{s1}^{2} \left( x \right)} \right. + 4w_{s1}^{3} \left( x \right)} \right)} \right)dx \hfill \\ k_{21} = \sqrt {\lambda_{2,2}^{4} \delta^{2} - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {q_{2,2} \phi^{\prime\prime}_{2,2} } \right)\phi_{2,2} \mathop \int \limits_{0}^{1} \left( {w^{\prime}_{s2} \left( x \right)^{2} } \right)dxdx - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {w^{\prime\prime}_{s2} \left( x \right)} \right)\phi_{2,2} \mathop \int \limits_{0}^{1} \left( {2q_{2,2} \phi^{\prime}_{2,2} w^{\prime}_{s2} \left( x \right)} \right)dxdx - N_{2} \mathop \sum \limits_{i = 1}^{n} \mathop \int \limits_{0}^{1} \left( {q_{2,2} \phi^{\prime\prime}_{2,2} } \right)\phi_{2,2} dx} \hfill \\ k_{22} = - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {q_{2,2} \phi^{\prime\prime}_{2,2} } \right)\phi_{2,2} \mathop \int \limits_{0}^{1} \left( {2q_{2,2} \phi^{\prime}_{2,2} w^{\prime}_{s2} \left( x \right)} \right)dxdx \hfill \\ \quad \quad - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {w^{\prime\prime}_{s2} \left( x \right)} \right)\phi_{2,2} \mathop \int \limits_{0}^{1} \left( {q_{2,2}^{2} \phi^{\prime}_{2,2} } \right)dxdx \hfill \\ k_{23} = - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {q_{2,2} \phi^{\prime\prime}_{2,2} } \right)\phi_{2,2} \mathop \int \limits_{0}^{1} \left( {q_{2,2}^{2} \phi^{\prime}_{2,2} } \right)dxdx \hfill \\ k_{c3} = \frac{{2V_{c}^{2} \alpha_{2} }}{{R^{3} \delta }}\mathop \int \limits_{0}^{1} \left( {q_{1,3} \phi_{1,3} } \right)\phi_{2,2} H_{2} \left( x \right)dx \hfill \\ k_{c4} = - \frac{{2V_{c}^{2} \alpha_{2} }}{{R^{3} \delta }}\mathop \int \limits_{0}^{1} \left( {q_{2,2} \phi_{2,2} } \right)\phi_{2,2} H_{2} \left( x \right)dx \hfill \\ \end{gathered} $$

(28)

Appendix B: Analytical solution using the method of multiple scales

The timescales T_n are introduced depending on the parameter ε and defined by:

$$ T_{n} = \varepsilon^{n} t \, \left( {\varepsilon < 1} \right) $$

(29)

The partial differential of time t becomes:

$$ \begin{gathered} \frac{d}{dt} = \frac{\partial }{{\partial T_{0} }}\frac{{dT_{0} }}{dt} + \frac{\partial }{{\partial T_{1} }}\frac{{dT_{1} }}{dt} + \frac{\partial }{{\partial T_{2} }}\frac{{dT_{2} }}{dt} + \cdots = D_{0} + \varepsilon D_{1} + \varepsilon^{2} D_{2} + \cdots \hfill \\ \frac{{d^{2} }}{{dt^{2} }} = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} \left( {D_{1}^{2} + 2D_{0} D_{2} } \right) + \cdots \hfill \\ \end{gathered} $$

(30)

where σ₁ is the detuning parameter in Eq. (23) and

$$ \sigma_{2} = \frac{{\omega_{1} - \omega_{2} }}{{\varepsilon^{2} }} $$

(31)

The solution of Eq. (22) is assumed by a second-order timescales form as follows:

$$ \begin{aligned} q_{1} & = q_{10} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon q_{11} \left( {T_{0} ,T_{1} ,T_{2} } \right) \\ \quad + \varepsilon^{2} q_{12} \left( {T_{0} ,T_{1} ,T_{2} } \right) \\ \end{aligned} $$

(32)

$$ \begin{aligned} q_{2} & = q_{20} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon q_{21} \left( {T_{0} ,T_{1} ,T_{2} } \right) \\ \quad + \varepsilon^{2} q_{22} \left( {T_{0} ,T_{1} ,T_{2} } \right) \\ \end{aligned} $$

(33)

By substituting Eqs. (32) and (33) into Eq. (22), the equations of each order of ε can be obtained:

Order ε⁰:

$$ D_{0}^{2} q_{10} + k_{11}^{2} q_{10} = 0 $$

(34)

$$ D_{0}^{2} q_{20} + k_{21}^{2} q_{20} = 0 $$

(35)

Order ε¹:

$$ D_{0} \left( {D_{0} q_{11} + D_{1} q_{10} } \right) + D_{1} D_{0} q_{10} + k_{11}^{2} q_{11} = - k_{12} q_{10}^{2} $$

(36)

$$ D_{0} \left( {D_{0} q_{21} + D_{1} q_{20} } \right) + D_{1} D_{0} q_{20} + k_{21}^{2} q_{21} = - k_{22} q_{20}^{2} $$

(37)

Order ε²:

$$ \begin{gathered} D_{0} \left( {D_{0} q_{12} + D_{1} q_{11} + D_{2} q_{10} } \right) + D_{1} \left( {D_{0} q_{11} + D_{1} q_{10} } \right) + D_{2} D_{0} q_{10} + k_{11}^{2} q_{12} \hfill \\ \quad = - c_{1} D_{0} q_{10} - \left( {k_{c1} q_{10} + \kappa_{c2} q_{20} } \right) - k_{13} q_{10}^{3} - k_{12} q_{10} q_{11} - f_{1} \cos \left( {k_{11} T_{0} + \sigma_{1} T_{2} } \right) \hfill \\ \end{gathered} $$

(38)

$$ \begin{gathered} D_{0} \left( {D_{0} q_{22} + D_{1} q_{21} + D_{2} q_{20} } \right) + D_{1} \left( {D_{0} q_{21} + D_{1} q_{20} } \right) + D_{2} D_{0} q_{20} + k_{21}^{2} q_{22} \hfill \\ \quad = - c_{2} D_{0} q_{20} - \left( {k_{c3} q_{10} + k_{c4} q_{20} } \right) - k_{23} q_{20}^{3} - k_{22} q_{20} q_{21} \hfill \\ \end{gathered} $$

(39)

The solutions of Eqs. (34) and (35) are given by:

$$ q_{10} = X_{1} e^{{ik_{11} T_{0} }} + \overline{{X_{1} }} e^{{ - ik_{11} T_{0} }} $$

(40)

$$ q_{20} = X_{2} e^{{ik_{21} T_{0} }} + \overline{{X_{2} }} e^{{ - ik_{21} T_{0} }} $$

(41)

where X₁ and X₂ are complex functions and $\overline{{X_{1} }}$ and $\overline{{X_{2} }}$ are the complex conjugates. Then, substituting q₁₀ and q₂₀ into Eqs. (36) and (37) we obtain:

$$ D_{0}^{2} q_{11} + k_{11}^{2} q_{11} = - e^{{ - 2iT_{0} k_{11} }} k_{12} \overline{{X_{1} }}^{2} - 2k_{12} \overline{{X_{1} }} X_{1} - {\text{e}}^{{2iT_{0} k_{11} }} k_{12} X_{1}^{2} - 2i{\text{e}}^{{iT_{0} k_{11} }} k_{11} D_{1} X_{1} + 2i{\text{e}}^{{ - iT_{0} k_{11} }} k_{11} D_{1}^{2} \overline{{X_{1} }} X_{1} $$

(42)

$$ D_{0}^{2} q_{21} + k_{21}^{2} q_{21} = - e^{{ - 2iT_{0} k_{21} }} k_{22} \overline{{X_{2} }}^{2} - 2k_{22} \overline{{X_{2} }} X_{2} - {\text{e}}^{{2iT_{0} k_{21} }} k_{22} X_{2}^{2} - 2i{\text{e}}^{{iT_{0} k_{21} }} k_{21} D_{1} X_{2} + 2i{\text{e}}^{{ - iT_{0} k_{21} }} k_{21} D_{1}^{2} \overline{{X_{2} }} X_{2} $$

(43)

Eliminating the secular terms in Eqs. (42) and (43) results in:

$$ D_{1} X_{1} = D_{1} X_{2} = 0 $$

(44)

And the solutions of Eqs. (38) and (39) are:

$$ q_{11} = \frac{{{\text{e}}^{{ - 2iT_{0} k_{11} }} \overline{{X_{1} }}^{2} k_{12} }}{{3k_{11}^{2} }} - \frac{{2k_{12} \overline{{X_{1} }} X_{1} }}{{k_{11}^{2} }} + \frac{{{\text{e}}^{{2iT_{0} k_{11} }} k_{12} X_{1}^{2} }}{{3k_{11}^{2} }} $$

(45)

$$ q_{21} = \frac{{{\text{e}}^{{ - 2iT_{0} k_{21} }} \overline{{X_{2} }}^{2} k_{22} }}{{3k_{21}^{2} }} - \frac{{2k_{22} \overline{{X_{2} }} X_{2} }}{{k_{21}^{2} }} + \frac{{{\text{e}}^{{2iT_{0} k_{21} }} k_{22} X_{2}^{2} }}{{3k_{21}^{2} }} $$

(46)

By substituting the solutions of q₁₁ and q₂₁ into Eqs. (38) and (39), the secular terms can be obtained as:

$$ \begin{gathered} \frac{1}{2}e^{{iT_{0} \varepsilon^{2} \sigma_{1} }} f_{1} + k_{c1} X_{1} + ik_{11} c_{1} X_{1} - \frac{{10k_{12}^{2} \overline{{X_{1} }} X_{1}^{2} }}{{3k_{11}^{2} }} \hfill \\ \quad + 3k_{13} \overline{{X_{1} }} X_{1}^{2} + k_{c2} e^{{ - iT_{0} \varepsilon^{2} \sigma_{2} }} X_{2} + 2ik_{11} D_{2} X_{1} + D_{1}^{2} X_{1} = 0 \hfill \\ \end{gathered} $$

(47)

$$ \begin{gathered} k_{c3} e^{{iT_{0} \varepsilon^{2} \sigma_{2} }} X_{1} + k_{c4} X_{2} + ik_{21} c_{2} X_{2} - \frac{{10k_{22}^{2} \overline{{X_{2} }} X_{2}^{2} }}{{3k_{21}^{2} }} \hfill \\ \quad + 3k_{23} \overline{{X_{2} }} X_{2}^{2} + 2ik_{21} D_{2} X_{2} + D_{1}^{2} X_{2} = 0 \hfill \\ \end{gathered} $$

(48)

Let X₁ and X₂ be as follows:

$$ X_{1} = \frac{{a_{1} }}{2}e^{{i\gamma_{1} }} ,X_{2} = \frac{{a_{2} }}{2}e^{{i\gamma_{2} }} $$

(49)

Substituting Eq. (49) into Eqs. (47) and (48) and multiplying Eq. (47) and Eq. (48) by ${\text{e}}^{{ - {\text{i}}\gamma_{1} }}$ and ${\text{e}}^{{ - {\text{i}}\gamma_{2} }}$, respectively, then separating the real part and the imaginary part, the following relationships can be obtained:

$$ \begin{gathered} \frac{1}{2}\cos \left( {\phi_{2} } \right)f_{1} - \frac{{5a_{1}^{3} k_{12}^{2} }}{{12\kappa_{11}^{2} }} + \frac{3}{8}a_{1}^{3} k_{13} + \frac{1}{2}a_{1} k_{c1} \hfill \\ \quad + \frac{1}{2}a_{2} \cos \left( {\phi_{1} } \right)k_{c2} - a_{1} k_{11} \sigma_{1} + a_{1} k_{11} \phi^{\prime}_{2} = 0 \hfill \\ \end{gathered} $$

(50)

$$ \begin{gathered} \frac{1}{2}\sin \left( {\phi_{2} } \right)f_{1} - \frac{1}{2}a_{2} \sin \left( {\phi_{1} } \right)k_{c2} \hfill \\ \quad + \frac{1}{2}a_{1} k_{11} c_{1} + k_{11} a^{\prime}_{1} = 0 \hfill \\ \end{gathered} $$

(51)

$$ \begin{gathered} - \frac{{5a_{2}^{3} k_{22}^{2} }}{{12k_{21}^{2} }} + \frac{3}{8}a_{2}^{3} k_{23} + \frac{1}{2}a_{1} \cos \left( {\phi_{1} } \right)k_{c3} \hfill \\ \quad + \frac{1}{2}a_{2} k_{c4} - a_{2} k_{21} \sigma_{1} - a_{2} k_{21} \sigma_{2} + a_{2} k_{21} \phi^{\prime}_{1} + a_{2} k_{21} \phi^{\prime}_{2} = 0 \hfill \\ \end{gathered} $$

(52)

$$ \frac{1}{2}a_{1} \sin \left( {\phi_{1} } \right)k_{c3} + \frac{1}{2}a_{2} k_{21} c_{2} + k_{21} a^{\prime}_{2} = 0 $$

(53)

where ϕ₁ and ϕ₂ are:

$$ \begin{gathered} \phi_{1} = T_{0} \varepsilon^{2} \sigma_{2} + \gamma_{1} - \gamma_{2} \hfill \\ \phi_{2} = T_{0} \varepsilon^{2} \sigma_{1} - \gamma_{1} \hfill \\ \end{gathered} $$

(54)

In the steady state, we have the conditions $a^{\prime}_{1} = a^{\prime}_{2} = \phi^{\prime}_{1} = \phi^{\prime}_{2} = 0$; then, we get

$$ \sin \left( {\phi_{1} } \right) = - \frac{{a_{2} k_{21} c_{2} }}{{a_{1} k_{c3} }} $$

(55)

$$ \cos \left( {\phi_{1} } \right) = \frac{{10a_{2}^{3} k_{22}^{2} + 3a_{2} k_{21}^{2} \left( { - 3a_{2}^{2} k_{23} - 4k_{c4} + 8k_{21} \left( {\sigma_{1} + \sigma_{2} } \right)} \right)}}{{12a_{1} k_{21}^{2} k_{c3} }} $$

(56)

$$ \sin \left( {\phi_{2} } \right) = - \frac{{a_{1}^{2} k_{11} k_{c3} c_{1} + a_{2}^{2} k_{21} k_{c2} c_{2} }}{{a_{1} f_{1} k_{c3} }} $$

(57)

$$ \cos \left( {\phi_{2} } \right) = \frac{{\left( {\frac{{10a_{1}^{4} k_{12}^{2} }}{{k_{11}^{2} }} + 24a_{1}^{2} k_{11} \sigma_{1} + \frac{1}{{k_{c3} }}\left( \begin{gathered} - \frac{{10a_{2}^{4} k_{22}^{2} k_{c2} }}{{k_{21}^{2} }} + 3\left( {3a_{2}^{4} k_{23} k_{c2} - 3a_{1}^{4} k_{13} k_{c3} - 4a_{1}^{2} k_{c1} k_{c3} + 4a_{2}^{2} k_{c2} k_{c4} } \right) \hfill \\ - 24a_{2}^{2} k_{21} k_{c2} \left( {\sigma_{1} + \sigma_{2} } \right) \hfill \\ \end{gathered} \right)} \right)}}{{12a_{1} f_{1} }} $$

(58)

From $\sin \left( {\phi_{1} } \right)^{2} + \cos \left( {\phi_{1} } \right)^{2} = 1$ and $\sin \left( {\phi_{2} } \right)^{2} + \cos \left( {\phi_{2} } \right)^{2} = 1$, Eqs. (24) and (25) can be obtained.