Skip to main content
SpringerLink
Log in

Darboux transformation, exact solutions and conservation laws for the reverse space-time Fokas–Lenells equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

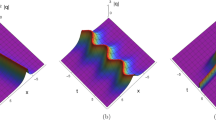
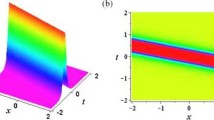
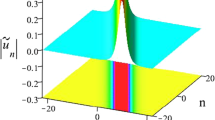
In this paper, we firstly deduce a reverse space-time Fokas–Lenells equation which can be derived from a rather simple but extremely important symmetry reduction of corresponding local equation. Next, the determinant representations of one-fold Darboux transformation and N-fold Darboux transformation are expressed in detail by special eigenfunctions of spectral problem. Depending on zero seed solution and nonzero seed solution, exact solutions, including bright soliton solutions, kink solutions, periodic solutions, breather solutions, rogue wave solutions and several types of mixed soliton solutions, can be presented. Furthermore, the dynamical behaviors are discussed through some figures. It should be mentioned that the solutions of nonlocal Fokas–Lenells equation possess new characteristics different from the ones of local case. Besides, we also demonstrate the integrability by providing infinitely many conservation laws. The above results provide an alternative possibility to understand physical phenomena in the field of nonlinear optics and related fields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

The authors declare that all data generated or analyzed during this study are included in this article.

References

  1. Fokas, A.S.: On a class of physically important integrable equations. Phys. D 87(1–4), 145–150 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  2. Lenells, J.: Exactly solvable model for nonlinear pulse propagation in optical fibers. Stud. Appl. Math. 123(2), 215–232 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  3. Lenells, J., Fokas, A.S.: On a novel integrable generalization of the nonlinear Schrödinger equation. Nonlinearity 22(1), 11–27 (2009)

  4. Lenells, J.: Dressing for a novel integrable generalization of the nonlinear Schrödinger equation. J. Nonlinear Sci. 20(6), 709–722 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  5. Vekslerchik, V.E.: Lattice representation and dark solitons of the Fokas-Lenells equation. Nonlinearity 24(4), 1165–1175 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Lü, X., Peng, M.S.: Nonautonomous motion study on accelerated and decelerated solitons for the variable-coefficient Lenells-Fokas model. Chaos 23(1), 013122 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  7. Matsuno, Y.: A direct method of solution for the Fokas-Lenells derivative nonlinear Schrödinger equation: I Bright soliton solutions. J. Phys. A 45(23), 235202 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  8. Matsuno, Y.: A direct method of solution for the Fokas-Lenells derivative nonlinear Schrödinger equation: II Dark soliton solutions. J. Phys. A 45(47), 475202 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  9. He, J.S., Xu, S.W., Porsezian, K.: Rogue waves of the Fokas-Lenells equation. J. Phys. Soc. Japan 81(12), 124007 (2012)

  10. Xu, S.W., He, J.S., Cheng, Y., Porsezian, K.: The n-order rogue waves of Fokas-Lenells equation. Math. Meth. Appl. Sci. 38(6), 1106–1126 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  11. Xu, J., Fan, E.G.: Long-time asymptotics for the Fokas-Lenells equation with decaying initial value problem: without solitons. J. Differ. Equ. 259(3), 1098–1148 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Wang, B., Zhang, Z., Li, B.: Two types of smooth positons for nonlocal Fokas-Lenells equation. Int. J. Mod. Phys. B 34(17), 2050148 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hanif, Y., Sarfraz, H., Saleem, U.: Dynamics of loop soliton solutions of PT symmetric nonlocal short pulse equation. Nonlinear Dyn. 100(2), 1559–1569 (2020)

    Article  Google Scholar 

  14. Song, C.Q., Zhu, Z.N.: An integrable reverse space-time nonlocal Sasa-Satsuma equation. Acta Phys. Sin.-Ch Ed 69(1), 010204 (2020)

    Article  Google Scholar 

  15. Hanif, Y., Saleem, U.: Broken and unbroken PT-symmetric solutions of semi-discrete nonlocal nonlinear Schrödinger equation. Nonlinear Dyn. 98(1), 233–244 (2019)

    Article  MATH  Google Scholar 

  16. Yang, B., Yang, J.K.: Rogue waves in the nonlocal PT-symmetric nonlinear Schrödinger equation. Lett. Math. Phys. 109(4), 945–973 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  17. Wazwaz, A.M.: A new integrable nonlocal modified KdV equation: abundant solutions with distinct physical structures. J. Ocean Eng. Sci. 2(1), 1–4 (2017)

    Article  Google Scholar 

  18. Ji, J.L., Zhu, Z.N.: Soliton solutions of an integrable nonlocal modified Korteweg-de Vries equation through inverse scattering transform. J. Math. Anal. Appl. 453(2), 973–984 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Wazwaz, A.M.: On the nonlocal Boussinesq equation: multiple-soliton solutions. Appl. Math. Lett. 26(11), 1094–1098 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  20. Li, H.M., Tian, B., Xie, X.Y., Chai, J., Liu, L., Gao, Y.T.: Soliton and rogue-wave solutions for a (2+1)-dimensional fourth-order nonlinear Schrödinger equation in a Heisenberg ferromagnetic spin chain. Nonlinear Dyn. 86(1), 369–380 (2016)

    Article  Google Scholar 

  21. Bender, C.M., Boettcher, S.: Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 80(24), 5243–5246 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  22. Bender, C.M., Boettcher, S., Meisinger, P.N.: PT-symmetric quantum mechanics. J. Math. Phys. 40(5), 2201–2229 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  23. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 110, 064105 (2013)

    Article  Google Scholar 

  24. Yan, Z.Y.: Integrable PT-symmetric local and nonlocal vector nonlinear Schrödinger equations: a unified two-parameter model. Appl. Math. Lett. 47, 61–68 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. Fokas, A.S.: Integrable multidimensional versions of the nonlocal nonlinear Schrödinger equation. Nonlinearity 29, 319–324 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  26. Ablowitz, M.J., Musslimani, Z.H.: Integrable nonlocal nonlinear equations. Stud. Appl. Math. 139, 7–59 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  27. Lou, S.Y., Huang, F.: Alice-Bob physics: coherent solutions of nonlocal KdV systems. Sci. Rep. 7, 869 (2017)

    Article  Google Scholar 

  28. Hu, X.R., Chen, Y.: Nonlocal symmetries, consistent Riccati expansion integrability, and their applications of the (2+1)-dimensional Broer-Kaup-Kupershmidt system. Chin. Phys. B 24(9), 090203 (2015)

    Article  Google Scholar 

  29. Li, M., Zhang, Y., Ye, R.S., Lou, Y.: Exact solutions of the nonlocal Gerdjikov-Ivanov equation. Commun. Theor. Phys. 73(10), 105005 (2021)

    Article  MathSciNet  Google Scholar 

  30. Ruschhaupt, A., Delgado, F., Muga, J.G.: Physical realization of PT-symmetric potential scattering in a planar slab waveguide. J. Phys. A Math. Gen. 38(9), L171–L176 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  31. Cartarius, H., Wunner, G.: Model of a PT-symmetric Bose-Einstein condensate in a delta-function double-well potential. Phys. Rev. A 86(1), 013612 (2012)

    Article  Google Scholar 

  32. Gadzhimuradov, T.A., Agalarov, A.M.: Towards a gauge-equivalent magnetic structure of the nonlocal nonlinear Schrödinger equation. Phys. Rev. A 93(6), 062124 (2016)

    Article  Google Scholar 

  33. Schindler, J., Li, A., Zheng, M.C., Ellis, F.M., Kottos, T.: Experimental study of active LRC circuits with PT symmetries. Phys. Rev. A 84(4), 040101 (2011)

    Article  Google Scholar 

  34. Bender, C.M., Berntson, B.K., Parker, D., Samuel, E.: Observation of PT phase transition in a simple mechanical system. Am. J. Phys. 81(3), 173–179 (2013)

    Article  Google Scholar 

  35. Zhang, R.F., Bilige, S.: Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equation. Nonlinear Dyn. 95, 3041–3048 (2019)

    Article  MATH  Google Scholar 

  36. Zhang, R.F., Bilige, S., Liu, J.G., Li, M.C.: Bright-dark solitons and interaction phenomenon for p-gBKP equation by using bilinear neural network method. Phys. Scr. 96, 025224 (2021)

    Article  Google Scholar 

  37. Zhang, R.F., Bilige, S., Chaolu, T.: Fractal solitons, arbitrary function solutions, exact periodic wave and breathers for a nonlinear partial differential equation by using bilinear neural network method. J. Syst. Sci. Complex. 34, 122–139 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  38. Hu, C.C., Tian, B., Zhao, X.: Rogue and lump waves for the (3+1)-dimensional Yu-Toda-Sasa-Fukuyama equation in a liquid or lattice. Int. J. Mod. Phys. B (2021)

  39. Hu, C.C., Tian, B., Qu, Q.X., Yang, D.Y.: The higher-order and multi-lump waves for a (3+1)-dimensional generalized variable-coefficient shallow water wave equation in a fluid. Chinese J. Phys. (2021)

  40. Wen, X.Y., Wang, H.T.: Breathing-soliton and singular rogue wave solutions for a discrete nonlocal coupled Ablowitz-Ladik equation of reverse-space type. Appl. Math. Lett. 111, 106683 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  41. Yang, B., Chen, Y.: Several reverse-time integrable nonlocal nonlinear equations: Rogue-wave solutions. Chaos 28(5), 053104 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  42. Meng, X.H., Wen, X.Y., Piao, L.H., Wang, D.S.: Determinant solutions and asymptotic state analysis for an integrable model of transient stimulated Raman scattering. Optik 200, 163348 (2020)

    Article  Google Scholar 

  43. Guo, R., Liu, Y.F., Hao, H.Q., Qi, F.H.: Coherently coupled solitons, breathers and rogue waves for polarized optical waves in an isotropic medium. Nonlinear Dyn. 80(3), 1221–1230 (2015)

    Article  MathSciNet  Google Scholar 

  44. Li, N.N., Guo, R.: Nonlocal continuous Hirota equation: Darboux transformation and symmetry broken and unbroken soliton solutions. Nonlinear Dyn. 105, 617–628 (2021)

    Article  Google Scholar 

  45. Guo, R., Tian, B., Wang, L.: Soliton solutions for the reduced Maxwell-Bloch system in nonlinear optics via the N-fold Darboux transformation. Nonlinear Dyn. 69(4), 2009–2020 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  46. Chen, S.S., Tian, B., Qu, Q.X., Li, H., Sun, Y., Du, X.X.: Alfvén solitons and generalized Darboux transformation for a variable-coefficient derivative nonlinear Schrödinger equation in an inhomogeneous plasma. Chaos Solitons Fractals 148, 111029 (2021)

    Article  Google Scholar 

  47. Chen, S.S., Tian, B., Zhang, C.R.: Odd-fold Darboux transformation, breather, rogue-wave and semirational solutions on the periodic background for a variable-coefficient derivative nonlinear Schrödinger equation in an inhomogeneous plasma. Ann. Phys. 2100231 (2021)

  48. Shen, J.L., Wu, X.Y.: Periodic-soliton and periodic-type solutions of the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation by using BNNM. Nonlinear Dyn. 106, 831–840 (2021)

  49. Zhang, R.F., Li, M.C., Yin, H.M.: Rogue wave solutions and the bright and dark solitons of the (3+1)-dimensional Jimbo-Miwa equation. Nonlinear Dyn. 103, 1071–1079 (2021)

    Article  Google Scholar 

  50. Zhang, R.F., Li, M.C., Albishari, M., Zheng, F.C., Lan, Z.Z.: Generalized lump solutions, classical lump solutions and rogue waves of the (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada-like equation. Appl. Math. Comput. 403, 126201 (2021)

    MathSciNet  MATH  Google Scholar 

  51. Zhang, Q.Y., Zhang, Y., Ye, R.: Exact solutions of nonlocal Fokas-Lenells equation. Appl. Math. Lett. 98, 336–343 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  52. Imai, K.: Generalization of the Kaup-Newell inverse scattering formulation and Darboux transformation. J. Phys. Soc. Japan 68(2), 355–359 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  53. Ma, Y.C.: The perturbed plane-wave solution of the cubic Schrödinger equation. Stud. Appl. Math. 60, 43–58 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  54. Zhang, Y., Yang, J.W., Chow, K.W., Wu, C.F.: Solitons, breathers and rogue waves for the coupled Fokas-Lenells system via Darboux transformation. Nonlinear Anal. RWA 33, 237–252 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  55. Akhmediev, N.N., Eleonskii, V.M., Kulagin, N.E.: Exact first-order solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 72, 809–818 (1987)

    Article  MATH  Google Scholar 

  56. Zuo, D.W., Gao, Y.T., Feng, Y.J., Xue, L.: Rogue-wave interaction for a higher-order nonlinear Schrödinger-Maxwell-Bloch system in the optical-fiber communication. Nonlinear Dyn. 78(4), 2309–2318 (2014)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work has been supported by the National Natural Science Foundation of China under Grant No. 11771111.

Author information

Authors and Affiliations

  1. School of Mathematics, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China

    Jiang-Yan Song, Yu Xiao & Chi-Ping Zhang

Authors
  1. Jiang-Yan Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu Xiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chi-Ping Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu Xiao.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work has been supported by the National Natural Science Foundation of China (NNSFC) under Grant No. 11771111.

Appendices

Appendix A

From Eq. (2.5a), comparing the coefficients of \(\lambda ^{j}, j=3, 2, 1, 0, -1\), we can get

$$\begin{aligned}&\lambda ^{3}: b_{1}=0, c_{1}=0,\\&\quad \lambda ^{2}: 2\,i\,b_{0}+a_{1}\,q_{x}-d_{1}\\&\quad q^{[1]}_{x}=0, -2\,i\,c_{0}+d_{1}\\&\quad q_{x}(-x,-t)-a_{1}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{1}: a_{1x}+b_{0}\,q_{x}(-x,-t)-c_{0}\\&\quad q^{[1]}_{x}=0, 2\,i\,b_{-1}+a_{0}\,q_{x}-d_{0}\,q^{[1]}_{x}=0,\\&\quad -2\,i\,c_{-1}+d_{0}\,q_{x}(-x,-t)-a_{0}\\&\quad q^{[1]}_{x}(-x,-t)=0, d_{1x}+c_{0}\,q_{x}\\&\quad -b_{0}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{0}: a_{0x}+b_{-1}\,q_{x}(-x,-t)-c_{-1}\,q^{[1]}_{x}=0, \\&\quad b_{0x}+a_{-1}\,q_{x}-d_{-1}\,q^{[1]}_{x}=0,\\&\quad c_{0x}+d_{-1}\,q_{x}(-x,-t)-a_{-1}\,q^{[1]}_{x}(-x,-t)=0, \\&\quad d_{0x}+c_{-1}\,q_{x}-b_{-1}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{-1}: a_{-1x}=0, b_{-1x}=0, c_{-1x}=0, d_{-1x}=0. \end{aligned}$$

Similarly, from Eq. (2.5b), comparing the coefficients of \(\lambda ^{j}, j=2, 1, 0, -1, -2, -3\) under the condition \(b_{1}=0, c_{1}=0\), we can get

$$\begin{aligned}&\lambda ^{2}: 2\,i\,b_{0}+a_{1}\,q_{x}-d_{1}\,q^{[1]}_{x}=0, \\&\quad -2\,i\,c_{0}+d_{1}\,q_{x}(-x,-t)\\&\quad -a_{1}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{1}: d_{0}\,q_{x}(-x,-t)-a_{0}\,q^{[1]}_{x}(-x,-t)=0, \\&\quad a_{0}\,q_{x}-d_{0}\,q^{[1]}_{x}=0,\\&\quad -\frac{1}{2}\,i\,a_{1}\,q(-x,-t)\,q+\frac{1}{2}\,i\,a_{1}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+a_{1t}+b_{0}\,q_{x}(-x,-t)\\&\quad -c_{0}\,q^{[1]}_{x}=0,\\&\quad \frac{1}{2}\,i\,d_{1}\,q(-x,-t)\,q-\frac{1}{2}\,i\,d_{1}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+d_{1t}+c_{0}\,q_{x}\\&\quad -b_{0}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{0}: -\frac{1}{2}\,i\,a_{0}\,q(-x,-t)\,q+\frac{1}{2}\,i\,a_{0}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+a_{0t}=0,\\&\quad \frac{1}{2}\,i\,d_{0}\,q(-x,-t)\,q-\frac{1}{2}\,i\,d_{0}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+d_{0t}=0,\\&\quad -2ib_{0}+\frac{1}{2}ia_{1}\,q+\frac{1}{2}ib_{0}q(-x,-t)q\\&\quad -\frac{1}{2}id_{1}q^{[1]}+\frac{1}{2}ib_{0}q^{[1]}(-x,-t)q^{[1]}+b_{0t}\\&\quad +a_{-1}q_{x} -d_{-1}q^{[1]}_{x}=0,\\&\quad 2\,i\,c_{0}-\frac{1}{2}\,i\,d_{1}\,q(-x,-t)\\&\quad -\frac{1}{2}\,i\,c_{0}\,q(-x,-t)\\&\quad q+\frac{1}{2}\,i\,a_{1}\,q^{[1]}(-x,-t)\\&\quad -\frac{1}{2}\,i\,c_{0}\,q^{[1]}(-x,-t)\,q^{[1]}\\&\quad +c_{0t}+d_{-1}\,q_{x}(-x,-t)-a_{-1}\\&\quad q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{-1}: a_{0}\,q-d_{0}\,q^{[1]}=0, \\&\quad -d_{0}\,q(-x,-t)+a_{0}\,q^{[1]}(-x,-t)=0,\\&\quad -\frac{1}{2}\,i\,b_{0}\,q(-x,-t)-\frac{1}{2}\,i\,a_{-1}\\&\quad q(-x,-t)\,q-\frac{1}{2}\,i\,c_{0}\,q^{[1]}\\&\quad +\frac{1}{2}\,i\,a_{-1}\,q^{[1]}(-x,-t)\,q^{[1]}+a_{-1t}=0,\\&\quad \frac{1}{2}\,i\,c_{0}\,q+\frac{1}{2}\,i\,d_{-1}\,q(-x,-t)\,q\\&\quad +\frac{1}{2}\,i\,b_{0}\,q^{[1]}(-x,-t)-\frac{1}{2}\,i\,d_{-1}\,q^{[1]}(-x,-t)\,q^{[1]}\\&\quad +d_{-1t}=0,\\&\quad \lambda ^{-2}: b_{0}+a_{-1}\,q-d_{-1}\,q^{[1]}=0, \\&\quad c_{0}+d_{-1}\,q(-x,-t)-a_{-1}\,q^{[1]}(-x,-t)=0,\\&\quad \lambda ^{-3}: b_{-1}=0, c_{-1}=0. \end{aligned}$$

Appendix B

The \(a_{1}, d_{1}, b_{0}, c_{0}\) for one-fold Darboux matrix \(T^{[1]}\) yield

$$\begin{aligned} a_{1}= & {} \frac{\left| \begin{array}{cc} -\lambda _{1}^{-1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ -\lambda _{2}^{-1}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ d_{1}= & {} \frac{\left| \begin{array}{cc} -\lambda _{1}^{-1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ -\lambda _{2}^{-1}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| },\\ b_{0}= & {} \frac{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}-\lambda _{1}^{-1}\,\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}-\lambda _{2}^{-1}\,\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ c_{0}= & {} \frac{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}-\lambda _{1}^{-1}\,\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}-\lambda _{2}^{-1}\,\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| }. \end{aligned}$$

In other words, we can deduce

$$\begin{aligned} T^{[1]}_{11}= & {} \frac{\left| \begin{array}{ccc} \lambda &{}0 &{}\lambda ^{-1}\\ \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t) &{}\lambda _{1}^{-1}\,\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t) &{}\lambda _{2}^{-1}\,\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ T^{[1]}_{12}= & {} \frac{\left| \begin{array}{ccc} 0 &{}1 &{}0\\ \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t) &{}\lambda _{1}^{-1}\,\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t) &{}\lambda _{2}^{-1}\,\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ T^{[1]}_{21}= & {} \frac{\left| \begin{array}{ccc} 0 &{}1 &{}0\\ \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t) &{}\lambda _{1}^{-1}\,\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t) &{}\lambda _{2}^{-1}\,\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| },\\ T^{[1]}_{22}= & {} \frac{\left| \begin{array}{ccc} \lambda &{}0 &{}\lambda ^{-1}\\ \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t) &{}\lambda _{1}^{-1}\,\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t) &{}\lambda _{2}^{-1}\,\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| }. \end{aligned}$$

Appendix C

The \(W^{[N]}, \widetilde{T^{[N]}_{11}}, \widetilde{T^{[N]}_{12}}, \widetilde{W^{[N]}}, \widetilde{T^{[N]}_{21}}, \widetilde{T^{[N]}_{22}}\) for N-fold Darboux matrix \(T^{[N]}\) read

$$\begin{aligned}&W^{[N]}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(x,t) &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(x,t) &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| ,\\&\widetilde{T^{[N]}_{11}}=\left| \begin{array}{cccccccc} \lambda ^{N} &{}0 &{}\cdots &{}0 &{}\lambda ^{-N}\\ \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{-N}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{-N}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\&\widetilde{T^{[N]}_{12}}=\left| \begin{array}{cccccccc} 0 &{}\lambda ^{N-1} &{}\cdots &{}\lambda ^{-(N-1)} &{}0\\ \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{-N}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{-N}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\&\widetilde{W^{[N]}}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\ {}&\widetilde{T^{[N]}_{21}}=\left| \begin{array}{ccccccc} 0 &{}\lambda ^{N-1} &{}\cdots &{}\lambda ^{-(N-1)} &{}0\\ \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(x,t) &{}\lambda _{1}^{-N}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(x,t) &{}\lambda _{2}^{-N}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| ,\\&\widetilde{T^{[N]}_{22}}=\left| \begin{array}{ccccccc} \lambda ^{N} &{}0 &{}\cdots &{}0 &{}\lambda ^{-N}\\ \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(x,t) &{}\lambda _{1}^{-N}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(x,t) &{}\lambda _{2}^{-N}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| . \end{aligned}$$

Appendix D

The \(\varOmega _{-(N-1)}, \widetilde{\varOmega _{-(N-1)}}\) for N-soliton solutions (\(q^{[N]}, q^{[N]}(-x, -t)\)) arrive at

$$\begin{aligned}&\varOmega _{-(N-1)}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(x,t) &{}-\lambda _{1}^{-N}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(x,t) &{}-\lambda _{2}^{-N}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(x,t) &{}-\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(x,t) &{}-\lambda _{2N}^{-N}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\&\widetilde{\varOmega _{-(N-1)}}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(-x,-t) &{}-\lambda _{1}^{-N}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(-x,-t) &{}-\lambda _{2}^{-N}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(-x,-t) &{}-\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(-x,-t) &{}-\lambda _{2N}^{-N}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| . \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, JY., Xiao, Y. & Zhang, CP. Darboux transformation, exact solutions and conservation laws for the reverse space-time Fokas–Lenells equation. Nonlinear Dyn 107, 3805–3818 (2022). https://doi.org/10.1007/s11071-021-07170-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-07170-z

Keywords

Search

Navigation