Abstract
This paper deals with the problem of distributed fault detection and isolation in multi-agent systems with disturbed high-order dynamics subject to communication uncertainties and faults. Distributed finite-frequency mixed \({\mathcal {H}}_-\) \(/{\mathcal {H}}_\infty \) unknown input observers are designed to detect and distinguish actuator, sensor and communication faults. Furthermore, an agent is capable of detecting not only its own faults but also faults in its neighbouring agents. Sufficient conditions are then derived in terms of a set of linear matrix inequalities while adding additional design variables to reduce the conservatism. A numerical simulation is carried out in order to demonstrate the effectiveness of the proposed approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the past couple of decades, multi-agent systems have received considerable amount of attention from researchers thanks to their wide range of potential applications in different areas, such as formation control, constellations in satellite systems [1, 2], cooperative unmanned aerial vehicles [3], transport systems [4], power grids and mobile robots [5,6,7], to mention a few.
The growing size and complexity of such systems render their safe operation and reliability critical topics of research. Indeed, in order to achieve their mission, the agents communicate between themselves over a given network. Hence, their vulnerability does not only stem from the fact that each agent can be faulty at any given time instant but also from the fact that the communication links between them can be faulty or subject to an attack. Indeed, on top of actuator and sensor faults, MASs can be subjected to multiple types of cyber-attacks [8,9,10,11,12,13].
In fact, many cyber-attacks have recently occurred around the world. Some examples include: multiple power blackouts in some countries like Brazil [14], the attack on the water distribution system in Australia [15], the Stuxnet attack that took control of actuators and sensors in an Iranian nuclear facility prompting the replacement of thousands of failed centrifuges [16], the cyber-attack against an Ukrainian power grid [17], etc. Clearly, these types of malicious attacks aim at degrading or interrupting the operation of connected systems, exploit their aforementioned vulnerabilities and can have extremely detrimental effects, not only from a process point of view but also from an environmental and financial one as well. It is shown in [18] that information security techniques such as adding encryption and authentication schemes can help make some attacks more difficult to succeed, but that they are far from being sufficient against cyber-attacks. Indeed, these malicious attacks may go unnoticed and lead to erroneous behaviours in the overall MAS’s dynamics and compromising the mission. This makes understanding their effects on the MAS dynamics, modelling them, detecting them, identifying them as well as isolating them, important issues.
There is a multitude of ways to detect and isolate faults and cyber-attacks in MASs. The reader is referred to [19] for a recent comprehensive survey. Some works proposed centralised architectures to detect faults or attacks [20, 21], due to their simplicity, whereby the analysis of all data is done by a central unit. However, in order to avoid long-distance data transmissions, reduce complexity and improve scalability, namely in larger systems, the detection and isolation process should be distributed.
A great deal of existing works in the literature either focuses on linear MASs [22,23,24,25,26,27,28,29], do not consider the effect of disturbances [22, 30], or do not consider the effect of measurement and communication noise [23, 31, 32]. However, it is a well-known fact that disturbances and noise are practically inevitable. Furthermore, some works focus only actuator faults [23, 29, 31, 33] or on sensor faults [25,26,27].
In [26, 30, 31, 34], UIOs were used for fault detection. Nevertheless, most of the existing works on fault detection using UIOs consider that the generated residual signals are completely decoupled from the unknown input. Indeed, they usually require a strict rank condition to decouple the unknown input vector, which can be infeasible. In [31] for instance, an UIO residual-based scheme for nonlinear homogeneous MASs with actuator faults was proposed, where faults and disturbances were decoupled from the error dynamics assuming some rank conditions. In [26], UIOs were combined with the mixed \({\mathcal {H}}_-/{\mathcal {H}}_\infty \) method for fault detection purpose where only sensor faults were considered. Furthermore, the \({\mathcal {H}}_-\) performance index method proposed therein, as well as in [25, 27] for instance, is only applicable when the distribution matrix of the sensor faults is of full column rank. In our work, one contribution is to relax such condition using the finite-frequency approach introduced in [35]. Furthermore, in [27, 36] for instance, multiple faults cannot occur in the MAS, which is a drawback, especially in large-sized MASs.
In [23, 27,28,29, 31], information from neighbouring FDI filters was transmitted among agents, which may weaken the distributed property of the detection scheme. Indeed, if and when an observer fails to accurately give an estimate at a given instant for an agent, all surrounding observers in its neighbourhood are compromised, which in turn compromises their respective neighbours’ observers, thus creating a destructive snowball effect that might lead to confusing results, trigger false alarms, etc. In our work, such drawback is removed since observers do not communicate between themselves.
Unlike [23, 28, 29, 31], where the topology is assumed to be undirected, a directed communication graph is considered in this work. Additionally, the proposed scheme in this paper does not require knowledge beyond its 1-hop neighbourhood and is independent on the graph topology of the overall MAS, making it more scalable. Furthermore, as opposed to the detection filters proposed in [23, 29, 31, 33] where their size increases as the graph topology grows, in the proposed scheme, the size of the filter is only limited to the size of the neighbourhood of each agent independently, hence improving the scalability and reducing the computational burdens.
Given the limitations discussed above with respect to the existing studies, the main contributions of this work are summarised as follows:
-
A more general problem is studied where actuator, sensor and communication faults are considered in the robust detection and isolation process for Lipschitz nonlinear heterogeneous MASs with disturbances and communication parameter uncertainties, without global knowledge about the communication graph and under-directed graphs.
-
A distributed finite-frequency mixed \({\mathcal {H}}_-/{\mathcal {H}}_\infty \) nonlinear UIO-based FDI scheme is designed such that actuator and sensor faults along with the communication faults are treated separately. Hence, the rank condition on the measurement fault distribution matrix as required by [27, 28] for instance is relaxed. Additionally, the scheme is capable of detecting and distinguishing multiple faults and attacks at a given time instant.
-
Sufficient conditions in terms of a set of LMIs are provided for the proposed finite-frequency \({\mathcal {H}}_-/{\mathcal {H}}_\infty \) UIO-based method, where the coupling between Lyapunov matrices and the observer matrices is avoided. This LMI characterisation enables to reduce conservatism by introducing additional design variables.
A brief comparison of the proposed method with some existing works in the literature is given in Table 1. To the best of the authors’ knowledge, a distributed finite-frequency mixed \({\mathcal {H}}_-/{\mathcal {H}}_\infty \) nonlinear UIO-based scheme for FDI in heterogeneous networked MASs subject to disturbances, noise, actuator faults, sensor faults and communication attacks, is investigated for the first time in this paper.
The rest of the manuscript is organised as follows. Section 2 presents the problem formulation and some preliminaries. The proposed finite-frequency \({\mathcal {H}}_-/{\mathcal {H}}_\infty \) UIO-based method and the corresponding algorithms are laid out in Sect. 3. In Sect. 4, an illustrative example is given to show the effectiveness of the proposed scheme. Finally, some conclusions are inferred in Sect. 5.
Notations: Given a transfer function \(T_{xy}(s)\) linking y to x, its \({\mathcal {H}}_\infty \) norm is defined as
where \({\bar{\sigma }}\) is the maximum singular value of \(T_{xy}(s)\). Its \({\mathcal {H}}_-\) index is defined as
where \({\underline{\sigma }}\) is the minimum singular value of \(T_{xy}(s)\). For a square matrix A, \(\mathbf{He} (A)= A+A^*\) where the superscript \(A^*\) corresponds to the conjugate of A. \(\text {tr}(A)\) is the trace of A. \(\mathbf{1 }_n\) and \(I_n\) refer to a column of all entries 1 and an identity matrix, respectively, and of dimensions n. \(0_{m \times n}\) denotes a null matrix of dimension \(m \times n\). \(\text {diag}(a_1, a_2,\ldots , a_n)\) denotes the diagonal matrix containing \(a_1, a_2, \ldots , a_n\) on the diagonal. \(\text {Blkdiag}(A_1, A_2,\ldots , A_n)\) denotes the block diagonal matrix with matrices \(A_1, A_2, \ldots , A_n\) on the diagonal. \(\text {Col}(A_1, A_2, \ldots , A_n)\) denotes the column block matrix \((A_1^T, A_2^T, \ldots , A_n^T)^T\). Throughout this paper, for a real square matrix \(P \in {\mathbb {R}}^{n \times n}\), \(P > 0\) implies that P is symmetric and positive-definite.
2 Problem formulation
Consider a heterogeneous MAS composed of N agents labelled by \(i \in \{1, \ldots , N\}\) and described by the following uncertain dynamics
where \(x_i \in \mathrm{I\!R}^{n_x}\), \(u_i \in \mathrm{I\!R}^{n_u}\), \(y_i \in \mathrm{I\!R}^{n_y}\), \(d_i \in \mathrm{I\!R}^{n_d}\), \(f_{a_i} \in \mathrm{I\!R}^{n_{f_a}}\), \(f_{s_i} \in \mathrm{I\!R}^{n_{f_s}}\) are the state vector, the control input, the output, the \(L_2\)-norm bounded disturbances and noise, the actuator fault and the sensor fault signals, respectively. Matrices \(A_i \in \mathrm{I\!R}^{n_x \times n_x}\), \(B_{u_i} \in \mathrm{I\!R}^{n_x \times n_u}\), \(B_{d_i}\in \mathrm{I\!R}^{n_x \times n_d}\), \(B_{f_i}\in \mathrm{I\!R}^{n_x \times n_{f_a}}\), \(C_i \in \mathrm{I\!R}^{n_y \times n_x}\), \(D_{d_i} \in \mathrm{I\!R}^{n_y \times n_d}\), \(D_{f_i} \in \mathrm{I\!R}^{n_y \times n_{f_s}}\) are known constant matrices. \(\varphi _i(x_i(t)) \in \mathrm{I\!R}^{n_x}\) is a known function representing the nonlinearity of agent i.
2.1 Graph theory and communication faults
The topology is represented by a directed graph \({\mathcal {G}}=({\mathcal {V}},{\mathcal {E}})\), where \({\mathcal {V}}=\{1,\ldots ,N \}\) is the node set and \({\mathcal {E}} \subseteq {\mathcal {V}} \times {\mathcal {V}}\) is the edge set. It is described by an adjacency matrix \({\mathcal {A}} \in \mathrm{I\!R}^{N \times N}\) that contains positive weight entries. If information flows from node j to i, then \(a_{ij}>0\), otherwise \(a_{ij}=0\). The neighbouring set of node i, denoted by \({\mathcal {N}}_i \subseteq {\mathcal {V}}\), is the subset of nodes that node i can sense and interact with. Alternatively, one could note \( {\mathcal {N}}_i = \{i_1,i_2,\ldots ,i_{N_i}\} \subseteq [1,N]\), where \(N_i = |{\mathcal {N}}_i|\).
The measured outputs are exchanged between neighbouring agents. Hence, an agent i receives from each neighbour \(j \in {\mathcal {N}}_i\) its output (resp. input), corrupted by parameter uncertainties associated with the communication link between i and j, \(\Delta a_{ij}(t) \in \mathrm{I\!R}\) and by faults due to link faults, packet losses or potential cyber-attacks denoted \(f^z_{ij}(t) \in \mathrm{I\!R}^{n_{f_{z_{ij}}}}\) (resp. \(f^u_{ij}(t) \in \mathrm{I\!R}^{ n_{{f_u}}} \)), i.e.
with \(z_{ii}(t)=y_i(t)\) and \(u_{ii}(t)=u_i(t)\). \(D_{z_{ij}} \in \mathrm{I\!R}^{n_y \times n_{f_{z_{ij}}}}\) and \(D_{u_{ij}} \in \mathrm{I\!R}^{n_u \times n_{{f_u}}}\) are known constant matrices. It is also assumed that the parameter uncertainties \(\Delta a_{ij}(t)\) satisfy \(|\Delta a_{ij}(t)| < a_{ij}\).
Remark 1
It is worth noting that the considered faults cover a wide range of cyber-attacks that have been studied in the literature. For instance, assume that \(\Delta a_{ij}=0\) for the sake of clarity,
-
In the case of a communication parametric fault [30] for i, affecting all its incoming information from agent j, one has
$$\begin{aligned} \begin{aligned} z_{ij}(t)&= (a_{ij}+ f_{a_{ij}(t)}(t)) y_j(t) \\&= a_{ij} y_j(t) + f_{a_{ij}}(t) y_j(t), \end{aligned} \end{aligned}$$where analogously to (2), one could note that \(f^z_{ij}(t)=f_{a_{ij}}(t) y_j(t)\) and \(D_{z_{ij}}=I_{n_y}\). \(f_{a_{ij}}(t)\) represents a parametric fault affecting the communication parameter \(a_{ij}\).
-
In a denial of service attack situation affecting all incoming information from agent j, one has \(f^z_{ij}(t)=-a_{ij} \delta (t-t_{ij}) y_j(t)\) and \(D_{z_{ij}}=I_{n_y}\) [39], where
$$\begin{aligned} \delta (t-t_{ij}) = \left\{ \begin{array}{ll} 1, \quad t \geqslant t_{ij}\\ 0, \quad \text {else} \end{array}, \right. \end{aligned}$$and \(t_{ij} \) is the instant at which the attack occurs.
-
Conversely, in a false data injection situation in the transmitted information, agent j transmits or agent i receives fake/invalid information, that is, \(f^z_{ij}(t)\) contains the injected malicious information [12]. In the case where the malicious information \(f^z_{ij}(t) \in \mathrm{I\!R}\) affects all incoming transmitted data equally, then one could set \(D_{z_{ij}}=\mathbf{1 }_{n_y}\).
-
Under replay attacks, the attacker intercepts the transmitted information and replays it with a delay instead of the actual information. In this case, one could write [10], \(f^z_{ij}(t)= \delta _{ij}(t-t_{ij}) (-a_{ij} y_j(t)+ y_j(t-{\mathcal {T}}_{ij}))\) and \(D_{z_{ij}}=I_{n_y}\), where
$$\begin{aligned} \delta _{ij}(t-t_{ij}) = \left\{ \begin{array}{ll} 1, \quad t \geqslant t_{ij}\\ 0, \quad \text {else} \end{array}, \right. \end{aligned}$$and \(t_{ij} > 0\) is the instant at which the attack occurs and \({\mathcal {T}}_{ij} \in \mathrm{I\!R}\) is the time delay.
The same remarks could be made w.r.t. \(u_{ij}(t)\). Contrary to agent/node attacks or faults in the form of the signals \(f_{a_i}(t),\;f_{s_i}(t)\), edge/communication attacks cannot be detected locally by an emitting agent j and thus need its neighbours to detect them. It is worth mentioning that the introduced problem can represent many potential practical applications to FDI in networked MASs. As discussed in introduction section, such applications include electric power networks and micro-grids, multi-robot and multi-vehicle systems, etc. [37, 38, 40].
2.2 Concatenated local model
In this subsection, a concatenated model is developed for each agent. Let us first denote
the concatenated state, disturbance, fault signals, relative information, output and input of agent i (\(i_{j}\in {\mathcal {N}}_i\)), where \(n^i_x=n_x (N_i+1)\), \(n^i_d=n_d (N_i+1)\), \(n^i_{f_a}=n_{f_a} (N_i+1)\), \(n^i_{f_s}=n_{f_s}(N_i+1)\), \({\underline{n}}^i_z=n_y N_i\) and \({\underline{n}}^i_u= n_u N_i\). A virtual output is given as
where
with \({\underline{n}}^i_{f_z}= \sum _{j\in {\mathcal {N}}_i} n_{f_{z_{ij}}} \ne 0\), \(n^i_z=n_y (N_i+1)\). \(z_{v_i}\) and \(f^z_i\) are the concatenated measured vector available for agent i and the associated communication fault signals, respectively. \(\bar{{\mathcal {A}}}_i={\mathcal {A}}_i+\Delta {\mathcal {A}}_i \in \mathrm{I\!R}^{{\underline{n}}^i_z \times {\underline{n}}^i_z}\) is the actual local adjacency matrix of agent i which takes into account the parametric uncertainty associated with the communication links. Replacing outputs and inputs with their respective values from (1) yields
where
\({\widetilde{C}}_i\), \({\widetilde{D}}_{d_i}\) and \({\widetilde{D}}_{f_i}\) correspond to the following tilde notation
with \({\widetilde{A}}_{i} \in \mathrm{I\!R}^{n^i_x \times n^i_x}\), \({\widetilde{B}}_{u_i} \in \mathrm{I\!R}^{n^i_x \times n^i_u}\), \({\widetilde{B}}_{f_i} \in \mathrm{I\!R}^{n^i_x \times n^i_{fa}}\), \({\widetilde{C}}_{i} \in \mathrm{I\!R}^{n^i_z \times n^i_x}\), \({\widetilde{D}}_{d_i} \in \mathrm{I\!R}^{n^i_z \times n^i_d}\), \({\widetilde{D}}_{f_i} \in \mathrm{I\!R}^{n^i_z \times n^i_{fs}}\). Let us make the following assumption on the parametric uncertainties
Assumption 1
There exist a time-varying matrix \(\nu _i(t)\) \(\in \mathrm{I\!R}^{{\underline{n}}^i_z \times {\underline{n}}^i_z}\) and known matrices \(\mathbf{X }_i\) and \(M_i\) with appropriate dimensions such that
with \({\bar{\sigma }}(\nu _i) \le \delta _M\).
Remark 2
It is worth noting that this assumption stems from the definition of the graph topology in this paper and is standard for bounded uncertainties [41].
Under this assumption, one could rewrite system (5) as
where \( {\mathcal {F}}_i(t) = \begin{pmatrix} f_{vs_i}(t) \\ f^z_i(t) \end{pmatrix} \), \( D_{{\mathcal {F}}_i} = \begin{pmatrix} Z^i{\widetilde{D}}_{f_i}&D_{vz_i} \end{pmatrix} \),
\( \phi _i(t) =-\nu _i(t) D_{\phi _i} \begin{pmatrix} x_{v_i}(t) \\ d_{v_i}(t) \\ f_{vs_i}(t) \end{pmatrix} \),
\( D_{\phi _i} = M_i \begin{pmatrix} \text {Blkdiag}(C_{i}^T,\ldots ,C_{i_{N_i}}^T)\\ \text {Blkdiag}(D_{d_i}^T,\ldots ,D_{d_{i_{N_i}}}^T)\\ \text {Blkdiag}(D_{f_i}^T,\ldots ,D_{f_{i_{N_i}}}) \end{pmatrix}^T \).
Note that, in the case where \({\widetilde{D}}_{f_i}=0\), \(D_{{\mathcal {F}}_i}\) is selected as \(D_{{\mathcal {F}}_i} =D_{vz_i}\). The robust distributed FDI objective is the design of residual generators for each agent using locally exchanged information capable of detecting and isolating not only the agent’s own faults but also the faults of its neighbours as well as attacks targeting incoming communication links.
The following assumption and lemma are going to be used in the next section.
Assumption 2
The nonlinear functions \(\varphi _i(x_i(t))\) are Lipschitz, with Lipschitz constant \(\theta _i\), \(\forall i=\{1,2,\ldots ,N\}\), i.e. \(\forall x_i,{\hat{x}}_i \in \mathrm{I\!R}^{n_x}\)
Remark 3
It is worth noting that Assumption 2 restricts the class of considered nonlinearities in Eq. (1) and has been considered in many works [42].
Lemma 1
[43] Given real matrices \(F_i\) and \(J_i\) of appropriate dimensions, then the following inequality holds for any strictly positive scalar \(\varepsilon _i\):
3 Distributed fault detection and isolation scheme
The aim here is to design robust residual generators which are sensitive to all types of faults in spite of the presence of uncertainties using UIOs. Consider the following observer
where \(U_i(t) = \text {Col}(u_{ii_1}(t),\ldots ,u_{ii_{N_i}}(t))\). The matrices \(N_i\), \(G_{1i}\), \(G_{2i}\), \(L_i\), \(T_i\) and \(H_i\) will be described hereafter. Define the state estimation error as \(e_{v_i}(t)=x_{v_i}(t)-{\hat{x}}_{v_i}(t)\). Then
where \( {\mathcal {D}}_i(t) = \begin{pmatrix} d_{v_i}(t) \\ \phi (t) \end{pmatrix} \), \( V_{v_i} = \begin{pmatrix} Z^i{\widetilde{D}}_{d_i}&-\mathbf{X }_i&D_{{\mathcal {F}}_i} \end{pmatrix} \) and \( v_i(t) = \begin{pmatrix} {\mathcal {D}}_i(t) \\ {\mathcal {F}}_i(t) \end{pmatrix} \). Therefore, its dynamics is expressed as
where
\(\varphi _{v_i}^{e_{v_i}}(t) = \varphi _{v_i}(x_{v_i}(t))-\varphi _{v_i}({\hat{x}}_{v_i}(t))\), and
with \(\nu _i(t)=\Delta {\mathcal {A}}_{i}\). By imposing the following
(9) becomes
By setting new concatenated uncertainties vector as \({\underline{\phi }}_i(t)= \begin{pmatrix} \phi _i(t) \\ \Delta {\mathcal {A}}_{u,i} u_{v_i}(t) \end{pmatrix}\), the error dynamics becomes
where \( {\mathcal {B}}_i = \begin{pmatrix} -{\widetilde{B}}_{f_i}&{\widetilde{B}}_{u_i} {\mathcal {A}}_{u,i}^{-1} D_{u_i} \end{pmatrix}\), \( \underline{{\mathcal {F}}}_i(t) = \begin{pmatrix} f_{a_i}(t) \\ f_{u_i}(t) \end{pmatrix} \), \(\underline{\mathbf{X }}_i=\begin{pmatrix} \mathbf{X }_i&0_{n^i_z \times (n_{u}\cdot N_i)} \end{pmatrix}\), \(\bar{\mathbf{X }}_i=\begin{pmatrix} 0_{n^i_x \times {\underline{n}}^i_z}&- {\widetilde{B}}_{u_i} \end{pmatrix}\).
On the other hand, define the following residual vector
where \(W_i\) is a pre-set post-residual gain matrix used to highlight the effects of the faults on the residual signals. In this work, since it does not directly affect the residual signals, it is considered that \(\underline{{\mathcal {F}}}_i(t)\) affects the residual signals over a finite-frequency domain, which can be uniformly expressed as [44]
where \(\kappa \in \{1,-1\}\), \(\omega _{f_1}\) and \(\omega _{f_2}\) are given positive scalars characterizing the frequency range of the fault vector \(\underline{{\mathcal {F}}}_i\). Indeed, if one selects
-
\(\kappa = 1\) and \(\omega _{f_1} < \omega _{f_2}\), then the set \(\varOmega _{\underline{{\mathcal {F}}}_i}\) corresponds to the middle frequency range
$$\begin{aligned} \varOmega _{\underline{{\mathcal {F}}}_i} := \{ \omega _f \in \mathrm{I\!R} \ | \ \ \omega _{f_1} \leqslant \omega _{f} \leqslant \omega _{f_2} \}. \end{aligned}$$ -
\(\kappa = 1\) and \(-\omega _{f_1} = \omega _{f_2} = \omega _{f_l}\), then the set \(\varOmega _{\underline{{\mathcal {F}}}_i}\) corresponds to the low-frequency range
$$\begin{aligned} \varOmega _{\underline{{\mathcal {F}}}_i} := \{ \omega _f \in \mathrm{I\!R} \ | \ \ \mathopen | \omega _f \mathclose | \leqslant \omega _{f_l} \}. \end{aligned}$$ -
\(\kappa = -1\) and \(-\omega _{f_1} = \omega _{f_2} = \omega _{f_h}\), then the set \(\varOmega _{\underline{{\mathcal {F}}}_i}\) corresponds to the high-frequency range
$$\begin{aligned} \varOmega _{\underline{\mathcal {F}} _i} := \{ \omega _f \in \mathrm{I\!R} \ | \ \ \mathopen | \omega _f \mathclose | \geqslant \omega _{f_h} \}. \end{aligned}$$
The objective here is to simultaneously achieve local state estimation (asymptotic stability of the error dynamics) and fault/attack detection. Theorems 1, 2 and 3 are proposed in this section to solve this problem through a set of matrix inequalities using the \({\mathcal {H}}_\infty , \ {\mathcal {H}}_-\) performance indexes. Hence, to summarise, the proposed fault/attack detection scheme is obtained through simultaneously satisfying the following, for some performance scalar variables \(\gamma _i, \varrho _i \beta _i\) and \(\eta _i \forall i \in \{1,\ldots ,N\}\).
-
(i)
To guarantee asymptotic stability of error dynamics (13).
-
(ii)
To ensure a reasonable sensitivity of the residuals to the possible output attacks/faults over all frequency ranges, by satisfying
$$\begin{aligned} \begin{array}{lll} ||T_{r_{{\mathcal {F}}_i} {\mathcal {F}}_i}||_{-} > \gamma _i, \end{array} \end{aligned}$$(16)where \(r_{{\mathcal {F}}_i}\) is the residual signal defined for the case with no disturbance \(d_{v_i}=0\), no uncertainty \({\underline{\phi }}_i=0\) and no fault \(\underline{{\mathcal {F}}}_i=0\).
-
(iii)
To ensure a reasonable sensitivity of the residuals to the possible input attacks/faults over a finite-frequency range defined in the set \(\varOmega _{\underline{{\mathcal {F}}}_i}\), by satisfying
$$\begin{aligned} \begin{array}{lll} ||T_{r_{\underline{{\mathcal {F}}}_i} \underline{{\mathcal {F}}}_i}||_- > \varrho _i, \end{array} \end{aligned}$$(17)for all solutions of (13) such that,
$$\begin{aligned} \begin{array}{ll} \int ^\infty _0 \Big ( \kappa (\omega _{f_1} e_{v_i}(t) + j{\dot{e}}_{v_i}(t))(\omega _{f_2} e_{v_i}(t) -j{\dot{e}}_{v_i}(t))^T\Big ) \mathrm{d}t \\ \leqslant 0, \end{array}\nonumber \\ \end{aligned}$$(18)where \(\kappa \), \(\omega _{f_1}\), \(\omega _{f_2}\) are as defined in \(\varOmega _{\underline{{\mathcal {F}}}_i}\), and \(r_{\underline{{\mathcal {F}}}_i}\) is the residual signal defined for the case with no disturbance \(d_{v_i}=0\), no uncertainty \({\underline{\phi }}_i=0\) and no fault \({\mathcal {F}}_i=0\).
-
(iv)
To guarantee a good disturbances and uncertainties rejection performance w.r.t. to the residual signals over all frequency ranges, i.e.
$$\begin{aligned} \begin{array}{lll} ||T_{r_{{\mathcal {D}}_i} d_{v_i}}||_\infty< \eta _i, \quad ||T_{r_{{\mathcal {D}}_i} {\underline{\phi }}_i}||_\infty < \beta _i , \end{array} \end{aligned}$$(19)where \(r_{{\mathcal {D}}_i}\) is the residual signal defined without fault \({\mathcal {F}}_i=0\) and \(\underline{{\mathcal {F}}}_i=0\).
For the rest of the manuscript, the time argument is omitted where it is not needed for clarity.
Theorem 1
For \(d_{v_i}=0\), \({\underline{\phi }}_i=0\), \(\underline{{\mathcal {F}}}_i=0\), \({\mathcal {F}}_i \ne 0\), let \(\gamma _i\), \(\theta _{m_i}\), \(\sigma _{1i}\) and \(\varepsilon _i\) be strictly positive scalars, error dynamics (13) is asymptotically stable and performance index (16) is guaranteed if \(\forall i \in \{1,\ldots ,N\}\), there exist symmetric positive definite matrices \(P_i\), matrices \(U_i\), \(R_i\) and unstructured nonsingular matrices \(Y_i\) such that the following optimisation problem is solved
subject to
where
and the observer gains are specified as
Proof
Performance index (16) corresponds to the following function
Let us select the candidate Lyapunov function
\(V_i(e_{v_i})=e^T_{v_i} P_i e_{v_i}\), then
On the other hand, (23) can be expressed as
According to Assumption 2, it can be shown that
where \(\theta _{M_i}=\text {max}(\theta _i^2,\theta _{i_1}^2,\ldots ,\theta _{i_{N_i}}^2)\).
Since \(V(e_{v_i})=e_{v_i}^T P_i e_{v_i} \ge 0\) and using Lemma 1 and equation (26), (25) can be shown to be equivalent to
where \( \varUpsilon _i=N_i^T P_i + P_i N_i + \varepsilon _i \theta _{M_i} I +\varepsilon _i^{-1} P_i T_i T_i^T P_i -(Z^i {\widetilde{C}}_i)^T W^T_i W_i Z^i {\widetilde{C}}_i \). Using the Schur complement, (27) can be re-written as
with
Using the congruence transformation \(\begin{pmatrix} I&{\mathcal {T}}_{1i}^T \end{pmatrix}\), (28) is equivalent to
for new general matrices \({\mathcal {K}}_{1i}\) and \({\mathcal {Y}}_{1i}\). Hence, by selecting
for a scalar \(\sigma _{1i}\) and a nonsingular general matrix \(Y_i\), one can obtain the following sufficient condition
with
Replacing \(N_i\) and \(T_i\) with their respective values, and applying the linearising change of variables \(U_i = Y_i H_i\), \(R_i = Y_i S_i\), (20) is obtained. Furthermore, pre-multiplying (11a) with \(Y_i\) yields (21). Therefore, solving (20) under imposed constraints (21) and using observer gains (22) guarantees residual performance index (16) and the asymptotic stability of error dynamics (9). \(\square \)
Theorem 2
For \(d_{v_i}=0\), \({\underline{\phi }}_i=0\), \({\mathcal {F}}_i=0\), \(\underline{{\mathcal {F}}}_i \ne 0\), let \(\varrho _i\), \(\theta _{M_i}\), \(\sigma _{2i}\) and \(\varepsilon _i\) be strictly positive scalars, an arbitrary design matrix \(K_i\), error dynamics (13) is asymptotically stable and performance index (17) is guaranteed if \(\forall i \in \{1,\ldots ,N\}\) over a finite-frequency domain defined in (15), there exist symmetric positive definite matrices \(X_i\), symmetric matrices \({\mathcal {X}}_i\), matrices \(U_i\), \(R_i\) and unstructured nonsingular matrices \(Y_i\) such that the following optimisation problem is solved
subject to
where
and \({\mathcal {B}}_i=\begin{pmatrix} -{\widetilde{B}}_{f_i}&{\widetilde{B}}_{u_i} {\mathcal {A}}_{u,i}^{-1} D_{u_i} \end{pmatrix}\). The observer gains are then computed as in (22).
Proof
Let us select the candidate Lyapunov function \(V_i(e_{v_i})=e^T_{v_i} X_i e_{v_i}\), then
To solve (17) over a finite-frequency domain as defined in (15), one could define the following function
where \( {\mathcal {W}}_i = (\omega _{f_1} e_{v_i} + j{\dot{e}}_{v_i})(\omega _{f_2} e_{v_i} +j{\dot{e}}_{v_i})^*\) and \({\mathcal {X}}_i\) is a symmetric matrix. From (18), one gets
Moreover, it can be shown through the Parseval’s theorem [45] that
where \(\check{\mathbf{e }}_i(\omega )\) is the Fourier transform of \(e_{v_i}(t)\). Choosing \({\mathcal {X}}_i\) such that \(\kappa {\mathcal {X}}_i \geqslant 0\), it yields
or equivalently, \(\text {tr}(\mathbf{He} ({\mathcal {W}}_i){\mathcal {X}}_i) \leqslant 0 \). Therefore, (17) is guaranteed for all solutions of (13) satisfying (18), if
By setting \(\omega _{f_a}=\frac{\omega _{f_1}+\omega _{f_2}}{2}\), then
On the other hand, using Lemma 1 and (26), one has
Replacing (34) and (35) into (33) gives
where
It can be re-written as
with
Similar to Theorem 1, (37) can be shown to be equivalent to
for new general matrices \({\mathcal {K}}_{2i}\) and \({\mathcal {Y}}_{2i}\). Hence, by selecting
for a scalar \(\sigma _{2i}\), an arbitrary matrix \(K_i\) and a nonsingular general matrix \(Y_i\), one can obtain the following sufficient condition
with
By replacing \(N_i\) and \(T_i\) with their respective values, and applying the linearising change of variables \(U_i = Y_i H_i\), \(R_i = Y_i S_i\), (30) is obtained. This guarantees residual performance index (17) and the asymptotic stability of error dynamics (9). \(\square \)
Remark 4
Given that LMIs (30) \(\forall i\) are in the complex domain, most solvers cannot directly handle them. Hence, the following equivalent statements are used for a complex Hermitian matrix L(x)
-
1.
\( L(x) < 0.\)
-
2.
\( \begin{pmatrix} \text {Re}(L(x)) &{} \text {Im}(L(x)) \\ -\text {Im}(L(x)) &{} \text {Re}(L(x)) \end{pmatrix} < 0 .\)
where \(\text {Re}(L(x))\) represents the real part of L(x) and \(\text {Im}(L(x))\) its imaginary part. More details can be found in [46].
Theorem 3
For \({\mathcal {F}}_i=0\), \(\underline{{\mathcal {F}}}_i = 0\), \(d_{v_i} \not =0\), \({\underline{\phi }}_i \not =0\), let \(\beta _i\), \(\eta _i\), \(\theta _{M_i}\), \( \sigma _{3i}\) and \(\varepsilon _i\) be strictly positive scalars, error dynamics (13) is asymptotically stable and performance indexes (19) are guaranteed if \(\forall i \in \{1,\ldots ,N\}\), there exist symmetric positive definite matrices \(Q_i\), matrices \(U_i\), \(R_i\) and unstructured nonsingular matrices \(Y_i\) such that for all possible uncertainties, under imposed constraint (21)
subject to
where
The observer gains are then computed as in (22).
Proof
Let us select the candidate Lyapunov function \( V_i(e_{v_i})=e^T_{v_i} Q_i e_{v_i} \), then
The performance index is equivalent to
Combining the two yields
The above inequality can be expressed as
where \( \varGamma _{i1} = N_i^T Q_i + Q_i N_i + (Z^i {\widetilde{C}}_i)^T W^T_i W_i Z^i {\widetilde{C}}_i + \varepsilon _i \theta _{M_i} I + \varepsilon _i^{-1} Q_i T_i T_i^T Q_i \),
\(\varGamma _{i2}=Q_i \begin{pmatrix} T_i{\widetilde{B}}_{d_i} - S_i Z^i{\widetilde{D}}_{d_i}&(S_i\underline{\mathbf{X }}_i- T_i\bar{\mathbf{X }}_i) \end{pmatrix}\),
\(\varUpsilon ^{de}_i = \begin{pmatrix} Z^i {\widetilde{C}}_i W_i^T W_i Z^i{\widetilde{D}}_{d_i}&-(Z^i {\widetilde{C}}_i)^T W^T_i W_i \underline{\mathbf{X }}_i \end{pmatrix}\) and
\(\varUpsilon ^{dd}_i=\begin{pmatrix} (Z^i{\widetilde{D}}_{d_i})^T W^T_i W_i Z^i{\widetilde{D}}_{d_i} -\eta _i^2I &{} -\underline{\mathbf{X }}_i^T W^T_i W_i Z^i{\widetilde{D}}_{d_i} \\ \star &{}\underline{\mathbf{X }}_i^T W^T_i W_i \underline{\mathbf{X }}_i -\beta _i^2I \end{pmatrix}\).
Similar to Theorem 1, the above is equivalent to
where
By selecting
for a scalar \(\sigma _{3i}\) and a nonsingular general matrix \(Y_i\), one can obtain the following sufficient condition
where
Replacing \(N_i\) and \(T_i\) with their respective values, and applying the linearising change of variables \(U_i = Y_i H_i\), \(R_i = Y_i S_i\), (39) is obtained. This guarantees residual performance index (19) and the asymptotic stability of error dynamics (9). \(\square \)
Remark 5
One could note that it is possible to relax constraint (21). Indeed, this equality constraint implies that the span of the rows of \(U_i\) is included in \(\text {ker}(V_{v_i})\). Hence, one could turn this into a minimisation of its maximum singular value which could be minimised, i.e. for a scalar \(\vartheta _i>0\)
subject to
Applying the Schur complement to (44) yields the following LMI
Remark 6
Note that here, as opposed to what is typically done in literature, we do not impose that \(T_i{\widetilde{B}}_{d_i} - S_i Z^i{\widetilde{D}}_{d_i} = S_i \mathbf{X }_i=0\). Indeed, maintaining this constraint while solving the proposed inequalities can be unfeasable for some systems. Contrary to other works using unknown input observer, our approach does not require invertibility conditions except on \(Y_i\) which is inherently required by the proposed LMIs. Thus, no rank condition is required for the existence of the unknown input observer to solve the LMIs.
3.1 Residual evaluation
In order to isolate the faulty element (the specific faulty agent and/or faulty link), the residuals are evaluated by comparing them with an offline computed threshold defined hereafter. For this purpose, let us select the following root-mean-square evaluation functions [41], \(\forall p \in {\mathcal {N}}_i \cup i\)
where \(T_w\) is a finite evaluation window with
and \(r_i^p(t) \in \mathrm{I\!R}^{n_y}, \forall p \in {\mathcal {N}}_i \cup i\). Noise, disturbances, communication uncertainties (etc.) are treated as unstructured unknown inputs, and the RMS threshold is computed as
where one could set \(J^e_{i{th}}=\max \{J^e_{ii_{th}},\ldots ,J^e_{{ii_{N_i}}_{th}}\}\). For isolation purpose, let us define the secure detection flags \(\pi _i\), such that if \(J^e_{i,i}(t) \leqslant J^e_{i{th}}\) then \(\pi _i = 0\) and \(\pi _i = 1\) when \(J^e_{i,i}(t) > J^e_{i{th}}\). An agent i is assumed to request the secure detection flag of its neighbours when a fault or an attack has been detected through the generated residual functions \(J^e_{i,j}(t)\), \(j \in {\mathcal {N}}_i\).
In order to summarise the proposed scheme, two algorithms are proposed hereafter. Optimisation Algorithm 1 is ran offline and proposes steps to compute the observer matrix gains using a finite-frequency mixed \({\mathcal {H}}_\infty /{\mathcal {H}}_-\) approach by simultaneously combining Theorems 1–3 and Remark 5. Define the multi-objective cost function
where \(\lambda _{i1},\lambda _{i2},\lambda _{i3},\lambda _{i4}, \lambda _{i5}\) are positive trade-off weighing constants.

Remark 7
It should be noted that Algorithm (48) ensures that the best solution with respect to cost function (48) is obtained. This renders the residual functions as sensible as possible to the fault and attack signals while guaranteeing the best possible attenuation performance of the disturbances and communication uncertainties with respect to the residual evaluation functions. It is also worth mentioning that the proposed method introduces additional design variables to the optimisation problem (e.g. matrix variables \(Y_i\)), and no products between Lyapunov matrices (\(P_i\), \(Q_i\) or \(X_i\)) and the observer matrices \(N_i\). It allows the use of different Lyapunov matrices for each Theorem, and solving Algorithm 1 with the common design variable \(Y_i\) which, unlike Lyapunov matrices, is only required to be nonsingular. This fact, along with the addition of variables \(\sigma _{1i}\), \(\sigma _{2i}\), \(\sigma _{3i}\) and matrix \(K_i\), allows more degree of freedom and reduces the conservatism of the overall solution.
Algorithm 2 given in the following is ran online and summarises the detection and isolation logic where an agent i is said to be faulty if \(f_{a_i}(t)\ne 0\) and/or \(f_{s_i}(t)\ne 0\).

4 Illustrative example
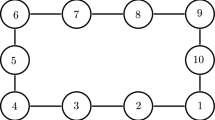
To show the effectiveness of the proposed algorithm, let us consider a heterogeneous MAS composed of one-link flexible joint manipulator robots. In the following, there are three followers labelled 1 to \(N=3\) and one virtual leader labelled 0. They are connected according to the directed graph topology represented in Fig. 1. The associated adjacency matrix is given as
Their dynamics is expressed as [42]
where \(\theta _{m_i}\) is the rotation angle of the motor, \(\theta _{l_i}\) is the rotation angle of the link, \(\omega _{m_i}\) and \(\omega _{l_i}\) are their angular velocities. The following table summarises the parameters.
Parameter | Unit |
|---|---|
Link inertia \(J_{l_i}\) | kg m\(^2\) |
Motor inertia \(J_{m_i}\) | kg m\(^2\) |
Viscous friction coefficient \(B_i\) | Nm V\(^{-1}\) |
Amplifier gain \(K_{\tau _i}\) | Nm V\(^{-1}\) |
Torsional spring constant \(k_i\) | Nm rad\(^{-1}\) |
Link length \(h_i\) | m |
Mass \(m_i\) | kg |
Gravitational acceleration g | ms\(^{-1}\) |
By setting, for all \(i=1,2,3\), \(x_i^T = \begin{pmatrix}\theta _{m_i}&\omega _{m_i}&\theta _{l_i}&\omega _{l_i}\end{pmatrix}=\begin{pmatrix}x_{i1}&x_{i2}&x_{i3}&x_{i4}\end{pmatrix}\) and \(x_0^T = \begin{pmatrix}x_{01}&x_{02}&x_{03}&x_{04}\end{pmatrix}\) where \(x_0\) is the virtual leader state, the state space representation can be given as
\(D_{z_{13}} = \mathbf{1 }\), \(D_{u_{13}} = 1\), \(D_{z_{31}} = \mathbf{1 }\), \(D_{u_{31}} = 1\), \(D_{z_{12}} =I\), \(D_{u_{12}} =1\), \(D_{z_{21}} =I\), \(D_{u_{21}} =1\).
In the following simulations, the parameter uncertainties are considered as \(\Delta a_{ij}(t)=0.1\sin (a_{ij}t)\) and the perturbations \(d_i(t)\) as Gaussian white noise with values in \([-0.2 , 0.2]\). For the followers, the parameters are chosen as \(m_1=m_2=m_3=0.21 kg\), \(k_1=0.18 Nm\cdot rad^{-1}\), \(k_2=0.1 Nm\cdot rad^{-1}\), \(k_3=0.22 Nm\cdot rad^{-1}\), \(B_1=4.6 \times 10^{-2} Nm V^{-1}\), \(B_2=3.6 \times 10^{-2} Nm V^{-1}\), \(B_3=5.6 \times 10^{-2} Nm V^{-1}\), \(J_{m_1}=J_{m_2}=J_{m_3}=3.7 \times 10^{-3} kgm^2\), \(J_{l_1}=J_{l_2}=J_{l_3}=9.3 \times 10^{-3} kgm^2\), \(K_{\tau _1}=0.08 Nm V^{-1}\), \(K_{\tau _2}=0.085 Nm V^{-1}\), \(K_{\tau _3}=0.09 Nm V^{-1}\), \(g= 9,8 m/s^2\), \(h= 0.3 m\). The leader parameters are given as \(m_0=0.21 kg\), \(k_0=0.18 Nm\cdot rad^{-1}\), \(B_0=4.6 \times 10^{-2} Nm V^{-1}\), \(J_{m_0}=3.7 \times 10^{-3} kgm^2\), \(J_{l_0}=9.3 \times 10^{-3} kgm^2\), \(K_{\tau _0}=0.08 Nm V^{-1}\).
It is thus easy to verify that \(\theta _{M_1}=\theta _{M_2}=\theta _{M_3}=3.3\). The initial conditions are given as \(x_{0}(0)=(0,0,0,0)\), \(x_{1}(0)=(0.1,0,0.2,0)\), \(x_{2}(0)=(0.5,0,0.1,0)\), \(x_{3}(0)=(0.3,0,0.4,0)\). In this example, a tweaked version of the leader–follower control algorithm proposed in [47] is used based on the estimated state:
where \({\hat{x}}_{v_i}^T = \begin{pmatrix} {\hat{x}}_i^i&{\hat{x}}_i^{i_1}&\ldots&{\hat{x}}_i^{i_{N_i}}\end{pmatrix}\), \(e_{v_i}^T = \begin{pmatrix} e_i^i&e_i^{i_1}&\ldots&e_i^{i_{N_i}}\end{pmatrix} = \begin{pmatrix} e_{i1}^i&\ldots&e_{i4}^i&e_{i1}^{i_{N_i}}&\ldots&e_{i4}^{i_{N_i}} \end{pmatrix} \), \({\hat{x}}_i^p \in \mathrm{I\!R}^{4}\), \(e_i^p = x_p - {\hat{x}}_i^p \in \mathrm{I\!R}^{4}, \ \forall p \in {\mathcal {N}}_i \cup i\), \(M_i\) is a control gain matrix and \(g_{0i}\) defines the communication link between agent i and leader 0 (\(g_{0i}=1\) when 0 communicates with i and \(g_{0i}=0\) otherwise). The control gains are given as
The multi-objective weights are chosen as \(\lambda _{i1}=\lambda _{i2}=\lambda _{i3}=\lambda _{i4}=\lambda _{i5}=1, \ \forall i\). The vector \(\underline{{\mathcal {F}}}_i\) is assumed to belong to the finite-frequency domain [0, 0.1). It is worth noting that inequalities (20), (30), (39) and (45) can be solved using an appropriate solver (YALMIP, etc. [48]).
\(\forall i \in \{1,2,3\}\), Algorithm 1 is applied for \( \sigma _{1i}=1\), \(\sigma _{2i}=0.2\), \(\sigma _{3i}=0.1\), \(K_i=-2B_{u_i}\), \(\varepsilon _i=0.04\) and \(W_i=I\), yielding \( \eta _1=0.2, \beta _1=0.2, \vartheta _1=0.01, \gamma _1=0.1, \varrho _1=0.81\), \( \eta _2=0.15, \beta _2=0.15, \vartheta _2=0.02, \gamma _2=0.1, \varrho _2=0.85\), \( \eta _3=0.04, \beta _3=0.4, \vartheta _3=0.01, \gamma _3=0.7, \varrho _3=0.77\).
Remark 8
It should be highlighted that the computation of the matrix gains is done offline and once. Based on Theorems 1–3, for each agent, the observer matrix gains are computed according to Algorithm 1. Therefore, a set of LMIs has to be solved offline and once. One can note that the dimension and number of LMIs linearly increase as the state and number of agents increase. Here, 4N LMIs (N is the number of agents) should be solved. For an agent i, their dimensions are: \((3n^i_x + n^i_{f_s} + {\underline{n}}^i_{f_z} ) \times (3n^i_x + n^i_{f_s} + {\underline{n}}^i_{f_z} )\) for Theorem 1, \((3n^i_x + n^i_{f_a} + N_i n_{f_u} ) \times (3n^i_x + n^i_{f_a} + N_i n_{f_u} )\) for Theorem 2, \((3n^i_x + n^i_d + {\underline{n}}^i_z+{\underline{n}}^i_u ) \times (3n^i_x + n^i_d + {\underline{n}}^i_z+{\underline{n}}^i_u)\) for Theorem 3 and \(n^i_x \times n^i_x\) for Remark 5. These dimensions are given in Table 2 for the illustrative example. Additionally, for each agent, the size of the FDI modules (i.e. Eq. (8)) is only dependent on the number of neighbouring agents regardless of the agents’ control inputs, which makes the proposed scheme highly scalable.
Remark 9
It is interesting to note that for implementation of the method proposed in this work, each agent sends its corrupted output and its corrupted control input (dimension \(n_u+n_y\)). This can increase the communication cost in contrast with [27] for instance, where the FDI modules only require estimated outputs to be broadcasted (dimension \(n_y\)). However, as opposed to [27], the proposed method does not require the agents to be equipped with relative information sensors. Indeed, requiring that the agents are equipped with both relative information sensors and wireless communication modules, can limit the cost-effectiveness of the method proposed therein.
Let us consider hereafter two scenarios. In the first one, two faults occur in the network: a sensor fault \(f_{s_1}(t)\) at agent 1 and an actuator fault \(f_{a_3}(t)\) at agent 3, as represented in Fig. 2. Figures 3, 4 and 5 show the generated residual evaluation functions by agents 1, 2 and 3, respectively. The worst case analysis of the evaluation functions corresponding to the nonfaulty operation of the network under disturbances and uncertainties leads to the following thresholds \(J^e_{1{th}}=0.048, J^e_{2{th}}=0.03\) and \(J^e_{3{th}}=0.027\) under the evaluation window \(T_w=10s\). It is usually not easy to accurately compute the value of the supremum of the RMS function in (47) to simultaneously prevent false alarms and avoid missed detections. As such, a series of Monte Carlo simulations have been conducted where the supremum of the RMS function in (47) is calculated under the healthy operation of the MAS, with different noises, disturbances and uncertainties. The corresponding maximum value has been taken as an appropriate threshold. The sampling period is set as \(T_s = 10^{-1}\) s. One could see from Figs. 3, 4 and 5 that the faults could be clearly distinguished. Additionally, according to Algorithm 2, one can see from Fig. 3 that all generated functions \(J_{1,1}^e(t)\), \(J_{1,2}^e(t)\) and \(J_{1,3}^e(t)\) increase at around \(t=20s\) and exceed the defined threshold due to the sensor fault \(f_{s_1}(t)\) occurring at agent 1. This confirms that a fault has occurred at agent 1. Figure 4 further confirms this, since only \(J_{2,1}^e(t)\) increases due to this fault. At \(t=40s\), the actuator fault \(f_{a_3}(t)\) occurs at agent 3, where one can see in Fig. 3 that agent 1 detects it (its residual evaluation function for agent 3, i.e. \(J_{1,3}^e(t)\), is greater than \(J^e_{1{th}}\) even though both \(J_{1,1}^e(t)\) and \(J_{1,2}^e(t)\) are lower than \(J^e_{1{th}}\)). Hence, according to Algorithm 2, agent 1 can distinguish that the fault \(f_{s_1}(t)\) has disappeared and that agent 3 is now faulty. This is confirmed for agent 3 in Fig. 5.
Estimation errors: a at agent 1 in the faultless and attackless case, b at agent 2 in the faultless and attackless case, c at agent 3 in the faultless and attackless case, d at agent 1 in scenario 1, e at agent 2 in scenario 1, f at agent 3 in scenario 1, g at agent 1 in scenario 2, h at agent 2 in scenario 2 and i at agent 3 in scenario 2
Remark 10
It is worth mentioning that the sensor fault matrices \(D_{f_2}\) and \(D_{f_3}\) are not full column rank. Hence, the methods proposed in [27, 28] for instance cannot be applied. Moreover, the effectiveness of the proposed method has been shown for heterogeneous MASs under directed topologies. Besides, compared with the decentralised observer proposed in [49] for example, in which faults occurring at agent i can only be detected by the agent itself, our distributed observer can detect both the agent’s faults and its neighbours’ faults. At last, it can be noticed that the matching condition, i.e. \(rank(C_i B_{f_i})=n_{f_a}\), required in many existing works (e.g. [50]), is not needed in our methodology. Indeed, this condition is not satisfied for agents 2 and 3.
In the second scenario, two types of faults are considered: a data injection attack incident to agent 1 targeting the link going from agent 3 to 1, i.e. \(f^z_{13}(t)=f^u_{13}(t)\) occurring at \( 15s \leqslant t \leqslant 40s\), and a replay attack incident to agent 2 at the link going from agent 1 to 2 at \(t=70s\), i.e. \(f^z_{21}(t)\) and \(f^u_{21}(t)\) with a delay of \({\mathcal {T}}_{12}=70s\). \(f^z_{13}(t)\), \(f^u_{13}(t)\), \(f^z_{21}(t)\) and \(f^u_{21}(t)\) are represented in Fig. 6. Figures 7, 8 and 9 show the generated evaluation functions by agents 1, 2 and 3, respectively, in the second scenario. The worst case analysis of the evaluation functions corresponding to the attack-less operation of the network under disturbances and uncertainties leads to the following thresholds \(J^e_{1{th}}=0.016, J^e_{2{th}}=0.017, J^e_{3{th}}=0.02\). It is clear from the evaluation functions that the attacks can be distinguished when surpassing the computed thresholds. Indeed, from Fig. 7, one can see that the data injection attack in the link from 3 to 1 has been detected according to Algorithm 2. It is confirmed that this fault is an edge fault upon requesting agent 3’s detection flag, as \(J^e_{3,3}\) stays below the defined threshold throughout the duration of the attack. From Fig. 8, the replay attack in the link from agent 1 to 2 has been detected by \(J_{2,1}^e(t)\) at \(t=70s\) which is confirmed by the fact that \(J^e_{1,1}\) does not react to the attack.
The control efforts corresponding to the faultless case and scenarios 1 and 2 are depicted in Fig. 10. Figure 11 shows the estimation errors generated by the FDI modules for agents 1, 2 and 3, respectively. It can clearly be seen that the estimation errors converge to zero in the absence of any fault or attack.
From these simulations, it can be seen that the proposed FDI scheme is able to detect and isolate attacks, actuator faults and sensor faults in the presence of disturbances, noise and communication uncertainties.
5 Conclusion
In this paper, the problem of FDI in Lipschitz nonlinear MASs with disturbances, subject to actuator, sensor and communication faults has been addressed. A multi-objective finite-frequency \({\mathcal {H}}_-/{\mathcal {H}}_\infty \) design along with nonlinear UIOs has been proposed. Sufficient conditions have been derived in terms of a set of LMIs. The combination of UIOs, removal of strict rank conditions and finite-frequency method has been shown to provide extra degrees of freedom in the FDI filter design. Additionally, the multi-objective method guarantees that the evaluation functions are robust with respect to all admissible disturbances and uncertainties and sensitive to all types of faults. A numerical example has been studied in order to showcase the effectiveness of the proposed scheme. As future works, instead of considering Lipschitz nonlinear systems, one could investigate other classes of nonlinear uncertain systems including chained-form dynamics. Based on the proposed FDI scheme, it would also be possible to design some fault accommodation strategies.
Data availability
The authors declare that the manuscript has no associated data.
References
Carpenter, J.R.: Decentralized control of satellite formations. Int. J. Robust Nonlinear Control 12(2–3), 141–161 (2002)
Schetter, T., Campbell, M., Surka, D.: Multiple agent-based autonomy for satellite constellations. Artif. Intell. 145(1–2), 147–180 (2003)
Beard, R.W., McLain, T.W., Goodrich, M.A., Anderson, E.P.: Coordinated target assignment and intercept for unmanned air vehicles. IEEE Trans. Robot. Autom. 18(6), 911–922 (2002)
Olfati-Saber, R.: Flocking for multi-agent dynamic systems: algorithms and theory. IEEE Trans. Autom. Control 51(3), 401–420 (2006)
Anggraeni, P., Defoort, M., Djemai, M., Zuo, Z.: Control strategy for fixed-time leader-follower consensus for multi-agent systems with chained-form dynamics. Nonlinear Dyn. 96(4), 2693–2705 (2019)
Trujillo, M., Aldana-López, R., Gómez-Gutiérrez, D., Defoort, M., Ruiz-León, J., Becerra, H.: Autonomous and non-autonomous fixed-time leader-follower consensus for second-order multi-agent systems. Nonlinear Dyn. 102(4), 2669–2686 (2020)
Taoufik, A., Defoort, M., Djemai, M., Busawon, K., Sánchez-Torres, J.D.: Distributed global fault detection scheme in multi-agent systems with chained-form dynamics. Int. J. Robust Nonlinear Control 31(9), 3859–3877 (2021)
Zhang, J., Sahoo, S., Peng, J.C.-H., Blaabjerg, F.: Mitigating concurrent false data injection attacks in cooperative dc microgrids. IEEE Trans. Power Electron. 36(8), 9637–9647 (2021)
Khalaf, M., Youssef, A., El-Saadany, E.: Joint detection and mitigation of false data injection attacks in AGC systems. IEEE Trans. Smart Grid 10(5), 4985–4995 (2018)
Gallo, A.J., Turan, M.S., Boem, F., Ferrari-Trecate, G., Parisini, T.: Distributed watermarking for secure control of microgrids under replay attacks. In: 2018 7th IFAC Workshop on Distributed Estimation and Control in Networked Systems (NECSYS), pp. 182–187. IEEE (2018)
Lu, A.-Y., Yang, G.-H.: Distributed consensus control for multi-agent systems under denial-of-service. Inf. Sci. 439, 95–107 (2018)
Boem, F., Gallo, A.J., Ferrari-Trecate, G., Parisini, T.: A distributed attack detection method for multi-agent systems governed by consensus-based control. In: 2017 IEEE 56th Annual Conference on Decision and Control (CDC), pp. 5961–5966. IEEE (2017)
Smith, R.S.: Covert misappropriation of networked control systems: presenting a feedback structure. IEEE Control Syst. Mag. 35(1), 82–92 (2015)
Conti, J.P.: The day the samba stopped [power blackouts]. Eng. Technol. 5(4), 46–47 (2010)
Slay, J., Miller, M.: Lessons learned from the maroochy water breach. In: International Conference on Critical Infrastructure Protection, pp. 73–82. Springer, Berlin (2007)
Lindsay, J.R.: Stuxnet and the limits of cyber warfare. Secur. Stud. 22(3), 365–404 (2013)
Sullivan, J.E., Kamensky, D.: How cyber-attacks in Ukraine show the vulnerability of the US power grid. Electr. J. 30(3), 30–35 (2017)
Cardenas, A.A., Amin, S., Sastry, S.: Secure control: towards survivable cyber-physical systems. In: 2008 The 28th International Conference on Distributed Computing Systems Workshops, pp. 495–500. IEEE (2008)
Song, J., He, X.: Model-based fault diagnosis of networked systems: a survey. Asian J. Control. 1–11 (2021). https://doi.org/10.1002/asjc.2543
Pasqualetti, F., Dörfler, F., Bullo, F.: Attack detection and identification in cyber-physical systems. IEEE Trans. Autom. Control 58(11), 2715–2729 (2013)
Jan, M.A., Nanda, P., He, X., Liu, R.P.: A sybil attack detection scheme for a centralized clustering-based hierarchical network. In: 2015 IEEE Trustcom/BigDataSE/ISPA, vol. 1, pp. 318–325. IEEE (2015)
Khan, A.S., Khan, A.Q., Iqbal, N., Sarwar, M., Mahmood, A., Shoaib, M.A.: Distributed fault detection and isolation in second order networked systems in a cyber-physical environment. ISA Trans. 103, 131–142 (2020)
Quan, Y., Chen, W., Wu, Z., Peng, L.: Distributed fault detection and isolation for leader-follower multi-agent systems with disturbances using observer techniques. Nonlinear Dyn. 93(2), 863–871 (2018)
Menon, P.P., Edwards, C.: Robust fault estimation using relative information in linear multi-agent networks. IEEE Trans. Autom. Control 59(2), 477–482 (2013)
Davoodi, M.R., Khorasani, K., Talebi, H.A., Momeni, H.R.: Distributed fault detection and isolation filter design for a network of heterogeneous multiagent systems. IEEE Trans. Control Syst. Technol. 22(3), 1061–1069 (2013)
Chadli, M., Davoodi, M., Meskin, N.: Distributed state estimation, fault detection and isolation filter design for heterogeneous multi-agent linear parameter-varying systems. IET Control Theory Appl. 11(2), 254–262 (2017)
Davoodi, M., Meskin, N., Khorasani, K.: Simultaneous fault detection and consensus control design for a network of multi-agent systems. Automatica 66, 185–194 (2016)
Li, S., Chen, Y., Zhan, J.: Simultaneous observer-based fault detection and event-triggered consensus control for multi-agent systems. J. Franklin Inst. 358(6), 3276–3301 (2021)
Liang, D., Yang, Y., Li, R., Liu, R.: Finite-frequency \(h_-\)/\(h_\infty \) unknown input observer-based distributed fault detection for multi-agent systems. J. Franklin Inst. 358(6), 3258–3275 (2021)
Teixeira, A., Shames, I., Sandberg, H., Johansson, K.H.: Distributed fault detection and isolation resilient to network model uncertainties. IEEE Trans. Cybernet. 44(11), 2024–2037 (2014)
Liu, X., Gao, X., Han, J.: Observer-based fault detection for high-order nonlinear multi-agent systems. J. Franklin Inst. 353(1), 72–94 (2016)
Han, J., Liu, X., Gao, X., Wei, X.: Intermediate observer-based robust distributed fault estimation for nonlinear multiagent systems with directed graphs. IEEE Trans. Industr. Inf. 16(12), 7426–7436 (2019)
Wu, Y., Wang, Z., Huang, Z.: Distributed fault detection for nonlinear multi-agent systems under fixed-time observer. J. Franklin Inst. 356(13), 7515–7532 (2019)
Liu, X., Gao, X., Han, J.: Robust unknown input observer based fault detection for high-order multi-agent systems with disturbances. ISA Trans. 61, 15–28 (2016)
Iwasaki, T., Hara, S., Fradkov, A.L.: Time domain interpretations of frequency domain inequalities on (semi) finite ranges. Syst. Control Lett. 54(7), 681–691 (2005)
Li, Y., Fang, H., Chen, J., Yu, C.: Distributed cooperative fault detection for multiagent systems: a mixed \({\cal{H}}_\infty / {\cal{H}}_2\) optimization approach. IEEE Trans. Ind. Electron. 65(8), 6468–6477 (2017)
Teixeira, A., Sandberg, H., Johansson, K.H.: Networked control systems under cyber attacks with applications to power networks. In: Proceedings of the 2010 American Control Conference, pp. 3690–3696. IEEE (2010)
Taoufik, A., Defoort, M., Busawon, K., Dala, L., Djemai, M.: A distributed observer-based cyber-attack identification scheme in cooperative networked systems under switching communication topologies. Electronics 9(11), 1912 (2020)
Rezaee, H., Parisini, T., Polycarpou, M.M.: Resiliency in dynamic leader-follower multiagent systems. Automatica 125, 109384 (2021)
Ren, W., Atkins, E.: Distributed multi-vehicle coordinated control via local information exchange. Int. J. Robust Nonlinear Control 17(10–11), 1002–1033 (2007)
Ding, S.X.: Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools. Springer, Berlin (2008)
Raghavan, S., Hedrick, J.K.: Observer design for a class of nonlinear systems. Int. J. Control 59(2), 515–528 (1994)
Boyd, S., El Ghaoui, L., Feron, E., Balakrishnan, V.: Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia (1994)
Li, X.-J., Yang, G.-H.: Fault detection in finite frequency domain for Takagi-Sugeno fuzzy systems with sensor faults. IEEE Trans. Cybernet. 44(8), 1446–1458 (2013)
Zhou, K., Doyle, J.C.: Essentials of Robust Control, vol. 104. Prentice Hall, Upper Saddle River (1998)
Gahinet, P., Nemirovski, A., Laub, A.J., Chilali, M.: LMI Control Toolbox. The Math Works Inc, Natick (1996)
Ding, L., Zheng, W.X.: Network-based practical consensus of heterogeneous nonlinear multiagent systems. IEEE Trans. Cybernet. 47(8), 1841–1851 (2016)
Lofberg, J.: Yalmip: A toolbox for modeling and optimization in matlab. In: 2004 IEEE international Conference on Robotics and Automation (ICRA), pp. 284–289. IEEE (2004)
Chen, G., Lin, Q.: Observer-based consensus control and fault detection for multi-agent systems. Control Theory Appl. 31(5), 584–591 (2014)
Zhang, K., Jiang, B., Cocquempot, V.: Adaptive technique-based distributed fault estimation observer design for multi-agent systems with directed graphs. IET Control Theory Appl. 9(18), 2619–2625 (2015)
Funding
This study was funded by the ANR and Region Hauts-de-France under project I2RM.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Taoufik, A., Defoort, M., Djemai, M. et al. A distributed fault detection scheme in disturbed heterogeneous networked systems. Nonlinear Dyn 107, 2519–2538 (2022). https://doi.org/10.1007/s11071-021-07129-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-07129-0