Stability and local bifurcation analyses of two-wheeled trailers considering the nonlinear coupling between lateral and vertical motions

Abstract

The nonlinear dynamics of two-wheeled trailers is investigated using a spatial 4-DoF mechanical model. The non-smooth characteristics of the tire forces caused by the detachment of the tires from the ground and other geometrical nonlinearities are taken into account. Beyond the linear stability analysis, the nonlinear vibrations are analyzed with special attention to the nonlinear coupling between the vertical and lateral motions of the trailer. The center manifold reduction is performed leading to a normal form up to third degree terms. The nature of the emerging periodic solutions, and, thus, the sense of the Hopf bifurcations are verified semi-analytically and numerically. Simplified models of the trailer are also used in order to point out the practical relevance of the study. It is shown that the linearly independent pitch motion affects the sense of the Hopf bifurcations at the linear stability boundary. Namely, the constructed spatial trailer model provides subcritical bifurcations for higher center of gravity positions, while the commonly used simplified mechanical models explore the less dangerous supercritical bifurcations only. Domains of loss of contact of tires are also detected and shown in the stability charts highlighting the presence of unsafe zones. Experiments are carried out on a small-scale trailer to validate the theoretical results. A good agreement can be observed between the measured and numerically determined critical speeds and vibration amplitudes.

1 Introduction

Vehicle handling and stability are critical factors in road transportation; hence, they became relevant research topics a long time ago. First, analyses of linear vehicle models were in focus (see, for example, [22, 36]), which provided the basic rules of vehicle design. However, some of the phenomena of the field remained unexplored since they are related to the nonlinear dynamics of the vehicles. Thanks to the developed mathematical tools and computational methods, the nonlinear analysis could come to the front in the academic area and started to be utilized in the industry too. Stability charts, phase portraits and nonlinear bifurcation diagrams were composed for the most intricate nonlinear problems of vehicle dynamics, like the shimmy motions of steered wheels (see [2,3,4, 19, 21, 25]) and aircraft landing nose gears (see [33, 34]), the wobble motion of motorcycles and bicycles (see [9, 17, 18, 20, 23, 26, 27]). Vehicle handling in close to critical maneuvers is also in the focus of recent studies (see [12, 24]), which allow the development of the new generation of vehicle motion control that utilizes the results of nonlinear analyses.

In this paper, the very interesting and complex stability problem of trailers is under investigation. Trailers are very commonly used on the roads in very different combinations with respect to the mass ratio of the towing vehicle and the trailer. Several road accidents happen due to the not appropriately chosen amount of payload and/or payload position/distribution, which easily leads to the so-called snaking and/or rocking motions of the trailer. These unwanted vibrations are also often associated with high towing speeds and are often generated by some initial impulses/perturbations caused by the driver or other circumstances (such as wind gusts or uneven roads), see [1, 5, 7, 16, 28, 35]. In the past, theoretical and numerical investigations have been made on the stability properties of car-trailer combinations considering different level of complexity of the investigated mechanical models, see the 3-DoF model of [5, 16], the 4- or 6-DoF models of [1] or the 32-DoF model of [28]. A systematic experimental investigation by Darling et al. [7] was also carried out using a car-adjustable trailer combination and drew the conclusions that the key factors that affect the stability properties are the yaw inertia, the mass distribution and the position of the trailer axle.

In theoretical stability analyses, the bounce, roll and pitch motions of the trailer are often separated from the lateral dynamics, which is a commonly used and accepted approach in vehicle dynamics. Namely, the use of in-plane models is a conventional solution in the field. Sometimes, the single track model, the so-called bicycle model, is also applied to simplify the analysis, see, e.g., [2,3,4, 19]. As a result, the governing equations have a relatively simple form and analytical calculations can be performed regarding the nonlinear properties of car-trailer systems. These models partially explain unsafe parameter zones and related nonlinear phenomena. For example, it is shown in [2, 4] that the Hopf bifurcations emerging at the critical towing speed are subcritical. Namely, the global stability of the rectilinear motion is not ensured in the linearly stable towing speed range, and large enough perturbations may lead to unwanted large amplitude vibrations of the trailer.

In this study, a spatial mechanical model of a two-wheeled trailer with non-rigid wheel suspensions is used, where all the yaw, pitch and roll motions are considered, see Model A in Fig. 1a. In order to have a relatively low degree-of-freedom model, the towing car is imitated by a lateral spring and damping at the king pin. This simplification may seem inappropriate, but in this study, we focus on the effect of the pitch motion on the nonlinear vibrations. The main contribution of the paper is the analysis of the nonlinear coupling between the vertical and lateral motions of the trailer. Our hypothesis is that the linearly independent pitch motion affects the local bifurcations, namely it changes the sense of the Hopf bifurcations at the linear stability boundaries. In order to verify this assumption, three models are compared to each other in our analysis, see Fig. 1. These models represent different levels of complexity, beginning with the most complex, spatial model (Model A) with 4 DoF, see panel (a). Model B in panel (b) is a reduced model with blocked bounce/pitch motion, but it considers the effect of the roll motion on the stability. Model C is the simplest, 2-DoF in-plane model with blocked pitch and roll motions, see panel (c).

The rest of the paper is organized as follows. The mechanical model of towed, two-wheeled trailers and the main sources of the nonlinearities are presented in Sect. 2. In Sect. 3, the governing equations are linearized around the rectilinear motion and linear stability charts are shown for the mechanical models of Fig. 1. The effects of the wheel suspension parameters and the payload positions on the linear stability are analyzed. The nonlinear vibrations are investigated in Sect. 4. Namely, we perform local bifurcation analysis with the center manifold reduction and numerical investigations using continuation. The limit cycles of the three different models are compared to each other both analytically and numerically. Unsafe zones and regions where the loss of contact of tires happens are also shown for the spatial model. Based on the mechanical model, a small-scale experimental rig is designed on which some measurements are performed. The experimental setup and experimental results are shown in Sect. 5. Finally, our theoretical, numerical and experimental results are concluded in Sect. 6.

Fig. 1

Mechanical models of a trailer with different levels of complexity: a full spatial model, b reduced model with blocked bounce/pitch motion, c in-plane model

2 Modeling

2.1 Mechanical model and generalized coordinates

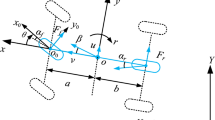
The spatial mechanical model (represented as Model A in Fig. 1) of two-wheeled trailers can be seen in Fig. 2. The trailer is moving in the (X, Y, Z) ground-fixed coordinate system. The towing speed v is kept constant in the X direction, while the movement of the king pin (point A) is not constrained in the Y direction. The trailer is considered as a rigid body with mass m and mass moment of inertia tensor ${\mathbf {J}}_{\mathrm{C}}$ at the center of gravity C with respect to the moving reference frame (x, y, z). The longitudinal and vertical positions of the center of gravity are given relative to the axle of the wheels by the parameters e and $h$, respectively. We consider that the trailer is symmetric with respect to the (x, z) plane, i.e., point C is located in this center plane of the trailer. The constant vertical distance between the king pin and the ground is denoted by $h_0$, the track width is 2b and the caster length, i.e., the longitudinal distance between the axle of the massless wheels and the king pin, is l. In the mechanical model, the pitch dynamics of the trailer is considered; accordingly, the overall stiffness and the damping of the tires and their suspensions are denoted by the parameters k and c, respectively. The interaction between the towing vehicle and the trailer is modeled here by the lateral stiffness $k_{\mathrm{lat}}$ and by the lateral damping $c_{\mathrm{lat}}$. However, this assumption seems to be an oversimplification, but it is often used in the literature (see [31, 32]) in order to keep the complexity of vehicle models and the corresponding mathematical formulas on a manageable level. Accordingly, the number of parameters is moderate in our model. However, in order to help the understanding of the following sections, all the parameters with their notations and names are listed in Table 1, close to the stability charts where their numerical values are first referred.

Fig. 2

The spatial, 4-DoF model of towed two-wheeled trailers. a Axonometric view with the generalized coordinates and geometrical parameters. b The interpretations of the distances $d_{\mathrm{R}}$ and $d_{\mathrm{L}}$ and the lateral tire forces

The spatial motion of the trailer would have six degrees of freedom without any constraints. However, the constant towing speed assumption manifests in the rheonomic geometric constraint $X_{\mathrm{A}}=vt$. In addition, the vertical position of the towing point is fixed $Z_{\mathrm{A}} \equiv h_0$. As a result, the system has $n=6-2=4$ degrees of freedom, and the vector of generalized coordinates can be composed as:

$$\begin{aligned} {\mathbf {q}}= \begin{bmatrix} \psi&\vartheta&\varphi&u \end{bmatrix}^{\mathrm{T}}\,, \end{aligned}$$

(1)

where $\psi$ is the yaw angle, $\vartheta$ is the pitch angle, $\varphi$ is the roll angle of the trailer, and u is the lateral displacement of the king pin, see Fig. 2a.

In order to avoid the presence of kinematic constraints, which could be originated in the rolling of the wheels, we rather use an elastic tire model that is based on the creep-force idea considering the side slip of the wheels [21]. Thus, no kinematic constraint is taken into account; correspondingly, the system is holonomic and the equations of motion can be derived with the Lagrange equation of the second kind [11].

2.2 Nonlinearities

Details of the derivation of the governing equations can be found in [14, 15]. Here, we present the essential assumptions of the mechanical model, pointing out the different sources of the relevant nonlinearities and non-smoothness. On the one hand, geometric nonlinearities are present in the model, but we do not emphasize them here, since they are straightforwardly provided by the derivation of the equations of motion with mathematical rigor. On the other hand, nonlinearities originated in the tire forces and in the suspension system have crucial roles in the nonlinear behavior of the trailer. Thus, they are in focus in this subsection.

The active forces acting on the trailer are the gravitational force G; the lateral tire forces $F^{\mathrm{tire}}_{\mathrm{R}}$ and $F^{\mathrm{tire}}_{\mathrm{L}}$ (see Fig. 2b) acting at the (possible) contact points $\mathrm R'$ and $\mathrm L'$ of the right and the left tires, respectively; the wheel suspension forces $F_{\mathrm{R}}$ and $F_{\mathrm{L}}$; the lateral force $F_{\mathrm{lat}}=-k_{\mathrm{lat}} u - c_{\mathrm{lat}} {\dot{u}}$ acting at point A due to the deformation of the lateral spring and damper.

The effect of the tires is taken into account by means of the lateral tire forces only, which are calculated based on Pacejka’s Magic Formula [21] via the side slip angles $\alpha _{\mathrm{R}}$ and $\alpha _{\mathrm{L}}$ of the right and left wheels, respectively. Thus,

$$\begin{aligned} F^{\mathrm{tire}}_\square = \mu (\alpha _\square ) N_\square \,, \end{aligned}$$

(2)

where $\square$ refers to R or L accordingly to the right or left wheel. With this formula, we assume that the lateral tire force depends linearly on the vertical load $N_\square =F_{\square }\cos {\vartheta }\cos {\varphi }$, which is calculated as the vertical Z-component of the suspension force $F_{\square }$. Namely, we neglect the effect of the unsprung mass by considering zero masses for the wheels. The characteristics $\mu (\alpha )$ are

$$\begin{aligned} \mu (\alpha )= & {} D \sin \left( C \arctan \left( B \alpha - E\left( B \alpha -\arctan (B \alpha ) \right) \right) \right) \,,\nonumber \\ \end{aligned}$$

(3)

where B is the stiffness factor, C is the shape factor, D is the peak factor, and E is the curvature factor. In practice, these parameters are not constant, and they may depend on the vertical load, the static and dynamic coefficients of friction, the temperature, the camber angle, etc., see [21]. For the sake of simplicity, we neglect these dependencies and consider fixed values in our analysis. We also notice that we neglect the self-aligning moments of the tires, which have negligible effect on the final results.

On the contrary, we pay special attention to the rocking motion of the trailer, namely we take into account that the tires can detach from the ground and the vertical load $N_\square$ becomes zero. As mentioned above, this corresponds to zero suspension forces in our model. Hence, we introduce the piece-wise smooth formula:

$$\begin{aligned} F_{\mathrm{s}}(d)= & {} \mathrm {ReLU}\left( F_0 \cdot H(L_{\mathrm{max}}-d) \right. \nonumber \\&\left. + F_\infty \cdot H(L_{\mathrm{min}}-d) \right) \end{aligned}$$

(4)

for both of the right $F_{\mathrm{R}}=F_{\mathrm{s}}(d_{\mathrm{R}})$ and the left $F_{\mathrm{L}}=F_{\mathrm{s}}(d_{\mathrm{L}})$ suspension forces, where the distances $d_{\mathrm{R}}$ and $d_{\mathrm{L}}$ are measured between the points R and $\mathrm R'$ and L and $\mathrm L'$, respectively, as shown in Fig. 2b. To handle the non-smooth characteristic of the suspension force, we use the so-called Heaviside step-function H(s) [8], often defined as $H(s) = \int _{-\infty }^s \delta (s) \mathrm{d}s$, where $\delta (s)$ is the Dirac-delta function. Thus, in Eq. (4), $L_{\mathrm{min}}$ corresponds to the minimal distance, where the spring of the suspension is compressed to its minimal length. Namely, for $d < L_{\mathrm{min}}$, we consider higher stiffness and damping for the suspension. The distance $L_{\mathrm{max}}$ relates to the maximal distance, where the suspension of the wheel is totally expanded. Accordingly,

$$\begin{aligned} F_0 = -k (d-L_0) - c \, {\dot{d}} \,, \end{aligned}$$

(5)

and

$$\begin{aligned} F_\infty = -k_{\infty } (d-L_{\mathrm{min}}) - c_{\infty } {\dot{d}} \,, \end{aligned}$$

(6)

where $L_0$ is the free length of the spring. To imitate the collision in the suspension, one should choose $k_{\infty } \gg k$ and $c_{\infty } \gg c$. Note that we did not take into account that the suspension dampers can be highly nonlinear. We used this simplification because most caravans only have leaf springs without any dampers.

Note that the $\mathrm{ReLU}(s)=\max \{0, s \}$ function in Eq. (4) guarantees that the suspension force cannot be negative even when the suspension expands rapidly (i.e., ${\dot{d}} \gg 0$). For the steady-state condition ${\dot{d}}=0$, the schematic characteristics of the suspension forces can be seen in Fig. 3.

Fig. 3

The schematic non-smooth characteristic of the suspension force $F_{\mathrm{s}}(d)$ for the steady-state condition ${\dot{d}}=0$ together with the switchings

Considering all the above-mentioned nonlinearities, the equations of motion can be written in the general form:

$$\begin{aligned} {\mathbf {M}}({\mathbf {q}}) \, \ddot{{\mathbf {q}}} +{\mathbf {C}}({\mathbf {q}},\dot{{\mathbf {q}}}) = {\mathbf {0}} \end{aligned}$$

(7)

where ${\mathbf {M}}({\mathbf {q}})$ is the mass matrix and ${\mathbf {C}}({\mathbf {q}},\dot{{\mathbf {q}}})$ is a vector containing the remaining parts of the equation including all the nonlinear and non-smooth characteristics.

3 Linear stability analysis

For the linear stability analysis of the rectilinear motion of the trailer, the equations of motion are linearized around ${\mathbf {q}}(t) \equiv {\mathbf {q}}_0$. For the sake of simplicity, we consider the case ${\mathbf {q}}_0={\mathbf {0}}$, namely

$$\begin{aligned} \begin{aligned} \psi (t)&\equiv \psi _0=0\,, \\ \vartheta (t)&\equiv \vartheta _0=0\,, \\ \varphi (t)&\equiv \varphi _0=0\,, \\ u(t)&\equiv u_0=0\,. \end{aligned} \end{aligned}$$

(8)

Due to the symmetry of our model, $\varphi _0=0$ is satisfied for any parameter setup. Moreover, we tune the free length of the spring in the suspensions to maintain zero pitch angle $\vartheta _0=0$ in steady state, i.e.,

$$\begin{aligned} L_0 =h_0+\frac{mg(l-e)}{2kl}\,. \end{aligned}$$

(9)

We assume that none of the switches in Eq. (4) occur in case of small amplitude vibrations around the rectilinear motion. This can be guaranteed by the proper choices of $L_{\mathrm{min}}$ and $L_{\mathrm{max}}$. Using the perturbation ${\mathbf {y}}(t)={\mathbf {q}}(t)-{\mathbf {q}}_0$ around the rectilinear motion, the linearized equations of motion can be written as:

$$\begin{aligned} {\mathbf {M}}_{\mathrm{lin}} \ddot{{\mathbf {y}}}+ {\mathbf {C}}_{\mathrm{lin}} \dot{{\mathbf {y}}} + {\mathbf {K}}_{\mathrm{lin}} {\mathbf {y}} = {\mathbf {0}}\,, \end{aligned}$$

(10)

where ${\mathbf {M}}_{\mathrm{lin}}$ is the mass matrix, ${\mathbf {C}}_{\mathrm{lin}}$ is the damping matrix and ${\mathbf {K}}_{\mathrm{lin}}$ is the stiffness matrix of the linearized system:

$$\begin{aligned} {\mathbf {M}}_{\mathrm{lin}}= & {} \begin{bmatrix} J _{\mathrm{A}z} &{} 0 &{} mh(l-e) &{} -m(l-e)\\ 0 &{} J _{\mathrm{A}y} &{} 0 &{} 0\\ mh(l-e) &{} 0 &{} J _{\mathrm{A}x} &{} -mh\\ -m(l-e) &{} 0 &{} -mh&{} m \end{bmatrix}\,, \end{aligned}$$

(11)

$$\begin{aligned} {\mathbf {C}}_{\mathrm{lin}}= & {} \begin{bmatrix} 2 {\overline{c}} l^2 &{} 0 &{} -2 {\overline{c}} h_0l &{} -2 {\overline{c}} l\\ 0 &{} 2 c l^2 &{} 0 &{} 0 \\ -2 {\overline{c}} h_0l &{} 0 &{} 2 c b^2 + 2 {\overline{c}} h_0^2&{} 2 {\overline{c}} h_0\\ -2 {\overline{c}} l &{} 0 &{} 2 {\overline{c}} h_0&{} 2{\overline{c}} + c_{\mathrm{lat}} \end{bmatrix}\,, \end{aligned}$$

(12)

$$\begin{aligned} {\mathbf {K}}_{\mathrm{lin}}= & {} \begin{bmatrix} 2 BCD {\overline{N}} l &{} 0 &{} -mg(l-e) &{} 0 \\ 0 &{} 2 k l^2 -mgh&{} 0 &{} 0 \\ -2 BCD {\overline{N}} h_0&{} 0 &{} 2 k b^2 -mgh&{} 0 \\ -2 BCD {\overline{N}} &{} 0 &{} -\frac{mg}{l}(l-e) &{} k_{\mathrm{lat}} \end{bmatrix}\,,\nonumber \\ \end{aligned}$$

(13)

where we use the mass moments of inertia about the (x, y, z) axes with respect to the king pin:

$$\begin{aligned} J _{\mathrm{A}x}&= J _{\mathrm{C}x}+mh^2 \,, \end{aligned}$$

(14)

$$\begin{aligned} J _{\mathrm{A}y}&= J _{\mathrm{C}y}+m(l-e)^2+mh^2 \,, \end{aligned}$$

(15)

$$\begin{aligned} J _{\mathrm{A}z}&= J _{\mathrm{C}z}+m(l-e)^2 \,. \end{aligned}$$

(16)

In Eqs. (12) and (13), we also introduce the nominal vertical load

$$\begin{aligned} {\overline{N}} = \frac{mg}{2} \left( 1-\frac{e}{l} \right) \end{aligned}$$

(17)

and the tire related damping

$$\begin{aligned} {\overline{c}}= \frac{BCD}{v} {\overline{N}} \end{aligned}$$

(18)

in order to shorten the formulas. Note that the stiffness matrix ${\mathbf {K}}_{\mathrm{lin}}$ is asymmetric due to the terms related to the lateral tire forces. See also [3] for similar asymmetry properties introduced by tire forces.

As it can be seen in Eqs. (11), (12) and (13), the linearized system can be separated into two subsystems: One differential equation can be disjointed, namely the pitch motion can be analyzed alone (1-DoF subsystem with generalized coordinate $\vartheta$), while the remaining equations are coupled (3-DoF subsystem with generalized coordinates $\psi$, $\varphi$ and u). Hence, the pitch motion does not affect the linear stability of the rectilinear motion of the trailer. In vehicle dynamics, this type of separation of the lateral (handling) and the vertical dynamics (bouncing and pitching) is commonly used for linear analysis. For the dynamics of the trailer, this approach is also confirmed by our mechanical model.

Using the exponential trial solution of the 3-DoF subsystem, one can determine the characteristic equation of the system in the form of a sixth-order polynomial with respect to the characteristic root. The stability of the rectilinear motion can be investigated by means of the Routh–Hurwitz criteria [11] based on the coefficients of the characteristic equation. On the one hand, no closed-form formula can be derived for the critical towing speed, which is an essential parameter in stability analyses of vehicles. On the other hand, one can evaluate the Routh–Hurwitz criteria numerically for a specific set of parameters. Here, we utilize the parameter values of the experimental study of Darling et al. [7], which were also used in [3] to validate an in-plane car-trailer combination model. Some of the parameters, which are also necessary for our spatial trailer model, are not involved in the analysis [7]. Hence, we tried to identify and/or estimate these parameters based on the available information and our physical sense. Moreover, we tuned the lateral stiffness $k_{\mathrm{lat}}$ and damping $c_{\mathrm{lat}}$ in our model with respect to the critical towing speed and vibration frequencies detected in [7]. Note that these parameters are used to imitate the interaction between the trailer and the towing vehicle, and one can tune them based on the natural frequency of the vibration mode that is related to the stability loss of the car-trailer system. We collect all the parameters in Table 1 called as realistic trailer setup.

For this setup, our mechanical model provides a Hopf bifurcation (dynamic/oscillatory loss of stability) at the critical towing speed 29.9 m/s, which agrees with the theoretical calculations of [3]. Namely, the real part of the rightmost complex conjugate pair of characteristic roots is negative for $v<29.9$ m/s, i.e., the rectilinear motion is linearly stable and the oscillations decay in time. For $v>29.9$ m/s, these roots have positive real parts; accordingly, the rectilinear motion is linearly unstable and the oscillations of the trailer increase in time.

Fig. 4

The effects of the stiffness a and the damping b of the wheel suspension on the linear stability. The dashed horizontal lines correspond to the realistic trailer setup of Table 1 providing the critical towing speed 29.9 m/s marked by red dots

In addition, one can also investigate the effect of different parameters on the linear stability. In Fig. 4, we construct linear stability charts in wide speed range for the stiffness k and damping c of the wheel suspension. We use these parameters because they can be varied independently from the other parameters of the trailer, and their effects are not considered in the in-plane models (like Model C). In the figure, the original setup is illustrated by dashed horizontal lines. Shaded areas correspond to linearly unstable rectilinear motion, where snaking, rocking, roll-over of the trailer may appear in practice; the white areas correspond to linearly stable rectilinear motion. The theoretical vibration frequency related to the stability boundary is not plotted in the figure, but it is in the range of $0.8-1.3$ Hz for our system parameters. These values have good agreement with the experimental results in [7].

As it can be observed in Fig. 4, the investigated parameters influence the value of the critical speed strongly. The stiffness k of the wheel suspension has a relevant role since small variation of the original value can significantly increase the critical speed. Thus, these stability charts may suggest suitable parameter values for the trailers and can support the engineering design process.

Fig. 5

The effects of the vertical a and the horizontal b positions of the center of gravity on the linear stability. The dashed horizontal lines correspond to the realistic trailer setup of Table 1

Road accidents involving trailers are often related to inappropriate values of the mass moment of inertia and/or the vertical position of the payload. Hence, in Fig. 5, stability charts are also constructed with respect to the vertical $h$ and longitudinal e positions of the center of gravity C. Note that the mass moments of inertia of the trailer may depend on these parameters, and to consider these effects we use the approximations $J_{\mathrm{C}x}=m (4 b^2 + 4 h^2)/6$, $J_{\mathrm{C}y}=m (l^2+ 4 h^2)/6$ and $J_{\mathrm{C}z}=m (l^2 + 4 b^2)/6$. These formulas are based on the mass and mass moment of inertia data given by Darling et al. [7], namely, $J_{\mathrm{C}z}$ provides the same value as their experimental setup and $J_{\mathrm{C}x}$ and $J_{\mathrm{C}y}$ are formulated using the same approach. As shown in Fig. 5a, the critical towing speed can be relevantly increased by increasing the height $h$. However, the critical speed drops again for high payload positions, what has good agreement with our physical sense. The effect of the longitudinal position e is illustrated in Fig. 5b. The plotted stability boundary suggests that the larger e is, the higher the critical speed is. Note that our model does not take into account that the so-called nose weight (the load on the towing hook) increases together with e, which may cause other stability issues. More detailed mechanical models of the car-caravan combination describe this phenomenon better and may give somewhat different results with respect to the effect of the longitudinal position e, see, e.g., [3, 7].

Table 1 Parameter values for the realistic trailer and the experimental rig

4 Bifurcation analysis

In practice, the linear stability analysis given in Sect. 3 does not provide enough information about the behavior of the trailer since the nonlinear vibrations often have a key role in the dynamics. In several cases, the presence of unstable limit cycles in linearly stable speed ranges may cause safety critical large amplitude vibrations when large perturbations occur. These limit cycles can relate to subcritical Hopf bifurcations emerging at the linear stability boundaries. In this section, first, the local bifurcation of the system is investigated by means of the center manifold reduction [6, 29], which is accomplished semi-analytically only due to the complexity of the system. Then, we perform numerical bifurcation analysis using continuation techniques in order to obtain information about the global dynamics of the trailer.

4.1 Local bifurcation analysis

Although the theory of the center manifold reduction [6, 29] is well known, it is rarely applied to higher dimensional systems. Due to the complexity of the method, even the sense of the Hopf bifurcation cannot be determined analytically for such systems, because at a certain point of the algorithm, one should evaluate the formulas numerically. The scenario is the same for our mechanical model, too. However, as we will show, essential information is provided by the center manifold reduction with respect to the nonlinear coupling between the vertical and the lateral motions of the trailer. Such information may never be obtained if numerical continuation is applied only.

Although the algorithm of the center manifold reduction is very conventional, we provide all the details of the calculation in order to emphasize the key steps where the above-mentioned nonlinear coupling emerges and can be identified.

For the local bifurcation analysis, we rewrite the equations of motion into a system of first order differential equations. To do this, let us introduce the vector of state variables

$$\begin{aligned} {\mathbf {z}}= \begin{bmatrix} {\mathbf {y}} \\ \dot{{\mathbf {y}}} \end{bmatrix} \,, \end{aligned}$$

(19)

where ${\mathbf {y}}$ is the perturbation around the rectilinear motion (cf. Eq. (10)). Based on this, the governing equations (7) can be rewritten and expanded in power-series form up to the third degree terms:

$$\begin{aligned} \varvec{\dot{\mathrm{z}}} = \mathbf {A} \mathbf {z} + \mathbf {F}_2+\mathbf {F}_3 \end{aligned}$$

(20)

where the coefficient matrix ${\mathbf {A}}$ reads

$$\begin{aligned} {\mathbf {A}}= \begin{bmatrix} {\mathbf {0}} &{} {\mathbf {I}} \\ -{{\mathbf {M}}_{\mathrm{lin}}}^{-1} {\mathbf {K}}_{\mathrm{lin}} &{} -{{\mathbf {M}}_{\mathrm{lin}}}^{-1} {\mathbf {C}}_{\mathrm{lin}} \end{bmatrix}\,. \end{aligned}$$

(21)

The vectors ${\mathbf {F}}_2$ and ${\mathbf {F}}_3$ contain the second and third degree terms, respectively. Since we are interested in the local bifurcation, the non-smooth characteristics of the suspension forces (4) do not appear in Eq. (20). But it is worth to mention that our system is asymmetric even in the linear domain due to the characteristics of the lateral tire forces (see Eq. (13)). The second degree terms (${\mathbf {F}}_2 \ne {\mathbf {0}}$) are also related to the tire forces, and they make coupling between the linearly independent lateral (described by $\psi$, $\varphi$ and u) and the vertical (described by $\vartheta$) motions of the trailer. For example, the first component of the vector ${\mathbf {F}}_2$ contains a term related to $\vartheta {\dot{\psi }}$.

By means of the center manifold reduction, our eight-dimensional system is reduced to a two-dimensional one [6]. First, the normal form of the governing equations is determined by transforming the equations of motion to the basis of the eigenvectors of the linear part. Let the eigenvalues and the eigenvectors of ${\mathbf {A}}$ be denoted by $\lambda _j$ and ${\mathbf {s}}_j$, respectively. Here, we investigate the case when six eigenvalues have nonzero imaginary parts and two real eigenvalues exist, which case holds for the parameter setup analyzed in this section. At the linear stability boundary, a complex conjugate pair of eigenvalues exists with zero real part (see the red dot corresponding to the linear stability boundary of the realistic trailer setup in Fig. 5):

$$\begin{aligned} \lambda _{1,2}= \pm \mathrm {i} \omega \,, \end{aligned}$$

(22)

while the other eigenvalues are

$$\begin{aligned} \lambda _{j}&= \sigma _{j} \,, \quad j=3,4 \,, \end{aligned}$$

(23)

$$\begin{aligned} \lambda _{j,j+1}&= \sigma _{j} \pm \mathrm{i} \omega _j\,, \quad j=5,7 \,, \end{aligned}$$

(24)

with $\sigma _j <0$ and $\omega _j>0$. Thus, the eigenvectors corresponding to the complex eigenvalues are:

$$\begin{aligned} {\mathbf {s}}_1 = \overline{{\mathbf {s}}}_2\,, \qquad {\mathbf {s}}_5 = \overline{{\mathbf {s}}}_6 \,, \qquad {\mathbf {s}}_7 = \overline{{\mathbf {s}}}_8\,, \end{aligned}$$

(25)

where the overline refers to the complex conjugate. Since the lateral and the vertical (pitch) motions are not coupled linearly through ${\mathbf {A}}$ (cf. Eqs. (11-13)), the eigenvectors corresponding to these linearly independent motions are perpendicular to each other. Let us denote $\lambda _{7,8}$ and ${\mathbf {s}}_7 = \overline{{\mathbf {s}}}_8$ to be the eigenvalues and the eigenvectors of the 1-DoF subsystem of the pitch motion, respectively. Namely, ${\mathbf {s}}_1 \cdot {\mathbf {s}}_7 = {\mathbf {s}}_3 \cdot {\mathbf {s}}_7 = {\mathbf {s}}_4 \cdot {\mathbf {s}}_7 = {\mathbf {s}}_5 \cdot {\mathbf {s}}_7 = 0$.

The columns of the transformation matrix can be composed by means of the eigenvectors (for more details, see [13]):

$$\begin{aligned} {\mathbf {T}} = \begin{bmatrix} {\mathrm{Re}} \, {\mathbf {s}}_1&{\mathrm{Im}} \, {\mathbf {s}}_1&{\mathbf {s}}_3&{\mathbf {s}}_4&{\mathrm{Re}} \, {\mathbf {s}}_5&{\mathrm{Im}} \, {\mathbf {s}}_5&{\mathrm{Re}} \, {\mathbf {s}}_7&{\mathrm{Im}} \, {\mathbf {s}}_7 \end{bmatrix}\,, \end{aligned}$$

(26)

which has the following structure due to the linear independence of the lateral and vertical motions:

$$\begin{aligned} {\mathbf {T}} = \begin{bmatrix} \square &{} \dots &{} \square &{} 0 &{} 0 \\ 0 &{} \dots &{} 0 &{} \square &{} \square \\ \square &{} \dots &{} \square &{} 0 &{} 0 \\ \square &{} \dots &{} \square &{} 0 &{} 0 \\ \square &{} \dots &{} \square &{} 0 &{} 0 \\ 0 &{} \dots &{} 0 &{} \square &{} \square \\ \square &{} \dots &{} \square &{} 0 &{} 0 \\ \square &{} \dots &{} \square &{} 0 &{} 0 \\ \end{bmatrix}\,. \end{aligned}$$

(27)

In the matrix, symbols $\square$ refer to nonzero elements. By means of this transformation matrix, we introduce the new variable ${\mathbf {x}}= [x_1 \, x_2 \, \ldots \, x_8]^{\mathrm{T}}$ as

$$\begin{aligned} {\mathbf {x}}={\mathbf {T}}^{-1} {\mathbf {z}}\,. \end{aligned}$$

(28)

Note that after the transformation, the new variables $x_7$ and $x_8$ still describe the pitch motion of the trailer. The system in the new basis can be formulated as:

$$\begin{aligned} \varvec{\dot{\mathrm{x}}} =\mathbf {T}^{-1} \mathbf {A} \mathbf {T} \mathbf {x} + \mathbf {T}^{-1} \left( \mathbf {F}_2(\mathbf {T} \mathbf {x}) + \mathbf {F}_3(\mathbf {T}\mathbf {x}) \right) , \end{aligned}$$

(29)

where ${\mathbf {T}}^{-1} {\mathbf {A}} {\mathbf {T}}$ is the so-called Jordan matrix, which enables the separation of (29) as:

$$\begin{aligned} \varvec{\dot{\mathrm{x}}}_\mathrm{c}&=\mathbf {B}\mathbf {x}_\mathrm{c} +\mathbf {f}(\mathbf {x}_\mathrm{c},\mathbf {x}_\mathrm{s}), \end{aligned}$$

(30)

$$\begin{aligned} \varvec{\dot{\mathrm{x}}}_\mathrm{s}&=\mathbf {C}\mathbf {x}_\mathrm{s} +\mathbf {g} (\mathbf {x}_\mathrm{c},\mathbf {x}_\mathrm{s})\,, \end{aligned}$$

(31)

where the subscript c refers to the so-called center manifold [6, 29] with the center variables, while s denotes the stable variables, which are in our case:

$$\begin{aligned} {\mathbf {x}}_{\mathrm{c}} = \begin{bmatrix} x_1&x_2 \end{bmatrix}^{\mathrm{T}} \quad \mathrm{and} \quad {\mathbf {x}}_{\mathrm{s}} = \begin{bmatrix} x_3&x_4&x_5&x_6&x_7&x_8 \end{bmatrix}^{\mathrm{T}}\,.\nonumber \\ \end{aligned}$$

(32)

In Eqs. (30) and (31), matrices ${\mathbf {B}}$ and ${\mathbf {C}}$ are

$$\begin{aligned} {\mathbf {B}}=\begin{bmatrix} 0 &{} \omega \\ -\omega &{} 0 \end{bmatrix}\,, \quad {\mathbf {C}} = \begin{bmatrix} \sigma _3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \sigma _4 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \sigma _5 &{} \omega _5 &{} 0 &{} 0 \\ 0 &{} 0 &{} -\omega _5 &{} \sigma _5 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \sigma _7 &{} \omega _7 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\omega _7 &{} \sigma _7 \end{bmatrix}\,,\nonumber \\ \end{aligned}$$

(33)

respectively. Vectors ${\mathbf {f}}$ and ${\mathbf {g}}$ contain second and third degree terms. Again, we notice that ${\mathbf {f}}$ have mixed second degree terms related to $x_7$, $x_8$ and the center variables $x_1$, $x_2$. Thus, terms like $x_1 x_7$, $x_1 x_8$, $x_2 x_7$ and $x_2 x_8$ with nonzero coefficients occur in ${\mathbf {f}}$. Later, we will show how the pitch motion affects the sense of the Hopf bifurcation through these mixed terms.

In order to eliminate the stable variable ${\mathbf {x}}_{\mathrm{s}}$ and to describe the dynamics of the system on the center manifold by means of the center variables ${\mathbf {x}}_{\mathrm{c}}$, the center manifold can be approximated as a purely quadratic surface:

$$\begin{aligned} {\mathbf {x}}_{\mathrm{s}} = {\mathbf {h}}({\mathbf {x}}_{\mathrm{c}}) = \begin{bmatrix} h_3(x_1^2, x_1 x_2, x_2^2) \\ \vdots \\ h_8(x_1^2, x_1 x_2, x_2^2) \end{bmatrix} \,, \end{aligned}$$

(34)

where $h_k = c_{k20} x_1^2 + c_{k11} x_1 x_2 + c_{k02} x_2^2$ for $k=3, \ldots , 8$ contains 18 unknown constant coefficients. We take the time derivative of Eq. (34):

$$\begin{aligned} \varvec{\dot{\mathrm{x}}}_\mathrm{s} =D_{\mathbf {x}_\mathrm{c}} \mathbf {h} (\mathbf {x}_\mathrm{c})\dot{\mathbf {x}}_\mathrm{c}, \end{aligned}$$

(35)

where $D_{{\mathbf {x}}_{\mathrm{c}}}$ refers to the partial derivative with respect to ${\mathbf {x}}_{\mathrm{c}}$. We substitute the expression of the quadratic surface of the center manifold in Eqs. (30) and (31); thus, we obtain the following set of equations:

$$\begin{aligned} \varvec{\dot{\mathrm{x}}}_\mathrm{c}&=\mathbf {B}\mathbf {x}_\mathrm{c} + \mathbf {f}(\mathbf {x}_\mathrm{c},\mathbf {h}(\mathbf {x}_\mathrm{c})), \end{aligned}$$

(36)

$$\begin{aligned} \varvec{\dot{\mathrm{x}}}_\mathrm{s}&=\mathbf {C}\mathbf {h} (\mathbf {x}_\mathrm{c})+ \mathbf {g}(\mathbf {x}_\mathrm{c}, \mathbf {h}(\mathbf {x}_\mathrm{c})) \,. \end{aligned}$$

(37)

Let us substitute Eq. (36) in (35):

$$\begin{aligned} \varvec{\dot{\mathrm{x}}} _\mathrm{s} = D_{\mathbf {x}_\mathrm{c}} \mathbf {h} (\mathbf {x}_\mathrm{c}) \left( \mathbf {B} \mathbf {x}_\mathrm{c} + \mathbf {f} (\mathbf {x}_\mathrm{c}, \mathbf {h} (\mathbf {x}_\mathrm{c})) \right) . \end{aligned}$$

(38)

We subtract Eq. (37) from Eq. (38):

$$\begin{aligned} \begin{aligned}&D_{{\mathbf {x}}_{\mathrm{c}}} {\mathbf {h}}({\mathbf {x}}_{\mathrm{c}}) \left( {\mathbf {B}} {\mathbf {x}}_{\mathrm{c}} + {\mathbf {f}}({\mathbf {x}}_{\mathrm{c}}, {\mathbf {h}}({\mathbf {x}}_{\mathrm{c}})) \right) +\\&\quad - {\mathbf {C}} {\mathbf {h}}({\mathbf {x}}_{\mathrm{c}}) - {\mathbf {g}}({\mathbf {x}}_{\mathrm{c}}, {\mathbf {h}}({\mathbf {x}}_{\mathrm{c}})) = {\mathbf {0}}\,, \end{aligned} \end{aligned}$$

(39)

from which the coefficients $c_{kij}$ can be calculated. Equation (39) consists of 6 scalar algebraic equations with 18 unknowns. Equating coefficients of the polynomials, one can solve this equation and can obtain that $h_3 = h_4 = h_5 = h_6 = 0$. However, $h_7$ and $h_8$ are not zeros; consequently, the variables $x_7$ and $x_8$ related to the pitch motion influence the local nonlinear dynamics on the center manifold. Namely, ${\mathbf {f}}$ in Eq. (30) provides third degree terms with respect to $x_1$ and $x_2$ when the $x_7 = h_7(x_1^2, x_1 x_2, x_2^2)$ and $x_8 = h_8(x_1^2, x_1 x_2, x_2^2)$ are substituted in the mixed second degree terms (e.g., $x_1 x_7$) mentioned above.

In our system, after substituting the calculated coefficients into Eq. (30), namely using the second degree approximation of the center manifold, the reduced order system is given by

$$\begin{aligned} \begin{bmatrix} {\dot{x}}_1 \\ {\dot{x}}_2 \end{bmatrix} = \begin{bmatrix} 0 &{} \omega \\ -\omega &{} 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+ \begin{bmatrix} \sum _{i+j={3}} a_{ij} x_1^i x_2^j \\ \sum _{i+j={3}} b_{ij} x_1^i x_2^j \end{bmatrix}\,. \end{aligned}$$

(40)

Thus, there are no second degree terms in the nonlinear part anymore, and the Poincaré–Lyapunov parameter can be calculated via the third degree terms only, see [30]:

$$\begin{aligned} \varDelta = \frac{1}{8}\left( 3 a_{30} + a_{12} + b_{21} + 3 b_{03}\right) \,. \end{aligned}$$

(41)

The sense of the bifurcation can be identified by investigating the sign of the Poincaré–Lyapunov parameter $\varDelta$. If $\varDelta$ is positive, then the corresponding Hopf bifurcation is subcritical and the emerging periodic solutions are unstable. If $\varDelta$ is negative, then the corresponding Hopf bifurcation is supercritical and the emerging periodic solutions are stable [30].

As mentioned before, due to the complexity of the governing equations and the large number of parameters of our mechanical model, no closed-form formula can be derived for the Poincaré–Lyapunov parameter. However, for a certain parameter setup, the sign of $\varDelta$, thus the sense of the Hopf bifurcation can be obtained semi-analytically. Here we consider our realistic trailer parameters given in Table 1 with the height $h=1$ m of the center of gravity. We apply the same approximation formulas for the mass moments of inertia like in Sect. 3 to assume the dependence of these parameters on the value of $h$. For this setup, the above detailed center manifold reduction is applied (see Appendix A for details) providing $\varDelta =6.475 \cdot 10^{-4} >0$, namely the Hopf bifurcation at the linear stability boundary is subcritical. This is the more dangerous case from engineering point of view, since an unstable periodic solution coexists with the stable rectilinear motion.

If the nonlinear effect of the pitch motion is neglected, i.e., the nonlinear coupling between the vertical (pitch) and the lateral motions is omitted by considering $h_7 = h_8 = 0$ (see Appendix B), then we obtain $\varDelta =-8.031 \cdot 10^{-4} <0$. Therefore, the Hopf bifurcation is supercritical, which suggests that using models neglecting pitch motion may not identify the presence of the more dangerous subcritical Hopf bifurcation case.

In Fig. 6, stability charts are constructed in the plane of the towing speed v and the height $h$ of the center of gravity. The subcritical and supercritical Hopf bifurcations are illustrated by dashed red and solid blue curves, respectively. The sense of the Hopf bifurcation is determined by means of numerical continuation, detailed later in the next subsection. Panel (a) corresponds to our spatial trailer model (Model A), while panel (b) is related to the simplified model (Model B) in which the pitch motion is blocked. As shown in Sect. 3, the linear stability boundaries coincide for both models. However, the sense of the Hopf bifurcation disagrees for certain parameter setups. In the figures, we marked the original $h=0.21$ m and the modified $h=1$ m trailer setups with dashed horizontal lines. For $h=1$ m, subcritical and supercritical bifurcations take place for Model A and Model B, respectively. Thus, the numerical continuation confirms the results of the semi-analytical bifurcation analysis.

In Fig. 6c, the stability chart of the in-plane model (Model C) is constructed, which does not describe the dependence of the critical towing speed on the vertical position of the center of gravity. By the way, this model provides supercritical Hopf bifurcation at a smaller critical speed, namely, $v=23.8$ m/s.

Fig. 6

Linear stability charts of the full spatial model a, the reduced model with blocked bounce/pitch motion b and the in-plane model c. Supercritical/subcritical Hopf bifurcations related to the stability boundaries are denoted with solid blue/dashed red lines, respectively

Fig. 7

Stability chart of the nonlinear system in the plane of the towing speed v and the vertical position $h$ of the center of gravity. Bifurcation diagrams are constructed in Fig. 8 for the parameters marked by dashed horizontal lines

4.2 Numerical bifurcation analysis

In order to validate the analytical calculations, numerical bifurcation analysis is performed with the help of DDE Biftool, see [10]. Namely, the Hopf bifurcations corresponding to the linear stability boundaries are located and the branches of the emerging periodic solutions are followed. As it was already shown in Fig. 6, the sense of the Hopf bifurcation is determined by this methodology.

Of course, numerical continuation is not limited to local bifurcation analysis, but it can also provide information about the large amplitude vibrations of the trailer. However, for this, one has to consider the non-smooth nature of the governing equations detailed in Sect. 2.2.

We approximate the Heaviside function by

$$\begin{aligned} {\tilde{H}}(s;\varepsilon ) = \frac{1}{2} \left( 1+\tanh \left( \frac{s}{\varepsilon } \right) \right) \,, \end{aligned}$$

(42)

where $\varepsilon$ is the so-called smoothing parameter. The smaller $\varepsilon$ is, the more sudden the switching is. Using this function, the H(s) and the $\mathrm {ReLU}(s)$ functions in Eq. (4) are formulated as: ${H}(s)={\tilde{H}}(s;\varepsilon _{d})$ and $\mathrm {ReLU}(s)={\tilde{H}}(s;\varepsilon _{F}) \cdot s$. The smoothing parameters $\varepsilon _{d}\,[\mathrm{m}]$ and $\varepsilon _{F}\,[\mathrm{N}]$ are related to the smoothings with respect to the suspension displacement d and the resulted suspension force $F_{\mathrm{s}}$. Thus, the originally non-smooth governing equations are approximated by their smoothed version during the continuation. In order to tend to the real scenario, the limit case $\varepsilon _{d} \rightarrow 0$ and $\varepsilon _{F} \rightarrow 0$ is investigated by choosing smaller and smaller $\varepsilon _{d}$ and $\varepsilon _{F}$ values as long as the numerical stability of the computation is ensured.

Accordingly, parameters $\varepsilon _{d}=10^{-3}$ m and $\varepsilon _{F}=10^{-3}$ N are used in our calculations, which leads to sudden changes within one time step of the detected periodic solutions related to the suspension forces (cf. Eq. (4)). We also take care how the number of mesh points and the degree of the interpolation function are selected in the collocation method. Namely, we increased the number of mesh points to 144, while linear interpolation was applied. This set of the parameters ensures an adequate convergence with acceptable computational time.

A nonlinear stability chart is constructed in Fig. 7, where the domains of different colors refer to different nonlinear properties of the trailer. In the white area, the rectilinear motion is globally stable. In the light and dark gray domains, the rectilinear motion is linearly unstable and a stable limit cycle takes place in the state space. We differentiate the limit cycles with respect to the minimum suspension forces (minimum vertical force on the tires) corresponding to them. In the dark gray zones, this minimum force is zero, namely the tires lose contact with the ground. The red unsafe zone refers to the parameter domain where the linearly stable rectilinear motion is not globally stable due to the presence of an unstable limit cycle. Namely, large enough perturbations may lead to large amplitude vibrations of the trailer. Such unsafe zones typically appear at subcritical Hopf bifurcations, but saddle-node bifurcations of periodic orbits can also provide such zones at supercritical Hopf bifurcations. This latter case also happens for our system parameters, see the figure.

Fig. 8

Bifurcation diagrams: supercritical case without unsafe zone a, supercritical case with unsafe zone b, subcritical case with unsafe zone c for low positions of the center of gravity; subcritical case with negligible unsafe zone d for a high position of the center of gravity. Dashed red curves correspond to unstable, solid blue curves relates to stable motions. Thick blue segments of the bifurcation branches of periodic orbits refer to motions with loss of contact of tires

To present more information about the nonlinear properties of the system, bifurcation diagrams related to dashed horizontal lines of Fig. 7 are plotted in Fig. 8. The amplitudes of the generalized coordinates $\psi$, $\vartheta$, $\varphi$ and u are plotted as functions of the towing speed v. Dashed red lines and solid blue lines refer to unstable and stable motions, respectively. Red dots denote the critical speeds where Hopf bifurcations take place. Black dots characterize the towing speed above which the loss of contact of the tires happen. This latter type of limit cycles is marked with thick blue lines. Based on the continuation, one can observe that symmetric solutions exist for the lateral motion ($\psi$, $\varphi$, u), while the pitch motion ($\vartheta$) is asymmetric. Thus, both the min/max values of the periodic solutions are illustrated for $\vartheta$.

Figure 8a shows the results of the original parameters of [7], providing supercritical Hopf bifurcation without unsafe zone. More precisely, saddle-node bifurcations of periodic orbits are within the linearly unstable speed range. At the first sharp folding point on the periodic bifurcation branch, the full compression of the wheel suspension appears leading to a qualitative change of the motion of the trailer thanks to the non-smooth nature of the suspension force.

In Fig. 8b, we present an example for the case where supercritical Hopf bifurcation and unsafe zone coexist. In Fig. 8c, a simpler structure of the limit cycles can be observed, namely subcritical Hopf bifurcation leads to the unsafe zone.

Figure 8d relates to the parameter setup for which we presented the results of the semi-analytical local bifurcation analysis. The sense of the Hopf bifurcation corresponding to the linear stability boundary is subcritical. As suggested by the small absolute value of the calculated Poincaré–Lyapunov parameter $\varDelta =6.475 \cdot 10^{-4}$, the numerical continuation provides a steeply rising branch of unstable periodic solutions. The saddle-node bifurcation of periodic solutions emerges resulting in a narrow bistable speed region, which is the reason why no red unsafe zone can be observed in Fig. 7 for the larger values of $h$. Although our spatial trailer model (Model A) shows subcritical Hopf bifurcation instead of the supercritical one (related to Model B), this phenomenon may not have any practical relevance.

As shown by the bifurcation diagrams presented here, the non-smooth characteristic of the suspension forces influences relevantly the nonlinear behavior of the system. The full compression/expansion of the wheel suspension and the loss of contact of tires occur for all investigated parameters. We will show more details about these scenarios in Sect. 5 with respect to our experiments.

5 Experiments

Fig. 9

The small-scale experimental setup

Based on the mechanical model described in Sect. 2, a small-scale experimental rig was designed and manufactured, see Fig. 9. The trailer is placed on a conveyor belt, whose speed can be tuned between 0 m/s and 5 m/s. The motion of the king pin is constrained in the towing direction by a roller bearing linear guide, while the king pin can move in the lateral direction against the spring and damper imitated by a rubber band in our experiment. In order to be able to compare the experimental results with the theoretical ones, the spring stiffness and the damping of the rubber band were measured. The position of the center of mass and the mass moment of inertia of the trailer can be tuned by the positioning of the dummy payloads. The caster length l can also be modified by shifting the wheel suspension along the longitudinal direction.

Fig. 10

The normalized tire force characteristic (black curve) $\mu (\alpha )$ plotted for positive side slip angle $\alpha$ (see Eq. (3)). Blue dots refer to the mean value of measurement data. The standard deviation of the measurement points is marked by blue bars

Fig. 11

Experimental results. The detected amplitude $u_{\mathrm{max}}$ a and frequency f b of the vibrations versus the towing speed v. Black crosses refer to measurement data, blue curves represent numerically determined stable solutions. Thick segments refer to motions with loss of contact of tires. Stability chart c for the damping c of the suspension; the dashed horizontal line corresponds to the experimental setup. Numerically determined min and max values of the suspension displacements d d and the suspension force $F_{\mathrm{s}}$ e

Fig. 12

Numerically determined time histories (solid lines) of generalized coordinates, suspension displacements d and suspension forces $F_{\mathrm{s}}$. Dashed black curves correspond to the measured lateral position of the king pin. Panels refer to the parameter points marked in Fig. 11c

Measurements were carried out to determine the tire force characteristics of the experimental rig. A pair of wheels were towed on the conveyor belt by a rigid caster. The side slip angle $\alpha$ was measured, while a constant lateral force was applied to the wheels. The measurement points normalized by the vertical load are shown in Fig. 10. The parameters B, C, D and E of the Magic Formula (3) were identified via the fitting of the formula to the measurement data.

Since the mass moment of inertia depends on the position of the payload, we fixed the parameters e and $h$ during the experiments, as well as the caster length l. Thus, we set different towing speed values for the conveyor belt and examined the linear stability and the nonlinear vibrations of the trailer. We measured the lateral displacement of the king pin with a laser sensor and collected and evaluated the data in Matlab.

Measurement data are compared to theoretical results in Fig. 11 for the parameter setup of the experimental rig (see Table 1). In panel (a) and (b), the measured amplitude $u_{\mathrm{max}}$ of the lateral displacement and the frequencies f of detected vibrations are plotted versus the towing speed v, respectively. Measurement points denoted by black crosses are compared to the results of the numerical continuation shown by blue curves. Relatively good agreement can be observed for the amplitudes; however, some shift occurs with respect to the linear stability boundary. In addition, there is somewhat larger difference between the predicted and the measured frequencies.

In Fig. 11c, a stability chart is constructed by numerical continuation for the experimental setup in the plane of the towing speed v and the damping c of the wheel suspension. As shown, there is a domain where the loss of contact of the tires occurs. The experimental setup is marked with a horizontal dashed line, for which the minimum and maximum values of suspension distance d (see Fig. 3) are also plotted in panel (d), highlighting that neither full compression nor full expansion of the suspension happen for this setup. The minimum and maximum values of the suspension force $F_{\mathrm{s}}$ are plotted in panel (e).

In Fig. 12, we present some numerical results for the parameter points $\mathrm{M}_1$, $\mathrm{M}_2$ and $\mathrm{P}$ of Fig. 11. We plot the periodic solutions for all four generalized coordinates ($\psi$, $\vartheta$, $\varphi$ and u) by solid blue lines for one period T of the oscillation. The suspension displacements d and suspension forces $F_{\mathrm{s}}$ are also illustrated with thin black and thick gray curves corresponding to the right and left wheels, respectively.

The measured time signals of the lateral displacement u at parameter points $\mathrm{M}_1$ and $\mathrm{M}_2$ (see Fig. 12a–b) are also plotted by dashed black curves. In order to compare the shapes of the theoretical and the measured periodic motions meanwhile we neglect the difference of the vibration frequencies (cf. Fig. 11b), we plot one period of the measured signal, too. A good agreement can be observed between the shapes of the measured and the theoretically calculated time histories. As mentioned before, a loss of contact happens for the parameter point $\mathrm{M}_2$, but the amplitude of the vibrations remains almost the same as for $\mathrm{M}_1$, no large amplitude, so-called rocking motion of the trailer occurs. This was also the case in the experiment, namely no gap between the wheels and the conveyor belt was visible. The wheel suspension was neither fully compressed nor fully expanded as suggested by the theoretical results, see the evolution of the suspension displacement in the figures.

Point $\mathrm{P}$ is in the parameter domain of Fig. 11 where full compression and full expansion of the wheel suspensions occur together with the loss of contact of the tires. The corresponding time signals are shown in Fig. 12c. In this case, the vibration amplitudes are significantly larger than in the former cases, namely a rocking motion may occur in practice.

6 Conclusions

In this study, we performed linear and nonlinear analyses of three possible mechanical models of trailers, see Fig. 1. The in-plane model, which is commonly used in vehicle dynamics, neglects the pitch and roll motions of the trailer, and it provides a smaller critical speed and supercritical Hopf bifurcation for the investigated parameter setup. Model B, the reduced model with blocked bounce/pitch motion, yields the same linear stability boundaries as the full spatial model (Model A). However, the linearly independent pitch motion affects the sense of the Hopf bifurcation at the linear stability boundary. The full spatial model provides subcritical Hopf bifurcation for higher center of gravity positions, but this does not lead to the occurrence of relevant unsafe parameter domains. Nevertheless, as the critical speed is crossed, large amplitude vibrations can suddenly appear, which means a relevant safety risk on roads that can be identified only by the use of the full spatial trailer model.

The different types of motions of the trailer were also explored by our study. Domains of loss of contact of tires were shown for the realistic trailer setup. An unsafe zone with practical relevance was detected at lower center of gravity positions, which significantly reduces the speed range, where the rectilinear motion is globally stable.

Laboratory experiments were used to validate the theoretical results. The numerically determined stable limit cycles were compared to the measured vibration amplitudes and frequencies, and a good qualitative agreement was established.

Appendices

Appendix A

By considering our realistic trailer parameters given in Table 1 with the height $h=1$ m of the center of gravity and applying the same approximation formulas for the mass moments of inertia like in Sect. 3, the coefficient matrix ${\mathbf {A}}$ of Eq. (21) reads

$$\begin{aligned} {\mathbf {A}}= \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ -\,19.112 &{} 0. &{} 0.730 &{} -\,16.242 &{} -2.501 &{} 0 &{} 0.232 &{} -\,0.298 \\ 0 &{} -\,58.114 &{} 0 &{} 0 &{} 0 &{} -\,1.860 &{} 0 &{} 0 \\ 256.153 &{} 0 &{} -\,48.087 &{} -\,10.764 &{} 33.517 &{} 0 &{} -\,4.650 &{} -\,9.527 \\ 429.268 &{} 0 &{} -\,54.702 &{} -\,81.817 &{} 56.169 &{} 0 &{} -\,6.753 &{} -\,19.740 \end{bmatrix} \,. \end{aligned}$$

(43)

Thus, the characteristic roots of the system are

$$\begin{aligned} \begin{aligned} \lambda _{1,2}&= \pm 8.732 \, \mathrm {i}\,, \\ \lambda _{3}&= -\,18.944 \,, \\ \lambda _{4}&= -\,7.328 \,, \\ \lambda _{5,6}&= -\,0.309 \pm 3.872 \, \mathrm {i}\,, \\ \lambda _{7,8}&= -\,0.930 \pm 7.566 \,\mathrm {i}\,, \end{aligned} \end{aligned}$$

(44)

while the eigenvectors are

$$\begin{aligned} {\mathbf {s}}_{1,2}= & {} \begin{bmatrix} 25.479 \pm 8.443 \, \mathrm {i} \\ 0 \\ 8.715 \mp 34.930 \, \mathrm {i}\\ 102.318 \mp 21.410 \, \mathrm {i}\\ -\,73.726 \pm 222.493 \, \mathrm {i}\\ 0 \\ 305.028 \pm 76.107 \, \mathrm {i} \\ 186.966 \pm 893.491 \, \mathrm {i} \end{bmatrix} \cdot 10^{-3} \,, \end{aligned}$$

(45)

$$\begin{aligned} {\mathbf {s}}_{3}= & {} \begin{bmatrix} -\,1.755\\ 0 \\ 26.363 \\ 45.614 \\ 33.252 \\ 0 \\ -\,499.419 \\ -\,864.116 \end{bmatrix} \cdot 10^{-3} \,, \end{aligned}$$

(46)

$$\begin{aligned} {\mathbf {s}}_{4}= & {} \begin{bmatrix} 27.781 \\ 0 \\ -\,84.489 \\ -\,101.830 \\ -\,203.593 \\ 0 \\ 619.173 \\ 746.254 \end{bmatrix} \cdot 10^{-3} \,, \end{aligned}$$

(47)

$$\begin{aligned} {\mathbf {s}}_{5,6}= & {} \begin{bmatrix} 22.409 \pm 22.567 \, \mathrm {i} \\ 0 \\ 170.580 \pm 179.038 \, \mathrm {i}\\ 2.519 \pm 1.683 \, \mathrm {i}\\ --\,.287 \pm 79.790 \, \mathrm {i}\\ 0 \\ -\,745.819 \pm 605.133 \, \mathrm {i} \\ -\,7.295 \pm 9.232 \, \mathrm {i} \end{bmatrix} \cdot 10^{-3} \,, \end{aligned}$$

(48)

$$\begin{aligned} {\mathbf {s}}_{7,8}= & {} \begin{bmatrix} 0\\ 121.110 \mp 47.422 \, \mathrm {i} \\ 0 \\ 0 \\ 0 \\ 246.237 \pm 960.443 \,\mathrm {i} \\ 0 \\ 0 \end{bmatrix} \cdot 10^{-3} \,. \end{aligned}$$

(49)

Equating the coefficients of Eq. (39), we obtain the quadratic surface for the center manifold as $h_3 = h_4 = h_5 = h_6 = 0$ and

$$\begin{aligned} \begin{aligned} h_7&= -18.619 \cdot 10^{-4} \, x_1^2 -27.855 \cdot 10^{-4} \, x_1 x_2 \\&\quad + 2.139 \cdot 10^{-4} \, x_2^2 \,, \end{aligned} \end{aligned}$$

(50)

$$\begin{aligned} \begin{aligned} h_8&= 11.691 \cdot 10^{-4} \, x_1^2 -55.094 \cdot 10^{-4} \, x_1 x_2 \\&\quad -7.466 \cdot 10^{-4} \, x_2^2 \,, \end{aligned} \end{aligned}$$

(51)

therefore, the coefficients of the third degree terms of the reduced system are

$$\begin{aligned} a_{30}&= 35.764 \cdot 10^{-4} \,, \end{aligned}$$

(52)

$$\begin{aligned} a_{12}&= -110.033 \cdot 10^{-4} \,, \end{aligned}$$

(53)

$$\begin{aligned} b_{21}&= -84.875 \cdot 10^{-4} \,, \end{aligned}$$

(54)

$$\begin{aligned} b_{03}&= 46.471 \cdot 10^{-4}\,. \end{aligned}$$

(55)

The value of the Poincaré–Lyapunov parameter is $\varDelta =6.475 \cdot 10^{-4} >0$, and the Hopf bifurcation at the linear stability boundary is subcritical.

Appendix B

If the nonlinear effect of the pitch motion is neglected, namely, the nonlinear coupling between vertical (pitch) and lateral motions is omitted, the quadratic surface of the center manifold simplifies to $h_3 = h_4 = h_5 = h_6 = h_7 = h_8 = 0$. In this case, the coefficients of the third degree terms of the reduced system are

$$\begin{aligned} a_{30}&= -29.733 \cdot 10^{-4} \,, \end{aligned}$$

(56)

$$\begin{aligned} a_{12}&= -121.558 \cdot 10^{-4} \,, \end{aligned}$$

(57)

$$\begin{aligned} b_{21}&= 22.911 \cdot 10^{-4} \,, \end{aligned}$$

(58)

$$\begin{aligned} b_{03}&= 41.200 \cdot 10^{-4} \,. \end{aligned}$$

(59)

The value of the Poincaré–Lyapunov parameter is $\varDelta =-8.031 \cdot 10^{-4} <0$, and the Hopf bifurcation at the linear stability boundary is supercritical.