Abstract
A unique feature of flexible cantilevered beams, which is used in a range of applications from energy harvesting to bio-inspired actuation, is their capability to undergo motions of extremely large amplitudes. The well-known third-order nonlinear cantilever model is not capable of capturing such a behaviour, hence requiring the application of geometrically exact models. This study, for the first time, presents a thorough experimental investigation on nonlinear dynamics of a cantilever under base excitation in order to capture extremely large oscillations to validate a geometrically exact model based on the centreline rotation. To this end, a state-of-the-art in vacuo base excitation experimental set-up is utilised to excite the cantilever in the primary resonance region and drive it to extremely large amplitudes, and a high-speed camera is used to capture the motion. A robust image processing code is developed to extract the deformed state of the cantilever at each frame as well as the tip displacements and rotation. For the theoretical part, a geometrically exact model is developed based on the Euler–Bernoulli beam theory and inextensibility condition, while using Kelvin–Voigt material damping. To ensure accurate predictions, the equation of motion is derived for the centreline rotation and all terms are kept geometrically exact throughout the derivation and discretisation procedures. Thorough comparisons are conducted between experimental and theoretical results in the form of frequency response diagrams, time histories, motion snapshots, and motion videos. It is shown that the predictions of the geometrically exact model are in excellent agreement with the experimental results at both relatively large and extremely large oscillation amplitudes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cantilevered structural elements are present in a wide range of mechanical systems and civil structures [6, 9, 17, 19, 33, 56]. They can be found in numerous engineering applications including, but not limited to, vibration energy harvesters, micro-gyroscopes, electromechanical systems, bio-inspired propulsion, and piezoelectric sensors and actuators [1, 7, 24, 31, 40, 43, 55, 59]. The key feature that differentiates cantilevers from other structures/elements that are supported from more than one side is their capability of undergoing large-amplitude deflections/oscillations. Such a behaviour makes cantilevers very suitable for applications where large-amplitude oscillations are desirable such as in-flow energy harvesters using inverted flag configurations [22, 28, 37]. Analysing the large-amplitude behaviour of cantilevers, however, is a difficult task, not only due to the presence of different sources of nonlinearity, but also the fact that a cantilever oscillation amplitude could grow extremely large, rendering the commonly used third-order nonlinear model insufficient and requiring more accurate models capable of predicting such behaviour.
Many investigators have examined the dynamical characteristics of cantilevers over the last few decades. An early investigation on this topic was carried out by Crespo da Silva and Glynn [45, 46], who derived the analytical equations of motion of a cantilever undergoing in-plane and out-of-plane motions using inextensibility assumption and retaining nonlinearities up to third order; they examined the dynamics of the cantilever via use of the method of multiple scales. Further investigations were conducted by Nayfeh and Pai [34, 38], who studied the planar lateral vibration of cantilevers under base excitations; they derived the third-order nonlinear equation of motion of the cantilever while assuming an inextensible centreline and examined the dynamical response of the system using the method of multiple scales. Nayfeh and co-investigators [3] continued the investigation by examining the nonlinear nonplanar dynamics of cantilevers under parametric excitation. Further investigations were conducted by Hsieh et al. [18], who employed an invariant manifold method to obtain the nonlinear vibration modes for examining relatively large-amplitude response of a cantilever, Feng and Leal [14], who examined the symmetries in inextensible cantilevered beam equations, and Oh and Nayfeh [36], who analysed the combination resonances in cantilevered composite plates.
Dwivedy and Kar [11] continued the investigations by examining the nonlinear dynamics of a slender cantilevered beam carrying a tip mass under base excitation in the presence of internal resonances. Zhang et al. [58] examined the chaotic dynamics and bifurcations for the nonlinear vibrations of a cantilever under harmonic axial and transverse excitations; they utilised the method of multiple scales together with the Galerkin technique to study the response of the system. Yoo et al. [57] conducted experiments to examine the relatively large-amplitude oscillations of a cantilever to demonstrate the validity of the absolute nodal coordinate formulation method in analysing the nonlinear dynamics of cantilevers. Mahmoodi et al. [27] conducted a theoretical-experimental investigation on relatively large-amplitude nonlinear vibration of cantilever viscoelastic beams; they employed the method of multiple scales to obtain the frequency response of the system and verified the theoretical findings with experimental observations. McHugh and Dowell [29] developed a computational model to examine the relatively large-amplitude nonlinear motion of an inextensible cantilevered and free-free beam; they utilised the Rayleigh–Ritz method together with Lagrange’s equations to derive the discretised equations of motion of the system and employed a fourth-order Runge–Kutta time integration solver to analyse the system response. Thomas et al. [49] studied the nonlinear behaviour of a rotating cantilever beam using a third-order nonlinear model; they utilised a continuation method to construct the frequency response curves and examined the softening/hardening nonlinear behaviour of the cantilever. Furthermore, Touzé and Thomas [51] examined the large-amplitude oscillations of a cantilevered beam utilising a third-order nonlinear model; they utilised the method of nonlinear normal modes [50, 52, 53] to obtain the reduced-order model and examined the dynamics using a time integration method. The investigations were continued by Colin et al. [8], who conducted an experimental/numerical study of structures undergoing very-large-amplitude oscillations and proposed a quadratic air damping model. In a recent study, Shen et al. [44] presented a thorough comparison of model-order reduction techniques for geometrically nonlinear structures using different finite element procedures.
Truncated cantilever beam models have been utilised in many other studies for examining the behaviour of vibration energy harvesters, piezoelectrically actuated systems, and sensors [15, 20, 23, 25, 26, 39, 54]. Further investigation was conducted by Meesala and Hajj [30], who examined the response sensitivity of a parametrically excited cantilevered beam with a proof mass to small variations in stiffness and mass. Farokhi et al. [12, 13] continued the investigations by developing a dynamical version of the rotation-based geometrically exact nonlinear cantilever model, which was originally used for static buckling of an elastic continuum [4], capable of examining vibrations of extreme amplitudes. The rotation-based inextensible exact cantilever model has also been used in the context of fluid–structure interaction of inverted flags by Tavallaeinejad et al. [47, 48].
It should be noted that there have been many studies on the so-called geometrically exact beam model; however, the proposed model in this study is different in the way it sets up the equation of motion since it uses the beam rotation as the main motion variable and utilises inextensibility to relate beam displacements to rotation. The reader is referred to the book by Géradin and Cardona [16] and the studies by Meier et al. [32] and Zupan et al. [60] for general overviews of geometrically exact models and details of their finite-element discretisations. Furthermore, Lang et al. [21] proposed a viscoelastic rod model based on Cosserat’s geometrically exact theory of rods [2], which is capable of analysing extension, shearing, bending, and torsion. In an interesting study, Bergou et al. [5] proposed the method of discrete elastic rods, which was initially developed for use in computer graphics for simulating hair motion; however, their approach was different for both kinematics and dynamics treatment, and they validated their proposed discrete rod model via comparison to experiments. Romero et al. [41] continued the investigations and proposed a new framework to assess the physical validity of computer graphics numerical simulators for rods, plates, and frictional contact. It should be noted that all these valuable studies utilise time integrations to solve the spatially discretised equations of motions.
To the knowledge of the authors, there has been no attempt to date to experimentally investigate the extremely large oscillations of a base-excited cantilever and compare that against theoretical predictions. The present study, for the first time, reports detailed experimental results on extreme vibrations of a cantilever and utilises those results to validate a geometrically exact model based on the centreline rotation. It is shown that the geometrically exact model predictions are very close to the experimental observations even for the case when the cantilever undergoes oscillations of extremely large amplitude. Additionally, a detailed comparison is conducted between the predictions of the geometrically exact model and those of the third-order nonlinear model to show the range of amplitudes that the third-order model can be used reliably.
2 Geometrically exact model development
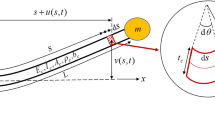
The geometrically exact model for a homogeneous cantilevered beam is developed in this section utilising the Euler–Bernoulli beam theory together with Kelvin–Voigt material damping; furthermore, the cantilever centreline is assumed to be inextensible. To this end, a cantilevered beam is considered, which is of length L, cross-sectional area A, second moment of area I, Young’s modulus E, mass per unit length m, and material damping coefficient \(\eta \). The (x; y) coordinate system is shown in Fig. 1, which is associated with the undeformed geometry of the cantilever. s is the curvilinear coordinate denoting the distance of an element on the beam from the clamped end. The cantilevered beam is in a vertical configuration, with the clamped end being at the bottom (as shown in Fig. 1), and the base is under harmonic excitation in the form of \(z_0 \sin (\omega _z t)\). The gravity is included in the model, and the acceleration due to gravity (i.e. g) is acting downward as shown in Fig. 1.
In what follows, the Euler–Bernoulli beam theory is utilised to derive the exact equation governing the rotational motion of the beam centreline while taking advantage of the centreline inextensibility assumption. The key advantage of the centreline rotation equation of motion over the transverse displacement equation of motion is that the former allows examining extremely large oscillations, while the latter loses accuracy at large oscillation magnitudes (as examined in detail in Sect. 5). It should be noted that the derivation procedure in this study follows the works of Nayfeh and co-investigators (e.g. Ref. [35]) in relating the strain to displacements and rotation; hence, an engineering strain measure is utilised together with a stress measure that is a consequence of the constitutive laws (for more details, refer to Ref. [49]).
The general expressions for the relationship between the centreline rotation and displacements are given by [35]:
where e represents the centreline strain and \(\partial _s \equiv \partial /\partial s\). It should be noted that even at very-large-motion amplitudes, the centreline strain remains small which allows the application of the centreline inextensibility assumption, i.e. \(e=0\), which relates both longitudinal and transverse displacements (denoted by u and w, respectively) to the centreline slope \(\psi \). Hence, the cantilevered beam displacements, with respect to the base, can be obtained in terms of the centreline rotation as
Taking into account the rotational inertia and the harmonic motion of the base, the kinetic energy can be formulated as:
in which \(J=\rho I\) with \(\rho \) being the mass density.
As mentioned before, in this study, the Kelvin–Voigt model is used to account for the damping in the system. Noting that the axial strain of the cantilevered beam centreline can be formulated in terms of the centreline rotation as \(\varepsilon _{xx}=-z\partial _s \psi (s,t)\), the stress–strain relationship based on the Kelvin–Voigt model can be formulated as:
Denoting the variational operator by \(\delta \), the expressions for the variation of the potential strain energy of the cantilevered beam can be formulated as:
The variation of the gravitational potential energy is given by:
which, using an integral identity equation [42], can be further simplified to
Finally, the virtual work of the viscous stress component can be expressed as:
Inserting Eqs. (3), (5), (7), and (8) into the extended Hamilton’s principle
one can obtain the geometrically exact equation governing the rotational motion of the centreline of the cantilevered beam as
Next, the following dimensionless quantities are defined:
where \(T=L^2\left( m/(EI) \right) ^{1/2}\). Inserting these quantities into Eq. (10) yields the following dimensionless geometrically exact equation governing the rotational motion of the cantilevered beam
To numerically solve the geometrically exact nonlinear integro-partial differential equation governing the cantilever centreline rotational motion (i.e. Eq. (12)), it needs to be first discretised into a set of nonlinear ordinary differential equations (ODEs). To this end, a suitable basis function is utilised to define the slope \(\psi \) as the following series expansion:
in which \(q_k(\tau )\) represents the unknown time-dependent generalised coordinate for the centreline slope and \(\Xi _k(\varsigma )\) denotes its corresponding basis function defined as \(\partial _{\varsigma }\Phi _k(\varsigma )/\beta _k\), with \(\Phi _k(\varsigma )\) being the kth eigenfunction for the transverse oscillation of a linear cantilevered beam and \(\beta _k\) being the kth root of its transcendental equation.
Substituting Eq. (13) into Eq. (12) and applying the Galerkin technique lead to the following set of N nonlinear second-order ODEs:
In this study, N is set to 6, resulting in a 6-degree-of-freedom (dof) discretised model, which ensures converged results (refer to Sect. 7 for a convergence analysis). The 6-dof second-order discretised model is transformed into a set of first-order ODEs via a change of variables; a pseudo-arclength continuation technique [10] is then utilised to examine the nonlinear primary resonance response of the system.
One of the main challenges associated with discretising Eq. (12) is that, being a geometrically exact model, the spatial integrations, unlike the case of a truncated nonlinear model, cannot be carried out in a closed form and need to be conducted numerically while ensuring that sufficient terms are retained for convergence. This process results in a very large set of discretised equations, but ensures accurate predictions even at extremely large amplitudes of oscillation. Furthermore, the key advantage of obtaining the equation of motion for the centreline rotation is that it allows capturing extremely large oscillations that are not possible to predict using truncated nonlinear models, as shown in Sect. 5. It should be noted that once the discretised set is solved numerically and the rotational generalised coordinates are obtained, the centreline displacements are calculated using Eq. (1).
3 In vacuo base excitation experimental set-up
Figure 2 shows the experimental set-up used in this study to excite the cantilever in the primary resonance region and to capture oscillations of extremely large amplitude. To achieve very-large-oscillation amplitudes without causing plastic deformation, a thin 1095 blue-tempered spring steel cantilever, with material properties and geometric parameters listed in Table 1, was selected. Additionally, the cantilever was placed in a vacuum chamber to minimise the air damping and enable very-large-oscillation amplitudes. More specifically, the spring steel cantilever was clamped upright inside a vacuum chamber mounted on the armature of an APS-113 long stroke shaker as shown in Fig. 2. The shaker was driven by an APS-125 amplifier and controlled by a SPEKTRA VCS-201 for the purpose of achieving harmonic base excitation at specified frequencies and acceleration amplitudes with feedback control (for constant base acceleration sweep). The base acceleration was measured by an accelerometer mounted on the clamp, and the signal was fed back to a VCS-201 controller. The vacuum chamber was realised by using a JB vacuum pump. The pressure was continuously measured by a pressure sensor at the base of the chamber and kept around 9% atmospheric pressure during the experiments.
A Polytec OFV-505 laser Doppler vibrometer (LDV) measured the velocity close to the middle point along the beam (39 mm from the clamped end). The LDV measurement was mainly used for obtaining the natural frequency of the cantilever. It should be noted that due to large oscillations of the cantilever, LDV cannot be used for high-fidelity measurements for model comparison. Instead, a high-speed camera system (Phantom FASTCAM Mini AX200 900K) was used to capture the side view of vibration response of the entire cantilever at various frequencies and different acceleration levels. Then, a robust image processing code was developed to analyse each frame and to extract the deformed beam shape, from which the tip longitudinal and transverse displacements as well as the tip rotation were obtained (see Fig. 3). Using this method, oscillations of extremely large amplitude can be analysed accurately, as explained in more detail in the following section.
4 Comparison between theoretical and experimental results
In this section, extensive comparisons are made between the experimental results and the theoretical predictions based on the geometrically exact model. It should be noted that both theoretical and experimental results are presented in the nondimensional form.
Two sets of experiments are conducted at base excitation magnitudes of 0.2g and 0.5g RMS (root mean square), with g denoting the gravitational acceleration. For each base acceleration level, the oscillation of the cantilever is recorded at 34 frequencies in the primary resonance region, in the range of 8–11 Hz. The videos are captured at 1600 frames per second; each video is then analysed frame by frame to extract the deformed shape and the tip displacements and rotation (as shown in Fig. 3), allowing for construction of the frequency response of the cantilever. A robust image processing code is developed in MATLAB to extract the deformed shape of the cantilever and then its tip displacements. More specifically, for the image processing, an edge detection algorithm is used in MATLAB.Footnote 1 After extracting the edges of the beam in a deformed configuration, different post-processings are applied to remove the clamped base, remove the motion of the base, and convert the edge into a line, representing the deformed configuration. The accuracy of the method is examined in more detail in Fig. 9.
Figure 4 shows the comparison between the experimental and theoretical frequency responses of the cantilever for transverse and longitudinal motions at 0.2g RMS acceleration level, which is equivalent to \(a_z=0.1211\). \(w_d\) and \(u_d\) represent the dimensionless transverse and longitudinal displacements, which are related to their dimensional counterparts (i.e. w and u, respectively) via \(w_d=w/L\) and \(u_d=u/L\). The rest of the system parameters are set to \(\gamma =0.4280\) and \(\chi =7.28\)e\(-8\), based on the material properties and geometric parameters given in Table 1. Finally, the nondimensional material damping \(\eta _d\) is set to 0.0037, which results in a theoretical peak amplitude almost the same as the experimental one. It should be noted that the damping parameter is calibrated once based on the experimental frequency response at 0.2g RMS and then is kept intact for the case of 0.5g RMS to examine how well the Kelvin–Voigt damping model works for the case with increased oscillation amplitudes.
The comparison in Fig. 4 shows that the geometrically exact model does a very good job of predicting the primary resonance response of the cantilever at 0.2g RMS base acceleration level. In particular, the exact model predicts almost the same transverse and longitudinal displacement amplitudes at oscillations near the peak, but deviates slightly from the experiment at other frequencies. It is seen that the cantilever displays a weak nonlinear hardening behaviour at this excitation level.
Figures 5 and 6 are constructed to provide a more detailed comparison between the theoretical and experimental predictions at the peak oscillation amplitude. Figure 5 shows the motion of the cantilever in one period of oscillation obtained via the exact model (solid lines) and experiment (circles). The figure shows excellent agreement between the experimental observations and the geometrically exact model predictions. Figure 6 shows the time histories of the tip displacements and tip rotation in one period of oscillation, for the system of Fig. 5. To extract the tip rotation from the experimental data, the coordinates of the last 5% of the length of the cantilever (near the tip) were extracted, a straight line was fitted to those points, and the slope of that line was calculated, resulting in the tip rotation curve. In all sub-figures, \(t_n\) denotes the time normalised with respect to the period of oscillation. The figure shows an excellent agreement between experimental and theoretical results for tip transverse and longitudinal displacements as well as tip rotation.
Next, in order to examine oscillations of extremely large amplitudes, the base acceleration is increased to 0.5g RMS. Similar to the previous case, the cantilevered beam motion is recorded at 34 frequencies in the range of 8–11 Hz, and the detailed dynamical response of the cantilever is extracted via comprehensive image processing of each video. The theoretical and experimental frequency responses of the cantilever at base acceleration of 0.5g RMS (i.e. \(a_z=0.3027\)) are illustrated in Fig. 7, showing the transverse and longitudinal displacements in sub-figures (a) and (b), respectively. The material damping coefficient \(\eta _d\) is kept at 0.0037 (as in the previous excitation level) to examine whether the Kelvin–Voigt damping works well at different base acceleration magnitudes without readjusting and recalibration. As shown in Fig. 7, the geometrically exact model works very well even at this extreme oscillation amplitude and predicts amplitudes very close to the experimental results. As shown in the figure, the hardening behaviour is more pronounced for this case. Additionally, it is worth noting that at extremely large oscillations like the case of Fig. 7, the transverse displacement does not increase much with increasing base excitation magnitude. This is due to the fact that the cantilever bends backwards (flapping motion) at this excitation level, and by increasing the excitation magnitude, only the tip rotation and longitudinal displacement increase, while the maximum transverse oscillation amplitude does not change much. This is explained further later in Fig. 10. It should be mentioned that for the vertical configuration studied here, taking into account the effect of gravity slightly reduces the natural frequency and slightly increases the hardening behaviour.
Motion of the cantilever of Fig. 4 at peak amplitude in one period of oscillation. Circles: experimental results. Solid line: geometrically exact model predictions. For a video comparison, refer to the electronic supplementary materials in the online version of the article
Time histories of the cantilever tip displacements and rotation for the system of Fig. 5 in one period of oscillation. a Tip transverse displacement, b tip longitudinal displacement, and c tip rotation. Circles: experimental results. Solid line: geometrically exact model predictions
To conduct a more detailed comparison between theoretical and experimental results, the oscillation of the cantilever at its peak resonance amplitude in one period of oscillation is constructed in Fig. 8. It is observed that the geometrically exact model does an excellent job at capturing the extreme vibrations of the cantilever, as confirmed by the experimental observation. The figure shows that the exact model slightly overestimates the tip rotation at the two ends, but it should be mentioned that the damping coefficient was kept unchanged, which shows the capabilities of the Kelvin–Voigt damping model in adjusting its effect at large oscillation magnitudes when calibrated once for relatively small base excitation magnitudes. It should be noted that although the Kelvin–Voigt damping model appears as a linear term in the centreline rotation equation of motion, it has a nonlinear relationship with transverse and longitudinal displacements. Hence, it increases nonlinearly as the transverse and longitudinal displacements are increased, and it works well with the same coefficient at various excitation magnitudes. Of course, the damping coefficient can be adjusted slightly here so that the theoretical predictions better match the experimental ones. However, this comparison shows that the proposed model is very robust and once the damping coefficient is calibrated at one excitation level, it does not need to be changed at other excitation magnitudes (as a result of eliminating other damping mechanisms, such as fluid damping, in the carefully conducted in vacuo experiments).
To better show the robustness of the developed image processing code and the capability of the geometrically exact model in capturing the deformed states of the cantilever, Fig. 9 is constructed, showing the experimental and theoretical snapshots of the cantilever oscillation in one period (corresponding to the case of Fig. 8). More specifically, the left column of Fig. 9 shows snapshots of the experimental results and the extracted deformed state via image processing (red circles). As can be seen, the developed image processing code is very robust and capable of extracting the deformed shape of the cantilever from the experimental results accurately. The right column of Fig. 9 shows the comparison between the extracted results from experiments (red circles) and the results obtained via the geometrically exact model (solid line). It is observed that the geometrically exact model captures the experimental deformed shapes of the cantilever very well.
Motion of the cantilever of Fig. 7 at peak amplitude in one period of oscillation. Circles: experimental results. Solid line: geometrically exact model predictions. For a video comparison, refer to the electronic supplementary materials in the online version of the article
The time histories of the tip displacements and rotation at peak resonance amplitude (corresponding to the case of Fig. 8) are shown in Fig. 10 in one period of oscillation. One interesting aspect of the extreme oscillation shown in Fig. 8 is that the oscillation grows so large that the cantilever tip bends backwards. As a result of this, the occurrence of the maximum transverse displacement does not coincide with that of the maximum tip rotation. This is shown clearly in Fig. 10; sub-figure (a) shows that the transverse displacement magnitude increases until reaching a maximum and then decreases until reaching a local minimum. This local minimum corresponds to the maximum tip rotation magnitude, i.e. the two extreme ends in Fig. 8. This behaviour appears only when the oscillation amplitude is large enough so that the cantilever tip bends backwards. A comparison between the theoretical and experimental results shows a very good agreement between the predictions of the exact model and the experimental observations. It is seen that the exact model slightly overestimates the tip rotation, which translates to a slight overestimation of the longitudinal displacement and a slightly sharper reduction in transverse motion amplitude at peak tip rotation.
Finally, for a visual comparison between theoretical and experimental results, two videos are provided as supplementary materials, showing the experimental and theoretical oscillations of the cantilever in one period of oscillation at peak amplitude for the two base acceleration cases examined in this study. (The reader is referred to the online version of the article for access to the multimedia contents.) The video comparisons clearly show the high accuracy of the geometrically exact model in reproducing the experimental results. In conclusion, the thorough comparisons conducted in this section fully verifies the accuracy and reliability of the centreline-rotation-based geometrically exact model of the cantilever for analysing oscillations of any magnitude.
Experimental and theoretical snapshots of the oscillation of the cantilever of Fig. 7 at peak amplitude. The sub-figures in left column a show snapshots of the experimental results and the extracted result via the image processing (red circles). The sub-figures in the right column b show a comparison between the extracted experimental results (red circles) and the results obtained via the geometrically exact model (solid line)

Time histories of the cantilever tip displacements and rotation for the system of Fig. 8 in one period of oscillation. a Tip transverse displacement, b tip longitudinal displacement, and c tip rotation. Circles: experimental results. Solid line: geometrically exact model predictions
Comparison between the geometrically exact cantilever model and the truncated third-order nonlinear model. Maximum transverse motion amplitude at a \(a_z=0.025\), b \(a_z=0.10\), c \(a_z=0.20\), and d \(a_z=0.40\). Dotted line: third-order nonlinear model; solid and dashed lines: geometrically exact model
5 Significance of the geometrically exact model
In order to further highlight the significance of the geometrically exact model, the primary resonance responses of a cantilever under various base excitation magnitudes are obtained via the exact model and compared to those obtained via the well-known third-order nonlinear inextensible cantilever model [35, 45]. In particular, the dimensionless equation of motion for the third-order nonlinear model can be obtained as:
in which a Kelvin–Voigt damping is utilised (to be consistent with the proposed exact model), and both geometric and inertial nonlinearities are taken into account. Equation (15) is discretised utilising the Galerkin technique, following a similar procedure as in Sect. 2, i.e. by defining \(w_d=\sum _{k=1}^{N}\Phi _k(\varsigma ) p_k(\tau )\) with \(\Phi _k(\varsigma )\) being the kth eigenfunction for the transverse motion of a cantilevered beam and \(p_k\) being the kth generalised coordinate. Similar to the case of the geometrically exact model, six modes are retained in the Galerkin discretisation resulting in a 6-dof system, which ensures converged results.
The comparison between the primary resonance response predictions of the two models is shown in Fig. 11. To better highlight the differences between the two models, the frequency responses are obtained for four dimensionless base acceleration amplitudes, i.e. \(a_z=0.025\), 0.10, 0.20, and 0.40; the rest of the system parameters are set to those of the system of Fig. 4. Sub-figure (a) shows that at relatively small base acceleration magnitude of 0.025, both models predict the same resonance response and amplitudes. By increasing the dimensionless base acceleration to 0.10 (as shown in sub-figure (b)), slight differences appear between the result obtained by the third-order model and that obtained via the exact model. More specifically, the third-order model predicts larger oscillation amplitudes and is unable to capture the nonlinear hardening behaviour of the cantilever (which does exist, as verified via experimental results). The difference between the two models is exacerbated at larger base acceleration magnitudes, as shown in Figs. 11(c) and (d). It is seen in Fig. 11(c) (corresponding to \(a_z=0.20\)) that the third-order model predicts transverse oscillation amplitudes larger than 1.0 (i.e. larger than the length of the cantilever from a dimensional perspective) which is impossible. The peak amplitude predicted by the geometrically exact model, on the other hand, increases only slightly as the base acceleration is increased, since at relatively large base accelerations, the cantilever bends backwards and a further increase in the base acceleration has almost no effect on the peak transverse motion amplitude. This comparison further highlights the limitations of the third-order nonlinear model and the significance of the geometrically exact model in capturing large-amplitude oscillations.
6 Concluding remarks
In this study, the nonlinear dynamics of a cantilever undergoing extreme motions was examined experimentally and theoretically. The cantilever was base excited in the primary resonance region using an in vacuo experimental set-up to minimise the air damping and to drive the cantilever to motions of extremely large amplitudes. A high-speed camera was used to capture the motion, from which snapshots of deformed shapes and displacements were extracted using an image processing code. A geometrically exact model based on the centreline rotation was developed for the theoretical part. The exact model was discretised using the Galerkin method while retaining six modes, and the resultant equations were solved through use of a continuation technique. Extensive comparisons were then conducted between experimental and theoretical results.
Two sets of experiments were conducted at base acceleration magnitudes of 0.2g and 0.5g (RMS). The comparison between theoretical and experimental results at 0.2g base acceleration level showed that the geometrically exact model predicts oscillation amplitudes, which are very close to the experimental data. Comparing the experimental and theoretical motion of the cantilever in one period of oscillation showed an excellent agreement between the exact model predictions and the experimental results.
For the second sets of comparisons, the base acceleration magnitude was increased to 0.5g to capture extremely large oscillation amplitudes. For this case, the material damping coefficient was kept the same as the previous case to examine how well the Kelvin–Voigt damping works when the base acceleration is increased. The comparison in this case also showed a very good agreement between experimental observations and theoretical predictions. It was shown that the geometrically exact model is fully capable of capturing extreme motions even when the oscillation grows so large that the tip of the cantilever bends backwards. It was shown that even though the same damping coefficient was used for both cases, the exact model was able to capture peak amplitudes very close to those obtained experimentally for both cases.
Convergence analysis of the primary resonance response of the cantilever at \(a_z=0.40\), showing the frequency responses for a tip rotation, b tip transverse displacement, and c tip longitudinal displacement, obtained via several discretised models of the geometrically exact model.  Stable periodic solution,
Stable periodic solution,  unstable periodic solution
unstable periodic solution
Finally, a comparison between the geometrically exact model and third-order truncated model showed that the latter works reliably only for relatively small base acceleration magnitudes. It was shown that the third-order model cannot capture the hardening nonlinearity and leads to wrong results at relatively large base accelerations.
Data availability statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request. The video comparisons of experimental and theoretical results for two cases are provided as supplementary materials.
References
Alben, S., Madden, P.G., Lauder, G.V.: The mechanics of active fin-shape control in ray-finned fishes. J. Royal Soc. Interface 4(13), 243–256 (2007)
Antman, S.: Dynamical problems for geometrically exact theories of nonlinearly viscoelastic rods. Mech. Theory Comput. pp. 1–18 (2000)
Arafat, H.N., Nayfeh, A.H., Chin, C.M.: Nonlinear nonplanar dynamics of parametrically excited cantilever beams. Nonlinear Dyn. 15(1), 31–61 (1998)
Bažant, Z.J., Cedolin, L.: Stability of Structures: Elastic, Inelastic, Fracture and Damage Theories. World Scientific, Singapore (2010)
Bergou, M., Wardetzky, M., Robinson, S., Audoly, B., Grinspun, E.: Discrete elastic rods. In: ACM SIGGRAPH 2008 papers, pp. 1–12 (2008)
Bilal, N., Tripathi, A., Bajaj, A.: On experiments in harmonically excited cantilever plates with 1: 2 internal resonance. Nonlinear Dynamics pp. 1–18 (2020)
Caliskan, T.D., Bruce, D.A., Daqaq, M.F.: Micro-cantilever sensors for monitoring carbon monoxide concentration in fuel cells. J. Micromech. Microeng. 30(4), 045005 (2020). https://doi.org/10.1088/1361-6439/ab6df2
Colin, M., Thomas, O., Grondel, S., Cattan, É.: Very large amplitude vibrations of flexible structures: experimental identification and validation of a quadratic drag damping model. J. Fluids Struct. 97, 103056 (2020)
Ding, H., Li, Y., Chen, L.Q.: Nonlinear vibration of a beam with asymmetric elastic supports. Nonlinear Dyn. 95(3), 2543–2554 (2019)
Doedel, E.J., Champneys, A.R., Dercole, F., Fairgrieve, T.F., Kuznetsov, Y.A., Oldeman, B., Paffenroth, R., Sandstede, B., Wang, X., Zhang, C.: Auto-07p: Continuation and bifurcation software for ordinary differential equations (2007)
Dwivedy, S., Kar, R.: Nonlinear dynamics of a cantilever beam carrying an attached mass with 1: 3: 9 internal resonances. Nonlinear Dyn. 31(1), 49–72 (2003)
Farokhi, H., Ghayesh, M.H.: Extremely large oscillations of cantilevers subject to motion constraints. J. Appl. Mech. 86(3), 031001 (2019)
Farokhi, H., Ghayesh, M.H.: Geometrically exact extreme vibrations of cantilevers. Int. J. Mech. Sci. 168, 105051 (2020)
Feng, Z., Leal, L.: Symmetries of the amplitude equations of an inextensional beam with internal resonance. J. Appl. Mech. 62(1), 235–238 (1995)
Friswell, M.I., Ali, S.F., Bilgen, O., Adhikari, S., Lees, A.W., Litak, G.: Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 23(13), 1505–1521 (2012)
Géradin, M., Cardona, A.: Flexible Multibody Dynamics: A Finite Element Approach. Wiley, Hoboken (2001)
Hirwani, C.K., Panda, S.K.: Numerical nonlinear frequency analysis of pre-damaged curved layered composite structure using higher-order finite element method. Int. J. Non-Linear Mech. 102, 14–24 (2018). https://doi.org/10.1016/j.ijnonlinmec.2018.03.005
Hsieh, S.R., Shaw, S.W., Pierre, C.: Normal modes for large amplitude vibration of a cantilever beam. Int. J. Solids Struct. 31(14), 1981–2014 (1994)
Katariya, P.V., Mehar, K., Panda, S.K.: Nonlinear dynamic responses of layered skew sandwich composite structure and experimental validation. Int. J. Non-Linear Mech. 125, 103527 (2020). https://doi.org/10.1016/j.ijnonlinmec.2020.103527
Lallart, M., Zhou, S., Yang, Z., Yan, L., Li, K., Chen, Y.: Coupling mechanical and electrical nonlinearities: The effect of synchronized discharging on tristable energy harvesters. Appl. Energy 266, 114516 (2020). https://doi.org/10.1016/j.apenergy.2020.114516
Lang, H., Linn, J., Arnold, M.: Multi-body dynamics simulation of geometrically exact cosserat rods. Multibody Syst. Dyn. 25(3), 285–312 (2011)
Latif, U., Uddin, E., Younis, M., Aslam, J., Ali, Z., Sajid, M., Abdelkefi, A.: Experimental electro-hydrodynamic investigation of flag-based energy harvesting in the wake of inverted c-shape cylinder. Energy 215, 119–195 (2021)
Leadenham, S., Erturk, A.: Unified nonlinear electroelastic dynamics of a bimorph piezoelectric cantilever for energy harvesting, sensing, and actuation. Nonlinear Dyn. 79(3), 1727–1743 (2015)
Li, W., Wierschem, N.E., Li, X., Yang, T., Brennan, M.J.: Numerical study of a symmetric single-sided vibro-impact nonlinear energy sink for rapid response reduction of a cantilever beam. Nonlinear Dyn. pp. 1–21 (2020)
Liu, H., Lee, C., Kobayashi, T., Tay, C.J., Quan, C.: Piezoelectric mems-based wideband energy harvesting systems using a frequency-up-conversion cantilever stopper. Sensors Actuat. A Phys. 186, 242–248 (2012). https://doi.org/10.1016/j.sna.2012.01.033
Mahmoodi, S.N., Jalili, N., Ahmadian, M.: Subharmonics analysis of nonlinear flexural vibrations of piezoelectrically actuated microcantilevers. Nonlinear Dyn. 59(3), 397–409 (2010)
Mahmoodi, S.N., Jalili, N., Khadem, S.E.: An experimental investigation of nonlinear vibration and frequency response analysis of cantilever viscoelastic beams. J. Sound Vibrat. 311(3), 1409–1419 (2008). https://doi.org/10.1016/j.jsv.2007.09.027
Mazharmanesh, S., Young, J., Tian, F.B., Lai, J.C.: Energy harvesting of two inverted piezoelectric flags in tandem, side-by-side and staggered arrangements. Int. J. Heat Fluid Flow 83, 108–589 (2020)
McHugh, K., Dowell, E.: Nonlinear responses of inextensible cantilever and free-free beams undergoing large deflections. J. Appl. Mech. 85(5),(2018)
Meesala, V.C., Hajj, M.R.: Parameter sensitivity of cantilever beam with tip mass to parametric excitation. Nonlinear Dyn. 95(4), 3375–3384 (2019)
Meesala, V.C., Hajj, M.R., Abdel-Rahman, E.: Bifurcation-based mems mass sensors. Int. J. Mech. Sci. 180, 105–705 (2020). https://doi.org/10.1016/j.ijmecsci.2020.105705
Meier, C., Popp, A., Wall, W.A.: Geometrically exact finite element formulations for slender beams: Kirchhoff-love theory versus simo-reissner theory. Archives Comput. Methods Eng. 26(1), 163–243 (2019)
Mojahed, A., Liu, Y., Bergman, L.A., Vakakis, A.F.: Modal energy exchanges in an impulsively loaded beam with a geometrically nonlinear boundary condition: computation and experiment. Nonlinear Dyn. 103(4), 3443–3463 (2021)
Nayfeh, A.H., Pai, P.F.: Non-linear non-planar parametric responses of an inextensional beam. Int. J. Non-Linear Mech. 24(2), 139–158 (1989)
Nayfeh, A.H., Pai, P.F.: Linear and Nonlinear Structural Mechanics. Wiley, Hoboken (2008)
Oh, K., Nayfeh, A.H.: Nonlinear combination resonances in cantilever composite plates. Nonlinear Dyn. 11(2), 143–169 (1996)
Ojo, O., Shoele, K., Erturk, A., Wang, Y.C., Kohtanen, E.: Numerical and experimental investigations of energy harvesting from piezoelectric inverted flags. In: AIAA Scitech 2021 Forum, p. 1323 (2021)
Pai, P.F., Nayfeh, A.H.: Non-linear non-planar oscillations of a cantilever beam under lateral base excitations. Int. J. Non-Linear Mech. 25(5), 455–474 (1990)
Panyam, M., Daqaq, M.F.: Characterizing the effective bandwidth of tri-stable energy harvesters. J. Sound Vibrat. 386, 336–358 (2017). https://doi.org/10.1016/j.jsv.2016.09.022
Rhoads, J.F., Shaw, S.W., Turner, K.L.: Nonlinear dynamics and its applications in micro- and nanoresonators. J. Dyn. Syst. Measure. Control (2010). https://doi.org/10.1115/1.4001333
Romero, V., Ly, M., Rasheed, A.H., Charrondière, R., Lazarus, A., Neukirch, S., Bertails-Descoubes, F.: Physical validation of simulators in computer graphics: A new framework dedicated to slender elastic structures and frictional contact. ACM Trans. Graphics (2021)
Semler, C., Li, G., Païdoussis, M.: The non-linear equations of motion of pipes conveying fluid. J. Sound Vibrat. 169(5), 577–599 (1994). https://doi.org/10.1006/jsvi.1994.1035
Shaw, A., Gatti, G., Gonçalves, P., Tang, B., Brennan, M.: Design and test of an adjustable quasi-zero stiffness device and its use to suspend masses on a multi-modal structure. Mech. Syst. Signal Process. 152, 107–354 (2021). https://doi.org/10.1016/j.ymssp.2020.107354
Shen, Y., Vizzaccaro, A., Kesmia, N., Yu, T., Salles, L., Thomas, O., Touzé, C.: Comparison of reduction methods for finite element geometrically nonlinear beam structures. Vibration 4(1), 175–204 (2021)
Crespo da Silva, M., Glynn, C.: Nonlinear flexural-flexural-torsional dynamics of inextensional beams i equations of motion. J. Struct. Mech. 4(6), 437–448 (1978)
Crespo da Silva, M., Glynn, C.: Nonlinear flexural-flexural-torsional dynamics of inextensional beams ii forced motions. J. Struct. Mech. 6(4), 449–461 (1978)
Tavallaeinejad, M., Legrand, M., Paidoussis, M.P.: Nonlinear dynamics of slender inverted flags in uniform steady flows. J. Sound Vibrat. 467, 115048 (2020)
Tavallaeinejad, M., Païdoussis, M.P., Legrand, M., Kheiri, M.: Instability and the post-critical behaviour of two-dimensional inverted flags in axial flow. J. Fluid Mech. 890,(2020)
Thomas, O., Sénéchal, A., Deü, J.F.: Hardening/softening behavior and reduced order modeling of nonlinear vibrations of rotating cantilever beams. Nonlinear Dyn. 86(2), 1293–1318 (2016)
Touzé, C., Amabili, M.: Nonlinear normal modes for damped geometrically nonlinear systems: application to reduced-order modelling of harmonically forced structures. J. Sound Vibrat. 298(4–5), 958–981 (2006)
Touzé, C., Thomas, O.: Reduced-order modeling for a cantilever beam subjected to harmonic forcing. In: proceedings of EUROMECH Colloquium, vol. 457, pp. 165–168 (2004)
Touzé, C., Thomas, O., Chaigne, A.: Hardening/softening behaviour in non-linear oscillations of structural systems using non-linear normal modes. J. Sound Vibrat. 273(1–2), 77–101 (2004)
Touzé, C., Thomas, O., Huberdeau, A.: Asymptotic non-linear normal modes for large-amplitude vibrations of continuous structures. Comput. Struct. 82(31–32), 2671–2682 (2004)
Wang, J., Geng, L., Yang, K., Zhao, L., Wang, F., Yurchenko, D.: Dynamics of the double-beam piezo-magneto-elastic nonlinear wind energy harvester exhibiting galloping-based vibration. Nonlinear Dyn. 100(3), 1963–1983 (2020)
Wang, W., Cao, J., Bowen, C.R., Zhang, Y., Lin, J.: Nonlinear dynamics and performance enhancement of asymmetric potential bistable energy harvesters. Nonlinear Dyn. 94(2), 1183–1194 (2018)
Yang, Z., Han, Q., Chen, Y., Jin, Z.: Nonlinear harmonic response characteristics and experimental investigation of cantilever hard-coating plate. Nonlinear Dyn. 89(1), 27–38 (2017)
Yoo, W.S., Lee, J.H., Park, S.J., Sohn, J.H., Dmitrochenko, O., Pogorelov, D.: Large oscillations of a thin cantilever beam: physical experiments and simulation using the absolute nodal coordinate formulation. Nonlinear Dyn. 34(1), 3–29 (2003)
Zhang, W., Wang, F., Yao, M.: Global bifurcations and chaotic dynamics in nonlinear nonplanar oscillations of a parametrically excited cantilever beam. Nonlinear Dyn. 40(3), 251–279 (2005)
Zhang, Y., Cao, J., Wang, W., Liao, W.H.: Enhanced modeling of nonlinear restoring force in multi-stable energy harvesters. J. Sound Vibrat. 494, 115–890 (2021). https://doi.org/10.1016/j.jsv.2020.115890
Zupan, E., Saje, M., Zupan, D.: Dynamics of spatial beams in quaternion description based on the newmark integration scheme. Comput. Mech. 51(1), 47–64 (2013)
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
H.F., Y.X., and A.E. done conceptualisation; H.F. performed methodology and formal analysis, software, and visualization; Y.X. and A.E were involved in investigation and resources. Y.X. and H.F performed validation and writing—original draft preparation; and A.E. and H.F. done writing—review and editing.
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Code availability
The open-source code package used in this study for numerical simulations can be downloaded from https://github.com/auto-07p/auto-07p. More information can be found in Ref. [10].
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary material 1 (mp4 240 KB)
Supplementary material 2 (mp4 234 KB)
Appendix: convergence analysis
Appendix: convergence analysis
A convergence analysis is performed in this section by analysing the primary resonance of the cantilever using various discretised models of the geometrically exact model. More specifically, four discretised models are considered, i.e. 1-degree-of-freedom (1-dof), 2-dof, 3-dof, and 6-dof ones. The nonlinear primary resonance response of the cantilever is examined via each of these models to determine the required number of modes to ensure converged results. Figure 12 shows the convergence analysis results for the tip rotation and tip displacements. As shown in the figure, the 1-dof model overestimates the hardening behaviour of the cantilever and the peak tip rotation. The 2-dof model predictions are more reliable than those of the 1-dof model, but it still does not give converged results. The results obtained via the 3-dof and 6-dof models are very close, indicating convergence. Hence, the 6-dof model utilised in the present study gives fully converged results.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Farokhi, H., Xia, Y. & Erturk, A. Experimentally validated geometrically exact model for extreme nonlinear motions of cantilevers. Nonlinear Dyn 107, 457–475 (2022). https://doi.org/10.1007/s11071-021-07023-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-07023-9







 Stable periodic solution,
Stable periodic solution,  unstable periodic solution)
unstable periodic solution)


 Stable periodic solution,
Stable periodic solution,  unstable periodic solution)
unstable periodic solution)



