Dynamic response of multi-degree-of-freedom systems with a Coulomb friction contact under harmonic excitation

Abstract

This paper investigates the steady-state response of a harmonically excited multi-degree-of-freedom (MDOF) system with a Coulomb contact between: (1) a mass and a fixed wall; (2) two different masses; (3) a mass and an oscillating base. Although discrete MDOF models are commonly used at early design stages to analyse the dynamic performances of engineering structures, the current understanding of the friction damping effects on MDOF behaviour is still limited due to the absence of analytical solutions. In this contribution, closed-form expressions of the continuous time response, the displacement transmissibility and the phase angle of each mass of the system are derived and validated numerically for 2DOF and 5DOF systems. Moreover, the features of the analytical response are investigated, obtaining the following results: (i) the determination of the minimum amounts of friction for which the resonant peaks become finite and (ii) for which stick-slip motion can be observed at high frequencies; (iii) an equation for the evaluation of invariant points for the displacement transmissibilities; (iv) a better understanding of phenomena such as the inversions of the transmissibility curves and the onset of additional resonant peaks due to the permanent sticking of the mass in contact. All these results show that MDOF systems exhibit significantly different dynamic behaviours depending on whether the friction contact and the harmonic excitation are applied to the same or different masses.

1 Introduction

Many engineering structures are characterised by the presence of frictional interfaces. When subject to dynamic loadings, the dry friction generated by the relative motion between the structural components in contact can have detrimental effects, such as noise, wear, loss of efficiency and failures. However, friction can also enhance the performance of vibrating structures, if used for purposes such as energy dissipation and vibration control [1,2,3]. Friction dampers present many advantageous properties, such as the ability to perform in harsh or inaccessible environments, to operate simultaneously along different directions and to adapt to a wide excitation bandwidth [4]. Therefore, their use is common in many engineering systems, such as bladed disks and civil buildings [4,5,6]. Nevertheless, the current understanding of the dynamic behaviour of friction damped structures is still limited.

One of the main challenges for the research in this field is the development of models and constitutive laws for describing the friction-related phenomena. Several models have been proposed throughout the years, in the attempt of describing the dependence of the friction force on the sliding velocity between the surfaces in contact [7,8,9,10] or introducing state variables accounting for the elastic deformation of the surface asperities [11,12,13,14,15]. Further details can be found in reviews [16, 17]. Another important challenge is understanding how friction can affect the performances of vibrating systems. In fact, even when Coulomb friction and simplified mass–spring models are considered, the determination of closed-form solutions for the dynamic response of these systems is a difficult task, due to the nonlinearity of the problem. The limited availability of analytical solutions also poses an important limitation to the conceptual design of engineering structures. In fact, single-degree-of-freedom (SDOF) and multi-degree-of-freedom (MDOF) mechanical models are commonly used during the early design stages to explore the vibration performance of frictional damping solutions. Analytical solutions could speed up the exploration of suitable designs, avoiding the use of more complicated and computationally expensive models while carrying out parameter investigations, optimisations and statistical model updating.

This paper proposes analytical expressions for the steady-state response of MDOF systems with a single Coulomb friction contact subjected to harmonic excitation and an exploration of their dynamic behaviour based on these derived solutions. In particular, Coulomb damping effects on the resonances and, more in general, on the response amplitude and phase of each mass of the system will be assessed. The investigation will also include the motion regimes determined by the periodic or permanent sticking of the mass in contact, focusing on their effects on these response features.

The research on the forced vibration of Coulomb damped systems has its roots in Den Hartog’s work [18]. Den Hartog determined an exact solution for the steady-state time response of SDOF systems in continuous non-sticking regimes, also providing analytical expressions for the response amplitude and phase; furthermore, he also provided a formulation for the boundary between continuous and stick-slip motion regimes. SDOF systems with a ground-fixed wall contact have lately been explored by several authors [19,20,21,22,23,24,25,26,27]. Hong and Liu [19] proposed a different closed-form expression for the response to harmonic excitation, enabling the evaluation of the velocity transmissibility and providing a different formulation for the boundary between continuous and stick-slip regimes. Hundal [21] determined an analytical solution for base-excited systems with combined viscous and Coulomb damping. Other authors [22,23,24] investigated the stability of these SDOF systems. Shaw [22] also extended Den Hartog’s solution taking into account different static and kinetic friction coefficients. Yeh [28] investigated a 2DOF system with viscous and Coulomb damping. Finally, SDOF systems with a friction contact between the mass and an oscillating wall have been investigated by Levitan [29] and, more recently, by Marino et al. [27, 30].

The response of more complex systems, involving more DOFs, multiple contacts or different friction models is usually investigated with approaches such as harmonic and multi-harmonic balances (see, e.g. [31,32,33,34,35,36,37]). However, these methods operate in the frequency domain and cannot be used to investigate directly nonlinear behaviours such as stick-slip motion [6]. Therefore, numerical integration in the time domain is still used to investigate these phenomena, despite its significant computational cost. For instance, Popp and Stelter [38] used a numerical approach to investigate the stick-slip vibration of a 2DOF system with both masses in contact with a moving rigid belt. Further details on the semi-analytical and numerical approaches used in the last decades for the investigation of friction damped systems can be found in reviews [4, 6, 16]. More recently, fundamental research has focused on the numerical and experimental investigation of the stability of SDOF and MDOF frictional oscillators, showing that multiple stable vibration states may exist in both self-excited and externally excited systems [39,40,41,42].

In reference [6], Rizvi et al. affirm that Den Hartog’s approach cannot handle systems with multiple nonlinearities due to its piecewise linear nature. Nonetheless, this approach can also be used for dealing with MDOF systems if a single friction contact is considered. In fact, Yeh [28] used Den Hartog’s approach to derive a closed-form solution for the response of a harmonically base-excited 2DOF system where the masses are interconnected by two springs and two viscous dampers in parallel and a Coulomb contact is applied on the lower mass. However, to the best of the authors’ knowledge, analytical expressions have not yet been derived for the response of systems with a larger number of DOFs and with the harmonic excitation and/or the friction force acting on different masses. These are the focus of the present contribution.

In this paper, the continuous steady-state response of a MDOF system with a Coulomb contact under harmonic loading is investigated. In particular, exact solutions are derived for the time response of all the masses of the system and for the response amplitude and phase of the mass in contact, while approximated analytical expressions are proposed for the response amplitudes and phases of the other masses. The domain of validity of these solutions, i.e. the boundary between continuous and stick-slip regimes, is also obtained and its expression coincides with the one proposed in reference [43] if a simplifying assumption is considered. In addition, the formulation presented in this paper also holds if different static and kinetic friction forces are considered. All these solutions hold for any number of DOFs and take into account harmonic and friction forces applied to different masses of the system. Therefore, they can be applied to the analysis of early design stages of engineering systems where MDOF models with a single contact are of interest, including the implementation of a friction damper in buildings [44], car suspensions [45], taxing of airplanes models [46] and energy harvesters [47]. MDOF systems with multiple friction contacts cannot be addressed with the proposed approach. Nonetheless, the general understanding developed in this work can be beneficial to a wide range of applications and support the exploration of engineering solutions exploiting the presence of a frictional damper.

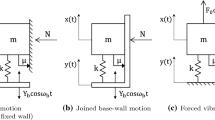
Finally, it can be observed that while mechanical models with a contact between a mass and a fixed wall are usually considered in theoretical works (see, e.g. [18,19,20, 22, 24, 25, 28]), it is more often the case in real applications that a friction contact occurs between two oscillating components of the system, as shown in references [44,45,46,47]. To address this aspect, the solutions derived in this paper are also extended to MDOF systems with a Coulomb contact (i) between two of the masses of the system or (ii) between a mass and a harmonically oscillating base.

The paper is structured as follows. The analytical expressions are derived in Sect. 2. In Sect. 3, these analytical expressions are used to investigate the features of the dynamic response, focusing on: (1) resonant, low- and high-frequency behaviour; (2) the presence of invariant points in the transmissibility curves; (3) the effects of the permanent sticking of the mass in contact. Section 4 presents a numerical validation of the solutions presented in Sect. 2 in the cases of a 2DOF and a 5DOF system with harmonic excitation and friction contact occurring either on the same or on different masses. The displacement transmissibilities are also evaluated numerically when stick-slip motion occurs, in order to achieve a complete overview of the dynamic response of these systems across the different motion regimes. Finally, Sect. 5 focuses on the extension of the solutions derived in Sect. 2 to MDOF systems with a contact between oscillating components.

2 Analytical evaluation of the steady-state response

2.1 Formulation of the problem

Let us consider a MDOF system where N masses $m_i$ are connected between each other and to the base by N springs of stiffness $k_i$, as shown in Fig. 1. The system is subjected to a harmonic load of amplitude P and frequency $\omega$, applied to the lth mass; the case of a harmonic base motion of amplitude Y can be accounted for by assuming that a harmonic load of amplitude $P=k_1Y$ is applied to the mass $m_1$. A Coulomb contact characterised by a friction force of amplitude F occurs on the jth mass of the system. The generic ith governing equation of this system can be written as:

$$\begin{aligned}&m_i\ddot{x}_i-k_ix_{i-1}+(k_i+k_{i+1})x_i-k_{i+1}x_{i+1}\nonumber \\&\quad +\delta _{ji}F\mathrm {sgn}(\dot{x}_j)=\delta _{li}P\cos (\omega t) \end{aligned}$$

(1)

where $x_{i-1}=0$ for $i=1$, $x_{i+1}=k_{i+1}=0$ for $i=N$ and:

The sgn() function is defined as follows:

where $\mu \ge 1$ is the ratio between the static and the kinetic values of the friction force. The so-defined function is mathematically undetermined when $\dot{x}_j=0$. The value assumed in this static condition, included between -$\mu$ and $\mu$, will be such that the system is in equilibrium when the mass $m_j$ is stuck on the wall.

Fig. 1

MDOF system with a friction contact on the jth mass subjected to a harmonic excitation on the lth mass

The dynamic behaviour of this system can be described by referring to $2N+1$ non-dimensional groups only:

• the frequency ratio $r_1=\omega \sqrt{m_1/k_1}$;

• the friction ratio $\beta =F/P$;

• the ratio between static and kinetic friction forces $\mu$;

• the $N-1$ mass ratios $\gamma _i=m_i/m_1$;

• the $N-1$ stiffness ratios $\kappa _i=k_i/k_1$.

It is worth noting that $\gamma _1$ and $\kappa _1$ are equal to 1, by definition, and therefore will not be considered as parameters of the system. By introducing the non-dimensional time:

$$\begin{aligned} \tau = \omega t \end{aligned}$$

(4)

and the non-dimensional mass displacements:

$$\begin{aligned} \bar{x}_i = \dfrac{x_i}{P/k_1} \end{aligned}$$

(5)

it is possible to rewrite Eq. (1) in a non-dimensional form where these parameters appear explicitly:

$$\begin{aligned}&\gamma _ir_1^2\bar{x}''_i-\kappa _i\bar{x}_{i-1}+(\kappa _i+\kappa _{i+1})\bar{x}_i-\kappa _{i+1}\bar{x}_{i+1}\nonumber \\&\quad +\delta _{ji}\beta \mathrm {sgn}(\bar{x}'_j)=\delta _{li}\cos \tau \end{aligned}$$

(6)

The symbol $'$ will be used to indicate derivatives with respect to the non-dimensional time $\tau$.

Fig. 2

Harmonic excitation and continuous responses of the mass in contact $m_j$ and of the generic mass not in contact $m_k$ in the steady-state period included between two maxima of the response $\bar{x}_j$ of the mass in contact

2.2 General assumptions and limitations

The assumptions required for the analytical approach proposed in this paper for MDOF systems are the same used by Den Hartog for the SDOF case [18]:

• periodic and continuous steady-state response

• presence of a single nonlinearity in the system

The existence of a periodic steady-state response and its independence of the assigned initial conditions have been investigated by several authors (see, e.g., [22,23,24]) for SDOF systems; however, to the best of the authors’ knowledge, stability properties have not been explored for MDOF systems with a friction contact. Nevertheless, the numerical investigations carried out in this study have shown a convergence of the response to a unique steady-state solution for most sets of parameters. Specific exceptions, including the case of infinite resonant peaks, are reported and discussed in the following sections.

The second assumption is satisfied if only a single contact is considered. Therefore, the proposed approach cannot deal with MDOF systems with multiple Coulomb contacts occurring simultaneously on different masses.

The harmonic excitation and the motions of the mass in contact $m_j$ and of a generic mass $m_k$ are shown in Fig. 2 in the steady-state period included between two maxima of $\bar{x}_j$. If the above assumptions are verified, the governing equations of the MDOF system will be linear in each interval included between two subsequent stationary points of $\bar{x}_j$, independently of the number of DOFs of the system. If the non-dimensional time interval $[0,\pi ]$ is considered, where $\tau =0$ coincides with a maximum of the periodic displacement of the mass in contact and $\tau =\pi$ with the subsequent minimum, the velocity of $m_j$ will be equal to zero at both ends of the interval and negative in all the internal points. Therefore, the non-dimensional friction force will be constant within the interval and equal to $-\beta$. Thus, it will be possible to rewrite Eq. (6) as:

$$\begin{aligned}&\gamma _ir_1^2\bar{x}''_i-\kappa _i\bar{x}_{i-1}+(\kappa _i+\kappa _{i+1})\bar{x}_i-\kappa _{i+1}\bar{x}_{i+1}\nonumber \\&\quad =\delta _{ji}\beta +\delta _{li}\cos (\tau +\phi _j) \end{aligned}$$

(7)

where it is assumed that an unknown phase angle $\phi _j$ is present between the maxima of the excitation and of the response of $m_j$ when a steady-state condition is reached, due to friction damping effect. It is worth underlining that this phase angle only refers to the maxima of the harmonic excitation and of the jth response. Since the response is not a monoharmonic function, the phase angle between their zeros will be, in general, different from $\phi _j$.

2.3 Modal analysis procedure

The linearity of the non-dimensional governing equations in Eq. (7) enables the use of standard modal analysis for its resolution. These equations can be written in a matrix form as:

$$\begin{aligned} \overline{\mathbf {M}}\bar{\mathbf {x}}''+\overline{\mathbf {K}}\bar{\mathbf {x}}=\bar{\mathbf {f}}+\bar{\mathbf {p}} \end{aligned}$$

(8)

where:

• $\overline{\mathbf {M}}$ is the mass matrix:

  $$\begin{aligned} \overline{\mathbf {M}}=\begin{bmatrix} r_1^2 &{} &{} 0 &{} &{} \ldots &{} &{} 0 \\ 0 &{} &{} \gamma _2 r_1^2 &{} &{} \ldots &{} &{} 0 \\ \vdots &{} &{} \vdots &{} &{} \vdots &{} &{} \vdots \\ 0 &{} &{} 0 &{} &{} \ldots &{} &{} \gamma _N r_1^2 \end{bmatrix} \end{aligned}$$

  (9)

• $\overline{\mathbf {K}}$ is the stiffness matrix:

  $$\begin{aligned} \overline{\mathbf {K}}=\begin{bmatrix} 1+\kappa _2 &{} &{} -\kappa _2 &{} &{} 0 &{} &{} \ldots &{} &{} 0 \\ -\kappa _2 &{} &{} \kappa _2+\kappa _3 &{} &{} -\kappa _3 &{} &{} \ldots &{} &{} 0 \\ \vdots &{} &{} \vdots &{} &{} \vdots &{} &{} \vdots &{} &{} \vdots \\ 0 &{} &{} 0 &{} &{} \ldots &{} &{} -\kappa _N &{} &{} \kappa _N \end{bmatrix} \end{aligned}$$

  (10)

• $\bar{\mathbf {f}}$ is the friction force vector, whose only nonzero component is $\beta$ in the jth position;

• $\bar{\mathbf {p}}$ is the harmonic force vector, whose only nonzero component is $\cos (\tau +\phi _j)$ in the lth position.

The N non-dimensional natural frequencies $\Omega _i$ and the corresponding N mode shapes $\varvec{\psi }_i=\begin{bmatrix} \psi _{1i}&\,&\psi _{2i}&\,&\ldots&\,&\psi _{Ni} \end{bmatrix}^T$ of the system described by Eq. (7) can be found as solutions of the generalised eigenvalue problem [48]:

$$\begin{aligned} (\overline{\mathbf {K}}-\Omega _i^2\overline{\mathbf {M}})\varvec{\psi }_i=\varvec{0} \end{aligned}$$

(11)

The obtained mode shapes $\varvec{\psi }_i$ are defined up to a constant [48] and, therefore, they need to be normalised according to some criteria in order to have a unique definition. In this paper, a mass normalisation is considered, i.e. it is imposed that the modal mass:

$$\begin{aligned} \hat{m}_i=\varvec{\psi }_i^T\overline{\mathbf {M}}\varvec{\psi }_i \end{aligned}$$

(12)

is unitary.

Standard modal analysis allows the rewriting of the governing equations of a linear system with N DOFs as a set of N uncoupled equations, which can be considered as the governing equations of N separate SDOF systems [48]. This transformation is performed by using the modal matrix $\varvec{\Psi }=\begin{bmatrix} \varvec{\psi }_1&\,&\varvec{\psi }_2&\,&\ldots&\,&\varvec{\psi }_N \end{bmatrix}$, which is defined as the matrix whose columns are the mode shapes of the system. Thus, it is possible to introduce the modal coordinates $\eta _i$ as the components of the vector $\varvec{\eta }$ obtained from the linear transformation:

$$\begin{aligned} \bar{\mathbf {x}}=\varvec{\Psi }\varvec{\eta } \end{aligned}$$

(13)

By introducing Eq. (13) into Eq. (8) and pre-multiplying both sides by $\varvec{\Psi }^T$, it is possible to write:

$$\begin{aligned} \varvec{\Psi }^T\overline{\mathbf {M}}\varvec{\Psi } \varvec{\eta }''+\varvec{\Psi }^T\overline{\mathbf {K}}\varvec{\Psi }\varvec{\eta } =\varvec{\Psi }^T\bar{\mathbf {f}}+\varvec{\Psi }^T\bar{\mathbf {p}} \end{aligned}$$

(14)

As the mode-shapes are mass-normalised, $\varvec{\Psi }^T\overline{\mathbf {M}}\varvec{\Psi }$ is equal to an identity matrix and $\varvec{\Psi }^T\overline{\mathbf {K}}\varvec{\Psi }$ is a diagonal matrix whose nonzero elements are equal to $\Omega _i^2$. Therefore, the ith equation of the system in Eq. (14) can be written as:

$$\begin{aligned} \eta _i''+\Omega _i^2\eta _i=\psi _{ji}\beta +\psi _{li}\cos (\tau +\phi _j) \end{aligned}$$

(15)

Equation (15) can be seen as the governing equation of a SDOF system of unitary mass and stiffness equal to $\Omega _i^2$, subjected to a constant force of amplitude $\psi _{ji}\beta$ and to a harmonic load $\psi _{li}\cos (\tau +\phi _j)$.

2.4 Solution of the modal problem

The forced vibration problem formulated in Eq. (15) is similar to that solved by Den Hartog [18], and its general solution can be written as:

$$\begin{aligned} \eta _i= & {} A_i\cos \left( \dfrac{\tau }{R_i}\right) + B_i\sin \left( \dfrac{\tau }{R_i}\right) \nonumber \\&+\psi _{ji}R_i^2\beta +\psi _{li}R_i^2v_i\cos (\tau +\phi _j) \end{aligned}$$

(16)

In this expression, the ith modal frequency ratio has been introduced as:

$$\begin{aligned} R_i = \dfrac{1}{\Omega _i} \end{aligned}$$

(17)

while the function:

$$\begin{aligned} v_i=\dfrac{1}{1-R_i^2} \end{aligned}$$

(18)

is the response function associated to the ith mode. Finally, $A_i$ and $B_i$ are two unknown constants whose expression can be determined by considering the initial conditions of this problem.

The initial and the final conditions to be imposed on $\eta _i$ are, in general, different from those considered by Den Hartog for the response of a SDOF system. In fact, in the SDOF case, the non-dimensional time instants $\tau =0$ and $\tau =\pi$ coincide with a maximum and a minimum of the response. However, this is not the case, in general, for the ith modal coordinate a MDOF system. Therefore, the initial conditions will be:

where the terms $\eta _{i0}$ and $\eta '_{i0}$ are both unknown at this stage.

Substituting Eq. (16) into Eq. (19) and rearranging the terms, the expressions of $A_i$ and $B_i$ are obtained:

Substituting these expressions into Eq. (16), it is possible to express the ith modal displacement as:

$$\begin{aligned}&\eta _i = \eta _{i0}\cos \left( \dfrac{\tau }{R_i}\right) +\eta '_{i0}R_i\sin \left( \dfrac{\tau }{R_i}\right) \nonumber \\&\quad +\psi _{ji}R_i^2\left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) \right] \beta \nonumber \\&\quad +\psi _{li}R_i^2v_i\left[ \cos \tau -\cos \left( \dfrac{\tau }{R_i}\right) \right] \cos \phi _j\nonumber \\&\quad +\psi _{li}R_i^2v_i\left[ R_i\sin \left( \dfrac{\tau }{R_i}\right) -\sin \tau \right] \sin \phi _j \end{aligned}$$

(21)

Due to the symmetry of the steady-state response, the final values of $\eta _i$ and $\eta '_i$ in the interval considered will be equal to:

Therefore, substituting Eq. (21) into Eq. (22), a system of algebraic equations is obtained in the form:

where:

The unknown values of $\cos \phi _j$ and $\sin \phi _j$ can be obtained from Eq. (23) as:

$$\begin{aligned} \cos \phi _j = \dfrac{\mathscr {B}\mathscr {R}-\mathscr {C}\mathscr {Q}}{\mathscr {A}\mathscr {Q}-\mathscr {B}\mathscr {P}} \qquad \qquad \sin \phi _j = \dfrac{\mathscr {C}\mathscr {P}-\mathscr {A}\mathscr {R}}{\mathscr {A}\mathscr {Q}-\mathscr {B}\mathscr {P}} \end{aligned}$$

(25)

Substituting Eq. (24) into Eq. (25), it is obtained that:

$$\begin{aligned} \cos \phi _j = \dfrac{\eta _{i0}}{\psi _{li}R_i^2v_i} \end{aligned}$$

(26)

and:

$$\begin{aligned} \sin \phi _j = -\dfrac{\eta '_{i0}}{\psi _{li}R_i^2v_i}-\dfrac{\psi _{ji}\sin (\pi /R_i)}{\psi _{li}R_iv_i\left[ 1+\cos (\pi /R_i)\right] }\beta \end{aligned}$$

(27)

Let us introduce the damping function of the ith mode of the system as:

$$\begin{aligned} u_i = \dfrac{\sin (\pi /R_i)}{R_i\left[ 1+\cos (\pi /R_i)\right] } \end{aligned}$$

(28)

in the same form as the damping function introduced by Den Hartog [18] for SDOF systems. Thus, it is possible to rewrite Eq. (27) as:

$$\begin{aligned} \sin \phi _j = -\dfrac{\eta '_{i0}+\psi _{ji}R_i^2u_i\beta }{\psi _{li}R_i^2v_i} \end{aligned}$$

(29)

By substituting Eqs. (26) and (29) into Eq. (21), it is possible to express the ith modal coordinate as:

$$\begin{aligned}&\eta _i = \eta _{i0}\cos \tau +(\eta '_{i0}+\psi _{ji}R_i^2u_i)\sin \tau \nonumber \\&\quad +\psi _{ji}R_i^2\left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) -u_iR_i\sin \left( \dfrac{\tau }{R_i}\right) \right] \beta \nonumber \\ \end{aligned}$$

(30)

In this expression, the initial values of the modal coordinate and of its derivative are still to be determined.

2.5 Response of the mass in contact

As specified in Sect. 2.2, the extremes of the non- dimensional time interval $[0,\pi ]$ coincide, respectively, with a maximum and a minimum of the response of the mass in contact $m_j$. Therefore, the initial conditions for this motion can be expressed as:

where $\overline{X}_j$ indicates the amplitude of the non-dimensional displacement of the mass $m_j$. As the amplitude of the non-dimensional excitation is unitary, this value also represents the jth magnification factor or displacement transmissibility of the system. These initial conditions can be imposed to determine the unknown amplitude and phase angle of the response $\bar{x}_j$. By introducing the jth coordinate transformation from Eq. (13) into Eq. (31), it is obtained that $\eta _{i0}$ and $\eta '_{i0}$ must verify the conditions:

$$\begin{aligned} \sum _{i=1}^N \psi _{ji}\eta _{i0} = \overline{X}_j \end{aligned}$$

(32)

and

$$\begin{aligned} \sum _{i=1}^N \psi _{ji}\eta '_{i0} = 0 \end{aligned}$$

(33)

respectively. These relations can be used to eliminate $\eta _{i0}$ and $\eta '_{i0}$ from the expression of the phase angle $\phi _j$. Let us multiply both numerator and denominator of the RHS of Eq. (26) by $\psi _{ji}$, obtaining:

$$\begin{aligned} \cos \phi _j = \dfrac{\psi _{ji}\eta _{i0}}{\psi _{ji}\psi _{li}R_i^2v_i} \end{aligned}$$

(34)

For each modal contribution, the quantity on the RHS of Eq. (34) is constant. As a result, by taking the sum of the N modal contributions of the numerator and denominator, the ratio will remain unchanged:

$$\begin{aligned} \cos \phi _j = \dfrac{\sum \nolimits _{i=1}^N\psi _{ji}\eta _{i0}}{\sum \nolimits _{i=1}^N\psi _{ji}\psi _{li}R_i^2v_i} \end{aligned}$$

(35)

Similarly, the generic kth response function of an undamped MDOF system of N masses subjected to a harmonic load acting on the lth mass can be expressed as [43]:

$$\begin{aligned} V_k =\sum \nolimits _{i=1}^N\psi _{ki}\psi _{li}R_i^2v_i \end{aligned}$$

(36)

Substituting Eqs. (32) and (36) for $j=k$, it is possible to rewrite Eq. (35) as:

$$\begin{aligned} \cos \phi _j = \dfrac{\overline{X}_j}{V_j} \end{aligned}$$

(37)

In a similar fashion, starting from Eq. (29), it is possible to obtain the relation:

$$\begin{aligned} \sin \phi _j = -\dfrac{\sum \nolimits _{i=1}^N\psi _{ji}\eta '_{i0}+\beta \sum \nolimits _{i=1}^N \psi _{ji}^2R_i^2u_i}{\sum \nolimits _{i=1}^N\psi _{ji}\psi _{li}R_i^2v_i} \end{aligned}$$

(38)

Let us introduce the generic kth damping function of a MDOF system of N masses with a contact on the jth mass as:

$$\begin{aligned} U_k =\sum \limits _{i=1}^N\psi _{ki}\psi _{ji}R_i^2u_i \end{aligned}$$

(39)

consistently with the formulation used in Eq. (36) for the response function. Substituting Eq. (33), Eq. (36) and Eq. (39) into Eq. (38) for $j=k$, it can be obtained that:

$$\begin{aligned} \sin \phi _j = -\dfrac{\beta U_j}{V_j} \end{aligned}$$

(40)

Substituting Eqs. (37) and (40) in the relation $\cos ^2\phi _j+\sin ^2\phi _j = 1$ and rearranging, it is possible to obtain the jth displacement transmissibility as:

$$\begin{aligned} \overline{X}_j=\sqrt{V_j^2-(\beta U_j)^2} \end{aligned}$$

(41)

It is worth observing that these expressions of the displacement transmissibility and of the phase angle are formally identical to those obtained by Den Hartog for SDOF systems [18] and reduce to the same expressions if $N=1$.

Finally, the following expression is obtained for the non-dimensional time response of the mass $m_j$ in the interval $[0,\pi ]$ by applying the jth equation of the transformation from modal to physical coordinates from Eq. (13) to Eq. (30):

$$\begin{aligned}&\bar{x}_j= \sum \limits _{i=1}^N\psi _{ji}\eta _{i0}\cos \tau \nonumber \\&\quad +\left( \sum \limits _{i=1}^N\psi _{ji}\eta '_{i0}+\beta \sum \limits _{i=1}^N\psi _{ji}^2R_i^2u_i\right) \sin \tau \nonumber \\&\quad +\beta \sum \limits _{i=1}^N\psi _{ji}^2R_i^2\left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) -u_iR_i\sin \left( \dfrac{\tau }{R_i}\right) \right] \nonumber \\ \end{aligned}$$

(42)

Considering Eqs. (32), (33) and (39), it is possible to rewrite the above expression as:

$$\begin{aligned}&\bar{x}_j= \overline{X}_j\cos \tau +\beta U_j\sin \tau \nonumber \\&\quad +\beta \sum \limits _{i=1}^N\psi _{ji}^2R_i^2\left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) -u_iR_i\sin \left( \dfrac{\tau }{R_i}\right) \right] \nonumber \\ \end{aligned}$$

(43)

Also in this case, Den Hartog’s expression for the time response of a SDOF system [18] is retrieved for $N=1$.

2.6 Response of a generic mass of the system

The time response of the generic mass $m_k$ of the MDOF system can be found with a similar approach. In fact, by introducing the kth equation from Eq. (13) into Eq. (30), it is obtained that:

$$\begin{aligned} \bar{x}_k&= \bar{x}_{k0}\cos \tau +(\bar{x}'_{k0}+\beta U_k)\sin \tau \nonumber \\&\quad +\beta \sum \limits _{i=1}^N\psi _{ji}\psi _{ki}R_i^2\left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) -u_iR_i\sin \left( \dfrac{\tau }{R_i}\right) \right] \nonumber \\ \end{aligned}$$

(44)

where $\bar{x}_{k0}$ and $\bar{x}'_{k0}$ are, respectively, the initial values of the displacement and of the velocity of $m_k$ in the interval considered; these values are unknown at this stage.

In order to determine $\bar{x}_{k0}$ and $\bar{x}_{k0}'$, let us multiply numerator and denominator of the RHS of Eq. (26) and Eq. (29) by $\psi _{ki}$ and consider their summations from $i=1$ to N, proceeding as in Sect. 2.5. The expressions obtained are:

$$\begin{aligned} \cos \phi _j = \dfrac{\sum \nolimits _{i=1}^N\psi _{ki}\eta _{i0}}{\sum \nolimits _{i=1}^N\psi _{ki}\psi _{li}R_i^2v_i}=\dfrac{\bar{x}_{k0}}{V_k} \end{aligned}$$

(45)

from Eq. (26) and

$$\begin{aligned} \sin \phi _j =-\dfrac{\bar{x}_{k0}'+\beta U_k}{V_k} \end{aligned}$$

(46)

from Eq. (29). The initial displacement of $m_k$ can be determined by substituting Eq. (37) into Eq. (45):

$$\begin{aligned} \bar{x}_{k0} =\dfrac{V_k}{V_j}\overline{X}_j=\dfrac{V_k}{V_j}\sqrt{V_j^2-(\beta U_j)^2} \end{aligned}$$

(47)

Similarly, considering Eqs. (40) and (46), the initial velocity can be formulated as:

$$\begin{aligned} \bar{x}'_{k0} =\beta \left( \dfrac{V_k}{V_j}U_j-U_k\right) \end{aligned}$$

(48)

The time response of the generic mass $m_k$ can now be evaluated by substituting Eqs. (47) and (48) into Eq. (44), obtaining:

$$\begin{aligned} \bar{x}_k&= \dfrac{V_k}{V_j}\left( \overline{X}_j\cos \tau +\beta U_j\sin \tau \right) +\beta \sum \limits _{i=1}^N\psi _{ji}\psi _{ki}R_i^2\nonumber \\&\quad \times \left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) -u_iR_i\sin \left( \dfrac{\tau }{R_i}\right) \right] \end{aligned}$$

(49)

It can be observed that this expression reduces to Eq. (43) if $j=k$.

The amplitude and the phase angle of $\bar{x}_k$ cannot be easily determined from the expression of the time response $\bar{x}_k$. In general, the evaluation of the maximum absolute value of $\bar{x}_k$ within the non-dimensional time interval $[0,\pi ]$ can be performed numerically and its value will coincide with the kth displacement transmissibility. Moreover, if the maximum value of $|\bar{x}_k|$ is verified at $\tau =\tau _{k,\mathrm {max}}$, the phase angle between the excitation and the displacement of the mass $m_k$ can be calculated as:

This approach for the determination of $\overline{X}_k$ and $\phi _k$ does not yield information on their dependency on the parameters of the problem. Therefore, an approximated approach for determining explicit analytical expressions for the displacement transmissibility and the phase angle of a generic mass of the system is proposed in what follows.

A monoharmonic approximation of the motion of the mass $m_j$ in the interval $[0,\pi ]$ could simply be obtained as $\bar{x}_j\cong \overline{X}_j\cos \tau$. Such a formulation would neglect the non-harmonic behaviour of the response due to nonlinearity but would agree with the exact solution from Eq. (43) at both ends of the interval, thus providing the exact amplitude and phase angle of the response. Nevertheless, the same approximation cannot be directly introduced for the motion of the generic mass $m_k$. In fact, a certain phase shift $\phi _{kj}$ is generally present between the displacements of $m_j$ and $m_k$; as a consequence, the initial and the final points of $\bar{x}_k$ in $[0,\pi ]$ are not stationary points. Comparing Eq. (43) and Eq. (44), it is possible to observe that this effect is expressed by the term $\bar{x}'_{k0}\sin \tau$, which is equal to zero in the case $j=k$. This term cannot be disregarded in a monoharmonic approximation. Thus, the formulation hereby proposed is:

$$\begin{aligned} \bar{x}_k \cong \bar{x}_{k0}\cos \tau + \bar{x}'_{k0}\sin \tau =\overline{X}_{k}\cos (\tau -\phi _{kj}) \end{aligned}$$

(51)

where

$$\begin{aligned} \overline{X}_{k}=\sqrt{\bar{x}_{k0}^2+\bar{x}_{k0}'^2}=\sqrt{V_k^2+ \left( 1-2\dfrac{V_k}{V_j}\dfrac{U_j}{U_k}\right) (\beta U_k)^2} \end{aligned}$$

(52)

is the approximated kth displacement transmissibility of the MDOF system, while the phase angle $\phi _{kj}$ can be determined as:

$$\begin{aligned} \cos \phi _{kj} = \dfrac{\bar{x}_{k0}}{\overline{X}_{k}} \qquad \qquad \sin \phi _{kj} =\dfrac{\bar{x}'_{k0}}{\overline{X}_{k}} \end{aligned}$$

(53)

The phase angle between the excitation and the displacement of the kth mass will be finally obtained as $\phi _k=\phi _j+\phi _{kj}$. Equations (52) and (53) offer a very good approximation of the exact transmissibilities and phase angles of the mass not in contact and will be used in the remaining of the paper. The absolute errors introduced with the respect to the exact quantities are mostly negligible for all the cases investigated.

2.7 Boundaries between continuous and stick-slip motion regimes

The solutions presented in this section have been determined under the assumption of continuous non-sticking response. In Sect. 2.2, it has been specified that the proposed mathematical procedure only holds if the velocity of the mass in contact $m_j$ is negative in all the internal points of the non- dimensional time interval $[0,\pi ]$. In addition, in order to observe a continuous response, it is also required that the sum of all the non-inertial forces acting on the mass $m_j$ is larger than the static friction force at both ends of this time interval, where $\bar{x}'_j=0$. Differently, a sticking phase would take place. These non-sticking conditions can be expressed as:

These two conditions can be used to obtain the maximum value of the friction ratio for which the steady-state response is non-sticking.

Let us consider the derivative of the jth mass motion from Eq. (43), so that Eq. (54a) can be rewritten as:

$$\begin{aligned}&-\overline{X}_j\sin \tau +\beta U_j\cos \tau \nonumber \\&\quad +\beta \sum \limits _{i=1}^N\psi _{ji}^2R_i^2\left[ \dfrac{1}{R_i}\sin \left( \dfrac{\tau }{R_i}\right) -u_i\cos \left( \dfrac{\tau }{R_i}\right) \right] <0\nonumber \\ \end{aligned}$$

(55)

from which

$$\begin{aligned}&\overline{X}_j>\beta \sum \limits _{i=1}^N\psi _{ji}^2\nonumber \\&\quad \dfrac{R_i\sin (\tau /R_i)+u_iR_i^2\left[ \cos \tau -\cos (\tau /R_i)\right] }{\sin \tau } \end{aligned}$$

(56)

This relation is verified if $\overline{X}_j$ is larger than the maximum value assumed by the RHS in the interval $]0,\pi [$. Thus, introducing the function:

$$\begin{aligned} S_j = \sum \limits _{i=1}^N\psi _{ji}^2s_i \end{aligned}$$

(57)

where:

$$\begin{aligned} s_i =\max \limits _{{0<\tau <\pi }} \dfrac{R_i\sin (\tau /R_i)+u_iR_i^2\left[ \cos \tau -\cos (\tau /R_i)\right] }{\sin \tau }\nonumber \\ \end{aligned}$$

(58)

it is possible to rewrite Eq. (56) as:

$$\begin{aligned} \overline{X}_j>\beta S_j \end{aligned}$$

(59)

Substituting Eq. (41) into Eq. (59) and rearranging, it is possible to express this relation in terms of the friction ratio as:

$$\begin{aligned} \beta <\sqrt{\dfrac{V_j^2}{U_j^2+S_j^2}} \end{aligned}$$

(60)

Let us now consider the second non-sticking condition, expressed in Eq. (54b). Due to the symmetry of the steady-state response, only the case $\tau =0$ needs to be considered. By introducing the transformation from Eq. (13), it is possible to rewrite this condition in terms of the ith modal coordinate as:

$$\begin{aligned} |\Omega _i^2\eta _{i0}-\psi _{li}\cos \phi _j|>\psi _{ji}\mu \beta \end{aligned}$$

(61)

By substituting Eq. (26) into Eq. (61), it is obtained that:

$$\begin{aligned} |\eta _{i0}|>\psi _{ji}\mu \beta \end{aligned}$$

(62)

from which, multiplying both sides by $\psi _{ji}$ and considering the sums from 1 to N, it can be written that:

$$\begin{aligned} \overline{X}_j>\mu \beta \sum _{i=1}^N\psi _{ji}^2 \end{aligned}$$

(63)

Considering that, from the jth equation of the system in Eq. (12):

$$\begin{aligned} \sum \limits _{i=1}^N\psi _{ji}^2=\dfrac{1}{\gamma _jr_1^2} \end{aligned}$$

(64)

and substituting Eq. (41), it is possible to express this condition in terms of the friction ratio as:

$$\begin{aligned} \beta <\sqrt{\dfrac{V_j^2}{U_j^2+\bigg (\dfrac{\mu }{\gamma _jr_1^2}\bigg )^2}} \end{aligned}$$

(65)

Finally, Eqs. (60) and (65) can be merged in the following overall condition for obtaining a continuous non-sticking response:

$$\begin{aligned} \beta <\sqrt{\dfrac{V_j^2}{U_j^2+\left[ \max \bigg (S_j,\dfrac{\mu }{\gamma _jr_1^2}.\bigg )\right] ^2}} \end{aligned}$$

(66)

The RHS of the above inequality represents the value of the friction ratio at the boundary between continuous and stick-slip motion regimes and will be referred to as $\beta _\mathrm {lim}$ in the remaining of this paper. Furthermore, it is possible to express the boundary between continuous and stick-slip motion in terms of any of the displacement transmissibilities or phase angles of the MDOF system by simply substituting Eq. (66) into their expression.

It is worth observing that in the limit case of $\mu =1$, when static and kinetic friction forces are assumed to be equal, the boundary can simply be expressed referring to Eq. (60). In fact, as stated by Den Hartog [18], the function $s_i$ is always equal or larger than unity and therefore from Eq. (57) and Eq. (64):

$$\begin{aligned} S_j\ge \dfrac{1}{\gamma _j r_1^2} \end{aligned}$$

(67)

This implies that the condition in Eq. (54b) is always verified if Eq. (54a) is verified. Moreover, Den Hartog affirms that $s_i$ is unitary for most values frequency ratio [18]. If the assumption of $s_i=1$ is considered, the expression of the upper bound for continuous motion reduces to:

$$\begin{aligned} \beta <\sqrt{\dfrac{V_j^2}{U_j^2+\bigg (\dfrac{1}{\gamma _jr_1^2}\bigg )^2}} \end{aligned}$$

(68)

which is the expression of the boundary proposed in [43]. This approximated expression can be advantageous since it does not require to compute $s_i$ from the time response for each value of $r_1$. Although it has been observed that Eq. (60) and Eq. (68) give slightly different results only when low frequency ratios are considered, the exact formulation will be used in this paper.

Fig. 3

3DOF system with unitary mass and stiffness ratios, a Coulomb friction contact on $m_2$ and a harmonic excitation on $m_1$: (a) schematic representation of the system, (b) analytical displacement transmissibility on $m_1$ for varying $r_1$ and $\beta$ in continuous motion regime and (c) stuck configuration of the system. The black dashed line represents the boundary between continuous and stick-slip regimes, while the black dotted line portrays the transmissibility in stuck configuration. The invariant points $P_1$ and $P_2$ are highlighted in magenta

3 Features of the dynamic response

This section focuses on investigating features of the dynamic response of a MDOF system with a contact on the jth mass and subjected to a harmonic excitation acting on the lth mass. This investigation is based on the analytical solutions derived in Sect. 2 for its continuous steady-state response and the boundaries between continuous and stick-slip motion regimes and focuses on: (i) resonant, low- and high-frequency behaviours, (ii) the presence of invariant points in the transmissibility curves and (iii) the effect of stuck friction contacts on the dynamic response of the system. A 3DOF system with unitary stiffness and mass ratios, a friction contact occurring on the $m_2$, characterised by equal static and kinetic friction forces, and a harmonic load applied on $m_1$, shown in Fig. 3a, will be used to show these response features.

3.1 Resonant behaviour

The effect of friction damping on the resonant behaviour of a system is very different from that provided, for instance, by viscous or hysteretic damping (see, e.g. [49]). In the case of SDOF systems, it is well-known that friction does not affect the damped natural frequency of the system and does not provide a finite resonance if $\beta <\pi /4$ (see, e.g. [18, 24]). This value represents the minimum friction ratio for which stick-slip occurs in the response of a SDOF system when the ratio between driving and natural frequency is unitary [30]. Thus, it can be deduced that friction can avoid infinite resonant peaks only by introducing stick-slip in the response.

Let us denote with $\beta _{n,i}$ the threshold value of the friction ratio for which the ith resonant peak of a MDOF system with a Coulomb contact becomes finite. $\beta _{n,i}$ can be determined by evaluating the value of the boundary between continuous and stick-slip motion from Eq. (60) for $R_i\rightarrow 1$. Observing that in the expressions of the response and of the damping functions, in Eqs. (36) and (39), respectively, only the ith terms of the summations tend to infinity, it is possible to write:

$$\begin{aligned} \beta _{n,i}=\lim _{R_i\rightarrow 1}\beta _\mathrm {lim}=\left| \dfrac{\psi _{li}}{\psi _{ji}}\right| \lim _{R_i\rightarrow 1}\dfrac{\dfrac{1}{1-R_i^2}}{\dfrac{\sin (\pi /R_i)}{R_i[1+\cos (\pi /R_i)]}} \end{aligned}$$

(69)

The limit in Eq. (69) has already been evaluated in [30], and it is equal to $\pi /4$. Therefore, the minimum friction ratio required for observing a finite ith resonant peak will be:

$$\begin{aligned} \beta _{n,i}=\dfrac{\pi }{4}\left| \dfrac{\psi _{li}}{\psi _{ji}}\right| \end{aligned}$$

(70)

It must be observed that, in the above equation, the ratio between $\psi _{li}$ and $\psi _{ji}$ is always independent of the frequency ratio.

In the 3DOF system shown in Fig. 3a, the threshold values of the friction ratio calculated from Eq. (70) are equal to $\beta _{n,1}=0.436$, $\beta _{n,2}=1.765$ and $\beta _{n,3}=0.630$. These results are in agreement with the resonant behaviour exhibited by the transmissibility curves shown in Fig. 3b for the mass $m_1$ of this system.

Equation (70) shows that, in general, the different resonant peaks of a MDOF system will become finite for different values of $\beta$. However, if the harmonic excitation and the friction force act on the same mass, i.e. if $j=l$, $\beta _{n,i}$ will be equal to:

$$\begin{aligned} \beta _{n,i}=\dfrac{\pi }{4}\cong 0.785 \end{aligned}$$

(71)

for any i, meaning that all the resonant peaks of the system will become finite for the same threshold value of the friction ratio.

3.2 Quasi-static conditions

The dynamic response of SDOF systems with Coulomb friction in quasi-static conditions is usually characterised by the occurrence of stick-slip motion. Moreover, when the frequency ratio approaches to zero, the number of stops per cycle can increase significantly, as shown by many authors (see, e.g. [20, 50]).

It can be shown that stick-slip motion usually occurs at very low frequency ratios also in the MDOF case. In fact, the evaluation of the boundary friction ratio from Eq. (60) for $\omega \rightarrow 0$ and, therefore, for $R_i\rightarrow 0$ yields:

$$\begin{aligned} \beta _0=\lim _{R_i\rightarrow 0}\beta _\mathrm {lim}=0 \end{aligned}$$

(72)

This equation reveals that any nonzero value of the friction ratio would lead to stick-slip in quasi-static conditions.

The numerical investigations carried out in this study showed that the dynamic response of MDOF systems is characterised, as in the SDOF case, by an increasing number of stops for $r_1\rightarrow 0$. However, the starting point of the transmissibility curves at $r_1=0$ can be evaluated analytically, avoiding the complications which may arise in numerical approaches due to the large number of stops per cycle.

Let us rewrite the governing equations of the problem from Eq. (8) in static conditions. If $\omega =0$, then both $r_1$ and $\tau$ will also be equal to zero. Thus, the harmonic excitation will reduce to a constant force, which will be opposed by a constant friction force. Therefore, the governing equations will reduce to:

$$\begin{aligned} \overline{\mathbf {K}}\bar{\mathbf {x}}_{\mathbf {0}}=\bar{\mathbf {p}}_{\mathbf {0}}-\bar{\mathbf {f}}_{\mathbf {0}} \end{aligned}$$

(73)

where

• $\bar{\mathbf {x}}_{\mathbf {0}}=\begin{bmatrix} \overline{X}_{10}, \ldots , \overline{X}_{N0} \end{bmatrix}^T$ is the vector of the displacement transmissibilities for $r_1=0$;

• $\bar{\mathbf {p}}_{\mathbf {0}}$ is a vector whose only nonzero component is equal to 1 in the lth position;

• $\bar{\mathbf {f}}_{\mathbf {0}}$ is a vector whose only nonzero component is equal to $\beta$ in the jth position.

The starting points of the transmissibilities curves can be evaluated as solutions of the linear algebraic system expressed in Eq. (73). In the case of a SDOF system, the solution is given by $\overline{X}_0=1-\beta$, in agreement with the starting value observed by Csernak et al. in reference [24], while for the 3DOF system in Fig. 3a the values obtained are $\overline{X}_{10}=1-\beta$, $\overline{X}_{20}=1-2\beta$ and $\overline{X}_{30}=1-2\beta$.

The validity of these results is limited to the cases where either continuous and stick-slip motion regimes occur in quasi-static conditions, while a different approach is required if the mass in contact is permanently stuck. This case will be discussed in Sect. 3.5.

3.3 High-frequency behaviour

In reference [30], the behaviour at high frequency ratios of a SDOF system with Coulomb friction subjected to harmonic excitation is analysed. This investigation revealed that, although the amplitude of the response always converges to zero when the driving frequency tends to infinity, the boundary between continuous and stick-slip motion converges to a specific value, which is:

$$\begin{aligned} \beta _\infty =\dfrac{2}{\sqrt{4+\pi ^2}}\cong 0.537 \end{aligned}$$

(74)

assuming equal values for the static and the kinetic friction forces. The meaning of this result is that stick-slip can occur at high frequencies in SDOF systems only if the friction ratio is larger than the above value.

The occurrence of stick-slip motion at high frequency ratios in the response of a MDOF system can be investigated by evaluating the limit of the boundary friction ratio from Eq. (60) for $\omega \rightarrow \infty$. Considering that $R_i$ will also tend to infinity in this case, it is possible to write:

$$\begin{aligned} \beta _\infty =\lim _{ {R_i\rightarrow \infty }}\beta _\mathrm {lim}=\sqrt{\dfrac{\left( \sum \limits _{i=1}^N\psi _{li}\psi _{ji}\right) ^2}{\left( \mu +\dfrac{\pi ^2}{4}\right) \left( \sum \limits _{i=1}^N\psi _{ji}^2\right) ^2}} \end{aligned}$$

(75)

Given the orthogonality conditions of the mode shapes, the boundary friction ratio will be equal to:

Therefore,

• when the harmonic and the friction forces act on the same mass of the MDOF system, stick-slip will occur at high frequencies only if the friction ratio is larger than the above value, which coincides with the result of Eq. (74) if $\mu =1$;

• otherwise, stick-slip will occur for $r_1\rightarrow \infty$ for any nonzero value of $\beta$.

In the case of the 3DOF system shown in Fig. 3a, the harmonic load and the friction contact are applied on different masses and, therefore, stick-slip occurs at high frequencies for any value of the friction ratio; this is also observed in Fig. 3b.

3.4 Invariant points

In Fig. 3b, it can be observed that the transmissibility curves, illustrated for the bottom mass of the 3DOF system in continuous motion regime, pass through two points denoted as $P_1$ and $P_2$, which are commonly defined as invariant points. In these points, the response amplitude is independent of the damping, which is represented in this case by the friction ratio.

The presence of invariant points in the transmissibility curves is regarded as an important aspect in the design of mechanical systems such as dynamic vibration absorbers [51,52,53] and car suspensions [54, 55]. In particular, according to the Den Hartog’s theory illustrated in reference [56], these points can be used to determine the optimal configuration of a viscous damper acting as vibration absorber for a main undamped SDOF system. An approach for determining the presence of invariant points in the transmissibilities of the MDOF system investigated in this section is proposed in what follows.

Let us consider the expression of the displacement transmissibility provided by Eq. (41) for mass in contact of the MDOF system. It appears clear that the transmissibility will not depend on the friction ratio if:

$$\begin{aligned} U_j=0 \end{aligned}$$

(77)

Thus, this equation can be used to find the invariant points for the response of the mass $m_j$. From Eq. (41), it can also be deduced that, at any other frequency ratios, $\overline{X}_j$ will always decrease for increasing $\beta$; therefore, no inversion of the transmissibility curves will be observed across the invariant points in this case. Moreover, from Eq. (37) and Eq. (40), it is possible to observe that the points determined from Eq. (77) will also be invariant for the phase angle $\phi _j$. Particularly, from Eq. (40), it can be deduced that the corresponding value of $\phi _j$ will be equal to 0 or 180 degrees, i.e. the excitation and the jth mass motion will be in phase or in phase-opposition. The phase angle curves will also exhibit an inversion across these points.

Let us now consider the generic kth displacement transmissibility of the system. From Eq. (52), it is possible to deduce that the invariant points can be obtained not only from the equation $U_k=0$, but also from:

$$\begin{aligned} 1-2\dfrac{V_k}{V_j}\dfrac{U_j}{U_k}=0 \end{aligned}$$

(78)

The points determined as solutions of the latter equation are associated to an inversion of the transmissibility curves. This behaviour can only be observed in the transmissibilities of the masses not in contact. Furthermore, these points are not invariant for the phase angle $\phi _k$.

It is important to note that Eqs. (77) and (78) hold only for a continuous response of the MDOF system. In general, transmissibility curves will not pass through an invariant point if stick-slip or permanent sticking of the mass in contact occurs at the corresponding frequency ratio. Finally, it is worth observing Eqs. (77) and (78) are transcendental equations and have infinite solutions. Nevertheless, as shown in Sect. 5, the vast majority of these solutions are characterised by very small values of frequency ratio, where usually stick-slip motion occurs, and can therefore be disregarded.

3.5 Stuck configurations

In friction damped systems, sliding can occur between two components in contact either continuously or in alternation with sticking phases. However, it is well known that friction contacts can also become permanently stuck under certain conditions (see, e.g., [43]).

In the case of a SDOF system with a fixed wall contact under harmonic excitation, mass motion occurs only when the amplitude of the harmonic load exceeds the value of the static friction force, i.e. if $\mu \beta <1$ [43]. The same principle holds, more in general, for the mass in contact of a MDOF system. In this case, the static friction force must be compared to the sum of all the spring and harmonic forces acting directly on this mass [43]. However, even when the mass in contact is stuck, some masses of the system can still exhibit a dynamic response, depending on where the harmonic and the friction forces are applied. The reduced system which remains active when $m_j$ is stuck will be referred to as stuck configuration of the MDOF system and its response can be evaluated as proposed in reference [43]:

• if $j>l$, only the masses $m_1,\ldots ,m_{j-1}$ will be excited. Thus, the stuck configuration of the system will be represented by an undamped system with $j-1$ DOFs, where the stuck jth mass is replaced by a fixed wall. The response of this system can be evaluated from standard modal analysis and will be characterised by the presence of $j-1$ infinite resonant peaks located, in general, at different frequencies with respect to those of the original system;

• if $j<l$, only the masses $m_{j+1},\ldots ,m_N$ will be excited and, therefore, the stuck configuration of the system will include $N-j$ DOFs. All the above considerations apply, except that, in this case, the stuck system will exhibit $N-j$ infinite resonant peaks;

• finally, if $j=l$, the harmonic excitation is applied to the stuck mass and, therefore, is not transmitted to any of the other masses, leaving the MDOF system fully stuck. Obviously, this is also the case for a SDOF system.

Denoting with $\overline{X}^*_i$ the ith displacement transmissibility of the system in stuck configuration, it is therefore possible to write the conditions for observing sliding motion between the mass $m_j$ and the wall as:

In the example of the 3DOF system in Fig. 3a, the stuck configuration consists in the SDOF system shown in Fig. 3c, where the bottom mass is the only remaining active DOF, while the intermediate mass is replaced by a fixed wall. The displacement transmissibility for $m_1$ in stuck conditions can be obtained as:

$$\begin{aligned} \overline{X}^*_1=\dfrac{1}{|2-r_1^2|} \end{aligned}$$

(80)

and is represented by a dotted line in Fig. 3b. According to Eq. (79), sliding occurs between the mass $m_2$ and the wall if $\overline{X}^*_1>\beta$. This implies that, for each value of $\beta$, the system will operate in a non-stuck configuration only in the frequency ratio range:

$$\begin{aligned} \sqrt{\dfrac{2\beta -1}{\beta }}<r_1<\sqrt{\dfrac{1+2\beta }{\beta }} \end{aligned}$$

(81)

The lower bound of Eq. (81) reduces to $r_1=0$ if $\beta \le 0.5$, while the upper bound is defined for any nonzero value of $\beta$. Therefore, in the presence of friction damping, the mass $m_2$ will always become stuck at high frequency ratios beyond the threshold expressed in the above inequality. Moreover, these bounds will converge to a single point at $r_1=\sqrt{2}$ only for $\beta \rightarrow \infty$. Therefore, even when the friction ratio is very large, sliding motion will always occur in the contact in a small range of frequencies around the resonance of the stuck configuration and the transmissibility will assume a finite value in this range.

Fig. 4

2DOF system with a friction contact and a harmonic load on the lower mass (a) and comparison between analytical (continuous lines) and numerical (round markers) steady-state time responses for two different sets of mass, stiffness, friction and frequency ratios (b, c)

The last two properties, regarding high-frequency and resonant behaviours, can easily be generalised to any MDOF systems with $j\ne l$. In fact, since the transmissibility curves of any undamped system tend to zero for $r_1\rightarrow \infty$ and tend to infinity at resonance, Eqs. (79a) and (79b) are not verified for any value of $\beta$ in the first case and always met in the latter.

4 Numerical validation and stick-slip response

In this section, the analytical solutions introduced in Sect. 2 for the continuous response of MDOF systems are compared to the results yielded by the numerical approach introduced in reference [43]. Moreover, the response is also evaluated numerically in stick-slip regimes, providing a validation of the analytical boundaries between continuous and stick-slip motion regimes and a complete overview of the dynamic behaviour for varying frequency and friction ratios. The stick-slip responses have been evaluated, for simplicity, in the case of $\mu =1$; different results would be obtained, in general, if a different value of the static friction force is considered.

In Sect. 3, it has been shown that the continuous response features can be significantly different depending on whether the friction and the harmonic forces are applied on the same or on different masses. Therefore, these two different classes of MDOF systems will be dealt with separately. In each case, analytical and numerical results will be first compared and discussed in detail for the 2DOF case and then generalised to systems with a larger number of DOFs, referring to the case of a 5DOF system. Moreover, for each of these systems, the analytical boundaries among continuous, stick-slip and permanent sticking regimes will be represented in a 2-D parameter space for varying frequency and friction ratios in the assumption of $\mu =1$, while their variation with the static friction force is shown in Appendix A.

Fig. 5

Displacement transmissibilities and phase angles of a 2DOF system with a Coulomb contact and a harmonic load on $m_1$ for varying friction ratio and unitary mass and stiffness ratios, displayed on $m_1$ (a) and on $m_2$ (b). Analytical results are represented by the continuous lines, while numerical results are represented with round (continuous motion) and with diamond markers (stick-slip motion). The black dashed line represents the boundary between continuous and stick-slip regimes

4.1 Systems with excitation and contact on the same mass

4.1.1 2DOF system with excitation and contact on $m_1$

The analytical and numerical results for the dynamic response of the 2DOF system with $j=l=1$ shown in Fig. 4a are discussed in what follows.

Figures 4b, c present a comparison between the analytical and numerical time responses of the masses $m_1$ and $m_2$. These results have been plotted in the non-dimensional time interval $[0,\pi ]$ for two different sets of the parameters $r_1$, $\beta$, $\kappa$ and $\gamma$, exhibiting in both cases an excellent agreement. The harmonic excitation $\cos (\tau +\phi _1)$ is also represented and appears perfectly aligned to the numerical forcing function, showing that a very good agreement is also achieved for the phase angle $\phi _1$.

Fig. 6

Motion regimes of a 2DOF system with a Coulomb contact and a harmonic load on $m_1$ for varying frequency and friction ratios. The black continuous lines represent the exact boundaries, while the red dashed curve represents the approximated boundary proposed in [43]

The analytical and the numerical displacement transmissibilities and phase angles are shown in Fig. 5a, b for varying frequency and friction ratios and unitary stiffness and mass ratios. Specifically, the frequency ratio varies in the range 0 : 2.5 and the friction ratios 0 : 0.2 : 0.8 are considered. In these figures, it is possible to observe an excellent agreement between the analytical (continuous lines) and numerical results (rounded markers) when the motion of $m_1$ is continuous. The analytical boundaries between continuous and stick-slip regimes are represented by a black dashed line. Numerical transmissibilities for stick-slip responses are also included (diamond markers). It can be observed that stick-slip motion occurs in the numerical responses only when the transmissibility is smaller than the boundary value, showing that the motion regimes occurring in the numerical results are in agreement with the analytical prediction. Numerical phase angles have only been evaluated for continuous responses. In fact, in this paper, the phase angle between the excitation and the response of each mass is referred to their maxima (see Sect. 2.2), but this definition cannot be used for stick-slip motion, where the maximum response of the mass in contact usually coincides with a sticking phase rather than a single point.

The following features of the dynamic response of this 2DOF system are observed in Fig. 5.

• Both resonant peaks are finite only in the case $\beta =0.8$, in agreement with Eq. (71).

• From Eq. (73), it can be calculated the starting values of the transmissibility curves at $r_1=0$ are $\overline{X}_{10}=\overline{X}_{20}=1-\beta$. These values are in agreement with those displayed in both transmissibility plots.

• At low frequency ratios, the response of the system is characterised by the occurrence of stick-slip motion. For most values of the friction ratio, the response is continuous starting from $r_1=0.559$. Among those displayed, only in the case $\beta =0.2$ continuous motion occurs at lower frequencies, specifically in the range $0.372<r_1<0.524$. The patterns exhibited by the transmissibility curves in the low frequency ratio range are very similar to those observed for SDOF systems (see, e.g. Fig. 11 in reference [27]).

• It can be observed that stick-slip motion occurs at high frequencies for $\beta =0.8$ and it has been verified that this is also the case for $\beta =0.6$, even though the transition from continuous to stick-slip regime does not occur within the range of frequencies displayed in Fig. 5. This behaviour is in agreement with Eq. (76).

• The invariant points of $\overline{X}_1$ can be evaluated from Eq. (77). These points are observed in Fig. 5a as the intersections between the undamped and the boundary curves, which are particularly well-visible in the phase angle plot. As anticipated in Sect. 3.2, most of these points are located in the low-frequency region, where the response is discontinuous for most values of $\beta$. Since Eq. (77) only holds for continuous regime, the transmissibility and the phase angle curves will not pass through these points, which can therefore be disregarded. The only relevant solutions are $r_1=0.559$ and $r_1=1.123$, which represent the main points of transition from continuous to stick-slip regime for most curves.

• The invariant points of $\overline{X}_2$, which can be obtained from Eq. (78), are associated with local inversions of the transmissibility curves, occurring at $0.527<r_1<0.576$ and $1<r_1<1.201$. However, as shown in Fig. 5b, none of these is associated with a significant increase of $\overline{X}_2$ with $\beta$.

• It can be observed that $\phi _2\cong \phi _1$ for $r_1<\sqrt{\kappa /\gamma }$ and $\phi _2\cong \phi _1+\pi$ for $r_1\ge \sqrt{\kappa /\gamma }$. This result can be explained by observing that mass $m_2$ is only excited, through the upper spring, by the motion of the lower mass, which is nearly monoharmonic in most cases.

Fig. 7

5DOF system with a Coulomb contact and a harmonic load on $m_1$ and unitary mass and stiffness ratios (a), displacement transmissibilities (b) and phase angles (c) for varying friction ratios. Analytical results for continuous motions are represented with continuous lines, while numerical results for stick-slip motions with dashed lines. The black dashed line represents the boundary between continuous and stick-slip regimes

Fig. 8

Analytical (continuous lines) and numerical (round markers) steady-state time response (a) and phase angle curves (b) of a 5DOF system with a Coulomb contact and a harmonic load on $m_1$ and unitary mass and stiffness ratios. The grey regions indicate stick-slip and stuck regimes

Finally, Fig. 6 shows the analytical boundaries among continuous, stick-slip and permanent sticking motion regimes, obtained by using Eqs. (66) and (79), respectively. The boundary between continuous and stick-slip regimes obtained using the approximated formulation from Eq. (68), which had already been proposed and numerically validated in reference [43], is represented by the red curve. The exact and approximated boundary curves are very similar but some differences can be observed at low frequency ratios, where the exact boundary presents a smoother pattern and does not intersect the boundary between sliding and permanent sticking regimes.

4.1.2 5DOF system with excitation and contact on $m_1$

Most of the response features discussed for the 2DOF case can also be observed in systems with a larger number of DOFs if excitation and contact are applied to the same mass.

Let us consider, for instance, the case of a 5DOF system with unitary stiffness and mass ratios where $j=l=1$, as shown in Fig. 7a. The analytical transmissibilities and phase angles are plotted in Fig. 7b, c, for the same frequency ratio range and values of friction ratio considered in Sect. 4.1.1; in Fig. 7b, the numerical transmissibilities in stick-slip regime have also been included. The analytical and the numerical time responses of this system are shown, for a specific set of parameters, in Fig. 8a, exhibiting an excellent agreement. Analytical and numerical phase angles curves, associated with the different masses of the system, are shown in Fig. 8b for varying $r_1$ and $\beta =0.4$; also in this case, a very good agreement can be observed. Finally, the boundaries among continuous, stick-slip and permanent sticking motion regimes are represented in Fig. 9.

Fig. 9

Motion regimes of a 5DOF system with equal masses and springs, with a Coulomb contact and a harmonic load on $m_1$ for varying frequency and friction ratios

Fig. 10

2DOF system with a friction contact on $m_1$ and a harmonic load on $m_2$ (a) and comparison between analytical (continuous lines) and numerical (round markers) steady-state time responses for two different sets of mass, stiffness, friction and frequency ratios (b, c)

From these figures, the following behaviours can be observed:

• the transmissibility curves present finite resonant peaks only in the case $\beta =0.8$, among those considered;

• the displacement transmissibilities are generally decreasing for increasing values of $\beta$. Local inversions can be observed for the masses not in contact, but they always occur in small intervals of $r_1$ and only present a slight increase in the transmissibility;

• the motion of each mass of the system is approximatively in phase or in phase-opposition with the motion of the other masses. This is clearly observed in Fig. 8a, b.

• the boundary between continuous and stick-slip regimes exhibits a similar pattern to that observed for the 2DOF case in Fig. 6. In particular, the boundary has an irregular behaviour at low frequency ratios and presents five maxima which are all characterised by the friction ratio $\beta \cong 0.83$. All these maxima are reached smoothly, except the one occurring at the lowest frequency ratio.

Figure 8b shows that the phase angle curves, particularly those of the mass in contact $m_1$, present slightly different patterns only in proximity of the transition to stick-slip regimes and at high frequency ratios. This behaviour can be explained observing that in these two cases the response of the mass in contact, which is usually nearly monoharmonic in continuous regime, is significantly affected by the higher harmonics.

Fig. 11

Displacement transmissibilities and phase angles of a 2DOF system with a contact on $m_2$ and a harmonic load on $m_1$ for varying friction ratios and unitary mass and stiffness ratios, displayed on $m_1$ (a) and on $m_2$ (b). Analytical results are represented by the continuous lines, while numerical results are represented with round (continuous motion) and with diamond markers (stick-slip motion). The black dashed line represents the boundary between continuous and stick-slip regimes, while the dotted black line represents the response in stuck configuration

4.2 Systems with harmonic excitation applied to a mass not in contact

4.2.1 2DOF system excited on $m_1$ with $m_2$ in contact

Let us consider a 2DOF system with a friction contact on the mass $m_2$ and excited by a harmonic load applied on $m_1$, as shown in Fig. 10a. A comparison between the analytical and the numerical time responses of this system in the non-dimensional time interval $[0,\pi ]$ is portrayed in Fig. 10b, c for two different sets of parameters, showing an excellent agreement. Analytical and numerical results for the displacement transmissibilities and the phase angles are compared in Fig. 11a, b, for varying frequency ratios within the range 0 : 2.5 and for the friction ratios [0, 0.2, 0.4, 0.5, 1, 1.5, 2, 5]. Also in this case, the agreement between analytical and numerical results in continuous motion regime is very good. Furthermore, stick-slip motion occurs in the numerical responses only when the transmissibility of the mass in contact is smaller than the boundary value, as expected.

The main features of the dynamic response of this 2DOF system, which can be observed in Fig. 11, are summarised in what follows.

• It can be observed that the first and the second resonant peaks become finite starting from the cases $\beta =0.5$ and $\beta =1.5$, respectively. This result agrees with the values obtained from Eq. (71), which are $\beta _{n,1}=0.485$ and $\beta _{n,2}=1.271$.

• The stuck configuration of this 2DOF system is represented by an undamped SDOF system where the mass $m_1$ is connected to a fixed wall on both sides through the springs $k_1$ and $k_2$, respectively. The transmissibility and the phase angle associated with this stuck configuration are represented in Fig. 11a with a black dotted line. Particularly, the displacement transmissibility can be expressed as [43]:

  $$\begin{aligned} \overline{X}^*_1=\dfrac{1}{|1+\kappa -r_1^2|} \end{aligned}$$

  (82)

  and the phase angle is equal to 0 degrees before the natural frequency ratio $r_1=\sqrt{1+\kappa }$ and 180 degrees afterwards. It can be observed as the transitions between stuck and sliding configurations always occur at $\overline{X}^*_1=\beta /\kappa$, as predicted from Eq. (79a).

Fig. 12

Motion regimes of a 2DOF system with a Coulomb contact on $m_2$ and a harmonic load on $m_1$ for varying frequency and friction ratios. The black continuous lines represent the exact boundaries, while the red dashed curve represents the approximated boundary proposed in [43]

Fig. 13

5DOF system with a Coulomb contact on $m_3$, a harmonic load on $m_1$ and unitary mass and stiffness ratios (a), displacement transmissibilities (b) and phase angles (c) for varying friction ratios. Analytical results for continuous motions are represented with continuous lines and numerical results for stick-slip motions with dashed lines. The black dashed line represents the boundary between continuous and stick-slip regimes, while the dotted black line represents the response in stuck configuration

Fig. 14

Analytical (continuous lines) and numerical (round markers) steady-state continuous time response (a) and phase angle curves (b) of a 5DOF system with a Coulomb contact on $m_3$, a harmonic load on $m_1$ and unitary mass and stiffness ratios. The grey regions indicate stick-slip and stuck regimes

• According to Eq. (73), the starting values of the transmissibility curves are $\overline{X}_{10}=1-\beta$ and $\overline{X}_{20}=1-(1+\kappa )\beta /\kappa$. These values agree well with those shown from the transmissibilities curves up to $\beta =0.4$. Starting from $\beta =0.5$, the mass $m_2$ will be stuck for $r_1\rightarrow 0$.

• As discussed in Sect. 3.2 and Sect. 3.5, respectively, both boundaries between continuous and stick-slip regimes and between sliding and stuck regimes tend to zero for $r_1\rightarrow \infty$ when $j\ne l$. In Figs. 11 and 12, it is possible to observe that stick-slip motion always occurs at high frequencies before the transition to the stuck configuration.

• All the transmissibility and the phase angle curves associated with the mass in contact $m_2$, shown in Fig. 11b, intersect at $r_1=1.450$. This value corresponds to the larger solution of Eq. (77), while the other solutions of this equation represent the other intersections occurring between the undamped and the boundary curves, as already observed in the 2DOF case discussed in Sect. 4.2.1.

• Two main invariant points for $\overline{X}_1$ are observed in Fig. 11a at $r_1=0.828$ and $r_1=1.549$. These values of $r_1$ correspond to the two largest solutions of Eq. (78) and are associated with a significant inversion of the transmissibility curves. In fact, in the frequency ratio interval included between these points, the transmissibility increases with $\beta$, leading the gradual onset of the resonant peak associated with the stuck configuration.

• The evolution of the phase angle $\phi _1$ is quite irregular for varying friction ratios. However, it can be observed that its value is always smaller than $\phi _2$, showing that $m_1$ oscillate with an intermediate phase angle between those of the excitation and of the response of $m_2$.

Finally, Fig. 12 shows the boundaries among continuous and stick-slip regimes and between sliding and permanent sticking regimes. It can be observed that also in this case the exact and the approximated boundary between continuous and stick-slip regimes are nearly identical. The boundary between sliding and permanent sticking regimes exhibits the same infinite peak shown in the transmissibility curves of the stuck configuration, as expected from Eq. (79a).

4.2.2 5DOF system excited on $m_1$ with $m_3$ in contact

The 5DOF system with a contact on $m_3$ and a harmonically load on $m_1$ shown in Fig. 13a represents a more general example of system with $j\ne l$. The displacement transmissibility curves, obtained analytically for continuous motion and numerically in stick-slip regime, are plotted in Fig. 13b, while the analytical phase angles are depicted in Fig. 13c for continuous response only. Analytical and numerical time responses are compared in Fig. 14a for a specified set of parameters, showing an excellent agreement. Analytical and numerical phase angles on the different masses of the system are represented in Fig. 14b. Finally, the boundaries among continuous, stick-slip and permanent sticking regimes are shown in Fig. 15. In these figures, many of the patterns and features described in the 2DOF case can be observed. In particular:

• the transmissibility of the mass in contact $m_3$ always decreases with $\beta$, except that in the invariant points. In Fig. 11, it can be observed that all the curves pass through two invariant points, located in proximity of the natural frequencies of the stuck configuration. In general, it has been verified that the number of these invariant points is always equal to the number of peaks of the stuck configuration. Despite this, invariant points and stuck resonant peaks occur at close but not coincident frequency ratios;

• the masses $m_4$ and $m_5$ oscillate in phase or in-phase opposition with $m_3$ for most values of frequency and friction ratios and their transmissibility curves have similar patterns to those of $\overline{X}_3$. This behaviour is typical of the masses located on the opposite side of the harmonic excitation with respect to the mass in contact and has already been described for the 5DOF system investigated in Sect. 4.2.2.

• the masses $m_1$ and $m_2$ do not oscillate in phase with $m_3$ or between each other. Their transmissibility curves exhibit significant inversions which lead to the onset of the two resonant peaks of the stuck configuration. In general, this behaviour is observed in the masses located on the same side of the excitation with respect to the mass in contact. The inversions of the transmissibility curves leading to the stuck resonant peaks always occur through two invariant points.

Fig. 15

Motion regimes of a 5DOF system with equal masses and springs, with a Coulomb contact on $m_3$ and a harmonic load on $m_1$ for varying frequency and friction ratios

Fig. 16

2DOF systems under harmonic base excitation with a Coulomb contact: a between the $m_1$ and the mass $m_2$ and b between the $m_1$ and the base

5 Extension to MDOF systems with a contact between oscillating parts

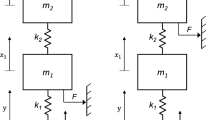
In this section, the analytical solution derived for the response of a MDOF system with a Coulomb contact between one of the masses and a fixed wall in Sect. 2 is extended to address the cases where the contact occurs: (i) between two different masses of the system and (ii) between a mass and a harmonically excited base. The features of the dynamic response of these systems will be discussed referring as example to 2DOF models where the contact is achieved between $m_1$ and $m_2$ (Fig. 16a) and between the base and $m_1$ (Fig. 16b), respectively. These mechanical models are similar to those used in references [44,45,46,47] if viscous damping is neglected. In fact, the schematic representation of the system shown in Fig. 16a is used in the energy harvester case in [47], while the model in Fig. 16b is used in the remaining cases: in [44], the upper mass, spring and friction contact represent a friction damper which is applied to the main building (represented by $m_1$ and $k_1$); in [45], the 2DOF system represents a quarter-car model where a friction contact is included in the connection between the tyre and the car; in [46], the contact between $m_1$ and $m_2$ refers to the presence of friction in the taxi system of an aircraft between the outer cylinder and the piston rod.

5.1 Contact between two masses

5.1.1 Evaluation of the continuous steady-state response

Let us consider a MDOF system with N masses and N springs excited by the harmonic load $P\cos (\omega t)$ applied to the lth mass, where a friction contact occurs between the masses $m_A$ and $m_B$, with $A<B$. The generic ith governing equation can be written as:

$$\begin{aligned}&m_i\ddot{x}_i-k_ix_{i-1}+(k_i+k_{i+1})x_i-k_{i+1}x_{i+1}\nonumber \\&\quad +(\delta _{Bi}-\delta _{Ai})F\mathrm {sgn}(\dot{x}_B-\dot{x}_A)=\delta _{li}P\cos (\omega t) \end{aligned}$$

(83)

or, in non-dimensional terms, as:

$$\begin{aligned}&\gamma _ir_1^2\bar{x}''_i+\sum _{k=1}^N \overline{K}_{ik}\bar{x}_k\nonumber \\&\quad +(\delta _{Bi}-\delta _{Ai})\beta \mathrm {sgn}(\bar{x}'_B-\bar{x}'_A)=\delta _{li}\cos \tau \end{aligned}$$

(84)

In order to apply to this system the analytical procedure introduced in Sect. 2, let us indicate the relative motion in the friction contact as:

$$\begin{aligned} \bar{z}=\bar{x}_B-\bar{x}_A \end{aligned}$$

(85)

and consider the non-dimensional time interval $[0,\pi ]$ included between a maximum and the subsequent minimum of $\bar{z}$, under the assumption of continuous steady-state motion. Equation (84) will then reduce to the linear equation:

$$\begin{aligned} \gamma _ir_1^2\bar{x}''_i+\sum _{k=1}^N\overline{K}_{ik}\bar{x}_k=(\delta _{Bi}-\delta _{Ai})\beta +\delta _{li}\cos (\tau +\phi _z) \end{aligned}$$

(86)

where $\phi _z$ is the phase angle between the excitation and the relative motion $\bar{z}$. Introducing the coordinate transformation from Eq. (13), it is possible to write the governing equation for the generic ith modal coordinate as:

$$\begin{aligned} \eta _i''+\Omega _i^2\eta _i=(\psi _{Bi}-\psi _{Ai})\beta +\psi _{li}\cos (\tau +\phi _z) \end{aligned}$$

(87)

Comparing Eq. (87) with Eq. (15), it can be noted that the term $\psi _{ji}$ is here replaced by $\psi _{Bi}-\psi _{Ai}$. This can also be observed in the initial conditions for the relative motion:

if compared to the initial conditions for the mass in contact written in Eq. (31). In the above conditions, $\overline{Z}$ indicates the amplitude of the non-dimensional relative motion. Therefore, it can easily be shown that the phase angle $\phi _z$ and the amplitude $\overline{Z}$ of the relative motion, as well as the steady-state time response, can be obtained from Eqs. (37), (40), (41) and (43) by replacing $\psi _{ji}$ with $\psi _{Bi}-\psi _{Ai}$. The expression of time response of the generic kth mass of the system will be:

$$\begin{aligned}&\bar{x}_k= \dfrac{V_k}{V_z}\left( \overline{Z}\cos \tau +\beta U_z\sin \tau \right) +\beta \sum \limits _{i=1}^N(\psi _{Bi}-\psi _{Ai}) \nonumber \\&\quad \cdot \psi _{ki}R_i^2\left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) -u_iR_i\sin \left( \dfrac{\tau }{R_i}\right) \right] \end{aligned}$$

(89)

where

$$\begin{aligned} \overline{Z}=\sqrt{V_z^2-(\beta U_z)^2} \end{aligned}$$

(90)

The response and the damping functions $V_z$ and $U_z$ are obtained from Eqs. (36) and (39) by applying the substitution specified above. Similarly, the displacement transmissibility of the generic mass $m_k$ of the system could be written in a closed form, from Eq. (52), as:

$$\begin{aligned} \overline{X}_{k}\cong \sqrt{V_k^2+ \left( 1-2\dfrac{V_k}{V_z}\dfrac{U_z}{U_k}\right) (\beta U_k)^2} \end{aligned}$$

(91)

following the monoharmonic approximation introduced in Sect. 2.6. However, it has been observed that Eq. (91) does not describe accurately the transmissibility curves of the masses in contact. In fact, the response of these masses is more markedly non-monoharmonic compared to that of the other masses. Therefore, it is not advised to refer to Eq. (91) if an accurate evaluation of the displacement transmissibility is required; in this case, the numerical evaluation of the maximum absolute value of Eq. (89) within the time interval $[0,\pi ]$ is preferred and has been considered when plotting Fig. 17. Nonetheless, Eq. (91) can be considered for other purposes, such as determining whether invariant points and inversions occur across the transmissibility curves and their approximative location. More details are given in Sect. 5.1.4.

5.1.2 Boundary between continuous and stick-slip regimes

In order to observe the continuous non-sticking response described in the previous paragraph, two conditions need to be met:

• the relative velocity in the contact must be different from zero in all the internal points of the time interval $[0,\pi ]$. In particular, it has been assumed that $\bar{z}'<0$ in this interval;

• the amplitude of the resultant dynamic load acting in the contact must overcome the static friction force when the relative velocity is zero, i.e. at $\tau =0$ and $\tau =\pi$.

While the first condition will simply lead to the boundary expressed by Eq. (60) if $\psi _{ji}$ is replaced by $\psi _{Bi}-\psi _{Ai}$, more attention needs to be paid to the second condition. As shown in reference [43], this non-sticking condition can be obtained by subtracting from the Bth governing equation of the system the Ath governing equation multiplied by the ratio between the two masses in contact:

$$\begin{aligned} \gamma _{AB}=\dfrac{m_B}{m_A}=\dfrac{\gamma _B}{\gamma _A} \end{aligned}$$

(92)

From Eq. (84), it can be obtained that:

$$\begin{aligned}&\gamma _Br_1^2\bar{z}''+\sum _{k=1}^N\left( \overline{K}_{Bk}-\gamma _{AB}\overline{K}_{Ak}\right) \bar{x}_k\nonumber \\&\quad +\beta (1+\gamma _{AB})\mathrm {sgn}(\bar{z}')=(\delta _{lB}-\gamma _{AB}\delta _{lA})\cos \tau \end{aligned}$$

(93)

When the relative velocity is zero, sticking will not occur if:

$$\begin{aligned}&\left| \sum _{k=1}^N\left( \overline{K}_{Bk}-\gamma _{AB}\overline{K}_{Ak}\right) \bar{x}_k\right. \nonumber \\&\quad \left. -(\delta _{lB}-\gamma _{AB}\delta _{lA})\cos \tau \right| >\mu \beta (1+\gamma _{AB}) \end{aligned}$$

(94)

Introducing Eq. (13) and after some algebraic manipulations, it is possible to write this condition in modal terms as:

$$\begin{aligned} |\Omega _i^2\eta _{i0}-\psi _{li}\cos \phi _z|>(\psi _{Bi}-\psi _{Ai})\mu \beta \end{aligned}$$

(95)

which can be eventually expressed in terms of the friction ratio as:

$$\begin{aligned} \beta <\sqrt{\dfrac{V_z^2}{U_z^2+\bigg [\bigg (\dfrac{1}{\gamma _A}+\dfrac{1}{\gamma _B}\bigg )\dfrac{\mu }{r_1^2}\bigg ]^2}} \end{aligned}$$

(96)

The boundary between continuous and stick-slip regimes can finally be obtained by merging Eq. (23), rewritten posing $\psi _{ji}=\psi _{Bi}-\psi _{Ai}$, and Eq. (96):

$$\begin{aligned} \beta <\sqrt{\dfrac{V_z^2}{U_z^2+\left[ \max \bigg (S_z,\bigg (\dfrac{1}{\gamma _A}+\dfrac{1}{\gamma _B}\bigg )\dfrac{\mu }{r_1^2}\bigg )\right] ^2}} \end{aligned}$$

(97)

All the considerations reported at the end of Sect. 2.7 also apply to this contact configuration.

5.1.3 Stuck configuration

In order to have a complete overview of the dynamic response of MDOF systems with a contact between two masses, it is also necessary to determine which are the conditions leading to permanent sticking between these masses and how the response of the system can be characterised when this happens.

In reference [43], it has been shown that the masses $m_A$ and $m_B$ are permanently stuck, they oscillate together as a single mass $m_A+m_B$ and their motion can be evaluated referring to the coordinate of their centroid:

$$\begin{aligned} \bar{x}_c=\dfrac{m_A\bar{x}_A+m_B\bar{x}_B}{m_A+m_B} \end{aligned}$$

(98)

The governing equation for $\bar{x}_c$ can be obtained by summing the equations governing the motion of the masses $m_A$ and $m_B$ and substituting Eq. (98):

$$\begin{aligned} (m_A+m_B)\bar{x}''_c+\sum _{k=1}^N\left( \overline{K}_{Ak}+\overline{K}_{Bk}\right) \bar{x}_i=(\delta _{Ai}+\delta _{Bi})\cos \tau \end{aligned}$$

(99)

Equation (99) can be coupled with the governing equations of the masses not involved in the contact, obtaining a system of $N-1$ linear equations in the form:

$$\begin{aligned} \overline{\mathbf {M}}^{*}\bar{\mathbf {x}}^{*''}+\overline{\mathbf {K}}^{*}\bar{\mathbf {x}}^{*}=\bar{\mathbf {p}}^{*} \end{aligned}$$

(100)

where the matrices $\overline{\mathbf {M}}^{*}$ and $\overline{\mathbf {K}}^{*}$ can be obtained from $\overline{\mathbf {M}}$ and $\overline{\mathbf {K}}$ (in Eqs. (9) and (10), respectively) by removing the original Ath and Bth rows and columns and including a new row and a new column with the terms provided in Eq. (99). Similarly, the vector $\bar{\mathbf {p}}^{*}$ can be obtained removing the Ath and the Bth components and adding the new component $(\delta _{Ai}+\delta _{Bi})\cos \tau$ given by Eq. (99).

Modal analysis can be used to determine the response of the system. In particular, the response amplitudes $\overline{X}^*_1$, ..., $\overline{X}^*_N$, where $\overline{X}^*_A=\overline{X}^*_B\equiv \overline{X}^*_c$ allow the determination of boundary between sliding and permanent sticking regimes. In fact, bearing in mind that a contact becomes permanently stuck if the maximum load acting on it does not overcome the static friction force and considering Eq. (94), it is possible to express such a boundary as:

$$\begin{aligned}&\beta <\dfrac{1}{\mu (1+\gamma _{AB})}\bigg |\sum _{k=1}^N\left( \overline{K}_{Bk}-\gamma _{AB}\overline{K}_{Ak} \right) \overline{X}^*_k\nonumber \\&\quad -(\delta _{lB}-\gamma _{AB}\delta _{lA})\bigg | \end{aligned}$$

(101)

5.1.4 Numerical validation and discussion

The analytical solutions derived in this section have been compared, for varying parameters, with the results obtained via numerical integration following the approach introduced in [43]. The agreement was excellent in all the cases investigated. In particular, the comparison between analytical and numerical transmissibilities is shown in Fig. 17 for the 2DOF system shown in Fig. 16a, in the frequency ratio range 0 : 2.5 and for varying friction ratio, assuming both stiffness and mass ratios equal to 0.5 and a unitary ratio between static and kinetic friction forces. The agreement between the transmissibilities is very good when the response is continuous. The motion regimes occurring in the numerical response are always in accordance with the analytical predictions. The analytical boundaries of these motion regimes are also shown in the parameter space $r_1-\beta$ in Fig. 18.

Fig. 17

Displacement transmissibilities of a harmonically excited 2DOF system with a contact between $m_1$ and $m_2$ for varying friction ratio and $\gamma =\kappa =0.5$: (a) absolute motions of $m_1$ and $m_2$ and (b) relative motion in the contact. Analytical results are represented by the continuous lines, while numerical results are represented with round (continuous motion) and with diamond markers (stick-slip motion). The black dashed line represents the boundary between continuous and stick-slip regimes, while the dotted black line represents the response in stuck configuration

Fig. 18

Motion regimes of a 2DOF system with a Coulomb contact and a harmonic load on $m_1$ for varying frequency, friction ratios and static friction forces

The general features of the dynamic response of MDOF systems with a Coulomb contact between two masses are discussed in what follows.

• The value $\beta _{n,i}$ of the friction ratio for which the ith resonant peak becomes finite can be evaluated by calculating the limit of Eq. (97) for $R_i\rightarrow 1$, as proposed in Sect. 3.5, and is given by:

  $$\begin{aligned} \beta _{n,i} = \dfrac{\pi }{4} \left| \dfrac{\psi _{li}}{\psi _{Bi}-\psi _{Ai}}\right| \end{aligned}$$

  (102)

  In the 2DOF case considered in this section, the values obtained from Eq. (102) are $\beta _{n,1} =0.785$ and $\beta _{n,2}=0.393$, in agreement with the curves shown in Fig. 17.

• Evaluating the limit value of the boundary between continuous and stick-slip motion for $r_1\rightarrow 0$, it can be shown that, as in the fixed wall case, any nonzero value of the friction ratio will prevent the relative motion in the contact from being continuous in quasi-static conditions. The starting value of the boundary between sliding and permanent sticking regimes can instead be evaluated from Eqs. (100) and (101), imposing that $r_1=0$. While this is not true in general, it has been observed that the system is always stuck in quasi-static conditions if $l=1$. This behaviour also occurs in the example presented in this section, as shown in Fig. 18.

• The high-frequency behaviour of these MDOF systems can significantly change depending on where the friction contact and the harmonic load are applied. In fact, when $r_1\rightarrow \infty$, the boundary between continuous and stick-slip regimes expressed in Eq. (97) tends to:

Furthermore, evaluating Eq. (101) for $r_1\rightarrow \infty$, it can be determined that the boundary between sliding and permanent sticking regimes tends to:

In the 2DOF case dealt with in this section, since $l=A=1$ and $\gamma _{AB}=\gamma =0.5$, it is obtained that $\beta _\infty =0.179$ and $\beta ^*_\infty =0.333$, in agreement with Fig. 18. It can be concluded that if the harmonic excitation is applied to one of the masses in contact, both boundaries will tend to nonzero asymptotic values, below which continuous and stick-slip motions can be observed, respectively. Conversely, if the excitation is applied to any other masses, both boundaries will tend to zero, meaning that the contact will always get stuck at high frequencies.

• In Fig. 17a, it can be observed that for both masses an inversion of the transmissibility curves occurs across two invariant points and leads to the onset of the resonant peak associated to the stuck configuration. It is possible to obtain an estimate of the position of these points from Eq. (91), as explained in Sect. 5.1.1. For instance, the points estimated for $\overline{X}_1$ are $r_1=0.778$ and $r_1=1.213$, while it has been observed that the actual inversion occurs between two small regions (rather than single points) located at $r_1\cong 0.770$ and $r_1\cong 1.226$. Finally, the amplitude of the relative motion in the contact (from Fig. 17b) always decreases with $\beta$, similarly to the motion of the mass in contact in systems with a fixed wall. In this case, the invariant points can be evaluated exactly from the condition $U_z=0$.

5.2 Joined base-wall excitation

5.2.1 Evaluation of the continuous steady-state response

Let us consider a MDOF mass–spring system excited by the harmonic base motion $y=Y\cos (\omega t)$. A Coulomb contact characterised by the friction force F occurs between the oscillating base and the mass $m_j$. The ith governing equation of the system is given by:

$$\begin{aligned}&m_i\ddot{x}_i-k_ix_{i-1}+(k_i+k_{i+1})x_i-k_{i+1}x_{i+1}\nonumber \\&\quad +\delta _{ji}F\mathrm {sgn}(\dot{x}_j-\dot{y})=\delta _{1i}k_1Y\cos (\omega t) \end{aligned}$$

(105)

Considering $P=k_1Y$ in Eq. (5), Eq. (105) can also be expressed in a non-dimensional form as:

$$\begin{aligned} \gamma _ir_1^2\bar{x}''_i+\sum _{k=1}^N \overline{K}_{ik}\bar{x}_k+\delta _{ji}\beta \mathrm {sgn}(\bar{x}'_j-\bar{y}')=\delta _{1i}\cos \tau \end{aligned}$$

(106)

A possible approach for extending the theory presented in Sect. 2 to a system with this contact configuration has been proposed in reference [43] and consists in introducing a coordinate transformation such that the given system can be studied as an equivalent system with a fixed wall. Alternatively, it is possible to use the approach introduced in Sect. 5.1.1, by indicating the relative motion between the mass in contact and the base as:

$$\begin{aligned} \bar{z} = \bar{x}_j - \bar{y} \end{aligned}$$

(107)

and rewriting Eq. (106) in the non-dimensional time interval $[0,\pi ]$ included between a maximum and a minimum of $\bar{z}$, under the assumption of continuous response, as:

$$\begin{aligned} \gamma _ir_1^2\bar{x}''_i+\sum _{k=1}^N \overline{K}_{ik}\bar{x}_k=\delta _{ji}\beta +\delta _{1i}\cos (\tau +\phi _z) \end{aligned}$$

(108)

Applying the modal transformation from Eq. (13), the same set of modal equations as that expressed by Eq. (15) is obtained from Eq. (106). The initial conditions for the relative motion will instead be given by:

Substituting Eqs. (109a) and (109b) into Eqs. (37) and (40), respectively, it is possible to obtain the following expressions for the phase angle between excitation and relative motion $\bar{z}$:

$$\begin{aligned}&\cos \phi _z = \dfrac{\overline{Z}}{V_j-1} \end{aligned}$$

(110)

$$\begin{aligned}&\sin \phi _z = \dfrac{-\beta U}{V_j-1} \end{aligned}$$

(111)

while the non-dimensional amplitude of the relative motion will be:

$$\begin{aligned} \overline{Z}= \sqrt{(V_j-1)^2-(\beta U)^2} \end{aligned}$$

(112)

It can be observed that these expressions are equivalent to those obtained in Sect. 2.5 for the fixed wall case if $V_j$ is substituted with $V_j-1$. The response of the generic mass $m_k$ can also be obtained from Eq. (43), introducing such a substitution, as:

$$\begin{aligned}&\bar{x}_k= \dfrac{V_k}{V_j-1}\left( \overline{Z}\cos \tau +\beta U_j\sin \tau \right) +\beta \sum \limits _{i=1}^N\psi _{ji}\psi _{ki}R_i^2\nonumber \\&\quad \times \left[ 1-\cos \left( \dfrac{\tau }{R_i}\right) -u_iR_i\sin \left( \dfrac{\tau }{R_i}\right) \right] \end{aligned}$$

(113)

It can be observed that Eqs. (112) and (113) reduce to the expressions provided in reference [30] for a SDOF system under joined base-wall excitation if $N=1$.

Also for this contact configuration, a closed-form expression can be obtained for the generic kth displacement transmissibility, by using the monoharmonic approximation introduced in Sect. 2.6, as:

$$\begin{aligned} \overline{X}_{k}\cong \sqrt{V_k^2+ \left( 1-2\,\dfrac{V_k}{V_j-1}\dfrac{U_j}{U_k}\right) (\beta U_k)^2} \end{aligned}$$

(114)

However, as in the case of the friction contact occurring between two masses, this approximation does not provide an accurate result for the mass in contact $m_j$ and, therefore, its use is not advised for obtaining an accurate evaluation of the response amplitudes, while it can similarly be used for investigating the presence of invariant points across the transmissibility curves.

5.2.2 Boundary between continuous and stick-slip regimes

The assumption of continuous steady-state response is verified, as in the other contact configurations explored in this paper, when the relative velocity in the contact is negative in all the internal points of the time interval $[0,\pi ]$ and, simultaneously, the sum of all the non-inertial forces acting in the contact is larger than the static friction force at both ends of this interval. Following the procedure described in Sect. 2.7, it can be shown that the first condition can be expressed in terms of the friction ratio by substituting $V_j-1$ to $V_j$ in Eq. (60). In order to write the second condition, it is necessary to derive the governing equation for the relative motion $\bar{z}$. This equation can be obtained by substituting Eq. (107) into Eq. (106), written for $i=j$:

$$\begin{aligned} \gamma _jr_1^2\bar{z}''+\sum _{k=1}^N \overline{K}_{jk}\bar{x}_k+\beta \mathrm {sgn}(\bar{z}')=(\delta _{1j}+\gamma _jr_1^2)\cos \tau \end{aligned}$$

(115)

The second non-sticking condition can therefore be expressed as:

$$\begin{aligned} \left| \sum _{k=1}^N\overline{K}_{jk}\bar{x}_k-(\delta _{1j}+\gamma _jr_1^2)\cos \tau \right| >\mu \beta \end{aligned}$$

(116)

Introducing Eq. (13), this inequality can be rewritten in modal terms as:

$$\begin{aligned} |\Omega _i^2\eta _{i0}-(\psi _{li}+\gamma _jr_1^2)\cos \phi _z|>\psi _{ji}\mu \beta \end{aligned}$$

(117)

With a similar procedure to that introduced in Sect. 2.7, this equation can be formulated in terms of the friction ratio in the same form as in Eq. (65), where $V_j$ is replaced with $V_j-1$. Finally, the boundary between continuous and stick-slip motion can be expressed, merging the two conditions derived, as:

$$\begin{aligned} \beta <\sqrt{\dfrac{(V_j-1)^2}{U_j^2+\left[ \max \bigg (S_j,\dfrac{\mu }{\gamma _jr_1^2}\bigg )\right] ^2}} \end{aligned}$$

(118)

5.2.3 Stuck configuration

As shown in Sects. 3.3 and 5.1.3, two main steps are required for deriving the boundary between sliding and permanent sticking motion regimes: (i) deriving the steady-state response of the system in the stuck configuration and (ii) using the derived response amplitudes for determining the maximum dynamic load acting in the contact and comparing it to the static friction force.

In this contact configuration, when sticking occurs, the mass in contact will oscillate jointly to the wall. Therefore, its motion can simply be written as $\bar{x}_j=\cos \tau$. The motion of the remaining masses can be determined from a linear system of $N-1$ equations written in the form expressed in Eq. (100), where the stuck mass and stiffness matrices are obtained by removing the jth rows and columns from $\overline{\mathbf {M}}$ and $\overline{\mathbf {K}}$, while the generic ith component of the stuck force vector will be:

$$\begin{aligned} \bar{p}^*_i = (\delta _{1i}+\delta _{j-1,i}\kappa _j+\delta _{ji}\kappa _{j+1})\cos \tau \end{aligned}$$

(119)

In other words, since its motion is already known, the mass $m_j$ will act as a further source of harmonic excitation in the stuck system. Therefore, a harmonic load $\kappa _j\cos \tau$ will be applied onto the mass $m_{j-1}$ and a load $\kappa _{j+1}\cos \tau$ will act on the mass $m_{j+1}$.

The formulation of the upper bound for the sliding motion regime can be obtained, at this stage, from Eq. (116), considering the maximum amplitude of the resultant force acting in the friction contact:

$$\begin{aligned} \beta <\dfrac{1}{\mu }\left| \sum _{k=1}^N\overline{K}_{jk}\overline{X}^*_k-\delta _{1j}-\gamma _jr_1^2\right| \end{aligned}$$

(120)

5.2.4 Numerical validation and discussion

The analytical results obtained for MDOF systems under joined base-wall harmonic excitation have been compared to numerical results for varying frequency, friction, mass and stiffness ratios, showing a very good agreement in all the cases investigated. The comparison between the analytical and numerical response amplitudes for the 2DOF system represented in Fig.16b is reported in Fig.19; the results shown in these plots have been obtained for unitary mass, stiffness and static/kinetic friction force ratios. An excellent agreement is observed for both absolute mass motions (in Fig. 19a) and for the relative motion in the contact (in Fig. 19b). Numerical results obtained in stick-slip regime are also reported in Fig. 19a, b to provide a complete overview of the dynamic behaviour of the system, while the boundaries among continuous, stick-slip and stuck motion regimes are depicted in Fig. 20.

Fig. 19

Displacement transmissibilities of a 2DOF system with a contact on $m_1$ under harmonic joined base-wall motion for varying friction ratio and unitary mass and stiffness ratios: (a) absolute motions of $m_1$ and $m_2$ and (b) relative motion in the contact. Analytical results are represented by the continuous lines, while numerical results are represented with round (continuous motion) and with diamond markers (stick-slip motion). The black dashed line represents the boundary between continuous and stick-slip regimes, while the dotted black line represents the response in stuck configuration

The main dynamic response features are presented for MDOF systems under joined base-wall excitation in what follows, referring as example to the results shown in Figs.19 and 20.

Fig. 20

Motion regimes of a 2DOF system with a Coulomb contact and a harmonic load on $m_1$ for varying frequency, friction ratios and static friction forces

• The evaluation of limit value assumed by the boundary between continuous and stick-slip regimes when $R_i\rightarrow 1$ provides the same result obtained in Sect. 3.5 for the fixed wall configuration and reported in Eq. (70). Therefore, all the resonant peaks exhibited by systems undergoing joined base-wall excitation also become finite at $\beta =\pi /4$ if the friction contact occurs on the mass $m_1$. This is also observed in Fig. 19a, b, where both peaks are finite starting from the curves associated to the case $\beta =0.8$.

• The behaviour of these systems at low frequency ratios can easily be explained by evaluating the values assumed by both boundaries for $r_1\rightarrow 0$. As in all the contact configurations explored in this paper, also in this case the boundary between continuous and stick-slip regimes tends to zero. It can be demonstrated that also the boundary between sliding and permanent sticking regimes is equal to zero at $r_1=0$. In fact, when permanent sticking occurs, the static response of the system can simply be obtained by the equation $\overline{\mathbf {K}}^*\bar{x}^{*}=\bar{\mathbf {p}}^{*}$. However, it can be observed that substituting the response amplitudes obtained from this equation into Eq. (120) and imposing $r_1=0$, the resulting value of the boundary will be equal to zero. Therefore, it can be concluded that systems under joined base-wall motion are always stuck in quasi-static conditions, as already observed for the SDOF case in reference [30].

• The behaviour of these MDOF systems is also similar to that described for the SDOF case in [30] at high frequency ratios. In fact, both boundaries grows to infinity when $r_1\rightarrow 0$. This means that, increasing the driving frequency, it will always be possible to observe a sliding motion in the friction contact at some point.

• Inversions of the transmissibility curves can be seen for both masses in Fig. 19a. In particular, two different kinds of inversions can be observed. In the case of the mass not in contact, inversions are mostly similar to those described in the other contact configurations, i.e. they occur across two invariant points and show the gradual onset of a new resonant peak associated with the stuck configuration of the system. However, it can also be noted that another inversion occurs for all the masses of the system after the last resonant peak, so that the transmissibility always increases with the friction ratio at high frequency ratios. This inversion occurs across a small region rather than a single invariant point. This behaviour had already been observed in [30] for SDOF systems, where such an inversion occurs at $r_1\cong 1.5$.

6 Concluding remarks

Analytical solutions have been derived for the continuous steady-state response of a harmonically excited MDOF system with a Coulomb friction contact between: (1) a mass and a fixed wall; (2) two different masses; (3) a mass and an oscillating base. In particular, the expressions of the displacement transmissibility, the phase angle and the time response have been obtained for all the masses of the system. Moreover, the domain of validity of these solutions has also been determined, providing an analytical formulation for the boundary between continuous and stick-slip regimes which also takes into account the case where different static and kinetic friction forces are considered.

The closed-form expressions of the continuous response and of the boundaries have been used to investigate the features of the dynamic response of these MDOF systems. Specifically, the resonant, low- and high-frequency behaviours have been analysed and an analytical approach for the determination of the invariant points for the transmissibility and the phase angle curves have been proposed. Moreover, the response to harmonic excitation has also been determined in the case where the mass in contact is permanently stuck.

Finally, the analytical solutions for the continuous response have been validated numerically in the cases of: (i) a 2DOF system with a harmonic load on the lower mass and a friction contact on either on the lower or the upper mass: (ii) a 5DOF system with a harmonic load on the bottom mass and a friction contact either on the same or on the third mass. Numerical transmissibilities have also been evaluated in stick-slip regime for all these systems, providing a complete overview of their dynamic behaviour for varying non-dimensional exciting frequencies and friction forces. The comparison between analytical and numerical results showed an excellent agreement in all the cases investigated.

Fig. 21

Motion regimes of a 2DOF system with a Coulomb contact and a harmonic load on $m_1$ for varying frequency, friction ratios and static friction forces

Fig. 22

Motion regimes of a 2DOF system with a Coulomb contact on $m_2$ and a harmonic load on $m_1$ for varying frequency, friction ratios and static friction forces

The main results obtained from investigation of the response features were: (i) the determination of the minimum friction ratio for which the generic ith resonant peak of the response becomes finite; (ii) the determination of starting values of the transmissibility curves in quasi-static regime; and (iii) the evaluation of the asymptotic values assumed from the boundary between continuous and stick-slip regimes when the exciting frequency tends to infinity. In addition, the presence of invariant points, inversions across the transmissibility curves for varying non-dimensional friction force and the onset of additional resonant peaks due to the transition from the sliding to the stuck configurations have been observed in both analytical and numerical curves. All these results have shown that MDOF systems can exhibit a significantly different dynamic behaviour depending on whether the contact and the harmonic excitation occur on the same or on different masses.

In conclusion, the results presented in this paper contribute to the development of a fundamental understanding of the Coulomb damping effects on mechanical systems. These solutions have been obtained under the assumptions that dry friction is the only source of damping in the system and that Coulomb’s law can be used to model friction. Experimental investigations carried out on a single-storey shear frame with a brass-to-steel contact [27] have shown that these assumptions can be considered when describing the dynamic behaviour of simple structures where damping effects are mainly due to the presence of a friction contact. The shear frame set up has been extended to include two storeys to investigate the behaviour of a 2DOF system and preliminary results have shown a good agreement with the analytical results presented in this paper. These experimental results will be presented in a separate publication.

Overall, the presented results can be used for exploring design solutions of structures that can be modelled as MDOF mass–spring systems with a friction damper required to operate in a non-sticking continuous vibration regime. For example, they can be implemented to investigate the performance of a car suspension system with a friction damper. Moreover, the proposed analytical solutions for such systems can be exploited for carrying out parameter investigations, optimisations and statistical model updating with a reduced computational cost compared to numerical approaches.

Further work on this topic is currently focusing on: (i) the extension of the results presented in this contribution to MDOF systems with combined Coulomb and viscous damping: (ii) the comparison of the dynamic response features observed by considering different friction models. Moreover, future work will focus on MDOF systems with multiple friction contacts.

Appendix A

The boundaries among continuous, stick-slip and permanent sticking motion regimes of a 2DOF system with unitary stiffness and mass ratios are represented in Figs. 21 and 22 for varying ratios between static and friction forces. In particular, Fig.21 refers to case of the lower mass in contact shown in Fig.4a, while in Fig. 22 the case of the upper mass in contact shown in Fig. 10a is considered. In these figures, it can be observed that intersections between the boundaries may occur when $\mu \ne 1$. In this case, the portion of the boundary between continuous and stick-slip regimes falling into the permanent sticking region will be disregarded and there will be a direct transition from continuous motion to permanent sticking.