Analytic exploration of safe basins in a benchmark problem of forced escape

Abstract

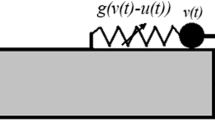
The paper presents an analytical approach to predicting the safe basins (SBs) in a plane of initial conditions (ICs) for escape of classical particle from the potential well under harmonic forcing. The solution is based on the approximation of isolated resonance, which reduces the dynamics to a conservative flow on a two-dimensional resonance manifold (RM). Such a reduction allows easy distinction between escaping and non-escaping ICs. As a benchmark potential, we choose a common parabolic-quartic well with truncation at varying energy levels. The method allows accurate predictions of the SB boundaries for relatively low forcing amplitudes. The derived SBs demonstrate an unexpected set of properties, including decomposition into two disjoint zones in the IC plane for a certain range of parameters. The latter peculiarity stems from two qualitatively different escape mechanisms on the RM. For higher forcing values, the accuracy of the analytic predictions decreases to some extent due to the inaccuracies of the basic isolated resonance approximation, but mainly due to the erosion of the SB boundaries caused by the secondary resonances. Nevertheless, even in this case the analytic approximation can serve as a viable initial guess for subsequent numeric estimation of the SB boundaries.

Appendix: Comparison of the escape criteria

As it was mentioned before, the two escape criteria—maximum energy and maximum displacement—are not equivalent. It is obvious that the energy criterion immediately follows from the displacement criterion, and therefore, the SB based on the energy criterion (ESB) is always included in the corresponding SB defined through the maximum displacement criterion (DSB). However, the other way is not necessarily true.

In order to compare two criteria, the following numeric test is performed. For each value of the forcing amplitude F, we pick 10,000 random ICs from the square $\left[ { - 1,1} \right] \times \left[ { - 1,1} \right]$. Then, we perform numerical time integration of system (1) starting from the chosen set selecting only the non-escaped trajectories according to the ESB. Next, we run the simulations again for the rest of ICs but with the displacement criterion to obtain the set belonging to the DSB but not to the ESB. Let $A_{q}$ and $A_{E}$ denote the number of points that belong to the DSB and the ESB, respectively. The difference between $A_{q}$ and $A_{E}$ relative to $A_{E}$ exhibits the discrepancy between the two criteria.

The experiment is repeated five times for the values of the external forcing amplitude F ranging from 0.001 to 0.071 with a step ${\Delta }F = 0.005$. The results are presented in Fig. 

Fig. 21

Comparison of SB areas for different values of the external force amplitude F. Blue, orange, and green markers correspond to the minimum, the mean, and the maximum of five experiments. Other parameters are the following: Ω = 0.9, Ψ = 0, ξ_max = 0.25. (Color figure online)

21. As one can see, for the small values of the external forcing amplitude F, SBs for both criteria are almost identical. However, with increasing F the difference becomes substantial, see Fig. 21.

Furthermore, our findings reveal that the choice of the escape criterion also strongly affects the shape of the SBs. The maximum energy escape criterion yields SBs with smoother boundary.

Figure 

Fig. 22

Zoomed SB Escape Chart simulation for F = 0.0876, Ω = 0.95, Ψ = π, ξ_max = 0.25, the resolution is 300 $\times$ 300. Left: t_eval = 500EC. Right: t_eval = 11,000EC, DSB (grey) and by ESB (black). (Color figure online)

22 presents a comparison of SBs in the (q₀, p₀) plane for two superimposed escape criteria for a short evaluation time t_eval (left) and a long t_eval (right). Colors grey and black correspond to the displacement and the energy criteria, respectively.

For a short evaluation time t_eval, the boundaries of SBs for both criteria look irregular representing the transient behavior. For a long time t_eval after the transient dynamics fades out, the SB boundary becomes clearer and smoother. The full view of SB for the same values of parameters as in Fig. 22 is shown in Fig. 

Fig. 23

Entire SB Escape Chart simulation for F = 0.0876, Ω = 0.95, Ψ = π, ξ_max = 0.25, the resolution is 300 $\times$ 300. Left: t_eval = 500EC. Right: t_eval = 11,000EC, DSB (grey) and by ESB (black). (Color figure online)

23.

Figure 

Fig. 24

Log of SB area in pixels fading with t_eval for DSB (dashed) and ESB (solid) F = 0.0876, Ω = 0.95, Ψ = π, ξ_max = 0.25, the resolution is 300 $\times$ 300

24 presents the change of the SB area with time. As one can see, the area undergoes a rapid shrinking for about 2000EC, followed by almost no change after. Each point on the graph is a natural logarithm of the SB area computed numerically at a given evaluation time.