Friction-induced traveling wave coupling in tuned bladed-disks

Abstract

Flutter is a major constraint on modern turbomachines; as the designs move toward more slender, thinner, and loaded blades, they become more prone to experience high cycle fatigue problems. Dry friction, present at the root attachment for cantilever configurations, is one of the main sources of energy dissipation. It saturates the flutter vibration amplitude growth, producing a limit cycle oscillation whose amplitude depends on the balance between the energy injected and dissipated by the system. Both phenomena, flutter and friction, typically produce a small correction of the purely elastic response of the structure. A large number of elastic cycles is required to notice their effect, which appears as a slow modulation of the oscillation amplitude. Furthermore, even longer time scales appear when multiple traveling waves are aerodynamically unstable and exhibit similar growth rates. All these slow scales make the system time integration very stiff and CPU expensive, bringing some doubts about whether the final solutions are properly converged. In order to avoid these uncertainties, a numerical continuation procedure is applied to analyze the solutions that set in, their traveling wave content, their bifurcations and their stability. The system is modeled using an asymptotic reduced order model and the continuation results are validated against direct time integrations. New final states with multiple traveling wave content are found and analyzed. These solutions have not been obtained before for the case of microslip friction at the blade attachment; only solutions consisting of a single traveling wave have been reported in previous works.

1 Introduction

Flutter onset is currently a very important limitation in modern turbomachinery, where blade designs are getting more slender and closer to their mechanical limit. It is an aeroelastic instability where the gas flowing around the blades tends to amplify the small elastic oscillations of the blades. As a consequence, the blade vibration amplitude grows exponentially until nonlinear effects, typically due to friction forces at the blade root in the case of Low Pressure Turbines (LPT), become relevant. Hopefully, the dissipation produced by nonlinear friction is strong enough to limit the growth of the aeroelastic instability and avoid a catastrophic blade failure. In this case, there is a balance between nonlinear friction damping and unstable flutter growth such that a final Limit Cycle Oscillation (LCO) state sets in with a bounded blade vibration amplitude.

The determination of this final vibration amplitude is crucial to estimate the blade fatigue level. This typically requires a CFD description of the aerodynamic flow coupled with a FEM for the motion of the bladed-disk with nonlinear friction effects. These simulations can include a number of simplifications (linearized CFD, partial fluid-structure coupling, reduced number of modes for the motion of the structure,...), but they are always quite involved and CPU costly.

In a tuned configuration, if the final state is made of a single Traveling Wave (TW), then the calculations can be reduced to just one flow passage and one sector of the bladed-disk. This constitutes a huge computational reduction in the usual case of large blade counts.

For this reason, there has recently been some research activity looking into the expected TW composition of the final LCO state. Aeroelastic models of the bladed-disk with different levels of detail have been used to try to decide whether, in a tuned rotor, the final LCO state is always made of a single TW or if there can also be multi-TW final states.

In [4], a mass-spring model with microslip friction is used to analyze the problem. The system is integrated in time with fully coupled and semi-uncoupled linearized aerodynamic effects. Both formulations produce very similar results, indicating that, in the usual case of small vibration amplitude, aerodynamic forces can be safely assumed to be linear. Time evolution of the system first showed the slow growth of the unstable TWs and, afterward, the nonlinear interaction of unstable TWs through the effect of friction at the fir-tree, which takes place on an even longer time scale. In all cases reported, this interaction always ended up selecting a final state composed of just one single TW, the most aeroelastically unstable one.

A multiple scales method is applied in [9, 10] to further simplify the mass-spring model. The resulting asymptotically reduced equations describe the evolution of the system directly in the slow time scale (associated with the small effects of flutter and friction), with the fast elastic oscillations filtered out and can be integrated with a much lower computational cost. Again, the simulations performed always produced single TW final states, although other unstable TWs close to the most unstable one were also found as possible final states of the system. The selection of the final single TW state is sensitive to the initial conditions. These initial conditions were picked from a random distribution [9] or both from a random distribution and starting from a pure TW [10].

Multi-TW solutions were reported as another possible final state in [8]. The model used consisted of 7 blades with linear aerodynamic effects and Coulomb friction forces to describe the effect of the contact between adjacent blades. In order to obtain the multi-TW states, the linear aeroelastic characteristics of the system were selected to have two unstable TWs with a quite high negative aerodynamic damping value. A realistic model of a LPT bladed-disk with linear aerodynamic forces and contact interaction at the tip shroud was considered in [7]. Here, it was shown that the inclusion of strong nonlinear coupling effects at the tip shroud can produce multi-TW final states. The analysis was continued in [2], to show that nonlinear tip contact effects change the vibration modes and frequencies of the system with respect to those obtained with linearized contact conditions. These changes in frequencies and mode shapes have to be considered in order to correctly estimate the amplitude of the resulting limit cycle oscillations.

In the present work, we consider the case of flutter vibrations with microslip contact forces at the blade fir-tree, where the effect of friction does not substantially change the natural vibration modes. As it was mentioned above, previous works on this configuration [4, 9, 10] have only found final vibration states consisting of just one single TW. The idea is to apply numerical continuation techniques [6] to analyze the stability of the solutions and search for multi-TW states. This procedure eliminates the need for direct time integration of the system, which requires very long integration times and always leaves some uncertainty about whether the final state is fully converged.

To this end, first, we briefly introduce the asymptotic model used, study the stability of the zero solution (no blade vibration) and compute the single TW solutions that appear when the magnitude of the flutter instability is increased. Then, we analyze the linear stability of single TW solutions and perform numerical continuation to follow new branches of multi-TW solutions that bifurcate from single TW solutions when they lose stability. New multi-TW states are obtained, with very rich TW content. They have two different frequencies and propagate around the rotor with nonuniform blade to blade amplitude.

2 Asymptotic model

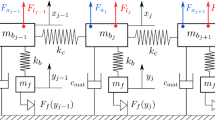
A simple mass-spring model is used to represent the bladed-disk (Fig. 1). The system has 2 degrees of freedom per sector, one for the blade motion $x_j$ and one for the friction displacement $y_j$. It includes: elastic coupling among the different blades to account for the effect of the disk ${\varvec{\mathrm{K_{c}}}}$, linear aerodynamic forces ${\varvec{\mathrm{F_{\mathrm {a}}}}}$, and microslip friction forces ${\varvec{\mathrm{F}}}_{f}({\varvec{\mathrm{y}}})$ at the blade attachment. Similar models have been successfully used in previous works for the description of flutter vibration of a nearly flat modal family (see [9, 10]).

Fig. 1

Mass-spring model of the bladed-disk

The equations of motion of the mass-spring system are given by

$$\begin{aligned} \begin{aligned}&m_{b}\ddot{{\varvec{\mathrm{x}}}}+k_{b}({\varvec{\mathrm{x}}}-{\varvec{\mathrm{y}}})+{\varvec{\mathrm{K_{c}}}}{\varvec{\mathrm{x}}}+c_{\mathrm {{mat}}}{\dot{{\varvec{\mathrm{x}}}}}+{\varvec{\mathrm{F_{\mathrm {a}}}}}={\varvec{\mathrm{0}}},\\&m_{f}\ddot{{\varvec{\mathrm{y}}}}+k_{b}({\varvec{\mathrm{y}}}-{\varvec{\mathrm{x}}})+{\varvec{\mathrm{F}}}_{f}({\varvec{\mathrm{y}}})={\varvec{\mathrm{0}}}, \end{aligned} \end{aligned}$$

(1)

where $m_b$ is the mass of the blade and $m_f$ is the mass of the nonlinear friction Degree of Freedom (DOF) in each sector. The elastic coupling between both DOF is $k_b$. It is convenient to rewrite this set of equations in dimensionless variables in order to clearly compare the relative importance of the different terms. Dividing Eq. (1) by the characteristic elastic force of the system $F_c = m_b\omega _b^2x_c$, one gets

$$\begin{aligned} \begin{aligned}&\tilde{{\varvec{\mathrm{x}}}}_{TT}+({\tilde{{\varvec{\mathrm{x}}}}}-\theta \tilde{{\varvec{\mathrm{y}}}})+{\tilde{{\varvec{\mathrm{K}}}}_{c}}{\tilde{{\varvec{\mathrm{x}}}}}+2\xi _{\mathrm {mat}}{\tilde{{\varvec{\mathrm{x}}}}}_{T}+{\tilde{{\varvec{\mathrm{F}}}}}_a={\varvec{\mathrm{0}}},\\&\gamma \theta {\tilde{{\varvec{\mathrm{y}}}}}_{TT}+(\theta {\tilde{{\varvec{\mathrm{y}}}}}-{\tilde{{\varvec{\mathrm{x}}}}})+{\tilde{{\varvec{\mathrm{F}}}}}_{f}({\tilde{{\varvec{\mathrm{y}}}}})={\varvec{\mathrm{0}}}, \end{aligned} \end{aligned}$$

(2)

where ${\tilde{{\varvec{\mathrm{x}}}}}={\varvec{\mathrm{x}}}/(F_{c}/k_{b})$, ${\tilde{{\varvec{\mathrm{y}}}}}={\varvec{\mathrm{y}}}/y_{c}$ ($y_{c}$ is the microslip characteristic displacement), the time is made dimensionless $T = \omega _bt$ with the blade alone natural frequency $\omega _{b}=\sqrt{k_{b}/m_{b}}$, $\gamma =m_{f}/m_{b}$, and $\theta =y_{c}/x_{c}=k_{b}/(F_{c}/y_{c})$. The dimensionless forces are expressed as ${\tilde{{\varvec{\mathrm{F}}}}}_a = {\varvec{\mathrm{F}}}_a/F_c$ and ${\tilde{{\varvec{\mathrm{F}}}}}_f = {\varvec{\mathrm{F}}}_f/F_c$.

The nondimensional parameter $\theta$ is usually very small because the displacement of the fir-tree is typically much smaller than the modal displacement of the blade (or, in other words, the stiffness of the friction is much larger than that of the blade elastic mode).

There are two very different time scales in this problem. One corresponds to oscillations with the elastic frequency of the blade and, the other, which is much slower, is associated with the small effects of flutter and nonlinear friction. A multiple scales method (see, e.g., [1]) can be applied to obtain, in the limit $\theta \ll 1$, an asymptotic model with the fast elastic oscillations filtered out. The derivation of the asymptotic model is completely analogous to that explained in detail in [9, 10] and is omitted here.

The asymptotic model expressed in terms of complex TW amplitudes $A_{j}$ and the slow time scale $\tau = \theta T$, can be written in the form

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau }\begin{pmatrix}A_{1}\\ \vdots \\ A_{N} \end{pmatrix}=({\varvec{\mathrm{M}}}_{\mathrm {{elastic}}}+{\varvec{\mathrm{M}}}_{\mathrm {{aero}}}+{\varvec{\mathrm{M}}}_{\mathrm {friction}})\begin{pmatrix}A_{1}\\ \vdots \\ A_{N} \end{pmatrix},\nonumber \\ \end{aligned}$$

(3)

where $N=24$ is the number of blades of the rotor. The elastic and aerodynamic matrices are diagonal in the TW basis

$$\begin{aligned} {\varvec{\mathrm{M}}}_{\mathrm {{elastic}}} = \begin{bmatrix}-\frac{\xi _{\mathrm {{mat}}}}{\theta }+i\frac{\Delta \omega _{1}}{\theta } &{} \cdots &{} 0\\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots - &{} \frac{\xi _{\mathrm {{mat}}}}{\theta }+i\frac{\Delta \omega _{N}}{\theta } \end{bmatrix}, \end{aligned}$$

(4)

$$\begin{aligned} {\varvec{\mathrm{M}}}_{\mathrm {{aero}}}= \begin{bmatrix}-\frac{\xi _{a}^{1}}{\theta }+i\frac{\eta _{a}^{1}}{\theta } &{} \cdots &{} 0\\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots - &{} \frac{\xi _{a}^{N}}{\theta }+i\frac{\eta _{a}^{N}}{\theta } \end{bmatrix}, \end{aligned}$$

(5)

and the friction matrix is diagonal in the displacement basis

$$\begin{aligned} {\varvec{\mathrm{M}}}_{\mathrm {friction}}=-\frac{i}{2}{\varvec{\mathrm{E}}}^{H}\begin{bmatrix}Q(|X_{1}|) &{} \cdots &{} 0\\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} Q(|X_{N}|) \end{bmatrix}{\varvec{\mathrm{E}}}. \end{aligned}$$

(6)

${\varvec{\mathrm{E}}}$ is the change matrix from TW amplitudes to blade displacements, and ${\varvec{\mathrm{E}}}^{H}$ denotes the conjugate transpose of ${\varvec{\mathrm{E}}}$. This matrix represents the discrete Fourier transform and is given by

$$\begin{aligned} {\varvec{\mathrm{E}}} = \frac{1}{\sqrt{N}} \begin{bmatrix} e^{i\left( \frac{2\pi 1}{N}\right) 1} &{} \cdots &{} e^{i\left( \frac{2\pi N}{N}\right) 1}\\ \vdots &{} \ddots &{} \vdots \\ e^{i\left( \frac{2\pi 1}{N}\right) N} &{} \cdots &{} e^{i\left( \frac{2\pi N}{N}\right) N} \end{bmatrix}. \end{aligned}$$

(7)

The complex blade displacements are represented by $X_{j}$, and they are related to the dimensionless displacements $\tilde{x}_j$ by

$$\begin{aligned} \tilde{x}_j = X_j(\tau )e^{iT} + \mathrm {c.c.}, \end{aligned}$$

(8)

which corresponds to the first order in the asymptotic expansion [9, 10]. Furthermore, the complex displacements $X_j$ are related to the TW amplitudes $A_{j}$ by ${\varvec{\mathrm{X}}}={\varvec{\mathrm{E}}}{\varvec{\mathrm{A}}}$.

The coefficients $\Delta \omega _{j}$ in the elastic matrix represent the small deviations of the natural frequencies of the modal family from the blade alone normalized frequency (see Fig. 2). The material damping coefficient of the structure has the value $\xi _{\mathrm {{mat}}}=c_{\mathrm {{mat}}}/2\sqrt{{k_{b}m_{b}}}=2\times 10^{-4}$ (much smaller than the aerodynamic damping).

Fig. 2

Elastic frequencies of the bladed-disk

The Olofsson model [11] is used to describe the microslip friction at the blade attachment. The dimensionless friction force $\tilde{F}_{f_j}$ is related to the DOF $\tilde{y}_j$ by a loading–unloading cycle, which is shown in Fig. 3. The magnitude of the friction force corresponding to the unloading part of the cycle is given by

$$\begin{aligned} \tilde{F}_{f_j} = \tilde{F}^L-2\left( 1 - \left( 1 - \frac{\tilde{y}^L - \tilde{y}_j}{2}\right) ^{5/2}\right) , \end{aligned}$$

(9)

and, the subsequent loading part is obtained as

$$\begin{aligned} \tilde{F}_{f_j} = -\tilde{F}^U+2\left( 1 - \left( 1 - \frac{\tilde{y}^U + \tilde{y}_j}{2}\right) ^{5/2}\right) . \end{aligned}$$

(10)

Fig. 3

Olofsson model for the friction force in the microslip regime

The complex friction coefficient $Q(|X_{j}|)$ in the friction matrix ${\varvec{\mathrm{M}}}_{\mathrm {friction}}$ used in the asymptotic model is related to the first term of the Fourier series expansion of $\tilde{y}_j$ (see [9]). This coefficient accounts for the nonlinear dissipation and frequency change produced by friction at the fir-tree and depends on the amplitude of the blade elastic cycle $|X_{j}|$. Real and imaginary parts of $Q(|X_{j}|)$ are shown in Fig. 4. The microslip regime is bounded by $|X| \le 0.5$.

Fig. 4

Real (top) and imaginary (bottom) parts of the complex friction coefficient Q(|X|)

The coefficients in ${\varvec{\mathrm{M}}}_{\mathrm {{aero}}}$ are the aerodynamic damping and frequency correction of the TW modes. A sinusoidal shape (blade aerodynamic interaction with itself and with its adjacent blades only) has been selected to mimic the typical data in a realistic LPT (see, e.g., [3])

$$\begin{aligned} \xi _{a}^{j}=\xi _{a_{0}}-\xi _{a_{1}}\sin \left( \frac{2\pi j}{N}+\xi _{a_{2}}\right) \ \ \ \ (\%), \end{aligned}$$

(11)

$$\begin{aligned} \eta _{a}^{j}=\eta _{a_{0}}-\eta _{a_{1}}\cos \left( \frac{2\pi j}{N}\right) \ \ \ \ (\%), \end{aligned}$$

(12)

where j is the TW wavenumber, $\xi _{a_{0}}=0.25,\ \xi _{a_{1}}=0.75,\ \xi _{a_{2}}=-0.05\ ,\eta _{a_{0}}=1.4\$ and $\eta _{a_{1}}=1$. The aerodynamic coefficients are shown in Fig. 5. The aerodynamically unstable TW modes (i.e., $\xi _{a}^{k}<0$) are represented with a shaded area. Note that the mean aerodynamic damping is stable and there are 9 unstable TWs. Also, as it is usual in the turbomachinery field we also use the term number of Nodal Diameters (ND) to refer to the wavenumber of a TW.

The coefficient $\xi _{a_{1}}$ will be used later on as the bifurcation parameter to explore the solutions of the system. By changing this parameter, we explore different levels of the flutter instability increasing or decreasing the number of unstable TW modes and their damping.

Fig. 5

Aerodynamic damping and frequency correction coefficients

3 Traveling wave solutions

Equation (3) admits the trivial solution, which corresponds to no blade motion. Linearizing the problem around this solution $A_j = 0 + a_j$ yields

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}\tau }\begin{pmatrix}\vdots \\ a_{j}\\ \vdots \end{pmatrix}\nonumber \\&\quad =\mathbf{diag} \left[ -{\tilde{\xi }}_j+i\left( \omega -\frac{\mathfrak {R}[Q(0)]}{2}\right) \right] \begin{pmatrix}\vdots \\ a_{j}\\ \vdots \end{pmatrix}, \end{aligned}$$

(13)

where $a_j$ represents the perturbed TW amplitude, with $|a_j|\ll 1$, ${\tilde{\xi }}_j = (\xi _{a}^{j}+\xi _{\mathrm {mat}}) /\theta$, and ${\tilde{\omega }}_j = (\Delta \omega _{j}+\eta _{a}^{j}) / \theta$.

This is a diagonal constant coefficient system, and the eigenvalues of the matrix are given by

$$\begin{aligned} \lambda _{j}=-{\tilde{\xi }}_j + i\left( {\tilde{\omega }}_j-\frac{\mathfrak {R}[Q(0)]}{2}\right) . \end{aligned}$$

(14)

As the flutter intensity is increased through the parameter $\xi _{a_{1}}$ [see Eq. (11)], the trivial solution becomes unstable for the first time at ${\tilde{\xi }}_j=\frac{\xi _{a}^{j}+\xi _{\mathrm {mat}}}{\theta }=0$ for any j. As it can be seen in Fig. 5, this happens first for $j=6$, which is the most aeroelastically unstable TW mode. For higher values of $\xi _{a_{1}}$, the adjacent TW modes become also unstable. The effect of friction is just a shift in frequency of magnitude $\mathfrak {R}[Q(0)]/2$ in the aeroelastic modes.

There is another type of simple solutions of the system which corresponds to a single TW with wavenumber r, with all blades vibrating with the same amplitude and frequency

$$\begin{aligned}&A_{r}=\sqrt{N}R_{r}e^{i(m_{r}\tau +\alpha )}, \nonumber \\&\quad A_{j}=0\ \ \mathrm {{for}}\ \ j=1,\ldots ,N\ \ \mathrm {{and}\ \ }j\ne r, \end{aligned}$$

(15)

where $\sqrt{N}R_{r}$ is the modulus of the TW amplitude, $m_{r}$ is the frequency correction of the single TW solution and $\alpha$ represents an arbitrary phase. Note that the magnitude of the blade displacements $|X_j| = R_r$ for every j, so all the entries in the friction matrix in Eq. (3) are equal to $Q(R_r)$. Therefore, after introducing the expression (15) in system (3), the following nonlinear equations are obtained

$$\begin{aligned} \mathfrak {J}[Q(R_{r})]=2{\tilde{\xi }}_r, \end{aligned}$$

(16)

which determines the value of $R_r$ for a given aerodynamic level ${\tilde{\xi }}_r$, and

$$\begin{aligned} m_{r}={\tilde{\omega }}_r-\frac{{1}}{2}\mathfrak {R}[Q(R_{r})], \end{aligned}$$

(17)

which directly gives the frequency of this periodic solution once the value $R_r$ is known. Equation (16) indicates that the amplitude of the single TW periodic solution is the result of the balance between the growth rate of the aeroelastic instability and the nonlinear damping of the friction [10].

Since $\mathfrak {J}[Q(|X|)] \le 0$, the existence of single TW solutions requires ${\tilde{\xi }}_r < 0$. Therefore, for each unstable TW mode with wavenumber $j=r,$ there is a single TW solution with complex amplitude $A_{r}$ that bifurcates from the trivial solution precisely when the real part of the eigenvalue $\lambda _{r}$ from (14) becomes positive. The stability of these single TW solutions is analyzed in the next section

4 Stability of the traveling wave solutions

Single TW solutions [Eq. (15)] are periodic solutions of system (3). To study their stability, we introduce a change of variable to make these solutions steady in the new formulation. By factoring out the frequency of single TW solutions, $m_r$, we have

$$\begin{aligned} {\varvec{\mathrm{A}}}={\varvec{\mathrm{B}}}e^{im_{r}\tau }. \end{aligned}$$

(18)

Introducing the change of variable (18) in Eq. (3), and substituting the value of $m_r$ from (17), gives

$$\begin{aligned} \begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}\tau }\begin{pmatrix} \vdots \\ B_{j}\\ \vdots \end{pmatrix}\\&\quad =-\frac{i}{2}{\varvec{\mathrm{E}}}^{H}{} \mathbf{diag} \left[ Q(|X_{j}|)-Q(R_{r})\right] {\varvec{\mathrm{E}}}\begin{pmatrix} \vdots \\ B_{j}\\ \vdots \end{pmatrix}\\&\quad +\mathbf{diag} \left[ -({\tilde{\xi }}_j - {\tilde{\xi }}_r)+i({\tilde{\omega }}_j - {\tilde{\omega }}_r)\right] \begin{pmatrix} \vdots \\ B_{j}\\ \vdots \end{pmatrix}, \end{aligned} \end{aligned}$$

(19)

where single TW solutions are now steady solutions of this autonomous system.

The stability characteristics of single TW solutions can now be obtained by computing the eigenvalues of the Jacobian matrix of Eq. (19), evaluated at one of these solutions. To this end, we linearize the system writing the solution as a single TW with wavenumber r plus a small perturbation

$$\begin{aligned} \begin{pmatrix}B_{1}\\ \vdots \\ B_{r}\\ \vdots \\ B_{N} \end{pmatrix}=\left( \begin{pmatrix}0\\ \vdots \\ 1\\ \vdots \\ 0 \end{pmatrix}+\begin{pmatrix}a_{1}\\ \vdots \\ a_{r}\\ \vdots \\ a_{N} \end{pmatrix}\right) \sqrt{N}R_{r}e^{i\alpha }. \end{aligned}$$

(20)

Expression (20) is introduced in the system of eqs. (19) and only linear terms in the perturbation are retained. The resulting linear system for the time evolution of the TW perturbations can be expressed as

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau }\begin{pmatrix}\vdots \\ a_{r-1}\\ a_{r}\\ a_{r+1}\\ \vdots \end{pmatrix}=-\frac{i}{4}Q'(R_{r})R_{r}(\begin{pmatrix}\vdots \\ a_{r-1}\\ a_{r}\\ a_{r+1}\\ \vdots \end{pmatrix}+&\begin{pmatrix}\vdots \\ {\bar{a}}_{r+1}\\ {\bar{a}}_{r}\\ {\bar{a}}_{r-1}\\ \vdots \end{pmatrix})\\ +\mathbf{diag} \left[ -({\tilde{\xi }}_j - {\tilde{\xi }}_r)+i({\tilde{\omega }}_j - {\tilde{\omega }}_r)\right]&\begin{pmatrix}\vdots \\ a_{r-1}\\ a_{r}\\ a_{r+1}\\ \vdots \end{pmatrix}, \end{aligned} \end{aligned}$$

(21)

where $Q'(R_r)$ is the derivative of the complex friction coefficient Q(|X|) evaluated at $R_r$. System (21) has some particular characteristics that are worth noting.

The complex conjugate of the perturbation, ${\bar{a}}_{j}$, appears through the linearization of the modulus of the blade displacement $|X_{j}|$, present in the friction terms $Q(|X_{j}|)$. A perturbation with wavenumber $r+k$ on a TW with wavenumber r produces also a complex conjugate component with wavenumber $r-k$. As a consequence, despite the fact that the system is tuned (that is, all sectors of the bladed-disk are identical), different TW perturbations are not uncoupled. Because of the nonlinearity of the friction terms, the TW perturbations $a_{r+k}$ and $a_{r-k}$ are coupled in pairs, and the perturbation $a_{r}$ is decoupled from the rest.

The second term in system (21) contains the damping differences ${\tilde{\xi }}_j - {\tilde{\xi }}_r$. Near the most aeroelastically unstable TW, the aerodynamic damping values are very similar (see Fig. 5). Their differences are thus very small and generate even longer time scales, associated with the selection of a particular TW as the final state.

This long time scale has been noticed in previous works [4, 9, 10], and it can be clearly seen in Fig. 6, where system (3) is integrated in time starting from a small initial condition ($A_{j}=0.01$ for every j) and with $\xi _{a_{1}}=0.75$. Initially, there is an exponential growth of the aeroelastically unstable TW modes (straight lines due to logarithmic scale). The slope of this growth (blued dashed line) is practically given by the most unstable aerodynamic damping $\xi _{a}^{6}$ (the material damping of the structure is much smaller). However, the slope of the TW decay in the nonlinear interaction region (red dashed line), which is related to the difference of aerodynamic dampings $\xi _{a}^{j} - \xi _{a}^{r}$, is much smaller and it takes a very long time to select the final TW with wavenumber 6. Direct time integration, even for this asymptotic model, requires long computation times, and there is always a certain level of doubt about whether the convergence to the final state has been reached.

Fig. 6

Time evolution of the solution of system (3) with initial condition $A_j = 0.01$ for every j

Now, expanding the small perturbation ${\varvec{\mathrm{a}}} = {\varvec{\mathrm{u}}} + i {\varvec{\mathrm{v}}}$, Eq. (21) can be written in real and imaginary part as

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau } \begin{pmatrix} {\varvec{\mathrm{u}}}\\ {\varvec{\mathrm{v}}} \end{pmatrix} = {\varvec{\mathrm{J}}}(R_r) \begin{pmatrix} {\varvec{\mathrm{u}}}\\ {\varvec{\mathrm{v}}} \end{pmatrix}, \end{aligned}$$

(22)

where ${\varvec{\mathrm{J}}}(R_r)$ is the Jacobian matrix evaluated at the amplitude $R_r$ of a single TW solution with wavenumber r. Therefore, a single TW solution branch is stable if the real part of all the eigenvalues of the Jacobian matrix are less or equal to zero or unstable if the real part of any of the eigenvalues is positive.

As an example, for wavenumber 8, the single TW solution curve is computed for values of the bifurcation parameter $\xi _{a_{1}}\in [0.2, 1.0]$. Its stability is determined by the eigenvalues of the Jacobian matrix at each point, as shown in Fig. 7. For values close to $\xi _{a_{1}} = 0.2$, only the trivial solution exists, which becomes unstable at the point ${\tilde{\xi }}_6 = 0$, since the TW with wavenumber 6 is the most unstable. When the bifurcation parameter is increased and ${\tilde{\xi }}_8 = 0$, the single TW8 branch emerges from the trivial solution, and it is initially unstable. Then, after a Hopf Bifurcation (HB) point, the LCO corresponding to TW8 becomes a stable solution.

Fig. 7

Bifurcation diagram for the single TW solution with wavenumber 8. Solid (dashed) line indicates stable (unstable) solution

The same process is repeated again for every TW mode that becomes aerodynamically unstable in the interval $\xi _{a_{1}}\in [0.2, 1.0]$. Gathering the information of each individual bifurcation diagram (as in Fig. 7), the stability of every single TW solution and the trivial solution is represented in Fig. 8. The trivial solution corresponds to the horizontal plane and is stable when there is no aerodynamically unstable TW mode present in the system. The straight dotted line corresponds to ${\tilde{\xi }}_6 = 0$, where the trivial solution becomes unstable. The single TW solutions emerge from the trivial solution when a TW mode becomes unstable (This condition is represented by the curved dotted line and is given by ${\tilde{\xi }}_r = 0$).

The single TW solution with wavenumber 6 (which corresponds to the most unstable aerodynamic damping) is always stable, but adjacent ones (with slightly less aerodynamic damping) only become stable as the bifurcation parameter $\xi _{a_1}$ is increased. Every single TW that changes stability does it through a HB. Also, for a given value of the bifurcation parameter $\xi _{a_{1}}$, even though multiple single TW solutions exist, not every one of them has a stable LCO.

Previous works only reported the most aerodynamically unstable TWs as final states of single TW solutions [10] after performing numerical integration. Also, the most unstable mode seemed to have the largest basin of attraction. In this work, the stability results show that, for example, when $\xi _{a_{1}} = 1$, only 5 out of the 10 aerodynamically unstable TW modes have a stable LCO. These TW modes are precisely the most aerodynamically unstable ones, and their stability region is larger the more unstable a TW mode is.

Fig. 8

Bifurcation diagram of the traveling wave solutions from the trivial solution. Solid (dashed) line indicates stable (unstable) solutions

5 Multi-traveling wave solutions

We now look for more complicated stable solutions that can bifurcate from the HB in single TW solutions. The approach to track these branches and compute their stability is to use numerical continuation. In particular, the numerical continuation software AUTO [6] is used. AUTO is a package that can continue steady solutions of ordinary differential equations and determine its bifurcation points using one (or more) free parameters. Furthermore, it continues periodic solutions, determining the Floquet multipliers at each step to compute the stability of these branches. The algorithms implemented in this software are explained in detail in [5].

Even though single TW solutions are periodic, recall that they became steady in Eq. (19) after performing a change of variable and eliminating the frequency $m_r$ (which is the small correction of the elastic frequency). Therefore, periodic solutions of Eq. (19) are actually solutions with two frequencies in the original system (3).

The change in stability of single TW solutions occurred through a HB, so we apply numerical continuation to track the branches that emerge from these points. The results show that a stable state only emerges from TW4. From the other single TW solutions, the new branch was always unstable.

The new solutions are represented in Fig. 9. Here, from the single TW with wavenumber 4 a multi-TW solution appears from the HB point. This multi-TW solution is stable for a very narrow range of values of the bifurcation parameter $(\xi _{a_{1}} \sim 0.5-0.515)$, but its TW components grow to a considerable amplitude (see the inset in Fig. 9 where the TW modes with largest amplitudes are represented). As one continues decreasing the bifurcation parameter, a Torus Bifurcation (TB) occurs and the multi-TW solution loses stability. In addition, the new frequency associated with this multi-TW branch is represented in Fig. 10. This frequency grows along the multi-TW branch and coexist with the single TW frequency $m_4$.

Fig. 9

Bifurcation diagram for the TW with wavenumber 4. Solid (dashed) line indicates stable (unstable) solutions

Fig. 10

Multi-TW frequency branch. Solid (dashed) line indicates stable (unstable) solutions

The TW content of the stable multi-TW solution found is illustrated in Fig. 11 for different values of the bifurcation parameter $\xi _{a_{1}}$. As the bifurcation parameter moves closer to the end of their stability region, there is more modal content of different TWs, except for the TW with wavenumber 4, which corresponds to the single TW solution from which this new multi-TW branch emerged.

Numerical time integration of system (3) has also been performed in order to check the results of the numerical continuation. The time evolution of the different TW components of the solution is presented in Fig. 12 for $\xi _{a_{1}}=0.502$, showing the convergence of the system to a multi-TW state. The initial condition for this simulation is the single TW4 solution plus a small perturbation of 0.01 to every TW mode. Nevertheless, for this value of the aerodynamic damping there are 4 stable single TW LCOs that coexist with the multi-TW solution, so for different initial conditions the final state can be a single TW. Also, notice that, in contrast to the case where the final state was a single TW solution (Fig. 6), the required time integration for multi-TW solutions is now roughly an order of magnitude larger.

Fig. 11

TW content of the multi-TW solution for different values of the aerodynamic damping

Fig. 12

Time evolution of the system to a multi-TW solution. The system evolves from the single TW4 solution plus a 0.01 perturbation to every TW component

Finally, the displacements of the blades $|X_{j}|$ of the new multi-TW solution for $\xi _{a_{1}}=0.502$ are plotted in Fig. 13. The multi-TW solution takes the form of a traveling wave with non-uniform amplitude that rotates around the bladed-disk. The solution represented in this figure is actually the envelope of the fast elastic oscillation (which was filtered in the asymptotic model) of blade j. The period of this envelope (roughly $\sim 300$) is the one associated with the new frequency present in the multi-TW solution (see Fig. 10).

Despite the complexity of the multi-TW solutions that are obtained in this work, the maximum blade displacement that they produce is always smaller than that associated with the single TW solution with highest amplitude (corresponding to the most aerodynamically unstable wavenumber 6). As presented in Table 1, the maximum blade displacement of the TW solution is $17\%$ higher than that of the multi-TW solution. Therefore, from the point of view of the calculation of the fatigue of the blades, it seems that it is conservative to consider only the highest amplitude TW solution.

Fig. 13

Multi-TW solution: blade displacements

Table 1 Comparison of the maximum blade displacements

In order to have a wider range of existence of stable multi-TW solutions, we have explored a number of modifications of the parameters in system (3): (i) increase/reduce the spread of the elastic frequencies (Fig. 2), (ii) increase/reduce the values aerodynamic frequency correction (top plot in Fig. 5), and (iii) change the aerodamping (bottom plot in Fig. 5) to have more/less unstable modes with similar aerodamping values.

Modifications (i) and (ii) changed the stability regions of single TW solutions. Decreasing the frequency correction of both the structure and the aerodynamic matrix enlarged the single TW instability regions. However, by doubling the frequency terms, the stability region of TW solutions grew with respect to the case shown in Fig. 8. Nevertheless, after performing numerical continuation it was found that there were no stable multi-TW states in neither of these cases. The changes in aerodynamic damping characteristics are represented in Fig. 14. The baseline configuration is the one already used throughout this paper. Two new configurations are explored: (a) Wide, where the damping coefficients of the unstable region are more similar, and (b) Peak, with more variation in the unstable aerodynamic dampings.

It was found that the only modification that ended up producing more stable multi-TW solutions was the one that made the unstable aerodynamic damping values more similar (Wide in Fig. 14).

Fig. 14

Aerodynamic damping modifications

For the Wide case, the multi-TW solution bifurcates from the TW solution with wavenumber 2 through a HB and connects again with the same branch at a second HB point (Fig. 15). With respect to the baseline case, this new solution is now stable for a much larger interval of values of the bifurcation parameter $\xi _{a_{1}}$. Furthermore, as before, the maximum displacement of the blades produced by the multi-TW solution remains below that of the single TW solution with highest amplitude (see Table 2), even though their difference is now much smaller.

Fig. 15

Bifurcation diagram for the TW solution with wavenumber 2 (Wide case). Solid (dashed) line indicates stable (unstable) solutions

Table 2 Comparison of the maximum blade displacements

6 Conclusions

Multi-TW stable states are found in a simplified model of a bladed-disk with microslip friction at the bladed-disk attachment. The model describes the vibration of a nearly flat modal family with several aerodynamically unstable modes and is derived through the application of a multiple scales method that allows to filter out the fast elastic blade oscillation. Numerical continuation techniques are applied to follow the branches of new multi-TW solutions that bifurcate from single TW solutions at the stability change. Previous works reported only single TW final states, which were obtained through direct time integrations of the model. The continuation method directly computes the final states and their stability, avoiding the need of performing very long time integrations to reach a converged final state.

The following final remarks summarize the main results of this work:

• 1. The stability analysis of the zero solution (no blade vibration) indicates that nonlinear friction only produces a frequency shift in the aeroelastic modes.

• 2. Single TW solutions bifurcate from the trivial solution as the flutter intensity is increased. The stability analysis of these solutions shows that there is a long time scale associated with the difference between the aerodynamic damping values of unstable modes, which is responsible for the very slow selection of the final state. This long time scale had been detected in time integrations presented in previous works [4, 9, 10].

• 3. There is always a stable single TW solution, which corresponds to the most unstable aerodynamic mode and has the largest amplitude of all single TW solutions. The adjacent TW solutions are first unstable, and they can become stable as the intensity of flutter is increased. There may be several stable single TW limit cycles for the same parameter values.

• 4. At the point of stability change of single TW solutions, new multi-TW solutions appear. Multi-TW solutions have two different frequencies, with non-uniform blade vibration amplitude, and rotate around the bladed-disk. The range of stability of these multi-TW solutions is seen to be related to the presence of unstable aeroelastic modes with similar aerodynamic damping values. The closer the unstable aerodynamic damping values, the larger the region of stability of the multi-TW solutions.

• 5. Multi-TW solutions give rise to blade vibration amplitudes that are always below that of the single TW solution. Therefore, from the point of view of blade fatigue calculation, it seems that it is conservative to consider only the highest amplitude single TW solution.