Discontinuous dynamics for a class of 3-DOF friction and collision system with symmetric bilateral rigid constraints

Abstract

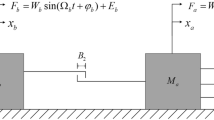
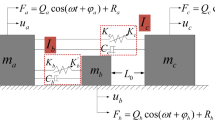
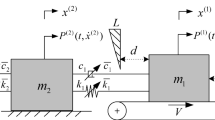
This paper deals with the discontinuous dynamic behaviors of a class of three-degree-of-freedom friction and collision system with symmetric bilateral rigid constraints by using the flow switching theory of discontinuous dynamical systems. The model takes into account the inequality of static and dynamic friction forces, which is more common in practice. The external excitation of the object contains a negative feedback, which can change with the variation of the velocity of the object, so that the system can adapt to different external environment. And the connection between the objects adopts nonlinear springs and viscous dampers in order to achieve a better vibration reduction effect. The model can be applied to mechanical equipment such as shock absorbers etc. According to the discontinuity caused by friction and collision, the dynamic domain and boundary of the object’s motion are defined in phase space, which requires the introduction of absolute coordinates and relative coordinates respectively to discuss the motion between objects. The vector field for the respective domain in the system is given, which can control the motion of object in each domain. The corresponding normal vector on the discontinuous boundary is introduced to determine the positive direction of the flow. The sufficient and necessary conditions for the switching motion of such dynamical system are given based on $\mathrm{G}$-function and its higher order. These switching conditions can be used to predict or even control the motion of the object on the separation boundary. In addition, several typical motions, such as sliding, stick, grazing, impact motions and periodic motion, are numerically simulated to better explain the complexity of the switching motion in the discontinuous dynamic system. Finally, the stick bifurcation scenarios for excitation frequency or amplitude are presented. The research results obtained can provide a theoretical basis for better use or control of friction and collision in practical applications.

Appendices

Appendix A

Without appearance of stick, the different domains of the masses $m_1$ and $m_2$ are defined as

$$\begin{aligned} \left\{ \begin{array}{l} \Omega _{1}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;\dot{x }_{1}>\dot{x }_{2},\;|{x }_{1}-{x }_{2}|<H\},\\ \Omega _2^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;\dot{x }_{1}<\dot{x }_{2},\;|{x }_{1}-{x }_{2}|<H\},\\ \Omega _{\xi ^\theta }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;{(-1)^\xi }\dot{x }_{2}>{(-1)^\xi }\dot{x }_{1},\;{(-1)^\theta }\dot{x }_{2}>0,\;|{x }_{2}-{x }_{1}|<H\}, \end{array}\right. \end{aligned}$$

(80)

and the corresponding boundaries are denoted by

$$\begin{aligned}&\left\{ \begin{array}{l} \partial \Omega _{12}^{(1)}=\partial \Omega _{21}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{12}^{(1)}=\varphi _{21}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;|{x }_{1}-{x }_{2}|<H\bigr \},\\ \partial \Omega _{{1^\theta }{2^\theta }}^{(2)}\!=\!\partial \Omega _{{2^\theta }{1^\theta }}^{(2)}\!=\!\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{{1^\theta }{2^\theta }}^{(2)}\!=\!\varphi _{{2^\theta }{1^\theta }}^{(2)}\!\equiv \! \dot{x }_{2}\!-\!\dot{x }_{1}\!=\!0,\;{(-1)^\theta }\dot{x }_{2}\!>\!0,\;|{x }_{2}\!-\!{x }_{1}|\!<\!H\bigr \},\\ \partial \Omega _{{\xi ^0}{\xi ^1}}^{(2)}\!=\!\partial \Omega _{{\xi ^1}{\xi ^0}}^{(2)}\!=\!\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{{\xi ^0}{\xi ^1}}^{(2)}\!=\!\varphi _{{\xi ^1}{\xi ^0}}^{(2)}\!\equiv \! \dot{x }_{2}\!=\!0,\;{(-1)^\xi }\dot{x }_{2}\!>\!{(-1)^\xi }\dot{x }_{1},\;|{x }_{2}\!-\!{x }_{1}|\!<\!H\bigr \}, \end{array}\right. \end{aligned}$$

(81)

$$\begin{aligned}&\left\{ \begin{array}{l} {}^+\!\partial \Omega _{1\infty }^{(i)}=\bigl \{(x _{i},\dot{x }_{i})\;|\;{}^+\!\varphi _{1\infty }^{(i)}\equiv x _{i}-x _{\overline{i}}+(-1)^{i}H=0,\;(-1)^{i}\dot{x }_{i}<(-1)^{i}\dot{x }_{\overline{i}}\},\\ {}^+\!\partial \Omega _{2\infty }^{(i)}=\bigl \{(x _{i},\dot{x }_{i})\;|\;{}^+\!\varphi _{2\infty }^{(i)}\equiv x _{i}-x _{\overline{i}}+(-1)^{i}H=0,\;(-1)^{i}\dot{x }_{i}>(-1)^{i}\dot{x }_{\overline{i}}\},\\ {}^-\!\partial \Omega _{1\infty }^{(i)}=\bigl \{(x _{i},\dot{x }_{i})\;|\;{}^-\!\varphi _{1\infty }^{(i)}\equiv x _{i}-x _{\overline{i}}-(-1)^{i}H=0,\;(-1)^{i}\dot{x }_{i}<(-1)^{i}\dot{x }_{\overline{i}}\},\\ {}^-\!\partial \Omega _{2\infty }^{(i)}=\bigl \{(x _{i},\dot{x }_{i})\;|\;{}^-\!\varphi _{2\infty }^{(i)}\equiv x _{i}-x _{\overline{i}}-(-1)^{i}H=0,\;(-1)^{i}\dot{x }_{i}>(-1)^{i}\dot{x }_{\overline{i}}\}, \end{array}\right. \end{aligned}$$

(82)

where $i\ne \overline{i}\in \{1,2\},\,\xi \in \{1,2\}\,\,\mathrm and\,\,\theta \in \{0,1\}$.

The vertex of boundaries are defined as

$$\begin{aligned}&\angle \Omega _{12}^{(2)}=\partial \Omega _{{1^0}{1^1}}^{(2)} \bigcap {\partial \Omega _{{2^0}{2^1}}^{(2)}}\bigcap {\partial \Omega _{{1^0}{2^0}}^{(2)}} \bigcap {\partial \Omega _{{1^1}{2^1}}^{(2)}}\nonumber \\&\quad \!=\!\bigl \{(x _{2},\dot{x }_{2})\; |\;\varphi _{{1^\theta }{2^\theta }}^{(2)}\!=\!\varphi _{{2^\theta }{1^\theta }}^{(2)}\!\equiv \! \dot{x }_{2}\!-\!\dot{x }_{1}\!=\!0,\;\nonumber \\&\quad \varphi _{{\xi ^0}{\xi ^1}}^{(2)}\!=\!\varphi _{{\xi ^1}{\xi ^0}}^{(2)} \!\equiv \! \dot{x }_{2}\!=\!0,\;|{x }_{2}\!-\!{x }_{1}|\!<\!H\},\nonumber \\ \end{aligned}$$

(83)

where $\xi \in \{1,2\}\,\,\mathrm{and}\,\,\theta \in \{0,1\}$.

The above domains and boundaries are shown in Fig. 10a, b. The domains $\Omega _1^{(1)}$ and $\Omega _2^{(1)}$ represent the domains where the mass $m _{1}$ does free-flight motion without stick and are expressed in gray and purple, respectively. The domains $\Omega _{\xi ^0}^{(2)}$ and $\Omega _{\xi ^1}^{(2)}$ $(\xi =1,2)$ represent the domains where the mass $m _{2}$ does free-flight motion without stick and are expressed in different shades of gray and purple, respectively. The velocity boundaries $\partial \Omega _{12}^{(1)}$, $\partial \Omega _{{1^0}{2^0}}^{(2)}$ and $\partial \Omega _{{1^1}{2^1}}^{(2)}$ are expressed in red dashed lines and the impact-chatter boundaries ${}^+\!\partial \Omega _{\tau \infty }^{(i)}$ and ${}^-\!\partial \Omega _{\tau \infty }^{(i)}$ $(i=1,2 ,\tau =1,2)$ are expressed in black dashed curves. Furthermore, the stuck boundaries $\partial \Omega _{{1^0}{1^1}}^{(2)}$ and $\partial \Omega _{{2^0}{2^1}}^{(2)}$ for the mass $m _{2}$ are expressed in orange dashed lines.

Fig. 10

Absolute domains and boundaries without appearance of stick: a mass $m_{1}$ and b mass $m_{2}$

Fig. 11

Absolute domains and boundaries with appearance of stick for the two masses: a mass $m_{1}$ and b mass $m_{2}$

With appearance of stick, the different domains of the masses $m_1$ and $m_2$ are defined as

$$\begin{aligned}&\left\{ \begin{array}{l} \Omega _{1}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;\dot{x }_{1}>\dot{x }_{2},\;{x }_{1}\in ({x }_{cr}^{(2)}-H, {x }_{cr}^{(2)}+H)\},\\ \Omega _2^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\; \dot{x }_{1}<\dot{x }_{2},\;{x }_{1}\in ({x }_{cr}^{(2)}-H, {x }_{cr}^{(2)}+H)\},\\ \Omega _3^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\; \dot{x }_{1}=\dot{x }_{2},\;{x }_{1}\in ( {x }_{cr}^{(2)}+H, +\infty )\},\\ \Omega _4^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\; \dot{x }_{1}=\dot{x }_{2},\;{x }_{1}\in (-\infty , {x }_{cr}^{(2)}-H)\}, \end{array}\right. \end{aligned}$$

(84)

$$\begin{aligned}&\left\{ \begin{array}{l} \Omega _{\xi ^\theta }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;{(-1)^\xi }\dot{x }_{2}>{(-1)^\xi }\dot{x }_{1},\;{(-1)^\theta }\dot{x }_{2}>0,\;{x }_{2}\in ({x }_{cr}^{(1)}-H, {x }_{cr}^{(1)}+H)\},\\ \Omega _{3^\theta }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\; \dot{x }_{1}=\dot{x }_{2},\;{(-1)^\theta }\dot{x }_{2}>0,\;{x }_{2}\in (-\infty , {x }_{cr}^{(1)}-H)\},\\ \Omega _{4^\theta }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\; \dot{x }_{1}=\dot{x }_{2},\;{(-1)^\theta }\dot{x }_{2}>0,\;{x }_{2}\in ( {x }_{cr}^{(1)}+H, +\infty )\}, \end{array}\right. \end{aligned}$$

(85)

and the corresponding boundaries are denoted by

$$\begin{aligned}&\left\{ \begin{array}{l} \partial \Omega _{12}^{(1)}=\partial \Omega _{21}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{12}^{(1)}=\varphi _{21}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;{x }_{1}\in ({x }_{cr}^{(2)}-H, {x }_{cr}^{(2)}+H)\bigr \},\\ \partial \Omega _{{1^\theta }{2^\theta }}^{(2)}=\partial \Omega _{{2^\theta }{1^\theta }}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{{1^\theta }{2^\theta }}^{(2)}=\varphi _{{2^\theta }{1^\theta }}^{(2)}\!\equiv \! \dot{x }_{2}-\dot{x }_{1}=0,{(-1)^\theta }\dot{x }_{2}>0,{x }_{2}\in ({x }_{cr}^{(1)}-H, {x }_{cr}^{(1)}\!+\!H)\!\bigr \},\\ \partial \Omega _{{\xi ^0}{\xi ^1}}^{(2)}=\partial \Omega _{{\xi ^1}{\xi ^0}}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{{\xi ^0}{\xi ^1}}^{(2)}=\varphi _{{\xi ^1}{\xi ^0}}^{(2)}\!\equiv \! \dot{x }_{2}=0,{(-1)^\xi }\dot{x }_{2}\!>\!{(-1)^\xi }\dot{x }_{1},{x }_{2}\!\in \!({x }_{cr}^{(1)}-H, {x }_{cr}^{(1)}\!+\!H)\!\bigr \},\\ \partial \Omega _{{3^0}{3^1}}^{(2)}=\partial \Omega _{{3^1}{3^0}}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{{3^0}{3^1}}^{(1)}=\varphi _{{3^1}{3^0}}^{(1)}\equiv \dot{x }_{2}=0,\;\dot{x }_{2}=\dot{x }_{1},\;{x }_{2}\in (-\infty , {x }_{cr}^{(1)}-H)\bigr \},\\ \partial \Omega _{{4^0}{4^1}}^{(2)}=\partial \Omega _{{4^1}{4^0}}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{{4^0}{4^1}}^{(1)}=\varphi _{{4^1}{4^0}}^{(1)}\equiv \dot{x }_{2}=0,\;\dot{x }_{2}=\dot{x }_{1},\;{x }_{2}\in ({x }_{cr}^{(1)}+H, +\infty , )\bigr \}, \end{array}\right. \end{aligned}$$

(86)

$$\begin{aligned}&\left\{ \begin{array}{l} \partial \Omega _{\tau 3}^{(i)}=\partial \Omega _{3\tau }^{(i)}=\bigl \{(x _{i},\dot{x }_{i})\;|\;\varphi _{\tau 3}^{(i)}=\varphi _{3\tau }^{(i)}\equiv \dot{x }_{i}-\dot{x }_{cr}^{(\overline{i})}=0,\;x _{i}=x _{cr}^{(\overline{i})}-(-1)^{i}H\},\\ \partial \Omega _{\tau 4}^{(i)}=\partial \Omega _{4\tau }^{(i)}=\bigl \{(x _{i},\dot{x }_{i})\;|\;\varphi _{\tau 4}^{(i)}=\varphi _{4\tau }^{(i)}\equiv \dot{x }_{i}-\dot{x }_{cr}^{(\overline{i})}=0,\;x _{i}=x _{cr}^{(\overline{i})}+(-1)^{i}H\}, \end{array}\right. \end{aligned}$$

(87)

Fig. 12

Absolute domains and boundary with appearance of stuck for the mass $m _{3}$

where $i\ne \overline{i}\in \{1,2\},\,\, \xi ,\tau \in \{1,2\}\,\,\mathrm and\,\,\theta \in \{0,1\}$. The above domains and boundaries are shown in Fig. 11a, b. The domains $\Omega _3^{(1)}$ and $\Omega _4^{(1)}$ represent the domains where the mass $m _{1}$ does stick motion, which are expressed in green and blue, respectively. The domains $\Omega _{\xi ^0}^{(2)}$ and $\Omega _{\xi ^1}^{(2)}$ $(\xi =3,4)$ represent the domains where the mass $m _{2}$ does stick motion, which are expressed in different shades of green and blue, respectively. The stick boundaries $\partial \Omega _{\tau 3}^{(i)}$ and $\partial \Omega _{\tau 4}^{(i)}$ are expressed in black dotted lines. And the stuck boundaries $\partial \Omega _{{3^0}{3^1}}^{(2)}$ and $\partial \Omega _{{4^0}{4^1}}^{(2)}$ for the mass $m _{2}$ are expressed in green and blue dashed lines.

For the free motion of the mass $m _{3}$, the absolute domains $\Omega _1^{(3)}$ and $\Omega _2^{(3)}$ and stuck boundary $\partial \Omega _{12}^{(3)}$ are defined as

$$\begin{aligned}&\Omega _1^{(3)}=\bigl \{(x _{3},\dot{x }_{3})\; |\; \dot{x }_{3}>0\bigr \},\,\,\nonumber \\&\Omega _2^{(3)}=\bigl \{(x _{3},\dot{x }_{3})\; |\; \dot{x }_{3}<0\bigr \}, \end{aligned}$$

(88)

$$\begin{aligned}&\partial \Omega _{12}^{(3)}=\partial \Omega _{21}^{(3)} =\bigl \{(x _{3},\dot{x }_{3})\;|\;\varphi _{12}^{(3)} =\varphi _{21}^{(3)}\equiv \dot{x }_{3}=0\bigr \}.\nonumber \\ \end{aligned}$$

(89)

Herein, the phase plane is partitioned into two domains by a boundary, which are sketched in Fig. 12. The domains $\Omega _1^{(3)}$ and $\Omega _2^{(3)}$ represent the domains of free motion for the mass $m_{3}$, which are represented by the light gray and light purple areas, respectively. The boundary $\partial \Omega _{12}^{(3)}$ is the velocity boundary, and it is depicted by the orange dashed line.

Appendix B

Fig. 13

Relative domains and boundaries with appearance of stick for the two masses: a mass $m_{1}$ and b mass $m_{2}$

The relative domains for the motions of the masses $m_i\;(i=1,2)$ are defined as

$$\begin{aligned}&\left\{ \begin{array}{l} \Omega _{1}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;\dot{z }_{1}>0,\;|z _{1}|<H\},\\ \Omega _2^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;\dot{z }_{1}<0,\;|z _{1}|<H\},\\ \Omega _3^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;\dot{z }_{1}=0,\;{z }_{1}=H\},\\ \Omega _4^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;\dot{z }_{1}=0,\;{z }_{1}=-H\}, \end{array}\right. \end{aligned}$$

(90)

$$\begin{aligned}&\left\{ \begin{array}{l} \Omega _{\xi ^\theta }^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;{(-1)^\xi }\dot{z }_{2}>0,\;{(-1)^\theta }\dot{z }_{2}>{(-1)^{\theta +1}}\dot{x }_{1},\;|z _{2}|<H\},\\ \Omega _{3^\theta }^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;\dot{z }_{2}=0,\;{z }_{2}=-H\},\\ \Omega _{4^\theta }^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;\dot{z }_{2}=0,\;{z }_{2}=H\}, \end{array}\right. \end{aligned}$$

(91)

and the corresponding boundaries are denoted by

$$\begin{aligned}&\left\{ \begin{array}{l} \partial \Omega _{12}^{(1)}=\partial \Omega _{21}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{12}^{(1)}=\varphi _{21}^{(1)}\equiv \dot{z }^{(1)}=0,\;|z _{1}|<H\bigr \},\\ \partial \Omega _{{1^\theta }{2^\theta }}^{(2)}=\partial \Omega _{{2^\theta }{1^\theta }}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{{1^\theta }{2^\theta }}^{(2)}=\varphi _{{2^\theta }{1^\theta }}^{(2)}\equiv \dot{z }_{2}=0,\;{(-1)^\theta }\dot{z }_{2}>{(-1)^{\theta +1}}\dot{x }_{1},\;|z _{2}|<H\},\\ \partial \Omega _{{\xi ^0}{\xi ^1}}^{(2)}=\partial \Omega _{{\xi ^1}{\xi ^0}}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{{\xi ^0}{\xi ^1}}^{(2)}=\varphi _{{\xi ^1}{\xi ^0}}^{(2)}\equiv \dot{z }_{2}=-\dot{x }_{1},\;{(-1)^\xi }\dot{z }_{2}>0,\;|z _{2}|<H\},\\ \partial \Omega _{{3^0}{3^1}}^{(2)}=\partial \Omega _{{3^1}{3^0}}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{{3^0}{3^1}}^{(2)}=\varphi _{{3^1}{3^0}}^{(2)}\equiv \dot{z }_{2}=-\dot{x }_{1},\;\dot{z }_{2}=0,\;z _{2}=-H\},\\ \partial \Omega _{{4^0}{4^1}}^{(2)}=\partial \Omega _{{4^1}{4^0}}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{{4^0}{4^1}}^{(2)}=\varphi _{{4^1}{4^0}}^{(2)}\equiv \dot{z }_{2}=-\dot{x }_{1},\;\dot{z }_{2}=0,\;z _{2}=H\}, \end{array}\right. \end{aligned}$$

(92)

$$\begin{aligned}&\left\{ \begin{array}{l} \partial \Omega _{\tau 3}^{(i)}=\partial \Omega _{3\tau }^{(i)}=\bigl \{(z _{i},\dot{z }_{i})\;|\;\varphi _{\tau 3}^{(i)}=\varphi _{3\tau }^{(i)}\equiv \dot{z }_{i}=0,\;z _{cr}^{(i)}=(-1)^{i+1}H\},\\ \partial \Omega _{\tau 4}^{(i)}=\partial \Omega _{4\tau }^{(i)}=\bigl \{(z _{i},\dot{z }_{i})\;|\;\varphi _{\tau 4}^{(i)}=\varphi _{4\tau }^{(i)}\equiv \dot{z }_{i}=0,\;z _{cr}^{(i)}=(-1)^{i}H\},\\ {}^+\!\partial \Omega _{1\infty }^{(i)}=\bigl \{(z _{i},\dot{z }_{i})\;|\;{}^+\!\varphi _{1\infty }^{(i)}\equiv z _{i}+(-1)^{i}H=0,\;(-1)^{i}\dot{z }_{i}<0\},\\ {}^+\!\partial \Omega _{2\infty }^{(i)}=\bigl \{(z _{i},\dot{z }_{i})\;|\;{}^+\!\varphi _{2\infty }^{(i)}\equiv z _{i}+(-1)^{i}H=0,\;(-1)^{i}\dot{z }_{i}>0\},\\ {}^-\!\partial \Omega _{1\infty }^{(i)}=\bigl \{(z _{i},\dot{z }_{i})\;|\;{}^-\!\varphi _{1\infty }^{(i)}\equiv z _{i}-(-1)^{i}H=0,\;(-1)^{i}\dot{z }_{i}<0\},\\ {}^-\!\partial \Omega _{2\infty }^{(i)}=\bigl \{(z _{i},\dot{z }_{i})\;|\;{}^-\!\varphi _{2\infty }^{(i)}\equiv z _{i}-(-1)^{i}H=0,\;(-1)^{i}\dot{z }_{i}>0\}, \end{array}\right. \end{aligned}$$

(93)

where $i\ne \overline{i}\in \{1,2\},\,\xi \in \{1,2\},\,\theta \in \{0,1\}\,\,\mathrm{and}\,\,\tau =1,2$. The relative domains and boundaries are shown in Fig. 13a, b. The stick domains and stick boundaries in relative coordinates become the blue points.