Automatic locking of a parametrically resonating, base-excited, nonlinear beam

Abstract

Described is a closed-loop control scheme capable of stabilizing a parametrically excited nonlinear structure in several vibration modes. By setting the relative phase between the spatially filtered response and the excitation, the open-loop unstable solution branches are stabilized under a 2:1 parametric excitation of a chosen mode of vibration. For a given phase, the closed-loop automatically locks on a limit cycle, through an Autoresonance scheme, at any desired point on the solution branches. Axially driven slender beams and nanowires develop large transverse vibration under suitable amplitudes and frequency base-excitation that are sensitive to small potential coupled field. To utilize such a structure as a sensor, stable and robust operation are made possible by the control scheme. In addition, an optimal operating point with large sensitivity to the sensed potential field can be set using phase as a tunable parameter. Detailed analysis of the dynamical behavior, experimental verifications, and demonstrations sheds light on some features of the system dynamics.

1 Introduction and motivation

This paper is the preliminary result of an effort to produce an ultrasensitive sensor for measuring Nano-scale interaction forces in high-aspect ratio scenarios. Vibrating sensors are often employed to sense small interaction forces [1, 2] and thereby to measure topographic height related to the intermolecular forces between a vibrating sensor’s tip and the nearest molecules on the measured specimen [3]. In the emerging world of 3D-shaped electronic devices, there is a need to measure the actual geometry of deep trenches and steep walls. The motivation behind this paper is the idea of employing a transversely vibrating nanowire so that its interaction forces with side walls can be accurately measured. To achieve this goal, it is necessary to excite vibrations in a stable and predictable manner and choose an operating point for this slender structure so that it is sensitive to small, nano-scale interaction forces. By connecting a nanowire to a vibrating base, typically this is done with a piezoelectric element (e.g., a quartz tuning fork [4]), one can produce axial motion along the structure that would cause transverse motion orthogonal to the axial excitation [4]. The transverse motion takes place at a narrow frequency range and under a suitable excitation amplitude. In the context of the proposed work, a control method to automatically generate transverse vibrations of a nanowire in a desired mode of vibration is developed here. Presented is the physical and mathematical model of a base excited structure, its dynamic behavior in open-loop and the proposed closed-loop realizing automatic resonance of principle parametric resonance. Asymptotic Galerkin and multiple scales (MS) analysis are compared with large-scale experiments.

1.1 Background and literature review

The utilization of parametric resonance to generate large amplitude vibrations under a small excitation levels is a well-known phenomenon, occurring in numerous physical systems [5]. One of its characteristics is a non-unique solution that leads to the jump phenomenon [6] at some frequencies, which makes the prediction and control of the response amplitude at some frequencies, hard. In this paper, an automatic feedback scheme able to realize a resonance-based control loop is put forward. This scheme can track the stable or the open-loop unstable solutions of a nonlinear systems with principal parametric resonance. The latter relies on the control of the relative phase between excitation and response in a similar manner to Sokolov and V. I. Babitsky [7] that numerically demonstrated similar results for single degree of freedom (DOF) linear and nonlinear systems, and a two DOF linear system. Miller et al. [8] experimentally demonstrated the ability to stabilize the open-loop unstable branch of a single DOF parametric oscillator using PID-based phase control scheme, which they termed parametric PLL. Villanueva et al. [9] produced a similar scheme using analogue feedback of a MEMS resonator. Here, we analyze and experimentally demonstrate the ability to control the open-loop unstable branches of a 2:1 parametrically excited continuous system, with a different scheme employing Autoresonance [7] combined with modal filtering [10]. We demonstrate the ability to stabilize the open-loop unstable branches of the first and second vibration modes of a continuous system using digital feedback, without the need to tune the PID control parameters as done in [8, 11].

Another approach to find and track unstable solutions is control-based continuation [12,13,14,15]. This approach requires a repetitive experiment (or simulation) where a small step to a neighboring point on the nonlinear frequency response needs to be first estimated. Whereas the proposed scheme can reach any point of the response curve without the need for scanning the curve. Another advantage of the proposed scheme is that unlike control-based continuation the response and the control signal frequencies are automatically tuned by the dynamics of the scheme, and the control tracks frequency changes upon drifts in the physical model parameters. In addition, in the proposed approach there is no need for tuning a controller as in control-based continuation. Another alternative approach that was previously reported [11, 16] employs a PLL to stabilize unstable solution branches, as demonstrated in both experiments and simulations. But the PLL-based methods demand a monotonous evolution of the phase and an initial guess for the desired frequency. However, as mentioned before, the proposed scheme neither requires prior knowledge of the frequency nor a monotonous evolution of the phase.

A case study of a nonlinear vibrating beam is developed throughout this paper to demonstrate the proposed scheme and to point toward possible sensing applications. The analysis is carried out via analytical, numerical, and experimental realizations. An explanation and a proof for the obtained response stability under the proposed close-loop scheme are provided.

The paper is structured as following: Sect. 2 briefly outlines the mathematical model of a base-excited beam, its asymptotic solution leading to some analysis of this system special features, and the inter-relations between the amplitude, phase, and frequency, unique to this construct. In Sect. 3, an automatic, a nonlinear closed-loop control scheme capable of exciting the vibrating beam in parametric resonance in several regions is described, modeled, and analyzed for stability. The same section demonstrates and verifies the mathematical derivations with numerical simulations and provides digital signal processing details required for the implementation. The extensive experimental campaign described in Sects. 3.4 and 3.5 verifies the assumptions regarding the stability of the closed-loop control and demonstrates an application of a device as a sensor capable of sensing magnetic forces.

2 Dynamic model

Before describing the control scheme, a model of the system under consideration is outlined. The model expands slightly the published description of an inextensional nonlinear beam under base excitation.

2.1 Introducing the model

The full nonlinear equation of motion (EOM) of a beam is well known and was first derived by Silva and Glynn[17] back in 1978. Later, Nayfeh and Perngjin [18] used this model to investigate the behavior of a clamped beam with internal resonance (two degrees of freedom system). A simpler model for a clamped beam carrying lumped mass under base excitation (single degree of freedom) was investigated by Zavodney and Nayfeh [19] among others.

In the present paper, the model is an extension of the combined results of the above-mentioned papers and is described by Eq. (1).

$$ \begin{aligned} \rho Av_{tt} + cv_{t} + EIv_{ssss} & = - EI\left( {v_{ss}^{3} + 4v_{s} v_{ss} v_{sss} + v_{s}^{2} v_{ssss} } \right) \\ & \quad - \rho A\left( {v_{s} \int_{L}^{s} {\left[ {x_{tt} + \frac{1}{2}\int_{0}^{s} {\left( {v_{s}^{2} } \right)_{tt} ds} } \right]ds} } \right)_{s} \\ \end{aligned} $$

(1)

with the associated boundary conditions (clamped-free beam):

$$ v(0) = v_{s} (0) = 0,\,\,\,\,v_{ss} (L) = v_{sss} (L) = 0 $$

(2)

where $v$ is the deflection of the beam, $x$ is the base displacement, $s$ is the arc length coordinate along the beam, $\rho$ is the density, $A$ is the cross-sectional area, $E$ is Young’s modulus, $c$ is the damping coefficient and the sub-indexing $\cdot_{t,s}$ denotes derivatives with respect to time and s, respectively.

The LHS of Eq. (1) is the ordinary damped linear EOM of a vibrating beam. The RHS of Eq. (1) is related to the nonlinear terms up to a third order. The first term in the RHS is related to the cubic stiffness of the beam due to curvature. The second term is related to the coupling force between the base axial acceleration, the beam bending motion and to nonlinear inertial terms.

Normalizing $v,s$ and $x$ by $L$, and scaling the time by $\sqrt {\frac{{\rho AL^{4} }}{EI}}$, we arrive at the normalized equation, where $\hat{ \cdot }$ denotes normalized parameters:

$$ \begin{aligned} \hat{v}_{{\hat{t}\hat{t}}} + \hat{c}\hat{v}_{{\hat{t}}} + \hat{v}_{{\hat{s}\hat{s}\hat{s}\hat{s}}} & = - \left( {\hat{v}_{{\hat{s}\hat{s}}}^{3} + 4\hat{v}_{{\hat{s}}} \hat{v}_{{\hat{s}\hat{s}}} \hat{v}_{{\hat{s}\hat{s}\hat{s}}} + \hat{v}_{{\hat{s}}}^{2} \hat{v}_{{\hat{s}\hat{s}\hat{s}\hat{s}}} } \right) \\ & \quad - \frac{1}{2}\left( {\hat{v}_{{\hat{s}}} \int_{1}^{{\hat{s}}} {\left[ {\int_{0}^{{\hat{s}}} {\left( {\hat{v}_{{\hat{s}}}^{2} } \right)_{{\hat{t}\hat{t}}} d\hat{s}} } \right]d\hat{s}} } \right)_{{\hat{s}}} - \left( {\left( {\hat{s} - 1} \right)\hat{v}_{{\hat{s}\hat{s}}} + \hat{v}_{{\hat{s}}} } \right)\hat{x}_{{\hat{t}\hat{t}}} \\ \end{aligned} $$

(3)

In order to reduce the partial differential equation to an ordinary differential equation, the Galerkin method [20] is employed.

First, the linear conservative homogeneous model describing small vibrations is considered, from which the natural frequencies and the normal modes can be found:

$$ \hat{v}_{{\hat{t}\hat{t}}} + \hat{v}_{{\hat{s}\hat{s}\hat{s}\hat{s}}} = 0. $$

(4)

The normalized natural frequencies, ω_n, are the roots of the following transcendental equation:

$$ 1 + \cos \left( {\sqrt {\omega_{n} } } \right)\cosh \left( {\sqrt {\omega_{n} } } \right) = 0, $$

(5)

and the normal modes, serving as basis for the Galerkin method, are:

$$ \begin{aligned} \phi_{n} & = \cosh \left( {\sqrt {\omega_{n} } \hat{s}} \right) - \cos \left( {\sqrt {\omega_{n} } \hat{s}} \right) \\ & \quad - \frac{{\cos \left( {\sqrt {\omega_{n} } } \right) + \cosh \left( {\sqrt {\omega_{n} } } \right)}}{{\sin \left( {\sqrt {\omega_{n} } } \right) + \sinh \left( {\sqrt {\omega_{n} } } \right)}}\left[ {\sinh \left( {\sqrt {\omega_{n} } \hat{s}} \right) - \sin \left( {\sqrt {\omega_{n} } \hat{s}} \right)} \right] \\ \end{aligned} $$

(6)

Now, by approximating the response of the beam using a single mode, i.e.

$$ \hat{v}\left( {\hat{s},\hat{t}} \right) \approx \phi_{n} \left( {\hat{s}} \right)w_{n} \left( {\hat{t}} \right), $$

(7)

and integrating over the beam’s length, one can obtain the weak formulation of the equation:

$$ \ddot{w}_{n} + \hat{c}\dot{w}_{n} + \alpha_{2} w_{n} + \alpha_{3} w_{n}^{3} + \alpha_{4} w_{n} \left( {\dot{w}_{n}^{2} + w_{n} \ddot{w}_{n} } \right) + \alpha_{5} w_{n} \hat{\ddot{x}} = 0. $$

(8)

The numerical values of the constants $\alpha_{i}$ are detailed in Appendix A.

Normalizing the time again by the natural frequency $\tau = \sqrt {\alpha_{2} } \hat{t}$ and substituting¹$w_{n} = \varepsilon y$, where ε is a small parameter added for bookkeeping, and choosing the damping coefficient to be of order ε (i.e.,$\hat{c} = 2\varepsilon \zeta \omega_{n}$ _s), we arrive at:

$$ y^{\prime\prime} + 2\varepsilon \zeta y^{\prime} + \left[ {1 + \alpha_{5} \hat{x}^{\prime\prime}} \right]y + \varepsilon^{2} \kappa_{3} y^{3} + \varepsilon^{2} \alpha_{4} y\left( {y^{{\prime}{2}} + yy^{\prime\prime}} \right) = 0, $$

(9)

where $\cdot ^{\prime}$ denotes derivative with respect to $\tau$.

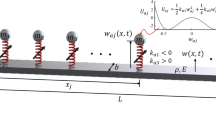
The physical realization described by the former equation is depicted in Fig. 1.

Fig. 1

Vibrating beam whose shape v(s,t) is proportional to a single mode $\phi_{n} \left( s \right)$ via Eq. (7), with non-normalized parameters

It should be stressed that Eq. (9) describes the dimensionless EOM of a beam vibrating in a specific, single mode under base excitation with nonlinear inertia and stiffness terms, linear damping, scaled to the chosen order of ε.

2.2 Asymptotic solution

Substituting the following acceleration into Eq. (9):

$$ \begin{array}{*{20}l} {\Omega = 2 + \varepsilon \sigma } \hfill \\ {\hat{x}^{\prime\prime} = 4\varepsilon \gamma \alpha _{5}^{{ - 1}} \cos \left( {\Omega \tau } \right){\mkern 1mu} } \hfill \\ \end{array} $$

(10)

the solution can be analytically approximated for the case of principle parametric resonance using the method of MS [21], and the full solution is outlined in Appendix B. There are three possible steady-state solutions as detailed in Eqs. (11)–(14).

$$ w_{n} = a_{k} \varepsilon \cos \left( {\frac{\Omega }{2}\tau - \frac{{\psi_{k} }}{2}} \right) + O\left( {\varepsilon^{2} } \right) $$

(11)

where a_k, k = 1,2,3 can obtain these values:

$$ a_{1,2} = \sqrt 6 \sqrt {\frac{{\varepsilon \left( {3\gamma^{2} - 2\zeta^{2} } \right) - 2\sigma + 2\left( {2 - \varepsilon \sigma } \right)\gamma \cos \left( {\psi_{1,2} } \right)}}{{\varepsilon \left( {6\alpha_{4} - 9\kappa_{3} } \right)}},\,\,\,} a_{3} = 0 $$

(12)

and the matching phase ψ_k is the solution of

$$ \sin \left( {\psi_{k} } \right) = - \frac{2\zeta }{{\left( {2 - \varepsilon \sigma } \right)\gamma }}, $$

(13)

that are given by

$$ \begin{array}{*{20}l} {\psi_{1,2} = 2\pi n - \frac{\pi }{2} \pm \Delta \,\,\,,} & {\,\,\,} \\ \end{array} n \in {\mathbb{Z}},\,\,\,\,\,\,\,\,\,\Delta = \frac{\pi }{2} - \arcsin \left( {\frac{2\zeta }{{\left( {2 - \varepsilon \sigma } \right)\gamma }}} \right). $$

(14)

Notice that the phase ψ₃ is omitted, as it is meaningless and may attain any value.

The solution is used for analyzing the dynamical response below.

2.2.1 On the phase unique role and use in the dynamic response

Examining Eq. (12), one can notice that there are two possible solutions for the amplitude as function of the response frequency, emanating from two solutions of the phase, which will be addressed as the response curve. One of the solutions can be shown to be stable, while the other is unstable (Appendix B). It is customary to plot the response curve as the amplitude versus frequency, a = f(ω), but in fact, the full response curve is contained in R³ and should be presented as such, with the phase $\left( {\begin{array}{*{20}l} a & \psi \\ \end{array} } \right)^{T} = g\left( \omega \right)$. Sokolv and Babitsky have already produced this kind of curve in their paper [7] for a linear system with weak nonlinearity. The same representation was also used by the authors of [11] for controlling a nonlinear system. The present paper expands this perspective for a system subjected to parametric resonance, in a manner that is useful for devising an automatic, closed-loop control, as shown later.

In linear systems, the importance of plotting both phase and amplitude versus frequency is well known, and the Bode diagram shows both. Moreover, in linear system analysis the Nichols diagram shows the amplitude as a function of the phase, which is just another projection of the 3D response curve onto the phase-amplitude plane. The same can be done with the response curve in the case of parametric excitation, which has an extended meaning, particularly for nonlinear systems.

When changing the excitation amplitude, unlike linear system, the present system being nonlinear undergoes a transformation other than pure scaling, resulting in a 2D manifold contained in a 4D space $\left( {\begin{array}{*{20}l} a & \psi \\ \end{array} } \right)^{T} = g\left( {\omega ,\gamma } \right)$, where γ is related to the response amplitude [see Eq. (10)]. This fact is significant in understanding the behavior of the system when applying a closed-loop control scheme.

It is possible to graphically present Eqs. (12)–(14) for several amplitude levels of the parametric excitation. These are provided in Fig. 2, considering the first normal mode, ϕ₁.

Fig. 2

a Response curve of mode ϕ₁, γ = 1.03ζ and its projections. Note that the MS analysis predicts a closed response curve. The curve is continuous in all 3 projections shown here. Continuous (dashed) lines indicate a stable (unstable) solution branch. b Several response curves of mode ϕ₁ and the backbone curve. The discrete curves are embedded in the surface of the response manifold. Damping coefficient is εζ = 0.01

While the first mode exhibits a single, continuous curve, the second mode curve, shown in Fig. 3, is split into two divergent response curves.

Fig. 3

a Response curve of mode ϕ₂, γ = 1.03ζ and its projections. Note that the MS analysis predicts an open response curve. Continuous (dashed) lines indicate a stable (unstable) solution branch. b Several response curves of mode ϕ₂. The discrete curves are embedded in the surface of the response manifold. Damping coefficient is εζ = 0.01

It is worth emphasizing that the multiple solutions are uniquely determined for a given triplet of amplitude, frequency, and phase. E.g., in Fig. 3a one can clearly distinguish the two response curves defined for different values of the phase. The same applies to Fig. 2a where for a given frequency there could theoretically be two different amplitudes, one stable and the other unstable. Adding the phase information would distinguish these points.

2.3 Sensitivity

One of the characteristics of the principal parametric resonance phenomenon is the high sensitivity of the amplitude to small changes of parameters in the EOM. This feature candidates the phenomenon to be a felicitous base for nanowire sensors. Such sensors can be used for measuring accurately small interaction forces (namely Van Der Wall's forces) acting between the nanowire and the desired sample, similar to AFM devices. These interaction forces are nonlinear forces and can be treated as linear spring whose stiffness depends on the distance between the sensor and the measured sample. Thus, as we analyze the sensitivity of the system, we will regard the small changes in the EOM to appear in the linear natural frequency, i.e., the coefficient $\alpha_{2}$ in Eq. (8) will be replaced with $\alpha_{{2{\text{new}}}}$:

$$ \begin{aligned} \alpha _{2} \to \alpha _{{2{\text{new}}}} & = \alpha _{2} + \kappa \ddot{w}_{n} + \hat{c}\dot{w}_{n} + \alpha _{{2{\text{new}}}} w_{n} \\ & \quad + \alpha _{3} w_{n}^{3} + \alpha _{4} w_{n} \left( {\dot{w}_{n}^{2} + w_{n} \ddot{w}_{n} } \right) + \alpha _{5} w_{n} \hat{\ddot{x}} = 0^{,} \\ \end{aligned} $$

(15)

and we define the change in the natural frequency in percentage as:

$$ \Delta \omega_{n} \left[ \% \right] = \frac{{\sqrt {\alpha_{{2{\text{new}}}} } - \sqrt {\alpha_{2} } }}{{\sqrt {\alpha_{2} } }} \times 100. $$

(16)

In Fig. 4a, the response curve projection on the amplitude-frequency plane can be seen for two realizations, the original EOM and a modified EOM with change of $\Delta \omega_{n}$ = 0.5%. Due to the shape of this curve which behave as $\sqrt \sigma$, under a constant excitation frequency, $\sigma = \sigma_{0}$, a drastic change in the steady state amplitude takes place, which amplifies the ability to detect it. Figure 4b demonstrates the amplitude changes due to a shift in the potential coupling the beam to an external element, (e.g., magnet in this case). The latter shifts the natural frequency and therefore, alters the response curves. The simulated curves represent slightly different coupling potentials that alter the small amplitude natural frequency. It is convenient to show the amplitude sensitivity, shown in Fig. 4c. The sensitivity to a parameter, $\kappa$ representing a change in the stiffness, is said to be $S = \frac{da}{{d\kappa }}$ and as can be seen (Fig. 4c) it become infinity large at lower amplitudes. The amplitude and its derivative were calculated using Eqs. (12)–(16).

Since the system is very sensitive and parametric resonance occurs at a narrow frequency band, a small deviation would make it lose stability, thus causing the vibrations to decay. The latter leads to the conclusion that open-loop operation could be impractical when excitation the frequency and force amplitude are set. Thus, a method to automatically excite the system in principal parametric resonance is needed, and this is the motivation for the automatic control presented below.

Fig. 4

a Response of mode $\phi_{1}$ for 2 cases, original coefficients, and a change in the linear natural frequency by 0.5 [%]. The black arrow emphasizes the drastic change in amplitude under constant frequency of excitation. b Four curves of amplitude as function of $\Delta \omega_{n}$, under different constant frequencies of excitation. c The sensitivity of the system to small changes in $\omega_{n}$, namely the derivative of the four curves displayed in b

3 Automatic excitation of principal parametric resonance

3.1 Closed-loop architecture

While the control scheme proposed in this paper is implemented on an axially driven clamped-free beam, its architecture, as described below, can be applied to a wider range of nonlinear systems with parametric resonance having 2:1 frequency ratio.

The injected control signal, u, is equivalent (in theory) to the acceleration x_tt and can be written as:

$$ u = x_{tt} = K \cdot h\left( {\mathcal{G}\left( {\mathcal{F}\left( {w_{n}^{2} } \right)} \right)} \right) $$

(17)

where K is the gain of the closed loop, and $\mathcal{F,}\,\,\mathcal{G}$, and h are the following operators:

$$ \mathcal{F}\,{\text {- }}{\text{High}}\,{\text{Pass}}\,{\text{Filter}},\,\,\,\mathcal{G}\,{\text {- }}{\text{Phase}}\,{\text{Shift}},\,\,\,\,h\,{\text {- }}{\text{Sign,}} $$

(18)

and w_n is the modal coordinate [see Eq. (7)] filtered out from the measured deflection of the beam using a modal filter [19] (further details are provided in Sect. 3.1.1).

When the control loop was implemented during experiments (Sects. 3.4, 3.5), the control signal u was treated as the voltage sent to the voice coil (actuator). The base acceleration was the response (of a linear system) to the voltage, same frequency, different phase, and amplitude proportional to the voltage amplitude.

In principal parametric resonance, the control signal needs to be twice the response signal frequency. When the squaring operation shown in Fig. 5 acts on a sinusoidal signal, it gives rise to an average (DC) value and a sinusoid signal with a doubled frequency. The unwanted DC is removed with a high-pass filter. A phase shifter is added to control the relative phase between excitation and response. The signum function implements the automatic excitation part, capable of locking onto a single frequency, while limiting the amplitude, in the spirit of Autoresonance [10, 22]. The post-multiplying gain is added to set the control signal level to a desired constant amplitude, regardless of the measured response signal amplitude—w_n.

Fig. 5

Closed-loop Architecture. Shown are the key blocks, the modal filter isolates a desired mode using spatial filtering, the squaring element produces a double frequency, a high-pass filter removes the DC part, the phase shifter controls the relative phase of the response with respect to the excitation, and the signum function realizes the required automatic switching of the control signal that produces the locking on the correct frequency

3.1.1 Modal filter for multiple degrees of freedom system

When dealing with parametric resonance of a clamped-free beam, the continuous system exhibits vibrations comprising several vibration modes and it is unclear which one will be excited by the scheme in Fig. 5 under the 2:1 frequency ratio. Normally, the mode most visible by the sensors, i.e., the first mode prevails. By adding a combination of a spatial modal-filter and a bandpass filter, it is possible to automatically excite selected modes.

Let ${\mathbf{x}}_{{\mathbf{s}}} \in R^{m \times 1}$ be all points along the beam where the response is measured, and N denotes the number of participating modes. It is possible to express the measurements vector, z as:

$$ {\mathbf{z}} = {\mathbf{v}}\left( {{\mathbf{x}}_{{\mathbf{s}}} ,t} \right) = \sum\limits_{n = 1}^{N} {\phi_{n} \left( {{\mathbf{x}}_{{\mathbf{s}}} } \right)w_{n} \left( t \right)} . $$

(19)

Recasting using matrix notations

$$ {\mathbf{z}} = {\mathbf{Cw}} = \left( {\begin{array}{*{20}l} {\phi_{1} \left( {x_{1} } \right)} & {\phi_{2} \left( {x_{1} } \right)} & \cdots & {} \\ {\phi_{1} \left( {x_{2} } \right)} & \ddots & {} & {} \\ {\phi_{1} \left( {x_{3} } \right)} & {} & {} & {} \\ \vdots & {} & {} & {\phi_{N} \left( {x_{m} } \right)} \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {w_{1} \left( t \right)} \\ {w_{2} \left( t \right)} \\ \vdots \\ {w_{N} \left( t \right)} \\ \end{array} } \right). $$

(20)

Since normally not all of the modes are being excited, and assuming that there are more sensors than participating modes (m > N), Eq. (20) is overdetermined. A least-squares solution for the contribution of each mode can be found using the pseudo-inverse of C [23]. Where C can be obtained experimentally by measuring the normal modes at the sensor locations, thus realizing a modal filter:

$$ {\mathbf{w}} = {\mathbf{C}}^{\dag } {\mathbf{z}}. $$

(21)

Having found the required modal coordinates, w_n(t), the scheme in Fig. 5 is used to make the corresponding mode dominant as described below.

3.2 Stability analysis of the closed-loop system

Having described the schematics of the closed-loop parametric excitation realization, ensuring a 2:1 excitation for a single mode, there is no guarantee that the structure will exhibit a stable limit cycle. In addition, it is desirable to understand the system's dynamical behavior under the proposed scheme. In the following sections, the behavior of the closed-loop scheme is analyzed for stability.

3.2.1 Stability and automatic excitation

As exemplified later through numerical simulation (Sect. 3.3), the closed-loop scheme stabilizes the otherwise unstable solution branch. Thus, the purpose of this section is to show that the closed-loop system converges to the nontrivial solution even though it is unstable in the open loop.

We start by assuming that a steady-state solution of the closed-loop system exists, and that the dynamical system response (i.e., output) is a periodic signal with a dominating component, having an amplitude A and frequency ω:

$$ w_{n} \left( t \right) = A\cos \left( {\omega t} \right) + \varepsilon F\left( t \right),\,\,\,\,\,\,\,F\left( t \right) = F\left( {t + \frac{2\pi }{\omega }} \right). $$

(22)

Then, the control signal is [using a truncated Fourier series, [24], Eq. (17)]:

$$ u\left( t \right) \approx K\,Sign\left( {\cos \left( {2\omega t + \psi } \right)} \right) \approx \frac{4K}{\pi }\cos \left( {2\omega t + \psi } \right). $$

(23)

Due to the recursive nature of the closed loop, one can now calculate the response of the dynamical system to the input u Eq. (23) and check if it is identical to the one assumed in Eq. (22). The result as calculated in the open-loop system shows this assumption holds. Comparing Eqs. (10), (11) to Eqs. (22), (23), respectively, reveals that the inputs and outputs in both cases are identical provided that the closed-loop gain is $K = \varepsilon \pi \alpha_{2} \alpha_{5}^{ - 1} \gamma$.This shows that the steady state solutions of both open and closed-loop system are identical.

As discussed in Sect. 2.2.1, the full response of the nonlinear system for a given excitation amplitude can be described as a curve in a 3D space. While in the open-loop, one should determine the control signal frequency, in proposed closed-loop scheme, it is automatically determined by the chosen signal's phase lag with respect to the response. Moreover, the automatically generated control signal’s frequency ensures that it is twice the response frequency.

When tuning the frequency to a certain value (open-loop situation), there are two possible solutions based on the MS analysis (see Eq. (14), and Fig. 6). In addition, a trivial solution can exist, for which the amplitude nullifies and the phase is not well-defined.

Fig. 6

Difference between closed- and open-loop. When choosing a specific frequency, there are two nontrivial solutions to the phase (and amplitude), alternatively for a specified phase there is only one nontrivial solution for a given frequency (and amplitude). Same response curve as Fig. 2

Therefore, tuning the frequency in the open-loop system results in multiple solutions and gives rise to stable and unstable stationery points in the (a, ψ) plane. In practice, the system locks on the trivial solution stable nontrivial solution, depending on the initial state.

In contrast, the closed-loop system sets ψ to a certain dictated value. Thus, according to Eq. (14) the solution is unique, and there is only one nontrivial solution corresponding to the specific values of σ and ψ (see Fig. 6). Setting $\psi > - \pi /2$ or $\psi < - \pi /2$ determines the system response (i.e., on which branch, stable or unstable, the solution resides). It should be emphasized that for the first mode, $\psi = - \pi /2$ corresponds to the point of maximum amplitude, as can be deduced from Eqs. (12)–(14).

Since the trivial solution is mathematically possible, it is shown later that under the closed-loop control, the focal point (i.e., the trivial solution, a = 0) becomes unstable. Consequently, the nontrivial and originally unstable solution becomes stable.

The original EOM and control law are given by Eqs. (8), (17) and (18), respectively. By choosing a control law as follows:

$$ \mathcal{F}\left( x \right) = \mathop x\limits^{ \cdot } ,\quad \mathcal{G}\left( x \right) = \beta_{1} x + \beta_{2} \mathop x\limits^{ \cdot } $$

(24)

the operators $\mathcal{F}$ and $\mathcal{G}$ realize Eq. (18) requirements. Taking the derivative of a signal eliminates any constant values (DC). By further taking the linear combination of the periodic signal and its derivative, using the constants β_i, it is possible to set ψ to any desired value.

By substituting Eq. (24) into Eq. (17), the control signal becomes:

$$ \begin{gathered} \mathcal{F}\left( {w^{2} } \right) = 2w\dot{w},\,\,\,\,\mathcal{G}\left( {\mathcal{F}\left( {w^{2} } \right)} \right) = 2\left( {\beta_{1} w\dot{w} + \beta_{2} \left( {\dot{w}^{2} + w\ddot{w}} \right)} \right) \hfill \\ \,\,u = K \cdot sign\left( {\beta_{1} w\dot{w} + \beta_{2} \left( {\dot{w}^{2} + w\ddot{w}} \right)} \right) \hfill \\ \end{gathered} $$

(25)

Substituting the control signal, Eq. (25), to Eq. (8), one obtains:

$$ \begin{aligned}& \ddot{w} + c_{v} \dot{w} + \alpha_{2} w + \alpha_{3} w^{3} + \alpha_{4} w\left( {\dot{w}^{2} + w\ddot{w}} \right) \hfill \\ & + K\alpha_{5} w \cdot sign\left( {\beta_{1} w\dot{w}w + \beta_{2} \left( {\dot{w}^{2} + w\ddot{w}} \right)} \right) = 0 \hfill \\ \end{aligned} $$

(26)

This representation is useful since now the system is autonomous and in contrast to the open-loop system, the phase-space is a 2D space instead of 3D. Moreover, using Eq. (26) one can find the full response curve using numerical simulations without need of tuning frequency selective filters at all. Still, Eqs. (25), (26) represent a recursive relationship between $u$ and $\ddot{w}$ which is non-standard for the subsequent analysis 2D phase-space. Furthermore, the acceleration in Eq. (26) appears as a nonlinear term and there is no guarantee for a unique or any solution. To remedy this difficulty, we set $u = \pm K$ and solve for the acceleration which leads to:

$$ \ddot{w}_{ \pm } = - \frac{{\overbrace {{c_{v} \dot{w} + \alpha_{2} w + \alpha_{3} w^{3} + \alpha_{4} w\dot{w}^{2} }}^{{C_{1} }} \pm K\alpha_{5} w\,}}{{\underbrace {{\left( {1 + \alpha_{4} w^{2} } \right)}}_{{C_{0} }}}} $$

(27)

Now, we can substitute Eq. (27) into Eq. (25) to recast $u$ as a function of $w,\dot{w}$:

$$ u = \left\{ {\begin{array}{*{20}l} { + K\quad f\left( {w,\dot{w}} \right) > K\beta_{2} } \\ { - K\quad f\left( {w,\dot{w}} \right) < - K\beta_{2} } \\ \end{array} } \right. $$

(28)

where

$$ f\left( {w,\dot{w}} \right) = \frac{{C_{2} C_{0} - C_{3} C_{1} }}{{\alpha_{5} w^{2} }},\,\,C_{2} \triangleq \beta_{1} w\dot{w} + \beta_{2} \dot{w}^{2} \,,\,\,C_{3} \triangleq \beta_{2} w\, $$

(29)

The controlled parameter $\beta_{2}$ can be both positive or negative, this creates a problem in Eq. (28) since in the region $- K\left| {\beta_{2} } \right| < f\left( {w,\dot{w}} \right) < K\left| {\beta_{2} } \right|$ there may be two or zero solutions for the control signal. In order to avoid this problem, we will define the control signal in this region to be $u = 0$. Since K is a small parameter, the uncertain region appears to be negligibly small and hence, the latter has no visible effect on the dynamic behavior.

Under closed-loop control, the governing equation is 2D instead of 3D, and there are four possibilities for the behavior in phase-space, where we use our prior knowledge that there is a periodic solution and a focal point as illustrated in Fig. 7.

Fig. 7

Possible behavior in phase-space under the closed-loop system. The vector field represents the phase portrait of the system. There are two known solutions in steady-state—one is trivial represented by the markers in the origins, and the other is nontrivial (limit cycle), represent by the circles. A full (hollow) marker represents stable (unstable) focal point, and a continuous line represent a stable, while dashed line indicates an unstable, the occurrence of both is a semi-stable limit cycle

The illustrated behaviors in panels C and D are not possible at low gains since a semi-stable limit cycle is a bifurcation point of two limit cycles—stable and unstable [25] meeting each other. Such bifurcation point can occur if a line of constant phase is tangential to the response curve, then a small change in the parameters of the system (or in the control system) can change the tangent point to zero or into two intersection points, two nontrivial solution, i.e., two limit cycles. This is not the case as can deduced from Fig. 6.

It is now shown that for some gain values K, the trivial solution becomes unstable, while under closed-loop, for both the stable or unstable branches. The analysis being used is based on energy balance. Multiplying Eq. (26) by $\dot{w}$ and integrating over the time and transferring all the non-conservative and control related terms to the RHS, the latter becomes²:

$$ \begin{aligned} \Delta E & = - c_{v} \int\limits_{0}^{t} {\dot{w}^{2} dt} - K\alpha_{5} \beta_{1} \int\limits_{0}^{t} {\frac{{\left( {w\dot{w}} \right)^{2} }}{{\left| {\beta_{1} w\dot{w} + \beta_{2} \left( {\dot{w}^{2} + w\ddot{w}} \right)} \right|}}dt} \\ & \quad - K\alpha_{5} \beta_{2} \int\limits_{0}^{t} {\frac{{w\dot{w}\frac{d}{dt}\left( {w\dot{w}} \right)}}{{\left| {\beta_{1} w\dot{w} + \beta_{2} \left( {\dot{w}^{2} + w\ddot{w}} \right)} \right|}}dt} \\ \end{aligned} $$

(30)

leading to

$$ \Delta E = \left. {\frac{1}{2}\dot{w}^{2} + \frac{1}{2}\alpha_{2} w^{2} + \frac{1}{4}\alpha_{3} w^{4} + \frac{1}{2}\alpha_{4} \left( {w\dot{w}} \right)^{2} } \right|_{0}^{t} . $$

(31)

Now, we examine the case where:

$$ \beta_{1} \approx \pm 1,\beta_{2} \approx \varepsilon , $$

(32)

whose meaning is that we focus on solution regions where the phase is around $\psi = \pm \,\pi /2$ (because $\mathcal{F}$ adds π/2 for these values). Substituting Eq. (32) to Eq. (30) and neglecting small terms yields:

$$ \Delta E = - c_{v} \int\limits_{0}^{t} {\dot{w}^{2} dt} - K\alpha_{5} sign\left( {\beta_{1} } \right)\int\limits_{0}^{t} {\frac{{\left( {w\dot{w}} \right)^{2} }}{{\left| {w\dot{w}} \right|}}dt} $$

(33)

Denoting that both integrals are positive, the sign of ΔE depends on the controlled coefficients K and β₁.

When considering small linear vibrations around the origin, the trivial solution is unstable if ΔE > 0, and vice versa [followed from Eq. (31)]. Hence, β₁ needs to be negative to lose stability and the phase should be in the vicinity of $\psi = - \pi /2$. In regions where the phase is around π/2, the system dissipates energy, and this can be used to design an active damping system (see Appendix D).

When setting the phase to be around $\psi = - \pi /2$, and slowly increasing the gain, a Hopf bifurcation occurs (i.e., the origin loses its stability, and a limit cycle takes place). Thus, we are left with the solution shown in panel A in Fig. 7 as the one in panel B is proven impossible, i.e., an unstable node and a stable limit cycle. It does not matter whether the phase is larger or smaller than $\psi = - \pi /2$, in both cases the sign and value of $\beta_{1}$ is the same. Thus, whether the closed-loop system response follows the originally stable or unstable branches, the control loop destabilizes the trivial solution and stabilizes the nontrivial solution.

Fig. 8

Response curve a and its projections b–d for mode $\phi_{1}$. The cubic stiffness was increased to${\mathrm{\alpha }}_{3}=10{\mathrm{\alpha }}_{3,\mathrm{mode }1}$, $\mathrm{\epsilon \gamma }=10.5\mathrm{\epsilon \zeta }$ $,\mathrm{ \epsilon \zeta }=0.01$. As can be seen, the MS, open-loop, and closed-loop are the same, in relatively small amplitudes. The closed-loop can stabilize the unstable branch. The response is symmetric around $\uppsi =-\frac{\uppi }{2}\left[\mathrm{rad}\right]$

The bifurcation point can be found using the averaging method of [26]. By considering small linear vibrations with slowly changing amplitude:

$$ \begin{aligned} & {t = \tau_{0} + \varepsilon \tau_{1} } \\ & {w\left( t \right) = A\left( {\tau_{1} } \right)\cos \left( {\sqrt {\alpha_{2} } \tau_{0} } \right)} \\ \end{aligned} $$

(34)

the change in amplitude:

$$ \begin{aligned} A^{\prime}A & = \frac{{\left. {\Delta E} \right|_{0}^{T} }}{{2\pi \sqrt {\alpha_{2} } }} = \frac{ - 1}{{2\pi \sqrt {\alpha_{2} } }}\left( {c_{v} \int\limits_{0}^{T} {\frac{dw}{{d\tau_{0} }}^{2} d\tau_{0} } + K\alpha_{5} sign\left( {\beta_{1} } \right)\int\limits_{0}^{T} {\frac{{\left( {w\frac{dw}{{d\tau_{0} }}} \right)^{2} }}{{\left| {w\frac{dw}{{d\tau_{0} }}} \right|}}d\tau_{0} } } \right) \hfill \\ A^{\prime} & = - \frac{A}{{2\pi \sqrt {\alpha_{2} } }}\left( {\pi c_{v} \sqrt {\alpha_{2} } + 2K\alpha_{5} sign\left( {\beta_{1} } \right)} \right) \hfill \\ \end{aligned} $$

(35)

where T is a unit period,³ so the bifurcation point is:

$$ K > - \frac{{\pi c_{v} \sqrt {\alpha_{2} } }}{{2\alpha_{5} sign\left( {\beta_{1} } \right)}} > 0. $$

(36)

Now, assuming that:

$$ \beta_{1} \approx \varepsilon ,\beta_{2} \approx \pm 1 $$

(37)

substituting Eq. (36) to Eq. (30) and neglecting small terms, we are left with:

$$ \Delta E = - c_{v} \int\limits_{0}^{t} {\dot{w}^{2} dt} - K\alpha_{5} {\text{sign}}\left( {\beta_{2} } \right)\int\limits_{0}^{t} {w\dot{w}\,{\text{sign}}\left( {\frac{d}{dt}\left( {w\dot{w}} \right)} \right)dt} $$

(38)

Using the averaging theory once more and assuming small linear vibrations [namely using Eq. (34)], the second term in Eq. (38) becomes:

$$ \int\limits_{0}^{T} {w\frac{dw}{{d\tau_{0} }}{\text{sign}}\left( {\frac{d}{{d\tau_{0} }}\left( {w\frac{dw}{{d\tau_{0} }}} \right)} \right)d\tau_{0} } = 0. $$

(39)

Now, one can conclude that around $\psi = 0,\pi /2$ the control loop has little effect on the dynamics of the system. The change in energy in one period is

$$ \Delta E \approx - c_{v} \int\limits_{0}^{T} {\dot{w}^{2} dt} $$

(40)

Now, we examine what happens in some comparable values of $\beta_{1}$ and $\beta_{2}$

$$ \beta_{1} \sim \beta_{2} \sim O\left( 1 \right) $$

(41)

As we change β₁ and β₂ continuously (thus changing the phase), the energy fed to the system due to the closed-loop controller also changes smoothly. By controlling the phase, it is possible to cause a transition between injecting energy, having negligible effect, dissipating energy, and having negligible effect again.

It should be noted that although we started this section from the assumption that there are two solutions when setting the phase: trivial and not trivial, we cannot know that from the MS analysis applied to the second mode, which predicts that there is no solution at $\psi = - \pi /2$. Nevertheless, the trivial solution does loose its stability as concluded from the energy balance analysis, regardless of the mode.

Now, the following question arises: is the system globally unstable in the second mode around this point? As deduced from Figs. 9, 10 and 11 and elaborated below, the answer is no. A limit cycle exists due to the cubic stiffness and the damping far from 2ω_n with some finite amplitude. Moreover, while the MS analysis does not predict that the system's response curve is closed, as can be concluded from the energy balance, once we find that there is a solution at $\psi = - \pi /2$.

Fig. 9

Response curve a and its projections (b-d) for mode $\phi_{2}$. $\mathrm{\epsilon \gamma }=10.5\mathrm{\epsilon \zeta },\mathrm{ \epsilon \zeta }=0.01$. There are two regions of the response, far and close to $2{\upomega }_{\mathrm{n}}$(with high or low amplitude). The high amplitude region contains only the closed-loop response. Between the two region- a jump

Fig. 10

Zoom on Fig. 9 onto a region of frequencies close to $2{\omega }_{n}$. In b, the closed-loop, open-loop. And MS all agree perfectly with each other. In c, d, the open-loop and closed-loop match while there are small errors relative to the MS solution

Fig. 11

Simulation for the closed-loop for mode ϕ₂. A modification to the closed-loop enabled us to stabilize the whole curve and remove the jump. The closed loop at first behave as the MS predicts, the two solutions at first are getting further apart from each other, but as it turns out, the response curve is closed, and symmetric around $\uppsi =-\frac{\uppi }{2}\left[\mathrm{rad}\right].$ Note that for certain phases there are two possible solutions. Experimental Verification

3.3 Numerical simulations and comparison with an open-loop system

Using the Matlab™ function ode45 and Simulink, we simulated the open- and closed-loop systems. In the open-loop, the control parameter was the frequency, and in the closed-loop, the control parameter was the relative phase. Figure 8 shows the simulation results for the first mode where the cubic stiffness was increased so that the results from the MS analysis agree with the simulation (otherwise it agrees only qualitatively). From Fig. 8, we can see that the closed and open-loops dynamics resemble, but the closed-loop system can stabilize the unstable branch. The MS analysis assumes small deviations around $\sigma = 0$ and small vibration amplitudes. Hence, in the region of low frequencies and amplitudes, the MS solution agrees with both the open and closed-loop simulations as can be seen in Fig. 8, while in the region of high amplitudes and frequencies it differs.

When we explored the closed-loop system dynamics for the second mode (shown in Fig. 9), two response regions were obtained: a low amplitude region with frequency close to 2ω_n and a high amplitude region with frequencies far from 2ω_n and between the two, a jump. We can note that in both regions the frequency ratio between the control signal and the response signal is 2:1. In the low amplitude region, when looking at the amplitude–frequency plane (Fig. 10b), the closed-loop, open-loop, and MS analysis resemble, and the closed-loop is able to stabilize the unstable branch. But, when we look at the other planes (Fig. 10), there are deviations in the relative phase between the numerical simulations and the analytical solution. Somehow, the MS analysis predicts the amplitude as function of frequency accurately, but not the phase. The second region seems to behave in an unusual manner since a principal parametric resonance was achieved at a frequency far from the linear natural frequency. As discussed before, if the response is globally stable, it should have a maximum amplitude at $\psi = - \frac{\pi }{2}$$,$ be symmetric in a small region around this phase, and the response curve should be continuous and closed despite that the MS analysis does not predict it. From the simulation shown in Fig. 9, it appears that the closed-loop system did not stabilize the whole response curve, and hence the jump. By modifying the closed-loop system as discussed in Appendix C, we succeeded to stabilize the unstable parts, and to eliminate the discontinuous jump, additionally the second mode’s response curve is continuous (Fig. 11). Examination of Fig. 11 shows that for the second mode, there are two possible amplitudes for some phase values, which explains the jump. In this case, the phase shifter can be constrained to avoid ambiguity as detailed in Appendix C.

Last note regarding the numerical simulation, when the system was simulated, it was noticed that the phase was relatively sensitive to the time steps and convergence criteria, while the amplitude and frequency converged quickly. The latter should be considered when simulating the response curve.

3.4 The experimental system

The experimental system comprises a voice coil which was used for the base excitation. It is connected to a mass resting on a spring that can move in the longitudinal direction. A steel beam of length 273 mm and rectangular cross section of 6 × 0.5 mm was clamped to the mass. An accelerometer was connected to the mass measuring the axial motion. Up to four Keyence™, optical sensors were connected externally to the mechanical system to measure the bending deflections of the beam at several points (Fig. 12). The control algorithm was implemented using Simulink and dSPACE, with a sampling rate of 5 kHz. The natural frequencies of the beam were first estimated by applying a Fourier transform to the beam’s response to transverse impact. The first four frequencies were found to be: 5.167, 32.11, 90.22, 176.3 Hz, which are sufficiently smaller than 5 kHz.

Fig. 12

Design (left) and implementation (right) of the experimental system in the laboratory. Left: CAD model. Right: photograph. One can observe these main components: Voice-coil actuator driving the based on the right which is connected by 2 parallel flexures to ground, several optical laser sensors. Accelerometer measuring the base axial motion and the vibrating beam under investigation

3.4.1 Numerical estimation of the experimental system characteristics

For verification, the beam’s normal modes were numerically estimated using finite elements analysis, using the commercial software ANSYS™. The computed normal modes are shown in Fig. 13. As can be seen, there is no linear coupling between the base movement and the beam’s deflection (i.e., bending and axial motion occur separately).

Fig. 13

Simulated modes of the experimental system using ANSYS™. The first mode a enabled us to accelerate the system in the longitude direction of the beam. As can be seen, the bending related modes of the beam b, c are decoupled from the mode exhibiting axial motion of the base

3.5 Comparison, analysis of the results and their significance

3.5.1 Automatic excitation

The automatic parametric excitation is a useful and significant characteristic of the closed-loop. While the first mode was parametrically excited effortlessly in both open-loop and close-loop configurations, bringing the system to parametrically resonate at the second mode was more challenging. In open-loop, to achieve parametric excitation at the second mode, the control signal had to be set initially with high precision to the correct frequency, and then the appropriate initial conditions had to be applied to the beam. Even though in theory, for some frequencies, the zero-amplitude solution should be unstable, in practice it remained stable. Since we could not control the initial state in practice, we applied random impacts to the system until it got the right initial state and started vibrating in parametric resonance. However, using the closed-loop control, the system was automatically excited in parametric resonance.

For the implementation of the closed-loop, we employed a modal filter and several digital and analog filters to reduce noisy sensor signals and high-frequency-related components. Since the first mode exhibited high amplitudes, it was easily and automatically excited and did not require any significant changes from the architecture described in Fig. 5. The results can be seen in Fig. 14a. In contrast, to excite the second mode we had to take a more complex route. First, the second mode was excited in an open-loop choosing a fundamental parametric resonance with frequency ratio of 1:1, and then, the system switched to the closed-loop operation. Without this procedure, the first mode prevailed and overcome the second mode, thus preventing the closed-loop from locking on it. The results can be seen in Fig. 14b. Once the closed-loop was able to automatically excite the second mode in parametric resonance, the second mode excitation in parametric resonance in an open-loop became easier. First, the closed-loop was switched on, then a signal with same frequency phase and amplitude was synchronized to the control signal and replaced it. This procedure ensured that the initial state in the open-loop configuration was close enough to the steady state response.

Fig. 14

a, b First mode Automatic Excitation and zoom to the transient part of the excitation and response, at steady-state the response approached a pure sinusoid. Even though higher modes were present, the closed-loop was able to lock on the first mode. As the amplitude is developed, the higher modes decayed. c, d Show the second mode behavior under automatic excitation. Until t < 5.98[s], an open loop 1:1 excitation was applied to the system, then switching to closed-loop parametric resonance the parametric excitation kicks in and full locking takes place

3.5.2 Stabilizing unstable branches

In these experiments, the response manifolds of both modes were measured by controlling the excitation amplitude and phase using the closed-loop. During the open-loop experiments, the excitation frequency and the excitation amplitude were controlled.

Figure 15 shows the measured response manifold and their projections on each of the planes, as measured in both open- and closed-loop systems for the first mode. As can be seen, while in the open-loop system, the response curve is cut off in the left branch before it gets to zero smoothly (Fig. 15b, a jump to zero occurred in the experiment when the frequency decreased), the closed-loop is able to measure this branch. This demonstrates that the closed-loop system works as expected. Moreover, the open- and closed-loop response of the system are on the same manifold, meaning that the closed-loop is indeed non-intrusive and keeps the dynamics of the system unchanged.

Fig. 15

The first mode response manifold as measured in both closed- and open-loop. It can be seen that the unstable branch become stable under the closed-loop

In addition, the arch-shaped amplitude versus phase graph is formed as can be seen in Fig. 15d and it is symmetric around $\psi = - \frac{\pi }{2}$. In contrast, the frequency is not an arch-shaped graph (Fig. 15c), which is also reflected in the steep slope of the unstable branch in Fig. 15b. A possible cause for this phenomenon may be due to the additional dynamics that is not included in the model, such as square-law damping $f = - c\dot{w}_{n} \left| {\dot{w}_{n} } \right|$ [27].

Several final notes regarding this experiment seem appropriate. When the first mode is excited, the system exhibits a softening behavior instead of hardening as predicted by the model and the set of parameters chosen in the simulation (Sects. 2.2, 3.3). It is suspected that it is due to the initial curvature of the beam that is not included in the model and the fact that the clamping at the base was not completely rigid. This disagreement has no effect on the closed-loop architecture that overcomes this discrepancy by setting the reference phase. The scheme is suitable for controlling parametrically excited nonlinear systems, as described, making this system more robust and controllable and less sensitive to modeling fine details. Additionally, the closed-loop adds robustness to the system which results in smooth measured curves, as can be seen in Fig. 15, while in the open-loop exhibits somewhat noisier curves stemming from additional dynamics. The closed-loop operation seems to reduce these additional effects.

For the second mode, the results of the measurements in both open- and closed-loop system can be seen in Fig. 16. Again, we observe that the closed-loop was able to stabilize the unstable branch of the response, and that it is indeed non-intrusive and keeps the dynamics of the system the same. Here, we can clearly see the arch-shaped amplitude versus phase and frequency versus phase graphs. Like the first mode, they exhibit a symmetry around $\psi = - \frac{\pi }{2}$. Moreover, while the open-loop experienced a noisy behavior, the closed-loop added robustness to the system, resulting in smoother curves.

Fig. 16

Second mode response manifold as measured in both closed- and open-loop. The unstable branch becomes stable under the closed-loop

In conclusions, it should be mentioned that the measured and theoretical response manifolds are somewhat different (Sects. 2.2, 3.3) in both in the first and second mode as discussed above. These could be explained by the unknown initial curvature of the vibrating beam, non-ideal clamping, and additional forces such as square-law damping. Nevertheless, the closed-loop seems to work properly and the observed behavior is generally as expected according to Sects. 3.2, 3.3 and in fact assists in overcoming model uncertainties.

3.5.3 Sensing—maintaining resonance while changing system parameters

One of the great advantages of the autoresonance controller is that if the system parameters changed (e.g., the natural frequency shifts), it automatically tracks and remains locked to the resonance, although at a different frequency and amplitude. In the following experiments, we examined the closed-loop behavior when some changes are introduced to the system, imitating the change in Van der Waals (VdW) forces under gap change. Changes in the system were achieved using a small magnet that was moved closer and further away from the vibrating ferromagnetic beam. We measured the first and second mode response curves for three fixed gaps of the magnet from the beam, and results are shown in Figs. 17, 18. The curve is mostly moving parallel to the frequency axis (due to change in natural frequency). This result can be useful for maintaining resonance under varying parameters, which is an important characteristic for sensors based on parametric resonance such as AFM based nanowires [2].

Fig. 17

First mode, system response measured in closed-loop for different magnet-beam distances. The result of varying the distance cause the system response to move mostly parallel along the frequency axis. The phase at which maximum amplitude is achieved remains the same, and that fact can be used for maintaining parametric resonance during changes in the system parameters

Fig. 18

Second mode, system response measured in closed-loop for different magnet-beam distances. The response is mainly moving parallel along the frequency axis, while the amplitude seems to exhibit the most sensitivity

Moreover, the sensitivity exhibited by the system was evaluated in this experiment. The sensitivity to small changes in the gap between a constant magnet and the vibrating beam was evaluated by placing it at a gap of 20 [mm]. The curve indicated by 0 [mm] and 3 [mm] (blue and yellow) in Fig. 17b illustrates the small change in frequency required to keep the vibration level of a = 0.2 and the large change in vibration amplitude when the oscillation frequency is kept constant. The points of intersection are marked in black and yellow squares, respectively. From the point of intersection on the 3 [mm] response curve, a vertical line of constant frequency (f = 10.19 [Hz]) was drawn and the intersection with the 0 [mm] response curve is once again marked in black square. Under the constant frequency of excitation, the change in natural frequency represented by $\Delta \omega$ in Fig. 17(b), which is relatively small, would cause the amplitude to drastically drop by amount of $\Delta A$ Using Eq. (16), the numerical values of $\Delta A$, and $\Delta \omega_{1}$ were obtained:

$$ \Delta A = \frac{0.2 - 0.549}{{0.549}} \cdot 100 = - 60.38\% $$

$$ \Delta \omega_{1} = \frac{10.190 - 10.230}{{10.230}} \cdot 100 = - 0.392\% $$

(42)

Despite the fact that this calculation is rough and simple, it demonstrates the large sensitivity of the amplitude to small interaction forces. The sensitivity of course depends on the specific point along the response curve, and it is much higher on the unstable branch since its slope is higher.

Similar results are shown for the second mode where the change in natural frequency was $\Delta \omega_{2}$ = − 0.15%, while the change in amplitude is $\Delta A$ = − 45.88% under frequency of excitation f = 63.85 [Hz]. (Fig. 18b).

This experiment verifies the stated elevated sensitivity shown in the analytical analysis in Sect. 2.3, even though the measured response manifolds are not those exactly what is expected from theory, but is in general agreement, as discussed in the previous section.

Figure 18 demonstrates that under a fixed excitation frequency (i.e., Figure 18b), the response amplitude changes by more than 40% for a fractional percent change in the response frequency upon small movement of the magnet. This fact illustrates the sensitivity of the parametrically excited system to small changes in the external potential field of the parametrically excited system.

4 Conclusions

The paper presents a method to automatically excite principal parametric resonance with a frequency ratio of 2:1 in a closed-loop using phase control and modal filtering. It has been shown that the proposed closed-loop control scheme can stabilize the open-loop unstable solution branches by three steps. First, it was explained why there is only one steady-state solution (a limit cycle) when setting the phase in the closed-loop rather than setting the frequency in the open-loop, as usually done. Then, it is shown that the closed-loop system can be expressed in a reduced number of state variable (2 instead of 3). Lastly, it is proven that the origin of the state-space becomes unstable under the chosen control law using energy balance therefore a limit cycle must arise. From these three steps, it can be concluded that the existing limit cycle is stable. The latter explains why the system is automatically excited while maintaining resonance even under drifts in parameters of the system. Numerical simulation and experiments were conducted to support the analytical proof given in the paper. All three methods demonstrated the closed-loop behavior on a clamped-free cantilever, both in first and second mode, and the results can be possibly applied to similar systems with driven in resonance under parametric excitation with frequency ratio of 2:1. A comparison between the three methods, asymptotic, numerical and experimental, was done. In the first mode, the MS solution was able to predict accurately the numerically simulated response curve simulated numerically. In the second mode, the amplitude–frequency prediction was accurate, the phase prediction less, and additional segments of the response curve that are not predicted by the MS were revealed using the closed-loop. The experimental system demonstrated the different characteristics and robustness of the closed-loop that can possibly aid in conducting such experiments with refined operating point control. Measurements of the same response manifold were carried out both by the open- and closed-loops, while in the closed-loop the otherwise unstable branch is stabilized. The latter is done both in the first and second mode, using an appropriate modal and frequency filters for each case. The observed dynamics did not match the theory (softening instead of hardening), yet the closed-loop seems to work well, thus supporting the need for the proposed control scheme.

The ability of the closed-loop to track the resonance under drift in parameters of the system can be exploited to construct a sensor based on parametric excitation, such as an Atomic force microscope (AFM) where the change in potential intermolecular forces depends on the gap from the vibrating sensor. The method shows greater robustness and stability than an open-loop driven parametric excitation and can be used to study the nonlinear dynamics of systems, as well as for automatic actuation in large vibration amplitudes. The principle parametric resonance exhibits large amplitude sensitivity as shown both analytically and experimentally to changes in the potential which make it a good candidate for measuring potential changes. A change of $\Delta \omega$ ₁ = -0.39% in the first natural frequency caused the amplitude to change of $\Delta A$ = 60.38%.

Appendices

Appendix A

Calculating the constants appearing in Eq. (8). Using $\phi_{n}$ from Eq. (6), we can evaluate (Table

Table 1 The values for mode 1 and 2 when using Eq. (43) are:

1):

$$ \begin{aligned} \alpha _{1} & = \int_{0}^{1} {\phi _{n}^{2} ds} = 1\quad \quad \quad \alpha _{2} = \int_{0}^{1} {\phi _{n} \phi _{n}^{{\left( 4 \right)}} ds} \\ \alpha _{3} & = \int_{0}^{1} {\phi _{n} \left( {\phi _{n} ^{{\prime \prime 3}} + 4\phi _{n} ^{\prime } \phi _{n} ^{{\prime \prime }} \phi _{n}^{{\left( 3 \right)}} + \phi _{n} ^{{\prime 2}} \phi _{n}^{{\left( 4 \right)}} } \right)ds} \\ \alpha _{4} & = \int_{0}^{1} {\phi _{n} \left\{ {\phi _{n} ^{\prime } \int_{1}^{s} {\left[ {\int_{0}^{s} {\left( {\phi _{n} ^{{\prime 2}} } \right)ds} } \right]ds} } \right\}_{s} ds\quad \quad \alpha _{5} = \int_{0}^{1} {\phi _{n} \left( {\left( {s - 1} \right)\phi _{n} ^{{\prime \prime }} + \phi _{n} ^{\prime } } \right)ds} } \\ \end{aligned} $$

(43)

Appendix B

The multiple-scales analysis described in (9) can be solved by expanding $y$ and $\tau$:

$$ \begin{gathered} \tau = \tau_{0} + \varepsilon \tau_{1} + \varepsilon^{2} \tau_{2} \hfill \\ y\left( {\varepsilon ,\tau } \right) = y_{0} \left( {\tau_{0} ,\tau_{1} ,\tau_{2} } \right) + \varepsilon y_{1} \left( {\tau_{0} ,\tau_{1} ,\tau_{2} } \right) + \varepsilon^{2} y_{2} \left( {\tau_{0} ,\tau_{1} ,\tau_{2} } \right), \hfill \\ \end{gathered} $$

(44)

By substituting Eq. (44) back to Eq. (9) and separating orders of $\varepsilon$, one obtains:

$$ \varepsilon^{0} :D_{0}^{2} y_{0} + y_{0} = 0 $$

(45)

$$ \varepsilon^{1} :D_{0}^{2} y_{1} + y_{1} = - 2D_{0} D_{1} y_{0} - 2\zeta D_{0} y_{0} - 4\gamma \cos \left( {\Omega \tau } \right)y_{0} $$

(46)

$$ \begin{aligned} \varepsilon^{2} :D_{0}^{2} y_{2} + y_{2} & = - D_{1}^{2} y_{0} - 2D_{0} D_{2} y_{0} - 2D_{0} D_{1} y_{1} - \alpha_{4} \left[ {y_{0} \left( {D_{0} y_{0} } \right)^{2} + y_{0}^{2} D_{0}^{2} y_{0} } \right] \\ & \quad - 2\zeta \left( {D_{1} y_{0} + D_{0} y_{1} } \right) - \kappa_{3} y_{0}^{3} - 4\gamma \cos \left( {\Omega \tau } \right)y_{1} \\ \end{aligned} $$

(47)

The zero-order solution, expressed in complex form, is (cc stands for complex conjugate):

$$ y_{0} = A\left( {\tau_{1} ,\tau_{2} } \right){\text{e}}^{{i\tau_{0} }} + cc, $$

(48)

The secular equation from Eq. (46) is:

$$ - 2iD_{1} A - 2i\zeta A - 2\gamma \overline{A}{\text{e}}^{{i\sigma \tau_{1} }} = 0, $$

(49)

and the particular solution of Eq. (46) is:

$$ y_{1} = \frac{2\gamma A}{{\Omega \left( {2 + \Omega } \right)}}{\text{e}}^{{{\text{i}}\left( {1 + \Omega } \right)\tau_{0} }} + cc. $$

(50)

Using Eqs. (49, 50), the secular equation from Eq. (47) can be found:

$$ \left( {\zeta^{2} - \gamma^{2} - \frac{{4\gamma^{2} }}{{\Omega \left( {2 + \Omega } \right)}}} \right)A + \left( {2\alpha_{4} - 3\kappa_{3} } \right)A^{2} \overline{A} - \gamma \sigma \overline{A}e^{{i\sigma \tau_{1} }} - 2iD_{2} A = 0. $$

(51)

By combining the two secular equations, we arrive at:

$$ - 2iA^{\prime} + \left[ {\left( {\zeta^{2} - \gamma^{2} - \frac{{4\gamma^{2} }}{{\Omega \left( {2 + \Omega } \right)}}} \right)\varepsilon - 2i\zeta } \right]\varepsilon A + \left( {2\alpha_{4} - 3\kappa_{3} } \right)\varepsilon^{2} A^{2} \overline{A} - \left( {2 - \varepsilon \sigma } \right)\gamma \overline{A}{\text{e}}^{{i\sigma \tau_{1} }} = 0 $$

(52)

where $A^{\prime} = \left( {\varepsilon D_{1} + \varepsilon^{2} D_{2} } \right)A = \frac{d}{dt}A$.

Substituting the polar form:

$$ A\left( \tau \right) = \frac{1}{2}a\left( \tau \right){\text{e}}^{i\phi \left( \tau \right)} , $$

(53)

and separating to real and imaginary parts, yields:

$$ \underline{{\Re}} :\,\, \phi ^{\prime}a = - \frac{1}{{24}}a\varepsilon \left( \begin{aligned} & \varepsilon \left( { - 18\gamma ^{2} + 12\zeta ^{2} + a^{2} \left( {6\alpha _{4} - 9\kappa _{3} } \right)} \right) \\ & - 12\gamma \left( {2 - \varepsilon \sigma } \right)\cos \left( {\varepsilon \tau _{1} - 2\phi } \right) \\ \end{aligned} \right) $$

(54)

$$ \underline{\Im } :a^{\prime} = - \frac{1}{2}a\varepsilon \left( {2\zeta + \gamma \left( {2 - \varepsilon \sigma } \right)\sin \left( {\varepsilon \tau _{1} - 2\phi } \right)} \right) $$

(55)

In order to transform Eqs. (54), (55) into an autonomous system, the following function is defined:

$$ \begin{array}{*{20}l} {\psi = \varepsilon \sigma \tau - 2\phi } & \Rightarrow & {\psi^{\prime} = \varepsilon \sigma - 2\phi^{\prime}} & \Rightarrow & {2\phi^{\prime} = } \\ \end{array} \varepsilon \sigma - \psi^{\prime} $$

(56)

Substituting Eq. (56) into Eqs. (54), (55) simplifies into:

$$ \underline{\Re } :\psi ^{\prime}a = \frac{1}{{12}}a\varepsilon \left( \begin{aligned} & a^{2} \varepsilon \left( {6\alpha _{4} - 9\kappa _{3} } \right) + 6\left( { - 3\gamma ^{2} \varepsilon + 2\varepsilon \zeta ^{2} + 2\sigma } \right) \\ & - 12\gamma \left( {2 - \varepsilon \sigma } \right)\cos \left( \psi \right) \\ \end{aligned} \right) = af_{1} \left( {a,\psi } \right) $$

(57)

$$ \begin{gathered} \underline{\Im}: \hfill a^{\prime} = - \frac{1}{2}a\varepsilon \left( {2\zeta + \gamma \left( {2 - \varepsilon \sigma } \right)\sin \left( \psi \right)} \right) = f_{2} \left( {a,\psi } \right) \hfill \\ \end{gathered} $$

(58)

Seeking the steady-state solution, $a^{\prime} = \psi^{\prime} = 0$, the equations reduce into:

$$ \underline{\Re } :0 = \frac{1}{{12}}a\varepsilon \left( \begin{aligned} & a^{2} \varepsilon \left( {6\alpha _{4} - 9\kappa _{3} } \right) + 6\left( { - 3\gamma ^{2} \varepsilon + 2\varepsilon \zeta ^{2} + 2\sigma } \right) \\ & - 12\gamma \left( {2 - \varepsilon \sigma } \right)\cos \left( \psi \right) \\ \end{aligned} \right) $$

(59)

$$ \underline{\Im } :0 = - \frac{1}{2}a\varepsilon \left( {2\zeta + \gamma \left( {2 - \varepsilon \sigma } \right)\sin \left( \psi \right)} \right) $$

(60)

and the solution of Eqs. (59), (60) is outlined in Eqs. (11)–(14).

The stability of the nontrivial solutions can be found using linearization of Eqs. (57), (58), around the solution Eqs. (11)–(14):

$$ \frac{d}{dt}\left( {\begin{array}{*{20}l} \psi \\ a \\ \end{array} } \right) = M\left( {\begin{array}{*{20}l} {\Delta \psi } \\ {\Delta a} \\ \end{array} } \right) = \left. {\left( {\begin{array}{*{20}l} {\frac{{\partial f_{1} }}{\partial \psi }} & {\frac{{\partial f_{1} }}{\partial a}} \\ {\frac{{\partial f_{2} }}{\partial \psi }} & {\frac{{\partial f_{2} }}{\partial a}} \\ \end{array} } \right)} \right|_{{\left( {\begin{array}{*{20}l} a \\ \psi \\ \end{array} } \right)\, = \left( {\begin{array}{*{20}l} {a_{k} } \\ {\psi_{k} } \\ \end{array} } \right)}} \left( {\begin{array}{*{20}l} {\Delta \psi } \\ {\Delta a} \\ \end{array} } \right) $$

(61)

and finding the numeric values of the eigenvalues of the matrix M.

Appendix C

It is described in this appendix how to avoid multiple solution in closed-loop, when following a solution curve. As will was shown above, when setting the phase, mode 2 may have multiple solutions, but we are still able to stabilize the whole curve by exploiting the architecture of the phase shifter. A common frequency shifter (the one that we used throughout this paper) is described in Fig. 19.

Fig. 19

Architecture of the phase shifter. Part of the automatic parametric resonance excitation that effectively controls the response along a possible response curve

A simplified (steady-state) description of the adaptive AGC (Automatic gain control) function [28], effectively employed in the experiment, can be described as:

$$ AGC\left( {A_{0} \sin \left( {\omega t + \phi_{0} } \right)} \right) = \left\{ {\begin{array}{*{20}l} {MA\,_{0} \,\sin \left( {\omega t + \phi_{0} } \right)} & {M\,A_{0} < \,A_{set} } \\ {A_{set} \sin \left( {\omega t + \phi_{0} } \right)} & {M\,A_{0} > \,A_{set} } \\ \end{array} } \right. $$

(62)

The desired output amplitude of the signal is $A_{set}$, and the maximal gain applied to the signal is $M$—both constants are pre-chosen in the AGC.

If the input signal to the phase shifter is

$$ y_{in} = A\sin \left( {\omega t} \right) $$

(63)

the output from the phase shifter will be:

$$ y_{out} = AGC\left[ {AK_{1} \omega \cos \left( {\omega t} \right)} \right]\,\,\,\,\sin \left( \varphi \right) + AGC\left[ {AK_{2} \sin \left( {\omega t} \right)} \right]\,\,\,\,\,\cos \left( \varphi \right) $$

(64)

Assuming that:

$$ \begin{gathered} \,A_{set} < MAK_{1} \omega \hfill \\ \,A_{set} > MAK_{2} = \beta A_{set} \hfill \\ \end{gathered} $$

(65)

then the output will be:

$$ y_{out} = A_{set} \sqrt {\sin \left( \varphi \right)^{2} + \beta^{2} \cos \left( \varphi \right)^{2} } \sin \left( {\omega t + \arctan \left( {\frac{\sin \left( \varphi \right)}{{\beta \cos \left( \varphi \right)}}} \right)} \right) $$

(66)

$$ \phi = \arctan \left( {\frac{\sin \left( \varphi \right)}{{\beta \cos \left( \varphi \right)}}} \right),\,\,\,\,\tan \left( \phi \right)A = \frac{{A_{set} \tan \left( \varphi \right)}}{{MK_{2} }} = Const. $$

(67)

The relation described in Eq. (67) is the actual condition in steady-state that the closed-loop must obey, therefore, instead of forcing the phase in system to be set on a certain value, we forcing the system to obey a relation between the phase and the amplitude. Then, instead of looking on vertical lines and theirs intersection with the response curve in the Amplitude-Phase plane as shown in Fig. 6, one should look on curves described by Eq. (67) and theirs intersection with the response curve. The intersection point will be the response in steady state. And this is why we could have tracked the whole curve of mode 2 displayed in Fig. 9, despite the multiple possibilities for a certain phase ($K_{2}$ reduced from value of 1 to 1/10).

Figures 

Fig. 20

Simulated system for this section using Simulink. Chosen parameters were $\omega_{n}$ = 40 [rad/s], $\zeta$ = 0.01, K₂ = 1/30, and the phase was $\phi$ = {10,15,…,170}[deg]

20, 21 describe the theory of enforcing a unique solution, demonstrated for a linear system in simulation. While on a linear system finding the curves related to the constrained made by the closed loop is easy, in the nonlinear system, the response consists of multiple frequencies, and the description of the AGC function becomes more complicated, making it hard to visualize in a figure.

Fig. 21

Simulations results. Each of the blue lines represents a different constrain as $\phi$ changes between simulations. The results of the simulations are indeed on the intersection points between the constrain curves and the response curve

Appendix D

As mentioned in Sect. 3.2.1, the control system can not only inject energy in to the system, but also dissipate energy from the system by setting the phase to be $\psi = \frac{\pi }{2}$. Figure 

Fig. 22

a Vibrations of the beam freely and under the control system. The phase of the control system was set to dissipate energy from the system. b Model fitting to the results to extract the original and modified damping coefficients. A bias to the free response was added for visual purposes

22a describes an experiment where the beam vibrates freely due to an impact, and once under the closed-loop system which was set to dissipate energy. The time taking to the free system to settle is much longer relative to the controlled system. A function $f\left( t \right) = A\sin \left( {\omega_{n} \sqrt {1 - \zeta^{2} } t + \phi } \right)e^{{ - \zeta \omega_{n} t}}$ was fitted to the result (Fig. 22b), and the damping coefficient was calculated. The results depend on the control effort and can be set to higher or lower values and the increase in damping is found to be $\frac{{\zeta_{controlles} }}{{\zeta_{free} }} = \frac{0.0089}{{0.0032}} = 2.78$.