1 Introduction

Polynomial control systems have been successfully applied to fulfilling different control objectives due to its rigorous mathematical framework and the ability to deal with nonlinearity. Based on the technique of sum-of-squares (SOS), there are promising research outcomes for polynomial control systems and SOS. For example, in [1], fault-tolerant control for nonlinear systems was conducted in the polynomial control systems. In [2], the fault-tolerant control was extended to polynomial fuzzy control systems. Converse SOS was discussed in [3] and the existence of a global polynomial Lyapunov function was discussed in [4]. In [5], the output-feedback sampled-data polynomial controller for nonlinear systems was designed. In [6], the input-delay for the sampled-data \(H_\infty \) control of polynomial systems was reported. The research on control design of polynomial systems with input saturation was reported in [7]. The research works focus on the domains of attraction for polynomial nonlinear systems were reported in [8, 9] Also the approaches in [10,11,12,13,14,15,16,17,18] adopted polynomial terms in the fuzzy-model-based (FMB) control. It is worth mentioning that the SOS-based techniques also have the potential to be applied to solve the dynamic problems in the heat transfer investigation [19,20,21].

Polynomial control systems can also be regarded as a polynomial extension of linear control systems, in which the polynomial terms can be processed. When the order of all the polynomial terms in the polynomial control systems is reduced to 0, the polynomial control systems become linear control systems, suggesting its generalizability. For many reported control systems, such as the linear control systems and Takagi-Sugeno (T–S) FMB control systems, the techniques of linear matrix inequalities (LMIs) can be used to solve the stability conditions efficiently. For example, in [22,23,24], the \(H_\infty \) problem was investigated through LMIs. In [25,26,27], the LMIs techniques were adopted to deal with the time-delay control issues. Also, LMIs in T-S FMB control can be found in [28,29,30,31,32].

Despite the success of LMIs in control applications, LMIs can no longer be used for polynomial control systems due to the polynomial terms in the model and controller, which cannot be handled by the LMI solver. In contrast, the stability conditions of polynomial control systems can be represented by SOS and solved efficiently by a third party MATLAB\(^{\textregistered }\) toolbox SOSTOOLS [33]. Adopting the polynomial control systems can have a range of applications. However, due to the polynomial Lyapunov function candidate, the stability conditions are not convex in most cases for general polynomial control systems.

It should be pointed out that in most of the literature regarding polynomial control systems, there are some constraints that need to be imposed on the polynomial Lyapunov function candidate. In [10,11,12,13,14], the polynomial Lyapunov function candidates are constrained to be dependent on only part of the state variables according to nonzeros rows in the input matrix B(x(t)). This constraint is considered to be strong since it often makes the polynomial Lyapunov function candidate in the form of constant Lyapunov function candidate in cases that B(x(t)) does not have all-zero rows. Therefore, this constraint introduces conservativeness into the stability analysis, forgoing the advantages of polynomial Lyapunov function candidates.

To make the stability analysis of general polynomial control systems possible, in [1, 2], the polynomial Lyapunov function candidate can be dependent on all the state variables, and thus the general polynomial control systems can be analyzed. However, there is a bound/index required for the non-convex terms in the general polynomial control system, which is another constraint imposed on the stability analysis.

To remove the constraints on the general control systems, in [15], a two-step stability analysis was provided to solve the general polynomial control systems without any other constraints on the stability conditions. The results are more general, and thus more general forms of the polynomial Lyapunov function candidate can be adopted in the stability analysis and control synthesis. However, in the two-step approach, when the stability analysis fails to find a feasible solution in the first step or the second step, the solving process is terminated and no feasible solution can be found.

Motivated by this specific difficulty in general polynomial control systems, the non-convex problem is investigated in this paper. The purpose of this paper is to propose an iterative stability analysis for general polynomial control systems. In the proposed approach, the non-convex terms in the stability conditions are firstly omitted to make the stability conditions convex, then a predefined convex term will be added manually into the stability conditions to make the convex stability conditions easier to find a feasible initial solution. In order to keep the impact of the manually added term as small as possible, the stability conditions are rewritten as an optimization problem. By solving the optimization problem, the value of the manually added term will be minimized. Once the initial solutions are obtained, the non-convex terms are approximated by the initial solutions, which makes the non-convex stability conditions into convex and can be further solved by SOSTOOLS. If the newly obtained solutions satisfy the original non-convex stability conditions, the newly obtained solutions are qualified as feasible solutions for the general polynomial control system. If not, the non-convex terms are approximated by the newly obtained initial solutions to obtain the most updated solutions iteratively. The novelty and contribution of the paper are summarized as follows:

  1. (1)

    The approximation of non-convex terms is presented to render the stability conditions into convex form for the general polynomial control systems.

  2. (2)

    An iteration approximation approach is proposed that the intermediate solutions dependent on the solutions in both the previous and current iterations. The solutions are verified by the original non-convex stability conditions to guarantee the asymptotic stability of the general polynomial system.

  3. (3)

    In the proposed stability analysis for general polynomial control systems, no constraint is imposed on the polynomial Lyapunov function candidate. Therefore, the polynomial Lyanpunov function candidate can depend on any system state variables.

  4. (4)

    Compared with the works reported in [1, 2, 10,11,12,13,14], there is no constraints imposed on the polynomial Lyapunov functions in the proposed approach; Compared with the works reported in [15], the proposed approach is more general and has more potential to find feasible solutions.

This paper is organized as follows. In Sect. 2, the preliminaries of general polynomial control systems and polynomial Lyapunov function candidate will be introduced. In Sect. 3, the algorithm for iterative stability will be presented and discussed in detail. The simulation example and the comparison with the state-of-the-art are provided in Sect. 4. A conclusion is drawn in Sect. 5.

Notation: The following notations are employed throughout the paper, the monomial vector \(x(t) = [x_1(t), \ldots , x_n(t)]^T\), the superscript T stands for matrix transposition, the superscript \(-1\) in the expression \(X(x(t))^{-1}\) stands for matrix inverse, the expressions of \(P(x(t)) > 0\) represents the corresponding polynomial \(p(x(t), \upsilon ) = \upsilon ^TP(x(t))\upsilon \) can be decomposed into SOS, where \(\upsilon \) is a nonzero arbitrary vector with proper dimensions.

2 Preliminaries

Consider the following polynomial control system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t) = A(x(t))x(t) + B(x(t))u(t) \\ u(t) = G(x(t))x(t), \end{array}\right. } \end{aligned}$$
(1)

where \(A(x(t)) \in {\mathbb {R}}^{n \times n}\) and \(B(x(t)) \in {\mathbb {R}}^{n\times m}\) are the system and input polynomial matrices. \(G(x(t)) \in {\mathbb {R}}^{m \times n}\) is the polynomial feedback gain matrix and \(u(t) \in {\mathbb {R}}^{m}\) is the control input.

The dynamics of closed-loop polynomial control system can be written as:

$$\begin{aligned} \dot{x}(t) = A(x(t))x(t) + B(x(t))G(x(t))x(t) \end{aligned}$$

or

$$\begin{aligned} \dot{x}(t) = (A(x(t)) + B(x(t))G(x(t)))x(t). \end{aligned}$$

To derive the stability conditions, it firstly needs to define the polynomial Lyapunov function candidate V(t) as:

$$\begin{aligned} V(t) = x(t)^TX(x(t))^{-1} x(t), \end{aligned}$$
(2)

where \(X(x(t)) = X(x(t))^T > 0\).

The differential of V(t) should be guaranteed to always be negative to ensure the asymptotic stability of the polynomial control system:

$$\begin{aligned} \dot{V}(t)&= \dot{x}(t)^TX(x(t))^{-1} x(t) + x(t)^TX(x(t))^{-1} \dot{x}(t)\nonumber \\&\quad + {x}(t)^T\dot{X}(x(t))^{-1} x(t). \end{aligned}$$
(3)

The expression \(\dot{V}(t)\) can be further deducted using the dynamics of the closed-loop control system in (1) as follows:

$$\begin{aligned} \dot{V}(t)&= x(t)^T(A(x(t)) \nonumber \\&\quad + B(x(t))G(x(t)))^TX(x(t))^{-1}x(t)\nonumber \\&\quad + x(t)^TX(x(t))^{-1}(A(x(t))\nonumber \\&\quad + B(x(t))G(x(t)))x(t) + x(t)^T\nonumber \\&\quad \left( \sum _{c=1}^{n} \frac{\partial X(x(t))^{-1}}{\partial x_c(t)} \frac{dx_c(t)}{dt}\right) x(t) < 0, \end{aligned}$$
(4)

where \(\frac{dx_c(t)}{dt} = A^{c}(x(t))x(t) +B^{c}(x(t))G(x(t))x(t)\), \(A^{c}(x(t)) \in {\mathbb {R}}^n\) and \(B^{c}(x(t)) \in {\mathbb {R}}^m\) are the c-th rows of the matrices A(x(t)) and B(x(t)), respectively. To deal with the term \(\sum _{c=1}^{n}\frac{\partial X(x(t))^{-1}}{\partial x_c(t)}\frac{dx_c(t)}{dt}\) in (4), let us introduce the following lemma [10] here.

Lemma 1

$$\begin{aligned}&\frac{\partial X(x(t))^{-1}}{\partial x_c(t)} \nonumber \\&\quad = - X(x(t))^{-1} \frac{\partial X(x(t))}{\partial x_c(t)} X(x(t))^{-1}, \forall c = 1, \ldots , n. \end{aligned}$$
(5)

Proof of Lemma 1

Given that

$$\begin{aligned} \frac{\partial I}{\partial x_c(t)} = 0, \end{aligned}$$
(6)

replacing I by \(X(x(t))^{-1}X(x(t))\), then (6) can be rewritten as

$$\begin{aligned} \frac{\partial X(x(t))^{-1}X(x(t))}{\partial x_c(t)} = 0. \end{aligned}$$
(7)

\(\square \)

Then it follows that:

$$\begin{aligned} X(x(t))^{-1}\frac{\partial X(x(t))}{\partial x_c(t)} +\frac{\partial X(x(t))^{-1}}{\partial x_c(t)}X(x(t)) = 0. \end{aligned}$$
(8)

In addition, to make the stability analysis numerically feasible, adopting \(z(t) = X(x(t))^{-1}x(t)\) to do variable replacement, we can further define:

$$\begin{aligned} \dot{V}(t) = z(t)^TQ(x(t))z(t) \end{aligned}$$
(9)

where \(Q(x(t)) = A(x(t))X(x(t)) + X(x(t))A(x(t))^T + B(x(t))N(x(t)) + N(x(t))^TB(x(t))^T - \sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(A^c(x(t)) +B^c(x(t))N(x(t))X(x(t))^{-1})x(t)\). The variable \(N(x(t)) =G(x(t))X(x(t))\) is introduced, in which X(x(t)) and N(x(t)) are the decision variables. The polynomial feedback gains can be calculated through the relationship \(G(x(t)) = N(x(t))X(x(t))^{-1}\) after solving the values of X(x(t)) and N(x(t)).

By guaranteeing \(Q(x(t)) < 0\) (or \(-Q(x(t))\) as SOS matrix), the closed-loop control system can be guaranteed to be stable. However, it can be found that this stability condition is not convex due to the non-convex terms in Q(x(t)), which makes SOSTOOLS cannot be applied to solve the stability conditions.

Remark 1

When compared with other non-general condition in [10,11,12,13,14], the existing conditions therein can be considered as the sub-set of the proposed approach since there are constraints imposed on the Lyapunov function candidate. To make it possible for SOSTOOLS to solve the stability conditions in a numerical way, the non-convex (nonlinear) term \(\sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(A^c(x(t)) +B^c(x(t))N(x(t))X(x(t))^{-1})x(t)\) needs special attention. In the following section, an iterative stability analysis is introduced to deal with this non-convex issue.

3 Iterative stability analysis

To process the non-convex term \(\sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(A^c(x(t)) + B^c(x(t))N(x(t))X (x(t))^{-1})x(t)\) through SOS programming, an iterative stability analysis approach is presented in this paper.

From the definition of N(x(t)) and \(X(x(t))^{-1}\), it can be shown that the following equation is always hold:

$$\begin{aligned} G(x(t)) = N(x(t))X(x(t))^{-1}. \end{aligned}$$
(10)

It can be found that \(\sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(A^c(x(t)) + B^c(x(t))N(x(t))X(x(t))^{-1})x(t)\) can be rewritten as \(\sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(A^c(x(t)) +B^c(x(t))G(x(t)))x(t)\).

Remark 2

It should be pointed out that using the variable substitution \(\sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c} (A^c(x(t)) +B^c(x(t))G(x(t)))x(t)\) will not make the stability condition convex. Since the variable G(x(t)) is not independent with the other two decision variables N(x(t)) and X(x(t)), therefore, all the three variables cannot all be the decision variables at the same time. In the following analysis, we will use initial solutions of N(x(t)) and X(x(t)) to approximate G(x(t)), which makes the iterative stability conditions convex.

The stability conditions can be rewritten as:

$$\begin{aligned} Q(x(t))&= A(x(t))X(x(t)) + X(x(t))A(x(t))^T \nonumber \\&\quad + B(x(t))N(x(t)) + N(x(t))^TB(x(t))^T \nonumber \\&\quad - \sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(A^c(x(t))\nonumber \\&\quad + B^c(x(t))G(x(t)))x(t) < 0, \end{aligned}$$
(11)
$$\begin{aligned} X(x(t))&> 0. \end{aligned}$$
(12)

To apply iterative stability analysis, let us start with \(\sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(A^c(x(t)) +B^c(x(t))G(x(t)))x(t) = 0\) as the 1-st iterative stability condition and solve the SOS-based iterative stability condition:

$$\begin{aligned}&\text {minimize } \alpha \text { subject to:} \nonumber \\&A(x(t))X(x(t)) + X(x(t))A(x(t))^T + B(x(t))N(x(t))\nonumber \\&\qquad + N(x(t))^TB(x(t))^T -\alpha M(x(t)) < 0, \end{aligned}$$
(13)
$$\begin{aligned}&X(x(t)) > 0, \end{aligned}$$
(14)

where \(M(x(t)) \in {\mathbb {R}}^{n\times n} \) is a predefined polynomial matrix and \(M(x(t)) > 0\). \(\alpha M(x(t))\) is a manually added term to make the condition easier to be feasible. In the corresponding SOS conditions, X(x(t)) and N(x(t)) are the decision variables to be solved by SOSTOOLS.

It can be seen that (13) and (14) are convex conditions, and thus it can be solved by SOS solver. After (13) and (14) are solved, \(X^{(1)}(x(t)), N^{(1)}(x(t))\) are used as the initial solutions for the 1-st iteration as the superscript (1) indicates. From the initial solutions \(X^{(1)}(x(t)), N^{(1)}(x(t))\), \(G^{(1)}(x(t))\) can be calculated as \(G^{(1)}(x(t)) = N^{(1)}(x(t))X^{(1)}(x(t))^{-1}\).

It should be noted that the term \(X^{(1)}(x(t))^{-1}\) will still make the stability conditions non-convex. From the definition of the inverse matrix, we have:

$$X^{(1)}(x(t))^{-1} = \frac{\text {adj}(X^{(1)}(x(t)))}{\text {det}(X^{(1)}(x(t)))},$$

where \(\text {adj}(X^{(1)}(x(t)))\) is the adjoint matrix of \(X^{(1)}(x(t))\) and \(\text {det}(X^{(1)}(x(t)))\) is the determinant of \(X^{(1)}(x(t))\).

Adopting \(\text {adj}(X^{(1)}(x(t)))\) and \(\text {det}(X^{(1)}(x(t)))\), we have:

$$\begin{aligned} G^{(1)}(x(t))&= N^{(1)}(x(t))X^{(1)}(x(t))^{-1} \nonumber \\&= N^{(1)}(x(t))\frac{\text {adj}(X^{(1)}(x(t)))}{\text {det}(X^{(1)}(x(t)))}. \end{aligned}$$
(15)

For any \(X(x(t)) > 0\), it is always true that \(\text {det}(X(x(t))) > 0\). Therefore, the iterative stability conditions can be defined as following:

$$\begin{aligned}&Q^{(1)}(x(t)) \nonumber \\&\quad = \text {det}(X^{(1)}(x(t)))\big ( A(x(t))X^{(1)}(x(t))\nonumber \\&\qquad + X^{(1)}(x(t))A(x(t))^T \nonumber \\&\qquad + B(x(t))N^{(1)}(x(t)) + N^{(1)}(x(t))^TB(x(t))^T \big ) \nonumber \\&\qquad - \sum _{c=1}^{n}\frac{\partial X^{(1)}(x(t))}{\partial x_c} (\text {det}(X^{(1)}(x(t)))A^c(x(t)) \nonumber \\&\qquad + B^c(x(t))N^{(1)}(x(t)) \text {adj}(X^{(1)}(x(t))))x(t) < 0, \end{aligned}$$
(16)
$$\begin{aligned}&X^{(1)}(x(t)) > 0. \end{aligned}$$
(17)

The following stability conditions can be verified:

$$\begin{aligned}&Q^{(1)}(x(t)) < 0, \end{aligned}$$
(18)
$$\begin{aligned}&X^{(1)}(x(t)) > 0. \end{aligned}$$
(19)

If the stability conditions in (18) and (19) are valid, the polynomial control system is guaranteed to be stable, X(x(t)), N(x(t)) and G(x(t)) are feasible solutions. Otherwise, substitute \(G^{(1)}(x(t))\) into (11), and solve (11) again with \(G(x(t)) = G^{(1)}(x(t))\) as a prior:

$$\begin{aligned}&\text {det}(X^{(1)}(x(t)))( A(x(t))X(x(t)) + X(x(t))A(x(t))^T \nonumber \\&\quad + B(x(t))N(x(t)) + N(x(t))^TB(x(t))^T ) \nonumber \\&\quad - \sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(\text {det} (X^{(1)}(x(t)))A^c(x(t)) \nonumber \\&\quad + B^c(x(t))N^{(1)}(x(t))\text {adj} (X^{(1)}(x(t))))x(t) < 0, \end{aligned}$$
(20)
$$\begin{aligned}&X(x(t)) > 0, \end{aligned}$$
(21)
$$\begin{aligned}&X(x(t)) - X^{(1)}(x(t)) - \beta _1^{(1)}I < 0, \end{aligned}$$
(22)
$$\begin{aligned}&X^{(1)}(x(t)) - X(x(t)) - \beta _2^{(1)}I < 0, \end{aligned}$$
(23)
$$\begin{aligned}&N(x(t)) - N^{(1)}(x(t)) - \beta _3^{(1)}I < 0, \end{aligned}$$
(24)
$$\begin{aligned}&N^{(1)}(x(t)) - N(x(t)) - \beta _4^{(1)}I < 0 \end{aligned}$$
(25)

where \(\beta _1^{(1)}, \beta _2^{(1)}, \ldots , \beta _4^{(1)}\) are predefined sufficiently small constants for the 1-st iteration. By solving the SOS-based stability condition in (20) to (25), we can obtain the solution for the 2-nd iteration: \(X^{(2)}(x(t))\) and \(N^{(2)}(x(t))\). Also, \(G^{(2)}(x(t)) = N^{(2)}(x(t))X^{(2)} (x(t))^{-1}\). In the stability conditions, since the non-convex terms are approximated by the initial solutions, the feasible solutions are dependent on both the current and the initial solutions. Therefore, the parameters \(\beta _1^{(1)}, \beta _2^{(1)}, \ldots , \beta _4^{(1)}\) are used to relate the current and initial solutions in a numerical way.

Remark 3

It is worth mentioning that in the above stability conditions, the non-convex terms are approximated by \(\sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c}(\text {det}(X^{(1)}(x(t)))A^c(x(t)) +B^c(x(t))N^{(1)}(x(t)) \text {adj}(X^{(1)}(x(t)))x(t)\), which are the solutions from the previous iteration and do not need to be solved again in the current iteration. Therefore, the stability conditions are convex for SOS programming.

Let’s check whether the iterative stability conditions are SOS:

$$\begin{aligned}&Q^{(2)}(x(t)) < 0, \end{aligned}$$
(26)
$$\begin{aligned}&X^{(2)}(x(t)) > 0, \end{aligned}$$
(27)

if not, repeat the iteration using solutions \(X^{(2)}(x(t))\) and \(N^{(2)}(x(t))\) as a prior.

In a more general form, for the k-th iteration, the iterative stability conditions can be expressed as follows:

$$\begin{aligned}&\text {det}(X^{(k)}(x(t)))( A(x(t))X(x(t)) + X(x(t))A(x(t))^T \nonumber \\&\quad + B(x(t))N(x(t)) + N(x(t))^TB(x(t))^T ) \nonumber \\&\quad - \sum _{c=1}^{n}\frac{\partial X(x(t))}{\partial x_c} (\text {det}(X^{(k)}(x(t)))A^c(x(t)) \nonumber \\&\quad + B^c(x(t))N^{(k)}(x(t))\text {adj}(X^{(k)}(x(t))))x(t) < 0, \end{aligned}$$
(28)
$$\begin{aligned}&X(x(t)) > 0, \end{aligned}$$
(29)
$$\begin{aligned}&X(x(t)) - X^{(k)}(x(t)) - \beta _1^{(k)}I < 0, \end{aligned}$$
(30)
$$\begin{aligned}&X^{(k)}(x(t)) - X(x(t)) - \beta _2^{(k)}I < 0, \end{aligned}$$
(31)
$$\begin{aligned}&N(x(t)) - N^{(k)}(x(t)) - \beta _3^{(k)}I < 0, \end{aligned}$$
(32)
$$\begin{aligned}&N^{(k)}(x(t)) - N(x(t)) - \beta _4^{(k)}I < 0 \end{aligned}$$
(33)

where \(\beta _1^{(k)}, \beta _2^{(k)}, \ldots , \beta _4^{(k)}\) are predefined sufficiently small constants to be determined for k-th iteration. In the iterative stability analysis, since the non-convex terms are approximated by the previous solutions, the feasible solutions are dependent on both the current solutions and the previous solutions. Therefore, the parameters \(\beta _1^{(k)}, \beta _2^{(k)}, \ldots , \beta _4^{(k)}\) are used to relate the solutions in two consecutive iterations in a numerical way.

By solving the SOS-based stability conditions in (28) to (33), we can obtain the \(k+1\)-th iterative solution: \(X^{(k+1)}(x(t))\) and \(N^{(k+1)}(x(t))\). Also, \(G^{(k+1)}(x(t)) = N^{(k+1)}(x(t))X^{(k+1)}(x(t))^{-1}\).

Until

$$\begin{aligned} Q^{(k+1)}(x(t))&< 0, \end{aligned}$$
(34)
$$\begin{aligned} X^{(k+1)}(x(t))&> 0. \end{aligned}$$
(35)

Then \(X^{(k+1)}(x(t))\), \(N^{(k+1)}(x(t))\) and \(G^{(k+1)}(x(t))\) are feasible solutions for the general polynomial control system.

The iterative stability analysis of the general polynomial control system is summarized in Algorithm. 1.

figure a

4 Simulation example

In this section, a numerical example is provided to verify the effectiveness of the iterative stability analysis. Let us consider a polynomial control system, where \(x(t) = [x_1(t), x_2(t)]^T\):

$$\begin{aligned}&A{(x(t))} \\&\quad = \left[ \begin{array}{cc} -1 + x_1(t) + \frac{3}{4}x_1(t)^2 - \frac{3}{2}x_2(t)^2 &{} \frac{1}{4} - x_1(t)^2 \\ x_1(t) &{} x_2(t) \end{array}\right] ,\\&B{(x(t))} = \left[ \begin{array}{cc} 1 &{} 0 \\ x_1(t) &{} 2 \end{array}\right] . \end{aligned}$$

In the simulation, X(x(t)) is chosen as a polynomial matrix with 2-nd order of \(x_1(t)\) and \(x_2(t)\), N(x(t)) is chosen as a polynomial matrix with 2-nd order of \(x_1(t)\). M(x(t)) is chosen as the identity matrix. \(\beta _1^{(k)} = \beta _2^{(k)} = 0.2\) and \(\beta _3^{(k)} = \beta _4^{(k)} = 0.05\) for every iteration.

Firstly, the stability conditions in (13) and (14) are adopted to find the initial solutions. Then the solutions \(X^{(1)}(x(t)), N^{(1)}(x(t))\) can be obtained. Using the initial solution to approximate the non-convex term and re-solve the solutions for the convex stability conditions, after the 1-st iteration feasible solution can be found.

For the N(x(t)) matrix, we rewrite N(x(t)) as:

$$\begin{aligned} N(x(t)) = \left[ \begin{array}{cc} N_{11}(x(t)) &{} N_{12}(x(t)) \\ N_{21}(x(t)) &{} N_{22}(x(t)) \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} N_{11}(x(t))&= - 3.746\times 10^{-6}x_1(t)^2 \\&\quad - 0.0001958x_1(t) - 0.5418, \\ N_{12}(x(t))&= - 1.112\times 10^{-6}x_1(t)^2 \\&\quad + 0.003416x_1(t) + 0.07179, \\ N_{21}(x(t))&= 0.03998x_1(t)^2 + 0.09521x_1(t) + 0.282, \\ N_{22}(x(t))&= - 0.278x_1(t)^2 - 0.02907x_1(t) - 1.009. \end{aligned}$$

For the X(x(t)) matrix, we define

$$\begin{aligned} X(x(t)) = \left[ \begin{array}{cc} X_{11}(x(t)) &{} X_{12}(x(t)) \\ X_{21}(x(t)) &{} X_{22}(x(t)) \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} X_{11}(x(t))&= 5.266\times 10^{-9}x_1(t)^2 + 6.099\times 10^{-7}x_1(t)\\&\quad + 1.299\times 10^{-8}x_2(t)^2 + 0.1238, \\ X_{12}(x(t))&= 2.785\times 10^{-9}x_1(t)^2 - 3.664\times 10^{-7}x_1(t)\\&\quad + 8.491\times 10^{-10}x_2(t)^2 + 0.1132, \\ X_{21}(x(t))&= 2.785\times 10^{-9}x_1(t)^2 - 3.664\times 10^{-7}x_1(t)\\&\quad + 8.491\times 10^{-10}x_2(t)^2 + 0.1132, \\ X_{22}(x(t))&= 3.536\times 10^{-9}x_1(t)^2 - 7.849\times 10^{-7}x_1(t)\\&\quad + 1.918\times 10^{-9}x_2(t)^2 + 0.155. \end{aligned}$$

In order to have a better understanding of the time-response of states \(x_1(t)\) and \(x_2(t)\), the time response of \(x_1(t)\) and \(x_2(t)\) can be viewed in Figs. 1 and 2. In the figures, it can be observed that the polynomial control system can be stabilized swiftly from 4 different initial states: the bold blue curve represents the state response with initial state \(x(0) = [-1.5, 3]^T\); The dashed bold red curve represents the state response with initial state \(x(0) = [1.5, 3]^T\); The green curve represents the state response with initial state \(x(0) = [3, -1]^T\); The dashed black curve represents the state response with initial state \(x(0) = [-3, -1]^T\).

Fig. 1
figure 1

The time-response simulation for \(x_1(t)\) from different initial states

Full size image
Fig. 2
figure 2

The time-response simulation for \(x_2(t)\) from different initial states

Full size image

In addition, the 2-dimensional control input during the control process can be viewed in Figs. 3 and 4. In these figures, it can be seen that the two control inputs are within reasonable ranges. As the same in the time-response simulations: the bold blue curve represents the control input with initial state \(x(0) = [-1.5, 3]^T\); The dashed bold red curve represents the control input with initial state \(x(0) = [1.5, 3]^T\); The green curve represents the control input with initial state \(x(0) = [3, -1]^T\); The dashed black curve represents the control input with initial state \(x(0) = [-3, -1]^T\).

Fig. 3
figure 3

The control input \(u_1(t)\) from 4 different initial states

Full size image
Fig. 4
figure 4

The control input \(u_2(t)\) from 4 different initial states

Full size image

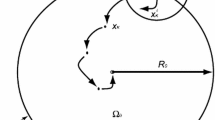
The vector field and phase plot of the polynomial control system with 12 initial start states can be viewed in Fig. 5. In the figure, the black circles represent the initial state for every trajectory. The blue arrows represent the vector fields in terms of size and direction. From Fig. 5, it can be seen that all the phase flows (red trajectories) start from different initial states (black circles) follow the vector field (blue arrows) into the stabilization state smoothly.

Fig. 5
figure 5

Phase plot of the polynomial control system

Full size image

To compare our method with the two-step approach reported in [15], detailed simulations have been done using the two-step approach with the same polynomial model and all the other parameters, such as the same degrees of X(x(t)), N(x(t)), etc.

From the simulation results, it is found that the two-step approach is also able to find a feasible solution N(x(t)) as:

$$\begin{aligned} N_{11}(x(t))&= -3.746\times 10^{-6}x_1(t)^2 \\&\quad - 0.0001975x_1(t) - 0.5249, \\ N_{12}(x(t))&= -1.112\times 10^{-6}x_1(t)^2 \\&\quad - 0.003686x_1(t) + 0.07221, \\ N_{21}(x(t))&= 0.002368x_1(t)^2 + 0.2854x_1(t) + 0.1736, \\ N_{22}(x(t))&= -0.278x_1(t)^2 - 0.02918x_1(t) - 1.003. \end{aligned}$$

and X(x(t)) as:

$$\begin{aligned} X_{11}(x(t))&= 3.877\times 10^{-9}x_1(t)^2 - 9.467\times 10^{-9}x_1(t) \\&\quad + 1.36\times 10^{-8}x_2(t)^2 + 0.0002032, \\ X_{12}(x(t))&= 3.351\times 10^{-9}x_1(t)^2 - 2.408\times 10^{-9}x_1(t) \\&\quad + 9.92\times 10^{-10}x_2(t)^2 + 0.0002164, \\ X_{21}(x(t))&= 3.351\times 10^{-9}x_1(t)^2 - 2.408\times 10^{-9}x_1(t) \\&\quad + 9.92\times 10^{-10}x_2(t)^2 + 0.0002164, \\ X_{22}(x(t))&= 2.259\times 10^{-9}x_1(t)^2 - 3.979\times 10^{-9}x_1(t) \\&\quad + 3.048\times 10^{-9}x_2(t)^2 + 0.004621. \end{aligned}$$

However, when the order of N(x(t)) is set to 0, the two-step approach cannot find a feasible solution while the iterative stability analysis is still able to find a feasible solution at the 2-nd iteration. The feasible solutions are:

$$\begin{aligned} N(x(t)) = \left[ \begin{array}{cc} -0.05362 &{} -0.006776 \\ 0.1625 &{} -1.285 \end{array}\right] \end{aligned}$$

and X(x(t)) as

$$\begin{aligned} X_{11}(x(t))&= 1.204\times 10^{-8}x_1(t)^2 + 3.592\times 10^{-7}x_1(t) \\&\quad + 4.43\times 10^{-8}x_2(t)^2 + 0.07741, \\ X_{12}(x(t))&= 8.896\times 10^{-9}x_1(t)^2 + 1.581\times 10^{-7}x_1(t) \\&\quad + 4.474\times 10^{-9}x_2(t)^2 + 0.08018, \\ X_{21}(x(t))&= 8.896\times 10^{-9}x_1(t)^2 + 1.581\times 10^{-7}x_1(t) \\&\quad + 4.474\times 10^{-9}x_2(t)^2 + 0.08018, \\ X_{22}(x(t))&= 7.972\times 10^{-9}x_1(t)^2 + 1.051\times 10^{-7}x_1(t) \\&\quad + 2.68\times 10^{-9}x_2(t)^2 + 0.09714. \end{aligned}$$

Remark 4

From the comparison with the two-step approach reported in [15], it can be found that the proposed approach has more potential to find feasible solutions for the general polynomial control systems. In addition, when the manually convex term added in the first step of the two-step approach to form the optimization problem, the two-step approach can be considered as a special case in the iteration approach with only 1 iteration.

Remark 5

Having demonstrated the merits of the iterative approach, the shortcoming of the proposed method is that it demands more computational resources when compared with the existing methods. In this paper, the simulations are conducted based on Matlab\(^{\textregistered }\) 2018a, and the computer is equipped with Intel Core i7-7700K along with 16GB memory. The compared two-step approach took 9.60s, the proposed method took 20.46s. From the simulation time, it can be found that it takes longer for the iterative method to find feasible solutions.

5 Conclusion

In conclusion, to confront the non-convex problem directly, an iterative stability analysis is presented for general polynomial control systems. Unlike most of the methods reported in the literature, there is no constraint imposed on the forms of the polynomial Lyapunov function candidates or the non-convex terms. Furthermore, the relationship between the solutions of successive iterations is utilized to obtain the feasible solutions, which are verified by the original non-convex conditions. In addition, the comparison between the proposed approach and the current state-of-the-art has been conducted. From the comparison results, it demonstrates that the proposed method has more potential to find feasible solutions than the reported methods, which shows the effectiveness of the method in this paper.