Skip to main content
SpringerLink
Log in

Soliton molecules, rational positons and rogue waves for the extended complex modified KdV equation

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

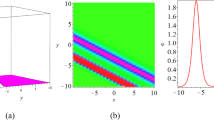
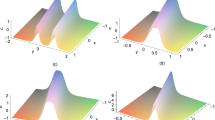
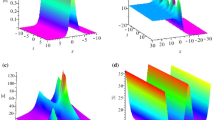
In this paper, we consider the integrable extended complex modified Korteweg–de Vries equation. Based on Darboux transformation, we obtain soliton molecules, positon solutions, rational positon solutions and rogue waves for integrable extended complex modified Korteweg–de Vries equation. Further, under the standard decomposition, we divide the rogue waves into three patterns: fundamental pattern, triangular pattern and ring pattern. On the basis of fundamental pattern, we define the length and width of rogue waves and discuss the effect of different parameters on rogue waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data Availability Statement

All data generated or analyzed during this study are included in this article.

References

  1. Ablowitz, M.J., Kaup, D.J., Newell, A.C., Segur, H.: The inverse scattering transform-Fourier analysis for nonlinear problems. Stud. Appl. Math. 53, 249–315 (1974)

    Article  MathSciNet  Google Scholar 

  2. Ablowitz, M.J., Segur, H.: Solitons and the Inverse Scattering Transform. Society for Industrial and Applied Mathematics, Philadelphia (1981)

    Book  Google Scholar 

  3. Belokolos, E.D., Bobenko, A.I., Enolskij, V.Z., Its, A.R., Matveev, V.B.: Algebro-Geometrical Approach to Nonlinear Integrable equations. Springer, Berlin (1994)

    MATH  Google Scholar 

  4. Bluman, G.W., Cole, J.D.: Similarity Methods for Differential equations. Springer, Berlin (1974)

    Book  Google Scholar 

  5. Erbay, H.A.: Nonlinear transverse waves in a generalized elastic solid and the complex modified Korteweg-de Vries equation. Phys. Scr. 58, 9–14 (1998)

    Article  MathSciNet  Google Scholar 

  6. Erbay, S., Suhubi, E.S.: Nonlinear wave propagation in micropolar media-II, special cases, solitary waves and Painlevé analysis. Int. J. Eng. Sci. 27, 915–919 (1989)

    Article  Google Scholar 

  7. Guo, B.L., Ling, L.M., Liu, Q.P.: Nonlinear Schrödinger equation: generalized Darboux transformation and rogue wave solutions. Phys. Rev. E. 85, 026607 (2012)

    Article  Google Scholar 

  8. Gorbacheva, O.B., Ostrovsky, L.A.: Nonlinear vector waves in a mechanical model of a molecular chain. Phys. D 8, 223–228 (1983)

    Article  MathSciNet  Google Scholar 

  9. Guo, B.L., Tian, L.X., Yan, Z.Y., Ling, L.M., Wang, Y.F.: Rogue Waves: Mathematical Theory and Applications in Physics. Zhejiang Science and Technology Press, Zhejiang (2017)

    Book  Google Scholar 

  10. Gu, C.H., Zhou, Z.X., Hu, H.S.: Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry. Springer, Berlin (2004)

    Google Scholar 

  11. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  Google Scholar 

  12. He, J.S., Charalampidis, E.G., Kevrekidis, P.G., Frantzeskakis, D.J.: Rogue waves in nonlinear Schrödinger models with variable coefficients: application to Bose-Einstein condensates. Phys. Lett. A 378, 577–583 (2014)

    Article  Google Scholar 

  13. Herink, G., Kurtz, F., Jalali, B., Solli, D.R., Ropers, C.: Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 356, 50–54 (2017)

    Article  Google Scholar 

  14. He, J.S., Wang, L.H., Li, L.J., Porsezian, K., Erdélyi, R.: Few-cycle optical rogue waves: Complex modified Korteweg-de Vries equation. Phys. Rev. E 89, 062917 (2014)

    Article  Google Scholar 

  15. He, J.S., Zhang, H.R., Wang, L.H., Porsezian, K., Fokas, A.S.: Generating mechanism for higher-order rogue waves. Phys. Rev. E 87, 052914 (2013)

    Article  Google Scholar 

  16. Kharif, C., Pelinovsky, E., Slunyaev, A.: Rogue Waves in the Ocean. Springer, Berlin (2009)

    MATH  Google Scholar 

  17. Karney, C.F.F., Sen, A., Chu, F.Y.F.: Nonlinear evolution of lower hybrid waves. Phys. Fluids 22, 940–952 (1979)

    Article  Google Scholar 

  18. Liu, N.: Soliton and breather solutions for a fifth-order modified KdV equation with a nonzero background. Appl. Math. Lett. 104, 106256 (2020)

    Article  MathSciNet  Google Scholar 

  19. Lou, S.Y.: Soliton molecules and asymmetric solitons in three fifth order systems via velocity resonance. J. Phys. Commun. 4, 041002 (2020)

    Article  Google Scholar 

  20. Liu, N., Guo, B.L.: Painlevé-type asymptotics of an extended modified KdV equation in transition regions. J. Differ. Equ. 280, 203–235 (2021)

    Article  Google Scholar 

  21. Liu, N., Guo, B.L., Wang, D.S., Wang, Y.F.: Long-time asymptotic behavior for an extended modified Korteweg-de Vries equation. Commun. Math. Sci. 17, 1877–1913 (2019)

    Article  MathSciNet  Google Scholar 

  22. Lakomy, K., Nath, R., Santos, L.: Spontaneous crystallization and filamentation of solitons in dipolar condensates. Phys. Rev. A 85, 033618 (2012)

  23. Liu, W., Zhang, Y.S., He, J.S.: Dynamics of the smooth positons of the complex modified KdV equation. Waves Random Complex 1–12,(2017)

  24. Miura, R.M. (ed.): Bäcklund transformations, the inverse scattering method, solitons, and their applications. In: Proceedings of the NSF Research Workshop on Contact Transformations, held in Nashville, Tennessee, 1974. Springer, Berlin (1976)

  25. Matveev, V.B., Salle, M.A.: Darboux Transformation and Solitons. Springer, Berlin (1991)

    Book  Google Scholar 

  26. Moslem, W.M., Sabry, R., El-Labany, S.K., Shukla, P.K.: Dust-acoustic rogue waves in a nonextensive plasma. Phys. Rev. E 84, 066402 (2011)

    Article  Google Scholar 

  27. Ren, B., Lin, J., Liu, P.: Soliton molecules and the CRE method in the extended mKdV equation. Commun. Theor. Phys. 75, 055005 (2020)

    Article  MathSciNet  Google Scholar 

  28. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450, 1054–1057 (2007)

    Article  Google Scholar 

  29. Tao, Y.S., He, J.S.: Multisolitons, breathers, and rogue waves for the Hirota equation generated by the Darboux transformation. Phys. Rev. E 85, 026601 (2012)

    Article  Google Scholar 

  30. Walker, D.A.G., Taylor, P.H., Taylor, R.E.: The shape of large surface waves on the open sea and the Draupner New Year wave. Appl. Ocean Res. 26, 73–83 (2004)

    Article  Google Scholar 

  31. Wazwaz, A.M., Xu, G.Q.: An extended modified KdV equation and its Painlevé integrability. Nonlinear Dyn. 86, 1455–1460 (2016)

    Article  Google Scholar 

  32. Wang, X., Zhang, J.L., Wang, L.: Conservation laws, periodic and rational solutions for an extended modified Korteweg-de Vries equation. Nonlinear Dyn. 92, 1507–1506 (2018)

    Article  Google Scholar 

  33. Xing, Q.X., Wu, Z.W., Mihalache, D., He, J.S.: Smooth positon solutions of the focusing modified Korteweg-de Vries equation. Nonlinear Dyn. 89, 2299–2310 (2017)

    Article  MathSciNet  Google Scholar 

  34. Yan, Z.Y.: Vector financial rogue waves. Phys. Lett. A 375, 4274–4279 (2011)

    Article  Google Scholar 

  35. Yin, H.M., Tian, B., Zhang, C.R., Du, X.X., Zhao, X.C.: Optical breathers and rogue waves via the modulation instability for a higher-order generalized nonlinear Schrödinger equation in an optical fiber transmission system. Nonlinear Dyn. 97, 843–852 (2019)

    Article  Google Scholar 

  36. Yin, H.M., Tian, B., Zhao, X.C., Zhang, C.R., Hu, C.C.: Breather-like solitons, rogue waves, quasi-periodic/chaotic states for the surface elevation of water waves. Nonlinear Dyn. 97, 21–31 (2019)

    Article  Google Scholar 

  37. Zhang, Z., Yang, X.Y., Li, B.: Soliton molecules and novel smooth positons for the complex modified KdV equation. Appl. Math. Lett. 103, 106168 (2020)

Download references

Acknowledgements

The authors thank the two referees for valuable comments. The research was supported by the National Natural Science Foundation of China, Grant No. 11901141.

Author information

Authors and Affiliations

  1. School of Science, Hangzhou Dianzi University, 310018, Zhejiang, China

    Lin Huang & Nannan Lv

Authors
  1. Lin Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nannan Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nannan Lv.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

$$\begin{aligned} L_{2}&=34560000\,{\beta }^{4}{t}^{4}{c}^{21}-27648000\,\alpha \,{\beta }^{3}{t}^ {4}{c}^{19}\\&\quad +4608000\,{\beta }^{3}{t}^{3}x{c}^{17}+8294400\,{\alpha }^{2} {\beta }^{2}{t}^{4}{c}^{17}\\&\quad -1105920\,{\alpha }^{3}\beta \,{t}^{4}{c}^{15} -2764800\,\alpha \,{\beta }^{2}{t}^{3}x{c}^{15}\\&\quad +55296\,{\alpha }^{4}{t}^{ 4}{c}^{13}+230400\,{\beta }^{2}{t}^{2}{x}^{2}{c}^{13}\\&\quad +552960\,{\alpha }^ {2}\beta \,{t}^{3}x{c}^{13}\\&\quad -36864\,{\alpha }^{3}{t}^{3}x{c}^{11}-92160\, \alpha \,\beta \,{t}^{2}{x}^{2}{c}^{11}\\&\quad +364800\,{\beta }^{2}{t}^{2}{c}^{ 11}+9216\,{\alpha }^{2}{t}^{2}{x}^{2}{c}^{9}\\&\quad +5120\,\beta \,t{x}^{3}{c}^{ 9}-8\,c\\&\quad -115200\,\alpha \,\beta \,{t}^{2}{c}^{9}-1024\,\alpha \,t{x}^{3}{c}^{7}\\&\quad +8448\,{\alpha }^{2}{t}^{2}{c}^{7}+14080\,\beta \,tx{c}^{7}\\&\quad +{\frac{128 \,{x}^{4}{c}^{5}}{3}}-1792\,\alpha \,tx{c}^{5}+64\,{x}^{2}{c}^{3}, \end{aligned}$$
$$\begin{aligned} L_{3}&\quad =-20736000000\,{\beta }^{6}{t}^{6}{c}^{30}+24883200000\,\alpha \,{\beta }^ {5}{t}^{6}{c}^{28}\\&\quad -12441600000\,{\alpha }^{2}{\beta }^{4}{t}^{6}{c}^{26} -4147200000\,{\beta }^{5}{t}^{5}x{c}^{26}\\&\quad +4147200000\,\alpha \,{\beta }^{ 4}{t}^{5}x{c}^{24}+3317760000\,{\alpha }^{3}{\beta }^{3}{t}^{6}{c}^{24}\\&\quad - 1658880000\,{\alpha }^{2}{\beta }^{3}{t}^{5}x{c}^{22}-345600000\,{\beta } ^{4}{t}^{4}{x}^{2}{c}^{22}\\&\quad -497664000\,{\alpha }^{4}{\beta }^{2}{t}^{6}{c }^{22}+167040000\,{\beta }^{4}{t}^{4}{c}^{20}\\&\quad +276480000\,\alpha \,{\beta }^{3}{t}^{4}{x}^{2}{c}^{20}+331776000\,{\alpha }^{3}{\beta }^{2}{t}^{5}x {c}^{20}\\&\quad +39813120\,{\alpha }^{5}\beta \,{t}^{6}{c}^{20}-115200000\, \alpha \,{\beta }^{3}{t}^{4}{c}^{18}\\&\quad -1327104\,{\alpha }^{6}{t}^{6}{c}^{18 }-82944000\,{\alpha }^{2}{\beta }^{2}{t}^{4}{x}^{2}{c}^{18}\\&\quad -33177600\,{ \alpha }^{4}\beta \,{t}^{5}x{c}^{18}-15360000\,{\beta }^{3}{t}^{3}{x}^{3} {c}^{18}\\&\quad +16128000\,{\beta }^{3}{t}^{3}x{c}^{16}+29030400\,{\alpha }^{2}{ \beta }^{2}{t}^{4}{c}^{16}\\&\quad +9216000\,\alpha \,{\beta }^{2}{t}^{3}{x}^{3}{c }^{16}+11059200\,{\alpha }^{3}\beta \,{t}^{4}{x}^{2}{c}^{16}\\&\quad +1327104\,{ \alpha }^{5}{t}^{5}x{c}^{16}-3133440\,{\alpha }^{3}\beta \,{t}^{4}{c}^{14 }\\&\quad -7833600\,\alpha \,{\beta }^{2}{t}^{3}x{c}^{14}-1843200\,{\alpha }^{2} \beta \,{t}^{3}{x}^{3}{c}^{14}\\&\quad -384000\,{\beta }^{2}{t}^{2}{x}^{4}{c}^{14 }-552960\,{\alpha }^{4}{t}^{4}{x}^{2}{c}^{14}\\&\quad +119808\,{\alpha }^{4}{t}^{ 4}{c}^{12} +499200\,{\beta }^{2}{t}^{2}{x}^{2}{c}^{12}\\&\quad +1198080\,{\alpha } ^{2}\beta \,{t}^{3}x{c}^{12}\\&\quad +153600\,\alpha \,\beta \,{t}^{2}{x}^{4}{c}^{ 12}+122880\,{\alpha }^{3}{t}^{3}{x}^{3}{c}^{12}\\&\quad -606400\,{\beta }^{2}{t}^ {2}{c}^{10}\\&\quad -55296\,{\alpha }^{3}{t}^{3}x{c}^{10}-138240\,\alpha \,\beta \,{t}^{2}{x}^{2}{c}^{10}\\&\quad -15360\,{\alpha }^{2}{t}^{2}{x}^{4}{c}^{10}- 5120\,\beta \,t{x}^{5}{c}^{10}\\&\quad +145280\,\alpha \,\beta \,{t}^{2}{c}^{8}\\&\quad +7680\,{\alpha }^{2}{t}^{2}{x}^{2}{c}^{8}+{\frac{12800\,\beta \,t{x}^{3} {c}^{8}}{3}}\\&\quad +1024\,\alpha \,t{x}^{5}{c}^{8}-{\frac{256\,{x}^{6}{c}^{6} }{9}}-8896\,{\alpha }^{2}{t}^{2}{c}^{6}\\&\quad -8000\,\beta \,tx{c}^{6}-{\frac{ 512\,\alpha \,t{x}^{3}{c}^{6}}{3}}\\&\quad +1088\,\alpha \,tx{c}^{4}-{\frac{64\, {x}^{4}{c}^{4}}{3}}-48\,{x}^{2}{c}^{2}-4. \end{aligned}$$

Appendix B

$$\begin{aligned} A_{1}&=100{c}^{2}{a}^{8}{\beta }^{2}{t}^{2}-800{t}^{2}{a}^{6}{\beta }^{2}{c }^{4}+6000{t}^{2}{a}^{4}{\beta }^{2}{c}^{6}\\&\quad +3600{c}^{10}{\beta }^{2} {t}^{2}+120{c}^{2}{a}^{6}\beta {t}^{2}\alpha \\&\quad -720{t}^{2}{a}^{4} \beta {c}^{4}\alpha +720{t}^{2}{a}^{2}\beta {c}^{6}\alpha \\&\quad -1440{c}^{8}\beta {t}^{2}\alpha +36{c}^{2}{a}^{4}{\alpha }^{2}{t}^{2}+144{c }^{6}{\alpha }^{2}{t}^{2}\\&\quad +40{c}^{2}{a}^{4}\beta tx+40{c}^{2}{a}^{4 }\beta ts_{{0}}-480{c}^{4}{a}^{2}\beta tx\\&\quad -480 {c}^{4}{a}^{2}\beta ts_{{0}}\\&\quad +240{c}^{6}\beta tx+240 {c}^{6}\beta ts_{{0}}+24{c}^{2}{a}^{2}\alpha tx\\&\quad +24 {c}^{2}{a}^{2}\alpha ts_{{0}}-48{c}^{4}\alpha tx-48{c}^{4}\alpha ts_{{0}}+4{c}^{2}{x}^{2}\\&\quad +8{c}^{2}xs_{{0}}+4\,{c}^{2}{s_{{0}}}^{2}.\\ A_{2}&=16\,{x}^{4}+ ( 160\,{a}^{4}t-1824\,{a}^{2}t+768\,t ) {x}^{3 }\\&\quad + ( 600\,{a}^{8}{t}^{2}-10480\,{t}^{2}{a}^{6}\\&\quad +66456\,{t}^{2}{a}^ {4}-42336\,{t}^{2}{a}^{2}+13824\,{t}^{2}\\&\quad +40 ) {x}^{2}+ ( 1000\,{a}^{12}{t}^{3}-18200\,{a}^{10}{t}^{3}+135480\,{a}^{8}{t}^{3}\\&\quad - 631464\,{a}^{6}{t}^{3}+196128\,{a}^{4}{t}^{3}\\&\quad +200\,{a}^{4}t-228096\,{a }^{2}{t}^{3}\\&\quad -2280\,{a}^{2}t+110592\,{t}^{3}+960\,t ) x\\&\quad +625\,{a}^ {16}{t}^{4}-8500\,{t}^{4}{a}^{14}\\&\quad +95350\,{t}^{4}{a}^{12}-442860\,{t}^{ 4}{a}^{10}+1733841\,{t}^{4}{a}^{8}\\&\quad +250\,{a}^{8}{t}^{2}+282600\,{t}^{4}{a}^{6}\\&\quad -8100\,{t}^{2}{a}^{6}+1563408\,{t}^{4}{a}^{4}\\&\quad +47850\,{t}^{2}{a} ^{4}+207360\,{t}^{4}{a}^{2}\\&\quad -44856\,{t}^{2}{a}^{2}+331776\,{t}^{4}\\&\quad +5760\,{t}^{2}-7. \end{aligned}$$
$$\begin{aligned} A_{3}&=-8\,{x}^{4}+ ( -80\,{a}^{4}+912\,{a}^{2}-384 ) t{x}^{3}\\&\quad + [28+ ( -300\,{a}^{8}+5240\,{a}^{6}\\&\quad -33228\,{a}^{4}+21168\,{a}^{2}-6912 ) {t}^{2} ] {x}^{2}\\&\quad + [( -500\,{a}^{12}+9100\,{a}^{10}-67740\,{a}^{8}\\&\quad +315732\,{a}^{6}-98064\,{a}^{4}\\&\quad + 114048\,{a}^{2}-55296 ) {t}^{3} +(140\,{a}^{4}-1596\,{a}^{2}\\&\quad +672 ) t ]x+ (-165888+4250\,{a}^{14}\\&\quad -{\frac{625}{2}}{a}^{16}-103680\,{a}^{2} -781704\,{a}^{4}\\&\quad -141300\,{a}^{6}-{\frac{1733841}{2}}{a}^{8}\\&\quad +221430\,{a}^{10}-47675\,{a}^{12}){t}^{4}+( 175\,{a}^{8}-7590\,{a}^{6}\\&\quad +43863\,{a}^{4}-45396\,{a}^{2}+4032) {t}^{2}-{\frac{17}{2}}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, L., Lv, N. Soliton molecules, rational positons and rogue waves for the extended complex modified KdV equation. Nonlinear Dyn 105, 3475–3487 (2021). https://doi.org/10.1007/s11071-021-06764-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-06764-x

Keywords

Search

Navigation