Existence of quasi-periodic responses in quasi-periodically forced nonlinear mechanical systems

Abstract

Forced responses of mechanical systems are crucial design and performance criteria. Hence, their robust and reliable calculation is of vital importance. While numerical computation of periodic responses benefits from an extensive mathematical basis, the literature for quasi-periodically forced systems is limited. More specifically, the absence of applicable and general existence criterion for quasi-periodic orbits of nonlinear mechanical systems impedes definitive conclusions from numerical methods such as harmonic balance. In this work, we establish a general existence criterion for quasi-periodically forced vibratory systems with nonlinear stiffness terms. Our criterion does not rely on any small parameters and hence is applicable for large response and forcing amplitudes. On explicit numerical examples, we demonstrate how our existence criterion can be utilized to justify subsequent numerical computations of forced responses.

1 Introduction

Quasi-periodic oscillations are vibrations containing multiple incommensurate frequencies. They have been reported in physics, chemistry and engineering. For example, Ditto et al. [21] study quasi-periodic oscillations of a magneto-elastic ribbon and Hauck and Schneider [30] observe quasi-periodic oscillations in an oxidation reaction. Engineering applications include Gendelman et al. [26] who utilize the emergence of quasi-periodic oscillations for vibration absorption in an electric circuit. Moreover, Coudeyras et al. [16] observe quasi-periodic vibrations impacting break squeal and Kim and Noah [37] examine quasi-periodic responses of a nonlinear Jeffcott rotor with bearing clearance.

It seems naturally to expect quasi-periodic vibrations in mechanical systems when the applied external loads are quasi-periodic. This expectation, however, is generally not true even for the periodic case, as we have investigated in depth for mechanical systems [8]. Consequently, the question arises when we can rigorously expect a quasi-periodic steady-state response of a forced nonlinear mechanical system.

Numerical time integration seems to be a natural candidate to compute the response of nonlinear mechanical systems. Due to the low damping in modern engineering structures, however, long integration times are required to observe a steady-state response. Moreover, quasi-periodic orbits lack a fixed period after which the steady-state response repeats itself. Thus, additional signal processing tools, such as Fourier transformations are required to even recognize a quasi-periodic steady state. For example Kreider and Nayfeh [40] observed “unexplained sidebands” in the measured forced response of a clamped–clamped beam. Later, Emam et al. [22] explained these sidebands with the occurrence of quasi-periodic motions. Moreover, Held and Jefferies [32], Cumming and Linsay[17] and He et al. [31] use Poincare sections (cf. Guckenheimer and Holmes [28]) to recognize quasi-periodicity. A periodic motion occurs as single point inside a Poincare section, whereas a quasi-periodic orbit with two incommensurate frequencies leaves a densely filled orbit inside the trap. Orbits with more incommensurate frequencies generally generate more complicated patterns inside a Poincare section (cf. Cumming and Linsay [17] Fig. 2b for an example). Other techniques have been used by, e.g., Walden et al. [60] who assess the number of incommensurate basis frequencies to decompose their measurements of a Rayleigh–Bérnard convection. Moreover, Laskar [42] presents a mathematically basis to decompose a signal into its quasi-periodic components including a convergence proof.

Motivated by the computational success of the harmonic balance procedure in computing periodic orbits (e.g., Mickens [46]), Chua and Ushida [14] extended the harmonic balance method to the quasi-periodic case. In this procedure, an assumed quasi-periodic solution is expanded in a multi-frequency Fourier series and the governing ordinary differential equations of the nonlinear system are projected onto a finite set of Fourier modes. The arising nonlinear algebraic system is then solved with, e.g., the Newton–Raphson iteration. Recently, the harmonic balance procedure has been generalized by Schilder et al. [57], who also proposed a finite difference approximation. Their version is also implemented in the continuation package coco (cf. Dankowicz and Schilder [19]). The error due to the truncation of the generally infinite number of Fourier modes of quasi-periodic solutions, however, is unknown and the convergence of this method is a priori unclear. Furthermore, if the existence of a quasi-periodic is not shown, the expansion of the solution in a multi-frequency Fourier series is unjustified. Thus, the harmonic balance method is generally unreliable in those cases.

If the mechanical system is close to a solvable limit, perturbation methods can rigorously compute quasi-periodic orbits. Examples of general perturbation methods are the method of averaging (cf. Sanders et al. [55]), normal forms (cf. Murdock [47]) or the method of multiple time scales (cf. Nayfeh [48]). Moreover, Samoilenko [54] establishes a perturbation approach of quasi-periodic tori relying on a Green’s function. Similarly, the KAM-Theorem (cf. Guckenheimer and Holmes [28]) can guarantee the existence of quasi-periodic orbits in Hamiltonian systems under suitable conditions. The validity of all these methods, however, is restricted to a small neighborhood of the solvable, i.e., unphysical, limit. Whether the actual physical system is contained within this neighborhood is generally uncertain.

Fixed point theorems such as Brouwer’s or Schauder’s fixed point theorem (cf. Bobylev et al. [5] or Precup [51]) are powerful tools to prove the existence of solutions in the absence of small parameters. While the existence of periodic solutions is extensively treated in the literature (cf. Farkas [23], Rouche and Mawhin [52] or Bobylev [5]) the quasi-periodic or almost-periodic¹ case is less prominent (cf. Fink [24] and Corduneanu [15]).

Fink [24] guarantees the existence of an almost-periodic solution for one-dimensional first-order systems, if a monotonicity condition is met. Still relying on a monotonicity condition, Dafermos [18] extends the scalar results to abstract evolution equations in Hilbert spaces. His results can guarantee the existence of quasi-periodic responses in a fairly general setting for multi-dimensional first-order systems. The monotonicity condition, however, is not satisfied for simple mechanical systems such as the linear damped oscillator as we examine in Appendix A. Hence, the results of Dafermos [18] are inapplicable in the structural dynamics context.

Berger and Chen [3] give conditions for the existence of almost- and quasi-periodic solutions for second-order systems. Their results have been extended by, e.g., Carminati [11], Bolt et al. [4] and Mahwin [45], who also cover the case of bounded and almost-periodic solutions. Moreover, their theorems can guarantee the uniqueness of the bounded solution. These results, however, require again a monotonicity condition on the geometric nonlinearities (i.e., position dependent terms). In structural engineering this condition requires the stiffness to be negative definite (cf. Appendix A). This condition, however, is generally not met for oscillatory systems.

Alonso and Ortega [1], notably, derive an existence criterion for bounded solutions of second-order equations, which can be directly applied to oscillatory systems having a positive definite stiffness matrix. Their result guarantees the existence of a unique, asymptotically stable and bounded solution. The condition of their theorem, however, requires the Hessian of the nonlinear stiffness terms to the globally positive definite. This requirement excludes softening nonlinearities which have been observed experimentally by, e.g., Cho et al. [13] in a micro-mechanical system and by Yuan [61] in energy harvesting applications. Furthermore, the theorem by Alonso and Ortega [1] suffers from a restrictive linear global upper bound on the nonlinear terms.

In summary, the existence criteria for quasi-periodic solutions from the literature are inapplicable even for simple nonlinear oscillators. For the periodic case, however, various results can establish the existence of periodic solutions even for high amplitude oscillations. In our previous work [8], we identified a strengthened version of a theorem by Rouche and Mawhin [52] to be the most relevant for periodically driven mechanical systems. Here, we extend our result to the quasi-periodic case.

2 Set-up

We consider the general N-dimensional mechanical system of the form

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {q}}+\mathbf {C}\dot{\mathbf {q}}+\mathbf {S}(\mathbf {q})= \mathbf {f}(t), \qquad \mathbf {q}\in \mathbb {R}^N, \end{aligned}$$

(1)

where the mass matrix $\mathbf {M}\in \mathbb {R}^{N\times N}$ is symmetric and positive definite and the damping matrix $\mathbf {C}\in \mathbb {R}^{N\times N}$ is symmetric. The vector $\mathbf {S}(\mathbf {q})$ collects all position dependent forces, such a linear and nonlinear stiffness forces or non-potential forces (cf. Bolotin [6] for examples). The external forcing $\mathbf {f}(t)$ is assumed to be quasi-periodic according to the following definition

Definition 2.1

The function $\mathbf {f}(\varvec{\phi }(t))$ is quasi-periodic, if it maps the K-dimensional torus$\mathbb {T}^K:=\left[ 0,2\pi \right] \times \left[ 0,2\pi \right] \times \ldots \times \left[ 0,2\pi \right]$ to $\mathbb {R}^N$

$$\begin{aligned} \mathbf {f}: \mathbb {T}^K \mapsto \mathbb {R}^N,\qquad \varvec{\phi }\mapsto \mathbf {f}(\varvec{\phi }), \end{aligned}$$

(2)

where the time evolution of the angles $\varvec{\phi }$ is generated by K incommensurate frequencies

$$\begin{aligned}&\dot{\varvec{\phi }}=\varvec{\Omega },\qquad \varvec{\Omega }\in \mathbb {R}^K,\qquad \langle \varvec{\kappa } , \varvec{\Omega } \rangle \ne 0, \nonumber \\&\quad \text {for all}~~ \varvec{\kappa }\in \mathbb {Z}^K-\{0\}. \end{aligned}$$

(3)

A forced response of system (1) is most commonly computed by evaluating Eq. (1) along an assumed quasi-periodic solution $\mathbf {q}^*(\varvec{\Omega }t)$ to E. (1). Projecting $\mathbf {q}^*(\varvec{\Omega }t)$ on the torus $\mathbb {T}^K$ Eq. (1) yields a partial differential equation on the bounded domain $\mathbb {T}^K$, which can be discretized by, e.g., Fourier modes to yield the harmonic balance method (cf. Chua and Ushida [14]). Alternatively, Schilder et al. [57] propose a finite difference approximation. Since these methods evaluate Eq. (1) along a quasi-periodic orbit, they are only justifiable if a quasi-periodic solution to Eq. (1) actually exists. Applying the harmonic balance to a system without clarifying the existence of a steady-state response, can lead to erroneous conclusions as we have demonstrated on an explicit, periodically driven mechanical system [8]. To aid the existing numerical tools, it is thus of fundamental importance to guarantee the existence of quasi-periodic solutions to Eq. (1).

For periodically excited nonlinear mechanical systems numerous existence criteria are readily available (e.g., Farkas [23], Rouche and Mawhin [52] or Bobylev [5]). For the quasi-periodic case, however, the literature lacks applicable existence results for realistic nonlinear mechanical systems as previously detailed (see also Appendix A). Due to their resemblance, one could intuitively expect that the quasi-periodic case does not significantly differ from the periodic case. Unfortunately, this expectation is false and existence criteria from the periodic case do not straightforwardly extend to the quasi-periodic case. To demonstrate a delicate differences between periodic and quasi-periodic oscillations, we consider the linear oscillator

$$\begin{aligned}&\ddot{q}+\omega _0^2 q=f(\varvec{\phi }),\qquad \dot{\varvec{\phi }}=\varvec{\Omega }, \qquad q\in \mathbb {R},\quad \varvec{\phi } \in \mathbb {T}^K,\nonumber \\&\langle \varvec{\Omega },\varvec{\kappa }\rangle \ne 0, \quad \text {for all}~~\varvec{\kappa }\in \mathbb {Z}^K-\{0\}. \end{aligned}$$

(4)

For the periodic case ($K=1$ in Eq. (4)), a periodic response exists if the forcing is non-resonant, i.e., $n \Omega \ne \omega _0$ holds for all integers n (cf. Burd [10] Remark 2.1). Extending these results to the more general quasi-periodic case ($K>1$) one would intuitively expect that as long as the frequencies of the quasi-periodic forcing $\langle \varvec{\Omega },\varvec{\kappa }\rangle$ are not equal to the natural frequency $\omega _0$ (i.e., $|\langle \varvec{\Omega },\varvec{\kappa }\rangle |\ne \omega _0$), then a quasi-periodic solution to system (4) exists. This expectation, however, is false. Even worse, for any incommensurate frequency basis $\varvec{\Omega }$ there exists a quasi-periodic forcing such that the linear oscillator has no quasi-periodic solution (4). More specifically, in Appendix B we show the following:

Fact 2.1

For any incommensurate frequency basis $\varvec{\Omega }\in \mathbb {R}^K$ with at least two frequencies ($K\ge 2$), there exists a continuous and bounded forcing $f(\varvec{\phi })$ such that system (4) has no quasi-periodic solution.

Proof

We rely on the occurrence of small denominators, which arise in system (4) for any incommensurate frequency basis. We detail the derivations leading to the above fact in Appendix B. $\square$

In summary, applying a quasi-periodic excitation to the undamped linear oscillator (4) does not guarantee a quasi-periodic response (cf. Fact 2.1), while for almost all periodic forcings (i.e., except forcing at exact resonance) a periodic steady-state response arises. This observation demonstrates that results from the periodic system do not always straightforwardly extend to the quasi-periodic case.

3 Existence of quasi-periodic solutions

We prove the following general result:

Theorem 3.1

Assume that the quasi-periodic forcing $\mathbf {f}(t)$ (cf. Definition 2.1) is continuous and the following conditions hold:

• (C1) The damping matrix $\mathbf {C}$ is positive or negative definite, which implies that there exists a constant $C_0>0$ such that

  $$\begin{aligned} |\mathbf {x}^{\mathrm{T}}\mathbf {C}\mathbf {x}|>C_{0}|\mathbf {x}|^2, \qquad \text { for all ~} \mathbf {x}\in \mathbb {R}^N, \end{aligned}$$

  (5)

  holds.

• (C2) The stiffness terms $\mathbf {S}(\mathbf {q})$ derive from a potential, i.e., there exists a continuously differentiable scalar function $V(\mathbf {q})$ such that

  $$\begin{aligned} \mathbf {S}(\mathbf {q})=\frac{\partial V(\mathbf {q})}{\partial \mathbf {q}}, \end{aligned}$$

  (6)

  holds.

• (C3) The stiffness terms $\mathbf {S}(\mathbf {q})$ are continuous and globally Lipschitz, i.e., there exists a constant $L>0$ such that

  $$\begin{aligned}&|\mathbf {S}(\mathbf {q}_1)-\mathbf {S}(\mathbf {q}_2)|\le L|\mathbf {q}_1-\mathbf {q}_2|,\qquad \nonumber \\&\qquad \text {for all}~~\mathbf {q}_1,\mathbf {q_2}\in \mathbb {R}^N, \end{aligned}$$

  (7)

  holds.

• (C4) The inner product of the stiffness terms $\mathbf {S}(\mathbf {q})$ with the coordinates $\mathbf {q}$ grows sufficient far away from the origin. Specifically, there exists a radius r and a minimal growths $\alpha >0$, such that

  $$\begin{aligned}&\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})>\alpha |\mathbf {q}|^2,~~\text {or}~~-\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})>\alpha |\mathbf {q}|^2,\nonumber \\&\qquad \text { for all ~} |\mathbf {q}|>r, \end{aligned}$$

  (8)

  holds.

Then, system (1) has a differentiable quasi-periodic solution $\mathbf {q}(\varvec{\Omega }t)$.

Proof

We base our proof of Theorem 3.1 on a fixed point theorem by Schäfer [56] (also see Smart [59]). We establish a homotopy between system (1) and the equation $\mathbf {M}\ddot{\mathbf {q}}+\mathbf {C}\dot{\mathbf {q}}\pm \mathbf {M} \mathbf {q}=0$. Conditions (C1)–(C4) guarantee that the solutions remains bounded for all homotopy parameters. We detail our derivations in Appendix C and give a concise proof referring to relevant preliminary results and definitions in Sect. C.5. $\square$

Remark 3.1

Since periodic orbits are a special case of quasi-periodic solutions (i.e., $K=1$ in Definition 2.1), one can also establish the existence of periodic solutions via Theorem 3.1. Comparing with our previous result [8] conditions (C1) and (C2) are identical. In the quasi-periodic case, however, we require inner product of the coordinates $\mathbf {q}$ and the stiffness terms $\mathbf {S}(\mathbf {q})$ to grow sufficient far from the origin (cf. condition (C4)), while in the periodic case it is sufficient that the stiffness terms are element-wise above or below the mean forcing value. Furthermore, we require the existence of a global Lipschitz constant in condition (C3). These deviations arise from the different fixed point theorems employed in the proofs of both results.

Remark 3.2

We emphasize that our Theorem 3.1 guarantees the existence of a quasi-periodic solution to Eq. (1) with the frequency base $\varvec{\Omega }$ arising from the external excitation. This enables to approximate the steady-state solutions by Fourier series with known frequencies basis $\varvec{\Omega }$. In practice this is the most common approach to compute quasi-periodic orbits (e.g., Schilder et al. [57] or Chua and Ushida [14]). Competing results in a similar setting of our Theorem 3.1, e.g., by Alonso and Ortega [1] Lemma 3.2, can only guarantee the existence of a bounded solution. Hence, an approximation by Fourier series is generally not justified by such a result.

Generally, results guaranteeing the existence of a bounded solution, such as Alonso and Ortega’s Lemma, can be strengthened to establish that an existing bounded solution is quasi-periodic with the same frequency base (or module) as the external loads. Thereby, Fourier series approximations with the frequency basis $\varvec{\Omega }$ are again justified. In practice, however, the necessary arguments rely on very restrictive assumptions. For example, if the bounded solution is unique and stable, then general results on module containment (cf. Fink [24]) guarantee that the bounded solution is quasi-periodic with the same frequencies as the forcing. For nonlinear mechanical systems of the form (1), however, already in the periodic case multiple co-existing steady-state solutions and unstable periodic orbits are frequently observed (e.g., Nayfeh and Mook [49]).

In the case of multiple coexisting solutions, it is non-trivial whether these are actually even almost-periodic. For such a result one would need to show that only finitely many, semi-separated solutions exist (cf. Fink [24]). However, the periodically forced damped Duffing oscillator, a prominent example of system (1), can have infinite number of periodic orbits if a homoclinic tangle occurs (cf. Guckenheimer and Holmes [28]). Even if one achieves to establish that only finitely many semi-separated solutions exist, then the frequency basis of these almost-periodic solutions is generally not the same as the module of the time-varying terms (see Fink [24] for an explicit example). Thereby, an expansion of the solution in a Fourier series with frequency basis $\varvec{\Omega }$ is generally unjustified.

Remark 3.3

If the stiffness terms in system (1) are polynomials such as in the classical Duffing oscillator, then condition (C3) is not satisfied. However, the Lipschitz constant L in Eq. (7) can be chosen arbitrarily large, which allows to conclude that condition (C4) is generally uncritical for realistic structures. Since any physical system will not allow for arbitrarily large displacements and velocities, equations of the form (1) modeling a realistic system are generally only valid in a bounded domain $U\subset \mathbb {R}^N$. Outside this domain of validity, Eq. (1) does not represent the reality. Thus, it is justified to modify Eq. (1) outside U such that the stiffness terms are globally Lipschitz. Such a truncation can always be carried out if $\mathbf {S}(\mathbf {q})$ is continuous. Then, $\mathbf {S}(\mathbf {q})$ is uniformly continuous on the compact domain U. Hence, $\mathbf {S}(\mathbf {q})$ is locally Lipschitz and there exists a Lipschitz constant L such that condition (C3) holds for all $\mathbf {q}_1$ and $\mathbf {q}_2$ in U.

We explicitly construct an example of such an envisioned truncation. We select a ball of radius r containing U ($U\subset \mathcal {B}_r \subset \mathbb {R}^N$) and denote the point on the boundary of $\mathcal {B}_r$ with minimal distance to $\mathbf {q}$ by $\mathbf {q}^*(\mathbf {q})$. With this notation, we define the nonlinearities

$$\begin{aligned} \mathbf {S}_1(\mathbf {q})= & {} {\left\{ \begin{array}{ll} \mathbf {S}(\mathbf {q}) &{} |\mathbf {q}|<r,\\ \mathbf {S}(\mathbf {q}^*(\mathbf {q})), &{} |\mathbf {q}|\ge r, \end{array}\right. }\nonumber \\ \mathbf {S}_2(\mathbf {q})= & {} {\left\{ \begin{array}{ll} 0 &{} |\mathbf {q}|<r,\\ \mathbf {K}^*(\mathbf {q}-r\frac{\mathbf {q}}{|\mathbf {q}|}), &{} |\mathbf {q}|\ge r, \end{array}\right. }, \end{aligned}$$

(9)

where $\mathbf {K}^*$ is a positive or negative definite matrix. We note that $\mathbf {S}_2$ satisfies condition (C3) and hence if $\mathbf {S}$ is continuous, then the system

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {q}}+\mathbf {C}\dot{\mathbf {q}}+\mathbf {S}_1(\mathbf {q})+\mathbf {S}_2(\mathbf {q})= \mathbf {f}(t), \qquad \mathbf {q}\in \mathbb {R}^N, \end{aligned}$$

(10)

is Lipschitz continuous and satisfies condition (C3). Thus, if the remaining conditions (C1), (C2) and (C4) of our Theorem 3.1 are met, a quasi-periodic response exists.

Remark 3.4

We have restricted our Theorem 3.1 to time independent nonlinearities, which are customary in structural dynamics. However, our results can be extended to include time dependent nonlinearities $\mathbf {S}(\mathbf {q},\varvec{\Omega } t)$, if the time dependence is quasi-periodic. Then, if conditions (C2)–(C4) are satisfied for all times, then the assertion of Theorem 3.1 still holds.

Remark 3.5

The existence of a quasi-periodic orbit, e.g., established by our Theorem 3.1 does not rule out the existence of other invariant objects such as periodic orbits, fixed points or chaotic attractors. Indeed, the coexistence of multiple stable or unstable attractors is a fundamental characteristic of nonlinear dynamical systems (e.g., Guckenheimer and Holmes [28]). Moreover, a general connection between quasi-periodic motion and chaos has been established by Ruelle and Takens [53] and Newhouse et al. [50]. A quasi-periodic route to chaos has been experimentally observed by, e.g., Held and Jeffries [32], Cumming and Linsay [17] and He et al. [31]. Since Theorem 3.1 can guarantee the existence of quasi-periodic motions, it can be applied in numerical investigation of the quasi-periodic route to chaos in the nonlinear mechanical system (1).

Remark 3.6

From the existence Theorem 3.1, we can conclude, that one can observe a quasi-periodic motion if the dynamical system (1) is initialized on one of the quasi-periodic orbits. Whether other initial conditions are attracted to this quasi-periodic orbit or whether it is stable with a basin of attraction cannot be inferred from our Theorem 3.1. Moreover, to the best of our knowledge, a robust and universal tool to conclude about the stability of a quasi-periodic orbit is not available. Although only stable orbits are observable, it is also of interest to compute unstable orbits. For example, Denis et al. [20] utilize unstable periodic orbits for system identification.

Condition (C4) specifies the sign of the inner product of the nonlinearity $\mathbf {S}(\mathbf {q})$ and the coordinate $\mathbf {q}$. Geometrically this implies that far away from the origin the vector $\mathbf {S}(\mathbf {q})$ points either toward the origin ($\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})<0$) or away from the origin ($\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})>0$). These considerations play a major role in the construction of guiding functions and also index theory (cf. Krasonosel’skii et al. [39], Krasnosel’skii and Zabreĭko [38] or Bobylev et al.  [5]). The application reported, however, focus on either periodic or bounded solutions (see also Remark 3.2).

If the nonlinearities are continuously differentiable, then condition (C4) of Theorem 3.1 can be replaced by a more intuitive condition.

Theorem 3.2

If the nonlinearities $\mathbf {S}(\mathbf {q})$ are continuously differentiable, condition (C4) holds if

• (C4*) The Hessian of $V(\mathbf {q})$ is positive or negative definite for $|\mathbf {q}|>\tilde{r}$, i.e., for some constant $C_S>0$

  $$\begin{aligned}&\!\!\!\mathbf {x}^{\top } \frac{\partial ^2 V(\mathbf {q})}{\partial \mathbf {q}^2} \mathbf {x}> C_S |\mathbf {x}|^2,\quad \text {or}\nonumber \\&\!\!\!\quad -\mathbf {x}^{\top } \frac{\partial ^2 V(\mathbf {q})}{\partial \mathbf {q}^2} \mathbf {x}> C_S |\mathbf {x}|^2 ,\nonumber \\&\!\!\!\quad \qquad \text {for all ~} |\mathbf {q}|>\tilde{r},~~ \mathbf {x}\in \mathbb {R}^N, \end{aligned}$$

  (11)

  holds.

Proof

We proof the above theorem in Appendix D. $\square$

Remark 3.7

We note that condition (C4*) requires differentiable nonlinearities, which is not required by condition (C4). Condition (C4*) is, however, generally easier to verify, since positive or negative definiteness can be checked through direct eigenvalue computation, leading minor criteria (or Sylvester’s criterion) or Cholesky decomposition (cf. Horn and Johnson [33]).

On our way to Theorem 3.1, we have established an analogous result for non-smooth but $L_2$-integrable external forcing, i.e.,

$$\begin{aligned} ||\mathbf {f}(t)||_{L_2}:= & {} \left( \frac{1}{(2\pi )^K}\int _{\mathbb {T}^K} \mathbf {f}^{\top }(\varvec{\phi })\mathbf {f}(\varvec{\phi })~{\mathrm{d}}\varvec{\phi } \right) ^{\frac{1}{2}}\nonumber \\= & {} \left( \lim _{T\rightarrow \infty }\frac{1}{2T}\int _{-T}^{T} \mathbf {f}^{\top }(t)\mathbf {f}(t)~{\mathrm{d}}t \right) ^{\frac{1}{2}} < \infty .\nonumber \\ \end{aligned}$$

(12)

Equation (12) is satisfied by, e.g., saw-tooth or square wave functions. For such non-smooth forcing functions, we have the following result:

Theorem 3.3

Assume that that the conditions (C1)–(C4), or equivalently condition (C4*) instead of condition (C4), are satisfied and the quasi-periodic forcing $\mathbf {f}(t)$ (cf. Definition 2.1) satisfies Eq. (12). Then, system (1) has a quasi-periodic solution $\mathbf {q}(\varvec{\Omega }t)$ with finite $L_2$-norm. Moreover, the time derivative of this solution is bounded in the $L_2$-norm.

Proof

Our proof of the above theorem is also based on a fixed point theorem by Schäfer [56] (also see Smart [59]). We detail our derivations in Appendix C and give an overview of the proof in Sect. C.4. $\square$

Moreover, basic results on the smoothness of solutions to ordinary differential equation (e.g., Hale [29] or Arnol’d [2]) for finite time guarantee the smoothness of the quasi-periodic solution

Corollary 3.1

(Smoothness) Assume the stiffness terms $\mathbf {S}(\mathbf {q})$ and the forcing $\mathbf {f}(t)$ of system (1) are s-times continuously differentiable ($s>0$) and the conditions of Theorem 3.1 hold. Then, the quasi-periodic solution guaranteed by Theorem 3.1s-times continuously differentiable.

Proof

Assume the contrary, i.e., the quasi-periodic solution $\mathbf {q}^*$ of system (1) is non-smooth at some time instance $t^*$. This statement is a direct contradiction to the existence of s-times continuous differentiable solutions for finite times proven by, e.g., Hale [29] or Arnol’d [2]. Hence, the quasi-periodic solutions are smooth as claimed in corollary (3.1). $\square$

4 Numerical examples

We demonstrate the applicability of our Theorem 3.1 on two oscillatory systems. First, we investigate a chain of oscillators proposed by Breunung and Haller [7]. This system is a natural extension of the classical Duffing oscillator or the Shaw–Pierre example [58] to higher dimensions. Subsequently, we apply Theorem 3.1 to a discretized slender beam. After concluding about the existence of a quasi-periodic steady-state response, we calculate it with the automated package proposed by Jain et al. [35].

4.1 Chain oscillator

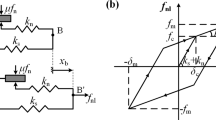
In the following, we utilize our Theorem 3.1 to compute a steady-state response of a system of N masses depicted in Fig. 1. Two adjacent masses are connected with spring elements and linear dampers. The first mass is suspended to the wall, while the last mass is suspended to the moving base u(t). Additional to the base point excitation, the external loads $f_j(t)$ are applied to the jth mass. For a first assessment, we assume purely external loads and select forcing frequencies in resonance with the first two eigenfrequencies. Subsequently, we show that our Theorem 3.1 also allows for complex loading scenarios, e.g., excitations arising from the natural roughness of a road surface.

Fig. 1

Oscillator chain with base excitation

4.1.1 External loading

For the case $u(t)=0$, the equation of motion for the jth mass is given by

$$\begin{aligned}&m_j\ddot{q}_j-c_j(\dot{q}_{j-1}-\dot{q}_{j})+c_{j+1}(\dot{q}_{j}-\dot{q}_{j+1})\nonumber \\&\quad -S_{j}(q_{j-1}-q_{j})+S_{j+1}(q_{j}-q_{j+1})=f_j(t),\nonumber \\&\qquad j=1,\ldots ,N, \end{aligned}$$

(13)

where the coordinates $q_0$ and $q_{N+1}$ are set to zero. The example (13) includes the classical Duffing oscillator in the case $N=1$ and $S_1(q_1)=\omega _0^2q+\kappa q^3$. Higher-dimensional variants of this system have been investigated by, e.g., Shaw and Pierre [58], Breunung and Haller [7] or Jain et al. [35]. In our previous work [8], we showed that if all the stiffness terms were hardening ($\partial S_j(p)/\partial p>0$) then periodic forcing leads to a periodic response of system (13). For the quasi-periodic case, we have a similar statement

Fact 4.1

Assume the masses $m_j$ and damping coefficients $c_j$ are positive and the forcing functions $f_j(t)$ are quasi-periodic and continuous. If additionally all springs are either hardening or softening far away from the origin, i.e., for some $\gamma >0$ and $r>0$

$$\begin{aligned} \begin{aligned}&S_{j}(q_{j-1}-q_{j})> \gamma (q_{j-1}-q_{j}), \\&\qquad |q_{j-1}-q_{j}|>r,\quad j=1,\ldots , N+1, \\&\text {or } \qquad -S_{j}(q_{j-1}-q_{j})> \gamma (q_{j-1}-q_{j}), \\&\qquad |q_{j-1}-q_{j}|>r,\quad j=1,\ldots ,N+1, \end{aligned} \end{aligned}$$

(14)

holds, then system (13) has a quasi-periodic steady-state response.

Proof

We verify that system (13) satisfies the conditions of Theorem 3.1 in Appendix 5. $\square$

Fact 4.1 extends the result of our previous work [8] to the case of quasi-periodic forcing and also includes softening nonlinearities. As an example, we consider a chain of five masses with the parameters $m_j=1$, $c_j=0.02$ and softening springs of the form $S_j(d)=d-0.5d^3$. For this configuration, Fact 4.1 guarantees the existence of a quasi-periodic steady-state response.

Selecting the quasi-periodic forcing $f_1=0.006 (\sin (\Omega _1 t)+\sin (\Omega _2 t))$ and $f_j=0$ for $j=2,3,\ldots ,N$, we use the automated package of Jain et al. [35] to compute a quasi-periodic steady state. In this algorithm, the steady-state response is approximated with a finite number of Fourier coefficients. The arising nonlinear algebraic equations are solved either with the Picard or the Newton–Raphson iteration, where the response of the corresponding linear system serves as initial guess. While the existence criterion of Jain et al. [35] fails for forcing in resonance with an eigenfrequency, our Theorem 3.1 guarantees the existence of a quasi-periodic response for any forcing amplitude and frequency. We chose the forcing frequency $\Omega _1$ to be close to the first eigenfrequency $\omega _1\approx 0.52$ and $\Omega _2$ in the vicinity of the second eigenfrequency $\omega _2 \approx 1$. In Fig. 2, we depict the $L_2$-norm of the quasi-periodic steady-state response of the chain oscillator (13).

Fig. 2

Quasi-periodic steady-state responses of system (13) with five masses and parameters $m_j=1$, $c_j=0.02$ and $S_j(d)=d-0.5d^3$ to the external loads $f_1=0.006(\sin (\Omega _1 t)+\sin (\Omega _2 t))$ and $f_j=0$. We select the forcing frequencies $\Omega _1$ and $\Omega _2$ in resonance with the first two natural frequencies $\omega _1\approx 0.52$ and $\omega _2 \approx 1$

4.1.2 Base excitation through road roughness

Many engineering systems are subject to complex or even random excitations. For example, various norms (e.g., MIL-STD-810G, ISO 4866 or ISO 1032) require the assessment of vibration amplitudes to loads with a specified power spectral density. Often it is assumed that these complex loading scenarios can be accurately modeled with a finite set of Fourier modes (cf. Loprencipe and Zoccali [43]). In such a setting the arising external loads are naturally quasi-periodic. In the following, we use our Theorem 3.1 to reliably compute an arising steady-state response to a complex excitation generate by a road surface.

We assume that the base point u(t) (cf. Fig. 1) moves with a constant speed v along a rough street. We envision, e.g., parts of a vehicle. Road profiles are often classified by their spatial spectral density according to the norm ISO 8608 [34] (cf. Loprencipe and Zoccali [43]). Furthermore, the smoothened power spectral densities given in [34] are commonly used for dynamical analysis of vehicles. We follow this approach to generate a road roughness profile according to ISO 8608. The smoothened spatial power spectral density from the standard [34] is given by

$$\begin{aligned} \hat{u}(\Omega )= C \left( \frac{\Omega }{\Omega _0}\right) ^{-2} \cdot 10^{-6}, \qquad \nonumber \\ 0.022\pi \le \Omega \le 5.66\pi , \qquad \nonumber \\ \Omega _0=1~ \mathrm {rad/m},\quad C=64~ \mathrm {m}^3, \end{aligned}$$

(15)

where $\Omega$ is the frequency in $\mathrm {rad/m}$ and the amplitudes $\hat{u}(\Omega )$ are given in meters. The normalization constant $\Omega _0$ is $1~ \mathrm {rad/m}$ and the constant C is quantifies the road quality. For our analysis, we assume that the road belongs to the class with the second highest quality and set C to be $64~ \mathrm {m}^3$. Following Loprencipe and Zoccali [43], we create an artificial road profile by selecting a finite number of frequencies $\Omega _k$ whereby the amplitudes are given by Eq. (15). Then, the road profile is given by

$$\begin{aligned} u(s)=\sum _{k=1}^K \sqrt{\hat{u}(\Omega _k)}\sin ( \Omega _k s+\phi _k), \end{aligned}$$

(16)

where s is the distance traveled and $\phi _k$ denote phases. We select the frequencies $\Omega _k$ by drawing random samples from the specified frequency interval (15). To emphasize the presence of low frequency terms, we assume an underlying beta distribution (e.g., Jonson et al. [36]) with the parameters $\alpha =1$ and $\beta =5$. Moreover, we sample the angles $\phi _k$ from a uniform distribution. We depict such a road profile with ten frequencies ($K=10$ in Eq. (16)) in Fig. 3a.

Fig. 3

Randomly generated road profile generated according to the norm ISO 8608 [34] and frequency spectrum of the forcing arising through base excitation with then base frequencies ($K=10$). We consider system (17) with five masses and the parameters $k=100 ~\mathrm {N/m}$, $k_r=10^4~ \mathrm {N/m}$, $c=2~ \mathrm {Ns/m}$, $\kappa =5000~\mathrm {N/m^3}$ and $v=10~\mathrm {m/s}$. a Road profile. b Force arising from the road profile 3a and eigenfrequencies of system (17).

We consider the chain of oscillators depicted in Fig. 1 with five masses. Assuming springs with linear and cubic coefficients the equations of motion are

$$\begin{aligned} \begin{aligned}&m\ddot{q}_j+c(2\dot{q}_{j}-\dot{q}_{ j-1}-\dot{q}_{j+1}) +k(2q_{j}-q_{j-1}-q_{j+1})\\&\quad -\kappa (q_{j-1}-q_{j})^3\\&\quad + \kappa (q_{j}-q_{j+1})^3=0, \quad j=1,\ldots ,N-1,\\&m\ddot{q}_{N}+c(2\dot{q}_{N}-\dot{q}_{N-1}) +k( q_{N}-q_{N-1})\\&\quad +k_rq_n=k_r u(vt)+c \dot{u}(t)=f_r(vt), \end{aligned} \end{aligned}$$

(17)

where we selected a linear force displacement relationship for the last spring $S_{N+1}$ with stiffness $k_r$ and v denotes the constant speed (cf. Fig. 1). The forcing $f_r(t)$ arising through the base point excitation is analytic and quasi-periodic for any finite number of frequencies K. The frequency spectrum of the forcing arising from the road profile shown in Fig. 3a is depicted in Fig. 3b. Selecting the positive mass $m=1~\mathrm {kg}$, positive stiffness coefficients $k=100 ~\mathrm {N/m}$, $k_r=10^4~ \mathrm {N/m}$, $\kappa =5000~\mathrm {N/m^3}$ and positive damping coefficient $c=2~ \mathrm {Ns/m}$, Eq. (17) satisfies Fact 4.1, hence a quasi-periodic steady-state response exists.

Figure 3b shows that in the frequency band between 10 and $20~\mathrm {rad/s}$ three eigenfrequencies and four forcing frequencies are in an immediate vicinity. Additionally, at $6~\mathrm {rad/s}$ one of the forcing frequencies is in resonance with the lowest eigenfrequency. Due to these multiple resonances, we expect considerable vibration amplitudes.

We compute the arising steady-state response via the harmonic balance procedure with ten base frequencies, whereby the arising nonlinear algebraic equations are solved the Newton–Raphson iteration. As initial guess, we select the response of the linearization of system (17) at the origin. In Fig. 4, we depict the arising quasi-periodic steady-state response for the first one hundred meters. Additionally, we include the linear solution and a time series obtained by numerical time integration with matlab’s ode45 algorithm serving as benchmark solution. To this end, we consider the system to be at rest one thousand seconds before reaching $s=0$, i.e., we select the initial condition $\mathbf {q}(t=-10^{3})=\dot{\mathbf {q}}(t=-10^{3})=\mathbf {0}$. Figure 4 reveals that the harmonic balance solution matches very well with the numeric time integration, while the linear response differs. The maximal displacement of $q_3$ along the arising steady-state response is $97.2~\mathrm {mm}$, while a linear analysis leads to a maximal displacement of $83.6~\mathrm {mm}$. Hence, linear analysis underestimates the response amplitude by more than 15 percent. Thus, it is essential to perform a nonlinear analysis on our example. Therein, Theorem 3.1 justifies the expansion the coordinates of system (17) in a Fourier series.

4.2 A slender beam

After applying our existence criterion 3.1 to the spring-mass systems (13), we advance to a beam serving as more realistic engineering structure. Beam elements are frequently used to model complex engineering structures and are readily implemented in common computational packages such as Abaqus, Autodesk or ANSYS. These computational packages discretize the model’s governing partial differential equations in space. Through the discretization high-dimensional ordinary differential equations arise. In the following, we apply our existence criterion 3.1 to such a high-dimensional oscillatory system. Subsequently, it justifies numerical computations of quasi-periodic responses.

We consider the clamped–clamped beam of length L depicted in Fig. 5. The material properties and geometry such as cross-sectional area A and moment of inertia I are assumed to be constant. Nayfeh and Mook [49] derive a partial differential equation governing the vertical vibrations of slender beams. They assume that the Euler–Bernoulli hypothesis is met (i.e., plane cross sections initially perpendicular to the neutral axis remain plane and perpendicular the neutral axis after deformation), linear elastic material properties (Hooke’s law) and use a third-order approximation of the Green–Lagrange strain tensor (van Kármán strains). With the additional assumption of a small radius of gyration r, i.e., $r=\sqrt{I/A}\ll 1$, Nayfeh and Mook state the non-dimensional partial differential equation

$$\begin{aligned}&r^2(w_{tt}+2\mu w_t+w_{xxxx})-\left( \frac{1}{2L}\int _{0}^{L} w_x^2{\mathrm{d}}x\right) w_{xx}\nonumber \\&\quad =f(x,t),~\qquad w(0)=w_x(0)\nonumber \\&\quad =w(L)=w_x(L)=0, \end{aligned}$$

(18)

where w(x, t) denotes the vertical displacement as a function of the non-dimensional horizontal position x and the non-dimensional time t (cf. Fig. 5). The subscripts of w in Eq. (18) refer to partial differentiation with respect to time t or space x and the constant $\mu$ is a damping parameter.

Fig. 4

Steady-state response of the third mass $q_3$ of system (17) exited by the forcing 3b. We select the parameters $k=100 ~\mathrm {N/m}$, $k_r=10^4~ \mathrm {N/m}$, $c=2~ \mathrm {Ns/m}$ and $\kappa =5000~\mathrm {N/m^3}$

Fig. 5

Clamped–clamped beam: undeformed configuration in black and deformed configuration in gray

We discretize the partial differential equation (18) in the spatial coordinate following a finite difference scheme with N equally space nodes $x_j$ ($j=1,\ldots ,N$). The parameter h denotes the distance between neighboring nodes. We use a forward scheme for to odd spatial derivative $w_x$ and a central scheme for the even spatial derivatives which yields

$$\begin{aligned}&w_x(x_j)=\frac{w(x_{j+1})-w(x_{j}) }{h}+\mathcal {O}(h),\nonumber \\&w_{xx}(x_j)=\frac{w(x_{j+1})-2w(x_{j})+w(x_{j-1})}{h^2}0+\mathcal {O}(h^2),\nonumber \\&w_{xxxx}(x_j)\nonumber \\&\quad =\frac{w(x_{j+2})-4w(x_{j+1})+6w(x_{j}) -4w(x_{j-1})+w(x_{j-2}) }{h^4}\nonumber \\&\qquad +\mathcal {O}(h^2).\nonumber \\ \end{aligned}$$

(19)

To approximate the spatial derivative at the node $x_N=L$, we use a backward-difference scheme, i.e., $w_x(L)=(w(x_{N})-w(x_{N-1}))/h+\mathcal {O}(h))$. Moreover, we approximate the integral in Eq. (18) via the trapezoidal rule yielding

$$\begin{aligned}&\int _{0}^{L} w_x^2{\mathrm{d}}x \nonumber \\&\quad = \frac{h}{2} \left( w_x^2 (x_1)+2 \sum _{j=2}^{N-1} w_x^2 (x_j)+w_x^2 (x_N)\right) +\mathcal {O}(h^2) \nonumber \\&\quad = \frac{1}{2h} \left[ (w(x_{2})-w(x_1))^2+(w(x_N)-w(x_{N-1}))^2\right] \nonumber \\&\qquad + \frac{1}{h} \sum _{j=2}^{N-1} (w(x_{j+1})-w(x_{j}))^2+ \mathcal {O}(h), \end{aligned}$$

(20)

where we have used the discretization (19). Moreover, we concentrate the distributed load f(x, t) onto the closest mesh point by defining the nodal forcing functions

$$\begin{aligned} f_j(t):=\int _{x_j-h/2}^{x_j+h/2} f(x,t)~{\mathrm{d}}x. \end{aligned}$$

(21)

The boundary conditions (18) imply that the vertical displacements of the first and last two elements are zero, i.e., $w(x_1)=w(x_2)=w(x_{N-1})=w(x_N)=0$. We collect the remaining degrees of freedom in the vector $\mathbf {w}:=[w(x_3),w(x_4),\ldots ,w(x_{N-2})]^{\top }$ and note that for all these nodes ($x_3,x_4\ldots ,x_{N-2}$) the finite differences (19) are well defined. To formulate a spatially discretized version of the partial differential equation (18), we define the forcing vector $\mathbf {f}:= [f_3(t),f_4(t),\ldots ,f_{N-2}(t)]^{\top }$ and the banded matrices

$$\begin{aligned} \displaystyle \mathbf {K}_1:= & {} \begin{bmatrix} 2 &{} -1&{}0 &{} 0 &{} \\ -1 &{} 2 &{}-1 &{} 0 &{} \\ 0 &{} \ddots &{} \ddots &{}\ddots \end{bmatrix}\nonumber \\ \mathbf {K}_2:= & {} \begin{bmatrix} 6 &{} -4&{} 1 &{} 0 &{} \\ -4 &{} 6 &{}-4 &{} 1 &{} 0 \\ 1 &{}-4 &{} 6 &{}-4 &{} 1 &{} 0 \\ 0 &{} \ddots &{} \ddots &{}\ddots &{} \ddots &{}\ddots \end{bmatrix}\nonumber \\&\quad \mathbf {K}_1,\mathbf {K}_2\in \mathbb {R}^{N-4\times N-4}. \end{aligned}$$

(22)

With the notation (22), a discretized version of the partial differential equation (18) is given by

$$\begin{aligned}&\ddot{\mathbf {w}} +2\mu \dot{\mathbf {w}} + \frac{1}{h^4} \mathbf {K}_2 \mathbf {w} +\frac{1}{2 L r^2 h^3 } (\mathbf {w}^{\top }\mathbf {K}_1\mathbf {w}) \mathbf {K}_1\mathbf {w}\nonumber \\&\quad =\frac{1}{r^2} \mathbf {f}(t). \end{aligned}$$

(23)

After deriving Eq. (23) as a discretization of the partial differential(19), we will now show that our Theorem 3.1 guarantees the existence of a quasi-periodic response of system (23). We emphasize that our result is especially relevant for Eq. (23). Competing perturbations methods commonly extract a steady-state response from linearizing Eq. (23) around the origin ($\mathbf {w}=\dot{\mathbf {w}}=0$). Subsequently, those approaches argue that a steady-state response of the linearization implies a close by steady-state response of the full nonlinear system if the nonlinearity is small enough. The nonlinearity in Eq. (23), however, is dominant , since the slenderness parameter r is small. Hence, the validity of regular perturbation methods is restricted to a tiny neighborhood of the origin. Our result 3.1 does not suffer from such a shortcoming.

We proceed by verifying that conditions (C1)–(C4) are satisfied for system (23). Indeed, for any nonzero value $\mu$ condition (C1) is satisfied. Furthermore, differentiation of the function $V(\mathbf {w}):= 1/(2 h^4) \mathbf {w}^{\top }\mathbf {K}_2 \mathbf {w}+1/(4 L r^2 h^3) (\mathbf {w}^{\top }\mathbf {K}_1\mathbf {w})^2$ yields

$$\begin{aligned} \frac{\partial V(\mathbf {w})}{\partial \mathbf {w}}=\frac{1}{h^4} \mathbf {K}_2 \mathbf {w}+\frac{1}{2 L r^2 h^3} (\mathbf {w}^{\top }\mathbf {K}_1\mathbf {w} ) \mathbf {K}_1\mathbf {w}, \end{aligned}$$

(24)

where we have used the symmetry of $\mathbf {K}_1$ and $\mathbf {K}_2$ (cf. Definition (22)). Equation (24) implies that $V(\mathbf {w})$ is a potential for the stiffness terms in Eq. (23) and hence condition (C2) holds.

As noted in Remark 3.3, system (23) can be modified such that condition (C3) holds. In the current setting, a truncation of the nonlinearity for large displacements is justified, since the partial differential equation (18) was obtained by expanding the Green–Lagrange strain tensor in a Taylor series up to order three. Such an approximation is generally only valid for small enough displacements.

To verify condition (C4), we note that Eq. (8) for the discretized beam (23) is given by

$$\begin{aligned} \mathbf {w}^\top \mathbf {S}(\mathbf {w})=\frac{1}{h^4} \mathbf {w}^{\top } \mathbf {K}_2 \mathbf {w} +\frac{1}{2 r^2 h^3} \mathbf {w}^{\top }\mathbf {K}_1\mathbf {w} \mathbf {w}^{\top } \mathbf {K}_1\mathbf {w}.\nonumber \\ \end{aligned}$$

(25)

Since $\mathbf {K}_1$ is a tridiagonal Toeplitz matrix with positive eigenvalues (e.g., Gover [27]), it is positive definite. Thus, the second summand in Eq. (25) is positive for all displacements, i.e., $\mathbf {w}^{\top }\mathbf {K}_1\mathbf {w} \mathbf {w}^{\top } \mathbf {K}_1\mathbf {w}>0$. To analyze the first term in Eq. (25), we split the matrix $\mathbf {K}_2$ as follows

$$\begin{aligned}&\!\!\!\mathbf {K}_2=\mathbf {K}_1^2 +\mathbf {B}(1)+\mathbf {B}(N-4),\nonumber \\&\!\!\!B_{jl}(k):= {\left\{ \begin{array}{ll} 1 &{} l=j=k \\ 0 &{} \text {otherwise} \end{array}\right. }, \quad j,l=1,\ldots ,N-4\nonumber \\ \end{aligned}$$

(26)

where all entries of the matrices $\mathbf {B}(1)$ and $\mathbf {B}(N-4)$ are zero expect for the first, respectively, the last entry on the main diagonal which is equal to one. Both matrices ($\mathbf {B}(1)$ and $\mathbf {B}(N-4)$) are positive semi-definite. Furthermore, we note that the square of the symmetric and positive definite matrix $\mathbf {K}_1$ is also positive definite. Since $\mathbf {K}_2$ can be expressed as sum of the positive definite matrix $\mathbf {K}_1^2$ with the positive semi-definite matrices $\mathbf {B}(1)$ and $\mathbf {B}(N-4)$, it is positive definite. The positive definiteness of $\mathbf {K}_2$, ensures that condition (C4) is satisfied for some $\alpha >0$ and $r=0$, since the second summand in Eq. (25) is always positive as we have noted earlier. In summary, all conditions (C1)–(C4) are met, and our Theorem 3.1 guarantees an arising quasi-periodic response of system (23) to external quasi-periodic forcing.

We calculate a forced response of the discretized beam (23) with the numerical package proposed by Jain et al. [35] and choose $N=10$ node points for the spatial discretization of the partial differential equation (18). The arising system (23) has six degrees of freedom. Moreover, we select the parameter values $r=0.01$, $\mu =0.05$ and $L=1$ and assume quasi-periodic forcing of the form $f(x,t)=0.06 r^2 (\sin (2\pi x /L)+1) (\sin (\Omega _1 t)+\sin (\Omega _2 t))$. We sweep the forcing frequencies $\Omega _1$ and $\Omega _2$ close to the first two eigenfrequencies $\omega _1\approx 7.13 ~\mathrm {rad/s}$ and $\omega _2 \approx 19 ~\mathrm {rad/s}$ and depict the $L_2$-norm of the arising quasi-periodic steady-state response in Fig. 6.

Fig. 6

Quasi-periodic steady-state responses of system (23) with six degrees-of-freedom and non-dimensional parameters $\mu =0.05$, $r=0.01$ and $L=1$ and forcing $f(x,t)=0.06 r^2 (\sin (2\pi x/L )+1) (\sin (\Omega _1 t)+\sin (\Omega _2 t))$. We select the forcing frequencies $\Omega _1$ and $\Omega _2$ in resonance with the first two natural frequencies $\omega _1\approx 7.13$ and $\omega _2 \approx 19$

The results depicted in Fig. 6 arise from two incommensurate frequencies. Our Theorem 3.1, however, guarantees the existence of a quasi-periodic steady-state response for any finite number of incommensurate frequencies. To illustrate the applicability of Theorem 3.1 in the case of more than two incommensurate forcing frequencies, we consider the excitation

$$\begin{aligned} f(x,t,\alpha )=0.05r^2(\sin (2\pi x /L)+1) \sum _{k=1}^3 \sin ( \gamma \omega _k t) \nonumber \\ \end{aligned}$$

(27)

where $\omega _k$ denote the eigenfrequencies of the discretized beam (23). For $\gamma$ close to one, the forcing (27) is in resonance with the first three eigenfrequencies. As previously, Theorem 3.1 guarantees the existence of a quasi-periodic steady-state response also for the forcing (27). Once again, we use the numerical package proposed by Jain et al. [35] and compute a quasi-periodic steady-state response. While the package handles two-dimensional tori fast and efficiently, its memory requirements become challenging and computation times increase significantly for three incommensurate frequencies.

We depict the maximal displacement of the arising quasi-periodic steady-state response of the discretized beam (23) for the forcing (27) in resonance with the first three eigenfrequencies in Fig. 7. Moreover, we include a solution by direct time integration with Matlab’s ode45 algorithm serving as a benchmark solution, which we initialize on the computed quasi-periodic orbit at $t=0$. While the maximal vibration amplitude of the nonlinear response agrees well with the benchmark solution, the linear response differs significantly. Thus, a nonlinear analysis of system (23) is essential to accurately predict the response amplitudes.

Fig. 7

Quasi-periodic steady-state responses of system (23) with three incommensurate base frequencies ($K=3$). We consider system (23) with six degrees-of-freedom, non-dimensional parameters $\mu =0.05$, $r=0.01$ and $L=1$ and select the forcing (27) to be in resonance with the first three natural frequencies

5 Conclusions

We have presented a criterion guaranteeing the existence of a quasi-periodic response for wide class of externally driven multi-degree-of-freedom vibratory systems. Our Theorem 3.1 guarantees the existence of a quasi-periodic orbit for arbitrary large forcing and response amplitudes, whereby it overcomes the major shortcoming of competing perturbation results. Thus, it can provide a priori justification for formal perturbation methods or numerical methods such as harmonic balance. Thereby, the results of such heuristic approaches become valid and computational resources can be efficiently employed.

Our criterion requires the damping to act on all coordinates, the stiffness terms to be derived from a potential and satisfy a growths conditions far away from the origin. These conditions are similar to our results in the periodic case [8] except for the growth condition (C4) which is stricter compared to the sign condition in the periodic case. Moreover, the nonlinear terms are required to be globally Lipschitz, which is generally satisfied if Eq. (1) accurately model a physical system (cf. Remark 3.3). We also cover the case of discontinuous external forcing, such as square waves or saw-tooth functions (cf. Theorem 3.3).

We utilize our results to revisit a chain of oscillators investigated by Breunung and Haller [7] and a slender beam model proposed by Nayfeh and Mook [49]. Both systems satisfy the conditions of our Theorem 3.1 and hence an approximation of the solution in a Fourier series is justified. We compute the arising steady-state vibrations with the numerical package proposed by Jain et al. [35]. Moreover, we consider a complex loading scenario, where the vibrations are excited by the natural roughness of a road. In this scenario, quasi-periodic functions arise naturally and our Theorem 3.1 justifies subsequent computations with the harmonic balance procedure.

We have limited our discussion to position depending nonlinearities, since these are customary in the vibrations literature. For more complex damping forces or oscillatory systems derived from Lagrangian with position dependent mass matrix arising in, e.g., robotics, an extension to account for velocity dependent nonlinearities is desirable.

After computing a steady-state response, it is important to assess its stability, since only stable solutions are observable. Numerical calculation of the monodromy matrix and calculating its eigenvalues (often referred as Floquet theory) is a well-established and universal procedure to assess the stability of periodic orbits. To the best of our knowledge such a procedure is absent for quasi-periodic orbits.

Furthermore, we have focused on quasi-periodic solutions, since these type of vibrations have been reported for a variety of mechanical and even more general systems (cf. Introduction 1). From a theoretical perspective, an extension of our results to the case of almost-periodic or bounded solutions seems tempting.

Appendices

A Existence results applied to vibratory systems

In this section, we examine known results guaranteeing the existence of quasi-periodic solutions. Thereby, we demonstrate that the available existence results are inapplicable in a structural dynamics context. We differ between Dafermos’ results [18] for first-order systems and the results of Bolt et al. [4] covering second-order systems. We show that both results are inapplicable to the simple single-degree-of-freedom oscillator in the form

$$\begin{aligned} \ddot{x}+c\dot{x}+k x=f(t). \end{aligned}$$

(28)

1.1 A.1 First-order systems

Dafermos [18] applies his abstract result to the equation

$$\begin{aligned} \dot{\mathbf {y}}+\mathbf {g}(\mathbf {y})=\mathbf {f}(t),\qquad \mathbf {y}\in \mathbb {R}^{N}, \end{aligned}$$

(29)

where we restrict our attention to N-dimensional Euclidean spaces. Originally, Dafermos [18] considers more abstract Hilbert spaces. He proves the existence of an weak solution to Eq. (29) which is unique and almost-periodic, if there exists a positive constant $\alpha >0$ such that

$$\begin{aligned} \langle \mathbf {g}(\mathbf {y}) -\mathbf {g}(\mathbf {z}), \mathbf {y}-\mathbf {z} \rangle > \alpha | \mathbf {y}-\mathbf {z} |^2, \qquad \forall ~\mathbf {y},\mathbf {z}\in \mathbb {R}^{N},\nonumber \\ \end{aligned}$$

(30)

holds. We evaluate condition (30) for the linear oscillator (28) reformulated in the form of Eq. (29) and obtain

$$\begin{aligned}&\left[ w_1,w_2 \right] \begin{bmatrix} 0 &{} -1 \\ k &{} c \end{bmatrix} \begin{bmatrix} w_1\\ w_2 \end{bmatrix}\nonumber \\&\quad = (k-1 )w_1w_2+cw_2^2 \overset{!}{>} \alpha (w_1^2+w_2^2) \end{aligned}$$

(31)

where we have set $y_1-z_1=:w_1$ and $y_2-z_2=:w_2$. Considering the case $w_2=0$, Eq. (31) cannot be satisfied for any $\alpha >0$ and $w_1 \ne 0$. Hence, Dafermos’ results on first-order systems is not relevant in the structural dynamics context.

1.2 A.2 Second-order systems

Extending earlier work of Berger and Chen [3], Bolt et al. [4] study systems of the form

$$\begin{aligned} \ddot{\mathbf {x}}+\left[ b(t)\mathbf {I}+\mathbf {B}(t)\right] \dot{\mathbf {x}}-\mathbf {F}(\mathbf {x},t)=\mathbf {f}(t), \end{aligned}$$

(32)

where the time dependence of all coefficients is continuous and bounded or almost-periodic. Besides technical assumptions on the coefficients in Eq. (32), the main condition of Bolt et al. [4] is requirement that there exists a positive constant $\alpha >0$ such that

$$\begin{aligned}&\langle \mathbf {F}(\mathbf {y},t)-\mathbf {F}(\mathbf {x},t)-\frac{1}{4}\mathbf {B}(t)\mathbf {B}(t)^{\top } (\mathbf {y}-\mathbf {x}) , \mathbf {y}-\mathbf {x}\rangle \nonumber \\&\quad > \alpha |\mathbf {y}-\mathbf {x}|^2,\qquad \mathbf {y},\mathbf {x}\in \mathbb {R}^{N},~~t\in \mathbb {R}, \end{aligned}$$

(33)

holds. While their result appears to be very general and also guarantees a unique bounded solution, it is inapplicable in the structural dynamics context. This is due to the negative sign in front of the nonlinearity $\mathbf {F}(\mathbf {x},t)$ in Eq. (32). For the linear oscillator (28) condition (33) requires

$$\begin{aligned} - k |\mathbf {y}-\mathbf {x}|^2>\alpha |\mathbf {y}-\mathbf {x}|^2, \qquad \mathbf {y},\mathbf {x}\in \mathbb {R}^{N},\qquad \alpha >0, \nonumber \\ \end{aligned}$$

(34)

where we have set $\mathbf {B}(t)=0$ and $\mathbf {b}(t)=c$. Equation (34) clearly holds only if the stiffness k is negative. The example considered by Bolt et al. [4] (gyroscopic stabilization) falls exactly in this class. In the structural dynamics context, however, stiffness matrices are commonly positive definite. Hence, the results of Bolt et al. [4] are insignificant for oscillatory systems.

For the linear oscillator (28) one can also absorb the damping c into the matrix $\mathbf {B}(t)$. Then, Eq. (34) would change and condition (33) requires the linear oscillator (28) to be either overdamped or the stiffness k to be negative. Again, both cases are uncommon in structural engineering.

B Non-existence of a quasi-periodic solution to the undamped-linear oscillator (4)

In the following, we show that for any incommensurate frequency basis $\varvec{\Omega }$ with at least two frequencies (i.e., $K \ge 2$) there exists a forcing $f(\varvec{\phi }(t))$ such that no quasi-periodic response to system (4) exists. First, we assume resonant forcing, i.e.,

$$\begin{aligned} | \langle \varvec{\kappa }^*,\varvec{\Omega }\rangle | = \omega _0,\qquad \text {for some } \varvec{\kappa }^* \in \mathbb {Z}^K, \end{aligned}$$

(35)

holds. Then, for the periodic forcing $f(t)=\cos ( \langle \varvec{\kappa }^*,\varvec{\Omega } \rangle t)$ system (4) is the undamped harmonic oscillator forced at resonance. Since all solutions of the undamped harmonic oscillator forced at resonance are unbounded, no quasi-periodic solution exists.

Next, we focus on the non-resonant case, i.e.,

$$\begin{aligned} |\langle \varvec{\kappa },\varvec{\Omega }\rangle | \ne \omega _0,\qquad \varvec{\kappa } \in \mathbb {Z}^K-\{0\}, \end{aligned}$$

(36)

holds and construct a forcing such that no quasi-periodic solution to Eq. (4) exists. To this end, we consider the forcing

$$\begin{aligned} f(\varvec{\phi })=\sum _{n=1}^{\infty } \frac{1}{n^2}\cos (\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle t), \qquad \varvec{\kappa }_n \in \mathbb {Z}^2, \end{aligned}$$

(37)

which only depends on the first two frequencies of the vector $\varvec{\Omega }$. The forcing (37) is bounded and continuous. Assuming the existence of a quasi-periodic solution $q^*$ to Eq. (4) we utilize the linearity of system (4) and obtain a steady-state response for every summand of the forcing individually, i.e.,

$$\begin{aligned} q^*=\sum _{n=1}^{\infty }q^*_n,\qquad \ddot{q}^*_n+\omega _0^2 q^*_n= \frac{1}{n^2}\cos (\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle t), \end{aligned}$$

(38)

which yields

$$\begin{aligned} q^*_n= & {} \frac{1}{n^2 (\omega _0^2-\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle ^2 )} \cos (\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle t) \nonumber \\= & {} \frac{1}{n^2 (\omega _0+\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle ) (\omega _0-\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle ) } \cos (\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle t) .\nonumber \\ \end{aligned}$$

(39)

Then, by superposition the assumed steady-state response of system (4) is given by

$$\begin{aligned} q^*(t)= & {} \sum _{n=1}^{\infty } \frac{1}{n^2 (\omega _0+\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle ) (\omega _0-\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle ) } \nonumber \\&\cos (\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle t). \end{aligned}$$

(40)

At the time $t=0$ the displacement $q^*$ of the assumed quasi-periodic solution is given by

$$\begin{aligned} |q^*(0)|=\sum _{n=1}^{\infty } \frac{1}{n^2 |\omega _0+\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle | |\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle -\omega _0| }. \end{aligned}$$

(41)

In the following, we obtain a lower bound on Eq. (41). To this end, we derive an upper bound onto the denominator of (41) and rewrite the last part of the denominator as

$$\begin{aligned}&|\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle -\omega _0|\nonumber \\&\quad = |\Omega _2| \left| \kappa _1^n \frac{\Omega _1}{|\Omega _2|}+\kappa _2^n {{\,\mathrm{sign}\,}}(\Omega _2) -\frac{\omega _0}{|\Omega _2|}\right| , \end{aligned}$$

(42)

where the integers $\kappa _1^n$ and $\kappa _2^n$ denote the first, respectively, second entry of the vector $\varvec{\kappa }_n=\left[ \kappa _1^n,\kappa _2^n,0,\dots \right]$. We use the following Theorem by Minkowski to establish an upper bound onto Eq. (42):

Theorem B.1

For any irrational number $\theta$ and any $\alpha \ne m \theta + n$ for all integers n and m, there are infinitely many integers p such that

$$\begin{aligned} |p| \min _{l\in \mathbb {Z}}|p \theta -\alpha -l| \le \frac{1}{4}, \end{aligned}$$

(43)

holds.

Proof

For a proof of the above theorem, we refer to Cassels [12] (Theorem IIA p. 48). $\square$

To show that Theorem (B.1) applies to Eq. (42), we note that the fraction $\theta =\Omega _1/|\Omega _2|$ is irrational, since $\varvec{\Omega }$ is incommensurate. Moreover, the non-resonance (36) yields

$$\begin{aligned}&\omega _0 \ne | \kappa _1 \Omega _1+\kappa _2\Omega _2| \quad \Leftrightarrow \quad \left| \kappa _1 \frac{\Omega _1}{|\Omega _2|}+ \kappa _2 {{\,\mathrm{sign}\,}}(\Omega _2) \right| \nonumber \\&\quad \ne \frac{\omega _0}{|\Omega _2|} =: \alpha ,\qquad \text {for all}~~\kappa _1,\kappa _2\in \mathbb {Z}, \end{aligned}$$

(44)

which implies that the second condition of Theorem (B.1) is satisfied. Equation (43) holds for infinitely many integers. Hence, for every $n=1,2,\ldots$ we can find some $|p_n|>n$ such that Eq. (43) holds. We utilize this observation by setting $\kappa _1^n=p_n$ in Eq. (42). Furthermore, we note that $\min _{l\in \mathbb {Z}}|p \theta -\alpha -l|$ in Eq. (43) returns the distance of the irrational number $p \theta -\alpha$ to the integer l closest to $p \theta -\alpha$. We select $\kappa _2^n$ such that ${{\,\mathrm{sign}\,}}(\Omega _2) \kappa _2^n$ (cf. Eq. (42)) is exactly this integer, i.e.,

$$\begin{aligned} \kappa _2^n \in \left\{ \kappa _2^n\in \mathbb {Z}~|~\min _{l\in \mathbb {Z}}|p_n \theta -\alpha -l|=|p_n \theta -\alpha + {{\,\mathrm{sign}\,}}(\Omega _2) \kappa _2^n| \right\} .\nonumber \\ \end{aligned}$$

(45)

Thus, for Eq. (42) we obtain

$$\begin{aligned} \begin{aligned}&|\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle -\omega _0|\\&\quad = |\Omega _2| \left| \kappa _1^n \frac{\Omega _1}{|\Omega _2|}+\kappa _2^n {{\,\mathrm{sign}\,}}(\Omega _2) -\frac{\omega _0}{|\Omega _2|} \right| \\&\quad = |\Omega _2| \left| p_n \theta -\alpha +\kappa _2^n{{\,\mathrm{sign}\,}}(\Omega _2) \right| \\&\quad = |\Omega _2| \min _{l\in \mathbb {Z}} \left| p_n \theta -\alpha -l \right| \\&\quad \le \frac{|\Omega _2|}{4|p_n|}\le \frac{|\Omega _2|}{4n},\qquad n=1,2,\ldots , \end{aligned}\nonumber \\ \end{aligned}$$

(46)

where we have used Eq. (45) and the assertion of Theorem B.1. We proceed by deriving an upper bound onto the first part of the denominator of Eq. (41) and obtain

$$\begin{aligned} |\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle +\omega _0|&\le 2|\omega _0|+ |\langle \varvec{\kappa }_n,\varvec{\Omega }\rangle -\omega _0|\nonumber \\&\le 2|\omega _0|+ \frac{|\Omega _2|}{4n}\le 2|\omega _0|+ |\Omega _2| ,\nonumber \\&\qquad n=1,2,\ldots , \end{aligned}$$

(47)

where we have used the upper bound (46). The bounds (46) and (47) imply for assumed steady-state response evaluated at $t=0$ (cf. Eq. (41))

$$\begin{aligned} |q^*(0)|\ge & {} \sum _{n=1}^{\infty } \frac{1}{n^2 ( 2|\omega _0|+|\Omega _2|) \frac{|\Omega _2|}{4n} } \nonumber \\\ge & {} \frac{4}{(2|\omega _0|+|\Omega _2|) |\Omega _2|}\sum _{n=1}^{\infty } \frac{1}{n }, \end{aligned}$$

(48)

which is diverges. Therefore, the assumed quasi-periodic response for system (4) does not exist and the claim of Fact 2.1 is proven.

C Proof of the main theorem

We base result guaranteeing the existence of a quasi-periodic solutions to system (1), on the following fixed point theorem by Schäfer:

Theorem C.1

Let X be a normed space and $\mathcal {A}$ a continuous mapping of X into X which is compact on each bounded subset $U\in X$. Then, either

• (i) the equation

  $$\begin{aligned} \mathbf {x}=\kappa \mathcal {A}(\mathbf {x}), \end{aligned}$$

  (49)

  has a solution for $\kappa =1$, or

• (ii) the set of all solutions $\mathbf {x}$ to Eq. (49) for $0<\kappa <1$ is unbounded.

Proof

Smart [59] states and proves the above theorem. We also refer to the original proof by Schäfer [56]. $\square$

Remark C.1

Fixed point theorems such as Banach’s fixed point theorem, Brouwer’s fixed point theorem or Schauder’s fixed point theorem are commonly formulated for complete metric spaces (cf. Bobylev et al. [5], Precup [51] or Smart [59]). Schäfer’s fixed point theorem C.1, however, does not require the underlying space X to be complete. As Smart [59] details, the requirement on $\mathcal {A}$ to map every bounded set into a compact set implies the existence of a complete metric space.

The key observation is to consider the closure of the space A(X) instead of X itself. Indeed, assuming that $\mathcal {A}(X)$ is compact implies that the closure of $\mathcal {A}(X)$ (i.e., $\overline{\mathcal {A} (X)}$) is compact. Moreover, assuming that the operator $\mathcal {A}$ maps X onto X, $\mathcal {A}$ maps $\overline{\mathcal {A}( X)}$ onto $\overline{\mathcal {A} (X)}$ by construction. Hence, we obtain the compact and therefore complete metric space $\overline{\mathcal {A}( X)}$ and the operator $\mathcal {A}$ mapping $\overline{\mathcal {A}( X)}$ to itself.

Having constructed an underlying complete metric space $\overline{\mathcal {A}( X)}$, standard versions of either Banach’s fixed point theorem ($\mathcal {A}$ is a contraction), Brouwer’s fixed point theorem ($\overline{\mathcal {A}( X)} \subset \mathbb {R}^N$) or Schauder’s fixed point theorem (cf. Smart [59]) formulated in complete spaces can subsequently guarantee the existence of a fixed point. An extensive treatment of continuation theorems of fixed points in normed spaces (not necessarily complete) can be found in Gaines and Mawhin [44] and Mawhin [25].

Before proving Theorem 3.1, we establish some preliminary results. First, we define the relevant metric spaces (cf. section C.1) and we rewrite the mechanical system (1) in the operator form (49) (cf. section C.2). Subsequently, we derive the relevant bounds to show that the second case of Schäfer’s theorem does not hold. Thus, by the virtue of Theorem C.1 Eq. (1) has a solution.

1.1 C.1 The relevant function spaces

We denote the set of all continuous quasi-periodic functions (cf. Definition 2.1) with $C(\mathbb {T}^K)$. The set of quasi-periodic functions with a continuous quasi-periodic time derivative is denoted by $C^1(\mathbb {T}^K)$. Defining the norm

$$\begin{aligned}&||\mathbf {x}(\varvec{\phi }(t))||_{C^0}=\sup _{ \varvec{\phi } \in \mathbb {T}^K }\left| \mathbf {x}( \varvec{\phi } )\right| ,\nonumber \\&||\mathbf {x}( \varvec{\phi }(t))||_{C^1}=|| \mathbf {x}(\varvec{\Omega } t)||_{C^0}+ \left\Vert \dot{ \mathbf {x}}(\varvec{\Omega } t)\right\Vert _{C^0}, \end{aligned}$$

(50)

the set $C^1(\mathbb {T}^K)$ is a Banach space (cf. Corduneanu [15]), which we will denote by $B(C^1(\mathbb {T}^K),||\cdot ||_{C^1})$. Analogously, we define the Banach space $B(C(\mathbb {T}^K),||\cdot ||_{C^0})$, which can also be introduced by considering trigonometric polynomials in the form

$$\begin{aligned} \mathcal {T}_L:=\sum _{l=1 }^{L} \mathbf {x}^{\varvec{\kappa }_l} {\mathrm{e}}^{ i \langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t}, \qquad \mathbf {x}^{ \varvec{\kappa }_l}\in \mathbb {C}^{N}, \varvec{\kappa }_l \in \mathbb {Z}^K. \end{aligned}$$

(51)

Then, $B(C(\mathbb {T}^K),||\cdot ||_{C^0})$ is the closure with respect to the $C^0$-norm of all trigonometric polynomials of the form (51) (cf. Corduneanu [15]). Hence, $\mathbf {x}$ is an element of $B(C(\mathbb {T}^K),||\cdot ||_{C^0})$ if and only if it can be uniformly approximated by a series of trigonometric polynomials $\mathcal {T}_L$ , i.e., there exists trigonometric polynomials of the form (51) such that

$$\begin{aligned} \mathbf {x}( \varvec{\phi }(t))&=\lim _{L\rightarrow \infty } \mathcal {T}_L=\lim _{L\rightarrow \infty } \sum _{l=1}^{L} \mathbf {x}^{\varvec{\kappa }_l} {\mathrm{e}}^{ i \langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t},\nonumber \\&\qquad \varvec{\kappa }_l \in \mathbb {Z}^K, \end{aligned}$$

(52)

holds.

Moreover, we introduce the map

$$\begin{aligned}&\mathbf {x} \mapsto \left( \frac{1}{(2\pi )^K} \int _{\mathbb {T}^K} \mathbf {x}^{\top }(\varvec{\phi })\mathbf {x}(\varvec{\phi })~d \varvec{\phi }\right) ^{\frac{1}{2}}\nonumber \\&\quad = \left( \lim _{T\rightarrow \infty } \frac{1}{2T} \int _{-T}^{T} \mathbf {x}^{\top }(\varvec{\phi }(t))\mathbf {x}(\varvec{\phi }(t))~{\mathrm{d}}t \right) ^{\frac{1}{2}}, \end{aligned}$$

(53)

which is a norm on the set $C(\mathbb {T}^K)$ (cf. Corduneanu [15]). We will denote the norm (53) by $||\cdot ||_{L_2}$, which we extend by including the first time derivative as follows

$$\begin{aligned} ||\mathbf {x}( \varvec{\phi }(t) )||_{L^1_2}= ||\mathbf {x}( \varvec{\phi }(t))||_{L_2}+ \left\Vert \dot{ \mathbf {x}}( \varvec{\phi }(t))\right\Vert _{L_2}. \end{aligned}$$

(54)

Then, the set $C^1(\mathbb {T}^K)$ together with the $L^1_2$-norm is a normed space which we denote by $N(C^1(\mathbb {T}^K),||\cdot ||_{L_2^1})$. We emphasize that $N(C^1(\mathbb {T}^K),||\cdot ||_{L_2^1})$ is not complete and hence not Banach with respect to the $L^1_2$-norm.

Extending $C^1(\mathbb {T}^K)$ by all quasi-periodic functions with finite $L_2$-norm and a time derivative bounded in the $L_2$-norm, we obtain the set $L_2^1(\mathbb {T}^K)$. We note that $L_2^1(\mathbb {T}^K)$ together with the $L_2^1$-norm (54) is a Banach space. Similar to the Banach space $B(C(\mathbb {T}^K),||\cdot ||_{C^0})$, the space $B(L_2(\mathbb {T}^K),||\cdot ||_{L_2})$ can also be introduced by considering the closure of the trigonometric polynomials (51) with respect to the $L_2$-norm. Therefore, any function $\mathbf {x}\in L_2(\mathbb {T}^K)$ can be uniformly (in the $L_2$-norm) approximated by an infinite series of trigonometric functions of the form (51). In summary, all functions in either $C^1(\mathbb {T}^K)$ or $L_2^1(\mathbb {T}^K)$ can be represented by an infinite Fourier series.

Schäfer’s Theorem C.1 requires the operator $\mathcal {A}$ to be compact on bounded sets. Before establishing compactness of a specific operator arising for the mechanical system (1), we clarify compactness of bounded subsets of the metric spaces $B(L^1_2(\mathbb {T}^K),||\cdot ||_{L^1_2})$ and $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_2})$. We collect our first result in the following proposition:

Proposition C.1

The closure of any bounded set $U \subset B(L^1_2(\mathbb {T}^K),||\cdot ||_{L_2^1})$ is compact.

Proof

We base the proof of the above Proposition on the following theorem

Theorem C.2

(Fréchet–Kolmogorov) A subset U of $L_2(\mathbb {T}^K)$ is relatively compact if and only if the following conditions are satisfied

• Y is bounded, i.e., there exists a constant C such that

  $$\begin{aligned} \left\Vert \mathbf {u}(\varvec{\phi })\right\Vert _{L_2}<C, \end{aligned}$$

  (55)

  holds for all $\mathbf {u}\in U$.

• for every $\varepsilon >0$ there exists a $\delta >0$ such that

  $$\begin{aligned} \left\Vert \mathbf {u}(\varvec{\phi }+\varvec{\delta })-\mathbf {u}(\varvec{\phi })\right\Vert _{L_2}<\varepsilon , \end{aligned}$$

  (56)

  holds for all $\mathbf {u} \in U$, whenever $|\varvec{\delta }|<\delta$.

Proof

For a proof of the above theorem, we refer to Precup [51] or Brezis [9]. $\square$

We show that the above theorem applies to any bounded set $U \subset B(L^1_2(\mathbb {T}^K),||\cdot ||_{L^1_2})$. Since U is bounded in the $L_2$ norm by assumption, for any U there exists some $C_U>0$ such that

$$\begin{aligned} \left\Vert \mathbf {x}(\varvec{\phi })\right\Vert _{L_2}\le \left\Vert \mathbf {x}(\varvec{\phi })\right\Vert _{L^1_2}\le C_U, \end{aligned}$$

(57)

holds. Equation (57) implies that condition (55) holds. Moreover, we note that any function $\mathbf {x}\in L_2(\mathbb {T}^K)$ satisfies Parseval’s identity

$$\begin{aligned} ||\mathbf {x}(\varvec{\phi })||^2_{L_2}= & {} ||\lim _{L\rightarrow \infty } \sum _{l=1}^{L} \mathbf {x}^{\varvec{\kappa }_l}{\mathrm{e}}^{\mathrm {i} \langle \varvec{\kappa },\varvec{\phi } \rangle }||^2_{L_2}\nonumber \\= & {} \lim _{L\rightarrow \infty } \sum _{l=1}^{L} |\mathbf {x}^{\varvec{\kappa }_l}|^2. \end{aligned}$$

(58)

Now, we claim that the $L_2$-norm along the orbit $\varvec{\phi }=\varvec{\Omega } t$ on the tours $\mathbb {T}^K$ is the same as $L_2$-norm along any other orbit of the form $\tilde{\varvec{\phi }}=\tilde{\varvec{\Omega }} t$ if $\tilde{\varvec{\Omega }}\in \mathbb {R}^K$ is incommensurate. Indeed, we define

$$\begin{aligned} \mathbf {x}(\varvec{\phi }(t))&=\lim _{L\rightarrow \infty } \sum _{l=1}^{L} \mathbf {x}^{\varvec{\kappa }_l}{\mathrm{e}}^{\mathrm {i} \langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} ,\nonumber \\&\Rightarrow ~~ \mathbf {x}(\tilde{\varvec{\phi }}(t)):= \lim _{L\rightarrow \infty } \sum _{l=1}^{L} \mathbf {x}^{\varvec{\kappa }_l}{\mathrm{e}}^{\mathrm {i} \langle \varvec{\kappa }_l,\tilde{\varvec{\Omega }}\rangle t}. \end{aligned}$$

(59)

Since $\tilde{\varvec{\phi }}$ is defined on a K-dimensional torus, Parseval’s identity holds and we obtain

$$\begin{aligned} ||\mathbf {x}(\tilde{\varvec{\phi }})||^2_{L_2}= \lim _{L\rightarrow \infty } \sum _{l=1}^{L} |\mathbf {x}^{\varvec{\kappa }_l}|^2= ||\mathbf {x}(\varvec{\phi })||^2_{L_2}. \end{aligned}$$

(60)

For any function $\mathbf {x}(\varvec{\phi })\in B(L^1_2(\mathbb {T}^K),||\cdot ||_{L^1_2})$, the identity (60) holds also for the velocity $\dot{\mathbf {x}}(\varvec{\phi })$. This observation implies

$$\begin{aligned} \left\Vert \frac{{\mathrm{d}}}{{\mathrm{d}}t}\mathbf {x}( \varvec{\phi }(t))\right\Vert _{L_2}= & {} \left\Vert \frac{{\mathrm{d}}}{{\mathrm{d}}t}\mathbf {x}( \tilde{\varvec{\phi }} (t))\right\Vert _{L_2}\nonumber \\= & {} \left\Vert \frac{\partial }{\partial \varvec{\phi }} \mathbf {x}( \tilde{\varvec{\phi }}(t) ) \tilde{\varvec{\Omega }}\right\Vert _{L_2}, \end{aligned}$$

(61)

where we have used the chain rule. The last equality in Eq. (61) implies that the directional derivative of $\mathbf {x}$ in the direction $\tilde{\varvec{\Omega }}$ is bounded in the $L_2$-norm. We rely on this observation to verify condition (56) of Theorem C.2. We permute $\varvec{\Omega }$ to generate K linearly independent vectors of the form

$$\begin{aligned}&\varvec{\Omega }_1=\varvec{\Omega },~~ \varvec{\Omega }_2=\left[ \Omega _2, \Omega _{3},\ldots ,\Omega _{K},\Omega _1 \right] ^{\top },\nonumber \\&~~\varvec{\Omega }_k=\left[ \Omega _k, \Omega _{k+1},\ldots ,\Omega _{K},\Omega _1,\Omega _2,\ldots ,\Omega _{k-1} \right] ^{\top },~~\nonumber \\&\qquad 2<k\le K, \end{aligned}$$

(62)

and collect the vectors $\varvec{\Omega }_k$ as columns of the matrix $\varvec{\Omega }_{\varvec{\Omega }}:=[\varvec{\Omega }_1,\varvec{\Omega }_2,\ldots ,\varvec{\Omega }_K]$. By construction, the vectors $\varvec{\Omega }_k$ are linearly independent and hence the matrix $\varvec{\Omega }_{\varvec{\Omega }}$ is invertible, i.e., $||\varvec{\Omega }_{\varvec{\Omega }}^{-1}||<C_{\varvec{\Omega }}$ holds for some finite constant $C_{\varvec{\Omega }}>0$. We observe that the vector $\varvec{\delta }$ in condition (56) can be represented as a linear combination of the basis vectors $\varvec{\Omega }_k$, i.e.,

$$\begin{aligned}&\varvec{\eta }:= \varvec{\Omega }_{\varvec{\Omega }}^{-1} \varvec{\delta },~~\Rightarrow ~~\varvec{\delta }=\varvec{\Omega }_{\varvec{\Omega }}\varvec{\eta } =\sum _{k=1}^K\eta _k \varvec{\Omega }_k,\nonumber \\&\qquad |\eta _k|\le C_{\varvec{\Omega }}|\varvec{\delta }| . \end{aligned}$$

(63)

Equation (63) also includes an upper bound onto the entries $\eta _k$ of the vector $\varvec{\eta }$. We substitute Eq. (63) into condition (56) and obtain

$$\begin{aligned} \begin{aligned}&\left\Vert \mathbf {x}(\varvec{\phi } +\varvec{\delta })-\mathbf {x}(\varvec{\phi })\right\Vert _{L_2}\\&\quad =\left\Vert \mathbf {x}\left( \varvec{\phi } +\sum _{k=1}^K\eta _k \varvec{\Omega }_k\right) -\mathbf {x}(\varvec{\phi })\right\Vert _{L_2}\\&\quad \le \sum _{j=1}^K \left\Vert \mathbf {x}\left( \varvec{\phi } +\sum _{k=1}^j\eta _k \varvec{\Omega }_k\right) -\mathbf {x}\left( \varvec{\phi }+\sum _{k=1}^{j-1}\eta _k \varvec{\Omega }_k\right) \right\Vert _{L_2}, \end{aligned}\nonumber \\ \end{aligned}$$

(64)

where we have used the Cauchy–Schwarz inequality. Introducing the notation $\varvec{\phi }_j(t):=\varvec{\Omega }_k t$ and $\varvec{\phi }_0(j):=\sum _{k=1}^{j-1}\eta _k \varvec{\Omega }_k$ for each summand in Eq. (64), we obtain

$$\begin{aligned}&\left\Vert \mathbf {x}\left( \varvec{\phi }(t) +\sum _{k=1}^j\eta _k \varvec{\Omega }_k\right) -\mathbf {x}\left( \varvec{\phi }(t)+\sum _{k=1}^{j-1}\eta _k \varvec{\Omega }_k\right) \right\Vert _{L_2}\nonumber \\&\quad = \left\Vert \mathbf {x}\left( \varvec{\phi }_j(t) + \eta _j \varvec{\Omega }_j +\varvec{\phi }_0(j)\right) -\mathbf {x}\left( \varvec{\phi }_j(t)+\varvec{\phi }_0(j)\right) \right\Vert _{L_2} \nonumber \\&\quad = \left\Vert \int _0^{\eta _j} \frac{d}{ds}\mathbf {x}\left( \varvec{\phi }_j(t)+ s \varvec{\Omega }_j +\varvec{\phi }_0(j)\right) ~ds \right\Vert _{L_2} \nonumber \\&\quad \le \left\Vert |\eta _j| \sup _{-|\eta _j| \le s \le |\eta _j| } \left| \frac{\partial }{\partial \varvec{\phi }} \mathbf {x}\left( \varvec{\phi }_j(t)+ s \varvec{\Omega }_j + \varvec{\phi }_0(j)\right) \varvec{\Omega }_j \right| ~\right\Vert _{L_2} \nonumber \\&\quad \le |\eta _j| \sup _{\varvec{\varphi }\in \mathbb {T}^K } \left\Vert \dot{\mathbf {x}}\left( \varvec{\phi }_j(t)+\varvec{\varphi } \right) \right\Vert _{L_2}, \end{aligned}$$

(65)

where we have use the identity (60) for the quasi-periodic function $\mathbf {y}(\varvec{\phi }(t)):=\mathbf {x}\left( \varvec{\phi }(t)+ \eta _j \varvec{\Omega }_j +\varvec{\phi }_0(j)\right) -\mathbf {x}\left( \varvec{\phi }(t)+\varvec{\phi }_0(j)\right)$, i.e., $||\mathbf {y}(\varvec{\phi }(t))||_{L_2}=||\mathbf {y}(\varvec{\phi }_j(t))||_{L_2}$ holds. Since $L_2$-norm is independent of the initial angle $\varvec{\varphi }$, Eq. (65) is bounded by $C_{\varvec{\Omega }}|\varvec{\delta }|C_U$ where we have used Eqs. (57) and (63). Inserting this upper bound into Eq. (64), we obtain

$$\begin{aligned} \begin{aligned} \left\Vert \mathbf {x}(\varvec{\phi } +\varvec{\delta })-\mathbf {x}(\varvec{\phi })\right\Vert _{L_2}&\le KC_{\varvec{\Omega }}|\varvec{\delta }|C_U. \end{aligned} \end{aligned}$$

(66)

Selecting $\delta =\varepsilon /(KC_UC_{\varvec{\Omega }})$ for the second condition of Theorem C.2, Eq. (56) is satisfied. Hence, the closure of the bounded set $U \subset B(L^1_2(\mathbb {T}^K),||\cdot ||_{L^1_2})$ is compact.$\square$

Following Proposition (C.1), we have the following Corollary

Corollary C.1

The closure of any bounded set $U \subset N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_2})$ is compact.

Proof

We have the inclusion $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_2}) \subset B(L_2^1(\mathbb {T}^K),||\cdot ||_{L^1_2})$. Thereby, the closure of any bounded set in $U\subset N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_2})$ is a closed subset of some bounded set $\tilde{U}\in B(L_2^1(\mathbb {T}^K),||\cdot ||_{L^1_2})$. By Proposition C.1$\tilde{U}$ is compact. Since a closed subset of a compact space is compact (cf. Lang [41]), $U \subset N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_2})$ is compact. $\square$

1.2 C.2 The operator $\mathcal {A}$

To identify the operator $\mathcal {A}$ of the homotopy (49), we rewrite the mechanical system (1) into the form (49). To this end, we note that condition (C4) implies that the continuous function $\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})$ is either positive or negative for $|\mathbf {q}|>r$. Depending on the sign of $\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})$ for large displacements, we define the following matrix

$$\begin{aligned} \mathbf {K}:= {\left\{ \begin{array}{ll} \mathbf {M},\qquad &{} \text {if~} \mathbf {q}^{\top }\mathbf {S}(\mathbf {q})> 0, \quad \forall ~|\mathbf {q}|>r, \\ -\mathbf {M},\qquad &{} \text {if~} \mathbf {q}^{\top }\mathbf {S}(\mathbf {q})< 0, \quad \forall ~ |\mathbf {q}|>r. \end{array}\right. } \end{aligned}$$

(67)

Then, we consider the following homotopy

$$\begin{aligned}&\mathbf {M}\ddot{\mathbf {q}}+ \mathbf {C} \dot{\mathbf {q}} +\mathbf {K}\mathbf {q}+\kappa ( \mathbf {S}(\mathbf {q}) -\mathbf {K} \mathbf {q})= \kappa \mathbf {f}(t) ,\qquad \nonumber \\&\qquad 0\le \kappa \le 1, \end{aligned}$$

(68)

which is equivalent to system (1) if $\kappa$ equals one. To transform the differential equation (68) into the operator form (49), we collect properties of the continuous stiffness terms into the following proposition:

Proposition C.2

Assume the stiffness terms $\mathbf {S}(\mathbf {q})$ are continuous. Then, $\mathbf {S}$ maps $C(\mathbb {T}^K)$ to $C(\mathbb {T}^K)$ continuously with respect to the $C^0$-norm.

Proof

By assumption $\mathbf {S}(\mathbf {q}(\varvec{\phi }))$ maps the torus $\mathbb {T}^K$ to $\mathbb {R}^N$ continuously, i.e., $\mathbf {S}: C(\mathbb {T}^K)\mapsto C(\mathbb {T}^K)$ holds. $\square$

We have the analogous statement for the $L_2$ case, if the global Lipschitz condition (C3) holds.

Proposition C.3

Assume that the stiffness terms $\mathbf {S}(\mathbf {q})$ satisfy condition (C3). Then, $\mathbf {S}$ maps $L_{2}(\mathbb {T}^K)$ to $L_{2}(\mathbb {T}^K)$ and is continuous with respect to the $L_2$-norm.

Proof

First, we note that $\mathbf {S}(\mathbf {q}(\varvec{\phi }))$ maps the torus $\mathbb {T}^K$ to $\mathbb {R}^N$, hence $\mathbf {S}(\mathbf {q}(\varvec{\phi }))$ is quasi-periodic with the same frequency base $\varvec{\Omega }$ as the coordinates $\mathbf {q}$. For the $L_2$-norm, we obtain

$$\begin{aligned}&\left\Vert \mathbf {S}(\mathbf {q}(\varvec{\phi }))\right\Vert _{L_2}^2\nonumber \\&\quad = \lim _{T\rightarrow \infty } \frac{1}{2T}\int _{-T}^{\mathrm{T}} |\mathbf {S}(\mathbf {q})|^2~{\mathrm{d}}t\nonumber \\&\quad =\lim _{T\rightarrow \infty } \frac{1}{2T}\int _{-T}^{\mathrm{T}} |\mathbf {S}(\mathbf {q})-\mathbf {S}(\mathbf {0})+\mathbf {S}(\mathbf {0})|^2~{\mathrm{d}}t\nonumber \\&\quad \le L^2 ||\mathbf {q}||^2_{L_2}+|\mathbf {S}(\mathbf {0})|^2, \end{aligned}$$

(69)

where we have used Eq. (7). For continuity, we select $||\mathbf {q}_1-\mathbf {q}_2||_{L_2}\le \varepsilon /L$ yielding

$$\begin{aligned}&\left\Vert \mathbf {S}(\mathbf {q}_1(\varvec{\phi }))-\mathbf {S}(\mathbf {q}_2(\varvec{\phi }))\right\Vert _{L_2}\nonumber \\&\qquad < L \left\Vert \mathbf {q}_1(\varvec{\phi })-\mathbf {q}_2(\varvec{\phi } )\right\Vert _{L_2}\le \varepsilon . \end{aligned}$$

(70)

Equation (70) implies that $\mathbf {S}(\mathbf {q}(\varvec{\phi }))$ is continuous for any $\mathbf {q}(\varvec{\phi })\in L_{2}(\mathbb {T}^K)$. This completes the proof of Proposition (C.3). $\square$

We apply Schäfer fixed point Theorem C.1 in the normed spaces $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ and $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$. In both spaces the coordinate $\mathbf {q}(\varvec{\Omega }t)$ can be represented as a trigonometric series with coefficients $\mathbf {q}^{\varvec{\kappa }_l}$. Then, Propositions C.3 and C.2 establish that $\mathbf {S}(\mathbf {q})$ can be expanded in an infinite trigonometric series of the form (51) with the same frequency base $\varvec{\Omega }$ as the coordinate $\mathbf {q}(\varvec{\Omega }t)$. We denote the coefficients of the trigonometric series approximating $\mathbf {S}$ evaluated along $\mathbf {q}(\varvec{\phi })$ by $\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q})$ and rewrite Eq. (68) as

$$\begin{aligned}&\lim _{L\rightarrow \infty }\sum _{l=1}^L \left[ -\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \mathbf {M}+ \mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle \mathbf {C} + \mathbf {K} \right] \nonumber \\&\qquad \mathbf {q}^{\varvec{\kappa }_l} {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t}= \kappa \lim _{L\rightarrow \infty }\sum _{l=1}^L \nonumber \\&\qquad \times \left( \mathbf {K}\mathbf {q}^{\varvec{\kappa }_l} -\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q}) + \mathbf {f}^{\varvec{\kappa }_l} \right) {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} . \end{aligned}$$

(71)

We introduce the matrices

$$\begin{aligned} \mathbf {H}(\varvec{\kappa }_l):= -\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2\mathbf {M}+ \mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle \mathbf {C} + \mathbf {K}, \end{aligned}$$

(72)

which are the well known linear transfer functions with the mass matrix as stiffness matrix (cf. Definition (67)). Due to the definition of the stiffness matrix (67), the matrices $\mathbf {H}(\varvec{\kappa }_l)$ are diagonalizable. To this end, we note that the positive definite mass matrix $\mathbf {M}$ has a positive definite square root $\mathbf {M}^{1/2}\mathbf {M}^{1/2} := \mathbf {M}$. Then, the product $\mathbf {M}^{-1/2}\mathbf {C}\mathbf {M}^{-1/2}$ is symmetric, which implies the existence of an orthogonal change of coordinates, such that

$$\begin{aligned}&\mathbf {D}:=\mathbf {T}^{\top }\mathbf {M}^{-1/2} \mathbf {C} \mathbf {M}^{-1/2} \mathbf {T}, \qquad D_{jl}=0, \qquad \nonumber \\&j,l=1,\ldots ,N,~~j\ne l, \quad \mathbf {T}\mathbf {T}^{\top }=\mathbf {I},\qquad ||\mathbf {T}||=||\mathbf {T}^{\top }||=1,\nonumber \\ \end{aligned}$$

(73)

holds. In Eq. (73) we have additionally normalized the transformation matrix $\mathbf {T}$ such that the norm of $\mathbf {T}$ and its transpose are one. We diagonalize the matrices $\mathbf {H}(\varvec{\kappa }_l)$ by left multiplying $\mathbf {T}^{\top }\mathbf {M}^{-1/2}$ and right multiplying $\mathbf {M}^{-1/2} \mathbf {T}$ and obtain

$$\begin{aligned} \begin{aligned} \tilde{\mathbf {H}}(\varvec{\kappa }_l)&:= \mathbf {T}^{\top } \mathbf {M}^{-1/2}\mathbf {H}(\varvec{\kappa }_l)\mathbf {M}^{-1/2} \mathbf {T} \\&= \mathbf {T}^{\top } \left( -\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \mathbf {I}+ \mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle \mathbf {M}^{-1/2} \mathbf {C}\mathbf {M}^{-1/2} \pm \mathbf {I} \right) \mathbf {T} \\&=-\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \mathbf {I} + \mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle \mathbf {D} \pm \mathbf {I}=:\tilde{\mathbf {H}}(\varvec{\kappa }_l), \end{aligned} \end{aligned}$$

(74)

where we have used the definitions (67) and (72). We denote the minimal entry of the diagonalized damping matrix by $D_{\min }:=\min _{1\le j\le N}(|\tilde{D}_{jj}|)>0$, which is greater than zero due to condition (C1). With this notation, we derive an upper bound onto the inverse of the diagonal matrix $\tilde{\mathbf {H}}(\varvec{\kappa }_l)$ by noting

$$\begin{aligned} \begin{aligned}&||(\tilde{\mathbf {H}} (\varvec{\kappa }_l))^{-1}||^2\\&\quad =\max _{1\le j\le N}\left( \frac{1}{(-\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \pm 1 )^2+ \langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2D_{jj}^2} \right) \\&\quad \le {\left\{ \begin{array}{ll} \frac{1}{(-\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \pm 1 )^2}< 4,&{} \text { for } 2\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2< 1 , \\ \frac{1}{\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 D_{\min }^2}< \frac{2}{ D_{\min }^2 },&{} \text { for } 2\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \ge 1, \end{array}\right. } \end{aligned}\nonumber \\ \end{aligned}$$

(75)

where we have differentiated between low frequencies $2\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2<1$ and higher frequencies. In summary, the inverse of the matrix $\tilde{ \mathbf {H}} (\varvec{\kappa }_l)$ is bounded from above by $\max (4,2/( D_{\min }^2))$. For the later purpose, we derive an upper bound onto the norm of $||\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle (\tilde{\mathbf {H}} (\varvec{\kappa }_l))^{-1}||$ by the following

$$\begin{aligned} \begin{aligned}&||\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle (\tilde{\mathbf {H}} (\varvec{\kappa }_l))^{-1}||^2&\\&\quad =\max _{1\le j\le N}\left( \frac{\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2}{(-\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \pm 1 )^2+ \langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2D_{jj}^2} \right) \\&\quad \le {\left\{ \begin{array}{ll} \frac{\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2}{(-\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \pm 1 )^2}< 2,&{} \text { for } 2\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2< 1 , \\ \frac{\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2}{\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 D_{\min }^2}< \frac{1}{ D_{\min }^2 },&{} \text { for } 2\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle ^2 \ge 1. \end{array}\right. } \end{aligned}\nonumber \\ \end{aligned}$$

(76)

The bound (75) implies that the inverse of the transfer functions $\mathbf {H}(\varvec{\kappa }_l)$ is well defined for any excitation frequency $\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle$, i.e., we obtain

$$\begin{aligned} \begin{aligned}&||\mathbf {H}^{-1}(\varvec{\kappa }_l)||^2=|| \mathbf {M}^{1/2} \mathbf {T} \mathbf {T}^{\top } \mathbf {M}^{-1/2} \mathbf {H}(\varvec{\kappa }_l)\\&\qquad \mathbf {M}^{-1/2} \mathbf {T} \mathbf {T}^{\top } \mathbf {M}^{1/2}|| \\&\quad \le || \mathbf {M}^{1/2}||^2 || \tilde{\mathbf {H}}(\varvec{\kappa }_l)||\\&\quad \le || \mathbf {M}^{1/2}||^2 \max \left( 4 ,\frac{2}{ D_{\min }^2}\right) =: h_1^2. \end{aligned} \end{aligned}$$

(77)

Similarly, for $||\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle (\mathbf {H} (\varvec{\kappa }_l))^{-1}||$ we obtain

$$\begin{aligned}&||\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle \mathbf {H}^{-1}(\varvec{\kappa }_l)||^2\le || \nonumber \\&\quad \mathbf {M}^{1/2}||^2 \sup \left( 2 ,\frac{1}{ D_{\min }^2}\right) =: h_2^2. \end{aligned}$$

(78)

Equation (77) implies that the inverse of $\mathbf {H}(\varvec{\kappa }_l)$ exists for all $\varvec{\kappa }_l\in \mathbb {Z}^K$, therefore we can rewrite Eq. (71) as

$$\begin{aligned} \mathbf {q}(\varvec{\Omega }t)= & {} \lim _{K\rightarrow \infty }\mathbf {q}^{\varvec{\kappa }_l}{\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} \nonumber \\= & {} \kappa \lim _{L\rightarrow \infty } \sum _{l=1}^L \mathbf {H}^{-1}(\varvec{\kappa }_l) \left[ \mathbf {K} \mathbf {q}^{\varvec{\kappa }_l} -\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q})+\mathbf {f}^{\varvec{\kappa }_l} \right] \nonumber \\&\times {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t}, \end{aligned}$$

(79)

which is in the form (49) by defining the operator

$$\begin{aligned} \mathcal {A}(\mathbf {q}):= & {} \lim _{L\rightarrow \infty } \sum _{l=1}^L \mathbf {H}^{-1}(\varvec{\kappa }_l) \left[ \mathbf {K} \mathbf {q}^{\varvec{\kappa }_l} -\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q})+\mathbf {f}^{\varvec{\kappa }_l} \right] \nonumber \\&\times {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t}. \end{aligned}$$

(80)

After identifying the operator $\mathcal {A}$, we establish that $\mathcal {A}$ satisfies the requirements of Schäfer’s theorem. To this end, we proceed by showing that the operator $\mathcal {A}$ indeed maps the space $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$, respectively, $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$. Moreover, we establish continuity in the $L_2^1$-norm and compactness on bounded subsets. By inspection the right-hand side of Eq. (80) can be written as a Fourier series with the base frequencies $\varvec{\Omega }$. Hence, the operators maps quasi-periodic functions to quasi-periodic functions.

For the normed space $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ we collect our results in the following lemma:

Lemma C.1

Assume that conditions (C1), (C3) and (C4) hold and the external forcing is quasi-periodic and continuous, i.e., $\mathbf {f}(t)\in C(\mathbb {T}^K)$. Then, the operator $\mathcal {A}$ (cf. Definition (80)) maps $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ continuously and is compact on any bounded set $U \subset N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$.

Proof

We derive the following bounds in the $C^0$-norm

$$\begin{aligned} \begin{aligned} \left\Vert \mathcal {A}(\mathbf {q})\right\Vert _{C^0}&= \left\| \lim _{K\rightarrow \infty } \sum _{k=1}^K \mathbf {H}^{-1}(\varvec{\kappa }_l) \left[ \mathbf {K} \mathbf {q}^{\varvec{\kappa }_l} -\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q})+\mathbf {f}^{\varvec{\kappa }_l} \right] {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} \right\| _{C^0} \\&\le h_1 \left( || \mathbf {K} \mathbf {q}||_{C^0}+|| \mathbf {S}(\mathbf {q})||_{C^0}+ || \mathbf {f} ||_{C^0}\right) , \end{aligned}\nonumber \\ \end{aligned}$$

(81)

where we have used the bound (77). Similarly, for the time derivative we obtain

$$\begin{aligned} \begin{aligned}&\left\Vert \frac{{\mathrm{d}}}{{\mathrm{d}}t}\mathcal {A}(\mathbf {q})\right\Vert _{C^0} \\&\quad = \left\| \lim _{K\rightarrow \infty } \sum _{k=1}^K \mathrm {i} \langle \varvec{\kappa }_l , \varvec{\Omega } \rangle \mathbf {H}^{-1}(\varvec{\kappa }_l) \left[ \mathbf {K} \mathbf {q}^{\varvec{\kappa }_l} -\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q})+\mathbf {f}^{\varvec{\kappa }_l} \right] {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} \right\| _{C^0} \\&\quad \le h_2 \left( || \mathbf {K} \mathbf {q}||_{C^0}+|| \mathbf {S}(\mathbf {q})||_{C^0}+ || \mathbf {f} ||_{C^0}\right) , \end{aligned}\nonumber \\ \end{aligned}$$

(82)

where we have used the bound (78). We note that the right-hand side of Eqs. (81) and (82) are bounded for any $\mathbf {q}\in C(\mathbb {T}^K)$. Hence, $\mathcal {A}$ maps $C^1(\mathbb {T}^K)$ to $C^1(\mathbb {T}^K)$. Furthermore, selecting $\left\Vert \mathbf {q}_1-\mathbf {q}_2\right\Vert _{L^1_{2}}\le \delta =\varepsilon /\left[ (h_1+h_2)(\left\Vert \mathbf {K}\right\Vert +L)\right]$, we obtain

$$\begin{aligned} \begin{aligned}&||\mathcal {A}(\mathbf {q}_1)-\mathcal {A}(\mathbf {q}_2)||_{L^1_{2}}\\&\quad \le (h_1+h_2)\left( \left\Vert \mathbf {K} (\mathbf {q}_1-\mathbf {q}_2)\right\Vert _{L_{2}}+ \left\Vert \mathbf {S} (\mathbf {q}_1)-\mathbf {S} (\mathbf {q}_2)\right\Vert _{L_{2}}\right) \\&\quad \le (h_1+h_2)(\left\Vert \mathbf {K}\right\Vert +L) \left\Vert \mathbf {q}_1-\mathbf {q}_2)\right\Vert _{L_{2}}\le \varepsilon , \end{aligned}\nonumber \\ \end{aligned}$$

(83)

which implies continuity of the operator $\mathcal {A}$ in the $L^1_{2}$-norm.

To show compactness for any bounded set U, we apply the Fréchet–Kolmogorov theorem C.2. We denote the constant bounding the set U in the $L_2^1$-norm by $C_U$. Then, for the condition (55) we have

$$\begin{aligned} \begin{aligned}&\left\Vert \mathcal {A}(\mathbf {q}(\varvec{\phi }))\right\Vert _{L_2} \\&\quad = h_1 \left\| \lim _{K\rightarrow \infty } \sum _{k=1}^K \left[ \mathbf {K} \mathbf {q}^{\varvec{\kappa }_l} -\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q})+\mathbf {f}^{\varvec{\kappa }_l} \right] {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} \right\| _{L_2}\\&\quad \le h_1 \left[ (|| \mathbf {K}||+L) || \mathbf {q}||_{L_2} + |\mathbf {S}(\mathbf {0})|+ || \mathbf {f} ||_{L_2}\right] \\&\quad \le h_1 \left[ (|| \mathbf {K}||~ +L )C_U + |\mathbf {S}(\mathbf {0})|+ || \mathbf {f} ||_{L_2}\right] \le \infty , \end{aligned}\nonumber \\ \end{aligned}$$

(84)

where we have used Proposition C.3, i.e., the fact that $\mathbf {S}(\mathbf {q})$ is bounded in the $L_2$-norm (cf. Eq. (69)). The upper bound (84) implies that condition (55) of Theorem C.2 is satisfied. For condition (56), we obtain

$$\begin{aligned} \begin{aligned}&\left\Vert \mathcal {A}(\mathbf {q}(\varvec{\phi }+\varvec{\delta }))-\mathcal {A}(\mathbf {q}(\varvec{\phi }))\right\Vert _{L_2}\\&\quad =h_1 \left\| \lim _{K\rightarrow \infty }\sum _{k=1}^K \left[ \mathbf {K} \left( \mathbf {q}^{\varvec{\kappa }_l} {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\delta } \rangle }-\mathbf {q}^{\varvec{\kappa }_l} \right) \right. \right. \\&\qquad \left. \left. +\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q}(\varvec{\phi }))-\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q}(\varvec{\phi }+\varvec{\delta }))\right] {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} \right\| _{L_2}\\&\quad \le h_1 \left( || \mathbf {K}|| \left\Vert \mathbf {q}(\varvec{\phi }\!+\!\varvec{\delta })-\mathbf {q}(\varvec{\phi })\right\Vert _{L_2} \!+\!L \left\Vert \mathbf {q}(\varvec{\phi }+\varvec{\delta })\!-\!\mathbf {q}(\varvec{\phi })\right\Vert _{L_2} \right) \\&\quad \le h_1 \left( || \mathbf {K}||+L\right) K C_{\varvec{\Omega }}|\varvec{\delta }| C_U, \end{aligned} \end{aligned}$$

where we have used the upper bound (66) in the proof of Proposition C.1. Selecting $|\varvec{\delta }|<\delta =\varepsilon /\left( h_1 \left( || \mathbf {K}||+L\right) KC_{\varvec{\Omega }}C_U\right)$ Eq. (85) implies that condition (56) holds. Hence, $\mathcal {A}$ is compact on any bounded subset of $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$. This completes our proof of Lemma C.1. $\square$

Analogous to Lemma C.1 we have the same statement for the normed space $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$

Lemma C.2

Assume conditions (C1), (C3) and (C4) are met and that the external forcing is quasi-periodic and $L_2$-integrable, i.e., $\mathbf {f}(t)\in L_2(\mathbb {T}^K)$. Then, the operator $\mathcal {A}$ (cf. def. (80)) maps $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ continuously and is compact on any bounded set $U\subset B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$.

Proof

We begin by showing that $\mathcal {A}$ maps $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $B(L^1_{2}(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$. To this end, we obtain

$$\begin{aligned} \begin{aligned}&\left\Vert \mathcal {A}(\mathbf {q})\right\Vert _{L_2^1}= \left\Vert \mathcal {A}(\mathbf {q})\right\Vert _{L_2}+ \left\Vert \frac{{\mathrm{d}}}{{\mathrm{d}}t}\mathcal {A}(\mathbf {q})\right\Vert _{L_2} \\&\quad = (h_1+h_2) \left\| \lim _{K\rightarrow \infty } \sum _{k=1}^K \left[ \mathbf {K} \mathbf {q}^{\varvec{\kappa }_l} -\mathbf {S}^{\varvec{\kappa }_l}(\mathbf {q})+\mathbf {f}^{\varvec{\kappa }_l} \right] {\mathrm{e}}^{\mathrm {i}\langle \varvec{\kappa }_l , \varvec{\Omega } \rangle t} \right\| _{L_2} \\&\quad \le (h_1+h_2) \left( || \mathbf {K}|| ~ ||\mathbf {q}||_{L_2}+L || \mathbf {q}||_{L_2} + |\mathbf {S}(\mathbf {0})| + || \mathbf {f} ||_{L_2}\right) , \end{aligned}\nonumber \\ \end{aligned}$$

(85)

where we have used the bounds (77) and (78). The right-hand side of Eq. (85) is bounded. Thus, the operator $\mathcal {A}$ maps $B(L_2^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $B(L^1_2(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$. The remainder of Lemma C.2, i.e., continuity in the $L_2^1$-norm and compactness on bounded sets, is analogous to the proof of Lemma C.1. $\square$

1.3 C.3 Bound on the solution

In this section, we show that all solutions to Eq. (49) with the operator (80) are bounded. To his end we note that any quasi-periodic function in $C(\mathbb {T}^K)$ is also almost-periodic, i.e., the following holds

Property C.1

(Almost-periodic in the sense of Bohr) The continuous and bounded function $\mathbf {f}(t)$ is almost-periodic, if for any $t_0,\tau \in \mathbb {R}$ and $\varepsilon >0$ there exists $T=T(\varepsilon )>0$, such that

$$\begin{aligned}&|\mathbf {f}(t_1)-\mathbf {f}(t_0)|<\varepsilon ,\qquad \varepsilon >0,\qquad \nonumber \\&\qquad \tau<t_1<\tau +T(\varepsilon ), \end{aligned}$$

(86)

holds (cf. Corduneanu [15]).

For the periodic case $T(\varepsilon )$ is the period. Therefore, $T(\varepsilon )$ is also considered as quasi-period.

Property (C.1) only holds for continuous quasi-periodic functions. To make use of property (C.1) in the non-smooth case, we approximate the non-smooth functions $\mathbf {q}\in L_{2}^1(\mathbb {T}^K)$ by continuous functions. Indeed, any function $\mathbf {q}\in L_{2}^1(\mathbb {T}^K)$ can be approximated arbitrarily well by a continuous function, e.g., the trigonometric polynomial of the form (51). Therefore, for any solution $\mathbf {q}\in L_2^1(\mathbb {T}^K)$ to Eq. (49) we can find some $\mathbf {p}\in C^1(\mathbb {T}^K)$ such that

$$\begin{aligned} ||\mathbf {p}-\mathbf {q}||_{L_2^1}<\varepsilon , \end{aligned}$$

(87)

holds. With the notation $\mathbf {f}^*(\mathbf {p},\mathbf {q},\kappa ):=\mathbf {p}-\mathbf {q}+\kappa (\mathcal {A}(\mathbf {q})- \mathcal {A}(\mathbf {p}))$, we observe that $\mathbf {p}$ approximately satisfies the operator equation (49)

$$\begin{aligned} \mathbf {p}= & {} \kappa \mathcal {A}(\mathbf {p}) +\mathbf {p}-\kappa \mathcal {A}(\mathbf {p})\nonumber \\= & {} \kappa \mathcal {A}(\mathbf {p}) +\mathbf {p}-\mathbf {q}-\kappa \mathcal {A}(\mathbf {p})+\kappa \mathcal {A}(\mathbf {q})\nonumber \\= & {} \kappa \mathcal {A}(\mathbf {p})+\mathbf {f}^*(\mathbf {p},\mathbf {q},\kappa ). \end{aligned}$$

(88)

Equation (87) implies the error term $\mathbf {f}^*$ is small for all $\mathbf {q}\in \L _2^1(\mathbb {T}^K)$, i.e., we have the following upper bound

$$\begin{aligned}&||\mathbf {f}^*(\mathbf {p},\mathbf {q},\kappa )||_{L_2}\nonumber \\&\quad \le ||\mathbf {p}-\mathbf {q}||_{L_2}+|| \mathcal {A}(\mathbf {q})- \mathcal {A}(\mathbf {p})||_{L_2}\nonumber \\&\quad \le \varepsilon + h_1(||\mathbf {K}||+L )||\mathbf {q}-\mathbf {p}||_{L_2}\nonumber \\&\quad =(1+h_1||\mathbf {K}||+h_1L)\varepsilon =:\delta , \end{aligned}$$

(89)

Rewriting the homotopy (88) as a differential equation, we obtain

$$\begin{aligned}&\mathbf {M}\ddot{\mathbf {p}}+ \mathbf {C} \dot{\mathbf {p}} +\mathbf {K}\mathbf {p}+\kappa ( \mathbf {S}(\mathbf {p}) -\mathbf {K} \mathbf {p})= \kappa \tilde{\mathbf {f}}(t,\mathbf {p},\mathbf {q},\kappa ), \nonumber \\&\qquad \mathbf {p}\in C^1(\mathbb {T}^K),~~\mathbf {q}\in L_2^1(\mathbb {T}^K) ,~~0\le \kappa \le 1, \end{aligned}$$

(90)

where we have defined the forcing

$$\begin{aligned}&\tilde{\mathbf {f}}:=\mathbf {f}(t)+\mathbf {f}^*(\mathbf {p},\mathbf {q},\kappa ),\nonumber \\&\qquad \left\Vert \tilde{\mathbf {f}}\right\Vert _{L_2}\le ||\mathbf {f}||_{L_2}+\delta ,\nonumber \\&\quad \forall ~ \mathbf {p}\in C^1(\mathbb {T}^K),~~\mathbf {q}\in L_2^1(\mathbb {T}^K) ,~~0\le \kappa \le 1. \end{aligned}$$

(91)

In the continuous case, i.e., for $\mathbf {q}\in N(C^1(\mathbb {T}^K),||\cdot ||_{L_2^1})$ the approximation with smooth functions is not necessary and hence $\tilde{\mathbf {f}}(t)=\mathbf {f}(t)$ holds.

Lemma C.3

Assume that conditions (C1) and (C2) hold and $\mathbf {f}(t)\in L_2(\mathbb {T}^K)$. Then, for all solutions $\mathbf {p}\in C^1(\mathbb {T}^K)$ to (90), the upper bound

$$\begin{aligned} ||\dot{\mathbf {p}}||_{L_2}\le \frac{ ||\mathbf {f}||_{L_2}+ \delta }{ C_0} =:C_{\dot{\mathbf {p}}}, \end{aligned}$$

(92)

holds, where $\delta$ can be made arbitrarily small.

Proof

We begin by defining the following scalar quasi-periodic auxiliary functions

$$\begin{aligned}&\eta _1(t):=\frac{1}{2}\dot{\mathbf {p}}^{\mathrm{T}}\mathbf {M}\dot{\mathbf {p}}+ \frac{1}{2} \mathbf {p}^{\mathrm{T}}\mathbf {K}\mathbf {p}\in C(\mathbb {T}^K),\nonumber \\&\eta _2(t):= V(\mathbf {p})- \frac{1}{2} \mathbf {p}^{\mathrm{T}}\mathbf {K}\mathbf {p}\in C(\mathbb {T}^K). \end{aligned}$$

(93)

Then, the function

$$\begin{aligned} \xi (t,t_0) = |\eta _1(t)-\eta _1(t_0)|+|\eta _2(t)-\eta _2(t_0)|, \end{aligned}$$

(94)

is quasi-periodic for any fixed $t_0$. Thus, property C.1 implies that inside any interval of length $T(\varepsilon )$ the function $\xi (t,t_0)$ is $\varepsilon$-close its value at $t_0$, i.e., zero. We collect these time instances in the set $\mathbb {Q}(\mathbf {p},t_0,\varepsilon )$

$$\begin{aligned} \mathbb {Q}(\mathbf {p},t_0,\varepsilon )=\left\{ t\in \mathbb {R}~|~ |\Xi (t,t_0)|<\varepsilon \right\} . \end{aligned}$$

(95)

To obtain an upper bound onto the velocities of system (90), we right multiply Eq. (90) with $\dot{\mathbf {p}}^{\top }$ and integrate from $t_0$ to $t_1$, which yields

$$\begin{aligned}&\int _{t_0}^{t_1} \dot{\mathbf {p}}^{\top }\mathbf {M}\ddot{\mathbf {p}}+ \dot{\mathbf {p}}^{\top }\mathbf {K}\mathbf {p} ~{\mathrm{d}}t +\kappa \int _{t_0}^{t_1} \dot{\mathbf {p}}^{\top } \mathbf {S}(\mathbf {p}) -\dot{\mathbf {p}}^{\top }\mathbf {K}\mathbf {p} ~{\mathrm{d}}t\nonumber \\&\quad +\int _{t_0}^{t_1}\dot{\mathbf {p}}^{\top }\mathbf {C}\dot{\mathbf {p}}~{\mathrm{d}}t =\kappa \int _{t_0}^{t_1}\dot{\mathbf {p}}^{\top } \kappa \tilde{\mathbf {f}}(t)~{\mathrm{d}}t. \end{aligned}$$

(96)

With the definition (93), we simplify the left-hand side of Eq. (96) and obtain

$$\begin{aligned} \begin{aligned}&\int _{t_0}^{t_1} \dot{\mathbf {p}}^{\top }\mathbf {M}\ddot{\mathbf {p}}+ \dot{\mathbf {p}}^{\top }\mathbf {K}\mathbf {p} ~{\mathrm{d}}t +\kappa \int _{t_0}^{t_1} \dot{\mathbf {p}}^{\top } \mathbf {S}(\mathbf {p}) -\dot{\mathbf {p}}^{\top }\mathbf {K}\mathbf {p} ~{\mathrm{d}}t\\&\quad =\int _{t_0}^{t_1} \frac{1}{2} \frac{{\mathrm{d}}}{{\mathrm{d}}t}\left( \dot{\mathbf {p}}^{\top }\mathbf {M}\dot{\mathbf {p}} + \mathbf {p}^{\top }\mathbf {K}\mathbf {p}\right) {\mathrm{d}}t + \kappa \int _{t_0}^{t_1} \frac{{\mathrm{d}}}{{\mathrm{d}}t}\\&\quad \left( V(\mathbf {p}) - \frac{1}{2} \mathbf {p}^{\top }\mathbf {K}\mathbf {p}\right) {\mathrm{d}}t\\&\quad = \eta _1(t_1)-\eta _1(t_0) +\kappa (\eta _2(t_1)-\eta _2(t_0)). \end{aligned} \end{aligned}$$

(97)

Rearranging terms in Eq. (96) and taking the absolute value, we obtain

$$\begin{aligned}&\left| \int _{t_0}^{t_1}\dot{\mathbf {p}}^{\top } \mathbf {C}\dot{\mathbf {p}}~{\mathrm{d}}t\right| \nonumber \\&\quad =\left| -\int _{t_0}^{t_1} \dot{\mathbf {p}}^{\top }\mathbf {M}\ddot{\mathbf {p}}- \dot{\mathbf {p}}^{\top }\mathbf {K}\mathbf {p} ~{\mathrm{d}}t\right. \nonumber \\&\qquad +\kappa \int _{t_0}^{t_1} \dot{\mathbf {p}}^{\top } \mathbf {S}(\mathbf {p}) -\dot{\mathbf {p}}^{\top }\mathbf {K}\mathbf {p} ~{\mathrm{d}}t \left. + \kappa \int _{t_0}^{t_1}\dot{\mathbf {p}}^{\top }\tilde{\mathbf {f}}(t)~{\mathrm{d}}t \right| \nonumber \\&\quad \le \left| \int _{t_0}^{t_1}\dot{\mathbf {p}}^{\top } \tilde{\mathbf {f}}(t)~{\mathrm{d}}t\right| \nonumber \\&\qquad +\left| \eta _2(t_1)-\eta _2(t_0) \right| +\left| \eta _1(t_1)-\eta _1(t_0)\right| . \end{aligned}$$

(98)

Condition (C1), implies the following lower bound onto the left-hand side of Eq. (98):

$$\begin{aligned} C_0\int _{t_0}^{t_1} |\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t\le |\int _{t_0}^{t_1}\dot{\mathbf {p}}^{\top } \mathbf {C} \dot{\mathbf {p}}~{\mathrm{d}}t|. \end{aligned}$$

(99)

Moreover, using the Cauchy–Schwarz inequality we obtain

$$\begin{aligned} \begin{aligned} \left| \int _{t_0}^{t_1}\dot{\mathbf {p}}^{\top } \tilde{\mathbf {f}}(t) ~{\mathrm{d}}t\right|&\le \int _{t_0}^{t_1}\left| \dot{\mathbf {p}}^{\top } \tilde{\mathbf {f}}(t)\right| ~{\mathrm{d}}t\\&\le \left( \int _{t_0}^{t_1}|\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t\right) ^{1/2} \left( \int _{t_0}^{t_1}|\tilde{\mathbf {f}}|^2 ~{\mathrm{d}}t\right) ^{1/2} . \end{aligned}\nonumber \\ \end{aligned}$$

(100)

The upper bound (100) and the lower bound (99) imply for Eq. (98)

$$\begin{aligned}&C_0\int _{t_0}^{t_1} |\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t \le \left( \int _{t_0}^{t_1}|\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t\right) ^{1/2} \left( \int _{t_0}^{t_1}|\tilde{\mathbf {f}}|^2 ~{\mathrm{d}}t\right) ^{1/2} \nonumber \\&\quad + \varepsilon ,\qquad t_1\in \mathbb {Q}(\mathbf {p},t_0,\varepsilon ), \end{aligned}$$

(101)

where we have selected the final integration time $t_1$ to be in the set $\mathbb {Q}(\mathbf {p},t_0,\varepsilon )$ (cf. Definition (95)). We observe, that the left-hand side of a Eq. (101) is a parabola in the dummy variable $y:=(\int _{t_0}^{t_1} |\dot{\mathbf {p}}|~{\mathrm{d}}t)^{1/2}$, whereas the right-hand side is linear in y. Therefore, Eq. (101) only holds in the closed interval

$$\begin{aligned}&\int _{t_0}^{t_1} |\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t\le \left( \frac{\sqrt{\int _{t_0}^{t_1}| \tilde{\mathbf {f}}|^2 ~{\mathrm{d}}t}}{2C_0} +\sqrt{\frac{\int _{t_0}^{t_1}|\tilde{\mathbf {f}}|^2 ~{\mathrm{d}}t }{4C_0^2} +\frac{ \varepsilon }{C_0} } \right) ^2 ,\nonumber \\&\qquad t_1\in \mathbb {Q}(\mathbf {p},t_0,\varepsilon ). \end{aligned}$$

(102)

We select $t_0=-T$ in Eq. (102), then the upper bound (102) holds all time instances $t_1$ inside the set $\mathbb {Q}(\mathbf {p},-T,\varepsilon )$. By construction, for any T there exists a time instance $t_1$ inside the set $\mathbb {Q}(\mathbf {p},-T,\varepsilon )$ such that $T<t_1<T+T(\varepsilon )$ holds, where $T(\varepsilon )$ is the finite quasi-period of the quasi-periodic function $\Xi (t,-T)$ (cf. Definition (94)). Indeed, the set $\mathbb {Q}(\mathbf {p},-T,\varepsilon )$ collects all time instances such that the quasi-periodic function $\Xi$ is $\varepsilon$-close to zero. Selecting $\tau =T$ and $t_0=-T$ property C.1 implies that for any T there exists $T<t_1<T+T(\varepsilon )$ such that $|\Xi (t_1,t_0))|<\varepsilon$ holds. By construction, $t_1$ is in the set $\mathbb {Q}(\mathbf {p},t_0,\varepsilon )$. Hence, for Eq. (102) we obtain

$$\begin{aligned}&\int _{-T}^{t_1} |\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t\le \left( \frac{\sqrt{\int _{t_0}^{t_1}| \tilde{\mathbf {f}}|^2 ~{\mathrm{d}}t}}{2C_0} +\sqrt{\frac{\int _{t_0}^{t_1}| \tilde{\mathbf {f}}|^2 ~{\mathrm{d}}t }{4C_0^2}+\frac{ \varepsilon }{C_0} } \right) ^2 ,\nonumber \\&\qquad T<t_1<T+T(\varepsilon ),~~\forall ~\mathbf {p}\in C^1(\mathbb {T}^K). \end{aligned}$$

(103)

In general, we have the following upper bound onto the $L_2$-norm of the velocity:

$$\begin{aligned} \begin{aligned}&\lim _{T\rightarrow \infty } \frac{1}{2T} \int _{-T}^{T} |\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t\\&\quad \le \lim _{T\rightarrow \infty } \frac{1}{1+\frac{T-t_1}{T+t_1}} \frac{1}{T+t_1} \int _{-T}^{t_1} |\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t,\\&\quad t_1>T,\quad \forall ~ \mathbf {p}\in C^1(\mathbb {T}^K). \end{aligned} \end{aligned}$$

(104)

Selecting $T<t_1<T+T(\varepsilon )$ in Eq. (104), the bound (103) holds. Now, taking the limit $T\rightarrow \infty$ the first fraction in Eq. (104) approaches one since $T-t_1 \le T(\varepsilon )<\infty$ for any $\mathbf {p}\in C(\mathbb {T}^K)$. Then, the bound (104) together with Eq. (102) implies

$$\begin{aligned} ||\dot{\mathbf {p}}||^2_{L_2} \le \lim _{T\rightarrow \infty } \frac{1}{T+t_1} \int _{-T}^{t_1} |\dot{\mathbf {p}}|^2 ~{\mathrm{d}}t \le \left( \frac{ ||\tilde{\mathbf {f}}||_{L_2} }{ C_0} \right) ^2. \end{aligned}$$

(105)

Equation (105) together with the bound onto the error term (91) proves Lemma (C.3). $\square$

Following Lemma C.3, we derive an upper bound onto the $L_2$-norm of the positions $\mathbf {p}$ of all quasi-periodic solutions to Eq. (90). To this end, we denote the maximum value of the continuous functions $| \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})|$ in the bounded interval of $|\mathbf {p}|<r$ by

$$\begin{aligned} S_m:=\sup _{|\mathbf {p}|\le r } | \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})|. \end{aligned}$$

(106)

Furthermore, the positive definite mass matrix satisfies

$$\begin{aligned} C_M |\mathbf {x}| \le \mathbf {x}^{\top } \mathbf {M}\mathbf {x}\le C_M^*|\mathbf {x}|,\qquad \forall ~\mathbf {x}\in \mathbb {R}^{N}, \end{aligned}$$

(107)

for some positive constants $C_M^*\ge C_M>0$. Finally, we denote the minimum of the two positive constants $C_M$ and $\alpha$ (cf. condition (C4)) by $\beta$, i.e.,

$$\begin{aligned} \beta :=\min (\alpha , C_M)>0. \end{aligned}$$

(108)

With the introduced notation (106), (107) and (108), we state the following Lemma yielding an upper bound onto the $L_2$-norm of the positions.

Lemma C.4

Assume that conditions (C1)–(C4) hold and $\mathbf {f}\in L_2(\mathbb {T}^K)$. Then, for all solutions $\mathbf {p}\in C^1(\mathbb {T}^K)$ to (90), the upper bound

$$\begin{aligned}&||\mathbf {p}||_{L_2}\le \frac{ ||\mathbf {f}||_{L_2}+\delta }{2 \beta } \nonumber \\&\quad + \sqrt{ \frac{ \left( ||\mathbf {f}||_{L_2}+\delta \right) ^2 }{4\beta ^2}+ \frac{C_M^*}{\beta } \frac{\left( ||\mathbf {f}||_{L_2}+\delta \right) ^2}{C_0^2} +\frac{ (\alpha r^2+S_m)}{\beta } } =:C_{\mathbf {p}},\nonumber \\ \end{aligned}$$

(109)

holds, where $\delta$ can be made arbitrarily small.

Proof

We start our proof of the above Lemma by left multiplying Eq. (90) with $\mathbf {p}^{\top }$ and integrate, which yields

$$\begin{aligned}&\int _{t_0}^{t_1} \mathbf {p}^{\top }\mathbf {M}\ddot{\mathbf {p}}+\mathbf {p}^{\top }\mathbf {C}\dot{\mathbf {p}} ~{\mathrm{d}}t\nonumber \\&\qquad + \int _{t_0}^{t_1} (1-\kappa )\mathbf {p}^{\top }\mathbf {K}\mathbf {p} +\kappa \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})~{\mathrm{d}}t\nonumber \\&\quad = \int _{t_0}^{t_1} \kappa \mathbf {p}^{\top }\tilde{\mathbf {f}}(t)~{\mathrm{d}}t . \end{aligned}$$

(110)

Condition (C4) implies that the quantity $\mathbf {p}^{\top }\mathbf {S}(\mathbf {p})$ is either positive or negative for $|\mathbf {p}|>r$. In the later case ($\mathbf {p}^{\top }\mathbf {S}(\mathbf {p})<0$ for $|\mathbf {p}|>r$) we multiply Eq. (110) with negative one. Then, rearranging terms and taking the absolute value of Eq. (110) yields

$$\begin{aligned}&\left| \pm \int _{t_0}^{t_1} (1-\kappa )\mathbf {p}^{\top }\mathbf {K}\mathbf {p} +\kappa \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})~{\mathrm{d}}t \right| \nonumber \\&\quad =\left| \mp \int _{t_0}^{t_1} \mathbf {p}^{\top }\mathbf {M}\ddot{\mathbf {p}}+\mathbf {p}^{\top }\mathbf {C}\dot{\mathbf {p}} ~{\mathrm{d}}t \pm \int _{t_0}^{t_1} \kappa \mathbf {p}^{\top }\tilde{\mathbf {f}}(t)~{\mathrm{d}}t \right| \nonumber \\&\quad \le \left| \int _{t_0}^{t_1} \frac{{\mathrm{d}}}{{\mathrm{d}}t} \left( \mathbf {p}^{\top }\mathbf {M}\dot{\mathbf {p}} + \frac{1}{2}\mathbf {p}^{\top }\mathbf {C} \mathbf {p} \right) ~{\mathrm{d}}t\right| + \left| \int _{t_0}^{t_1} \dot{\mathbf {p}}^{\top }\mathbf {M}\dot{\mathbf {p}}~ {\mathrm{d}}t\right| \nonumber \\&\qquad + \left( \int _{t_0}^{t_1} | \mathbf {p}|^2~{\mathrm{d}}t \right) ^{1/2} \left( \int _{t_0}^{t_1} | \tilde{\mathbf {f}}|^2~{\mathrm{d}}t \right) ^{1/2} , \end{aligned}$$

(111)

where we have used integration by parts and the Cauchy–Schwarz inequality. For the case $\mathbf {p}^{\top }\mathbf {S}(\mathbf {p})>0$ for $|\mathbf {p}|>r$ the upper signs in Eq. (111) are valid, whereas the lower signs hold for $\mathbf {p}^{\top }\mathbf {S}(\mathbf {p})<0$ for $|\mathbf {p}|>r$. Now, we differ between the two cases and continue by obtaining a lower bound on the left-hand side of Eq. (111). For the case $\mathbf {p}^{\top }\mathbf {S}(\mathbf {p})>0$ for $|\mathbf {p}|>r$, we have the following global lower bound

$$\begin{aligned} \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})> {\left\{ \begin{array}{ll} -S_m\ge -S_m+(\alpha |\mathbf {p}|^2-\alpha r^2),&{} |\mathbf {p}|\le r, \\ \alpha |\mathbf {p}|^2\ge \alpha |\mathbf {p}|^2 -S_m-\alpha r ^2, &{} |\mathbf {p}|>r, \end{array}\right. }\nonumber \\ \end{aligned}$$

(112)

where we have used the definition (106) and Eq. (8). With the lower bound (112) we obtain for left-hand side of Eq. (111)

$$\begin{aligned}&\left| \int _{t_0}^{t_1} (1-\kappa )\mathbf {p}^{\top }\mathbf {K}\mathbf {p} +\kappa \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})~{\mathrm{d}}t \right| \nonumber \\&\quad \ge \left| \int _{t_0}^{t_1} (1-\kappa )\mathbf {p}^{\top }\mathbf {M}\mathbf {p}+ \kappa (\alpha |\mathbf {p}|^2 -S_m-\alpha r^2) ~{\mathrm{d}}t \right| ,\nonumber \\ \end{aligned}$$

(113)

where we have used the definition of the matrix $\mathbf {K}$ in Eq. (67). For the case $\mathbf {p}^{\top }\mathbf {S}(\mathbf {p})<0$ for all $|\mathbf {p}|>r$ , we obtain

$$\begin{aligned} -\mathbf {p}^{\top }\mathbf {S}(\mathbf {p})> {\left\{ \begin{array}{ll} -S_m\ge -S_m+(\alpha |\mathbf {p}|^2-\alpha r^2),&{} |\mathbf {p}|\le r, \\ \alpha |\mathbf {p}|^2\ge \alpha |\mathbf {p}|^2 -S_m-\alpha r ^2, &{} |\mathbf {p}|>r . \end{array}\right. }\nonumber \\ \end{aligned}$$

(114)

Now, Eq. (111) holds with the negative sign on left-hand side, which yields

$$\begin{aligned}&\left| - \int _{t_0}^{t_1} (1-\kappa )\mathbf {p}^{\top }\mathbf {K}\mathbf {p} +\kappa \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})~{\mathrm{d}}t \right| \nonumber \\&\quad \ge \left| \int _{t_0}^{t_1} (1-\kappa )\mathbf {p}^{\top }\mathbf {M}\mathbf {p}+ \kappa ( \alpha |\mathbf {p}|^2 -S_m-\alpha r^2) ~{\mathrm{d}}t \right| ,\nonumber \\ \end{aligned}$$

(115)

where we have used the definition of the matrix $\mathbf {K}=-\mathbf {M}$ in Eq. (67). We note that both lower bounds (113) and (115) are identical. Hence, we can proceed without separating the two cases.

With the definition of $\beta$ (cf. Eq. (108)) we refine the lower bounds (113), respectively, (115) to

$$\begin{aligned}&\left| \pm \int _{t_0}^{t_1} (1-\kappa )\mathbf {p}^{\top }\mathbf {K}\mathbf {p} +\kappa \mathbf {p}^{\top }\mathbf {S}(\mathbf {p})~{\mathrm{d}}t \right| \nonumber \\&\quad \ge \left| \int _{t_0}^{t_1} \left( (1-\kappa ) C_M + \kappa \alpha \right) |\mathbf {p}|^2 -\kappa (S_m+\alpha r^2) ~{\mathrm{d}}t \right| \nonumber \\&\quad \ge \left| \int _{t_0}^{t_1} \left( (1-\kappa ) \beta + \kappa \beta \right) |\mathbf {p}|^2 -\kappa (S_m+\alpha r^2) ~{\mathrm{d}}t \right| \nonumber \\&\quad \ge \beta \int _{t_0}^{t_1} |\mathbf {p}|^2 ~~{\mathrm{d}}t- (S_m+\alpha r^2)|t_1-t_0|. \end{aligned}$$

(116)

To derive an upper bound for the first term on the right-hand side of Eq. (111), we define the continuous quasi-periodic auxiliary function

$$\begin{aligned} \gamma (t,t_0):= & {} |\mathbf {p}^{\top }(t)\mathbf {M}\dot{\mathbf {p}}(t) + \frac{1}{2}\mathbf {p}^{\top }(t)\mathbf {C} \mathbf {p}(t)\nonumber \\&-\mathbf {p}^{\top }(t_0)\mathbf {M}\dot{\mathbf {p}}(t_0) + \frac{1}{2}\mathbf {p}^{\top }(t_0)\mathbf {C} \mathbf {p}(t_0)|, \end{aligned}$$

(117)

which is quasi-periodic for any fixed $t_0$. Hence, property C.1 implies that $\gamma (t,t_0)$ is $\varepsilon$-close to zero at least once in any time interval of the length $T(\varepsilon )$. We collect all these time instances in the set $\mathbb {P}(\mathbf {p},t_0,\varepsilon )$, i.e.,

$$\begin{aligned} \mathbb {P}(\mathbf {p},t_0,\varepsilon ):=\left\{ t\in \mathbb {R}~|~ |\gamma (t,t_0)|<\varepsilon \right\} . \end{aligned}$$

(118)

Substituting the upper bound on the quadratic form of the mass matrix (107), the definition (117) and the lower bound (116) into Eq. (111), we obtain

$$\begin{aligned}&\beta \int _{t_0}^{t_1} |\mathbf {p}|^2~{\mathrm{d}}t \nonumber \\&\quad \le \sqrt{\int _{t_0}^{t_1}|\mathbf {p}|^2~{\mathrm{d}}t} \sqrt{ \int _{t_0}^{t_1} | \tilde{\mathbf {f}}|^2~{\mathrm{d}}t } \nonumber \\&\qquad + C_M^* \int _{t_0}^{t_1}|\dot{\mathbf {p}}|^2~{\mathrm{d}}t + (\alpha r^2+S_m)|t_1-t_0|+\varepsilon ,\quad \nonumber \\&\qquad t_1\in \mathbb {P} . \end{aligned}$$

(119)

Analogous to the proof of Lemma C.3, we observe that the left side of Eq. (119) is quadratic in the dummy variable $y:=(\int _{t_0}^{t_1} |\mathbf {p}|^2 ~{\mathrm{d}}t)^{1/2}$, whereas the right-hand side is linear in y. Solving for y, yields

$$\begin{aligned}&\int _{t_0}^{t_1} |\mathbf {p}|^2 ~{\mathrm{d}}t\nonumber \\&\quad \le \left( \frac{ \sqrt{ \int _{t_0}^{t_1} | \tilde{\mathbf {f}}|^2~{\mathrm{d}}t } }{2 \beta } + \sqrt{ \frac{ \int _{t_0}^{t_1} | \tilde{\mathbf {f}}|^2~{\mathrm{d}}t }{4\beta ^2}+ \frac{C_M^*}{\beta } \int _{t_0}^{t_1}|\dot{\mathbf {p}}|^2~{\mathrm{d}}t +\frac{ (\alpha r^2+S_m)|t_1-t_0|+\varepsilon }{\beta } } \right) ^2 , \quad t_1\in \mathbb {P} . \end{aligned}$$

(120)

Now, we set $t_0=-T$ and divide Eq. (120) by 2T. Since $\gamma (t,t_0)$ is quasi-periodic, property C.1 implies that for any $\mathbf {p}\in C^1(\mathbb {T}^K)$ and any $T\in \mathbb {R}^+$ we can select some $t_1 \in \mathbb {P}(\mathbf {p},-T,\varepsilon )$, such that $t_1$ is greater than T and less than $T+T(\varepsilon )$. Thereby, we obtain

$$\begin{aligned} \begin{aligned} ||\mathbf {p}||^2_{L_2}&= \lim _{T\rightarrow \infty } \frac{1}{2T} \int _{-T}^{T} |\mathbf {p}|^2~{\mathrm{d}}t\le \lim _{T\rightarrow \infty } \frac{1}{2T} \int _{-T}^{t_1} |\mathbf {p}|^2 ~{\mathrm{d}}t\\&\le \lim _{T\rightarrow \infty }\frac{1}{1+\frac{T-t_1}{T+t_1}} \frac{1}{T+t_1} \int _{-T}^{t_1} |\mathbf {p}|^2 ~{\mathrm{d}}t \\&\le \left( \frac{ ||\tilde{\mathbf {f}}||_{L_2}}{2 \beta } + \sqrt{ \frac{ ||\tilde{\mathbf {f}}||_{L_2}^2 }{4\beta ^2}+ \frac{C_M^*}{\beta } \frac{||\tilde{\mathbf {f}}||_{L_2}^2}{C_0^2} +\frac{ (\alpha r^2+S_m)}{\beta } } \right) ^2, \end{aligned}\nonumber \\ \end{aligned}$$

(121)

where we have used the upper bound (105) from Lemma (C.3). Together with the upper bound on the error term (91) the upper bound (121) gives the upper bound of Lemma C.4. $\square$

1.4 C.4 Existence of non-smooth solutions

In the following, we collect our results to show that Eq. (1) has a solution in $L_2^1(\mathbb {T}^K)$.

Theorem C.3

Assume that conditions (C1)–(C4) are met and $\mathbf {f}(t)\in L_2(\mathbb {T}^K)$. Then, system (1) has a solution bounded in $L_2^1(\mathbb {T}^K)$.

Proof

We base our proof on Schäfer’s fixed point theorem C.1 and consider the homotopy (68), respectively, its equivalent form (79) in the Banach space $B(L_2^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$. Equation (79) is in the form of Eq. (49) of Schäfer’s theorem C.1, whereby the operator $\mathcal {A}$ is defined in Eq. (80).

Lemma C.2 guarantees that the operator $\mathcal {A}$ maps $B(L_2^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $B(L_2^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$, is continuous and compact on bounded sets. Hence, Schäfer’s fixed point theorem C.1 applies. The upper bounds stated in Lemmata C.3 and C.4 and Eq. (87) guarantee, that the set of solutions to Eq. (49) is bounded by

$$\begin{aligned} ||\mathbf {q}||_{L_2^1}\le C_{\mathbf {p}}+C_{\dot{\mathbf {p}}}+\varepsilon , \end{aligned}$$

(122)

where $\varepsilon$ is an arbitrarily small constant. Thus, the second case of Schäfer’s fixed point does not hold and hence Eq. (68) has a solution for $\kappa =1$. Since Eq. (68) is equivalent to system (1) for $\kappa =1$, system (1) has a solution bounded in $L_2^1(\mathbb {T}^K)$ by Eq. (122). This proves the claim of Theorem C.3, which is equivalent to Theorem 3.3. $\square$

1.5 C.5 Existence of smooth solutions

If the forcing is continuous, then the result from Theorem C.3 can be strengthened to guarantee a continuously differentiable quasi-periodic solution.

Theorem C.4

Assume that conditions (C1)–(C4) are met and the forcing is quasi-periodic and continuous, i.e., $\mathbf {f}\in C(\mathbb {T}^K)$. Then, system (1) has a solution in $C^1(\mathbb {T}^K)$.

Proof

Our proof is based on Schäfer’s fixed point theorem C.1. We consider the homotopy (68), respectively, its equivalent form (79) in the normed space $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$. Equation (79) is in the form of Eq. (49) of Schäfer’s theorem C.1, whereby the operator is defined in Eq. (80).

Moreover, Lemma C.1 guarantees that $\mathcal {A}$ maps $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$ to $N(C^1(\mathbb {T}^K),||\cdot ||_{L^1_{2}})$, is continuous and compact on bounded sets. Thus, all requirements of Schäfer’s fixed point theorem C.1 are met. The upper bounds provided by Lemmata C.3 and C.4 imply that the set of solutions to Eq. (49) is bounded by

$$\begin{aligned} ||\mathbf {q}||_{L_2^1}\le C_{\mathbf {p}}+C_{\dot{\mathbf {p}}}, \end{aligned}$$

(123)

where the constant $\delta$ in the bounds (92) and (109) can be set to zero. Once again, the second case of Schäfer’s fixed point theorem C.1 does not hold. Hence, Eq. (68) has a solution for $\kappa =1$. Since (68) is equivalent to system (1) for $\kappa =1$, system (1) has a solution in $C^1(\mathbb {T}^K)$. More specifically, there exists a solution $\mathbf {q}^*$ to Eq. (1) for which

$$\begin{aligned} \mathbf {q}^*\in C^1(\mathbb {T}^K),~~\text {and}~~||\mathbf {q}^*||_{L_2^1}\le C_{\mathbf {p}}+C_{\dot{\mathbf {p}}}, \end{aligned}$$

(124)

holds. This proves Theorem C.4, which is a restatement of Theorem 3.1. $\square$

Remark C.2

Our Theorem (C.4) guarantees that at least one solution to Eq. (1) is continuous and bounded. With the knowledge of such a solution $\mathbf {q}^* \in C^1(\mathbb {T}^K)$, we can apply Schäfer’s fixed point theorem C.1 in the Banach space $B(C^1(\mathbb {T}^K),\left\Vert \cdot \right\Vert _{C^1})$. Since the first case holds (i.e., $\mathbf {q}^*$ exists), the second cases does not hold, i.e., the set of solutions to the homotopy (49) is bounded in the $C^1$-norm.

D Proof of Theorem 3.2

To proof Theorem 3.2, we show that condition (C4*), implies that condition (C4) holds. To this end, we assume that the nonlinearity $\mathbf {S}(\mathbf {q})$ evaluated at $\mathbf {q}=\mathbf {0}$ is zero. We can make this assumption without the loss of generality. Indeed, subtracting $\mathbf {S}(\mathbf {0})$ on both sides of Eq. (1) and defining the new nonlinearities $\tilde{\mathbf {S}}(\mathbf {q}):=\mathbf {S}(\mathbf {q})-\mathbf {S}(\mathbf {0})$ and forcing $\tilde{\mathbf {f}}(t):=\mathbf {f}(t)-\mathbf {S}(\mathbf {0})$, we obtain an equivalent system in the from of Eq. (1) with $\tilde{\mathbf {S}}(\mathbf {0})=\mathbf {0}$.

First, we assume that the Hessian is positive definite for $\mathbf {q}>\tilde{r}$ and note that within the bounded domain $|\mathbf {q}|< \tilde{r}$ there exists a constant $0<C_{\min }<\infty$ such that the real and symmetric Hessian matrix $\partial ^2 V(\mathbf {q})/\partial \mathbf {q}^2$ satisfies

$$\begin{aligned}&\mathbf {x}^{\top } \frac{\partial ^2 V(\mathbf {q})}{\partial \mathbf {q}^2} \mathbf {x}> - C_{\min } |\mathbf {x}|^2,\nonumber \\&\qquad |\mathbf {q}|<\tilde{r},\qquad C_{\min }>0, \qquad \forall ~\mathbf {x}\in \mathbb {R}^N. \end{aligned}$$

(125)

In the following, we show that Eq. (11) ensures that Eq. (8) holds with

$$\begin{aligned} r=2 \tilde{r} \left( 1 + \frac{ C_{\min }}{C_S}\right) ,\qquad \text {and} \qquad \alpha >C_S/2, \end{aligned}$$

(126)

where the constant $C_S$ is a lower bound on the magnitude of the Hessian for $|\mathbf {q}|>r$ (cf. Eq. (11)). To this end, a Taylor series expansion of the nonlinearity yields

$$\begin{aligned} \begin{aligned} \mathbf {q}^{\top }\mathbf {S}(\mathbf {q})&=\mathbf {q}^{\top }\mathbf {S}(\mathbf {0})\\&\quad +\int _0^1\mathbf {q}^{\top } \frac{\partial ^2 V(s\mathbf {q})}{\partial \mathbf {q}^2} \mathbf {q}~ds \\&= \int _0^{\tilde{s}}\mathbf {q}^{\top } \frac{\partial ^2 V(s\mathbf {q})}{\partial \mathbf {q}^2} \mathbf {q}~ds \\&\quad +\int _{\tilde{s}}^{1}\mathbf {q}^{\top } \frac{\partial ^2 V(s\mathbf {q})}{\partial \mathbf {q}^2} \mathbf {q}~ds, \qquad \forall ~|\mathbf {q}|>r, \end{aligned} \end{aligned}$$

(127)

where we have denoted $\tilde{s}=\tilde{r}/|\mathbf {q}|$ as the value for which the argument of the Hessian matrix $s\mathbf {q}$ leaves the bounded domain $|\mathbf {q}|< \tilde{r}$. Due to the choice of the radius r in Eq. (126), $\tilde{s}$ is upper bounded by

$$\begin{aligned} \tilde{s}\le \frac{C_S}{2\left( C_S+C_{\min } \right) }\le 1. \end{aligned}$$

(128)

For $|\mathbf {q}|>\tilde{r}$ , i.e., for the second integral in Eq. (127), the lower bound (11) from Theorem 3.2 holds, whereas for the first integral the lower bound (125) holds. Together these bounds imply for Eq. (127)

$$\begin{aligned}&\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})> (-\tilde{s} C_{\min } +(1-\tilde{s})C_S) |\mathbf {q}|^2\nonumber \\&\quad>\frac{C_S}{2} |\mathbf {q}|^2, \qquad \forall ~|\mathbf {q}|>r. \end{aligned}$$

(129)

where we have used the lower bound on the parameter $\tilde{s}$ from Eq. (128). Equation (129) implies, that condition (8) is satisfied for the radius defined in Eq. (126) and $\alpha =C_S/2>0$.

The proof in the case of a negative definite Hessian matrix for $|\mathbf {q}|>r$ is analogous. The only difference is that instead of a lower bound on the quadratic form (125) one needs to work with an upper bound of the quadratic form (125) inside a bounded domain.

E Theorem 3.1 applies to the oscillator chain

In the following, we show that the chain of oscillators depicted in Fig. 1 satisfies the conditions of our existence Theorem 3.1. In our previous work [8], we have shown that the damping matrix is positive definite and have derived a potential for the stiffness terms of Eq. (13). Thus, conditions (C1) and (C2) of Theorem 3.1 hold.

For the Lipschitz condition (C3), we point out Remark 3.3 where we have constructed a Lipschitz continuous truncation of system (1). Selecting the radius of the truncation large, i.e., in the overflow our computation package (Matlab), this truncation does not necessarily need to be implemented.

For condition (C4), we first assume $dS_{j}(d)>0$ for $|d|>r$ and all $j=1,\ldots ,N+1$. Each continuous function $|dS_{j}(d)|$ has a maximum value inside the bounded interval $|d|<r$, which we denote by $S_j$. With this notation, we obtain the following

$$\begin{aligned} dS_{j}(d)> {\left\{ \begin{array}{ll} -S_j>-S_j+(\gamma d^2-\gamma r^2),\quad &{} |d|<r, \\ \gamma d^2>\gamma d^2 -S_j -\gamma r^2, &{} |d|>r, \end{array}\right. }\nonumber \\ \end{aligned}$$

(130)

where we have used Eq. (14). Computing the inner product $\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})$ yields

$$\begin{aligned} \begin{aligned} \mathbf {q}^{\top }\mathbf {S}(\mathbf {q})&= \sum _{j=1}^{N } q_j (-S_{j}(q_{j-1}-q_{j})+S_{j+1}(q_{j}-q_{j+1}))\\&=\sum _{j=1}^{N+1} (q_{j-1}-q_j)S_j(q_{j-1}-q_j) \\&> \gamma \sum _{j=1}^{N+1} (q_{j-1}-q_j)^2-(N+1) (\gamma r^2\\&\quad +\sup _{1\le j\le N+1}(S_j) ) . \end{aligned} \end{aligned}$$

(131)

We rewrite the sum in Eq. (131) as the following quadratic form

$$\begin{aligned}&\sum _{j=1}^{N+1} (q_{j-1}-q_j)^2=\mathbf {q}^{\top }\mathbf {A} \mathbf {q},\nonumber \\&\qquad \mathbf {A}:= \begin{bmatrix} 2 &{} -1 &{} 0 &{} \cdots &{}\\ -1 &{} 2 &{} -1 &{} 0 &{} \cdots \\ 0 &{} \ddots &{}\ddots &{}\ddots &{} 0 \\ \end{bmatrix}\in \mathbb {R}^{N \times N}. \end{aligned}$$

(132)

The matrix $\mathbf {A}$ is a tridiagonal Toeplitz matrix, with the eigenvalues $\lambda _n=2+2\cos (\pi n /(n+1))$ for $n=1,\ldots ,N$ (e.g., Gover [27]). We observe that all eigenvalues of the matrix $\mathbf {A}$ are positive, since $N/(N+1)$ is less than one. Thus, $\mathbf {A}$ is positive definite, i.e., $\mathbf {q}^{\top }\mathbf {A}\mathbf {q}>C_A |\mathbf {q}|^2$ holds for some positive $C_A>0$. Hence, for Eq. (131) we obtain

$$\begin{aligned} \mathbf {q}^{\top }\mathbf {S}(\mathbf {q})>C_A |\mathbf {q}|^2-(\sup _{1\le j\le N+1} S_j+ \gamma r^2)(N+1).\nonumber \\ \end{aligned}$$

(133)

Selecting $r=\sqrt{2(N+1) (\sup _{1\le j\le N+1} S_j+ \gamma r^2)/C_A}$, Eq. (133) yields

$$\begin{aligned}&\mathbf {q}^{\top }\mathbf {S}(\mathbf {q})>\left( C_A -\frac{(N+1)(\sup _{1\le j\le N+1} S_j+ \gamma r^2)}{|\mathbf {q}|^2}\right) |\mathbf {q}|^2\nonumber \\&\quad>\frac{C_A}{2}|\mathbf {q}|^2,\qquad |\mathbf {q}|>r, \end{aligned}$$

(134)

which implies that condition (C4) is satisfied with $\alpha =C_A/2$. The proof for softening springs (i.e., $dS_{j}(d)<0$ for $|d|>r$) is analogous.