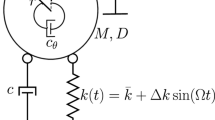When does a periodic response exist in a periodically forced multi-degree-of-freedom mechanical system?

Abstract

While periodic responses of periodically forced dissipative nonlinear mechanical systems are commonly observed in experiments and numerics, their existence can rarely be concluded in rigorous mathematical terms. This lack of a priori existence criteria for mechanical systems hinders definitive conclusions about periodic orbits from approximate numerical methods, such as harmonic balance. In this work, we establish results guaranteeing the existence of a periodic response without restricting the amplitude of the forcing or the response. Our results provide a priori justification for the use of numerical methods for the detection of periodic responses. We illustrate on examples that each condition of the existence criterion we discuss is essential.

Appendices

A Proofs of the main theorems

In the following, we prove the main Theorems 3.1 and 3.2 and derive an upper bound on the amplitudes of the periodic orbits.

1.1 A1 Proof of Theorem 3.1

We base our proof of Theorem 3.1 on a theorem by Rouche and Mawhin [36], who analyze systems of the following form

$$\begin{aligned} \ddot{{\mathbf {q}}}+\bar{{\mathbf {C}}}\dot{{\mathbf {q}}}+\frac{\partial {\bar{V}}({\mathbf {q}})}{\partial {\mathbf {q}}}={\mathbf {g}}(t), \quad {\mathbf {g}}(t)={\mathbf {g}}(t+T),~~{\bar{V}}\in C^1. \nonumber \\ \end{aligned}$$

(33)

Theorem A.1

Assume system (33) satisfies the following conditions:

• (RM1) The damping matrix $\bar{{\mathbf {C}}}$ is positive or negative definite.

• (RM2) There exists a distance $r\!>\!0$ and an integer $1\!\le \!n\!\le N$ such that

  $$\begin{aligned} \begin{aligned} q_j\frac{\partial {\bar{V}}({\mathbf {q}})}{\partial q_j}&>0, \quad |q_j|>r,~~j=1,\ldots ,n, \\ q_j\frac{\partial {\bar{V}}({\mathbf {q}})}{\partial q_j}&<0, \quad |q_j|>r,~~j=n+1,\ldots ,N. \end{aligned} \end{aligned}$$

  (34)

• (RM3) The forcing ${\mathbf {g}}$ is continuous with zero mean value, i.e.,

  $$\begin{aligned} \bar{{\mathbf {g}}}=\frac{1}{T}\int _{0}^{T}{\mathbf {g}}(t)\hbox {d}t={\mathbf {0}} . \end{aligned}$$

  (35)

Then, system (33) has at least one T-periodic solution.

Proof

The proof relies on a homotopy of Eq. (33) to the equation $\ddot{{\mathbf {q}}}=0$. Conditions (RM1)–(RM3) ensure a bound on the solution for all homotopy parameters. In addition, condition (RM2) ensures a nonzero Brouwer degree, i.e., the existence of at least one T-periodic solution during the homotopy. For a detailed proof, we refer to Rouche and Mawhin [36]. $\square$

We transform system (1) such that it is in the form (33) and then show that the conditions of Theorem 3.1 imply that Theorem A.1 applies. First, we absorb the mean forcing into the potential by setting

$$\begin{aligned} {\tilde{V}}({\mathbf {q}})=V({\mathbf {q}})-{\mathbf {q}}^T\bar{{\mathbf {f}}}, \quad \tilde{{\mathbf {f}}}={\mathbf {f}}-\bar{{\mathbf {f}}}. \end{aligned}$$

(36)

The equation of motion with nonlinearity derived from the potential ${\tilde{V}}$ and forcing $\tilde{{\mathbf {f}}}$ is equivalent to system (1). Since the mass matrix is positive definite by assumption, its square root $\mathbf{M}^{-1/2}{} \mathbf{M}^{-1/2} :=$M is exists and is positive definite. Performing the change of coordinates $\mathbf{p} = \mathbf{M}^{1/2}{} \mathbf{q}$ in Eq. (1) and further right-multiplying with $\mathbf{M}^{-1/2}$, we obtain

$$\begin{aligned} \ddot{{\mathbf {p}}}+{\mathbf {M}}^{-\frac{1}{2}}{\mathbf {CM}}^{-\frac{1}{2}}\dot{\mathbf {p}}+\frac{\partial {\tilde{V}}}{\partial {\mathbf {p}}}={\mathbf {M}}^{-\frac{1}{2}}\tilde{\mathbf {f}}(t). \end{aligned}$$

(37)

The potential for the geometric nonlinearities of system (37) is given by ${\bar{V}}({\mathbf {p}})\!:=\!{\tilde{V}}({\mathbf {M}}^{-1/2}{\mathbf {p}})$. Therefore, system (37) can be rewritten in the form (33). Since the mass matrix is positive definite by assumption, the product $\bar{{\mathbf {C}}}\!:=\!{\mathbf {M}}^{-1/2}{\mathbf {CM}}^{-1/2}$ is positive or negative definite. Therefore, condition (C1) of Theorem 3.1 implies that condition (RM1) of Theorem A.1 is satisfied.

Rewriting condition (C3) for the potential ${\bar{V}}({\mathbf {p}})$, one recovers the equivalent condition (RM2). Since $\tilde{{\mathbf {f}}}$ has zero mean, condition (RM3) holds. Therefore, the conditions in Theorem 3.1 ensure that Theorem A.1 applies, and hence, the existence of a periodic orbit can be guaranteed.

1.2 A2 Maximal amplitude of the periodic response

Essential to the proof of Rouche and Mawhin [36] is an upper bound on the periodic solution of Eq. (1). In the following, we show that this can be obtained for system (1) in its original form. Therefore, a transformation to Eq. (33) is not necessary. We derive an upper bound on the solutions of

$$\begin{aligned} {\mathbf {M}} \ddot{{\mathbf {q}}}+{\mathbf {C}}\dot{{\mathbf {q}}}+{\mathbf {S}}({\mathbf {q}})= {\mathbf {f}}(t),~\quad {\mathbf {q}}\in C^2(T), \end{aligned}$$

(38)

in the $C^0$ norm defined by

$$\begin{aligned} ||{\mathbf {q}}||_{C^0}=\max _{0\le t\le T}\left| {\mathbf {q}}\right| . \end{aligned}$$

(39)

First, we follow the derivation by Rouche and Mawhin [36] by left-multiplying Eq. (38) with $\dot{{\mathbf {q}}}^T$ and integrating over one period to obtain

$$\begin{aligned}&\int _0^T\dot{{\mathbf {q}}}^T{\mathbf {M}}\ddot{{\mathbf {q}}}~\hbox {d}t+ \int _0^T\dot{{\mathbf {q}}}^T{\mathbf {C}}\dot{{\mathbf {q}}}~\hbox {d}t + \int _0^T\dot{{\mathbf {q}}}^T{\mathbf {S}}({\mathbf {q}})~\hbox {d}t\nonumber \\&\quad = \int _0^T\dot{{\mathbf {q}}}^T{\mathbf {f}}(t)~\hbox {d}t. \end{aligned}$$

(40)

Observing that

$$\begin{aligned} \int _0^T\dot{{\mathbf {q}}}^T{\mathbf {M}}\ddot{{\mathbf {q}}}~\hbox {d}t= \int _0^T \frac{\hbox {d}}{\hbox {d}t}\left( \frac{1}{2} \dot{{\mathbf {q}}}^T{\mathbf {M}}\dot{{\mathbf {q}}}\right) \hbox {d}t=0, \end{aligned}$$

(41)

where we have used the symmetry of the mass matrix (${\mathbf {M}}={\mathbf {M}}^T$) and the periodicity of ${\mathbf {q}}$. Similarly,

$$\begin{aligned} \int _0^T\dot{{\mathbf {q}}}^T{\mathbf {S}}({\mathbf {q}})~\hbox {d}t= \int _0^T\frac{\hbox {d}}{\hbox {d}t}\left( V({\mathbf {q}})\right) \hbox {d}t=0, \end{aligned}$$

(42)

where we have used the fact that the geometric nonlinearities arise from a potential (10) and again the periodicity of ${\mathbf {q}}$. Therefore, from Eq. (40), we obtain

$$\begin{aligned} \left| \int _0^T \dot{{\mathbf {q}}}^T{\mathbf {C}}\dot{{\mathbf {q}}} ~\hbox {d}t\right| =\left| \int _0^T\dot{{\mathbf {q}}}^T {\mathbf {f}}~ \hbox {d}t \right| . \end{aligned}$$

(43)

With the assumption of a positive or negative definite ${\mathbf {C}}$ matrix (cf. Eq. (9)), we obtain a lower bound on the left-hand side of Eq. (43) to

$$\begin{aligned} C_0\int _0^T |\dot{{\mathbf {q}}}|^2 \hbox {d}t\le \left| \int _0^T \dot{{\mathbf {q}}}^T{\mathbf {C}}\dot{{\mathbf {q}}} \hbox {d}t\right| . \end{aligned}$$

(44)

For the right-hand side of Eq. (43), we obtain an upper bound by using the Cauchy–Schwartz inequality

$$\begin{aligned} \left| \int _0^T\dot{{\mathbf {q}}} {\mathbf {f}} ~\hbox {d}t\right| \le \left( \int _0^T |\dot{{\mathbf {q}}} |^2 ~\hbox {d}t\right) ^{1/2} \left( \int _0^T |{\mathbf {f}} |^2 ~\hbox {d}t\right) ^{1/2}. \nonumber \\ \end{aligned}$$

(45)

Using the definition (12) of $C_f$ and combining the estimates (44) and (45), we obtain from Eq. (43) that

$$\begin{aligned} \left( \int _0^T |\dot{{\mathbf {q}}} |^2 ~\hbox {d}t\right) ^{1/2}\le \frac{C_f}{C_0}. \end{aligned}$$

(46)

Equation (46) is an upper bound on the $L_2$-norm of the velocity of the periodic orbit. Rouche and Mawhin [36] derive the same bound. Now we depart from the derivations by Rouche and Mawhin [36] and integrate system (38) for one period, which yields

$$\begin{aligned} \int _0^T {\mathbf {S}}({\mathbf {q}})~\hbox {d}t=T\bar{{\mathbf {f}}},\quad \Leftrightarrow \quad \int _0^T \left( {\mathbf {S}}({\mathbf {q}}) -\bar{{\mathbf {f}}}\right) \hbox {d}t=0, \nonumber \\ \end{aligned}$$

(47)

where we used the definition (8) of the mean forcing $\bar{{\mathbf {f}}}$. Applying the mean-value theorem to (47), we conclude that there exist $t_j$ such that

$$\begin{aligned} S_j({\mathbf {q}}(t_j))-{\bar{f}}_j=0,\quad 0\le t_j\le T,\quad j=1,\ldots ,N. \nonumber \\ \end{aligned}$$

(48)

From condition (11), we conclude that Eq. (48) is only satisfied if $|q_j(t_j)|<r$. We conclude

$$\begin{aligned} \begin{aligned} q_j^2(t)&=\left( q_j(t_j)+\int _{t_j}^t{\dot{q}}_j(s)ds\right) ^2= q_j(t_j)^2\\&\quad +2q_j(t_j)\int _{t_j}^t{\dot{q}}_j(s)ds+\left( \int _{t_j}^t{\dot{q}}_j(s)ds\right) ^2 \\&\le r^2+2r|t-t_j|^{\frac{1}{2}}\left( \int _{t_j}^t{\dot{q}}_j^2(s)ds\right) ^{1/2}\\&\quad + |t-t_j|\int _{t_j}^t{\dot{q}}_j^2(s)ds \\&\le r^2+2r\sqrt{T}\left( \int _{0}^T{\dot{q}}_j^2(s)ds\right) ^{1/2}\\&\quad + T\int _{0}^T{\dot{q}}_j^2(s)ds\le \left( r+\sqrt{T}\frac{C_f}{C_0}\right) ^2, \end{aligned} \end{aligned}$$

(49)

where we have used the upper bound (46). Therefore, for the $C^0$-norm of the positions, we obtain

$$\begin{aligned}&||{\mathbf {q}}||_{C^0} < \left( \sum _{j=1}^N \sup _{0\le t \le T} (q_j^2(t)) \right) ^{1/2}\nonumber \\&\quad \le \sqrt{N}\left( r+\sqrt{T} \frac{C_f}{C_0} \right) , \end{aligned}$$

(50)

In contrast, Rouche and Mawhin [36] use the bound (46) to obtain an upper estimate on the oscillatory part of the position $\tilde{{\mathbf {q}}}:={\mathbf {q}}-1/T\int _0^T{\mathbf {q}}\,\hbox {d}t$ to $||\tilde{{\mathbf {q}}}||_{C^0}\le TC_f/C_0$. From Eq. (47), they directly obtain that each component of the mean $\bar{{\mathbf {q}}}:=1/T\int _0^T{\mathbf {q}}\,\hbox {d}t$ is bounded by $r+TC_f/C_0$. Adding the mean and oscillatory part, Rouche and Mawhin [36] derive the bound

$$\begin{aligned} ||{\mathbf {q}}||_{C^0} \le \sqrt{N}\left( r+\sqrt{T} \frac{C_f}{C_0} \right) +\frac{TC_f}{C_0}, \end{aligned}$$

(51)

which includes the additional summand $TC_f/C_0$ compared to our bound (50).

1.3 A3 Proof of Theorem 3.2

In the following, we show that condition (C3*) implies that condition (C3) is satisfied. We note that each continuous function $S_j({\mathbf {q}})$ has a maximum value and a minimum value in a ball of radius $r^*$, which we label with $S_{\max }^j$ and $S_{\min }^j$. Choosing the radius

$$\begin{aligned} r_j=r^*+\max \left( 0,\frac{{\bar{f}}_j-S^j_{min}}{C_v},\frac{S_{\max }^j-{\bar{f}}_j}{C_v}\right) , \end{aligned}$$

(52)

ensures that the quantity $q_j(S_j({\mathbf {q}})-{\bar{f}}_j)$ has a constant, nonzero sign for all

$$\begin{aligned} {\mathbf {q}}\in {\mathbb {Q}}_j:=\{{\mathbf {q}}\in {\mathbb {R}}^N|~|q_j|> r_j \}. \end{aligned}$$

(53)

First, we assume a positive definite Hessian outside a ball of radius $r^*$. Using a Taylor series expansion of the nonlinearity, we note that outside the $r^*$ ball the following holds:

$$\begin{aligned}&{\mathbf {h}}^T({\mathbf {S}}({\mathbf {q}}+{\mathbf {h}})-{\mathbf {S}}({\mathbf {q}})) =\int _0^1 {\mathbf {h}}^T \frac{\partial ^2 V ({\mathbf {q}}+s{\mathbf {h}})}{\partial {\mathbf {q}}^2}{\mathbf {h}} ds\nonumber \\&\quad>C_v|{\mathbf {h}}|^2,\quad {\mathbf {q}},{\mathbf {h}}\in {\mathbb {R}}^N,\quad 0\le s \le 1,\nonumber \\&\quad |{\mathbf {q}}+s{\mathbf {h}}|>r^*. \end{aligned}$$

(54)

For every point ${\mathbf {q}}\!\in \!{\mathbb {Q}}_j$, we select ${\mathbf {h}}$ to be the vector pointing from the $q_j$-axis to ${\mathbf {q}}$ with minimal length. Denoting the j-th unit vector by ${\mathbf {e}}_j$, we set ${\mathbf {h}}\!=\!{\mathbf {q}}-q_j{\mathbf {e}}_j$ and ${\mathbf {q}}=q_j{\mathbf {e}}_j$. Since $|q_j|\!>\!r^*$, line connecting $q_j{\mathbf {e}}_j$ and ${\mathbf {q}}$ is in the region, where the potential $V({\mathbf {q}})$ is positive definite. From Eq. (54), we obtain

$$\begin{aligned}&({\mathbf {q}}-q_j{\mathbf {e}}_j)^T({\mathbf {S}}({\mathbf {q}})-{\mathbf {S}}(q_j{\mathbf {e}}_j))\nonumber \\&\quad = \sum _{\begin{array}{c} n=1 \\ n\ne j \end{array}}^N q_n\left[ S_n({\mathbf {q}})-S_n(q_j{\mathbf {e}}_j)\right] >0. \end{aligned}$$

(55)

Further, we reduce the j-th coordinate until we reach $|q_j|=r^*$. The line connecting between the points ${{\,\mathrm{sign}\,}}(q_j)r^*{\mathbf {e}}_j$ and $q_j{\mathbf {e}}_j$ lies in the region with a positive definite Hessian. We evaluate (54) for ${\mathbf {q}}={{\,\mathrm{sign}\,}}(q_j)r^*{\mathbf {e}}_j$ and ${\mathbf {h}}\!=\!{\mathbf {q}}-{{\,\mathrm{sign}\,}}(q_j)r^*{\mathbf {e}}_j$ to obtain

$$\begin{aligned}&({\mathbf {q}}-{{\,\mathrm{sign}\,}}(q_j)r^*{\mathbf {e}}_j)^T({\mathbf {S}}({\mathbf {q}})-{\mathbf {S}}({{\,\mathrm{sign}\,}}(q_j)r^*{\mathbf {e}}_j)\nonumber \\&\quad = \sum _{\begin{array}{c} n=1 \\ n\ne j \end{array}}^N q_n\left[ S_n({\mathbf {q}})-S_n(q_j{\mathbf {e}}_j)\right] \nonumber \\&\qquad + (q_j-{{\,\mathrm{sign}\,}}(q_j)r^*)\\&\qquad \left[ S_j({\mathbf {q}})-S_j({{\,\mathrm{sign}\,}}(q_j)r^*{\mathbf {e}}_j)\right] \nonumber \\&\quad>(q_j-{{\,\mathrm{sign}\,}}(q_j)r^*)\left[ S_j({\mathbf {q}})-S_j({{\,\mathrm{sign}\,}}(q_j)r^*{\mathbf {e}}_j)\right] \nonumber \\&\quad >C_v(q_j-{{\,\mathrm{sign}\,}}(q_j)r^*)^2,\quad {\mathbf {q}}\in {\mathbb {Q}}_j.\nonumber \end{aligned}$$

(56)

For $q_j\!>\!0$, Eq. (52) implies that $(q_j-{{\,\mathrm{sign}\,}}(q_j)r^*)$ is positive. Therefore, we obtain from Eq. (56) that

$$\begin{aligned}&S_j(\mathbf {q})>C_v(q_j-r^*)+S_j(r^*{\mathbf {e}}_j)> C_v(q_j-r^*)\nonumber \\&\quad +S^j_{\min }> C_v(r^*+\frac{{\bar{f}}_j-S_{\min }^j}{C_v}-r^*)+S_{\min }^j={\bar{f}}_j,\nonumber \\&\qquad q_j>r_j. \end{aligned}$$

(57)

Similarly, for $q_j\!<\!0$ the quantity $S(q_j-{{\,\mathrm{sign}\,}}(q_j)r^*)$ is negative, therefore Eq. (56) implies

$$\begin{aligned}&S_j({\mathbf {q}})<C_v(q_j+r^*)+\,S_j(-r^*{\mathbf {e}}_j)<C_v(q_j+r^*)\nonumber \\&\quad +S_{\max }^j<C_v(-r^*-\frac{S_{\max }^j-{\bar{f}}_j}{C_v}+r^*)+S_{\max }^j={\bar{f}}_j,\nonumber \\&\qquad q_j^*<-r_j. \end{aligned}$$

(58)

Equations (57) and (58) together imply

$$\begin{aligned} q_j(S_j({\mathbf {q}})-{\mathbf {f}}_j)>0,\quad {\mathbf {q}}\in {\mathbb {Q}}_j, \end{aligned}$$

(59)

which is equivalent to the upper condition (11), if we set $r:=\max _j(r_j)$.

The same argument can be repeated for potentials having a negative definite Hessian. The sign in Eq. (54) changes, and therefore, one obtains

$$\begin{aligned} q_j(S_j({\mathbf {q}})-{\mathbf {f}}_j)<0,\quad {\mathbf {q}}\in {\mathbb {Q}}_j, \end{aligned}$$

(60)

which is equivalent to the lower condition (11), if we set $r:=\max _j(r_j)$.

B Derivations for specific examples

1.1 B1 Necessary bound on the forcing amplitude for system (3)

In the following, we prove a necessary bound on the forcing amplitude (4) for the existence of periodic solutions for system (3) with parameters (5). Specifically, we assume the existence of a twice continuous differentiable periodic orbit ${\mathbf {q}}^*$. Transforming system (3) to modal coordinates, we obtain

$$\begin{aligned}&q_1^*=x_1+x_2,\quad q_2^*=x_1-x_2,\nonumber \\&\ddot{x}_1+c_1{\dot{x}}_1+k_1 x_1 +2\kappa x_1^2=-2\kappa x_2^2, \end{aligned}$$

(61a)

$$\begin{aligned}&\ddot{x}_2+c_1{\dot{x}}_2+(k_1+2k_2) x_2 =f_1. \end{aligned}$$

(61b)

The equation of motion of the second modal degree-of-freedom (61b) is linear, and therefore, the assumed periodic response of the second degree of freedom $x_2$ can be obtained analytically:

$$\begin{aligned} \begin{aligned} x_2&=\frac{8f_m}{\pi ^2}\sum _{k=0}^{\infty } \frac{(-1)^k\sin ((2k+1)\Omega t-\varphi _k)}{(2k+1)^2\sqrt{((k_1+2k_2)-(2k+1)^2\Omega ^2)^2+((2k+1)c_1\Omega )^2}}=\frac{8f_m}{\pi ^2}\sum _{k=0}^{\infty } c_k\sin ((2k+1)\Omega t-\varphi _k) , \\ \varphi _k&=\tan ^{-1}\left( \frac{(2k+1)c_1\Omega }{(k_1+2k_2)-(2k+1)^2\Omega ^2}\right) , \end{aligned} \end{aligned}$$

(62)

Here, we have relabeled the amplitudes for notational convenience. Next, we integrate (61a) over one period and impose periodicity to obtain

$$\begin{aligned}&\int _0^T \left( k_1 x_1+2 \kappa x_1^2 \right) \hbox {d}t= -2 \kappa \int _0^T x_2^2 \hbox {d}t,\nonumber \\&\quad = - T \kappa \frac{64f_m^2}{\pi ^4} \sum _{k=0}^{\infty }|c_k|^2. \end{aligned}$$

(63)

The infinite sum converges to the limit $c_{\infty }$, since it can be majorized by $1/k^6$, i.e.,

$$\begin{aligned} \begin{aligned}&c_{\infty }:=\sum _{k=0}^{\infty }|c_k|^2= \sum _{k=0}^{\infty }\frac{1}{(2k+1)^4(((k_1+2k_2)-(2k+1)^2\Omega ^2)^2+((2k+1)c_1\Omega )^2)}\\&\quad \le \frac{1}{c_1^2\Omega ^2}\sum _{k=0}^{\infty }\frac{1}{(2k+1)^6}\le \frac{1}{c_1^2\Omega ^2}\sum _{k=1}^{\infty }\frac{1}{k^6}. \end{aligned} \end{aligned}$$

(64)

For the parameters (5), we compute the value $c_{\infty }$ numerically and obtain

$$\begin{aligned} c_{\infty }:= 1371.7577441>1371.757744027918. \end{aligned}$$

(65)

By the mean-value theorem applied to Eq. (63), there must be a time instance $t^*\!\in \! \left[ 0,T\right]$ at which the integrand on the left-hand side multiplied by T is equal to the infinite sum on the right-hand side. Calculating the minimum of the parabola in that integrand and inserting the numerical parameter values (5) yields

$$\begin{aligned}&-\frac{k_1^2}{8\kappa }T\le \left( k_1{\tilde{x}}_1(t^*)+2 \kappa {\tilde{x}}_1^2(t^*) \right) T\nonumber \\&\quad =-\kappa T\frac{64f_m^2}{\pi ^4}c_{\infty }, \quad 0\le t^*<T. \end{aligned}$$

(66)

Solving (66) for the forcing amplitude, we obtain

$$\begin{aligned} |f_m|<\sqrt{\frac{k_1^2\pi ^4}{512 \kappa ^2 c_{\infty }}}=0.011777,\quad \kappa >0. \end{aligned}$$

(67)

Since the forcing amplitude (5) is above the threshold (67), the periodic orbit indicated by the harmonic balance method does not exist.

1.2 B2 Failure of the harmonic balance with infinite harmonics

In the following, we construct a forcing for the linear system (6), such that even for infinite number of harmonics in ansatz (2), the harmonic balance procedure yields a periodic orbit that differs from the actual periodic orbit significantly. Generally speaking, the computability of a finite number of terms in a Fourier series of a periodic solution does not guarantee the pointwise convergence of that series to the periodic orbit. We consider the function

$$\begin{aligned}&f_f=\sum _{k=1}^{K}\frac{2}{k^2}\sin (p_k t)\sum _{l=1}^{q_k}\frac{1}{l}\sin (l t),\nonumber \\&\quad p_k=2^{k^3+1},\quad q_k=2^{k^3}, \end{aligned}$$

(68)

which is a truncated version of a classic example due to Fejér (c.f. Edwards [12]). We note that the function (68) is analytic and therefore the forcing

$$\begin{aligned} f(t)=\ddot{f}_f+c{\dot{f}}_f+kf_f, \end{aligned}$$

(69)

is well defined. Applying this forcing in system (6), we obtain the periodic orbit in the form $q^*\!=\!f_f$. The harmonic balance procedure, therefore, produces a Fourier series of the function (68). As Edwards [12] details, the function $f_f$ can be bounded from above by a constant independent of K, while its Fourier series at $t\!=\!0$ is unbounded for $K\!\rightarrow \!\infty$. Therefore, for large enough K the Fourier series of $f_f$ will deviate from the function (68) at $t\!=\!0$. Choosing an appropriately large K leads to a large deviation of the approximative periodic orbit obtained by the harmonic balance from the unique periodic orbit of system (6) with forcing (68). Therefore, the harmonic balance fails to approximate the periodic orbit at $t\!=\!0$.

1.3 B3 Proof of Fact 4.1

In the following, we show that no periodic orbit for system (22) exists, for an appropriately chosen set of parameters. For these sets of parameters, one of the Floquet multipliers of the unforced limit of system (22) equals to one in norm. This introduces the possibility of resonance between the external periodic forcing and the non-trivial solution of the homogeneous part (23), under which no periodic orbit for system (22) can exist.

For further analysis, we introduce the matrices and vectors

$$\begin{aligned}&\mathbf {x}:= \begin{bmatrix} q_1^*\\ \dot{q}^*_1 \end{bmatrix},\nonumber \\&{\mathbf {A}}(t):= \begin{bmatrix} 0&1\\ -k_1-\frac{\kappa A^2}{2}+\frac{\kappa A^2}{2} \cos (2\Omega t -2 \psi )&-c_1 \end{bmatrix}, \nonumber \\&{\mathbf {g}}(t):= \begin{bmatrix} 0\\ f_1(t) \end{bmatrix}. \end{aligned}$$

(70)

With the notation (70), we express system (22) in first-order form

$$\begin{aligned}&\dot{{\mathbf {x}}}={\mathbf {A}}(t){\mathbf {x}}+{\mathbf {g}}(t),\quad {\mathbf {A}}(t+T/2)={\mathbf {A}}(t),\nonumber \\&T=2\pi /\Omega , \end{aligned}$$

(71)

and denote its homogeneous part by

$$\begin{aligned} \dot{{\mathbf {x}}}={\mathbf {A}}(t){\mathbf {x}}. \end{aligned}$$

(72)

Furthermore, we define the adjoint problem,

$$\begin{aligned} \dot{{\mathbf {y}}}=-{\mathbf {A}}(t)^T{\mathbf {y}}. \end{aligned}$$

(73)

To show the nonexistence of a periodic orbit of system (71), we use the following theorem:

Theorem A.2

Assume that system (72) has k linearly independent, non-trivial T-periodic solutions and denote k linearly independent T-periodic solutions to the adjoint system (73) by $\tilde{{\mathbf {y}}}_1$, $\tilde{{\mathbf {y}}}_2$, ..., $\tilde{{\mathbf {y}}}_k$. Then, the non-autonomous system (71) has a T-periodic solution if and only if the orthogonality conditions

$$\begin{aligned} \int _0^T\tilde{{\mathbf {y}}}_j^T{\mathbf {g}}(t)\hbox {d}t=0,\quad j=1,\ldots ,k, \end{aligned}$$

(74)

hold.

Proof

For a proof, we refer to Farkas [13]. $\square$

First, we note system (72) is periodic with period T / 2 (cf. Eq. (71)), where T is determined by the external forcing $f_2$ (cf. Eq. (22)). We denote the complex conjugate Floquet multipliers of system (71) by $\rho _1$ and $\rho _2$ and further obtain from Liouville’s theorem that

$$\begin{aligned} \rho _1\rho _2=e^{\int _{t_0}^{t_0+T/2} {{\,\mathrm{Tr}\,}}\left[ {\mathbf {A}}(s)\right] ds}=e^{-\frac{c_1T}{2}}, \quad \rho _1={\bar{\rho }}_2. \end{aligned}$$

(75)

Equation (75) implies that the Floquet multipliers are located either on the circle with radius $e^{-c_1T/4}$ (red circle in Fig. 8) or on the real axis (blue line in Fig. 8) in the complex plane.

If the forcing $f_2$ is zero, then the parameter A in system (22) is zero and, due to the positive damping value $c_1$, the trivial solution of system (72) stable. Therefore, the Floquet multipliers are located on the red circle in Fig. 8. If we observe instability of the trivial solution to Eq. (72) for some nonzero forcing ($A\!\ne \! 0$), then the Floquet multipliers must have crossed the unit circle in the complex plane. In this critical case, one of the Floquet multipliers is either one or negative one, which we mark with a black square in Fig. 8.

Fig. 8

Locations of the Floquet multipliers of system (72) in the complex plane. The two critical cases, $\rho _1=1$ and $\rho _1=-1$, are marked with black squares. (Color figure online)

If one of the multipliers, $\rho _1$, is one, there exists a non-trivial T / 2-periodic solution of the homogeneous part of system (71). In the case of a Floquet multiplier of negative one, a non-trivial T-periodic solution exists (cf. Farkas [13]). As Farkas details further, in both cases, the adjoint system (72) has a non-trivial T / 2 or T-periodic solution, which we denote by $\tilde{{\mathbf {y}}}$. Analyzing Eq. (73), we conclude that a non-trivial $\tilde{{\mathbf {y}}}$ implies a non-constant value of both coordinates ${\tilde{y}}_1(t)$ and ${\tilde{y}}_2(t)$. We choose the forcing

$$\begin{aligned} f_1(t)=\tilde{y}_2(t). \end{aligned}$$

(76)

Then, the orthogonality condition is

$$\begin{aligned} \begin{aligned} \int _0^{T} \tilde{{\mathbf {y}}}{\mathbf {g}}(t) \text{ d }t= \int _0^{T} {\tilde{y}}_2^2\text{ d }t\ne 0, \end{aligned} \end{aligned}$$

(77)

Clearly, the orthogonality condition (77) is not satisfied and therefore, by Theorem A.2, system (22) has no periodic solution.

1.4 B4 Proof of Fact 4.2

In the following, we show that no periodic orbit for system (1) exists if the geometric nonlinearities possess a global minimum, and the mean forcing is below this minimum value (i.e., Eq. (25) is satisfied). To prove the nonexistence of a T-periodic orbit, we proceed as in Appendix B1, assuming the existence of a twice differentiable periodic orbit ${\mathbf {q}}^*$ for system (1). Integrating Eq. (1) for one period and imposing periodicity yields

$$\begin{aligned} \int _0^T {\mathbf {S}}( {\mathbf {q}}^*(t)) \hbox {d}t=T\bar{{\mathbf {f}}},\quad \Leftrightarrow \quad \int _0^T \left( {\mathbf {S}}({\mathbf {q}}^*(t)) -\bar{{\mathbf {f}}} \right) \hbox {d}t=0 . \nonumber \\ \end{aligned}$$

(78)

By the mean-value theorem, there exist time instances $t^*_j$ within the period at which the integrand in Eq. (78) is equal to zero, i.e.,

$$\begin{aligned} S_j({\mathbf {q}}^*(t^*_j))-{\bar{f}}_j=0,\quad j=1,\ldots ,N,\quad 0\le t_j\le T. \nonumber \\ \end{aligned}$$

(79)

However, due to the choice of the forcing (25), we obtain for $j\!=\!l$ that

$$\begin{aligned} S_l({\mathbf {q}}^*(t^*))-{\bar{f}}_l>0, \end{aligned}$$

(80)

which contradicts (79). Therefore, the periodic orbit cannot exist.

1.5 B5 Proof of Fact 4.3

In the following, we prove that if the forcing amplitude f in the oscillator (28) is above the threshold (29), then no periodic solution to system (28) exists. Again, we assume the existence of a twice continuous differentiable periodic orbit $q^*$ and split the coordinate $q^*$ into a constant and a purely oscillatory part, i.e.,

$$\begin{aligned} {\bar{q}}:=\frac{1}{T}\int _0^Tq^*(t)\hbox {d}t,\quad {\tilde{q}}(t)=q^*-{\bar{q}}. \end{aligned}$$

(81)

Substituting the definitions (81) into the equation of motion (28) yields

$$\begin{aligned}&\ddot{{\tilde{q}}}+c{\dot{q}}+\omega _0^2({\bar{q}}+{\tilde{q}})+\kappa ({\bar{q}}^2+2{\bar{q}}{\tilde{q}}+{\tilde{q}}^2) \nonumber \\&\quad =f\cos (\Omega t). \end{aligned}$$

(82)

Integrating Eq. (82) over one period, we obtain

$$\begin{aligned} \int _0^T {\tilde{q}}^2\hbox {d}t =-T\left( \frac{\omega ^2}{\kappa }{\bar{q}}+{\bar{q}}^2\right) \le \frac{T\omega ^4}{4\kappa ^2}, \end{aligned}$$

(83)

where we have used that ${\tilde{q}}$ has zero mean (cf. definition (81)). Furthermore, we note that the left-hand side of (83) is positive. Since the right-hand side of Eq. (83) is a parabola which is concave downward, it is positive on a closed interval. We thus obtain the upper bound on ${\bar{q}}$ in the form

$$\begin{aligned} |{\bar{q}}|<\frac{\omega ^2}{|\kappa |}, \end{aligned}$$

(84)

which is independent of the sign of $\kappa$. Since $q^*$ is twice continuously differentiable, it can be expressed in a convergent Fourier series. We denote the Fourier coefficients of ${\tilde{q}}$ by

$$\begin{aligned} {\tilde{q}}^k:=\frac{1}{T}\int _0^Tq_t e^{-\mathrm {i} k \Omega t} \hbox {d}t,~\quad k\in {\mathbb {Z}}. \end{aligned}$$

(85)

Using Parseval’s identity and Eq. (83), we obtain an upper bound on the Fourier coefficients of the assumed periodic orbit as follows:

$$\begin{aligned}&|{\tilde{q}}^k|\le \left( \sum _{k\in {\mathbb {Z}}}|{\tilde{q}}^k|^2\right) ^{1/2}=\left( \frac{1}{T} \int _0^T {\tilde{q}}^2\hbox {d}t\right) ^{1/2}\nonumber \\&\quad \le \frac{ \omega ^2}{2|\kappa |},\quad k\in {\mathbb {Z}}. \end{aligned}$$

(86)

Multiplying Eq. (82) with $e^{-\mathrm {i}\Omega t}$ and integrating over one period yields

$$\begin{aligned}&\int _0^T(\ddot{{\tilde{q}}}+c\dot{{\tilde{q}}}+\omega _0^2{\tilde{q}}+2\kappa {\bar{q}}{\tilde{q}}) e^{-i \Omega t} \hbox {d}t\nonumber \\&\quad +\int _0^T\kappa {\tilde{q}}^2 e^{-i \Omega t} \hbox {d}t=\frac{f}{2}. \end{aligned}$$

(87)

From Eq. (87), we obtain

$$\begin{aligned} \begin{aligned} \left| \frac{f}{2}\right|&\le \left| \int _0^T(\ddot{{\tilde{q}}}+c\dot{{\tilde{q}}}+\omega _0^2{\tilde{q}}+2\kappa {\bar{q}}{\tilde{q}}) e^{-i \Omega t} \hbox {d}t\right| \\&\quad +|\kappa |\int _0^T |{\tilde{q}}^2(t)||e^{-i\Omega t}| \hbox {d}t \\&\le |(-\Omega ^2+\mathrm {i}c\Omega +\omega ^2+2\kappa {\bar{q}}){\tilde{q}}^1|+|\kappa |\frac{\omega ^4}{4\kappa ^2}\\&\le \frac{ \omega ^2}{ 2|\kappa |} \left( |-\Omega ^2+\mathrm {i}c\Omega +\omega ^2|+ 2\omega ^2 \right) +|\kappa |\frac{\omega ^4}{4\kappa ^2}, \end{aligned} \end{aligned}$$

(88)

where we have used the upper bounds (84) and (86). Equation (88) gives an upper bound for the forcing amplitude f of the oscillator (28). For forcing amplitudes exceeding this threshold, we obtain a contradiction and therefore no periodic orbit can exist for the oscillator (28).

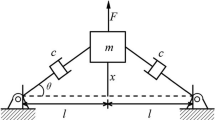
1.6 B6 Proof of Fact 4.4

We show that the chain system (31) with the parameters (32) satisfies the conditions of Theorem 3.1 and hence a steady-state response exists. First, we show that the conditions (C2) and (C3*) on the geometric nonlinearities are satisfied for the set of parameters (32). The definiteness of the damping matrix (i.e., condition (C1)) can be shown in a fashion  similar to the definiteness of the Hessian.

As for condition (C2), the spring forces of system (31) can be derived from the potential

$$\begin{aligned} V({\mathbf {q}})= & {} \int _0^{q_1}S_{1}(-p) dp +\sum _{j=2}^{N} \int _0^{q_{j-1}-q_j} S_{j}(p) \hbox {d} p\nonumber \\&+\int _0^{q_N}S_{N+1}(p) \hbox {d}p. \end{aligned}$$

(89)

Since the spring forces in of system (31) are continuous by assumption, the integrals in Eq. (89) exist. With the notation

$$\begin{aligned} S_{j,l}:=\frac{\partial }{\partial q_l}\left( S_j(q_{j-1}-q_j)\right) , \end{aligned}$$

(90)

the Hessian of the potential is given by

$$\begin{aligned} {\mathbf {H}}:=\frac{\partial ^2 V({\mathbf {q}})}{\partial {\mathbf {q}}^2}= \begin{bmatrix} -S_{1,1}+S_{2,1}&S_{2,2}&0&&\\ -S_{2,1}&-S_{2,2}+S_{3,2}&S_{3,3}&0&\\ 0&-S_{3,2}&-S_{3,3}+S_{4,3}&S_{4,4}&0&\\&0&\ddots&\ddots&\ddots&0 \\&0&-S_{N\!-\!1,N\!-\!2}&-S_{N\!-\!1,N\!-\!1} + S_{N,N\!-\!1}&S_{N,N} \\&&0&-S_{N,N\!-\!1}&-S_{N,N}+S_{N\!+\!1,N} \end{bmatrix}.\nonumber \\ \end{aligned}$$

(91)

Due to the choice of parameters (32), we have following identities

$$\begin{aligned} S_{j,j}<0,\quad S_{j+1,j}>0,\quad S_{j,j}=-S_{j,j-1}, \end{aligned}$$

(92)

which implies that the main diagonal entries of the Hessian (91) are positive and the off-diagonal elements negative. We define the matrices

$$\begin{aligned} {\mathbf {H}}^j=\begin{bmatrix} -S_{1,1}-S_{2,2}&S_{2,2}&0&&\\ S_{2,2}&-S_{2,2}-S_{3,3}&S_{3,3}&0&\\ 0&S_{3,3}&-S_{3,3}-S_{4,4}&S_{4,4}&0&\\&0&\ddots&\ddots&\ddots&S_{j,j} \\&&0&S_{j,j}&-S_{j,j} \end{bmatrix}\in {\mathbb {R}}^{j\times j}, \end{aligned}$$

(93)

which are equivalent to the leading minors of the Hessian, except for the last term in the main diagonal where the term $-S_{j+1,j}$ is missing. Therefore, ${\mathbf {H}}^N$ is not equal to ${\mathbf {H}}$. The matrices ${\mathbf {H}}^j$ can be constructed recursively as follows:

$$\begin{aligned} {\mathbf {H}}^1=-S_{1,1}, \quad {\mathbf {H}}^{j+1}= \begin{bmatrix} {\mathbf {H}}^j&{\mathbf {0}} \\ {\mathbf {0}}&0 \end{bmatrix} + \begin{bmatrix} {\mathbf {0}}&{\mathbf {0}}&{\mathbf {0}} \\ {\mathbf {0}}&-S_{j,j}&S_{j,j} \\ {\mathbf {0}}&S_{j,j}&-S_{j,j} \end{bmatrix}.\nonumber \\ \end{aligned}$$

(94)

We show that the matrices ${\mathbf {H}}^j$ are positive definite by induction. As a first step, we note that ${\mathbf {H}}^1$ is positive definite. Performing the induction step, we have

$$\begin{aligned} {\mathbf {x}}^T{\mathbf {H}}^{j}{\mathbf {x}}= {\mathbf {x}}^T \begin{bmatrix} {\mathbf {H}}^{j-1}&{\mathbf {0}} \\ {\mathbf {0}}&0 \end{bmatrix} {\mathbf {x}}+ {\mathbf {x}}^T \begin{bmatrix} {\mathbf {0}}&{\mathbf {0}}&{\mathbf {0}} \\ {\mathbf {0}}&-S_{j,j}&S_{j,j} \\ {\mathbf {0}}&S_{j,j}&-S_{j,j} \end{bmatrix} {\mathbf {x}}. \nonumber \\ \end{aligned}$$

(95)

Since the matrix ${\mathbf {H}}^{j-1}$ is positive definite, the first summand in (95) is always positive unless ${\mathbf {x}}$ aligns with the $x_j$-axis, i.e., $x_1 {=}x_2 {=}\cdots {=} x_{j- 1} {=} 0$. Along this axis the first quadratic form is zero and the second quadratic form, however, yields $-S_{j,j}x_j^2$ which is positive. For the case $x_j {=} 0$ and $|\tilde{{\mathbf {x}}}| {=}|\left[ x_1,\dots ,x_{j-1}\right] ^T| {>} 0$, we obtain

$$\begin{aligned}&\tilde{{\mathbf {x}}}^T{\mathbf {H}}^{j-1} \tilde{{\mathbf {x}}}+{\mathbf {x}}^T \begin{bmatrix} {\mathbf {0}}&{\mathbf {0}}&{\mathbf {0}} \\ {\mathbf {0}}&-S_{j,j}&S_{j,j} \\ {\mathbf {0}}&S_{j,j}&-S_{j,j}\nonumber \\ \end{bmatrix} {\mathbf {x}} \ge \tilde{{\mathbf {x}}}^T{\mathbf {H}}^{j-1} \tilde{{\mathbf {x}}},\nonumber \\&\quad |\tilde{{\mathbf {x}}}|>0, \end{aligned}$$

(96)

where we have used the fact that the matrix in the second quadratic form in Eq. (95) is positive semi-definite. Merging both cases

$$\begin{aligned} {\mathbf {x}}^T{\mathbf {H}}^{j}{\mathbf {x}}\ge \left\{ \begin{array}{l l l} -S_{j,j} x_j^2>0, &{}\quad |\tilde{{\mathbf {x}}}|=0, &{}\quad |x_j|>0, \\ \tilde{{\mathbf {x}}}^T{\mathbf {H}}^{j-1} \tilde{{\mathbf {x}}}>0, &{}\quad |\tilde{{\mathbf {x}}}|>0, &{}\quad x_j=0, \end{array} \right. \nonumber \\ \end{aligned}$$

(97)

which implies positive definiteness of all matrices ${\mathbf {H}}^j$. Since the Hessian can be written as the sum of the positive definite matrix ${\mathbf {H}}^N$ and a positive semi-definite the matrix, i.e.,

$$\begin{aligned} {\mathbf {H}}={\mathbf {H}}^N+ \begin{bmatrix} {\mathbf {0}}&{\mathbf {0}}\\ {\mathbf {0}}&-S_{N+1,N} \end{bmatrix}, \end{aligned}$$

(98)

we conclude that the Hessian (91) positive definite.

Since the damping matrix is in the form of the Hessian (91), the positive definiteness proof applies for the damping matrix as well. Therefore, we have verified the remaining condition (C1) of Theorem 3.1, and the existence of a periodic orbit is guaranteed by Theorem 3.1.

We note that in the case of $S_{N+1,N}\!=\!0$, the Hessian ${\mathbf {H}}$ coincides with the matrix ${\mathbf {H}}^N$, which is positive definite. Therefore, the assumptions on the parameters (32) can be relaxed to include this case.