1 Introduction

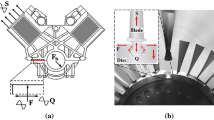
A complex mechanical structure such as a turbomachine is made up of many individual components connected through mechanical joints. These joints create interfaces between the components. Some of the crucial joints such as blade root, shroud contact, under-platform dampers are designed to undergo relative motion at the interfaces to provide friction damping and reduce the peak vibration levels. The partial or full slip occurring at the interfaces during vibration excitation could lead to fretting wear [1, 2]. Wear is a multi-physics and multi-scale phenomenon. Fretting wear leads to loss of material over accumulated millions of cycles and damage the contact interface. The damages could amplify especially when the operating frequencies of the system are close to the resonant frequencies of the structure. Turbomachines are carefully designed for performance and efficiency. Unintended degradation of the interfaces due to wear could hamper the performance and lead to undesirable consequences.

The cyclically symmetric nature of the turbomachinery components such as bladed discs leads to high modal density in certain frequency ranges. As a result, in case of synchronous excitation, avoiding resonances within the operating range is often not possible, especially in aero-engines, that operate at different speeds. Hence, controlling the maximum vibration amplitudes at resonances is crucial to prevent high cycle fatigue damage accumulation and failure. This can be achieved by introducing additional friction damping. This damping is caused by the relative motion of surfaces sliding against each other and can be well represented with a structural damping model. Due to the nonlinear nature of friction damping, performing numerical simulations based on linear models to predict the vibration amplitude of frictionally damped systems is not sufficient. To achieve reliable designs, accurate analytical/numerical structural and dynamic models considering the nonlinear effect of joints are necessary to have high fidelity simulations. The recent book by Brake [3] provides a holistic view on trends and advancements in the field of the mechanics of jointed structures. To model these joints, there are many contact models available in the literature. The commonly used heuristic models are 2D and 3D Jenkins elements, Iwan, LuGre, Bouc–Wen, etc. [4,5,6,7,8,9,10,11,12,13]. They can be classified into node-to-node and patch-to-patch models with relative strengths and weaknesses. The commercial Finite Element codes available today are not capable of solving these large nonlinear dynamic problems in an efficient manner. Botto [14] proposed to reduce with a lossless static reduction the matrices that characterize a contact problem. The small dimensions of the reduced matrices make the iterative solution of the contact problem very fast. FE codes that usually use time-domain techniques [15, 16] are very computationally intensive and have scalability issues for large problems. To circumvent this problem, in-house research codes were developed in many research institutes and industries. These codes use the Harmonic Balance Method (HBM), assuming periodic response of the system under periodic excitation [17]. HBM allows to compute directly steady-state conditions, considering the friction contact nonlinearity with a reasonable complexity and substantially short computational times. Within the HBM framework, the Dynamic Lagrangian Frequency Time (DLFT) [18] method was developed. This approach does not use contact elements to couple bodies in contact but enforces direct coupling by means of Lagrange Multipliers.

Considering the effect of fretting wear to predict the complex nonlinear dynamic response is gaining attraction in the research community. The work done by Salles et al. [18, 19] is one of the first studies in this regard that used DLFT technique to analyse the effect of fretting wear at the under-platform dampers and at the blade root. Armand et al. [20, 21] used a combination of semi-analytical solver using BEM (Boundary Element Method) and HBM technique to predict the effect of wear numerically on the dynamic response. In a previous work [22], the authors used a realistic coupled static/dynamic HBM technique to study the effect of wear at the shrouds of a bladed disc. Predicting the effect of wear at the shroud differs largely from the blade-root or under-platform dampers. The major difference is that the contact preload at the coupled shroud varies as wear progresses, while the contact preload is relatively constant at the root joint or at the under-platform contact. Shrouds are usually assembled with an initial preload to provide certain designed structural stiffness and sealing. However, over its operational lifetime wear could result due to micro-slip at the contact interfaces and cause loss of preload and then lead to fretting wear and high vibrational amplitudes. Amplitudes exceeding a certain limit could be detrimental to the engine and lead to degraded functioning. In the worst case, when the preload reduces to zero, the blade becomes a free-standing cantilever beam undergoing large vibrations leading to unexpected high stresses.

Albeit, these studies are so far only numerical predictions. Today’s need is to assess the effect of wear on the dynamics of structures and then to use these data for an experimental validation of the proposed numerical models. Later, the correlated models can be successfully used to develop predictive tools to supplement parametric sensitivity study with sufficient confidence. Several detailed studies focussing on fretting wear and evolution of contact parameters are available in the literature [23,24,25,26,27,28,29,30,31,32,33,34,35].

Despite these crucial studies gave many insights into the contact behaviour, the effect of fretting wear on structural dynamics is still an open field. To the author’s knowledge, only one study so far—Fantetti et al. [23]—experimentally studied the effect of fretting wear, on a fretting test rig available at Imperial College London. This study uncovered important revelations on the evolution of contact interface and contact parameters such as friction coefficient, tangential contact stiffness and energy dissipation tracking the evolution of hysteresis cycles. The Bouc–Wen contact model was used to numerically predict the effect of wear. Nevertheless, there is the need for more experimental studies to better describe the effect of wear, for example a parametric analysis with different loading conditions could be very useful. In particular, when the amount of static preload depends on the amount of wear accumulated during the vibration, as in shrouded blades. To study the effect of static preload varying with wear, as in blade shrouds, needs specially designed test rigs.

There are a few fretting test rigs specifically designed to study the fretting wear and its effects on bladed disc contacts. Two fretting rigs [36, 37] were designed at Politecnico di Torino AERMEC to study the effect of large number of wear cycles also at high temperatures on the contact parameters, namely friction coefficient, contact stiffness and energy dissipation. Studying the effect of wear on the dynamics of this rig is not so straightforward. The fretting test rig at Imperial College London [38] was built to study the effect of fretting wear and the evolution of contact stiffness over small to large number of wear cycles. In [23], the effect of wear on the dynamics of the friction rig was investigated together with the steady-state evolution of contact parameters.

This paper describes a novel test rig purposely designed and developed to study the effect of fretting wear on the forced response of a mechanical system. To this end, the contact surfaces must undergo a very large number of fretting wear cycles. The test rig was also designed with the capability to study the effect of changing contact preload with progressing wear as seen at the shroud contacts. The first part of the paper describes the design, instrumentation and set-up of the test rig. The second part presents the results with long-term effects of wear. Results are given in terms of hysteresis loops, wear volume and evolution of frequency response at various wear conditions. The optical images of the specimen surface scans tracking the real worn area and its evolution are also presented. The goal of the study is to emphasize the change in dynamics of the test rig with the progressing wear until full loss of contact. The test rig is suitable to perform variety of experimental campaigns and build a database of collection of test results for future exploitation and validation of currently available numerical solvers studying nonlinear forced response with friction contacts and fretting wear.

2 Novel test rig

2.1 Description of the test rig

The goal of the new test rig is to experimentally study the effect of fretting wear on the dynamic response of a mechanical system. The system is loaded with a steady state excitation and undergoes a large number of fretting wear cycles.

The following criteria were adopted for the design of the test rig:

  • The mechanical system must have well separated resonance peaks in the dominant slip direction.

  • The set-up should permit experiment for a wide range of contact preload to dynamic excitation ratio.

  • The replacement of contact specimens is allowed for testing different materials and surface roughness.

  • The design should allow for accurate displacement and force measurements to be performed as close as possible to the contact region.

  • The tangential relative displacement at the contact is large enough to generate high dissipated energy and simulate severe wear.

This type of response must be exhibited for various normal contact loads so that the changes due to fretting wear are easily detected in the selected range of frequencies. The test article is thought of as analogous to a blade with tip shroud in a turbine bladed disc, namely a cantilever beam with a friction contact at the free end. The contact is loaded with a known preload given by means of interference fit, as in the tip shroud. For a full characterization of the contact behaviour, the measurement system must be capable of measuring the static and dynamic contact forces during operation. The measurement of relative displacement at the contact is also needed to record the slip-stick behaviour and plot hysteresis loops at each fretting cycle.

The rig is made of two main parts, as shown in Fig. 1. The first part includes the cantilever beam, connected to a column whose base is fixed to a table. The free length of the beam is 310 mm with a rectangular cross section of 60 mm × 10 mm, having a dominant bending mode well separated from other modes. The beam length and cross-sectional dimensions can be customized in future to simulate different natural frequencies. The column, a bulk component, houses the beam with 15 screw-pair and a cover plate for even tightening and load distribution to enable a connection as rigid as possible. The column is attached to the table via 8 screws. The actual images of the test rig can be seen in Fig. 2. The second part includes a contact loading mechanism designed to load the contact with certain preload. A detailed explanation of the contact loading mechanism is given in Sect. 2.1.

Fig. 1
figure 1

Rendered image of the test rig along with the named reference axes

Full size image
Fig. 2
figure 2

Actual images of the test rig, shaker, L-separator assembly, top and bottom specimens

Full size image

The beam has a slot at the free end in which one specimen (the upper specimen) could be mounted via three screws. The other specimen (the lower specimen) is mounted onto the L-separator via three screws. An L-separator, a right-angled component, is mounted on the top of the moving platform with two force transducers mounted at a 45° angle to the normal contact direction. The two force transducers can record the static and dynamic force components throughout the test. Because of its geometry, this device “separates” the contact force into two components along the load cell axis so that the load cell measures the forces without crosstalk effect. Since this device is made of two limbs at 90 degrees to each other, it makes a “L-shape”. Hence the name “L-separator”. The design criteria and the functioning of the L-separator are described in detail in [39]. The top specimen has a contact surface of 2 mm × 5 mm with a nominal area of 10 mm2, while the bottom specimen has a larger flat counter surface.

The specimen couple is designed as replaceable parts, which can be customized with known contact geometry and surface properties beforehand. The contact geometry can be modified with different nominal contact area and combinations of flat, cylinder or sphere. Theoretically, the contact area can be modified to as low as 1 mm2 and up to 25 mm2. Figure 3 shows the rendered and real images of the contact pair with partial and fully worn specimens. The upper and lower specimens are fixed to their respective housing components by inserting into the ‘slots’ with mating walls and screwed using 3 × M3 screws. This way the specimens are secured well and any possible uncertainty arising due to the clamping is reduced. Moreover, this clamping system allows assembling the specimen in the same position, at least within the machining tolerances, after disassembling and reassembling the specimen for the surface measurements. Figure 4 shows the cross section of the specimens and its mounting arrangement and a real image of the assembly.

Fig. 3
figure 3

Contact pair, mid-wear and fully worn specimens

Full size image
Fig. 4
figure 4

Close-up view and cross section at the contact a rendered image b real image

Full size image

A split beam laser velocimeter, in combination with its controller, is used to measure the relative velocity between the contact surfaces during the wear test. The displacement is calculated by integrating the velocity signal. The two laser beams are pointed one to the top specimen and the other to the bottom specimen, as close as possible to the contact point. The relative velocity is obtained by taking the difference of the two signals. The time signal is read by the Data Acquisition System (DAQ).

The cantilever beam is excited by an electromagnetic shaker close to the fixed support at low mobility point. This helps to inject the energy into the beam with relatively low amplitudes of the moving mass of the shaker. The shaker is rated up to 100 N. The beam is excited at a fixed frequency for the wear test and a frequency sweep to observe the dynamic response. A load cell is placed between the beam excitation point and the stinger to measure the applied force. A uniaxial accelerometer is mounted onto the tip of the beam in the tangential direction to record the acceleration during the frequency sweep to record the response of the system.

The whole test rig is mounted on a pneumatic table. The material used for all the components is AISI 304. The test rig is set up at the LAQ AERMEC Lab in Politecnico di Torino.

2.2 Contact loading mechanism

This section provides a detailed description of the contact loading mechanism. The requirement of the loading assembly is to have precise, stable and separated natural frequencies from that of vibrating beam modes. In this way, the modal participation of the support when the contact is engaged is minimum. One can visualize the effect of wear on the response peaks and frequency shifts if any. During the design phase, modal analysis has been carried out to study the natural frequencies of the L-separator and the contact loading mechanism so as to not interfere in the interested frequency range. The first modes obtained are over 2000 Hz, and this has been verified using experimental modal analysis and found to be over 1200 Hz, which is well beyond the interested frequency range. Also, to accommodate the changing preload condition with progressing wear, the platform must be stable and locked at a certain determined height during the test. The principle is based on a standard screw-lift system with a vertical moving platform. The exploded view of the loading assembly is depicted in Fig. 5.

Fig. 5
figure 5

Exploded view of the contact loading system

Full size image

The moving platform translates up and down by rotating the loading nut. This motion produces interference fit between the two contact surfaces so that the prescribed static preload is applied. The cross section of the assembly is shown in Fig. 6. The figure also shows the forces measured from the two load cells and resolved to obtain the tangential and normal contact forces by means of the following equations:

$$ \begin{aligned} F_{t} & = F_{1} *\cos \left( {45^{ \circ } } \right) - F_{2} *\cos \left( {45^{ \circ } } \right) \\ F_{n} & = F_{1} *\cos \left( {45^{ \circ } } \right) + F_{2} *\cos \left( {45^{ \circ } } \right). \\ \end{aligned} $$
(1)
Fig. 6
figure 6

Cross section of the screw lift contact loading mechanism

Full size image

The highlight of this arrangement is that there is the possibility of simulating the ‘changing preload’ with wear. The platform is raised to any desirable height and locked at that position. The height of the platform governs the resulting static preload. In this way, the contact between the two elements of the contact pair is engaged and the cantilever beam has a certain deflection. The load cells connected to the L-separator allows measuring the value of static contact preload when the contact is engaged. As wear occurs and there is loss of material at the contact, the interference between the two bodies in contact reduces as well as the cantilever beam deflection reduces and the normal static preload. This type of changing preload with wear is commonly observed in bladed discs with shroud contacts.

The base has a 140 mm diameter male screw threads with 40 mm screw length and 2 mm pitch. A loading nut with counter female threads is mounted to the base and flushes onto moving platform as shown in Fig. 6. A lock nut is provided to ensure the loading nut is secured in place. Two guide pins passing through the moving plate and the base constrain the rotating DOF and maintain the alignment of the platform and contact orientation. Now, there is still one DOF left to constrain, i.e. the vertical direction. Six screws with nut and washer connects the moving platform with the loading nut at any given desirable platform height. To achieve this, the loading nut has elongated slots and the moving plate has 18 through holes. This ensures at any given rotation angle, there are at least six locations where the screws can be used to constraint the moving plate to the loading nut. In this way, all DOFs are constrained.

2.3 Instrumentation and data acquisition system

A 16 channel SCADAS Mobile data acquisition system is used to acquire the time signals of the shaker stinger-beam force transducer, L-separator left and right force transducers, relative displacement laser, accelerometers and to control the shaker input signal. The Simcenter Testlab software modules clubbed to SCADAS Mobile hardware are used to perform the wear tests and to measure FRFs at defined intervals. Figure 7 shows the instrumentation and sensors used by the test rig. The DAQ is connected to the computer, and the time signals are recorded during wear test and FRFs during frequency sweep.

Fig. 7
figure 7

Instrumentation of the test rig

Full size image

2.4 Test plan

To study the impact of fretting wear on the dynamics of the test rig, the beam must be excited at a fixed frequency for a set number of cycles. The choice of the frequency of excitation and excitation force is discussed in the results section. In a typical metal to metal contact with nominal loading conditions subjected to fretting wear, the amount of wear occurred is minuscule in one vibration cycle. A few millions of fretting cycles are needed to substantially observe a loss of material at the contact and to visualize the effect on the system FRFs. It would also be useful to record surface scans using optical interferometer at various wear intervals. To avoid uncertainty due to disassembling and assembling the specimens at various intervals for specimen scans during the full length test, the frequency sweeps have to be performed before the removal and after fixing the specimens at each interval and ensure the contact is loaded to the same level. To achieve this, the height of the moving platform is closely monitored, and the same height is ensured throughout the test. Hence, a smart test plan is needed to capture surface scans, frequency sweeps and a number of wear cycles at fixed frequency. Figure 8 shows a schematic representation of the test plan to study the effect of wear on the forced response dynamics. The whole test is carried out at room temperature.

Fig. 8
figure 8

Test plan embedding surface scans, frequency sweeps and wear cycles at a fixed frequency

Full size image

The plan for one full range test is devised to be:

  • Scan the specimen surfaces of the contact pair using a non-contact 3D optical profilometer.

  • Run the frequency sweep with pristine specimen contact pair.

  • Run a set number of vibration cycles at a fixed frequency, for example 0.5 million cycles.

  • Run the frequency sweep.

  • Remove the specimens and obtain intermediate worn out surface profiles using profilometer.

  • Reassemble the contact pair and repeat the frequency sweeps, fixed frequency wear cycles and surface scans until a desired total number of wear cycles are obtained or full loss of contact.

3 Experimental results and discussion

3.1 System identification

The first step before proceeding with the actual full range test plan is to characterize the test rig and understand its actual dynamic behaviour under open and closed contact conditions by means of an experimental modal analysis. The bolted joints and contact interfaces such as the connections between the beam and the column, column and the table, loading mechanism could differ from the dynamic behaviour as computed by the numerical FE models. The bolted joints are never perfect and can introduce flexibility and damping, undesirable from the numerical analysis point of view. To collect the FRF curves necessary to the experimental modal analysis of a system, two methods were contemplated, namely, roving hammer test and roving accelerometer test. In this case, roving hammer test was selected as a more suitable option because the accelerometers can be fixed, and numerous hammer impacts could be performed freely and avoid accelerometer mass loading. Hence, a roving hammer test was performed on various locations on the test rig. Figure 9 shows the roving hammer impact points set-up on the test rig and the 3 accelerometer locations in tangential, normal and axial direction from the contact point of view. Total of 107 impact locations were chosen to visualize experimental mode shapes with a fine mesh distribution.

Fig. 9
figure 9

Roving hammer impact locations to characterize the test rig and visualize the experimental mode shapes

Full size image

Table 1 shows the experimental modal analysis results obtained using roving hammer test for open and stuck contact. The mode shapes are visualized at different natural frequencies to understand the behaviour of the test rig by plotting and connecting the mesh using 107 impact locations. The dominant displacement direction for each of the first modes is shown in the table to understand the behaviour of the test rig. Nevertheless, due to the design of the test rig and the lateral connection of the beam to the column (refer Fig. 1), in mode shapes dominated by bending in the tangential direction, displacement in normal direction also occurs.

Table 1 Experimental modal analysis results obtained using roving hammer test for open and stuck contact
Full size table

Figure 10 shows the dynamic response of the test rig for open and closed contact conditions in tangential, normal and axial direction with respect to the contact with shaker excitation. The open case is generated by not engaging the contact and the beam acting as a free cantilever. The stuck case is generated by applying a very high contact preload. For over 150 N contact preloads, no relative displacement at the contact was observed by the laser. These curves can be used as linear reference open case and stuck case to highlight the nonlinearity due to friction contact and the impact of fretting wear on the evolution of system dynamics.

Fig. 10
figure 10

Frequency response function of the test rig with shaker excitation for open and closed contacts (tangential, normal and axial directions are with respect to the contact)

Full size image

3.2 Effect of excitation amplitude

The resonance peaks of interest are the modes which correspond to the maximum relative displacement in the tangential direction. The frequency range corresponding to these peaks for closed contact is between 240 and 450 Hz. There are two dominant modes to look-out for around 280 Hz and 400 Hz. The upper plot in Fig. 11 shows the FRFs when the beam is excited using a shaker and a frequency sweep is run in this frequency range for various excitation forces under a fixed contact preload. The FRFs are recorded using an accelerometer attached in the tangential direction on the beam close to the contact. Also, the lower plot in Fig. 11 shows the corresponding receptance as measured by the relative displacement laser close to the contact. The excitation force is varied from 5 to 80 N in 9 intervals. It is interesting to see the effect of increasing excitation has on the 400 Hz peak. Due to the nonlinearity in the system induced by friction contact, the level of excitation affects the system configuration leading to different operational deflection shapes at different excitation force levels. As a result, the accelerance of the measured DOF becomes force dependent as shown in Fig. 11.

Fig. 11
figure 11

FRF of the test rig for various excitation at a fixed preload as recorded by the accelerometer in tangential direction (top). Corresponding receptance as recorded by the relative displacement laser (bottom)

Full size image

3.3 Determination of excitation frequency and excitation force

So far, the test rig dynamic behaviour under various loading conditions has been experimentally characterized. The next step was to decide the frequency at which the fretting wear to be run for a few millions of cycles to obtain substantial wear up to the potential full loss of contact. From the previous section, it was clear that the contact experiences the maximum relative displacement for the shaker excitation force around 70 N at 280–290 Hz. The energy dissipation is the area under the curve of hysteresis loops, i.e. the product of friction force and the relative tangential displacement. Figure 12 shows the hysteresis loops obtained at 290 Hz frequency for various excitation forces. The hysteresis loops acquisition is performed by collecting 60 data points per cycle. It is clear that a large excitation force determined a wider area of the hysteresis cycle, corresponding to a higher value of dissipated energy per cycle. The asymmetry of the hysteresis cycles, clearly visible in Fig. 12, is due to a variation of normal load during vibration [40] possibly due to:

  • Asymmetry in the test rig design, already mentioned in Sect. 3.1;

  • Non-perfect alignment of the contact surfaces.

Fig. 12
figure 12

Hysteresis loops for various excitation at 290 Hz frequency (each curve plots 100 cycles at each excitation)

Full size image

Table 2 shows the relationship between the dissipated energy per cycle, the relative displacement and the periodic excitation amplitude. For excitation forces larger than 50 N, the contact experiences stick and full slip behaviour. The transition between stick to slip can also be observed. For excitation forces below 50 N, the contact does not experience full sliding and only stick to micro-slip regime.

Table 2 Energy dissipated per cycle for various excitation
Full size table

From the above-mentioned results, it was concluded that, for the accelerated wear test, the best option was to excite the test rig at 70–80 N at 290 Hz for the maximum energy dissipation at each cycle amounting to approximately 1400 µJ with a relative displacement of 50 µm. The energy dissipation and the relative displacement are very sensitive to the magnitude of excitation force in the nonlinear range due to the nonlinearity introduced by the friction contact. Hence, even small variation in the excitation amplitude could result in large swings in the energy dissipation at each cycle.

Figure 13 shows the normal and tangential contact force at one vibration cycle as recorded by the force transducers (\(F_{1} \;\& \;F_{2}\)). The coefficient of friction can be computed by drawing an envelope above and below the friction contact force for the \(+ \mu N\) and \(- \mu N\) friction limit. In this way, the coefficient of friction is computed to be approximately 0.9 for the plain AISI 304 metal to metal dry contact as shown in the figure. Figure 13 also shows a high frequency component of the contact forces. A Fourier analysis of the response showed the contribution of the 4th harmonic, whose frequency was very close to one of the higher natural frequencies of the test rig, experimentally identified at around 1160 Hz.

Fig. 13
figure 13

Normal and tangential contact force at one cycle

Full size image

3.4 Full range test results

After the set-up and commissioning of the test rig, the full range test was performed as per the test plan. The test parameters are set to 70 N as excitation force, 31 N contact preload, 290 Hz as excitation frequency for wear test, 240 to 450 Hz frequency range for the frequency sweep. The test was run until the full loss of contact is observed. The full loss of contact occurred for 16 million wear cycles resulting in 8 intervals for the specimen surface scans and 32 intervals for the intermediate frequency sweeps every 0.5 million cycles to record the effect of wear on the FRFs. The repeatability after disassembly and reassembly procedure of the specimens for surface scans was ensured by performing before and after frequency sweeps, and monitoring and ensuring the moving platform height is precisely the same throughout the test. During the test, the evolution of following quantities was tracked: contact area, hysteresis loop, contact preload, wear volume, dissipated energy and forced response.

3.4.1 Contact area evolution

The surface scans of the upper and lower specimen were obtained using a high-resolution optical 3D surface measurement device. The vertical and lateral resolution achieved during the surface measurements were 2.2 and 0.5 μm, respectively. The measured surface topology was then exported to and analysed in a topology analysis software. The specimen surfaces were obtained by milling and polishing and resulted in average surface roughness of 1 μm. The specimens were cleaned before the surface scans were obtained. For the worn specimens, the oxide debris was removed, cleaned and then, the surface scans were done. For the full test plan, a whole of 8 scans were done at 0 cycles, 0.5 million, 1.5 million, 4 million, 7 million, 10 million, 13 million and 16 million cycles. Figure 14 presents the worn surface images of upper and lower specimens at various intervals. The surface is levelled and oriented so that one-on-one visual comparison can be made at the optimal scale. It can be seen through the images that, though the nominal contact area is around 10 mm2, only a partial initial contact area is established at the beginning of the wear test. This is due to the fact that the cantilever beam deflected by the application of normal load through the loading mechanism makes only an ‘edge contact’ at the inner edge closest to the column. Also, the ridges at the inner edge of the upper specimen contribute to the localized edge contact. As the wear progresses, more and more area is engaged and can be seen through the evolution of the surface images. Such a localization of the contact area is fully in line with what actually happens in shrouded blades [41], where a small portion of the theoretical contact area ends up being actually in contact.

Fig. 14
figure 14

Worn surface images of upper and lower specimens at various wear intervals

Full size image

The worn area is representatively similar on the upper and lower specimens. Figure 15 shows a better representation of close-up through real images of the upper and lower specimens at different wear intervals. It is calculated that the true area available after machining of the specimens is 7.8 mm2, though the nominal area mentioned in the design was 10 mm2. The marginal area is lost at the edges and during the manufacturing process. The figure also highlights the actual perimeter of the worn area for the worn images. The 3D images also show that the specimen surfaces are not completely flat. The upper specimen has two ridges along the longer edges, and these ridges would be the first ones to come in contact and wear out to proceed to establish larger contact area. The reduction in the ridge is clearly visualized in the intermediate images.

Fig. 15
figure 15

Optical images of the evolution of surface areas of upper and lower specimens

Full size image

The worn area profile boundaries from Fig. 15 are extracted and plotted over the cumulative energy dissipated to give an idea about the evolution of established contact area. Final worn area after 16 million wear cycles and total loss of contact corresponds to only around 80% of the nominal area. At the end of the test, though there was complete loss of contact, one can see that the whole available area is not fully engaged. There are two primary reasons for the same. Firstly, the surface waviness is not even, and the exciting mode shape is not perfectly parallel to the tangential contact plane as discussed before. The mode shape around 290 Hz, the beam is slightly inclined with respect to the nominal contact plane due to the geometry of the test rig and the dynamic behaviour at that mode. The second reason is the beam deflection is dependent on the starting contact preload. Since the starting contact preload is around 31 N, which is quite low and the magnitude of deflection of the beam is comparable to the surface profile and the ridge height. The contact preload is chosen in such a way to obtain the maximum energy dissipation to accelerate wear with relatively low number of cycles. Hence, when the surfaces worn out the ridges, the contact preload was almost zero leading to loss of contact. The worn area profiles stand out because of its asymmetric wear also attributing to the starting surface profiles and the mode shape of the system as that frequency. In case, there was a large contact preload providing large deflection of the beam, though compromising with lower energy dissipation and larger number of fretting cycles needed, the worn area would be fully established (Fig. 16).

Fig. 16
figure 16

Worn area with respect to the cumulative energy dissipated

Full size image

3.4.2 Evolution of hysteresis loops and contact preload

Figure 17 shows the evolution of hysteresis loops with the progressing wear up to 16 million cycles. The contact undergoes stick and full slip at each cycle for the given loading conditions. The initial hysteresis loops during the running-in phase are ignored as the interest is in the steady state behaviour that was achieved in the first few minutes of the test.

Fig. 17
figure 17

Evolution of hysteresis loops with wear for 16 million cycles

Full size image

The plot reveals that, as the wear progresses, the height of the hysteresis loops reduces and the shape changes. The height of the hysteresis loops is governed by the upper \(\left( { + \mu N} \right)\) and lower \(\left( { - \mu N} \right)\) friction limit. The friction coefficient is computed during the test, using the normal and tangential contact force time signals, using the procedure described in Sect. 3.3 about the single cycle. As a result, the value of the friction coefficient is obtained to be quite constant at 0.9 throughout the wear test. As a result, the reduction in the height of the hysteresis loops with wear is due to the loosing contact preload. The shape of hysteresis loops (Fig. 17) sticks out especially in the later stages of wear. Apart from the overall reduced height of the hysteresis loops corresponding to low contact preloads, the ‘left stick region’ is also missing with progressing wear indicating direct transition from negative slip to positive slip without sticking region. For various reasons, many of the wear tests performed in the literature are under a constant normal load; hence, the variation in height of the hysteresis loops is minimal in the steady-state region. Hence, the huge variation in evolution of hysteresis loops is not commonly found in the literature for comparison.

Figure 18 shows the evolution of contact preload with wear. The figure is plotted against the cumulative energy dissipated and also for the cumulative number of cycles. One can clearly see the difference in trend in evolution. The reason being the energy dissipation in each cycle reduces because of the smaller hysteresis loops due to wear with increasing number of cycles. Ideally, if the hysteresis loops were all the same under constant load, the graphs plotted versus energy dissipated or number of cycles would have been the same. Hence, tracking the cumulative energy dissipated is a better choice of parameter to track the impact of wear. The full range test is performed until the complete loss of contact. For the given specimens and loading conditions, it took roughly 16 million fretting cycles resulting in around 12,000 Joules of dissipated energy.

Fig. 18
figure 18

Evolution of contact preload with wear until full loss of contact versus a energy dissipated b number of cycles

Full size image

The impact of the loosing contact preload has a direct impact on the hysteresis loops in terms of dissipated energy in each cycle and the average tangential slip at each cycle. Figure 19 shows the evolution of average dissipated energy at each cycle with respect to the cumulative number of cycles. Basically, as the contact preload decreases, the dissipated energy at each cycle decreased due to reduced height of hysteresis loops and the tangential slip increases due to the reduced normal load.

Fig. 19
figure 19

Evolution of average dissipated energy in one cycle versus number of cycles

Full size image

3.4.3 Wear volume versus dissipated energy

The wear volumes of the upper and lower specimens are calculated by superimposing the worn surface profile over the unworn surface profile. This method eliminates the computation error introduced due to non-flat initial surface waviness if any. The procedure is repeated for all wear intervals and for the upper and lower specimens separately. Topology analysis software is used to perform the operations and compute the wear volume. The total wear volume is calculated by summing up the wear volume obtained at upper and lower specimen. The unevenness of worn area is due to initial contact profile and waviness of the surfaces. This poses a certain difficulty in measuring the total wear volume at low number of cycles. The confidence is greater with larger wear volumes as there is more loss of volume. Figure 20 shows the relationship between the total wear volume corresponding to the cumulative energy dissipated during the wear test. A linear relationship can be seen by the plotted data indicating the total wear volume is proportional to the cumulative energy dissipated. A linear regression (dotted blue-line) is performed to obtain an approximate relationship between the total wear volume and cumulative energy dissipated. This is in line with the energy form of the classical Archard wear model in which the product sliding distance times the normal load—that is the work done on the system—has been substituted by the dissipated energy. The slope of the best fit line represents the wear energy coefficient (α). This is a particularly important parameter for the given material pair as it can be used in numerical prediction software for better wear prediction and accurate number of wear cycles. Most of the numerical studies in the literature [20, 22, 42, 43] studying the effect of fretting wear on the forced response dynamics using Harmonic Balance Method uses this parameter as an input. The wear energy approach [44] using wear energy coefficient (α) is a convenient method in terms of the accuracy and ease of implementation in large nonlinear dynamic solvers as it is relatively straightforward compared to complex methods such as in [45,46,47,48,49,50] requiring many variables as inputs.

Fig. 20
figure 20

Total wear volume versus cumulative energy dissipated

Full size image

3.4.4 Impact of wear on the FRFs

As the contact loses material due to progressing wear, as seen in the contact evolution images in Figs. 14 and 15, the beam static deflection reduces, while the height of the moving platform is kept fixed throughout the full test. As a result, the static contact preload gets smaller as wear is accumulated. This reduction in static contact preload affects the FRFs of the system, measured at every 0.5 million cycles during the test.

In Fig. 21, the FRF evolution at different excitation levels is plotted. In each plot, corresponding to a certain excitation level (70 N, 50 N, 25 N and 10 N), the FRF curves correspond to different levels of wear, accumulated during the test. The nonlinear behaviour of the system is clearly visible in the plots.

Fig. 21
figure 21

Effect of wear on the FRFs subject to different excitation amplitudes for 16 million wear cycles

Full size image

At the beginning of the test, the peak around 400 Hz is sharper, being the system closer to the stuck case. As the wear progresses, the FRFs show a softening behaviour of the system, associated with larger relative displacements as the preload is progressively reduced. The increase in relative displacements affects both the stiffness and the damping provided by the contact. Towards the end of the test, corresponding to full loss of contact and zero contact preload, the FRF matches the response of the system with open contact. This successfully captures the impact of wear and the evolution of contact surface from pristine surface and nonzero contact load to a worn surface with complete separation.

To the authors knowledge, this is the first study, where: (i) a step-by-step experimental analysis of wear evolution and its effect on structural dynamics is performed; (ii) the focus is on the effect of wear evolution on the magnitude of contact preload. Such a study was possible due to the purposely designed test rig and to the experimental procedure followed during the tests. Thanks to this approach, incremental effect of wear on the hysteresis loops, contact surface evolution and system dynamics were tracked until loss of contact.

From the above results, it can be clearly seen that though the amount of wear at the contact is only in the order of a few micrometres, there can be substantial effect in terms of energy dissipation, contact preloads, real contact area engaged, etc. Over a few million cycles, these cumulative effects can be amplified and affect the dynamic response significantly. This strengthens the point that considering realistic contact interface conditions and its evolution is important in designing high-performance components and predicting the actual lifetime of the components. Robust and efficient nonlinear solvers are needed to predict the effects numerically and conduct parametric studies for optimized turbomachinery components. Taking into account the changes in the contact preload, loss of material, shift in vibration amplitudes and change in the resonance frequencies are crucial in designing the high-performance turbomachinery components for safety and efficiency. Having a robust prediction tool will help for better design for operational performance at the design stage itself and better components in a short turnaround time. The results presented here are the initial set obtained from the test rig; however, a wide range of studies can be performed using this test rig. For example, a parametric study of contact pair material, contact preload, excitation forces, contact geometry, contact area, etc., can be performed and isolated individually to better understand the impact of wear on dynamics in each case. In turn, these experimental results can be used to update the numerical models and iterate to develop a robust prediction tool. This would result in positive iterative loop strengthening the robustness of the prediction tool.

4 Conclusions

This paper presented a novel test rig to study the effect of fretting wear on the forced response dynamics with a friction contact and changing preload. The paper outlined the brief description of the test rig, design intent, instrumentation, test plan and the initial set of results. A long-term wear test with 16 million wear cycles was carried out until full loss of contact. The dynamic response and specimen surface scans were captured at various intervals throughout the test.

The major outcomes from the study are:

  • A first of its kind experimental test rig to study the effect of fretting wear on the dynamic response with changing preload.

  • The results presented evolution of contact surfaces, hysteresis loops, wear, and the impact on the FRFs.

  • Fretting wear over millions of cycles alters contact interface significantly over large cumulative energy dissipation.

  • The wear affects the dynamic response of the system by changing vibration amplitudes, frequency and damping.

  • The wear also affects the contact conditions by changing the effective engaged contact area, contact preload, relative displacement for different forcing conditions.

As it is shown from the current study, it is crucial to include the time effects of fretting wear and the contact behaviour in the design of components for dynamic performance and reliability. This study acts as an experimental observation and validation for the numerical prediction tools which are used in the turbomachinery field. This novel test rig is of particular importance to validate the wear on dynamics of shroud tip of the bladed disc which experience a changing contact preload. It is quite different from the under-platform dampers which is studied extensively in the last years.

The equivalent numerical model of the test rig for the validation of the experimental results using Harmonic Balance Method (HBM) is currently being done, and the results will follow in the subsequent articles.