Model reduction of the tippedisk: a path to the full analysis

Abstract

The tippedisk is a mechanical-mathematical archetype for friction-induced instability phenomena that exhibits an interesting inversion phenomenon when spun rapidly. The inversion phenomenon of the tippedisk can be modeled by a rigid eccentric disk in permanent contact with a flat support, and the dynamics of the system can therefore be formulated as a set of ordinary differential equations. The qualitative behavior of the nonlinear system can be analyzed, leading to slow–fast dynamics. Since even a freely rotating rigid body with six degrees of freedom already leads to highly nonlinear system equations, a general analysis for the full system equations is not feasible. In a first step the full system equations are linearized around the inverted spinning solution with the aim to obtain a local stability analysis. However, it turns out that the linear dynamics of the full system cannot properly describe the qualitative behavior of the tippedisk. Therefore, we simplify the equations of motion of the tippedisk in such a way that the qualitative dynamics are preserved in order to obtain a reduced model that will serve as the basis for a following nonlinear stability analysis. The reduced equations are presented here in full detail and are compared numerically with the full model. Furthermore, using the reduced equations we give approximate closed form results for the critical spinning speed of the tippedisk.

1 Introduction

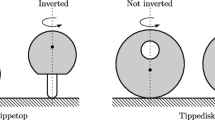
Various gyroscopic systems which are interacting with a horizontal frictional support, such as Euler’s disk [19, 22, 26], the rattleback [5, 13] and the tippetop [6, 10, 25, 29], form a scientific playground for friction-induced instability phenomena. Even though the early research on the tippetop dates back to the 1950s, it is still a topic of current scientific interest [4, 18, 20]. In [30] we introduced a new mechanical-mathematical archetype, called the tippedisk, to this scientific playground and provided a suitable model. The tippedisk is essentially an eccentric disk, for which the center of gravity (COG) does not coincide with the geometric center of the disk. Neglecting dissipation due to spinning friction (i.e., pivoting friction), two stationary motions can be distinguished. For ‘noninverted spinning’, the COG is located below the geometric center and the disk is spinning with a constant velocity about the in-plane axis through the COG and the geometric center. The second stationary motion is referred to as ‘inverted spinning’, being similar to ‘noninverted spinning’, but with the COG located above the geometric center of the disk.

Fig. 1

Inversion phenomenon showing the rise of the COG (black dot)

If the noninverted tippedisk is spun fast around an in-plane axis, one observes that the COG rises until the disk remains in an inverted configuration, similar to the inversion of the tippetop shown in Fig. 1. For dissipative systems, people tend to intuitively assume trajectories to end in equilibria or stationary solutions with lower potential energy. Since the potential energy for the noninverted configuration is lower than in the case of inverted solutions, this energetic intuition contradicts our experiments from Fig. 2. The experimental observations qualitatively indicate that for a fastly spinning tippedisk the noninverted spinning is unstable and a stable inverted spinning motion attracts nearly all trajectories.

Fig. 2

Tippedisk: inversion phenomenon

In this paper we aim to conduct an in-depth stability analysis for the tippedisk. We therefore have to reduce the complexity of the model, to pave the way for a closed form stability analysis. This reduction has to be understood as simplification of the full model and will be validated through various numerical models and the results will be compared to experimental data in future research. In this paper, the main focus is on linear stability analysis and a physically motivated reduction of the system.

In Sect. 2, we introduce the kinematics and briefly recapitulate the model developed in [30]. Moreover, we discuss the dimensions of our specimen and illustrate the two stationary solutions whose stability is studied in the following. Section 3 attempts to explain the local stability behavior of the tippedisk using Lyapunov’s indirect method. Physical constraints are numerically and analytically introduced in Sect. 4, to obtain a reduced system which qualitatively describes the inversion phenomenon. The corresponding simulation results are compared in Sect. 5. In Sect. 6, the reduced system is locally approximated to obtain the linear behavior. In addition, a closed form approximation of the critical spinning speed is derived in this section. The behavior of the linear system is subsequently discussed together with the applied approximations in Sect. 7.

2 Model of the tippedisk

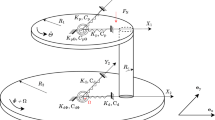
We introduce an orthonormal inertial frame $I=(O,{\mathbf {e}}_x^I,{\mathbf {e}}_y^I,{\mathbf {e}}_z^I)$ attached to the origin O, where ${\mathbf {e}}_z^I$ is perpendicular to the flat support. The body fixed B-frame, $B=(G,{\mathbf {e}}_x^B,{\mathbf {e}}_y^B,{\mathbf {e}}_z^B)$, is attached to the geometric center G of the disk, such that ${\mathbf {e}}_z^B$ is normal to the surface of the disk. The axis ${\mathbf {e}}_x^B$ is defined as the normalized vector of ${\mathbf {r}}_{GS}$, which points from the geometric center G to the center of gravity S. The inertia tensor with respect to G expressed in the body fixed B-frame is given as $_B\varvec{\Theta }_G=\text {diag}(A,B,C)$, where $B<A<C$ holds. To describe the interaction between disk and support, the point with minimal height is introduced as C. The contact distance between the contact point C and the corresponding point D is measured as $g_N$ (Fig. 3).

Fig. 3

Mechanical model: tippedisk

2.1 Equations of motion

In [30] we provide a suitable mechanical model of the tippedisk, which is able to describe the inversion phenomenon. Using the parameterization

$$\begin{aligned} _I{\mathbf {r}}_{OG} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \end{aligned}$$

(1)

of the geometric center G together with Euler angles $\varvec{\varphi }=\left[ \alpha , \beta , \gamma \right] ^{\mathop {{\mathrm {T}}}}$, in z–x–z convention, we obtain equations of motion in the form of

$$\begin{aligned} {\mathbf {M}}({\mathbf {q}}) \ddot{{\mathbf {q}}} - {\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}}) = {\mathbf {f}}_G + {\mathbf {w}}_N {\lambda }_N + {\mathbf {W}}_T \varvec{\lambda }_T, \end{aligned}$$

(2)

in the coordinates ${\mathbf {q}}= [x, y, z, \alpha , \beta , \gamma ]^{\mathop {{\mathrm {T}}}}\in {\mathbb {R}}^6$. For a detailed explanation of Euler angles, we refer to [27]. As mentioned in [17], Euler angles can lead to singularities. Euler angle singularities are often mistakenly confused with gimbal lock [17]. In [30] we additionally present a quaternion-based approach and showed that the model in Euler angles is suitable to describe the inversion of the tippedisk, since the motion occurs far from singularities of the chosen parameterization. The vector ${\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}})$ contains all gyroscopic terms. On the right-hand side of Eq. (2) appear the gravitational force ${\mathbf {f}}_G$, the normal contact force $\lambda _N \in {\mathbb {R}}$, with corresponding normal force direction ${\mathbf {w}}_N$, as well as the tangential contact force $\varvec{\lambda }_T \in {\mathbb {R}}^2$ in the contact plane $({\mathbf {e}}_x^I,{\mathbf {e}}_y^I)$, with associated matrix of tangential force directions ${\mathbf {W}}_T$. Equation (2) represents the equations of motion of a single rigid body in the sense of nonlinear mechanics, which has structurally the same form as a general rigid multibody system. Constraint forces are thereby represented through Lagrange multipliers resulting from constraint equations and set-valued force laws [1, 9, 15]. In the field of Nonsmooth Mechanics, there are a variety of set-valued frictional force laws such as dry Coulomb friction, spinning friction and contour friction [15, 21, 24]. Often different friction laws are considered in isolation. In [11] it was shown that spatial Coulomb friction and spinning friction (i.e., pivoting friction) must be considered in a coupled fashion. This leads to more advanced and realistic friction laws such as the Coulomb–Contensou friction presented in [23]. Simplified, Coulomb–Contensou friction law results from a microscopic consideration in which a tangential force distribution in the sense of Coulomb it is assumed to act on a contact patch. The macroscopic contact force and contact torque are then obtained by integrating the force distribution over the contact area. If the tippedisk is spun around an in-plane axis, the contact patch is forced into the state of sliding. This sliding then leads to a smoothing of Coulombs friction law for sliding friction. In [30] we showed that the smooth Coulomb friction law

$$\begin{aligned} \varvec{\lambda }_T = - \mu \lambda _N \frac{\varvec{\gamma }_T}{||\varvec{\gamma }_T||+\varepsilon }, \end{aligned}$$

(3)

with friction coefficient $\mu$ and smoothing parameter $\varepsilon$ is sufficient to describe the inversion phenomenon of the disk. The kinematic quantity $\varvec{\gamma }_T$ describes the relative slip velocity¹ between the contact points C and D in the inertial frame. Moreover, the normal contact force $\lambda _N$ is given through Signorini’s law

$$\begin{aligned} 0 \le g_N \perp \lambda _N \ge 0, \end{aligned}$$

(4)

where the expression $a \perp b$ means $ab=0$.

To obtain more compact expressions in the following, we introduce the notations ${\text {s}\vartheta }=\sin \vartheta$, ${\text {s}^{2}\vartheta }=\sin ^2\vartheta$, ${\text {c}\vartheta }=\cos \vartheta$ and ${\text {c}^{2}\vartheta }=\cos ^2\vartheta$. The corresponding mass matrix ${\mathbf {M}}({\mathbf {q}})$ and the gyroscopic ${\mathbf {h}}$-vector, as well as the generalized normal and tangential force directions ${\mathbf {w}}_N$ and ${\mathbf {W}}_T$, are given in “Appendix A”.

2.2 Dimensions

Similar to [30], a stainless steel disk is considered, with dimensions depicted in Fig. 4. The nonlinearities induced by the rounding of the edge are not responsible for the inversion of the tippedisk. Neglecting these additional geometric effects, we model the tippedisk as an infinitely thin disk with mass m, radius r and eccentricity e. For the experimental investigations, a disk with a rounded edge has been constructed, as a sharp edge cuts grooves in the support and leaves marks on it, resulting in inhomogeneous frictional properties. In addition, a sharp edge is not as resistant as a rounded one, such that a flattening of the tread can occur. Such flattening of the running surface can lead to micro-jumps of the tippedisk. The dimensions and inertia properties for the considered specimen are given in Table 1. For a more detailed derivation of the principal moments of inertia, we refer to [30]. In the following numerical simulations, the smoothing parameter is set to $\varepsilon = 0.1 \frac{\mathrm{m}}{\mathrm{s}}$ and the friction coefficient is chosen as $\mu = 0.3$.

Fig. 4

Dimensions of the tippedisk

Table 1 Dimensions of the tippedisk

2.3 Stationary solutions

In accordance with the model presented in [30], the tippedisk has two stationary solutions for which dissipation is absent. The stationary solutions are characterized by a constant spinning speed ${\dot{\alpha }}=\varOmega$, a constant height $z=r$ and a constant inclination angle $\beta = \frac{\pi }{2}$. The COG is below G ($\gamma = -\frac{\pi }{2}$) for noninverted spinning and above G ($\gamma = +\frac{\pi }{2}$) for inverted spinning. The stationary solutions can be expressed in the coordinates ${\mathbf {q}}(t)$ as

$$\begin{aligned} {\mathbf {q}}_\text {n}^*(t)= \begin{bmatrix} 0 \\ 0 \\ r \\ \varOmega t \\ +\frac{\pi }{2} \\ -\frac{\pi }{2} \end{bmatrix} ; \quad {\mathbf {q}}_\text {i}^*(t)= \begin{bmatrix} 0 \\ 0 \\ r \\ \varOmega t \\ +\frac{\pi }{2} \\ +\frac{\pi }{2} \end{bmatrix} \end{aligned}$$

(5)

with generalized velocities ${\mathbf {u}}_\text {n}^*(t)={\mathbf {u}}_\text {i}^*(t)=[ 0 \quad 0 \quad 0 \varOmega \quad 0 \quad 0 ]^{\mathop {{\mathrm {T}}}}$. In the following, we aim to analyze the stability properties of both stationary spinning solutions, depicted in Fig. 5.

Fig. 5

Stationary solutions of the tippedisk

3 Linear stability analysis (6 DOF)

As a first step in the analysis of the dynamic behavior of the tippedisk, the local stability properties of inverted an noninverted spinning solutions are analyzed using Lyapunov’s indirect method. The experiments and simulations from [30] show that the inverted spinning solution seems to be locally attractive for a large spinning speed $\varOmega$. We may try to apply Lyapunov’s indirect method, i.e., use an eigenvalue analysis, to prove local attractivity. Hence, we linearize the system equations around the noninverted and inverted stationary spinning solutions. Both stationary spinning solutions Eq. (5) are characterized by the constant rotational velocity ${\dot{\alpha }}=\varOmega$ and thus by a linear time dependence $\alpha (t)=\varOmega t+\alpha _0$ of the angle $\alpha$. If we linearize the equations of motion around the noninverted and inverted spinning solutions ${\mathbf {q}}^*(t)$, we obtain a linear system of the form

$$\begin{aligned} {\mathbf {M}}(t) \ddot{{\mathbf {y}}} + {\mathbf {B}}(t){\dot{{\mathbf {y}}}} + {\mathbf {C}}(t){{\mathbf {y}}} = 0, \end{aligned}$$

(6)

with ${\mathbf {y}}(t)={\mathbf {q}}(t)-{\mathbf {q}}^*(t)$ and ${\mathbf {M}}(t)={\mathbf {M}}({\mathbf {q}}^*(t))$. The time dependent matrices ${\mathbf {B}}(t)$ and ${\mathbf {C}}(t)$ are extracted from ${\mathbf {h}}({\mathbf {q}}^*,{\mathbf {u}}^*)$, the normal contact force $\lambda _N(t)=\lambda _N({\mathbf {q}}^*,{\mathbf {u}}^*)$ and the friction force $\varvec{\lambda }_T(t)=\varvec{\lambda }({\mathbf {q}}^*,{\mathbf {u}}^*)$. Since the mass matrix ${\mathbf {M}}(t)={\mathbf {M}}({\mathbf {q}}^*(t))$ here depends on $\alpha$ and is thus time-dependent, the linear system is nonautonomous. As a consequence, Lyapunov’s indirect method is not applicable due to time-dependent matrices and one would need to resort to Floquet theory which is not feasible in closed form [12]. In contrast, the physical interpretation suggests that the system does not explicitly depend on time t. For this reason, it is presumed that a non-autonomous description exists, so that this time dependency vanishes. In Sect. 3.1, it is shown that a non-autonomous description can be achieved through a coordinate transformation, so that subsequently Lyapunov’s indirect method can be applied. The above linearization motivates the introduction of new minimal coordinates for the nonlinear system.

3.1 Reparametrization

The parameterization of the reference point G with respect to the I-frame leads to a time-dependent mass matrix ${\mathbf {M}}$ and therefore to a non-autonomous system in coordinates

$$\begin{aligned} {\mathbf {q}}= \begin{bmatrix} x&\quad y&\quad z&\quad \alpha&\quad \beta&\quad \gamma \end{bmatrix}^{\mathop {{\mathrm {T}}}}\in {\mathbb {R}}^6. \end{aligned}$$

(7)

Since this time dependence is an artifact of the chosen parameterization, we introduce a second parameterization in new minimal coordinates

$$\begin{aligned} {\mathbf {z}}= \begin{bmatrix} {\bar{x}}&\quad {\bar{y}}&\quad z&\quad \alpha&\quad \beta&\quad \gamma \end{bmatrix}^{\mathop {{\mathrm {T}}}}\in {\mathbb {R}}^6, \end{aligned}$$

(8)

where the position

$$\begin{aligned} _R{\mathbf {r}}_{OG} = \begin{bmatrix} {\bar{x}} \\ {\bar{y}} \\ z \end{bmatrix} \end{aligned}$$

(9)

of the geometric center G is expressed with respect to the co-rotating R-frame, which results from rotation of the I-frame with the angle $\alpha$ around the ${\mathbf {e}}_z^I$-vector. The corresponding transformation matrix ${\mathbf {A}}_{IR}$ yields the relationship

$$\begin{aligned} {\mathbf {q}}= \begin{bmatrix} {\mathbf {A}}_{IR} &{}\quad 0 \\ 0 &{}\quad {\mathbf {I}}\end{bmatrix} {\mathbf {z}}={\mathbf {H}}({\mathbf {z}}){\mathbf {z}}={\mathbf {q}}({\mathbf {z}}) \end{aligned}$$

(10)

between coordinates ${\mathbf {q}}$ and ${\mathbf {z}}$. The kinematic relation between ${\dot{{\mathbf {q}}}}$ and ${\dot{{\mathbf {z}}}}$ can be derived by taking the time derivative of Eq. (10) as

$$\begin{aligned} {\dot{{\mathbf {q}}}} = {\mathbf {H}}({\mathbf {z}}) {\dot{{\mathbf {z}}}} + {\dot{{\mathbf {H}}}}({\mathbf {z}}) {\mathbf {z}}= {\mathbf {B}}({\mathbf {z}}){\dot{{\mathbf {z}}}}, \end{aligned}$$

(11)

from which one extracts the kinematic matrix

(12)

Together with Eq. (10) and Eq. (12), the equation of motion

$$\begin{aligned} {\mathbf {M}}({\mathbf {q}})\ddot{{\mathbf {q}}}-{\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}})={\mathbf {f}}+{\mathbf {w}}_N \lambda _N +{\mathbf {W}}_T \varvec{\lambda }_T \end{aligned}$$

(13)

from Eq. (2) transforms to

$$\begin{aligned}&{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {M}}{\mathbf {B}}\ddot{{\mathbf {z}}}-{\mathbf {B}}^{\mathop {{\mathrm {T}}}}\left[ {\mathbf {h}}({\mathbf {q}}({\mathbf {z}}),{\mathbf {B}}{\dot{{\mathbf {z}}}})-{\mathbf {M}}{\dot{{\mathbf {B}}}}{\dot{{\mathbf {z}}}}\right] \nonumber \\&\quad ={\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {f}}+{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {w}}_N \lambda _N +{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {W}}_T \varvec{\lambda }_T, \end{aligned}$$

(14)

which can be written in short form as

$$\begin{aligned} {\bar{{\mathbf {M}}}}({\mathbf {z}})\ddot{{\mathbf {z}}}-{\bar{{\mathbf {h}}}}({\mathbf {z}},{\dot{{\mathbf {z}}}})={\bar{{\mathbf {f}}}}+{\bar{{\mathbf {w}}}}_N \lambda _N +{\bar{{\mathbf {W}}}}_T \varvec{\lambda }_T, \end{aligned}$$

(15)

using the notation ${\bar{{\mathbf {M}}}}({\mathbf {z}}) := {\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {M}}{\mathbf {B}}$, $\bar{{\mathbf {h}}}({\mathbf {z}},\dot{{\mathbf {z}}}):={\mathbf {B}}^{\mathop {{\mathrm {T}}}}\left[ {\mathbf {h}}({\mathbf {q}}({\mathbf {z}}),{\mathbf {B}}\dot{{\mathbf {z}}})-{\mathbf {M}}\dot{{\mathbf {B}}}\dot{{\mathbf {z}}}\right]$, ${\bar{{\mathbf {f}}}}({\mathbf {z}})={\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {f}}({\mathbf {q}}({\mathbf {z}}))$, ${\bar{{\mathbf {w}}}}_N={\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {w}}_N$ and ${\bar{{\mathbf {W}}}}_T={\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {W}}_T$. Equation (15) corresponds to the equation of motion in new minimal coordinates ${\mathbf {z}}$. The symmetric mass matrix ${\bar{{\mathbf {M}}}}$ and the vector of gyroscopic forces ${\bar{{\mathbf {h}}}}$ are given as

$$\begin{aligned} {\bar{{\mathbf {M}}}} = \begin{bmatrix} {\bar{{\mathbf {M}}}}_{11} &{}\quad {\bar{{\mathbf {M}}}}_{12}\\ {\bar{{\mathbf {M}}}}_{21} &{}\quad {\bar{{\mathbf {M}}}}_{22} \end{bmatrix}, \end{aligned}$$

(16)

with

$$\begin{aligned}&{\bar{{\mathbf {M}}}}_{11} = \begin{bmatrix} m &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad m &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad m \end{bmatrix}, \quad {\bar{{\mathbf {M}}}}_{21} = {\bar{{\mathbf {M}}}}_{12}^{\mathop {{\mathrm {T}}}}, \end{aligned}$$

(17)

$$\begin{aligned}&{\bar{{\mathbf {M}}}}_{12} = \begin{bmatrix} -m{\bar{y}}-me\text {c}\beta \text {s}\gamma &{}\quad 0&{}\quad -me\text {s}\gamma \\ m{\bar{x}}+me\text {c}\gamma &{}\quad -me\text {s}\beta \text {s}\gamma &{}\quad me\text {c}\beta \text {c}\gamma \\ 0&{}\quad me\text {c}\beta \text {s}\gamma &{}\quad me\text {s}\beta \text {c}\gamma \end{bmatrix},\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned}&{\bar{{\mathbf {M}}}}_{22} = \begin{bmatrix} {\bar{M}}_{22,11}&{}\quad \cdot &{}\quad \mathrm{sym.}\\ {\bar{M}}_{22,12}&{}\quad A\text {c}^2\gamma +B\text {s}^2\gamma &{}\quad \cdot \\ {\bar{M}}_{22,13}&{}\quad 0&{}\quad C \end{bmatrix}, \end{aligned}$$

(19)

$$\begin{aligned}&{\bar{M}}_{22,11} = m({\bar{x}}^2+{\bar{y}}^2)+2me({\bar{x}}\text {c}\gamma +{\bar{y}}\text {c}\beta \text {s}\gamma ) \nonumber \\&\qquad +(A\text {s}^2\gamma +B\text {c}^2\gamma )\text {s}^2\beta +C\text {c}^2\beta , \end{aligned}$$

(20)

$$\begin{aligned}&{\bar{M}}_{22,12} = (A-B)\text {s}\beta \text {s}\gamma \text {c}\gamma -me{\bar{x}}\text {s}\beta \text {s}\gamma , \end{aligned}$$

(21)

$$\begin{aligned}&{\bar{M}}_{22,13} = me{\bar{x}}\text {c}\beta \text {c}\gamma +me{\bar{y}}\text {s}\gamma +C\text {c}\beta , \end{aligned}$$

(22)

where the notation $\text {c}\gamma =\cos \gamma$ and $\text {c}^2\gamma =\cos ^2\gamma$ has been used and

$$\begin{aligned} {\bar{{\mathbf {h}}}}({\mathbf {z}},{\dot{{\mathbf {z}}}}) :=&\begin{bmatrix} {\bar{h}}_1&\quad {\bar{h}}_2&\quad {\bar{h}}_3&\quad {\bar{h}}_4&\quad {\bar{h}}_5&\quad {\bar{h}}_6 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(23)

with

$$\begin{aligned} {\bar{h}}_1&= m \big [ {\bar{x}}{\dot{\alpha }}^2+2\dot{{\bar{y}}}{\dot{\alpha }} \big ] \nonumber \\&\quad +\,me \big [ ({\dot{\alpha }}^2 + {\dot{\gamma }}^2)\text {c}\gamma - 2{\dot{\alpha }}{\dot{\beta }}\text {s}\beta \text {s}\gamma \nonumber \\&\quad +\, 2{\dot{\alpha }}{\dot{\gamma }}\text {c}\beta \text {c}\gamma \big ], \end{aligned}$$

(24)

$$\begin{aligned} {\bar{h}}_2&= m \big [ {\bar{y}}{\dot{\alpha }}^2-2\dot{{\bar{x}}}{\dot{\alpha }} \big ] \nonumber \\&\quad +\, me \big [ ({\dot{\alpha }}^2 + {\dot{\beta }}^2 + {\dot{\gamma }}^2)\text {c}\beta \text {s}\gamma \nonumber \\&\quad +\,2{\dot{\alpha }}{\dot{\gamma }}\text {s}\gamma + 2{\dot{\beta }}{\dot{\gamma }}\text {s}\beta \text {c}\gamma \big ], \end{aligned}$$

(25)

$$\begin{aligned} {\bar{h}}_3&= me \big [ {\dot{\beta }}^2\text {s}\beta \text {s}\gamma + {\dot{\gamma }}^2\text {s}\beta \text {s}\gamma - 2{\dot{\beta }}{\dot{\gamma }}\text {c}\beta \text {c}\gamma \big ], \end{aligned}$$

(26)

$$\begin{aligned} {\bar{h}}_4&= -2m \big [ {\bar{x}}\dot{{\bar{x}}}{\dot{\alpha }} + {\bar{y}}\dot{{\bar{y}}}{\dot{\alpha }} \big ] \nonumber \\&\quad -\,me \big [ 2\dot{{\bar{x}}}{\dot{\alpha }}\text {c}\gamma + (2\dot{{\bar{y}}}{\dot{\alpha }} -{\bar{x}}{\dot{\beta }}^2 -{\bar{x}}{\dot{\gamma }}^2)\text {c}\beta \text {s}\gamma \nonumber \\&\quad -\,2{\bar{x}}{\dot{\alpha }}{\dot{\gamma }}\text {s}\gamma -\,2{\bar{x}}{\dot{\beta }}{\dot{\gamma }}\text {s}\beta \text {c}\gamma +{\bar{y}}{\dot{\gamma }}^2\text {c}\gamma \nonumber \\&\quad -\,2{\bar{y}}{\dot{\alpha }}{\dot{\beta }}\text {s}\beta \text {s}\gamma +\,2{\bar{y}}{\dot{\alpha }}{\dot{\gamma }}\text {c}\beta \text {c}\gamma \big ] \nonumber \\&\quad -\,(A-B) \big [ {\dot{\beta }}^2\text {c}\beta \text {s}\gamma \text {c}\gamma + 2{\dot{\alpha }}{\dot{\gamma }}\text {s}^2\beta \text {s}\gamma \text {c}\gamma \nonumber \\&\quad + {\dot{\beta }}{\dot{\gamma }}\text {s}\beta (\text {c}^2\gamma -\text {s}^2\gamma ) \big ] \nonumber \\&\quad -\,2(A\text {s}^2\gamma +B\text {c}^2\gamma -C){\dot{\alpha }}{\dot{\beta }}\text {s}\beta \text {c}\beta +C{\dot{\beta }}{\dot{\gamma }}\text {s}\beta , \end{aligned}$$

(27)

$$\begin{aligned} {\bar{h}}_5&= me \big [ 2\dot{{\bar{x}}}{\dot{\alpha }} - {\bar{y}}{\dot{\alpha }}^2 \big ]\text {s}\beta \text {s}\gamma + (A-B) \big [ 2{\dot{\beta }}{\dot{\gamma }}\text {s}\gamma \text {c}\gamma \nonumber \\&\quad -\,{\dot{\alpha }}{\dot{\gamma }}\text {s}\beta (\text {c}^2\gamma -\text {s}^2\gamma ) \big ] \nonumber \\&\quad +\,(A\text {s}^2\gamma +B\text {c}^2\gamma ){\dot{\alpha }}^2\text {s}\beta \text {c}\beta \nonumber \\&\quad -C\big [ {\dot{\alpha }}^2\text {s}\beta \text {c}\beta +{\dot{\alpha }}{\dot{\gamma }}\text {s}\beta \big ], \end{aligned}$$

(28)

$$\begin{aligned} {\bar{h}}_6&= -me \big [ 2\dot{{\bar{y}}}{\dot{\alpha }} + {\bar{x}}{\dot{\alpha }}^2 \big ]\text {s}\gamma -me \big [ 2\dot{{\bar{x}}}{\dot{\alpha }} -{\bar{y}}{\dot{\alpha }}^2 \big ]\text {c}\beta \text {c}\gamma \nonumber \\&\quad +\,(A-B) \big [ ({\dot{\alpha }}^2\text {s}^2\beta - {\dot{\beta }}^2)\text {s}\gamma \text {c}\gamma \nonumber \\&\quad +\,{\dot{\alpha }}{\dot{\beta }}(\text {c}^2\gamma -\text {s}^2\gamma )\text {s}\beta \big ] +C{\dot{\alpha }}{\dot{\beta }}\text {s}\beta . \end{aligned}$$

(29)

Equations (16)–(29) define the left-hand side of the equation of motion, see Eq. (15). The generalized gravitational force yields

$$\begin{aligned} {\bar{{\mathbf {f}}}}= \begin{bmatrix} 0&\quad 0&\quad -mg&\quad 0&\quad -mge\text {c}\beta \text {s}\gamma&\quad -mge\text {s}\beta \text {c}\gamma \end{bmatrix}^{\mathop {{\mathrm {T}}}}.\nonumber \\ \end{aligned}$$

(30)

The generalized normal and tangential force directions are given with respect to the coordinates ${\mathbf {z}}$ as

$$\begin{aligned} {\bar{{\mathbf {w}}}}_N= \begin{bmatrix} 0&\quad 0&\quad 1&\quad 0&\quad -r\text {c}\beta&\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(31)

and

$$\begin{aligned} {\bar{{\mathbf {W}}}}_T= \begin{bmatrix} 1&{}\quad 0&{}\quad 0&{}\quad r\text {c}\beta -{\bar{y}}&{}\quad 0&{}\quad r\\ 0&{}\quad 1&{}\quad 0&{}\quad {\bar{x}}&{}\quad r\text {s}\beta &{}\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}. \end{aligned}$$

(32)

With $\varvec{\gamma }_T={\bar{{\mathbf {W}}}}_T^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {z}}}}$ the smooth Coulomb friction law Eq. (3) can be evaluated.

3.2 Linear stability analysis of the autonomous system

In Sect. 3.1, the reparameterization of the equations of motion to new minimal coordinates ${\mathbf {z}}$ has been introduced. The resulting equations of motion Eq. (15) can be linearized together with the smooth Coulomb friction law (3) and the condition $g_N=z-r\text {s}\beta =0$ around the inverted and noninverted stationary spinning solutions of the tippedisk. Due to symmetry, the linearized equations for noninverted spinning solutions are similar to the linearized equations of motions for inverted spinning and differ only in the sign of the eccentricity e. For this reason the linearization is here only performed for the inverted spinning tippedisk. In the inverted orientation $\beta = +\pi /2$ and $\gamma = +\pi /2$ are valid. Introducing the shifted angles ${\bar{\beta }}=\beta -\pi /2\ll 1$ and ${\bar{\gamma }}=\gamma -\pi /2\ll 1$, we linearize the trigonometric expressions

$$\begin{aligned} \sin \beta&= \cos {\bar{\beta }} = 1 + {\mathcal {O}}({\bar{\beta }}^2), \end{aligned}$$

(33)

$$\begin{aligned} \cos \beta&= -\sin {\bar{\beta }} = -{\bar{\beta }} + {\mathcal {O}}({\bar{\beta }}^3), \end{aligned}$$

(34)

$$\begin{aligned} \sin \gamma&= \cos {\bar{\gamma }} = 1 + {\mathcal {O}}({\bar{\gamma }}^2), \end{aligned}$$

(35)

$$\begin{aligned} \cos \gamma&= -\sin {\bar{\gamma }} = -{\bar{\gamma }} + {\mathcal {O}}({\bar{\gamma }}^3). \end{aligned}$$

(36)

Instead of the linearization around an isolated state, we assume only

$$\begin{aligned} {\mathcal {O}}({\bar{x}})={\mathcal {O}}({\bar{y}})={\mathcal {O}}({\bar{\beta }})={\mathcal {O}}({\bar{\gamma }})\ll 1 \end{aligned}$$

(37)

to be small and define the vector

$$\begin{aligned} {\bar{{\mathbf {z}}}}:= \begin{bmatrix} {\bar{x}}&\quad {\bar{y}}&\quad z&\quad \alpha&\quad {\bar{\beta }}&\quad {\bar{\gamma }} \end{bmatrix}^{\mathop {{\mathrm {T}}}}. \end{aligned}$$

(38)

Note that z and $\alpha$ are not small. We define ${\hat{{\mathbf {z}}}}:= \begin{bmatrix} {\bar{x}}&\quad {\bar{y}}&\quad {\bar{\beta }}&\quad {\bar{\gamma }} \end{bmatrix}^{\mathop {{\mathrm {T}}}}$ of small quantities and use ${\mathcal {O}}(||{\hat{{\mathbf {z}}}}||)$ to qualify the deviation from the stationary solution. In [30], it is shown that during the inversion process the disk makes always contact with the flat support, i.e., the contact between the points C and D is closed so that $g_N=0$ holds. Accordingly, the vertical height of the geometric center G and therefore the coordinate z can be expressed as $z = r \sin \beta = r \cos {\bar{\beta }}$. With the assumption of slightly perturbed inverted motions, the second time derivative

$$\begin{aligned} \ddot{z} = -r (\ddot{{\bar{\beta }}}\sin {\bar{\beta }} - \dot{{\bar{\beta }}}^2\cos {\bar{\beta }}) = 0+{\mathcal {O}}(||{\hat{{\mathbf {z}}}}||^2) \end{aligned}$$

(39)

of z vanishes in the linear analysis. From the third row of the equation of motion Eq. (15), we then conclude

$$\begin{aligned} {\mathcal {O}}(||{\hat{{\mathbf {z}}}}||^2) = -mg +\lambda _N \Rightarrow \lambda _N = mg +{\mathcal {O}}(||{\hat{{\mathbf {z}}}}||^2) \end{aligned}$$

(40)

for motions in the vicinity of the inverted and noninverted stationary solutions of the tippedisk. If the disk moves in a stationary solution, the relative velocity $\varvec{\gamma }_T$ between contact points C and D is equal to zero. For motion in the vicinity of the stationary solutions, the smooth Coulomb friction law from Eq. (3) can be approximated as linear dissipative force law

$$\begin{aligned} \varvec{\lambda }_T = - \frac{\mu \lambda _N}{\varepsilon }\varvec{\gamma }_T+{\mathcal {O}}(||\varvec{\gamma }_T||^3) = - d\varvec{\gamma }_T+{\mathcal {O}}(||\varvec{\gamma }_T||^3),\nonumber \\ \end{aligned}$$

(41)

with dissipation constant $d=\frac{\mu \lambda _N}{\varepsilon }$. Inserting the relative velocity $\varvec{\gamma }_T = {\bar{{\mathbf {W}}}}_T^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {z}}}}$ yields the generalized force

$$\begin{aligned} {\bar{{\mathbf {W}}}}_T\varvec{\lambda }_T&= -d \, {\bar{{\mathbf {W}}}}_T {\bar{{\mathbf {W}}}}_T^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {z}}}} + {\mathcal {O}}(||\varvec{\gamma }_T||^3) \\&= -d \begin{bmatrix} 1&{}\quad 0&{}\quad 0&{}\quad -r{\bar{\beta }}-{\bar{y}}&{}\quad 0&{}\quad r\\ 0&{}\quad 1&{}\quad 0&{}\quad {\bar{x}}&{}\quad r&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad r &{}\quad 0 &{}\quad {\bar{x}}r &{}\quad r^2 &{}\quad 0 \\ r &{}\quad 0 &{}\quad 0 &{}\quad -r^2{\bar{\beta }}-r{\bar{y}} &{}\quad 0 &{}\quad r^2 \end{bmatrix} {\dot{{\mathbf {z}}}}\nonumber \\&\quad +{\mathcal {O}}(||{\hat{{\mathbf {z}}}}||^2).\nonumber \end{aligned}$$

(42)

Neglecting higher-order terms in the fourth row of Eq. (15) we obtain $\ddot{\alpha } = 0 +{\mathcal {O}}(||{\hat{{\mathbf {z}}}}||)^2$, such that ${\dot{\alpha }}=\varOmega$ and $\alpha (t) = \alpha _0 + \varOmega t$ follows. The associated solution

$$\begin{aligned}&{\bar{{\mathbf {z}}}}_0= \begin{bmatrix} 0&\quad 0&\quad r&\quad \alpha _0 + \varOmega t&\quad 0&\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(43)

$$\begin{aligned}&\dot{{\bar{{\mathbf {z}}}}}_0= \begin{bmatrix} 0&\quad 0&\quad 0&\quad \varOmega&\quad 0&\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(44)

which can be equivalently expressed in ${\mathbf {z}}$-coordinates

$$\begin{aligned}&{\mathbf {z}}_0= \begin{bmatrix} 0&\quad 0&\quad r&\quad \alpha _0 + \varOmega t&\quad \pi /2&\quad \pi /2 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(45)

$$\begin{aligned}&{\dot{{\mathbf {z}}}}_0= \begin{bmatrix} 0&\quad 0&\quad 0&\quad \varOmega&\quad 0&\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}} \end{aligned}$$

(46)

is similar to the inverted stationary solution of the tippedisk. Without loss of generality, the initial angle $\alpha _0$ can be set to zero since we assume an isotropic friction law. The stationary solution from Eqs. (43)–(46) is derived from the assumptions (37) neglecting higher-order terms. Consequently, the normal contact force $\lambda _N$ used in the tangential Coulomb friction law and the rotational velocity ${\dot{\alpha }}=\varOmega$ in the linearization are no longer degrees of freedom but become parameters of the reduced linear system. Since for each $\varOmega \in {\mathbb {R}}$, there exists a pair of inverted/noninverted stationary solutions, the parameter $\varOmega$ defines a foliation in the state-space. Together with the matrix

$$\begin{aligned} {\mathbf {C}}= \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ \end{bmatrix} \end{aligned}$$

(47)

and the linear relations ${\hat{{\mathbf {z}}}}={\mathbf {C}}{\bar{{\mathbf {z}}}}$ and $\dot{{\hat{{\mathbf {z}}}}}={\mathbf {C}}\dot{{\bar{{\mathbf {z}}}}}$, we obtain reduced coordinates ${\hat{{\mathbf {z}}}}= \begin{bmatrix}{\bar{x}}&\quad {\bar{y}}&\quad {\bar{\beta }}&\quad {\bar{\gamma }}\end{bmatrix}^{\mathop {{\mathrm {T}}}}$, in which stationary inverted spinning is represented by the equilibrium ${\hat{{\mathbf {z}}}}_0=\dot{{\hat{{\mathbf {z}}}}}_0={\mathbf {0}}$. To reduce the equations of motion Eq. (15), we have to pre-multiply with the ${\mathbf {C}}$ matrix, which resembles the deletion of the third and fourth line. Applying the linearization around zero and using ${\dot{\alpha }}=\varOmega$ yields the linear system

$$\begin{aligned} {\mathbf {M}}^{4\times 4}\ddot{{\hat{{\mathbf {z}}}}} + {\mathbf {G}}_{\mathbf {h}}^{4\times 4}\dot{{\hat{{\mathbf {z}}}}} + {\mathbf {K}}_{\mathbf {h}}^{4\times 4}{{\hat{{\mathbf {z}}}}} = - {\mathbf {K}}_{\mathbf {f}}^{4\times 4}{{\hat{{\mathbf {z}}}}} - {\mathbf {D}}_C^{4\times 4}\dot{{\hat{{\mathbf {z}}}}} - {\mathbf {B}}_C^{4\times 4}{{\hat{{\mathbf {z}}}}}\nonumber \\ \end{aligned}$$

(48)

with constant system matrices

$$\begin{aligned} {{\mathbf {M}}}^{4\times 4}= & {} \begin{bmatrix} m &{}\quad 0 &{}\quad 0&{}\quad -me \\ 0 &{}\quad m &{}\quad -me &{}\quad 0 \\ 0 &{}\quad -me &{}\quad B &{}\quad 0 \\ -me &{}\quad 0 &{}\quad 0 &{}\quad C \\ \end{bmatrix}, \end{aligned}$$

(49)

$$\begin{aligned} {{\mathbf {G}}_{\mathbf {h}}}^{4\times 4}= & {} \begin{bmatrix} 0 &{}\quad -2m\varOmega &{}\quad +2me\varOmega &{}\quad 0 \\ +2m\varOmega &{}\quad 0 &{}\quad 0 &{}\quad -2me\varOmega \\ -2me\varOmega &{}\quad 0 &{}\quad 0 &{}\quad -D\varOmega \\ 0 &{}\quad +2me\varOmega &{}\quad +D\varOmega &{}\quad 0 \\ \end{bmatrix},\nonumber \\ \end{aligned}$$

(50)

$$\begin{aligned} {{\mathbf {K}}_{\mathbf {h}}}^{4\times 4}= & {} \begin{bmatrix} -m\varOmega ^2 &{}\quad 0 &{}\quad 0 &{}\quad +me\varOmega ^2 \\ 0 &{}\quad -m\varOmega ^2 &{}\quad +me\varOmega ^2 &{}\quad 0 \\ 0 &{}\quad +me\varOmega ^2 &{}\quad (A-C)\varOmega ^2 &{}\quad 0 \\ +me\varOmega ^2 &{}\quad 0 &{}\quad 0 &{}\quad (A-B)\varOmega ^2 \\ \end{bmatrix},\nonumber \\ \end{aligned}$$

(51)

$$\begin{aligned} {{\mathbf {K}}_{\mathbf {f}}}^{4\times 4}= & {} - \begin{bmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad mg(e+r)&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad mge \end{bmatrix}, \end{aligned}$$

(52)

$$\begin{aligned} {{\mathbf {D}}_C}^{4\times 4}= & {} - \begin{bmatrix} d&{}\quad 0&{}\quad 0&{}\quad dr\\ 0&{}\quad d&{}\quad dr&{}\quad 0\\ 0 &{}\quad dr&{}\quad dr^2 &{}\quad 0 \\ dr &{}\quad 0&{}\quad 0 &{}\quad dr^2 \end{bmatrix} \end{aligned}$$

(53)

and

$$\begin{aligned} {{\mathbf {B}}_C}^{4\times 4}&= - \begin{bmatrix} 0&{}\quad -d\varOmega &{}\quad -dr\varOmega &{}\quad 0\\ d\varOmega &{}\quad 0&{}\quad 0&{}\quad 0\\ dr\varOmega &{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -dr\varOmega &{}\quad -dr^2\varOmega &{}\quad 0 \end{bmatrix}\nonumber \\&={{\mathbf {B}}}_{\mathrm{sym}}^{4\times 4}+{{\mathbf {B}}}_{\mathrm{skew}}^{4\times 4}. \end{aligned}$$

(54)

In Eq. (515253) the abbreviation $D=(A-B-C)$ is used. The linearization of the gyroscopic ${\mathbf {h}}$-vector leads to a skew-symmetric gyroscopic matrix ${{\mathbf {G}}_{\mathbf {h}}}^{4\times 4}$ and a symmetric stiffness matrix ${{\mathbf {K}}_{\mathbf {h}}}^{4\times 4}$. The gravitational and normal contact forces induce a symmetric ${{\mathbf {K}}_{\mathbf {f}}}^{4\times 4}$ matrix. The linearized Coulomb friction includes linear terms in $\dot{{\hat{{\mathbf {z}}}}}$, which are distributed by the symmetric matrix ${{\mathbf {D}}_C}^{4\times 4}$ on generalized coordinates ${\hat{{\mathbf {z}}}}$. Moreover, Coulomb friction leads to linear terms in ${\hat{{\mathbf {z}}}}$, which occur symmetrically with ${{\mathbf {B}}}_{\mathrm{sym}}^{4\times 4}$ and asymmetrically with ${{\mathbf {B}}}_{\mathrm{skew}}^{4\times 4}$. Defining ${\mathbf {D}}^{4\times 4}:={\mathbf {D}}_C^{4\times 4}$, ${\mathbf {G}}^{4\times 4}:={\mathbf {G}}_{\mathbf {h}}^{4\times 4}$, ${\mathbf {K}}^{4\times 4}:={\mathbf {K}}_{\mathbf {h}}^{4\times 4}+{\mathbf {K}}_{\mathbf {f}}^{4\times 4}+{\mathbf {B}}_\mathrm{sym}^{4\times 4}$ and ${\mathbf {N}}^{4\times 4}:={\mathbf {B}}_\mathrm{skew}^{4\times 4}$, the linearized equations of motion can be written as

$$\begin{aligned} {\mathbf {M}}^{4\times 4}\ddot{{\hat{{\mathbf {z}}}}} + \left( {\mathbf {D}}^{4\times 4} + {\mathbf {G}}^{4\times 4} \right) \dot{{\hat{{\mathbf {z}}}}} + \left( {\mathbf {K}}^{4\times 4} + {\mathbf {N}}^{4\times 4} \right) {{\hat{{\mathbf {z}}}}} = 0 \end{aligned}$$

(55)

and form a system of linear ordinary differential equations with constant coefficients. The matrices ${\mathbf {M}}^{4\times 4}$, ${\mathbf {D}}^{4\times 4}$ and ${\mathbf {K}}^{4\times 4}$ have a symmetric structure. The matrices ${\mathbf {G}}^{4\times 4}$ and ${\mathbf {N}}^{4\times 4}$ are skew symmetric. Since these matrices and hence the eigenvalues, depend on the spinning velocity $\varOmega$, the linear stability behavior of the system can be studied with respect to the bifurcation parameter $\varOmega$.

Due to the high dimension of the corresponding first-order system, the eigenvalues are calculated numerically. Figure 6 shows the real and imaginary part of the eigenvalues $\lambda _1-\lambda _6$ for $\varOmega \in [0,50\,\mathrm {rad}/\mathrm {s}]$. Both real eigenvalues $\lambda _7\approx -9\cdot 10^2 \; 1/\mathrm {s}$ and $\lambda _8\approx -1.5\cdot 10^3 \; 1/\mathrm {s}$ are strongly negative. As the real part does remain almost constant and does not change sign and therefore is not mainly responsible for the qualitative stability behavior, the corresponding two-dimensional subspace remains stable. The comparison of the upper left and right graph shows that the eigenvalues $\lambda _1$(red) and $\lambda _2$(red, dashed) are crossing the imaginary axis at the critical spinning velocity $\varOmega _{\mathrm{crit}_2} \approx 30.2 \, \mathrm{rad/s}$, such that the magnitude of their real part is negative for $\varOmega > \varOmega _{\mathrm{crit}_2}$. Since the eigenvalues are crossing the imaginary axis as complex conjugated pair, the bifurcation can be identified as Hopf bifurcation with corresponding stable two-dimensional eigenspace for super critical spinning velocities. The green pair of conjugated eigenvalues $\lambda _3$ and $\lambda _4$ are purely imaginary and their magnitude is directly related to the spinning velocity $\varOmega$. The eigenvalues $\lambda _5$(blue) and $\lambda _6$(blue, dashed) are crossing the imaginary axis simultaneously at $\varOmega _{\text {crit}_1} \approx 27.1 \, \text {rad/s}$. The bifurcation at $\varOmega _{\mathrm{crit}_1}$ can also be identified as a Hopf bifurcation leading to an unstable subspace for supercritical spinning velocities $\varOmega >\varOmega _{\mathrm{crit}_1}$. In the lower graph of Fig. 6, both critical velocities $\varOmega _{\mathrm{crit}_1}$ and $\varOmega _{\mathrm{crit}_2}$ are depicted in a magnified plot. The numerical eigenvalue analysis indicates that the equilibrium ${\hat{{\mathbf {z}}}}_0=\dot{{\hat{{\mathbf {z}}}}}_0={\mathbf {0}}$ corresponding to a inverted spinning solution is always unstable, since there exists for each $\varOmega$ an unstable subspace. This local stability analysis does not reflect the physical observation of an inverted spinning motion which, loosely speaking, seems to attract almost all trajectories. According to this contradiction, it is not possible to analyze the asymptotic dynamical behavior applying Lyapunov’s indirect method to the six-dimensional system Eq. (15). Just because of the vanishing real parts of $\lambda _3$ and $\lambda _4$, a stability statement about the nonlinear system by neglecting higher-order terms is not possible.

Fig. 6

Evolution of eigenvalues for the inverted tippedisk. (Color figure online)

For the sake of completeness, the eigenvalues for the noninverted spinning tippedisk are shown in Fig. 11 of “Appendix B”. Here we observe that noninverted stationary solutions are always unstable because of the positive real part of $\lambda _1$. This stability behavior is consistent with experimental observations, since it is not possible to rotate the disk so that it remains in a noninverted configuration. In summary, the linearized stability analysis contradicts the physical observation for inverted spinning solutions. The reason for this contradiction could be the restrictive assumption of small $|{\bar{x}}|\ll 1$ and $|{\bar{y}}|\ll 1$. This hypothesis is supported by the fact that in the real experiment we observe horizontal movements of the tippedisk during the inversion phenomenon. Although the linear analysis cannot properly describe the qualitative dynamics, it provides important results. On the one hand we observe that the inverted spinning of the disk, which is basically a stationary solution, manifests as equilibrium in generalized coordinated ${\hat{{\mathbf {z}}}}\in {\mathbb {R}}^4$. On the other hand the linearization of the six-dimensional system motivates a constant spinning velocity ${\dot{\alpha }} \approx \varOmega$ and a constant normal contact force $\lambda _N \approx mg$. Furthermore, the large difference in the eigenvalues implies that the qualitative behavior can be decomposed into slow and fast dynamics, suggesting the application of singular perturbation theory and thus the theory of slow–fast systems.

4 Reduction

In the previous section, it has been shown that the qualitative dynamic behavior of the tippedisk cannot be identified by an eigenvalue analysis of the full system. For this reason, a system reduction is sought which preserves the qualitative stability. Before introducing new constraints, the bilateral constraint of the contact point C is applied, such that an ordinary differential equation is obtained. This bilateral constraint was motivated in [30] and numerically validated. After this first reduction step, new physically motivated constraints are introduced which are validated numerically using simulations with fixed initial conditions. For the sake of clarity, Table 2 introduces the following model names with the assumptions made.

Table 2 Assumptions on constraints of various models introduced in this paper

As several constraints will be introduced in this section, the reduction procedure is explained in a general way. The starting point of any reduction step is an ‘unconstrained’ mechanical system of the form

$$\begin{aligned} \begin{aligned}&{\dot{{\mathbf {q}}}} = {\mathbf {u}}\\&{\mathbf {M}}({\mathbf {q}}){\dot{{\mathbf {u}}}} - {\mathbf {h}}({\mathbf {q}},{\mathbf {u}}) = {\mathbf {f}}({\mathbf {q}},{\mathbf {u}}). \end{aligned} \end{aligned}$$

(56)

The addition of a generic mechanical constraint equation ${\mathbf {c}}({\mathbf {q}},{\mathbf {u}},\varvec{\lambda }_C)=0\in {\mathbb {R}}^m$ induces the generalized constraint force ${\mathbf {f}}_C = {\mathbf {W}}_C \varvec{\lambda }_C$ into the right-hand side of the equation of motion (56), where ${\mathbf {W}}_C$ is the matrix of generalized force directions and $\varvec{\lambda }_C\in {\mathbb {R}}^m$ is the associated constraint force (i.e., Lagrange multiplier). This addition yields the constrained system

$$\begin{aligned} \begin{aligned}&{\dot{{\mathbf {q}}}} = {\mathbf {u}}\\&{\mathbf {M}}({\mathbf {q}}){\dot{{\mathbf {u}}}} - {\mathbf {h}}({\mathbf {q}},{\mathbf {u}}) = {\mathbf {f}}({\mathbf {q}},{\mathbf {u}}) + {\mathbf {W}}_C \varvec{\lambda }_C \\&{\mathbf {c}}({\mathbf {q}},{\mathbf {u}},\varvec{\lambda }_C)=0, \end{aligned} \end{aligned}$$

(57)

which forms a differential algebraic equation (DAE) [16]. In DAE-theory it is possible to obtain the underlying ordinary differential equation (ODE) by successive differentiation of the constraint equation. The (differentiation) index of a DAE counts the differentiations needed to obtain an ODE for all states and Lagrange multipliers [14, 16]. In mechanical systems, we restrict us to constraints on position, velocity or acceleration level. Constraints on position level $\varvec{g}_C({\mathbf {q}})=0$ can be differentiated once to obtain the corresponding constraint on velocity level

$$\begin{aligned} \varvec{\gamma }_C({\mathbf {q}},{\mathbf {u}})=\frac{\partial \varvec{g}_C({\mathbf {q}})}{\partial {\mathbf {q}}} {\dot{{\mathbf {q}}}} =\frac{\partial \varvec{g}_C({\mathbf {q}})}{\partial {\mathbf {q}}} {\mathbf {u}}=0. \end{aligned}$$

(58)

Subsequently, the differentiation of a constraint on velocity level yields the constraint on acceleration level

$$\begin{aligned} \begin{aligned} \dot{\varvec{\gamma }}_C({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})&=\frac{\partial \varvec{\gamma }_C({\mathbf {q}},{\mathbf {u}})}{\partial {\mathbf {u}}} {\dot{{\mathbf {u}}}}+\frac{\partial \varvec{\gamma }_C({\mathbf {q}},{\mathbf {u}})}{\partial {\mathbf {q}}} {\mathbf {u}}\\&=\frac{\partial \varvec{\gamma }_C({\mathbf {q}},{\mathbf {u}})}{\partial {\mathbf {u}}} {\dot{{\mathbf {u}}}}+ \varvec{\chi }=0. \end{aligned} \end{aligned}$$

(59)

Since the mass matrix ${\mathbf {M}}$ is symmetric, positive definite and thus invertible, we obtain the generalized acceleration

$$\begin{aligned} {\dot{{\mathbf {u}}}} = {\mathbf {M}}^{-1} \left( {\mathbf {h}}+ {\mathbf {f}}+ {\mathbf {W}}_C \varvec{\lambda }_C\right) . \end{aligned}$$

(60)

For perfect constraints it holds that the matrix ${\mathbf {W}}_C$ of generalized force directions follows from the kinematics:

$$\begin{aligned} {\mathbf {W}}_C = \left( \frac{\partial \varvec{g}_C}{\partial {\mathbf {q}}}\right) ^{\mathop {{\mathrm {T}}}}= \left( \frac{\partial \varvec{\gamma }_C}{\partial {\mathbf {u}}}\right) ^{\mathop {{\mathrm {T}}}}. \end{aligned}$$

(61)

Substitution of Eq. (60) allows to express the relative acceleration as a function of ${\mathbf {q}}$, ${\mathbf {u}}$ and $\varvec{\lambda }_C$

$$\begin{aligned} \dot{\varvec{\gamma }}_C({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})&=\frac{\partial \varvec{\gamma }_C({\mathbf {q}},{\mathbf {u}})}{\partial {\mathbf {u}}} {\mathbf {M}}^{-1} \left( {\mathbf {h}}+ {\mathbf {f}}+ {\mathbf {W}}_C \varvec{\lambda }_C\right) +\varvec{\chi }\nonumber \\&= \underbrace{{\mathbf {W}}_C^{\mathop {{\mathrm {T}}}}\, {\mathbf {M}}^{-1} {\mathbf {W}}_C}_{=:{\mathbf {D}}} \, \varvec{\lambda }_C\nonumber \\&\quad + {\mathbf {W}}_C^{\mathop {{\mathrm {T}}}}\, {\mathbf {M}}^{-1} \left( {\mathbf {h}}+ {\mathbf {f}}\right) + \varvec{\chi } \nonumber \\&= {\mathbf {c}}({\mathbf {q}},{\mathbf {u}},\varvec{\lambda }_C). \end{aligned}$$

(62)

The square matrix ${\mathbf {D}}= {\mathbf {W}}_C^{\mathop {{\mathrm {T}}}}\, {\mathbf {M}}^{-1} {\mathbf {W}}_C$, defined in Eq. (62), is called the Delassus matrix [8]. For linearly independent constraints $\dot{\varvec{\gamma }}$, the matrix ${\mathbf {W}}_C$ of generalized force directions is of full column rank. The Delassus matrix ${\mathbf {D}}$ is then symmetric, positive definite and thus invertible, such that an explicit equation for $\varvec{\lambda }_C$ can be found. Direct substitution of the explicit equation $\varvec{\lambda }_C({\mathbf {q}},{\mathbf {u}})$ into the equations of motion yields the underlying ODE. However, the DAE (57) with constraint Eq. (62) is a DAE of index 1, as the constraint equation needs to be differentiated once to obtain a differential equation in $({\mathbf {q}},{\mathbf {u}},\varvec{\lambda }_C)$. In summary, a constraint on acceleration level describes an index 1 problem, while constraints on velocity or position level lead to index 2 and index 3 DAEs, respectively. Instead of solving the related ODE, we use a numerical scheme, which solves the DAE of index 1 directly. Considering the constraint on acceleration level Eq. (62) in system (57), we obtain the DAE of index 1

$$\begin{aligned} \begin{aligned}&{\dot{{\mathbf {q}}}} = {\mathbf {u}}\\&{\mathbf {M}}({\mathbf {q}}){\dot{{\mathbf {u}}}} - {\mathbf {h}}({\mathbf {q}},{\mathbf {u}}) = {\mathbf {f}}({\mathbf {q}},{\mathbf {u}}) + {\mathbf {W}}_C \varvec{\lambda }_C \\&{\mathbf {c}}({\mathbf {q}},{\mathbf {u}},\varvec{\lambda }_C)= \dot{\varvec{\gamma }}_C({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})={\mathbf {W}}_{C}^{\mathop {{\mathrm {T}}}}\, {\dot{{\mathbf {u}}}}+ \varvec{\chi }=0. \end{aligned} \end{aligned}$$

(63)

which can be rewritten in matrix form as

$$\begin{aligned} \underbrace{ \begin{bmatrix} {\mathbf {I}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} \\ {\mathbf {0}} &{}\quad {\mathbf {M}}&{}\quad -{\mathbf {W}}_{C}\\ {\mathbf {0}} &{}\quad {\mathbf {W}}_{C}^{\mathop {{\mathrm {T}}}}&{}\quad {\mathbf {0}} \end{bmatrix} }_{{\mathbf {A}}} \begin{bmatrix} {\dot{{\mathbf {q}}}} \\ {\dot{{\mathbf {u}}}} \\ \varvec{\lambda }_C \end{bmatrix} = \begin{bmatrix} {\mathbf {u}}\\ {\mathbf {h}}+ {\mathbf {f}}\\ - \varvec{\chi } \end{bmatrix}. \end{aligned}$$

(64)

The square matrix ${\mathbf {A}}$ is of full rank, as it can be transformed into the upper triangular matrix

$$\begin{aligned} {\mathbf {A}}^{*} = \begin{bmatrix} {\mathbf {I}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} \\ {\mathbf {0}} &{}\quad {\mathbf {I}}&{}\quad -{\mathbf {M}}^{-1}\,{\mathbf {W}}_{C}\\ {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {W}}_{C}^{\mathop {{\mathrm {T}}}}\, {\mathbf {M}}^{-1}\,{\mathbf {W}}_{C} \end{bmatrix}, \end{aligned}$$

(65)

with a submatrix ${\mathbf {A}}_{33}^{*} = {\mathbf {W}}_{C}^{\mathop {{\mathrm {T}}}}\, {\mathbf {M}}^{-1}\,{\mathbf {W}}_{C}$, which is equal to the Delassus matrix ${\mathbf {D}}$ an thus of full rank. Equation (64) can be solved for each time step and therefore integrated with any standard integrator for ordinary differential equations (e.g., the stiff integrator ode15s from MATLAB). To avoid numerical difficulties, the initial conditions must be admissible, i.e., they must be compatible with the applied constraints. The used initial conditions are therefore listed in Table 3 and are chosen such that the following constraints are not violated.

Table 3 Initial conditions

4.1 Bilateral constraint

During the inversion process, one observes that the unilateral constraint $g_{N}\ge 0$ expressing the impenetrability of the contact remains closed, i.e., $g_{N}=0$ see [30]. The unilateral constraint can therefore be replaced with a bilateral one

$$\begin{aligned} g_{N}=z-r\sin \beta =0, \end{aligned}$$

(66)

which forces the contact point to be in touch with the flat support and prevents penetration. Of course, this bilateral restriction does not apply to general motion of the tippedisk, but it is indeed fulfilled during the inversion process and therefore not an approximation. The equations of motion from (15) together with the constraint equation (66) can be written in a differential algebraic form

$$\begin{aligned} \begin{aligned}&{\mathbf {M}}({\mathbf {q}}) \ddot{{\mathbf {q}}} - {\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}}) = {\mathbf {f}}_G + {\mathbf {w}}_N {\lambda }_N + {\mathbf {W}}_T \varvec{\lambda }_T(\lambda _N,\varvec{\gamma }_T),\\&g_{N}({\mathbf {q}})=0 \end{aligned} \end{aligned}$$

(67)

with generalized coordinates

$$\begin{aligned} {\mathbf {q}}= \begin{bmatrix} {\bar{x}}&\quad {\bar{y}}&\quad z&\quad \alpha&\quad \beta&\quad \gamma \end{bmatrix}^{\mathop {{\mathrm {T}}}}\in {\mathbb {R}}^6 \end{aligned}$$

(68)

and generalized force directions

$$\begin{aligned} {\mathbf {w}}_N&= \begin{bmatrix} 0&\quad 0&\quad 1&\quad 0&\quad -r\text {c}\beta&\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(69)

$$\begin{aligned} {\mathbf {W}}_T&= \begin{bmatrix} 1&{}\quad 0&{}\quad 0&{}\quad r\text {c}\beta -{\bar{y}}&{}\quad 0&{}\quad r\\ 0&{}\quad 1&{}\quad 0&{}\quad {\bar{x}}&{}\quad r\text {s}\beta &{}\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}= \begin{bmatrix} {{\mathbf {w}}}_{x}^{\mathop {{\mathrm {T}}}}\\ {{\mathbf {w}}}_{y}^{\mathop {{\mathrm {T}}}}\end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(70)

from Eqs. (31)–(32). The system Equation (67) forms a DAE of index 3, as the constraint (66) is formulated on position level. The associated Lagrange multiplier of the bilateral constraint is identified as the normal contact force $\lambda _N$ with corresponding generalized force direction

$$\begin{aligned} {\mathbf {w}}_N=\left( \frac{\partial g_{N}({\mathbf {q}})}{\partial {\mathbf {q}}}\right) ^{\mathop {{\mathrm {T}}}}. \end{aligned}$$

(71)

The tangential generalized contact force $\varvec{\lambda }_T$, described by the friction law (3), depends linearly on the normal contact force $\lambda _N$. The index of the DAE (67) can be reduced by differentiating the constraint equation, i.e., replacing it with the velocity constraint,

$$\begin{aligned} \gamma _{N}({\mathbf {q}},{\dot{{\mathbf {q}}}})= \frac{\partial g_{N}({\mathbf {q}})}{\partial {\mathbf {q}}}{\dot{{\mathbf {q}}}} = {\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {q}}}} = {\dot{z}}-r{\dot{\beta }}\cos \beta =0,\nonumber \\ \end{aligned}$$

(72)

yielding the DAE of index 2

$$\begin{aligned} \begin{aligned}&{\mathbf {M}}({\mathbf {q}}) \ddot{{\mathbf {q}}} - {\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}}) = {\mathbf {f}}_G + {\mathbf {w}}_N {\lambda }_N + {\mathbf {W}}_T \varvec{\lambda }_T(\lambda _N,\varvec{\gamma }_T),\\&\gamma _{N}({\mathbf {q}},{\dot{{\mathbf {q}}}})={\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {q}}}}=0. \end{aligned} \end{aligned}$$

(73)

Subsequently, we reduce the index of system (73) by formulating the constraint on acceleration level

$$\begin{aligned} {\dot{\gamma }}_{N}({\mathbf {q}},{\dot{{\mathbf {q}}}},\ddot{{\mathbf {q}}})&= {\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}\ddot{{\mathbf {q}}}+{\dot{{\mathbf {w}}}}_{N}^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {q}}}} \nonumber \\&= \ddot{z}-r\ddot{\beta }\cos \beta +r{\dot{\beta }}^2\sin \beta =0,\nonumber \\ \end{aligned}$$

(74)

to arrive at the DAE of index 1

$$\begin{aligned} \begin{aligned}&{\mathbf {M}}({\mathbf {q}}) \ddot{{\mathbf {q}}} - {\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}}) = {\mathbf {f}}_G + {\mathbf {w}}_N {\lambda }_N + {\mathbf {W}}_T \varvec{\lambda }_T(\lambda _N,\varvec{\gamma }_T),\\&{\dot{\gamma }}_{N}({\mathbf {q}},{\dot{{\mathbf {q}}}},\ddot{{\mathbf {q}}})={\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}\ddot{{\mathbf {q}}}+{\dot{{\mathbf {w}}}}_{N}^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {q}}}}=0. \end{aligned} \end{aligned}$$

(75)

As the first equation of (75) describes the equation of motion, which is basically a differential equation of second order, we introduce the kinematic equation

$$\begin{aligned} {\mathbf {u}}:= {\dot{{\mathbf {q}}}}, \end{aligned}$$

(76)

such that the system (75) can be rewritten in first-order form as

$$\begin{aligned} \begin{aligned}&{\dot{{\mathbf {q}}}} = {\mathbf {u}}\\&{\mathbf {M}}({\mathbf {q}}) {\dot{{\mathbf {u}}}} - {\mathbf {h}}({\mathbf {q}},{\mathbf {u}}) = {\mathbf {f}}_G + {\mathbf {w}}_N {\lambda }_N + {\mathbf {W}}_T \varvec{\lambda }_T(\lambda _N,\varvec{\gamma }_T),\\&{\dot{\gamma }}_{N}({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})={\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}{\dot{{\mathbf {u}}}}+{\dot{{\mathbf {w}}}}_{N}^{\mathop {{\mathrm {T}}}}{\mathbf {u}}=0. \end{aligned} \end{aligned}$$

(77)

Inserting the force law (3) of smooth Coulomb friction into the right-hand side of the kinetic equation, we obtain as right-hand side (RHS)

$$\begin{aligned} \begin{aligned} \mathrm{RHS}&= {\mathbf {f}}_G + {\mathbf {w}}_N {\lambda }_N + {\mathbf {W}}_T \varvec{\lambda }_T(\lambda _N,\varvec{\gamma }_T)\\&= {\mathbf {f}}_G + \underbrace{\left( {\mathbf {w}}_N - \mu {\mathbf {W}}_T\frac{\varvec{\gamma }_T}{||\varvec{\gamma }_T||+\varepsilon } \right) }_{=: {\mathbf {W}}_{NT}} \lambda _N. \end{aligned} \end{aligned}$$

(78)

The index-1 equations of motion Eq. (77) can be reformulated in matrix form using Eq. (78) as

$$\begin{aligned} \underbrace{ \begin{bmatrix} {\mathbf {I}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} \\ {\mathbf {0}} &{}\quad {\mathbf {M}}&{}\quad -{\mathbf {W}}_{NT}\\ {\mathbf {0}} &{}\quad {\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}&{}\quad {\mathbf {0}} \end{bmatrix} }_{{\mathbf {A}}_0} \begin{bmatrix} {\dot{{\mathbf {q}}}} \\ {\dot{{\mathbf {u}}}} \\ \lambda _N \end{bmatrix} = \begin{bmatrix} {\mathbf {u}}\\ {\mathbf {h}}+ {\mathbf {f}}_G \\ - {\dot{{\mathbf {w}}}}_{N}^{\mathop {{\mathrm {T}}}}\, {\mathbf {u}}\end{bmatrix}, \end{aligned}$$

(79)

depending on the kinematic quantities ${\dot{{\mathbf {q}}}}$, ${\dot{{\mathbf {u}}}}$ and the normal force $\lambda _N$. The $\lambda _N$-dependence in the Coulomb friction law renders the matrix ${\mathbf {A}}_0$ asymmetric and is therefore not guaranteed to be invertible. Using the results from the previous section, where the system was linearized with six degrees of freedom, the assumption $\lambda _N \approx mg$ for calculation of the friction force is motivated. Using this approximation, Eq. (79) is rewritten as

$$\begin{aligned} \underbrace{ \begin{bmatrix} {\mathbf {I}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} \\ {\mathbf {0}} &{}\quad {\mathbf {M}}&{}\quad -{\mathbf {w}}_{N}\\ {\mathbf {0}} &{}\quad {\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}&{}\quad {\mathbf {0}} \end{bmatrix} }_{{\mathbf {A}}_1} \begin{bmatrix} {\dot{{\mathbf {q}}}} \\ {\dot{{\mathbf {u}}}} \\ \lambda _N \end{bmatrix} = \begin{bmatrix} {\mathbf {u}}\\ {\mathbf {h}}+ {\mathbf {f}}_G + {\mathbf {W}}_T \varvec{\lambda }_T\\ - {\dot{{\mathbf {w}}}}_{N}^{\mathop {{\mathrm {T}}}}\, {\mathbf {u}}\end{bmatrix},\nonumber \\ \end{aligned}$$

(80)

with

$$\begin{aligned} \varvec{\lambda }_T = \begin{bmatrix} \lambda _{Tx} \\ \lambda _{Ty} \end{bmatrix} = -\mu m g \frac{\varvec{\gamma }_T}{||\varvec{\gamma }_{T}||+\varepsilon }, \end{aligned}$$

(81)

i.e., $\varvec{\lambda }_T=\varvec{\lambda }_T({\mathbf {q}},{\mathbf {u}})$. The assumption of a constant normal contact force mg in the Coulomb friction law has led to a symmetric matrix ${\mathbf {A}}_1$, having the same structure as the matrix ${\mathbf {A}}$ in Eq. (64), guaranteeing the solvability of Eq. (80). In Fig. 7, the angles $\beta$ and $\gamma$ are shown during the process of inversion.

Fig. 7

Simulation results for Model 1: bilateral constraint. (Color figure online)

The $\gamma$-graph (red, dashed) starts from $\gamma _0 = -{\pi }/{2} +0.1 \, \mathrm {rad}$ and converges in the interval $t \in \left[ 0\, \mathrm{s},\, 0.5\, \mathrm{s}\right]$ to $\gamma ={\pi }/{2}$. As the angle $\beta$ (blue, dotted) only changes slightly, we identify the increase in $\gamma$ with the inversion of the tippedisk. Both angles are superimposed with small oscillations occurring from $t\approx 0.5\, \mathrm{s}$. The colored angles were obtained by solving the DAE of index 1 from Eq. (79). The angles shown in black are calculated assuming a constant normal force $\lambda _N\approx mg$, i.e., by combining Eqs. (80) and (81). Since the normal force $\lambda _N$ is nearly constant, it is convenient to neglect the $\lambda _N$-dependence in the tangential friction law and to assume a constant scaling. This has already been motivated by the linear stability analysis. The difference between the solutions with constant and varying normal force is nearly zero. To be more specific, the absolute difference $|\Delta \beta |$ and $|\Delta \gamma |$ lies in the range of $10^{-2} \,\mathrm{rad}$. For the sake of simplicity, we will use only the approach of a constant normal force in the following.

4.2 COG constraint

The horizontal position of the tippedisk does not affect the dynamical behavior, since the equations of motion (w.r.t the inertial I-frame) do not explicitly depend on the horizontal position, see “Appendix A”. The only force acting in the horizontal direction is caused by friction and is therefore dependent on the relative sliding velocity at the contact point. The relative sliding velocity can be decomposed into a part caused by horizontal translation and a part induced by gyroscopic effects. As the gyroscopic effects dominate, the part induced by horizontal motion is negligible, motivating the assumption of a horizontally fixed center of gravity. In experiments, we observe that the disk only drifts slowly in the horizontal plane, supporting the hypothesis of a horizontally immobile COG. The COG constraint can be expressed on position level with

$$\begin{aligned} {\mathbf {r}}_{OS}={{\mathbf {r}}}_{OG}+e{\mathbf {e}}_x^B \end{aligned}$$

(82)

as

$$\begin{aligned} \varvec{g}_S({\mathbf {q}}) = \begin{bmatrix} {\mathbf {e}}_x^R \cdot {\mathbf {r}}_{OS} \\ {\mathbf {e}}_y^R \cdot {\mathbf {r}}_{OS} \end{bmatrix} = \begin{bmatrix} {\bar{x}}+ e \cos \gamma \\ {\bar{y}}+ e \cos \beta \sin \gamma \end{bmatrix} = 0\nonumber \\ \end{aligned}$$

(83)

and can be written with the matrix

$$\begin{aligned} {\mathbf {W}}_S&= \left( \frac{\partial \varvec{g}_S({\mathbf {q}})}{\partial {\mathbf {q}}} \right) ^{\mathop {{\mathrm {T}}}}\nonumber \\&= \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -e\sin \gamma \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad -e\sin \beta \sin \gamma &{}\quad +e\cos \beta \cos \gamma \end{bmatrix}^{\mathop {{\mathrm {T}}}}\nonumber \\ \end{aligned}$$

(84)

of generalized force directions as a velocity constraint

$$\begin{aligned} \varvec{\gamma }_S({\mathbf {q}},{\mathbf {u}}) = {\mathbf {W}}_S^{\mathop {{\mathrm {T}}}}{\mathbf {u}}= 0. \end{aligned}$$

(85)

In Fig. 8, the simulation results of angles $\beta$ and $\gamma$ are depicted during the inversion process under the assumption of a bilateral constraint together with a horizontally fixed center of gravity. The simulation results of Model 2 are very similar to the results of Model 1, both qualitatively and quantitatively. A high-frequency oscillation, present in Model 1, has disappeared in Model 2.

4.3 No tangential slip

The relative velocity between the moving contact point C and the inertial fixed support is equal to the horizontal projection of the velocity ${\mathbf {v}}_C$ of the contact point C and can be decomposed into two orthogonal parts. For a more physical interpretation, we use the co-rotating R-frame with

$$\begin{aligned} \begin{aligned} {\mathbf {e}}_x^R = \frac{{\mathbf {e}}_z^I \times {\mathbf {e}}_z^B}{||{\mathbf {e}}_z^I \times {\mathbf {e}}_z^B||}, \quad {\mathbf {e}}_z^R = {\mathbf {e}}_z^I, \quad {\mathbf {e}}_x^R = {\mathbf {e}}_z^R \times {\mathbf {e}}_x^R \end{aligned}\nonumber \\ \end{aligned}$$

(86)

and define the projected relative velocity components $\gamma _x: = {\mathbf {e}}_x^R \cdot {\mathbf {v}}_C$ and $\gamma _y: = {\mathbf {e}}_y^R \cdot {\mathbf {v}}_C$ as tangential and lateral slipping velocity. Motivated through experiments we assume that the tippedisk inverts without any slip in ${\mathbf {e}}_x^R$-direction, which justifies the velocity constraint

$$\begin{aligned} {\gamma }_{x}({\mathbf {q}},{\mathbf {u}}) = {\mathbf {w}}_{x}^{\mathop {{\mathrm {T}}}}{\mathbf {u}}= {\mathbf {e}}_x^R \cdot {\mathbf {v}}_C = 0. \end{aligned}$$

(87)

At his point we mention that the assumption of pure rolling (${\mathbf {v}}_C = 0$) does not lead to the inversion of the tippedisk and therefore does not describe the phenomenon under investigation. Figure 8 shows the simulation results of Model 3, using initial conditions of Table 3 under the assumption of a bilateral constraint, a horizontally fixed center of gravity and zero slip condition in ${\mathbf {e}}_x^R$-direction, introduced in (87). Qualitatively, the simulation results of Model 3 are similar to Model 2.

Fig. 8

Comparison of simulation results of the various models

4.4 Constant spinning velocity

The linearization of the system (15) reveals that the spinning velocity ${\dot{\alpha }}$ is constant for motion in the vicinity of an inverted spinning solution, such that ${\dot{\alpha }}=\varOmega$ holds. Furthermore, simulation results of the full model show that the angle $\alpha$ seems to increase almost linearly during the whole inversion process of the tippedisk. The assumption of a constant spinning velocity ${\dot{\alpha }}=\varOmega$ can be written with the generalized force direction

$$\begin{aligned} {\mathbf {w}}_{\alpha } = \begin{bmatrix} 0&\quad 0&\quad 0&\quad 1&\quad 0&\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(88)

and $\chi _{\alpha }=\varOmega =\mathrm{const}$ as a constraint on velocity level

$$\begin{aligned} \gamma _{\alpha }({\mathbf {q}},{\mathbf {u}})={\mathbf {w}}_{\alpha }^{\mathop {{\mathrm {T}}}}{\mathbf {u}}-\chi _{\alpha }={\dot{\alpha }}-\varOmega =0, \end{aligned}$$

(89)

Since Eq. (89) describes a holonomic constraint, we integrate the constraint on velocity level to obtain the rheonomic constraint

$$\begin{aligned} g_{\alpha }({\mathbf {q}},t)=\alpha (t) - \varOmega t - \alpha _0 = 0 \end{aligned}$$

(90)

on position level [7]. The equations of motion do not depend on $\alpha$ explicitly. For this reason $\alpha _0$ can be set to zero without loss of generality.

4.5 Reduced system

The application of a bilateral constraint, a horizontal fixed center of gravity, zero tangential slip in ${\mathbf {e}}_x^R$-direction and a constant spinning velocity yields the constrained system

$$\begin{aligned} \begin{aligned}&{\dot{{\mathbf {q}}}} = {\mathbf {u}}\\&{\mathbf {M}}({\mathbf {q}}) {\dot{{\mathbf {u}}}} - {\mathbf {h}}({\mathbf {q}},{\mathbf {u}}) = {\mathbf {f}}_G + {{\mathbf {w}}_N} {\lambda }_N + {{\mathbf {w}}_{y}} {\lambda }_{Ty} + {{\mathbf {W}}_S} \varvec{\lambda }_S \\&\qquad + {{\mathbf {w}}_{x}} {\lambda }_{Tx} + {{\mathbf {w}}_{\alpha }} {\lambda }_{\alpha } \\&{\dot{\gamma }}_{N}({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})=0 \\&\dot{\varvec{\gamma }}_S({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})=0 \\&{\dot{\gamma }}_{x}({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})=0 \\&{\dot{\gamma }}_{\alpha }({\mathbf {q}},{\mathbf {u}},{\dot{{\mathbf {u}}}})=0 \end{aligned} \end{aligned}$$

(91)

of index 1, which can be written in linear matrix form

$$\begin{aligned}&\underbrace{ \begin{bmatrix} {\mathbf {I}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}}\\ {\mathbf {0}} &{}\quad {\mathbf {M}}&{}\quad -{\mathbf {w}}_{N} &{}\quad -{\mathbf {W}}_{S} &{}\quad -{\mathbf {w}}_{x} &{}\quad -{\mathbf {w}}_{\alpha }\\ {\mathbf {0}} &{}\quad {\mathbf {w}}_{N}^{\mathop {{\mathrm {T}}}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}}\\ {\mathbf {0}} &{}\quad {\mathbf {W}}_{S}^{\mathop {{\mathrm {T}}}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}}\\ {\mathbf {0}} &{}\quad {\mathbf {w}}_{x}^{\mathop {{\mathrm {T}}}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}}\\ {\mathbf {0}} &{}\quad {\mathbf {w}}_{\alpha }^{\mathop {{\mathrm {T}}}}&{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}}\\ \end{bmatrix} }_{{\mathbf {A}}_\mathrm{red}} \begin{bmatrix} {\dot{{\mathbf {q}}}} \\ {\dot{{\mathbf {u}}}} \\ \lambda _N \\ \varvec{\lambda }_S \\ \lambda _{Tx} \\ \lambda _{\alpha } \\ \end{bmatrix} \nonumber \\&\quad = \begin{bmatrix} {\mathbf {u}}\\ {\mathbf {h}}+ {\mathbf {f}}_G + {{\mathbf {w}}_{y}} {\lambda }_{Ty}\\ - {\dot{{\mathbf {w}}}}_{N}^{\mathop {{\mathrm {T}}}}\, {\mathbf {u}}\\ - {\dot{{\mathbf {W}}}}_{S}^{\mathop {{\mathrm {T}}}}\, {\mathbf {u}}\\ - {\dot{{\mathbf {w}}}}_{x}^{\mathop {{\mathrm {T}}}}\, {\mathbf {u}}\\ - {\dot{{\mathbf {w}}}}_{\alpha }^{\mathop {{\mathrm {T}}}}\, {\mathbf {u}}\\ \end{bmatrix}. \end{aligned}$$

(92)

In (92) the constraints are applied on acceleration level so that the system can be solved numerically using explicit integration schemes. However, this formulation on acceleration level can lead to drift problems and therefore to excessive constraint violation (e.g., penetration). To prevent the constraints from drifting, one may choose a new set of minimal coordinates

$$\begin{aligned} {\mathbf {z}}= \begin{bmatrix} \beta \\ \gamma \end{bmatrix}, \end{aligned}$$

(93)

such that ${\mathbf {q}}={\mathbf {q}}({\mathbf {z}})$ fulfills all constraints on position level

$$\begin{aligned} \begin{aligned} g_{N}({\mathbf {q}}({\mathbf {z}}))&\equiv 0 \; \forall {\mathbf {z}}\\ \varvec{g}_S({\mathbf {q}}({\mathbf {z}}))&\equiv 0 \; \forall {\mathbf {z}}\\ g_{\alpha }({\mathbf {q}}({\mathbf {z}}))&\equiv 0 \; \forall {\mathbf {z}}\\ \end{aligned} \end{aligned}$$

(94)

intrinsically. In addition, we choose new minimal velocities

$$\begin{aligned} {\mathbf {v}}:={\dot{\beta }} \end{aligned}$$

(95)

and introduce the kinematic differential equation

$$\begin{aligned} {\mathbf {u}}= {\mathbf {B}}({\mathbf {z}}) {\mathbf {v}}+\varvec{\beta }({\mathbf {z}},t), \end{aligned}$$

(96)

with

$$\begin{aligned} \begin{aligned} {\mathbf {B}}({\mathbf {z}})&= \begin{bmatrix} 0\\ e\sin \beta \sin \gamma \\ +r\cos \beta \\ 0\\ 1\\ 0 \end{bmatrix}&\; \mathrm{and} \; \\ \varvec{\beta }({\mathbf {z}},t)&= \begin{bmatrix} -e\varOmega \cos \beta \sin \gamma \\ +e\varOmega \cos ^2\beta \sin \gamma \\ 0\\ \varOmega \\ 0\\ -\varOmega \cos \beta \end{bmatrix} \end{aligned} \end{aligned}$$

(97)

such that the velocity constraint

$$\begin{aligned} \begin{aligned} \gamma _{x}({\mathbf {q}}({\mathbf {z}}),{\mathbf {u}}({\mathbf {z}},{\mathbf {v}}))&\equiv 0 \\ \end{aligned} \end{aligned}$$

(98)

is automatically fulfilled for all ${\mathbf {z}}$ and for all ${\mathbf {v}}$. As the velocity constraint from Eq. (98) is non-integrable, it is identified as a nonholonomic constraint [2, 3]. The constraints from (91) are said to be perfect in the sense of d’Alembert, as

$$\begin{aligned} \begin{aligned}&{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {w}}_N = 0 \\&{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {W}}_S = 0 \\&{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {w}}_x = 0 \\&{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {w}}_\alpha = 0 \\ \end{aligned} \end{aligned}$$

(99)

holds [7, 28]. With Eqs. (97), (99), (91) and the matrix

$$\begin{aligned} {\mathbf {C}}= \begin{bmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{bmatrix}, \end{aligned}$$

(100)

we obtain the reduced system

$$\begin{aligned} \begin{aligned}&{\dot{{\mathbf {z}}}} = {\mathbf {C}}\left( {\mathbf {B}}({\mathbf {z}}){\mathbf {v}}+\varvec{\beta }({\mathbf {z}},t)\right) \\&{\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {M}}{\mathbf {B}}{\dot{{\mathbf {v}}}} - {\mathbf {B}}^{\mathop {{\mathrm {T}}}}\left( {\mathbf {h}}- {\mathbf {M}}({\dot{{\mathbf {B}}}}{\mathbf {v}}+\dot{\varvec{\beta }})\right) = {\mathbf {B}}^{\mathop {{\mathrm {T}}}}{\mathbf {f}}_G + {\mathbf {B}}^{\mathop {{\mathrm {T}}}}{{\mathbf {w}}_{y}} {\lambda }_{Ty}. \end{aligned} \end{aligned}$$

(101)

This reduced system in minimal coordinates ${\mathbf {z}}$ and minimal velocities ${\mathbf {v}}$ from Eq. (101) corresponds to a first-order ordinary differential equation of the form

$$\begin{aligned} \begin{aligned}&{\dot{{\mathbf {z}}}} = {\bar{{\mathbf {B}}}}({\mathbf {z}}){\mathbf {v}}+ \bar{\varvec{\beta }}({\mathbf {z}})\\&{\bar{{\mathbf {M}}}}({\mathbf {z}}){\dot{{\mathbf {v}}}} - {\bar{{\mathbf {h}}}}({\mathbf {z}},{{\mathbf {v}}})= {\bar{{\mathbf {f}}}}_G + {\bar{{\mathbf {w}}}}_{y} {\lambda }_{Ty}, \end{aligned} \end{aligned}$$

(102)

with mass matrix (here scalar)

$$\begin{aligned} {\bar{{\mathbf {M}}}} = {A}\cos ^2\gamma +{\bar{B}}\sin ^2\gamma +m(r+e\sin \gamma )^2\cos ^2\beta ,\nonumber \\ \end{aligned}$$

(103)

scalar gyroscopic force term

$$\begin{aligned} \begin{aligned} {\bar{{\mathbf {h}}}}&= +({A}\cos ^2\gamma +{\bar{B}}\sin ^2\gamma )\varOmega ^2 \sin \beta \cos \beta \\&\quad -\,2({A}-{\bar{B}})\varOmega {\dot{\beta }}\cos \beta \sin \gamma \cos \gamma \\&\quad +\,m(r+e\sin \gamma )^2{\dot{\beta }}^2\sin \beta \cos \beta \\&\quad +\,me(r+e\sin \gamma )\varOmega ^2\sin \beta \cos ^3\beta \sin \gamma \\&\quad -\,me(r+e\sin \gamma )(3\sin ^2\beta -2)\varOmega {\dot{\beta }}\cos \beta \cos \gamma , \end{aligned} \end{aligned}$$

(104)

generalized gravitational force

$$\begin{aligned} {\bar{{\mathbf {f}}}}_G = -mg(r+e\sin \gamma )\cos \beta \end{aligned}$$

(105)

and generalized friction force ${\bar{{\mathbf {w}}}}_{y} {\lambda }_{Ty}$ with corresponding force direction

$$\begin{aligned} {\bar{{\mathbf {w}}}}_y = (r+e\sin \gamma )\sin \beta , \end{aligned}$$

(106)

lateral sliding velocity

$$\begin{aligned} {\bar{\gamma }}_y = (r+e\sin \gamma ){\dot{\beta }}\sin \beta -e\varOmega \sin ^2\beta \cos \gamma \end{aligned}$$

(107)

and friction force

$$\begin{aligned} {\lambda }_{Ty} = -\mu m g\frac{{\bar{\gamma }}_y}{|{\bar{\gamma }}_y|+\varepsilon }. \end{aligned}$$

(108)

In Eqs. (103) and (104) the abbreviation ${\bar{B}}=B-me^2$ is used. The kinematic part of (102) yields

$$\begin{aligned} {\dot{{\mathbf {z}}}} = {\bar{{\mathbf {B}}}}({\mathbf {z}}){\mathbf {v}}+ \bar{\varvec{\beta }}({\mathbf {z}},t) \end{aligned}$$

(109)

with

$$\begin{aligned} {\bar{{\mathbf {B}}}}({\mathbf {z}}) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \quad \mathrm{and} \quad \bar{\varvec{\beta }}({\mathbf {z}}) = \begin{bmatrix} 0 \\ -\varOmega \cos \beta \end{bmatrix}. \end{aligned}$$

(110)

Equations (92) and (102) describe the bilaterally constrained tippedisk with horizontally fixed center of gravity, zero slip condition in ${\mathbf {e}}_x^R$-direction and a constant spinning velocity. Equation (92) describes a DAE of index 1, which can be solved numerically since all constraints are formulated on acceleration level. In contrast, Eq. (102) corresponds to a formulation in minimal coordinates ${\mathbf {q}}$ and minimal velocities ${\mathbf {v}}$ satisfying the introduced constraints, so that the behavior of the system is described by a first-order ordinary differential equation. Since both approaches consider the same constraints, they lead (in the absence of numerical errors such as drift) to the same simulation results, which are shown in Fig. 8.

5 Comparison

In the previous sections, we have presented several models by applying additional constraints on the system (15). The introduced constraints are used to reduce the number of degrees of freedom, step by step, and thus to obtain a minimal model which qualitatively describes the inversion behavior of the tippedisk. In this section, the solutions of all reduction stages are compared, starting from the initial conditions given in Table 3. The evolution of the angle $\gamma$ and the inclination angle $\beta$ is shown in Fig. 8 for Models 1–4.

Qualitatively, the trajectories of the inclination angle $\beta$ remain close to $\pi /2$ for all introduced models. The qualitative comparison of the derived models shows that the behavior is similar. However, it can be noted that the additional constraints lead to less overshooting and faster convergence to the inverted spinning solution. In Fig. 9, the evolution of the spinning velocity ${\dot{\alpha }}$ is depicted for the presented models.

Fig. 9

Evolution of the spinning velocity $\dot{\alpha }$. For $t>2\, \mathrm {s}$ the spinning velocity $\varOmega$ remains for Model 1, 2 and 3 almost constant. Model 4 assumes per definition a constant spinning speed $\varOmega$

The red graph describes the spinning velocity ${\dot{\alpha }}$ under the assumption of a bilateral constraint of the contact point, the green under assumption of a bilateral constraint and a horizontally fixed center of gravity. The blue ${\dot{\alpha }}$-graph is obtained from the model with an additional constraint on the tangential sliding velocity. The black graph is given using the model from Eq. (102), which assumes a constant spinning velocity and therefore implies directly a linear time dependency of $\alpha$. According to Fig. 9, the spinning velocity ${\dot{\alpha }}(t)$ drops slightly during the inversion phenomenon from ${\dot{\alpha }}_0=40 \,\mathrm {rad}/\mathrm {s}$ to ${\dot{\alpha }}\approx 35 \,\mathrm {rad}/\mathrm {s}$. This drop in ${\dot{\alpha }}$ stems from the fact that the kinetic energy has to decrease when the potential energy rises during the inversion process. The exact decrease here depends on the respective model, but is in a similar order of magnitude. After the disk inverts its orientation, the rotational velocity ${\dot{\alpha }}$ is kept nearly constant.

6 Linear stability analysis of the 3 DOF system

Similar to Sect. 3, the shifted angles ${\bar{\beta }}=\beta -\pi /2$ and ${\bar{\gamma }}=\gamma -\pi /2$ are introduced. The linearization of Eq. (102) around the equilibrium ‘inverted spinning’ yields the linear homogeneous system

$$\begin{aligned} {\dot{{\mathbf {x}}}}= \begin{bmatrix} \dot{{\bar{\beta }}} \\ \dot{{\bar{\gamma }}} \\ \ddot{{\bar{\beta }}} \end{bmatrix} = \begin{bmatrix} 0 &{}\quad 0 &{}\quad 1 \\ \varOmega &{}\quad 0 &{}\quad 0 \\ A_{31} &{}\quad A_{32} &{}\quad A_{33} \end{bmatrix} \begin{bmatrix} {\bar{\beta }} \\ {\bar{\gamma }} \\ \dot{{\bar{\beta }}} \end{bmatrix} = {\mathbf {A}}{\mathbf {x}}, \end{aligned}$$

(111)

with

$$\begin{aligned} \begin{aligned}&A_{31} =\frac{mg}{{\bar{B}}}(r+e)-\varOmega ^2 = {\mathcal {O}}\left( 1\right) \\&A_{32} = -\frac{\mu mg}{\varepsilon {\bar{B}}}e(r+e)\varOmega = {\mathcal {O}}\left( \tfrac{1}{\varepsilon }\right) \\&A_{33} = -\frac{\mu mg}{\varepsilon {\bar{B}}}(r+e)^2 = {\mathcal {O}}\left( \tfrac{1}{\varepsilon }\right) . \end{aligned} \end{aligned}$$

(112)

The eigenvalues $\lambda _i^\mathrm{n}$ from Eq. (111) are computed numerically and shown in color in Fig. 10 for varying $\varOmega$. The left graph shows the real part ${\mathcal {R}}(\lambda _i)$ of the eigenvalues $\lambda _i$ for $\varOmega \in [0,50\,\mathrm {rad}/\mathrm {s}]$. The right graph of Fig. 10 represents the corresponding imaginary part ${\mathcal {I}}(\lambda _i)$. Since the real part of the third eigenvalue $\lambda _3^\mathrm{n}$ yields $\mathcal {R}(\lambda _3^\mathrm {n})<-100 \; 1/\mathrm {s}\; \forall \,\varOmega \in [0,50\,\mathrm {rad}/\mathrm {s}]$, it is not shown in the left diagram. For $\varOmega =0$ the eigenvalues $\lambda _1^\mathrm{n}$ and $\lambda _2^\mathrm{n}$ are purely real and ${\mathcal {R}}(\lambda _1^\mathrm{n})>0$, ${\mathcal {R}}(\lambda _2^\mathrm{n})=0$ holds. If the rotation speed $\varOmega$ is increased, these two eigenvalues $\lambda _1$ and $\lambda _2$ with positive real part converge so that from $\varOmega _1\approx 12.5\,\mathrm {rad}/\mathrm {s}$ on they form a complex conjugate pair with equal positive real part. If the spinning velocity $\varOmega$ is further increased, the complex conjugate pair of eigenvalues $\lambda _1^\mathrm{n}$ and $\lambda _2^\mathrm{n}$ is crossing the imaginary axis, changing the sign of the real part at the numerically determined critical spinning velocity $\varOmega _{\mathrm{crit}}^\mathrm{n}\approx 31\,\mathrm {rad}/\mathrm {s}$. For $\varOmega >\varOmega _{\mathrm{crit}}^\mathrm{n}$ all eigenvalues have negative real part, such that the inverted spinning equilibrium is locally asymptotically attractive. As a complex conjugate pair of eigenvalues (i.e., the pair of $\lambda _1^\mathrm{n}$ and $\lambda _2^\mathrm{n}$) changes the stability behavior of the equilibrium, we identify the corresponding bifurcation as a Hopf bifurcation.

Fig. 10

Eigenvalues for the inverted tippedisk for varying spinning velocity $\varOmega$. (Color figure online)

Due to the dimension of the system (111), a linear stability analysis in closed form is not feasible. However, we can use the smoothing parameter $\varepsilon$ as perturbation parameter with $\lim \varepsilon \downarrow 0$ to approximate the eigenvalues. The characteristic polynomial $p(\lambda )$ can be calculated using the Laplace expansion as

$$\begin{aligned} \begin{aligned} p(\lambda )&= \det ({\mathbf {A}}-\lambda {\mathbf {I}}) \\&= (-\lambda ) (-\lambda (A_{33}-\lambda )) + (+1)(A_{32}\varOmega +A_{31}\lambda ) \\&= -\lambda ^3+A_{33}\lambda ^2+A_{31}\lambda +A_{32}\varOmega \overset{!}{=} 0. \end{aligned} \end{aligned}$$

(113)

Since the linear first-order system (111) has dimension three, there is at least one pure real eigenvalue such that the characteristic polynomial $p(\lambda )$ can be written as polynomial decomposition

$$\begin{aligned} \begin{aligned} p(\lambda )&=(a-\lambda )(\lambda ^2+b\lambda +c) \\&= -\lambda ^3 + (a-b) \lambda ^2 + (ab-c) \lambda + ac \overset{!}{=} 0. \end{aligned} \end{aligned}$$

(114)

The comparison of coefficients from Eqs. (113) and (114) yields with Eq. (112)

$$\begin{aligned} A_{31}&= ab-c = {\mathcal {O}}\left( 1\right) \end{aligned}$$

(115)

$$\begin{aligned} A_{32}&= \frac{ac}{\varOmega } = {\mathcal {O}}\left( \tfrac{1}{\varepsilon }\right) \end{aligned}$$

(116)

$$\begin{aligned} A_{33}&= a-b = {\mathcal {O}}\left( \tfrac{1}{\varepsilon }\right) , \end{aligned}$$

(117)

from which we derive the mathematical orders

$$\begin{aligned} a={\mathcal {O}}\left( \tfrac{1}{\varepsilon }\right) , \quad c={\mathcal {O}}\left( 1\right) , \quad b={\mathcal {O}}\left( \varepsilon \right) . \end{aligned}$$

(118)

From Eqs. (118), (117) and (112) we obtain the coefficients

$$\begin{aligned} \varepsilon \downarrow 0&\implies a \rightarrow A_{33} = -\frac{\mu mg}{\varepsilon {\bar{B}}}(r+e)^2 \end{aligned}$$

(119)

$$\begin{aligned}&\implies c \rightarrow \frac{A_{32}}{A_{33}}\varOmega = \frac{e}{r+e}\varOmega ^2 \end{aligned}$$

(120)

$$\begin{aligned}&\implies b \rightarrow \frac{1}{a}(A_{31}+c) \nonumber \\&\approx -129.04 \,\frac{\text {1}}{\mathrm {s}}. \end{aligned}$$

(121)

According to the polynomial decomposition (114), the purely real eigenvalue is identified as

$$\begin{aligned} \lambda _3 = a= & {} A_{33} + {\mathcal {O}}\left( \varepsilon \right) \nonumber \\= & {} -\frac{\mu mg}{\varepsilon {\bar{B}}}(r+e)^2 + {\mathcal {O}}\left( \varepsilon \right) \approx -129.04 \,\frac{\text {1}}{\mathrm {s}}. \end{aligned}$$

(122)

Solving the quadratic polynomial factor $\lambda ^2+b\lambda +c=0$ results in

$$\begin{aligned} \lambda _{1,2} = \frac{-b \pm \sqrt{b^2-4c}}{2}. \end{aligned}$$

(123)

In Eqs. (122) and (123), the eigenvalues $\lambda _{1,2,3}$ are approximately given in a closed form under the assumption of a small smoothing parameter $\varepsilon$. These eigenvalues of the closed form are depicted black in Fig. 10. The critical spinning speed $\varOmega _{\mathrm{crit}}$ can be calculated in closed form by requiring that the real part of the complex conjugate eigenvalues $\lambda _{1,2}$ in (123)

$$\begin{aligned} {\mathcal {R}}(\lambda _{1,2}(\varOmega _{\mathrm{crit}}))=0 \end{aligned}$$

(124)

has to vanish. For the limit of $\varepsilon \downarrow 0 \implies b \rightarrow 0$, the following expression

$$\begin{aligned} c = - A_{31} = -\frac{mg}{{\bar{B}}}(r+e)+\varOmega _{\mathrm{crit}}^2 \overset{!}{=} \frac{e}{e+r} \varOmega _{\mathrm{crit}}^2\nonumber \\ \end{aligned}$$

(125)

has to hold. The critical spinning velocity $\varOmega _{\mathrm{crit}}$ is thus given by

$$\begin{aligned} \varOmega _{\mathrm{crit}} = \sqrt{\frac{(r+e)^2}{r}\frac{mg}{{\bar{B}}}} = 30.92\, \frac{\mathrm{rad}}{\mathrm{s}}. \end{aligned}$$

(126)

The numerically determined critical spinning velocity $\varOmega _{\mathrm{crit}}^\mathrm{n} \approx 31 \, \frac{\mathrm{rad}}{\mathrm{s}}$ is close to $\varOmega _{\mathrm{crit}}$ from Eq. (126), such that $\varOmega _{\mathrm{crit}} \approx \varOmega _{\mathrm{crit}}^\mathrm{n}$ is a valid approximation. The corresponding complex eigenvalues are given as

$$\begin{aligned} \lambda _{1,2} = \pm \mathrm {i} \sqrt{c} = \pm 6.9 \mathrm {i} \,\frac{1}{\mathrm {s}} \end{aligned}$$

(127)

which also agrees with the numerically calculated eigenvalues.

With prior knowledge of a Hopf bifurcation, $\lambda = i \omega$ can be substituted directly into the characteristic polynomial (114), which yields

$$\begin{aligned} \mathrm {i}\omega ^3-A_{33}\omega ^2+\mathrm {i}A_{31}\omega +A_{32}\varOmega =0. \end{aligned}$$

(128)

Setting both real and imaginary part to zero, the two equations

$$\begin{aligned}&{\mathcal {R}}{:} \quad -A_{33}\omega ^2+A_{32}\varOmega \nonumber \\&\quad = \frac{\mu mg}{\varepsilon {\bar{B}}}\left( (r+e)^2\omega ^2-e(r+e)\varOmega ^2\right) =0 \end{aligned}$$

(129)

$$\begin{aligned}&{\mathcal {I}}{:} \quad \left( \omega ^2+A_{31}\right) \omega \nonumber \\&\quad = \left( \omega ^2+\frac{mg}{{\bar{B}}}(r+e)-\varOmega ^2\right) \omega =0 \end{aligned}$$

(130)

are obtained. From Eq. (129) it follows

$$\begin{aligned} \omega ^2=\frac{e}{r+e}\varOmega ^2, \end{aligned}$$

(131)

which can be inserted into Eq. (130) and solved for $\varOmega =\varOmega _\mathrm{crit}$, yielding

$$\begin{aligned} \varOmega _\mathrm{crit}^2 = \frac{(r+e)^{2}}{r}\frac{mg}{{\bar{B}}}. \end{aligned}$$

(132)

Hence, the critical spinning velocity $\varOmega _\mathrm{crit}$ given in Eq. (126) is exact and not an approximation for small values of the smoothing parameter $\varepsilon$. Moreover, it can be seen from Eq. (132) that the critical spinning velocity does not depend on the friction coefficient $\mu$ and the smoothing parameter $\varepsilon$.

7 Discussion

Experiments show that at high spinning velocities the tippedisk inverts so that the center of gravity lies above the geometric center of the disk, see Fig. 2. For lower spinning velocities the disk does not invert. These observations indicate that the inverted spinning solution is unstable for low spinning speeds and becomes attractive when the disk is spun fast enough.

In Sect. 3.2, the local stability of the inverted spinning solution of the full system was investigated using a linear eigenvalue analysis. Numerical computations for $\varOmega \in [0, \, 50] \frac{\mathrm{rad}}{\mathrm{s}}$ showed at low spinning velocities two eigenvalues with a pronounced positive real part. For larger values of $\varOmega$, the real part of these eigenvalues becomes negative. Furthermore, the real part of a second complex conjugate pair of eigenvalues increases from a noticeable negative value at lower speeds to a very small positive value at higher rotational speeds. Consequently, the inverted spinning solution of the full system is always unstable, since for all $\varOmega \in [0, \, 50] \frac{\mathrm{rad}}{\mathrm{s}}$ there exists at least one eigenvalue with positive real part, indicating an unstable subspace.

Numerical simulations of the full nonlinear system show the inversion during a first phase of motion. However, after the solutions reach the inverted spinning solution, they are eventually repelled. The eigenvalues of the full system indeed indicate that there are three different timescales involved. For supercritical spinning velocities, two strongly negative eigenvalues $\lambda _{7,8}$ with $\mathcal {R}(\lambda _{7,8})|\gg 1$ corresponding to fast asymptotic dynamics are obtained. Moreover, two complex conjugate eigenvalues $\lambda _{1,2}$ with negative real part describe a stable subspace with intermediate spinning velocity (i.e., the asymptotic behavior is neither very slow nor extremely fast). The third and thus slow timescale characterizes the long-term behavior, as the slightly positive real parts of $\lambda _{5,6}$ define an unstable subspace, such that the inverted tippedisk is not stable on longer timescales (because of the eigenvalues with slightly positive real part and also because the spinning speed ${\dot{\alpha }}$ decreases as the system dissipates energy), see [30]. Since we are only interested in the inversion process during the first stage of motion, the focus is on the fast and intermediate timescales on which the inversion process occurs.

Therefore, we need to somehow ‘block’ the slow unstable motion related to the eigenvalues with small positive real part. This is exactly what we do by adding physically motivated constraints, as done in Sect. 4. Clearly, these assumptions affect somewhat the quantitative behavior, as the comparison shows that the more constrained models converge faster to the inverted spinning solution. However, the qualitative behavior is preserved, i.e., the inversion process occurs only for supercritical initial spinning velocities and the evolution of the inclination angle $\beta$ and the angle $\gamma$ is not strongly affected by the four constraints which we introduced. Two constraints, namely the horizontally fixed center of gravity and the constant spinning speed ${\dot{\alpha }}=\varOmega$, require further discussion. As the inversion behavior does not strongly depend on the horizontal motion, the constraint of a horizontally fixed center of gravity seems justified, although actually not present for the real system. By introducing the horizontal constraint, the state space is reduced such that the inversion behavior is preserved and superfluous horizontal dynamics is neglected. According to the graphs in Fig. 9, the spinning velocity ${\dot{\alpha }}$ remains nearly constant (on an intermediate timescale) after the disk spins in an inverted orientation. Since a raise of the center of gravity implies an increase of the potential energy, the kinetic energy and thus the rotational speed must naturally decrease as a consequence of energetic consistency. The assumption of a constant spinning velocity ${\dot{\alpha }}$ correctly describes the qualitative dynamics, but leads to inconsistencies in energetic considerations. In [30] it is shown that the inversion phenomenon cannot be explained from an energetic viewpoint. Therefore, we argue that the violation of the energetic consistency is acceptable.

8 Conclusions and merits

The tippedisk shows an interesting inversion phenomenon that cannot be explained intuitively and must be studied in the context of nonlinear dynamics. From the stability analysis conducted in this paper, which serves as stepping stone to a more complete global analysis, the following conclusions are drawn:

• The asymptotic behavior of the tippedisk strongly depends on the considered timescale. On a ‘fast’ and ‘intermediate’ timescale, the inversion can be observed. On a ‘slow’ timescale, the motion reaches a static equilibrium state, for which the disk lies flat on the table.

• Comparison of the models at different reduction levels shows that the qualitative dynamical behavior is well described by the three-dimensional reduced system (102).

• Based on the reduced model, the linearization around the inverted spinning motion yields the local stability behavior. For $\varOmega =\varOmega _{\mathrm{crit}}$ we identify an eigenvalue $\lambda _3$ with negative real part and a complex conjugate pair $\lambda _{1,2}$ crossing the imaginary axis, implying a Hopf bifurcation. The classification as sub- or supercritical Hopf bifurcation will be studied in a follow-up paper.

• A closed form expression of the critical spinning velocity

  $$\begin{aligned} \varOmega _{\mathrm{crit}} =\sqrt{\frac{(r+e)^2}{r}\frac{mg}{{\bar{B}}}}= 30.92 \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned}$$

  was derived. The critical spinning velocity $\varOmega _\mathrm{crit}$ does not depend on the friction coefficient $\mu$ and smoothing parameter $\varepsilon$. However, these parameters affect the real part of the eigenvalue and thus characterize the asymptotic behavior of solutions, i.e., how fast solutions converge to the inverted spinning solution.

The reduced system will set the starting point for a further nonlinear dynamic analysis in follow-up papers.

Fig. 11

Evolution of eigenvalues for the noninverted tippedisk

Appendices

Equations of motion

The equations of motion of the system presented in [30] are given as:

$$\begin{aligned} {\mathbf {M}}({\mathbf {q}}) \ddot{{\mathbf {q}}} - {\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}}) = {\mathbf {f}}_G + {\mathbf {w}}_N {\lambda }_N + {\mathbf {W}}_T \varvec{\lambda }_T, \end{aligned}$$

(133)

with mass matrix

$$\begin{aligned}&{\mathbf {M}}({\mathbf {q}}) = \begin{bmatrix} {\mathbf {M}}_{11} &{} {\mathbf {M}}_{12}\\ {\mathbf {M}}_{21} &{} {\mathbf {M}}_{22} \end{bmatrix}\\&{\mathbf {M}}_{11} = \begin{bmatrix} m &{}\quad 0 &{}\quad 0\\ 0 &{}\quad m &{}\quad 0\\ 0 &{}\quad 0 &{}\quad m \end{bmatrix}, \quad {\mathbf {M}}_{21} = {\mathbf {M}}_{12}^{\mathop {{\mathrm {T}}}}\nonumber \\&{\mathbf {M}}_{12} = me \begin{bmatrix} -\text {c}\alpha \text {c}\beta \text {s}\gamma - \text {s}\alpha \text {c}\gamma &{}\quad \text {s}\alpha \text {s}\beta \text {s}\gamma &{}\quad -\text {c}\alpha \text {s}\gamma -\text {s}\alpha \text {c}\beta \text {c}\gamma \\ -\text {s}\alpha \text {c}\beta \text {s}\gamma + \text {c}\alpha \text {c}\gamma &{}\quad -\text {c}\alpha \text {s}\beta \text {s}\gamma &{}\quad -\text {s}\alpha \text {s}\gamma +\text {c}\alpha \text {c}\beta \text {c}\gamma \\ 0 &{}\quad \text {c}\beta \text {s}\gamma &{}\quad \text {s}\beta \text {c}\gamma \end{bmatrix} \nonumber \\&{\mathbf {M}}_{22} = \begin{bmatrix} (A\text {s}^2\gamma +B\text {c}^2\gamma )\text {s}^2\beta +C\text {c}^2\beta &{}\quad (A-B)\text {s}\beta \text {s}\gamma \text {c}\gamma &{}\quad C\text {c}\beta \\ (A-B)\text {s}\beta \text {s}\gamma \text {c}\gamma &{}\quad A\text {c}^2\gamma +B\text {s}^2\gamma &{}\quad 0\\ C\text {c}\beta &{}\quad 0 &{}\quad C \end{bmatrix}\nonumber \end{aligned}$$

(134)

and gyroscopic force vector

$$\begin{aligned}&{\mathbf {h}}({\mathbf {q}},{\dot{{\mathbf {q}}}}) = \begin{bmatrix} h_1&\quad h_2&\quad h_3&\quad h_4&\quad h_5&\quad h_6 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\end{aligned}$$

(135)

$$\begin{aligned} h_1&= me\, \big [ {\dot{\alpha }}^2(\text {c}\alpha \text {c}\gamma -\text {s}\alpha \text {c}\beta \text {s}\gamma ) -{\dot{\beta }}^2\text {s}\alpha \text {c}\beta \text {s}\gamma \nonumber \\&\quad +{\dot{\gamma }}^2(\text {c}\alpha \text {c}\gamma -\text {s}\alpha \text {c}\beta \text {s}\gamma ) \nonumber \\&\quad -2{\dot{\alpha }}{\dot{\beta }}\text {c}\alpha \text {s}\beta \text {s}\gamma -2{\dot{\alpha }}{\dot{\gamma }}(\text {s}\alpha \text {s}\gamma -\text {c}\alpha \text {c}\beta \text {c}\gamma )\nonumber \\&\quad -2{\dot{\beta }}{\dot{\gamma }}\text {s}\alpha \text {s}\beta \text {c}\gamma \big ], \end{aligned}$$

(136)

$$\begin{aligned} h_2&= me\, \big [ {\dot{\alpha }}^2(\text {s}\alpha \text {c}\gamma +\text {c}\alpha \text {c}\beta \text {s}\gamma ) +{\dot{\beta }}^2\text {c}\alpha \text {c}\beta \text {s}\gamma \nonumber \\&\quad +{\dot{\gamma }}^2(\text {s}\alpha \text {c}\gamma +\text {c}\alpha \text {c}\beta \text {s}\gamma ) \nonumber \\&\quad -2{\dot{\alpha }}{\dot{\beta }}\text {s}\alpha \text {s}\beta \text {s}\gamma +2{\dot{\alpha }}{\dot{\gamma }}(\text {c}\alpha \text {s}\gamma +\text {s}\alpha \text {c}\beta \text {c}\gamma )\nonumber \\&\quad +2{\dot{\beta }}{\dot{\gamma }}\text {c}\alpha \text {s}\beta \text {c}\gamma \big ], \end{aligned}$$

(137)

$$\begin{aligned} h_3&= me\, \big [ {\dot{\beta }}^2\text {s}\beta \text {s}\gamma + {\dot{\gamma }}^2\text {s}\beta \text {s}\gamma - 2{\dot{\beta }}{\dot{\gamma }}\text {c}\beta \text {c}\gamma \big ], \end{aligned}$$

(138)

$$\begin{aligned} h_4&= -{\dot{\beta }}^2(A-B)\text {c}\beta \text {s}\gamma \text {c}\gamma \nonumber \\&\quad -2{\dot{\alpha }}{\dot{\beta }}(A\text {s}^2\gamma + B\text {c}^2\gamma - C)\text {s}\beta \text {c}\beta \nonumber \\&\quad -2{\dot{\alpha }}{\dot{\gamma }}(A-B)\text {s}^2\beta \text {s}\gamma \text {c}\gamma \nonumber \\&\quad -{\dot{\beta }}{\dot{\gamma }}\text {s}\beta \big [(A-B)(\text {c}^2\gamma -\text {s}^2\gamma )-C\big ],\end{aligned}$$

(139)

$$\begin{aligned} h_5&= {\dot{\alpha }}^2\text {s}\beta \text {c}\beta (A\text {s}^2\gamma + B\text {c}^2\gamma - C)\nonumber \\&\quad -{\dot{\alpha }}{\dot{\gamma }}\text {s}\beta \big [(A-B)(\text {c}^2\gamma -\text {s}^2\gamma ) +C\big ] \nonumber \\&\quad + 2{\dot{\beta }}{\dot{\gamma }}(A-B)\text {s}\gamma \text {c}\gamma ,\end{aligned}$$

(140)

$$\begin{aligned} h_6&= {\dot{\alpha }}^2(A-B)\text {s}^2\beta \text {s}\gamma \text {c}\gamma - {\dot{\beta }}^2\text {s}\gamma \text {c}\gamma (A-B) \nonumber \\&\quad + {\dot{\alpha }}{\dot{\beta }}\text {s}\beta \big [(A-B)(\text {c}^2\gamma -\text {s}^2\gamma ) +C\big ]. \end{aligned}$$

(141)

The generalized normal and tangential force directions are given as

$$\begin{aligned} {{\mathbf {w}}_N}&= \left( \frac{\partial {\gamma }_{N_{1}}}{\partial {\dot{{\mathbf {q}}}}} \right) ^{\mathop {{\mathrm {T}}}}\nonumber \\&= \begin{bmatrix} 0&\quad 0&\quad 1&\quad 0&\quad -r\text {c}\beta&\quad 0 \end{bmatrix}^{\mathop {{\mathrm {T}}}}\in {\mathbb {R}}^{6 \times 1}, \end{aligned}$$

(142)

and

$$\begin{aligned} {{\mathbf {W}}_T}&= \left( \frac{\partial {\varvec{\gamma }}_{T_{1}}}{\partial {\dot{{\mathbf {q}}}}} \right) ^{\mathop {{\mathrm {T}}}}\nonumber \\&= \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad r\text {c}\alpha \text {c}\beta &{}\quad -r\text {s}\alpha \text {s}\beta &{}\quad r\text {c}\alpha \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad r\text {s}\alpha \text {c}\beta &{}\quad r\text {c}\alpha \text {s}\beta &{}\quad r\text {s}\alpha \end{bmatrix}^{\mathop {{\mathrm {T}}}}\nonumber \\&\quad \in {\mathbb {R}}^{6 \times 2}. \end{aligned}$$

(143)

Eigenvalues for noninverted spinning solutions

See Fig. 11.