1 Introduction

Transport processes of thin deformable structures are intrinsic for various technical solutions: belt drives, rolling mills, etc. Combined effects of flexibility, inertia and contact may prevent the structure from operating in a desired way. Practical importance and modelling complexity promote the rapid growth of the body of literature in the field of axially moving structures; here, we mention review articles [1,2,3], a comprehensive monograph [4], own works [5,6,7] as well as relevant papers [8,9,10,11]. Particularly interesting in the light of the present research are studies featuring the effect of frictional contact between moving deformable bodies; here, we refer to [12,13,14,15,16]. Most mentioned contributions address transient dynamic processes. Nevertheless, for certain kinds of problems, it may become important and challenging just to find a steady regime of motion. Such solutions remain unchanged for an observer in a spatially fixed frame, although the material particles of the structure are moving according to complicated laws, see, for example, [10, 12, 14, 15].

A new, seemingly simple and at the same time practically relevant statement of a problem, which allows for a non-trivial steady solution, is given in the present contribution. We consider the motion of a beam, which lies on a moving rough plane, see Fig. 1.

Fig. 1
figure 1

Beam travelling on a moving rough surface across a control domain between two misaligned guideways

Full size image

The kinematic boundary conditions in the form of the misaligned guideways at both sides of the control domain impose deformation, which is incompatible with the motion of the plane and thus make sliding inevitable in at least part of the considered domain. The interest to the topic of frictional interaction of slender rods with other rods or solid rough surfaces is also increasing over the recent years owing to both the practical relevance and the variety of particular effects, observed in the model problems, see, for example, already cited works [12, 13] as well as [17]. Papers [18,19,20,21,22] are particularly important in the context of the present research, as they address the microslip of a slender beam on a frictional foundation. While the authors of [19, 20] consider a semi-infinite beam under the force and moment loading, the research results demonstrated in [18, 21] are more practically oriented: cooling of long rails after hot-rolling leads to thermal bending moment with subsequent loss of the straight form of equilibrium despite the friction between the rail and the foundation. Even the solutions, obtained in the mentioned references [18,19,20,21,22], look similar to the one we obtain in the following: partial stick and a sequence of zones of sliding contact with alternating directions of sliding, which are analytically studied using considerations of self-similarity. Nevertheless, the present formulation is essentially different as it features an axially moving beam and is described by a different nonlinear boundary value problem. Also the transient evolution of the deformation of the beam makes perfectly sense now and is investigated numerically in Sect. 9 of the present contribution.

The current study is restricted to the slow motion of the system such that the inertia effects can be ignored. Nevertheless, the system possesses own dynamics because of the time evolution of the deformed state under the action of friction forces. We begin with a semi-analytic treatment of the stationary regime of motion, which depends on a single non-dimensional parameter of the model f and comprises one or several segments with alternating directions of sliding. This small difference between the velocities of contacting deformable bodies is known in the literature as microslip, see, for example, [23]. At higher values of f a zone of stick appears, followed by infinite many segments with alternating directions of sliding. The solution in the sliding zone becomes then self-similar, as each sliding segment is exactly the same as the previous one, just scaled by a fixed factor. A closed-form expression for the total length of the zone of stick in dependence on f is available also for the case of angular misalignment of the guideways relative to the overall direction of motion, when the zone of stick develops somewhere in the middle of the control domain and is not adjacent to the end points. The phenomenon of self-similarity is not conventional in structural mechanics, and we finally answer the questions regarding the stability of the obtained solution and the rate of convergence of a transient process to the stationary state with the help of a numerical simulation of the time evolution of the deformed state of the beam. A non-material finite element scheme [5, 6, 8] allows discretizing the control domain, while the material particles of the beam are travelling across the finite element mesh. A step of the time integration scheme consists of seeking a quasistatic equilibrium for the present distribution of friction forces, updating the friction forces as Lagrange multipliers according to the augmentation technique, suggested in [24] and then performing a time step for the transport (advection) equation to “promote” the solution further in the axial direction. Converged results of time integration fully justify the analytical outcome. They also demonstrate that each subsequent segment of sliding friction takes longer to appear, such that the limiting quasistationary solution would require infinite time to be established.

The discussed phenomena are observed within a geometrically linear formulation with small deflections of the beam. It is important that the considered model is far from being a mere mathematical abstraction. It directly describes the motion of a hot metal strip within a rolling mill on a roller table, when the finishing part at the exit has a small transverse or angular misalignment relative to the roughing mill at the entry to the considered domain. The complicated three-dimensional phenomena with partial transverse sliding of a flat belt on a rotating drum of a belt drive are also described by models, which are similar to the one used for the present study. The results may be used not only for validating advanced finite element procedures for modelling the frictional transport of slender elongated structures, but also for gaining insights regarding the frictional contact state for certain technological processes.

2 Transport without friction

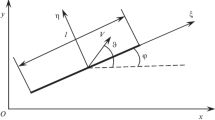
Consider an elastic Bernoulli–Euler (unshearable) beam, which is freely moving with a given velocity v across a domain with the length \(\ell \) in the direction of the x axis. The beam is travelling through guideways at the both ends of this control domain, which means that the deflection and the inclination angles are kinematically prescribed there. By now we consider just a small transverse misalignment between the guideways: the small transverse deflection h at the right end is given, see Fig. 2.

Fig. 2
figure 2

Axially travelling beam sliding on a moving surface owing to the misalignment of the guideways; the coordinate x grows from 0 at the entry to the control domain to \(\ell \) at the exit from it

Full size image

We ignore the geometrically nonlinear effects as well as the inertia and easily find the steady deformed configuration, described by the deflection w(x) of the points of the beam:

$$\begin{aligned} \begin{array}{l}\displaystyle w''''=0,\quad w(0)=0,\quad w'(0)=0,\\[7pt]\displaystyle w(\ell )=h,\quad w'(\ell )=0 {\quad \Rightarrow \quad }w=\frac{3hx^2}{\ell ^2}-\frac{2hx^3}{\ell ^3}. \end{array}\end{aligned}$$
(1)

The solution is a quasi-static one, as the particles of the beam are flowing across the domain along the computed line w(x) and

$$\begin{aligned} \dot{x}=v. \end{aligned}$$
(2)

The dot means a full material time derivative, computed for a given material particle. Further, we find

$$\begin{aligned} \dot{w}=vw', \end{aligned}$$
(3)

such that the transverse component of the velocity of particles at the steady motion is determined by the small inclination angle \(w'\), which is always positive in the considered solution Eq. (1). From the geometric linearity follows that \(w'\ll 1\) and \(\dot{w}\ll v\), such that the contribution of the transverse velocity component to the absolute value of velocity \(\sqrt{\dot{x}^2+\dot{w}^2}\) is negligible.

3 Statement of the problem and mathematical model

Now let us turn the attention to the actual problem and assume that the beam is supported by a rough plane, which is also moving with the velocity v in the direction of the x axis. For the present analysis with small deflections, it makes no difference whether the beam is pulled across the domain by some external action or it is the motion of the underlying plane that transports the beam from a guiding channel on the left into another one on the right. Important is that the x components of the velocity of material particles always coincide with the velocity of the plane in the present geometrically linear approximation. Relative sliding is thus possible only in the transverse direction according to Eq. (3). Alternatively, we can consider the plane being a roller table such that the rollers allow for friction-free motion in the axial direction, but the transverse component of the velocity of the beam causes sliding, which results into the same mathematical formulation.

We assume the ideal dry (Coulomb) friction law between the beam and the plane with the maximal friction force per unit length of the beam being \(q_0\). This value depends on the weight of the beam, the properties of the contacting materials, etc. In the configuration, depicted in Fig. 2, we have \(w'(x)>0\) everywhere such that the relative sliding velocity \(\dot{w}\) is directed upwards and the distributed force of sliding friction q(x) will be pointing in the opposing direction with its absolute value being equal to \(q_0\). The beam is assumed to be very thin such that the distributed friction moment owing to the rotation of cross sections with the angular velocity \(v w''\) is ignored in the present study.

As long as \(q_0\) is small compared to the stiffness of the beam, it will just slightly influence the solution Eq. (1). If, however, the friction force is getting higher, the sign of \(w'\) may change in the part of the domain, which will immediately change the direction of the relative sliding velocity according to Eq. (3) and, consequently, the sign of the friction force q(x). This finally provides us with the following essentially nonlinear boundary value problem for the considered stationary regime of motion, in which the deformed configuration w(x) does not change in time:

$$\begin{aligned} a w''''=q,\quad q=\left\{ \begin{array}{ll}-q_0,&{}w'>0\\ 0,&{}w'=0\\ q_0,&{}w'<0\end{array}\right. \end{aligned}$$
(4)

with a being the bending stiffness and boundary conditions as in Eq. (1). The intriguing question is whether continuous segments of stick with identically vanishing \(w'\) in a finite part of the domain are possible at sufficiently high friction forces \(q_0\).

The above statement that the static friction force q vanishes as soon as there is no relative velocity between the beam and the underlying surface because of \(w'=0\) requires additional discussion. If \(w'\) turns into zero in an isolated point, then the local value of the friction force is just not relevant, because no concentrated force is clearly possible and any finite value would not play a role. In a continuous segment of sticking contact with \(w'=0\) the beam is straight, such that the fourth-order derivative \(w''''\) must also vanish identically and \(q=0\) there. Note that this holds only in the stationary case with time-independent w(x). In the transient analysis, presented in Sect. 9, the static friction force varies from \(-q_0\) to \(q_0\) according to the Coulomb law.

The naive expectation that high friction and low beam stiffness would result in a solution, in which the beam remains straight after entering the domain and then begins sliding upwards closer to the right end as in Fig. 3 can be easily proven wrong. Indeed, sliding upwards in the right part of the domain \(x>x_*\) means that \(w'>0\) there and thus, the friction force is pointed downwards. In the left segment of stick \(x<x_*\), in which the straight beam and the plane are travelling together, all derivatives of w will vanish, see Fig. 3.

Fig. 3
figure 3

Solution with a segment of stick to the left of \(x_*\) and monotonous sliding upwards to the right of this point

Full size image

Now the contradiction is becoming clear. The beam is clamped at the right end \(x=\ell \) and loaded by a distributed force \(q_0\). As the bending moment \(M=aw''\) and the transverse force \(Q=-aw'''\) are continuous, they will also vanish in the boundary point \(x_*\) between the segments as if the two parts of the beam were separated here and the right segment was just a cantilever. But \(w'\) must also vanish at its left end, which will certainly not be the case: we cannot solve a linear inhomogeneous differential equation of the fourth order with five homogeneous boundary conditions.

In the remainder of this paper, we will demonstrate that the zone of sticking contact is nevertheless possible when the friction force is high, and the beam is flexible and the misalignment h is small. We will furthermore determine the limiting level of a non-dimensional parameter combination and show that the sliding zone will consist of infinitely many segments with alternating directions of relative motion. We will also briefly discuss the effect of the possible angular misalignment at the entry to the domain.

4 Evolution of the sliding solution at growing friction force

We know that the entire beam (except for several isolated points) is sliding when the friction force is small. Therefore, it makes sense to seek such solutions by solving the boundary value problem

$$\begin{aligned} \begin{array}{l}\displaystyle \eta ''''(\xi )+f{{\,\mathrm{sign}\,}}\eta '=0,\\[7pt]\displaystyle \eta (0)=0,\quad \eta '(0)=0,\quad \eta (1)=1,\quad \eta '(1)=0. \end{array}\end{aligned}$$
(5)

We have reformulated the differential equation and boundary conditions, replacing the physical deflection w, axial coordinate x and maximal friction force \(q_0\) by their non-dimensional counterparts according to the following substitutions:

$$\begin{aligned} \eta =\frac{w}{h},\quad \xi =\frac{x}{\ell },\quad f=\frac{q_0\ell ^4}{a h}. \end{aligned}$$
(6)

The prime in Eq. (5) means a derivative with respect to the new non-dimensional coordinate \(\xi \). The advantage (besides shorter formulas) is that everything is now determined by just a single force parameter f, which comprises all relevant physical quantities of the actual problem.

We expect \(\eta '>0\) at small f, and the entire domain is just a single segment with the beam sliding upwards. Solving Eq. (5) under this assumption is easy and results in

$$\begin{aligned} \begin{array}{l}\displaystyle \eta =\frac{1}{24}\left( (72-f)\xi ^2 - 2(24-f)\xi ^3 - f \xi ^4 \right) ,\\[7pt]\displaystyle \eta ''(0)=\frac{72-f}{12}. \end{array} \end{aligned}$$
(7)

We conclude that \(\eta '\) remains nonnegative as long as \(f<f_1=72\), such that \(f_1\) is the maximal value of the force parameter, until which the solution Eq. (7) with just one segment of sliding remains valid. Because \(\eta '(0)=0\), we find \(f_1\) as the value, at which the second-order derivative \(\eta ''\) becomes negative at \(\xi =0\). The conclusion is justified by plotting \(\eta '(\xi )\) in Fig. 4 for three values of f. Friction breaks the symmetry, and a zone with negative \(\eta '\) near \(\xi =0\) makes the solution with \(f=100>f_1\) invalid.

Fig. 4
figure 4

Rotation angle (derivative of the deflection) in the solution of the problem with just a single segment of sliding for three values of the force parameter; a zone with \(\eta '<0\) at \(f=100\) makes this last solution invalid

Full size image

Having established that the solution at \(f>f_1\) must consist of at least two segments, we construct such a solution analytically, see Fig. 5 for the result with \(f=200\). We denote by \(\xi _1\) the switching point between the segments, \(\eta _1(\xi )\) is the solution in the right one with sliding upwards, \(\eta _1'\ge 0\), and \(\eta _2(\xi )\) is the solution in the left segment with sliding downwards, \(\eta _2'\le 0\). The numbering is chosen such that new segments with higher numbers are always added at the left. Both solutions read

$$\begin{aligned} \eta _i(\xi )=(-1)^i\frac{f \xi ^4}{24}+c_{1,i}+c_{2,i}\xi +c_{3,i}\xi ^2+c_{4,i}\xi ^3, \end{aligned}$$
(8)

\(c_{k,i}\) are integration constants for each segment. There are no concentrated forces or moments acting on the beam at the switching point, the moment M and the force Q may not jump there. The entire piecewise defined function \(\eta (\xi )\) must therefore be \(C^3\) continuous. Recalling the general boundary conditions from Eq. (5) as well as the requirement that \(\xi _1\) is actually a switching point from negative \(\eta '\) to positive \(\eta '\), we arrive at a system of the following 9 nonlinear algebraic equations

$$\begin{aligned} \begin{array}{l}\displaystyle \eta _1(0)=0,\quad \eta _1'(0)=0,\quad \eta _2(1)=1,\quad \eta _2'(1)=0,\\[7pt]\displaystyle \eta _1(\xi _1)=\eta _2(\xi _1),\quad \eta _1'(\xi _1)=0,\quad \eta _2'(\xi _1)=0,\\[7pt]\displaystyle \eta _1''(\xi _1)=\eta _2''(\xi _1),\quad \eta _1'''(\xi _1)=\eta _2'''(\xi _1) \end{array} \end{aligned}$$
(9)

for 9 unknowns, namely 8 integration constants \(c_{k,i}\) and the coordinate \(\xi _1\). Using Wolfram Mathematica,Footnote 1 we symbolically obtained all 6 possible solutions, of which the single physically meaningful one needs to be chosen: the coordinate of the switching point needs to remain inside the domain and vanish for \(f=f_1\). The analytical expressions for the integration constants are lengthy, and here, we just provide an expression for the coordinate of the switching point:

$$\begin{aligned} \xi _1=\frac{1}{6}\left( 3-\sqrt{15-6\sqrt{7-\frac{432}{f}}}\right) . \end{aligned}$$
(10)

We observe that \(\xi _1|_{f=72}=0\). The obtained solution for \(f=200\) is shown in detail in Fig. 5.

Fig. 5
figure 5

Solution with two segments of sliding for the value of the force parameter \(f=200\), deflection \(\eta \) and rotation angle \(\eta '\)

Full size image

Clearly, the solution with two segments will lose validity as soon as \(\eta '\) changes its sign in the vicinity of the left end \(\xi =0\), which will happen when the segment with the friction force pointing upwards is sufficiently large. Again we find the corresponding critical value \(f_2\) by demanding \(\eta _2''(0)=0\). This equation has two roots, the first one being again \(f_1\) and the larger one is

$$\begin{aligned} f_2=\frac{144}{7}\left( 5+4\sqrt{2}\right) \approx 219.227, \end{aligned}$$
(11)

the switching point is \(\xi _1\approx 0.292893\).

Continuing the process, we construct a solution with three segments by solving a system of equations with 14 unknowns (2 coordinates \(\xi _{1,2}\) and 12 integration constants), the subsequent critical force value appears to be \(f_3\approx 308.259\). The solution with four segments for \(f>f_3\) can also be constructed, but the corresponding analytical expressions soon become very lengthy. Therefore, we implemented a routine, which solves the problem for sequentially increasing values of the force parameter f. The previous solution is always taken as an initial approximation as the system of equations with the actual number of segments n is solved numerically. We increase n by one and add a new segment at the left, as soon as the sign of \(\eta ''(0)\) (that is the sign of the third integration constant for the leftmost segment \(c_{3,n}\)) changes from one value of f to the next one.

With the adaptive incrementation of the parameter f, we collected resulting critical values of the force parameter, which are shown in Table 1.

Table 1 Critical values of the friction force parameter, at which new segments with different sliding direction appear in the solution of Eq. (5)
Full size table

The results clearly indicate that the sequence \(f_n\) converges to a limiting value \(f_\infty \approx 375.659\), and the solution with infinitely many segments of sliding friction is then reached. Prior to making conclusions regarding the behaviour of the system beyond this state when \(f>f_\infty \), i.e. when the force parameter is high, the beam is flexible and the end point deflection is small [see Eq. (6)], we analytically study the limiting solution at \(f=f_\infty \).

5 Self-similar limiting solution with infinitely many segments of sliding friction

Let us make another observation with the data of the numerical experiment from the previous section. Consider, for example, the solution at \(f=f_5\), when the sixth segment has not yet been appended (i.e. \(f=f_5-0\)), see Fig. 6.

Fig. 6
figure 6

Solution with \(n=5\) segments at \(f=f_5\)

Full size image

The coordinates of the switching points \(\xi _i\) are known, the length of the i-th segment is \(l_i=\xi _i-\xi _{i+1}\) (we use \(\xi _0=1\)), and the computed ratios of the lengths of the neighbouring segments \(l_i/l_{i+1}\) are presented in Table 2.

Table 2 Ratios of the lengths of the neighbouring segments in the solution at \(f=f_5\) and \(n=5\) segments
Full size table

Computing these ratios for higher n, we clearly see that the lengths of the segments further away from the left end form a geometric progression with the factor \(k\approx 2.61803\), which is by 1 larger than the famous golden ratio.Footnote 2 This observation gives us a clue that the limiting solution at \(f=f_\infty \) should be sought using the considerations of self-similarity. Noteworthy, self-similar solutions in the related problem of the static deformation of a loaded beam on a frictional foundation with microslip were demonstrated in [18,19,20,21,22].

We seek the limiting state by demanding that the solution in the second segment \(\eta _2\) is just a scaled and shifted solution in the first segment \(\eta _1\). This allows to continue the sequence by \(\eta _3\), \(\eta _4\), etc. To make the analysis simpler, we move the origin of the coordinate \(\xi \) to the switching point \(\xi _1\) between the segments, see Fig. 7 for the expected distribution of the rotation angle \(\eta '\) in the first two segments with lengths \(l_1=\xi _*\) and \(l_2=\xi _*/k\).

Fig. 7
figure 7

First two segments of a self-similar limiting solution at \(f=f_\infty \)

Full size image

Being solutions of Eq. (5), the sought functions are such that

$$\begin{aligned} \eta _{1,2}'(\xi )=\mp \frac{f \xi ^3}{6}+2c_3 \xi +3c_4 \xi ^2. \end{aligned}$$
(12)

We accounted for the \(C^3\) continuity of the compound function \(\eta (\xi )\) at the shifted switching point \(\xi =0\) by using the same integration constants and set \(c_2=0\) as both \(\eta _{1,2}'(0)=0\). Now we impose the condition of self-similarity and demand

$$\begin{aligned} \eta _1'(\xi )=-k_\eta \eta _2'((\xi -\xi _*)/k). \end{aligned}$$
(13)

The solution in the second segment repeats the solution in the first one with a negative sign, shrank by the factor k in the horizontal direction and by the factor \(k_\eta \) in the vertical one. Indeed, from Eq. (13) we see that \(\eta _1'(\xi _*)=-k_\eta \eta _2'(0)=0\), and \(\eta _2'(-\xi _*/k)=-\eta _1'(0)/k_\eta =0\), such that the derivatives vanish at the expected locations. Substituting Eq. (12) in Eq. (13) and balancing the coefficient at \(\xi ^3\), we immediately find that

$$\begin{aligned} k_\eta =k^3. \end{aligned}$$
(14)

Further balancing the coefficients at \(\xi ^0\), \(\xi ^1\) and \(\xi ^2\) in Eq. (13), we obtain the equations

$$\begin{aligned} \begin{array}{l}\displaystyle 12c_3 k^2 \xi _*-18 c_4 k \xi _*^2+f \xi _*^3=0,\\[7pt]\displaystyle 4c_3(1+k^2)-12c_4k \xi _*+f \xi _*^2=0,\\[7pt]\displaystyle 6c_4(1+k)-f \xi _*=0. \end{array} \end{aligned}$$
(15)

From the second and the third equations, we easily express \(c_3\) and \(c_4\) and substitute them into the first one and end up with a quadratic equation for the scaling factor

$$\begin{aligned} k^2-3k+1=0{\quad \Rightarrow \quad }k=\frac{1}{2}\left( 3+\sqrt{5}\right) \approx 2.61803. \end{aligned}$$
(16)

We chose the root of the quadratic equation, which is greater than 1. The experimental observation in Table 2 is thus justified. The inclination angles in the neighbouring segments are thus scaled by the factor \(k_\eta =9+4\sqrt{5}\approx 17.9443\) such that sliding is indeed pronounced only in the several segments further away from the entry point at the left end.

The length of the first segment is now easy to find, as the total length equals 1 and

$$\begin{aligned} \begin{array}{l}\displaystyle l_i=\frac{\xi _*}{k^{i-1}},\quad \sum _{i=1}^\infty l_i=\frac{k \xi _*}{k-1}=1 {\quad \Rightarrow \quad }\\[7pt]\displaystyle {\quad \Rightarrow \quad }\xi _*=1-\frac{1}{k}=\frac{1}{2}\left( \sqrt{5}-1\right) \approx 0.61803. \end{array} \end{aligned}$$
(17)

In the limiting state, the first switching point \(\xi _1=1-\xi _*\) divides the entire domain exactly in the proportion of the golden ratio!

Finally, we analytically determine the limiting force parameter \(f_\infty \) by computing the deflection of the right end of the beam

$$\begin{aligned} \eta (1)=\int _0^1\eta '(\xi )\,\mathrm {d}\xi =\sum _{i=0}^\infty (-k_\eta k)^{-i}\eta _1^\varSigma . \end{aligned}$$
(18)

Contribution of each subsequent segment to the total deflection is different by the factor \(-k_\eta k=-k^4\). The contribution of the right most segment is easy to compute by integrating the expression for \(\eta _1\) from Eq. (12) with shifted origin and resolved constants:

$$\begin{aligned} \eta _1^\varSigma =\int _0^{\xi _*}\eta _1'(\xi )\,\mathrm {d}\xi =\frac{f\xi _*^4}{24\sqrt{5}}. \end{aligned}$$
(19)

Now we sum the geometric series, find the limiting value \(f_\infty \) from the boundary condition at the right end and justify the results in Table 1:

$$\begin{aligned} \begin{array}{l}\displaystyle \eta (1)=\frac{k^4}{1+k^4}\eta _1^\varSigma =1 {\quad \Rightarrow \quad }\\[7pt]\displaystyle {\quad \Rightarrow \quad }f=f_\infty =168\sqrt{5}\approx 375.6594. \end{array} \end{aligned}$$
(20)

6 Solution with the zone of stick

Now the existence of a segment of sticking contact becomes clear. As soon as the force parameter f grows beyond \(f_\infty \), the solution will contain a continuous domain with \(\eta '=0\), in which the beam sticks to the moving surface. A high value of f does not necessarily mean that the friction force must grow itself. A flexible beam and a small transverse misalignment h between the two guideways at the entry to the domain and at the exit from it will have the same effect, see Eq. (6).

At \(f>f_\infty \), the above self-similar solution will establish in the right part of the beam \(\xi _\infty<\xi <1\). The left part \(0<\xi <\xi _\infty \) will be a sticking zone with vanishing deflection, \(\eta =0\). This resolves the contradiction, which was intrinsic to the solution shown in Fig. 3. Indeed, the transverse force Q (both the physical dimensional variable and its non-dimensional counterpart) at the ends of each sliding segment differs by the factor \(-k\):

$$\begin{aligned} Q(\xi _{i+1})=-Q(\xi _i)/k. \end{aligned}$$
(21)

The bending moment M decreases even faster. That means that the self-similar solution at \(f=f_\infty \) is such that \(\eta \), \(\eta '\), M and Q vanish at the left end \(\xi =0\), which makes this left end both kinematically clamped and free from reaction force and moment. The same will hold further at a transition point \(\xi _\infty \), in which the particles of the beam begin sliding relative to the underlying surface.

In order to determine the relation between the force parameter f and the length of the zone of sticking contact, we rewrite the condition Eq. (17). The total length of the sliding segments is now

$$\begin{aligned} \sum _{i=1}^\infty l_i=\frac{k \xi _*}{k-1}=1-\xi _\infty . \end{aligned}$$
(22)

The total deflection of all sliding segments must still fulfil the boundary condition, and we find the length of the rightmost sliding segment \(\xi _*\) using Eq. (19) and the first line in Eq. (20):

$$\begin{aligned} \xi _*=\left( \frac{84(7\sqrt{5}-15)}{f} \right) ^\frac{1}{4}. \end{aligned}$$
(23)

Substituting in Eq. (22), we find the length of the zone of stick as function of the force parameter, which after transformation obtains a simple form

$$\begin{aligned} \xi _\infty =1-\left( \frac{f_\infty }{f}\right) ^\frac{1}{4}. \end{aligned}$$
(24)

Evidently, \(\xi _\infty \big |_{f=f_\infty }=0\) and \(\xi _\infty \big |_{f\rightarrow \infty }=1\). We plot this dependence in Fig. 8.

Fig. 8
figure 8

Length of the zone of stick in dependence on the force parameter \(f>f_\infty \)

Full size image

7 Sticking contact for beams with physically meaningful parameters

Using Eq. (24), we compute the force parameter, at which the zone of stick is exactly the half of the entire domain:

$$\begin{aligned} \xi _\infty =1/2\quad \text {at}\quad f=16f_\infty \approx 6010.55. \end{aligned}$$
(25)

Is it much or not? Let us try computing with some physical parameters of an imaginary structure. Consider a steel beam \(\ell =1\) m long with a square cross section \(s=10^{-3}\,\mathrm m\) wide. With Young’s modulus \(E=2.1\cdot 10^{11}\,\mathrm {N/m^2}\), we find the bending stiffness

$$\begin{aligned} a=E \frac{s^4}{12}=0.0175\,\mathrm {N\,m^2}. \end{aligned}$$
(26)

This wire-like beam will weigh \(\rho g s^2\) per unit length. With the free-fall acceleration \(g=9.8\,\mathrm {m/s^2}\) and the friction coefficient \(\mu =0.2\), we find the maximal friction force per unit length to be \(q_0=\mu \rho g s^2=0.015288\,\mathrm {N/m}\). Using the computed values in Eq. (6), we find the relation connecting the dimensionless force parameter f and the transverse offset h between the ends of the beam:

$$\begin{aligned} h=\frac{0.8736\,\mathrm m}{f}. \end{aligned}$$
(27)

Substituting here \(f=f_\infty \), we see that the entire beam will be sliding as long as \(h>2.32551\cdot 10^{-3}\,\mathrm {m}\), i.e. sticking contact is possible only if the offset is below 2.3 millimeters. And the zone of sticking contact will be \(\ell /2\) long at \(h\approx 0.145\cdot 10^{-3}\,\mathrm m\), which is slightly above 0.1 millimeters and seems to be unrealistic in terms of inevitable imperfections in the geometry of the beam and angular orientation of the guideways at the ends!

Repeating the computations for a thick rubber beam with \(E=10^6\,\mathrm {N/m^2}\), \(\rho =1500\,\mathrm {kg/m^3}\), the size of the cross section \(s=10^{-2}\,\mathrm m\) and the coefficient of friction \(\mu =0.5\), we find that the onset of sticking contact takes place at \(h\approx 2.347\,\mathrm m\), which is far beyond the geometrically linear range. Part of the beam will be sticking for all realistic values of h. The half of the control domain will be sticking at \(h\approx 0.1467\,\mathrm m\).

8 Effect of angular misalignment

Until now we assumed that both guideways are perfectly directed along the axis of motion of the underlying plane. Now we briefly consider a small angular misalignment at the entry to the domain, such that the second boundary condition in the BVP Eq. (5) reads \(\eta '(0)=\alpha >0\). What will change in the above solution?

Evidently, a sliding zone must be present near \(\xi =0\). The zone of sticking contact does, however, effectively decouple the boundary domains. So, focussing on the case of a flexible beam with f essentially above \(f_\infty \), we expect that the beam slides in a domain \(0\le \xi \le \xi _*\). Further, we would observe a zone of sticking contact \(\xi _*<\xi <\xi _\infty \) and, finally, we again have a self-similar solution with alternating sliding directions in \(\xi _\infty \le \xi \le 1\). The coordinate of the transition point \(\xi _*\) follows from the following overdeterminate boundary value problem:

$$\begin{aligned} \begin{array}{l}\displaystyle \eta ''''+f=0,\quad \eta (0)=0,\quad \eta '(0)=\alpha ,\\[7pt]\displaystyle \eta '(\xi _*)=0,\quad \eta ''(\xi _*)=0,\quad \eta '''(\xi _*)=0. \end{array} \end{aligned}$$
(28)

A transition to the zone of stick requires that the beam is horizontal and that both the force and the moment vanish at \(\xi =\xi _*\), which is expressed by the last three conditions. A simple analysis shows that the problem is solvable only when

$$\begin{aligned} \xi _*=\left( \frac{6\alpha }{f}\right) ^{1/3}. \end{aligned}$$
(29)

The corresponding deflection at the transition point reads

$$\begin{aligned} \eta (\xi _*)=\left( \frac{3\alpha ^4}{32f}\right) ^{1/3}=\frac{\alpha }{4}\xi _*. \end{aligned}$$
(30)

Interestingly, this deflection may even exceed the transversal misalignment, \(\eta (\xi _*)>1\) (or even one may consider the case of angular misalignment only by setting \(h=0\) and using another scaling in Eq. (6)). Then, it is the role of the sliding domain at the right to bring the deflection back to the prescribed level. Anyway, the scheme of computation of the right boundary of the sticking zone \(\xi _\infty \) remains almost the same. One simply needs to adjust the condition Eq. (20), as the total deflection in the series of sliding zones with alternating directions must now be equal to \(1-\eta (\xi _*)\). If by chance we obtain that \(1-\eta (\xi _*)=0\), then it would mean that the zone of sticking contact reaches until the right end of the domain and \(\xi _\infty =1\).

The entire solution makes of course sense only if \(\xi _\infty >\xi _*\). Otherwise, there is no zone of sticking contact and we again return to the situation with a finite number of sliding zones, discussed in Sect. 4.

9 Transient behaviour: finite element analysis

The fascinating analytic solution for the stationary regime of motion is certainly possible only because of the strong idealization expressed in the use of the Bernoulli–Euler beam model, Coulomb friction law, geometrically linear formulation as well as neglecting frictional moment interaction between the beam and the moving rough surface. Not intending to release these assumptions in the framework of the present study, we wish to answer the questions of stability of the obtained regime of motion and to experimentally investigate, how long it takes for the many segments with alternating directions of sliding to develop. For this sake, a finite element simulation was designed, which features a geometrically linear counterpart of the non-material Eulerian–Lagrangian beam model, introduced in [5]. Choosing the non-dimensional deflection \(\eta \) and its derivative \(\eta '\) as nodal degrees of freedom, we use cubic approximation within an element and obtain the necessary \(C^1\) interelement continuity. The static solution Eq. (1) (or, after non-dimensionalization, Eq. (7) with \(f=0\)) is taken as the initial configuration, whose evolution in time t owing to the axial motion we intend to compute. Along with the time evolution of the displacement field \(\eta (\xi )\), we also consider the distribution of the transverse friction force \(\lambda (\xi )\) as part of solution, \(\lambda =-f\) in the segments currently sliding upwards and \(\lambda =f\) in the segments sliding downwards. In the zones of sticking contact \(\lambda \) plays the role of a Lagrange multiplier for the imposed kinematic constraint and takes on values \(-f<\lambda <f\).

In the first stage of each time step, we seek a new equilibrium configuration \(\eta _+(\xi )\) by minimizing the energy functional

$$\begin{aligned} \begin{array}{l}\displaystyle U^\mathrm {strain}[\eta _+]+U^\mathrm {contact}[\eta _+]\rightarrow \min ,\\[7pt]\displaystyle U^\mathrm {strain}=\int _0^1\frac{1}{2}\eta _+''^2\,\mathrm {d}\xi ,\\[7pt]\displaystyle U^\mathrm {contact}=\int _0^1\left( -\lambda \eta _++\frac{1}{2}P(\lambda )(\eta _+-\eta ^\mathrm {old})^2 \right) \,\mathrm {d}\xi . \end{array} \end{aligned}$$
(31)

The first term here represents the strain energy of bending deformation of the beam, and the second integral imposes the effect of friction forces. Here,

$$\begin{aligned} P(\lambda )=\left\{ \begin{array}{ll}P_0,&{}-f<\lambda <f\\ 0,&{}\lambda =f\ \text {or}\ \lambda =-f\end{array}\right. \end{aligned}$$
(32)

is the artificial stiffness, which takes on the large value \(P_0\) in the zones with current sticking behaviour and penalizes the relative transverse motion from the given configuration \(\eta ^\mathrm {old}(\xi )\). The contribution of each finite element to the total strain energy \(U^\mathrm {strain}\) is integrated analytically and is a quadratic form of the nodal degrees of freedom. The second integral \(U^\mathrm {contact}\) in the minimization problem above is evaluated using a quadrature rule with two Gaussian integration points such that the field values \(\lambda (\xi )\) are also stored and updated there. Initially, the beam is resting on the moving surface without sliding: \(\lambda |_{t=0}=0\).

During the second stage of a time step, we update the friction force distribution according to the technique of augmented Lagrange multipliers [24], which helps avoiding the effect of numerical drift even at moderate values of penalty stiffness \(P_0\). The new values in each point are computed according to the simple algorithm:

$$\begin{aligned} \begin{array}{l}\displaystyle \lambda ^\mathrm {trial}=\lambda ^\mathrm {old}-P_0(\eta _+-\eta ^\mathrm {old}),\\[7pt]\displaystyle \lambda _+=\left\{ \begin{array}{ll}-f,&{}\lambda ^\mathrm {trial}<-f\\ \lambda ^\mathrm {trial},&{}-f<\lambda ^\mathrm {trial}<f\\ f,&{}\lambda ^\mathrm {trial}>f.\end{array}\right. \end{array} \end{aligned}$$
(33)

Note that this update rule fully covers the conditions of switching from the sliding state to stick and back.

The third stage concludes a time step by accounting for the transport condition. For the advection equation

$$\begin{aligned} \frac{\partial \eta }{\partial t}+v\eta '=0 \end{aligned}$$
(34)

we perform a single explicit Eulerian time step and store the results in the integration points in the form of the reference deflection values for the subsequent time step:

$$\begin{aligned} \eta ^\mathrm {old}_+=\eta _+-v\tau \eta _+'. \end{aligned}$$
(35)

Here, \(\tau \) is the time step size and the derivative \(\eta _+'\) is directly available from the finite element discretization. Note that the values \(\eta ^\mathrm {old}\) are relevant only in the zones of stick with \(P\ne 0\) according to Eq. (32).

For the computations below we consider \(v=1\), such that \(t=1\) is the time period, within which a particle of the beam travels across the control domain of the unit length. We used the penalty stiffness value \(P_0=2\cdot 10^4\) as a compromise between the stability of time integration and the rate of convergence. Accurate presentation of the time evolution of the zones of sliding required a fine discretization; we used 600 finite elements. This in its own turn leads to the necessity of using a small time step such that the numerical integration of the advection equation does not suffer from inaccuracies, and we chose \(\tau =2.5\cdot 10^{-3}\) as practically converged solutions can be accomplished in reasonable time. The simulation was easily implemented within the Wolfram Mathematica environment.

In the first example, we consider the process with the force parameter value \(f=360\). According to the results in Table 1, we see that in the stationary regime the control domain shall be divided into 5 sliding segments with \(\xi _1\) ...\(\xi _4\) being the corresponding switching points between the them. The computed time evolution of the sliding segments in the transient solution is demonstrated in Fig. 9.

Fig. 9
figure 9

Time evolution of the segments of sliding friction (gray areas) for \(f=360\), full view on the left and enlarged initial stage on the right. Dashed lines represent the analytic values for the switching points in the stationary regime

Full size image

The horizontal axis represents here the time, and the vertical one—the control domain. One sees that the first large sliding segment is initiated almost immediately. Slightly after the beam travels the half of the domain the second sliding segment appears, and for the the third one it takes approximately 1.5 full travels of the beam to be born. It takes significantly longer for the fourth small sliding segment to appear soon after \(t\approx 17\). There is no doubt that the fifth very narrow segment would follow much later on (and, possibly, it would require finer discretization to actually observe it). All sliding segments grow to the limits, predicted by the analytic solution.

The second example featured \(f=500\), which is beyond the limiting value \(f_\infty \) and corresponds to the length \(\xi _\infty \approx 0.069\) of the zone of stick in the stationary regime according to Eq. (24). The simulation results are demonstrated in Fig. 10 and again stand in full correspondence with the analytic solution.

Fig. 10
figure 10

Time evolution of the segments of sliding friction (gray areas) for \(f=500\), full view on the left and enlarged initial stage on the right. Dashed line represents the analytic boundary of the zone of stick in the stationary regime

Full size image

Four sliding segments are visible up to the time point \(t=30\), and each subsequent one needs much longer to appear.

10 Conclusions

Various technological processes feature transport of objects with the help of axially moving beam-like strips. A slight misalignment between the transport direction and the guideways at the both sides of the domain gives rise to the phenomena studied in the present paper. For an observer, sitting on the beam and moving with it along the path with a zone of sticking contact and then the many segments with alternating direction of sliding, this motion will feel like highly oscillatory with decreasing frequency and increasing amplitude.

In the present paper, we introduced a seemingly simple essentially nonlinear boundary value problem, which governs the stationary transport of a beam on a moving rough surface. The obtained self-similar solution of the second kind, see [25], represents the most interesting feature of the analysis. This class of solutions, in which the self-similarity does not take part in the dimensional analysis but rather appears as a property of the solution of differential equations with non-dimensional coefficients, is seldom in problems of structural mechanics. Previously known self-similar solutions of this kind [18,19,20,21,22] were obtained in the static problem of a beam with microslip on a frictional foundation because of end-point mechanical loading or under the action of a temperature induced bending moment.

The analytical results are supported by the numerical analysis of the transient evolution of the deformed shape of the beam in time. Results obtained with a specially designed non-material finite element model demonstrate the stability of the considered stationary regime of motion and show that each subsequent segment of sliding takes significantly more time to appear than the previous ones.

To the opinion of the author, a whole new direction of research is expected to be initiated by the present contribution. One may, for example, consider effects, which are not covered by the presently used classical beam model. The currently ignored frictional moment interaction between the beam and the plane may become particularly important near the switching point \(\xi _\infty \) between the zones of stick and sliding. Implications of the natural curvature of the beam, its shear deformability and/or axial pre-tension need to be investigated. One may also consider the present problem in the context of continuum mechanics with plane deformation of a two-dimensional strip with finite width.

An important practical outcome of the presented research will be the possibility to validate advanced non-material finite element procedures for modelling the frictional transport of slender rods by rotating pulleys. Thus, with the moving rough plane occupying just a part of the length of the control domain, we obtain a prototype model problem for a flat belt drive. Being validated, the finite element scheme shall further be applied towards the practically relevant geometrically nonlinear study of the lateral run-off of the belt in a three-dimensional setting.