Abstract
We consider tracking control for multibody systems which are modeled using holonomic and non-holonomic constraints. Furthermore, the systems may be underactuated and contain kinematic loops and are thus described by a set of differential-algebraic equations that cannot be reformulated as ordinary differential equations in general. We propose a control strategy which combines a feedforward controller based on the servo-constraints approach with a feedback controller based on a recent funnel control design. As an important tool for both approaches, we present a new procedure to derive the internal dynamics of a multibody system. Furthermore, we present a feasible set of coordinates for the internal dynamics avoiding the effort involved with the computation of the Byrnes–Isidori form. The control design is demonstrated by a simulation for a nonlinear non-minimum phase multi-input, multi-output robotic manipulator with kinematic loop.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the present paper, we propose a combined feedforward and feedback tracking control strategy for underactuated non-minimum phase multibody systems. We follow a popular approach to two degrees of freedom controller design as proposed, e.g. in [53]. The feedforward control input design is based on a reference model of the system such that if the model truthfully captures reality, exact tracking of a given reference signal by the output is achieved. We utilize the so-called servo-constraints approach for feedforward control design.
In order to compensate (inevitable) modeling errors, uncertainties, disturbances, noise, etc. an additional feedback loop is used to stabilize the system around the given reference signal. Since a robust feedback controller is desired, and the output must respect prescribed error margins around the reference signal, we use the funnel controller first proposed in [39]. Since the funnel controller presented in [39] is not feasible for non-minimum phase systems, we use an extension recently developed in [9].
An important tool both in feedforward and feedback control design is the Byrnes–Isidori form, which allows a decoupling of the internal dynamics of the system. However, a calculation of the Byrnes–Isidori form and the accompanying nonlinear transformation requires a lot of computational effort in general. The approach presented in the present paper avoids this computation. In the feedforward control design, the servo-constraints constitute an approach which does not require the Byrnes–Isidori form for the solution of the inverse model. For the feedback control design, we present a new approach to choose a set of variables for the internal dynamics of the system directly in terms of the system parameters—circumventing the Byrnes–Isidori form. The feedback controller is then based on this representation of the internal dynamics.
More details of the considered system class and the proposed control methodology are given in the following. Furthermore, we recall the concept of vector relative degree and the Byrnes–Isidori form. We like to emphasize that the proposed control design is potentially feasible in any open set where the vector relative degree is well defined.
Before continuing, we like to summarize the main contributions of the present paper in the following.
-
a)
A new method for computing the internal dynamics of a multibody system which avoids the DAE formulation is presented (Sect. 2).
-
b)
To circumvent the computational effort involved with the Byrnes–Isidori form of the auxiliary ODE arising in a), a feasible set of coordinates which directly yields the internal dynamics is derived (Sect. 3).
-
c)
A feedforward control strategy based on servo-constraints for model inversion of non-minimum phase systems is used. For the required solution of the arising boundary value problem, we apply newly proposed boundary conditions, which significantly simplify the inversion process (Sect. 4).
-
d)
We present a new funnel control design for nonlinear non-minimum phase systems which only have a vector relative degree (Sect. 5).
-
e)
We demonstrate that the combination of the feedforward and feedback control strategies is able to achieve tracking with prescribed performance for a nonlinear, non-minimum phase robotic manipulator with kinematic loop (described by a DAE that cannot be reformulated as an ODE)—the controller performance of the combination is favorable compared to the individual controllers (Sect. 6).
1.1 Nomenclature
-
\({\mathbb {N}}\), \({\mathbb {R}}\), \({\mathbb {C}}\) the set of natural, real and complex numbers, resp.
-
\({\mathbb {R}}_{\ge 0}\) \(=[0,\infty )\),
-
\({\mathbb {C}}_{+}\) \(\big ({\mathbb {C}}_-\big )\) the open set of complex numbers with positive (negative) real part
-
\({\mathbb {R}}^{n\times m}\) the set of real \(n\times m\) matrices
-
\( \mathbf {Gl}_n\) the group of invertible matrices in \({\mathbb {R}}^{n\times n}\)
-
\(\sigma (A)\) the spectrum of a matrix \(A\in {\mathbb {R}}^{n\times n}\)
-
\({\mathscr {L}}^\infty _{{{\,\mathrm{loc}\,}}}(I\!\rightarrow \!{\mathbb {R}}^n)\) the set of locally essentially bounded functions \(f:I\!\rightarrow \!{\mathbb {R}}^n\), \(I\subseteq {\mathbb {R}}\) an interval
-
\({\mathscr {L}}^\infty (I\!\rightarrow \!{\mathbb {R}}^n)\) the set of essentially bounded functions \(f:I\!\rightarrow \!{\mathbb {R}}^n\)
-
\(\Vert f\Vert _\infty \) = \(\mathrm{ess\ sup}_{t\in I} \Vert f(t)\Vert \)
-
\({\mathscr {W}}^{k,\infty }(I\!\rightarrow \!{\mathbb {R}}^n)\) the set of k-times weakly differentiable functions \(f:I\!\rightarrow \!{\mathbb {R}}^n\) such that \(f,\ldots , f^{(k)}\in {\mathscr {L}}^\infty (I\!\rightarrow \!{\mathbb {R}}^n)\)
-
\({\mathscr {C}}^k(V\!\rightarrow \!{\mathbb {R}}^n) \) the set of k-times continuously differentiable functions \(f:V\!\rightarrow \! {\mathbb {R}}^n\), \(V\subseteq {\mathbb {R}}^m\)
-
\({\mathscr {C}}(V\!\rightarrow \!{\mathbb {R}}^n) \) \(= {\mathscr {C}}^0(V\!\rightarrow \!{\mathbb {R}}^n) \)
-
\(\left. f\right| _{W}\) restriction of the function \(f:V\!\rightarrow \!{\mathbb {R}}^n\) to \(W\subseteq V\)
1.2 System class
We consider multibody systems which possibly contain kinematic loops as well as holonomic and non-holonomic constraints. The equations of motion are given by
with
-
the generalized coordinates \(q: I\rightarrow {\mathbb {R}}^n\) and generalized velocities \(v: I\rightarrow {\mathbb {R}}^n\) (in the case of no constraints), where \(I\subseteq {\mathbb {R}}_{\ge 0}\) is some interval,
-
the generalized mass matrix \(M:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times n}\),
-
the generalized forces \(f:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\),
-
the holonomic constraints \(g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^\ell \) and \(G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{\ell \times n}\),
-
the non-holonomic constraints \({J:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{p\times n}}\) and \({j:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^p}\) (which may incorporate a change of physical units),
-
the input distribution matrix \(B:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times m}\),
-
the output measurement function \(h:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^m\).
The functions \(u:{\mathbb {R}}\rightarrow {\mathbb {R}}^m\) are the inputs that influence the multibody system (1) in affine form. We explicitly allow for \({m < n - \ell }\), which means that if no non-holonomic constraints are present, underactuated multibody systems are encompassed by this formulation. The affine input has the interpretation of a force or torque; however, standard industrial actuators are typically velocity controlled and not force controlled, which may lead to different system properties [46, Sec. 4.4]. In the present paper, we assume that the actuators are force/torque controlled and that the multibody system is given in the form (1).
The functions \(y:{\mathbb {R}}\rightarrow {\mathbb {R}}^m\) are the outputs associated with the multibody system (1) and typically represent appropriate measurements. The generalized forces f usually encompass several terms, including applied forces, Coriolis, centrifugal and gyroscopic forces. The functions \(\lambda :{\mathbb {R}}\rightarrow {\mathbb {R}}^\ell \) and \(\mu :{\mathbb {R}}\rightarrow {\mathbb {R}}^p\) are the Lagrange multipliers corresponding to the holonomic and non-holonomic constraints, resp. The functions in (1) are assumed to be sufficiently smooth and to satisfy the natural assumptions \(\ell + p + m \le n\) and
Let us stress that invertibility of M(q) is not sufficient, we require that it is positive definite. This follows, for example, from deriving the equations of motion using the direct application of d’Alembert’s principle in the form of Lagrange.
System (1) is a differential-algebraic system, and its treatment needs special care. For an overview of important concepts for differential-algebraic control systems, we refer to [7, 43, 52] and the series of survey articles [38].
1.3 Vector relative degree
An important property of the system (1) is its vector relative degree, which, roughly speaking, is the collection of numbers of derivatives of each output component needed so that the input appears explicitly. We briefly recall the required concepts from [41] and, to this end, consider a general nonlinear system affine in the control given by
where \({f: {\mathbb {R}}^d \!\rightarrow \! {\mathbb {R}}^d}\), \({g: {\mathbb {R}}^d \!\rightarrow \! {\mathbb {R}}^{d \times m}}\) and \({h: {\mathbb {R}}^d \!\rightarrow \! {\mathbb {R}}^m}\) are sufficiently smooth and \(x:I\rightarrow {\mathbb {R}}^n\), where \(I\subseteq {\mathbb {R}}_{\ge 0}\) is some interval. Denote the components of h by \(h_1,\ldots ,h_m\), and recall the definition of the Lie derivative of \(h_i\), \(i\in \{1,\ldots ,m\}\), along a vector field f at a point \(z \in U \subseteq {\mathbb {R}}^d\), U open:
where \(h_i'\) is the Jacobian of \(h_i\), i.e., the transpose of the gradient of \(h_i\). We may gradually define \(L_f^k h_i = L_f(L_f ^{k-1} h_i)\) with \(L_f^0 h_i = h_i\). Furthermore, denoting with \(g_j(z)\) the columns of g(z) for \(j=1,\ldots ,m\), we define
Now, in virtue of [41], the system (3) is said to have vector relative degree \((r_1,\ldots ,r_m)\in \mathbb {N}^{1\times m}\) on U, if for all \(z \in U\) we have:
where \(\varGamma :U\rightarrow \mathbf {Gl}_m\) denotes the high-frequency gain matrix. If \(r_1 = \ldots = r_m =: r\in {\mathbb {N}}\), then system (3) is said to have strict relative degree r.
If system (3) has vector relative degree \({(r_1,\ldots ,r_m) \in \mathbb {N}^{1\times m}}\) on an open set \(U \subseteq {\mathbb {R}}^d\), then there exists a (local) diffeomorphism \({\varPhi : U \!\rightarrow \! W \!\subseteq \! {\mathbb {R}}^d}\), W open, such that the coordinate transformation \(\begin{pmatrix} \xi (t) \\ \eta (t) \end{pmatrix} = \varPhi (x(t))\), \(\xi (t) = (\xi _{ij}(t))_{i=1,\ldots ,m; j=1,\ldots ,r_i}\in {\mathbb {R}}^{{{\bar{r}}}}\), \(\eta (t)\in {\mathbb {R}}^{d-{{\bar{r}}}}\), where \({{\bar{r}}}= \sum _{i=1}^m r_i\), puts system (3) into Byrnes–Isidori form
The last equation in (4) represents the internal dynamics of system (3). The diffeomorphism \(\varPhi \) can be represented as
where \(\phi _i:U\rightarrow {\mathbb {R}}\), \(i={{\bar{r}}} +1,\ldots ,d\) are such that \(\varPhi '(z)\in \mathbf {Gl}_d\) for all \(z\in U\). By a distribution, we mean a mapping from an open set \(U\subseteq {\mathbb {R}}^d\) to the set of all subspaces of \({\mathbb {R}}^d\). If the distribution \(x\mapsto {\mathscr {G}}(x) := {{\,\mathrm{im}\,}}(g(x))\) in (3) is involutive, then the functions \(\phi _i\) in (5) can additionally be chosen such that
by which \(p(\cdot ) = 0\) in (4), cf. [41, Prop. 5.1.2]. Recall from [41, Sec. 1.3] that a distribution \({\mathscr {G}}\) is involutive, if for all smooth vector fields \(g_1, g_2: U \rightarrow {\mathbb {R}}^d\) with \(g_i(x)\in {\mathscr {G}}(x)\) for all \(x \in U\) and \(i=1,2\) we have that the Lie bracket \([g_1,g_2](x) = g_1'(x) g_2(x) - g_2'(x) g_1(x)\) satisfies \({[g_1,g_2](x) \in {\mathscr {G}}(x)}\) for all \(x\in U\).
1.4 Control methodology
As in our preliminary work [14], we follow the popular controller design methodology for mechanical systems undergoing large motions, where a feedforward controller is combined with a feedback controller, see, e.g., [53]. Both controllers are designed independently for tracking of a reference trajectory \(y_\mathrm{ref}:{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^m\). The feedforward control input \(u_\mathrm{ff}\) is designed using a reference (inverse) model of the system, while the feedback control input \(u_\mathrm{fb}\) is applied to the actual system. The latter may deviate from the reference model; the situation is depicted in Fig. 1.
As in [14], the feedforward control input \(u_\mathrm{ff}\) is computed using the method of servo-constraints introduced in [20], cf. also [21, 22]. In this framework, the equations of motion of the multibody system (1) are extended by constraints which enforce the output to coincide with the reference trajectory \(y_\mathrm{ref}\). The resulting set of differential-algebraic equations (DAEs) is solved numerically for the inverse system, by which the feedforward control input \(u_\mathrm{ff}\) is obtained. The details of the method are presented in Sect. 4.
Servo-constraints have been successfully used for the control of rotary cranes [19], overhead gantry cranes [21, 47], (infinitely long) mass–spring chains [2, 34] and flexible robots [25]. The addition of the servo-constraints to the system may result in a higher differentiation index, as shown in [26]; see [23, 35] and also [43] for a definition of the differentiation index. A higher index causes difficulties in the numerical solution, and hence, index reduction methods are frequently used, cf. [37]. Popular approaches are index reduction by projection onto the constrained and unconstrained directions [21] and index reduction by minimal extension [1, 18].
The feedback control input \(u_\mathrm{fb}\) is generated by a dynamic state feedback of the form
We choose a feedback control design based on the funnel control methodology [12, 39]. Recently, this method has been extended to linear non-minimum phase systems in [9]. Based on a linearization of the internal dynamics, the approach from [9] has been used for tracking control of a nonlinear non-minimum phase robotic manipulator in [11]. We stress that this approach to non-minimum phase systems, compared to classical funnel control, requires certain knowledge of system parameters and measurements of state variables.
As alternative suitable feedback control methods—not pursued in this work—we like to mention prescribed performance control [5, 28] and control barrier functions [42, 55].
The objective of funnel control is to design a feedback control law such that in the closed-loop system, the tracking error \({e(t) = y(t) - y_\mathrm{ref}(t)}\) evolves within the boundaries of a prescribed performance funnel
which is determined by a function \(\varphi \) belonging to
where \(k = \max _{i=1,\ldots , m} r_i\) and \((r_1,\ldots ,r_m)\) is the vector relative degree of the considered system. Furthermore, all involved signals should remain bounded.
The boundary of \({\mathscr {F}}_\varphi \) is given by the reciprocal of \(\varphi \), see Fig. 2. The case \(\varphi (0)=0\) is explicitly allowed, which means that no restriction is put on the initial value and the funnel boundary \(1/\varphi \) has a pole at \(t=0\) in this case.
Each performance funnel given by \({\mathscr {F}}_{\varphi }\) is bounded away from zero, since boundedness of \(\varphi \) implies existence of \(\lambda >0\) such that \(1/\varphi (t)\ge \lambda \) for all \(t > 0\). The funnel boundary is not necessarily monotonically decreasing and widening the funnel over some later time interval might be beneficial, e.g. in the presence of periodic disturbances.
The detailed design of a feedback controller of the form (7) yielding the feedback control input \(u_\mathrm{fb}\) is presented in Sect. 5 and extends the recent approach [9, 11]. The funnel controller was already successfully applied, e.g. in temperature control of chemical reactor models [40], DC-link power flow control [50], voltage and current control of electrical circuits [17], control of peak inspiratory pressure [48], adaptive cruise control [15, 16] and control of industrial servo-systems [36] and underactuated multibody systems [14].
1.5 Organization of the present paper
The present work is organized as follows. In Sect. 2, we present a novel procedure to compute the internal dynamics of a multibody system. To this end, we introduce an auxiliary input and output to avoid the DAE formulation. In Sect. 3, we present a feasible set of coordinates of the internal dynamics. Section 4 provides a presentation of the open-loop control strategy based on servo-constraints and in particular details the case of unstable internal dynamics. In Sect. 5, we present a funnel-based feedback-controller design which is based on recently developed results for linear non-minimum phase systems. Finally, in Sect. 6 we apply the findings of the present paper to achieve output tracking of a nonlinear, non-minimum phase, multi-input, multi-output multibody system with kinematic loop, namely a robotic manipulator, which is described by a DAE that cannot be conveniently reformulated as an ordinary differential equation (ODE).
2 Computing the internal dynamics
In this section, we present a novel approach to decouple the internal dynamics of the multibody system (1) avoiding the DAE formulation. In principle, it would be possible to obtain a Byrnes–Isidori form for a DAE directly, see [8]. Here, we define auxiliary inputs and outputs by removing the constraints and adding the Lagrange multipliers to the input functions. For this auxiliary ODE system, we derive the Byrnes–Isidori form as in (4) and then add the constraints which have been removed before, thus obtaining the internal dynamics.
2.1 The general case
Consider (1) and define an auxiliary input and output as follows:
With the state variables \(x_1 = q\), \(x_2 = v\) and \(x= (x_1^\top , x_2^\top )^\top \), we may now consider the auxiliary ODE system (omitting the argument t for brevity)
which is of the form (3), and decouple its internal dynamics using the Byrnes–Isidori form. After that we add the constraints \(y_\mathrm{aux,1} = O_1(x) = 0\) and \(y_\mathrm{aux,2} = O_2(x) = 0\) to derive the internal dynamics of (1).
First, we calculate the vector relative degree of (10). Let \(U\subseteq {\mathbb {R}}^{2n}\) be open such that the following Lie derivatives exist for \(x = (x_1^\top , x_2^\top )^\top \in U\):
and
as well as
Since both \(J(x_1)M(x_1)^{-1}J(x_1)^\top \) and \(G(x_1)M(x_1)^{-1} G(x_1)^\top \) are invertible, it follows that a vector relative degree of system (10), if it exists, is of the form \(r = (r_1, r_2, r_3)\) with \(r_1 = (1,\ldots ,1) \in {\mathbb {N}}^{1\times p}\), \(r_2 = (2,\ldots ,2)\in {\mathbb {N}}^{1\times \ell }\) and some \(r_3\in {\mathbb {N}}^{1\times m}\).
In the following, we restrict ourselves to the case where the multi-index \(r_3\) has equal entries, i.e.,
Then, it is necessary that, for all \(x\in U\),
and
The first two block rows are given above, and the last row strongly depends on the shape of the function h. In the special case that inputs and outputs are colocated, we may explicitly calculate \(\varGamma _3(x)\) and show that the relative degree is well defined, see Sect. 2.3.
Now, we can compute the Byrnes–Isidori form of (10) using the state-space transformation as in (5), which in this case reads
where \({{\bar{r}}} = p + 2\ell + {{\hat{r}}} m\) and \(\phi _i: U \rightarrow {\mathbb {R}}\) for \(i={{\bar{r}}} +1,\ldots ,2n\). Then, in the new coordinates
the system has the form
If the distribution \(x\mapsto {\mathscr {K}}(x) = {{\,\mathrm{im}\,}}K(x)\) is involutive, then the functions \(\phi _i\) can be chosen such that, for all \(x\in U\),
by which \(p(\cdot ) = 0\), cf. Sect. 1.3. For the auxiliary ODE (10), we have the following result.
Lemma 2.1
For \(K:U\rightarrow {\mathbb {R}}^{2n\times (p+\ell +m)}\) as in (10), the distribution \(x\mapsto {\mathscr {K}}(x) = {{\,\mathrm{im}\,}}K(x)\) is involutive on U.
Proof
First, recall that a distribution \({\mathscr {D}}(\cdot ) = {{\,\mathrm{span}\,}}\{ d_1(\cdot ),..., d_q(\cdot ) \}\) is involutive if, and only if, for any \(0 \le i,j \le q\) and \(x\in U\), we have
where \([d_i, d_j](x)\) denotes the Lie bracket of \(d_i\) and \(d_j\) at x. Observe that K in (10) has the following structure:
for all \(x = (x_1^\top , x_2^\top )^\top \in U\), where \(k_i: [I_n,0] U \rightarrow {\mathbb {R}}^n\) for \(i=1,...,p+\ell +m\). Now, calculate for any pair \({{\tilde{k}}}_i(x), {{\tilde{k}}}_j(x)\), \(0\le i,j \le p+\ell +m\) the Lie bracket \([{{\tilde{k}}}_i, {{\tilde{k}}}_j](x)\):
for all \(x = (x_1^\top , x_2^\top )^\top \in U\). Therefore, using (13) the distribution \({\mathscr {K}}(\cdot )\) is involutive on U.\(\square \)
Lemma 2.1 yields that it is always possible to choose the diffeomorphism \(\varPhi \) such that \(p(\cdot )=0\) in (12), which we assume is true henceforth.
We are now in the position to invoke the original constraints \(O_1(x) = 0\) and \(O_2(x) = 0\), which in the new coordinates simply read \(\xi _1 = 0\) and \(\xi _2 = 0\). Therefore, we obtain the system
which is equivalent to the original multibody system (1).
Considering the first two equations in (14), we obtain that
where \({{\bar{x}}}_1 = [I_n,0] \varPhi ^{-1}(0,y,\dot{y},\ldots ,y^{({{\hat{r}}}-1)},\eta )\). Since \(\varGamma (x)\) can be written as
and is invertible, it follows that K(x) has full column rank for all \(x\in U\). Therefore, \(\begin{bmatrix} J(x_1)^\top&G(x_1)^\top&B(x_1)\end{bmatrix}\) has full column rank and the matrix \(\begin{bmatrix} J(x_1)^\top&G(x_1)^\top \end{bmatrix}\) has full column rank as well; hence, by using that M is pointwise positive definite, we have that \(A(x_1) := \begin{bmatrix} J(x_1)\\ G(x_1)\end{bmatrix} M(x_1)^{-1} \begin{bmatrix} J(x_1)^\top&G(x_1)^\top \end{bmatrix}\) is positive definite for all \(x_1\in [I_n,0] U\). Therefore, we can solve for the Lagrange multipliers as follows:
for some appropriately chosen function \(b_4\). Inserting this into the third equation in (14) gives
where \({{\bar{x}}} = \varPhi ^{-1}(0,y,\dot{y},\ldots ,y^{({{\hat{r}}}-1)},\eta )\) and \({{\bar{x}}}_1 = [I_n, 0] {{\bar{x}}}\). Note that it is not clear in general whether the matrix S(x) is invertible for some or all \(x\in U\). The multibody system (1) is then equivalent to
where \(b_5\) is some appropriate function, \({{\tilde{S}}}(\cdot ) = S\big (\varPhi ^{-1}(0,\cdot )\big )\), and the internal dynamics are completely decoupled in (16).
Remark 2.2
We note that an alternative to the above described approach would be to simply differentiate the holonomic and non-holonomic constraints in (1) and solve for the respective Lagrange multipliers. When these have been inserted in (1) (and the still present holonomic and non-holonomic constraints are neglected), an ODE of the form (3) is obtained, for which the Byrnes–Isidori form as in Sect. 1.3 can be computed. This approach has some disadvantages compared to our approach presented above:
-
1)
Since differentiating the constraints does not remove them, it must be guaranteed that any solution of the resulting ODE is also a solution of the overall DAE, i.e., it satisfies the constraints for all times. Nevertheless, this can be ensured, provided that the initial values are chosen appropriately.
-
2)
It cannot be avoided to solve for the Lagrange multipliers first, while in our approach the internal dynamics in (16) are the same as obtained for the auxiliary system in (12), since \(p(\cdot )=0\) in the latter by Lemma 2.1. The system (12) can be computed without solving for the Lagrange multipliers and hence requires much less computational effort. Nevertheless, it is still important to choose the functions \(\phi _{{{\bar{r}}}+1},\ldots ,\phi _{2n}\) such that \(L_K \phi _i = 0\) for \(i={{\bar{r}}}+ 1,\ldots ,2n\); this problem is discussed in Sect. 3.
2.2 Position-dependent output with relative degree two
In the special case, \(h(q,v) = h(q)\), i.e., \(h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m\) and \(y(t) = h\big (q(t)\big )\), we obtain some additional structure. First of all, we may compute that
whence \({{\hat{r}}} \ge 2\). Assuming that \({{\hat{r}}} = 2\) (a typical situation), we obtain, for all \(x=(x_1^\top , x_2^\top )^\top \in U\),
Furthermore,
which is the Schur complement of \(A(x_1)\) in \(\varGamma (x)\).
2.3 The colocated case
Now, we consider the special case that the inputs and outputs of system (1) are colocated, which means that \(h(q,v) = h(q)\) as in Sect. 2.2 and
We show that in this case, the vector relative degree with respect to \(O_3\) is \({{\hat{r}}} = 2\). First, we calculate, for all \(x=(x_1^\top , x_2^\top )^\top \in U\),
and
Then, we obtain the high-gain matrix
Therefore, we find that, for some \(x = (x_1^\top , x_2^\top )^\top \in U\),
i.e., the latter matrix has full column rank. Roughly speaking, this condition means that (the components of) the Lagrange multipliers \(\mu \) and \(\lambda \) and the inputs u influence the system in a linearly independent (i.e., non-redundant) way, because in
the matrix \(\begin{bmatrix} J(q)^\top&G(q)^\top&B(q)\end{bmatrix}\) has full column rank, and thus, the auxiliary input \(u_\mathrm{aux}\) does not have any redundant components.
Then, the transformation which puts (10) into Byrnes–Isidori form is given by
where \({{\bar{r}}} = p + 2\ell + 2m\), and since \({\mathscr {K}}(\cdot )\) is involutive by Lemma 2.1, it is possible to choose \(\phi _i:U\rightarrow {\mathbb {R}}\), \(i={{\bar{r}}} +1,\ldots ,2n\), such that \((L_{K} \phi _i)(x) = \phi _i'(x) K(x) = 0\) and \(\varPhi '(x)\) is invertible for all \(x\in U\). Using the new coordinates
and invoking the original constraints \(O_1(x) = 0\) and \(O_2(x) = 0\), we may rewrite the original multibody system (1) in the form (14), which in the colocated case simplifies to
As in the general case, we may solve for the Lagrange multipliers \(\mu \) and \(\lambda \) and insert this in (18), and thus, (15) becomes
where \({{\bar{x}}} = \varPhi ^{-1}(0,y,\dot{y},\ldots ,y^{({{\hat{r}}}-1)},\eta )\), \({{\bar{x}}}_1 = [I_n, 0] {{\bar{x}}}\) and
for \(x = (x_1^\top , x_2^\top )^\top \in U\). In the colocated case, the matrix S(x) is the Schur complement of \(A(x_1)\) in \(\varGamma (x)\). It is a well-known result that since \(\varGamma (x)\) is positive definite, then the Schur complement \(S(x_1)\) is positive definite as well. Therefore, the decoupled system (16) is of the form
where \({{\tilde{S}}}\) is pointwise positive definite.
3 A feasible set of coordinates for the internal dynamics
In this section, we derive a representation of the internal dynamics which depends on the auxiliary output \(y_\mathrm{aux}\) and its derivative \(\dot{y}_\mathrm{aux}\). Consider a system (1) with holonomic and non-holonomic constraints and position-dependent output. Further set \(H(x_1) =: h'(x_1)\) and assume that, for some open set \(U_1 \subseteq {\mathbb {R}}^n\),
for all \(x_1\in U_1\), which means that the high-gain matrix \(\varGamma (\cdot )\) is invertible on \(U := U_1 \times {\mathbb {R}}^n\). Then, following Sect. 2.2, the auxiliary ODE (10) with (again omitting the argument t for brevity) \(u_\mathrm{aux}^\top = (\mu ^\top , \lambda ^\top , u^\top )\) and \(y_\mathrm{aux}^\top = \big ((J(x_1)x_2 + j(x_1))^\top , g(x_1)^\top , h(x_1)^\top \big )\) has vector relative degree \((1,\ldots ,1,2,\ldots ,2)\) on U, thus \(\bar{r} = p+2\ell +2m\). The diffeomorphism \(\varPhi :U\rightarrow W\) can be represented as
\(x = (x_1^\top , x_2^\top )^\top \in U\). For the internal dynamics \(\eta = \big (\phi _{{{\bar{r}}}+1}(x),\ldots ,\phi _{2n}(x)\big )^\top \), we make, with some abuse of notation, the structural ansatz
where \(\phi _1\in {\mathscr {C}}^1(U_1 \rightarrow {\mathbb {R}}^{n-\ell -m})\) and \(\phi _2\in {\mathscr {C}}(U_1 \rightarrow {\mathbb {R}}^{(n-p-\ell -m) \times n})\). If we now rearrange (21), i.e., we set
where \(P\in {\mathbb {R}}^{{{\bar{r}}}\times {{\bar{r}}}}\) is some permutation matrix, we see that \((\xi _1^\top , \xi _2^\top )^\top \) and \((\eta _1^\top , \eta _2^\top )^\top \) are of similar structure. Since \(\varPhi \) is a diffeomorphism, and system (10) has vector relative degree \((1,\ldots ,1,2,\ldots ,2)\) on U, its Jacobian is invertible on U:
where \(*\) is of the form \(\tfrac{\partial }{\partial x_1} \big (\zeta (x_1) x_2\big )\) with appropriate \(\zeta : U_1 \rightarrow {\mathbb {R}}^{q \times n}\) and \(q \in {\mathbb {N}}\). Since we are interested in the case \({p(\cdot ) = 0}\) in (12) (which can be achieved by Lemma 2.1), we aim to find \(\phi _2: U_1 \rightarrow {\mathbb {R}}^{(n-p-\ell -m) \times n}\) such that
We summarize this in the following result.
Lemma 3.1
Consider the multibody system (1) and assume that (20) holds on an open set \(U_1\subseteq {\mathbb {R}}^n\). For any \(x_1^0 \in U_1\), there exist an open neighborhood \(U_1^0 \subseteq U_1\) of \(x_1^0\) and \(\phi _1\in {\mathscr {C}}^1(U_1^0 \rightarrow {\mathbb {R}}^{n-\ell -m})\), \(\phi _2\in {\mathscr {C}}(U_1^0 \rightarrow {\mathbb {R}}^{(n-p-\ell -m) \times n})\) such that (24) and (25) hold locally on \(U_1^0\), resp.
Proof
We exploit [54, Lem. 4.1.5] which states the following: Consider \(W \in {\mathscr {C}}( U_1 \rightarrow {\mathbb {R}}^{w \times n})\) with \({{\,\mathrm{rk}\,}}W(x_1) = w\) for all \(x_1 \in U_1\). Then, for each \(x_1^0 \in U_1\) there exist an open neighborhood \(U_1^0 \subseteq U_1\) and \(T \in {\mathscr {C}}(U_1^0 \rightarrow \mathbf {Gl}_n)\) such that
Now, we use this to show the existence of \(\phi _1\). Since by (20) we have \({{\,\mathrm{rk}\,}}[G(x_1)^\top , H(x_1)^\top ] = \ell + m\) for all \({x_1 \in U_1}\), there exist for each \(x_1^0 \in U_1\) an open neighborhood \(U_1^0 \subseteq U_1\) and \(T = [T_1, T_2] \in {\mathscr {C}}(U_1^0 \rightarrow \mathbf {Gl}_n)\) such that
i.e., \({{\,\mathrm{im}\,}}T_2(x_1) = \ker [G(x_1)^\top , H(x_1)^\top ]^\top \) and \({{\,\mathrm{rk}\,}}T_2(x_1) = n-\ell -m\) for all \(x_1 \in U_1^0\). Define \(E :=T_2(x_1^0)^\top \), then
Since \({{\,\mathrm{rk}\,}}T_2(x_1^0) = n-\ell -m\), it follows that for \(x_1=x_1^0\), we have \(E T_2(x_1^0) = T_2(x_1^0)^\top T_2(x_1^0) \in \mathbf {Gl}_{n-\ell -m}\). Furthermore, by \(T_2 \in {\mathscr {C}}(U_1^0 \rightarrow {\mathbb {R}}^{n \times (n-\ell -m)})\), the mapping \(x_1 \mapsto \det (ET_2(x_1))\) is continuous on \(U_1^0\), and hence, there is an open neighborhood \(\bar{U}_1^0 \subseteq U_1^0\) of \(x_1^0\) such that \(\det (ET_2({{\bar{x}}}_1)) \ne 0\) for all \({{\bar{x}}}_1 \in {{\bar{U}}}_1^0\). Thus,
and, with \(\phi _1 : {{\bar{U}}}_1^0 \rightarrow {\mathbb {R}}^{n-\ell -m},\ x_1 \mapsto E x_1\), we have \(\phi _1 \in {\mathscr {C}}^1({{\bar{U}}}_1^0 \rightarrow {\mathbb {R}}^{n-\ell -m})\) and the first condition in (24) is satisfied on \({{\bar{U}}}_1^0\) since \(\phi _1'(x_1) = E\).
Now, we show the existence of \(\phi _2\). Observe that by (20), we have \( {{\,\mathrm{rk}\,}}[J(x_1)^\top , G(x_1)^\top , B(x_1)] = p+\ell + m\) and \({{\,\mathrm{rk}\,}}M(x_1) = n\) for all \(x_1 \in U_1\). Therefore, again via [54, Lem. 4.1.5], there exist for each \(x_1^0 \in U_1\) an open neighborhood \(U_1^0 \subseteq U_1\) and \(T = [T_1, T_2] \in {\mathscr {C}}(U_1^0 \rightarrow \mathbf {Gl}_n)\) such that
i.e., \({{\,\mathrm{im}\,}}T_2(x_1) = \ker [J(x_1)^\top , G(x_1)^\top , B(x_1)]^\top \) and \(T_2 \in {\mathscr {C}}(U_1^0 \rightarrow {\mathbb {R}}^{n \times (n-p-\ell -m)})\). Now, choosing \({\phi _2(\cdot ) = T_2(\cdot )^\top M(\cdot )}\) we obtain
which is invertible on \(U_1^0\) since by (20) the high-gain \(\varGamma (x_1)\) is invertible, and \({{\,\mathrm{rk}\,}}T_2(x_1) = n-p-\ell -m\) for all \(x_1 \in U_1^0\). Hence, the second condition in (24) is satisfied on \(U_1^0\). Furthermore, equation (25) holds on \(U_1^0\) by construction of \(\phi _2\). \(\square \)
Lemma 3.1 justifies the structural ansatz for the internal state \(\eta \) in (22). Note that the construction of \(\phi _1\) in the proof of Lemma 3.1 is not unique. There is a lot of freedom in the choice of \(\phi _1\), which is basically free up to (24). However, a straightforward choice is \(\phi _1(x_1) = Ex_1\) with \(E = T_2(x_1^0)^\top \) as in the proof of Lemma 3.1, which can be computed via \({{\,\mathrm{im}\,}}T_2(x_1^0) = \ker [G(x_1^0)^\top , H(x_1^0)^\top ]^\top \).
On the other hand, \(\phi _2\) is uniquely determined up to an invertible left transformation. To find all possible representations, assume that \(\phi _2\in {\mathscr {C}}(U_1 \rightarrow {\mathbb {R}}^{(n-p-\ell -m) \times n})\) is such that (24) and (25) hold. Then, there exist \(P: U_1\rightarrow {\mathbb {R}}^{n \times (p+\ell +m)}\) and \(V: U_1\rightarrow {\mathbb {R}}^{n \times (n-p-\ell -m)}\) such that
Furthermore, P, V have pointwise full column rank, by which the pseudoinverse of V is given by \(V^\dagger (x_1) = (V(x_1)^\top V(x_1))^{-1} V(x_1)^\top \) for \(x_1\in U_1\). Note that it follows from (26) that V is the pointwise basis matrix of a kernel, i.e.,
Lemma 3.2
Let \(\phi _2\in {\mathscr {C}}(U_1 \rightarrow {\mathbb {R}}^{(n-p-\ell -m) \times n})\) be such that (24) and (25) hold. Then, \(\phi _2\) is uniquely determined up to an invertible left transformation. All possible functions are given by
\(x_1\in U_1\), for feasible choices of V satisfying (26).
Proof
Assume that (24) and (25) hold, and hence, we have (26) for some corresponding P and V. Observe that multiplying (26) from the left by \(V(x_1)^\dagger \) gives
Invoking (25), we further obtain from (26) that
and hence, P is uniquely determined by M, J, G, H, B. Therefore, \(\phi _2\) is given as in (27). Furthermore, it follows from (26) that
from which we may deduce \(\phi _2(x_1) V(x_1) = I_{n-p-\ell -m}\) and \({{\,\mathrm{im}\,}}V(x_1) = \ker [J(x_1)^\top , G(x_1)^\top , H(x_1)^\top ]^\top \). Therefore, the representation of \(\phi _2\) in (27) only depends on the choice of the basis of \(\ker [J(x_1)^\top , G(x_1)^\top , H(x_1)^\top ]^\top \). Now, let \({{\tilde{V}}}(x_1) = V(x_1) R(x_1)\), \(x_1\in U_1\), for some \(R: U_1\rightarrow \mathbf {Gl}_{n-p-\ell -m}\) and set
Then, a short calculation shows the claim \({{\tilde{\phi }}}_2(x_1) = R(x_1)^{-1} \phi _2(x_1)\) for all \(x_1\in U_1\). \(\square \)
Now, let \(\phi _1\in {\mathscr {C}}^1(U_1 \rightarrow {\mathbb {R}}^{n-\ell -m})\) and \(\phi _2\in {\mathscr {C}}(U_1 \rightarrow {\mathbb {R}}^{(n-p-\ell -m) \times n})\) be such that (24) and (25) are satisfied and \(V: U_1\rightarrow {\mathbb {R}}^{n \times (n-p-\ell -m)}\) as in (26). We continue deriving a representation of the internal dynamics. We define \({{\bar{y}}}_\mathrm{aux} := [0,I_{\ell +m}] y_\mathrm{aux}\) and observe that, using the first equation in (10),
Then, with \(y_\mathrm{aux, 1} = O_1(x)\) we find
Thus, using (22) and (28) the dynamics of \(\eta _1\) are given by
Furthermore, we have that
for a continuously differentiable \(\vartheta : U_1 \rightarrow {\mathbb {R}}^n\), the Jacobian of which is invertible on \(U_1\) by (24). In order to ensure that \({\vartheta }\) is a diffeomorphism on \(U_1\), we need to additionally require that there exist a diffeomorphism \(\psi : U_1\rightarrow {\mathbb {R}}^n\) and \(\omega :[0,\infty )\rightarrow (0,\infty )\) which is continuous, non-decreasing and satisfies \(\int _0^\infty \frac{1}{\omega (t)} \, \mathrm{d}t = \infty \) such that
Then, [10, Thm. 2.1] yields that \({\vartheta }: U_1 \rightarrow W_1 := {\vartheta }(U_1)\) is a diffeomorphism. Then, we have
To combine (30) with (29), we define the following functions as concatenations on \(W_1\):
Therefore, we obtain the following representation of (29):
Now, we investigate the dynamics of \(\eta _2\). Define \(\phi '_2[x_1,x_2] := \tfrac{\partial }{\partial x_1} \big (\phi _2(x_1) x_2\big ) \in {\mathbb {R}}^{(n-p-\ell -m) \times n }\), then from (10), (22) and (25), we obtain
Let \(\phi _{2,\vartheta }(\cdot ) := \big (\phi _2 \circ \vartheta ^{-1} \big )(\cdot )\), \(H_{\vartheta }(\cdot ) := \big (H \circ \vartheta ^{-1} \big )(\cdot )\) on \(W_1\) and define for \(w \in W_1\), \(v \in {\mathbb {R}}^n\)
Then, the dynamics of \(\eta _2\) are given by
Finally, we invoke the original constraints, which means that \(y_\mathrm{aux,1} = 0\) and \({ {{\bar{y}}}}_\mathrm{aux} = \begin{pmatrix} 0 \\ y\end{pmatrix}\). With this, and omitting the argument \(({{\bar{y}}}_\mathrm{aux}^\top , \eta _1^\top )^\top = (0, y^\top , \eta _1^\top )^\top \) where it is obvious, the internal dynamics read
Remark 3.3
If no non-holonomic constraints are present, we may obtain further structure for the internal dynamics in (31). Consider the functions \(\phi _1\) and \(\phi _2\) as above and recall the concept of a conservative vector field. For \(U \subseteq {\mathbb {R}}^n\) open, a vector field \(\zeta : U \rightarrow {\mathbb {R}}^n\) is said to be conservative, if it is the gradient of a scalar field. More precisely, if there exists a scalar field \(\chi : U \rightarrow {\mathbb {R}}\) such that \(\chi '(x) = \zeta (x)^\top \).
Now, if every row \(\phi _{2,i}(\cdot )\) of \(\phi _2(\cdot )\) defines a conservative vector field, then the components of \(\phi _1(\cdot )\) can be chosen to be multiples of the associated scalar fields. More precisely, if there exist \(\chi _i\in {\mathscr {C}}^1(U_1\rightarrow {\mathbb {R}})\) such that \(\chi _i'(x_1) = \phi _{2,i}(x_1)\) for all \(x_1\in U_1\) and all \(i=1,\ldots ,n-\ell -m\), then we may choose \(\phi _1 = (\lambda _1 \chi _1,\ldots ,\lambda _{n-\ell -m}\chi _{n-\ell -m})^\top \) for some \(\lambda _i\in {\mathbb {R}}\), \(i=1,\ldots ,n-\ell -m\). This gives \(\phi '_{1} = \varLambda \phi _{2}\) for \(\varLambda = \mathrm{diag\,}(\lambda _1,\ldots ,\lambda _{n-\ell -m})\) and, likewise, \(\phi '_{1,\vartheta } = \varLambda \phi _{2,\vartheta }\). Hence, via (25) and Lemma 3.2 the dynamics of \(\eta _1\) in (31) simplify to
where the diagonal entries of \(\varLambda \) can be chosen as desired.
Hence, in this case the variables \(\eta _1 = \phi _1(q)\) can be interpreted as (transformed) positions and \(\eta _2 = \varLambda ^{-1} {{{\dot{\eta }}}}_1\) as velocities. Therefore, the states \(\eta = (\eta _1^\top , \eta _2^\top )^\top \) admit a partition which is structurally similar to that of the states \((q^\top , v^\top )^\top \) of the multibody system (1). In the presence of non-holonomic constraints, this simplification is not possible, because of the different dimensions of \(\phi _1'\) and \(\phi _2\).
Remark 3.4
The computation of the Byrnes–Isidori form leading to the decoupling of the internal dynamics as in (16) often requires a lot of effort. The choice of variables for the internal dynamics presented in this section offers an alternative, leading to the internal dynamics given in (31) directly in terms of the original system parameters; a computation of the Byrnes–Isidori form is not necessary.
4 Servo-constraints approach
We seek to find a feedforward control \(u_\mathrm{ff}\) regarding the control methodology described in Sect. 1.4 by inverting the system model. For minimum phase systems, the transformed system (16) can be used as an inverse model for feedforward control. Solving the respective first equation for the input u with \(y=y_\mathrm{ref}\) yields the feedforward control signal \(u_\mathrm{ff}\), provided the internal dynamics are integrated simultaneously. However, a direct integration of the internal dynamics is not possible for non-minimum phase systems, due to unstable dynamics. Thus, stable inversion is introduced in [27, 30] for finding a bounded solution based on a boundary value problem (BVP). This yields a non-causal solution, in the sense that a system input \(u_\mathrm{ff}(t)\ne 0\) is present in a pre-actuation phase \(t<t_0\) before the start of the trajectory at time \(t_0\). Thus, the BVP is solved on a time interval \(\left[ T_0\,, T_f\right] \) with \(T_0<t_0\) and \(T_f>t_f\), with \(t_f\) denoting the end of the desired trajectory \(y_\mathrm{ref}\). Provided that the equilibrium of the internal dynamics is hyperbolic, there are \(n^s\) eigenvalues in the left half plane and \(n^u\) eigenvalues in the right half plane, such that \(n^s+n^u=2n-{\bar{r}}\). The boundary conditions of the BVP are chosen such that the states \(\eta \) of the internal dynamics start on the unstable manifold \(W_0^u\in \mathbb {R}^{n^u}\) of the equilibrium point \(\eta _\mathrm{eq,0}\) at time \(T_0\). At the end \(T_f\), the boundary conditions constrain the states \(\eta \) to lie on the stable manifold \(W_f^s\in \mathbb {R}^{n^s}\) of the equilibrium point \(\eta _\mathrm{eq,f}\). This is summarized as
The case of non-hyperbolic equilibria is discussed in [29]. The BVP consisting of the dynamics (16) subject to the constraints (32) yields a bounded solution to the internal dynamics. It was recently demonstrated in the brief note [31] that the boundary conditions (32) can be simplified as
where the binary matrices \(L_0\in \mathbb {R}^{n^0 \times (2n-r)}\) and \(L_f\in \mathbb {R}^{n^f \times (2n-r)}\) select in total \(n^0+n^f=2n-{\bar{r}}\) conditions to constrain \(n^0\) states of the internal dynamics to the equilibrium point at time \(T_0\) and \(n^f\) states of the internal dynamics to the equilibrium point at time \(T_f\). Thus, the number of constraints equals the number of unknowns.
For higher relative degree and multi-input, multi-output systems, the symbolic derivation of the internal dynamics, and especially of the stable and unstable manifolds, becomes tedious and complex. Thus, the method of servo-constraints introduced in [20] is applied to demonstrate an alternative approach. Motivated from modeling of classical holonomic mechanical constraints, such as bearings, the equations of motion (1) are appended by m servo-constraints
which enforce the output to stay on the prescribed trajectory \(y_\mathrm{ref}\in {\mathscr {W}}^{r,\infty }({\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^m)\). This yields a set of DAEs
to be solved numerically for the coordinates q and v, the Lagrange multipliers \(\lambda \) and \(\mu \) and the input u. We stress that the initial values \(q^0, v^0, \lambda ^0, \mu ^0, u^0\) must be chosen so that they are consistent and the desired trajectory must be compatible with the possible motion of the system, i.e., it is required that a solution of (35) exists on \({\mathbb {R}}_{\ge 0}\). Note that (35) might have multiple solutions in the case that the desired output trajectory can be achieved by choosing different state trajectories. This is, for example, already the case for a 2-arm manipulator and most serial manipulators. However, from a control perspective, any solution that generates the desired output trajectory can be chosen. The freedom of choosing any solution can be utilized to optimize, e.g. input energy. The chosen solution \((q,v,\lambda ,\mu ,u):{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^n\times {\mathbb {R}}^n\times {\mathbb {R}}^\ell \times {\mathbb {R}}^p\times {\mathbb {R}}^m\) of (35) is used to define the feedforward control signal \(u_\mathrm{ff} := u\). As a consequence, if all the system parameters and initial values of the multibody system (1) are known exactly and the control \(u= u_\mathrm{ff}\) is applied to it, then the closed-loop system has a solution which satisfies \(y=y_\mathrm{ref}\). However, this result may not be true in the presence of disturbances, uncertainties and/or modeling errors. Then, a feedback controller can be added to reduce the tracking errors. This is demonstrated in the application example in Sect. 6.
While classical mechanical constraints are enforced by reaction forces orthogonal to the tangent of the constraint manifold, the servo-constraints (34) are enforced by the generalized input \( B\big (q(t)\big ) u(t)\) which is not necessarily perpendicular to the tangent of the constraint manifold. Different configurations are distinguished depending on the vector relative degree of the associated auxiliary ODE (10), see [21]. For example, if inputs and outputs are colocated as discussed in Sect. 2.3, then the system input can directly actuate the output and the inverse model is in so-called ideal orthogonal realization. Recall that this corresponds to a relative degree two framework. If less than m components of the system input directly influence the system output, then the inverse model is in so-called mixed tangential–orthogonal or purely tangential realization.
Remark 4.1
It is interesting to note that in the colocated case, i.e., \(h'(q) = B(q)^\top \) for all \(q\in {\mathbb {R}}^n\), and for \(y_\mathrm{ref} = 0\), the servo-constraints act like holonomic constraints in (35), where the corresponding Lagrange multipliers are given by the inputs u(t) of the system. Therefore, the system (35) can again be interpreted as a multibody system (without any inputs or outputs) in this case.
While DAEs describing mechanical systems dynamics with classical constraints are of differentiation index 3, the set of DAEs (35) might have a larger differentiation index. As a rule of thumb for single-input single-output systems, the differentiation index is larger by one than the relative degree of the respective system, if the internal dynamics is modeled as an ODE and not affected by a constraint [26].
It is shown in [24] that the original stable inversion problem solving the boundary value problem of (16) and (32) can be formulated and solved directly for the inverse model described by the DAEs (35). However, the derivation of the boundary conditions (32) is still tedious. In order to avoid the boundary conditions, it is proposed in [4] to reformulate the stable inversion problem as an optimization problem. Alternatively, the simplified boundary conditions (33) can also be formulated for the inverse model described by the DAEs (35). They then read
with the binary selection matrices \(L_0\in \mathbb {R}^{n^0 \times (2n+\ell +p+m)}\) and \(L_f\in \mathbb {R}^{n^f \times (2n+\ell +p+m)}\). These describe in total \(n^0+n^f=2n+\ell +p+m\) conditions, which constrain \(n^0\) states to the initial equilibrium and \(n^f\) states to the final equilibrium of the internal dynamics. Compared to the Byrnes–Isidori form, the resulting boundary value problem of the dynamics (35) subject to the constraints (36) greatly simplifies the problem setup, since less analytical derivations are required.
The boundary value problem needs to be solved numerically. Since high-index DAEs are difficult to solve numerically, see, e.g., [37], different index reduction strategies can be applied. In the context of servo-constraints, index reduction by projection is proposed in [21], minimal extension is proposed in [1, 18] and Baumgarte stabilization is applied in [6]. Available methods for solving BVPs are, for example, single shooting, multiple shooting or finite differences [3]. In the present paper, we utilize finite differences with Simpson discretization [51].
The computational effort for the solution of the BVP depends on the number of unactuated states. For systems with few unactuated states, this might be done within seconds or minutes. However, the solution of the boundary value problem has to be computed offline. This is due to the fact that the BVP requires the specification of the output trajectory over the complete time horizon. If real-time trajectory adaption is desired, one might have to use a different approach which allows real-time capable forward time integration of the servo-constraint problem, see, e.g., [46, 47]. However, this requires a differentially flat or minimum phase system. This could be achieved by changing the mechanical design of the system or by output redefinition, see, e.g., [45]. While output redefinition is quite simple, the close tracking of the original end-effector output is deteriorated.
Finally, it should be noted that the feedforward control of non-minimum phase systems, such as obtained by solving the BVP, is non-causal. This means that there is a so-called pre-actuation phase where some control action occurs before the trajectory tracking starts. During this pre-actuated phase, the system is driven into the required initial condition for exact trajectory tracking. If this pre-actuation phase is neglected, then there is a mismatch between the actual initial conditions of the system and the ones provided by the inverse model. However, this mismatch is often small and can be compensated quickly by the feedback controller.
5 Funnel-based feedback controller
In this section, we present a feedback-controller design for the multibody system (1), which is based on the funnel controller for systems with arbitrary vector relative degree recently developed in [13]. Furthermore, the design invokes a recently developed methodology for linear non-minimum phase systems from [9], which has been successfully applied to a nonlinear non-minimum phase robotic manipulator in [11]—however, here we extend this methodology to the case of vector relative degree. The method is based on the introduction of a new output, which is differentially flat for the unstable part of the internal dynamics, cf. [32] for differential flatness. With respect to the new output, the overall system has a higher vector relative degree (in some of the components), but the unstable part of the internal dynamics is eliminated. This allows to apply the controller from [13] to the system (1) with new output and appropriate new reference signal. Since the required differentially flat output does often not exist for real-world nonlinear multibody systems (cf. [11]), we first linearize the internal dynamics, i.e., the second equation in (16), around an equilibrium \((\eta _1^0,\eta _2^0)\in {\mathbb {R}}^{n-\ell -m}\times {\mathbb {R}}^{n-p-\ell -m}\) and \(y = \dot{y} = \ldots = y^{({{\hat{r}}}-1)} = 0\). With
we obtain the linearized internal dynamics (with some abuse of notation, again using \(\eta \) as state variable)
Note that \({{\tilde{q}}}\) and \({{\tilde{p}}}\) may also be given in the special form (31), obtained using the approach presented in Sect. 3. In the next step, as in [11], we need to transform (37) so that the derivatives of y are removed from the right-hand side. To this end, we define
and then, a straightforward induction shows that
With some abuse of notation, again using \(\eta \) as state variable, we set \(\eta := \zeta ^{{{\hat{r}}} -1}\) and obtain
where \(P = \sum _{i=1}^{{{\hat{r}}}} Q^{i-1} P_i\). In the following, we assume that \(\sigma (Q) \cap \overline{{\mathbb {C}}_+} \ne \emptyset \), so that the internal dynamics are not minimum phase.
In order to derive the controller design, we first require some assumptions which are extensions of those stated in [9]. Compared to the latter, here we increase each component of the vector relative degree separately (and possibly differently), instead of uniformly increasing the strict relative degree. To this end, choose \(T\in \mathbf {Gl}_{2n-{{\bar{r}}}}\) and \(k\in {\mathbb {N}}\) such that
where \({{\hat{Q}}}_1\in {\mathbb {R}}^{(2n-{{\bar{r}}}-k)\times (2n-{{\bar{r}}}-k)}\), \({{\hat{Q}}}_2\in {\mathbb {R}}^{(2n-{{\bar{r}}}-k)\times k}\), \({{\tilde{Q}}}\in {\mathbb {R}}^{k\times k}\), \({{\hat{P}}}\in {\mathbb {R}}^{(2n-{{\bar{r}}}-k)\times m}\), \({{\tilde{P}}}\in {\mathbb {R}}^{k\times m}\), with \(\sigma ({{\hat{Q}}}_1)\subseteq {\mathbb {C}}_-\) and \(\sigma ({{\tilde{Q}}})\subseteq \overline{{\mathbb {C}}_+}\). We assume:
- (A1):
-
There exist \(q\in \{1,\ldots ,m\}\) and \(k_i\in {\mathbb {N}}\), \(i=1,\ldots ,q\) such that \(k_1+\ldots +k_q = k\). Furthermore, there exist \({\rho } \in \{-1,1\}\), \(K_1, \ldots , K_q\in {\mathbb {R}}^{1\times k}\) and \(K_{q+1}, \ldots , K_m\in {\mathbb {R}}^{1\times m}\) such that, for the matrix-valued function \({{\tilde{S}}}:W\rightarrow {\mathbb {R}}^{m\times m}\), \(W = [0,I_{2n-p-2\ell }] \varPhi (U)\), that appears in (16) (which is basically the high-gain matrix of this equation), we have that
$$\begin{aligned} \forall \, i=1,\ldots ,q\ \forall \, j=0,\ldots ,k_i-2:\ K_i {{\tilde{Q}}}^j {{\tilde{P}}} = 0 \end{aligned}$$and the matrix
$$\begin{aligned} {\rho } \cdot \begin{bmatrix} K_1 {{\tilde{Q}}}^{k_1 - 1} {{\tilde{P}}}\\ \vdots \\ K_q {{\tilde{Q}}}^{k_q-1} {{\tilde{P}}}\\ K_{q+1} \\ \vdots \\ K_m\end{bmatrix} {{\tilde{S}}}(w) \end{aligned}$$is positive definite for all \(w\in W\).
- (A2):
-
Let \(y_\mathrm{ref}\in {\mathscr {W}}^{{{\hat{r}}},\infty }({\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^m)\) be a given reference signal and \(W\in \mathbf {Gl}_{k}\) be such that
$$\begin{aligned} W{{\tilde{Q}}} W^{-1} = \begin{bmatrix} Q_1&{}0\\ 0&{}Q_2\end{bmatrix},\quad W{{\tilde{P}}} = \begin{bmatrix} P_1\\ P_2\end{bmatrix}, \end{aligned}$$where \(Q_i\in {\mathbb {R}}^{l_i\times l_i}\), \(i=1,2\), with \(\sigma (Q_1)\subseteq {\mathbb {C}}_+\) and \(\sigma (Q_2)\subseteq \mathrm{i}{\mathbb {R}}\). Then, the equation
$$\begin{aligned} \dot{z}_2(t) = Q_2 z_2(t) + P_2 y_\mathrm{ref}(t),\quad z_2(0) = 0 \end{aligned}$$has a bounded solution \(z_2:{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^{l_2}\).
Note that in the colocated case discussed in Sect. 2.3, the matrix \(S(\cdot )\) (and hence also \({{\tilde{S}}}(\cdot )\)) is always pointwise positive definite, independent of the specific system parameters. Hence, the last condition in (A1) is satisfied, if, for instance, it is possible to choose \(K_1,\ldots K_m\) such that \(\begin{bmatrix} K_1 {{\tilde{Q}}}^{k_1 - 1} {{\tilde{P}}}\\ \vdots \\ K_q {{\tilde{Q}}}^{k_q-1} {{\tilde{P}}}\\ K_{q+1} \\ \vdots \\ K_m\end{bmatrix} = I_m\).
We may now define the new output. Let, for \(\eta \) as in (38) and T as in (39), \((\eta _1^\top , \eta _2^\top )^\top = T \eta \) (not to be confused with the variables introduced in Sect. 3). Then,
With this, we define \(y_\mathrm{new}:{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^m\) by
Similar to [9], it can be computed that the vector relative degree (of the auxiliary ODE (10)) increases when the output y is replaced by \(y_\mathrm{new}\). More precisely, in the context of Sect. 2 we find that \(r_3\) changes to \(({{\hat{r}}} + k_1,\ldots , {{\hat{r}}} +k_q, {{\hat{r}}}, \ldots , {{\hat{r}}})\in {\mathbb {N}}^{1\times m}\).
In order to track the original reference signal \(y_\mathrm{ref}\) with the original output y, we need to introduce a new reference signal for system (1) with new output (41). The new reference signal is generated by the subsystem (40) corresponding to the unstable part \(\eta _2\) when the output y is substituted by the reference \(y_\mathrm{ref}\), i.e.,
Equation (42) will be part of the controller design and constitutes a dynamic part of the overall controller. In order for the controller from [13] to be applicable, we require that \({{\hat{y}}}_{\mathrm{ref},i}\in {\mathscr {W}}^{{{\hat{r}}}+k_i,\infty }({\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^m)\) for \(i=1,\ldots ,q\). As shown in [9], this is the case, if, using the notation from (A2),
Furthermore, if the original reference \(y_\mathrm{ref}\) is generated by a linear exosystem (as in linear regulator problems, cf. [33]) of the form
where the parameters \(A_e\in {\mathbb {R}}^{n_e\times n_e}, C_e\in {\mathbb {R}}^{m\times n_e}\) and \(w^0\in {\mathbb {R}}^{n_e}\) are known, and \(\sigma (A_e)\subseteq \overline{{\mathbb {C}}_-}\) so that any eigenvalue \(\lambda \in \sigma (A_e)\cap \mathrm{i}{\mathbb {R}}\) is semisimple (note that this guarantees \(y_\mathrm{ref}\in {\mathscr {W}}^{{{\hat{r}}},\infty }({\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}^m)\)), then \(\eta ^0_{2,\mathrm ref}\) can be calculated via the solution \(X\in {\mathbb {R}}^{l_1\times n_e}\) of the Sylvester equation
as
Now, using the new output (41) and the new reference signal (42), the auxiliary tracking error is defined by
The application of the funnel control law from [13] requires the derivatives of \(y_\mathrm{new}\), and for implementation, we need to express them in terms of the original variables q and v of the multibody system (1). We use the linearization (40) to obtain these derivatives. We replace \(\eta _2\) in \(y_\mathrm{new}\) and its derivatives by the original coordinates from (1). To this end, we pretend that the coordinates of the linearization of the internal dynamics in (37) coincide with the original coordinates in the second equation of (16), which can be obtained via
Assume that the transformation from (37) to (38) is given by
then we consider
Now, we replace \(\eta _2(t) = \varPsi (q(t),v(t))\) in \(y_{\mathrm{new}, i}(t) = K_i \eta _2(t)\) and its derivatives for \(i=1,\ldots ,q\). To this end, observe that, similar as in [9], we may calculate that
Hence, we obtain the replacement rule
for \(i=1,\ldots ,q\), where the derivatives \(y^{(j)}(t)\) are to be expressed via Lie derivatives as in (11) and read
Similarly, we obtain the replacement rule
for \(i=q+1,\ldots ,m\) and \(j=0,\ldots ,{{\hat{r}}}-1\).
If the transformation \(\varPsi :U\rightarrow {\mathbb {R}}^k\) is not available or hard to compute, then \(\eta _2\) may instead be computed as the solution of the linear differential equation (40) with \(y(t) = h(q(t),v(t))\), which is inserted at the respective places above.
With this, the application of the controller from [13] to a multibody system (1) with new output (41) and reference signal as in (42) leads to the following overall control law:

with \({\eta }_{2,\mathrm ref}^0\) as in (43), \( \rho \) as in (A1), tuning parameters \({{\bar{\kappa }}}, \kappa _{i,j} > 0\), reference signal \(y_\mathrm{ref}\in {\mathscr {W}}^{{{\hat{r}}},\infty }({\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}})\) and funnel functions \(\varphi _{i,j} \in \varPhi _{{{\hat{r}}} + k_i-j}\) for \(i=1,\ldots ,q\), \(j=0,\ldots ,{{\hat{r}}} + k_i -2\), \(\varphi _{i,j} \in \varPhi _{{{\hat{r}}} -j}\) for \(i=q+1,\ldots ,m\), \(j=0,\ldots ,{{\hat{r}}} -2\) and \(\varphi \in \varPhi _1\).
We note that in (48), the variables \(e_{i,j}\) are only short-hand notations and they can be expressed in terms of \(y_\mathrm{new}, {{\hat{y}}}_\mathrm{ref}, \varphi _{i,j}\) and the derivatives of these. Therefore, the expressions in (46) must be used for the replacement of the derivatives of \(y_\mathrm{new}\) in terms of the original coordinates q and v. Further note that the controller (48) implicitly assumes that the physical dimensions of all input and output variables coincide. For systems in which these variables have different physical dimensions, a straightforward renormalization approach as presented in [14] can be used.
Remark 5.1
Since the controller design developed in this section involves numerous transformations, a summarizing remark is warranted. For a given multibody system (1) with unstable internal dynamics, we perform the following steps.
-
1.
Decouple the internal dynamics as in (16) using the method of Sect. 2 or, alternatively, that of Sect. 3.
-
2.
Linearize the internal dynamics around an equilibrium to obtain (37).
-
3.
Transform the linearization such that the derivatives of y are removed from the right-hand side and (38) is obtained.
-
4.
Decompose the internal dynamics via (39) such that the unstable part of the linearized internal dynamics is decoupled and given by (40).
-
5.
Define the new output \(y_\mathrm{new}\) as in (41) and express it as a function of the original variables q and v of (1).
-
6.
Calculate the new reference signal \({{\hat{y}}}_\mathrm{ref}\) via (42).
-
7.
Calculate the required derivatives of \(y_\mathrm{new}\) and \({{\hat{y}}}_\mathrm{ref}\) using (46), (47) and (42).
-
8.
Calculate the control input u via (48).
6 A robotic manipulator with kinematic loop
In this section, we illustrate our findings by a robotic manipulator which is described by a DAE that cannot be reformulated as an ODE and, at the same time, has unstable internal dynamics. The model is shown in Fig. 3. This example is motivated by a similar flexible manipulator in [44]. It consists of three bodies with mass \(m_i\), length \(L_i\) and moments of inertia \(I_i\). The first body is fixed to a translationally moving actuator on one end. The other end is connected to the end of body 2. The center of gravity of body 2 is mounted on a translationally moving actuator. Body 3 is attached to the end of body 2 by a linear spring–damper combination with coefficients c and D. Due to the described configuration, there exists a kinematic loop in the model and the resulting equations of motion in DAE form cannot be easily reformulated as an ODE.
With the variables \(q = (s_1, s_2, \alpha , \beta , \gamma )^\top \), \(\lambda = (\lambda _1, \lambda _2)^\top \) and the system input \(u=(u_1, u_2)^\top \), the equations of motion are given by
which are of the form (1) with f, g, M, G, B defined in (49) in a brief way. The model parameters are listed in Table 1. Note that a homogeneous mass distribution is assumed for bodies 1 and 2, while the center of gravity of body 3 can be varied by \(X_3\). The parameters of the reference model differ from the parameters for the forward simulation of the actual model in order to show robustness of the presented approach. For this example, the mass \(m_3\) of the third arm is chosen 20% larger compared to the reference model. This might be the case if the robot is hoisting an unknown mass with its third arm.
The reference model is inverted according to Sect. 4 to obtain the feedforward control input \(u_\mathrm{ff}\). Using identical parameters for both models would yield exact tracking of the feedforward controller. Therefore, the parameters for the simulated model differ from the ones of the inverted model. The funnel controller introduced in Sect. 5 decreases the tracking errors due to parameter mismatch of the pure feedforward control. However, note that the funnel controller (48) also requires some system parameters, for instance, to compute the matrices \({{\tilde{Q}}}\) and \({{\tilde{P}}}\), and hence relies on the reference model. Nevertheless, we will demonstrate that it is able to compensate the tracking error induced by feedforward control.
The output is chosen as
where the first component is the horizontal position of the second body and the second component corresponds to an auxiliary angle describing the end-effector position for small angles \(\gamma \). Both components may be used to approximate the end-effector position by
Note that in practice the output y(t) can be easily measured. The first component of y(t) is directly obtained by measuring the position \(s_2(t)\) of the second translational actuator. The second component of the output is computed from the measured joint angles \(\beta (t)\) and \(\gamma (t)\) and the known lengths \(L_2\) and \(L_3\), see Fig. 3. A detailed explanation and derivation of such an output to approximate the end-effector position can be found in [49].
To demonstrate the tracking capability of the proposed controller design, we choose the reference trajectory \(r_\mathrm{app,ref}\) in end-effector coordinates as the path
parameterized by r(t). The timing law of the scalar parameter r(t) is chosen as the polynomial
with initial time \(t_0={0}{\hbox {s}}\) and final transition time \(t_f={1}{\hbox {s}}\). The initial position is chosen as \(r_\mathrm{app,0}=\begin{bmatrix}1.6&-0.6\end{bmatrix}^\top \,\)m, and the final position is \(r_\mathrm{app,f}=\begin{bmatrix}0.9&-0.9\end{bmatrix}^\top \,\)m. The reference trajectory \(r_\mathrm{app,ref}\) is then transformed to the system output trajectory \(y_\mathrm{ref}\).
In the following, we aim to calculate the relative degree in a preferably large open set around the equilibrium point
To this end, we choose (and this will be justified later)
which accordingly restricts the operating range of the system. Henceforth, we identify M, G, g and h with their restrictions to \(U_q\) and f with its restriction to U. It is straightforward to check that the conditions in (2) are satisfied on \(U_q\). However, the inputs and outputs are not colocated here,
i.e., (17) does not hold. It is then easy to see that for all \(x = (q^\top , v^\top )^\top \in U\), we have \(L_{K(x)} O_3(x) = 0\) and
where
and a MATLAB calculation yields that
Let us assume in the following that the third body has a homogeneous mass distribution, and hence,
Now, for \(x = (q^\top , v^\top )^\top \in U\) we find that \(\sin (\alpha )>0\), \(\sin (\alpha +\beta )>0\) and \(\cos \gamma > \tfrac{2}{3}\), where the latter gives
thus \(\det \varGamma (x) < 0\), and hence, \(\varGamma (x)\) is invertible and the vector relative degree is well defined on U with \({{\hat{r}}} = 2\). As a consequence, we find that \({{\bar{r}}} = 4 + 4 = 8 < 10 = 2n\), so the system has non-trivial internal dynamics.
For later use, set \(\kappa := m_3 X_3^2 + I_3 = \frac{m_3 L_3^2}{3}\). In order to decouple the internal dynamics, we invoke the transformation \(\varPhi \) with
and following the ansatz (22) in Sect. 3, we set
where \(\phi _{10}(x) = {{\tilde{\phi }}}_{10}(q) v\). As in the proof of Lemma 3.1, we choose
and observe that \({{\tilde{\phi }}}_{10}(q) = [0,0,0,0,1]M(q)\). We check that
Further, we choose \(\phi _9: U_q \rightarrow {\mathbb {R}},\ q \mapsto \gamma \) and thus
Furthermore, the Jacobian of \(\varPhi \) is given by (53). Invertibility of the matrix in (53) is equivalent to invertibility of the submatrix
Since \(x\in U\) implies that \(\sin \alpha >0\), this matrix is invertible if, and only if, the determinant of the lower right \(2\times 2\) submatrix is nonzero, which is given by
since \(\cos \gamma > \tfrac{2}{3}\). Therefore, \(\varPhi '(x)\) is invertible everywhere for all \(x\in U\). In the next step, we aim to obtain the internal dynamics, i.e., the second equation in the decoupled system (16). First, we calculate that
In order to resolve the right-hand sides in the above equation, we calculate the inverse of the diffeomorphism \(\varPhi \). First, observe that the new coordinates admit the representation in (54). Upon solving, and invoking the original constraints \(\phi _1 = \ldots = \phi _4 = 0\), with \(\delta := \frac{2L_3}{L_2+ 2L_3}\) we obtain for the required coordinates \(s_2, \beta , \gamma \) and \(\dot{s}_2,\dot{\beta }\) and \({{{\dot{\gamma }}}}\) that
With this and \(\phi _5 = y_1\), \(\phi _6 = y_2\), \(\phi _7 = \dot{y}_1\), \(\phi _8 = \dot{y}_2\), \(\phi _9 = \eta _1\) and \(\phi _{10} = \eta _2\), the internal dynamics are given by (55).
Denote with \(J_{{\mathscr {F}},x}(x^0,y^0) \in {\mathbb {R}}^{p \times q}\) the Jacobian of a function \({\mathscr {F}}\in {\mathscr {C}}^1({\mathbb {R}}^q \times {\mathbb {R}}^k \rightarrow {\mathbb {R}}^p)\) with respect to x at a point \((x^0,y^0) \in {\mathbb {R}}^q \times {\mathbb {R}}^k\). Instead of linearizing (55) around the equilibrium point, in order to increase performance we linearize it around the starting point of the reference trajectory at \(t_0\) and the end point at \(t_f\) given by
and combine both points linearly to obtain \(Q, P_1\) and \(P_2\) as in Sect. 5 from the function \({\mathscr {F}}= ({\mathscr {F}}_1, {\mathscr {F}}_2)^\top \) defined in (55) by
With the coefficients
where \(\beta ^0, \beta ^f\) are the values of \(\beta \) at \(t_0\) and \(t_f\), resp., induced by the reference trajectory, these matrices are given by
and we consider the corresponding system in the form as in (37), that is
We may observe that Q has a positive and a negative eigenvalue, and hence, the system is not minimum phase, not even locally.
After the transformation \({{\bar{\eta }}}(t) = \eta (t) - P_2 y(t) \), we obtain
where \(P = Q P_2\). Now, we calculate that Q has eigenvalues \(\mu _{1,2} = \tfrac{D C_0}{2} \mp \sqrt{\big (\tfrac{D C_0}{2}\big )^2 + C_0 c}\). Note that for \(c {>}\) 0 we have \(\mu _1 {<} 0 {<} \mu _2\), thus (51) has a hyperbolic equilibrium, whence the linearized internal dynamics have an unstable part. Next, we seek a transformation which diagonalizes Q and hence separates the stable and the unstable part of the internal dynamics:
Using the transformation \({{\hat{\eta }}}(t) = T^{-1} {{\bar{\eta }}}(t)\), we obtain the linearized internal dynamics
According to (A1), we set \({{\tilde{P}}} = [0,1] T^{-1} P\), and then, this has exactly the form of (40) in Sect. 5:
where \({{\tilde{Q}}}, {{\tilde{P}}}\) satisfy (A1) with \(q = 1\), \(k_1=1\),
however, strictly speaking the last condition in (A1) is only satisfied in a neighborhood of the equilibrium point. (A2) is satisfied with \(W = 1\).
Hereinafter, \({{\hat{\eta }}}_2\) plays the role of \(\eta _2\) in Sect. 5 which is not to be confused with the expressions in (55). We have
To replace \({{\hat{\eta }}}_2\) and its derivatives in \(y_\mathrm{new,1}\), consider
Then, \({{\hat{\eta }}}_2(t) = \varPsi (q(t),v(t))\) and \(y_\mathrm{new,1}(t) = K_1 \varPsi (q(t),v(t))\). In order to implement the controller (48), we calculate the required derivatives of \(y_\mathrm{new,1}\) in terms of the system’s original variables. Recall \(y(t) = h(q(t))\) and \(\dot{y}(t) = h'(q(t))v(t)\). Then, using (56):
Further, we need to express \(e_{i,j}(t)\) in (48) in terms of the system’s original variables. Therefore, we need to calculate \({{\hat{y}}}_\mathrm{ref,1}\) according to (42):
where \({{\hat{\eta }}}_{2,\mathrm ref}^0\) is computed according to (43):
Now, for \(e_{1,0}(t) := y_\mathrm{new,1}(t) - {{\hat{y}}}_\mathrm{ref,1}(t)\) we define for \(\varphi _0 \in \varPhi _3\) and \(\kappa _0 > 0\) the expressions
where \({{\hat{y}}}_\mathrm{ref,1}\) is from (60) and \(y_\mathrm{new,1}^{[i]}\) are from (59), resp. For both errors, we choose the same funnel function, i.e., \(\varphi _{i,j} = \varphi _j \in \varPhi _{3-j}\) and the same amplification factor, i.e., \(\kappa _{i,j} = \kappa _j\) for \(i=1,2\) and \(j=0,\ldots ,2-i\). With this, the controller reads

for \({{\bar{\kappa }}} = \kappa _2\) and \(\varphi = \varphi _2\). For the simulation, we have chosen the funnel functions \(\varphi _j(t) = (p_j e^{-q_j t} + r_j)^{-1}\) for \(j=0,1,2\). The simulation parameters are given in Table 2. Based on the parameters for the reference model from Table 1, the matrices \(T^{-1} Q T\), and \(T^{-1} P\) are given by
and thus \({{\tilde{Q}}} = 28.3917\), \({{\tilde{P}}} = [-305.9704, 339.9671]\).
The feedforward control \(u_\mathrm{ff}\) is obtained from solving the boundary value problem described in Sect. 4, based on the inverse model in the DAE formulation (35). In order to apply the simplified boundary conditions (36) to this example, \(n^0+n^f=2n+\ell +p+m=14\) initial or final conditions have to be selected from the equilibrium points at time \(T_0\) and \(T_f\), while the remaining 14 entries in (36) remain as free bounds. There are many possible combinations to select these 14 conditions. Here, in an heuristic way one may choose, e.g.,
where free bounds are denoted by \(\star \). The initial angles \(\alpha _0\) and \(\beta _0\) are given by the geometry of the model as \(\alpha _0=\arccos \left( \frac{L_1^2+d^2-0.25L_2^2}{2L_1\,d}\right) \) and \(\beta _0=\arcsin \left( \frac{2\,L_1\sin (\alpha _0)}{L_2}\right) \). The BVP solution includes a pre-actuation phase before the start of the trajectory at time \(t_0={0}{\hbox {s}}\). However, here only the causal part for \(t\ge t_0\) is considered, such that
where \(u_\mathrm{bvp}\) denotes the solution of the BVP. Note that the clipping of the input signal will also yield small tracking errors, which have to be reduced by the feedback controller. Furthermore, the solution of the BVP does not only yield the feedforward control \(u_\mathrm{ff}\), but also the desired state trajectories \(q_\mathrm{ref},v_\mathrm{ref},\lambda _\mathrm{ref}\), which may be used for reference in a feedback control law.
In the simulations, three controller configurations are compared. The controller C\(_1\) is the combination \(u(t)=u_\mathrm{fb}(t) + u_\mathrm{ff}(t)\) of the feedback and feedforward strategy discussed above. The controller C\(_2\) is pure feedback control \(u(t)=u_\mathrm{fb}(t)\), and the controller C\(_3\) is pure feedforward control \(u(t)=u_\mathrm{ff}(t)\). The simulations over the interval \(0-2\,\mathrm s\) are performed on MATLAB with the solver ode15s (AbsTol and RelTol at default values).
Snapshots of an animation of the simulation with controller C\(_1\) are shown in Fig. 4 for different time instances. The motion of the complete robot is visualized, and the motion of the actuators attached to the moving bases with \(s_1(t)\) and \(s_2(t)\) can be seen. Moreover, the deflection \(\gamma (t)\) of the third, passive arm is visible at time \(t=0.4\;\text {s}\).
Figure 5 shows the associated states \(s_1(t)\), \(s_2(t)\), \(\alpha (t)\), \(\beta (t)\) and \(\gamma (t)\) during the motion, applying the combined controller \(\mathrm C_1\). The oscillation of the third, passive body due to the motion is visible as an oscillation of \(\gamma (t)\). This motion cannot be actuated directly and is therefore responsible for the involved controller design.
Figure 6 shows the end-effector position in the two-dimensional space under all three controller configurations C\(_1\)–C\(_3\). While at the beginning a good tracking is achieved, the pure feedforward controller C\(_3\) does not reach the desired final position at \((e_1,e_2)=(0.9,-0.9)\;\text {m}\). While both controllers C\(_1\) and C\(_2\) reach the correct desired final position, the controller C\(_1\) shows smaller tracking errors over the course of the trajectory. The tracking errors are evaluated in the following.
Figure 7(a) shows the errors between the original output y and the reference signal \(y_\mathrm{ref}\) and Fig. 7(b) the errors in end-effector coordinates \(\Vert r_\mathrm{app} - r_\mathrm{ref} \Vert \) under the controllers \(\mathrm C_1, C_2\) and C\(_3\), resp. The pure feedforward controller C\(_3\) cannot compensate the increasing tracking errors due to the mass \(m_3\), which is larger in the simulated model compared to the reference model used for controller design. In contrast, both controllers C\(_1\) and C\(_2\), which include a feedback channel, reduce the tracking error after an initial growth period. Applying the combined controller \(\mathrm C_1\) results in the smallest tracking error at the end time \(t_f = 2\,\mathrm s\). Moreover, the cumulative error of the controller C\(_1\) is considerably smaller compared to the controller C\(_2\). The controller C\(_1\) reduces the cumulative error of C\(_2\) by 40% and 50%, resp., for the coordinates of y and \(r_\mathrm{app}\).
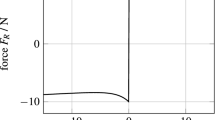
In Fig. 8, the input functions \(u_1\) and \(u_2\) are depicted. The controller C\(_3\) shows the smooth feedforward control signal from model inversion of the reference model. The funnel controller C\(_2\) varies strongly, especially in the first component \(u_1\). These large derivatives result in large accelerations of the physical system and should be avoided in order to reduce the loads on the mechanical parts. This can be achieved by the controller C\(_1\). Since it includes the smooth feedforward signal, which roughly moves the system on the desired path, the work load of the funnel feedback controller is reduced and the peaks and strong variations of the input signal can be completely avoided here. The input signals of C\(_1\) are smooth and therefore reduce the loads on the mechanical parts of the system.
In Fig. 9, the error norm \(\Vert \bar{e}(\cdot )\Vert \) and the funnel boundary \(\varphi (\cdot )^{-1}\) under the controllers \(\mathrm C_1\) and \(\mathrm C_2\) are depicted. In both controller configurations, the error lies within the funnel boundary. However, in the scenario \(\mathrm C_2\) when only the feedback controller is applied, the error is closer to the funnel boundary which results in a larger input, cf. Figure 8.
7 Summary and conclusion
In the present work, we successfully combined a feedforward control strategy based on servo-constraints with a novel high-gain feedback controller design in order to achieve output tracking for a multibody system with kinematic loop and unstable internal dynamics. First, we introduced auxiliary inputs and outputs in order to avoid the DAE formulation and decouple the internal dynamics. Then, we derived a feasible set of coordinates for the internal dynamics which allows a decoupling in terms of the original system parameters and avoids an explicit calculation of the Byrnes–Isidori form. In order to apply the recent result from [9] on funnel control of linear non-minimum phase systems, we considered a linearization of the internal dynamics of the multibody system. Furthermore, a system inversion based on servo-constraints is applied as a feedforward control. Due to the unstable internal dynamics, this includes solving a boundary value problem beforehand.
As a proof of concept, we applied the combination of both control strategies to a nonlinear multi-input, multi-output multibody system with unstable internal dynamics in a simulation and compared the results. We found the combination of both controllers to have the best tracking performance in terms of the error between the system output and the reference signal. Moreover, the combination reduces peaks and strong variations in the input signal compared to the pure feedback strategy. The results motivate further research on the combination of open-loop and closed-loop control strategies for non-minimum phase systems.
References
Altmann, R., Betsch, P., Yang, Y.: Index reduction by minimal extension for the inverse dynamics simulation of cranes. Multibody Sys. Dyn. 36(3), 295–321 (2016)
Altmann, R., Heiland, J.: Simulation of multibody systems with servo constraints through optimal control. Multibody Sys. Dyn. 40(1), 75–98 (2017)
Ascher, U., Mattheij, R., Russell, R.: Numerical Solution of Boundary Value Problems for Ordinary Differential Equations. Society for Industrial and Applied Mathematics (1995)
Bastos, G., Seifried, R., Brüls, O.: Inverse dynamics of serial and parallel underactuated multibody systems using a DAE optimal control approach. Multibody Syst. Dyn. 30(3), 359–376 (2013)
Bechlioulis, C.P., Rovithakis, G.A.: A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems. Automatica 50, 1217–1226 (2014)
Bencsik, L., Kovács, L.L., Zelei, A.: Stabilization of internal dynamics of underactuated systems by periodic servo-constraints. Int. J. Struct. Stabil. Dyn. 17(05), 1740004 (2017)
Berger, T.: On differential-algebraic control systems. Ph.D. thesis, Institut für Mathematik, Technische Universität Ilmenau, Universitätsverlag Ilmenau, Germany (2014)
Berger, T.: The zero dynamics form for nonlinear differential-algebraic systems. IEEE Trans. Autom. Control 62(8), 4131–4137 (2017)
Berger, T.: Tracking with prescribed performance for linear non-minimum phase systems. Automatica 115, 108909 (2020)
Berger, T., Haller, F.E.: On an extension of a global implicit function theorem (2020). Submitted for publication, preprint available at arXiv:2004.04427
Berger, T., Lanza, L.: Output tracking for a non-minimum phase robotic manipulator (2020). To appear in Proc. MTNS 2020. Preprint available at arXiv:2001.07535
Berger, T., Lê, H.H., Reis, T.: Funnel control for nonlinear systems with known strict relative degree. Automatica 87, 345–357 (2018)
Berger, T., Lê, H.H., Reis, T.: Vector relative degree and funnel control for differential-algebraic systems. In: S. Grundel, T. Reis, S. Schöps (eds.) Progress in Differential-Algebraic Equations II, Differential-Algebraic Equations Forum. Springer-Verlag, Berlin-Heidelberg (2020). To appear. Preprint available at arXiv:2001.05391
Berger, T., Otto, S., Reis, T., Seifried, R.: Combined open-loop and funnel control for underactuated multibody systems. Nonlinear Dyn. 95, 1977–1998 (2019)
Berger, T., Rauert, A.L.: A universal model-free and safe adaptive cruise control mechanism. In: Proceedings of the MTNS 2018, pp. 925–932. Hong Kong (2018)
Berger, T., Rauert, A.L.: Funnel cruise control. Automatica 119, 109061 (2020)
Berger, T., Reis, T.: Zero dynamics and funnel control for linear electrical circuits. J. Franklin Inst. 351(11), 5099–5132 (2014)
Betsch, P., Altmann, R., Yang, Y.: Numerical integration of underactuated mechanical systems subjected to mixed holonomic and servo constraints. In: Font-Llagunes, J.M. (ed.) Multibody Dynam., Comput. Method. Appl. Sci., vol. 42, pp. 1–18. Springer-Verlag, Cham (2016)
Betsch, P., Quasem, M., Uhlar, S.: Numerical integration of discrete mechanical systems with mixed holonomic and control constraints. J. Mech. Sci. Tech. 23(4), 1012–1018 (2009)
Blajer, W.: Index of differential-algebraic equations governing the dynamics of constrained mechanical systems. Appl. Math. Mod. 16(2), 70–77 (1992)
Blajer, W., Kołodziejczyk, K.: A geometric approach to solving problems of control constraints: Theory and a DAE framework. Multibody Sys. Dyn. 11(4), 343–364 (2004)
Blajer, W., Kołodziejczyk, K.: Improved DAE formulation for inverse dynamics simulation of cranes. Multibody Sys. Dyn. 25(2), 131–143 (2011)
Brenan, K.E., Campbell, S.L., Petzold, L.R.: Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations. North-Holland, Amsterdam (1989)
Brüls, O., Bastos, G.J., Seifried, R.: A stable inversion method for feedforward control of constrained flexible multibody systems. J. Comput. Nonlinear Dyn. 9(1), 011,014–011,014–9 (2013)
Burkhardt, M., Seifried, R., Eberhard, P.: Experimental studies of control concepts for a parallel manipulator with flexible links. J. Mech. Sci. Technol. 29(7), 2685–2691 (2015)
Campbell, S.L.: High-index differential algebraic equations. Mech. Struct. Mach. 23(2), 199–222 (1995)
Chen, D., Paden, B.: Stable inversion of nonlinear non-minimum phase systems. Int. J. Control 64(1), 81–97 (1996)
Dai, S.-L., He, S., Lin, H., Wang, C.: Platoon formation control with prescribed performance guarantees for USVs. IEEE Trans. Ind. Electron. 65(5), 4237–4246 (2018)
Devasia, S.: Approximated stable inversion for nonlinear systems with nonhyperbolic internal dynamics. IEEE Trans. Autom. Control 44(7), 1419–1425 (1999)
Devasia, S., Chen, D., Paden, B.: Nonlinear inversion-based output tracking. IEEE Trans. Autom. Control 41(7), 930–942 (1996)
Drücker, S., Seifried, R.: Stable inversion for flexible multibody systems using the ANCF. submitted to Proceedings in Applied Mathematics and Mechanics 2020 (2020)
Fliess, M., Levine, J., Martin, P., Rouchon, P.: Flatness and defect of non-linear-systems: introductory theory and examples. Int. J. Control 61, 1327–1361 (1995)
Francis, B.A.: The linear multivariable regulator problem. SIAM J. Control Optim. 15, 486–505 (1977)
Fumagalli, A., Masarati, P., Morandini, M., Mantegazza, P.: Control constraint realization for multibody systems. J. Comput. Nonlinear Dyn. 6(1), 011,002–011,002–8 (2010)
Gear, C.W.: Differential-algebraic equation index transformations. SIAM J. Sci. Stat. Comput. 9, 39–47 (1988)
Hackl, C.M.: Non-identifier Based Adaptive Control in Mechatronics-Theory and Application. Lecture Notes in Control and Information Sciences. Springer-Verlag, Switzerland (2017)
Hairer, E., Wanner, G.: Solving ordinary differential equations II: Stiff and differential-algebraic problems, Springer Series in Computational Mathematics, 2nd edn. Springer-Verlag, Berlin (1996)
Ilchmann, A., Reis, T. (eds.): Surveys in Differential-Algebraic Equations I–IV. Differential-Algebraic Equations Forum. Springer-Verlag, Berlin (2013–2019)
Ilchmann, A., Ryan, E.P., Sangwin, C.J.: Tracking with prescribed transient behaviour. ESAIM Control, Optimisation and Calculus of Variations 7, 471–493 (2002)
Ilchmann, A., Trenn, S.: Input constrained funnel control with applications to chemical reactor models. Syst. Control Lett. 53(5), 361–375 (2004)
Isidori, A.: Nonlinear Control Systems, 3rd edn. Communications and Control Engineering Series. Springer-Verlag, Berlin (1995)
Jin, X.: Adaptive fixed-time control for MIMO nonlinear systems with asymmetric output constraints using universal barrier functions. IEEE Trans. Autom. Control 64(7), 3046–3053 (2019)
Kunkel, P., Mehrmann, V.: Differential-Algebraic Equations. Analysis and Numerical Solution. EMS Publishing House, Zürich, Switzerland (2006)
Morlock, M., Meyer, N., Pick, M.A., Seifried, R.: Modeling and trajectory tracking control of a new parallel flexible link robot. IEEE International Conference on Intelligent Robots and Systems pp. 6484–6489 (2018)
Morlock, M., Meyer, N., Pick, M.A., Seifried, R.: Real-time trajectory tracking control of a parallel robot with flexible links. Mechan. Mach. Theor. 158, 104220 (2021)
Otto, S., Seifried, R.: Open-loop control of underactuated mechanical systems using servo-constraints: Analysis and some examples. In: Campbell, S., Ilchmann, A., Mehrmann, V., Reis, T. (eds.) Applications of Differential-Algebraic Equations: Examples and Benchmarks, Differential-Algebraic Equations Forum, pp. 81–122. Springer-Verlag, Cham (2018)
Otto, S., Seifried, R.: Real-time trajectory control of an overhead crane using servo-constraints. Multibody Sys. Dyn. 42(1), 1–17 (2018)
Pomprapa, A., Weyer, S., Leonhardt, S., Walter, M., Misgeld, B.: Periodic funnel-based control for peak inspiratory pressure. In: Proc. 54th IEEE Conf. Decis. Control, Osaka, Japan, pp. 5617–5622 (2015)
Seifried, R.: Dynamics of Underactuated Multibody Systems. Modeling, Control and Optimal Design. No. 205 in Solid Mechanics and Its Applications. Springer-Verlag (2014)
Senfelds, A., Paugurs, A.: Electrical drive DC link power flow control with adaptive approach. In: Proc. 55th Int. Sci. Conf. Power Electr. Engg. Riga Techn. Univ., Riga, Latvia, pp. 30–33 (2014)
Shampine, L.F., Gladwell, I., Thompson, S.: Solving ODEs with MATLAB. Cambridge University Press, Cambridge (2003). http://www.runet.edu/~thompson/webddes/
Simeon, B.: Computational Flexible Multibody Dynamics. Differential-Algebraic Equations Forum. Springer-Verlag, Heidelberg-Berlin (2013)
Skogestad, S., Postlethwaite, I.: Multivariable Feedback Control: Analysis and Design, 2nd edn. John Wiley and Sons Inc., Chichester (2005)
Sontag, E.D.: Mathematical Control Theory: Deterministic Finite Dimensional Systems, 2nd edn. Springer-Verlag, New York (1998)
Tee, K.P., Ren, B., Ge, S.S.: Control of nonlinear systems with time-varying output constraints. Automatica 47, 2511–2516 (2011)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Disclosure of potential conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the German Research Foundation (Deutsche Forschungsgemeinschaft) via the grants BE 6263/1-1 and SE 1685/6-1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Berger, T., Drücker, S., Lanza, L. et al. Tracking control for underactuated non-minimum phase multibody systems. Nonlinear Dyn 104, 3671–3699 (2021). https://doi.org/10.1007/s11071-021-06458-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06458-4