Skip to main content
SpringerLink
Log in

The stability analysis of a two-spool rotor system undergoing rub-impact

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

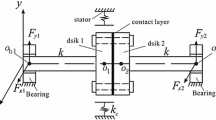
The main objective of the present paper is to determine the influence of rub parameters on the stability of a two-spool rotor system undergoing rub-impact. The parameters such as rotor–stator contact stiffness, coefficient of friction and clearance are varied for understanding their effects on the system response and stability. Moreover, the analysis is performed for two modes of rotor operations, namely co-rotation and counter-rotation, and determines their impacts on rotor–stator rubbing. A time variational method is employed to predict the nonlinear response of the system with a perturbation function applied at the steady-state solution points to investigate their stability. Two types of bifurcations, namely limit point and Neimark–Sacker bifurcations, are observed in the response by monitoring the Floquet exponents of the perturbed system. As the coefficient of friction is increased, the early onset of NS bifurcation has happened and the system enters into the quasi-periodic regime early. However, when the contact stiffness and clearance values are increased, the onset of NS bifurcation is delayed. It is also observed that the response characteristics of the co- and counter-rotating systems are entirely different. The separation between forward and backward whirling frequencies is reduced for the counter-rotating system due to the cancellation of gyroscopic moments. In addition, for the same set of parameters, the counter-rotating system enters into the quasi-periodic regime quickly once the disk starts rubbing.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32

Similar content being viewed by others

References

  1. Prabith, K., Krishna, I.P.: The numerical modeling of rotor-stator rubbing in rotating machinery: a comprehensive review. Nonlinear Dyn. 101, 1317–1363 (2020)

    Article  Google Scholar 

  2. Yang, Y., Cao, D., Yu, T., Wang, D., Li, C.: Prediction of dynamic characteristics of a dual-rotor system with fixed point rubbing-theoretical analysis and experimental study. Int. J. Mech. Sci. 115, 253–261 (2016)

    Article  Google Scholar 

  3. Wang, N., Jiang, D., Behdinan, K.: Vibration response analysis of rubbing faults on a dual-rotor bearing system. Arch. Appl. Mech. 87(11), 1891–1907 (2017)

    Article  Google Scholar 

  4. Yang, Y., Cao, D., Wang, D., Jiang, G.: Response analysis of a dual-disc rotor system with multi-unbalances-multi-fixed-point rubbing faults. Nonlinear Dyn. 87(1), 109–125 (2017)

    Article  Google Scholar 

  5. Yang, Y., Cao, D., Wang, D., Jiang, G.: Fixed-point rubbing characteristic analysis of a dual-rotor system based on the Lankarani–Nikravesh model. Mech. Mach. Theory 103, 202–221 (2016)

    Article  Google Scholar 

  6. Lankarani, H.M., Nikravesh, P.E.: A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 112(3), 369–376 (1990)

    Article  Google Scholar 

  7. Lu, Z., Zhong, S., Chen, H., Wang, X., Han, J., Wang, C.: Nonlinear response analysis for a dual-rotor system supported by ball bearing. Int. J. Non-Linear Mech. 128, 103–627 (2021)

    Article  Google Scholar 

  8. Gao, T., Cao, S., Zhang, T.: Theoretical and experimental study on the transient time-frequency characteristics of the bending-torsional coupling motions of a rub-impact dual-rotor system. Shock Vib. 2021, 8817228.1–17 (2021)

  9. Wang, N., Liu, C., Jiang, D., Behdinan, K.: Casing vibration response prediction of dual-rotor-blade-casing system with blade-casing rubbing. Mech. Syst. Signal Process. 118, 61–77 (2019)

    Article  Google Scholar 

  10. Yang, Y., Ouyang, H., Yang, Y., Cao, D., Wang, K.: Vibration analysis of a dual-rotor-bearing-double casing system with pedestal looseness and multi-stage turbine blade-casing rub. Mech. Syst. Signal Process. 143, 106–845 (2020)

    Article  Google Scholar 

  11. Sun, C., Chen, Y., Hou, L.: Steady-state response characteristics of a dual-rotor system induced by rub-impact. Nonlinear Dyn. 86(1), 91–105 (2016)

    Article  Google Scholar 

  12. Hou, L., Chen, Y., Fu, Y., Chen, H., Lu, Z., Liu, Z.: Application of the HB-AFT method to the primary resonance analysis of a dual-rotor system. Nonlinear Dyn. 88(4), 2531–2551 (2017)

    Article  Google Scholar 

  13. Hou, L., Chen, H., Chen, Y., Lu, K., Liu, Z.: Bifurcation and stability analysis of a nonlinear rotor system subjected to constant excitation and rub-impact. Mech. Syst. Signal Process. 125, 65–78 (2019)

    Article  Google Scholar 

  14. Sun, C., Chen, Y., Hou, L.: Nonlinear dynamical behaviors of a complicated dual-rotor aero-engine with rub-impact. Arch. Appl. Mech. 88(8), 1305–1324 (2018)

    Article  Google Scholar 

  15. Guskov, M., Thouverez, F.: Harmonic balance-based approach for quasi-periodic motions and stability analysis. J. Vib. Acoust. 134(3), 031 003.1-11 (2012)

    Article  Google Scholar 

  16. Rook, T.: An alternate method to the alternating time-frequency method. Nonlinear Dyn. 27(4), 327–339 (2002)

    Article  MathSciNet  Google Scholar 

  17. Krishna, I.P., Padmanabhan, C.: Improved reduced order solution techniques for nonlinear systems with localized nonlinearities. Nonlinear Dyn. 63(4), 561–586 (2011)

    Article  MathSciNet  Google Scholar 

  18. Praveen Krishna, I., Padmanabhan, C.: Experimental and numerical investigations on rotor-stator rub. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 232(18), 3200–3212 (2018)

    Article  Google Scholar 

  19. Prabith, K., Krishna, I.: A time variational method for the approximate solution of nonlinear systems undergoing multiple-frequency excitations. J. Comput. Nonlinear Dyn. 15(3), 031 006.1-11 (2020)

    Google Scholar 

  20. Wang, F., Luo, G.H., Yan, S., Cui, H.T.: A comparison study on co-and counterrotating dual-rotor system with squeeze film dampers and intermediate bearing. Shock Vib. 2017, 5493763.1–25 (2017)

  21. Ma, X., Ma, H., Zeng, J., Piao, Y.: Rubbing-induced vibration response analysis of dual-rotor-casing system. Trans. Nanjing Univ. Aeronaut. Astronaut. 35(1), 101–108 (2018)

    Google Scholar 

  22. Fei, Zx, Tong, Sg, Wei, C.: Investigation of the dynamic characteristics of a dual rotor system and its start-up simulation based on finite element method. Jo. Zhejiang Univ. Sci. A 14(4), 268–280 (2013)

    Article  Google Scholar 

  23. Friswell, M.I., Penny, J.E., Garvey, S.D., Lees, A.W.: Dynamics of Rotating Machines, 1st edn. Cambridge University Press, New York (2010)

    Book  Google Scholar 

  24. Detroux, T., Renson, L., Masset, L., Kerschen, G.: The harmonic balance method for bifurcation analysis of large-scale nonlinear mechanical systems. Comput. Methods Appl. Mech. Eng. 296, 18–38 (2015)

    Article  MathSciNet  Google Scholar 

  25. Xie, L., Baguet, S., Prabel, B., Dufour, R.: Bifurcation tracking by harmonic balance method for performance tuning of nonlinear dynamical systems. Mech. Syst. Signal Process. 88, 445–461 (2017)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering, Indian Institute of Space Science and Technology, Thiruvananthapuram, 695547, India

    K. Prabith & I. R. Praveen Krishna

Authors
  1. K. Prabith
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. R. Praveen Krishna
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. R. Praveen Krishna.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Prabith, K., Krishna, I.R.P. The stability analysis of a two-spool rotor system undergoing rub-impact. Nonlinear Dyn 104, 941–969 (2021). https://doi.org/10.1007/s11071-021-06370-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-06370-x

Keywords

Search

Navigation