Stability analysis of whirl flutter in rotor-nacelle systems with freeplay nonlinearity

Abstract

Tiltrotor aircraft are growing in prevalence due to the usefulness of their unique flight envelope. However, aeroelastic stability—particularly whirl flutter stability—is a major design influence that demands accurate prediction. Several nonlinearities that may be present in tiltrotor systems, such as freeplay, are often neglected for simplicity, either in the modelling or the stability analysis. However, the effects of such nonlinearities can be significant, sometimes even invalidating the stability predictions from linear analysis methods. Freeplay is a nonlinearity that may arise in tiltrotor nacelle rotation actuators due to the tension–compression loading cycles they undergo. This paper investigates the effect of a freeplay structural nonlinearity in the nacelle pitch degree of freedom. Two rotor-nacelle models of contrasting complexity are studied: one represents classical whirl flutter (propellers) and the other captures the main effects of tiltrotor aeroelasticity (proprotors). The manifestation of the freeplay in the systems’ dynamical behaviour is mapped out using Continuation and Bifurcation Methods, and consequently the change in the stability boundary is quantified. Furthermore, the effects on freeplay behaviour of (a) model complexity and (b) deadband edge sharpness are studied. Ultimately, the freeplay nonlinearity is shown to have a complex effect on the dynamics of both systems, even creating the possibility of whirl flutter in parameter ranges that linear analysis methods predict to be stable. While the size of this additional whirl flutter region is finite and bounded for the basic model, it is unbounded for the higher complexity model.

1 Introduction

Tiltrotor aircraft such as the XV-15 shown in Fig. 1 aim to combine the speed and range of turboprop aircraft with the VTOL capabilities of helicopters. This relatively large flight envelope makes them highly versatile and consequently they are attractive to both civil and military operators. It is in increasing their maximum cruising speed that the aeroelastic instability known as whirl flutter is encountered.

Fig. 1

XV-15 tiltrotor aircraft [1]

Whirl flutter affects propellers or rotors mounted on flexible structures. It is caused by the interaction of the wing’s elasticity, gyroscopic moments acting on the rotor as a whole and aerodynamic forces and moments acting on the rotor disc. Motion-dependent in-plane forces are the most significant contributor to the instability [2]. The physical origin is typically the coupling between the wing torsional motion and rotor in-plane forces [3]. Additionally, these in-plane forces may destabilise the whole aircraft’s short period flight modes [4]. From the designer’s perspective, an aircraft’s whirl flutter stability is a function of its various physical properties, such as the damping and stiffness of various structural components or the placement of wing modal frequencies relative to one another. However, from a pilot’s perspective, it is encountered at or beyond a certain onset speed, when the damping ratio of one or more whirl flutter modes becomes negative.

In its canonical form, the instability is usually referred to as “propeller whirl flutter” or “classical whirl flutter”. This usage strictly refers to a model of the form first derived in [5]: a basic system with rigid blades and a rigid shaft, all of which is able to pitch and yaw elastically about an effective pivot point. Although turboprop aircraft such as the Electra were the context for the first (classical) whirl flutter studies, the search for feasible high-speed V/STOL concepts had by that time recognised the promise of the tiltrotor configuration, and the aeroelastic properties of tiltrotor-like V/STOL configurations were considered as early as 1963 [6]. However, with slender, highly twisted and flexible blades and heavy engine nacelles mounted upon wingtips to provide clearance of the long blades from the fuselage, tiltrotors are prominently vulnerable to whirl flutter. The dynamics of a tiltrotor system—with flapping blades and a flexible wing—are more complex than the classical model. For instance, the manner in which the precession-generated aerodynamic loads act on the pylon/wing is significantly different [7] to the classical case. The phenomenon limits the performance of tiltrotor aircraft; it either imposes a direct limit on the maximum safe cruise speed, or the increased stiffness (and therefore thickness) of the wings necessary to guarantee aeroelastic stability up to a certain design speed results in reduced aerodynamic efficiency [8].

Several lines of research have been well explored in efforts to delay the onset airspeed of whirl flutter in tiltrotors. Active control has been applied to the proprotor swashplate and to various aerodynamic surfaces, while passive measures such as aeroelastic tailoring or installing winglets constitute design refinements that act against physical drivers of the whirl flutter instability. Furthermore, at the heart of any whirl flutter research lies the matter of accurate prediction, and to this end, dedicated research has been conducted, broadly focusing on closing gaps between the predictions of various tools and their experiment equivalents.

The vast majority of the available literature is limited in its treatment of nonlinearities present in real tiltrotor aircraft. In many cases, available studies restricted the modelling of the structural stiffness to linear approximations, which is contingent on the assumption of small deformations. Where nonlinear structural stiffnesses were used, linear stability analysis methods were ultimately employed once linearization about a nonlinear trim point had been obtained. Park et al. investigated whirl flutter with a nonlinear structural model [9], though the focus of the paper was an overall design optimization framework as opposed to impacts on the whirl flutter predictions made by using nonlinear elements in the model. Additionally, whirl flutter stability analysis in Park’s work was conducted using time-domain methods: a simulation was conducted for each case under examination to see if whirl flutter was encountered. Similarly, an investigation by Janetzke et al. [10] used nonlinear aerodynamic models adapted from aerofoil data, though the structural aspects of the model did not appear to have benefitted from the same approach.

However, nonlinearities of various types can have a significant impact on system behaviour, as has been evident in a number of works. Masarati et al. [11] showed within a tiltrotor context that deformability nonlinearities within the blades can have effects that manifest in the overall system stability. Krueger [12] showed that differences in the dynamic behaviour of a rotor between windmilling and thrust mode can arise from nonlinearities introduced by the influence of the drivetrain such as freeplay and backlash. In general, limit cycle oscillations (LCOs) are necessarily nonlinear phenomena and are commonly observed in practical aeroelastic contexts. Their study in computational works is not possible without consideration of the nonlinearities that give rise to their existence, such as Gandhi and Chopra’s work on an elastomeric lag damper that combats air and ground resonance in a bearingless helicopter main rotor [13], which models the damper as a nonlinear spring in series with a Kelvin chain to permit the prediction of LCOs. The consideration of nonlinearities is therefore key for aeroelastic study.

A prolific source of nonlinearity in tiltrotors is their structure. Their material properties may be non-uniform, and any property anisotropy may also introduce nonlinearity. Other specific sources of structural nonlinearities in a tiltrotor rotor-nacelle system may include the deformability of the rotor blades or joint deadband [11] or the drivetrain [12] as previously mentioned. The gimbal may itself be a source of structural nonlinearity if elastomeric materials are used therein to provide elastic restraint. Structural freeplay—a stiffness nonlinearity where a deadband of highly reduced or zero stiffness exists around an undeformed equilibrium position—may exist at hinges and other mechanical interfaces [14], in addition to backlash and saturation nonlinearities. It is only outside of this deadband region that appreciable structural restoring forces act [15]. A typical impact of freeplay in aerospace systems is to shrink stability envelopes. For example, Lee and Tron [16] demonstrated that the existence of freeplay in a control surface led to a significantly reduced flutter onset speed. This ability of freeplay to prematurely induce flutter in this manner has been long known, after it was described definitively by Woolston [17] in the 1950s. Other aerospace contexts with similarly reduced instability boundaries include landing gear shimmy [14], flutter of wing-mounted stores [18] and freeplay-induced oscillations in helicopter pitch-links [24]. Freeplay is well known to arise gradually in mechanical systems due to ordinary wear, though structural damage may cause freeplay deadbands to appear instantly. Additionally, freeplay oscillations themselves may directly cause the deadband to grow [19]. Exemplified by Breitbach [20], a significant body exists of nonlinear aeroelastic research by a number of authors into basic systems such as pitch-plunge models. Nonlinearity types are categorised and their respective detrimental impacts on stability characteristics are shown in isolation. However, tiltrotor aeroelastic systems have not received such treatment.

In order to fulfil their flight envelope, tiltrotor aircraft employ nacelle tilting actuators. These actuators are able to rotate each nacelle to any point between horizontal and vertical, and hold the nacelle still. The two-stage telescopic ballscrew design that is typically employed [21] undergoes a range of compressive and tensile loads within one operating cycle. Over time, wear of the lug end that attaches to the nacelle may cause the whole assembly to develop a degree of freeplay. The same effect could also be created through wear or damage of the trunnions that allow the actuator to fit into the wing end via split spindle arms. In view of freeplay’s known role in the premature onset of aeroelastic oscillations, its presence in the nacelle pitch of tiltrotors, affecting whirl flutter stability characteristics, is therefore a plausible eventuality worthy of investigation. Furthermore, tiltrotor nacelles with their tilting systems are in some respects counterparts to wing control surfaces with their actuation mechanisms. However, the investigation of freeplay in tiltrotor-nacelle tilting mechanisms has not been found in existing literature.

Regardless of what measures are taken to delay the onset airspeed of whirl flutter, nonlinearities in the system can make linear prediction of this speed inaccurate through the creation of whirl flutter solution branches that can exist in supposedly stable parameter regions. Compared to the aforementioned linear stability analysis methods, continuation and bifurcation methods (CBM) are much better suited to the stability analysis of nonlinear systems due to their output of a complete stability “picture” of the system. However, CBM is still in the process of proliferation within the field of helicopter dynamics and as a result their application has so far been limited to a small number of problems [22], such as flight mechanics, ground resonance and rotor vortex ring state. Their inclusion in rotary wing studies is steadily becoming more prevalent as they are powerful when applied to problems such as the identification of instability scenarios of rotor blades [23]. Continuation methods were used in the AW159/Wildcat Release To Service military certification document to assess the nonlinear dynamic behaviour of the tail rotor [24].

A significant opening still exists for the application of CBM to tiltrotor whirl flutter. Whirl flutter requires analysis methods that respect its intrinsic nonlinearities. However, much of the foregoing literature has either underestimated the role of nonlinearities in whirl flutter in its modelling or prevented the full discovery of their impacts through insufficient stability analyses. Eigen analysis of equilibria ignores the possibility of whirl flutter solutions coexisting with other solutions. Multibody approaches such as Masarati et al. [11] or Krueger [12] do well to model nonlinearities although they rely on time-domain simulations for their stability analyses, which can be costly. Furthermore, the discoverability of whirl flutter solutions is not always guaranteed as the simulation’s initial conditions may be outside of a solution’s basin of attraction if they are selected arbitrarily. Furthermore, if multiple solutions coexist, different initial conditions are required to find each solution. Time marching methods, when applied to high-fidelity multibody formulations, are able to find some solutions, though others—which may be unstable but still of relevance from a design perspective—may only be found by enhanced analytical processes, such as CBM. Some comprehensive analyses also rely on time-domain stability analysis and other methods grounded in linear systems theory, such as eigen analysis (as used by Acree [25]) or the Prony method (also used by Masarati et al. [11]), which extracts modal damping ratios from system time histories. Considering the use of CBM applied to low-order dynamical models, when compared to large, high-fidelity models used by comprehensive solvers, attention is drawn to the trade-off between the different kinds of insight that are available. While comprehensive models may fail to detect some whirl flutter behaviours, as mentioned previously, they will likely allow more accurate prediction of some dynamics due to their more precise and complete representation of the physical phenomena present in the system. While CBM is highly efficient in revealing solution branches, high-fidelity models may well be more suitable for the detailed study of known behaviours. By combining comprehensive analysis strategies operating on high-fidelity models with the CBM analysis laid out in this work, a comprehensive understanding of the stability of tiltrotor dynamical systems may be achieved.

Conversely, dedicated research investigating the aeroelastic impacts of nonlinearities such as freeplay do not have tiltrotor systems as their context. The body of such research, typified by such works as Dowell et al. [26] and Price et al. [27], generally uses simple systems such as pitch-plunge 2D aerofoils that bear no resemblance to tiltrotor systems. However, the works make use of several analysis methods that are highly suitable for the nonlinear results concerned, such as CBM and Poincaré sections. This article shows that applying similar methods to the tiltrotor whirl flutter problem can give powerful insight beyond existing approaches.

The research increment provided by this article is to investigate the effect of a freeplay nonlinearity on the whirl flutter stability characteristics of tiltrotor aeroelastic systems. There are three main research objectives of this investigation: (1) to establish how the presence of freeplay alters the whirl flutter behaviour over a range of design parameters; (2) to assess the effect of system complexity on the freeplay-induced behaviour alterations by considering two models of contrasting complexity; and (3) to investigate the effect of deadband edge sharpness on the predicted behaviour. The alterations to the systems’ dynamical behaviour are found by using CBM to conduct analysis of two rotor-nacelle models. Of the two models considered, the basic model depicts classical whirl flutter, which in the present day pertains to propellers on turboprop aircraft or more propeller-like designs on some future tiltrotor aircraft, while the more advanced gimballed hub model depicts tiltrotor aeroelasticity, which pertains to larger proprotors and includes several distinguishing features over the classical case such as blade and wing flexibility. The models are adopted from existing literature and have each formed the basis of several well-known studies. Their respective equations of motion and parameter values are publicly available and were implemented directly in MATLAB. CBM is selected for obtaining results as it enables comprehensive exploration of a range of nonlinear system steady-state behaviours, while identifying the bifurcations that interlink the branches of various solution types. The authors have previously used CBM to explore the effects of polynomial stiffness nonlinearities on the whirl flutter stability of a basic rotor-nacelle system [28, 29], and a higher complexity gimballed rotor-wing model [30]. In all cases, the effects of the nonlinearities were complex, though a recurring finding was the possibility of flutter behaviour when linear analysis predicted stability. Polynomial stiffness is a smooth nonlinearity that can provide a better representation than linear expressions of stiffness profiles over large deformations. It is, however, completely distinct from freeplay, which is a non-smooth nonlinearity that arises inherently in mechanical interfaces and joints, and is exacerbated by cyclic loading. A preliminary investigation of the effects of freeplay on the aforementioned basic model was presented in [31]. The work constitutes initial exploratory research and motivates a more systematic and structured analysis which is conducted in this work. Crucially, [31] suggested that model complexity was an axis of investigation that could provide an understanding of the effects of freeplay in tiltrotor aeroelastic systems. Although the basic model’s stability boundary was redrawn to take account of the whirl flutter behaviours found by CBM, it is, however, only in this article that both the basic model and the gimballed hub model are analysed, and in greater depth: the newly presented analyses of the gimballed hub model are substantially more comprehensive. Furthermore, the effect of the freeplay on the gimballed hub model’s stability boundary is presented in this work, and a summarising discussion of the implications for tiltrotor design is a further contribution of this paper.

The models are presented and described in Sect. 2. The original formulations as they appear in their respective original literature are given, followed by details of the freeplay adaptation made for this work. Section 3 describes the stability analysis methods used, and these are applied to the linear and nonlinear models as appropriate in Sect. 4. First, the linear versions of each model are treated with linear stability analysis to establish their baseline stability boundaries. CBM is then applied to the linear version of the basic model to illustrate the link between linear/eigen analysis and CBM. Freeplay is then introduced to both models and bifurcation diagrams are generated for a variety of parameter value cases for each. The stability boundaries are revised where possible to summarise the impact of the freeplay nonlinearity.

2 Whirl flutter models

Two models of contrasting complexity were used for the present research. To illustrate the influence of freeplay on classical whirl flutter, a basic 2-DoF model given by Bielawa [32] adapted from an original formulation by Reed [33] was used. For comparison, a more advanced 9-DoF model formulated by Johnson [34] was also used. This model resembles real tiltrotor rotor-nacelle systems more closely and features a gimballed hub, rotor blade dynamics and wing degrees of freedom.

Both models (as originally presented) are linear in nature and can therefore be written in the form

$$ {\mathbf{M}}{\ddot{\mathbf{{X}}}} + {\mathbf{C}}{\dot{\mathbf{{X}}}} + {\mathbf{KX}} = {\mathbf{0}} $$

(1)

where M is the mass matrix, C is the damping matrix, K is the stiffness matrix and X is the vector of generalised displacements. The C and K matrices contain both structural and aerodynamic terms. Additionally, both models received dedicated validation against experimental data in their original literature.

To facilitate computational implementation in MATLAB R2015a [35], the models were written in state space-form, shown in Eqs. (2) and (3):

$$ {\dot{\mathbf{Y}}} = f\left( {{\mathbf{Y}},{\mathbf{p}}} \right),\quad {\mathbf{Y}} \in \Re^{n} ,\;{\mathbf{p}} \in \Re^{m} $$

(2)

$$ {\mathbf{Y}} = \left[ {\begin{array}{*{20}c} {\mathbf{X}} \\ {{\dot{\mathbf{X}}}} \\ \end{array} } \right] $$

(3)

where Y is the state vector, X is the vector of generalised displacements as before and p is the vector of parameters. The generalised displacement vector for each model is provided below in the description of each.

2.1 Basic model

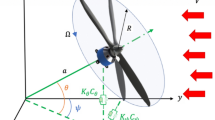
In this model, an N-bladed rotor of radius R and moment of inertia about its rotational axis I_x spins with angular velocity Ω about the end of a shaft of length aR pinned at the origin. It is able to move in pitch θ and yaw ψ about the origin with moment of inertia I_n. The dynamical contributions of the wing structure are modelled with lumped stiffness K and damping C properties in the pitching and yawing directions at the effective pivot point. A schematic of this basic system is shown in Fig. 2.

Fig. 2

Basic whirl flutter model schematic adapted from [33]

The equations of motion governing the system, as given by Bielawa, are stated in Eq. (4).

$$ \left[ {\begin{array}{*{20}c} {I_{n} } & 0 \\ 0 & {I_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{\theta }} \\ {\ddot{\psi }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {C_{\theta } } & { - I_{x} \Omega } \\ {I_{x} \Omega } & {C_{\psi } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{\theta }} \\ {\dot{\psi }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {K_{\theta } } & 0 \\ 0 & {K_{\psi } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \theta \\ \psi \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {M_{\theta } } \\ {M_{\psi } } \\ \end{array} } \right] $$

(4)

M_θ and M_ψ are aerodynamic moments in pitch and yaw, respectively, and are defined in Eqs. (5) and (6). The aerodynamic model may be classed as quasi-steady blade element theory, as developed by Ribner [36] in 1945. More advanced and improved models, such as those used by Kim et al. [37], have been developed, though the low complexity of Ribner’s aerodynamics is suitable for the other components of Bielawa’s model. These equations feature coupling only in stiffness and not in damping, i.e. proportional to angular displacement rather than velocity.

$$ M_{\theta } = \frac{{N_{B} }}{2}K_{a} R\left[ { - \left( {A_{3} + a^{2} A_{1} } \right)\frac{{\dot{\theta }}}{\Omega } - A_{2}^{\prime } \psi + aA_{1}^{\prime } \theta } \right] $$

(5)

$$ M_{\psi } = \frac{{N_{B} }}{2}K_{a} R\left[ { - \left( {A_{3} + a^{2} A_{1} } \right)\frac{{\dot{\psi }}}{\Omega } + A_{2}^{\prime } \theta + aA_{1}^{\prime } \psi } \right] $$

(6)

$$ K_{a} = \frac{1}{2}\rho c_{l,\alpha } R^{4} \Omega^{2} $$

K_a is simply a consolidation of terms for more concise presentation, with ρ denoting air density and c_l,α denoting the blade section lift slope. The A_i terms are aerodynamic integrals that arise from integrating the force expressions along each blade and summing the contributions from each and are defined as:

$$ A_{1} = \frac{c}{R}\int_{0}^{1} {\frac{{\mu^{2} }}{{\sqrt {\mu^{2} + \eta^{2} } }}d\eta } $$

(7)

$$ A_{1}^{\prime } = \mu A_{1} $$

(8)

$$ A_{2}^{\prime } = \frac{c}{R}\int_{0}^{1} {\frac{{\mu^{2} \eta^{2} }}{{\sqrt {\mu^{2} + \eta^{2} } }}d\eta } $$

(9)

$$ A_{3} = \frac{c}{R}\int_{0}^{1} {\frac{{\eta^{4} }}{{\sqrt {\mu^{2} + \eta^{2} } }}d\eta } $$

(10)

$$ \mu = \frac{V}{\Omega R} $$

The A₂ integral (without a hyphen) features only in the original text’s derivation of these expressions [32]; however, the original nomenclature has been retained here. The generalised displacement vector for this basic model is therefore:

$$ {\mathbf{X}} = \left[ {\begin{array}{*{20}c} \theta & \psi \\ \end{array} } \right]^{T} $$

(11)

The parameter values used throughout the investigation were retained where possible from Reed [5] and are listed in Table 1. Where ranges of parameter values were used, the midpoint value was chosen for this investigation. Although these parameters do not represent an actual tiltrotor model, the results achieved from the following analyses are qualitatively relevant for the demonstration of classical whirl flutter principles.

Table 1 Datum parameter values used for the basic model

2.2 Gimballed hub model

In this model, an N-bladed rotor of radius R spins with angular velocity Ω at the end of a shaft of length h. The shaft is attached to the tip of a single cantilever wing of span y_t and chord c_w that is rigidly supported at its root. The motion of the shaft is expressed in terms of the elastic deformation of the wing to whose tip it is connected: beamwise/flapwise bending q₁, chordwise bending q₂ and torsion p. The system schematic is shown in Fig. 3. A modal representation is used for these degrees of freedom, modelling only the first mode of each, as higher-frequency modes tend not to couple with the rotor degrees of freedom. Lumped damping and stiffness properties are associated with each wing degree of freedom. A gimballed hub connects the rotor to the end of the shaft, allowing the rotor disc to pitch and yaw separately from the motion of the wing. The flapping and lead-lag motions of the individual blades are transformed into multi-blade coordinates using Fourier coefficients, which enable the whole system to be viewed from the non-rotating frame of reference. Blade torsion is not modelled as its natural frequency is usually much higher than those of blade flapping or lead-lag. The multi-blade flapping of the blades in the non-rotating frame constitutes the aforementioned gimbal pitch and yaw degrees of freedom, β_1C and β_1S, respectively, while the cyclic lead-lag is modelled as the position of the rotor’s centre of gravity within the hub plane that occurs due to the sum of blade lead-lag motion. This location is specified with two coordinates: one parallel to the global y-axis (ζ_1C) and another parallel to the global x-axis (ζ_1S). The blades are also able to move in a collective sense: as coning β₀ (collective flap) and as rotor speed perturbations ζ₀ (collective lead-lag). Modelling in this way allows autorotation/windmilling to be depicted by relaxing the collective lead-lag elastic restraint. The Fourier coordinate definition allows for any number of rotor modes to be included; however, only the first mode is retained for each degree of freedom here, as higher modes only depict movement of the blades relative to each other and do not couple with the wing dynamics. The blade stiffnesses are modelled implicitly: rather than explicit stiffness values, the natural frequency (per-rev) of each blade motion is instead specified. Soft in-plane and stiff in-plane rotors behave significantly differently, and this representation allows simplified handling of the parameter sets referring to each type. The various blade degrees of freedom are considered to be uncoupled. Also neglected are the aircraft’s rigid body motions, since these typically have low frequency and are not strongly coupled with the wing and rotor motions. Modelling the system in this way—as a cantilever wing with a fixed end—is the configuration that was generally used in wind tunnel testing of proprotor models at the time the model was developed.

Fig. 3

Gimballed hub model schematic adapted from [34]

The aerodynamics of both the blades and the wing are modelled using the same quasi-steady strip theory [36] as in the basic model. The derivation uses integrals along each blade, summed and named according to their origin and the direction of their action. Johnson mentions that proprotor dynamics wind tunnel tests at the time of writing frequently operated the rotor in autorotation and uses it as the first point of reference in his results [34]. The present work uses the data pertaining to the powered condition for the purposes of consistency with the basic model and maintaining relevance to real operation of tiltrotor aircraft.

A simplified matrix equation of motion governing the system is given in [34, Eq. (198)] which omits any terms containing the wing sweep angle and neglects blade structural damping. The full equations of motion, as used in the present work, are obtained by re-deriving the constituent matrices with inclusion of wing sweep and blade damping terms. Though these full equations are too long to write here, they can be written in the compact form given in Eq. (1).

With separate rotor and wing degrees of freedom, this model provides higher modelling fidelity without excessive computational cost. The inclusion of the gimballed hub is key for representing tiltrotor systems and makes it a meaningful counterpart to the Reed model. The generalised displacement vector for this model is

$$ {\mathbf{X}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\beta_{1C} } & {\beta_{1S} } & {\zeta_{1C} } \\ \end{array} } & {\begin{array}{*{20}c} {\zeta_{1S} } & {\beta_{0} } & {\zeta_{0} } \\ \end{array} } & {\begin{array}{*{20}c} {q_{1} } & {q_{2} } & p \\ \end{array} } \\ \end{array} } \right]^{T} $$

(12)

The parameter values used for this model were retained from Johnson [34], and a selection of particularly relevant parameters is listed in Table 2. All dimensionless quantities have been normalised in the same manner as in [34]: rotor quantities with blade inertia I_b and wing quantities with I_b.N/2. Johnson gives the parameter values for a wing and two different full-size rotors: a gimballed stiff in-plane rotor and a hingeless soft in-plane rotor. Those describing the former, a 25-ft Bell rotor related to the XV-15, have been used here.

Table 2 Datum parameter values used for the gimballed hub model

2.3 Freeplay adaptation

In their original literature, both models use linear stiffness for all structural elements, that is, structural deflection and the resulting restoring force or moment are always in the same proportion. Their deflection-force/moment profile therefore has a constant slope, i.e. constant stiffness. To obtain a freeplay stiffness adaptation of each model, the arctangent expression [14] shown in Eq. (13) was implemented. While some freeplay investigations employ a bilinear stiffness profile to achieve “true” freeplay, an arctangent profile was chosen here to avoid gradient discontinuities at the deadband edges as these may cause difficulties for continuation solvers. Furthermore, deadbands in real freeplay systems are unlikely to be truly non-smooth [14].

$$ M = \frac{K}{\pi }\left[ {\left( {\alpha + d} \right)\left( {\frac{\pi }{2} + \tan^{ - 1} \frac{{ - \left( {\alpha + d} \right)}}{\varepsilon }} \right) + \left( {\alpha - d} \right)\left( {\frac{\pi }{2} + \tan^{ - 1} \frac{{\left( {\alpha - d} \right)}}{\varepsilon }} \right)} \right] $$

(13)

For some deflection quantity α that ordinarily has associated with it some linear restoring force or moment M = Kα, there instead exists a deadband of highly reduced M, centred about α = 0 and with width 2d. The tuning parameter ε primarily controls the turning radius of the line at the edges of the deadband. The width (in α) of the transition between the deadband and the rest of the stiffness profile is approximately 2ε; a smaller ε results in sharper edges. Additionally, ε influences the gradient within the deadband, with the gradient approaching zero as ε tends to zero. Outside of this region, the stiffness, hereafter termed “out-of-deadband gradient”, asymptotically approaches the original linear gradient K. Therefore, this smooth arctangent function converges asymptotically on representing “true” freeplay as ε tends to 0, in the sense of having perfectly sharp discontinuous edges and zero in-deadband stiffness. Furthermore, it is more intuitive to consider the ratio ε/d rather than ε by itself. The ratio ε/d more usefully gives an indication of what proportion of the deadband is used up in turning and is therefore of non-negligible gradient.

As zero ε cannot in practice be used due to its presence in the denominator, a non-zero deadband gradient is inevitable, though it can be minimised by using as small a value of ε as possible. As will be shown later, the sensitivity to ε/d of the two models exhibited varies in both nature and severity, and therefore the value chosen in each case requires dedicated discussion. Following consultation of other freeplay studies which are informed by the examination of real-world systems, a value of 0.1° for the deadband half-width d is, though small, deemed to be representative of wear accrued during the service life of an aerospace system [16, 38] and is therefore suitable for use in the present work. While the matrix format of the equations is retained in both models through their adaptation, the arctangent expression is integrated by calculating its value separately and adding the result into the relevant element of the matrix product KX, where K has had the original linear term (K_p) removed so that it does not feature in the multiplication. As the two models’ parameter sets differ by orders of magnitude, example profiles are shown in Fig. 4, with equivalent linear stiffness also included for comparison.

Fig. 4

Example freeplay stiffness profiles as described by Eq. (13), with K = 1, ε = [2, 1, 0.01], d = 2

The objective of this research is to investigate the impact of freeplay at the rotor tilting mechanism, where, as explained earlier, there is a strong case for it to exist. In the basic model, there is only one degree of freedom for nacelle pitch, θ, and therefore the freeplay adaption is applied in place of the associated stiffness. In the gimballed hub model, the wing torsion degree of freedom p has an assumed mode shape for the entire span of the wing, although it is only the resultant rotation in pitch at the tip that the quantity p represents. The wing torsion at any other point on the wing is not used anywhere in the model, for aerodynamic, structural or any other purposes. As the nacelle is mounted and rotated at the tip, any freeplay in the nacelle mechanism manifests within the wing torsion degree of freedom and it is therefore the most suitable part of the model to receive the freeplay adaptation. The original linear models were used as a baseline for comparison with the nonlinear stiffness adaptations.

3 Stability analysis methods

3.1 Linear methods

Initially, eigenvalue analysis was used to assess the stability of the baseline linear version of each model. This well-known method operates on the system’s Jacobian matrix J, which, when the system’s equations of motion are placed in linear state space form, is defined as

$$ {\dot{\mathbf{Y}}} = {\mathbf{JY}} $$

(14)

where Y, the state vector, is defined as in Eq. (3). The eigenvalues of the Jacobian matrix contain information about the decay rate (i.e. stability) and frequency of the system’s modes, and the corresponding right eigenvectors contain the mode shapes. An eigenvector is ordered in the same manner as the state vector, and the relative magnitudes of the eigenvector components and their relative arguments in the complex plane provide the relative amplitudes and relative phasing of each state’s participation in the mode in question. The undamped natural frequency ω and damping ratio ζ for a given mode are calculated using their standard contemporary definitions, as shown in Eqs. (15) and (16), respectively.

$$ \omega = \sqrt {{\text{Re}} \left( \lambda \right)^{2} + {\text{Im}} \left( \lambda \right)^{2} } $$

(15)

$$ \zeta = \frac{{ - {\text{Re}} \left( \lambda \right)}}{\omega } $$

(16)

In the present work, this analysis was written in MATLAB so that a direct interface with the model was possible.

3.2 Nonlinear methods

For nonlinear systems, CBM is used. Continuation is a numerical method that, given a starting solution associated with a particular parameter set, calculates the steady-state solution values of a dynamical system as one or more of its parameters, called the continuation parameter(s), is/are varied [22]. This constructs solution branches or “continues” the set of solutions. There are two kinds of solution found by continuation: fixed points and periodic solutions. At a fixed point (also known as an equilibrium), the system remains still, while periodic solutions—also known as limit cycle oscillations (LCOs)—are closed loops in the phase space that constitute motions that repeat periodically.

For each solution point calculated, its stability is also computed. For fixed points, an eigenvalue analysis of the type described in Sect. 3.1 can be used, requiring local linearization in the case of a nonlinear system. Periodic solutions require Floquet theory to determine stability [39], which views an arbitrary point on an LCO as a fixed point on a plane intersecting the LCO at that point. The stability of solutions determines the system’s behaviour when it is nearby; stable solutions attract the system within some neighbourhood around them, while unstable ones repel.

A bifurcation is a qualitative point change in the system stability or behaviour due to the variation of a parameter. In other words, when the stability of a system changes, or the type (fixed/periodic) or number of solutions changes, the system is said to bifurcate. The points at which these stability changes happen are called bifurcation points, and furthermore the technical definition of a bifurcation is the intersection of two or more solution branches [42]. Bifurcations are identified through characteristic changes in the Jacobian’s eigenvalues or the Floquet multipliers. If the system is nonlinear, new solution branches may emerge from the bifurcation points, leading to the coexistence of multiple solutions for a given set of system parameter values. Where this happens, the system’s behaviour may be dependent on the magnitude of a perturbation: a hallmark phenomenon of nonlinear systems. Additionally, nonlinearities may cause bending of solution branches within the parameter space, which may not be detected by linear analysis. The identification of these different solution branches helps to uncover the global dynamics of the system.

The results of continuation analysis are displayed on bifurcation diagrams, where the solution branches are shown as the continuation parameter value varies. The type (fixed/periodic) of each solution branch, along with the locations of any bifurcations it encounters, is also indicated. The typical form of a bifurcation diagram is a 2D graph with a chosen state on the y-axis and the continuation parameter on the x-axis. A plot of this kind is known as a “projection” or a “plane”, e.g. “θ projection” or “K_θ−θ plane”. As some solution branches may connect with each other at unlikely or even impossible parameter values, it is typical in bifurcation analysis to allow continuations to enter such parameter value ranges, and this practice will prove vital later in the present work. Additionally, CBM does not give much reliable indication of transient behaviour and therefore continuation results are frequently complemented with time simulations, i.e. numerical integration of the equations of motion.

The analysis methods discussed here and in Sect. 3.1 were employed according to the version of the system (linear/nonlinear) in question. Bifurcation diagrams were produced using the Dynamical Systems Toolbox by Coetzee [40], which is a MATLAB framework for an implementation of the AUTO-07P [41] continuation software. While a precise description of the various continuation methods is best left to the substantial body of dedicated literature, it is sufficient here to state that the AUTO-07P software employs the pseudo-arclength method [41]. Rather than taking steps only in the continuation parameter, the pseudo-arclength method moves along the solution curve in the phase space. This method contrasts with natural parameter continuation, where the solution of one point is used as the initial estimate for the next point, and simplicial/piecewise linear continuation, which uses simplexes within the solution-parameter space. The pseudo-arclength method used here is a predictor–corrector method, using the tangent at the last solution found to estimate the next solution point, before using Newton’s method or similar to refine the solution to within specified tolerances [42]. The stability of fixed points is determined through eigen analysis of a linearization about the point in question, while the monodromy matrix is calculated for periodic solutions whose eigenvalues describe the solution’s stability. These eigenvalues are more commonly known as Floquet multipliers. Time simulations were also used to corroborate the predictions of both stability methods using the ode45 solver within MATLAB, which uses an explicit Runge–Kutta (4,5) formula known as the Dormand–Prince pair. Differing magnitudes of the various gimballed hub model datum parameter values, shown in Table 2, mean that it is most convenient to deal with normalized quantities for this model’s results. Therefore, for the remainder of the present work all stiffness parameter values discussed for this model refer to their normalised values without a change in notation.

Two bifurcation types that are prevalent in the following results are Hopf bifurcations and pitchfork bifurcations. A Hopf bifurcation is the birth of a periodic solution branch from a fixed-point branch. The bifurcation manifests mathematically as a pair of complex conjugate eigenvalues crossing the complex plane imaginary axis, and the stability of the fixed point also changes. At a pitchfork bifurcation, two additional fixed-point branches emerge from an existing fixed-point branch which itself changes stability. The mathematical manifestation is the crossing of a single real eigenvalue over the complex plane imaginary axis. For more information on the subject, the reader is referred to [42].

4 Results and discussion

4.1 Linear analysis

The original literature of the two models both contain sufficiently complete presentation of results to allow validation of the present work’s corresponding computational implementations. A good agreement is found with both models, and the most likely source of discrepancies is the process of digitising of the original figures. Shown in Fig. 5 are frequency and damping plots of the basic model’s modes as the rotor angular velocity Ω is swept, compared to the corresponding figure [33], Fig. 6]. The “backward” whirl mode (BW)—where the whirl direction is in the opposite sense to the rotor spin direction—becomes progressively more unstable. The forward whirl mode (FW) is not capable of instability in this model. While the original axis labels are retained from the original figure, the scales shown here are adjusted to conform to the contemporary definitions of modal frequency and damping.

Fig. 5

Variation of modal frequency (top) and damping ratio (bottom) with rotor speed Ω of the implemented basic model (black dots) and results from [34] (solid coloured lines)

A similar comparison is made for the gimballed hub model in Fig. 6. Corresponding to [34], [Fig. 38] in the original work, plots of modal frequency and damping ratio for 7 of the 9 system modes over a sweep of airspeeds from 25 to 600 kts are shown. Johnson’s naming of the modes (as preserved in Fig. 6) closely follows the naming of the degrees of freedom. Johnson’s naming is based both on prominence of participation of the system’s degrees of freedom and on proximity of a mode’s natural frequency to the uncoupled natural frequencies of the system. Also shown on the right side of Fig. 6 are the mode shapes of the two modes that become unstable within the airspeed range considered: the q₁ mode at approximately 500 kts and the q₂ mode at approximately 575 kts.

Fig. 6

Variation of modal frequency (top) and damping ratio (bottom) of the implemented gimballed hub model’s modes as airspeed V is varied (black dots), with results from [34] (solid coloured lines)

It is prudent to establish the basic stability characteristics of the original linear systems prior to the nonlinear analysis. This is achieved most straightforwardly by using the linear analysis methods described in Sect. 3.1 to construct stability boundaries between parameters of interest to the designer. A range of values is considered for each of the parameters, and the resulting area is partitioned according to the stability of the system when configured with the combination of parameter values corresponding to each point. Additionally, the stability boundary will serve as a medium of comparison later in the present work, when assessing the impact of the freeplay nonlinearities introduced.

Baseline linear stability boundaries for the basic model (between pitch and yaw stiffnesses) and the gimballed hub model (between wing torsion and chordwise bending stiffnesses) are shown in Fig. 7. The pitch and yaw stiffnesses (K_θ and K_ψ, respectively) are chosen for the basic model as they are the only two stiffness parameters characterising the nacelle/wing structure. Furthermore, of the parameters present in the model they are likely the most controllable in practice by a designer. For consistency, the equivalent parameters in the gimballed hub model (K_p and K_q2) are chosen for the stability boundary. As previously described, the p degree of freedom in the gimballed hub model (wing torsion) is analogous to the θ degree of freedom (pitch) in the basic model, and the q₂ degree of freedom (wing chordwise bending) is similarly analogous to the ψ degree of freedom (yaw).

Fig. 7

Baseline (linear variant) stability boundaries for the basic model (a) and the gimballed hub model (b)

4.2 Nonlinear analysis of the basic model

Continuation methods are now applied to the linear version of the basic model. The undeformed position of the nacelle at rest (i.e. Y = 0) is intuitively an equilibrium that may be used as the initial solution for continuations. Setting yaw stiffness K_ψ (y-axis in Fig. 7a) to 0.3 N m rad⁻¹ and performing a continuation in K_θ (x-axis) produces the bifurcation diagram in b) of Fig. 8, showing the pitch θ projection. A key to the symbols and line colours used in the bifurcation diagrams in this paper is provided in Table 3. To show the relationship between eigen analysis and CBM, an Argand plot of the system’s eigenvalues over this sweep is shown on the left, with the corresponding damping ratios plotted in the bottom right.

Fig. 8

Stability results for the basic model, linear version, as K_θ is varied for K_ψ = 0.3. Root locus (a), bifurcation diagram, pitch projection, fixed points only (b) and modal damping ratio (c). BP: branch point, HB: Hopf bifurcation

Table 3 Key to symbols and line colours used in bifurcation diagrams herein

The changes in the system’s eigenvalues as K_θ is varied between 0 and 0.5 can be seen on the complex plane (a). Considering this sweep from the perspective of decreasing K_θ, the complex conjugate pair of roots pertaining to the backward whirl mode temporarily dips into the positive real half-plane before meeting on the real axis and diverging from each other, with one root gaining a positive real part. As a positive real part signifies instability, the damping plot (c) shows that the oscillatory instability happens between approximately K_θ = 0.09 and K_θ = 0.28, and the non-oscillatory instability happens below approximately K_θ = 0.03. The crossing of this single non-oscillatory root causes the damping ratio of the root in question to change from 1 to − 1 instantly. In terms of overall system behaviour, the parameter range K_θ = [0.09, 0.28] allows oscillatory behaviour growing to unbounded amplitude, while K_θ < 0.03 will see first-order “blow-up” of the solutions. The bifurcation diagram in b) indicates that these key eigenvalue crossings and their associated changes in system behaviour are detected by CBM as bifurcations. The crossings of the complex conjugate root pair over the imaginary axis are manifested as Hopf bifurcations (hollow squares) at the according K_θ values, and these are labelled HB1 and HB2. In general, Hopf bifurcations constitute the emergence of a periodic solution from an equilibrium branch. The crossing of the single real root manifests as the pitchfork bifurcation (black star). The forward whirl roots do not experience instability at any point in the sweep. The bifurcation diagram also shows that the solution remains at 0° pitch for the whole continuation. Furthermore, if Fig. 8 is compared to Fig. 7, it can be noted that the bifurcations and regions of instability are directly linked to the stability boundary: the locations of the bifurcations in K_θ are the same as the intersections of a horizontal line at K_ψ = 0.3 with the boundary.

The freeplay nonlinearity discussed in Sect. 2.3 may now be introduced. In this variant of the model, the undeformed at-rest position Y = 0 is uniformly unstable within the K_θ domain of analysis, due to the near-zero stiffness at θ = 0° causing a negative level of damping. For non-trivial continuation results, a new, stable equilibrium must be found for the initial solution. Intuitively, the nacelle must lie stably at some pitch angle outside of the deadband, where the structural restoring moment is non-zero and able to oppose the aerodynamic moments that act to push the nacelle further away from the undeflected position. Being deflected in pitch, the nacelle in turn experiences an aerodynamic yaw moment pushing it further away from Y = 0 that must be countered by yaw structural stiffness. Two such non-zero equilibria exist due to the structural symmetry of the system, mirrored in θ and ψ about 0. These new equilibria were found by solving the equations of motion with all time derivatives set to zero. Due to the presence of the arctangent terms, iterative numerical methods were employed.

Using a deadband half-width d of 0.1° (see Sect. 2.3), a continuation in K_θ similar to that shown for the linear system is now performed and is presented in Fig. 9, left side. An ε/d value of 10^–4 was used as it provides suitably sharp deadband edges without causing numerical difficulties for the AUTO solver. The periodic solution branches emanating from the Hopf bifurcations are also shown. The maximum/peak value of the state of interest within the LCO at each continuation parameter value is indicated with a thick line, and the minimum value with a thin line. As the freeplay deadband exists within the projection shown, it is indicated with black dash-dot lines. A phase plane taken at a cut of K_θ = 0.15 is shown on the right of the figure. The maximum and minimum values of the flutter LCOs on the bifurcation diagram can be cross-referenced with the full LCO in the phase plane, along with the positions of the zero and non-zero main branches which are indicated with ‘X’s, magenta to denote their instability.

Fig. 9

Bifurcation diagram of basic model with freeplay in pitch θ for K_ψ = 0.3, d = 0.1°, pitch projection, K_θ as the continuation parameter

The first notable feature of Fig. 9 is that for most of the range of the continuation parameter, three main solution branches exist instead of one as in the linear model. Either side of the uniformly unstable zero main branch (Y = 0), the two new non-zero main equilibria described earlier have appeared as branches either side of the zero main branch. These branches diverge to infinitely large solution values with decreasing K_θ. The divergence to infinity is asymptotic to the K_θ value of the pitchfork bifurcation in the linear system (~ 0.03), indicated on the figure as a dashed vertical line. With increasing K_θ, the non-zero main branches converge asymptotically on the boundaries of the deadband. This occurs as the structural restoring moments require non-zero deflection (beyond the deadband) in order to exist, regardless of the value of K_θ, to which the out-of-deadband stiffness tends. The Hopf bifurcations on the two new branches are the same as those observed in Fig. 8 and are unchanged in their K_θ location, and therefore their labels are retained.

Here, periodic solution branches link HB1 and HB2 together on each non-zero branch. At each K_θ value, an LCO exists: a trajectory within the state space that repeats periodically. Furthermore, these non-trivial solution branches may transcend their mathematical context and can be interpreted in terms of real-world phenomena. Specifically, these periodic solutions constitute the whirl flutter motion that the present work concerns, and they are almost entirely stable (i.e. attracting). Pitch stiffness decreases from the right side of the diagram to the left, so at HB2 the pylon has become loose enough to begin to oscillate, while at HB1 the stiffness has reduced to a level where it is not able to store sufficient potential energy when deflected for flutter motion to be sustained. Where each flutter branch joins HB2 at ~ 0.28, it first overhangs the stable non-zero main branch by a small amount, as shown in the zoomed inset box in the left plot. In plain terms, this means that flutter is possible for a slightly larger range of parameter values than the linear analysis predicts. The phase plane in θ and ψ at K_θ = 0.15 shown on the right side of the figure shows the path in this plane taken by the two LCOs found at this point on the bifurcation diagram.

Before any further analysis is conducted, some validation of the choice to use ε/d = 10^–4 is prudent. The bifurcations HB1 and HB2 define the topology of Fig. 9, and using two-parameter continuation in K_θ and ε/d, the location in K_θ of these bifurcations can be tracked over a range of ε/d values to detect any variation, indicating sensitivity to ε/d. More specifically, it can be said that ε/d = 10^–4 is a suitable choice if the bifurcations do not exhibit a sensitivity to further decreasing ε/d. This two-parameter continuation is shown in Fig. 10. The value of ε/d = 10^–4 as used in Fig. 9 is also indicated. With the exception of a very slight increase in the K_θ location of HB2 at ε/d = 10^–3 (right line, top of figure), the variation in either Hopf bifurcation is imperceptible below the chosen value of 10^–4, and therefore it may be concluded that this ε/d value is sufficient for the purposes of the present work.

Fig. 10

Two-parameter continuation of Hopf bifurcations at K_ψ = 0.3, d = 0.1° within the K_p−ε plane

As stated earlier, CBM does not indicate transient behaviour beyond a measure of stability close to the solution branches, and time simulations may be employed to this end. Figure 11 shows the same bifurcation diagram as in Fig. 9; however, time simulations in the pitch state θ are shown for two selected points. For this and the remaining figures, only the upper half of each figure (i.e. the positive pitch branch) is shown as the system is symmetrical about the origin in all states, and therefore so are any solution branches. Convergence on the stable flutter branch attached to the positive non-zero main branch is shown on the left of the figure (K_θ = 0.15). Divergence away from the unstable zero (equilibrium) main branch and convergence on the stable non-zero main branch is shown on the right (K_θ = 0.4).

Fig. 11

Bifurcation diagram of basic model with freeplay in pitch θ for K_ψ = 0.3, d = 0.1°, pitch projection, K_θ as the continuation parameter. Time simulations are shown in inset plots, with initial conditions indicated by red dots

The foregoing results exist only at K_ψ = 0.3 and further exploration of the K_θ-K_ψ plane is required. As K_ψ is lowered, the Hopf bifurcations HB1 and HB2 move apart from each other (see Fig. 7, left, for reference). Furthermore, the flutter branches grow in amplitude, reaching towards the unstable zero branch. Their eventual collision with the zero branch happens simultaneously due to the symmetry of the system. At this collision point, the two flutter LCOs make contact with each other at the unstable zero branch. The resulting orbit of infinite period that is created links the central fixed point to itself and is known as a homoclinic trajectory [42]. The fusing of orbits to form such a trajectory is known as a homoclinic bifurcation. It occurs below K_ψ = 0.28, when HB1 is no longer present to re-attach the flutter branches (that have emanated from HB2) to the non-zero main branches. A continuation in K_θ with K_ψ now set to 0.2 is shown in Fig. 12, accompanied by a phase plane showing the trajectories before (K_θ = 0.346), at (K_θ = 0.366) and after (K_θ = 0.389) fusing. At K_θ values above the homoclinic collision point (~ 0.366), the homoclinic trajectory opens up into a new LCO of finite period which, near the collision, resembles a bowtie. It is a product of the fusing of the two flutter branches and is of comparatively large amplitude.

Fig. 12

Bifurcation diagram (a) of basic model with freeplay in pitch θ for Kψ = 0.2, d = 0.1°, pitch projection, K_θ as the continuation parameter. Selection of phase planes (b) at the cuts indicated in the inset plot of (a)

As Fig. 12 shows, the “bowtie” LCO branch folds back and forth between K_θ = 0.32 and 0.62 as it increases in amplitude. However, it can also be seen that throughout this parameter range, the non-zero main (equilibrium) branches are stable, and in literature employing linear stability analysis methods it is effectively only equilibrium branches that are considered when determining overall system stability. The linear methods discussed earlier only show the parameter values at which periodic solution branches emanate from fixed point. Any bending of periodic solution branches back into fixed-point-stable regions due to nonlinearities—as has happened here—is not captured by linear theory and therefore goes undetected. Linear stability analysis declares the system to be stable for K_θ > 0.32 based on the location of HB2, though clearly this is not correct. The hazard posed by the “bowtie” LCO branch is therefore threefold: it is largely stable (and therefore attracts), has a comparatively large amplitude and overhangs the non-zero main branches at K_θ values as high as 0.62: well into the supposedly stable region of the stability boundary.

The fact that part of the overhanging bowtie branch is stable means that the system can be attracted to it following a sufficient perturbation. In practice, such a perturbation might be supplied by a gust, or by manoeuvring of the aircraft. Figure 13a shows two time simulations with K_ψ = 0.2, K_θ = 0.55, showing one insufficient perturbation causing the system to join the upper non-zero main equilibrium branch (green line), and a similar but sufficient perturbation causing the system being attracted to the bowtie LCO (blue line). For comparison, a phase plane of the system is shown on the right side, b). Two parts of this LCO branch are present at K_θ = 0.55; in addition to the stable LCO of pitch amplitude ~ 0.3° shown in the time simulation, a smaller unstable LCO with a pitch amplitude of ~ 0.25° is also present, surrounded by the stable LCO.

Fig. 13

Time simulations with K_ψ = 0.2, K_θ = 0.55 (a). Starting from two different initial conditions, the system can join one of the non-zero main branches (green) or join the bowtie LCO (blue). The various solutions nearby are shown in a phase plane (b). (Color figure online)

The existence of the bowtie LCO—specifically created by the presence of the freeplay nonlinearity—is a significant problem. In practical terms, a whirl flutter oscillation is possible in parameter ranges declared safe by linear stability analysis, a commonly used standard prediction tool. Strictly speaking, this new parameter range cannot really be termed “unstable” as the danger lies in attraction to stable solutions, and so “unsafe” is a more suitable term. The extent (in K_θ) of the bowtie LCO’s overhang can be tracked in the K_θ− K_ψ plane to see what range of K_ψ it occurs at. This adds a new “unsafe” region to the stability boundary and is presented in Fig. 14.

Fig. 14

Redrawn stability boundary for the basic model, based on overhang of bowtie LCO

The discontinuity in the boundary of the new unsafe region at approximately K_θ = 0.6 is caused by a rapid distension of one of the features on the bowtie LCO. The overhang extent is mostly defined by the position of the fold seen at K_θ = 0.65, θ = 0.2° in Fig. 12, marked ‘F1′. However, the second fold underneath it marked ‘F2′, at K_θ = 0.41, θ = 0.15°, begins to move rightward with decreasing K_ψ. By K_ψ =  ~ 0.18 , it emerges from underneath the first fold and becomes the furthest-right feature on the bifurcation diagram, defining the extent of the unsafe region.

4.3 Nonlinear analysis of the gimballed hub model

K_q2 = 0.4 (that is, 40% of the datum value used in [34]) is selected as the level on the stability boundary at which to conduct the gimballed hub model’s analysis. The freeplay nonlinearity now exists in the wing torsion degree of freedom p as this represents the pitch of the wingtip and therefore the wingtip. A deadband half-width d of 0.1° was used, as with the basic model. However, reprising ε/d = 10^–4 for the deadband edge sharpness introduces intricate complications into the periodic solution branches that cause great difficulties for the AUTO solver.

An alternate method to obtain a bifurcation diagram for the gimballed hub model is to employ a similar method to the ε/d sensitivity analysis shown in Fig. 10. The strategy is to start with a value of ε that is too large to represent freeplay fairly but is amenable to the application of AUTO, and subsequently sweep ε downwards, noting how the bifurcation diagram changes as the stiffness profile becomes more representative of freeplay. This approach not only allows numerical complexities to be circumvented but also lends further insight into how the freeplay nonlinearity alters the system’s solution branch structure. Figure 15 shows bifurcation diagrams with ε/d set to 0.010, 0.007 and 0.005, continuing in K_p. The boundaries of the deadband are once again indicated with dash-dot lines.

Fig. 15

Bifurcation diagram for gimballed hub model, K_q2 = 0.4, d = 0.1°, ε/d = [0.010, 0.007, 0.005]

Some of the changes seen here caused by the nonlinearity are similar to those in the basic model. For instance, the zero branch becomes unstable, two non-zero equilibrium branches are created, mirrored about the zero (undeflected) branch, and a bowtie LCO is spawned. However, the zero branch is only unstable at K_p values below a Hopf bifurcation, labelled ‘HB0′, which is the source of the bowtie LCO. The bowtie LCO exists over the rest of the domain of analysis and reaches unbounded amplitude as K_p tends to 0. It is stable over its entire extent. The zero branch also has a pitchfork bifurcation, labelled ‘BP’, between K_p = 0 and HB0, from which the two double main branches emanate. When ε/d <  = 0.007, a region of stability exists on both, bounded by a pair of Hopf bifurcations (‘HBR’ and ‘HBL’) that attach a small unstable LCO (i.e. whirl flutter) branch. HBR, BP and HB0 all move rightward as ε/d is lowered, while HBL moves slightly leftward. While Fig. 15 bears several similarities to Fig. 11 and Fig. 12, crucially both the bowtie LCO and the double main branches are attached to the zero main branch, and there is no homoclinic bifurcation connecting the bowtie LCO to the whirl flutter branch from each double main branch. In [31], this bowtie LCO was demonstrated through time simulations though no analysis of any kind was conducted.

With the basic topology of the bifurcation diagram established, further lowering of ε/d is achieved by conducting two-parameter continuations in ε/d and K_p on each of the aforementioned topology-defining bifurcations (HB0, etc.). Their loci in the K_p-ε/d plane as ε/d is lowered down to 0.001 are shown in Fig. 16a. The positions in K_p of the bifurcations can be cross-referenced with the relevant diagrams in Fig. 15. A plot of the stiffness at p = 0 when K_p = 1 is also shown in b).

Fig. 16

Two-parameter continuation of bifurcations found at K_q2 = 0.4, d = 0.1°, within the K_p−ε plane (a), with plot of torsional stiffness at deadband centre (p = 0)

The double main branch Hopf bifurcations HBL and HBR are coincident with each other slightly above ε/d = 0.007 and do not exist above this value. Meanwhile, the distance moved leftward by HBL decreases with each further downward increment of ε/d; however, the rightward movement of HB0, BP and HBR increases. For clarity, a logarithmic scale is used for the K_p axis.

Physically speaking, this runaway occurs due to the flattening of the gradient within the deadband: as the structure becomes softer in-deadband, the out-of-deadband stiffness (K_p in this case) becomes less and less influential as a stabilising influence. Outside the deadband, K_p still controls the amplitude of the bowtie LCO, and at the Hopf bifurcation HB0 it has increased to a level sufficient to prevent oscillatory motion. An interesting effect is the lowering of ε/d causing a stabilisation of a portion of the double main branches. This region is around the deadband edge and at low values of K_p, which flatten the stiffness profile. A sufficient edge sharpness, however, can introduce enough curvature into the profile so as to produce a stable point. The unstable flutter LCOs attached to the Hopfs bounding these portions act as separatrices in the phase space between the basins of attraction of these stable double main branch portions and of the bowtie LCO.

The movement of the bifurcations HBR, BP and HB0 to infinity in K_p as ε/d tends to 0 is intuitive as no amount of out-of-deadband stiffening would be able to stabilise a truly zero-stiffness deadband. The form of the bifurcation diagram for bilinear or “true” freeplay, within a physically reasonable range of analysis, is already provided by that for ε/d = 0.005 shown in Fig. 15 (right). Specifically, the ε/d = 0 diagram would resemble the ε/d = 0.005 diagram for K_p <  ~ 1.2, that is, up to but not including HBR on the double main branches. The diagram therefore comprises two non-zero equilibrium branches which are stable except below HBL, the uniformly unstable zero main branch, all surrounded by the bowtie LCO.

Figure 16 tracks the positions of HBR, BP and HB0 as far as ε/d = 0.001. However, time simulations reveal that, as this value is approached, complex dynamical structures begin to surround the nominal bowtie LCO branch. At first, patches of quasiperiodic behaviour caused by the creation of torus bifurcations emerge at various points on the bowtie branch. Further obfuscation of the torus structures with decreasing ε/d leads to the collapse of some precipitating pockets of chaotic behaviour. Other pockets of chaos in the region may exist due to other onset mechanisms, such as period doubling cascades or intermittency [43, 44]. A subsection of the bifurcation diagram for ε/d = 0.001 is shown in Fig. 17, overlaid with a selection of phase planes showing the various steady-state behaviours present at some points on the bowtie LCO branch. The flutter branch attached to the double main branch shown could not be computed in full due to strong numerical issues prevalent at this value of ε/d (0.001), and it is therefore not shown. Each phase plane shows the wing torsion p and gimbal pitch β_1C coordinates of the various forms of the bowtie LCO. These states are chosen to give simultaneous insight into how the bowtie LCO manifests in both the rotor and the wing, the two macro-components of the system. An ordinary period-1 oscillation is present at K_p = 1.468, while a period-2 variation is at K_p = 0.636 where the trajectory approaches its starting point but completes another similar cycle before closing as a loop. A well-formed torus can be seen at K_p = 0.918 and a chaotic trajectory is found at K_p = 0.646.

Fig. 17

Subsection of bowtie LCO for ε/d = 0.001 within the region of K_p = [0 2.5], pitch projection. The inset windows contain p−β_1C phase planes. The hollow circles indicate Neimark–Sacker (torus) bifurcations

Some torus bifurcations were sufficiently well-defined for AUTO to detect and they are indicated with hollow circles. However, efforts in the present work to create a complete behaviour map of this branch region proved to be impossible due to its fractal nature: no amount of “zooming in” revealed a fundamental structure or resolution for the intervals in which these behaviours exist. Fractal structuring of this kind is a common feature of chaotic regimes [44].

A well-known tool for analysing chaotic behaviour is to use a Poincaré section. This stroboscopic method places a plane in the phase space where the trajectories are known to pass and simulates the system in the time-domain, recording a dot at each point that the system’s state intersects the plane. In this way, some insight into the underlying structure of the chaotic attractor can be gained. Figure 18 shows a Poincaré section defined by p = 0°, monitoring transitions from positive to negative p, for the chaotic trajectory found in Fig. 17. Created by the folding and mixing of the state space [44], the chaotic attractor’s layered structure is clearest in the ζ_1S–ζ₀ plane.

Fig. 18

Poincaré section at p = 0° for chaotic trajectory found at K_p = 0.646 showing values of rotor CG lateral offset ζ_1S and rotor collective lead-lag ζ₀ upon intersecting the section over the period of 5 × 10⁷ rotor revolutions

Although the presence of freeplay creates plenty of overhanging bowtie LCO, it is not possible to redraw the stability boundary for the “true” freeplay case of ε = 0. The position in K_p of HB0 may at first seem like a robust definition of the new boundary: it bounds the extent of the bowtie LCO and its overhang of the double main branches, the zero branch is stable thereafter and its position is in theory always finite and findable for ε > 0. However, as previously discussed, for ε = 0 it lies at infinity and therefore the overhang is unbounded in K_p. Attracting solution structures of various kinds (i.e. periodic, quasiperiodic and chaotic) are therefore predicted to exist on the bowtie branch at all values of K_p, constituting a risk of whirl flutter without the possibility of restabilising using K_q2 or any other parameter. The runaway effect of HB0 and the correspondingly growing “unsafe” region on the stability boundary is shown in Fig. 19. The K_p values of the three boundaries at the level K_q2 = 0.4 can be cross-referenced with Fig. 16.

Fig. 19

Redrawn stability boundaries for gimballed hub model, based on overhang of bowtie LCO for ε/d = [0.010, 0.009, 0.008]. The original linear boundary is shaded grey

Even if a real-world system’s deadband has appreciable edge smoothness, the associated HB0 is most likely to exist at a value of K_p so extreme that it is not physically realisable, if it even exists at all. For instance, at ε/d = 0.001 it exists at K_p = 1856; recalling that K_p has been normalised by its datum value, the wing structure would need to be stiffened by a factor of at least 1856 in order to obviate the possibility of whirl flutter of any of the kinds shown in Fig. 17. In practical terms, no safe region is predicted to exist, and therefore some responsibilities exist surrounding preventative measures. The designer must ensure that the structure has sufficient strength and stiffness for the tiltrotor to fulfil its required performance envelope. If possible, it must also be resistant to the fatigue-induced stresses of the components that may undergo very small whirl flutter LCOs in the course of ordinary operation. As the amplitude of these small whirl flutter oscillations is not reduced meaningfully by increasing the out-of-deadband gradient K_p to large values, a design optimum may be reached by a structure that fulfils its required performance envelope but is not excessively strong (and therefore needlessly heavy). From an operational perspective, a preventative approach may be adopted, involving periodic monitoring of the deadband width and conducting component replacement as appropriate when the deadband width reaches some critical value. The selection of this critical value could be based on the growth rate of the deadband as a function of its width and would benefit from practical investigation via experimental testing. As mentioned previously, freeplay oscillations induce their own deadband to widen through cyclic wear, and such monitoring would prevent whirl flutter oscillations reaching a size that could lead to structural failure. Preloading of the tilting mechanism could also be employed, to reduce the effects of the deadband’s presence.

5 Summary

This article demonstrated the use of continuation and bifurcation methods to provide nonlinear dynamic analysis of whirl flutter in two rotor-nacelle system models of contrasting complexity. Both linear and freeplay nonlinearity stiffness profiles were used for the nacelle pitch degree of freedom in both models. The freeplay expression used arctangent terms to create a smooth-edged deadband in an otherwise quasi-linear profile that via its tuning parameter can approximate a sharp-edged profile. Appropriate stability analysis methods were described and employed for both the linear and nonlinear models. Bifurcation diagrams were generated for a number of pitch stiffness cases for both models.

The primary impact of the freeplay’s presence, for both models, is to create new whirl flutter behaviours in parametric regions that are predicted to be stable by linear analysis methods applied to the main equilibrium branches. Specifically, the linear stability methods are not able to predict these new whirl flutter behaviours, as the nonlinear model variants appear linear to them. The zero branch present in the linear version of both models becomes unstable, and two non-zero equilibrium branches are created, mirrored about the zero (undeflected) branch, just outside of the freeplay deadband. In both models, a large, mostly attracting LCO that was termed “the bowtie LCO” was created which, through overhanging of the non-zero equilibrium branches, existed over large parametric regions that the linear analysis claimed to be stable. Regions overhung in this manner were termed “unsafe” on account of the possibility of the system experiencing whirl flutter following a gust or other perturbation.

Regarding the differences caused by the model complexity, the extent of the overhang was finite in the basic model but unbounded in the gimballed hub model. Furthermore, the bowtie LCO in each case was created by different mechanisms. In the basic model, it was created through a homoclinic collision between the individual flutter branches connected to each of the non-zero equilibrium branches, while in the gimballed hub model it originates from a Hopf bifurcation on the zero main branch, located at high stiffness values. Furthermore, the complexity of the two models’ results scales with the complexity of the models themselves. The gimballed hub model’s results feature quasiperiodicity and chaotic behaviour, which were not observed in the basic model. Increasing the sharpness of the deadband edges (via the tuning parameter ε) caused the gimballed hub model’s dynamical behaviours to complicate, spawning quasiperiodic and chaotic regions, while such an effect was not observed in the basic model.

6 Conclusions

Regarding the ramifications of this work for real-world systems, the large oscillation amplitudes of the LCO or the other attracting structures in the system (torus/chaos) would likely cause a rapid degradation in the structural properties of the aircraft, most likely leading to structural failure. Even if this degradation were not to occur immediately, the oscillations would present a fatigue hazard to aircraft nacelle mounts and degrade the ride quality for any onboard the aircraft.

Furthermore, the only way to remove the bowtie LCO is to remove the freeplay entirely, as the bowtie originates from a Hopf bifurcation at infinite stiffness. A more practical adjustment to the design approach is to make the tiltrotor structure as fatigue-resistant as possible. A design optimum may be reached by a structure that fulfils its required performance envelope but is not excessively strong (and therefore needlessly heavy). From an operational perspective, periodic monitoring of the deadband width is advisable, with component replacement to be conducted as appropriate when the deadband width reaches some critical value. Preloading of the tilting mechanism could also be employed, to reduce the effects of the deadband’s presence.

The findings also show that the presence of freeplay in a system can invalidate previous guidance regarding structural stiffness. Several publications on classical whirl flutter explain that the elongation of the Hopf-bulge (as seen in Fig. 7) along its axis of symmetry means that a design point with particularly dissimilar values of pitch and yaw stiffness will have a greater stability margin (in speed) than one with similar or equal values. However, in the case of low yaw stiffness, very much the opposite was found in the present work and therefore following the guidance in this manner could prove to be ruinous.