Zoonotic MERS-CoV transmission: modeling, backward bifurcation and optimal control analysis

Abstract

Middle East Respiratory Syndrome Coronavirus (MERS-CoV) can cause mild to severe acute respiratory illness with a high mortality rate. As of January 2020, more than 2500 cases of MERS-CoV resulting in around 860 deaths were reported globally. In the absence of neither effective treatment nor a ready-to-use vaccine, control measures can be derived from mathematical models of disease epidemiology. In this manuscript, we propose and analyze a compartmental model of zoonotic MERS-CoV transmission with two co-circulating strains. The human population is considered with eight compartments while the zoonotic camel population consist of two compartments. The expression of basic reproduction numbers are obtained for both single strain and two strain version of the proposed model. We show that the disease-free equilibrium of the system with single stain is globally asymptotically stable under some parametric conditions. We also demonstrate that both models undergo backward bifurcation phenomenon, which in turn indicates that only keeping $R_0$ below unity may not ensure eradication. To the best of the authors knowledge, backward bifurcation was not shown in a MERS-CoV transmission model previously. Further, we perform normalized sensitivity analysis of important model parameters with respect to basic reproduction number of the proposed model. Furthermore, we perform optimal control analysis on different combination interventions with four components namely preventive measures such as use of masks, isolation of strain-1 infected people, strain-2 infected people and infected camels. Optimal control analysis suggests that combination of preventive measures and isolation of infected camels will eventually eradicate the disease from the community.

1 Introduction

An outbreak of Middle East respiratory syndrome coronavirus (MERS-CoV) is ongoing in the Arabian Peninsula, with the first case identified in Jeddah, Saudi Arabia, in June 2012 [36]. Phylogenetic analyses have indicated that the virus emerged in July 2011, with a broad uncertainty range, and that the outbreak results from multiple introductions of a weakly transmissible virus that is geographically dispersed [8]. Since September 2012, WHO has been notified of more than 2500 laboratory-confirmed cases of infection with MERS-CoV and at least 860 deaths related to MERS-CoV. Sporadic cases have been imported to Europe, Africa, Asia and North America via returning travelers from the Middle East, but no sustained transmission has been reported in those regions. Sporadic introductions of MERS-CoV into humans are suspected to involve bats [15] and/or camels [27] with camels implicated as the likely source of most zoonotic infections of MERS-CoV in Saudi Arabia. Meanwhile, there is considerable uncertainty about the extent of human-to-human transmission and it is unclear whether MERS-CoV has the potential for epidemic spread. Transmission appears limited among family members but may be amplified in health care settings [8]. An understanding of the MERS-CoV epidemiology and transmission pathways are critically needed to devise effective surveillance, prevention and control strategies.

Fig. 1

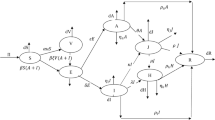
Compartmental flow diagram of the proposed model. Here green color indicates the susceptible compartment and the red color is for the infected compartment. The dotted double arrows denote the contacts between susceptible and infected populations and single sided blue solid arrows represent transition from one compartment to another. Here the green dotted line represents the contact within the human population and the red dotted line represents the contact between the human and camel population

Mathematical models provide a suitable framework in this situation to understand the transmission dynamics and design of prevention strategies. There are few modelling approaches related to MERS-CoV epidemics. [6] proposed a data-driven model for MERS-CoV transmission and they found strong support for $R_0<1$ ( $R_0$ measures the average number of secondary cases from each infected person) in the initial stage of the epidemic in Saudi Arabia. [14] used the Richards model to trace the temporal course of the South Korea MERS-CoV outbreak. In 2016, a dynamic transmission model for the 2015 MERS-CoV outbreak in the Republic of Korea was considered [19]. Later on, an SEIR type mathematical model for the MERS-CoV outbreak in South Korea was considered to perform optimal control analysis [18]. A stochastic epidemiological model of MERS-CoV with zoonotic and human-to-human transmission was considered by [26] to quantify the rates of generation of cases from those two transmission routes. However, these models were based on single a strain of MERS-CoV. There is strong evidence in the literature that there are multiple strains of MERS-CoV co-circulating in the community [5, 28, 38]. [29], proposed a two strain model of MERS-CoV to understand the epidemiological characteristics in three affected provinces of Saudi Arabia. They found that Riyadh province is likely to have cases from two strains. Motivated by this we consider a two strain model to have some insight into the intervention strategies. There is, however, no mathematical analysis considering two strain models of MERS-CoV as far as our knowledge is concerned. The objective of this study is to investigate the qualitative effect of both human-to-human and zoonotic disease transmission on the spread of MERS-CoV. To achieve this goal, a two-strain mathematical model for MERS-CoV is proposed and analyzed. We consider transmission from camels to humans as a zoonotic infection in our analysis [10, 21]. For classical epidemic models, it is common that the basic reproduction number is a threshold in the sense that a disease will survive if the basic reproductive number is greater than one, and it will die out if it is less than one. In some cases, the basic reproduction number may not reflect the elimination effort required; instead, the value of the critical parameter represents the effort at the turning point. This phenomenon is known as backward bifurcation. Thus, it is important to examine the occurrence of backward bifurcations to achieve thresholds for disease control. The presence of a backward bifurcation and the circumstances for its appearance in epidemic models have been extensively studied over the years. The problem of determining the causes of backward bifurcation in some standard deterministic models for the spread of some emerging and re-emerging diseases were studied by Gumel [13]. Recently, the necessary and sufficient conditions for the occurrence of backward bifurcation in general epidemic models have been studied by [23]. Backward bifurcation has been studied for several epidemic diseases [11, 24, 32]. However, we have studied this phenomenon here for our proposed models of MERS-CoV transmission. Our objective is not only to investigate the qualitative effect of disease transmission but also to effectively control the disease as quickly and efficiently as possible. Improving control and finally eradicating MERS-CoV from the population is one of the key reasons for investigating this infectious disease. There are various types of control mechanisms that have been studied in literature over the years. In the literature, several nonlinear control methods are also suggested. The rapid growth of Networked control systems has been followed by some thorny issues, such as network delay, imperfect communication links and limited communication bandwidth [31]. They studied the state estimation problem for the set of switched complex dynamic networks affected by the quantization, in which the switching mechanism is presumed to obey persistent dwell-time switching regulations. Many researchers have studied to unify a variety of different performance indexes within a uniform framework. More general performance called extended dissipative performance, which addressed four common performance indexes in a detailed manner within the same framework [37]. Extended dissipation was used in several systems analysis. The analyses of the extended dissipative performance of the closed-loop PDT SPSSs and a preferable decoupling method deriving the mode-dependent controller gains are given in [30]. Time-dependent control strategies may be applied over a finite time interval to prevent a disease. Optimal control is a powerful mathematical method that can be used in this situation to make decisions [20]. Here, we conduct optimal control analysis on various combined interventions with four components, namely preventive measures such as mask use, isolation of strain-1 infected individuals, strain-2 infected individuals and infected camels.

The rest of the paper is organized as follows: in Sect. 2, we formulate the compartmental model of MERS-CoV; the single strain version of the proposed model is analyzed in Sect. 3; optimal control analysis and numerical simulations for the proposed two strain model is presented in Sect. 4; finally, the obtained results are discussed for prevention strategies in Sect. 5.

2 Model formulation

We consider two heterogeneous population groups as host and vector population. Time-dependent state variables are taken to describe the compartments of the two populations. Let at time t, $N_h(t)$ represents total host population and $N_c(t)$ represents total camel population as vector. We consider an extension of ’SEIR’ type model for the host population and a ’SI’ type model for the vectors. We subdivide the host population into eight mutually disjoint classes: susceptible, $S_h$; Exposed with strain-i, $E_i$; un-notified infected with strain-i, $I_i$; Hospitalized or notified with strain-i, $H_i$; recovered, $R_h$ (i=1,2). Thus, at any time t, the size of the human population is given by $N_h = S_h + \sum _{i=1}^{2} (E_i+I_i +A_i)+ R_h$. The vector population is divided into two classes such that at time t, there are susceptible, $S_c$; and infected, $I_c$ vectors. With this division, the size of the vector population at time t is given by $N_c(t)=S_c(t)+I_c(t)$. A flow diagram of the proposed model is depicted in Fig. 1.

Table 1 Description of variables used in the model

Table 2 Description of parameters used in the model

We assume all newborn hosts are fully susceptible. The susceptible host population increases at a constant rate $\varPi _h$. The susceptible population decreases due to getting infection from infected vectors and infected hosts and natural mortality at a rate $\mu _h$, hence the average life span of the human population in endemic region is $\frac{1}{\mu _h}$. After getting infection the susceptible hosts progress to either $E_1$ or $E_2$. From $E_1$, people may progress to either $I_1$ or $H_1$ after incubation period is over. Similar progression is assumed for strain-2. The infected human populations $I_i$ and $H_i$ decreases as a result of natural death and recovery. We also consider disease induced mortality in the hospitalized compartment as MERS-CoV has a high case fatality rate. The average life span of vector population is $\frac{1}{\mu _c}$, that means $\mu _c$ is the natural mortality rate of camels. The susceptible camel population increases at a constant rate $\varPi _c$. All the parameters used in the system are described in Table 2. The above assumptions lead to the following set of ordinary differential equations:

$$\begin{aligned} \displaystyle { \frac{\mathrm{d}S_h}{\mathrm{d}t} }= & {} \varPi _h-\beta _1 \frac{S_h}{N_h}(I_1+\alpha _1 H_1)\nonumber \\&-\beta _2 \frac{S_h}{N_h}(I_2+\alpha _2 H_2)-\beta _d\frac{S_h}{N_h}I_c-\mu _h S_h,\nonumber \\ \displaystyle { \frac{\mathrm{d}E_1}{\mathrm{d}t} }= & {} \beta _1 \frac{S_h}{N_h}(I_1+\alpha _1 H_1)\nonumber \\&+\,m\beta _d\frac{S_h}{N_h}I_c-\mu _h E_1-\gamma _1 E_1,\nonumber \\ \displaystyle { \frac{\mathrm{d}E_2}{\mathrm{d}t} }= & {} \beta _2 \frac{S_h}{N_h}(I_2+\alpha _2 H_2)\nonumber \\&+\,(1-m)\beta _d\frac{S_h}{N_h}I_c-\mu _h E_2-\gamma _2 E_2,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_1}{\mathrm{d}t} }= & {} r_1\gamma _1 E_1-(\mu _h+k_{11}+\eta _1)I_1,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_2}{\mathrm{d}t} }= & {} r_2\gamma _2 E_2-(\mu _h+k_{12}+\eta _2)I_2,\nonumber \\ \displaystyle { \frac{\mathrm{d}H_1}{\mathrm{d}t} }= & {} (1-r_1)\gamma _1E_1+\eta _1 I_1-(\mu _h+k_{21}+\delta _1)H_1, \nonumber \\ \displaystyle { \frac{\mathrm{d}H_2}{\mathrm{d}t} }= & {} (1-r_2)\gamma _2E_2+\eta _2 I_2-(\mu _h+k_{22}+\delta _2)H_2, \nonumber \\ \displaystyle { \frac{\mathrm{d}R_h}{\mathrm{d}t} }= & {} k_{11}I_1+k_{12}I_2+k_{21}H_1+k_{22}H_2-\mu _hR_h,\nonumber \\ \displaystyle { \frac{\mathrm{d}S_c}{\mathrm{d}t} }= & {} \varPi _c -\beta _3\frac{S_c I_1}{N_h}-\beta _4\frac{S_c I_2}{N_h}-\mu _c S_c,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_c}{\mathrm{d}t} }= & {} \beta _3\frac{S_c I_1}{N_h}+\beta _4\frac{S_c I_2}{N_h}-\mu _c I_c. \end{aligned}$$

(1)

The variables and all the parameters and their biological interpretation are given in Tables 1 and 2, respectively.

3 Model analysis for single strain

In this section, we analyze the single starin version of model 1 mathematically. Here we consider the single strain model as follows:

$$\begin{aligned} \displaystyle { \frac{\mathrm{d}S_h}{\mathrm{d}t} }= & {} \varPi _h-\beta _1 \frac{S_h}{N_h}(I_1+\alpha _1 H_1)-\beta _d\frac{S_h}{N_h}I_c-\mu _h S_h,\nonumber \\ \displaystyle { \frac{\mathrm{d}E_1}{\mathrm{d}t} }= & {} \beta _1 \frac{S_h}{N_h}(I_1+\alpha _1 H_1)+\beta _d\frac{S_h}{N_h}I_c-\mu _h E_1-\gamma _1 E_1,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_1}{\mathrm{d}t} }= & {} r_1\gamma _1 E_1-(\mu _h+k_{11}+\eta _1)I_1,\nonumber \\ \displaystyle { \frac{\mathrm{d}H_1}{\mathrm{d}t} }= & {} (1-r_1)\gamma _1E_1+\eta _1 I_1-(\mu _h+k_{21}+\delta _1)H_1, \nonumber \\ \displaystyle { \frac{\mathrm{d}R_h}{\mathrm{d}t} }= & {} k_{11}I_1+k_{21}H_1-\mu _hR_h,\nonumber \\ \displaystyle { \frac{\mathrm{d}S_c}{\mathrm{d}t} }= & {} \varPi _c -\beta _3\frac{S_c I_1}{N_h}-\mu _c S_c,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_c}{\mathrm{d}t} }= & {} \beta _3\frac{S_c I_1}{N_h}-\mu _c I_c. \end{aligned}$$

(2)

3.1 Mathematical analysis

3.1.1 Positivity and boundedness of the solution

Proposition 1

The system (2) is bounded in the region

$\varOmega =\lbrace (S_h,E_1,I_1,H_1,R_h,S_c,I_c)\in R_+^{7}|S_h+E_1+I_1+H_1+R_h\le \frac{\varPi _h}{\mu _h},S_c+I_c\le \frac{\varPi _c}{\mu _c}\rbrace$, which is positively invariant.

Proof

We observed from the system that

$$\begin{aligned}&\frac{\mathrm{d}N_h}{\mathrm{d}t}=\varPi _h-\mu _h N_h-\delta _1 H_1\le \varPi _h-\mu _h N_h\\&\Longrightarrow \lim \limits _{t\rightarrow \infty }sup N_h(t)\rightarrow \frac{\varPi _h}{\mu _h} \end{aligned}$$

and

$$\begin{aligned}&\frac{\mathrm{d}N_c}{\mathrm{d}t}=\varPi _c-\mu _c N_c \\&\Longrightarrow \lim \limits _{t\rightarrow \infty }sup N_c(t)\rightarrow \frac{\varPi _c}{\mu _c} \end{aligned}$$

Now the system (2) can be written as

$$\begin{aligned} \frac{\mathrm{d}X}{\mathrm{d}t}&=MX+N \end{aligned}$$

where $X=(S_h,E_1,I_1,H_1,R_h,S_c,I_c)^T$. The matrix M is given by

$$\begin{aligned} M&=\begin{pmatrix} -(\theta _1+\theta _2+\mu _h) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \theta _1+\theta _2 &{} -(\mu _h+\gamma _1) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} r_1 \gamma _1 &{} -(\mu _h+k_{11}+\eta _1) &{} 0 &{} 0&{} 0 &{} 0\\ 0 &{} (1-r_1)\gamma _1 &{} \eta _1 &{} -(\mu _h+k_{21}+\delta _1) &{} 0 &{} 0&{} 0\\ 0 &{} 0 &{} k_{11} &{} k_{21} &{} -\mu _h &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -(\theta _3+\mu _c) &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \theta _3 &{} -\mu _c\\ \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} \theta _1&= \frac{\beta _1(I_1+\alpha _1 H_1)}{N_h}, \theta _2=\frac{\beta _d I_c}{N_h}, \theta _3=\frac{\beta _3 I_1}{N_h} \end{aligned}$$

The vector $N=(\varPi _h, 0, 0, 0, 0, 0, \varPi _c, 0)^T$. Note that MX is a Metzler matrix for all $X\in R_+^{7}$. Since $N\ge 0$, system (2) is positively invariant in $R_+^{7}$ [1]. Therefore, every trajectory of the system (2) starting from an initial state in $R_+^{7}$ remains trapped in $R_+^{7}$.

Therefore, all mathematically and biologically feasible solutions of the model system (2) are attractive to the region $\varOmega$. Of this reason, it is now sufficient to analyze the dynamic properties of the Model (2) in $\varOmega$. $\square$

3.1.2 Diseases-free equilibrium and basic reproduction number

The diseases-free equilibrium can be obtained for the system (2) by putting $E_1=0, I_1=0, H_1=0, I_c=0$, which is denoted by $P_0=(S_h,0,0,0,R_h,S_c,0),$ where

$$\begin{aligned} S_h=\frac{\varPi _h}{\mu _h},S_c=\frac{\varPi _c}{\mu _c},R_h=0. \end{aligned}$$

The basic reproduction number, a key idea in the study of the spread of infectious diseases, is the threshold value that specifies the number of infected individuals generated by one infected individual in a completely susceptible population. It is denoted by $R_{01}$ and calculated as $R_d+R_v$, where $R_d$ is the direct transmission reproduction number and $R_v$ is the vector transmission reproduction number [3]. This dimensionless number is determined by the next generation operator method at DFE. For this reason, we assemble the compartments that are infected from the system (2) and decompose the right side as ${\mathcal {F}}-{\mathcal {V}}$, where ${\mathcal {F}}$ is the transmission part, which expresses the generation of new infections, and the transition part is ${\mathcal {V}}$, which describes the change in state.

$$\begin{aligned} {\mathcal {F}}&=\begin{pmatrix} \beta _1 \frac{S_h}{N_h}(I_1+\alpha _1 H_1)+\beta _d\frac{S_h}{N_h}I_c \\ 0\\ 0\\ \beta _3\frac{S_c}{N_h}I_h \end{pmatrix},\\ {\mathcal {V}}&=\begin{pmatrix} \mu _h E_1+\gamma _1 E_1\\ -r_1 \gamma _1 E_1+(\mu _h+k_{11}+\eta _1)\\ -(1-r_1)\gamma _1 E_1-\eta _1 I_1+(\mu _h+k_{21}+\delta _1) H_1\\ \mu _c I_c \end{pmatrix} \end{aligned}$$

Now we calculate the Jacobian of ${\mathcal {F}}$ and ${\mathcal {V}}$ at DFE $P_0$

$$\begin{aligned} F&=\frac{\partial {\mathcal {F}}}{\partial X}=\begin{pmatrix} 0 &{}\beta _1 &{} \alpha _1 \beta _1 &{}\beta _d \\ 0&{}0 &{} 0 &{}0 \\ 0 &{}0 &{} 0 &{}0 \\ 0 &{}\beta _3\frac{\varPi _c \mu _h}{\varPi _h \mu _c} &{}0 &{}0 \\ \end{pmatrix},\\ V&=\frac{\partial {\mathcal {V}}}{\partial X}=\begin{pmatrix} \mu _h+\gamma _1 &{}0 &{} 0 &{}0 \\ -r_1\gamma _1 &{}\mu _h+k_{11}+\eta _1 &{} 0 &{}0 \\ -(1-r_1)\gamma _1 &{}-\eta _1 &{} \mu _h+k_{21}+\delta _1 &{}0 \\ 0 &{}0 &{}0 &{}\mu _c \\ \end{pmatrix}. \end{aligned}$$

Now the $V^{-1}$ is given by

$$\begin{aligned} V^{-1}=\begin{pmatrix} \frac{1}{\mu _h+\gamma _1} &{}0 &{} 0 &{}0 \\ \frac{r_1\gamma _1}{(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)} &{}\frac{1}{\mu _h+k_{11}+\eta _1} &{} 0 &{}0 \\ \frac{r_1 \gamma _1 \eta _1+(1-r_1)\gamma _1(\mu _h+k_{11}+\eta _1)}{(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)(\mu _h+k_{21}+\delta _1)} &{}\frac{\eta _1}{(\mu _h+k_{11}+\eta _1)(\mu _h+k_{21}+\delta _1)} &{} \frac{1}{\mu _h+k_{21}+\delta _1} &{}0 \\ 0 &{}0 &{}0 &{}\frac{1}{\mu _c} \\ \end{pmatrix} \end{aligned}$$

Thus, the matrix $FV^{-1}$ is given as

$$\begin{aligned} FV^{-1}=\begin{pmatrix} \frac{\beta _1 r_1 \gamma _1}{m_1 m_2}+\frac{\alpha _1 \beta _1[r_1 \gamma _1 \eta _1+(1-r_1)\gamma _1m_2]}{m_1 m_2 m_3} &{}\frac{\beta _1}{m_2}+\frac{\alpha _1 \beta _1 \eta _1}{m_2 m_3} &{} \frac{\alpha _1 \beta _1}{m_3} &{}\frac{\beta _d}{\mu _c} \\ 0&{}0 &{} 0 &{}0 \\ 0 &{}0 &{} 0 &{}0 \\ \beta _3\frac{\varPi _c \mu _h}{\varPi _h \mu _c}\frac{r_1 \gamma _1}{m_1 m_2} &{}\beta _3\frac{\varPi _c \mu _h}{\varPi _h \mu _c}\frac{1}{m_2} &{}0 &{}0 \\ \end{pmatrix}, \end{aligned}$$

where $m_1=\mu _h+\gamma _1$, $m_2=\mu _h+k_{11}+\eta _1$ and $m_3=\mu _h+k_{21}+\delta _1$.

To find $R_d$ we use $\beta _d=0$ and $\beta _3=0$ in F, then the direct transmission reproduction number $R_d$ for the Model (2) is given by

$$\begin{aligned}&F_{1}=\begin{pmatrix} 0 &{}\beta _1 &{} \alpha _1 \beta _1 &{}0 \\ 0&{}0 &{} 0 &{}0 \\ 0 &{}0 &{} 0 &{}0 \\ 0 &{}0 &{}0 &{}0 \\ \end{pmatrix},\\&V=\begin{pmatrix} \mu _h+\gamma _1 &{}0 &{} 0 &{}0 \\ -r_1\gamma _1 &{}\mu _h+k_{11}+\eta _1 &{} 0 &{}0 \\ -(1-r_1)\gamma _1 &{}-\eta _1 &{} \mu _h+k_{21}+\delta _1 &{}0 \\ 0 &{}0 &{}0 &{}\mu _c \\ \end{pmatrix}. \end{aligned}$$

Now the direct transmission reproduction number $R_d$ is the spectral radius of $F_{1}V^{-1}$, therefore

$$\begin{aligned} R_d&=\frac{\beta _1 r_1 \gamma _1}{(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)}\\&\quad +\frac{\alpha _1 \beta _1 r_1 \gamma _1 \eta _1}{(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)(\mu _h+k_{21}+\delta _1)}\\&\quad +\frac{\alpha _1 \beta _1 (1-r_1) \gamma _1}{(\mu _h+\gamma _1)(\mu _h+k_{21}+\delta _1)} \end{aligned}$$

To find $R_v$ we use $\beta _h=0$ in F. Therefore, the vector transmission reproduction number $R_v$ is given by

$$\begin{aligned}&F_2=\begin{pmatrix} 0 &{}0 &{} 0 &{}\beta _d \\ 0&{}0 &{} 0 &{}0 \\ 0 &{}0 &{} 0 &{}0 \\ 0 &{}\beta _c\frac{\varPi _c \mu _h}{\varPi _h \mu _c} &{}0 &{}0 \\ \end{pmatrix},\\&V=\begin{pmatrix} \mu _h+\gamma _1 &{}0 &{} 0 &{}0 \\ -r_1\gamma _1 &{}\mu _h+k_{11}+\eta _1 &{} 0 &{}0 \\ -(1-r_1)\gamma _1 &{}-\eta _1 &{} \mu _h+k_{21}+\delta _1 &{}0 \\ 0 &{}0 &{}0 &{}\mu _c \\ \end{pmatrix}. \end{aligned}$$

Now the vector transmission reproduction number $R_v$ is the spectral radius of $F_{2}V^{-1}$, therefore

$$\begin{aligned} R_v&= \sqrt{\frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \mu _h}{\mu _c^{2}\varPi _h(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)}} \end{aligned}$$

In this calculation, the transition is considered as two generations. In studying vector transmitted diseases it is common to consider this as one generations and use the value by direct approach

$$\begin{aligned} R_v&= \frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \mu _h}{\mu _c^{2}\varPi _h(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)} \end{aligned}$$

Therefore, the basic reproduction number is

$$\begin{aligned}&R_{01}=R_d+R_v \\&\quad =\frac{\beta _1 r_1 \gamma _1}{(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)}\\&\quad +\frac{\alpha _1 \beta _1 r_1 \gamma _1 \eta _1}{(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)(\mu _h+k_{21}+\delta _1)}\\&\quad +\frac{\alpha _1 \beta _1 (1-r_1) \gamma _1}{(\mu _h+\gamma _1)(\mu _h+k_{21}+\delta _1)} \\&\quad +\frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \mu _h}{\mu _c^{2}\varPi _h(\mu _h+\gamma _1)(\mu _h+k_{11}+\eta _1)} \end{aligned}$$

3.1.3 Stability of DFE

Theorem 1

The diseases free equilibrium(DFE) $P_{0}=(\frac{\varPi _h}{\mu _h},0,0,0,0,\frac{\varPi _c}{\mu _c},0)$ of the system (2) is locally asymptotically stable if $R_{01}<1$ and unstable if $R_{01}>1$.

Proof

We calculate the Jacobian of the system (2) at DFE, and is given by

$$\begin{aligned} J_{P_{0}}={\begin{pmatrix} -\mu _h &{} 0 &{} -\beta _1 &{} -\alpha _1 \beta _1 &{} 0 &{} 0 &{} -\beta _d \\ 0 &{} -(\mu _h+\gamma _1) &{} \beta _1 &{} \alpha _1 \beta _1 &{} 0 &{} 0 &{} \beta _d\\ 0 &{} r_1 \gamma _1 &{} -(\mu _h+k_{11}+\eta _1) &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} (1-r_1)\gamma _1 &{} \eta _1 &{} -(\mu _h+k_{21}+\delta _1) &{} 0 &{} 0 &{}0\\ 0 &{} 0 &{} k_{11} &{} k_{21} &{} -\mu _h &{} 0 &{} 0\\ 0 &{} 0 &{} -\beta _3\frac{\varPi _c \mu _h}{\varPi _h \mu _c} &{} 0 &{} 0 &{} -\mu _c &{} 0\\ 0 &{} 0 &{} \beta _3\frac{\varPi _c \mu _h}{\varPi _h \mu _c} &{} 0 &{} 0 &{} 0 &{} -\mu _c\\ \end{pmatrix}}, \end{aligned}$$

Let $\lambda$ be the eigenvalue of the matrix $J_{P_{0}}$. Then the characteristic equation is given by $det(J_{P_{0}}-\lambda I)=0$.

which implies

$$\begin{aligned}&\beta _1 r_1 \gamma _1\mu _c(\mu _h+k_{21}+\delta _1+\lambda )+\alpha _1 \beta _1 r_1 \gamma _1 \mu _c\\&\quad +\,\alpha _1 \beta _1 \gamma _1 \mu _c (1-r_1)(\mu _h+k_{11}+\eta _1+\lambda )\\&\quad +\,\beta _d \beta _c r_a \gamma _1 (\mu _h+k_{21}+\delta _1+\lambda )\frac{\varPi _c \mu _h}{\varPi _h \mu _c}\\&\quad -\,(\mu _h+\gamma _1+\lambda )(\mu _h+k_{11}+\eta _1+\lambda )\\&\quad \quad (\mu _h+k_{21}+\delta _1+\lambda )=0 \end{aligned}$$

Which can be written as

$$\begin{aligned}&\frac{\beta _1 r_1 \gamma _1}{(\mu _h+\gamma _1+\lambda )(\mu _h+k_{11}+\eta _1+\lambda )}\\&\quad +\frac{\alpha _1 \beta _1 r_1 \gamma _1 \eta _1}{(\mu _h+\gamma _1+\lambda )(\mu _h+k_{11}+\eta _1+\lambda )(\mu _h+k_{21}+\delta _1+\lambda )}\\&\quad +\frac{\alpha _1 \beta _1 (1-r_1) \gamma _1}{(\mu _h+\gamma _1+\lambda )(\mu _h+k_{21}+\delta _1+\lambda )} \\&\quad +\frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \mu _h}{\mu _c^{2}\varPi _h(\mu _h+\gamma _1+\lambda )(\mu _h+k_{11}+\eta _1+\lambda )}=1. \end{aligned}$$

Denote

$$\begin{aligned} G(\lambda )&=\frac{\beta _1 r_1 \gamma _1}{(\mu _h+\gamma _1+\lambda )(\mu _h+k_{11}+\eta _1+\lambda )}\\&\quad +\frac{\alpha _1 \beta _1 r_1 \gamma _1 \eta _1}{(\mu _h+\gamma _1+\lambda )(\mu _h+k_{11}+\eta _1+\lambda )(\mu _h+k_{21}+\delta _1+\lambda )}\\&\quad +\frac{\alpha _1 \beta _1 (1-r_1) \gamma _1}{(\mu _h+\gamma _1+\lambda )(\mu _h+k_{21}+\delta _1+\lambda )}\\&\quad +\frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \mu _h}{\mu _c^{2}\varPi _h(\mu _h+\gamma _1+\lambda )(\mu _h+k_{11}+\eta _1+\lambda )}. \end{aligned}$$

We rewrite $G(\lambda )$ as $G(\lambda )=G_1(\lambda )+G_2(\lambda )+G_3(\lambda )+G_4(\lambda )$

Now if $Re(\lambda )\ge 0$, $\lambda =x+iy$, then

$$\begin{aligned} |G_1(\lambda )|&\le \frac{\beta _1 r_1 \gamma _1}{|\mu _h+\gamma _1+\lambda ||\mu _h+k_{11}+\eta _1+\lambda |}\\&\le G_1(x)\le G_1(0)\\ |G_2(\lambda )|&\le \frac{\alpha _1 \beta _1 r_1 \gamma _1 \eta _1}{|\mu _h+\gamma _1+\lambda ||\mu _h+k_{11}+\eta _1+\lambda ||\mu _h+k_{21}+\delta _1+\lambda |}\\&\le G_2(x)\le G_2(0)\\ |G_3(\lambda )|&\le \frac{\alpha _1 \beta _1 (1-r_1) \gamma _1}{|\mu _h+\gamma _1+\lambda ||\mu _h+k_{21}+\delta _1+\lambda |}\\&\le G_3(x)\le G_3(0)\\ |G_4(\lambda )|&\le \frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \mu _h}{\mu _c^{2}\varPi _h|\mu _h+\gamma _1+\lambda ||\mu _h+k_{11}+\eta _1+\lambda |}\\&\le G_4(x)\le G_4(0) \end{aligned}$$

Then $G_1(0)+G_2(0)+G_3(0)+G_4(0)=G(0)=R_{01}<1$, which implies $|G(\lambda )|\le 1$.

Thus for $R_{01}<1$, all the eigenvalues of the characteristics equation $G(\lambda )=1$ has negative real parts.

Therefore, if $R_{01}<1$, all eigenvalues are negative and hence DFE $P^{0}$ is locally asymptotically stable.

Now if we consider $R_{01}>1$ i.e $G(0)>1$, then

$$\begin{aligned} \lim \limits _{\lambda \rightarrow \infty } G(\lambda )=0. \end{aligned}$$

Then there exist $\lambda _1^{*}>0$ such that $G(\lambda _1^{*})=1$.

That means there exists positive eigenvalue $\lambda _1^{*}>0$ of the Jacobian matrix.

Hence, DFE $P_{0}$ is unstable whenever $R_{01}>1$. $\square$

3.1.4 Global stability of DFE:

Now set $X_1 =(S_h,R_h,S_c)$ and $X_2 =(I_1,H_1,I_1,E_1)$. Then the system can be written on the set $\varOmega$, in a pseudo-triangular form

$$\begin{aligned} \dot{X_1}&=A_1(X)(X_1-X_1^*)+A_{12}(X) X_2 \nonumber \\ \dot{X_2}&=A_2(X)X_2 \end{aligned}$$

(3)

We express the sub-system $\dot{X_1}=A_1(X)(X_1-X_1^*)+A_{12}(X) X_2$

$$\begin{aligned} \dot{S_h}&=\varPi _h-\mu _h S_h \nonumber \\ \dot{R_h}&=-\mu _h R_h \nonumber \\ \dot{S_c}&=\varPi _c-\mu _c S_c \end{aligned}$$

(4)

This is a linear system which is globally asymptotically stable at the equilibrium $(\frac{\varPi _h}{\mu _h},0,\frac{\varPi _c}{\mu _c})$ corresponding to the DFE which satisfies H1 and H2 [17].

The matrix $A_2(X)$ is given by $A_2(X)=$$\begin{pmatrix} -\mu _c &{} 0 &{} \beta _3 \frac{S_c}{N_h} &{} 0\\ 0 &{} -(\mu _h+k_{21}+\delta _1) &{} \eta _1 &{} (1-r_1)\gamma _1\\ 0 &{} 0 &{} -(\mu _h+k_{11}+\eta _1) &{} r_1\gamma _1\\ \beta _d \frac{S_h}{N_h} &{} \alpha _1 \beta _h \frac{S_h}{N_h} &{} \beta _h \frac{S_h}{N_h} &{} -(\mu _h+\gamma _1) \end{pmatrix}$

which is an irreducible matrix.

The upper bound for $X\in \varOmega$ is given by $\bar{A_2}=$$\begin{pmatrix} -\mu _c &{} 0 &{} \beta _3 \frac{\varPi _c(\mu _h+\delta _1)}{\varPi _h \mu _c} &{} 0\\ 0 &{} -(\mu _h+k_{21}+\delta _1) &{} \eta _1 &{} (1-r_1)\gamma _1\\ 0 &{} 0 &{} -(\mu _h+k_{11}+\eta _1) &{} r_1\gamma _1\\ \beta _d &{} \alpha _1 \beta _h &{} \beta _h &{} -(\mu _h+\gamma _1) \end{pmatrix}$

which is not attained on $\varOmega$ and which is not the corresponding block in Jacobian matrix of the system at the DFE. Thus we obtain only sufficient condition.

It is straightforward to check that all hypothesis of Theorem 4.3 of [17] are satisfied. Hence, we obtained the condition

$$\begin{aligned} R_{01}+\frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \delta _1}{\mu _c^{2}\varPi _h(\mu _h+\gamma _1) (\mu _h+k_{11}+\eta _1)} < 1 \end{aligned}$$

Which implies

$$\begin{aligned} R_{01}<1-\frac{\beta _3 \beta _d r_1 \gamma _1 \varPi _c \delta _1}{\mu _c^{2}\varPi _h(\mu _h+\gamma _1) (\mu _h+k_{11}+\eta _1)}=R_{01}^{c}\le 1 \end{aligned}$$

Obviously $R_{01}<R_{01}^{c}$ and this condition is stronger.

Theorem 2

The diseases free equilibrium(DFE) $P_0=(S_h,0,0,0,R_h,S_c,0)$ of the system (1) is globally stable if $R_{01}<R_{01}^{c}$.

3.1.5 Endemic equilibrium

In this section we discuss the existence of endemic equilibria and its stability conditions. Let $P^*=(S_h^*,E_h^*,I_h^*,H_h^*,R_h^*,S_c^*,I_c^*)$ be an arbitrary endemic equilibrium of the system (1). Therefore, equating the right hand sides of the equations of system (1) to zero, we have

$$\begin{aligned} S_h^*= & {} \frac{1}{\mu _h}\Big [\varPi _h-(\gamma +\mu _h)E_h^*\Big ]\\ I_h^*= & {} \frac{r \gamma _h}{\mu _h+k_1+\eta _1}E_h^*\\ H_h^*= & {} \frac{1}{b}\Big \lbrace (1-r)\gamma _h+\frac{\eta _1 r \gamma _h}{\mu _h+k_1+\eta _1}\Big \rbrace E_h^*\\ R_h^*= & {} \frac{1}{\mu _h}\Big [\frac{k_1 r \gamma _h}{\mu _h+k_1+\eta _1}\\&+\frac{k_2}{b}\Big \lbrace (1-r)\gamma _h+\frac{\eta _1 r \gamma _h}{\mu _h+k_1+\eta _1}\Big \rbrace \Big ]E_h^*\\ S_c^*= & {} \frac{\frac{\varPi _c}{\mu _h}\Big [\varPi _h-\frac{\delta }{b}\Big \lbrace (1-r)\gamma _h+\frac{\eta _1 r \gamma _h}{\mu _h+k_1+\eta _1}\Big \rbrace E_h^*\Big ]}{\frac{\beta _c r \gamma _h}{\mu _h+k_1+\eta _1}E_h^*+\frac{\mu _c}{\mu _h}\Big [\varPi _h-\frac{\delta }{b}\Big \lbrace (1-r)\gamma _h+\frac{\eta _1 r \gamma _h}{\mu _h+k_1+\eta _1}\Big \rbrace E_h^*\Big ]}\\ I_c^*= & {} \frac{\frac{\beta _c \varPi _c r \gamma _h}{\mu _c(\mu _h+k_1+\eta _1)}E_h^*}{\frac{\beta _c r \gamma _h}{\mu _h+k_1+\eta _1}E_h^*+\frac{\mu _c}{\mu _h}\Big [\varPi _h-\frac{\delta }{b}\Big \lbrace (1-r)\gamma _h+\frac{\eta _1 r \gamma _h}{\mu _h+k_1+\eta _1}\Big \rbrace E_h^*\Big ]} \\ N_h^*= & {} \frac{1}{\mu _h}\Big [\varPi _h-\frac{\delta }{b}\Big \lbrace (1-r)\gamma _h+\frac{\eta _1 r \gamma _h}{\mu _h+k_1+\eta _1}\Big \rbrace E_h^*\Big ] \end{aligned}$$

and $E_h^*$ comes from the equation

$$\begin{aligned} \begin{array}{lll} f(E_h^*)=Q_1 {E_h^*}^{2}+Q_2 {E_h^*}+Q_3=0\\ \end{array} \end{aligned}$$

(5)

where,

$$\begin{aligned} Q_1= & {} \frac{c \beta _h}{\mu _h}\Big (\frac{r \gamma _h}{a}+ d\alpha \Big )\Big (\frac{\mu _c \delta d}{\mu _h}-\frac{\beta _c r \gamma _h}{a}\Big )\\&-\frac{c}{\mu _h}\Big (\frac{\mu _c \delta d}{\mu _h}-\frac{\beta _c r \gamma _h}{a}\Big )\delta d\\ Q_2= & {} \frac{\beta _h \varPi _h}{\mu _h}\Big (\frac{r \gamma _h}{a}+ d\alpha \Big )\Big [\Big (\frac{\beta _c r \gamma _h}{a}-\frac{\mu _c \delta d}{\mu _h}\Big )-\frac{ c \mu _c}{\mu _h}\Big ]\\&-\frac{\beta _d \beta _c \varPi _c r \gamma _h c}{\mu _h \mu _c a}-\frac{\varPi _h c}{\mu _h}\Big (\frac{\beta _c r \gamma _h}{a}-\frac{\mu _c \delta d}{\mu _h}\Big )\\&+\frac{\varPi _h c \mu _c \delta d}{\mu _h^{2}}\\ Q_3= & {} \frac{\varPi _h^{2}c\mu _c}{\mu _h^{2}}(R_{01}-1) \end{aligned}$$

Here

• $a=\mu _h+k_1+\eta _1$,

• $b=\mu _h+k_2+\delta$,

• $c=\mu _h+\gamma _h$,

• $d=\frac{1}{b}\Big \lbrace (1-r)\gamma _h+\frac{\eta _1 r \gamma _h}{\mu _h+k_1+\eta _1}\Big \rbrace$.

Therefore, if $R_{01}>1$, then endemic equilibrium exists.

Now $E_h^*=\frac{-Q_2\pm \sqrt{Q_2^{2}-4Q_1Q_3}}{2Q_1}$

• Case I If $Q_2^{2}-4Q_1Q_3>0$, there may exist two endemic equilibrium

• Case II If $Q_2^{2}-4Q_1Q_3=0$, there may exists unique endemic equilibrium.

• Case III If $Q_2^{2}-4Q_1Q_3<0$, there exist no endemic equilibrium..

Table 3 When $R_{01}>1$

Table 4 When $R_{01}<1$

Now from the Tables 3 and 4, it is clear from Case (II) of both table that, the model (2) has a unique endemic equilibrium whenever $R_{01} > 1$ and $R_{01} < 1$. In case (I) in Table 4, we observed that, if $Q_1<0$, $Q_2>0$ and $Q_3<0$ then the model (2) may have the possibility of backward bifurcation where stable disease-free equilibrium coexists with a stable endemic equilibrium whenever the basic reproduction number $R_{01}$ is less than unity. We explore the details analysis of backward bifurcation in the next section. This phenomenon is illustrated numerically by simulation of the model (2)(See Fig. 2).

Fig. 2

Backward bifurcation diagram and related time series for the single strain model 2. The region in the box is the bistable zone. The following set of hypothetical parameter values are used: $\varPi _h$=0.007, $\varPi _c$ =0.4817, $\mu _h$ = 0.00154, $\mu _c$ = 0.009, $\beta _h$ = 0.200, $\beta _d$ = 0.0025, $\beta _c$ = 0.17, $\alpha$ = 0.005, $\gamma _h$ =0.035, r = 0.98, $k_1$ = 0.001, $k_2$ = 0.0039, $\eta _1$ = 1.01 and $\delta$ =0.04

3.1.6 Backward bifurcation analysis

In this section, we explore the phenomenon of backward bifurcation in system (1). First, we carry out bifurcation analysis by applying the Center Manifold Theorem [4]. Let $x = (x_1, x_2, x_3, x_4, x_5, x_7)^T = ( S_h, E_1, I_1, H_1, R_h, S_c, I_c)^T$. Thus, the model (2) can be re-written in the form $\frac{dx}{\mathrm{d}t}=f(x)$, with $f(x) = (f_1 (x),..., f_7(x))$, as follows:

$$\begin{aligned} \displaystyle { \frac{dx_1}{\mathrm{d}t} }= & {} f_1 = \varPi _h-\frac{\beta _1 x_1(x_3+\alpha _1x_4)}{x_1+x_2+x_3+x_4+x_5}\nonumber \\&-\frac{\beta _d x_1 x_7}{x_1+x_2+x_3+x_4+x_5}-\mu _h x_1\nonumber \\ \displaystyle { \frac{dx_2}{\mathrm{d}t} }= & {} f_2 =\frac{\beta _1 x_1(x_3+\alpha _1x_4)}{x_1+x_2+x_3+x_4+x_5}\nonumber \\&-\frac{\beta _d x_1 x_7}{x_1+x_2+x_3+x_4+x_5}-(\mu _h+\gamma _1)x_2,\nonumber \\ \displaystyle { \frac{dx_3}{\mathrm{d}t} }= & {} f_3 =r_1 \gamma _1 x_2-(\mu _h+k_{11}+\eta _1)x_3,\nonumber \\ \displaystyle { \frac{dx_4}{\mathrm{d}t} }= & {} f_4 = (1-r_1)\gamma _1 x_2+\eta _1 x_3-(\mu _h+k_{21}+\delta _1)x_4, \nonumber \\ \displaystyle {\frac{dx_5}{\mathrm{d}t} }= & {} f_5 =k_{11}x_3+k_{21}x_4-\mu _h x_5, \nonumber \\ \displaystyle {\frac{dx_6}{\mathrm{d}t} }= & {} f_6 =\varPi _c-\frac{\beta _3 x_6 x_3}{x_1+x_2+x_3+x_4+x_5}-\mu _c x_6, \nonumber \\ \displaystyle { \frac{dx_7}{\mathrm{d}t} }= & {} f_7 =\frac{\beta _3 x_6 x_3}{x_1+x_2+x_3+x_4+x_5}-\mu _c x_7 . \end{aligned}$$

(6)

The Jacobian of the system (6) at the DFE $P_0$ is given as,

$$\begin{aligned} J_{P_0}={\begin{pmatrix} -\mu _h &{}0 &{}-\beta _1 &{}-\alpha _1 \beta _1 &{} 0 &{}0 &{}-\beta _d \\ 0 &{}-(\mu _h+\gamma _1)&{}\beta _1 &{}\alpha _1 \beta _1 &{} 0 &{}0 &{}\beta _d \\ 0 &{}r_1 \gamma _1 &{}-(\mu _h+k_{11}+\eta _1) &{}0 &{} 0 &{}0 &{}0 \\ 0 &{}(1-r_1)\gamma _1 &{}\eta _1 &{}-(\mu _h+k_{21}+\delta _1) &{} 0 &{}0 &{}0 \\ 0 &{}0 &{}k_{11} &{}k_{21} &{} -\mu _h &{}0 &{}0 \\ 0 &{}0 &{}-\frac{\beta _3\varPi _c \mu _h}{\varPi _h \mu _c}&{}0 &{} 0 &{}-\mu _c &{}0 \\ 0 &{}0 &{}\frac{\beta _3\varPi _c \mu _h}{\varPi _h \mu _c}&{}0 &{} 0 &{}0&{}-\mu _c \\ \end{pmatrix}}, \end{aligned}$$

Choose $\beta _1$ as the bifurcation parameter, then setting $R_{01}=1$ gives

$$\begin{aligned} \beta _1&=\beta _1^*\nonumber \\&=\frac{abc(\mu _c^2 \varPi _h a c -\beta _3 \beta _d r_1 \gamma _1\varPi _c \mu _h)}{\mu _c^2 \varPi _h a c (r_1 \gamma _1 b+\alpha _1 r_1 \gamma _1 \eta _1+\alpha _1(1-r_1)\gamma _1 a)} \end{aligned}$$

(7)

The system (6) at the DFE $P_0$ evaluated for $\beta _1=\beta _1^*$ has a simple zero eigenvalue and all other eigenvalues having negative real parts. Hence, we apply the Center Manifold Theorem to analyze the dynamics of (6) near $\beta _1=\beta _1^*$.

The Jacobian of (6) at $\beta _1=\beta _1^*$ denoted by $J_{P_0}|{\beta _1=\beta _1^*}$ has a right eigenvector (associated with the zero eigenvalue) given by $w = ( w_1 , w_2 , w_3 , w_4 , w_5 , w_6, w_7)^T$ , where

$$\begin{aligned} w_1&=-\frac{(\mu _h+\gamma _1)}{\mu _h}w_2, w_2=w_2>0, \nonumber \\ w_3&=\frac{r_1 \gamma _1}{(\mu _h+k_{11}+\eta _1)}w_2,\nonumber \\ w_4&=\frac{(1-r_1)\gamma _1(\mu _h+k_{11}+\eta _1)+\eta _1 r_1 \gamma _1}{(\mu _h+k_{11}+\eta _1)(\mu _h+k_{21}+\delta _1)}w_2, \nonumber \\ w_5&=\frac{k_{11}w_3+k_{21}w_4}{\mu _h},\nonumber \\ w_6&=-\frac{\beta _3 \varPi _c \mu _h r_1 \gamma _1}{\varPi _h \mu ^2_c(\mu _h+k_{11}+\eta _1)}w_2, \nonumber \\ w_7&=\frac{\beta _3 \varPi _c \mu _h r_1 \gamma _1}{\varPi _h \mu ^2_c(\mu _h+k_{11}+\eta _1)}w_2. \end{aligned}$$

(8)

Similarly, from $J_{P_0}|{\beta _1=\beta _1^*}$, we obtain a left eigenvector $v=( v_1 , v_2 , v_3 , v_4 , v_5 , v_6, v_7)^T$ (associated with the zero eigenvalue), where

$$\begin{aligned}&v_1=0, v_2=v_2>0, v_3\nonumber \\&\quad =\frac{1}{(\mu _h+k_{11}+\eta _1)}\Big [\beta _1+\frac{\alpha _1 \beta _1 \eta _1}{(\mu _h+k_{21}+\delta _1)}\nonumber \\&\quad \quad +\frac{\beta _d \varPi _c \mu _h}{\varPi _h \mu ^2_c}\Big ]v_2,\nonumber \\ v_4&=\frac{\alpha _1 \beta _1}{(\mu _h+k_{21}+\delta _1)}v_2, v_5=0, v_6=0, v_7=\frac{\beta _d}{\mu _c}v_2. \end{aligned}$$

(9)

To show the existence of backward bifurcation, we calculate the following second-order partial derivatives of $f_i$ at the disease-free equilibrium $\varepsilon _0$ and obtain

$$\begin{aligned} \frac{\partial f_2}{\partial x_3 \partial x_2}&=\frac{\partial f_2}{\partial x_2 \partial x_3}=\frac{\partial f_2}{\partial x_5 \partial x_3}\nonumber \\&\quad =\frac{\partial f_2}{\partial x_3 \partial x_5}\nonumber \\&\quad =-\frac{\beta _1 \mu _h}{\varPi _h}, \frac{\partial f_2}{\partial x_7 \partial x_2}=\frac{\partial f_2}{\partial x_7 \partial x_3}=\frac{\partial f_2}{\partial x_7 \partial x_4}\nonumber \\&\quad =\frac{\partial f_2}{\partial x_7 \partial x_5} =\frac{\partial ^2 f_2}{\partial ^2 x_2 \partial x_6}=\frac{\partial ^2 f_2}{\partial x_3 \partial x_6}\nonumber \\&\quad =\frac{\partial ^2 f_2}{\partial x_4 \partial x_6}=\frac{\partial ^2 f_2}{\partial x_5 \partial x_6}=-\frac{\beta _d \mu _h}{\varPi _h}, \frac{\partial ^2 f_2}{\partial x_3 \partial x_3}\nonumber \\&\quad =-\frac{2 \beta _1 \mu _h}{\varPi _h}, \frac{\partial ^2 f_2}{\partial x_4\partial x_2}= \frac{\partial ^2 f_2}{\partial x_2\partial x_4}\nonumber \\&\quad =\frac{\partial ^2 f_2}{\partial x_5\partial x_4}=\frac{\partial ^2 f_2}{\partial x_4\partial x_5}=-\frac{\alpha _1 \beta _1 \mu _h}{\varPi _h}, \frac{\partial ^2 f_2}{\partial x_4\partial x_4}\nonumber \\&\quad =-\frac{2 \alpha _1 \beta _1 \mu _h}{\varPi _h}, \frac{\partial ^2 f_2}{\partial x_4\partial x_3}=-\Big (\frac{\beta _1 \mu _h}{\varPi _h}+\frac{\alpha _1 \beta _1 \mu _h}{\varPi _h}\Big ) \frac{\partial ^2 f_7}{\partial x_3\partial x_1}\nonumber \\&\quad =\frac{\partial ^2 f_7}{\partial x_3\partial x_2}=\frac{\partial ^2 f_7}{\partial x_1\partial x_3}=\frac{\partial ^2 f_7}{\partial x_2\partial x_3}\nonumber \\&\quad =\frac{\partial ^2 f_7}{\partial x_4\partial x_3}=\frac{\partial ^2 f_7}{\partial x_5\partial x_3}=-\frac{\beta _3 \varPi _c \mu _h}{\varPi _h \mu _c},\nonumber \\&\qquad \frac{\partial ^2 f_7}{\partial x_3\partial x_3}=-\frac{2 \beta _3 \varPi _c \mu _h}{\varPi _h \mu _c}, \frac{\partial ^2 f_7}{\partial x_6\partial x_3}\nonumber \\&\quad =\frac{\partial ^2 f_7}{\partial x_3\partial x_6}=\frac{\beta _3\mu _h}{\varPi _h}, \frac{\partial ^2 f_7}{\partial x_3\partial x_4}=\frac{\partial ^2 f_7}{\partial x_3\partial x_5}\nonumber \\&\quad =-\frac{\beta _3 \varPi _c \mu _h}{\varPi _h \mu _c} \end{aligned}$$

(10)

Now we calculate the coefficients a and b defined in Theorem 4.1 [4] of Castillo-Chavez and Song as follow

$$\begin{aligned} a&= \sum _{k,i,j=1}^{6} v_k w_i w_j\frac{\partial ^2 f_k(0,\beta ^*)}{\partial x_i \partial x_j}\nonumber \\&=\frac{2 \varPi _c \mu _h v_7 \beta _3}{\varPi _h \mu _c}\nonumber \\&\quad \times (w_3w_6-w_3(w_1+w_2+w_3+w_4+w_5))\nonumber \\&\quad -\frac{2\beta _1 v_2 \mu _h}{\varPi _h}(w_2 w_3+w_3 w_3\nonumber \\&\quad +w_2 w_4+(1+\alpha _1)w_3 w_4+w_3 w_5\nonumber \\&\quad +\alpha _1 w_4 w_4++\alpha _1 w_4 w_5)\nonumber \\&\quad -\frac{2 v_2 \mu _h}{\varPi _h}\beta _d w_7(w_2+w_3+w_4+w_5) \end{aligned}$$

(11)

and

$$\begin{aligned} b= \sum _{k,i=1}^{6} v_k w_i\frac{\partial ^2 f_k(0, 0)}{\partial x_i \partial \beta }=v_2(w_3+\alpha _1 w_4)>0. \end{aligned}$$

(12)

Since the coefficient b is always positive, system (1) undergoes backward bifurcation at $R_{01}=1$, if $a>0$, namely if

$$\begin{aligned} \beta _3>\frac{\mu _c \beta _1 v_2(w_2 w_3+w_3 w_3+w_2 w_4+(1+\alpha _1)w_3 w_4+w_3 w_5+\alpha _1 w_4 w_4+\alpha _1 w_4 w_5)+\mu _c v_2 \beta _d w_7 (Z_w-w_1)}{v_7 \beta _3 \varPi _c(w_3 w_6-w_3 Z_w)},\nonumber \\ \end{aligned}$$

(13)

where, $Z_w=w_1+w_2+w_3+w_4+w_5$.

We have established the following conclusion.

Theorem 3

System (1) undergoes a backward bifurcation at $R_{01}=1$ whenever the inequality 13 holds.

We numerically shown the existence of backward bifurcation for the model (2), which verifies our analytical finding. The bifurcation diagram and related time series is presented in Fig. 2.

Fig. 3

Time series for the full model 1 showing bistability of the equilibrium values

Table 5 Normalized sensitivity indices

This implies that even if the basic reproduction number is less than unity, the disease may not be eradicated. To ensure the global stability of DFE one must reduce $R_{01}$ below a certain threshold namely, $R_{01}^c$.

4 Two strain model analysis

4.1 Diseases-free equilibrium and basic reproduction number

The diseases-free equilibrium can be obtained for the system (2) by putting $E_1=0, E_2=0, I_1=0, I_2=0, H_1=0, H_2=0, I_c=0$, which is denoted by $P_{01}=(S_h,0,0,0,0,0,0,R_h,S_c,0),$ where

$$\begin{aligned} S_h=\frac{\varPi _h}{\mu _h},S_c=\frac{\varPi _c}{\mu _c},R_h=0. \end{aligned}$$

4.1.1 Basic reproduction number

The basic reproduction number has been computed by next generation approach [16]. It is defined as the average number of secondary infections produced by a single infected individual in a susceptible population and it is given as

$$\begin{aligned} R_0=max\lbrace R_{01}, R_{02} \rbrace \end{aligned}$$

where

$$\begin{aligned} R_{0i}&=\frac{\beta _i r_i \gamma _i}{(\mu _h+\gamma _i)(\mu _h+k_{1i}+\eta _1)}\\&\quad +\frac{\alpha _i \beta _i r_i \gamma _i \eta _i}{(\mu _h+\gamma _i)(\mu _h+k_{1i}+\eta _i)(\mu _h+k_{2i}+\delta _i)}\\&\quad +\frac{\alpha _i \beta _i (1-r_i) \gamma _i}{(\mu _h+\gamma _i)(\mu _h+k_{2i}+\delta _i)}\\&\quad +\frac{\beta _{i+2} \beta _d r_i \gamma _i \varPi _c \mu _h}{\mu _c^{2}\varPi _h(\mu _h+\gamma _i)(\mu _h+k_{1i}+\eta _i)} \end{aligned}$$

4.2 Backward bifurcation analysis of the full model

We could not analytically find the conditions for the existence of backward bifurcation in case of the full model. Thus, we checked numerically whether this phenomenon occurs for the full model or not. Interestingly, we find parameters for which the full model undergoes bistable dynamics even if the basic reproduction number is below unity. The time series of bistability is depicted in Fig. 3.

The following set of hypothetical parameter values are used: $\varPi _h$=0.007, $\varPi _c$ =0.4817, m = 0.5, $\alpha _1 =\alpha _2 =0.0005$; $\gamma _1 =\gamma _2 =0.035$; $\mu _h$ = 0.00154, $\mu _c$ = 0.009, $\beta _1$ = 0.2; $\beta _2$ = 0.17; $\beta _3$ = 0.2; $\beta _4$ = 0.17; $\beta _d$=0.0025; $r_1$ = 0.98, $r_2$=0.7; $k_{11}=k_{21}$ = 0.001, $k_{12}$ = 0.0039, $k_{22}=0.0017$ $\eta _1=\eta _2$ = 1.01 and $\delta _1=\delta _2$ =0.04. For this parameter values, the basic reproduction number is found to be $0.7941<1$. This indicates that backward bifurcation or existence of bistability for $R_0<1$ is an inherent property of MERS-CoV transmission dynamics. In turn, this point out that the control efforts will need more careful considerations.

4.3 Normalized sensitivity analysis

Due to the complex dynamical behavior of the model, we calculate the normalized sensitivity indices of the model parameters with respect to $R_0$ in order to find the most influential parameters. We consider the following parameters for this analysis: $\beta _1$, $\beta _2$, $\beta _3$, $\beta _4$, $\beta _d$, $r_1$, $r_2$, $k_{11}$, $k_{12}$, $k_{21}$ and $k_{22}$. We use the parameter values from Table 2 for the baseline values. However, the mathematical definition of the normalized forward sensitivity index of a variable z with respect to a parameter $\tau$ (where z depends explicitly on the parameter $\tau$) is given as:

$$\begin{aligned} X^\tau _z=\frac{\partial z}{\partial \tau }\times \frac{\tau }{z}. \end{aligned}$$

It is important to note that we used the following expression for $R_0$: $R_0= \frac{R_{01}+R_{02} + |R_{01}-R_{02}|}{2}$. The sensitivity indices of $R_0$ with respect to the most important parameters are given in Table 5.

All other parameters have sensitivity indices less than 0.001. However, the fact that $X^{\beta _1}_{R_0}=0.0431$ means that if we increase 1% in $\beta _1$, keeping other parameters fixed, will produce 0.0431% increase in $R_c$. Similarly, $X^{k_21}_{R_0}=-0.0183$ means increasing the parameter $k_21$ by 1%, the value of $R_0$ will be decreased by 0.0183% keeping the value of other parameters be fixed. Biologically, this indicates that the transmission rate from strain-1 infected humans to susceptible camels and transmission rate from camels to susceptible humans are very crucial. These two quantities can be decreased by using personal protection measures. On the other hand, the recovery rate of un-notified infected with strain-1 should be increased to reduce the $R_0$ below unity. This can be achieved by tracing and treating un-notified infected humans with strain-1.

4.4 Optimal control analysis

In countries such as Saudi Arabia, Republic of Korea, United Arab Emirates etc, MERS-CoV is of great concern. For MERS-CoV transmission dynamics we formulate an optimal control problem [25]. The goal here is to demonstrate that time-dependent anti-MERS control strategies that can be implemented while minimizing the cost of implementing these measures. There are several control mechanisms that are put in place to minimize disease transmission. We consider four types of individual control mechanisms to mitigate MERS-CoV in the community. These single strategies are explained below:

• 1. Personal protection ($u_1(t)$): Preventing transmission of MERS-CoV in society requires the application of personal protective measures such as the use of face masks [7]. In this strategy, the susceptible humans are expected to reduce contacts with infected humans and camels.

• 2. Isolation of strain-1 infected notified people ($u_2(t)$): In this control mechanism, the strain-1 infected people who are notified are isolated from the other patients. These patients are given special attention so as to reduce contact with other people.

• 3. Isolation of strain-2 infected notified people ($u_3(t)$): Similarly, strain-2 infected people who are notified are specially isolated.

• 4. Isolation of infected camels ($u_4(t)$): Infected camels are to be found and are to be isolated in a special healthcare setting.

Note that for bounded Lebesgue measurable controls and non-negative initial conditions, non-negative bounded solutions to the state system exist [22]. The control functions $u_1(t)$, $u_2(t)$, $u_3(t)$ and $u_4(t)$ are bounded and Lebesgue integrable functions, where the associated force of infection in the human population is reduced by a factor of (1 - $u_1$(t)), where $u_1$(t) measures the level of successful prevention efforts and the control functions $u_2$(t), $u_3$(t) and $u_4$(t) represent the isolation of notified humans infected with strain-1 or strain-2 and isolation of infected camels, respectively.

Taking the above-mentioned interventions into account, the model (1) takes the following form

$$\begin{aligned} \displaystyle { \frac{\mathrm{d}S_h}{\mathrm{d}t} }= & {} \varPi _h-\beta _1 \frac{(1-u_1)S_h}{N_h}(I_1+\alpha _1 H_1)\nonumber \\&-\beta _2 \frac{(1-u_1)S_h}{N_h}(I_2+\alpha _2 H_2)\nonumber \\&-\beta _d\frac{(1-u_1)S_h}{N_h}I_c-\mu _h S_h,\nonumber \\ \displaystyle { \frac{\mathrm{d}E_1}{\mathrm{d}t} }= & {} \beta _1 \frac{(1-u_1)S_h}{N_h}(I_1+\alpha _1 H_1)\nonumber \\&+m\beta _d\frac{(1-u_1)S_h}{N_h}I_c-\mu _h E_1-\gamma _1 E_1,\nonumber \\ \displaystyle { \frac{\mathrm{d}E_2}{\mathrm{d}t} }= & {} \beta _2 \frac{(1-u_1)S_h}{N_h}(I_2+\alpha _2 H_2)\nonumber \\&+(1-m)\beta _d\frac{(1-u_1)S_h}{N_h}I_c-\mu _h E_2-\gamma _2 E_2,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_1}{\mathrm{d}t} }= & {} r_1\gamma _1 E_1-(\mu _h+k_{11}+\eta _1)I_1,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_2}{\mathrm{d}t} }= & {} r_2\gamma _2 E_2-(\mu _h+k_{12}+\eta _2)I_2,\nonumber \\ \displaystyle { \frac{\mathrm{d}H_1}{\mathrm{d}t} }= & {} (1-r_1)\gamma _1E_1+\eta _1 I_1\nonumber \\&-(\mu _h+k_{21}+\delta _1)H_1-u_2 H_1, \nonumber \\ \displaystyle { \frac{\mathrm{d}H_2}{\mathrm{d}t} }= & {} (1-r_2)\gamma _2E_2+\eta _2 I_2 \nonumber \\&-(\mu _h+k_{22}+\delta _2)H_2-u_3 H_2, \nonumber \\ \displaystyle { \frac{\mathrm{d}R_h}{\mathrm{d}t} }= & {} k_{11}I_1+k_{12}I_2+k_{21}H_1+k_{22}H_2-\mu _hR_h,\nonumber \\ \displaystyle { \frac{\mathrm{d}S_c}{\mathrm{d}t} }= & {} \varPi _c -\beta _3\frac{S_c I_1}{N_h}-\beta _4\frac{S_c I_2}{N_h}-\mu _c S_c,\nonumber \\ \displaystyle { \frac{\mathrm{d}I_c}{\mathrm{d}t} }= & {} \beta _3\frac{S_c I_1}{N_h}+\beta _4\frac{S_c I_2}{N_h}-\mu _c I_c-u_4 I_c. \end{aligned}$$

(14)

The problem is to minimize the cost function [12, 20, 25] given as follows:

$$\begin{aligned}&J(u_1, u_2, u_3, u_4)\nonumber \\&\quad =\int _{0}^{T} (C_1 H_1+C_2 H_2+C_3 I_c+\frac{1}{2}C_4 u_1^2\nonumber \\&\quad \quad +\frac{1}{2}C_5 u_2^2+\frac{1}{2}C_6 u_3^2+\frac{1}{2}C_7 u_4^2) \mathrm{d}t \end{aligned}$$

(15)

subject to the state system given by (14). The goal is to minimize the hospitalized infected human populations, infected camel population and the cost of implementing the control. Basically, we assume that the costs are proportional to the square of the corresponding control function. Our goal is to find optimal control functions $(u_1^*, u_2^*, u_3^*, u_4^*)$ such that

$$\begin{aligned}&J(u_1^*, u_2^*, u_3^*, u_4^*)\\&\quad =min\lbrace J(u_1, u_2, u_3, u_4)|(u_1, u_2, u_3, u_4)\in \varGamma \rbrace \end{aligned}$$

subject to the system of equations given by (14), where

$$\begin{aligned}&\varGamma =\lbrace (u_1, u_2, u_3, u_4)|u_i(t) \text { is Lebesgue measurable}\nonumber \\&\qquad \text {on } [0,T], 0\nonumber \\&\quad \le u_i(t)\le b_i, i=1, 2, 3, 4 \rbrace \end{aligned}$$

(16)

is the control set.

Pontryagin’s maximum principle [20] can be applied to find the optimal rates of different interventions and layered combinations. This principle converts system (14) into a minimizing problem. The Hamiltonian H, with respect to $u_1$, $u_2$, $u_3$ and $u_4$, can be written as:

$$\begin{aligned} H&=(C_1 H_1+C_2 H_2+C_3 I_c+\frac{1}{2}C_4 u_1^2+\frac{1}{2}C_5 u_2^2\nonumber \\&\quad +\frac{1}{2}C_6 u_3^2+\frac{1}{2}C_7 u_4^2) \nonumber \\&\quad +\lambda _1\Big [\varPi _h-\beta _1 \frac{(1-u_1)S_h}{N_h}(I_1+\alpha _1 H_1)\nonumber \\&\quad -\beta _2 \frac{(1-u_1)S_h}{N_h}(I_2+\alpha _2 H_2)\nonumber \\&\quad -\beta _d\frac{(1-u_1)S_h}{N_h}I_c-\mu _h S_h\Big ]\nonumber \\&\quad +\lambda _2\Big [\beta _1 \frac{(1-u_1)S_h}{N_h}(I_1+\alpha _1 H_1)\nonumber \\&\quad +m\beta _d\frac{(1-u_1)S_h}{N_h}I_c-\mu _h E_1-\gamma _1 E_1\Big ]\nonumber \\&\quad +\lambda _3\Big [\beta _2 \frac{(1-u_1)S_h}{N_h}(I_2+\alpha _2 H_2)\nonumber \\&\quad +(1-m)\beta _d\frac{(1-u_1)S_h}{N_h}I_c-\mu _h E_2-\gamma _2 E_2\Big ]\nonumber \\&\quad +\lambda _4[r_1\gamma _1 E_1-(\mu _h+k_{11}+\eta _1)I_1] \nonumber \\&\quad +\lambda _5[r_2\gamma _2 E_2-(\mu _h+k_{12}+\eta _2)I_2]\nonumber \\&\quad +\lambda _6[(1-r_1)\gamma _1E_1+\eta _1 I_1\nonumber \\&\quad -(\mu _h+k_{21}+\delta _1)H_1-u_2 H_1] \nonumber \\&\quad +\lambda _7[(1-r_2)\gamma _2E_2+\eta _2 I_2\nonumber \\&\quad -(\mu _h+k_{22}+\delta _2)H_2-u_3 H_2] \nonumber \\&\quad +\lambda _8[k_{11}I_1+k_{12}I_2+k_{21}H_1+k_{22}H_2-\mu _h R_h]\nonumber \\&+\lambda _9\Big [\varPi _c -\beta _3\frac{S_c I_1}{N_h}-\beta _4\frac{S_c I_2}{N_h}-\mu _c S_c\Big ]\nonumber \\&+\lambda _{10}\Big [\beta _3\frac{S_c I_1}{N_h}+\beta _4\frac{S_c I_2}{N_h}-\mu _c I_c-u_4 I_c\Big ] \end{aligned}$$

(17)

where $\lambda _i$, $i = 1,....,10$ are the adjoint variables. In the following theorem, we present the adjoint system and control characterization. To simplify notation, we let $\hbar =\frac{1}{N_h}$.

Theorem 4

Given an optimal control $(u_1^*, u_2^*, u_3^*, u_4^*)$, and corresponding state solutions $S_h$, $E_1$, $E_2$, $I_1$, $I_2$, $H_1$, $H_2$, $R_h$, $S_c$, $I_c$ of the corresponding state system (14), there exists adjoint variables, $\lambda _i$ ,for $i = 1,...,10$, satisfying

$$\begin{aligned}&\frac{\partial \lambda _1}{\partial t}=-(\lambda _2-\lambda _1)[\beta _1(1-u_1(t))(I_1+\alpha _1 H_1)(\hbar -S_h \hbar ^2)]\nonumber \\&\quad -(\lambda _3-\lambda _1)[\beta _2(1-u_1(t))(I_2+\alpha _2 H_2)(\hbar -S_h \hbar ^2)]\nonumber \\&\quad -(\lambda _2 m+\lambda _3(1-m)-\lambda _1)\nonumber \\&\quad \quad [\beta _d(1-u_1(t))I_c(\hbar -S_h \hbar ^2)]+\lambda _1 \mu _h, \nonumber \\&\frac{\partial \lambda _2}{\partial t}=-(\lambda _1-\lambda _2)[\beta _1(1-u_1(t))S_h(I_1+\alpha _1H_1)\hbar ^2]\nonumber \\&\quad -(\lambda _1-\lambda _3)[\beta _2(1-u_1(t))S_h(I_2+\alpha _2 H_2)\hbar ^2]\nonumber \\&\quad -(\lambda _1-\lambda _2m+\lambda _3(1-m))[\beta _d(1-u_1(t))S_h I_c \hbar ^2]\nonumber \\&\quad +\lambda _2(\mu _h+\gamma _1)-(\lambda _4-\lambda _6)r_1 \gamma _1-\lambda _6 \gamma _1,\nonumber \\&\frac{\partial \lambda _3}{\partial t}=-(\lambda _1-\lambda _2)[\beta _1(1-u_1(t))S_h(I_1+\alpha _1H_1)\hbar ^2]\nonumber \\&\quad -(\lambda _1-\lambda _3)[\beta _2(1-u_1(t))S_h(I_2+\alpha _2 H_2)\hbar ^2] \nonumber \\&\quad -(\lambda _1-\lambda _2m+\lambda _3(1-m))[\beta _d(1-u_1(t))S_h I_c \hbar ^2]\nonumber \\&\quad +\lambda _3(\mu _h+\gamma _2)-(\lambda _5-\lambda _7)r_2 \gamma _2-\lambda _7 \gamma _2,\nonumber \\&\frac{\partial \lambda _4}{\partial t}=-(\lambda _2-\lambda _1)[\beta _1(1-u_1(t))S_h(\hbar -(I_1+\alpha _1H_1)\hbar ^2)]\nonumber \\&\quad -(\lambda _1-\lambda _3)[\beta _2(1-u_1(t))S_h(I_2+\alpha _2 H_2)\hbar ^2] \nonumber \\&\quad -(\lambda _1-\lambda _2m-\lambda _3(1-m))[\beta _d(1-u_1(t))S_h I_c \hbar ^2]\nonumber \\&\quad +\lambda _4(\mu _h+k_{11}+\eta _1)-\lambda _6\eta _1-\lambda _8 k_{11} \nonumber \\&\quad -(\lambda _{10}-\lambda _9)[\beta _3 S_c(\hbar -I_1 \hbar ^2)-\beta _4 S_c I_2 \hbar ^2] \nonumber \\&\frac{\partial \lambda _5}{\partial t}=-(\lambda _1-\lambda _2)[\beta _1(1-u_1(t))S_h(I_1+\alpha _1H_1)\hbar ^2]\nonumber \\&\quad -(\lambda _3-\lambda _1)[\beta _2(1-u_1(t))S_h(\hbar -(I_2+\alpha _2H_2))\hbar ^2] \nonumber \\&-(\lambda _1-\lambda _2m+\lambda _3(1-m))[\beta _d(1-u_1(t))S_h I_c \hbar ^2]\nonumber \\&\quad +\lambda _5(\mu _h+k_{12}+\eta _2)-\lambda _7\eta _2-\lambda _8 k_{12} \nonumber \\&\quad -(\lambda _9-\lambda _{10})[\beta _3 S_c I_1\hbar ^2-\beta _4 S_c(\hbar -I_2 \hbar ^2)] \nonumber \\&\frac{\partial \lambda _6}{\partial t}=-C_1-(\lambda _2-\lambda _1)\nonumber \\&\quad [\beta _1(1-u_1(t))S_h(\alpha _1\hbar -(I_1+\alpha _1H_1)\hbar ^2)] -(\lambda _1-\lambda _3)\nonumber \\&\quad [\beta _2(1-u_1(t))S_h(I_2+\alpha _2 H_2)\hbar ^2] \nonumber \\&\quad -(\lambda _1-\lambda _2m-\lambda _3(1-m))[\beta _d(1-u_1(t))S_h I_c \hbar ^2]\nonumber \\&\quad +\lambda _6[(\mu _h+k_{21}+\delta _1)+u_2(t)]-\lambda _8 k_{21} \nonumber \\&\quad -(\lambda _9-\lambda _{10})[\beta _3 S_c I_1 \hbar ^2+\beta _4 S_c I_2 \hbar ^2] \nonumber \\&\frac{\partial \lambda _7}{\partial t}=-C_2-(\lambda _1-\lambda _2)[\beta _1(1-u_1(t))S_h(I_1+\alpha _1H_1)\hbar ^2]\nonumber \\&\quad -(\lambda _3-\lambda _1)[\beta _2(1-u_1(t))S_h(\alpha _2\hbar -(I_2+\alpha _2H_2))\hbar ^2] \nonumber \\&-(\lambda _1-\lambda _2m-\lambda _3(1-m))[\beta _d(1-u_1(t))S_h I_c \hbar ^2]\nonumber \\&\quad +\lambda _7[(\mu _h+k_{22}+\delta _2)+u_3(t)]-\lambda _8 k_{22} \nonumber \\&\quad -(\lambda _9-\lambda _{10})[\beta _3 S_c I_1\hbar ^2+\beta _4 S_c I_2 \hbar ^2] \nonumber \\&\frac{\partial \lambda _8}{\partial t}=-(\lambda _1-\lambda _2)[\beta _1(1-u_1(t))S_h(I_1+\alpha _1H_1)\hbar ^2]\nonumber \\&\quad -(\lambda _1-\lambda _3)[\beta _2(1-u_1(t))S_h(I_2+\alpha _2 H_2)\hbar ^2] \nonumber \\&\quad -(\lambda _1-\lambda _2m-\lambda _3(1-m))[\beta _d(1-u_1(t))S_h I_c \hbar ^2]\nonumber \\&\quad +\lambda _8\mu _h-(\lambda _9-\lambda _{10})[\beta _3 S_c I_1 \hbar ^2+\beta _4 S_c I_2 \hbar ^2] \nonumber \\&\frac{\partial \lambda _9}{\partial t}=-(\lambda _{10}-\lambda _9)\nonumber \\&\quad \quad [\beta _3 I_1 (\hbar -S_c \hbar ^2)+\beta _4 I_2(\hbar -S_c \hbar )] \nonumber \\&\frac{\partial \lambda _{10}}{\partial t}=-C_3-(\lambda _3(1-m)+\lambda _2 m-\lambda _1) \nonumber \\&\quad \quad [\beta _d(1-u_1(t))S_h \hbar ]+\lambda _{10}(\mu _c+u_4(t)). \end{aligned}$$

(18)

Fig. 4

Time series in presence of optimal control and without control for a Un-notified cases with strain-1, b Un-notified cases with strain-2, c Notified cases with strain-1, d Notified cases with strain-1 and e infected camels. The optimal control strategy is the combination of $U_1(t)$ and $U_4(t)$

The terminal conditions are

$$\begin{aligned} \lambda _i(T)=0 \text { for } i = 1,......,10. \end{aligned}$$

(19)

Furthermore, the optimal controls $u_1^*, u_2^*, u_3^*, u_4^*$ and are represented by

$$\begin{aligned} u_1^*&=\text {max}\Big \lbrace 0, \text {min}\Big \lbrace 1, \frac{1}{C_4}[\beta _1 S_h \hbar (I_1+\alpha _1 H_1)(\lambda _2-\lambda _1)\nonumber \\&\quad +\beta _2 S_h \hbar (I_2+\alpha _2 H_2)(\lambda _3-\lambda _1) \nonumber \\&\quad +\beta _d S_h I_c \hbar (\lambda _3 (1-m)+\lambda _2 m-\lambda _1)]\Big \rbrace \Big \rbrace \nonumber \\ u_2^*&= \text {max}\Big \lbrace 0, \text {min}\Big \lbrace 1,\frac{1}{C_5}\lambda _6 H_1 \Big \rbrace \Big \rbrace \nonumber \\ u_3^*&=\text {max}\Big \lbrace 0, \text {min}\Big \lbrace 1,\frac{1}{C_6}\lambda _7 H_2 \Big \rbrace \Big \rbrace \nonumber \\ u_4^*&= \text {max}\Big \lbrace 0, \text {min}\Big \lbrace 1,\frac{1}{C_7}\lambda _{10} I_c \Big \rbrace \Big \rbrace \end{aligned}$$

(20)

Proof

The adjoint system results from Pontryagin’s maximum Principle [20]

$$\begin{aligned} \frac{\partial \lambda _1}{\partial t}=-\frac{\partial H}{\partial S_h}, \frac{\partial \lambda _2}{\partial t}=-\frac{\partial H}{\partial E_1},....., \frac{\partial \lambda _{10}}{\partial t}=-\frac{\partial H}{\partial I_c} \end{aligned}$$

with zero final time conditions (transversality).

To get the characterization of the optimal control given by (20), we solve the equations on the interior of the control set,

$$\begin{aligned} \frac{\partial H}{\partial u_1}=0, \frac{\partial H}{\partial u_2}=0, \frac{\partial H}{\partial u_3}=0, \frac{\partial H}{\partial u_4}=0 \end{aligned}$$

Using the bounds on the controls, we obtain the desired characterization. $\square$

Fig. 5

Time evolution of optimal control profiles a $u_1(t)$ and b $u_4(t)$

The optimality system consists of the state system (14) with the initial conditions, the adjoint system with the terminal conditions and the control characterization.

We now numerically study the optimal strategies for the effect of combined control interventions by using a forward backward sweep fourth order Runge–Kutta method. The objective is to optimize the controls, $u_1$, $u_2$, $u_3$ and $u_4$. The values for the parameters used are given in Table 2 and the cost coefficients are taken as $C1=300$, $C_2=300$, $C_3=100$, $C_4=50$, $C_5=400$, $C_6=400$ and $C_7=200$. We consider six scenarios combining the four individual controls. We calculate two quantities to distinguish between interventions strategies, Infection Averted Ratio (IAR) and Average Cost-Effectiveness Ratio (ACER) [25]. IAR and ACER are defined as follows:

$$\begin{aligned}&IAR =\frac{Number of infection averted }{Number of successfully recovered }, \\&ACER =\frac{Total cost of intervention }{Number of infection averted }. \end{aligned}$$

These two measures are reported in the Table 6. These values indicate that combination of $u_1$ and $u_4$ is the best strategy to apply. We further give the graphical representation of the cases and control profiles in Figs. 4 and 5 respectively.

Table 6 Cost effectiveness of control strategies

These results indicate that reducing the contacts with infected people as well as infected camels along with isolation of infected camels is a very useful control strategy. This strategy is the most cost effective in terms of ACER and IAR.

5 Discussion and conclusion

In this paper, we introduce a general autonomous model that considers human and camel populations and probe further to understand the effect of optimal control strategies on the MERS-CoV infected populations. We mathematically analyze the single strain model to derive the basic reproduction number $R_{01}$ for the model and show that the disease-free equilibrium of the proposed model is globally asymptotically stable if $R_{01}< R_{01}^c < 1$. Further, we prove the existence of backward bifurcation phenomenon for the single strain version of the proposed model under some parametric conditions. We also numerically showed the existence of backward bifurcation, see Fig. 2. The basic reproduction number ($R_0$) of the full model is obtained and we numerically depicted the bistability even if $R_0<1$, see Fig. 3. Thus, the existence of bistability may be an inherent property of the MERS-CoV transmission dynamics. This phenomenon also indicates that the control interventions will require additional efforts to eradicate the disease from the community. To find the most influential parameters on $R_0$, we performed the normalized sensitivity analysis. Results indicate that, transmission rate from strain-1 infected humans to susceptible camels and transmission rate from camels to susceptible humans cam be decreased by using personal protection measures to reduce the epidemic potential. Additionally, the recovery rate of un-notified infected with strain-1 should be increased to reduce the $R_0$ below unity. This can be achieved by finding and treating un-notified infected humans with strain-1.

Time dependent intervention strategies can be implemented to curtail a disease on a finite time interval. Using optimal control analysis, we further investigated the effects of intervention strategies on infected human and camel populations in the model (1). We consider four types of control, i.e. effect of self-protection measures by susceptible humans, the isolation of notified humans infected with strain-1 or strain-2 and isolation of infected camels. Optimal control policy suggests that the combination of self-protection measures by susceptible humans and isolation of infected camels give cost-effective and efficient results for reducing disease prevalence. From Fig. 4, it can be observed that this combination strategy significantly reduces MERS-CoV cases. Finally, we conclude that cutting the transmission cycle between camels and humans is the key factor to eradicate the disease from the community.