1 Introduction

There are several examples in engineering for structures constituted by mechanical elements arranged in a cyclic and symmetric fashion, which range from aeroengine fans [1], turbine and compressor rotors [2], wind turbine rotors [3], propellers [4], blisks [5] and space structures [6,7,8]. Some of them are illustrated in Fig. 1. The repeating sector (unit cell) is typically constituted by a slender beam (the blade in aeroengines), which is connected to the hub through a mechanical joint, which provides the weak elastic coupling between different sectors. Since the ‘50s, it was recognized in solid state physics that a small disorder added to a linear crystal lattice may lead to spatial localization of vibration energy [9], which, in turn, may strongly influence the lattice transport properties [10]. Later on, the problem of vibration localization became central in engineering as for the relevance it has in turbomachinery [2, 11, 12]. Indeed, small deviations in the inertia or elastic properties of the rotor blades (unavoidable due to the manufacturing tolerances and wear) substantially change the underlying mode shapes of the system leading to spatial localization of vibration, up to remarkable amplification factor, e.g., about \(\simeq 6\) in a rotor with 121 blades [11] (although extreme cases are unlikely to happen). Clearly, such an event may be life-threatening for the blade [13,14,15], hence design strategies opt for considerable damping when large vibration amplitudes are reached, e.g., by introducing frictional dampers [16,17,18,19,20].

More recent studies have shown that vibration localization may take place also in nonlinear systems, due to the mode shape dependence on may lead to energy confinement [21,22,23,24,25,26,27,28,29]. For example Sato and co-authors [23, 24] first observed localization in an array of few hundreds micro-mechanical cantilever oscillators, in the presence of external excitation, disorder and damping. Even perfectly cyclic symmetric structures may suffer spatial localization of vibrations, with only a small part of the full structure vibrating with a considerable amplitude. This is mainly due to the system’s strong nonlinearities, such as nonlinear damping [30, 31], impacts [32] or nonlinear stiffness [33] (see also [34,35,36]). A key characteristic of these systems is that the “unit cell” is nonlinear and has multiple coexisting stable solutions (fixed points and/or periodic orbits) in a certain range of the operation conditions and parameters [33, 37, 38]. When the unit cells are assembled in a cyclic symmetric structure they may experience several coexisting stable states, which are typically obtained with few of the unit cells being on the excited state (typically a high amplitude limit cycle), while the others vibrate with a smaller amplitude.

Fig. 1
figure 1

Engineering applications with rotors with slender blades. In clockwise sense: high bypass ration turbofan engine, wind turbine, merchant ship propeller, aircraft turboprop engine (right panels). Images adapted from Wikipedia (https://en.wikipedia.org/wiki/Main_Page). Evolution of the turbofan engine bypass ratio (top-right panel) through years, entailing an increase in the fan blade slenderness; data taken from [39]. Evolution of the blade length of off-shore and on-shore wind turbines through the years; data take from [40]

Full size image

The claim for high power output and low energy consumption constantly pushes the design of new-generation turbomachinery toward larger rotors with higher blade aspect-ratio (see Fig. 1). Slender blades, alike those in the new-generation turbofan [41] or in wind turbines, undergoing large deformations are a perfect candidate to show localization in weakly coupled structures. In this work, we consider a cyclic symmetric structure constituted of three blades connected to the same hub. Each blade (the unit cell) is modeled as a thin airfoil with two degrees of freedom (2-DOF, pitch and plunge) loaded by a uniform airstream at a certain velocity V. When, at the critical flutter speed, the bifurcation is subcritical, the blade shows a range of bistability, which gives rise to multiple spatially localized stable states when a rotor, constituted by several elastically coupled blades, is considered. By following the solution branches along the airstream velocity for an isolated airfoil, we show that for low airstream velocities a stable fixed point and a periodic orbit may coexist, and that for high airstream velocity a stable limit cycle or irregular motion is exhibited, with a different degree of localization if measured on the plunge or on the pitch DOF. Finally, the concept of basin stability as a global stability metric is briefly introduced and the probability of the system to asymptotically approach a certain state (localized or not localized) is determined for a set of operational conditions, i.e., varying airstream velocity and various sets of initial conditions. It is shown that the system more likely converges on homogeneous or slightly localized solutions, while strongly localized states are restricted to a quite narrow range of airstream velocity .

2 Single airfoil

First, the dynamical response of a system constituting the unit cell, i.e., the 2-DOF airfoil system, is studied via time integration.

Fig. 2
figure 2

Sketch of the isolated airfoil with relevant dimensions. The pitch \(\alpha \) and plunge h are denoted with their positive displacement

Full size image

2.1 Governing equations for the single airfoil

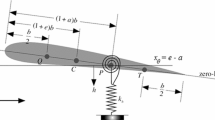
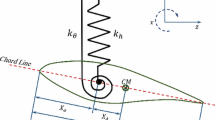
The model analyzed in the present work describes a planar oscillator by the plunge h and pitch \(\alpha \) degrees-of-freedom (DOF). The equations of motion provide a direct coupling between pitch and plunge by the inertial contributions. The nonlinear response of the system is provided by the cubic stiffness coefficients on the pitch and on the plunge (see Fig.  2). The pitch angle about the elastic axis is considered positive with the nose up; the plunge deflection is considered positive in the downward direction. The elastic center \(C^E\) is located at a distance ab from the mid-chord point (b represents half the chord length while a is a dimensionless parameter), while the mass center \(C^M\) is located at a distance e from the elastic center. \(C^A\) represents the aerodynamic center of the system. Both distances are positive when measured toward the trailing edge of the airfoil.

Hence, the governing equations of motion for the aeroelastic system under consideration are

$$\begin{aligned} \begin{aligned}&\mathrm{m} \ddot{{\tilde{\mathrm{h}}}} + \mathrm{me} \ddot{\alpha } + c_\mathrm{h} \dot{{\tilde{h}}} + k_{\mathrm{h}0}{\tilde{h}} + k_{\mathrm{h}3} {\tilde{h}}^3 = -L(t), \\&I_{\alpha } \ddot{\alpha } + \mathrm{me} \ddot{{\tilde{h}}} + c_{\alpha } {\dot{\alpha }} + k_{\alpha 0} \alpha + k_{\alpha 3} \alpha ^3 = M(t), \end{aligned} \end{aligned}$$
(1)

where the expression \({\tilde{\cdot }}\) denotes a dimensional variable. In the above equations, m is the mass of the blade, \(I_{\alpha }\) is the mass moment of inertia about the elastic axis. Viscous damping coefficients for plunge and pitch motion are represented by \(c_\mathrm{h}\) and \(c_{\alpha }\), respectively. L(t) and M(t) represent the aerodynamic force and moment at the aerodynamic center. In Eq. (1), t is the time variable and a dot superimposed represents a time derivative. For both pitch and plunge, a linear and a cubic stiffness coefficients are considered, respectively \(\{k_{\alpha 0},k_{\alpha 3}\}\) and \(\{k_{\mathrm{h}0},k_{\mathrm{h}3}\}\).

Modeling the time-dependent load, without prior assumptions on the airfoil motion periodicity is a challenging tasks in lumped-parameter models. According to the theory of isolated oscillating airfoil in an incompressible stream [42], the lift force L(t) and the aerodynamic moment M(t), reduced to the aerodynamic center, are given by

$$\begin{aligned} \begin{aligned} L(t)&= \rho U^2 b \, c_{\mathrm{L}} \left( \alpha ^e \right) , \\ M(t)&= \rho U^2 b \left( \frac{1}{2}+a \right) c_{\mathrm{L}} \left( \alpha ^e \right) , \end{aligned} \end{aligned}$$
(2)

being U the airstream velocity, \(\rho \) the air density and \(c_L\) the lift coefficient, expressed as a function of the equivalent pitch angle \(\alpha ^e\). Under the assumption of infinitesimal variation of the angle of attack, the lift coefficient can also be expressed as the product of the lift coefficient in the reference configuration \(c_\mathrm{L}^0\) and the equivalent pitch angle

$$\begin{aligned} c_\mathrm{L} \left( \alpha ^e \right) = c_\mathrm{L}^0 \, \alpha ^e . \end{aligned}$$
(3)

The equivalent pitch angle is defined under the assumptions of incompressible, inviscid flow past a zero-thickness airfoil at infinitesimal angle of attack. Following the theory of isolated oscillating airfoils in a uniform freestream [42], the equivalent pitch angle can be obtained from the summation of three components: (i) a uniform downwash angle corresponding to the pitching angle \(\alpha \); (ii) a uniform downwash due to vertical translation h; (iii) a nonuniform downwash due to \({\dot{\alpha }}\) at the 3/4 chord point

$$\begin{aligned} \alpha ^e = \alpha + \frac{{\dot{h}}}{U} + b \left( \frac{1}{2}-a \right) \frac{ {\dot{\alpha }}}{U} . \end{aligned}$$
(4)

In this scenario, the aerodynamic forces are configuration-dependent parameters which actively affect the dynamic behavior of the system

$$\begin{aligned} \begin{aligned} L(t)&= \rho U^2 b c^0_\mathrm{L} \left( \alpha + \frac{{\dot{h}}}{U} + b \left( \frac{ 1}{2}-a \right) \frac{{\dot{\alpha }}}{U} \right) \, , \\ M(t)&= \rho U^2 b c^0_\mathrm{L} \left( \frac{1}{2} + a \right) \\&\quad \left( \alpha + \frac{{\dot{h}}}{U} + b \left( \frac{1}{2}-a \right) \frac{{\dot{\alpha }}}{U} \right) . \end{aligned} \end{aligned}$$
(5)

From (1) and (5) the equations of motion yield

$$\begin{aligned} \begin{aligned}&\mathrm{m} \ddot{{\tilde{\mathrm{h}}}} + \mathrm{me} \ddot{\alpha } + c_\mathrm{h} \dot{{\tilde{h}}} + k_{\mathrm{h}0} {\tilde{h}} + k_{\mathrm{h}3} {\tilde{h}}^3 \\&\quad = -\rho U^2 b c^0_L \left( \alpha + \frac{{\dot{h}}}{U} + b \left( \frac{1}{2}-a \right) \frac{{\dot{\alpha }}}{U} \right) , \\&I_{\alpha } \ddot{\alpha } + me \ddot{{\tilde{h}}} + c_{\alpha } {\dot{\alpha }} + k_{\alpha } \alpha + k_{\alpha } \alpha ^3 \\&\quad = \rho U^2 b c^0_\mathrm{L} \left( \frac{1}{2} + a \right) \left( \alpha + \frac{{\dot{h}}}{U} + b \left( \frac{1}{2}-a \right) \frac{{\dot{\alpha }}}{U} \right) . \end{aligned} \end{aligned}$$
(6)

An equivalent dimensionless formulation can be obtained using the definitions

$$\begin{aligned} h=\frac{{\tilde{h}}}{b}; \quad t={\tilde{t}} \omega _{\alpha }; \quad \varepsilon = \frac{{\tilde{e}}}{b}, \end{aligned}$$
(7)

where \(\omega _\alpha = \sqrt{k_\alpha /m}\). Thus, by substituting these into Eq. (6), and introducing the dimensionless parameters

$$\begin{aligned} \begin{aligned} r^2&=\frac{I_{\alpha }}{\mathrm{mb}^2}; \quad \mu _h=\frac{c_h}{m \omega _{\alpha }}; \quad \mu _{\alpha }=\frac{c_{\alpha }}{\mathrm{mb}^2 \omega _{\alpha }}; \\ \xi _{\mathrm{h}0}&= \frac{k_{\mathrm{h}0}}{m \omega _{\alpha }^2}; \\ \xi _{\alpha 0}&=\frac{k_{ \alpha 0} }{\mathrm{mb}^2 \omega _{\alpha }^2}; \\ \xi _{\mathrm{h}3}&=\frac{k_{\mathrm{h}3} \mathrm{b}^2}{m \omega _{\alpha }^2}; \quad \xi _{\alpha 3}= \frac{k_{ \alpha 3}}{\mathrm{mb}^2 \omega _{\alpha }^2}; \\ \xi _\mathrm{u}&=\frac{\rho c_\mathrm{L}^0}{ \mathrm{mb}^2 \omega _{\alpha }^2}; \quad V=\frac{U}{b \omega _{\alpha }}, \end{aligned} \end{aligned}$$
(8)

the equations of motion finally read

$$\begin{aligned} \begin{aligned}&\ddot{h} + \varepsilon \ddot{\alpha } + \mu _\mathrm{h} {\dot{h}} + \xi _{\mathrm{h}0} h + \xi _{\mathrm{h}3} h^3 \\&\quad = - \xi _\mathrm{u} V^2 \left( \alpha + \frac{{\dot{h}}}{V} + \left( \frac{1}{2}-a \right) \frac{{\dot{\alpha }}}{V} \right) , \\&\varepsilon \ddot{h} + r^2 \ddot{\alpha } + \mu _a {\dot{\alpha }} + \xi _{\alpha 0} \alpha + \xi _{\alpha 3} \alpha ^3 \\&\quad = \xi _\mathrm{u} V^2 \left( \frac{1}{2 } + a \right) \left( \alpha + \frac{{\dot{h}}}{V} + \left( \frac{1}{2}-a \right) \frac{{\dot{\alpha }}}{V} \right) , \end{aligned} \end{aligned}$$
(9)

which can be written in matrix form as

$$\begin{aligned} {\mathbf{M}}{\ddot{\mathbf{q}}}(t) + {\mathbf{C}}{\dot{\mathbf{q}}}(t) + {\mathbf {K}}_1 {\mathbf {q}}(t) + {\mathbf {K}}_3 {\mathbf {q}}^3(t) = {\mathbf {0}} \, \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{aligned}&{\mathbf {q}}= \begin{bmatrix} h \\ \alpha \end{bmatrix}, \\&{\mathbf {M}}= \begin{bmatrix} 1 &{} \varepsilon \\ \varepsilon &{} r^2 \end{bmatrix}, \\&{\mathbf {C}}= \begin{bmatrix} \mu _\mathrm{h}+\xi _\mathrm{u} V &{} \xi _\mathrm{u} V \left( \frac{1}{2}-a \right) \\ - \xi _\mathrm{u} V \left( \frac{1}{2}-a \right) &{} \mu _{\alpha }-\xi _\mathrm{u} V \left( \frac{1}{4}-a^2 \right) \end{bmatrix} \, , \\&\mathbf {K_1}= \begin{bmatrix} \xi _{\mathrm{h}0} &{} \xi _\mathrm{u} V^2 \\ 0 &{} \xi _{\alpha 0}-\xi _\mathrm{u} V^2 \left( \frac{1}{2}+a \right) \end{bmatrix}, \\&\mathbf {K_3}= \begin{bmatrix} \xi _{\mathrm{h}3} &{} 0 \\ 0 &{} \xi _{\alpha 3} \end{bmatrix} . \end{aligned} \end{aligned}$$
(11)

Following [43, 44], the set of nondimensional parameters describing the system behavior is summarized in Table 1.

Table 1 Summary of system parameters of the single airfoil system
Full size table

2.2 Methodology

The integration of the equations of motion is performed by means of a state–space formulation, where the state vector is defined as:

$$\begin{aligned} {\mathbf {z}}= & {} \left[ z_1,z_2,z_3,z_4 \right] ^\mathrm{T} \nonumber \\= & {} \left[ h,\alpha ,{\dot{h}},{\dot{\alpha }} \right] ^T . \end{aligned}$$
(12)

With this arrangement, the governing equations can be conveniently expressed in the state-space form, which yields to four first-order ordinary differential equations

$$\begin{aligned} \begin{bmatrix} {\mathbf {I}} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {M}} \end{bmatrix} {\dot{\mathbf{z}}} = \begin{bmatrix} {\mathbf {0}} &{} {\mathbf {I}} \\ -{\mathbf {K}}_1 &{} -{\mathbf {C}} \end{bmatrix} {\mathbf {z}} + \begin{bmatrix} {\mathbf {0}} &{} {\mathbf {0}} \\ -{\mathbf {K}}_3 &{} {\mathbf {0}} \end{bmatrix} {\mathbf {z}}^3. \end{aligned}$$
(13)

2.3 Bifurcation behavior

By numerical time-marching integration of the equations of motion one can detect only stable solutions. However, it represents a valuable tool for the understanding of the DOF coupling effects as well as it can be exploited to find the critical speed under which bifurcations occur. Time integration of the equations of motion easily detects periodic, quasi-periodic or chaotic solutions showing how the final state of the system depends on the initial conditions. Furthermore, this choice of method will allow us to exploit the concept of basin stability analysis, which will be introduced later in Sect. 3.3. The equations of motion are integrated by an explicit Runge–Kutta scheme with adaptive time step size update by means of the MATLAB function ode23t with a relative and absolute tolerance equal to \(10^{-9}\). The integrations are initialized with two different disturbances on the plunge and pitch position: \({\mathbf {z}}_{0}^{(1)} =\left[ 0.01, 0, 0, 0\right] ^{\top }\) and \({\mathbf {z}}_{0}^{(2)} =\left[ 0.5, 0.5, 0, 0\right] ^{\top }\). Figure 3 depicts the root-mean-squared (RMS) steady-state amplitudes \(\left( \, {\hat{\cdot }} \, \right) \) of the plunge h and the pitch \(\alpha \) for a range of airstream velocities V. With the aim of investigating the effect of the stiffness nonlinearity on the system dynamics, we change the plunge stiffness nonlinear coefficient \(\xi _{\mathrm{h}3}=[100,180,260]\). For \(\xi _{\mathrm{h}3}=100\), a stable equilibrium position (fixed point) can be observed up to airstream velocities \(V=7.6\), then the fixed point loses stability to a stable periodic orbit. As the airstream velocity increases further, the oscillation amplitudes increase for both DOFs. However, the plunge starts to saturate at \({\hat{h}} \approx 0.07\) after \(V=12.0\), while the pitch amplitude keeps growing (see Fig. 3, green triangles). These trends suggest that the coupling between the DOFs (through the inertial term) has minimal influence on the system dynamics for the considered set of parameters. The steady-state motion is the same for trajectories starting from either initial conditions, such that no bistability regime can be observed for \(\xi _{\mathrm{h}3}=100\). This picture changes as the stiffness value is increased: for \(\xi _{\mathrm{h}3}=260\), we can observe a bistability regime for \(7.2 \le V \le 7.6\), where the stable equilibrium position and a stable periodic orbit coexist. Increasing the nonlinear stiffness value, the bistability regime stretches out along V, as shown in the lower panels in Fig. 3. Trajectories starting from the first initial condition \({\mathbf {z}}_{0}^{(1)}\) converge toward the fixed point, while trajectories starting from \({\mathbf {z}}_{0}^{(2)}\) are attracted by the stable periodic orbit.

Fig. 3
figure 3

Oscillation RMS \({\hat{h}}\) and \({\hat{\alpha }}\) as function of the airstream velocity obtained through time integrations. Open markers relate to solutions starting from \({\mathbf {z}}_{0}^{(1)} =\left[ 0.01, 0, 0, 0\right] ^{\top }\) and filled markers relate to initial conditions \({\mathbf {z}}_{0}^{(2)} =\left[ 0.5, 0.5, 0, 0\right] ^{\top }\). The second row provides two close-ups of the bifurcation diagrams in the first bistability region

Full size image

As the airstream velocity is increased further, at \(V=9.6\) (for \(\xi _{\mathrm{h}3}=260\)) another bifurcation point can be identified: trajectories starting from the two different initial solutions converge to different steady-state amplitudes: in case of the plunge, trajectories starting from \({\mathbf {z}}_0^{(1)}\) converge to a solution branch of larger amplitude, while trajectories starting from \({\mathbf {z}}_0^{(2)}\) converge to the previously observed solution path. Hence, for \(V\ge 9.6\) there coexist two stable dynamical equilibria for the airfoil. Depending on the choice of initial conditions, the system tends to converge to one of them. Interestingly, the second branch of oscillatory solutions in the pitch DOF appears at a significantly lower amplitude compared to the previous solution path. As a consequence, severe jumping phenomena may occur if the system is slightly perturbed, e.g., at \(V=10.0\): the plunge amplitude may suddenly jump to a motion of larger amplitude, while the pitch at the same time will jump to a significantly smaller amplitude motion. For \(\xi _{\mathrm{h}3}=260\), the single airfoil system in Eq. 9 exhibits two bistability regimes for the airstream velocity: for \(V \in {\mathcal {R}}_1 = \left[ 7.2, 7.6\right] \), a periodic orbit coexists with the stable equilibrium position (fixed point). For \(V \ge 9.6\), two stable dynamical equilibria exist. Eventually, one can notice from Figure 3 that the two DOFs provides significantly different oscillation amplitudes, which might be relevant for structural integrity. Notice that the sensitivity of the flutter behavior on the initial conditions has been experimentally measured in several nonlinear systems, including airfoil and shell structures [28, 29, 45, 46].

Fig. 4
figure 4

Plunge trajectories of the airfoil system for three airstream velocity values (from top to bottom), one row corresponds to the initial condition indicated on the left. Left column: trajectories; center column: steady-state response depicted in the state space of the plunge degree-of-freedom; right column: Poincar section displaying the intersections of the trajectories with the plane of zero pitch \(\alpha =0\)

Full size image
Fig. 5
figure 5

Pitch trajectories of the airfoil system for three airstream velocity values (from top to bottom), one row corresponds to the initial condition indicated on the left. Left column: trajectories; center column: steady-state response depicted in the state space of the pitch degree-of-freedom; right column: Poincar section displaying the intersections of the trajectories with the plane of zero plunge \(h=0\)

Full size image

Next, the dynamics are studied in more detail in Figs 4 and  5 for \(\xi _{\mathrm{h}3}=260\) at three different airstream velocity values: (a) in the first bistability regime \({\mathcal {R}}_1\) at \(V=7.3\), (b) in the regime of a unique periodic solution at \(V=8.0\), and (c) in the second bistability regime \({\mathcal {R}}_2\) at \(V=11.0\). The trajectories of the plunging and pitching motions are depicted for two representative initial conditions that illustrate the bistability behavior. It becomes visible that the steady-state vibrations are not given by trivial period-1 cycles. At \(V=7.3\), the Poincar sections of both pitch and plunge indicate that the orbit is in fact a period-7 cycle with an amplitude-modulating behavior visible from the time series. In the mono-stable regime at \(V=8.0\), the dynamics of the plunge motion turns out to have a more complicated temporal behavior, whereas the pitch motion keeps a vibration with one dominating frequency. The Poincar section states that this motion is a regular period-9 cycle, even if the time traces may appear to be irregular. In the second bistability regime at \(V=11.0\), a small-amplitude period-1 orbit exists for initial conditions starting from very small deflections on both DOFs. Larger initial conditions on the plunge converge to an orbit of larger amplitudes that exhibits irregular dynamics. No clear attractor can be observed in the phase diagram of the plunge, and the Poincar section displays a point cloud with some structure. On the other hand the same initial conditions provide a much more regular trajectory on the pitch and a clearly circular structure of the Poincar section.

Figure 6 concisely summarizes the results of Figs. 4 and 5. For the same loading conditions, it shows the RMS oscillation amplitude \({\hat{A}}\) as a function of the ratio \(\xi _{\mathrm{h}3}/\xi _{\alpha 3}\), (with \(\xi _{\alpha 3}=20\)) and for three airstream velocity \(V = [7.3, 8, 11]\). Up to \(\xi _{\mathrm{h}3}/\xi _{\alpha 3}\) about 5, both h and \(\alpha \) have unique dynamical equilibria independently on the initial conditions. For larger \(\xi _{\mathrm{h}3}/\xi _{\alpha 3}\), the system dynamics changes consistently. The system is attracted by different solutions which depend on the initial conditions. In a real rotor, severe jumps from one solution to the other may take place, which may be life-threatening for the airfoil. Further, in the next section, it will be shown that the existence of multiple equilibria for the unit cell in a rotor configuration may lead to strongly spatially localized vibrating states that coexist for the same airstream velocity.

Fig. 6
figure 6

RMS vibration amplitude against nonlinear stiffness ratio. Plunging and pitching amplitudes are displayed with red and blue markers, respectively, whereas the line type is associated with the initial perturbation

Full size image

3 Rotor model

In Sect. 2, the dynamical behavior of a single airfoil immersed in a uniform airstream was studied. Nevertheless, the single and slender airfoil constitutes only the unit cell of a larger cyclic-symmetric structure. Here, we consider a ’rotor model,’ which is constituted by \(N=3\) unit cells, elastically connected through a linear spring connecting the plunge degrees-of-freedom (Fig. 7), which accounts for the mechanical coupling originated at the common hub at which all the airfoils are mechanically connected.

Fig. 7
figure 7

Sketch of the rotor mode configuration with three airfoils connected through the plunge DOF. Each airfoil represents the unit illustrated in Fig. 2

Full size image

3.1 Governing equations

Assuming that all airfoils have the same mechanical properties, and are excited by the same aerodynamic load, the nondimensional governing Equations written for the n-th airfoil as:

$$\begin{aligned}&\ddot{h}_\mathrm{n} + \varepsilon \ddot{\alpha }_\mathrm{n} + \mu _\mathrm{h} {\dot{h}}_\mathrm{n} + \xi _{\mathrm{h}0} h_\mathrm{n}+ \xi _{\mathrm{h}3} h_\mathrm{n}^3 \nonumber \\&\quad + \eta _\mathrm{c} \left( 2h_\mathrm{n} -h_{\mathrm{n}+1}-h_{\mathrm{n}-1} \right) = \nonumber \\&\quad -\xi _\mathrm{u} V^2 \left( \alpha _n + \frac{{\dot{h}}_\mathrm{n}}{V} + \left( \frac{1}{2}-a \right) \frac{{\dot{\alpha }}_n}{V} \right) , \end{aligned}$$
(14)
$$\begin{aligned}&\varepsilon \ddot{h}_\mathrm{n} + r^2 \ddot{\alpha }_\mathrm{n} + \mu _a {\dot{\alpha }}_\mathrm{n} + \xi _{\alpha 0} \alpha _\mathrm{n} + \xi _{\alpha 3} \alpha _\mathrm{n}^3 \nonumber \\&\quad = \xi _\mathrm{u} V^2 \left( \frac{ 1}{2} + a \right) \left( \alpha _\mathrm{n} + \frac{{\dot{h}}_\mathrm{n}}{V} + \left( \frac{1}{2} -a \right) \frac{{\dot{\alpha }}_\mathrm{n}}{V} \right) . \end{aligned}$$
(15)

where the nondimensional plunge coupling coefficient \(\eta _\mathrm{c}\) is related to its dimensional counterpart \(k_\mathrm{c}\) by:

$$\begin{aligned} \eta _\mathrm{c}=\frac{k_c}{\mathrm{mb}^2 \omega _{\alpha }^2} . \end{aligned}$$
(16)

Following the state-space arrangement used for the single airfoil characterization, the state vector for a chain of airfoil is defined as:

$$\begin{aligned}&{\mathbf {z}}= \left[ z_1,\dots , z_{4N} \right] ^\mathrm{T} \nonumber \\&\quad = \left[ h_1,\alpha _1,\dots , h_N,\alpha _N, {\dot{h}}_1,{\dot{\alpha }}_1,\dots , {\dot{h}}_N,{\dot{\alpha }}_N \right] ^\mathrm{T}.\nonumber \\ \end{aligned}$$
(17)

With this arrangement, the matrix formulation corresponding to Eq. (14) can be conveniently implemented by means of the local coefficient matrices (10). Each blade within the oscillator chain is assumed to have the same values of nondimensional coefficients of the single airfoil case. The other system parameters are chosen as

$$\begin{aligned} N=3, \quad \eta _\mathrm{c}=0.02 . \end{aligned}$$
(18)

3.2 Bifurcation behavior

Figure 8 shows the rotor bifurcation plots with the same parameter setting and the load range of V used for the unit cell analysis. Specifically, we selected the largest value of nonlinear plunge stiffness \(\xi _{\mathrm{h}3}=260\), i.e., where the unit cell exhibits two bistable regimes. The flutter amplitude of the rotor is computed as a root mean square value of the RMS amplitude of each blade:

$$\begin{aligned} {\tilde{A}}= \sqrt{\frac{1}{N} \sum _{i=1}^{N} {\hat{A}}_i^2 \,,} \end{aligned}$$
(19)

The different localization states are identified by performing two time stepping simulations (increasing-V sweep and decreasing-V sweep) for each of the following initial conditions

$$\begin{aligned} {\mathbf {z}}_{0}^{(1)}= & {} \left[ 0.01,0.01,0.01,0.01,0.01,0.01,0,\ldots ,0\right] ^{\top } \nonumber \\ {\mathbf {z}}_{0}^{(2)}= & {} \left[ 0.5,0.5,0.01,0.01,0.01,0.01,0,\ldots ,0\right] ^{\top } \nonumber \\ {\mathbf {z}}_{0}^{(3)}= & {} \left[ 0.5,0.5,0.5,0.5,0.01,0.01,0,\ldots ,0\right] ^{\top } \nonumber \\ {\mathbf {z}}_{0}^{(4)}= & {} \left[ 0.5,0.5,0.5,0.5,0.5,0.5,0,\ldots ,0\right] ^{\top }. \end{aligned}$$
(20)

According to Fig. 8 (panels a, b), several bifurcations of the equilibrium solutions take place and multiple stable states coexist. Depending on the sweep directionFootnote 1 and the initial values, the rotor converges to different states at the same loading condition. These states correspond to different patterns of vibration localization, which can be observed by looking at the normalized RMS amplitude of each blade in Fig. 9.

Fig. 8
figure 8

Bifurcation diagrams (a,b) of plunge h (left panel) and pitch \(\alpha \) (right panel) as function of the airstream velocity for a cyclic symmetric chain of \(N=3\) blades. The coexisting stable states are identified by applying \(n=4\) combinations of small and large initial perturbation. The normalized vibration RMS amplitude of the solutions labeled with numbers from 1–6 are shown in Fig. 9. The corresponding localization coefficients from Eq. (21) are displayed in (c,d)

Full size image

To quantify the degree of localization, the localization coefficient L is introduced

$$\begin{aligned}&L \left( \hat{{\mathbf {z}}}\right) = \left( \frac{\mathrm {max} \left( {\hat{z}} \right) }{\sum _i^N {\hat{z}}_i} - \frac{1}{N} \right) \frac{N}{N-1}, \quad L \in \left[ 0, 1\right] , \nonumber \\&\quad \hat{{\mathbf {z}}} = \left[ {\hat{z}}_1, \dots , {\hat{z}}_N\right] \end{aligned}$$
(21)

where \({\hat{z}}_i\) denotes the RMS steady-state amplitude of the ith state, and N denotes the number of blades, e.g., \(N=3\) in this study. Essentially, the localization coefficient represents a measure for the degree of spatial localization for a given vibration pattern, such that for an exemplary set of vibration patterns the following localization coefficients result:

$$\begin{aligned}&L \left( \left[ 1, 1, 1 \right] \right) = 0.0, \nonumber \\&L \left( \left[ 1, 0, 0 \right] \right) = 1.0, \nonumber \\&L \left( \left[ 2, 2, 1 \right] \right) = 0.1. \end{aligned}$$
(22)

Hence, L is vanishing for the case of a homogeneous vibration pattern, and it is equal to unity in the limiting case in which a single blade vibrates, while the two others remain at the fixed point solution. In Fig. 8c, d, we have reworked the bifurcation diagrams shown in Fig. 8a, b to show the localization coefficient L as a function of the airstream velocity V for the different solutions found. These results indicate that the localization characteristics are different in the two multistable regimes: at lower V values, there exist states that are highly localized with L close to 1, i.e., where one blade vibrates while the other two remain at the fixed point solution. For different initial values, two blades vibrate and one stays at the fixed point, resulting in \(L \approx 0.25\). Lastly, all blades can either vibrate or collectively stay at the fixed point, i.e., resulting in \(L=0\). In the velocity range \(V=[7.6,9.6]\) homogeneous vibration patterns can be observed in between the two multistable regimes. In the second multistable regime at larger V values, significantly lower L values are found, i.e., less pronounced localization characteristics are observed.

Fig. 9
figure 9

For the solutions labeled with numbers from 1 to 6 in Figure 8 the normalized RMS vibration amplitude of each blade \({\hat{A}}_i\) and the resulting localization coefficient L is displayed. The plunge amplitude \({\hat{A}}_\mathrm{h}\) is normalized by the value \(A_{\mathrm{hn}}=0.25\), whereas the pitch amplitude \({\hat{A}}_{\alpha }\) is normalized by the value \(A_{\alpha \mathrm{n}}=0.8\). Red bars refer to the plunging DOF and blue bars refer to the pitching DOF. The load parameter for each labeled solution is \(V_1=7.4103\), \(V_2=V_3=7.5385\) and \(V_4=V_5=V_6=10.359\)

Full size image

Looking at the vibration patterns reported in Fig. 9, one can observe that solution (1) is strongly localized, while solutions (3,4) are homogeneous in space (compare Fig. 8a,b with Fig. 9). Some degree of localization can be observed for the other solutions. In the first multistable region (\(7.2 \le V \le 7.7\)), the localization pattern directly relates to the initial perturbances on each DOF: larger initial values on the first blade excite a strongly localized vibration where the first blade is in the ’excited state,’ while the two other blades remain close to the fixed point solution showing a very small vibration amplitude. Larger initial conditions on two blades cause excited states in these two DOFs, which is a behavior that one would expect from the analysis of the unit cell. The interaction between the unit cells is not strong enough to excite neighboring blades irrespective of their initial perturbances. Interestingly, in the second multistable region (\(V>9.6\), points (4–6)) the localization of pitch and plunge vibrations is ’opposite’: when the plunge shows weak localization, the pitch shows significantly stronger localization, and vice versa. So, in real-life applications, when measuring amplitudes on either of these DOFs, one would come to different conclusions about the localization in the system with strong localization in the torsional motion and slight localization in the bending motion. Overall, in the parameter range of larger airstream velocities there are no strong localizations as the blades vibrate either on the lower-amplitude periodic solution, or on the higher-amplitude irregular state.

It has been shown that the rather simple rotor model constituted of three bistable units cells can exhibit several different vibration patterns, both homogeneous and localized. As a strongly localized vibration may cause serious threats (enhancing wear, exceeding critical mechanical resistance, reducing fatigue life, etc.) to realistic cyclic structures, we are interested in the likelihood of occurrence of specific vibration patterns. In the following basin stability analysis, we aim at quantifying how likely all of the observed vibration patterns are for a given range of initial perturbances prescribed on each blade.

3.3 Basin stability

The concept of basin stability was recently introduced by Menck et al. [47] and denotes a probabilistic approach to assessing the global stability of a solution in a multistability scenario. Local stability metrics such as the Lyapunov exponent indicate stability against small perturbations. Hence, they characterize the attractiveness of a solution in its neighborhood, and quantify the rate of trajectories approaching/diverging from that solution. However, local stability measures do not resolve the largest permissible perturbation that will still converge back to that solution. In multistable nonlinear systems, even small perturbations may let the trajectory jump to a different basin of attraction, such that the trajectory will be attracted by another solution. Explicit knowledge of the basins of attraction would allow to state permissible perturbations, i.e., the global stability of a solution. However, expressions for the basin boundaries are difficult to obtain even for low-dimensional systems. The concept of basin stability aims at approximating the basins’ volumes through Monte Carlo simulations, and thereby measuring the global stability of a solution by the volume of its basin of attraction in the state space.

To derive the basin stability value, a reference subset \({\mathcal {Z}}\) of the state space must be chosen such that the Monte Carlo simulations can draw samples for the initial conditions from this set. The selection of \({\mathcal {Z}}\) affects the final basin stability values, and is obviously subject to the domain expert that has some a priori knowledge about reasonable perturbations of the system’s state of operation. Then, a number of n samples is drawn uniformly at random from \({\mathcal {Z}}\). The resulting long-term trajectories are obtained through time marching solutions of the system, and the steady-state behavior is classified to have converged to one of the multiple attractors. Finally, the basin stability value \({\mathcal {S}}_{{\mathcal {B}}}\left( {\mathcal {A}} \right) \) of the attractor \({\mathcal {A}}\) is derived from the ratio of \(n\left( {\mathcal {A}} \right) / n\) solutions that converged to it. Hence, the basin stability measures the likelihood of the system to converge to a specific attractor given a reference set of initial conditions at a given probability density function. The basin stability analysis in this work was performed using the open-source and MATLAB-based bSTAB code [48].

We study the probability of localized vibrations for a strictly prescribed range of initial conditions. As a reference set \({\mathcal {Z}}^{(0)}\) of initial solutions, we choose all plunge \(h_\mathrm{i}\) and pitch \(\alpha _\mathrm{i}\) DOFs to be limited to the interval \(\left( h_\mathrm{i}, \alpha _\mathrm{i} \right) \in \left[ -0.01, 0.01\right] \). For the Monte Carlo simulations, \(n=2000\) initial conditions are drawn from a uniform random distribution within this interval. All velocities initial conditions, i.e., \({\dot{h}}_\mathrm{i}\) and \({\dot{\alpha }}_\mathrm{i}\), are fixed to 0

$$\begin{aligned} {\mathcal {Z}}^{(0)} = \begin{bmatrix} h_1 \\ \alpha _1 \\ h_2 \\ \alpha _2 \\ h_3 \\ \alpha _3 \\ {\dot{h}}_1 \\ \vdots \\ {\dot{\alpha }}_3\\ \end{bmatrix}_{t=0} = \quad \begin{bmatrix} -0.01, \ldots , 0.01 \\ -0.01, \ldots , 0.01 \\ -0.01, \ldots , 0.01 \\ -0.01, \ldots , 0.01 \\ -0.01, \ldots , 0.01 \\ -0.01, \ldots , 0.01 \\ 0 \\ \vdots \\ 0 \end{bmatrix}. \end{aligned}$$
(23)

Variants of \({\mathcal {Z}}^{(0)}\) are studied in the remainder of this section: First, larger initial conditions \({\mathcal {Z}}^{(1)}\): \(h_1 \in \left[ -0.15, 0.15\right] \), \(\alpha _1 \in \left[ -0.5, 0.5 \right] \) for the first blade are introduced. Secondly, larger initial conditions are allowed for two blades \({\mathcal {Z}}^{(2)}\): \(h_{1,2} \in \left[ -0.15, 0.15\right] \), \(\alpha _{1,2} \in \left[ -0.5, 0.5 \right] \), and lastly all blades are subjected to larger initial conditions \({\mathcal {Z}}^{(3)}\): \(h_{1, 2, 3} \in \left[ -0.15, 0.15\right] \), \(\alpha _{1, 2, 3} \in \left[ -0.5, 0.5 \right] \). The basin stability analysis will then compute the probability of specific vibration pattern. Four classes of (potentially localized) vibration patterns are defined through the localization coefficient in Eq. 21:

$$\begin{aligned} \begin{aligned}&L_{0.0-0.05}: \quad 0.00 \le L< 0.05 \\&\quad \text {homogeneous vibrations} \\&L_{0.05-0.15}: \quad 0.05 \le L< 0.15 \\&\quad \text {slightly localized vibrations} \\&L_{0.15-0.45}: \quad 0.15 \le L < 0.45 \\&\quad \text {moderately localized vibrations} \\&L_{0.45-1.0}: \quad 0.45 \le L \le 1.00 \\&\quad \text {strongly localized vibrations.} \\ \end{aligned} \end{aligned}$$
(24)

Basin stability values are computed for these localization classes along the parameter variation of V, thus indicating which localization pattern is the most probable for the given choice of initial conditions at a specific airstream velocity value. Localization coefficients and related classes are computed for the plunge DOF.

3.3.1 Localization after perturbation of a single blade

First, larger initial conditions are allowed for the first blade only. Practically, this setup may correspond to one blade of the rotor experiencing a severe perturbation, due to a foreign object impact, like a bird strike. Figure 10 displays the state space of the first blade and the sampling points for the basin stability at \(V=7.3\). For small initial conditions, all blades remain at their fixed points, such that the resulting dynamics do not exhibit any localized vibrations. For larger initial conditions, high-amplitude vibrations are excited in the first blade, such that strongly localized vibrations are observed and quantified by \(L_{0.45-1.0}\). For the choice of \({\mathcal {Z}}^{(1)}\), \(L_{0.45-1.0}\) localized vibrations are the most probable to occur at \(95\%\) for the plunge h and the plunge \(\alpha \). Weakly or moderately localized vibrations do not occur at all at this airstream velocity value. This result may be somewhat expected: larger perturbations of a single blade will in most cases lead to vibration that are strongly localized at that blade.

Fig. 10
figure 10

State-space sampling at \(V=7.3\) (\(n=2000\) samples) for larger initial conditions of the first blade (\({\mathcal {Z}}^{(1)}\)) and the corresponding localization behavior in (a). The resulting basin stability values for the localization classes of the plunge DOF are displayed in (b)

Full size image

However, a constant airstream velocity may not be a realistic assumption, and the picture at \(V=7.3\) is a rather limited viewpoint. Figure 11 depicts the basin stability values of all stable solutions along V. In correspondence with Fig. 8, no flutter (and hence no localized vibrations) are observed for \(V<7.2\). For larger airstream velocities in the first multistable range, the strongly localized state is the most probable, and only few trajectories remain in the homogeneous state. This picture changes instantly as the multistable regime is left at \(V=7.7\), and all blades oscillate homogeneously. In the second multistable range \(9.7 \le V \le 10.4\), localized vibrations can be observed along with homogeneous vibrations, before the homogeneous state becomes the dominating characteristic again.

Fig. 11
figure 11

Basin stability values of the localized solutions for larger initial conditions of the first blade (\({\mathcal {Z}}^{(1)}\)) as a function of the airstream velocity

Full size image

3.3.2 Localization after perturbation of two and three blades

Next, the first two blades are chosen for larger initial conditions, such that \(\left( h_{1,2}, \alpha _{1,2}\right) \in \left[ -0.5, 0.5\right] \), denoted as \({\mathcal {Z}}^{(2)}\). The aim is to study which vibration pattern, i.e., which localization, will happen in multistability ranges for a set of initial conditions drawn from \({\mathcal {Z}}^{(2)}\). The resulting basin stability values are depicted in Fig. 12 (a). For most of the first multistability range, the moderately localized states, i.e., two excited blades, are the most likely at \(>95\%\) , while only less than \(5\%\) of all initial conditions converge to strong localization. Notice that in the transition between homogeneous and moderately localized states \((V\approx 7.2)\) strongly localized patterns appear with a probability of about \(50\%\). This behavior can be expected for our choice of initial conditions. The second multistable regime exhibits two sub-regimes, where first the slight localization and, then the homogeneous vibration compete with each other. Hence, even though the rotor model has four stable solutions depicted in Fig. 8, for our choice of initial conditions the behavior reduced mostly to a bistable-alike system for most of the airstream velocities. However, transitions to localized states happen instantaneously, thus representing potentially dangerous jumping phenomena.

Fig. 12
figure 12

Basin stability values for a larger initial conditions of two blades (\({\mathcal {Z}}^{(2)}\)) and b larger initial conditions of all three blades (\({\mathcal {Z}}^{(3)}\)) as a function of the airstream velocity

Full size image

If all three blade DOFs are subjected to larger initial conditions \(\left( h_{1,2, 3}, \alpha _{1,2,3}\right) \in \left[ -0.5, 0.5\right] \), denoted as \({\mathcal {Z}}^{(3)}\), the basin stability values show a significantly different behavior, see Fig. 12b. At the lower end of the multistability range the moderate and strong localization compete for a narrow airstream velocity \((V \approx 7.2)\). Hereafter, the homogeneous pattern becomes the strongly dominating vibration behavior, and only few observations of moderate localization are made. In the upper multistable range, the homogeneous and weakly localized patterns compete at almost equal probability, while no relevant amounts of stronger localization patterns can be observed.

Overall, the basin stability analysis shows that strongly localized vibration patterns are obtained rarely, only in the low velocity multistability range and only when a single blade is strongly excited. If larger perturbations are selected on two or three blades, then only slight or moderate localization was found. Our results suggest that in real-world applications, homogeneous (or slightly localized) states should be more likely to happen, which is beneficial for the mechanical components as vibration localization is usually cause of severely localized wear, damage and loss of stiffness. Nevertheless, strongly localized states may not be excluded a priori; hence, the knowledge of the nonlinear dynamical response of the mechanical rotor remains essential.

4 Conclusion

In this paper, the nonlinear dynamical behavior of a rotor constituted by \(N=3\) slender airfoils with 2-DOF each and subjected to flutter instability has been studied. For a single airfoil (with 2 DOFs, plunge and pitch), it has been shown that for large plunge cubic stiffness coefficient multiple coexisting dynamical equilibria exist which, at low airstream velocity, are a fixed point and a limit cycle, while for large airstream velocity, are a limit cycle and an irregular motion. By considering the full rotor as \(N=3\) elastically coupled airfoils, the existence of multiple localized vibration states has been shown. By restricting the state space to a certain hypervolume of initial conditions, the concept of basin stability has been exploited to determine the likelihood of the system to converge to localized states. A localization parameter was defined to classify the possible states obtained, which equals 1 for highly localized states and 0 for homogeneous states. It has been shown that the external perturbation, imposed as different initial conditions on the three blades, correlates with the probability of localized vibrations: if a single airfoil is strongly excited, then strongly localized vibrations are the most likely system state to observe. If all airfoils are subjected to a similar range of perturbations, the homogeneous or weakly localized vibration state dominates the system dynamics. Overall, these results show that strongly localized vibration patterns are obtained more rarely than slightly or moderate localized solutions. Nevertheless, strongly localized states may not be excluded a priori; hence, a detailed knowledge of the nonlinear rotor dynamics remains essential to avoid local wear and damage of a single blade. Further studies are needed to assess the severity and likelihood of nonlinear localization in more realistic rotor models, able to capture the complex aerodynamic phenomena. For instance, further studies should account for the effects of stall on the lift and moment exerted by the flow on the airfoil, as well as for the aerodynamic coupling between the blades [49, 50].