Nonlinear vibrations and time delay control of an extensible slowly rotating beam

Abstract

Nonlinear dynamics of a rotating flexible slender beam with embedded active elements is studied in the paper. Mathematical model of the structure considers possible moderate oscillations thus the motion is governed by the extended Euler–Bernoulli model that incorporates a nonlinear curvature and coupled transversal–longitudinal deformations. The Hamilton’s principle of least action is applied to derive a system of nonlinear coupled partial differential equations (PDEs) of motion. The embedded active elements are used to control or reduce beam oscillations for various dynamical conditions and rotational speed range. The control inputs generated by active elements are represented in boundary conditions as non-homogenous terms. Classical linear proportional (P) control and nonlinear cubic (C) control as well as mixed ($P-C$) control strategies with time delay are analyzed for vibration reduction. Dynamics of the complete system with time delay is determined analytically solving directly the PDEs by the multiple timescale method. Natural and forced vibrations around the first and the second mode resonances demonstrating hardening and softening phenomena are studied. An impact of time delay linear and nonlinear control methods on vibration reduction for different angular speeds is presented.

1 Introduction

Slender beam-like elements play an important role in engineering and structural design. Typical applications might be cranes, aircraft wings, diving boards at swimming pools, overhang structural elements of civil engineering like masts or roof supports. When rotary motion of the structure is considered further examples might be wind turbines blades, helicopter blades, aircraft propellers, etc.

Advances over the years in composite materials technology as well as increasing demands particularly from aeronautics and off-shore engineering have stimulated the extensive use of light and flexible elements. Predominantly, they are subjected to large elastic deformations that affect the precision and stability of the structure motion. Moreover, large deformations combined with low structural damping may lead to fatigue damage and shorten the lifespan of the design. Therefore, the attenuation of large vibrations observed in highly flexible beam-like elements is a problem of primary importance.

Driven by practical needs as well as theoretical challenges, efficient and accurate modeling of flexible beams dynamics and their control have received great attention in the literature. Depending on complexity, current compact beam theories can be divided into three main groups: (a) un-shearable theory including the classical Euler–Bernoulli one, (b) shear deformable models— e.g., Timoshenko theory, the third-order shear theory etc., and (c) three-dimensional beam theories capturing different phenomena neglected by the former two approaches. Typically, each of commonly accepted theories can be formulated within linear or nonlinear framework. Linear models are very useful in a case of relatively stiff systems, performing small oscillations. For thin slender flexible elements that undergo large deformations, use of nonlinear theories is much more favorable [32].

The dynamics of a rotating beam system within nonlinear framework was examined by several researchers. Weidenhammer [44] studied rotating beams by adopting a (not-complete) nonlinear theory of Bernoulli–Euler beams; the governing equations of motion were derived applying Hamilton’s principle. The influential work presenting a comprehensive nonlinear beam analysis was published by Crespo da Silva and Glynn in [8, 9]. The nonlinear-order three differential governing equations were derived by Hamilton’s method accounting for contributions resulting from nonlinear curvature as well as nonlinear inertia. It was shown that both these effects may had a significant influence on the non-planar moderately large oscillations of the system. This initial research was later enhanced to consider complex deformations involving flexure along two principal directions as well as torsion [7]. Later, author extended his analytical model to a rotating beams case with the main application to helicopter rotor blades [10].

Hamdan and El-Sinawi in [16] studied the inextensible nonlinear Euler–Bernoulli beam model accounting for relatively large planar deformations and exact expression for the beam curvature. Influence of a setting angle and other selected structural parameters on rotor response characteristics for a prescribed hub torque scenarios was discussed. It was shown that for a soft base and a low preset angle unstable vibrations of the rotor might have occur.

Fenili et al. [13] presented a nonlinear mathematical model of a flexible beam-like structure in slewing motion. Authors used the method of multiple timescales to find analytical solutions in selected primary and secondary resonance states. Recently, the importance of nonlinear effects coming from the large displacement oscillations observed in rotating inextensible beams leading to rich dynamic behavior has been presented by Thomas et al. in [38]. The performed analysis demonstrated both softening or hardening frequency response characteristics dependent on the resonance order. Interestingly, the observed softening effect originating from geometric nonlinearities prevailed the centrifugal stiffening phenomenon. Also Tian et al. [39] presented a general formulation for nonlinear vibration analysis of rotating beams. The numerical solutions demonstrated that Coriolis effect could essentially change dynamics of the hub–beam system in the case of small hub radius, large beam slenderness, and high angular velocity.

When considering structures made of composite materials the kinematic relations become much more complicated since geometrically originated couplings are accompanied by strong directional properties of the constituent material. Studies accounting for coupling between flexural and longitudinal vibrations were published recently by Lenci and Rega [27] and next by Babilio and Lenci [3, 4]. Besides the mentioned bending–axial couplings, authors took into account the shear effect and imperfect boundary conditions. The importance of the adopted definition of geometric curvature was discussed by Lenci and his group in [24, 26]. The proposed strict nonlinear shearable beam model was solved analytically by attacking directly the nonlinear partial differential equations and the results were verified by the Abaqus/CAE finite element analysis [18, 19]. The results showed softening versus hardening dichotomy in the resonance curves and also strong interactions between flexural and longitudinal (axial) vibrations leading to internal resonances occurring for specific combinations of beam to axial end spring stiffness ratios. Analytical and numerical predictions were accompanied by experimental studies on a slender beam–spring system subject to kinematic excitation in [20].

Widely reported large amplitudes observed in oscillations of highly flexible beam-like elements motivated practicing engineers and scholars to extensively study the methods of oscillations suppression and to improve structural positioning accuracy. The fundamental idea was the application of any control methods, that is passive or active ones. Possibly the most promising results can be obtained by closed-loop control strategy achieved by the feedback of the system state recorded by sensors to drive actuation forces/moments generated by, e.g., piezoelectric devices [14].

With reference to large oscillations of the cantilever beams the problem of structural control by means of piezo sensor-actuator layers was studied by Rechdaoui et al. in [36]. To mitigate vibrations the proportional and time derivative potential feedback control was formulated. It was shown by tuning the control parameters and gains the nonlinear dynamic behavior of the structure could be actively suppressed. The problem of large amplitude oscillations of beams and their control was studied also by Nguyen et al. in [33] with reference to marine risers represented by long tensioned Euler–Bernoulli beam undergoing bending in two orthogonal planes. Based on the set of equations, the boundary controller applied at the top end of the riser was designed using Lyapunov’s direct method. The proposed algorithm was used to effectively stabilize the riser at its equilibrium position. Similar problem was studied by Do in [12]. The structure was modeled analytically as extensible and shearable slender beam undergoing large 3D translational and cross-section rotary motions. The control design and stability analysis were based on two Lyapunov-type theorems developed for a class of evolution systems in Hilbert space.

The control of complex flexural-torsional vibrations of a rotating composite beam was studied also by co-authors of this paper in [43]. It was proposed to use the saturation control method to reduce vibrations of flexible beam clamped to the hub that was excited by the prescribed harmonic torque. Conducted tests showed narrowing down the zones of effective suppression of beam vibrations while increasing the rotating speed of the structure. Other control methods exploited by piezo actuator devices for beam oscillations suppressing include LQR technique [5], LQG [30], P control [28], PID control [35]. Further reading on beam vibrations and various control laws can be found in a comprehensive book by He and Liu [17].

A significant effort and research works are also focused on accounting for the effect of time delays as present in all actual dynamical systems with system control. Daqaq et al. [11] examined the effect of feedback delays on the nonlinear vibrations of a piezoelectric actuated cantilever beam and analyzed the effect of feedback delays on a blade when subjected to harmonic base excitations. Alhazza et al. [1] investigated the effect of time delays on the stability, amplitude and frequency–response characteristics of a beam. The authors found that even the small time delays could completely altered the behavior and stability of the parametrically excited beam and might lead to unexpected structural phenomena. Liu et al [29] studied the piezoelectric based optimal delayed feedback control method when applied to large amplitude nonlinear vibrations of a beam. The time-delayed feedback control to reduce the nonlinear resonant vibration of a piezoelectric elastic beam was studied also by Peng et al. in [34]. Authors tested three different single-input linear time-delayed feedback control methodologies, namely displacement, velocity and acceleration time-delayed feedback. It was shown the time-delayed feedback control could act as a vibration absorber at specific values of time delay magnitude.

It is interesting to note the vast majority of papers proposing the use of piezoelectric transducers for feedback structural control adopt the simplified mechanical model of the piezoelectric active elements and their mutual interaction with hosting structure. Most of them capture just the phenomenological behavior of the combined system involving functional material and the host member. These models consider solely the converse piezoelectric effect where the commanded actuation strain is transferred as a shear force to the master structure along the actuator–subsystem interface. This force–since located off beam mid-line–generates the control moment.

Fig. 1

Configuration of beam–hub structure with embedded PZT element with control subsystem (a), orientation of the preset angle $\theta$ (b)

The discussed above new results obtained for nonlinear stationary beams, followed by the observed interactions between transversal and longitudinal vibrations and the dichotomy of softening and hardening response behavior as well as the potential of feedback control methods motivated authors of the present contribution to a more detailed study of the problem under discussion. In particular, the nonlinear phenomena observed for the rotating inextensible beams [38, 39] and provided conclusions suggested to analyze a more general case of an extensible beam. As reported in the literature, the effect of longitudinal vibrations can be even more important if the rotating beam carries a heavy tip mass. A preliminary study of a rotating extensible beam model which takes into account transversal and also longitudinal vibrations was presented in [41] and then extended in [42]. In the current work, we consider the configuration of the system corresponding to an arbitrary preset angle of the beam and added tip mass. We also modify definition of the beam curvature adopted in the mathematical model, according to the comments presented by Lenci in [25]. The model studied in this paper considers an active structure with embedded piezo-layers and a boundary control method with time delay. On the basis of the proposed complete active beam model we determine approximate solutions on the basis of the multiple timescales method applied directly to the partial differential equations with time delay and associated dynamic boundary conditions.

Following the given above comments the rest of this manuscript is organized as follows: In Sect. 2, the dynamic nonlinear model of a highly flexible beam is derived using the Hamilton’s principle and then solved by the multiple timescales method in Sect. 2.2. Next, identification of model parameters based on laboratory experiment is presented (Sect. 3). Finally, results of numerical simulations are presented in Sect. 4. The paper is concluded by results discussion and final remarks. “Appendix” contains listing of adopted shape functions of the first- and second-order perturbation solution.

2 Mathematical model of the rotor and extensible beam

2.1 Derivation of governing equations

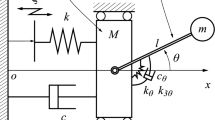
We consider a rotating hub–beam structure which is carrying a tip mass $m_\mathrm {t}$ as shown in Fig. 1. The highly elastic isotropic and slender beam with spanwise embedded piezo-layers is attached to the hub at an arbitrary preset angle $\theta$ (Figs. 1b and 2b). In order to describe motion of the structure, we introduce a fixed $(X_0,Y_0,Z_0)$ coordinates system originated at the hub centre C, a set of coordinates $(X,Y,Z\equiv Z_0)$ rotating with the hub and with the same origin, and a set of local coordinates (x, y, z) fixed to the beam and oriented along the symmetry axes of the undeformed blade with the origin at clamping point 0. We assume the rotation is performed about $Z\equiv Z_0$ axis and it is described by a temporary position angle $\psi (T)$.

Fig. 2

Top view on beam deformation plane xy (a), kinematics of infinitesimal beam element at arbitrary longitudinal position x (b)

The longitudinal and transversal displacements u(x, T) and v(x, T) of an elementary segment attributed to point A, which is next moved to $A'$ position, are defined in the rotating coordinate frame as presented in Fig. 2a. Due to its high slenderness and low stiffness, the beam can be deformed with large amplitudes. The kinematics of the beam deformations at any arbitrary time instant is shown in Fig. 2b where $\mathrm {d}x$ denotes the initial length of an infinitesimal beam element, while $\mathrm {d}s$ is its extended length. Moreover, we assume that the beam is allowed to deform only in (x, y) plane because of its high stiffness in the orthogonal direction z. For the specific preset angle $\theta =0$, this plane would overlap with the plane of rotation. Moreover, in the presented analysis, twist of the beam is neglected leaving these more general cases for future developments.

In its reference configuration, the beam has length L, cross section A, second moment of inertia I, and mass per unit length $\rho _1$; finally the hub radius is denoted $R_\mathrm {h}$ and its mass moment of inertia $J_\mathrm {h}$.

The kinematic relations in the extensible-unshearable (Euler–Bernoulli) beam element are given as

$$\begin{aligned} \cos {\varphi }= & {} \frac{1+u'}{\sqrt{\left( 1+u'\right) ^2+v'^2}}, \qquad \tan {\varphi }=\frac{v'}{1+u'}, \nonumber \\ \varphi '= & {} \frac{v''+u'v''-v'u''}{\left( 1+u'\right) ^2+v'^2}, \end{aligned}$$

(1)

where $\left( ...\right) '$ denote derivative with respect to spatial coordinate $\frac{\partial ...}{\partial x}$, in the following notation $\dot{\left( ...\right) }$ describes a time derivative $\frac{\partial ...}{\partial T}$.

Assuming the material to be uniform (the Young modulus E is constant), the axial force N along the deformed beam element is related to the axial stiffness EA, and the bending moment M to the mechanical curvature and bending stiffness EI as

$$\begin{aligned} N=EA\hat{e}, \qquad M=EI \kappa _m, \end{aligned}$$

(2)

where elongation due to extension of the beam’s mid-plane $\hat{e}$ and mechanical curvature $\kappa _m$ are given as

$$\begin{aligned} \hat{e}=\sqrt{\left( 1+u'\right) ^2+v'^2}-1, \qquad \kappa _m=\varphi '. \end{aligned}$$

(3)

Assuming the linear elastic behavior of the material and given above kinematic relations, the potential energy of the beam element is

$$\begin{aligned} \widetilde{V}=\frac{1}{2}\int _0^L \left( EA\hat{e}^2+ EI\varphi '^2 \right) \mathrm {d}x. \end{aligned}$$

(4)

The kinetic energy of the beam-hub system has three components, which arise from motion of the hub $\widetilde{T}_\mathrm {h}$, beam $\widetilde{T}_\mathrm {b}$ and tip mass $\widetilde{T}_\mathrm {t}$:

$$\begin{aligned} \widetilde{T}= \widetilde{T}_\mathrm {h}+\int _0^L \widetilde{T}_\mathrm {b} \mathrm {d}x + \widetilde{T}_\mathrm {t}, \end{aligned}$$

(5)

where

$$\begin{aligned} \begin{aligned} \widetilde{T}_\mathrm {h}&=\frac{1}{2} J_\mathrm {h} \dot{\psi }^2,\\ \widetilde{T}_\mathrm {b}&=\frac{1}{2} \rho _1 \Big \{ \dot{u}^2 + \dot{v}^2 + 2 \Big [(R_\mathrm {h}+x+u) \dot{v} - v \dot{u} \Big ] \dot{\psi }\cos \theta \\&\quad +\, \left[ (R_\mathrm {h}+x+u)^2 + v^2 \cos ^2\theta \right] \dot{\psi }^2 \Big \},\\ \widetilde{T}_\mathrm {t}&=\frac{1}{2} m_\mathrm {t} \Big \{\dot{u}_\mathrm {t}^2 + \dot{v}_\mathrm {t}^2 + 2 \Big [(R_\mathrm {h}+L+u_\mathrm {t}) \dot{v}_\mathrm {t} - v_\mathrm {t} \dot{u}_\mathrm {t} \Big ]\dot{\psi }\cos \theta \\&\quad +\, \left[ (R_\mathrm {h}+L+u_\mathrm {t})^2 + v_\mathrm {t}^2 \cos ^2\theta \right] \dot{\psi }^2 \Big \}. \end{aligned} \end{aligned}$$

(6)

The equations of motion are derived using the Hamilton’s principle of the least action

$$\begin{aligned} \int _{T_0}^{T_1}\left( \delta \widetilde{T}-\delta \widetilde{V}+\delta \widetilde{D} - \delta \widetilde{W}\right) \mathrm {d}T=0, \end{aligned}$$

(7)

where $\widetilde{D}$ and $\widetilde{W}$ are works done by dissipative and nonconservative forces in the system, respectively

$$\begin{aligned} \widetilde{D}= & {} \frac{1}{2}c_u \dot{u}^2 + \dfrac{1}{2}c_v \left[ \dot{v}^2+2(R_\mathrm {h}+x)\dot{\psi }\dot{v}\cos {\theta }\right] , \nonumber \\&\widetilde{W}=f_v(x,T)v+f_u(x,T)u, \end{aligned}$$

(8)

Terms $c_u$, $c_v$ are two independent linear viscous damping coefficients in longitudinal (x) and transverse (y) directions of the beam, respectively. Note that the y-direction damping (second component of Eq. (8)$_1$) contains terms responsible for beams oscillation about xz plane and slewing motion of the rotor. External excitation applied to the structure can be represented by any time-dependent force functions $f_v(x,T)$ and $f_u(x,T)$.

Variations of kinetic and potential energies, dissipation, and external works are given by

$$\begin{aligned} \begin{aligned}&\delta \widetilde{V} = \frac{\partial \widetilde{V}}{\partial u'}\delta u' + \frac{\partial \widetilde{V}}{\partial v'}\delta v' + \frac{\partial \widetilde{V}}{\partial u''}\delta u'' +\,\frac{\partial \widetilde{V}}{\partial v''}\delta v'', \\&\delta \widetilde{D} = \frac{\partial \widetilde{D}}{\partial \dot{u}}\delta \dot{u}+\frac{\partial \widetilde{D}}{\partial \dot{v}}\delta \dot{v},\\&\delta \widetilde{T} = \frac{\partial \widetilde{T}}{\partial u}\delta u+\frac{\partial \widetilde{T}}{\partial v}\delta v+\,\frac{\partial \widetilde{T}}{\partial \dot{u}}\delta \dot{u} +\frac{\partial \widetilde{T}}{\partial \dot{v}}\delta \dot{v},\\&\delta \widetilde{W} = \frac{\partial \widetilde{W}}{\partial u}\delta u+\frac{\partial \widetilde{W}}{\partial v}\delta v. \end{aligned} \end{aligned}$$

(9)

Substituting Eqs. (1)–(6) and (8)–(9) into Eq. (7), then integrating by parts, we get a set of partial differential equations of motion and corresponding boundary conditions. Due to computational difficulties, we limit ourselves to the specific case of constant hub speed $\dot{\psi }(T)=\mathrm{const}$. Moreover, since the problem will be solved by the multiple timescales method up to the third order of approximation, the formulas (1) and (3) are expanded in Taylor series up to fourth order of geometric nonlinearities. After some mathematical manipulations, one arrives at the system of two nonlinear partial differential equations governing the longitudinal and transverse motion:

$$\begin{aligned}&\rho _1 \left[ \ddot{u} - (R_\mathrm {h}+x)\dot{\psi }^2 - 2\dot{\psi }\cos {\theta } \dot{v} - \dot{\psi }^2u\right] + c_u \dot{u}\nonumber \\&\quad +EA\left( -u''-v'v''+v'^2v''+2u'v'v''\right) \nonumber \\&\quad +EI\left( -v''v'''-v'v''''+2u''v''^2+4v'v''u'''\right. \nonumber \\&\quad +5v'u''v''' \left. +3u'v''v'''+v'^2u''''+3u'v'v''''\right) = f_u \end{aligned}$$

(10)

$$\begin{aligned}&\rho _1\left( \ddot{v}+2\dot{u}\dot{\psi }\cos {\theta }-v\dot{\psi }^2\cos ^2{\theta }\right) + c_v \left[ \dot{v} \right. \nonumber \\&\quad \left. +\left( R_\mathrm {h}+x\right) \cos {\theta } \dot{\psi }\right] \nonumber \\&\quad +EA\left( -v'u''-u'v''+2u'v'u''+u'^2v''-\frac{3}{2}v'^2v''\right) \nonumber \\&\quad +EI\left( v'''' -3v''u''' -4u''v''' -v'u'''' +2u'v''''\right. \nonumber \\&\quad +\,8v''^2v''-2v''^3+7v'u''u'''\nonumber \\&\quad +\,9u'v''u''' +12u'u''v''' -8v'v''v''' \nonumber \\&\quad \left. +\,3u'v'u'''' +3u'^2v'''' -2v'^2 v'''' \right) = f_v, \end{aligned}$$

(11)

as well as the associated boundary conditions

$\bullet$ At $x=0$

$$\begin{aligned} u=0, \qquad v=0, \qquad v'=0 \end{aligned}$$

(12)

$\bullet$ At $x=L$

$$\begin{aligned} \begin{aligned}&m_\mathrm {t} \left[ \ddot{u} - \left( R_\mathrm {h}+L\right) \dot{\psi }^2 - 2 \dot{v} \dot{\psi } \cos \theta - u\dot{\psi }^2 \right] \\&\qquad +EA\left( u'+\frac{1}{2} v'^2-u'v'^2\right) \\&\qquad +EI\left( v'v'''-2v'u''v''-v'^2u'''-3u'v'v'''\right) \\&\quad = \underline{Q_{u\mathrm {p}}}+\underline{Q_{u\mathrm {c}}}\\&m_\mathrm {t} \left( \ddot{v} + 2 \dot{u} \dot{\psi } \cos \theta \right. \\&\qquad \left. - v \dot{\psi }^2 \cos ^2 \theta \right) \\&\qquad +EA\left( u'v'-u'^2v'+\frac{1}{2}v'^3\right) \\&\qquad +EI\left( -v'''+2u''v''+v'u'''+2u'v'''-2v'u''^2 \right. \\&\qquad \left. -6u'u''v''+v'v''^2-3u'v'u'''-3u'^2v'''+2v'^2v'''\right) =0\\&EI\left( v'' -v'u''-2u'v''+3u'v'u''+3u'^2v''-2v'^2v''\right) \\&\quad =\underline{Q_{v\mathrm {p}}}+\underline{Q_{v\mathrm {c}}} \end{aligned} \end{aligned}$$

(13)

The underlined terms $Q_{u\mathrm {p}}, Q_{u\mathrm {c}}, Q_{v\mathrm {p}}$ and $Q_{v\mathrm {c}}$ present on the right-hand side of conditions (13)$_1$ and (13)$_3$ are artificiality introduced control generalized loads resulting from the action of piezoelectric actuators. It can be shown if the active layer is distributed along the whole span of hosting specimen (e.g., beam or plate), the action of the piezoelectric actuators is mathematically represented as non-homogenous boundary conditions at the free end of the structure. These nonzero terms represent the induced dynamic moment/shear force and are effective and robust computational ways toward the implementation of a feedback control in mathematical models of active structures. Since the proposal by Lagnese [21] this boundary control moment/force methodology has been successfully adopted by many investigators to study the behavior of the plates, shells, and beam structures with feedback control [6, 15, 22, 31].

The subsequent terms $Q_{u\mathrm {p}}$, $Q_{v\mathrm {p}}$, and $Q_{u\mathrm {c}}$, $Q_{v\mathrm {c}}$ represent proportional (subscript ’p’) and cubic (subscript ’c’) functions of longitudinal and transverse displacements, respectively. Considering the time delay $\tau$ in the system, these are expressed by formulas

$$\begin{aligned} \begin{aligned} Q_{u\mathrm {p}}(L,T-\tau )&= \widehat{g}_{u\mathrm {p}} u_\tau (L,T-\tau ), \\ Q_{v\mathrm {p}}&=\widehat{g}_{v\mathrm {p}} v_\tau (L,T-\tau ), \\ Q_{u\mathrm {c}}(L,T-\tau )&= \widehat{g}_{u\mathrm {c}} u^3_\tau (L,T-\tau ), \\ Q_{v\mathrm {c}}&=\widehat{g}_{v\mathrm {c}} v^3_\tau (L,T-\tau ). \end{aligned} \end{aligned}$$

(14)

2.2 Solution by perturbation method

The analysis is applied for the pure nth flexural mode without internal resonance interactions. To solve the problem, we introduce three timescales

$$\begin{aligned} t_0=T,\qquad t_1=\varepsilon T,\qquad t_2=\varepsilon ^2 T, \end{aligned}$$

(15)

where $t_0$, $t_1$, $t_2$ are fast and slow timescales, respectively. Parameter $\varepsilon$ is a formal small parameter and serves as a book keeping device grouping small terms in a proper perturbation order. Thus using the chain rule the first- and second-order time derivatives are

$$\begin{aligned} \begin{aligned} \dot{v}(x,T)&= \frac{\partial v(x,T)}{\partial t_0}+\varepsilon \frac{\partial v(x,T)}{\partial t_1}+\varepsilon ^2\frac{\partial v(x,T)}{\partial t_2} + \mathcal {O}(\varepsilon ^3),\\ \ddot{v}(x,T)&= \frac{\partial ^2 v(x,T)}{\partial t_0^2}+\varepsilon \frac{\partial ^2 v(x,T)}{\partial t_0 \partial t_1}\\&\quad +\varepsilon ^2 \left[ \frac{\partial ^2 v(x,T)}{\partial t_0 \partial t_2}+\frac{\partial ^2 v(x,T)}{\partial t_1^2}\right] + \mathcal {O}(\varepsilon ^3). \end{aligned} \end{aligned}$$

Next, we seek the solutions in a series of small parameter at the subsequent three orders of perturbation:

$$\begin{aligned} \begin{aligned} v(x,T)&= \varepsilon v_0(x,t_0,t_1,t_2) + \varepsilon ^2 v_1(x,t_0,t_1,t_2) \\&\quad + \varepsilon ^3 v_2(x,t_0,t_1,t_2)+ \mathcal {O}(\varepsilon ^4),\\ v_\tau (x,T,\tau )&= \varepsilon v_{\tau 0}(x,\tau ,t_0,t_1,t_2) \\&\quad + \varepsilon ^2 v_{\tau 1}(x,\tau ,t_0,t_1,t_2) \\&\quad + \varepsilon ^3 v_{\tau 2}(x,\tau ,t_0,t_1,t_2)+ \mathcal {O}(\varepsilon ^4), \end{aligned} \end{aligned}$$

(16)

where v(x, T) denotes the solution without time delay, and $v_\tau (x,T,\tau )$ is its counterpart when time delay $\tau$ is considered. The variables u corresponding to the longitudinal direction are expanded in the similar way. For the sake of text brevity, they are deliberately omitted here.

To decouple linear response of the structure, we assume the angular speed to be of $\varepsilon$ order (relatively small quantity) and write

$$\begin{aligned} \dot{\psi }=\varepsilon \Omega . \end{aligned}$$

(17)

By this assignment, the small book-keeping parameter $\varepsilon$ shifts the angular velocity $\Omega$ term from first to the second and higher orders of the problem. Furthermore, eliminating $\Omega$ from the first-order solution will result in a classical cantilever beam equation (linear part of the solution). Without this assumption, static predeformations due to constant angular speed could be studied.

The external excitations $f_u$, $f_v$ present on RHS in (10) and (11) as well as damping coefficients and control loads are shifted to the third and second perturbation order of the problem, respectively. Following this assumption, they are declared by

$$\begin{aligned} \begin{aligned} f_v (x,T)&= \varepsilon ^3 \xi _v (x) \cos \left( \omega _v T\right) \\&=\varepsilon ^3 \xi _v (x) \cos \left( \omega _{0v} t_0+ \sigma _v t_2 \right) , \\ f_u (x,T)&= \varepsilon ^3 \xi _u (x) \cos \left( \omega _u T\right) \\&=\varepsilon ^3 \xi _u (x) \cos \left( \omega _{0u} t_0+ \sigma _u t_2 \right) ,\\ c_u&= \varepsilon ^2 C_u,\qquad c_v=\varepsilon ^2 C_v,\\ \widehat{g}_{u\mathrm {p}}&=\varepsilon ^2 g_{u\mathrm {p}},\qquad \widehat{g}_{v\mathrm {p}}=\varepsilon ^2 g_{v\mathrm {p}},\\ \widehat{g}_{u\mathrm {c}}&=\varepsilon ^0 g_{u\mathrm {c}},\qquad \widehat{g}_{v\mathrm {c}}=\varepsilon ^0 g_{v\mathrm {c}} \end{aligned} \end{aligned}$$

(18)

where $\xi _v$ ($\xi _u$) describe the amplitudes of uniformly distributed external excitations at frequencies $\omega _v$ ($\omega _u$). The later ones are expressed by corresponding natural frequencies $\omega _{0v}$ ($\omega _{0u}$) at the fast timescale and detuning parameters $\sigma _v$ ($\sigma _u$) attributed to the second slow timescale $t_2$.

Inserting equations (15)–(18) into expressions (10)–(13) and collecting $\varepsilon$ power-like terms, we obtain the following sets of equations and corresponding boundary conditions

$\bullet \; \mathcal {O}(\varepsilon ^1)$:

$$\begin{aligned} \rho _1 \frac{\partial ^2 u_0}{\partial t_0^2} - E A u_0'' = 0 \qquad \rho _1 \frac{\partial ^2 v_0}{\partial t_0^2} + EI v_0'''' = 0 \end{aligned}$$

(19)

boundary conditions at $x=0$

$$\begin{aligned} u_0=0,\qquad v_0=0,\qquad v_0'=0, \end{aligned}$$

(20)

and $x=L$

$$\begin{aligned}&m_\mathrm {t} \frac{\partial ^2 u_0 }{\partial t_0^2} + EA u_0' = 0,\nonumber \\&\quad m_\mathrm {t} \frac{\partial ^2 v_0 }{\partial t_0^2} - EI v_0''' = 0, \qquad v_0''=0 \end{aligned}$$

(21)

$\bullet \; \mathcal {O}(\varepsilon ^2)$:

$$\begin{aligned} \begin{aligned} \rho _1\frac{\partial ^2 u_1}{\partial t_0^2} - E A u_1'' =&-2 \rho _1 \frac{\partial ^2 u_0}{\partial t_0\partial t_1} + 2\rho _1\Omega \cos {\theta }\frac{\partial v_0 }{\partial t_0}\\ {}&+ \rho _1\left( R_\mathrm {h}+x\right) \Omega ^2 \\&+ EA v_0' v_0'' + EI \left( v_0'' v_0''' + v_0' v_0''''\right) \\ \rho _1\frac{\partial ^2 v_1}{\partial t_0^2} + EI v_1'''' =&-2\rho _1 \frac{\partial ^2 v_0}{\partial t_0\partial t_1}-2\rho _1\Omega \cos {\theta }\frac{\partial u_0 }{\partial t_0}\\&+ EA\left( v_0' u_0''+ u_0' v_0''\right) \\&+EI\left( 3 v_0''u_0'''+EI\left( 3 v_0''u_0'''\right. \right. \\&\left. +\, 4 u_0''v_0''' + v_0'u_0''''+ 2 u_0' v_0''''\right) \end{aligned} \end{aligned}$$

(22)

boundary conditions at $x=0$

$$\begin{aligned} u_1=0,\qquad v_1=0,\qquad v_1'=0, \end{aligned}$$

(23)

and at $x=L$

$$\begin{aligned}&m_\mathrm {t}\left[ \frac{\partial ^2 u_1 }{\partial t_0^2} + 2\frac{\partial ^2 u_0 }{\partial t_0\partial t_1} - 2\cos {\theta }\frac{\partial v_0 }{\partial t_0}\Omega -\left( R_\mathrm {h}+L\right) \Omega ^2\right] \nonumber \\&\quad + EA \left( u_1' +\frac{1}{2} v_0'^2\right) + E I v_0' v_0''' = 0,\nonumber \\&m_\mathrm {t}\left( \frac{\partial ^2 v_1 }{\partial t_0^2}+2\frac{\partial ^2 v_0 }{\partial t_0\partial t_1}+2\cos {\theta }\frac{\partial u_0 }{\partial t_0}\Omega \right) \nonumber \\&\quad +E A u_ 0'v_0'+E I \left( -v_1'''+2 u_0'' v_ 0'' + v_ 0' u_ 0''' + 2 u_ 0' v_ 0''' \right) =0,\nonumber \\&EI\left( v_1''-v_ 0' u_ 0'' - 2 u_ 0' v_ 0''\right) =0 \end{aligned}$$

(24)

$\bullet \; \mathcal {O}(\varepsilon ^3)$:

(25)

boundary conditions at $x=0$

$$\begin{aligned} u_2=0,\qquad v_2=0,\qquad v_2'=0, \end{aligned}$$

(26)

and at $x=L$

$$\begin{aligned} \begin{aligned}&m_\mathrm {t}\left[ \frac{\partial ^2 u_2 }{\partial t_0^2}+\frac{\partial ^2 u_0 }{\partial t_1^2}+2\frac{\partial ^2 u_0 }{\partial t_0\partial t_2}-\Omega ^2 u_0+2\frac{\partial ^2 u_1 }{\partial t_0\partial t_1}\right. \\&\quad \left. -2\cos {\theta }\Omega \left( \frac{\partial v_0 }{\partial t_1}+\frac{\partial v_1 }{\partial t_0}\right) \right] \\&\quad + EA \left( u_2' - u_0'v_0'^2 + v_0'v_1'\right) \\&\quad +EI \left( -2 v_0'u_0''v_0'' - v_0'^2 u_0''' - 3 u_0'v_0'v_0''' + v_1'v_0''' \right. \\&\quad \left. + v_0'v_1'''\right) = g_{u\mathrm {p}} u_\tau (L,T-\tau ) + g_{u\mathrm {c}} u^3_\tau (L,T-\tau ),\\&m_\mathrm {t}\left[ \frac{\partial ^2 v_2 }{\partial t_0^2} +2 \cos {\theta }\left( \frac{\partial u_0 }{\partial t_1}+\frac{\partial u_1 }{\partial t_0}\right) \Omega \right. \\&\quad \left. +\frac{\partial ^2 v_0 }{\partial t_1^2}+2\frac{\partial ^2 v_0 }{\partial t_0 \partial t_1}-\cos ^2{\theta }v_0\Omega ^2+2\frac{\partial ^2 v_1 }{\partial t_0\partial t_1}\right] \\&\quad + EA \left[ -u_0'^2 v_0' + u_1' v_0' + 0.5 v_0'^3 + u_0 v_1' \right] \\&\quad + EI \left[ -v_2''' -\,2 v_0'u_0''^2 - 6 u_0' u_0''v_0''\right. \\&\quad \left. + \, 2 u_1'' v_0'' + 2 v_0' v_0''^2 + 2 u_0''v_1'' - 3 u_0'v_0'u_0'''\right. \\&\quad + v_1'u_0''' + v_0'u_1'''\\&\quad \left. -\, 3 u_0'^2 v_0''' + 2 u_1'v0''' + 2 v_0'^2 v_0''' + 2 u_0'v_1'''\right] = 0,\\&\quad EI\left[ v_2'' - v_1'u_0'' - v_0'u_1'' + 3 u_0'^2 v_0'' - 2 u_1' v_0'' \right. \\&\quad \left. -\, 2 v_0'^2 v_0'' + u_0'(3v_0'u_0'' - 2v_1'')\right] \\&\quad = g_{v\mathrm {p}} v_\tau (L,T-\tau ) +g_{v\mathrm {c}} v^3_\tau (L,T-\tau ). \end{aligned} \end{aligned}$$

(27)

2.2.1 First-order solution

The solutions to the first-order problem Eqs. (19)–(22) are given as products of time dependent functions and linear mode shapes

$$\begin{aligned} u_0(x,T)&= \left[ A(t_1,t_2){\text {e}}^{\mathrm {i}\omega _{0u} t_0} + \bar{A}(t_1,t_2){\text {e}}^{-\mathrm {i}\omega _{0u} t_0}\right] \hat{\phi }_u(x),\nonumber \\ v_0(x,T)&= \left[ B(t_1,t_2){\text {e}}^{\mathrm {i}\omega _{0v} t_0} + \bar{B}(t_1,t_2){\text {e}}^{-\mathrm {i}\omega _{0v} t_0}\right] \hat{\phi }(x),\nonumber \\ \hat{\phi }_u(x)&=\sin (\phi _u x),\nonumber \\ \hat{\phi }(x)&= r_1 \sin (\phi x)+r_2 \cos (\phi x)\nonumber \\&\quad +\,r_3 \sinh (\phi x)+r_4 \cosh (\phi x), \end{aligned}$$

(28)

where $A(t_1,t_2)$, $\bar{A}(t_1,t_2)$ and $B(t_1,t_2)$, $\bar{B}(t_1,t_2)$ are complex amplitudes dependent on both slow timescales and the over bar symbol denotes complex conjugate. Parameters $r_1$-$r_4$ are trigonometric coefficients which satisfy the boundary value problem (20)–(21).

When considering the time delay the sought delayed solutions to the first-order problem $u_{\tau 0}, v_{\tau 0}$ are again defined as products of time dependent amplitude functions and linear mode shapes. However, the former ones are shifted by appropriate time delays $\tau _u$ and $\tau _v$ whereas the deformation modes stay similar to their counterparts in regular solution as given by Eq. (28)$_{3,4}$

$$\begin{aligned} \begin{aligned} u_{\tau 0}(x,T,\tau )&= \left[ A(t_1,t_2){\text {e}}^{\mathrm {i}(\omega _{0u} t_0-\tau _u)}\right. \\&\quad \left. + \bar{A}(t_1,t_2){\text {e}}^{-\mathrm {i}(\omega _{0u} t_0-\tau _u)}\right] \hat{\phi }_u (x),\\ v_{\tau 0}(x,T,\tau )&= \left[ B(t_1,t_2){\text {e}}^{\mathrm {i}(\omega _{0v} t_0-\tau _v)} \right. \\&\quad \left. + \bar{B}(t_1,t_2){\text {e}}^{-\mathrm {i}(\omega _{0v} t_0-\tau _v)}\right] \hat{\phi }(x). \end{aligned} \end{aligned}$$

(29)

This treatment of time delay effect within the multiple timescales method framework was successfully adopted by Rusinek et al. in [37].

The natural frequencies $\omega _{0u}$, $\omega _{0v}$ in axial and transverse directions are given by

$$\begin{aligned} \omega _{0u}=\sqrt{\frac{EA \phi _u^2}{\rho _1}}, \qquad \qquad \omega _{0v}=\sqrt{\frac{EI \phi ^4}{\rho _1}}, \end{aligned}$$

(30)

respectively, while $\phi _u$ and $\phi$ have to be found by solving the transcendental equations

$$\begin{aligned} \rho _1\cos (\phi _u L) - m_\mathrm {t} \phi _u\sin (\phi _u L) = 0, \quad \frac{\rho _1{+}\cosh (\phi L) [\rho _1 \cos (\phi L)- m_\mathrm {t} \phi \sin (\phi L)] {+} m_\mathrm {t} \cos (\phi L)\sinh (\phi L)}{\rho _1 [\cos (\phi L) {+} \cosh (\phi L)] + m_\mathrm {t} [\sinh (\phi L)-\sin (\phi L)]} = 0. \quad \end{aligned}$$

(31)

Subsequent roots determine the mode shapes Eq. (28)$_{3,4}$ and corresponding natural frequencies Eq. (30).

2.2.2 Second-order solution

Considering the second-order problem, we solve Eqs. (22)–(24). Namely, in the first attempt, we are focused on secular generating terms (the ones containing ${\text {e}}^{\pm \mathrm {i}\omega _{0u} t_0 }$ and ${\text {e}}^{\pm \mathrm {i}\omega _{0v} t_0}$) to vanish. Following this, the solvability conditions are

$$\begin{aligned} \begin{aligned}&\int _0^L\left( \rho _1\frac{\partial ^2 u_1}{\partial t_0^2} - EA u_1''\right) u_0 \mathrm {d}x \\&\quad = \int _0^L\left( -2\rho _1\frac{\partial ^2 u_0}{\partial t_0\partial t_1}\right) u_0\mathrm {d}x,\\&\int _0^L\left( \rho _1\frac{\partial ^2 v_1}{\partial t_0^2} + EI v_1''''\right) v_0 \mathrm {d}x\\&\quad = \int _0^L\left( -2\rho _1\frac{\partial ^2 v_0}{\partial t_0\partial t_1}\right) v_0\mathrm {d}x. \end{aligned} \end{aligned}$$

(32)

After integration by parts and substituting the boundary conditions Eqs. (23)–(24) and performing simple algebraic manipulations, we get

$$\begin{aligned} \frac{\partial A}{\partial t_1}=\frac{\partial \bar{A}}{\partial t_1}=\frac{\partial B}{\partial t_1}=\frac{\partial \bar{B}}{\partial t_1}=0. \end{aligned}$$

(33)

Then analyzing Eqs. (22)–(24), we decompose harmonics, calculate time derivatives, and then reduce partial differential equations to ordinary differential ones. Finally, the second-order solutions are given by

$$\begin{aligned} \begin{aligned} u_1(x,T)&= r_{5}\Omega ^2 + r_{6}R_\mathrm {h}\Omega ^2 + r_{7}B\bar{B} \\&\quad + \mathrm {i}r_8 \cos \theta \Omega B {\text {e}}^{\mathrm {i}\omega _{0v}t_0} \\&\quad - \mathrm {i}r_8\cos \theta \Omega \bar{B} {\text {e}}^{-\mathrm {i}\omega _{0v} t_0} \\&\quad + r_{9} B^2 {\text {e}}^{2\mathrm {i}\omega _{0v}t_0} + r_{9}\bar{B}^2 {\text {e}}^{-2\mathrm {i}\omega _{0v}t_0},\\ v_1(x,T)&= \mathrm {i}r_{10} \Omega \cos \theta A {\text {e}}^{\mathrm {i}\omega _{0u}t_0} - \mathrm {i}r_{10} \Omega \cos \theta \bar{A} {\text {e}}^{-\mathrm {i}\omega _{0u}t_0} \\&\quad + r_{11} A B {\text {e}}^{\mathrm {i}\omega _{0u} t_0}{\text {e}}^{\mathrm {i}\omega _{0v} t_0}\\&\quad + r_{11}\bar{A}\bar{B} {\text {e}}^{-\mathrm {i}\omega _{0u} t_0} {\text {e}}^{-\mathrm {i}\omega _{0v} t_0} \\&\quad + r_{12}A\bar{B}{\text {e}}^{\mathrm {i}\omega _{0u}t_0} {\text {e}}^{-\mathrm {i}\omega _{0v} t_0}\\&\quad + r_{12}\bar{A}B {\text {e}}^{-\mathrm {i}\omega _{0u} t_0} {\text {e}}^{\mathrm {i}\omega _{0v}t_0}. \end{aligned} \end{aligned}$$

(34)

where $r_5$–$r_{12}$ are real valued functions dependent on $A, E, I, \rho _1, \omega _{0u}, \omega _{0v}$ that represent mode shapes, while using parameters $R_\mathrm {h}$, $\Omega$ and $\theta$ we can manipulate their magnitudes. To keep the length of the paper concise these functions are reported just graphically only for a set of fixed parameters as given in “Appendix A”.

Studying the Eq. (22) and associated boundary conditions (23)–(24) one observes the time delays to be absent at this order of perturbation. Therefore, the second-order solution of time-delayed problem is identically zero.

2.2.3 Third-order solution

In the third-order problem Eqs. (25)–(27), we consider only terms proportional to ${\text {e}}^{\pm \mathrm {i}\omega _{0v} t_0}$ and ${\text {e}}^{\pm \mathrm {i}\omega _{0u} t_0}$, to which solvability conditions are applied (multiply functions by linear solutions and next integrate by parts in 0 to L limits). After cumbersome computations, taking into account boundary conditions (26)–(27), one obtains the following set of four modulation equations in the slow timescale $t_2$:

$$\begin{aligned} \begin{aligned} \frac{\partial A}{\partial t_2}&= q_{1}\xi _u {\text {e}}^{\mathrm {i}\sigma _u t_2} + q_2 C_u A + \mathrm {i}q_3 g_{u\mathrm {p}} A {\text {e}}^{-\tau _u}\\&\quad + \mathrm {i}q_4 g_{u\mathrm {c}}A^2\bar{A}{\text {e}}^{-\tau _u} + \mathrm {i}q_{5} A B\bar{B} \\&\quad + \mathrm {i}q_6 \Omega ^2 A + \mathrm {i}q_7\Omega ^2 A \cos ^2{\theta },\\ \frac{\partial \bar{A}}{\partial t_2}&= -q_{1}\xi _u {\text {e}}^{-\mathrm {i}\sigma _u t_2} + q_2 C_u \bar{A} \\&\quad - \mathrm {i}q_3 g_{u\mathrm {p}}\bar{A}{\text {e}}^{\mathrm {i}\tau _u}\\&\quad - \mathrm {i}q_4 g_{u\mathrm {c}}A\bar{A}^2{\text {e}}^{\mathrm {i}\tau _u} - \mathrm {i}q_5 \bar{A} B\bar{B} - \mathrm {i}q_6 \Omega ^2 \bar{A} \\&\quad - \mathrm {i}q_7 \Omega ^2\cos ^2{\theta } \bar{A},\\ \frac{\partial B}{\partial t_2}&= \mathrm {i}p_1 \xi _v {\text {e}}^{\mathrm {i}\sigma _v t_2} + p_2 C_v B + \mathrm {i}p_3 g_{v\mathrm {p}} B {\text {e}}^{-\mathrm {i}\tau _v} \\&\quad + \mathrm {i}p_4 A \bar{A} B + \mathrm {i}p_5 B^2 \bar{B}\\&\quad + \mathrm {i}p_6 g_{v\mathrm {c}} B^2 \bar{B}{\text {e}}^{-\mathrm {i}\tau _v} + \mathrm {i}p_7\Omega ^2 B + \mathrm {i}p_8 R_\mathrm {h} \Omega ^2 B \\&\quad + \mathrm {i}p_9\Omega ^2\cos ^2{\theta }B,\\ \frac{\partial \bar{B}}{\partial t_2}&= -\mathrm {i}p_1 \xi _v {\text {e}}^{-\mathrm {i}\sigma _v t_2} + p_2 C_v\bar{B} - \mathrm {i}p_3g_{v\mathrm {p}}\bar{B}{\text {e}}^{\mathrm {i}\tau _v} \\&\quad - \mathrm {i}p_4 A \bar{A}\bar{B} - \mathrm {i}p_5 B \bar{B}^2\\&\quad - \mathrm {i}p_6 g_{v\mathrm {c}} B \bar{B}^2 {\text {e}}^{\mathrm {i}\tau _v} - \mathrm {i}p_7\Omega ^2\bar{B}\\&\quad - \mathrm {i}p_8 R_\mathrm {h} \Omega ^2\bar{B} - \mathrm {i}p_9\Omega ^2\cos ^2{\theta }\bar{B}, \end{aligned} \end{aligned}$$

(35)

where $q_{1}$–$q_{7}$ and $p_{1}$–$p_{9}$ are real valued coefficients calculated during integration process. We preferentially convert the above equations expressing complex amplitudes in their polar form by introducing new variables

$$\begin{aligned} \begin{aligned} A&=\frac{1}{2}a(t_2){\text {e}}^{\mathrm {i}\beta _a(t_2)},&\bar{A}&=\frac{1}{2}a(t_2){\text {e}}^{-\mathrm {i}\beta _a(t_2)}, \\ B&=\frac{1}{2}b(t_2){\text {e}}^{\mathrm {i}\beta _{b}(t_2)},&\qquad \bar{B}&=\frac{1}{2}b(t_2){\text {e}}^{-\mathrm {i}\beta _b(t_2)}, \end{aligned} \end{aligned}$$

(36)

and obtain a modified set of four modulation equations of amplitudes a, b and phase angles $\beta _a$, $\beta _b$

$$\begin{aligned} \begin{aligned} \frac{\partial a}{\partial t_2}&= -2q_1 \xi _u\sin {\left( t_2 \sigma _u-\beta _a\right) } + q_2 C_u a \\&\quad + q_3 g_{u\mathrm {p}} a \sin {\tau _u} + \frac{1}{4} q_4 g_{u\mathrm {c}}a^3 \sin {\tau _u},\\ a \frac{\partial \beta _a}{\partial t_2}&= 2q_1\xi _u \cos {(t_2 \sigma _u - \beta _a)} + q_3 g_{u\mathrm {p}} a \cos {\tau _u}\\&\quad +\frac{1}{4} q_4 g_{u\mathrm {c}}a^3 \cos {\tau _u} + \frac{1}{4}q_5 a b^2 \\&\quad + q_6\Omega ^2a + q_7\Omega ^2 \cos ^2{\theta }a,\\ \frac{\partial b}{\partial t_2}&= -2p_1 \xi _v\sin {(t_2 \sigma _v-\beta _{b})} + p_2C_v b \\&\quad + p_3 g_{v\mathrm {p}} b \sin {\tau _v} + \frac{1}{4} p_6 g_{v\mathrm {c}}b^3 \sin {\tau _v},\\ b\frac{\partial \beta _b}{\partial t_2}&= 2p_1\xi _v \cos {(t_2 \sigma _v-\beta _b)} + p_3 g_{v\mathrm {p}}b \cos {\tau _v}\\&\quad +\frac{1}{4}p_4a^2b + \frac{1}{4}p_5 b^3 + \frac{1}{4} p_6 g_{v\mathrm {c}}b^3 \cos {\tau _v} \\&\quad + p_7 \Omega ^2 b + p_8 R_\mathrm {h}\Omega ^2 b + p_9\Omega ^2\cos ^2{\theta }b. \end{aligned} \end{aligned}$$

(37)

Coefficients $q_{1}$–$q_{7}$ and $p_{1}$–$p_{9}$ contain terms of first- and second-order solutions and can be calculated numerically for fixed properties of the beam. Material data and geometry of the structure used to derive approximate solution were measured within laboratory experiment described in Sect. 3. Further parametric analysis of the system is presented in Sect. 4.

Finally, the approximate solutions of Eq. (16) take the form

$$\begin{aligned} u(x,T)= & {} \varepsilon a \sin (\phi _u x)\cos (\omega _{0u} t_0 + \beta _a) \nonumber \\&+\, \varepsilon ^2\left[ (r_5 + r_6R_\mathrm {h})\Omega ^2 + \frac{r_7}{4} b^2 \right. \nonumber \\&-\,r_8\Omega \cos \theta b\sin (\beta _b+ \omega _{0v}t_0)\nonumber \\&\left. +\, \frac{r_9}{2}b^2\cos (2\omega _{0v}t_0+2\beta _b)\right] + \mathcal {O}(\varepsilon ^3), \end{aligned}$$

$$\begin{aligned} u_\tau (x,T,\tau )= & {} \varepsilon a \sin (\phi _u x)\cos (\omega _{0u}t_0+\beta _a-\tau _u)\\&+\, \mathcal {O}(\varepsilon ^3), \end{aligned}$$

$$\begin{aligned} v(x,T)= & {} \varepsilon b\left[ r_1 \sin \left( \phi x\right) +r_2 \cos \left( \phi x\right) +r_3 \sinh \left( \phi x\right) \right. \nonumber \\&\quad \left. +\,r_4 \cosh \left( \phi x\right) \right] \cos {\left( \omega _{0v} t_0+\beta _b \right) }\nonumber \nonumber \\&\quad +\, \varepsilon ^2 \left[ -r_{10} \Omega \cos {\theta }a\sin {\left( \omega _{0u} t_0+\beta _a \right) } \right. \nonumber \\&\quad + \frac{r_{11}}{2}ab\cos {\left( \omega _{0u}t_0+\omega _{0v}t_0+\beta _a+\beta _b \right) }\nonumber \\&\quad \left. +\,\frac{r_{12}}{2}ab\cos {\left( \omega _{0u}t_0-\omega _{0v}t_0+\beta _a-\beta _b \right) } \right] \nonumber \\&\quad +\mathcal {O}(\varepsilon ^3), \end{aligned}$$

$$\begin{aligned} v_\tau (x,T,\tau )= & {} \varepsilon b \left[ r_1 \sin \left( \phi x\right) +\,r_2 \cos \left( \phi x\right) \right. \nonumber \\&+\,r_3 \sinh \left( \phi x\right) \left. +\,r_4 \cosh \left( \phi x\right) \right] \nonumber \\&\times \, \cos (\omega _{0v} t_0 + \beta _b - \tau _v) + \mathcal {O}(\varepsilon ^3),\nonumber \\ \end{aligned}$$

(38)

where (38)$_{1,3}$ are solutions to the regular problem, and (38)$_{2,4}$ are their counterparts if time delay is accounted for.

2.3 Stability analysis

Stability analysis of analytical solutions is performed on the basis of modulation equations (37) which are rewritten in a shorter form

$$\begin{aligned} \begin{aligned} \dot{a}= & {} f_1 \left( a, \beta _a, b, \beta _b \right) ,\\ \dot{\beta }_a= & {} f_2 \left( a, \beta _a, b, \beta _b \right) ,\\ \dot{b}= & {} f_3 \left( a, \beta _a, b, \beta _b \right) ,\\ \dot{\beta }_b= & {} f_4 \left( a, \beta _a, b, \beta _b \right) , \end{aligned} \end{aligned}$$

(39)

where “dot” means time derivative with respect to timescale $t_2$. In the steady state the right-hand sides of Eq. (39) are equal to zero. The solutions of Eq. (39) are disturbed in the vicinity of the steady state. Substituting perturbed solutions into Eq. (39), then subtracting from unperturbed ones and expanding the disturbed functions $f_1, f_2, f_3, f_4$ in Taylor series in the neighborhood of the steady state and considering the linear terms we obtain a set of linear, homogeneous differential equations in variations

$$\begin{aligned} \begin{aligned} \dot{{\delta }_a}&= \frac{\partial {f_1}}{\partial {a}} \delta _a + \frac{\partial {f_1}}{\partial {\beta _a}} \delta _{\beta _a} + \frac{\partial {f_1}}{\partial {b}} \delta _b + \frac{\partial {f_1}}{\partial {\beta _b}} \delta _{\beta _b},\\ \dot{\delta }_{\beta _a}&= \frac{\partial {f_2}}{\partial {a}} \delta _a + \frac{\partial {f_2}}{\partial {\beta _a}} \delta _{\beta _a} + \frac{\partial {f_2}}{\partial {b}} \delta _b + \frac{\partial {f_2}}{\partial {\beta _b}} \delta _{\beta _b},\\ \dot{\delta }_b&= \frac{\partial {f_3}}{\partial {a}} \delta _a + \frac{\partial {f_3}}{\partial {\beta _a}} \delta _{\beta _a} + \frac{\partial {f_3}}{\partial {b}} \delta _b + \frac{\partial {f_3}}{\partial {\beta _b}} \delta _{\beta _b},\\ \dot{\delta }_{\beta _b}&= \frac{\partial {f_4}}{\partial {a}} \delta _a + \frac{\partial {f_4}}{\partial {\beta _a}} \delta _{\beta _a} + \frac{\partial {f_4}}{\partial {b}} \delta _b + \frac{\partial {f_4}}{\partial {\beta _b}} \delta _{\beta _b},\\ \end{aligned} \end{aligned}$$

(40)

Fig. 3

Experiment setup; a laser scanning head with camera, b computer with scanning unit, c anti-vibrational table, d composite specimen

Fig. 4

Section of the MFC patch (orange colour) bonded onto the composite specimen (black). (Color figure online)

where $\delta$ means variation of the selected variable and the derivatives are computed for a steady state. The stability of the solutions depends on eigenvalues of the Jacobian matrix

$$\begin{aligned} \mathbf {J}= \begin{bmatrix} \dfrac{\partial {f_1}}{\partial {a}} &{} \dfrac{\partial {f_1}}{\partial {\beta _a}} &{} \dfrac{\partial {f_1}}{\partial {b}} &{} \dfrac{\partial {f_1}}{\partial {\beta _b}} \\ \dfrac{\partial {f_2}}{\partial {a}} &{} \dfrac{\partial {f_2}}{\partial {\beta _a}} &{} \dfrac{\partial {f_2}}{\partial {b}} &{} \dfrac{\partial {f_2}}{\partial {\beta _b}} \\ \dfrac{\partial {f_3}}{\partial {a}} &{} \dfrac{\partial {f_3}}{\partial {\beta _a}} &{} \dfrac{\partial {f_3}}{\partial {b}} &{} \dfrac{\partial {f_3}}{\partial {\beta _b}} \\ \dfrac{\partial {f_4}}{\partial {a}} &{} \dfrac{\partial {f_4}}{\partial {\beta _a}} &{} \dfrac{\partial {f_4}}{\partial {b}} &{} \dfrac{\partial {f_4}}{\partial {\beta _b}} \\ \end{bmatrix} \end{aligned}$$

(41)

If any of the eigenvalue has a positive real part, the system becomes unstable.

3 Laboratory experiment

To identify the coefficients of the analytical model the laboratory experiment was conducted. The test stand comprised the laser vibrometer PSV-500 camera system—see Fig. 3 marks (a,b), and a highly flexible specimen (d) mounted to a dedicated grip fixed to an anti-vibrational slip table TIRA TGT MO 48XL (c). A series of reflective markers were sticked on the beam surface to be traced by the scanning laser. Moreover, piezoelectric macro fiber composite (MFC) patches M8528-P1 by Smart-Material Corp. were bonded on the tested blade as shown in Fig. 4. These are the elements operating in $d_{33}$ mode, so the piezoceramic poling direction (being in-plane of the transducer) when oriented along the beam span axis x excites the specimen bending (note also Fig. 1). To amplify the signal from the vibrometer generator, a dedicated MFC high-voltage amplifier was used.

The beam was made of multilayered ThinPreg^TM 120EP-513/CF resin reinforced with M40JB-12000-50B (TORAY) carbon fibers composite. The laminate stacking sequence was a special 18-layered configuration $[0,-60_2,0,-60,60_3,-60_2,0_2,-60,0_2,60_2,-60]$ ensuring the macroscopically isotropic properties of the material [40]. One of numerous advantages of this composite material is its susceptibility to large deformations within elastic regime. The geometric data of the beam and resulting material properties are gathered in Table 1, while outcomes of identification tests are displayed in Fig. 5.

Table 1 Dimensions of the blade (length, width, thickness) and laminate material properties: density, mass per unit length, longitudinal Young modulus, transversal Young modulus, shear modulus, Poisson’s ratio

Fig. 5

Experimental free oscillations of the beam and matched logarithmic decrement of damping (a); and fast Fourier transform of the beams response (b). Linear mode shapes corresponding to the first two flexural (c) and the first longitudinal (d) natural frequencies (FE analysis made in commercial Abaqus software)

The above data of the tested prototype have been adopted for the numerical investigations. In the further analysis, the governing equations and BCs are transformed to dimensionless forms. The space coordinates are normalized to the beam length: $\bar{x} = x/L$, $\bar{u}=u/L$, $\bar{v} = v/L$, ${\bar{R}_h=R_h/L}$ and angles remain as they are ${\bar{\theta } = \theta }, {\bar{\psi } = \psi }$. Dimensionless time is defined as $\bar{t} = t/\omega ^\star$, where $\omega ^\star =\sqrt{\frac{EI}{\rho _1 L^4}}$, and thus corresponding dimensionless natural frequencies and dimensionless angular velocity are now given by $\bar{\omega }_u=\omega _u/\omega ^\star$, $\bar{\omega }_v=\omega _v/\omega ^\star$, $\bar{\Omega }= \Omega /\omega ^\star$, respectively.

The adopted transformation rules result in the dimensionless bending and axial stiffnesses normalized as ${\bar{EI}=1}$, $\bar{EA}=\frac{EA L^2}{EI}$, dimensionless beam mass per unit length $\bar{\rho }_1=1$ and dimensionless tip mass $\bar{m}_t=\frac{m_t}{\rho _1 L}$. Dimensionless values of the physical parameters given in Table 1 are

$$\begin{aligned} \begin{aligned} \bar{L} =1, \quad \bar{EI} =1, \quad \bar{EA} = 5.24481\times 10^6, \quad \bar{\rho _1} =1, \end{aligned} \end{aligned}$$

(42)

and the tip mass is equal to zero for the studied case, $\bar{m_\mathrm {t}}=0$.

Coefficients $q_1$–$q_7$ and $p_1$–$p_9$ present in Eq. (35) were calculated for two basic cases:

$\bullet \;$ The combination of first longitudinal and the first flexural mode

$$\begin{aligned} q_1&= -0.00008848 \ q_2 = 0.5 \ q_3 = -0.00027798\nonumber \\ q_4&= -0.00083394 \ q_5 = 7070.1147 \ q_6 = -0.00013899 \nonumber \\ q_7&= 0.00055597\nonumber \\ p_1&= -0.11134646 \quad p_2 = 0.5 \quad p_3 = -0.78299175\nonumber \\ p_4&{=} {1.4467399}{\times }{10}^7\ p_5 = 0.272619\ p_6 {=} {-}2.34897526 \nonumber \\ p_7&= 0.16969987 \ p_8 = 0.22338865 \ p_9 = -0.14220694\nonumber \\ \end{aligned}$$

(43)

$\bullet \;$ The combination of first longitudinal and the second flexural mode

$$\begin{aligned} q_1&=-0.00008848 \ q_2 = 0.5 \ q_3 = -0.00027798 \nonumber \\ q_4&=-0.00083394 \quad q_5 =180241.709 \ q_6 =-0.00013899 \nonumber \\ q_7&= 0.00055597 \nonumber \\ p_1&=-0.00984674 \ p_2 =0.5 \ p_3 =-0.43393589 \nonumber \\ p_4&= 5.88527845\times 10^7\ p_5 = -569.351085 \ p_6 =-1.30180768 \nonumber \\ p_7&= 0.14700054 \ p_8 =0.19621623 \ p_9 =-0.02269225. \end{aligned}$$

(44)

These values are used in numerical analysis given in the following section.

4 Parametric studies of the system

The derived analytical solutions of the governing equations expanded up to $\varepsilon ^3$ approximation order as obtained in Sect. 2.2 enable comprehensive parametric study of the system. To this aim, bifurcation diagrams are constructed to present the effects of various structural parameters on system response characteristics. In particular, parameters $\Omega$, $\sigma _v$, $\xi$, $R_\mathrm {h}$, $\theta$ are kept in Eq. (37) and thus can be used in these analyses.

The modulation equations obtained from MTS method involve also control signals $C_u$, $C_v$. They can be modified according to the adopted control law to meet the required beam behavior. In this paper, we consider two control strategies, namely a proportional P control and cubic control C. Proportional strategy considers the input signal multiplied by a gain coefficient $g_\mathrm {p}$ and supplied with some time delay $\tau$ to the actuators. In the case of nonlinear cubic C control, the signal is raised to power 3, gained by $g_\mathrm {c}$ factor and than supplied with delay $\tau$.

Moreover, by calculating coefficients $p_i$ ($i=1,\ldots ,9$) and $q_i$ ($i=1,\ldots ,7$) as present in (35) for individual longitudinal and transverse vibration modes the multiple different dynamic states of the system can be considered.

We start the analysis from solving the modulation equations analytically. To this aim, we introduce new variables $\gamma$ like

$$\begin{aligned} \gamma _a(t_2) = \sigma _a t_2 - \beta _a(t_2), \qquad \gamma _b(t_2) = \sigma _b t_2 - \beta _b(t_2), \end{aligned}$$

and next substitute them into Eq. (37). In a steady state $a'(t_2)=0$, $\beta _a'(t_2)=0$, $b'(t_2)=0$, $\gamma '(t_2)=0$; therefore, the modulation formulas simplify to the set of nonlinear but algebraic equations. Solution to this system involve response amplitude as a function of selected bifurcation parameters including the detuning parameters $\sigma _u$ and $\sigma _v$. Moreover, these relations can be used to tune control parameters for effective vibration reduction.

We note that for a general case all four modulation Eq. (37) are involved in the solution. However, if we neglect axial excitation and control in this direction, one can set $a'(t_2)=0$ followed by $a(t_2)=0$ relation due to damping. Then, the dynamics of the structure is governed only by the third and the forth equations of the system. It should be emphasized this simplification can be done if we confine the transverse excitation frequency only to the vicinity of the corresponding natural frequency and exclude the possibility of internal resonance. Study of the structural dynamics involving the internal longitudinal–transversal resonances for simply supported beams can be found in [23]. This problem for rotating beams with a tip mass will be discussed in a separate contribution.

4.1 Natural vibrations

We start the analysis from analytical solutions to determine backbone curves which represent nonlinear natural vibrations around the first and second flexural frequencies. Dimensionless values of the linear natural frequencies corresponding to non-rotating system configuration are:

• The first flexural natural frequency: $\omega _{01}=3.51602$ (16.5774 rad/s),

• The second flexural natural frequency: $\omega _{02}=22.034492$ (103.889 rad/s),

• The first longitudinal natural frequency: $\omega _{0u}=3597.37$ (16 961.0 rad/s).

It can be observed for the adopted structural parameters the first longitudinal frequency $\omega _{0u}$ is located far away from the flexural ones. Thus, as it has been mentioned above, the internal resonance case does not occur in the given problem formulation.

To obtain the expressions for backbone curves, we substitute zero values on the excitation, damping, and control gains in Eq. (37). Then, we get the final expression

$$\begin{aligned} b^4 + \left( c_1 \sigma _v + c_2 \Omega ^2 \right) b^2 + c_3 \sigma _v^2 + c_4 \sigma _v \Omega ^2 + c_5 \Omega ^4 = 0 \end{aligned}$$

(45)

where $\sigma _v = \omega _{0v} - \omega _{0}$. The individual coefficients are

• $c_1=-29.345,\quad c_2=2.129, \quad c_3=215.282, c_4=-31.236, \quad c_5=1.133 \$ and

• $c_1 =0.014, c_2=-2.30\times 10^{-3}, c_3=4.94\times 10^{-5}, c_4=-1.628\times 10^{-5}$, $c_5=1.33\times 10^{-6}$

for the first and second flexural modes, respectively. When analyzing the relation (45), one observes the presence of terms involving the rotor angular velocity $\Omega$ in power 2 and 4.

The plotted shape of the backbone curve corresponding to fundamental vibration mode and zero angular velocity (non-rotating structure) is presented in Fig. 6a. The curve reveals the evident hardening nature. If the angular speed $\Omega$ is increased, the curve gets shifted right toward higher frequencies, and its hardening-like property is maintained (Fig. 6b). The linear natural frequency increases as a parabolic function of rotor angular speed $\Omega$ which is presented in Fig. 6c.

In contrast to the first mode, the backbone curve for second flexural mode exhibits a softening (Fig. 7a) behavior for non-rotating structure. This nature of the curve is preserved also for rotating system—cases of $\Omega =2$, $\Omega =3$, $\Omega =5$ presented in Fig. 7b. It is interesting to note that the inherent softening behavior is strong enough to prevail the stiffening effect due to centrifugal loadings.

Fig. 6

Backbone curves for selected angular velocities a $\Omega =0$ and b $\Omega =0$ (black), $\Omega =1$ (blue), $\Omega =2$ (red), and c effect of angular velocity on natural vibrations frequency; first flexural vibration mode. (Color figure online)

Fig. 7

Backbone curves for selected angular velocities a $\Omega =0$ and b $\Omega =0$ (black), $\Omega =2$ (blue), $\Omega =3$ (red), and $\Omega =5$ (green); second flexural vibration mode. (Color figure online)

The proposed analytical model of the structure and obtained approximate solutions show that both modes exhibit opposite characteristics. This fact is in an agreement with results published by Thomas [38] considering relatively small rotations, but in contrast to Arvin et al. [2] where the introduced so-called equivalent nonlinearity coefficient depends on the rotor angular speed as well. Based on the analytical results, we may conclude the angular velocity does not affect neither hardening nor softening features of the backbone curves but just shifts them toward higher frequencies. This means the linear part of the stiffness matrix gets larger if rotation increases. But the nonlinear effect resulting from large amplitude oscillations maintains the same magnitude revealing stiffening/softening features depending on mode order. The first and the second modes having opposite nature will be studied for excited vibrations and structural control.

4.2 Forced vibrations

Forced vibrations of the rotating beam structure are studied assuming the excitation is imposed in the transverse direction only. Presuming steady-state vibrations and neglecting excitation in axial direction in Eq. (37), the last two formulas yield

$$\begin{aligned} \begin{aligned}&C_v p_2 b(t_2) + \Big [g_{v\mathrm {p}} p_3 + \frac{1}{4} g_{v\mathrm {c}} p_6 b^2(t_2) \Big ] b(t_2)\sin \tau _v \\&\quad = 2 p_1 \xi _v \sin \gamma _b(t_2)\\&\sigma _v b(t_2) - \left( p_7 + p_8 R_\mathrm {h} + p_9 \cos ^2 \theta \right) \Omega ^2 b(t_2) \\&\qquad - \frac{1}{4} p_5 b^3(t_2) = 2 p_1 \xi _v \cos \gamma _b(t_2)\\&\qquad + \Big [g_{v\mathrm {p}} p_3 + \frac{1}{4} g_{v\mathrm {c}} p_6 b^2(t_2) \Big ] b(t_2) \cos \tau _v \end{aligned} \end{aligned}$$

(46)

Eliminating phase angle $\gamma _b(t_2)$ and after mathematical transformations, we get

$$\begin{aligned} \alpha _1 b(t_2)^6 + \alpha _2 b(t_2)^4 + \alpha _3 b(t_2)^2 - 2 p_1^2 \xi _v^2 = 0 \end{aligned}$$

(47)

where

$$\begin{aligned} \alpha _1= & {} \frac{1}{32} \left( p_5^2 + g_{v\mathrm {c}}^2 p_6^2 + 2 g_{v\mathrm {c}} p_5 p_6\cos \tau _v\right) \\ \alpha _2= & {} \frac{1}{4} \Big \{p_5 \left[ \Omega ^2 \left( p_7 + p_8 R_\mathrm {h} + p_9\cos ^2\theta \right) - \sigma _v \right] \\&+ g_{v\mathrm {p}} p_3 (g_{v\mathrm {c}} p_6 + p_5 \cos \tau _v)\\&+ C_v p_2 p_6 g_{vc}\sin \tau _v + p_6 g_{vc}\left[ \Omega ^2 \left( p_7 + p_8 R_\mathrm {h} \right. \right. \\&\left. \left. + p_9 \cos ^2\theta \right) - \sigma _v\right] \cos \tau _v \Big \}\\ \alpha _3= & {} \frac{1}{2} \left\{ C_v^2 p_2^2 + g_{v\mathrm {p}}^2 p_3^2 + \left[ \sigma _v - \Omega ^2 \left( p_7 \right. \right. \right. \\&\left. \left. \left. + p_8 R_\mathrm {h} + p_9 \cos ^2\theta \right) \right] ^2\right\} \\&+ g_{v\mathrm {p}} p_3 \left\{ C_v p_2\sin \tau _v - \left[ \sigma _v - \Omega ^2 \left( p_7 \right. \right. \right. \\&\left. \left. \left. + p_8 R_\mathrm {h} + p_9\cos ^2\theta \right) \right] \cos \tau _v \right\} \end{aligned}$$

In the above equation, we can distinguish terms dependent on angular velocity $\Omega$, hub radius $R_\mathrm {h}$, external excitation $\xi _v$, and related to linear $g_{v\mathrm {p}}$ and nonlinear $g_{v\mathrm {c}}$ control laws and time delay $\tau _v$. Equating to zero the control parameters, we get equations of the resonance curves around the first and the second resonance zones as a function of the angular velocity and the preset angle $\theta$. For the following analysis, we assume that the preset angle is equal zero ($\theta =0$). This correspond for the beam oscillating in the rotor plane (see Fig. 5). Modal damping is approximated on the base of experimental tests as $2\%$ of first natural frequency value: $C_v=0.07032$ and $1\%$ for the second mode $C_v=0.22035$. Amplitude of excitation $\xi _v$ is varied as reported in figure captions.

Resonance curves around the first flexural frequency are presented in Fig. 8. Despite that large oscillations in the system just a very faint stiffening effect is observed for this mode (Fig. 8a), much too small for the jump phenomenon to occur. This feature is observed for zero angular velocity and also for rotating structure—cases $\Omega =2$, $\Omega =3$ and $\Omega =5$ corresponding to blue, red and green curves, respectively (Fig. 8b). Again the results are similar to the backbone curves, the so-called stiffening effect due to rotation leads solely to the right shift of the curves without a change of the stiffening effect caused by the nonlinear beam oscillations.

Fig. 8

Resonance curves for selected angular velocities a $\Omega =0$ and b $\Omega =0$ (black), $\Omega =2$ (blue), $\Omega =3$ (red), and $\Omega =5$ (green); first flexural vibration mode; $\xi _v=0.1$, $C_v=0.07032$. (Color figure online)

Fig. 9

Resonance curves for selected angular velocities a $\Omega =0$ and b $\Omega =0$ (black), $\Omega =2$ (blue), $\Omega =3$ (red), and $\Omega =5$ (green); second flexural vibration mode; $\xi _v=0.4$, $c_v=0.220345$. (Color figure online)

For the second resonance zone, nonlinear softening is rather strong. In Fig. 9a, computed for $\Omega =0$, the softening behavior is observed for amplitudes below of $8\%$ of the beam length. As it is demonstrated in Fig. 9b the increased angular speed (cases $\Omega =2$, $\Omega =3$, $\Omega =5$) does not change the intensity of softening phenomenon but just shifts the resonance zone. Stability of frequency response curves is studied by computing eigenvalues of Jacobian matrix (41); dashed line represents unstable part of the solution and solid line defines stable solution in the following Figures.

The results presented in this section shall be used in the next steps when the proportional and cubic control strategies are engaged in order to reduce vibrations around the discussed resonance zones. The outcomes obtained in this section are consistent with authors previous work in [42].

5 Controlled forced vibrations

The derived analytical model of the active blade and approximate solutions to governing equations enable analysis of the system under assumed control law. This involves additional terms present in the boundary conditions Eq. (35) and later modulation equations—see terms with $g_{u\mathrm {p}}$, $g_{u\mathrm {c}}$, and $g_{v\mathrm {p}}$, $g_{v\mathrm {c}}$ in formulas (37). They represent loads generated by control unit according to the boundary control method approach adopted in this research. In a real set-up structural control can be achieved by the controlled voltage supplied to active elements. The mathematical model of the combined blade-control unit structure considers also a time delay $\tau _v$ which may occur due to inherent properties of actual devices or can be added intensionally to enhance system’s performance.

It was decided to study two control strategies, namely the linear control (P) and cubic control (C). In the linear control method, the input signal is multiplied by a gain coefficient $g_\mathrm {p}$ and supplied to the actuators. In the case of nonlinear C control the signal is raised to power 3 and gained by $g_\mathrm {c}$ factor.

Remembering that dynamics of the beam close to its first natural frequency is almost linear, we apply P control with time delay. Based on the Eq. (47), substituting $g_{v\mathrm {c}}=0$ we get

$$\begin{aligned} \begin{aligned}&b^6 + b^4 \left( c_{1p} \sigma _v + c_{2p} \Omega ^2 + c_{3p} g_{v\mathrm {p}} \cos \tau _v \right) \\&+ b^2 \left[ c_{4p} + c_{5p} g_{v\mathrm {p}}^2 + c_{6p} \sigma _v^2 + c_{7p} \Omega ^4 \right. \\&+ c_{8p} g_{v\mathrm {p}} \sigma _v \cos \tau _v\\&+ \Omega ^2 \left( c_{9p} \sigma _v + c_{10p} g_{v\mathrm {p}} \cos \tau _v \right) \\&\left. + c_{11p} g_{v\mathrm {p}} \sin \tau _v \right] + c_{12p}\xi _v^2 = 0, \end{aligned} \end{aligned}$$

(48)

where

$$\begin{aligned} \begin{aligned} c_{1p}&=-29.345,&c_{2p}&= 2.12886, \\ c_{3p}&=-22.9769,&c_{4p}&= 0.266137,\\ c_{5p}&=131.984,&c_{6p}&=215.282, \\ c_{7p}&= 1.13302,&c_{8p}&=337.128,\\ c_{9p}&=-31.2357,&c_{10p}&=-24.4573, \\ c_{11p}&=-11.8534,&c_{12p}&=-10.6763. \end{aligned} \end{aligned}$$

Fig. 10

Amplitude of system response for P control against detuning frequency $\sigma _v$ and time delay $\tau$ for a $\Omega =0$ and b $\Omega =2$; first flexural vibration mode; $g_{v\mathrm {p}}=0.2$, $\xi _v=0.1$, $c_v=0.07032$

Fig. 11

Resonance curves of the system with P control with various time delay; a for $\Omega =0$, $\tau _v=0$ (black), $\tau _v=0.5$ (blue), $\tau _v=1.0$ (green), $\tau _v=1.5$ (pink), $\tau _v=2.0$ (orange), $\tau _v=2.5$ (magenta), b $\Omega =2$, $g_{v\mathrm {p}}=0$ (magenta), $\tau _v=0$ (black), $\tau _v=0.5$ (blue), $\tau _v=1.0$ (green), $\tau _v=1.5$ (pink), c $\Omega =0$, $\tau _v=3.0$ (blue), $\tau _v=3.5$ (green), and d $\Omega =0$, $\tau _v=6$ (black), $\tau _v=6.5$ (red); grey line denotes resonance curve for $\Omega =0$ and no control; first flexural vibration mode; $g_{v\mathrm {p}}=0.2$, $\xi _v=0.1$, $c_v=0.07032$. (Color figure online)

Equation (48) depends on controller gain, time delay $\tau _v$, angular velocity $\Omega$, and amplitude and frequency of excitation, $\xi _v$ and $\sigma _v$, respectively. Therefore, we can evaluate the effectiveness of the controller at various combinations of excitation conditions.

The response of the system for fixed amplitude of excitation $\xi _v=0.1$ and activated linear controller is shown in Fig. 10. The figures present an overview of the response for fixed gain value $g_{v\mathrm {p}}=0.2$ with respect to detuning frequency $\sigma _v$ and time delay $\tau _v$ varied in $\langle -2\pi$, $2\pi \rangle$ interval. The computed 3D surface shows periodically repeated peaks where the applied control does not work properly. However, there are also valleys corresponding to small amplitudes and effective vibrations suppression. Comparing graphs for $\Omega =0$ (Fig. 10a) and $\Omega =2$ (Fig. 10b), we observe the controller works in a very similar way. The only difference is the shift of the response surface toward higher frequencies. This is visible by localization of peaks along $\sigma _v$ axis (note that scales for $\sigma _v$ are different on both plots). Studying these plots, one may also conclude about the influence of the time delay. It is evident the proper tuning of the $\tau _v$ parameter with respect to time delay the effective suppression of vibrations may be achieved.

Fig. 12

Response of the system with P control and various detuning parameter; a for $\Omega =0$, $\sigma _v=-0.2$ (blue), $\sigma _v=0$ (black), $\sigma _v=0.1$ (red), $\sigma _v=1.5$ (green), and b $\Omega =2$, $\sigma _v=-0.2$ (blu2), $\sigma _v=0$ (black), $\sigma _v=0.1$ (red), $\sigma _v=0.15$ (green); first flexural vibration mode; $g_{v\mathrm {p}}=0.2$, $\xi _v=0.1$, $c_v=0.07032$. (Color figure online)

The selected cross sections of these 3D surfaces are presented in Fig. 11a and b for the stationary and rotating configuration, respectively. In Fig. 11a the resonance curve of the system without control is sketched by the grey line. If the P controller is engaged and the input signal is supplied with zero time delay then the curve is just shifted toward lower frequencies without any amplitude change (black line). However, if the time delay is introduced, then we may simultaneously shift the resonance curve and reduce vibrations. As it is seen in Fig. 11a the amplitude can be decreased even over three times for $\tau _v=2.0$ (orange curve).

In the case of the rotating beam (Fig. 11b), the resonance curve without control due to rotation is shifted toward higher frequencies (magenta line with respect to grey curve as copied from (a)). Then if the P controller is operational without time delay ($\tau _v=0$) the curve is shifted back toward lower frequencies (black continuous line). Similar to the stationary configuration case, the proper selection of time delay $\tau _v$ may significantly reduce vibration amplitudes—see, e.g., orange curve corresponding to $\tau _v=2.0$. However, the optimal delays are different than for non-rotating system. It should be also noted the response amplitude can be not only reduced, but also magnified to large values if the time delay is tuned improperly. Meanwhile, the characteristics are shifted toward higher or lower frequencies as it is presented in Fig. 11c for $\tau _v=3$ (blue) and $\tau _v=6.5$ (red) in Fig. 11d, respectively.

Direct comparison of P control effectiveness around the first resonance zone for fixed excitation amplitude and frequency is presented in Fig. 12. The detuning of excitation frequency $\sigma _v$ is selected close to the first resonance and time delay is varied within $\langle -2\pi , 2\pi \rangle$ interval. As reported above, the proper selection of time delay results in a large reduction of vibration amplitudes both for stationary (Fig. 12a) and rotating beam (Fig. 12b). Furthermore, one observes the zones of effective vibrations suppression are significantly wider for the rotating beam case.

As the second option, we propose to apply the nonlinear cubic C controller. Thus the P control is switched off by setting $g_{v\mathrm {p}}=0$. Substituting the condition to equations (47) we get

$$\begin{aligned} \begin{aligned}&b^6 \Big (c_{1c} + c_{2c} g_{v\mathrm {c}}^2 + c_{3c} g_{v\mathrm {c}} \cos \tau _v \Big ) \\&\quad + b^4 \Big \{ c_{4c} \sigma _v + c_{5c} \Omega ^2 - g_{v\mathrm {c}} \Big [\Big (c_{6c} \sigma _v \\&\quad + c_{7c} \Omega ^2 \Big )\cos \tau _v + c_{8c} \sin \tau _v \Big ] \Big \} \\&\quad + b^2 \Big (c_{9c} + c_{10c} \sigma _v^2 + c_{11c} \sigma _v \Omega ^2 \\&\quad + c_{12c} \sigma _v \Omega ^4 \Big ) + c_{13c} \xi _v^2 = 0, \end{aligned} \end{aligned}$$

(49)

where:

$$\begin{aligned} \begin{aligned} c_{1c}&= 0.00232254,&c_{2c}&= 0.172428, \\ c_{3c}&= 0.0400235,&c_{4c}&=-0.0681548,\\ c_{5c}&= 0.00494436,&c_{6c}&=-0.587244, \\ c_{7c}&= 0.0426023,&c_{8c}&=0.0206475,\\ c_{9c}&= 0.000618113,&c_{10c}&= 0.5, \\ c_{11c}&=-0.0725461,&c_{12c}&= 0.00263147,\\ c_{13c}&=-0.0247961. \end{aligned} \end{aligned}$$

Fig. 13

Resonance curves of the system with C control and fixed time delay $\tau _v=0$ for a $\Omega =0$ and b $\Omega =2$; $g_{v\mathrm {c}}=0.2$ (blue), $g_{v\mathrm {c}}=0.5$ (green), $g_{v\mathrm {c}}=0.12$ (red), $g_{v\mathrm {c}}=-0.5$ (orange), $g_{v\mathrm {c}}=-1.0$ (magenta); grey line: $g_{v\mathrm {c}}=0$ and $\Omega =0$; first flexural vibration mode; $\xi _v=0.1$, $c_v=0.07032$. (Color figure online)

Solutions of Eq. (49) enable to determine impact of C control on the system response. The idea of this controller is to influence mainly the fundamental property of the structure characteristics that is represented by the slope of the backbone curve. In fact, setting time delay $\tau _v=0$ and varying gain $g_{v\mathrm {c}}$ we may modify the properties of the system from hardening to softening (Fig. 13a) behavior. For the gain $g_{v\mathrm {c}}=0.12$, we may obtain linear-like response (red curve in Fig. 13a).

Results of the rotating system analysis are presented in Fig. 13b. The introduced rotation does not affect the controller performance apart from the fact that the resonance curves are shifted and their slopes are modified around the shifted linear natural frequency value.

The effectiveness of the C controller as well as combined $P-C$ control we demonstrate for the second natural frequency. Due to its strong nonlinear softening effect, the comparison of nonlinear versus linear control strategy is more appealing.

The analysis of the second-mode dynamics is started from P control governed by Eq. (48). The coefficients for the second mode take values

$$\begin{aligned}&c_{1p} =0.0140511, c_{2p} =-\,0.00230271, \\&c_{3p} =0.00609727, c_{4p} =5.99109\times 10^{-7},\\&c_{5p} =9.29417\times 10^{-6}, c_{6p} =0.0000493582, \\&c_{7p} =1.32562\times 10^{-6}, c_{8p} =0.0000428366,\\&c_{9p} =-\,0.0000161778, \qquad \ c_{10p} = -\,7.02012\times 10^{-6}, \\&c_{11p} =-\,4.71942\times 10^{-6},\quad c_{12p} =-\,1.91428\times 10^{-8} \end{aligned}$$

Since vibrations amplitudes around this resonance zone are much smaller then for the first resonance the gain $g_{v\mathrm {p}}$ need to be adjusted to higher values. Based on experimental data, we accept $g_{v\mathrm {p}}=1$ as a reference value. The second-mode response surface plots are prepared keeping the excitation amplitude fixed $\xi _v=0.4$ and varying detuning parameter $\sigma _v$ (excitation frequency) and time delay $\tau _v$. The amplitudes of oscillations for the stationary and the rotating beam configuration $\Omega =5$ are presented in Fig. 14a and b, respectively.

Fig. 14

Amplitude of system response for P control against detuning frequency and time delay for a $\Omega =0$ and b $\Omega =5$; second flexural vibration mode; $g_{v\mathrm {p}}=1.0$, $\xi _v=0.4$, $c_v=0.220345$

The darker blue surfaces represent the desired controller performance with just a few hills corresponding to slightly increased amplitudes. Studying the plots it may be concluded for the given excitation frequency one may adjust the time delay to maximize the effectiveness of the controller and retain possibly lowest vibration amplitudes. The summits of pale blue hills are located right at the second natural frequency (i.e., for $\sigma _v=0$) in the case of the non-rotating beam or shifted toward higher frequencies to about $\sigma _v=4$ for the $\Omega =5$ rotating beam. This offset results purely from the centrifugal stiffening effect. Nevertheless, the inherent strong nonlinear behavior (softening type see Fig. 9) of the second mode brings additional large amplitudes solutions represented by orange surfaces in Fig. 14 even if P controller is on.

Fig. 15

Resonance curves of the system with P control for $\Omega =0$ and various time delay; a $\tau _v=0$ (green), $\tau _v=0.5$ (black), $\tau _v=1.0$ (red), $\tau _v=1.5$ (blue) and b $\tau _v=2.0$ (black), $\tau _v=2.5$ (blue), $\tau _v=3.0$ (green), $\tau _v=3.5$ (red); grey line denotes resonance curve for $\Omega =0$ and no control; second flexural vibration mode; $g_{v\mathrm {p}}=1.0$, $\xi _v=0.4$, $c_v=0.220345$. (Color figure online)

The individual response curves for selected time delays are clearly presented in Fig. 15. The resonance curve of the system without control is marked by grey line. When the control is triggered, the overall performance of the system is quite similar to the first mode. Increase in time delay first shifts the curves slightly toward lower frequencies (Fig. 15a), but next the trend is reversed and peaks are shifted a bit to the right (Fig. 15b). By proper tuning of the time delay parameter $\tau _v$, we can decrease amplitudes of the response while keeping the natural frequency almost unchanged. Meanwhile, the softening type of the characteristics is maintained. On the other hand the poor choice of time delay causes the dramatic increase in vibrations amplitudes and enhances nonlinearity of the system as presented in Fig. 15a for $\tau _v=0.5$ and Fig. 15b for $\tau _v=3.0$. These cases correspond to orange areas in Fig. 14. Possible consequences of the poorly tuned P control are presented also in Fig. 16. Adjusting time delay, we may get low amplitude oscillations but meanwhile above these low amplitude sections there are isolated closed loops representing large amplitude oscillations with unstable bottom part of the “isola.” For specific time delays where the “isolas” exist the basins of attractions of all possible solutions have to be carefully checked.

To eliminate the presented above drawbacks of P-control we propose to apply C strategy which—as it has been demonstrated earlier—allows to modify the slope of the resonance curve. The coefficients of the governing equation Eq. (49) for the second mode take values

$$\begin{aligned} \begin{aligned} c_{1c}&=324161.0,&c_{2c}&=1.6947, \\ c_{3c}&=-1482.37,&c_{4c}&=4554.81,\\ c_{5c}&=-746.448,&c_{6c}&=-10.4145, \\ c_{7c}&=1.70674,&c_{8c}&= 1.14739,\\ c_{9c}&=0.194208,&c_{10c}&= 16, \\ c_{11c}&= -5.2442,&c_{12c}&= 0.429713,\\ c_{13c}&=-0.00620533. \end{aligned} \end{aligned}$$

First it should be noted the value of the cubic control gain $g_{v\mathrm {c}}$ may get even two orders higher values than its counterpart applied for the first mode. This is related to the fact that the second mode dimensionless amplitudes are much smaller than the first mode ones. Since these values are put to the power 3 the difference must be “compensated” by higher magnitudes of gain at second mode. Accordingly, the second mode cubic gain may approach values of about 1500 but we decided to take a smaller value setting $g_{v\mathrm {c}}=\pm \,500$ as a reference level.

Fig. 16

Response of the system with P control and various detuning parameters for $\Omega =5$, $\sigma _v=2.5$, ${\sigma _v=3.0}$, $\sigma _v=3.5$, $\sigma _v=4.0$,$\sigma _v=4.5$, $\sigma _v=5.0$, $\sigma _v=5.5$; second flexural vibration mode; $g_{v\mathrm {p}}=1.0$, $\xi _v=0.4$, $c_v=0.220345$

Fig. 17

Resonance curves of the system with C control at fixed gain and varied time delay a $\tau _v=0$ (black); $\tau _{v}=0.2$ (blue), $\tau _{v}=0.5$ (green), $\tau _{v}=1.0$ (red); b $\tau _v=2.0$ (black); $\tau _{v}=2.5$ (blue), $\tau _{v}=3.0$ (green), $\tau _{v}=3.5$ (red), and c $\tau _v=-2.0$ (black); $\tau _{v}=-2.5$ (blue), $\tau _{v}=-3.0$ (green), $\tau _{v}=-3.5$ (red); second flexural vibration mode; $g_{v\mathrm {c}}=-500$, $\xi _v=0.4$, $c_v=0.220345$; grey line denotes resonance curve for $\Omega$=0 and no control. (Color figure online)

In contrast to the first-mode analysis now, we show that the C-control strategy applied to mode 2 can modify the slope of the response characteristics by tuning the time delay. The original resonance curve (grey line in Fig. 17a) can be modified in terms of amplitudes and also its slope can be changed from softening to hardening. Moreover, the further increase in time delay results in reduced amplitudes combined with amplified softening behavior evidenced by increased slope (Fig. 17b). However, for negative time delays, the reduction of response is not so evident. Furthermore, the double nonlinearities, namely the structural and control ones result in presence of additional solutions observed by isolated curves (Fig. 17c) of high amplitude. The spotted additional solutions are adverse events in terms of vibration reduction but they may be interesting while designing the energy harvesters.

Fig. 18

Amplitude of system response for $P-C$ control against detuning frequency and gain $g_{v\mathrm {p}}$; $\Omega =0$; second flexural vibration mode; $g_{v\mathrm {c}}=-500$, $\xi _v=0.4$, $c_v=0.220345$

Fig. 19

Resonance curves of system for $P-C$ control; second flexural vibration mode; a $\Omega =0$, $g_{v\mathrm {p}}=-1$, $\tau _v=1$ (black), $g_{v\mathrm {p}}=1$, $\tau _v=-1.5$ (red), and b $\Omega =5$, $g_{v\mathrm {p}}=-1$, $\tau _v=1$; $g_{v\mathrm {c}}=-500$, $\xi _v=0.4$, $c_v=0.220345$. (Color figure online)

Having above results now we apply mixed $P-C$ control for the nonlinear second mode resonance. To benefit from advantages of both controllers, we apply cubic controller to get a pseudo-linear system and then the linear controller to reduce vibrations. Therefore, we set $g_{v\mathrm {c}}=-500$ and $\tau _v=1$ for the analysis which correspond to linear-like response in Fig. 17 (red curve). Next, we are to adjust the settings of the additional P controller. The response surface in Fig. 18 presents the characteristics of the beam against detuning parameter $\sigma _v$ and gain $g_{v\mathrm {p}}$. Obviously, for $g_{v\mathrm {p}}=0$ we get purely cubic control strategy. To get more reduction, we have to avoid the peak and select value out of this zone.

The resonance curve with activated $P-C$ controller at time delay $\tau _v=1$ is presented in Fig. 19a by the black line. The vibrations amplitude is reduced and the only one solution exists. For comparison we study control setting $\tau _v=-1.5$ (red line) where the greater reduction of the amplitude can be achieved. However, in this case, additional isolated solutions exist (red isola), and they are of large amplitude. Such situation requires a careful detection of their basins of attraction to guarantee safe system dynamics. The parameters of the combined $P-C$ controller can be applied for rotating beam as well. The only difference is that the resonance curve is shifted toward higher frequencies, as presented in Fig. 19b.

Fig. 20

Functions $r_5$-$r_{12}$ for the first flexural mode

Fig. 21

Functions $r_5$-$r_{12}$ for second flexural mode

6 Conclusions

The presented mathematical model of the rotating cantilever beam structure with active elements enables analysis of free and forced oscillations of the structure corresponding to moderate-large amplitudes. The partial differential equations and associated boundary conditions are derived considering longitudinal and transversal vibrations of the beam rotating with fixed angular velocity $\Omega$ and preset to the hub at any arbitrary angle. The performance of active elements has been represented by non-homogenous terms in BCs. These involved linear and nonlinear (cubic) control signals with time delay. The set of partial differential equations and associated BCs have been solved directly by the multiple timescales method up to the third-order perturbation. The physical parameters of the model including electromechanical parameters of the active elements have been determined within the laboratory tests.

The analytically derived modulation equations of the beam dynamics include most important structural parameters and control gains that may be considered as bifurcation parameters. The performed analysis of the solutions revealed hardening for the first mode and softening of the second vibration bending mode. These effects are maintained also if angular velocity is increased. It has been shown the rotation does not change the curve slope (hardening or softening) but just shifts the resonance zones toward higher frequencies which is in an agreement with results presented in paper [38] if angular velocity is not high.

To reduce vibrations of the system the linear proportional P controller, nonlinear cubic C controller and finally mixed $P-C$ controller is proposed. It has been shown for the weakly nonlinear system around the first resonance the P controller is effective both for the stationary as well as rotating beam. For the moderate or strongly nonlinear system behavior corresponding to second natural frequency multiple solutions occur and thus more advanced control techniques are applied. The suggested strategy is based on the cubic or mixed linear-cubic control results. It has been shown these two approaches are capable to significantly reduce nonlinearities and to eliminate multiple solutions. By a proper tuning of control gains and time delay we can determine analytically domains of system parameters corresponding to unique (single) solution and zones with safe controller performance. Therefore, it is possible to adjust controller parameters for safe operation of the system at large oscillations and various angular speeds of the beam.

The additional nonlinearity coming from controller combined with beam’s second mode structural nonlinearity may lead to additional isolated solutions corresponding to large amplitudes. That specific operation of the system can be exploited in terms of energy harvesting when nonlinear oscillations are much desired effect. The obtained analytical results will be tested in the laboratory for actual implementations.

Appendix A

For the coefficients presented in the Eq. (34) the first longitudinal mode has coefficient $\phi _u=0.5 \pi$, while the flexural modes have ratios

$\bullet \;$First mode:

$$\begin{aligned} \phi= & {} 1.8751, \quad r_1=0.367048, \quad r_2=0.5, \\ r_3= & {} -0.367048, \quad r_4=-0.5, \quad \end{aligned}$$

$\bullet \;$Second mode:

$$\begin{aligned} \phi= & {} 4.69409, \quad r_1=0.509234, \quad r_2=-0.5, \\ r_3= & {} -0.509234, \quad r_4=0.5, \quad \end{aligned}$$

and graphical representation of functions $r_5$-$r_{12}$ get the forms shown in Figs. 20 and 21, respectively.