Small amplitude chimeras for coupled clocks

Abstract

We report the arise of small amplitude chimera states in three coupled pendulum clocks suspended on an oscillating base. Two types of chimeras are identified and described by the character of the behaviour of particular units (which can be both regular or irregular). The regions of the appearance of the dynamical patterns are determined and the scenarios of their coexistence with typical synchronization states are discussed. We investigate the chimeras’ basins of attraction, showing that the arise of complex dynamics is not straightforward and highly depends on the system’s parameters and the initial conditions. The latter is confirmed by the probability analysis, exhibiting the rare character of the observed attractors. The scenarios of bifurcations between the chimeric patterns are studied and supported using the energy balance method, which allows to describe the changes of the energy flows between particular nodes of the system. The results presented in this paper confirm the ones obtained for the previous models, extending the analysis with an additional degree of freedom.

1 Introduction

The spontaneous coexistence of coherence and incoherence in networks of coupled systems [1] is one of the most surprising phenomena observed in the nonlinear dynamics discipline. The so-called chimera state [2], named after a hybrid creature from the Greek mythology, combines both regular and irregular types of patterns, showing that even though the coupling scheme applied to the system is homogeneous, the oscillators can split into many groups of different behaviours, uncovering unexpected scenarios of partial synchronization and chaos.

Chimeras have been observed in various dynamical models, just to mention heterogeneous networks [3, 4], chemical oscillators [5], mechanical systems [6, 7] or the delayed ones [8, 9]. Patterns of coexistence are reported in neuronal problems [10,11,12,13,14] (including such classical systems as the FitzHugh-Nagumo [12] or the Hindmarsh-Rose [13] ones) and can be related to the complex brain dynamics [14]. In [15], the authors present a solvable model exhibiting chimeric behaviours, while in [16], the spectral properties of chimeras are discussed. Coexisting states arise naturally on the road from complete synchronization to pure spatial chaos, which has been studied in [17, 18] but can be also related to the transient dynamics occurring in the system (see, e.g. [19] for details). In [20], Sethia and Sen discuss the existence criteria for chimera states, while in [21], the classification scheme of the chimeric behaviour is described. A general study on the phenomenon can be found in [22].

Apart from typical large networks of coupled oscillators, as the ones referenced above, coexisting patterns can be also found in small models of connected units. This particular scenario of chimeras’ appearance has been introduced as the so-called weak chimeras [23, 24], which occur even for the simplest case of three coupled oscillators [25, 26]. Small/weak chimeras have been observed in Kuramoto model with inertia [26], experimental pendula [25] or delay-coupled lasers [27]. Some studies on their arise in systems with broken symmetry and complex, nonlinear interactions have been described in [28] and [29], respectively.

In this paper, we report the arise of small chimeras, investigating the amplitude of the oscillations of the connected units. The amplitude chimeras [30, 31], characterized by the coexistence of (at least) two groups of oscillators synchronized within different amplitudes appear universally in networks of coupled systems, e.g. in chaotic oscillators [32] or non-locally coupled maps [33]. The stability of amplitude chimeras has been studied in [34], while in [35], Banerjee et al. investigate their relation with classical, phase patterns.

The results presented in this study extend the ones discussed in the previous works [25, 26], introducing an additional degree of freedom, which corresponds to the dynamics of the supporting base. When the motion of the base is included, the scenario becomes more realistic (the oscillations of the support, on which the nodes are working cannot be excluded completely in practical implementations). Moreover, the relation between the motion of the oscillators and the base enables a new way of the energy distribution (the coupling scheme within the network becomes more complex). The inclusion of the support’s dynamics (i.e. the central hub node globally coupled with all of the units [36, 37]) can influence the behaviour of the oscillators and uncover new, complex states, just to mention the transient ones [38]. In this study, we focus on the smallest amplitude chimeras, which have not been described previously.

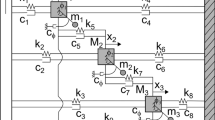
Namely, we investigate the dynamics of a simple system of three coupled pendulum clocks hanged on an oscillating base, which is schematically shown in Fig. 1.

Fig. 1

(colour online). The scheme of three coupled identical pendulum clocks (masses m marked in red, blue and green) hanged on an oscillating, supporting base (the motion is realized in 0xy plane)

The supporting base mounted at the origin of 0xy plane (the location of the mass centre) can oscillate around the axis, which is perpendicular to Figure’s plane (position denoted by $\theta$ variable). The properties of the base are described by the following parameters: $B_0 \, [\text {kg}m^2]$ (moment of inertia in regard to the origin), $k_{\theta } \, \text {[Nm]}$ (the stiffness of the spring connecting the base and the unmoving support) and $c_{\theta } \, \text {[Nms]}$ (the damping of the damper connecting the base and the unmoving support). The support is connected with three identical planar pendulum clocks (marked by red, blue and green), which are mounted at points $S_i$, $i = 1, 2, 3$ (shown as the brown dots). The suspension of the 1st pendulum (point $S_1$) is located above the origin, while the positions of the remaining two points ($S_2$ and $S_3$) are chosen to preserve the angular symmetry of the model, i.e. $\sphericalangle (\overline{0S}_i, \overline{0S}_{i+1}) = 120 ^{\circ }$ ($i = 1, 2, 3$; index i periodic mod 3). The distance between the origin and each of the suspension points is the same and has been denoted by parameter $r = \left| \overline{0 S}_i \right|$ ($i = 1, 2, 3$). The displacement of i–th pendulum is given by $\varphi _i$ variable, while the parameters of the nodes are as follows: m (the mass), l (the length) and $c_{\varphi }$ (the damping, not shown in Figure). The pendula shown in Fig. 1 are coupled via the supporting base, as well as the springs with stiffness coefficient $k_{\varphi } \, \text {[N/m]}$ (shown as the pink ones). Due to the number of the oscillators (three), the topology of the latter coupling scheme is both local and global [25, 26]. In the considered scenario, the motion of the nodes induces the oscillations of the base and the pendula are not parametrically excited as in classical models [39,40,41,42].

The Lagrange equations of motion determining the dynamics of the model shown in Fig. 1 can be described in the following way:

$$\begin{aligned} \left\{ \begin{array}{l} (B_0 + 3 m r^2 ) \ddot{\theta } + k_{\theta } \theta + c_{\theta } \dot{\theta } + \\ m r \sum \limits _{i=1}^3 \{ l [ \ddot{\varphi }_i \sin (\varphi _i - \theta - \alpha _i) + {\dot{\varphi }_i}^2 \cos (\varphi _i - \theta - \alpha _i) ] +\\ g \cos (\alpha _i + \theta ) \} + \Delta V_{\theta } = 0,\\ m l^2 \ddot{\varphi }_i + m g l \sin \varphi _i + c_{\varphi } \dot{\varphi }_i + \\ m r l [ \ddot{\theta } \sin (\varphi _i - \theta - \alpha _i) - {\dot{\theta }}^2 \cos (\varphi _i - \theta - \alpha _i) ] +\\ \Delta V_{\varphi _i} = M_{E_i}, \end{array} \right. \nonumber \\ \end{aligned}$$

(1)

where $i = 1, 2, 3$.

During our research, we have fixed the following parameters of model (1): $m = 1.0 \, \text {[kg]}$, $l = 0.24849 \, \text {[m]}$, $c_{\varphi } = 0.01 \, \text {[Nms]}$, $k_{\theta } = 34.0 \, \text {[Nm]}$, $g = 9.81 \, [\text {m}/s^2]$ (the standard gravity), $r = 1.0 \, \text {[m]}$, $\alpha _1 = \pi /2$, $\alpha _2 = 7 \pi /6$ and $\alpha _3 = 11 \pi /6$ (parameters $\alpha _i$ describe the angular position of suspension points $S_i$, i.e. $\alpha _i = \sphericalangle (0x, \overline{0 S}_i)$, where 0x denotes the positive x half axis. The damping of the supporting base $c_{\theta } \, \text {[Nms]}$ has been varied during the research to preserve fixed logarithmic decrement at $\Delta = \ln (2)$ (in reference to a simple 1 DOF system of an oscillating base with the same values of the parameters as described above).

The motion of the pendula in system (1) is induced by the build-in escapement mechanisms (not shown in Fig. 1), providing the moment of force described by functions $M_{E_i}$, $i = 1, 2, 3$ [43, 44]. The i-th function depends on both pendulum’s displacement ($\varphi _i$) and the position of the i-th mechanism’s cogwheel versus the mechanism’s pallet (parameter $\sigma _i \in \left\{ 1, 2 \right\}$; the cogwheel can rest on either left or the right pallet). Each of functions $M_{E_i}$ can be expressed as follows:

$$\begin{aligned} M_{E_i} = \left\{ \begin{array}{ll} M &{} : \sigma _i=1 \wedge 0< \varphi _i< \varepsilon ,\\ - M &{} : \sigma _i=2 \wedge -\varepsilon< \varphi _i < 0,\\ 0 &{} : \text {otherwise,} \end{array} \right. \end{aligned}$$

(2)

where $M = \, 0.075 \text {[Nm]}$ denotes the value of the fixed external momentum, while $\varepsilon = 5.0 ^{\circ }$ is the escapement’s threshold (the mechanism is working as long as the displacement of the pendulum exceeds the threshold). Components $\Delta V_{\varphi _i}$ and $\Delta V_{\theta }$ in eqs. (1) describe the moments of forces acting on the pendula (and indirectly on the base), which are provided by the coupling springs (see Fig. 1 for details). The values of components $\Delta V_{\theta }$ and $\Delta V_{\varphi _i}$ depend on both $s_i$ (the distance between the i–th and the $(i+1)$-th pendulum masses for the unmoving system, i.e. in the equilibrium state) and $\hat{s}_i$ (the distance between the masses when the nodes oscillate) and can be expressed using the following formulas:

$$\begin{aligned}&s_i = r \sqrt{2 \left( 1- \cos \left( \alpha _i - \alpha _{i+1} \right) \right) },\nonumber \\&\hat{s}_i = \sqrt{s^2_i + 2 l^2 \left( 1- \cos \left( \varphi _i - \varphi _{i+1} \right) \right) + 8 l r \sin \left( \frac{\varphi _i - \varphi _{i+1}}{2} \right) \sin \left( \frac{\alpha _i - \alpha _{i+1}}{2} \right) \sin \left( \frac{\varphi _i + \varphi _{i+1} - \alpha _i - \alpha _{i+1}}{2} - \theta \right) },\nonumber \\&\Delta V_{\theta } = 4 l r k_{\varphi } \sum \limits _{i=1}^3 \left( 1 - \frac{s_i}{\hat{s}_i} \right) \sin \left( \frac{\varphi _i - \varphi _{i+1}}{2} \right) \sin \left( \frac{\alpha _{i+1} - \alpha _{i}}{2} \right) \cos \left( \frac{\varphi _i + \varphi _{i+1} - \alpha _i - \alpha _{i+1}}{2} - \theta \right) ,\nonumber \\&\Delta V_{\varphi _i} = k_{\varphi } l \left( 1 - \frac{s_i}{\hat{s}_i} \right) \left[ l \sin \left( \varphi _i - \varphi _{i+1} \right) \right. \left. + 2 r \sin \left( \frac{\alpha _{i} - \alpha _{i+1}}{2} \right) \sin \left( \varphi _i - \frac{\alpha _i + \alpha _{i+1}}{2} - \theta \right) \right] \nonumber \\&\qquad +\, k_{\varphi } l \left( 1 - \frac{s_{i-1}}{\hat{s}_{i-1}} \right) \left[ l \sin \left( \varphi _i - \varphi _{i-1} \right) \right. \left. + 2 r \sin \left( \frac{\alpha _{i} - \alpha _{i-1}}{2} \right) \sin \left( \varphi _i - \frac{\alpha _i + \alpha _{i-1}}{2} - \theta \right) \right] . \end{aligned}$$

(3)

In this study, we have varied both $B_0$ and $k_{\varphi }$ (the moment of inertia of the supporting base and the stiffness of the springs, respectively), uncovering possible dynamical patterns of model (1). Our results are discussed in Sect. 2.

2 Results

The regions of different types of dynamics of system (1) in two-parameters plane $(B_0, k_{\varphi })$ are presented in Fig. 2, with corresponding examples of behaviours shown in Fig. 3. The description of the possible states is as follows.

Fig. 2

(colour online). The dynamics of system (1) in two-parameters plane $(B_0, k_{\varphi })$ (the moment of inertia of the supporting base versus the stiffness of the coupling springs). Each colour and label corresponds to a different behaviour as follows: CS (light grey)—Complete Synchronization; PAC (yellow)—Periodic Amplitude Chimeras; QAC (orange)—Quasiperiodic Amplitude Chimeras; PLS (dark grey)— Phase–Locked Synchronization; Q (brown)—Quasiperiodic motion. The regions of the coexistence of the dynamical patterns (except the CS state) are shown as the hatched ones (hatched yellow: the coexistence of PAC and QAC; brown: the coexistence of QAC and Q)

Fig. 3

(colour online). Typical dynamical patterns of model (1). The time plots and the phase–time plots of the pendula and the supporting base are shown in the left and the right panel, respectively. From the top to the bottom: a $B_0 = 5.115 \, [\text {kg}m^2]$, $k_{\varphi } = 17.75 \, \text {[N/m]}$ (PAC); b $B_0 = 3.465 \, [\text {kg}m^2]$, $k_{\varphi } = 18.75 \, \text {[N/m]}$ (QAC); c $B_0 = 3.045 \, [\text {kg}m^2]$, $k_{\varphi } = 11.75 \, \text {[N/m]}$ (PLS); d $B_0 = 0.585 \, [\text {kg}m^2]$, $k_{\varphi } = 9.35 \, \text {[N/m]}$ (Q). The Poincare sections for cases (b) and (d) are included in the inboxes in the left panel

The pendula of model (1) can completely synchronize ($\varphi _1 = \varphi _2 = \varphi _3$), which is one of the most typical behaviours observed in coupled mechanical systems. In this case, the synchronization pattern is stable in the whole region shown in Fig. 2. However, we have found that when the moment of inertia $B_0$ is small enough (region labeled ’CS’ and shown in the light grey in Fig. 2), the synchronization state becomes the general solution of the system, within which all of the pendula oscillate (the case when the escapement mechanisms of the units are partially switched off has not been investigated in this study).

During our research, we have observed two types of chimeric patterns possible for system (1). The first one is characterized by the periodic motion of the pendula and resides in the yellow region marked in Fig. 2. The Periodic Amplitude Chimera (labeled ’PAC’ in Fig. 2) can be observed, when the support’s moment of inertia $B_0$ and the coupling strength $k_{\varphi }$ are large enough. The example of this state is discussed in Fig. 3a for $B_0 = 5.115 \, [\text {kg}m^2]$ and $k_{\varphi } = 17.75 \, \text {[N/m]}$, where the time plots of the pendula ($\varphi _1$ – red; $\varphi _2$ – blue; $\varphi _3$ – green) and the base ($\theta$ – black) are presented in the left panel, while the phase–time plots of the nodes (the displacements) are shown in the right one. Parameter T in the horizontal axes in Fig. 3 equals $T = 2 \pi \sqrt{l/g} \approx 1 \, \text {[s]}$ (the natural period of the pendula for chosen length $l = 0.24849 \, \text {[m]}$). As one can see, in this case the lower nodes have clustered (the 2nd– $\varphi _2$ (blue) and the 3rd–$\varphi _3$ (green)) and oscillate in the anti–phase to the upper one (the 1st–$\varphi _1$ (red)). The amplitude of the latter pendulum is greater (different) than the amplitude of the remaining ones.

In the considered case of three coupled oscillators, the smallest amplitude chimera can be defined as the state, in which all of the nodes are frequency synchronized ($\omega _1 = \omega _2 = \omega _3$, where $\omega _i$ denotes the frequency of the oscillations of the i-th pendulum, $i = 1, 2, 3$), but only two of them are oscillating with the same amplitude (there exists a solitary node with different amplitude). For the case shown in Fig. 3a, the amplitudes $\Phi _i$ of the pendula satisfy the following relation: $\Phi _1 > \Phi _2 = \Phi _3$.

The yellow region shown in Fig. 2 is surrounded by the orange one, where another example of chimera has been found, i.e. the Quasiperiodic Amplitude Chimera, labeled ’QAC’ in Fig. 2. The latter pattern is shown in Fig. 3b for $B_0 = 3.465 \, [\text {kg}m^2]$ and $k_{\varphi } = 18.75 \, \text {[N/m]}$. In this case, the behaviour of the system becomes quasiperiodic, which can be observed in the Poincare sections in the inbox in the left panel in Fig. 3b. The motion of the base has been chosen as the reference for the creation of the maps, i.e. when $\dot{\theta } = 0$ and $\theta > 0$ (which means that the base has reached its maximum), both position $\varphi _i$ and velocity $\dot{\varphi }_i$ of each pendulum are marked in the map. In this case, the dynamics of the lower pendula, i.e. the 2nd (blue) and the 3rd (green) is almost the same (see the curves in the Poincare section) but the attractors are shifted in space, forming an anti-phase pattern. On the other hand, the upper, red pendulum is moving almost periodically (the small irregularities are caused by the quasiperiodic motion of the lower nodes; see the phase–time plot in the right panel in Fig. 3b), and its amplitude is qualitatively different (smaller) that the amplitude of the remaining two oscillators. As in the previous case (the PAC in Fig. 3a), one can identify two coexisting groups of patterns (the 1st node versus the 2nd and the 3rd one), which can be distinguished by the difference in the amplitudes ($\Phi _1 < \Phi _2 = \Phi _3$) and lead to the classification of the amplitude chimera.

Bifurcating system (1) (increasing parameter $B_0$), we have observed that the Quasiperiodic Amplitude Chimera (QAC) resides not only in the orange domain in Fig. 2 but can be also found in the yellow one, where the Periodic Amplitude Chimera (PAC) is present. The yellow region of the coexistence of both types of chimeric patterns (PAC and QAC) has been hatched in Fig. 2. However, with the decrease in the moment of inertia $B_0$ (or the springs’ stiffness $k_{\varphi }$), the QAC state vanishes and the model bifurcates into the phase-locked synchronization profile. The latter solution appears in the dark grey domain labeled ’PLS’ in Fig. 2 and is shown in Fig. 3(c) (parameters: $B_0 = 3.045 \, [\text {kg}m^2]$, $k_{\varphi } = 11.75 \, \text {[N/m]}$). In this scenario, each pendulum oscillates with the same frequency and different amplitudes (the motion is periodic), while the phases between the nodes are locked (see the phase–time plot in the right panel in Fig. 3c for details).

With further decrease in coefficients $B_0$, $k_{\varphi }$, the behaviour of the pendula loses periodicity and becomes quasiperiodic. The irregular domain is marked in Fig. 2 in the brown colour and can be observed in a wide region of the parameters values. The example of the dynamics corresponding to this scenario is presented in Fig. 3d ($B_0 = 0.585 \, [\text {kg}m^2]$ and $k_{\varphi } = 9.35 \, \text {[N/m]}$), where one can see that the motion of the pendula becomes more complex than in the case of the QAC state (this can be especially observed in the inbox in the left panel in Fig. 3d, where the Poincare maps for the oscillators are included). Due to the increase in the irregularity, which affects the dynamics of the 1st (red) pendulum (the oscillations of the node are more irregular, compared to an almost periodic motion discussed in Fig. 3b), we have not identified the states similar to the one presented in Fig. 3d with any kind of chimera. However, when the coupling strength $k_{\varphi }$ is small enough, one can observe an arise of patterns qualitatively similar to the one presented in Fig. 3b, i.e. characterized by an almost periodic motion of the upper pendulum (the 1st) and an anti-phase profile between the lower ones (the 2nd and the 3rd). The surprising appearance of the QAC states is marked in Fig. 2 as the brown, hatched region at the bottom of the map. The latter result uncovers that the additional connection of the oscillators through the springs (see Fig. 1 for details) is not necessary for the occurrence of the Quasiperiodic Amplitude Chimeras, i.e. the states are also possible when $k_{\varphi } = 0$. However, the local coupling is still required for the arise of the Periodic Amplitude Chimeras (PAC), as shown in the map in Fig. 2.

Dynamical patterns described in Fig. 2 reside in different regions of parameters plane $(B_0, k_{\varphi })$. To investigate the possible scenarios of their coexistence, we have calculated the basins of attraction for system (1), which are discussed in Fig. 4.

Fig. 4

(colour online). Basins of attraction of system (1). In the left (right) panel the initial conditions from ${IC}_L$ (${IC}_R$) subspace are considered (see the details in the text). The colour code corresponds to four possible states: CS (light grey)—Complete Synchronization; PAC (yellow)—Periodic Amplitude Chimeras; QAC (orange)—Quasiperiodic Amplitude Chimeras; Q (brown)—Quasiperiodic motion. From the top to the bottom: a $B_0 = 5.5 \, [\text {kg}m^2]$, $k_{\varphi } = 18.0 \, \text {[N/m]}$; b $B_0 = 4.8 \, [\text {kg}m^2]$, $k_{\varphi } = 9.0 \, \text {[N/m]}$; c $B_0 = 5.0 \, [\text {kg}m^2]$, $k_{\varphi } = 1.3 \, \text {[N/m]}$

The phase space of system (1) is an 8-dimensional subset of the $\mathbb {R}^8$ space. To present the cross sections of the basins of attraction (on the plane), we have considered the following two subsets of the initial conditions:

$$\begin{aligned} \left\{ \begin{array}{l} {IC}_L = \{ ( \theta ^0, \dot{\theta }^0, \varphi _1^0, \dot{\varphi }_1^0, \varphi _2^0, \dot{\varphi }_2^0, \varphi _3^0, \dot{\varphi }_3^0 ) :\\ \varphi _1^0 \in [ -\pi , \pi ), \varphi _2^0 = \varphi _3^0 \in [ -\pi , \pi ),\\ \theta ^0 = \dot{\theta }^0 = \dot{\varphi }_1^0 = \dot{\varphi }_2^0 = \dot{\varphi }_3^0 = 0 \};\\ {IC}_R = \{ ( \theta ^0, \dot{\theta }^0, \varphi _1^0, \dot{\varphi }_1^0, \varphi _2^0, \dot{\varphi }_2^0, \varphi _3^0, \dot{\varphi }_3^0 ) :\\ \varphi _1^0 \in [ -\pi , \pi ), \varphi _2^0 \in [ -\pi , \pi ),\\ \theta ^0 = \varphi _3^0 = \dot{\theta }^0 = \dot{\varphi }_1^0 = \dot{\varphi }_2^0 = \dot{\varphi }_3^0 = 0 \}. \end{array} \right. \end{aligned}$$

(4)

Scenario ${IC}_L$ corresponds to the case, when the motion of both lower pendula (the 2nd and the 3rd) is initiated from the same conditions ($\varphi _2^0 = \varphi _3^0$), which may support the appearance of the PAC state (in this pattern, the lower pendula are synchronized). On the other hand, ${IC}_R$ case involves the scenario, when the escapement mechanism of the 3rd pendulum (green in Fig. 2) is switched off ($\varphi _3^0 = 0$) and the motion has to be induced by the remaining two oscillators (the red and the blue ones, as shown in Fig. 2).

The methodology of the initial conditions selection has a major influence on the dynamics of the system, which has been shown further. The basins of attraction corresponding to scenarios ${IC}_L$ and ${IC}_R$ (calculated in $(\varphi _1, \varphi _2) \in {[-\pi , \pi )}^2$ cross section) are presented in the left and the right panel in Fig. 4, respectively.

In Fig. 4a, one can observe the results obtained for parameters $B_0 = 5.5 \, [\text {kg}m^2]$ and $k_{\varphi } = 18.0 \, \text {[N/m]}$. In this case, three dynamical patterns are possible, i.e. the Complete Synchronization (CS), the Periodic Amplitude Chimeras (PAC) and the Quasiperiodic Amplitude Chimeras (QAC), which are marked in the light grey, yellow and orange, respectively (see the legend in the bottom in Fig. 4). When the initial conditions are chosen from ${IC}_L$ set (left panel in Fig. 4a), one can see the basin of the PAS state (yellow), surrounded by the narrow, orange stripes corresponding to the QAS solution. However, when ${IC}_R$ scenario is considered (right panel in Fig. 4a), the middle of the phase–space is filled mainly by the irregular orange basin. The small area, where the yellow domain can be found (the hatched inbox) has been shown in the enlargement. In both cases, the basin of the complete synchronization (CS—light grey) is the dominant one.

A similar scenario but with the absence of the PAC state can be observed in Fig. 4b for $B_0 = 4.8 \, [\text {kg}m^2]$ and $k_{\varphi } = 9.0 \, \text {[N/m]}$. The orange basin (QAC) competes with the light grey one (CS), but the regime of the second state is dominating the phase space. It should be noted that the small, black region marked in the right panel in Fig. 4b corresponds to the scenario, when the escapement mechanism of the upper pendulum (the 1st one) has switched off and the dynamics is mainly induced by the oscillations of the lower nodes and the supporting base.

The dominant character of the CS attractor changes, when the general quasiperiodic dynamics occurs. The example of such a scenario is presented in Fig. 4c (parameters: $B_0 = 5.0 \, [\text {kg}m^2]$, $k_{\varphi } = 1.3 \, \text {[N/m]}$), where only the CS (light grey) and the Q (brown) dynamical patterns coexist. In this case, the measures of the regimes occupied by the basins are similar (in contrast to the results described in Fig. 4a and 4b) and their structure becomes more complex. The riddled nature of the domains (especially around $\varphi _1, \varphi _2 \approx \pm \pi$) implicates that the final behaviour of system (1) is very hard to predict and may change even for a slight perturbation of the initial conditions or parameters.

The results discussed in Fig. 4a exhibit that the choice of the initial conditions (sets ${IC}_L$ and ${IC}_R$) has a major influence on the appearance of the PAC and the QAC states (especially the former one, when ${IC}_R$ scenario is applied). To investigate the probabilities of the chimeras’ arise, we have performed a statistical analysis, which is discussed in Fig. 5.

Fig. 5

(colour online). Probabilities of the occurrence of the complete synchronization pattern (CS—light grey) and the amplitude chimeras (PAC—yellow; QAC—orange). In a- ${IC}_L$ initial conditions scenario is considered, while in b, the case of ${IC}_R$ is discussed. The vertical axes are shown in the logarithmic scale. Parameters: $k_{\varphi } = 18.0 \, \text {[N/m]}$, $B_0 \in [1.8, 20] \, [\text {kg}m^2]$

The results presented in Fig. 5 are obtained for fixed coupling strength $k_{\varphi } = 18.0 \, \text {[N/m]}$ and varied moment of inertia $B_0 \in \left[ 1.8, 20 \right] \, [\text {kg}m^2]$ (the latter denoted in the horizontal axes). The probabilities of the occurrence of different solutions (CS – light grey, PAC – yellow and QAS – orange) are marked in the logarithmic scale in the vertical axes. The scenarios corresponding to the choice of the initial conditions from subspaces ${IC}_L$ and ${IC}_R$ are shown in Fig. 5a and b, respectively. Each iteration point (marked by dots in Figure) has been examined for a total number of 2000 trials (the initial conditions randomly chosen from the uniform distribution using ${IC}_L$ or ${IC}_R$ subset).

As one can see, when scenario ${IC}_L$ is considered ($\varphi _2^0 = \varphi _3^0$; Fig. 5a, the probability of the occurrence of the PAC state is greater than the QAC one almost in whole $B_0$ interval (except the smallest possible values around $B_0 \approx 1.8 \, [\text {kg}m^2]$). With the increase in the moment of inertia, both probabilities also increase, reaching the stable levels around $p=0.11$ (yellow) and $p=0.02$ (orange) for $B_0 \approx 20 \, [\text {kg}m^2]$. On the other hand, the appearance of the complete synchronization pattern (CS – light grey) decreases from $p=0.99$ for $B_0 = 1.8 \, [\text {kg}m^2]$ to $p=0.87$ for $B_0 = 20 \, [\text {kg}m^2]$.

The second scenario, i.e. ${IC}_R$ one ($\varphi _3^0 = 0$) is shown in Fig. 5b and uncovers that the probability of the occurrence of the QAC state (orange) exceeds the one observed for the PAC pattern (yellow) for $B_0 < 10.9 \, [\text {kg}m^2]$. Moreover, the Periodic Amplitude Chimeras have not been observed during the analysis for $B_0 < 5.7 \, [\text {kg}m^2]$. The latter phenomenon is caused by the change of the initial conditions procedure. The arise of the PAC state is more probable, when the initial conditions for the lower pendula are the same, i.e. $\varphi _2^0 = \varphi _3^0$ (as in scenario ${IC}_L$), since the state involves the same motion of the lower nodes (see Fig. 3a for details); when one of the pendulum is switched off at the beginning ($\varphi _3^0 = 0$; case ${IC}_R$), the periodic chimeric pattern may not arise from the chosen initial conditions and parameters at all. With the increase in $B_0$ coefficient, the probabilities of the states stabilize around $p=0.09$ (yellow), $p=0.005$ (orange) and $p=0.905$ (light grey) for $B_0 = 20 \, [\text {kg}m^2]$.

We have found that with further increase in the moment of inertia $B_0$, the results do not change significantly, oscillating around the values obtained for $B_0 = 20 \, [\text {kg}m^2]$. The dominant character of the CS solution presented in Fig. 5 indicates that the basins of attraction for the parameters chosen from the orange and the yellow regions in Fig. 2 (where amplitude chimeras are possible) should be qualitatively similar to the ones presented in Fig. 4a and b (the value of $B_0$ parameter has a minor influence on the probability of the appearance of the complete synchronization attractor). Taking into account the obtained results, chimeras discussed above can be identified as the rare attractors [45,46,47,48] and their occurrence in the system from randomly chosen initial conditions is highly uncertain.

To study the transitions between different patterns appearing in system (1), we have performed the bifurcation analysis, applying the energy balance method [43, 44, 49, 50].

Multiplying the dynamical equation of the i-th pendulum in system (1) by its velocity, i.e. $\dot{\varphi }_i$ and integrating for one full period of oscillations, one can get the energy equation, describing the flows of the energy components for the node:

$$\begin{aligned}&\int \limits _{T} m l \left[ l \ddot{\varphi }_i + g \sin \varphi _i \right] \dot{\varphi }_i dt = \int \limits _{T} M_N \dot{\varphi }_i dt \nonumber \\&\quad - \int \limits _{T} c_{\varphi } {\dot{\varphi }_i}^2 dt + \nonumber \\&\quad - \int \limits _{T} m r l \left[ \ddot{\theta } \sin (\varphi _i - \theta - \alpha _i\right. )\nonumber \\&\quad \left. - {\dot{\theta }}^2 \cos (\varphi _i - \theta - \alpha _i) \right] \dot{\varphi }_i dt - \int \limits _{T} \Delta V_{\varphi _i} \dot{\varphi }_i dt. \end{aligned}$$

(5)

The left-hand side of eq. (5) describes the increase in the total energy of the i-th pendulum during one full period of oscillations and equals zero in the case of periodic motion. The components on the right-hand side of Eq. (5) can be denoted in the following way:

$$\begin{aligned} {W_i}^{\text {ESC}}= & {} \int \limits _{T} M_N \dot{\varphi }_i dt, \end{aligned}$$

(6)

$$\begin{aligned} {W_i}^{\text {DAMP}}= & {} \int \limits _{T} c_{\varphi } {\dot{\varphi }_i}^2 dt, \end{aligned}$$

(7)

$$\begin{aligned} {W_i}^{\text {BASE}}= & {} \int \limits _{T} m r l [ \ddot{\theta } \sin (\varphi _i - \theta - \alpha _i) + \nonumber \\&\quad - {\dot{\theta }}^2 \cos (\varphi _i - \theta - \alpha _i) ] \dot{\varphi }_i dt, \end{aligned}$$

(8)

$$\begin{aligned} {W_i}^{\text {SPRING}}= & {} \int \limits _{T} \Delta V_{\varphi _i} \dot{\varphi }_i dt, \end{aligned}$$

(9)

where $i = 1, 2, 3$.

Component (6) ${W_i}^{\text {ESC}} \, \text {[J]}$ describes the energy supplied to the i-th pendulum by its escapement mechanism, while (7) ${W_i}^{\text {DAMP}} \, \text {[J]}$ equals the energy dissipated by the i-th damper. On the other hand, components (8) ${W_i}^{\text {BASE}} \, \text {[J]}$ and (9) ${W_i}^{\text {SPRING}} \, \text {[J]}$ describe the energy transferred from the i-th node to the base and/or the other clock via the support and via the coupling springs, respectively. In this case, the sum ${W_i}^{\text {FLOW}} = {W_i}^{\text {BASE}} + {W_i}^{\text {SPRING}}$ represents the total energy flow from the pendulum to other elements of the system.

The results of the bifurcation and the energy analysis for model (1) are discussed in Fig. 6.

Fig. 6

(colour online). Bifurcation (a) and energy (b–d) diagrams of system (1) for fixed $B_0 = 4.005 \, [\text {kg}m^2]$. In the left panel, the transition from the PAC to the QAC states is presented ($k_{\varphi } \in [11.0, 11.5] \, \text {[N/m]}$), while in the right one, the road from the PLS to the Q pattern is shown ($k_{\varphi } \in [8.0, 9.6] \, \text {[N/m]}$). The energy components in (b–d) are marked in the following way: ${W_i}^{\text {ESC}}$ – white; ${W_i}^{\text {DAMP}}$ – cyan; ${W_i}^{\text {BASE}}$ – pink; ${W_i}^{\text {SPRING}}$ – violet; ${W_i}^{\text {FLOW}}$ – light blue (see the details in the text)

We investigate two bifurcation scenarios, i.e. (i) the transition from the PAC (Periodic Amplitude Chimera) to the QAC (Quasiperiodic Amplitude Chimera) – left panel in Fig. 6 and (ii) the transition from the PLS (Phase–Locked Synchronization) to the Q state (Quasiperiodic motion) – right panel in Fig. 6. In both cases, the moment of inertia is fixed at $B_0 = 4.005 \, [\text {kg}m^2]$ and the stiffness of the coupling springs is decreased in the following intervals: (i) $k_{\varphi } \in [11.0, 11.5] \, \text {[N/m]}$; (ii) $k_{\varphi } \in [8.0, 9.6] \, \text {[N/m]}$ (see the horizontal axes in Fig. 6). The bifurcation diagrams are presented in Fig. 6a, where we denote the local maxima of the supporting base ($\hat{\theta }$) and the pendula ($\hat{\varphi }_i$) during the oscillations (colour–code as in Fig. 3). On the other hand, the energy diagrams for the 1st, the 2nd and the 3rd pendulum are shown in Figs. 6b, c and d, respectively. The colour code used to distinguish different energy components is as follows: ${W_i}^{\text {ESC}}$–white; ${W_i}^{\text {DAMP}}$ – cyan; ${W_i}^{\text {BASE}}$–pink; ${W_i}^{\text {SPRING}}$ – violet and ${W_i}^{\text {FLOW}}$ – light blue.

The transition from the PAC to the QAC states is discussed in the left panel in Fig. 6. Beginning from $k_{\varphi } = 11.5 \, \text {[N/m]}$ and decreasing the parameter, one can observe that the periodic amplitude chimera (see Fig. 3a) is present for the coupling strength $k_{\varphi } > 11.3 \, \text {[N/m]}$. The higher amplitude of the 1st node (compared to pendula 2nd and 3rd) can be explained by the energy flows. Indeed, the energy dissipated by the 1st oscillator is higher than the energy supplied by its escapement mechanism: ${W_1}^{\text {DAMP}} > {W_1}^{\text {ESC}}$ (Fig. 6b). In order to preserve the same frequency of the oscillations for all of the units, this lack of energy has to be compensated by the decreased amplitudes of the remaining nodes (the 2nd and the 3rd). This is possible due to the fact that the escapement mechanisms of the latter units produce more energy than is required by their dampers: ${W_i}^{\text {DAMP}} < {W_i}^{\text {ESC}}$, $i = 2, 3$ (Fig. 6c and d). The first pendulum consumes the energy from the system: ${W_1}^{\text {FLOW}} < 0$, while the other two oscillators supply it: ${W_2}^{\text {FLOW}} > 0$, ${W_3}^{\text {FLOW}} > 0$. However, this scenario begins to change around $k_{\varphi } = 11.3 \, \text {[N/m]}$, when the amplitude of the 1st pendulum decreases (see the red curve in Fig. 6a). Dissipation ${W_1}^{\text {DAMP}}$ also decreases and the consumption of the energy is smaller (${W_1}^{\text {FLOW}}$ increases). Simultaneously, the amplitudes of the lower pendula change, i.e. the amplitude of the 2nd node decreases, while the amplitude of the 3rd one increases (blue and green curves in Fig. 6a, respectively), which corresponds to the changes in the energy flows: ${W_2}^{\text {DAMP}}$ (${W_3}^{\text {DAMP}}$) decreases (increases), while ${W_2}^{\text {FLOW}}$ (${W_3}^{\text {FLOW}}$) increases (decreases). The diagrams shown in Figs. 6c and d uncover the differences in the directions of the energy distribution for the pendula: the energy transferred via the base by the 2nd (the 3rd) oscillator decreases (increases), while the flow transferred via the coupling springs by the 2nd (the 3rd) node increases (decreases). The variation of the amplitudes continues until the occurrence of the sudden bifurcation to the QAC state around $k_{\varphi } = 11.18 \, \text {[N/m]}$. Interestingly, the bifurcation arises close to the point in which ${W_3}^{\text {DAMP}} = {W_3}^{\text {FLOW}}$ (the energy dissipated by the 3rd pendulum collides with the energy transferred to the system). With further decrease in coupling strength $k_{\varphi }$, the Quasiperiodic Amplitude Chimera can be observed, until the state bifurcates to the PLS pattern (Phase-Locked Synchronization). Due to the fact that the motion is no longer periodic in this scenario, the analysis of the energy balance cannot be longer followed.

The scenario presented in the right panel in Fig. 6 corresponds to the case, when the phase-locked synchronization (the PLS state) leads to the appearance of the quasiperiodic motion (Q). The analysis begins at $k_{\varphi } = 9.36 \, \text {[N/m]}$, when the motion becomes periodic (the system leaves the region of the QAC). In the first stage ($k_{\varphi } \in [9.17, 9.36] \, \text {[N/m]}$), the amplitude of the 3rd node is greater than the amplitude of the 2nd one (see the green and the blue curves in Fig. 6a). Indeed, the additional energy produced by the 2nd pendulum (${W_2}^{\text {DAMP}} < {W_2}^{\text {ESC}}$) can be transferred to the 3rd neighbour, for which ${W_3}^{\text {DAMP}} > {W_3}^{\text {ESC}}$ (Fig. 6c and d), respectively). Simultaneously, the amplitudes vary (blue increases, green decreases) and finally get even around $k_{\varphi } = 9.17 \, \text {[N/m]}$ (${W_2}^{\text {FLOW}} = {W_3}^{\text {FLOW}} = 0$; see the hatched, horizontal lines in Fig. 6c and d). With further decrease in parameter $k_{\varphi } < 9.17 \, \text {[N/m]}$, the energy scenario reverses. The amplitude of the 2nd node (blue) exceeds the amplitude of the 3rd one (green), which is accompanied by the following inequalities: ${W_2}^{\text {DAMP}} > {W_2}^{\text {ESC}}$, ${W_2}^{\text {FLOW}} < 0$ and ${W_3}^{\text {DAMP}} < {W_3}^{\text {ESC}}$, ${W_3}^{\text {FLOW}} > 0$. The distribution of components ${W_i}^{\text {BASE}}$, ${W_i}^{\text {SPRING}}$, $i = 2, 3$ shows the directions in which the energy is transferred. It should be noted that the whole process (during the PLS state) is supported by the 1st pendulum (red in Fig. 6a), which has the smallest amplitude and supplies the energy to the system: ${W_1}^{\text {DAMP}} < {W_1}^{\text {ESC}}$, ${W_1}^{\text {FLOW}} > 0$. With further decrease in coupling strength $k_{\varphi }$, the periodic motion vanishes (around $k_{\varphi } = 8.3 \, \text {[N/m]}$) and the behaviour becomes irregular. The latter bifurcation occurs around ${W_3}^{\text {DAMP}} = {W_3}^{\text {FLOW}}$ point, similarly to the case described previously (left panel in Fig. 6; see the details above).

The energy scenarios discussed in Fig. 6 seem universal and have been observed also for other values of parameters $B_0, k_{\varphi }$ during the study on system (1).

3 Conclusions

In this paper, we have studied the dynamics of three coupled pendulum clocks suspended on an oscillating supporting base. The inclusion of the support (an additional degree of freedom) expands the research performed before for small networks of coupled oscillators and allows to observe new types of solutions. We have distinguished two types of amplitude chimeras, characterized by the periodic and the quasiperiodic dynamics of the nodes. The regions of the occurrence of the dynamical patterns uncover that the states can coexist in different configurations, including the appearance of such classical states as the complete or the phase-locked synchronization. Typical examples of behaviours have been shown and discussed. Investigations on the basins of attraction (realized in various scenarios, depending on the methodology of the initial conditions selection) have shown that the chimeric dynamics may be hard to predict and can appear in the system spontaneously. The latter observations have been studied closely during the probability analysis, where the rare character of the patterns has been confirmed. We have shown that the investigations on the transitions between different types of attractors can be supported by the energy balance method, which follows the qualitative changes occurring in the model. Our results participate in the research on chimera states in small networks of coupled oscillators, confirming the universal appearance of complex, coexisting patterns in dynamical systems.