Skip to main content
SpringerLink
Log in

Synchronization and chimera state in a mechanical system

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

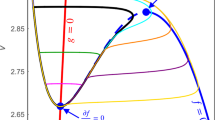
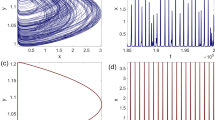
Abstract

Synchronization phenomenon appears in several natural systems being associated with physical, chemical and biological processes. In brief, synchronization may be understood as a harmonization of two or more system behaviors following some patterns. This paper deals with synchronization analysis of a mechanical pendulum-chart system composed by a hierarchical network of three pendula coupled to each other through their own chart that receives continuous supply of energy via a base excitation. Dynamical patterns are classified and investigated in order to understand the conditions to each one of them. Asynchronous behaviors are analyzed including the chimera state defined as a symmetry break of the behavior of identical oscillator network. Numerical simulations indicate that patterns do not have a direct relation with periodicity. An energetic approach is proposed in order to define a measure of synchronized states, providing new insights about the origin of chimera state and its relationship with natural frequencies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29

Similar content being viewed by others

References

  1. Huygens, C.: L’Horloge à pendule de 1651 à 1666. Travaux divers de physique, de mécanique et de technique de 1650 à 1666. Traité des couronnes et des parhélies (1662 ou 1663), vol. 17. Swets & Zeitlinger N. V., Amsterdam (1666)

  2. Huygens, C.: Correspondance 1664–1665, vol. 5. Société Hollandaise des sciences, Amsterdam (1665)

    Google Scholar 

  3. Kapitaniak, M., Czolczynski, K., Perlikowski, P., Stefanski, A., Kapitaniak, T.: Synchronization of clocks. Phys. Rep. 517, 1–69 (2012). https://doi.org/10.1016/j.physrep.2012.03.002

    Article  MATH  Google Scholar 

  4. Bennett, M., Schatz, M.F., Rockwood, H., Wiesenfeld, K.: Huygens’ s clocks. Proc. R. Soc. Lond. A 458, 563–79 (2002). https://doi.org/10.1098/rspa.2001.0888

    Article  MathSciNet  MATH  Google Scholar 

  5. Buck, J., Buck, E.: Mechanism of rhythmic synchronous flashing of fireflies. Science 159, 1319–27 (1968). https://doi.org/10.1126/science.159.3821.1319

    Article  Google Scholar 

  6. Ravasz, E., Néda, Z., Vicsek, T., Brechet, Y., Barabási, A.L.: Physics of the rhythmic applause. Phys. Rev. E 61, 6987–92 (2000). https://doi.org/10.1007/BF02068742

    Article  Google Scholar 

  7. Walker, T.J.: Acoustic synchrony: two mechanisms in the snowy tree cricket. Science 166, 891–4 (1969). https://doi.org/10.1126/science.166.3907.891

    Article  Google Scholar 

  8. Wiener, N.: Nonlinear Problems in Random Theory. MIT Press, Cambridge (1958)

    MATH  Google Scholar 

  9. Wiener, N.: The human use of human beings: cybernetics and society, vol. 20. Free Association Books, London (1989). https://doi.org/10.1109/TIT.1974.1055201

    Book  Google Scholar 

  10. Winfree, A.T.: Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 16, 15–42 (1967). https://doi.org/10.1016/0022-5193(67)90051-3

    Article  Google Scholar 

  11. Kuramoto, Y.: Self-entrainment of a population of coupled non-linear oscillators. In: Araki, H. (ed.) International Symposium on Mathematical Problems in Theoretical Physics, pp. 420–422. Springer, Berlin (1975). https://doi.org/10.1007/BFb0013365

    Chapter  Google Scholar 

  12. Czolczynski, K., Perlikowski, P., Stefanski, A., Kapitaniak, T.: Clustering of non-identical clocks. Prog. Theor. Phys. 125, 473–90 (2011). https://doi.org/10.1143/PTP.125.473

    Article  MATH  Google Scholar 

  13. Pantaleone, J.: Synchronization of metronomes. Am. J. Phys. 70, 1–9 (2002). https://doi.org/10.1119/1.1501118

    Article  Google Scholar 

  14. Ulrichs, H., Mann, A., Parlitz, U.: Synchronization and chaotic dynamics of coupled mechanical metronomes. Chaos 19, 1–6 (2009). https://doi.org/10.1063/1.3266924

    Article  Google Scholar 

  15. Czolczynski, K., Perlikowski, P., Stefanski, A., Kapitaniak, T.: Huygens’ odd sympathy experiment revisited. Int. J. Bifurc. Chaos 21, 2047–56 (2011). https://doi.org/10.1142/S0218127411029628

    Article  MATH  Google Scholar 

  16. Czolczynski, K., Perlikowski, P., Stefanski, A., Kapitaniak, T.: Clustering and synchronization of n Huygens’ clocks. Phys. A Stat. Mech. Appl. 388, 5013–23 (2009). https://doi.org/10.1016/j.physa.2009.08.033

    Article  MATH  Google Scholar 

  17. Czolczynski, K., Perlikowski, P., Stefanski, A., Kapitaniak, T.: Clustering of Huygens’ clocks. Prog. Theor. Phys. 122, 1027–33 (2009). https://doi.org/10.1143/PTP.122.1027

    Article  MATH  Google Scholar 

  18. Najdecka, A., Kapitaniak, T., Wiercigroch, M.: Synchronous rotational motion of parametric pendulums. Int. J. Nonlinear Mech. 70, 84–94 (2015). https://doi.org/10.1016/j.ijnonlinmec.2014.10.008

    Article  Google Scholar 

  19. Strzalko, J., Grabski, J., Wojewoda, J., Wiercigroch, M., Kapitaniak, T.: Synchronous rotation of the set of double pendula: experimental observations. Chaos 22, 1–7 (2012). https://doi.org/10.1063/1.4740460

    Article  Google Scholar 

  20. Kapitaniak, M., Lazarek, M., Nielaczny, M., Czolczynski, K., Perlikowski, P., Kapitaniak, T.: Synchronization extends the life time of the desired behavior of globally coupled systems. Sci. Rep. 4, 4391 (2014). https://doi.org/10.1038/srep04391

    Article  Google Scholar 

  21. Kapitaniak, M., Czolczynski, K., Perlikowski, P., Stefanski, A., Kapitaniak, T.: Synchronous states of slowly rotating pendula. Phys. Rep. 541, 1–44 (2014)

    Article  MathSciNet  Google Scholar 

  22. Strogatz, S.H., Abrams, D.M., McRobie, A., Eckhardt, B., Ott, E.: Crowd synchrony on the Millennium Bridge. Nature 438, 43–4 (2005). https://doi.org/10.1038/43843a

    Article  Google Scholar 

  23. Strogatz, S.H.: Exploring complex networks. Nature 410, 268–76 (2001). https://doi.org/10.1038/35065725

    Article  MATH  Google Scholar 

  24. Osipov, G.V., Kurths, J., Zhou, C.: Synchronization in Oscillatory Networks. Springer, Berlin (2007)

    Book  Google Scholar 

  25. Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., Hwang, D.U.: Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006). https://doi.org/10.1016/j.physrep.2005.10.009

    Article  MathSciNet  MATH  Google Scholar 

  26. Dörfler, F., Bullo, F.: Synchronization in complex networks of phase oscillators: a survey. Automatica 50, 1539–64 (2014). https://doi.org/10.1016/j.automatica.2014.04.012

    Article  MathSciNet  MATH  Google Scholar 

  27. Pikovsky, A., Rosenblum, M., Kurths, J.: Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press, Cambridge (2003). https://doi.org/10.1063/1.1554136

    Book  MATH  Google Scholar 

  28. Kapitaniak, T.: Continuous control and synchronization in chaotic systems system. Chaos Solitons Fractals 6, 237–44 (1995)

    Article  Google Scholar 

  29. Blazejczyk-Okolewska, B., Brindley, J., Czolczynski, K., Kapitaniak, T.: Antiphase synchronization of chaos by noncontinuous coupling: two impacting oscillators. Chaos Solitons Fractals 12, 1823–6 (2001). https://doi.org/10.1016/S0960-0779(00)00145-4

    Article  MATH  Google Scholar 

  30. Rosenblum, M.G., Pikovsky, A.S., Kurths, J.: Phase synchronization of chaotic oscillators. Phys. Rev. Lett. 76, 1804–7 (1996)

    Article  Google Scholar 

  31. Pecora, L.M., Carroll, T.L.: Synchronization in chaotic systems. Phys. Rev. Lett. 64, 821–4 (1990). https://doi.org/10.1103/PhysRevLett.64.821

    Article  MathSciNet  MATH  Google Scholar 

  32. Boccaletti, S., Kurths, J., Osipov, G., Valladares, D.L., Zhou, C.S.: The synchronization of chaotic systems. Phys. Rep. 366, 1–101 (2002). https://doi.org/10.1016/S0370-1573(02)00137-0

    Article  MathSciNet  MATH  Google Scholar 

  33. Kurths, J., Boccaletti, S., Grebogi, C., Lai, Y.C.: Introduction: control and synchronization in chaotic dynamical systems. Chaos 13, 126–7 (2003). https://doi.org/10.1063/1.1554606

    Article  Google Scholar 

  34. Pyragiene, T., Pyragas, K.: Anticipatory synchronization via low-dimensional filters. Phys. Lett. Sect. A Gen. At. Solid State Phys. 381, 1893–8 (2017). https://doi.org/10.1016/j.physleta.2017.04.005

    Article  MathSciNet  MATH  Google Scholar 

  35. Liu, X., Wu, C.: Fault-tolerant synchronization for nonlinear switching systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 23, 91–110 (2017). https://doi.org/10.1016/j.nahs.2016.06.005

    Article  MathSciNet  MATH  Google Scholar 

  36. Dörfler, F., Chertkov, M., Bullo, F.: Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. 110, 2005–10 (2013). https://doi.org/10.1073/pnas.1212134110

    Article  MathSciNet  MATH  Google Scholar 

  37. Blaabjerg, F., Teodorescu, R., Liserre, M., Timbus, A.V.: Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 53, 1398–409 (2006). https://doi.org/10.1109/TIE.2006.881997

    Article  Google Scholar 

  38. Witthaut, D., Timme, M.: Braess’s paradox in oscillator networks, desynchronization and power outage. New J. Phys. 14, 083036 (2012). https://doi.org/10.1088/1367-2630/14/8/083036

    Article  Google Scholar 

  39. Filatrella, G., Nielsen, A.H., Pedersen, N.F.: Analysis of a power grid using a Kuramoto-like model. Eur. Phys. J. B 61, 485–91 (2008). https://doi.org/10.1140/epjb/e2008-00098-8

    Article  Google Scholar 

  40. Rohden, M., Sorge, A., Timme, M., Witthaut, D.: Self-organized synchronization in decentralized power grids. Phys. Rev. Lett. 109, 1–5 (2012). https://doi.org/10.1103/PhysRevLett.109.064101

    Article  Google Scholar 

  41. Baldoni, R., Corsaro, A., Querzoni, L., Scipioni, S., Piergiovanni, S.T.: Coupling-based internal clock synchronization for large-scale dynamic distributed systems. IEEE Trans. Parallel Distrib. Syst. 21, 607–19 (2010). https://doi.org/10.1109/TPDS.2009.111

    Article  Google Scholar 

  42. Klein, D.J., Lee, P., Morgansen, K.A., Javidi, T.: Integration of communication and control using discrete time Kuramoto models for multivehicle coordination over broadcast networks. IEEE J. Sel. Areas Commun. 26, 695–705 (2008). https://doi.org/10.1109/CDC.2007.4434294

    Article  Google Scholar 

  43. Wang, Y., Nunez, F., Doyle III, F.J.: Increasing sync rate of pulse-coupled oscillators via phase response function design: theory and application to wireless networks. IEEE Trans. Control Syst. Technol. 21, 1455–62 (2013). https://doi.org/10.1109/TCST.2012.2205254

    Article  Google Scholar 

  44. Simeone, O., Spagnolini, U., Bar-Ness, Y., Strogatz, S.H.: Distributed synchronization in wireless networks. IEEE Signal Process. Mag. 25, 81–97 (2008). https://doi.org/10.1109/MSP.2008.926661

    Article  Google Scholar 

  45. Piqueira, J.R.C.: Using bifurcations in the determination of lock-in ranges for third-order phase-locked loops. Commun. Nonlinear Sci. Numer. Simul. 14, 2328–35 (2009). https://doi.org/10.1016/j.cnsns.2008.06.012

    Article  MathSciNet  Google Scholar 

  46. Correa, D.P.F., Wulff, C., Piqueira, J.R.C.: Symmetric bifurcation analysis of synchronous states of time-delayed coupled phase-locked loop oscillators. Commun. Nonlinear Sci. Numer. Simul. 22, 793–820 (2015). https://doi.org/10.1016/j.cnsns.2014.08.004

    Article  MathSciNet  MATH  Google Scholar 

  47. Piqueira, J.R.C., Oliveira, M.Q., Monteiro, L.H.A.: Synchronous state in a fully connected phase-locked loop network. Math. Probl. Eng. (2006). https://doi.org/10.1155/MPE/2006/52356

    Article  MathSciNet  Google Scholar 

  48. Giardina, I.: Collective behavior in animal groups: theoretical models and empirical studies. HFSP J. 2, 205–19 (2008). https://doi.org/10.2976/1.2961038

    Article  Google Scholar 

  49. Saber-Olfati, R., Fax, J.A., Murray, R.M.: Consensus and cooperation in networked multi-agent systems. Proc. IEEE 95, 215–33 (2007). https://doi.org/10.1109/JPROC.2010.2049911

    Article  MATH  Google Scholar 

  50. Bemporad, A., Heemels, M., Johansson, M.: Networked Control Systems. Springer, Berlin (1978)

    MATH  Google Scholar 

  51. Kuramoto, Y., Battogtokh, D.: Coexistence of coherence and incoherence in nonlocally coupled phase oscillators: a soluble case. Nonlinear Phenom. Complex Syst. 4, 380–5 (2002)

    Google Scholar 

  52. Abrams, D.M., Mirollo, R.E., Strogatz, S.H., Wiley, D.A.: Solvable model for chimera states of coupled oscillators. Phys. Rev. Lett. 101, 1–4 (2008). https://doi.org/10.1103/PhysRevLett.101.084103

    Article  Google Scholar 

  53. Abrams, D.M., Strogatz, S.H.: Chimera states for coupled oscillators. Phys. Rev. Lett. 93, 174102 (2004). https://doi.org/10.1103/PhysRevLett.93.174102

    Article  Google Scholar 

  54. Panaggio, M.J., Abrams, D.M.: Chimera states: coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity 28, 67–87 (2015). https://doi.org/10.1088/0951-7715/28/3/R67

    Article  MathSciNet  MATH  Google Scholar 

  55. Tinsley, M.R., Nkomo, S., Showalter, K.: Chimera and phase-cluster states in populations of coupled chemical oscillators. Nat. Phys. 8, 662–5 (2012). https://doi.org/10.1038/nphys2371

    Article  Google Scholar 

  56. Hagerstrom, A.M., Murphy, T.E., Roy, R., Hövel, P., Omelchenko, I., Schöll, E.: Experimental observation of chimeras in coupled-map lattices. Nat. Phys. 8, 658–61 (2012). https://doi.org/10.1038/nphys2372

    Article  Google Scholar 

  57. Martens, E.A., Thutupalli, S., Fourrière, A., Hallatschek, O.: Chimera states in mechanical oscillator networks. Proc. Natl. Acad. Sci. 110, 10563–7 (2013). https://doi.org/10.1073/pnas.1302880110

    Article  Google Scholar 

  58. Kapitaniak, T., Kuzma, P., Wojewoda, J., Czolczynski, K., Maistrenko, Y.: Imperfect chimera states for coupled pendula. DINAME 2015, 6 (2015). https://doi.org/10.1038/srep06379

    Article  Google Scholar 

  59. Wojewoda, J., Czolczynski, K., Maistrenko, Y., Kapitaniak, T.: The smallest chimera state for coupled pendula. Sci. Rep. 6, 34329 (2016). https://doi.org/10.1038/srep34329

    Article  Google Scholar 

  60. Wolf, A., Swift, J.B., Swinney, H.L., Vastano, J.A.: Determining Lyapunov exponents from a time series. Physica D 16, 285–317 (1985)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge the support of the Brazilian Research Agencies CNPq, CAPES and FAPERJ.

Funding

Funding was provides by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Conselho Nacional de Desenvolvimento Científico e Tecnológico and Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro.

Author information

Authors and Affiliations

  1. Center for Nonlinear Mechanics, COPPE – Department of Mechanical Engineering, Universidade Federal do Rio de Janeiro, 21.941.972, P.O. Box 68.503, Rio de Janeiro, RJ, Brazil

    Phablo R. Carvalho & Marcelo A. Savi

Authors
  1. Phablo R. Carvalho
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marcelo A. Savi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcelo A. Savi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Carvalho, P.R., Savi, M.A. Synchronization and chimera state in a mechanical system. Nonlinear Dyn 102, 907–925 (2020). https://doi.org/10.1007/s11071-019-05441-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05441-4

Keywords

Search

Navigation