Abstract
This paper introduces a procedure in the field of computational contact mechanics to analyze contact dynamics of beams undergoing large overall motion with large deformations and in self-contact situations. The presented contact procedure consists of a contact search algorithm which is employed with two approaches to impose contact constraint. The contact search task aims to detect the contact events and to identify the contact point candidates that is accomplished using an algorithm based on intersection of the oriented bounding boxes (OBBs). To impose the contact constraint, an approach based on the complementarity problem (CP) is introduced in the context of beam-to-beam contact. The other approach to enforce the contact constraint in this work is the penalty method, which is often used in the finite element and multibody literature. The latter contact force model is compared against the frictionless variant of the complementarity problem approach, linear complementarity problem approach (LCP). In the considered approaches, the absolute nodal coordinate formulation (ANCF) is used as an underlying finite element method for modeling beam-like structures in multibody applications, in particular. The employed penalty method makes use of an internal iteration scheme based on the Newton solver to fulfill the criteria for minimal penetration. Numerical examples in the case of flexible beams demonstrate the applicability of the introduced approach in a situation where a variety of contact types occur. It was found that the employed contact detection method is sufficiently accurate when paired with the studied contact constraint imposition models in simulation of the contact dynamics problems. It is further shown that the optimization-based complementarity problem approach is computationally more economical than the classical penalty method in the case of studied 2D-problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Contact between highly flexible bodies or self-contact situation in a flexible body is an important subject matter in many applications such as in wire ropes, belts, drapes and biomechanical implementations. The solutions to the contact problems above-mentioned are intrinsically rife with the three categories of nonlinearity known from the nonlinear finite element including material, geometry and boundary nonlinearities [71]. The presence of all these nonlinearities leads to undesired non-physical vibrations resulting in poor energy conservation, dynamic instability and moreover expensive, computational efforts for contact description including contact search procedures [9].
The above applications which account for large deformations have been the motivation for developing several formulations to discretize the beam-like structures using the nonlinear finite element method. Many of the nonlinear finite element formulations developed for beam-like continua have been characterized using the one-dimensional elastic line theory. This is also often referred to as the Simo-Reissner beam model [57, 62,63,64]. The Simo-Reissner beam model also forms the basis for many beam formulations in the framework of the geometrically exact beam (GEB) theory [24, 29, 58, 59]. Rather recently, the geometrically exact beam finite element was formulated according to the Kirchhoff–Love beam type by Meier et al. [44]. There, the proposed formulations fulfilled all the essential requirements that were already satisfied by the Simo-Reissner beam type, such as large deformation, dynamic problems involving slender beams, applicability in various anisotropic cross sections and avoidance of locking effects [46]. An alternative formulation for discretizing slender continua undergoing large deformation dynamics is the absolute nodal coordinate formulation (ANCF) introduced by Shabana [60]. Within a number of developments and extensions made to the original ANCF, it is capable of fulfilling all the above-mentioned essential requirements [58]. Among a large number of comparisons between the absolute nodal coordinate and the geometrically exact beam formulations, we cite in passing on the investigations by Gerstmayr et al. [23] on the performance and accuracy of the ANCF element. They further indicated a fourth order of convergence rate of a locking-free planar ANCF beam element when the strain energy is derived according to Simo and Vu-Quoc formulation [63, 64]. With the evolution of the formulation [19, 42, 43], capturing cross-sectional deformation in high-frequency modes became feasible using the higher-order derivations of position vector with respect to the beam transverse directions that was recently discussed by Bozorgmehri et al. [10]. The strain energy in the ANCF can be described using a number of nonlinear material laws known from the two- and three-dimensional elasticity. Moreover, ANCF is regarded as a suitable underlying formulation to incorporate the isogeometric analysis (IGA), and in particular to be combined with the isogeometric collocation method [5] due to the feasibility of enforcing Neumann boundary conditions [14] on the higher-order degrees-of-freedom of the ANCF nodes.
In the context of formulation related to contact between beams, Lee et al. [35] introduced a solution procedure for frictionless contact problems in two-dimensional beams undergoing large displacements. They used quadratic programming to solve the equivalent minimization problem. Speaking of three-dimensional beam contact, Wriggers et al. [72] proposed a computational algorithm to describe the contact between beams with circular cross sections subjected to large deformations. Subsequently, Zavarise et al. [77] extended the proposed algorithm to formulate the contact force model when friction is present. Later, a contact search strategy was developed with the contact model with rectangular cross-sectional beams in the case of large displacements and rotations [40, 41]. All the above-mentioned contributions were based on point-to-point contact interaction leading to discrete contact force acting on the contacting beams. Although using the point-to-point contact model results in an efficient and precise numerical implementation, it has an essential limitation when beams with arbitrary orientation i.e., when the contact angle between them is small (almost parallel), come into contact. In this situation, the requirement of the uniqueness and existence of closest point projection for all contact points is violated. To alleviate the point-to-point contact model limitation, Łitewka [37] proposed a smoothing procedure based on the Hermite polynomials for contact description to improve the smoothness of the normal and tangent contact vectors through the contact points. The limitation mentioned above, particularly when the contact beams are rather parallel was resolved to some extent by Litewka [38, 39], although it still necessitates solving two closest point projection problems (bilateral minimal distance problem) for the contacting beams. The above point-wise contact developments were classified as master-and-slave definition of the contacting entities. In contrary, Gay Neto et al. recently introduced a class of master-and-master formulations within which no distinction is made whether a point and surface is on a master or slave beam [51, 52].
As it is often the case with the general beam-to-beam contact when beams of arbitrary configuration come into contact, the enhanced multiple-point contact method in [38, 39] unable to guarantee the uniqueness of a closest point projection. Consequently, a contact region may remain undetected leading to inaccurate contact constraint enforcement, i.e., nonphysical penetration within a contact event. To alleviate this shortcoming, Durville introduced an intermediate geometry where a proximity zone can be defined to detect the contact point candidates in [18] and was later used in the case of a self-contact beam in [17]. Inspired by Durville’s geometrical contact detection approach, Weeger et al. [69] applied the point force as the contact force in a rod-to-rod surface contact in the framework of Cosserat beam model parameterized using the collocation isogeometric analysis (IGA-C). Chamekh et al. [12, 13] introduced a Gauss-point-to-segment approach to measure gap function between the contacting beams and in self-contact beam problems. To solve the particular contact when contacting beams are interacting along two curves, Konyukhov et al. [32] studied a curve-to-curve contact within a geometrically exact description in the covariant form. Further, they used a geometrical criteria whereby the existence and uniqueness of closest point projection [33] is ensured. As an alternative to the geometrical-based formulation proposed in [32, 33] Meier et al. [45] developed the Gauss-point-to-segment approach into a variant of line-to-line contact formulation with an emphasis on integration interval segmentation in the vicinity of strong discontinuity in the applied beam element formulation, i.e., in the end-points of contacting beams. The line-to-line formulations are considered as a very accurate and rather efficient (more computationally expensive than the point-to-point) contact model in the range of small contact angles for contacting beams (parallel or roughly parallel beams). But, the formulation becomes drastically inefficient when the contact angle exceeds a certain value [45, 47]. To deal with such a scenario, Meier et al. [47] introduced a transition procedure between the point-to-point and the line-to-line contact schemes in contact force level and the contact energy level.
Generally speaking, contact constraint can beimposed by different approaches such as penalty methods, Lagrange multipliers method and augmented Lagrangian method. The variation of contact energy in the penalty method is computed based on the selected penalty parameter which is critically important to ensure that the interpenetration between two bodies in contact is minimal [70]. This method typically needs small time steps in the time integration scheme and a carefully chosen penalty parameter due to the stability requirements. The penalty is widely used alongside the standard mortar contact approach [73] for analyzing contact problems. Yet, the combination of the penalty method with the mortar finite element method is computationally time consuming and not suitable for efficient computing such as real-time simulations. In the case of solid continua, in the presence of frictional contact, Puso et al. [56] enforced contact constraint by an augmented Lagrangian scheme using the mortar method. Speaking of contact between one-dimensional slender continua, Łitewka [36] compared the penalty and Lagrange multiplier methods and concluded that in expanse of higher computational effort, the Lagrange multiplier is more accurate than the penalty method and is trial-and-error free in contrast to the penalty method. On the other hand, Meier et al. [45] argued that the penalty method is more efficient than the Lagrange multiplier method, because of a lower amount of unknowns in the line-to-line contact model and also the penalty parameter has a physical role by taking into account the beam cross-sectional flexibility. Instead of using the standard penalty force law, Khude et al. [30] combined the discrete continuous contact force model with the absolute nodal coordinate formulation (ANCF) to describe the interactions between flexible bodies in multibody applications. The contact constraint can be characterized by inequality constraints, which in turn can be served with a complementarity problem [54]. This is analogous to the Lagrange multipliers method. But, the complementarity problem-based approaches are distinguished from the Lagrange multipliers method with the following features: in Lagrange multiplier method, the contact between two bodies is computed by solving a set of nonlinear constraint equations that establish that both surfaces are in contact without penetration or separation. The contact forces are described through the Lagrange multipliers, which are associated with the contact constraints. On the other hand, with the linear complementary problem approach (LCP), the contact constraints are included into the differential algebraic equations in terms of the complementarity conditions. The contact forces can be solved using a convex quadratic optimization method. The algorithms in this class lead to solving the differential variational inequality (DVI) classified in [53] that describes the interaction of bodies with contact and friction over the evolution of time. The complementarity problem (CP) is regarded as a special case of variational inequality (VI) and subsequently, the acronym DVI. Tasora et al. [4, 67] proposed cone complementarity problems by means of a fixed-point iteration algorithm to simulate contact problems with tens of thousands of colliding rigid bodies. They have enhanced the computational efficiency of the algorithms and formulas by tailoring the fixed-point iteration to obtain a matrix-free algorithm with O(n) space complexity [65]. Negrut et al. [50] proposed the non-penetration condition and the Coulomb dry friction model in a cone complementarity problem which can solve the multibody problems with frictional contact. All of the above applications of the complementarity problem approach were in the context of rigid body contact. Latterly, Tasora et al. [66] introduced a rigid-to-flexible contact model using second-order CCP in the frame work of geometrically exact beam with the isogeometric analysis (IGA) discretization. They concluded that the employed CCP method can be regarded as an acceptable alternative to the conventional penalty method. Accordingly, in the work of Yu et al. [76], the CCP approach is used to compare with the penalty method in the frame work of ANCF beam contact with rigid bodies. The damping component is included in the penalty method using the continuous contact model introduced by Hunt and Crossley [28]. They concluded that the kinematic results show a good agreement between both approaches when the coefficient of restitution is zero.
Prior to a contact event description, a collision detection procedure is needed if the contact points and/or the contact types are unknown. Collision detection is essential and often one of the most crucial steps when imposing an accurate contact procedure. As is often the case, a large overall motion in highly flexible bodies encompasses several contact events of different types, for example, a beam in self-contact situation. A general contact detection procedure was introduced by Zhong et al. [78]. They used a hierarchical algorithm within the contacting entities between bodies or in one self-contacting body. In the past decades, with the development of computer graphics, several numerically efficient algorithms to search for contact between moving bodies have been presented in the literature. In multibody system dynamics [34], computer games [21] and in efficient multi-physics engines [68], the concept of a bounding box approach is widely used to decrease the computational time associated with collision detection. Klosowski et al. [31] proposed a method based on a bounding-volume hierarchy for efficient collision detection for objects moving within highly complex environments. The bounding volumes used in their study were k-dops (discrete orientation polytopes). The k-dops form a natural generalization of axis-aligned bounding boxes. Van den Bergen [7] presented a collision detection scheme that relies on a hierarchical model representation and axis-aligned bounding boxes (AABBs). The work found AABB trees to be the method of choice for collision detection of complex models undergoing deformation. Yang et al. [74] introduced a contact searching algorithm based on bounding volume hierarchies. The procedure introduced was designed for use with the mortar finite element method, and it was employed to solve problems featuring large deformations and significant sliding. Their algorithm searches for potential contacting elements pairs and from which all the contributing points to the mortar integral are identified. They found that for large deformation problems, the bounding volume trees need to be updated in every iteration, which is computationally more costly than the contact searching algorithm itself. Haikal et al. [25] introduced an oriented volume contact search scheme to deal with non-smooth contact events e.g., corner-to-corner contact type. The contact constrained in their implementation relies on an oriented gap function which is evaluated according to the inner products of in-plane vectors defining the contact surface and the position vector of the closest node to the contact surface candidate. When dealing with large torsion loads, large displacements and rotations, self-contact may occur. Neto et al. [22] analyzed a self-contact situation of a highly flexible beam using a geometrically exact formulation. They used a contact search technique based on the overlap between imaginary spheres located at each element to find the candidates of contacting elements when the beam undergoes line-to-line contact in a loop formation. Recently, Sun et al. [16] introduced global and local strategies for contact detection. They have employed an AABBs in the global search stage to find an overlapping pair of AABBs in the frame work of an ANCF plate element.
This contribution proposes a contact procedure including a novel contact detection algorithm. This contact detection algorithm facilitates side-to-side (segment-to-segment), corner-to-side (point-to-segment) and corner-to-corner (point-to-point) contact scenarios. The method is applied with linear complementarity condition (LCP) and the penalty to enforce the contact constraint. The transition between the above beam contact scenarios is treated by means of the minimal contact angle criterion described in [47] and is further discussed in Sect. 4.5. The presented contact detection procedure accounts for the following three phases:
-
1.
A broad-phase (element-wise) search is performed to find the pairs of close-by elements either located in two beams or in the case of self-contact in one beam that might potentially come into contact.
-
2.
Upon identifying the closest contacting element pairs, the oriented bounding boxes enveloping the contacting element candidates are activated. Therein, an algorithm based on the separating axis test (SAT) is used to detect contact events.
-
3.
The intersection of the contacting bounding boxes is determined using Cyrus–Beck line clipping algorithm [27]. For the master beam, the reported intersection points are projected onto the corresponding contacting element surface to solve the closest point projection problem for the beam local parameter of the contact point. Depending on the orientation of the bounding boxes which is measured in terms of contact angles, there are the following possibilities:
-
For sufficiently small contact angles, the contact is regarded as a line-to-line model.
-
Otherwise, the contact model is of the point-to-segment (including point-to-point scenario).
-
The segment-to-segment contact scenario is formulated with respect to the line-to-line contact model (discussed in Sect. 3.3.3) and the other contact scenarios are regarded as the point-wise contact (discussed in Sects. 3.3.1 and 3.3.2). The line-to-line formulation also known as Gauss-point-to-segment (GPTS) formulation is preferred over the mortar methods in this work for a number of reasons: in the mortar methods, the contact constraints are expressed by introducing the special functions so-called mortar space functions on contact interface [75]. These constraint functions, which are composed of product of the shape functions on the slave and master bodies, are to be integrated across the contact surface. The required segmentation over the contact surface in the mortar methods is computationally expensive, yet it concretely contributes to the accuracy of the mortar integrals [15]. A discussion over the computational cost of the mortar methods was recently presented by Harish et al. in [26]. Meanwhile, the developed Gauss-point-to-segment formulation in this work incorporates the segmentation technique to parameterize the contact patch. The mortar methods are known for their optimal convergence properties thanks to satisfying the stability conditions known as the Ladyzhenskaya–Babuška–Brezzi (LBB) conditions in expense of performing mesh refinement [75]. On thec contrary, the presented GPTS formulation achieves a converged solution with a reasonable number of elements. Alongside the presented complementarity problem approach, a conventional penalty method with an embedded Newton solver is employed with the contact search scheme outlined above. The novelties with reference to the presented contact procedure can be stated as follows:
-
Proposal of a contact constraint enforcement model according to the complementarity problem method for beam-to-beam contact and in particular in the case of line-to-line contact i.e., Gauss-point-to-segment (GPTS).
-
Describing a narrow-phase contact search strategy to find the collision points to be applied with the point-to-segment, line-to-line and point-to-point contact scenarios.
-
Comparing the optimization-based LCP approach with the classical penalty formulation with respect to their performance and accuracy.
In a number of numerical examples, the DVI optimization scheme is compared to the conventional Newton iteration embedded in the penalty formulation within each time step. In order to compare against the friction-less penalty formulation, the linear complementarity problem (LCP) is selected with the Lemke’s optimizing algorithm.
2 The absolute nodal coordinate formulation (ANCF)
2.1 Kinematics of the element
In solving the dynamics of multibody applications, deformable bodies can be described in a number of different ways. The floating frame of reference formulation, the geometrically exact beam formulations (GEB) also known as the large rotation vector formulation in multibody literature, conventional nonlinear solid finite elements and the absolute nodal coordinate formulation (ANCF) are some of the examples. The ANCF is a finite element-based approach which is particularly designed to analyze large deformations in multibody applications. In this approach, the kinematics of deformable planar and spatial bodies, such as beams, plates and shells, can be described using polynomial-based shape functions. Absolute positions and their gradients are used as nodal degrees-of-freedom in the ANCF element [60]. The use of ANCF leads to a constant and symmetric mass matrix, however, the centrifugal and Coriolis forces are not expressed explicitly [8, 61]. Hence, the simpler dynamic equations in ANCF makes the formulation suitable in the optimized design of flexible multibody systems [20]. Although in the two-dimensional (2D) space the GEB formulations lead to constant mass matrix and the three-dimensional large rotations do not come into play in beam kinematics, 2D ANCF has some merits over the 2D GEB formulations. Some of the general advantages of the ANCF beam over the GEB formulations were already discussed in Sect. 1. In the following, we briefly point out those benefits which are prominent in the contact procedure presented:
-
As mentioned above, in the ANCF including 2D beams, the position of any particle in a physical beam or its surface is given in terms of the element shape function in the current (deformed) configuration. This solid element-like feature is beneficial when combining with the employed narrow-phase contact search procedure and particularly during the Cyrus-beck line clipping process. This feature is illustrated in Sect. 3.
-
In the case of ANCF, the transition from 2D to 3D is just a few simple steps because of using components of the deformation gradient to define the rotational degrees-of-freedom. One can easily replicate the presented procedure using the 3D variant of the element used [48].
This study employs a three-node quadratic ANCF planar beam element. In this element, the nodes are located at the ends and in the middle of the beam’s longitudinal axis as shown in Fig. 1 [49].
Beam kinematics defined in the reference and deformed configurations with description of the bi-normalized, the local elemental coordinates and the transformation between them, where \({\varvec{u}}_{h}\) is the displacement field
Each node has four degrees-of-freedom: two components of position vector \({\varvec{r}}\) and two components of the position vector gradient \({\varvec{r}}_{,y}\). Accordingly, the vector of the nodal coordinates can be written as:
where \(\varvec{r}_{,y}\) is the derivative of position vector with respect to y \(\frac{\partial \varvec{r}}{\partial \textit{y}}\). The shape functions are defined for the beam element in the element’s local bi-normalized coordinate system \(\varvec{\xi }=\{\xi ,\eta \}\) as:
where the non-dimensional quantities \(\varvec{\xi }=\{\xi ,\eta \}\) are defined as:
where \(\ell _x\) is the length and \(\ell _y\) is the height of the beam element in the undeformed configuration.
The shape function matrix for the beam element can be written with the help of Eq. 2 in the following way:
where \({\varvec{I}}\) is the 2-by-2 identity matrix. In the ANCF, an arbitrary particle within the element can be defined with respect to the global coordinates using the shape function matrix \({\varvec{N}}\), and the vector of the nodal degree-of-freedom \(\varvec{q}\) as
2.2 Equations of motion
In the absolute nodal coordinate formulation, the equations of motion in weak form can be derived using the concept of variational energy as follows:
where \(\varPi _{\text {kin}}\) is the kinetic energy of the element, \(\varPi _{\text {int}}\) is the strain energy of the element, \(\varPi _{\text {ext}}\) is the work done by externally applied forces, and \(\varPi _{\text {con}}({g}_\mathrm{N},{g}_\mathrm{T})\) relates to contact constraint terms due to normal \({g}_\mathrm{N}\) and tangential \({g}_\mathrm{T}\) gap functions. In Eq. (6), \(t_1\) and \(t_2\) are integration limits with respect to time t. The variations of the energies can be written as:
where \(\Big [\int _V\rho \dot{\varvec{r}}\delta \varvec{r}\text {d}V \Big ]_{t_1}^{t_2}=0\), because the position vector is specified at the end-points \(t_1\) and \(t_2\), \(\rho \) is the density of mass, \({\varvec{S}}\) is the second Piola–Kirchhoff stress tensor, \({\varvec{E}}\) is the Green–Lagrange strain tensor, \(:\) denotes the double dot product, \(\varvec{b}\) is the body force vector, which is \(\varvec{b}=\rho {g}\), where g is the field of gravity. The variation of kinetic energy \(\delta \varPi _{\text {kin}}\) can be represented as follows:
where \({\varvec{M}}\) is the mass matrix. The elastic force \(\varvec{F}_{\text {int}}\) can be derived from the variation of strain energy
In this work, the strain energy is derived in terms of generalized strains according to Simo and Vu-Quoc [63, 64] and was adapted for the employed ANCF beam originally introduced in [49]. This structural mechanics-based approach proposed in [49] is preferred over the continuum mechanics-based approach due to its higher rate of solution convergence in the case of lower-order ANCF beams. This topic was investigated in detail for two-dimensional cases in [23] and for three-dimensional beams in [10, 19]. The variations of strain energy associated with beam bending and torsion in terms of the nodal coordinate \(\varvec{q}\) can be expressed as follows:
where E and G are the Young’s modulus and shear modulus, respectively, \(\varGamma _1\) and \(\varGamma _2\) are the generalized strains, \(I_z\) is the second moment of inertia, \(k_\mathrm{s}\) is the shear correction factor and K measures the rotation of the cross section plane with respect to the reference length. The integration in Eq. 10 is computed along the beam center line x. The additional variations of the strain energy accounting for thickness deformation can be considered as follows:
where the transverse strain component \(E_{yy}\) is defined in the Green–Lagrange strain tensor:
where \({\varvec{I}}\) is the identity matrix and \({\varvec{F}}\) stands for the deformation gradient which is expressed as follows:
where \(\varvec{r}\) and \({\varvec{r}}_{0}\) are the current and initial reference configurations, respectively, and \(\varvec{u}_h\) is the displacement vector from the initial configuration to the current configuration.
The external force \(\varvec{F}_{\text {ext}}\) can be obtained using the variation of energy \(\delta {\varPi }_{\text {ext}}\) as follows:
The variation of energy \(\delta \varPi _{\text {con}}\) is contributed by contact force and can be written as:
where \(\varvec{F}_{\text {con}}\) represents the contact force, which will be explained in Sect. 4.
Substituting (8), (9) and (14) into Eq. (7), the weak form of the equations of motion can be expressed as follows:
2.3 Semi-implicit time integration with embedded Newton iteration
According to the semi-implicit Euler integration scheme, the new position \(\varvec{q}^{l+1}\) and the new velocity \(\dot{\varvec{q}}^{l+1}\) at the end of the new time step can be written as follows:
where \(\varDelta {t}\) is the time step size. To amend the position vector \(\varvec{q}^{l+1}\) of the contact points and in turn the velocity vector \(\dot{\varvec{q}}^{l+1}\) at each time step, the Newton iteration is employed and is embedded into the equations of motion of the system. After substituting the acceleration \(\ddot{\varvec{q}}^l=\dfrac{\varvec{q}^{l+1}-\varvec{q}^{l}-\varDelta {t}\dot{\varvec{q}}^{l}}{\varDelta {t}^2}\) at the current time into Eq. (16), the iterative form of the equations of motion is:
where index i indicates the evaluation of the corresponding variable at each Newton iteration.
Accordingly, \(\varvec{F}_{{\text {ext}}_i}\), \(\varvec{F}_{{\text {int}}_i}\) and \(\varvec{F}_{\text {con}_i}\) are the external force, elastic force and contact force at iteration i during the time period from \( t^{l}\) to \( t^{l+1}\). The trial position and velocity vectors to be amended through the iteration are denoted \(\varvec{q}_\mathrm{trial}^{l+1}=\varvec{q}_i^{l+1}\) and \(\dot{\varvec{q}}_\mathrm{trial}^{l+1}=\dot{\varvec{q}}_i^{l+1}\), respectively. The time integration form is created in terms of the velocities and positions, where multiple contact forces can be treated uniformly per step [2]. For the ith iteration, a new displacement is evaluated by taking the Jacobian matrix of the vector of residual forces \(\varvec{R}_e\) with respect to the total degrees-of-freedom of the system as follows:
Search for the contact element candidates. a Checking the closest potential contact elements i and j by comparing the distance between the mid-nodes from each pair of elements between two beams, \({{\varvec{r}}}_i^O\) and \({{\varvec{r}}}_j^O\) are the middle nodes from element i and j. b Checking the closest potential contact elements i and j by comparing the distance between the mid-nodes from each pair of elements in case of self-contact, \({{\varvec{r}}}_i^O\) and \({{\varvec{r}}}_j^O\) are the middle nodes from element i and j
One can express the tangent stiffness matrix of the flexible multibody system at the ith iteration using the finite difference method as follows:
where \(\varvec{\hat{I}}\,^{(m)}\) is the identity vector corresponding to the mth degree-of-freedom of the total n degrees-of-freedom of the system and h is the reasonable infinitesimal step [6, 70]. The next predicted-amended position vector \(\varvec{q}_{i+1}^{l+1}\) is given as follows to check if the converged solution has been achieved:
3 Contact search procedure
3.1 Determination of the elements in contact
In the beam-to-beam contact, the first task in contact search is to identify the possible pairs of contact zones i.e., the global contact search. In this work, the definition of a pair of entities is addressed based on the current position of the middle node \(\varvec{r}_{i}^O\) of element i from beam I and the middle node \(\varvec{r}_{j}^O\) of element j from beam J as shown in Fig. 2a. The position vectors of the middle nodes \(\varvec{r}_{i}^O\) and \(\varvec{r}_{j}^O\) are defined from Eq. (5) with local coordinate \((\xi =0,\eta =0)\) [17]. The pair of the elements A and B with minimum distance of \(d_{\mathrm {min}}\) can be expressed as follows:
where \(n_{I}\) is the number of elements of beam I and \(n_{J}\) is the number of element of beam J.
In the case of self-contact (Fig. 2b), the pair of closest elements needs to be considered within the beam. When contact occurs, the adjacent elements are assumed as not making contact with each other, which means element i cannot contact element \(i-1\) and element \(i+1\). To prevent the adjacent middle nodes from being detected, the pair of adjacent elements are not included in the calculation of the minimum distance \(d_{\mathrm {min}}\). As shown in Fig. 2b, the pair of elements A and B with a minimum distance \(d_{\mathrm {min}}\) can be expressed as follows:
where \(n_{I}\) is the element ID of element I.
Remark 1
Equations (22) and (23) form the loops to detect the pairs of closest elements in the case of the beam-to-beam and beam self-contact situations, respectively. The closest element pairs are recorded for activation in the narrow-phase discussed in the forthcoming Sections. So the value of \(d_{\text {min}}\) is not of interest.
3.2 Determination of the contact event
Planar contact phenomena between flexible bodies includes corner-to-corner, corner-to-side and side-to-side contact scenarios, as shown in Fig. 3. In multibody dynamic problems with flexible bodies, the contact type is not known before contact simulation.
Possibilities of contact between beams
To search for the existence of a contact event, a bounding box scheme is developed in this work. A bounding box is a single simple volume in three-dimensional space or a planar box in two-dimensional space encapsulating one or more objects of a more complex nature or those undergoing significant deformation. The main concept of this approach is to replace complex objects with simple geometrical representation, such as boxes and spheres to have efficient overlap tests [21].
In the oriented bounding box (OBB) approach, a rectangular block with an arbitrary orientation is employed. This approach is based on the separating axis test (SAT). A separating axis of two boxes is an axis for which the projections of two polygons onto that axis never overlap. In the planar case, the existence of the separating axis sufficiently ensures that two convex polygons never intersect. In other words, two polygons do not intersect if there exists a line that completely divides a polygon on one side of the line and the other polygon on the other side of the line. This line is known as the separating line, which is perpendicular to the separating axis. The above explanation is illustrated in Fig. 4 in which \(\varvec{L}\) denotes the separating axis. It is worth mentioning that in the spatial case, a separating axis is still defined, but there are 15 cases to check for existence of the separating axes instead of the four trials with the planar case. Moreover, instead of separating lines that are perpendicular to the separating axes, the separating planes separate the oriented bounding volumes. For the above reasons, the SAT algorithm may not be the most efficient way for three-dimensional contact detection, and therefore, some other contact detection approaches such as Gilbert–Johnson–Keerthi distance algorithm is usually preferred [27]. Using bounding volumes allows for fast overlap rejection tests because one only needs to check if there is a separating axis, and if it gives a positive result, the objects never intersect. As shown in Fig. 4, to have an intersection between the bounding boxes encapsulating the closest elements recorded by Eqs. (22) or (23), \(\varvec{L}\) must not be an instant separating axis. Then, the following condition should be satisfied:
Illustration of two rectangles to check the possible intersections through existence of separating axes. The vector \(\varvec{T}_c\) and half of rectangle A (\(\dfrac{W_A}{2}\varvec{A}_x\cdot \varvec{L}\)) and half of rectangle B (\(\dfrac{W_B}{2}\varvec{B}_x\cdot \varvec{L}+\dfrac{H_B}{2}\varvec{B}_y\cdot \varvec{L}\)) are projected onto axis \(\varvec{L}=\varvec{A}_x\) in this illustration. The other axis \(\varvec{L}=\varvec{A}_y\) and \(\varvec{L}=\varvec{B}_y\) are not separating axes for this case. The objects in this illustration do not intersect as the projection of A and B onto the separating axis \(\varvec{L}=\varvec{A}_x\) do not overlap
where \(\varvec{T}_c\) is a vector from the center of box B to the center of box A, \(\varvec{A}_x\) and \(\varvec{A}_y\) are the unit vectors representing the local x-axis or y-axis of A, \(\varvec{B}_x\) and \(\varvec{B}_y\) are the unit vectors denoting the local x-axis or y-axis of B, \(W_A\) is half the width of A, \(W_B\) is half of the width of B, \(H_A\) and \(H_B\) are half of the height of A and B, respectively, see Fig. 4. To establish a contact detection algorithm based on the oriented bounding box, a solid based mesh is used as a set of points in two-dimensional space. A convex hull is defined using the imported coordinates of the solid mesh. The mesh is created for an undeformed plane element in the bi-normalized coordinate system using the commercial finite element software ANSYS. For the i-th convex hull \({\varvec{C}}_{H_i}\) and the j-th convex hull \({\varvec{C}}_{H_j}\) correspond to the closest element pair, one side of the bounding box contains an edge of the convex hull. Hereafter, to simplify the notation, the subscripts i and j are dropped. The edge of convex hull \({\varvec{C}}_{H}\) is defined as follows:
where nc denotes the number of columns of the convex hull and ic is the column index and \(\varvec{X}\) and \(\varvec{Y}\) are the global coordinates of the points along the convex hull edges. The angle of the convex hull edges can be computed as follows:
Assigning a rotation matrix to \(n_a\) angles given by Eq. (26) gives a global rotation matrix of \({\varvec{R}}^{(2n_a\times 2)}\). The rotated convex hull then is of the form
The border size of each bounding box for all possible edges is computed as follows:
Subsequently, the area of the bounding boxes for all possible edges can be determined among which the smallest one belongs to the minimal-volume-oriented bounding box. Then, the coordinates of the corners of the minimal-volume bounding box can be determined in a straightforward manner. To this end, by the following transformation
all the possible bounding boxes are transformed on the rotated frame \(R_{\text {OBB}}\) which corresponds to the smallest bounding box whose index is identified by the minimum bounding boxes area according to Eq. (28). After identification of the borders of the minimum-oriented bounding box, its corners can be simply found using the corresponding rotation matrix.
3.3 Determination of the contact points
After detecting the pair of closest elements A and B described in Sect. 3.1, and determining an active contact between the contacting OBBs explained in Sect. 3.2, the next task is the placement of the contact point to measure the gap function in order to apply the contact constraint. Consequently, a line clipping process according to Cyrus–Beck algorithm [27] is started to determine the intersection between the colliding bounding boxes.
3.3.1 Point-to-segment contact model
Contact between the beam corner and beam edge is considered to be point-to-segment contact.
Kinematics of a contact event when a corner makes contact with a side. The master point \(\varvec{r}^P(\xi ^{p\prime })\) is found after solving two closest point projection problems (CPP) for \(\eta \) and \(\xi \), respectively
In the point-to-segment contact model, since the collision point between two OBBs is determined according to the Cyrus–Beck algorithm, the exact contact point is identified by solving a number of closest point projection problems (CPP), see Fig. 5. This approach leads to an accurate enough approximation of a contact point which would physically belong to the beam surface. The following closest projection point problem
is solved for the closest value of master beam parameter \(\eta ^\mathrm{CB}_A\) to the intersection point, where
and superscript \(^\mathrm{CB}\) denotes the intersection between lines given by the Cyrus–Beck clipping process. Then, the position of resulted point \(P^{\prime }\) is:
Since the contact takes place on the side of the ANCF beam, the value of the local coordinates \(\eta ^P\) and \(\eta ^Q\) can only be \(-1\) or 1 in the current configuration [24]. Thereto, local coordinates \(\xi _A^P\), ranging from \(-1\) to 1, respectively, is the solution of the following closest point projection problem [72]:
where
As shown in Fig. 6 assuming the connecting line between point P on beam A (master) and point Q of beam B (slave) is perpendicular to the tangent vector at point Q, the following unilateral minimal distance problem
should be solved for the unknown closest coordinate parameters \(\xi ^c_B\equiv \xi ^Q_B\) via the following orthogonality problem:
where
Contact detection when a corner makes contact with a side
The solution of the quadratic problems for \(\xi ^{^P}_A\) and \(\xi ^{Q}_B\), respectively, appeared in Eqs. (33) and (36) necessitates Newton’s iterative procedure. The contact points are thus as follows:
3.3.2 Point-to-point contact model
In this section, the collision point detection in the corner-to-corner contact scenario is analyzed. In this case, it is assumed that the closest points P and Q are located at the corner of two beams. The contact candidate points are represented by their coordinates \(\varvec{r}^P_{A}\) and \(\varvec{r}^Q_{B}\), which can be calculated analogous to the approach described in Sect. 3.3.1 for the point P. However, that procedure should be replicated here in the case of the other corner Q. Repeating the same routine as that formulated through Eqs. (30)–(34) ends up with the following bilateral minimal distance problem:
A side-to-side contact situation happens when contact angle is small enough according to Eq. (83)
Consequently, the additional orthogonality condition
should be satisfied, where
Therefore, in contrast to the unilateral distance problem (35) in the point-to-segment contact model, the bilateral distance problem (39) leads to two orthogonality conditions (36) and (40). This is equivalent to the point-to-point formulation originally introduced by Wriggers et al. [72]. It is classified as master-to-master formulation [51] as no distinction between the slave and master entities in contacting beams is made.
3.3.3 Line-to-line contact model
The approach presented in Sect. 3.3.1 was to find the exact contact points when point-wise contact happens i.e., in the case of a small contact patch between two beams or self-contact of one physical beam. However, when the contact patch is large compared to the other dimensions of the contacting beams (roughly parallel contacting elements), the point-to-point procedure described in the previous Section should be adjusted to find the contact patch end-points. As illustrated in Fig. 7, two points are given as the results of the line clipping process. Although in the previous Section, two intersection points were also screened, see Fig. 5, the second point is too close to \(P_\mathrm{CB}\). In Sect. 4, a measure to consider a contact being point- or patch-wise is further discussed. Analogous to the point-to-segment model, the following closest point projection problems
should be solved for the abscissa coordinate parameters \(\xi _A^{P_\mathrm{CB}}\) and \(\xi _A^{Q_\mathrm{CB}}\) corresponding to the intersections \(P_\mathrm{CB}\) and \(Q_\mathrm{CB}\). The contact patch boundaries
on master beam A are to be assigned onto the slave beam B to confine the contact patch RS via the following set of closest point projections:
where \(\xi ^R_B\) and \(\xi ^S_B\) are the abscissa coordinate parameters on beam B. The contact patch RS is thus confined at the following points:
and
Algorithm 1 is written in view of the procedure in [21]. It describes the proposed contact search approach based on the oriented bounding box, which detects and identifies the collision points, which are significantly important in the calculation of the vector of the contact force.
4 Contact constrain enforcement
This section discuses two methods used in this work for contact constraint enforcement. This includes the penalty presented in Sects. 4.1 and 4.2 and the linear complementarity problem (LCP) approach introduced in Sects. 4.3 and 4.4.
4.1 Penalty method based on the point-to-segment formulation
This section describes the application of the penalty method for enforcing contact constraints in the case of the point-to-segment contact formulation. The normal gap function \({g}_\mathrm{N}\) can be written in terms of the derived contact points in Eq. (38) as follows:
where \(\varvec{r}_{B}^{Q_0}={\varvec{N}}_m(\xi ^{Q_0}_B,0)\varvec{q}_B\) is the closest projection of the master point \(\varvec{r}_{A}^{P}\) on the slave beam B axis where \(\xi ^{Q_0}_B\) is the solution of
If the gap function \({g}_\mathrm{N}\) is positive (\({g}_\mathrm{N}>0\)), there is no contact between bodies (\({f}_\mathrm{N}=0\)), and consequently the variation of energy \(\delta \varPi _{\text {con}}\) based on the contact force is not introduced. In the opposite case (\({g}_\mathrm{N}\le 0\)), the contact occurs when (\({f}_\mathrm{N}>0\)), the contact contribution terms \(\delta \varPi _{\text {con}}\) should be taken into account in the weak form \(\delta \varPi \). In the absence of tangential force, the Signorini non-penetration conditions for the unilateral contact take the form
which coincides with the Karush–Kuhn–Tucker (KKT) non-penetration constraints. The penalty potential energy \(\varPi _{\text {con}}^\mathrm{PM}\) related to normal contact is expressed as follows:
where \(c_\mathrm{N}\) is the normal penalty parameter. The variation of the penalty potential energy (49)
is equivalent to the contact energy contribution in Eq. (15) where
is the contact normal vector. Thereto, the point-wise discrete contact force can be read from Eq. (50):
The variation of the normal gap function is expressed as follows:
where \((\varvec{r}_{A}^{P}-\varvec{r}_{B}^{Q})^\mathrm{T}\delta \varvec{n}_{A}^{P}=0\) and \(\delta \varvec{r}=\frac{\partial {\varvec{r}}}{\partial {\varvec{q}}}\delta \varvec{q}=\varvec{N}\delta \varvec{q}\). Therefore, the variation of the normal gap can be reduced to the following form:
Remark 2
In the case of the point-to-point contact model in Sect. 3.3.2, it is cumbersome to define the normal vector using Eq. (51) at the corner of beams and the gap function calculation cannot follow Eq. (46) function. On this account, an approach based on penetration check originally proposed by [41] is discussed in Sect. 5.4.
Remark 3
As it can be realized from Fig. 5, there is a scenario when the bounding boxes intersect, but still there is no intersection between the two beams. This usually happens when deformation is large. In such a situation, the bounding boxes continue to interpenetrate as a result of a positive gap function. This is also the case for the line-to-line formulation in the forthcoming Section.
4.2 Penalty method based on the line-to-line contact formulation
In the case of the beam line-to-line contact formulation, the unilateral minimum problem for two contacting beams is expressed in terms of the closest distance field between two contacting beams. The closest vector field on beam A (master) \(\varvec{r}^c_A(\varvec{\xi }_B)\) corresponds to the position field belonging to beam B (slave), \(\varvec{r}^B\) is obtained by solving the following minimal distance problem
where superscript \(^\mathrm{c}\) denotes the closest point coordinate assigned to the master element, and hereafter, it denotes the entity assigned to the coordinate given by closest point projection problem. In the line-to-line contact, the unique solution to (55) leads to one orthogonality condition in which the task is seeking for unknown \(\xi _A^\mathrm{c}(\xi _B)\) that is the master closest point coordinate corresponds to the slave point in terms of the coordinate field parameter \(\xi _B\)
where \(\varvec{r}_{A,\xi }(\xi _A)\) is the tangent of the position vector field \(\varvec{r}_A\) with respect to the local coordinate \(\xi _A\). The gap function field \(g\big (\xi _A(\xi _B),\xi _B\big )\) is defined to express the non-penetration condition
Illustration of the minimum distance gap function when side-to-side contact takes place
where position field \(\varvec{r}_{A}^{P_0Q_0}={\varvec{N}}_m(\xi ^{P_0Q_0}_A,0)\varvec{q}_A\) results from the projection of the intersections \({P_\mathrm{CB}}\) and \({P_\mathrm{CB}}\) on the master element axis and the position field \(\varvec{r}_{B}^{R_0S_0}={\varvec{N}}_m(\xi ^{R_0S_0}_B,0)\varvec{q}_B\), in the same way resulted from the projection of the closest points P and Q on the slave element axis. In the light of the segment-to-segment integration along the parameterized contact patch that was previously applied in the mortar contact method in [11, 16, 55], and with reference to the line-to-line contact formulation proposed by Meier et al. [45], the penalty potential energy in terms of the established contact patch shown in Fig. 8 is of the following form
Accordingly, the contribution of contact energy to the weak form of equation of motion (6) can be expressed as follows:
where
and RS indicates the integration domain on the slave beam B. The vector of distributed contact force can be identified in Eq. (59) in the form of
where
is the average magnitude of contact pressure on the entire contact patch and
the contact normal vector.
4.2.1 Parameterization of contact patch
Illustration of integration segmentation along the contact patch in the contacting master and slave beams
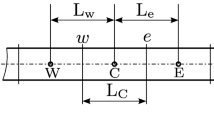
The variation of energy (59) can be expressed in discretized form by substituting the position vector \(\varvec{r}\) from Eq. (5) into Eq. (59):
where \(n_G\) is the number of Gauss points in a contacting element, \(w_j\) are the corresponding Gauss points weight, \(\xi ^j_B\) is the Gauss point coordinate in terms of the slave beam parameter \(\xi _B\), \(\xi ^c_A(\xi ^j_B)\) is the closest projected master point assigned to the Gauss slave point parameter \(\xi ^j_B\) and \(J\big (\xi ^c_A(\xi ^j_B)\big )\) and \(J(\xi _B^j)\) are the scaling factor between the increment of the Gauss point coordinates in the bi-normalized and the physical coordinate systems in the master and slave beams, respectively. The integration interval used in Eq. (64) can be further parameterized by assigning \(n_S\) segments for each beam slave element, see Fig. 9. Therefore, for \(n_S\) number of segments within a slave element, a new coordinate parameter in a slave beam element can be introduced as
where \(\xi _B^{1e}\) and \(\xi _B^{2e}\) are the integration boundaries at each integration segment. The parameter \(\xi ^s\) is equidistantly spaced within interval \([-1,1]\) unless there exists a projection for a master beam end-point to be assigned onto a slave beam segment such that \(\xi _B^{1e}\equiv \xi _{B}(\xi ^{P}_A)\) and/or \(\xi _B^{2e}\equiv \xi _{B}(\xi ^{Q}_A)\) where \(\xi ^{P}_A\) and \(\xi ^{Q}_A\) are the master beam end-points abscissa coordinate parameters. Therefore, according to Eq. (56)
Now, the discretized contact energy variation (64) can be expressed with a further parameterization consisting of the beam discretization and the contact segmentation. It is represented in the form of two sums over the number of Gauss points and over the integral segments:
where
in which \(L_B\) is the slave beam length and H is the element height.
Remark 4
As illustrated in Fig. 9, the established Gauss points on the slave beam characterized by coordinate parameter \(\xi ^{sj}_B\) are to be projected onto the master beam using Eq. (56). To this end, an internal search should be considered in the computation algorithm to find the closest master element to each Gauss points on the slave beam.
4.3 Linear complementarity method based on the point-to-segment formulation
In the absence of friction, the normal contact force vector \(\varvec{F}_{k,N}^{P}\) for the k-th contact is imposed on the beam A by the components of normal vector \(\varvec{n}_P\) on the contact point P, such that:
where \({\hat{\gamma }}_{k,N}\) is the Lagrange multiplier vector corresponding to the values of the normal contact forces.
It is worth noting that the discrete contact force \(\varvec{F}^{Q}_k\) on the beam in the point-to-point and point-to-segment formulation is the reaction force of \(\varvec{F}^{P}_k\) as:
The variation of energy \(\delta \varPi _{\text {con},N}^\mathrm{LCP}\) related to the contact force within the linear complementarity problem (LCP) associated with the contact force can be expressed as:
where
and
For the k-th contact, \({\varvec{D}}_{k}\) is a vector which can define the location and direction of the contact force in the global coordinate system. \({\varvec{D}}_{k}\) is computed based on the k-th pair of potential contact points. If there is \(N_k\) presence of contact events at same time step, \({\varvec{D}}\) and \(\hat{\varvec{\gamma }}\) can be constructed at the system level as:
where \(N_{\text {dof}}\) refers to total number of degrees-of-freedom of the system.
4.4 Linear complementarity method based on the line-to-line formulation
When dealing with line-to-line contact formulation, the contact energy contribution to the weak form has to be defined in terms of a distributed force model. In this way, the variation of contact energy is in the form of
where the first and the second terms represent the contact energy contribution with respect to beam A (master) and beam B (slave), respectively, in which \(\varvec{F}^{PQ}\) and \(\varvec{r}^{RS}_B\) are the corresponding continuous contact force over the entire contact patch defined with the position fields \(\varvec{r}_A^{PQ}\) and \(\varvec{r}_B^{RS}\). The variational contact energy (74) is in the form of
in which RS denotes the contact patch on the slave element B. Analogously to the definition for the discrete contact force given in Eq. (72b), the distributed contact force acting on each beam element are
where \({\varvec{D}}_{A,k}\) and \({\varvec{D}}_{B,k}\) are to be parameterized according to the Gauss-point-to-segment (or line-to-line) approach described in Sect. 4.2 in the form of
Applying of the same integration segmentation scheme as presented in Sect. 4.2.1 yields:
that are analogous to Eq. (72c). For \(N_k\) number of contact events per time step Eq. (73) is valid and consists of \(N_k\) surface-to-surface contact scenarios.
Remark 5
The gap function is calculated according to Eq. (57), but first, the contributions
and
and also those denoted \(\varvec{r}_{A}^{P_0Q_0}\) and \(\varvec{r}_{B}^{R_0S_0}\) defining the contact patch should be integrated separately with respect to the procedure described in Sect. 4.2.1.
4.5 Transition between point-wise and line-to-line formulations
As briefly pointed out in Sect. 1, the point-to-point and line-to-line beam contact formulations have their own limitations with respect to the angle range within which contact takes place. These limitations were already derived in [45] and circumvented in [47]. In this work, the transition between the point-to-segment and line-to-line contact scenarios is handled by means of measuring the contact angle with reference to the point-wise (point-to-segment or point-to-point) contact type. So that, in case of a sufficiently small contact angle, the line-to-line formulation is required. In the ANCF, the angle between two contacting beam elements is defined in terms of the angle between the tangent vectors at the contact points:
in which \(\alpha \in [0;\dfrac{\pi }{2}]\). The rate of rotation of the cross section rotation with respect to the beam undeformed center line is adopted according to [24] as follows:
where \(\varvec{r}_{,\xi \eta }=\frac{\partial r_{,\xi }}{\partial \eta }\). According to [45], as long as the contact angle \(\alpha \) is larger than the following lower bound
a unique solution for the closest point projection problem (36) is guaranteed, where
Concretely, for the contact angle values above \(\alpha _{\text {min}}\), the unique solution for the closest point projection problem (40) in the case of point-to-point contact is also guaranteed.
4.6 Customized time integration with contact impulse
The discretized equation of motion in terms of the k-th contact impulse \({\gamma }_k=\varDelta {t}{\hat{\gamma }}\) in the semi-implicit Euler scheme can be rewritten as:
where \(\perp \) means perpendicular [50], which is indeed \({\gamma }_{k,N} \perp g_{N,k}={\gamma }_{k,N}\cdot g_{N,k}\), based on the calculation of the contact contribution presented in Sects. 4.3 and Sect. 4.4, and contact impulse \({\gamma }^{(l+1)}=\hat{{\gamma }}^{(l+1)}\varDelta {t}\) is used in the rest of the paper [50].
The signed gap function at \(t^{(l+1)}\) can be approximated in terms of Taylor’s expansion as [4]:
where \(v_{k,N}^{(l+1)}\) is the normal component of relative velocity at a contact event between two contact points at \(t^{l+1}\). Recalling the definition of vector \(\varvec{D}\) in Eq. (72c), it can be interpreted as the differentiation of the gap function with respect to the nodal coordinates in the normal direction. Hereupon, the complementarity condition in Eq. (85c) can be expressed in the following form:
The corresponding composite velocity with respect to Eq. (86) takes the form of
For the k-th contact \(\gamma _{k,N}^{(l+1)}>0\) and \(\frac{1}{\varDelta {t}}{g}_{N,k}^{(l+1)}=\frac{1}{\varDelta {t}}{g}_{N,k}^{(l)}+\varvec{D}^{(l+1),T}_k\dot{\varvec{q}}_k^{(l+1)}=0\).
It is for this reason that:
according to which \({\gamma }_{k}^{(l+1)}\cdot d_{k}\ge {0}\).
At the initial time, the relative contact velocity will be zero, so the initial term of \(d_{k}\) is:
According to Eq. (88), the term of \(d_{k}\) can be rewritten as:
After substituting the nodal velocity vector at \(t^{l+1}\) from the first row of Eq. (85a) into Eq. (91) one gets
where
and in the absence of friction the second term in Eq. (92) containing
is a scalar.
4.7 Time integration scheme
Due to the use of the absolute nodal coordinate formulation, the mass matrix \({\varvec{M}}\) and the gravity external force \(\varvec{F}_{\text {ext}}\) are constant. It is for this reason that the mass matrix and gravity external force can be initialized before time integration. The initial elastic force \(\varvec{F}_{\text {int}}\) and the velocity \(\dot{\varvec{q}}\) can be set to be equal to zero by assuming that the simulation starts in an undeformed configuration. Algorithm 2 succinctly explicates the implementation of a semi-implicit integrator with the embedded iteration loop to calculate the corrected position vector of the collision points during a contact event [40, 72]. With the employed semi-implicit Euler time integration scheme, the contact force, the elastic force, the velocity and the position vectors are calculated and amended at each time step using the Newton’s iteration as summarized in Algorithm 2 when the penalty method is used. In the case of the LCP method, the vector \({\varvec{D}}\), and the gap function \(g_N\) is used to compute the new contact impulse \(\varvec{\gamma }^{(l+1)}\) using Eq. (96).
5 Numerical examples
The numerical examples presented in this Section aim to examine the performance and accuracy of the computational procedures introduced including point-wise (point-to-segment and point-to-point), contact formulation and line-wise formulation (line-to-line). One quasi-static and four dynamics cases of ANCF beams coming into contact are considered in this section. Contact cases between beams are described as corner contacts a corner, corner contacts a side and side contacts a side. All examples are solved using the linear complementarity problem (LCP) and the penalty method. The contact detection explained in Sect. 3 is used to help impose the contact constraints. A Semi-implicit Euler numerical scheme is utilized as the time integration scheme for both approaches used.
When using the penalty method, the corrector, Newton’s iteration presented in Sect. 2.3 is employed to provide a converged solution for the vector of nodal degrees-of-freedom at each time step during each contact event. This is needed to minimize the inter-penetration of the contact elements. The converged solution is achieved when the magnitude of the vector of the residual of the equation of motion given in Eq. (19) \(\left\| \varvec{R}_e^{l+1}\right\| \le 10^{-4}\).
The material and integrator setting used in the simulations are given in Table 1. The contact events are detected through the oriented bounding boxes (OBBs) scheme which is composed of a parent box that encapsulates the whole beam structure, and the children boxes that encompass the finite ANCF beam elements.
Then the complementarity problem can be displayed as:
According to Eq. (95), the linear complementarity problem (LCP) represents the first-order optimality conditions for the one-dimensional quadratic optimization problem and can be solved by Lemke’s algorithm [1, 3] to find the minimum for the impulse \(\gamma ^{l+1}\) which satisfies the KKT constraints:
whose solution is the normal contact impulse \({\gamma }^{(l+1)}\).
5.1 Double-cantilever beam
In this example, the performance and accuracy of the presented Gauss-point-to-segment (GPTS) contact formulation is examined by considering a classical example originally discussed in [55] and later in [25] using the bounding volumes scheme. The parameters used in the simulation are collected in Table 2. The structure underwent a large deformation at the end of the simulation in the maximum loading as shown in Fig. 10. In order to investigate the GPTS formulation discussed in Sect. 4.1, a convergence analysis was performed with an increasing number of ANCF elements.
Double cantilever beam in deformed configuration using 24 beam discretization and three integration segments per slave beam element
Rate of convergence of the double cantilever beam solution for the tip vertical displacement of the upper beam with increasing number of beam discretizations. Dashed line indicates third order of convergence
Comparison between the solutions for the slave beam center line position using the proposed contact formulation and ANSYS. A certain discretization of 24 and 72 number of ANCF and ANSYS BEAM189 are used, respectively
Initial configuration of two unconstrained beams and three stages of the contact process
Energy balance of the side-to-side contact type based on the LCP and the penalty methods. Eight ANCF elements are used for each beam structure
The number of Gauss point per integration interval \(n_S\) over each segment is given by the Gauss rule as follows:
with the total number of
Gauss points per slave beam element, where p is the order of the integrand polynomial appeared in Eq. (67)
Figure 11 shows the convergence rate of the solution for end point vertical displacement, therein, the relative errors were measured versus increasing number of beam discretization: 4, 8, 16, 24 and 32 to investigate the used beam element performance when applying the contact formulation. The solution given by the finest discretization (32 ANCF beams) is as to the reference value. It can be seen from the figure that the solution converges with a sharp pace when using 16 discretizations, and thereafter, the convergence rate follows a slighter rate. To investigate the accuracy of the above performance analysis, the simulation was replicated by a commercial finite element code ANSYS using a three-node beam element BEAM189. To properly replicate the contact model with ANSYS implementation, the contact element type CONTA170 acts to define a contact surface on the master beam (upper beam), and TARGE170 was used for definition of contact surface on the slave beam (lower beam). The contact elements’ options are set to replicate the contact constraint used in the proposed GPTS formulation. Therein, the contact model is set for parallel beam with distributed force and the penalty methods are chosen to enforce the contact constraint. Figure 12 shows the lower beam’s center line displacement based on the proposed formulation and ANSYS solution for maximum loading. The results are based on 24 ANCF elements with three integration segments per element and 72 BEAM189 elements when a nonlinear static solver is selected. Although, the comparison between two center line displacements are in an acceptable range for such a significant deformation, the X-displacement value for the beam end point is not in close agreement with the ANSYS solution. It is expected from the low-order ANCF beam that was comprehensively shown in [10].
Comparison of evolution of the gap function along the contact patch when using LCP and the penalty methods. The descritization of eight elements is used with the both beams
Energy balance of the corner-to-side contact type based on the penalty and the LCP methods. Eight ANCf elements are used for each beam structure
Initial configuration of two free moving beams and six stages of the contact process. The contact and the collision points are detected by the algorithm based on the intersecting of OBBs
5.2 Side-to-side contact problem
In this example, two unconstrained beams enter into contact demonstrating the side-to-side contact (segment-to-segment) type, see Fig. 13a. The beams are of two different lengths. The length of the upper beam is 1 m and the lower beam is 0.5 m. The beams are discretized using eight ANCF elements. The initial configuration and three stages of the contact process are shown in Fig. 13. To define the contact patch on the contacting element, the boundaries of the patch were found according to the procedure described in Sect. 4.2. The OBBs corresponding to the boundaries of the lower beam are considered with their counterparts from the upper beam for the line clipping process as was detailed in Sect. 3.3.3. The established contact patch was parameterized with three segments per contacting elements. The gap function in both the LCP and penalty methods were computed with respect to Eq. (57). In the case of the penalty method, four Gaussian points according to Eq. (97) are required to integrate the contact contribution appearing in Eq. (67). With the LCP method, the contributions to the distributed contact force Eq. 76 represented by Eq. (78) were integrated using three Gauss points. The deformation dependent abscissa coordinates confining the entire contact patch are iteratively obtained according to Eq. (66).
Figure 14a and b shows the potential, kinetic and strain energies associated with the LCP approach and the penalty method with the OBB contact detection algorithm, respectively.
The small drop appeared in the total energy with the penalty method could emanate from choosing a relatively large penalty parameter (\(2\cdot E\)) to compensate for the surface penetration in the pure line-to-line contact which contains more energy lost compared to the point-to-segment case discussed in Sect. 5.3. On the other hand, the LCP exhibits the flat level of the total energy excluding a tiny drop upon the first contact event. The fluctuations with the kinetic and strain energy interchange is expected from the LCP formulation. It is analogous to that in the Lagrange multipliers method. Figure 15 indicates that the evaluation of gap function with the LCP and penalty methods is in a close agreement in their values. The penalty method exhibits a number of swings within the contact duration which is expected from such formulation. Moreover, the average of the penetration with the penalty method is slightly less than that in the LCP method. As corroborated with the above energy conservation results, this is due to the relatively large penalty factor used. This supports the small drop in the total energy level shown in Fig. 14b.
5.3 Corner-to-side contact problem
In this example, a rotated free falling flexible beam and a horizontally moving beam make contact as shown in Fig. 17. The upper beam is rotated by an angle of \(45^{\circ }\) with respect to the ground level. The velocities of the upper and lower beams are − 3 m/s and 3 m/s, respectively. The contact events were detected according to the OBB scheme described in Sect. 3.2, and the contact points were identified based on the line clipping process explained in Sect. 3.3.1. In the LCP and penalty approaches, the contact energy contribution was evaluated according to the approach described in Sects. 4.3 and 4.1, respectively. In the case of negative values for the gap function, the contact force vector is iteratively updated during the contact events. Potential, kinetic and strain energies associated with the LCP approach and the penalty method are shown in Fig. 16a and b, respectively. As evidenced by the figures, the total energy remains constant in the case of the penalty formulation. This is due to the use of the Newton iteration within the contact events to re-evaluate the system’s tangent stiffness matrix (20).
Gap function variation during the simulation of the penalty and the LCP methods with OBB contact detection when mesh of eight ANCF beam elements is used for the beams
Figure 18 shows the gap function variation during the contact events in the LCP and the penalty approaches. As can be seen in the figure, a significant sliding takes place in the contact events due to the non-frictional contacts (see Fig. 17).
Figure 19a and b, respectively, shows the disposition of the solution convergence for the right-end-point of the upper beam when the LCP and penalty methods are used. Both methods delivered the converged results up to 12 discretizations that imply the robust computational performance of the contact implementation. While the solutions with the penalty method for 8 and 12 discretizations seem to closely resemble each other, in the case of the LCP method, the solutions for 8 and 12 beam elements are still discernible. This can be justified by the applied strict convergence criterion (19) with the penalty method.
A comparison was made between the converged solutions for the upper beam trajectory with the LCP and penalty methods in the X and Y directions that are illustrated in Fig. 20a and b. The figures indicate that the solutions from both methods are almost coincident in the X direction and for the Y direction they are in close agreement (see also Fig. 19).
Convergence of the displacements in the Y direction with increasing number of beam discretizations with respect to the contact constraint imposition using a: penalty and b: LCP methods
Comparison of the displacement of upper beam right-end-point a: in the X and b: Y directions when enforcing the contact constraint based on the LCP and penalty methods. The discretization of 12 beam elements are used with the both methods
The LCP method showed a significantly lower computational cost compared to the penalty method. The computational effort is given in terms of the CPU time in Table 3. This indicates that the optimization-based approach in evaluating the contact force components in CP method is more efficient than the classic Newton iterative solver used with the penalty method. This emanating from the fact that the local optimization used with the CP approach is dealing with evaluation of optimized value for the normal component of reaction force (the Lagrange multiplier) at each contact event per time integration step, whereas in the case of penalty method, the whole right-hand side of the motion differential equation is iteratively evaluated per each contact event within a time integration step. This accounts for the re-evaluation of the gap function at each Newton iteration. That means that the narrow-phase contact detection algorithm has to be repeated at each iteration.
5.4 Corner-to-corner contact problem
In this example, the corner-to-corner contact scenario is analyzed.
The gap calculation is accompanied by a specific penetration check according to [41]. Figure 21 shows the possibility of penetration for the closest points at the corners to satisfy Karush–Kuhn–Tucker conditions. The values of the angles between several vectors are also illustrated in Fig. 21. According to Fig. 21, the angle \(\alpha _1\) and \(\alpha _1\) can be defined as:
where contact points P and Q are found according to the discussion in Sect. 3.3.2. When penetration takes place between the corners [40], the angles \(\alpha _1\) and \(\alpha _2\) can be computed as follows:
Therefore, if the angles fulfill the condition of Eq. (99), the gap function is negative, and can be written as:
If the angles do not fulfill the condition, the gap function will be positive.
The example of two pendulums contacting each other is used to analyze the corner-to-corner contact type. The initial configuration and three stages of the contact process are shown in Fig. 23.
Penetration check: \(\alpha _1=\angle ({\varvec{{PQ}}},{\varvec{{PM}}})\), \(\alpha _2=\angle (-{\varvec{{PQ}}},{\varvec{{QN}}})\)
Energy balance of the corner-to-corner contact type based on the LCP and panalty methods. 16 ANCF elements are used for each beam
Initial configuration: a of two pendulums and five stages of the contact process: a–f. Two pendulum come into contact starting with the point-to-point contact events: b, and after separation: c, a line-to-line contact happens within their lower part: d, and subsequently, another round of point-to-point contact events: e is repeated
With this example, the transition between the contact scenarios discussed in Sect. 4.5 is illustrated. It is shown in Fig. 23 that first contact scenario is regarded as the point-to-point followed by a side-to-side contact scenario. Potential, kinetic and strain energy associated with the LCP approach and the penalty method are shown in Fig. 22a and b, respectively. There are small fluctuations during the transition from the point-wise formulation (described in Sects. 4.1 and 4.3) into the line-to-line formulation presented in Sects. 4.2 and 4.4. Nonetheless, the penalty and LCP method conserved the level of total energy within the contact events with respect to the different contact formulations; the point-to-point and line-to-line. The above-mentioned fluctuation could be arisen from switching between the contact formulation in the narrow-phase of contact detection level.
5.5 Self-contact problem
In this example, a highly flexible beam undergoing multiple self contact events is studied. The example parameters were adopted from [62] where the dynamics of the flexible beam denoted ”flying spaghetti” was originally contrived, see Fig. 24.
The quadratic ANCF beam element with discretization of 16, 24 and 32 beam elements is used in the formulation. A force of \(F(t)=8~\text {N}\) and a torque of \(M(t)=80~\text {N}\cdot \mathrm{m}\) are applied as shown in Fig. 24 within the time interval of \(t=[0,4.0]\) s to provide a motion composed of a large deformation and a large local displacement and rotation. According to the approach described in Sect. 3.1, the global search for the proximity zone leads to an efficient computational algorithm. This is because only the OBBs corresponding to the closest elements remain active in the identification of the collision points.
As shown in Fig. 25, the self-contact events including sliding and non-frictional contacts take place several times during the simulation from \(t=2.84~\text {s}\). To determine the contact points, Algorithm 1 is employed to detect the contact and the contact point candidates in the LCP and the penalty formulation approaches.
A flexible unconstrained beam with an applied force, moment and its problem data
Snapshots of the self-contact events in the flying spaghetti problem in the simulation when using the penalty force model. The number of meshes in beam is 32
To evaluate the accuracy of the presented approaches with the highly flexible beam, an energy balance analysis is provided in Fig. 26a and b. As can be seen from the figures, the total energy and its components for the LCP- and the penalty-based approaches are in an acceptable agreement.
Figure 27a and b compares the rate of convergence of the solution for the displacement in the Y direction of the beam lower end point in the case of the penalty and LCP methods, respectively. The figures indicate that the solution is converged up to 32 beam elements with both methods, and no distinction can be reported between the penalty and LCP methods from the convergence analysis perspective.
Energy balance of the flying spaghetti based on the LCP and the penalty methods. The number of beam elements are 32
Convergence of the displacements of the lower end point of the beam in the Y direction with increasing number of beam discretizations with respect to the contact constraint imposition using a: penalty and b: LCP methods
To gain an insight into the motion of the flying spaghetti problem during the contact events, the motion of the end node of the structure is considered. Figure 28 depicts the trajectory of the end node in the LCP and the penalty formulation approaches. The figure shows the coincident patterns recorded by the two methods within the contact events and by the end of the simulation time. The usage of Newton’s solver with the penalty method mitigates the inter-penetrations of contact elements. This is demonstrated in Fig. 29a and b where the convergence of the solution in the contact methods are shown in terms of the magnitude of the vector of the residuals \(\left\| \varvec{R}_e\right\| \). From Fig. 29a, it can interpreted that the penalty method proves the converged solution in every time step during contact events by satisfying the criterion given in Eq. (19). Figure 29b shows that the LCP method ensures zero norm of the residual vector within the contact events.
Trajectory of the lower end point of the beam during the simulation based the LCP and the penalty methods
Magnitude of the vector of the residual of the equation of motion over the simulation time based on the penalty and the LCP models when mesh of 16 beam elements is used
6 Conclusions
In this work, a contact procedure was introduced to analyze contact in the case of flexible beams and particularly in self-contact situations. The contact events and the collision points were, respectively, detected using the oriented bounding box scheme and the Cyrus–Beck line clipping process. The complementarity problem (CP) and penalty approaches were used for contact constraint imposition. Five numerical examples were presented to investigate the performance and accuracy of the introduced CP method in combination with the proposed contact detection procedure. To compare against the LCP method, a penalty method was developed with a particular stress on the line-to-line (GPTS) formulation with the contact patch segmentation inspired by Meier et al.’s work [45]. In the first static example, the developed line-to-line formulation was examined for further implementations in the large deformation dynamic problems with the LCP and penalty methods. Therein, a three-dimensional beam element in ANSYS was used to verify the results. In the dynamic examples, energy balance is presented to show the conservation of strain energy when a contact event occurs. Furthermore, the performance of the proposed contact formulations in respect of the LCP and penalty methods were investigated by a number of solution convergence analyses. In the numerical examples, the introduced contact detection procedure showed its accuracy and robustness in application of different contact formulations (point-to-segment, point-to-point and line-to-line), and also different contact constraint imposition (LCP and penalty) approaches. The gap functions evolution based on the two employed approaches are in acceptable agreement which is discussed in Sects. 5.2 and 5.3 where the segment-to-point and line-to-line formulation contact were studied. The numerical results show that the LCP method posses similar solution convergence properties as the penalty method when combined with the introduced contact detection procedure. However, the computational effort with the LCP is significantly lower than the penalty method and for this reason, the LCP method is more suitable in (real-time) simulation of large deformation contact problems in two-dimensional space. As demonstrated in this work, the combination of the introduced hierarchical contact detection procedure with the complementarity problem (CP) approach can be efficiently applied in the simulation of highly flexible beams undergoing self-contact. In our forthcoming contribution, we will introduce a novel surface-to-surface contact formulation in the frame-work of three-dimensional ANCF beam with arbitrary cross-sectional geometry.
References
Anitescu, M.: Optimization-based simulation of nonsmooth rigid multibody dynamics. Math. Program. 105(1), 113–143 (2006)
Anitescu, M., Hart, G.D.: A constraint-stabilized time-stepping approach for rigid multibody dynamics with joints, contact and friction. Int. J. Numer. Methods Eng. 60(14), 2335–2371 (2000)
Anitescu, M., Potra, F.: Formulating dynamic multi-rigid-body contact problems with friction as solvable linear complementarity problems. Nonlinear Dyn. 14(3), 231–247 (1997)
Anitescu, M., Tasora, A.: An iterative approach for cone complementarity problems for nonsmooth dynamics. Comput. Optim. Appl. 47(2), 207–235 (2010)
Auricchio, F., Da Veiga, L.B., Hughes, T.J.R., Reali, A., Sangalli, G.: Isogeometric collocation methods. Math. Models Methods Appl. Sci. 20(11), 2075–2107 (2010). https://doi.org/10.1142/S0218202510004878
Bathe, K., Bouzinov, P.: On the constraint function method for contact problems. Comput. Struct. 64(5–6), 1069–1085 (1997)
Bergen, G.V.D.: Efficient collision detection of com- plex deformable models using aabb trees. J. Graph Tools 2(4), 1–13 (1998)
Berzeri, M., Campanelli, M., Shabana, A.A.: Definition of the elastic forces in the finite element absolute nodal coordinate formulation and the floating frame of reference formulation. Multibody Syst. Dyn. 5(1), 21–54 (2001)
Bourago, N., Kukudzhanov, V.: A review of contact algorithms. Mech. Solids 40(1), 35–71 (2005)
Bozorgmehri, B., Hurskainen, V.V., Matikainen, M.K., Mikkola, A.: Dynamic analysis of rotating shafts using the absolute nodal coordinate formulation. J. Sound Vib. 453, 214–236 (2019). https://doi.org/10.1016/j.jsv.2019.03.022
Cavalieri, F.J., Cardona, A.: Numerical solution of frictional contact problems based on a mortar algorithm with an augmented Lagrangian technique. Multibody Syst. Dyn. 35(4), 353–375 (2015)
Chamekh, M., Mani-Aouadi, S., Moakher, M.: Modeling and numerical treatment of elastic rods with frictionless self-contact. Comput. Methods Appl. Mech. Eng. 198(47–48), 3751–3764 (2008)
Chamekh, M., Mani-Aouadi, S., Moakher, M.: Stability of elastic rods with self-contact. Comput. Methods Appl. Mech. Eng. 279, 227–246 (2014)
De Lorenzis, L., Evans, J., Hughes, T., Reali, A.: Isogeometric collocation: neumann boundary conditions and contact. Comput. Methods Appl. Mech. Eng. 284, 21–54 (2015). https://doi.org/10.1016/j.cma.2014.06.037
De Lorenzis, L., Wriggers, P., Hughes, T.J.: Isogeometric contact: a review. GAMM-Mitt. 37(1), 85–123 (2014)
Dewei, S., Cheng, L., Haiyan, H.: Dynamic computation of 2D segment-to-segment frictionless contact for a flexible multibody system subject to large deformation. Mech. Mach. Theory 140(2), 350–376 (2019)
Durvile, D.: Contact friction modeling within elastic beam assemblies: an application to knot tightening. Comput. Mech. 49(6), 687–707 (2012)
Durville, D.: Modelling of contact-friction interactions in entangled fibrous materials. In: VI World Wide Congress on Computational Mechanics, Beijing, China (2004)
Ebel, H., Matikainen, M.K., Hurskainen, V.V., Mikkola, A.: Higher-order beam elements based on the absolute nodal coordinate formulation for three-dimensional elasticity. Nonlinear Dyn. 88(2), 1075–1091 (2017). https://doi.org/10.1007/s11071-016-3296-x
Ebrahimi, M., Butscher, A., Cheong, H., Iorio, F.: Design optimization of dynamic flexible multibody systems using the discrete adjoint variable method. Comput. Struct. 213, 82–99 (2019)
Ericson, C.: Real-Time Collision Detection. Morgan Kaufmann Publishers, San Francisco (2004)
Gay Neto, A., Pimenta, P., Wriggers, P.: Self-contact modeling on beams experiencing loop formation. Comput. Mech. 55(1), 193–208 (2015)
Gerstmayr, J., Irschik, H.: On the correct representation of bending and axial deformation in the absolute nodal coordinate formulation with an elastic line approach. J. Sound Vib. 318(3), 461–487 (2008). https://doi.org/10.1016/j.jsv.2019.03.022
Gerstmayr, J., Matikainen, M., Mikkola, A.: A geometrically exact beam element based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 20(4), 359–384 (2008)
Haikal, G., Hjelmstad, K.D.: A finite element formulation of non-smooth contact based on oriented volumes for quadrilateral and hexahedral elements. Comput. Methods Appl. Mech Eng. 196, 4690–4711 (2007)
Harish, A.B., Wriggers, P.: Modeling of two-body abrasive wear of filled elastomers as a contact-induced fracture process. Tribol. Int. 138, 16–31 (2019)
Hughes, J.F., Van Dam, A., Foley, J.D., McGuire, M., Feiner, S.K., Sklar, D.F.: Computer Graphics: Principles and Practice. Pearson Education, London (2014)
Hunt, K., Crossley, E.: Coefficient of restitution interpreted as damping in vibroimpact. J. Appl. Mech. 7, 440–445 (1975)
Jelenic, G., Crisfield, M.: Geometrically exact 3d beam theory: implementation of a strain-invariant finite element for statics and dynamics. Comput. Methods Appl. Mech. Eng. 171(1–2), 141–171 (1999)
Khude, N., Stanciulescu, I., Melanz, D., Negrut, D.: Efficient parallel simulation of large flexible body systems with multiple contacts. J. Comput. Nonlinear Dyn. 8(4), 041003 (2013)
Klosowski, J.T., Held, J.M., Mitchell, J.S., Sowizral, H., Zikan, K.: Efficient collision detection using bounding volume hierarchies of k-dops. IEEE Trans. Vis. Comput. Graph. 4(1), 21–36 (1998)
Konyukhov, A., Schweizerhof, K.: On the solvability of closest point projection procedures in contact analysis: analysis and solution strategy for surfaces of arbitrary geometry. Comput. Methods Appl. Mech. Eng. 197(33), 3045–3056 (2008)
Konyukhov, A., Schweizerhof, K.: Geometrically exact covariant approach for contact between curves. Comput. Methods Appl. Mech. Eng. 199(37), 2510–2531 (2010)
Korkealaakso, P.M., Rouvinen, A.J., Moisio, S.M., Peusaari, J.K.: Development of a real-time simulation environment. Multibody Syst. Dyn. 17(2), 177–194 (2007)
Lee, G.B., Kwak, B.M.: Formulation and implementation of beam contact problems under large displacement by a mathematical programming. Comput. Struct. 31(3), 365–376 (1989)
Litewka, P.: The penalty and Lagrange multiplier methods in the frictional 3D beam-to-beam contact problem. Civil and Environmental Engineering Reports, pp. 189–207 (2005)
Łitewka, P.: Hermite polynomial smoothing in beam-to-beam frictional contact. Comput. Mech. 40(5), 815–826 (2007)
Łitewka, P.: Enhanced multiple-point beam-to-beam frictionless contact finite element. Comput. Mech. 52(6), 1365–1380 (2013)
Łitewka, P.: Frictional beam-to-beam multiple-point contact finite element. Comput. Mech. 56(2), 243–264 (2015)
Łitewka, P., Wriggers, P.: Contact between 3-D beams with rectangular cross-sections. Int. J. Numer. Methods Eng. 53(9), 2019–2041 (2002)
Łitewka, P., Wriggers, P.: Frictional contact between 3-D beams. Comput. Mech. 28(1), 26–39 (2002)
Matikainen, M.K., Dmitrochenko, O.: A study of three-node higher-order gradient beam elements based on the absolute nodal coordinate formulation. In: The 3rd Joint International Conference on Multibody System Dynamics. Busan, Korea (2014)
Matikainen, M.K., Dmitrochenko, O., Mikkola, A.: Beam elements with trapezoidal cross section deformation modes based on the absolute nodal coordinate formulation. In: International Conference of Numerical Analysis and Applied Mathematics, pp. 1266–1270. Rhodes, Greece (2010). https://doi.org/10.1063/1.3497930
Meier, C., Popp, A., Wall, W.A.: An objective 3D large deformation finite element formulation for geometrically ecaxt curved kirchhoff rods. Comput. Methods Appl. Mech. Eng. 278, 445–478 (2014)
Meier, C., Popp, A., Wall, W.A.: A finite element approach for the line-to-line contact interaction of thin beams with arbitrary orientation. Comput. Methods Appl. Mech. Eng. 308, 377–413 (2016)
Meier, C., Popp, A., Wall, W.A.: Geometrically exact finite element formulations for slender beams: Kirchhoff–Love theory versus simo-reissner theory. Arch. Comput. Methods Eng. 26, 163–243 (2017)
Meier, C., Popp, A., Wall, W.A.: A unified approach for beam-to-beam contact. Comput. Methods Appl. Mech. Eng. 315, 972–1010 (2017)
Nachbagauer, K., Gruber, P., Gerstmayr, J.: A 3D shear deformable finite element based on the absolute nodal coordinate formulation. In: Samin, J.C., Fisette, P. (eds.) Multibody System Dynamics, Computational Methods in Applied Sciences, pp. 77–96. Springer, Dordrecht (2013). https://doi.org/10.1007/978-94-007-5404-1_4
Nachbagauer, K., Pechstein, A.S., Irschik, H., Gerstmayr, J.: A new locking-free formulation for planar, shear deformable, linear and quadratic beam finite elements based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 26(3), 245–263 (2011)
Negrut, D., Serban, R., Tasora, A.: Posing multibody dynamics with friction and contact as a differential complementarity problem. J. Comput. Nonlinear Dyn. 13(1), 014503 (2017)
Neto, A.G., Wriggers, P.: Computing pointwise contact between bodies: a class of formulations based on master-master approach. Comput. Mech. 64(3), 585–609 (2019)
Neto, A.G., Wriggers, P.: Numerical method for solution of pointwise contact between surfaces. Comput. Methods Appl. Mech. Eng. 365, 112971 (2020)
Pang, J.S., Stewart, D.E.: Differential variational inequalities. Math. Program. 113(2), 345–424 (2008)
Pfeiffer, F., Glocker, C.: Multibody Dynamics with Unilateral Contacts. Wiley, New York (1996)
Puso, M.A., Laursen, T.: A mortar segment-to-segment contact method for large deformations solid elements. Comput. Methods Appl. Mech. Eng. 193, 601–629 (2003)
Puso, M.A., Laursen, T., Solberg, J.: A segment-to-segment mortar contact method for quadratic elements and large deformations. Comput. Methods Appl. Mech. Eng. 197(6), 555–566 (2008)
Reissner, E.: On one-dimensional finite strain beam theory: the plane problem. J. Appl. Math. Phys. 23(5), 795–804 (1972)
Romero, I.: A comparison of finite elements for nonlinear beams: the absolute nodal coordinate and geometrically exact formulations. Multibody Syst. Dyn. 20(1), 51–68 (2008). https://doi.org/10.1007/s11044-008-9105-7
Romero, I., Armero, F.: An objective finite element approximation of the kinematics of geometrically exact rods and its use in the formulation of an energy-momentum conserving scheme in dynamics. Int. J. Numer. Methods Eng. 54(12), 1683–1716 (2002). https://doi.org/10.1002/nme.486
Shabana, A.A.: Definition of the slopes and the finite element absolute nodal coordinate formulation. Multibody Syst. Dyn. 1(3), 339–348 (1997)
Shabana, A.A.: Flexible multibody dynamics: review of past and recent developments. Multibody Syst. Dyn. 1(2), 189–222 (1997)
Simo, J.: A finite strain beam formulation, the three-dimensional dynamic problem. Part I. Comput. Methods Appl. Mech. Eng. 49(1), 55–70 (1985)
Simo, J., Vu-Quoc, L.: On the dynamics of flexible beams under large overall motions-the plane case: I. J. Appl. Mech. 53(4), 849–854 (1986)
Simo, J., Vu-Quoc, L.: On the dynamics of flexible beams under large overall motions-the plane case: II. J. Appl. Mech. 53(4), 855–863 (1986)
Tasora, A., Anitescu, M.: A matrix-free cone complementarity approach for solving large-scale, nonsmooth, rigid body dynamics. Comput. Methods Appl. Mech. Eng. 200(5–8), 439–453 (2011)
Tasora, A., Benatti, S., Mangoni, D., Garziera, R.: A geometrically exact isogeometric beam for large displacements and contacts. Comput. Methods Appl. Mech. Eng. 358, 112635 (2020)
Tasora, A., Negrut, D., Anitescu, M.: Large-scale parallel multibody dynamics with frictional contact on the graphical processing unit. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 222(4), 315–326 (2008)
Tasora, A., Serban, R., Mazhar, H., Pazouki, A., Melanz, D., Fleischmann, J., Taylor, M., Sugiyama, H., Negrut, D.: Chrono: an open source multi-physics dynamics engine. In: Kozubek, T., Blaheta, R., Šístek, J., Rozložník, M., Čermák, M. (eds.) High Performance Computing in Science and Engineering, pp. 19–49. Springer, Cham (2016)
Weeger, O., Narayanan, B., De Lorenzis, L., Kiendl, J., Dunn, M.L.: An isogeometric collocation method for frictionless contact of cosserat rods. Comput. Methods Appl. Mech. Eng. 321, 361–382 (2017)
Wriggers, P.: Computational Contact Mechanics, 2nd edn. Springer, Berlin (2006)
Wriggers, P.: Nonlinear FInite Element Methods. Springer, Berlin (2008)
Wriggers, P., Zavarise, G.: On contact between three-dimensional beams undergoing large deflections. Commun. Numer. Methods Eng. 13(6), 429–438 (1997)
Yang, B.: Mortar Finite Element Methods for Large Deformation Contact Mechanics, 2nd edn. VDM Publishing, Saarbrücken (2009)
Yang, B., Laursen, T.A.: A contact searching algorithm including bounding volume trees applied to finite sliding mortar formulations. Comput. Mech. 41(2), 189–205 (2008)
Yang, B., Laursen, T.A., Meng, X.: Two dimensional mortar contact methods for large deformation frictional sliding. Int. J. Numer. Methods Eng. 62(9), 1183–1225 (2005)
Yu, X., Matikainen, M.K., Harish, A.B., Mikkola, A.: Procedure for non-smooth contact for planar flexible beams with cone complementarity problem. Proc. Inst. Mech. Eng. Part K J. Multibody Dyn. (2020). https://doi.org/10.1177/1464419320957450
Zavarise, G., Wriggers, P.: Contact with friction between beams in 3-D space. Int. J. Numer. Methods Eng. 49(8), 977–1006 (2000)
Zhong, Z.H., Nilsson, L.: A contact searching algorithm for general contact problems. Comput. Struct. 33(1), 197–209 (1989)
Acknowledgements
We would like to thank the Academy of Finland (Application No. 299033 for funding of Academy Research Fellow) for supporting Marko K. Matikainen.
Funding
Open access funding provided by LUT University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bozorgmehri, B., Yu, X., Matikainen, M.K. et al. A study of contact methods in the application of large deformation dynamics in self-contact beam. Nonlinear Dyn 103, 581–616 (2021). https://doi.org/10.1007/s11071-020-05984-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-020-05984-x