Skip to main content
SpringerLink
Log in

Improving the predictable accuracy of fluid Galerkin reduced-order models using two POD bases

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

A fundamental limitation of fluid flow reduced-order models (ROMs) which utilize the proper orthogonal decomposition is that there is little capability to determine one’s confidence in the fidelity of the ROM a priori. One reason why fluid ROMs are plagued by this issue is that nonlinear fluid flows are fundamentally multi-scale, often chaotic dynamical systems and a single linear spatial basis, however carefully selected, is incapable of ensuring that these characteristics are captured. In this paper, the velocity and the velocity gradient were decomposed using differently optimized linear bases. This enabled an optimization for several dynamically significant flow characteristics within the modal bases. This was accomplished while still ensuring the resulting model is accurate and without iterative methods for constructing the modal bases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. Many models of course do not reside exclusively in one category or another; a researcher’s goals in using a model are often just as important as the model itself when identifying an approach in this context.

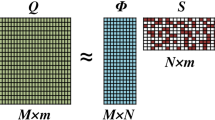
  2. Repeated indices denote summation throughout this paper; subscript indices reference modal sums and superscript indices reference spatial inner products.

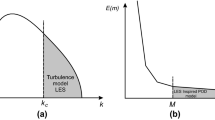
  3. Important characteristics of time, ensemble averages and the provided signal are not elaborated upon here; they are explored in detail in the literature [3, 14].

  4. The authors recognize the important differences between 2D and 3D turbulence and therefore refer to the flow as chaotic, in which it is known to be in a formal sense. One commonality between 2D and 3D turbulence is the cross-scale energy transfer; this characteristic is what is captured better in the two-basis POD approach and a 2D chaotic flow is therefore an adequate test case.

  5. The authors again nod to the SPOD and its capability to organize modes by frequency; the time-average-based POD modes in this and much existing work each present several frequencies, though their individual coherence is dynamically meaningful in other ways.

  6. The inclusion of this \(\epsilon \) term was found to modestly but notably improve the accuracy of the ROMs, especially at higher Reynolds numbers.

  7. The velocity gradient norm is still a global norm and thus does not ideally focus on exclusively on small-scale dynamics, but it is an improvement at identifying small scales relative to the energy norm.

  8. As has been discussed, the velocity gradient and the enstrophy norms are qualitatively comparable, albeit not identical.

References

  1. Pope, S.B.: Turbulent Flows. Cambridge University Press, Cambridge (2000)

    Book  MATH  Google Scholar 

  2. Kraichnan, R.H.: Direct-interaction approximation for shear and thermally driven turbulence. Phys. Fluids 7(7), 1048–1062 (1964)

    Article  MathSciNet  Google Scholar 

  3. Berkooz, G., Holmes, P., Lumley, J.L.: The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575 (1993)

    Article  MathSciNet  Google Scholar 

  4. Holmes, P., Berkooz, G., Lumley, J.L.: Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press, Cambridge (1996)

    Book  MATH  Google Scholar 

  5. Tu, J.H., Rowley, C.W., Luchtenburg, D.M., Brunton, S.L., Kutz, J.N.: On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1(2), 391–421 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kida, S., Goto, S.: A Lagrangian direct-interaction approximation for homogeneous isotropic turbulence. J. Fluid Mech. 345, 307–345 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bazilevs, Y., Calo, V.M., Cottrell, J.A., Hughes, T.J.R., Reali, A., Scovazzi, G.: Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Comput. Methods Appl. Mech. Eng. 197(1–4), 173–201 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hughes, T.J.R., Scovazzi, G., Franca, L.P.: Multiscale and stabilized methods. In: Stein, E., de Borst, R., Hughes, T.J. (eds.) Encyclopedia of Computational Mechanics, 2nd edn, pp. 1–64. Wiley, Chichester (2017)

    Google Scholar 

  9. Taira, K., Brunton, S.L., Dawson, S.T.M., Rowley, C.W., Colonius, T., McKeon, B.J., Schmidt, O.T., Gordeyev, S., Theofilis, V., Ukeiley, L.S.: Modal analysis of fluid flows: an overview. AIAA J. 55(12), 4013–4041 (2017)

    Article  Google Scholar 

  10. Iollo, A., Dervieux, A., Désidéri, J.A., Lanteri, S.: Two stable POD-based approximations to the Navier-Stokes equations. In: Wittum, G. (ed.) Computing and Visualization in Science, vol. 3, pp. 61–66. Springer, Berlin (2000)

    Google Scholar 

  11. Östh, J., Noack, B.R., Krajnović, S., Barros, D., Borée, J.: On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J. Fluid Mech. 747(3), 518–544 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Grimberg, S., Farhat, C., Youkilis, N.: On the stability of projection-based model order reduction for convection-dominated laminar and turbulent flows (2020). arXiv preprint

  13. Loève, M.: Probability Theory. Springer, Princeton (1955)

    MATH  Google Scholar 

  14. Lumley, J.L.: The structure of inhomogeneous turbulent flows. In: Yaglom, A.M., Tatarsky, V.I. (eds.) Atmospheric Turbulence and Radio Wave Propagation, pp. 166–178. Nauka, Moscow (1967)

    Google Scholar 

  15. Dowell, E.H., Tang, D.: Dynamics of Very High Dimensional Systems. World Scientific Publishing Company, Singapore (2003)

    Book  Google Scholar 

  16. Kerschen, G., Golinval, J., Vakakis, A.F., Bergman, L.A.: The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: an overview. Nonlinear Dyn. 41, 147–169 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  17. Liang, Y.C., Lee, H.P., Lim, S.P., Lin, W.Z., Lee, K.H., Wu, C.G.: Proper orthogonal decomposition and its applications—part 1: theory. J. Sound Vib. 252(3), 527–544 (2002)

    Article  MATH  Google Scholar 

  18. Balajewicz, M.J., Dowell, E.H., Noack, B.R.: Low-dimensional modelling of high-Reynolds-number shear flows incorporating constraints from the Navier–Stokes equation. J. Fluid Mech. 729, 285–308 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ravindran, S.S.: A reduced-order approach for optimal control of fluids using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 34(5), 425–448 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  20. Sirovich, L., Rodriguez, J.D.: Coherent structures and chaos: a model problem. Phys. Lett. A 120(5), 211–214 (1987)

    Article  MathSciNet  Google Scholar 

  21. Noack, B.R., Papas, P., Monkewitz, P.A.: The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 523, 339–365 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  22. Rowley, C.W., Colonius, T., Murray, R.M.: POD based models of self-sustained oscillations in the flow past an open cavity. In: 6th Aeroacoustics Conference and Exhibit (2000)

  23. Stabile, G., Hijazi, S., Mola, A., Lorenzi, S., Rozza, G.: POD-Galerkin reduced order methods for CFD using finite volume discretisation: vortex shedding around a circular cylinder. Commun. Appl. Ind. Math. 8(1), 210–236 (2017)

    MathSciNet  MATH  Google Scholar 

  24. Dowell, E.H., Hall, K.C.: Modeling of fluid-structure interaction. Annu. Rev. Fluid Mech. 33(1), 445–490 (2001)

    Article  MATH  Google Scholar 

  25. Smith, T.R., Moehlis, J., Holmes, P.: Low-dimensional modelling of turbulence using the proper orthogonal decomposition: a tutorial. Nonlinear Dyn. 41(1–3), 275–307 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  26. Lee, M., Dowell, E.: Fluid Galerkin reduced-order models: computational efficiency and sensitivity to methods of flow decomposition. Comput. Fluids (2020). A preprint is available at https://www.researchgate.net/publication/340849510_Fluid_Galerkin_Reducedorder_Models_Computational_Efficiency_and_Sensitivity_to_Methods_of_Flow_Decomposition

  27. Johnston, H., Liu, J.G.: Accurate, stable and efficient Navier–Stokes solvers based on explicit treatment of the pressure term. J. Comput. Phys. 199(1), 221–259 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  28. Picard, C., Delville, J.: Pressure velocity coupling in a subsonic round jet. Int. J. Heat Fluid Flow 21(3), 359–364 (2000)

    Article  Google Scholar 

  29. Towne, A., Schmidt, O.T., Colonius, T.: Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  30. Shen, J.: Hopf bifurcation of the unsteady regularized driven cavity flow. J. Comput. Phys. 95(1), 228–245 (1991)

    Article  MATH  Google Scholar 

  31. Shankar, P.N., Deshpande, M.D.: Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32, 93–136 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  32. Lee, M.W., Dowell, E.H., Balajewicz, M.J.: A study of the regularized lid-driven cavity’s progression to chaos. Commun. Nonlinear Sci. Numer. Simul. 71, 50–72 (2019)

    Article  MathSciNet  Google Scholar 

  33. Gollub, J.P., Swinney, H.L.: Onset of turbulence in a rotating fluid. Phys. Rev. Lett. 35(14), 927–930 (1975)

    Article  Google Scholar 

  34. Albeverio, S., Cruzeiro, A.B.: Global flows with invariant (Gibbs) measures for Euler and Navier–Stokes two dimensional fluids. Commun. Math. Phys. 129(3), 431–444 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  35. Dascaliuc, R., Foias, C., Jolly, M.S.: Estimates on enstrophy, palinstrophy, and invariant measures for 2-D turbulence. J. Differ. Equ. 248(4), 792–819 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  36. Liakopoulos, A., Blythe, P.A., Gunes, H.: A reduced dynamical model of convective flows in tall laterally heated cavities. Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 453(1958), 663–672 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  37. Gunes, H., Liakopoulos, A., Sahan, R.A.: Low-dimensional description of oscillatory thermal convection: the small prandtl number limit. Theoret. Comput. Fluid Dyn. 9(1), 1–16 (1997)

    Article  MATH  Google Scholar 

  38. Kostas, J., Soria, J., Chong, M.S.: A comparison between snapshot POD analysis of PIV velocity and vorticity data. Exp. Fluids 38(2), 146–160 (2005)

    Article  Google Scholar 

  39. Richardson, L.F.: The supply of energy from and to atmospheric eddies. Proc. R. Soc. Lond. 97(686), 345–373 (1920)

    Google Scholar 

  40. Kolmogorov, A.N.: On the degeneration of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 31(6), 319–323 (1941)

    Google Scholar 

Download references

Acknowledgements

The authors extend their appreciation to A. Bragg, H. Gavin, K. Hall, B. Mann, M. Balajewicz, and T. Witelski for their insight and counsel. The first author is supported by NSF Grant DGE-1644868.

Author information

Authors and Affiliations

  1. Duke University, 144 Hudson Hall, Durham, NC, 27708, USA

    Michael W. Lee & Earl H. Dowell

Authors
  1. Michael W. Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Earl H. Dowell
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael W. Lee.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lee, M.W., Dowell, E.H. Improving the predictable accuracy of fluid Galerkin reduced-order models using two POD bases. Nonlinear Dyn 101, 1457–1471 (2020). https://doi.org/10.1007/s11071-020-05833-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05833-x

Keywords

Search

Navigation