1 Introduction

With the introduction of useful computer software focused on solving dynamic problems, many researchers focused on identifying and predicting the behavior of various dynamic objects. These include double pendulums with torsional friction. Scientific research is based on a relatively simple theory of friction, describing this phenomenon in the contact zone between the surfaces of two bodies existing in nature. In this context, two main types of friction should be distinguished, i.e., the static and kinetic friction. Their occurrence depends on the phase of movement of interacting bodies. In dynamic systems, such as pendulums, friction has a structural form with energy dispersion, which is directly related to the contact surface properties and range of motion. Nevertheless, friction can be analyzed in both solids and liquids by testing for mechanical energy losses [1,2,3].

Looking at the history of the development of the description of the phenomenon of friction, one of the first models of full friction was developed by Coulomb. The author stated that static friction is not constant and causes kinetic friction fluctuations. In recent decades, based on this statement, engineering practice has developed various friction laws. One of the most important laws is related to the concept of viscous friction, the Stribeck effect and related phenomena occurring even in torsional vibrations with dry friction [2].

On the basis of several scientific publications presented below, the mathematical description of the real torsion pendulum with friction and other nonlinear phenomena was experimentally verified. Similarly to the study presented by Skup [4], in the first step, several basic aspects of the research were defined. It began with an analysis of the dynamics of a torsion pendulum with friction with two degrees of freedom and external forcing.

Deriving a more realistic dynamic model is an essential part of the semiempirical methodology. In the work by Bassian et al. [5], the existence of unpredictable forms of dynamic changes, existing in experimental tests and being not reflected in numerical modeling was emphasized. A mechanical model of the torsion pendulum was developed taking into account geometric imperfections, which allowed to continue the study of a number of unrecognized system properties related to pendulum motion and resonance.

One of the most significant dynamic models was developed by Miao et al. [6]. The work reproduces the dynamics of the torsion pendulum with kinematic excitation and depicts the bifurcation of vibrations with doubling of the period, transforming into chaotic vibrations. This demonstrates the unpredictable dynamics of behavior of this type of systems and the strongly nonlinear nature of mechanical vibrations. The mentioned article presents irregular transitions between various dynamic responses of the examined system.

A slightly different methodology for identifying and validating the parameters of the dynamic model was proposed by De Marchi et al. [7]. In the cited work, an eight-degree-of-freedom system derived using the Lagrange method was considered. The correct identification of friction forces was obtained that is directly related to the material and geometry of the contact zone in the tested torsion pendulum model. Based on the work of Coullet et al. [8], a kinematic excitation was introduced, where the dynamics of relative motion changes in the inverted pendulum was conditioned by sudden changes in acceleration caused by a torsion spiral spring [2].

Free and forced oscillation of the pendulum with a torsion spring, suppressed by dry and viscous Coulomb friction, was tested by Butikov [9]. The analytical methods were supported by a computer simulation. An idealized mathematical model of dry friction described by the so-called Z characteristics was adopted. The sinusoidal form of excitation of the pendulum with dry friction allowed to observe the linearly increasing amplitude of forced vibrations. The increase was unlimited if the system was in resonance after exceeding a certain value of forcing frequency. With sufficiently strong non-resonant sinusoidal excitation, dry friction caused a transient behavior, which usually, regardless of the initial conditions, led to a periodic steady-state symmetrical forced vibrations, but without any stick–slip behavior. However, assuming special conditioning of motion, the pendulum with dry friction showed complex stick–slip vibrations [10].

Impacts having an impulse character that were introduced in this work into the torsion pendulum with friction have various applications in many branches of modern industry. One of the most common applications relates to the torsional motion dynamics with impacts used in large drilling machines. Solutions to dynamic problems occurring in these systems are difficult to obtain and depend on various theories of nonlinear dynamics. For example, the stick–slip effect initiating the failure of drill-strings can be mentioned [11,12,13,14]. Further occurrence of impacts includes vibrations in steering systems of motor vehicles, which significantly affect driving comfort and safety aspects [15, 16] and microelectromechanical systems as well [17]. Recently, there is a growing interest in the use of modeling of impact phenomena in rotary elements of wind turbines, as well as the movement of parts of manipulators used in the transport industry [18].

The dynamical system studied in this work may also have other interesting applications from the borderline of textile metrology and biology—mainly in models that meet all the necessary conditions tailored to the dynamics of hybrids of such systems. Torsional movement devices with impulse vibration are also used to identify and simulate the rigidity of hemp fibers during torsion with the analysis of the influence of chemical treatment. The dynamic effects associated with vibrations during torsion have an impact on the stiffness of hemp fibers [19].

Moreover, the phenomenon of coupling of torsion pendulums at the microscopic level is subjected to torsional DNA dynamics. Here, the effects of nonlinear dynamics are key for studying the features and properties of the DNA structure [2, 20].

2 A physical model of the double torsion pendulum with friction and elastic barriers

The following part of the article is dedicated to an overall description of the investigated test stand. Figure 1 depicts the double torsion pendulum with electronics, barrier systems and an excitation mechanism powered by a stepper motor installed below the base plate. The presented construction is built as a torsion pendulum having two degrees of freedom about one common vertical axis of rotation of both system bodies. The applied vertical gravitational connection of both bodies gives the possibility to place a free disk body on the upper mounting ring (head) of the column. This way, a planar rotational friction contact is made; see red line in Fig. 4. The movement of the pendulum column depends on the dynamics and friction interface between the two contacting bodies, significantly influencing a rotational motion of the free disk’s body. The lower segment of the sleeve is joined with a movable cam supported by the torsional spiral spring that is designed as a bar spring (see in Fig. 4 an axial mounting below the rolling bearing).

Fig. 1
figure 1

An isometric view of the experimental double torsion pendulum presenting the physical model with barriers and electronics, where a stepper motor with driver is mounted under the base plate and drives the cam. The generalized coordinates \( \varphi_{1} \), \( \varphi_{2} \), as well as mass moments of inertia \( B_{1} \), \( B_{2} \) of the sleeve disk and the column are marked

Full size image
Fig. 2
figure 2

A side view of the very stiff barrier system and the kinematic forcing mechanism of the column

Full size image
Fig. 3
figure 3

A top view of the stand with the soft elastic barrier system of the free disk body of the investigated double torsion pendulum (a); view of the upper disk (\( B_{2} \)) after removal from the column’s head (two magnets fixed to the disk from inner side rotate about the Hall-effect sensor). (Color figure online)

Full size image
Fig. 4
figure 4

Physical model for the derivation of the mathematical model (c.m.—center of mass rotating about the vertical axis). (Color figure online)

Full size image

The kinematic forcing, including the mentioned spiral spring and also connecting the sliding disk with the upper ring of the column, activates the pendulum’s torsional dynamics measured by the vector of angles \( \varvec{q} = \left[ {\varphi_{1} \;\;\varphi_{2} } \right]^{\text{T}} \)—general coordinates. The device is also equipped with a ball bearing which allows for rotations of the column. It significantly reduces frictional resistance of the rotational motion. Considering the detailed visualization of the pendulum, the particular isometric view, including the numbered individual elements, is presented in Fig. 2. Starting from the bottom, the whole mechatronic structure is placed on the base plate on which the pendulum’s assembly is mounted.

The magnets shown in Fig. 3b generate a rotating magnetic field that is sensed by the Hall-effect sensor, the voltage readings of which are transformed into the angular positions accordingly to the experimentally identified sensor characteristics. The same method of a direct contactless measurement is applied for estimation of rotational motion of both system bodies, i.e., the column (denoted by \( \varphi_{1} \)) and the free disk body (denoted by \( \varphi_{2} \)).

Another significant part of the construction is related to the mechanism of kinematic forcing of the column presented in Fig. 2. The components labeled with numbers 1–6 consider the stepper motor with the attachment of a cam (5), while transmission of movement is realized by the connection of the motor’s shaft directly with the cam. The resulting motion of the arm (1) through the intermediate pin (4, translating linearly with respect to the gutter of arm 1) is driven by the described connection. The axis of the fastening pin (3) in the construction’s base (2) determines the point of rotation. The last element is the roller (6) working as a connector between the end of the mechanism’s arm and the end of the spiral spring connecting it with the column at the other end (see Fig. 4).

The final stage of the assembly required to design the systems blocking angular movements of both bodies, i.e., the column and the free body. Figure 3 shows the elastic blocking system of the upper free disk body of the pendulum realized by two beam springs of low stiffness. The two symmetric elements are made of plastic.

A more rigid mechanism for the restriction of column’s rotations shown in Fig. 2 is made of wood. The final model design of the unique experimental stand, shown in Fig. 1, fulfills all the considerations of the work, since the aim of this study will be to investigate the behavior of the free disk of double torsion pendulum with friction. A small-angle relative rotations in frictional contact mainly exhibit an interesting stick–slip dynamics of the disk, but also the second blocking mechanism of the column allows us to investigate the impulsive form of a transitory—periodically appearing elastic impact response.

3 Initial mathematical model of the double torsion pendulum with friction and elastic barriers

The topic of identification of elastic springs in the form of hit beams is not deeply explored, but one could mention an experimental system identification of the dynamics of a vibro-impact beam [21] or a survey [22], addressing a nonlinear system identification provided by discussing the central role played by the experimental models in the design cycle of engineering structures.

Our study is focused on a double torsion pendulum with friction and a kinematically excited column shown on the physical model in Fig. 4.

A device realizing that forcing provides a sinusoidal excitation of the spiral spring attached to the main column. A second flat disk body is positioned onto the first one, which introduces the frictional rotational planar contact and the second degree of freedom of the system. The study continues some aspects initiated in [2]. The main point is now related to an implementation of the proper mathematical model, which will represent the dynamical behavior of the pendulum. In Fig. 1, we define two-state variables \( \varphi_{1} \) and \( \varphi_{2} \) that constitute the vector of generalized coordinates

$$ \varvec{q} = \left[ {\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varphi_{1} } \\ {\varphi_{2} } \\ \end{array} } \right], $$
(1)

where \( q_{1} = \varphi_{1} \) (rad) is the angular displacement of the pendulum column relative to its base, and \( q_{2} = \varphi_{2} \) (rad) is the angular displacement of the free body relative to the column. The zero angle of the column is determined by the equilibrium position of the kinematically forced end of the spiral spring, which is attached at the center of the hollow bore’s opening in the construction base (see Figs. 1, 4). Existence of soft interaction of the two elastic beam springs fixed to the flat upper mounting ring of the column (see Fig. 1) with the tip fixed to the rotating disk (see Fig. 3) is taken into account. Then, in Sect. 3.2, the most appropriate models of barriers restricting rotational motion of both system bodies are introduced into the mathematical model. Hereafter, the term “contact zone” denotes a plane frictional contact interface (the main coupling) between the pendulum’s bodies of inertia B1 and B2.

3.1 Mathematical derivation of the double torsion pendulum model using the Lagrange method

Firstly, the kinetic energy of the double torsion pendulum is given by

$$ T = \frac{1}{2}B_{1} \dot{\varphi }_{1}^{2} + \frac{1 }{2}B_{2} \left( {\dot{\varphi }_{1} + \dot{\varphi }_{2} } \right)^{2} , $$
(2)

where \( B_{1} \) (kg m2) is the total mass moment of inertia of the pendulum column (a sleeve with the lower ring for placing the column in the ball bearing, and with the upper one, for realization of the contact surface with the free body of a disk shape), \( B_{2} \) (kg m2) stands for the mass moment of inertia of the free disk body.

Potential energy accumulated by elastic elements is given in the following form

$$ V = \frac{1 }{2}\kappa_{1} \varphi_{\text{f}}^{2} + \frac{1}{4}\kappa_{2} \varphi_{\text{f}}^{4} + \frac{1}{2}k_{1} \left( { - \varphi_{1}^{d} } \right)^{2} + \frac{1}{2}k_{2} \left( { - \varphi_{2}^{d} } \right)^{2} , $$
(3)

where \( \varphi_{\text{f}} (t) = f_{\text{e}} (t) - \varphi_{1} (t) \) and, respectively, \( \kappa_{1} \), \( \kappa_{2} \) (N m/rad) are the coefficients at linear and nonlinear terms of stiffness characteristics (symmetric along free length) of the torsional spiral spring, connecting the column and the arm of the excitation mechanism (see element 6 in Figs. 1, 2) [23]; \( k_{1} \) (N m/rad) is the coefficient of stiffness of the elastic contact modeled by a Voigt element that is created temporarily (to be turned on/off during/after contacts with barrier, see Fig. 2) at the bracket boundaries by a “pin barrier” and the wooden bracket arms attached to the column (see Fig. 2); \( k_{2} \) (N m/rad) is the coefficient of stiffness of two symmetric beam springs attached to the upper disk fixed on top of the column of inertia \( B_{1} \) and the tip fixed to the disk of inertia \( B_{2} \); \( f_{\text{e}} (t) = A\sin (\omega t + \phi ) \) is the function of the sinusoidal kinematic forcing coming from the external excitation mechanism of the first end of the torsional spiral spring; A (rad) denotes the amplitude of forcing, ω (rad/s) is the angular frequency, \( \phi \) is the phase shift (rad).

Moreover, the conditional presence of the time-dependent terms \( \varphi_{1}^{d} \) or \( \varphi_{2}^{d} \), appearing after hitting both pendulum barriers at \( \varphi_{i}^{s} \), for \( i = 1,2 \), respectively, is defined

$$ \varphi_{i}^{d} = \left\{ {\begin{array}{*{20}l} {{\text{sign}}\left( {\varphi_{i} } \right)\left( {\left| {\varphi_{i} } \right| - \varphi_{i}^{s} } \right)} \hfill & {{\text{if}}\;\left| {\varphi_{i} } \right| \ge \varphi_{i}^{s} ,} \hfill \\ 0 \hfill & {{\text{if}}\;\left| {\varphi_{i} } \right| < \varphi_{i}^{s} ,} \hfill \\ \end{array} } \right. $$
(4)

where \( \varphi_{i}^{s} > 0 \) are the given constant angles at which both elastic pendulum barriers modeled by Voigt elements have been placed. The first barrier, shown in Fig. 2, which restricts motion of the first pendulum body (a column), is marked by a pin barrier interacting during elastic impacts with the wooden bracket. It has large stiffness and small damping properties. The second barrier, composed of a fixed tip rotating between two beam springs (fixed at a constant distance to each other), is attached to the moving column softly and it restricts motion of the disk (a free body shown in Fig. 3). It has low stiffness and damping properties.

Before any mathematical model can be proposed, the vector \( \varvec{Q} \), denoting the generalized forces, is to be defined as follows

$$ \varvec{Q} = \left[ {\begin{array}{*{20}c} {Q_{1} } \\ {Q_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - M_{L} + M_{T} } \\ { - M_{T} } \\ \end{array} } \right], $$
(5)

where \( M_{L} \) (N m)—Coulomb static friction torque of the dry frictional resistance of the bearing, in which the first pendulum body, corresponding to the column is mounted, \( M_{T} \) (N m)—the frictional resistance torque between both pendulum bodies of inertia B1 and B2. We assume that the frictional resistance torque of the column depends on both, the viscous friction torque \( T_{\text{v1}} \dot{\varphi }_{1} \) and the maximum static friction torque \( {\text{sign}}\left( {\dot{\varphi }_{1} } \right)T_{\text{s1}} \), expressing the Coulomb friction—both acting in the contact zone [17]. Moreover, the discontinuity introduced by the dry friction Coulomb model is smoothened by the trigonometric function arctg as follows

$$ {\text{sign}}\left( {\dot{\varphi }_{1} } \right)T_{\text{s1}} \approx \frac{2}{\pi }{\text{arctg}}\left( {\varepsilon \dot{\varphi }_{1} } \right)T_{\text{s1}} , $$
(6)

which applies an approximation of the function \( {\text{sgn}}\left( {\dot{\varphi }_{1} } \right) \) of the sign of the angular velocity \( \dot{\varphi }_{1} \) of the column [1]. The smoothing has been applied to include some type of reality in the modeling. We get an additional parameter to tune if necessary, where the two observations appear: putting \( \varepsilon \) high we still numerically get an almost step increase, when comparing to the speed of the overall system dynamics; numerical integration in Scilab is seen to be much stable, since we sometimes observed, that using only a pure step functions can lead to unpredictable unstable solutions, smoothing of which has allowed to correct it. From the other side, the very ideal step of friction torque does not exist in reality, being assumed in this work as of an inertial increase (decrease) that appears after applying Eq. (6). We also consider the rolling resistance of motion of the ball bearing at the base of the column. For low velocity of motion of the bearing, the following constant torque is approximated

$$ T_{b} = \frac{{m g \mu D_{m} }}{2}, $$
(7)

where \( m \) (kg)—total mass of the column, \( g \) (m/s2)—the gravity constant, \( \mu \) (–)—the coefficient of rolling friction in the ball bearing, and \( D_{m} \) (m)—the average diameter between the internal and external diameters of the bearing, see Fig. 2. Then, we obtain the following first-stage expression for the first frictional resistance torque

$$ M_{L} \left( {\dot{\varphi }_{1} } \right) = T_{\text{v1}} \dot{\varphi }_{1} + T_{\text{s1}} \frac{2}{\pi }{\text{arctg}}\left( {\varepsilon_{1} \dot{\varphi }_{1} } \right) + {\text{sign}}\left( {\dot{\varphi }_{1} } \right)T_{b} , $$
(8)

where for the first frictional contact: \( T_{\text{v1}} \) (N m s/rad)—the coefficient of viscous friction in ball bearing, \( T_{\text{s1}} \) (N m)—maximum torque of static friction of the bearing, \( \varepsilon_{1} \) (s/rad) denotes the parameter determining accuracy of smoothing of mean Coulomb static friction torque acting in the bearing’s rotational contact surface.

It is worth noticing that the bearing is free of grease and we also assume that the friction can appear during changes in the direction of rotation of the column. The frictional resistance torque between bodies of inertia B1 and B2 depends on the viscous friction torque \( T_{\text{v2}} \dot{\varphi }_{2} \) and the smoothened relation for the Coulomb friction torque expressed by the formula

$$ {\text{sign}}\left( {\dot{\varphi }_{2} } \right)T_{\text{s2}} \approx \frac{2}{\pi }T_{\text{s2}} {\text{arctg}}\left( {\varepsilon_{2} \dot{\varphi }_{2} } \right). $$
(9)

We define

$$ M_{T} \left( {\dot{\varphi }_{2} } \right) = T_{\text{v2}} \dot{\varphi }_{2} + \frac{2}{\pi }T_{\text{s2}} {\text{arctg}}\left( {\varepsilon_{2} \dot{\varphi }_{2} } \right), $$
(10)

where for the second frictional contact: \( T_{\text{v2}} \) (N m s/rad)—the viscous friction coefficient, \( T_{\text{s2}} \) (N m)—the maximum static friction torque, \( \varepsilon_{2} \) (s/rad) denotes the parameter determining accuracy of smoothing of the Coulomb static friction torque, acting in the planar rotational frictional contact (see Fig. 1).

Bearing in mind Eqs. (8) and (10), the static friction parameters maximum values are usually greater than the kinetic friction parameters, but we intend to apply the most simple model of friction to reduce the number of parameters to identify. We assume also that both terms in Eq. (10) will sufficiently well capture the frictional behavior of the rotational frictional contact of the disk.

Expressing the kinetic and potential energy in the generalized coordinate system, the Lagrange function \( L \) is defined as the difference of the kinetic \( T \) and the potential energy \( V \)

$$ L = T - V, $$
(11)

where substitution of Eqs. (2) and (3) leads to the Lagrangian

$$ L = \frac{1}{2}B_{1} \dot{\varphi }_{1}^{2} + \frac{1 }{2}B_{2} \left( {\dot{\varphi }_{1} + \dot{\varphi }_{2} } \right)^{2} - \frac{1 }{2}\kappa_{1} \varphi_{\text{f}}^{2} - \frac{1}{4}\kappa_{2} \varphi_{\text{f}}^{4} - \frac{1}{2}k_{1} \left( { - \varphi_{1}^{d} } \right)^{2} - \frac{1}{2}k_{2} \left( { - \varphi_{2}^{d} } \right)^{2} . $$
(12)

Then, for the conservative system and the Lagrangian \( L \) with the presence of generalized forces

$$ \frac{\text{d}}{{{\text{d}}t}}\left( {\frac{ \partial L }{{\partial \dot{q}_{i} }}} \right) - \frac{\partial L }{{\partial q_{i} }} + \frac{ \partial D }{{\partial \dot{q}_{i} }} = Q_{i} ,\quad {\text{for}}\;\;i = 1,2, $$
(13)

where \( Q_{i} \) [ith component of \( \varvec{Q} \) in Eq. (5)] is understood to be the reminder of the \( i \)th generalized force when viscous damping of motion in both directions, after the elastic impacts with two barriers (see Figs. 2, 4) of the pendulum’s bodies, is accounted for with the Rayleigh dissipation function of the form

$$ D\left( {\dot{\varphi }_{1} ,\dot{\varphi }_{2} } \right) = \frac{1}{2}c_{1} \left( {\frac{{{\text{d}}\varphi_{1}^{d} }}{{{\text{d}}t}}} \right)^{2} + \frac{1}{2}c_{2} \left( {\frac{{{\text{d}}\varphi_{2}^{d} }}{{{\text{d}}t}}} \right)^{2} , $$
(14)

where the conditional presence of \( \varphi_{i}^{d} \), for \( i = 1,2 \), is defined by Eq. (4); \( c_{1} \) is the coefficient of linear damping of the connection between the column bracket and the pin barrier (see Fig. 2); adequately, \( c_{2} \) exists between the beam springs characterized by some small damping as well and the tip fixed to the rotating disk (see Fig. 3). The form of an isotropic nonlinear damping of motion of the rotating (vibrating) body studied in [24] is worth further attention. Moreover, some conditional presence of the time-dependent derivatives \( \dot{\varphi }_{i}^{d} \) appearing in the model discontinuously just after hitting both pendulum barriers at \( \varphi_{i}^{s} \), for \( i = 1,2 \), is defined

$$ \dot{\varphi }_{i}^{d} = \left\{ {\begin{array}{*{20}l} {{\text{sign}}\left( {\varphi_{i} } \right)\frac{{{\text{d}}\left( {\left| {\varphi_{i} } \right| - \varphi_{i}^{s} } \right)}}{{{\text{d}}t}} } \hfill & {{\text{if}}\;\left| {\varphi_{i} } \right| \ge \varphi_{i}^{s} ,} \hfill \\ 0 \hfill & {{\text{if}}\;\left| {\varphi_{i} } \right| < \varphi_{i}^{s} .} \hfill \\ \end{array} } \right. $$
(15)

The first second-order differential equation for the general coordinate \( \varphi_{1} \) is found from Eq. (13), for \( i = 1 \), by calculating the partial and ordinary derivatives with respect to time, obtaining the following result

$$ B_{1} \frac{{{\text{d}}^{2} \varphi_{1} }}{{{\text{d}}t^{2} }} + B_{2} \left( {\frac{{{\text{d}}^{2} \varphi_{1} }}{{{\text{d}}t^{2} }} + \frac{{{\text{d}}^{2} \varphi_{2} }}{{{\text{d}}t^{2} }}} \right) + k_{1} \varphi_{1}^{d} + c_{1} \frac{{{\text{d}}\varphi_{1}^{d} }}{{{\text{d}}t}} - f_{s} (t) = - M_{L} + M_{T} , $$
(16)

with some conditional presence of the state variables \( \varphi_{1}^{d} \), defined by Eq. (4) and \( \dot{\varphi }_{1}^{d} \), defined by Eq. (15), both for \( i = 1 \) and the nonlinear stiffness characteristics of the spiral spring \( f_{s} (t) = \kappa_{1} \varphi_{\text{f}} + \kappa_{2} \varphi_{\text{f}}^{3} \).

Substituting \( i = 2 \) in Eqs. (13) and (14), and taking the Lagrange equation for the coordinate \( \varphi_{2} \) from Eq. (12), the partial and ordinary derivatives are similarly calculated to obtain the second differential equation of second order

$$ B_{2} \left( {\frac{{{\text{d}}^{2} \varphi_{1} }}{{{\text{d}}t^{2} }} + \frac{{{\text{d}}^{2} \varphi_{2} }}{{{\text{d}}t^{2} }}} \right) + k_{2} \varphi_{2}^{d} + c_{2} \frac{{{\text{d}}\varphi_{2}^{d} }}{{{\text{d}}t}} = - M_{T} . $$
(17)

Again, a conditional presence of the state variables \( \varphi_{2}^{d} \), defined by Eq. (4) and \( \dot{\varphi }_{2}^{d} \), by Eq. (15), appears for \( i = 2 \).

The double torsion pendulum with a plane frictional contact together with an elastic reaction moments of forces between bodies is represented by the two-degree-of-freedom dynamical system and described by the general system of two second-order ordinary differential equations:

$$ \left\{ {\begin{array}{*{20}l} {B_{1} \frac{{{\text{d}}^{2} \varphi_{1} }}{{{\text{d}}t^{2} }} + k_{1} \varphi_{1}^{d} + c_{1} \frac{{{\text{d}}\varphi_{1}^{d} }}{{{\text{d}}t}} - \kappa_{1} \varphi_{\text{f}} - \kappa_{2} \varphi_{\text{f}}^{3} - k_{2} \varphi_{2}^{d} } \hfill \\ {\quad - \,c_{2} \frac{{{\text{d}}\varphi_{2}^{d} }}{{{\text{d}}t}} = - M_{L} + 2M_{T} ,} \hfill \\ {B_{2} \left( {\frac{{{\text{d}}^{2} \varphi_{1} }}{{{\text{d}}t^{2} }} + \frac{{{\text{d}}^{2} \varphi_{2} }}{{{\text{d}}t^{2} }}} \right) + k_{2} \varphi_{2}^{d} + c_{2} \frac{{{\text{d}}\varphi_{2}^{d} }}{{{\text{d}}t}} = - M_{T} .} \hfill \\ \end{array} } \right. $$
(18)

It is important to note that the terms at \( k_{1} \), \( k_{2} \), \( c_{1} \) and \( c_{2} \) in the general Eq. (18) vanish when the motion without any collisions of the column and the disk with the appropriate barriers is reported. In a consequence, there will appear four combinations of the mathematical model of the double pendulum system that will switch between four kinds of the dynamical behavior reflected in two elastically impacting bodies (the column and the disk), one impacting body (the column or the disk) or even shortly, a nonimpacting regime of operation (neither the column or the disk).

A system for the application of a numerical integration results directly from the system (18), i.e.,

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{2} \varphi_{1} }}{{{\text{d}}t^{2} }} = \frac{1}{{B_{1} }}\left( { - k_{1} \varphi_{1}^{d} - c_{1} \frac{{{\text{d}}\varphi_{1}^{d} }}{{{\text{d}}t}} + \kappa_{1} \varphi_{\text{f}} + \kappa_{2} \varphi_{\text{f}}^{3} } \right.} \hfill \\ {\left. {\quad + k_{2} \varphi_{2}^{d} + c_{2} \frac{{{\text{d}}\varphi_{2}^{d} }}{{{\text{d}}t}} - M_{L} + 2M_{T} } \right)} \hfill \\ {\frac{{{\text{d}}^{2} \varphi_{2} }}{{{\text{d}}t^{2} }} = - \frac{{{\text{d}}^{2} \varphi_{1} }}{{{\text{d}}t^{2} }} + \frac{1}{{B_{2} }}\left( {k_{2} \varphi_{2}^{d} - c_{2} \frac{{{\text{d}}\varphi_{2}^{d} }}{{{\text{d}}t}} - M_{T} } \right).} \hfill \\ \end{array} } \right. $$
(19)

In the potential switching of the dynamical behavior of the investigated double torsion pendulum between four regimes, a very interesting nature of mechanical vibrations is expected, which is characteristic for discontinuous dynamical systems.

3.2 Model of collisions of the pendulum column

The barrier system attached to the pendulum column provides some complicated elastic collisions with the fixed cylindrical barrier made of a thin steel shaft with the boundaries of the bracket made of soft wood.

In this case, an inelastic impact model could be applied at each time instant t, when an impact treated as an instantaneous inelastic collision occurs with the coefficient of restitution \( 0 < c_{\text{r}} < 1 \). A modified nonlinear Kelvin model of the impact of bodies, including relationships between object strains, elastic and damping forces of the impact represented by power functions is proposed in [25].

We tested the numerical model dynamics with the use of the following mapping:

$$ {\text{if}}\;\;\varphi_{1} \left( {t^{ - } } \right) \ge \bar{\varphi }_{1} \;\;{\text{then}}\;\;\varphi_{1} \left( {t^{ + } } \right) = \bar{\varphi }_{1} \;\;{\text{and}}\;\;\dot{\varphi }_{1} \left( {t^{ + } } \right) = - c_{\text{r}} \dot{\varphi }_{1} \left( {t^{ - } } \right), $$
(20)

where the impacts occurred at two boundaries located at \( \varphi_{1}^{s} \). Despite the large range of the coefficient of restitution tested in the simulation, the dynamical response was far from the real one registered on the test stand. Hence, the inelastic model of impact has been replaced by the elastic one.

Measurements and observations of the collisions of the pendulum column exhibit some very stiff, but still elastic type of coupling. Therefore, an attempt of using a simple Voigt model of a parallel spring-dashpot connection (similarly to the elastic collisions of the disk), represented by the components at \( \varphi_{1}^{d} \) of the model given in Eq. (19), has been introduced and tested below during identification of model parameters.

4 Measurements on the experimental mechatronic system

4.1 Data acquisition and signal processing

The measurement and motor driving system of the torsion pendulum consists of the following elements: two angular position sensors HMC1512 embedded in a dedicated electronic circuit based on the LM358 amplifier; a microcontroller FRDM-KL25Z for data acquisition and control; the motor driver SMC64v2 controlled by the microcontroller; the 2-phase DC stepper motor 57BYG081 [55 (N cm), 5 (V), 1 (A) with the basic step 1.8 (°)]; a computer for data reading in a serial connection with the SDA port of the microcontroller. After the acquisition, the two series of data shown in Fig. 5, corresponding to the angles of rotation of pendulum bodies, were obtained.

Fig. 5
figure 5

Time series of measurement data of real nonlinear motion of the column (a) and the disk (b) for a quasi-sinusoidal kinematic excitation of the pendulum. (Color figure online)

Full size image

Measurements were performed with the use of Hall-effect magnetic sensors of rotation (see [26] for other realizations). The characteristics of the sensors, both for the column and the free disk body, were obtained as linear. The range of the motion for the column is limited to 30 (°), which fits to the most linear part of the sensors range. Two sensors acquire the voltages, and then these signals are transferred to the angle of rotation in degrees. Results of measurements are shown in Fig. 5.

The two obtained characteristics of the sensors measuring the angles \( \varphi_{1} \) and \( \varphi_{2} \) (in degrees) of rotation of the column and the disk read, respectively: \( \varphi_{1} (i) = \left( {u_{1} (i) - 1.7907} \right)/0.0271 \) and \( \varphi_{2} (i) = \left( {u_{2} (i) + 0.0269} \right)/0.0323 \), where \( i \) denotes the number of the sample, and voltage readings \( u_{1} \) and \( u_{2} \) from the sensors measure displacements of the column and the disk. Due to the initial readings from the sensors at the assumed 0 angle values of both rotation coordinates, an offset of both amplitudes appears. It does not influence the character of the time trajectories.

4.2 Results of measurements

The most characteristic behavior, represented by the time series of measurement data of real motion of two bodies of the double torsion pendulum with friction, elastic barriers and a quasi-sinusoidal kinematic forcing, has been registered. The time characteristics of motion (sampled every 0.01 of a second) of both the column (a) and the disk-shaped free body (b) are shown in Fig. 5. The red time series for \( \varphi_{2} (t) \) illustrates the very characteristic stick–slip motion of the disk, which is observed in every period of motion.

At first glance, one can observe some periodicity of the series and asymmetry at lower and upper limits of motion of the disk (red line). The effect will be studied and identified in the subsequent sections. The red trajectory is composed of a slip phase, caused by an elastic contact of the tip fixed to the disk with the beam springs attached to the upper column’s ring (see Fig. 3), and a stick phase that holds when the disk sticks to the moving base while its moment of static friction (acting tangentially in the contact surface) exceeds the moments exerted on it by inertial effects coming from the column. One should note that there exists a small backslash—a free space between the tip and the beam springs. When neither the left nor the right beam spring forces the disk, then it can change its position only by the moment of friction caused by the rotating base of the column. As a consequence, any elastic impacts of the pendulum column with the barriers matched by the wooden bracket attached to the column and the pin barrier (see Fig. 2) will generate sufficiently high accelerations, causing the appearance of the moments of friction acting on the base and being able to break its stick phase with the disk.

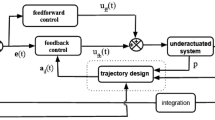
To conclude, a challenging problem of identification of the dynamics appears. It requires an adaptation of a suitable mathematical modeland, a numerical simulation supported by some methods helping in optimization of the problem. Next to the trial-and-error method, a simplex Nelder–Mead algorithm [27] will be used to identify the model of friction and its parameters.

5 Identification of system structure and parameters

5.1 The strategy

Identification of unmeasurable parameters is one of the most difficult engineering problems of any numerical virtualization of real mechatronic objects. The present study deals with the nonlinear discontinuous system with friction, elastic barriers and backlashes. Therefore, to find the proper set of system parameters for the numerical simulation, some special methods and a semiempirical identification strategy were applied.

Our strategy of identification of system parameters is based on the following steps.

  1. 1.

    Assessment of the main physical phenomena influencing the dynamics of the investigated system.

  2. 2.

    Derivation of the estimated mathematical model of the system.

  3. 3.

    Inclusion of flexible parts, which will capture the main physical phenomena (friction and impacts) and which are mostly responsible for the most specific character of the system response, in the mathematical description.

  4. 4.

    Observation of real dynamics on the experimental stand connected with acquisition of all possible experimental time series of state variables that are covered by the state variables of the assumed mathematical description, i.e., development of differential equations. The obtained time series will state for a multidimensional criterion of convergence in the process of identification. Having in mind that the series of data acquired with the time step will be evaluated by the algorithm of identification during a simultaneous integration of the numerical model, the selection of as short as possible experimental time series is suggested. On the other hand, the time series has to be the representative one, exhibiting the specific shape and nature of the dynamical response of the investigated system. The regular dynamics saved within two or three periods of changes of the system states should be sufficient.

  5. 5.

    Assumption of the simplest models of the physical phenomena governing the dynamics of the system connected with initialization of the set of the parameters, many of which can be identifiable by the basic experimental measurement on the stand, e.g., masses, mass moments of inertia, geometrical dimensions, placement of boundaries like frictional surfaces, springs, damping or barriers. The more information will be collected and verified at this stage, the better estimation of the associated dynamical phenomena will be possible.

  6. 6.

    Description of the effects that are assumed as important for the evaluation of the system, e.g., physical models of a friction or impact law. The estimation of an initial set of unknown system parameters of the effects.

  7. 7.

    Building of a numerical model of the system and checking if its solution gives some reliable results. The boundaries of variations of the numerical system states and their experimental counterparts should be at least roughly comparable. Slight changes in the initially assumed parameters of the numerical model should allow for better imitation of real characteristics that should be incorporated into the simulation, being a background for the numerical solutions.

  8. 8.

    Selection of a method of identification of system parameters with an inclusion of the numerical model into the optimization algorithm’s function of evaluation.

  9. 9.

    Assumption of the most probable system parameters as constant and the roughly estimated as the varying ones in the identification algorithm.

  10. 10.

    Running the numerical algorithm of identification, here Nelder–Mead, with observation and assessment of the rate of convergence of the numerical solution (to be found with the same step of integration as the time step of sampling—measurement of the real system’s multidimensional response).

  11. 11.

    Here, the expected convergence was not visible at the first attempt; therefore, a more advanced model of the still unidentified physical phenomena was modified by a trial-and-error method (see pt. 5).

  12. 12.

    The final results were mainly achieved after a few manipulations in the direction of changing the physical laws modeling the friction and impacts.

5.2 Defining the nonlinear problem of dynamics

In the study, continued after [2], we use a Nelder–Mead technique (functions optimset and fminsearch in Scilab) [27] from the library of simplex methods supported with an initial guess of regions of model parameters to be performed on the basis of some engineering experience as well as on many trial-and-error experiments.

First of all, some initial guess of the whole set of model parameters subjected to the identification has to be made. It is based on a rough identification of mechanical properties of the mechatronic system at hand, initial assumption of mathematical models of the physical phenomena governing, by assumption, the mechanical system’s dynamics and also on some experience of the mechanical engineer conducting the research. All the numerical simulations and the trials were made in Scilab, where the model system’s block diagram performed in Xcos (a dynamic system builder and simulator) was simulated during a few thousands of iterations of numerical solutions by taking a few periods only as the specific test signals of the solutions \( \varphi_{1} (t) \) and \( \varphi_{2} (t) \). One required to search for the sets of model parameters allowing for a reconstruction of the selected real trajectories (measured on the experimental stand, see Fig. 1.) to be computed during numerical tests.

The most difficult problem in such experiments is to find the parameters of both frictional contact models and the parameters of Voigt elements used in this case to simulate contacts of the pendulum with elastic barriers. Parameters of the models, assumed for \( M_{L} \) in Eq. (8), and for \( M_{T} \) in Eq. (10), were manipulated in some regions to obtain the best shape of the particular periods of real periodic steady-state motions of the two bodies of the mechatronic system. Such a procedure works very roughly and permits only for the placement of the numerically obtained time histories in proper regions of the variability of the trajectories \( \varphi_{1} (t) \) and \( \varphi_{2} (t) \), since mostly, the very characteristic dynamical behavior of the pendulum bodies remains undiscovered. Therefore, to achieve some better coincidence between the numerical and real-world objects, the Nelder–Mead algorithm was applied to obtain the closest possible mathematical model parameters, being in the best adequacy to the reality and the series of data obtained with the test stand.

5.3 Methodology

In the first approach, we focus on the investigation of the stick–slip dynamic response of the disk-shaped free body on a step input waveform of frequency \( f_{w} = 4.1 \) (Hz). In the identification process, the following strategy consisting of a few subsequent steps is applied.

(M1) Unknown physical parameters obtainable by simple measurements, like mass of the column, stiffness coefficient of the beam springs at \( \pm \varphi_{2}^{s} \), restricting the disk’s motion, mass moment of inertia of the disk, diameter of ball bearings, frequency of excitation of the pendulum, as well as parameters obtainable by the trial-and-error method, like mass moment of inertia of the column (due to its irregular geometry), moments of static and viscous friction, stiffness and damping of the column barrier at \( \pm \varphi_{1}^{s} \), are roughly estimated; see Fig. 6.

Fig. 6
figure 6

Initial discrepancy of time histories \( \varphi_{2}^{ \exp } (t) \) and \( \varphi_{2}^{\text{num}} (t) \) of a stick–slip motion of the disk for the symmetric models of friction (10) and (14) in the pendulum in the assumed test interval of time \( [0.41,\; 4.41] \) translated in time to 0 before the first optimization test

Full size image

(M2) In the first running of the numerical test, the parameters \( \varepsilon_{1} \), \( \varepsilon_{2} \), \( \mu \), \( B_{1} \), \( B_{2} \) are not optimized as well as some overvalued parameters of the moments of frictional resistance of the column, i.e., \( T_{\text{s1}} \), \( T_{\text{v1}} \) are assumed to obtain a step excitation allowing for attenuation of stick–slip effect in behavior of the disk-shaped free body of the pendulum.

(M3) In the second test, the parameters \( \varepsilon_{1} \), \( \varepsilon_{2} \), \( \mu \) are optimized as well, and the parameters \( T_{\text{s1}} \), \( T_{\text{v1}} \) are significantly decreased to the vicinity of intervals with the most expected values.

(M4) In the third test, the parameters \( B_{1} \), \( B_{2} \) are also optimized, because estimation of the column’s inertia, consisting of some mounting rings at the bearing and the upper free body, a hollow shaft and the wooden bracket of a material different than steel (see Figs. 1, 2), is rather very roughly known.

(M5) After running the third test with 50 iterations of the Nelder–Mead algorithm, the final set of parameters is found. Application of the set in the numerical integration solving the nonlinear dynamics problem of the investigated system results in the proper dynamic response represented by the time histories shown in Fig. 7. Such a characteristic behavior of torsional disks has been reported in [18].

Fig. 7
figure 7

Coincidence of time histories \( \varphi_{2}^{ \exp } (t) \) and \( \varphi_{2}^{\text{num}} (t) \) of a stick–slip motion of the disk for the symmetric models of friction (10) and (14) in the pendulum in the assumed test interval of time \( [0.41, \;4.41] \) translated in time to 0 after the third test of optimization

Full size image

The biggest discrepancy between the time histories results from asymmetry. Two slip phases per one period of the observed stick–slip motion are asymmetric. It means that the conditions of the planar frictional contact differ when the disk rotates to the left (counterclockwise) and to the right (clockwise). The main cause of the concave upward phenomenon is considered to be uneven friction, which may originate from the roughness of the surface, the asymmetry of the disk and from many other factors that cannot be considered in the ideal model. In the transition region, the motion of the disk alternates between at least two similar frictional behaviors.

(M6) With respect to that nonuniformity of the contact surface, the model of the frictional contact [see \( M_{T} \) in Eq. (10)] is expanded on two parameters of the static and viscous friction torque, for the positive and negative angular velocities of relative motion of the disk, respectively. Therefore, the friction model is defined again as follows

$$ M_{T} \left( {\dot{\varphi }_{2} } \right) = T_{\text{v2}} \dot{\varphi }_{2} + T_{\text{s2}} \frac{2}{\pi }{\text{arctg}}\left( {\varepsilon_{2} \dot{\varphi }_{2} } \right) $$
(21a)
$$ \left[ {\begin{array}{*{20}c} {T_{\text{s2}} } \\ {T_{\text{v2}} } \\ \end{array} } \right] = \left\{ {\begin{array}{*{20}c} {\left[ {T_{{{\text{s}}2l}} \;\;T_{{{\text{v}}2l}} } \right]} & {{\text{if}}\;\dot{\varphi }_{2} \ge 0,} \\ {\left[ {T_{{{\text{s}}2r}} \;\;T_{{{\text{v}}2r}} } \right]} & {{\text{if}}\;\dot{\varphi }_{2} < 0,} \\ \end{array} } \right. $$
(21b)

where for the second frictional contact: “l” and “r” stand for the positive and negative velocity of motion, respectively. One should note that we say about the velocity of motion relative to the motion of the column.

The next result of optimization with the improved mathematical model of asymmetric friction torque, acting on the disk and the column at the positive and negative rotational velocity is shown in Fig. 8.

Fig. 8
figure 8

Coincidence of time histories \( \varphi_{2}^{ \exp } (t) \) and \( \varphi_{2}^{\text{num}} (t) \) of a stick–slip motion of the disk after inclusion of modeling of asymmetry in the assumed test interval of time \( [0.41, \;4.41] \) translated in time to 0 after the fifth stage of optimization

Full size image

Moreover, the transitory sliding phase in slip phases takes a longer time in reality than in the numerical model. It seems that just after the elastic collisions with the beam springs, the resistance of motion is greater than it would be expected from the assumed Voigt model of the elastic barrier.

(M7) At the first step, we initiate a rough identification of the disk’s dynamic response by applying a step waveform of motion of the base at the frequency \( f_{w} = 4.1 \) (Hz), simulating motion of the column—motion of the base of the disk. Now, we try to identify the column’s dynamic response to fit it to the registered real measurement on the stand.

Similarly to the nonuniformity of the disk contact surface as well as with regard to an assessment of the time series of measurement data, the column’s asymmetric friction model is re-defined

$$ M_{L} \left( {\dot{\varphi }_{1} } \right) = T_{\text{v1}} \dot{\varphi }_{1} + {\text{sign}}\left( {\dot{\varphi }_{1} } \right)T_{b} , $$
(22a)
$$ T_{\text{v1}} = \left\{ {\begin{array}{*{20}c} {T_{{{\text{v}}1l}} } & {{\text{if}}\;\dot{\varphi }_{1} \ge 0,} \\ {T_{{{\text{v}}1r}} } & {{\text{if}}\;\dot{\varphi }_{1} < 0,} \\ \end{array} } \right. $$
(22b)

where comparing with the model in Eq. (8), the negligible static friction torque in the rolling bearing is removed.

Using the set of parameters (see Table 1), that are found initially by the trial-and-error method, and finally, by means of the Nelder–Mead algorithm, a quite good numerical fit is estimated (see Fig. 9).

Table 1 Identified estimates of parameters of asymmetric forcing and elastic contact models and friction
Full size table
Fig. 9
figure 9

Coincidence of the experimental (blue) and numerical (red) time history of displacements \( \varphi_{1}^{ \exp } (t) \) and \( \varphi_{1}^{\text{num}} (t) \) (a) and velocities \( \dot{\varphi }_{1}^{ \exp } (t) \) and \( \dot{\varphi }_{1}^{\text{num}} \) (b) of the column in the assumed test interval of time \( t \in [0.41, \;4.41] \) translated in time to 0. The presented solution takes into account modeling of asymmetry of elasticity of forcing of the pendulum body. (Color figure online)

Full size image
Fig. 10
figure 10

Coincidence of the experimental (blue) and numerical (red) time history of displacements \( \varphi_{2}^{ \exp } (t) \) and \( \varphi_{2}^{\text{num}} (t) \) (a) and velocities \( \dot{\varphi }_{2}^{ \exp } (t) \) and \( \dot{\varphi }_{2}^{\text{num}} \) (b) of the disk in the assumed test interval of time \( t \in [0.41, 4.41] \) translated in time to 0. The presented solution takes into account modeling of asymmetry of elasticity of barriers and contact friction of the pendulum body. (Color figure online)

Full size image

The time-dependent response of the pendulum column will be based on modeling of the asymmetric spiral spring and also asymmetry of the kinematic quasi-sinusoidal excitation of the cam mechanism, which has the following nonlinear form

$$ f_{s} (t) = \kappa_{1} \varphi_{\text{f}} + \kappa_{2} \varphi_{\text{f}}^{3} , $$
(23a)
$$ \left[ {\kappa_{1} \;\;\kappa_{2} } \right] = \left\{ {\begin{array}{*{20}c} {\left[ {\kappa_{1l} \;\;\kappa_{2r} } \right]} & {{\text{if}}\;\varphi_{1} \ge 0,} \\ {\left[ {\kappa_{1r} \;\;\kappa_{2r} } \right]} & {{\text{if}}\;\varphi_{1} < 0,} \\ \end{array} } \right. $$
(23b)

where \( \varphi_{\text{f}} (t) = f_{\text{e}} (t) - \varphi_{1} (t) = A\sin (\omega t + \phi ) - \varphi_{1} (t) \).

The disk’s mass moment of inertia is about 4.5 times smaller than the corresponding moment of the column. Therefore, the column dynamics is rather not so much influenced by the disk. Looking at the red and blue plots, one can notice that the numerical experiment sufficiently well captures the interaction of the column bracket with the barrier at \( \varphi_{1}^{s} \) (see Fig. 11a). There are some effects described in Sect. 6, the influence of which could be crucial.

Fig. 11
figure 11

The conditional presence of the time-dependent terms \( \varphi_{i}^{d} (t) \) [see Eq. (4)], appearing after hitting both pendulum barriers at \( \varphi_{i}^{s} \), for \( i = 1,2 \), respectively. (Color figure online)

Full size image

(M8) To improve quality of solution of the problem marked in point 6, we take into consideration the column dynamics represented by the time histories in Fig. 9. Additionally, based on observations, we introduce a more universal and well-developed model of frictional contact studied in [28]. Again, we define the model (21) of the contact zone of the disk and its base accordingly to the smoothed characteristics of kinetic dry friction taking into account the Stribeck effect. It follows

$$ M_{T} \left( {\dot{\varphi }_{2} } \right) = \frac{{T_{\text{s2}} }}{{1 + T_{02} \left| {\dot{\varphi }_{2} } \right|}}\left( {1 + \frac{\beta }{{\cos h\alpha \dot{\varphi }_{2} }}} \right)\tan h\alpha \dot{\varphi }_{2} , $$
(24a)
$$ \left[ {T_{\text{s2}} \;\;T_{02} } \right] = \left\{ {\begin{array}{*{20}c} {\left[ {T_{{{\text{s}}2l}} \;\;T_{02l} } \right]} & {{\text{if}}\;\dot{\varphi }_{2} \ge 0,} \\ {\left[ {T_{{{\text{s}}2r}} \;\;T_{02r} } \right]} & {{\text{if}}\;\dot{\varphi }_{2} < 0,} \\ \end{array} } \right. $$
(24b)

where \( T_{\text{s2}} \) (N m) is a constant parameter controlling the amplitude of the spike in the friction coefficient, assuming that the range of relative velocities (here \( \dot{\varphi }_{2} \)) is narrow enough, the parameter \( T_{02} \) (s/rad) is responsible for the decay of friction force as the modulus of relative velocity is increasing, \( \alpha \) (s/rad) controls the curve sharpness near zero and, finally, \( \beta \) (N m) controls the magnitude of spikes near zero, in other words, the rate of the original drop of the friction coefficient just after the moving mass quits the sticking (possibly a creeping in reality) area. A function of torque versus angular velocity of motion, established in [29], at a bit in drill-string torsional vibrations can be covered by the universal model introduced in Eq. (24).

The solutions presented in Fig. 10 in red color on the background of real trajectories of motion of the double pendulum mostly approximate the reality. Despite various configurations of the initial set of parameters and setting of parameters of the Nelder–Mead algorithm, the peaks on the numerically estimated velocity plots visible in Fig. 10b were impossible to remove. The identified model dynamics, including the introduced asymmetry, is qualitatively much better than the dynamics represented by the responses obtained at first stages of the identification process shown in Figs. 7 and 8, subsequently. A more detailed analysis of the possible sources of discrepancies is carried out in Sect. 6.

Table 1 contains a subset of the identified model parameters defining asymmetry of the nonlinear system. The remaining estimations are as follows: mass moments of inertia of the column \( B_{1} = 0.00135 \) (kg m2) and the disk \( B_{2} = 0.0003 \) (kg m2); amplitude of sinusoidal excitation \( A = 37.5\pi /180 \) (rad), frequency of the excitation \( \omega = 3.9 \) (rad/s) and phase shift \( \phi = 120\pi /180 \) (rad); constant torque \( T_{b} \) in Eq. (7) is determined by mass of the column \( m = 0.9 \) (kg), diameter \( D_{m} = 0.008 \) (m), coefficient of resistance of motion \( \mu = 0.001126 \) (−) and gravitational constant \( g = 9.81 \) (m/s2); positions of activation of elastic barriers modeled by Voigt elements: \( \varphi_{1}^{s} = \pm 13.6\pi /180 \) (rad), \( \varphi_{2}^{s} = \pm 1.1\pi /180 \) (rad); shaping parameters of dry and viscous friction models: \( \varepsilon_{1} = \varepsilon_{2} = 100 \) (s/rad); shaping coefficients of the improved friction model \( \alpha = 0.15 \) (s/rad), \( \beta = 2.2 \) (N m). Coefficients of stiffness and damping in the model of elastic barriers of the column and the disk, respectively: \( c_{1} = 120 \) (N m/rad) and \( k_{1} = 300 \) (N/rad), \( c_{2} = [c_{2l} \;\;c_{2r} ] = [0.018\;\;0.02] \) (N m/rad) and \( k_{2} \approx 0.7 \) (N/rad). The stiffness \( k_{2} \) of beam springs was preliminary estimated in a static characteristics test of force response versus linear deformation, since after the optimization it took about \( 0.7 \) (N/rad).

Parameters of the numerical integration: initial time of observation \( t_{0} = 0.41 \) (s); final time of observation \( t_{\text{f}} = 4.41 \) (s) (both are fit to the assumed part of real pendulum time characteristics taken into the Nelder–Mead algorithm); integration step \( \Delta t = 0.001 \) (s) (every 10-th point of the numerical solution was taken to fit the time series to the sampling of real measurement series of data of length 400 samples); initial conditions \( \varphi_{1} (0) = - \varphi_{1}^{s} \), \( \varphi_{2} (0) = 0 \) (rad), \( \dot{\varphi }_{1} (0) = 0 \), \( \dot{\varphi }_{2} (0) = 0 \) (rad/s); solver type: Sundials/CVODE—BDF—Newton, absolute tolerance: \( 10^{ - 6} \), relative tolerance: \( 10^{ - 6} \), tolerance on time: \( 10^{ - 10} \). Diagram of the numerical model is given in “Appendix”.

6 Discussion

Below, a few remarks on the effectiveness and accuracy of the numerical estimation of the set of parameters of the two-degree-of-freedom dynamical system are given.

A quasi-sinusoidal excitation in real experiment versus pure sinusoidal excitation applied in the numerical test may cause some discrepancies in the amplitude and phase shift of forcing acting on the column, and even indirectly, on the free disk body of the double torsion pendulum.

Usually, numerical solutions are more sharper at discontinuous boundaries that need an introduction of some additional corrections in the frictional or impact contact models and/or some additional inertial effects. For instance, friction may occur at stochastically changing parameters as reported in [30]. On the real stand, possible averaging of sensor readings, that is caused by its quantization errors and measurement noise, smoothens some peaks and the discontinuous boundaries. Moreover, time delays in the data acquisition from sensors of rotational motion can stand for another source of averaging of the real physical phenomena omitted after the measurements. Finally, elastic impacts or breaking of adhesion during stick–slip motions occur faster than the regular dynamical response, so not all data informing about the real physical response are acquired. All the mentioned adversities, but not all in overall, shade the true “sharper dynamic response” of the real system that is naturally exhibited by numerical experiments.

An unknown, but initially identified, hysteresis of the spiral spring provokes some modifications in the static characteristics of the spring that stands for the first identified source of asymmetry of the pendulum. The second significant source of asymmetry is related to the contact surface, which has different coefficients of static and kinetic friction, while the contacting surfaces of the pendulum bodies move relatively with positive or negative velocity of motion [see Eqs. (20) and (21) for \( \dot{\varphi }_{2} \) defined on intervals]. The coefficients slightly differ by assessment of the contact surface and confirmed asymmetric shapes of time histories of the displacement of the free disk body. It is caused by the process of rolling machining, causing low roughness of the planar rotational contact surface, the quality of which was sensitive to the direction and speed of machining.

Any numerical simulation based on the modeling of motion with the use of Lagrangian dynamics for point-focused (lump) masses of solid bodies is a priori a kind of simplification of the real dynamics distributed on the nonuniform properties of irregular surfaces of planar or rolling contacts (as in this case), not created by any point-focused masses of some not fully identified geometry and matrices of inertia. Next to that, some not captured scale effects can exist.

At the beginning, the assumed method of optimization based on the Nelder–Mead algorithm requires a quite precise selection of model parameters and the form of the mathematical and physical model as well. As it is confirmed in the above section, the simplest model does not guarantee enough number of directions of shaping of the characteristics of friction or elasticity. As a consequence, the Nelder–Mead algorithm might not be able to achieve the best optimal value of the objective function (in this case, the time history of motion of the pendulum bodies). Mostly, some incorrect assumptions of the initial set of parameters or even of the mathematical model do not lead to convergence of the searching algorithm. The real physical object is subject to the high-frequency vibrations (coming from the engine, rotations of balls in bearings, etc.) of small amplitudes, propagated through the whole construction. High-frequency vibrations are conducive to breaking the static friction forces and decreasing the sticking zones. The phenomenon brings also smoothing of the discontinuities dividing the regions of adhesion. In the present research, the form of propagation of such mechanical vibrations (associated also with some propagation of sound) of the pendulum’s construction is not possible for including in the mathematical model, and finally, in the numerical simulation.

7 Conclusions

Mathematical modeling and virtualization of the real nonlinear double torsion pendulum with asymmetric friction, hysteresis and elastic barriers have turned out to be a quite challenging problem. It allowed us to model and simulate interesting complex dynamics of the mechanical system.

Due to a good correlation between the real observations and numerical solutions, the most difficult engineering problem has been solved, since the identified model parameters will be useful in further investigation of other possible physical phenomena.

Some sources of discrepancies between the real and virtual models have been enumerated, but mostly, they could come from deeper aspects of viscous and dry friction acting on the pendulum bodies. Indeed, it is difficult to determine which of the physical effects is dominating.

We have identified many system parameters. It turns out that these parameters make the modeling much precise, but on the other hand, they bring a basic problem in this matter, i.e., their identification is difficult as we operate in multidimensional parameter space. Basing on the obtained results, one estimates that the attempt to identify the basic physical phenomena exhibited by the system was successful. We have found the approximated numerical solutions in the proper range of variation as well as we have modeled typical behaviors of a complex system, including some discontinuous phenomena of machine dynamics.

Finally, the mathematical model is sufficiently close to reality, and therefore it can be used for the torsion pendulum in further studies and in other problems associated with studying various kinds of excitation, checking its sensitivity to changes of initial conditions or even inspection of time delays.