Deformed breather and rogue waves for the inhomogeneous fourth-order nonlinear Schrödinger equation in alpha-helical proteins

Abstract

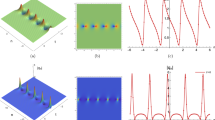
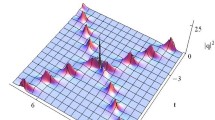
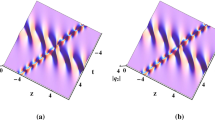
The inhomogeneous fourth-order nonlinear Schrödinger equation is investigated, which models the transport of energy along the inhomogeneous hydrogen bonding spines in alpha-helical proteins. The deformed breather and rogue waves solutions for the equation are derived via Darboux transformation. Thereinto, the modified limit procedure in generalized Darboux transformation is proposed to construct the expressions of higher-order rogue waves. Due to the presence of inhomogeneity, despite their diversity profiles, the shape, amplitude and pulse width of each deformed breather will change with time. When the coefficients of higher-order terms are varied, the propagating trajectories of breathers are changed. Head-on collision, partially coalesced, without interaction between two deformed breathers is found under diverse selected parameters. The temporal-spatial structures of the presented rogue waves exhibit certain valleys around one or several centers, and the peak heights of those rogue waves are more than three times that of the background. Additionally, the distributed area of the rogue wave will tend to be broaden/narrow along the temporal axis, with the variation of the coefficients of inhomogeneity and higher-order terms.

Appendices

Appendix A

The expressions for $d_1(t)$ and $d_2(t)$ in Eq. (12) are given as

$$\begin{aligned}&d_1(t)=-\frac{1}{2}\, \log \Bigg [\,\frac{m_2}{3 h_1^2 \left( \xi +2 t h_1\right) m_1}\nonumber \\&\quad -\frac{i \beta _1}{3 h_1 m_1}\sqrt{\frac{-m_1}{h_1^2 \left( \xi +2 t h_1\right) ^2 \beta _1}}\,\Bigg ]\nonumber \\&\quad +\frac{1}{2} \log \left( \xi +2 t h_1\right) \,\nonumber \\&\quad -\frac{1}{72 h_1^3}\,\sqrt{\frac{-m_1}{h_1^2 \left( \xi +2 t h_1\right) ^2 \beta _1}}\Bigg [-36 h_0 h_1^2 \nonumber \\&\quad -\frac{96 a^2 A \rho _1^2 \sigma _1^2 h_1^2}{\beta _1^2}+\frac{4 a^2 A h_1^2}{\left( \xi +2 t h_1\right) ^2} +\frac{a^2 A \sigma _1^2 m_3}{m_1\, \beta _1} \,\nonumber \\&\quad + \frac{4 a^2 A h_1^2 \sigma _1^2 \left( 2 h_1 \sigma _2-\xi \right) }{\left( \xi +2 t h_1\right) \, m_1}\Bigg ]\nonumber \\&\quad -\frac{1}{4}\log \left( \beta _1\right) -\log \Big [\delta _1(t)\Big ]+ \sigma _3\,, \end{aligned}$$

(A-1a)

$$\begin{aligned} d_2[t]&=\frac{1}{2}\, \log \Bigg [\,\frac{-m_2}{3 h_1^2 \left( \xi +2 t h_1\right) m_1}\nonumber \\&\quad +\frac{i \beta _1}{3 h_1 m_1}\sqrt{\frac{-m_1}{h_1^2 \left( \xi +2 t h_1\right) ^2 \beta _1}}\,\Bigg ]\nonumber \\&\quad +\frac{1}{2} \log \left( \xi +2 t h_1\right) \,\nonumber \\&\quad -\frac{1}{72 h_1^3}\,\sqrt{\frac{-m_1}{h_1^2 \left( \xi +2 t h_1\right) ^2 \beta _1}}\Bigg [36 h_0 h_1^2 \nonumber \\&\quad +\frac{96 a^2 A \rho _1^2 \sigma _1^2 h_1^2}{\beta _1^2}-\frac{4 a^2 A h_1^2}{\left( \xi +2 t h_1\right) ^2} -\frac{a^2 A \sigma _1^2 m_3}{m_1\, \beta _1} \,\nonumber \\&\quad -\frac{4 a^2 A h_1^2 \sigma _1^2 \left( 2 h_1 \sigma _2-\xi \right) }{\left( \xi +2 t h_1\right) \, m_1}\Bigg ]\nonumber \\&\quad -\frac{1}{4}\log \left( \beta _1\right) -\log \Big [\delta _2(t)\Big ]+ \sigma _4\,,\ \end{aligned}$$

(A-1b)

where $m_1=256 \rho _1^2 h_1^4+4 \sigma _1^2 \sigma _2^2 h_1^2-4 \xi \sigma _1^2 \sigma _2 h_1+\xi ^2 \sigma _1^2$, $m_2=-2 \sigma _1^2 \sigma _2 \left( t+\sigma _2\right) h_1+\xi \sigma _1^2 \left( t+\sigma _2\right) -128 \,\rho _1^2\, h_1^3$, $m_3=512 \rho _1^2 h_1^4 -4 t \sigma _1^2 \sigma _2 h_1^2+2 \xi \sigma _1^2 \left( t-\sigma _2\right) h_1+\xi ^2 \sigma _1^2$, and $\sigma _3$ and $\sigma _4$ are constants.

Appendix B

The definition of the coefficients in Eq. (24) are expressed as

$$\begin{aligned} \theta _1&=i+ \frac{5\,(t+1)\,i}{2 n_3}\left( x+\frac{1471435}{1572864}-\frac{8125 }{9216 n_3}+\frac{175 }{9 n_3^2}\right) \nonumber \\&\quad -\frac{12366125 i \arctan \left[ \frac{5 (t+1)}{16}\right] }{50331648}\,, \end{aligned}$$

(A-2a)

$$\begin{aligned} n_2&=\big (25 t^2+50 t+281\big )^4 \,, \end{aligned}$$

(A-2b)

$$\begin{aligned} n_1&=\big (25 t^2+50 t+281\big )^2\,\big (7500 t^4+30000 t^3\nonumber \\&\quad +182975 t^2+305950 t+1011907\big )\,, \end{aligned}$$

(A-2c)

$$\begin{aligned} n_0&=t^{12}+12 t^{11}+\frac{3186 t^{10}}{25}+\frac{4172 t^9}{5}+\frac{616583 t^8}{125}\nonumber \\&\quad +\frac{2693464 t^7}{125}+\frac{804569642 t^6}{9375}+\frac{815250884 t^5}{3125}\,\nonumber \\&\quad +\frac{2052241197593 t^4}{2812500}+\frac{1048962591593 t^3}{703125}\nonumber \\&\quad +\frac{167769855736561 t^2}{58593750}\,\nonumber \\&\quad +\frac{286743955611433 t}{87890625}+\frac{33761501393177141}{8789062500}\,, \end{aligned}$$

(A-2d)

$$\begin{aligned} m_0&=t^{12}+12 t^{11}+\frac{3186 t^{10}}{25}+\frac{4172 t^9}{5}+\frac{591583 t^8}{125}\nonumber \\&\quad +\big (\frac{2493464}{125}+\frac{400 i}{3}\big ) t^7\,\nonumber \\&\quad +\big (\frac{683082142}{9375}+\frac{2800 i}{3}\big ) t^6\nonumber \\&\quad +\big (\frac{642275884}{3125}+6896 i\big ) t^5\nonumber \\&\quad +\big (\frac{1382086641343}{2812500}+\frac{75440 i}{3}\big ) t^4\,\nonumber \\&\quad +\big (\frac{617270535343}{703125}+\frac{6567728 i}{75}\big ) t^3\nonumber \\&\quad +\big (\frac{70600528830311}{58593750}+\frac{4239728 i}{25}\big ) t^2\,\nonumber \\&\quad +\big (\frac{91685863955183}{87890625} +\frac{544515056 i}{1875}\big ) t\nonumber \\&\quad +\big (\frac{1684758372895891}{8789062500}+\frac{355008656 i}{1875}\big )\,,\ \end{aligned}$$

(A-2e)

with $n_3=(t+1)^2+\frac{256}{25}$.