Abstract
In this paper, a detailed review on the dynamics of axially moving systems is presented. Over the past 60 years, vibration control of axially moving systems has attracted considerable attention owing to the board applications including continuous material processing, roll-to-roll systems, flexible electronics, etc. Depending on the system’s flexibility and geometric parameters, axially moving systems can be categorized into four models: String, beam, belt, and plate models. We first derive a total of 33 partial differential equation (PDE) models for axially moving systems appearing in various fields. The methods to approximate the PDEs to ordinary differential equations (ODEs) are discussed; then, approximated ODE models are summarized. Also, the techniques (analytical, numerical) to solve both the PDE and ODE models are presented. The dynamic analyses including the divergence and flutter instabilities, bifurcation, and chaos are outlined. Lastly, future research directions to enhance the technologies in this field are also proposed. Considering that a continuous manufacturing process of composite and layered materials is more demanding recently, this paper will provide a guideline to select a proper mathematical model and to analyze the dynamics of the process in advance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Axially moving systems form part of several mechanisms in various engineering disciplines (Fig. 1). For example, they play an essential role in production and packaging lines, such as technical textile manufacturing (Fig. 1a), flexible robotic end-effectors (Fig. 1b), zinc galvanization (Fig. 1c), nanoscale metal printing for making electronic devices (Fig. 1d), and so on. In such applications, mechanical vibrations which occurred within the moving system constitute the principal factor tending to limit the performance and productivity of the said systems: This is especially true for high-speed precision systems. To enhance efficiency and optimize the design of such systems, numerous investigations have been performed over the past six decades concerning the vibration behavior of axially moving systems. The primary purpose of this paper is to present a comprehensive review of the studies undertaken thus far concerning the dynamics of axially moving systems. This paper discusses the development of mathematical models for axially moving systems along with the methods of vibration analysis employed over the past 60 years.
Figure 2 depicts an axially moving system with various boundary conditions (see also Sect. 2.5). The vibrations along the i-, j-, and k-axes are called the longitudinal, lateral, and transverse vibrations, respectively. Depending on the flexibility and geometric parameters of the system, four different models under tension (constant or time-varying) can be developed: String, beam, belt, and plate models. The string model is generally used to model components wherein the bending stiffness of the material is relatively small and can be ignored (i.e., threads in textile manufacturing processes (Fig. 1a), cables in automatic winding machines, and so on) [1,2,3,4,5]. The beam model assumes that the bending moment is significant in contrast to the string model (i.e., the Euler–Bernoulli beam), and further considers the area moment of inertia (i.e., the Rayleigh beam), and more also includes the shear force (i.e., the Timoshenko beam). Examples of the Euler–Bernoulli beam model include a steel rod in the continuous casting process and the moving beams in [6,7,8,9]. The flexible link with a prismatic joint in a robotic system in Fig. 1b is an example of the Timoshenko beam model. The belt model investigates the lateral and longitudinal vibrations [10,11,12,13] by considering the longitudinal inertia force. Such models sometimes involve only the bending moment and the longitudinal inertia force or all the bending moment, area moment of inertial, shear force, and the longitudinal inertia force. Examples of belt model include the steel strip in a zinc galvanization line (Fig. 1c) and a belt used in the power transmission system. These axially moving string/beam/belt models are one-dimensional model from the sense that one independent spatial variable x appears in the equation of motion. Instead, the plate model is a two-dimensional model that involves two independent spatial variables x and z in Fig. 2 and investigates both the lateral and transverse vibrations. A plate model can include the bending moment, shear force, and torsion in the middle surface of the plate. A membrane model is another two-dimensional model, but it considers only tension. The axially moving plate model is suitable for modeling axially moving materials with considerable width (e.g., the metal layer in nanoscale metal printing processes (Fig. 1d)) [14,15,16,17,18,19].
The very first works concerning axially moving systems were published by Sack [20] and Mahalingam [1]. Since then, various studies concerning the development of the equations of motion of axially moving systems have been conducted [21,22,23,24]. Subsequently, the effect of material damping on the dynamic response of the system has been investigated, and the mathematical models of translating viscoelastic materials have been developed using several viscoelastic models [25,26,27,28]. Moreover, the dynamics subject to nonlinear factors such as viscoelastic foundations [29, 30], hydrodynamic forces [31, 32], magnetic effects [33, 34], and thermal effects [35, 36] have also been reported. Dynamic behaviors of linear axially moving systems have been analyzed using methods such as the Laplace transform [37] and Lie group theory [27]. In contrast, nonlinear models have been investigated based on approximate methods such as perturbation techniques [26, 38,39,40,41,42,43], the Galerkin method [40,41,42], finite-element method (FEM) [44, 45], finite differential method (FDM) [46, 47], and differential quadrature method (DQM) [31, 48].
Besides the analysis of the dynamics, control of axially moving systems has also been considered in several existing studies. Numerous control strategies to suppress the vibrations of the system have been developed by utilizing the advanced control techniques including the passive damping method, active vibration control methods including feedback control [49], variable-structure control [50, 51], adaptive control [52,53,54], boundary control [55,56,57,58], etc. See [59] for a comprehensive review on control of axially moving systems.
This paper provides an insight into the investigations of the dynamics of axially moving systems. The significant studies on mathematical modeling of the string, beam, belt, and plate models are presented. Both the classical models and the complex nonlinear models describing axially moving systems are reported and classified in Sect. 2. This paper is also concerned with the dynamic models which are discretized by using the approximate methods such as the Galerkin method, the FEM, the FDM, or the DQM. Besides, the numerical and analytical approaches used to determine the vibrational responses of translating systems were also introduced. Furthermore, advanced knowledge on analyzing the stability, bifurcations, and chaotic motions of axially moving systems is also discussed. Finally, this paper proposes several suggestions for future studies in the field of the axially moving system.
Applications of axially moving systems: a Technical textile manufacturing process (https://www.global-safety-textiles.com), b flexible robotic end-effector (https://www.dlr.de/rm/en/desktopdefault.aspx/tabid-11673), c zinc galvanization line (https://www.sms-group.com/press-media/press-releases/press-detail/ssab-contracts-sms-group-to-modernize-hot-dip-galvanizing-line-no-3-in-finland-793/), d nanoscale metal printing process (https://engineering.purdue.edu/Papers/Goswami.pdf)
This paper is divided into six sections. Section 2 presents a review of the significant works on developing the dynamical equations and the associated boundary conditions concerning axially moving systems. Section 3 introduces approximate models. Section 4 presents various methods to solve the equations of motion, whereas Sect. 5 is a review of state-of-the-art studies concerning dynamical analyses. This paper ends with a discussion on the directions for future research in Sect. 6.
2 Dynamic models
2.1 String model
The string model forms the simplest model to describe axially moving systems under tension with negligible bending stiffness of the material. Figure 3 depicts an axially moving string model, wherein l denotes the string length, v denotes the axial velocity, and w(x, t) and u(x, t) denote the lateral and longitudinal displacements of the string, respectively.
2.1.1 Elastic string model
In an early study concerning axially moving systems, Mahalingam [1] used the uniform string model for describing the lateral displacement of a power transmission chain. Without considering axial deformation of the string, the kinetic and potential energies were obtained as \(K=1/2\int _0^l {\left[ {\left( {w_{t} +vw_{x} } \right) ^{2}+v^{2}} \right] } \mathrm{d}x\) and \(P=1/2\int _0^l {T_{0} } w_{x}^{2}\mathrm{d}x\), respectively, and the following partial differential equation (PDE) was developed:
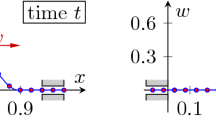
where \(\rho \) denotes the density of the string material, A denotes the cross-sectional area of the string, and \(T_{{0}}\) denotes the applied constant tension. Equation (1) represents the first formulation of the string model. The terms on the left side of Eq. (1) (from left to right) are associated with the lateral acceleration, Coriolis force (due to simultaneous axial and lateral motions), centrifugal acceleration, and tension, respectively, of the unit element of the string at x. The dynamic response of Eq. (1) with an initial condition \(w(x,0)=0.01\sin ({x\pi } \big / l)\) is depicted in Fig. 4. Later, Bapat and Srinivasan [21] and Mote [22] included the effect of axial deformation of the string in the potential energy \(P=1/2\int _0^l {\left( {T_{0} w_{x}^{2}+EAw_{x}^{4}/4} \right) \mathrm{d}x} \) and developed the following PDE.
where E denotes Young’s modulus. In the studies thus far, the strings were assumed nonaccelerating (i.e., constant speed). In reality, however, acceleration and deceleration tend to affect the vibrational behavior of such systems severely. Therefore, the cases that string’s moving velocity was prescribed as a function of time were considered. The following equation of motion for an axially moving string with time-dependent velocity was proposed by Pakdemirli et al. [60]:
where the second term is the additional Coriolis force due to the time-varying velocity.
In the investigation of a moving string with arbitrarily varying length, Fung et al. [44] formulated a set of nonlinear ordinary differential equations (ODE)—governing the motions of the string—via Hamilton’s principle and the variable-domain finite-element method. Later, Zhu and Ni [61] considered a string model with a mass–damper–spring system attached at its lower end, see Fig. 5. Consequently, the dynamic model of a vertically translating string with varying length and tension was derived as follows.
where c denotes the damping coefficient of the material, T(x, t) stands for the axially varying tension in the string, g is the gravitational acceleration, and \(m_{\mathrm{e}}\), \(k_{\mathrm{e}}\), and \(c_{\mathrm{e}}\) denote the “end” mass, the spring constant, and the damping coefficient, respectively, of the mass–damper–spring system attached at the end. Partial differential equation (4) (with (5)) represents the string motion, whereas the ordinary differential equation (6) describes the motion of the end mass. Equation (4) also considers the damping effect of the material by including the term \(c(w_{t} +\dot{{l}}w_{x} )\). The dynamic response of the end mass with an initial condition \(w(x,0)=0.01\sin ({x\pi } \big / l)\) is depicted in Fig. 6.
The vibration of a moving string on a uniform linearly elastic foundation was first investigated by Bhat et al. [62]. In their work, an axially moving string supported along its entire length by a foundation was modeled using Newton’s second law. In contrast, Zhang and Chen [63] used Hamilton’s principle to develop the equation of motion of a string-foundation coupled system as follows:
where \(T_{{0}}\) is the constant tension, and \(k_{\mathrm{f}}\) and \(c_{\mathrm{f}}\) denote the stiffness and the damping coefficient per unit length of the soft foundation, respectively. For investigating a string with a nonlinear foundation, Ghayesh [64] considered an axially accelerating string placed on a partial, nonlinearly elastic foundation, see Fig. 7: In his research, the string was considered to be a three-part system, the middle part of which was supported by a foundation with cubic nonlinear stiffness. The equation of motion for this system under axial deformation is expressed as follows:
where \(k_{\mathrm{l}}\) and \(k_{\mathrm{n}}\) denote the linear and nonlinear stiffness per unit length of the foundation, respectively, and H indicates the Heaviside function.
Vibration of the end mass in Fig. 5 with initial condition \(w(x,0)=0.01\sin ({x\pi } \big / l)\)
2.1.2 Viscoelastic string model
In most works considered thus far, the axially moving strings were considered made of linearly elastic materials. The effect of material damping in the dynamics analysis was usually either neglected or simplified. However, many engineering problems, such as the creep problem of magnetic tapes and conduit vibrations, require an accurate examination of viscoelastic material properties. Under such situations, it becomes necessary to consider viscoelastic strain–stress constitutive relations. Viscoelastic models, see Fig. 8, are usually used to model elastic and viscous properties of the material in the form of springs and dashpots, respectively. Various viscoelastic models have previously been proposed and adopted to describe the viscoelastic properties of the strings [4, 26, 27, 46, 65, 66]. Li et al. [27] and Zhang et al. [66] established a mathematical model for viscoelastic strings based on the Kelvin–Voigt model (Fig. 8a). In this model, the disturbed stress \(\sigma (x,t)\) corresponding to the strain \(\varepsilon (x,t)\) can be expressed using the following stress–strain relation:
where \(\mu \) denotes the dynamic viscosity of the dashpot. Using Eq. (9), the following nonlinear dynamic model for an axially moving viscoelastic string was derived:
In Eq. (10), the sixth term in the left side represents the internal Kelvin–Voigt damping while the last term models the simultaneous presence of axial velocity and Kelvin–Voigt damping. The Kelvin–Voigt model is a simple viscoelastic model that is commonly utilized. However, it is inadequate in the sense that it does not accommodate stress relaxations. Zhao and Chen [67] and Zhao et al. [47] adopted a more general viscoelastic model, known as the standard linear solid model (SLS model) (Fig. 8b, c), to analyze the vibration of axially moving strings. The SLS model is a three-parameter model that considers both creep and stress relaxation. In the SLS model, the stress–strain relationship can be expressed as follows:
where \(E_{{1}}\) and \(E_{{2}}\) denote Young’s moduli of two elastic components in the standard linear solid model.
In Zhao and Chen [67], another model, namely the Burgers model (Fig. 8d) (or it is also popularly called the Maxwell–Kelvin model [68]), was used to investigate the problems involving viscoelastic strings. This model is somewhat complicated in the sense that it is comprised of the Kelvin model with the elastic modulus \(E_{{1}}\) and the viscosity \(\mu _{{1}}\) and the Maxwell model with the elastic modulus \(E_{{2}}\) and the viscosity \(\mu _{{2}}\). In the Burgers model, the stress–strain relationship can be expressed as follows:
Besides the aforementioned differential constitutive laws, those of the integral type, such as Boltzmann’s superposition principle, were also used in modeling the viscoelastic strings. The stress–strain relationship prescribed by Boltzmann’s superposition principle takes the following form:
where \(E_{\mathrm{v}}\) denotes the stress relaxation function. Based on Boltzmann’s superposition principle, the following equation of motion of an axially accelerating viscoelastic string was proposed by Zhao and Chen [4]:
2.1.3 Applications of string model
As already mentioned, the string model is most fundamental in axially moving systems. It is usually used to describe the dynamics of an axially moving material that is entirely flexible concerning bending. These include threads in the technical textile manufacturing processes (Fig. 1a), cables in winding machines, narrow belts, and chains in power transmission systems [1], and papers in paper-making processes [52] to name a few. Many axially moving materials with small flexural stiffness can be modeled as strings by ignoring the flexural rigidity. For example, the string model with varying length was used to model a hoisting cable(s) in a container-crane system [54] and of an elevator [61].
2.2 Beam model
When the bending stiffness of an axially moving material is sufficiently large, it should be considered as a moving beam. In this case, the beam theories such as the Euler–Bernoulli, Timoshenko, and Rayleigh theories can be used to investigate the dynamics of the involved system.
2.2.1 Euler–Bernoulli beam
The Euler–Bernoulli beam model is the simplest and most commonly used one to describe an axially moving beam without shear deformation and rotation of the cross section (only bending). One of the earliest works devoted to the vibration analysis of axially moving Euler–Bernoulli beams was performed by Mote [69]. The potential energy of the beam under a constant tension was assumed as \(P=1/2\int _0^l {\left( {T_{0} w_{x} ^{2}+EIw_{xx} } \right) \mathrm{d}x} \). Subsequently, the equation of motion of a moving beam was obtained as follows [70]:
where EI denotes the flexural rigidity of the beam. For an axially accelerating beam with a time-varying velocity, the governing equation has been derived, and its vibrations were analyzed in [71, 72]. The effect of axial deformation on the dynamic behavior of a moving beam has been investigated in [73]. In 2005, Chen and Yang [74] derived a more general form of the governing equation in the following form:
where T(x, t) is the tension and M(x, t) is the bending moment. If the effect of material damping is simplified, the tension and the bending moment can be written as \(T_{{0}} + {EA}\varepsilon (x, t)\) and \({EIw}_{xx}\), respectively (where \(\varepsilon \) denotes the axial strain). By ignoring the longitudinal vibration completely, the axial strain was obtained as \(\varepsilon \left( {x,t} \right) =1/2w_{x}^{2}\), and (16) was rewritten as follows.
In [74], another form of the equation of motion for a moving beam was also introduced via the use of the quasi-static stretch assumption in [6]. Under this assumption, the tension was assumed to be a function of time alone (i.e., the axial strain \(\varepsilon \left( {x,t} \right) =u_{x} +1/2w_{x}^{2}\) is replaced by the averaged value of the disturbed strain as \(\varepsilon \left( {x,t} \right) =1/l\int _0^l {w_{x}^{2}\mathrm{d}x} )\). The equation of motion of the axially moving beam was obtained as follows:
Equation (18) is known as an integro-partial differential equation (IPDE) [6, 75, 76].
Most studies concerning moving beams involve double overhanging parts of constant length, whereas not many studies concerning axially moving cantilever beams with time-varying length are available in the literature. About this aspect, Wang et al. [77] considered a translating cantilever beam model to analyze the dynamics of a spacecraft antenna featuring time-dependent velocity. The governing equation of this cantilever beam model was expressed as follows:
Duan et al. [78] proposed a non-uniform cantilever beam model wherein the damping coefficient c(x), flexural rigidity EI(x), and mass per unit length \(\rho A(x)\) vary along the beam length. In addition, the lumped mass \(m_{\mathrm{e}}\) attached to one end of the beam was subjected to external load f(x, t); see Fig. 9. The equation of motion for this system is described as follows:
where the external force f(x, t) is given by
and \(\delta \) denotes the Dirac function.
With regard to viscoelastic beam models, the Kelvin–Voigt and SLS models were used to describe the effect of material damping on the dynamic behaviors of the beam. Chen and Yang [79] derived the following equation of motion by employing the Kelvin–Voigt constitutive relation:
In their research, the viscoelastic model did not include the steady dissipation term owing to the axial motion of the beam (i.e., the dissipation term can be neglected when the material enters the steady motion). In this model, the constitution relation can be simply described as \(\sigma =E\varepsilon +\mu \varepsilon _{t} \). The mathematical equations of axially moving strings and beams using the viscoelastic model with the steady dissipation term were proposed by Mockensturm and Gou [80] and Ding and Chen [81], respectively. In their works, the authors assumed that the steady dissipation resulted from the material time derivative, and the constitution relation was given by \(\sigma =E\varepsilon +\mu (\varepsilon _{t} +v\varepsilon _{x} )\). Later, Ghayesh and Amabili [82] used this constitution relation to derive the following bending moment M(x, t) and tension T(x, t) equations:
The following equation of motion was established by substituting (23) into the general governing equation (Eq. (16)) of the beam model.
Dynamical analyses of axially moving viscoelastic beams based on the IPDE model were carried out in [74, 83, 84]. In Chen and Yang [74], the following IPDE was used to investigate the Kelvin–Voigt viscoelastic beam model:
In this work, the axial velocity was supposed to be a harmonic variation about the constant mean speed, namely \(v=v_{0} +\varepsilon v_{1} \sin \Omega _{v} t\), where \(\varepsilon \) is a small parameter, and \(v_{{1}}\) denotes the variation magnitude of the axial velocity. This paper further provided a comparison of instability intervals with the amplitudes of non-trivial solutions obtained using the two viscoelastic beam models described by PDE and IPDE (i.e., Eqs. (22) and (25)). Their numerical results demonstrated that the models tend to change with the associated parameters in the same way: The instability intervals derived from Eqs. (22) and (25) were similar, and the intervals increased with an increase in \(v_{{1}}\) and a decrease in the viscosity coefficient. Meanwhile, the amplitudes of non-trivial solutions increased with a reduction in the nonlinear coefficient \(\sqrt{{EI} \big / {T_{0} l}} \). Additionally, the magnitudes of non-trivial solutions obtained by using Eq. (25) were slightly larger than those derived from Eq. (22).
The SLS model has been used in several studies to describe material properties of viscoelastic beams. Marynowski and Kapitaniak [85] derived the equation of motion of a translating beam via the use of the SLS model. In their work, the constitutive relation of the SLS model was obtained by considering it as a degenerate case of the generalized Maxwell model (Fig. 8b, i.e., the SLS model–Maxwell representation). In this case, the bending moment M(x, t) of the beam is expressed as
Later, Wang et al. [7] analyzed the dynamics of a translating viscoelastic cantilever beam based on the SLS model–Kelvin representation (i.e., a degenerate case of the generalized Kelvin–Voigt model, Fig. 8c). In this model, the bending moment M(x, t) of the beam is determined using the following equation:
The influence of other complicated effects such as thermal or fluid nature on the dynamic behavior of axially moving beams has also been examined. Kazemirad et al. [86] presented an analysis of thermal effects on the nonlinear vibrations of a translating beam attached to an intermediate spring–mass support through the following PDE:
where \(\alpha _{\mathrm{th}}\) denotes the thermal expansion coefficient of the beam, \(\Delta T_{\mathrm{th}}\) signifies the rise in temperature, and \(k_{\mathrm{l}}\), \(k_{\mathrm{n}}\), and \(x_{\mathrm{m}}\) represent the linear stiffness, nonlinear stiffness, and position of the spring–mass support, respectively. Gosselin et al. [87], Lin and Qiao [31], and Ni et al. [88] examined the vibrations of a translating cylindrical beam surrounded by fluid. These studies demonstrate that the dynamic behavior of a beam is influenced by the normal and longitudinal components of the viscous force (\(F_{\mathrm{N}}\) and \(F_{\mathrm{L}}\), respectively) per unit length. Values of \(F_{\mathrm{N}}\) and \(F_{\mathrm{L}}\) can be calculated using the linearization scheme in [87] as follows:
where
In Eq. (31), \(C_{\mathrm{F}}\) and \(C_{\mathrm{D}}\) denote the form coefficient and the friction coefficient of the cylindrical beam in the cross-flow, respectively, and \(v_{\mathrm{max}}\) is determined by using the following relation:
The dynamics of a fluid-conveying pipe, which is considered as a special type of axially moving systems, has also been investigated; see Païdoussis [89] for the detailed review. In contrast to an axially moving system that moves by itself, only the fluid inside the static pipe flows axially. However, from the dynamical point of view, the fluid-conveying tube is similar to an axially moving material. The fluid-conveying pipe can be modeled by linear [90,91,92,93] or nonlinear [94,95,96,97] models. In [90], a vertically fluid-conveying pipe was modeled by a uniform tubular beam, and the dynamic model of the pipe was established based on the Euler–Bernoulli beam theory as follows:
where \(\rho \) and \(A_{\mathrm{p}}\) are the mass density and the cross-sectional area of the tubular beam, respectively; M denotes the mass per unit length of the fluid, \( A_{\mathrm{f}}\) is the cross-sectional flow area, and V indicates the flow velocity; \({\bar{T}}_{0} \) and \({\bar{p}}\) are the externally applied tension and the internal pressure at the downstream end of the pipe, respectively. In [92, 93], the dynamics of fluid-conveying pipes were also analyzed via the simple mathematical formulations of fluid-conveying pipes, wherein the gravity, the internal damping, the externally imposed tension, and the pressurization effects were neglected. The simplified equation of motion of the pipe takes the following simple form [93]:
In addition, various nonlinear dynamic models of fluid-conveying pipes were also developed and analyzed based on diverse approaches and assumptions; see [94,95,96].
Besides the above macroscale beams, investigations on axially moving nanobeams were also performed [98,99,100,101]. Lim et al. [98] established a mathematical model of translating nanobeams using Eringen’s nonlocal elasticity approach [102] for the first time. Later, Li et al. [100] developed a dynamic model of an axially moving piezoelectric nanobeam under the thermoelectromechanical forces. In [101], the nonlocal strain gradient theory was utilized to derive the equation of motion of a translating Euler–Bernoulli nanobeam. In another work on axially moving beams, Sarigul [103] studied the dynamics of a beam with multiple edge cracks. In this work, the author separated the beam into two parts around the crack, and a highly stressed region due to the crack was modeled by considering the energies of two springs. Therefore, a hybrid axially moving system consisting of multiple Euler–Bernoulli beams connected by translational and rotational springs was investigated.
2.2.2 Timoshenko beam
The Timoshenko beam theory considers the effects of both shear deformation and rotational inertia. Therefore, it is more appropriate to describe the behavior of thick and short beams and to predict the frequencies of the high modes in the vibration, because the shear deformation becomes important in such cases. In [104], the equation of motion of an axially moving Timoshenko beam under uniform axial tension was used for spectral analysis of the lateral vibration of the beam. Later, An and Su [105] formulated an approximate model of a translating Timoshenko beam based on the previous PDE equation in [104]. In accordance with the Timoshenko beam theory, the dynamic model of an axially moving beam can be described using the following differential equations of two variables (i.e., the lateral vibration w(x, t) and the rotational angle of the cross section \(\theta (x\), t)):
where G denotes the shear modulus, and \(\kappa \) denotes the shear coefficient. The Timoshenko beam theory assumes that the distribution of shear deformation is uniform. The shear coefficient \(\kappa \) was introduced to compensate for the drawback of the uniformity assumption. Yan et al. [106] and Ding et al. [107] presented the following IPDEs to describe the dynamic behavior of a translating Timoshenko beam:
Similar to the Euler–Bernoulli beam theory, comprehensive studies concerning viscoelastic Timoshenko beams have also been performed. The lateral vibrations of an axially moving viscoelastic Timoshenko beam were investigated by Mokhtari and Mirdamadi [108] using the following equations:
The vibration characteristics of short conveying fluid pipes have also been investigated using the Timoshenko beam theory [109,110,111,112,113,114]. The early conveying fluid pipe model based on the Timoshenko beam theory was presented by Huang [109]. Later, Laithiers and Païdoussis [110] used the Hamilton principle to develop the equation of motion of an initially stressed Timoshenko pipe. Furthermore, the dynamic model of microscale conveying fluid pipes was also established via the Timoshenko beam theory in [113].
Ding et al. [105] investigated the supercritical natural frequencies of a moving beam using the Timoshenko beam theory. They numerically showed that the natural supercritical frequencies were affected by the system parameters such as bending stiffness, rotary inertia, and shear force. Subsequently, the authors compared the natural frequencies of the Timoshenko beam model with those using the Euler–Bernoulli beam model. When the axial velocity was in the vicinity of the critical speed, the first natural frequency of the moving Euler–Bernoulli beam was smaller than that of the Timoshenko beam. However, the natural frequencies of the Euler–Bernoulli beam became higher as the axial velocity increased.
2.2.3 Rayleigh beam
The Timoshenko beam theory predicts the dynamic behavior of a thick and short beam more accurately compared to the Euler–Bernoulli beam theory. The Timoshenko beam theory can lead to more complicated mathematics. In the early 1890s, Rayleigh proposed another beam-modeling theory, which includes the effect of rotation of the cross section without the consideration of the shear force. Mathematically, the Rayleigh beam equation is more straightforward compared to that of the Timoshenko beam. Besides, the Rayleigh beam theory can predict the vibrational behavior more accurately compared to the Euler–Bernoulli beam theory.
Ghayesh and Balar [26] investigated the nonlinear vibration of a Rayleigh beam made of a viscoelastic material that can be described by the Kelvin–Voigt constitutive relation. The governing equation of the beam was obtained in the fourth-order differential equation as follows:
With regard to the Rayleigh beam theory, Razaee and Lotfan [116] also performed a study concerning the nonlinear nonlocal vibration of an axially moving nanoscale beam. In the said study, the nonlocal beam theory (i.e., the congruity between the atomic theory of lattice dynamics and experimental observation) was also used to consider small-scale effects in the nanoscale beam. Accordingly, the nonlocal bending moment \(M_{\mathrm{n}}\) and axial force \(N_{\mathrm{n}}\) are expressed as follows:
where \(e_{{0}}\) is the material constant and a denotes the characteristic length. The term \(e_{{0}}a\) is a function of boundary conditions and molecular lattice [117]. Subsequently, the following equation of motion was developed to analyze the stability of the nanoscale beam:
2.2.4 Laminated composite beam
All formulations of axially moving systems introduced in the previous sections are exclusively applicable to isotropic materials. In recent years, however, in addition to isotropic materials, laminated composite materials comprising of two or more layers of orthotropic materials with different properties have also been used in axially moving systems, such as paper sheets, fluid pipes, band saws, and aerospace structures. Ghayesh [118] has discussed the dynamics of a translating symmetrically laminated composite beam with time-varying velocity. According to the classical laminate theory (an extension of the classical plate theory), the governing equation of such a system is expressed as follows:
where b denotes the width of the beam and \(D_{{11}}\) is the first element of the bending stiffness matrix expressed as
where \(h_{n}\) denotes the distance from the external boundary of the nth layer to the i-axis; \(\theta _{\mathrm{a}}\) represents the angle from the i-axis to the normal direction of the fibers, and \(Q_{ij}\) (i, \(j \quad = 1\), 2,..., 6) are the stiffness elements of the material used in each layer. Later, Li et al. [119] updated the dynamic model of an axially moving laminated composite beam by including the environmental effects such as thermal stresses and blast loads. Dynamic models of axially moving materials with a sandwich structure were also studied in [120,121,122,123,124,125,126]. Marynowski [120] developed the mathematical model of a translating sandwich beam (Fig. 10) wherein the core layer of the beam is viscoelastic material, and only shear deformation is considered in this layer. The equation of motion of the system is given as follows:
where \(h_{\mathrm{in}}\), \(h_{\mathrm{out}}\), and b are the geometrical parameters shown in Fig. 10, and G is the shear modulus. Later, Lv et al. [121] analyzed the lateral vibration of a similar viscoelastic sandwich beam, neglecting shear deformation, whereas Yang et al. [122] considered a sandwich beam with a soft core. Furthermore, Wei et al. [123] presented the dynamic behavior of an axially moving beam with a magnetorheological fluid core and aluminum outer layers under a magnetic field. Two years later, Hao and Gao [124] analyzed the lateral vibrations of a moving beam with shape memory alloy outer layers.
2.2.5 Applications of beam model
From the physical viewpoint, the beam model can be used to analyze the dynamics of thick axially moving systems more accurately compared to the string model owing to the consideration of bending moment. The saws of metal-cutting band-saw machines and the steel strips in automatic winding machines can be modeled using the beam model. In addition, the axially moving cantilever beam model can be used to describe the dynamics of a flexible robotic end-effector (Fig. 1b), a drill string [127], an aerospace structure [77], and a hosting rod with a free end [61].
2.3 Belt model
In modeling axially moving systems as strings or beams, the longitudinal vibrations are either neglected or simplified using the quasi-static stretch assumption [6]. In the belt model, the coupling between the lateral and longitudinal vibrations, which becomes significant with increasing slenderness ratio of the material (the ratio of length to the cross-sectional area), is investigated [13, 128,129,130,131,132,133,134,135,136,137]. In an early study published concerning the axially moving belt, Thurman and Mote [13] developed the nonlinear governing equations of a uniform translating strip based on the Euler–Bernoulli beam theory. In their work, the kinetic and the potential energies were obtained as follows:
where the strain \(\varepsilon \) is given by \(\varepsilon =\sqrt{w_{x} ^{2}+\left( {1+u_{x}^{2}} \right) } -1\). The equations of motion are expressed as follows:
Equations (50–51) represent a comprehensive dynamic model for axially moving belt. However, it is too complicated mathematically because of the nonlinear property of the strain \(\varepsilon \). Therefore, simpler models dealing with various approximated strains were developed in [12, 129,130,131] to facilitate the analysis of the dynamics of the moving belt. Ghayesh [131] used the approximate strain \(\varepsilon =u_{x} +1/2w_{x}^{2}\) to develop the following dynamic model of an axially moving belt:
Later, Ghayesh and Amabili [132, 133] investigated the nonlinear dynamics of an axially moving belt based on the Timoshenko beam theory. The following mathematical model for the longitudinal and lateral vibrations and the rotational angle of the cross section was established:
In an investigation on axially moving viscoelastic material, Chen and Ding [25] used the Kelvin–Voigt model to establish a set of PDEs describing a moving belt as follows.
In their study, the steady-state lateral responses of the belt model were also assessed and compared against those obtained using the beam model.
In contrast to the in-plane vibrations of the system (i.e., lateral and longitudinal vibrations in the plane of i- and j-axis), only a limited number of studies have been performed concerning the lateral, transverse, and longitudinal vibrations [134,135,136,137]. In [136], the following nonlinear PDEs were developed to analyze the vibrations in i-, j-, and k-axis of an axially accelerating material:
where u, w, and \(\eta \) denote the lateral, longitudinal, and transverse vibrations, respectively, and I and \(I_{\mathrm{z}}\) stand for the moments of inertia about the j- and k-axis, respectively.
To compare the dynamic characteristics of the beam models in Eqs. (17) and (18) and the belt model in Eqs. (50)–(51), Ding and Chen [138] investigated the effects of system parameters on the natural frequencies of the lateral vibration. The authors indicated that the tendencies of the first and second natural frequencies calculated from these models were similar when the axial velocity and the flexural stiffness increased. When increasing the nonlinear coefficient and the magnitude of the initial condition, the changes in natural frequencies corresponding to Eqs. (18) and (50)–(51) were not different, whereas those predicted by Eq. (17) tended to increase more than the other two. Later, Ding and Chen [10] presented non-trivial equilibrium solutions of an axially moving material in the supercritical regime, which were derived based on these three models. Using numerical simulations, the authors showed that the non-trivial equilibrium solutions of Eqs. (18) and (50)–(51) were the same, while the solution of Eq. (17) was different from those explicitly. Furthermore, in view of supercritical equilibrium solutions of axially moving systems with non-ideal boundary conditions, the similarity between the models described by Eqs. (18) and (50)–(51) was demonstrated in [139]. The above studies indicate that the dynamic characteristics of the beam model under the quasi-static stretch assumption (i.e., Eq. (18)) show an affinity with the one of the belt model (i.e., Eqs. (50)–(51)).
Due to consideration of both lateral and longitudinal vibrations, the belt model is suitable for modeling axially moving components with sufficient length, wherein the distance between two support points is significant. Strips and wires in zinc galvanization lines (Fig. 1c) and belts used in power transmission systems are typical examples. Besides, the belt model can also be used to model the systems wherein the longitudinal vibrations can seriously affect the quality and productivity, such as a roll-to-roll printing process to produce flexible circuits.
2.4 Plate model
The axially moving string/beam/belt models are one-dimensional model from the sense that one independent spatial variable x appears in the equation of motion. The use of such models leads to a satisfactory result in numerous cases. However, these one-dimensional models cannot be applied in situations that the material is of considerable width, such as a metal layer (Fig. 1d). In such circumstances, the plate model that is a two-dimensional model that involves two independent spatial variables x and z should be used to analyze the vibrations.
The earliest work in this aspect was reported by Ulsoy and Mote [140]. In their study, a PDE model describing the dynamics of the blade of a band saw was developed based on the Hamilton principle. An approximate solution of the equation of motion was also obtained by using both the classical Ritz and finite-element-Ritz methods. Later, Marynowski and Kolakowski [17] established a nonlinear model of an axially moving orthotropic plate: In Fig. 11, the length, width, and thickness of the plate are denoted by l, b, and h, respectively, while the lateral, longitudinal, and transverse vibrations are indicated by w(x, z, t), u(x, z, t), and \(\eta (x\), z, t), respectively. Based on the von Karman strain theory, the strain–displacement relations were obtained as follows:
where \(\varepsilon _{\mathrm{X}}\), \(\varepsilon _{\mathrm{Z}}\), and \(\varepsilon _{\mathrm{XZ}}\) denote the strain components for the middle plate in the x and z coordinates, whereas \(\kappa _{\mathrm{X}}\), \(\kappa _{\mathrm{Z}}\), and \(\kappa _{\mathrm{XZ}}\) represent the curvature modifications and torsions of the central surface of the plate. The stress functions \(\sigma _{\mathrm{X}}\), \(\sigma _{\mathrm{Z}}\), and \(\sigma _{\mathrm{XZ}}\) and the bending moments \(M_{\mathrm{X}}\), \(M_{\mathrm{Z}}\), and \(M_{\mathrm{XZ}}\) are given as follows:
where G denotes the shear modulus of the plate, \(E_{\mathrm{X}}\) and \(E_{\mathrm{Z}}\) are Young’s moduli of the plate along the i- and k-axis, respectively, the ratio \(\chi = E_{\mathrm{X}}/E_{\mathrm{Z}}\) indicates the orthotropic factor of the plate, and \(\upsilon \) is Poisson’s ratio. Based on the Hamilton principle, the dynamic model of the axially moving plate was written as follows:
where \(\rho \) denotes the mass density and F stands for the lateral loading. Compared to axially moving orthotropic plates, studies concerning translating isotropic plates have attracted greater interest owing to its diverse research prospects. For isotropic materials, expressions for the stress functions \(\sigma _{\mathrm{X}}\), \(\sigma _{\mathrm{Z}}\), and \(\sigma _{\mathrm{XZ}}\) are rewritten as follows:
where E denotes Young’s modulus of the isotropic material. Under the stresses in Eq. (67), mathematical models of axially moving isotropic plates were also established in [15, 28, 141].
Lin and Mote [142] and Liu et al. [143] analyzed the dynamics of axially moving plates with large displacements. In such cases, the stress induced by large deflections tended to influence the dynamic responses of the plate significantly. In their works, the von Karman large deflection theory that can model the plate stress arising from the plate curvature was used to develop the following governing equations for translating plates:
where \(D=Eh^{3}[12(1-\upsilon ^{2})]\) denotes the bending stiffness. Equations (68) and (69) are partial differential equations relating the large-amplitude vibration w(x, z, t) and the stress function \(\Phi (x\), z, t). The biharmonic operator \(\nabla ^{4}\) and the operator \(L\left( {\omega ,\Phi } \right) \) were defined as follows:
Similar to the string, beam, and belt models, the viscoelastic models have also been used to describe material properties while considering the vibration of axially moving plates. Based on the Kelvin–Voigt model, Zhou and Wang [48] investigated the dynamic behavior and the stability of an axially moving viscoelastic plate. Later, Abedi et al. [14] derived the dynamic model for an axially moving viscoelastic material obeying the von Karman large deflection theory. Marynowski [144] used the SLS model to establish a mathematical formulation describing a translating hybrid plate consisting of both elastic and viscoelastic regions. Subsequently, the author presented the solution to a simplified case wherein the pure viscoelastic plate.
Concerning axially moving laminated composite plates, Hamita et al. [145], based on the classical laminate theory, developed the governing equation of a moving laminated plate. Zhang et al. [146] employed the high-order shear deformation theory (HSDT) to establish the dynamic model of a laminated composite cantilever plate. The HSDT assumes that a displacement can be expanded to a cubic function in the thickness coordinate. Essentially, this theory is more efficient in comparison with the classical laminate theory in the analysis of laminated composite plates. Arani et al. [33] used a third-order shear deformation theory to develop the mathematical model of a moving plate on a visco-Pasternak foundation. In their work, the system was subjected to a longitudinal magnetic field, and the effect of this magnetic field on the critical velocity of the plate was investigated. In [147], the influence of the inherent small scale of a moving viscoelastic microplate was considered via the use of the modified coupled stress theory, and the sinusoidal shear deformation theory (SSDT) was used to develop the dynamic model of the plate. The authors also compared the results obtained via the use of SSDT with those obtained using the classical plate theory. In [148], a nanocomposite plate moving along the i- and k-axis was investigated based on various shear deformation theories. Furthermore, Liu et al. [149] established a mathematical model describing an axially moving nanoplate using the nonlocal elasticity theory proposed by Eringen and Edelen [150].
Besides the studies considering the influence of material properties on the dynamic behavior of moving plates, the effect of the external environment has also been discussed in numerous researches. Marynowski and Grabski [35] developed a mathematical model of an axially moving plate subjected to thermal loading. In their model, the potential energy of the plate included the strain energy due to heating to consider the effect of temperature on plate dynamics. Yao and Zhang [151] developed a dynamic model based on the thin-plate and linear potential-flow theories for the investigation on the dynamics of a moving plate subjected to surrounding airflow. Concerning the effect of fluid flow, Wang et al. [32, 152] revealed that the fluid pressure has a significant influence on the vibration characteristics and the stability of the moving plate-fluid system. This study not only presented the equation of motion of an axially moving plate partially immersed in fluid in a rigid container but also discussed the effect of parameters such as immersed-depth ratio and the distance between the plate and container walls on the vibration characteristics of the plate. Additionally, around the same time, Hu et al. [34] published a study concerning the influence of electromagnetic forces on a moving plate. In this work, the nonlinear governing equation describing an axially moving plate in the magnetic field was developed and subsequently used to analyze its complicated dynamic behaviors.
The plate model is a reasonable means for the analysis of axially moving components withstanding tensile stresses and bending. The axially moving plate model can accurately predict the vibration behavior of numerous systems such as the metal sheets in thin-metal production lines and coil-coating processes as well as the metal layers in the nanoscale metal printing (Fig. 1d).
2.5 Boundary conditions of axially moving systems
Boundary conditions significantly affect the vibration behavior of axially moving systems. Most studies usually deal with simply supported boundaries, which do not experience any deflection and torque. In this case, the considered system has the ideal boundary conditions. In practice, the boundary conditions, however, are non-ideal due to the operation of other machine elements or the influence of external excitations. Dynamic analyses of axially moving systems with non-ideal boundaries were presented in [153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168]. Wang and Mote [154] investigated the mathematical model of a band-wheel mechanical system, as shown in Fig. 12, wherein the wheels were supported by linear springs of stiffness \(k_{\mathrm{L}}\) and \(k_{\mathrm{R}}\) (i.e., left spring and right spring, respectively). In this work, the axially moving band with the following tension was modeled using the belt model.
where \({\bar{k}}\) is the equivalent support stiffness. Using Hamilton’s principle, the following equations of motion of the system were developed.
The non-homogeneous boundary conditions at \(x = 0\) are
and at \(x = l\)
where the lateral and longitudinal vibrations of the top and bottom spans are denoted by \((w_{1} ,u_{1} )\) and \((w_{2} ,u_{2} )\), respectively; \(J_{\mathrm{R}}\), \(m_{\mathrm{R}}\), and \(R_{\mathrm{R}}\) indicate the rotational inertia, the mass, and the radius of the right wheel; and \(J_{\mathrm{L}}\), \(m_{\mathrm{L}}\), and \(R_{\mathrm{L}}\) denote the corresponding variables for the left wheel; h indicates the band thickness. \(M_{\mathrm{R}}\) and \(M_{\mathrm{L}}\) are the constant moments at the ends of the span, which arise from the bending of the continuous band around the wheels. The authors then linearized the nonlinear equations of motion (i.e., Eq. (72)) and developed an ODE model based on the Galerkin method. Subsequently, the equilibrium configuration, vibration modes, and the influence of system parameters on the coupled vibrations were analyzed. In another investigation concerning the lateral vibration of a moving beam wrapped on fixed pulleys (Fig. 13b), Yue [155] examined the case in which the contacting points between the belt and the pulley were not fixed on the common tangent line between two pulleys during vibration; therefore, the span length was varying. Later, Hwang and Perkins [156] revisited the previous model in [154] and investigated large static band deflections described by the inextensible elastic theory, wherein the contacting points were not fixed. An approximated model that included the rod rigid body modes was developed by the Ritz method. The prediction of the system’s vibration behaviors was subsequently experimentally verified. In [157], two distinct vibration models of belt/pulley systems, i.e., Fig. 13a, b, were presented. The differences in these models in natural frequencies were also discussed via numerical analyses. In other studies, Orloske et al. [158, 159] investigated a full mathematical model describing both in-plane and out-plane displacements of a belt/pulley system undergoing parallel pulley misalignment. Under the misalignment, the boundary conditions were non-homogeneous, and the number of boundary conditions was fewer than the total order of spatial derivatives in the dynamic model. To handle this issue, the authors derived a simpler form of the dynamic model by assuming negligible geometric torsion and using Taylor’s serial expansion. The equilibria, bifurcation, stability, and vibration characteristics of this system were then analyzed based on this simple model.
Investigations on axially moving viscoelastic materials with non-ideal boundary conditions were introduced in [160,161,162,163,164,165,166]. In [160, 161], the belt in a belt/pulley system with a one-way clutch was modeled as a translating viscoelastic beam using the Kelvin–Voigt model. The equations of motion of the belt are given by
and the non-ideal boundary conditions are
where R denotes the radius of pulleys and \(T_{{1}}\) and \(T_{{2}}\) are the dynamic tensions, which correspond to the dynamics of the pulleys and one-way clutch. Later, Ding [162, 163] studied the vibration response of the above-mentioned belt/pulley system undergoing dual excitations. Furthermore, Ding et al. [164] experimentally investigated the damping effect of the one-way clutch on the previous belt/pulley system. In a study concerning axially moving systems with non-homogeneous boundary conditions, Ding et al. [165] presented a PDE model describing the dynamic of an axially moving viscoelastic belt wrapping around two pulleys with different radii. Based on the PDE model, the influence of the non-homogeneous boundary conditions on the equilibrium configuration and the natural frequencies was analyzed. Around the same time, Ding et al. [166] used the IPDE to model the system in [165] and then investigated the static equilibrium shape of the belt and the steady-state response of the forced vibration.
Axially moving systems with non-ideal boundary conditions due to the excitation of external forces were investigated in [167]. In this work, the right boundary of a moving string was excited by an arbitrary lateral force; and the lateral vibration behavior was then determined through the Laplace transforms method. Yurddas et al. [168] analyzed the nonlinear vibrations of a translating string subjected to four supports: Two supports at the ends of the string were considered as ideal supports, and two supports located in the middle of the string span allowed minimal deflections. These supports divide the string into three regions with different boundary conditions.
3 Approximate model
In many investigations concerning the analysis of the dynamics of axially moving systems, approximate methods have been used to convert the PDEs, describing system vibrations, into a low-dimensional system of ordinary differential equations (ODEs) to facilitate the use of certain techniques employed for solving discrete problems. One of the most well-known techniques is the Galerkin method, also known as the Galerkin approximation. This method has been widely used in axially moving systems. Wickert and Mote [43] developed ODEs of a string model using the classical Galerkin method, which assumes that the solution of the equation of motion takes the following form:
where \(q_{i}(t)\) is a set of generalized displacements of the string, and \(\varphi _{i}(x)\) represents the set of basis functions satisfying all boundary conditions. The said basis functions are chosen to be the eigenfunctions of a linear static string for given boundary conditions as follows:
According to the Galerkin method, a set of n coupled ODEs in the following generalized form is established.
where M, C, and K refer to the global matrices of the mass, damping coefficient, and string stiffness, respectively, while \({\ddot{\mathbf{q}}}\), \({\dot{{\mathbf{q}}}}\), and \({\mathbf{q}}\) represent the string accelerations, velocity, and deflection vectors, respectively. The Galerkin method, wherein basis functions are given by Eq. (78), has also been used to discretize the PDEs of the beam and coupled models [41, 76, 129, 169]. Apart from the classical Galerkin method, the complex-mode Galerkin method has also been used to solve the problems concerning axially moving strings, as proposed by Zhang et al. [66]. In this method, the basis functions must satisfy the boundary conditions and special orthonormality relations of the gyroscopic system. Additionally, through the comparison of numerical results, the authors also revealed that the convergence velocity of the complex-mode Galerkin method is higher compared to that observed when using the classical approach.
Marynowski and Kolaknowski [17], Marynowski and Grabski [35], and Wang et al. [170] extended the Galerkin method to discretize the equations of motion and boundary conditions of axially moving plate systems. The extended Galerkin method requires the basis functions to satisfy the kinetic boundary conditions while not necessarily satisfying the dynamic ones. With regard to two-dimensional plate models, out-of-plane deflection can be assumed to take the following form:
where \(q_{ij}(t)\) refers to the unknown functions of time; \(\varphi _{i}(x)\) and \(\psi _{j}(z)\) denote the basis functions; and \(n_{i}\) and \(n_{k}\) refer to the total number of basis functions concerning out-of-plane defections along the i and k directions. Basis functions \(\varphi _{i}(x)\) can be chosen similar to the case of a simply supported beam, whereas \(\psi _{j}(z)\) possesses the same form as the case of a free-free beam. By employing the extended Galerkin procedure, the governing equation, described by a set of \(n_{i}\).\(n_{k}\) coupled ODEs concerning out-of-plane deflections of a plate model, can be expressed in the matrix form similar to Eq. (79).
Shin et al. [171] used the extended Galerkin method to develop an approximate model for axially moving plates, wherein the equations of out-plane deflections (i.e., u(x, z, t) and \(\eta (x\), z, t) in the i–k plane) can be solved independently to w(x, z, t). Consequently, two matrix-vector equations, each concerning in-plane and out-of-plane deflections, were established as follows:
where \(\mathbf{q} _{\mathrm{u}\upeta } \) and \(\mathbf{q} _{\mathrm{w}}\) denote the \(2m_{i} \cdot m_{k}\) and \(n_{i}\cdot n_{k}\) vectors, respectively (\(m_{i}\) and \(m_{k}\) denote the total number of basis functions concerning the defections); \(\mathbf{M} _{\mathrm{u}\upeta }\), \(\mathbf{G} _{\mathrm{u}\upeta }\), \(\mathbf{H} _{\mathrm{u}\upeta }\), and \(\mathbf{K} _{\mathrm{u}\upeta }\) denote the global matrices for the mass, gyroscopic component, centrifugal component, and stiffness in the in-plane deflections, respectively. The corresponding notations for the out-of-plane deflections are \(\mathbf{M} _{\mathrm{w}}\), \(\mathbf{G} _{\mathrm{w}}\), \(\mathbf{H} _{\mathrm{w}}\), and \(\mathbf{K} _{\mathrm{w}}\). Lastly, \(\mathbf{f} _{\mathrm{u}\upeta } \) and \(\mathbf{f} _{\mathrm{w}}\) denote the external force vectors. It is noted that \(\mathbf{K} _{\mathrm{w}}\) is a function of \(\mathbf{q} _{\mathrm{u}\upeta }\). The vector \(\mathbf{q} _{\mathrm{u}\upeta }\) as well as the longitudinal and transverse displacements, u(x, z, t) and \(\eta (x\), z, t), can be obtained independently without considering the lateral displacement w(x, z, t) by solving Eq. (81). In addition, once \(\mathbf{q} _{\mathrm{u}\upeta }\) is determined, Eq. (82) can be solved to determine the lateral displacement. For a plate model with large displacement, the equations of motion become the PDEs of two variables, that is, the large-amplitude deflection w(x, z, t) and the stress function \(\Phi (x\), y, t) (refer to Eqs. (68) and (69)). To convert the said PDEs to ODEs through the use of the extended Galerkin method, Liu et al. [143] assumed that w(x, z, t) and \(\Phi (x\), z, t) are given as follows:
where \(q_{ij}(t)\) and \(\phi _{ij}(t)\) denote the sets of generalized displacements and stress variables concerning the plate. To obtain the set of ODEs, the stress function was first determined using the extended Galerkin method for Eq. (69), thereby yielding a function that depends on the generalized displacement \(q_{ij}(t)\). Subsequently, this stress function can be substituted into Eq. (68), and the extended Galerkin method can be used again to establish a set of ODEs.
Another approximate method to discretize the equation of motion, known as the finite-element method (FEM), has also been widely used in the studies related to axially moving systems [44, 45, 172,173,174], especially with regard to models involving time-varying material lengths. Fung et al. [44] and Chen and Ferguson [45] employed the FEM technique to establish ODEs concerning a translating string model with time-varying length. In their studies, since the length of the string was a function of time t, the FEM analysis pertaining to a fixed-sized domain proved to be unsuitable. Investigators, therefore, employed an FEM technique involving a variable-domain and constant number of elements, for instance, the work of Stylianou and Tabarrok [172, 173]. In these techniques, as long as the string length changes, the length of each element also changes correspondingly. The string is first discretized into n elements with the lateral displacement w(x, t) within a linear element j being expressed as follows:
where \(\mathbf{N} _{j}\) denotes the shape function—a function of x and length l(t), whereas \(\mathbf{q} _{j}\) represents the nodal variable vector. Subsequently, the governing equation for each element j can be derived by calculating the energy within each element j using Lagrange’s equation. Lastly, the global equation of motion described by ODEs can be established by assembling all elemental governing equations in the form expressed as follows:
where M, C, and K denote the global matrices for the mass, damping coefficient, and string stiffness, respectively, and S is the matrix of the nonlinear term of the nodal displacement. It is to be noted that matrix S is not constant, but a function of Q instead. Equation (86) becomes a nonlinear differential equation with time-dependent coefficients. It can be solved using numerical techniques, such as the Runge–Kutta [44] and Newmark-Beta [45] methods. For axially moving plate models, Hatami et al. [175] developed FEM-based formulations for each element of the plate, wherein the lateral, longitudinal, and transverse deflections of nodal points in the mid-plane were considered.
In addition to the Galerkin method and the FEM, the finite difference method (FDM) has also been utilized for discretizing the equations of motion of axially moving systems. The first step toward establishing an FDM-based approximate equation involves discretizing independent PDE variables (i.e., spatial and temporal variables) into a finite number of small segments \(\Delta x\) and \(\Delta t\) and establishing an equispaced mesh grid with grid points (\(x_{j}\), \(t_{j})\). Subsequently, derivative terms in the PDE at each grid point can be converted into algebraic approximations via Taylor-series expansion. For axially moving systems, Ding and Chen [138] employed the FDM method to derive the following equations for solving the lateral vibration responses of a translating beam at the grid point\(\left( {{\bar{x}}_{i} ,{\bar{t}}_{j} } \right) \):
where
The FDM is also a highly efficient numerical method for the analysis of axially moving strings considering viscoelastic material properties through the use of appropriate models, especially compound models such as the Burgers model and the standard linear solid model [47, 67]. Using the FDM, PDEs of the equations describing the stress–strain relationship can be discretized. Subsequently, the resulting equations can be combined to determine the vibration behavior of the string. Furthermore, to solve nonlinear PDEs describing the lateral vibrations of a translating viscoelastic plate, Yang et al. [176] used the FDM approach in both the spatial and temporal domains in consideration of spatial differentiation based on a \(3\times 3\) mesh grid.
Another approach for developing an approximate model involves the differential quadrature method (DQM) [31, 83, 177]. In the DQM, the spatial variable x is discretized into N nodes. Subsequently, the partial derivative of the function with respect to variable x at a node can be described by means of a weighted sum of the functions at all nodes. For example, in the investigation performed by Lin and Qiao [31], the partial derivative of the lateral vibration of a translating beam at the ith node was approximated as follows:
where d denotes the dth derivative and \(A_{ij}^{(d)} \)denotes the weighting-coefficient matrix to be determined. This approximation is substituted into the equation of motion with appropriate boundary conditions, thereby leading to the establishment of DQM-based ODEs. These ODEs can be expressed in the matrix form as follows:
where M, C, and K denote the global matrices for the mass, damping coefficient, and stiffness, respectively; \(\Omega \) and \({\bar{w}}\) denote the dimensionless frequency and amplitude of the vibration. In Eq. (90), \(\Omega \) can be determined by setting the determinant of the coefficient matrix equal to zero to obtain a non-trivial solution. DQM can also be used for solving translating-plate models, wherein both spatial variables x and z are discretized into discrete points. Zhou and Wang [48] and Robinson [178] developed approximate models for axially moving viscoelastic plates. With regard to dynamic models described by an IPDE (e.g., Eq. (18)), in conjunction with DQM, the integral quadrature method (IQM) can be used to derive the set of ODEs concerning system vibration [83, 84, 179]. In such systems, differential terms can be approximated using DQM, whereas the integral term can be expressed by using IQM as follows:
where \(I_{k}^{ij} \) denotes the integral weighting coefficients and g(x, t) is an arbitrary function.
4 Vibration solutions
To evaluate the influence of the parameters on the dynamic response of axially moving systems and to determine the parameters needed for vibration control, vibration behaviors are usually analyzed by solving the equations of motion pertaining to both linear and nonlinear cases. As regard to linear models, exact solutions can be determined using the techniques such as Laplace transform [37] and the Lie group theory [27]. However, it is impossible to determine exact solutions to the nonlinear equations of motion of axially moving systems. Therefore, approximate solutions have been obtained for analyzing the vibrations of a nonlinear model via the use of numerical, analytical, or combined numerical–analytical methods.
4.1 Numerical solutions
When using numerical methods [43, 44, 85, 170, 180, 181], an approximate model is usually established first based on a technique presented in Sect. 3. Subsequently, an approximate solution of the equations of motion can be obtained using techniques such as the Runge–Kutta and Newmark-Beta methods. In other words, the spatial discretization is performed based on the methods such as the Galerkin approximation, FEM, or DQM. In contrast, the temporal discretization can be performed using the Runge–Kutta or Newmark-Beta methods. For example, to investigate the dynamic response of an axially moving string with time-varying length, Fung et al. [44] solved the nonlinear FEM-based equations of motion using the Runge–Kutta method. In contrast, Chen and Ferguson [45] utilized the FEM technique along with the Newmark-Beta method to solve the vibration response of a nonlinear string model. Zhao and Chen [4] approximated an integro-differential equation involving a string model using the Galerkin method and subsequently employed an iterative algorithm to determine approximate solutions. Based on numerical results, the effectiveness of the iterative algorithm and the effects of the parameters on the vibration response of a translating viscoelastic string have also been evaluated. An and Su [182, 183] proposed the use of a hybrid method, known as the generalized integral transform technique (GITT), to analyze the lateral vibrations of an axially moving beam. The authors employed GITT to eliminate the spatial variables of PDEs and derive a system comprising second-order ODEs in time. Subsequently, the vibration response of the system was obtained by numerically solving the resulting ODEs.
4.2 Analytical solutions
Under certain circumstances, approximate solutions to the equations of motion can be expressed in a mathematical form by using analytical techniques for solving differential equations. The most common analytical method used to analyze the vibrations of axially moving systems is the perturbation technique. The perturbation technique is a powerful tool for solving the equations of motion [40, 184, 185] and investigates the steady-state responses of axially moving systems [29, 168, 186]. The perturbation technique is usually used for solving nearly linear and autonomous systems, wherein the terms that render the nonlinearity are relatively small and are referred to as perturbations. In such cases, it is possible to assume that the mathematical form of the solution would correspond to a power series of a small parameter. A drawback of the classical perturbation method is the appearance of a secular term in the solution that tends to increase indefinitely in time, thereby leading to loss of convergence of the solution. To address this concern, perturbation techniques, such as the multiple-scales, Krylov–Bogoliubov–Mitropolsky, Lindstedt–Poincaré, and harmonic balance methods that tend to eliminate the presence of secular terms, have been developed.
Mote [69] is recognized as a pioneer in using the perturbation method for analyzing the dynamic response of axially moving systems. Subsequently, Pakdemirli and Ulsoy [187] presented a detailed solution to the vibration of a translating string based on the discretization–multiple-scales method. This work first assumed the velocity function to be harmonically varying about a mean velocity \(v_{{0}}\) such that
where \(\varepsilon \) denotes a small parameter, and \(\Omega _{\mathrm{v}}\) indicates the frequency of the velocity. PDEs describing the system were also converted to ODEs, wherein the translating vibration was assumed to be a series of a generalized displacement \(q_{i}(t)\) of the string and basis functions \(\varphi _{i}(x)\) (refer to Eq. (78)). Subsequently, the multiple-scales method was applied by expressing the displacement \(q_{i}(t)\) in the form of the following power series.
where \({\begin{array}{*{20}c} {\tau _{i} =\varepsilon ^{i}t;} &{} {i=0,1,2,\ldots } \\ \end{array} }\) and the time derivatives can be written as follows.
By substituting Eqs. (93) and (94) into ODEs, the terms at each order of \(\varepsilon \) can be obtained, followed by attainment of the analytical solution for lateral vibration at each order of \(\varepsilon \), which can be expressed using a Fourier series. In addition, the multiple-scales method can also be directly used to solve the PDEs without the need to discretize the equation of motion [26, 127, 184, 187,188,189]. Unlike the discretization–multiple-scales method, the lateral vibrations can directly be expressed in the following power-series form:
This formulation can be substituted into a PDE model to determine analytical solutions at each order of \(\varepsilon \). For high-order perturbation schemes, the direct multiple-scales method is more straightforward, and the results are also more accurate compared to those based on the discretization–multiple-scales method. Malookani and Van Horssen [190] combined the multiple-scales method with the method of characteristic coordinates to develop an approximate solution of a translating string problem to avoid computational difficulties and occurrence of errors via eliminations of the Fourier series.
Wickert [6] and Moon and Wickert [191] used a perturbation technique, known as the Krylov–Bogoliubov–Mitropolsky method, to analyze the vibrations of an axially traveling beam. In contrast, Pellicano and Zirilli [192] employed the Lindstedt–Poincaré method to suppress secular terms present in the solution for nonlinear vibrations of an axially moving beam. Later, Chen et al. [73] analyzed the dynamics of an axially moving beam through the use of the multidimensional Lindstedt–Poincaré method (involving generalization of the Lindstedt–Poincaré method to multiple-degree-of-freedom systems). Their study revealed that the said method is more convenient and straightforward compared to other perturbation techniques employed in the analysis of the multiple-degree-of-freedom systems. Another investigation performed by Sze et al. [12] involved the use of the incremental harmonic balance (IHB) method [193] to solve ODEs describing the dynamics of a moving beam. In their work, an incremental equation in the matrix-vector form was developed from ODEs through the use of a new time variable \(\tau = \Omega _{\mathrm{f}}\).t (\(\Omega _{\mathrm{f}}\) denotes the frequency of an external excitation). This incremental equation was linearized using the Newton–Raphson procedure. The Galerkin procedure was then employed to establish a set of linear equations. The solution process began with a guessed solution. Subsequently, the nonlinear frequency–amplitude response curve is then solved point-by-point by incrementing the frequency \(\Omega _{\mathrm{f}}\) or incrementing a component of the coefficient vector of the set of linear equations.
Besides the perturbation techniques, the modal analysis method developed by Meirovitch [194] was also used to investigate the dynamics of axially moving systems via eigensolutions. Wickert and Mote [24] were among the early researchers who applied the modal analysis method to axially moving materials. In their work, the equation of motion of a translating beam was first expressed in the canonical state-space form, and a solution to this equation was obtained by analyzing the eigenvalue problem and using the following separable solution:
where \(\alpha \) is a complex number and \({{\varvec{\Theta }} }\left( x \right) \) is the complex-mode function vector. Consequently, a closed-form solution to the vibration response of the beam was obtained. Yang et al. [3, 195] used the invariant manifold method for deriving the linear and nonlinear complex mode functions of the axially moving material. The modal analysis method offers an efficient means to investigate free- and forced-vibration responses of axially moving systems. However, for a translating system with a viscoelastic foundation, the classical modal analysis method cannot be directly utilized owing to the influence of damping of the foundation. Zhang et al. [196], therefore, proposed a complex modal analysis method for investigating such systems. Their study revealed that the complex modal analysis method was applied efficiently to the non-self-adjoint systems, such as those with viscoelastic foundations.
5 Dynamic behavior analysis
Besides the approximate solutions of mathematical models, dynamical behaviors of axially moving systems including natural frequencies, equilibrium, bifurcation, and stability have also been discussed in detail in [197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213,214,215,216,217,218,219,220,221,222,223]. Wicket [6] investigated the equilibrium configurations of a moving beam described by the following equation of motion:
where the dimensionless parameters \({\bar{w}}\), \({\bar{v}}\), \({\bar{x}}\), \({\bar{t}}\), \(\lambda _{2} \), and \(\lambda _{1} \) are given as Eq. (88). In this work, the equilibrium solutions \(\hat{{w}}({\bar{x}})\) of the beam were obtained by solving the following equation:
Equation (98) has the trivial solution \({\bar{w}}_{0} \left( {{\bar{x}}} \right) =0\) and non-trivial solutions bifurcating from the straight configuration as follows:
where \(\gamma _{i} =\sqrt{1+\left( {i\pi \lambda _{1} } \right) ^{2}} \) denotes the critical velocity for the linear mode i. Based on Eq. (99), the author showed the relationship between the equilibrium of an axially moving beam and the axial velocity. The regime in which \({\bar{v}}\) is smaller than the first critical speed \(\gamma _{1} \) is called the subcritical, whereas the regime wherein \({\bar{v}}>\gamma _{1} \) is called the supercritical regime. In the former regime, the equilibrium configuration of the system is a straight line (i.e., \({\bar{w}}_{0} \left( {{\bar{x}}} \right) =0\)), while there exist \(2i+1\) equilibrium configurations corresponding to \(\gamma _{i}<{\bar{v}}<\gamma _{i+1} \) in the latter regime. In most studies on axially moving systems, dynamics analysis has been generally performed in the subcritical regime and investigated the behaviors around the trivial equilibrium. However, in nonlinear systems with high velocity, the trivial equilibrium can become unstable, and many complicated types of motions such as bifurcation, chaos, divergence, and flutter instabilities may occur. Therefore, the global dynamics of axially moving systems in the supercritical regime also are an interesting problem and have received considerable attention. Various investigations on the stability and bifurcation were published in [10, 46, 76, 115, 198, 200, 203,204,205,206,207].
5.1 Stability and bifurcation: String and beam models
Wang [197] is recognized for his study on the stability of the equilibrium configurations of an axially moving system in the supercritical regime. The author considered two translating beams: A straight beam and a beam with end curvatures due to applying bending moments to two supports. The author found that the trivial configuration of the former one became unstable in the supercritical regime showing the existence of a pitchfork bifurcation. In contrast, the equilibrium configuration of the latter one changed with an increase in the axial velocity, but it remained stable. Pakdemirli and Ulsoy [187] examined the influence of the frequency \(\Omega _{v} \) (i.e., Eq. (92)) on the stability of an axially moving string. Based on the approximated analytical solutions, the authors showed that when \(\Omega _{v} \) was close to twice any natural frequency of the system or close to the sum of any two natural frequencies, the string became unstable. Later, Öz and Pakdemirli [71] used the Euler–Bernoulli beam model to investigate the previous problem and achieved similar conclusions. Öz et al. [188] extended the study in [71] by using the nonlinear moving beam model in Eq. (97). Consequently, the stability and the bifurcations of steady-state solutions were analyzed, and the frequency–response curves were given. Concerning chaotic motions of axially moving systems, Ravindra and Zhu [76] investigated the bifurcation and the chaos of an axially moving beam based on a one-mode approximated model established by the Galerkin method. In the supercritical regime, the response of the system can become chaotic due to the nonlinear effects. A criterion for the occurrence of the chaos was obtained via Melnikov’s method. Furthermore, the authors proved that both the period-doubling and intermittency routes to chaos exist in the system as the system parameters vary. Later, Pellicano and Vestroni [169] discussed the stability of an axially moving beam in the supercritical regime based on an approximate model developed by using the four-term Galerkin truncate. Zhu and Ni [61] presented a study on the energetics and stability of an axially moving string/beam with varying length. In [198], Özhan investigated the stability of an axially moving beam, wherein both axial velocity and tension were time-dependent. According to the solutions of the equation of motion using the multiple-scales method, seven resonance conditions were obtained, and then the stability condition of each case was considered analytically. Besides the Euler–Bernoulli beam, the Rayleigh beam theory was also used for investigating the influence of rotary inertia on the dynamic behavior of an axially moving system. In [205], the dynamic behavior of a Rayleigh beam was analyzed in both the sub and supercritical regime.
Marynowski and Kapitaniak [208] examined the stability of an axially moving viscoelastic beam using both the Kelvin–Voigt and the Burgers models. The authors obtained several significant results related to the effects of axial velocity and dynamic viscosity \(\mu \) on the instability regions of the system and the occurrence of divergence and flutter instabilities in the supercritical regime. Concerning parametric excitations with time-dependent axial velocity, Sahoo and coauthors used the direct multiple-scales method to investigate the stability, the bifurcation in steady-state solution, and the chaotic dynamics of axially traveling viscoelastic beams under single excitation frequency in [209, 210] and two excitation frequencies in [211, 212] under the 3:1 internal resonance between the first and second natural frequencies. Marynowski [19] subsequently investigated the bifurcation and the chaotic motions of a viscoelastic beam with a time-varying axial force using the Kelvin–Voigt model. Furthermore, Sahoo [213] considered a viscoelastic moving beam under parametric excitations derived from both varying axial velocity and tension simultaneously. In his paper, the stability, bifurcations, and the chaotic behaviors of the beam were analyzed. Another viscoelastic model, the SLS model—Maxwell representation (Fig. 8b), was also used to develop a dynamic model of a translating beam in [85]. Based on this dynamic model, the authors concluded that the critical velocity obtained from the dynamic model using the SLS model is similar to the one using the Burgers model and smaller than the one using the Kelvin–Voigt model. In another study, Ghayesh [186] employed the Routh–Hurwitz criterion to obtain the stability conditions of a moving viscoelastic string placed on a partial foundation (Fig. 7). The author further analyzed the effects of axial velocity, the damping viscosity, and the length and stiffness of the foundation on natural frequencies, the stability, and the bifurcations of the system. Subsequently, an elastic string subject to a nonlinear foundation (i.e., Eq. (7)) and a translating viscoelastic Rayleigh beam (i.e., Eq. (41)) were analyzed in [64] and [26], respectively. Additionally, Ding et al. [83] examined the chaotic dynamics of a viscoelastic beam based on the numerical solutions obtained using two approaches; the high-order Galerkin truncations and the differential and integral quadrature methods. Comparisons of the bifurcation diagrams, the phase portraits, and the Poincaré maps of two-, four-, and six-term Galerkin’s truncations and the DQM & IQM were further conducted.
Studies on the stability and the bifurcation of translating systems under external excitations were also published [75, 201, 202, 214,215,216,217,218]. In [75], the bifurcation and the chaotic dynamics of an axially moving beam with a harmonic point-wise excitation were investigated in the supercritical regime. The bifurcation diagrams presented in [75] provide a panoramic view of the vibration behaviors as the axial velocity, and the amplitude and frequency of the excitation force are varied. In the supercritical regime, the authors found the existence of complicated dynamical phenomena, such as cascaded bifurcations, blue-sky catastrophes (i.e., a sudden disappearance of a chaotic orbit), and the coexistence of chaotic and periodic orbits. Concerning the stability of axially moving systems with an internal resonance, Huang et al. [214] analyzed a moving Euler–Bernoulli beam under harmonic lateral excitations. The nonlinear dynamic behaviors of the system were investigated based on the IHB and the multivariable Floquet theory. The authors presented the stable regions and bifurcation points for the case where the excitation frequency is near the first two natural frequencies of the system. Concurrently, Ghayesh [201] examined the relationship between the material damping and the bifurcations of an axially moving system tuned to internal resonances through considering a translating viscoelastic beam. The author showed that Neimark–Sacker bifurcations could occur in the subcritical regime, and the chance for the existence of these bifurcations increases as the damping viscosity decreases. Later, both the sub- and supercritical nonlinear dynamics of an axially moving beam with a 3:1 internal resonance were investigated in [202]. In this paper, the bifurcation diagrams and the Poincaré maps were analyzed via the direct time integration. In the supercritical regime, various dynamical phenomena, including the period-doubling, the quasiperiodic, and the chaotic motions, were exhibited. Additionally, Ding et al. [215] also discussed the influences of nonlinear vibrations on the stress distribution and fatigue life of a translating beam with a 3:1 internal resonance. In recent studies on axially moving material with complicated structure, Li et al. [216] and Zhu et al. [217] investigated the stability of translating viscoelastic sandwich beams, whereas Sarigul [218] discussed the internal resonance of a translating beam with multimass.
5.2 Stability and bifurcation: Belt model
The stability of axially moving systems described by the belt model was analyzed in [130, 133, 135, 219, 220]. Riedel and Tan [130] introduced the subcritical dynamics of a translating strip subject to harmonic lateral forces. Ghayesh et al. [219] presented both the local and global dynamic behaviors of a moving belt with an internal resonance based on the Euler–Bernoulli beam theory. Later, Ghayesh and Amabili [133] used the Timoshenko beam theory to analyze the dynamics of an axially moving belt with intermediate spring supports in the sub- and supercritical regimes. Furthermore, the global nonlinear dynamics of a translating viscoelastic belt were analyzed in [135]. The previous studies considered moving belts under lateral external excitations. In contrast, Farokhi et al. [220] investigated parametric resonances of an axially moving belt subject to a sinusoidal longitudinal excitation. In their work, the dynamic stability of the system in the subcritical regime was analyzed.
5.3 Stability and bifurcation: Plate model
Investigations on the stability and the bifurcation of the axially moving plates were presented in [143, 149, 176, 221,222,223,224,225,226,227,228,229]. Yang et al. [176] studied the natural frequencies of free vibration and the bifurcation and the chaotic dynamics of the forced vibration of a translating viscoelastic plate based on FDM. Bifurcation diagrams showed the effects of the axial velocity, the amplitude of the excitation, and the damping viscosity on the dynamic behavior of the system: When these parameters increase, the equilibrium becomes unstable and bifurcates into periodic motions, and the chaos occurs after a sequence of period-doubling bifurcation. In [222], the flutter and divergence instabilities of a translating viscoelastic plate with different boundary conditions were examined. In this paper, the complex eigenvalue equations were established using the power-series method. The authors also exhibited the influences of the viscosity coefficient, the geometrical ratio of plate, and boundary conditions on the system instability. The chaotic dynamics of axially moving plates using the von Karman large deflection theory (i.e., Eqs. (68–69)) were also discussed in [143] and [221]. Meanwhile, the stability analysis of a moving nanoscale plate in the sub- and supercritical regime was performed in Liu et al. [149]. In this work, the authors drew several conclusions concerning the relationship between and the dynamic behaviors of the system and the system parameters (i.e., small-scale parameter, axial velocity, and boundary constraints). Subsequently, Duan et al. [223] analyzed the stability of a translating nanoscale plate subjected to a viscoelastic foundation. Concerning composite materials, Yang and Chen [224] developed a dynamic model of a translating rectangular antisymmetric cross-ply composite plate and investigated the divergence and flutter instabilities analyzing the complex natural frequencies.
The stability of axially moving plates in diverse environments such as fluids, magnetic fields, and thermoelectromechanical fields was also discussed in [34, 100, 226,227,228,229]. In [227], the stability and chaotic motion of a translating plate immersed in a liquid were investigated. Later, Li et al. [228] performed a study on complicated dynamic behaviors of a moving plate immersed in a fluid with an internal resonance. In another investigation on axially moving plates in fluid, Wang and Zu [229] analyzed the instability of a viscoelastic plate. The authors derived unstable regions for different types of resonances using the solvability conditions and the Routh–Hurwitz criterion. They further showed the influences of the system parameters on the unstable boundaries. A study on the dynamics of a translating plate in a magnetic field was also performed by Hu et al. [34]. Based on bifurcation diagrams, they showed that the chaotic dynamics of the system are sensitive to the parameters: The magnetic induction intensity, the axial velocity, the tension, and the amplitude and frequency of the external excitation. Around the same time, Li et al. [100] studied the stability of an axially moving viscoelastic piezoelectric nanoscale plate under the multi-thermoelectromechanical field.
6 Conclusions and future prospects
This paper provided a detailed review of extant researches performed concerning the dynamics of axially moving systems. Mathematical models (linear and nonlinear) of the string, beam, belt, and plate models and boundary conditions are introduced in Sect. 2. Approximation methods used to discretize the equations of motion are presented in Sect. 3. The techniques to determine the solutions of axially moving systems are discussed in Sect. 4. Finally, the local and global dynamics of axially moving systems are examined in Sect. 5. Several key works on the dynamical analysis of axially moving systems are summarized in Table. 1. Based on the review presented in this paper, the following six specific aspects are outlined for initiating future research endeavors to be undertaken concerning axially moving systems.
Laminated composite materials: The laminated composite material is a material type that includes two or more layers of orthotropic materials with different properties. Recently, the use of these materials in axially moving systems instead of homogeneous materials has drawn considerable attention due to their improved properties. Although several studies on this aspect were published in recent years, the dynamic analyses of axially moving composite materials, however, are still limited, particularly investigation on its stability and complicated dynamics. The emphasis of laminated composite materials will reveal the diversity of dynamic behaviors due to the differential properties of material layers. In the future, this aspect is one of the most anticipated fields.
Axially moving materials in the nanoscale: Also, due to the broad applications of nanotechnology, the dynamics and stability analyses of axially moving systems in nanoscale, in which the small-scale effect and nanoscale surface effect are considered, should be investigated.
Axially moving materials with defects: In axially moving systems, the long-term effects of vibrations can cause potential damages for the system and lead to a failure of components. Furthermore, the existence of damages or cracks in the material seriously affects the safety and performance of the system. There are many studies on the vibrations of static beams and plates with crack defects. However, the works of moving materials with defects are rare yet. Therefore, investigation of the vibration responses of axially moving materials with defects must be pursued in the future.
Non-ideal boundary conditions: With regard to axially moving systems with non-ideal boundaries, especially non-homogeneous boundary conditions, most of the published works focused on analyzing the linear vibration of the system. Not much work concerning the effects of non-ideal boundary conditions, bifurcation, and chaotic motions has been reported. In the future, this aspect must be further studied.
Non-uniform materials: Most studies have considered axially moving systems made of uniform materials: Basic parameters such as mass density, cross-sectional area, and flexural rigidity were assumed constant. The use of non-uniform materials can be pursued with regard to future research endeavors.
Experimental analysis: Lastly, experimental analyses must be performed when investigating the vibration response of axially moving materials. This is all the more applicable to the system subject to affective environmental factors including fluid interactions, the presence of magnetic and thermal fields, etc.
Abbreviations
- DQM:
-
Differential quadrature method
- FDM:
-
Finite difference method
- FEM:
-
Finite-element method
- GITT:
-
Generalized integral transform technique
- HSDT:
-
High-order shear deformation theory
- IHB:
-
Incremental harmonic balance
- IPDE:
-
Integro-partial differential equation
- IQM:
-
Integral quadrature method
- ODE:
-
Ordinary differential equation
- PDE:
-
Partial differential equation
- SLS:
-
Standard linear solid
- SSDT:
-
Sinusoidal shear deformation theory
References
Mahalingam, S.: Transverse vibrations of power transmission chains. Br. J. Appl. Phys. 8(4), 145–148 (1957)
Nguyen, Q.C., Hong, K.-S.: Simultaneous control of longitudinal and transverse vibrations of an axially moving string with velocity tracking. J. Sound Vib. 331(13), 3006–3019 (2012)
Yang, X.D., Wu, H., Qian, Y.J., Zhang, W., Lim, C.W.: Nonlinear vibration analysis of axially moving strings based on gyroscopic modes decoupling. J. Sound Vib. 393, 308–320 (2017)
Zhao, W.J., Chen, L.Q.: Iterative algorithm for axially accelerating strings with integral constitutive law. Acta Mech. Solida Sin. 21(5), 449–456 (2008)
Zhu, W.D., Mote, C.D.: Free and forced response of an axially moving string transporting a damped linear-oscillator. J. Sound Vib. 177(5), 591–610 (1994)
Wickert, J.A.: Nonlinear vibration of a traveling tensioned beam. J. Non-linear Mech. 27(3), 503–517 (1992)
Wang, L.H., Hu, Z.D., Zhong, Z., Ju, J.W.: Dynamic analysis of an axially translating viscoelastic beam with an arbitrarily varying length. Acta Mech. 214(3–4), 225–244 (2010)
Özkaya, E., Pakdemirli, M.: Group-theoretic approach to axially accelerating beam problem. Acta Mech. 155(1–2), 111–123 (2002)
Fung, R.F., Lu, P.Y., Tseng, C.C.: Non-linearly dynamic modelling of an axially moving beam with a tip mass. J. Sound Vib. 218(4), 559–571 (1998)
Ding, H., Chen, L.Q.: Equilibria of axially moving beams in the supercritical regime. Arch. Appl. Mech. 81(1), 51–64 (2011)
Hong, K.-S., Kim, C.W., Hong, K.T.: Boundary control of an axially moving belt system in a thin-metal production line. Int. J. Control Autom. Syst. 2(1), 55–67 (2004)
Sze, K.Y., Chen, S.H., Huang, J.L.: The incremental harmonic balance method for nonlinear vibration of axially moving beams. J. Sound Vib. 281(3–5), 611–626 (2005)
Thurman, A.L., Mote, C.D.: Free, periodic, nonlinear oscillation of an axially moving strip. J. Appl. Mech. 36(1), 83–91 (1969)
Abedi, M., Asnafi, A., Karami, K.: To obtain approximate probability density functions for a class of axially moving viscoelastic plates under external and parametric white noise excitation. Nonlinear Dyn. 78(3), 1717–1727 (2014)
Hatami, S., Azhari, M., Saadatpour, M.M.: Exact and semi-analytical finite strip for vibration and dynamic stability of traveling plates with intermediate supports. Advant. Struct. Eng. 9(5), 639–651 (2006)
Hatami, S., Azhari, M., Saadatpour, M.M.: Stability and vibration of elastically supported, axially moving orthotropic plates. Iran. J. Sci. Technol. Trans. B Eng. 30(B4), 427–446 (2006)
Marynowski, K., Kolakowski, Z.: Dynamic behaviour of an axially moving thin orthotropic plate. J. Theor. Appl. Mech. 1(37), 109–128 (1999)
Nguyen, Q.C., Hong, K.-S.: Stabilization of an axially moving web via regulation of axial velocity. J. Sound Vib. 330(20), 4676–4688 (2011)
Marynowski, K.: Non-linear vibrations of an axially moving viscoelastic web with time-dependent tension. Chaos Solitons Fractals 21(2), 481–490 (2004)
Sack, R.A.: Transverse oscillations in travelling strings. Br. J. Appl. Phys. 5(6), 224 (1954)
Bapat, V.A., Srinivasan, P.: Nonlinear transverse oscillations in traveling strings by the method of harmonic balance. J. Appl. Mech. 34(3), 775–777 (1967)
Mote, C.D.: On the nonlinear oscillation of an axially moving string. J. Appl. Mech. 33(2), 463–464 (1966)
Swope, R.D.: Vibrations of a moving threadline. J. Frankl. Inst. Eng. Appl. Math. 275(1), 36–55 (1963)
Wickert, J.A., Mote, C.D.: Classical vibration analysis of axially moving continua. J. Appl. Mech. Trans. ASME 57(3), 738–744 (1990)
Chen, L.Q., Ding, H.: Steady-state transverse response in coupled planar vibration of axially moving viscoelastic beams. J. Vib. Acoust. Trans. ASME 132(1), 011009 (2010)
Ghayesh, M.H., Balar, S.: Non-linear parametric vibration and stability of axially moving visco-elastic Rayleigh beams. Int. J. Solids Struct. 45(25–26), 6451–6467 (2008)
Li, Y.H., Gao, Q., Jian, K.L., Yin, X.G.: Dynamic responses of viscoelastic axially moving belt. Appl. Math. Mech. Engl. Ed. 24(11), 1348–1354 (2003)
Tang, Y.Q., Chen, L.Q.: Stability analysis and numerical confirmation in parametric resonance of axially moving viscoelastic plates with time-dependent speed. Eur. J. Mech. A Solids 37, 106–121 (2013)
Ghayesh, M.H.: Stability characteristics of an axially accelerating string supported by an elastic foundation. Mech. Mach. Theory 44(10), 1964–1979 (2009)
Yang, X.D., Lim, C.W., Liew, K.M.: Vibration and stability of an axially moving beam on elastic foundation. Advant. Struct. Eng. 13(2), 241–247 (2010)
Lin, W., Qiao, N.: Vibration and stability of an axially moving beam immersed in fluid. Int. J. Solids Struct. 45(5), 1445–1457 (2008)
Wang, Y.Q., Huang, X.B., Li, J.: Hydroelastic dynamic analysis of axially moving plates in continuous hot-dip galvanizing process. Int. J. Mech. Sci. 110, 201–216 (2016)
Arani, A.G., Haghparast, E., Zarei, H.B.: Nonlocal vibration of axially moving graphene sheet resting on orthotropic visco-Pasternak foundation under longitudinal magnetic field. Physica B 495, 35–49 (2016)
Hu, Y.D., Hu, P., Zhang, J.Z.: Strongly nonlinear subharmonic resonance and chaotic motion of axially moving thin plate in magnetic field. J. Comput. Nonlinear Dyn. 10(2), 021010 (2015)
Marynowski, K., Grabski, J.: Dynamic analysis of an axially moving plate subjected to thermal loading. Mech. Res. Commun. 51, 67–71 (2013)
Kazemirad, S., Ghayesh, M.H., Amabili, M.: Thermo-mechanical nonlinear dynamics of a buckled axially moving beam. Arch. Appl. Mech. 83(1), 25–42 (2013)
Van Horssen, W.T., Ponomareva, S.V.: On the construction of the solution of an equation describing an axially moving string. J. Sound Vib. 287(1–2), 359–366 (2005)
Suweken, G., Van Horssen, W.T.: On the transversal vibrations of a conveyor belt with a low and time-varying velocity. Part II: the beam-like case. J. Sound Vib. 267(5), 1007–1027 (2003)
Suweken, G., Van Horssen, W.T.: On the transversal vibrations of a conveyor belt with a low and time-varying velocity. Part I: the string-like case. J. Sound Vib. 264(1), 117–133 (2003)
Suweken, G., Van Horssen, W.T.: On the weakly nonlinear, transversal vibrations of a conveyor belt with a low and time-varying velocity. Nonlinear Dyn. 31(2), 197–223 (2003)
Chen, L.Q., Yang, X.D.: Transverse nonlinear dynamics of axially accelerating viscoelastic beams based on 4-term Galerkin truncation. Chaos Solitons Fractals 27(3), 748–757 (2006)
Ghayesh, M.H., Amabili, M.: Nonlinear dynamics of axially moving viscoelastic beams over the buckled state. Comput. Struct. 112, 406–421 (2012)
Wickert, J.A., Mote, C.D.: Linear transverse vibration of an axially moving string-particle system. J. Acoust. Soc. Am. 84(3), 963–969 (1988)
Fung, R.F., Wang, P.H., Lee, M.J.: Nonlinear vibration analysis of a traveling string with time-dependent length by finite element method. J. Chin. Inst. Eng. 21(1), 109–117 (1998)
Chen, E.W., Ferguson, N.S.: Analysis of energy dissipation in an elastic moving string with a viscous damper at one end. J. Sound Vib. 333(9), 2556–2570 (2014)
Ding, H., Chen, L.Q.: Natural frequencies of nonlinear transverse vibration of axially moving beams in the supercritical regime. Adv. Vib. Eng. 10(3), 261–272 (2011)
Zhao, W.J., Chen, L.Q., Zu, J.W.: Finite difference method for simulating transverse vibrations of an axially moving viscoelastic string. Appl. Math. Mech. Engl. Ed. 27(1), 23–28 (2006)
Zhou, Y.F., Wang, Z.M.: Transverse vibration characteristics of axially moving viscoelastic plate. Appl. Math. Mech. Engl. Ed. 28(2), 209–218 (2007)
Yang, B., Mote, C.D.: Active vibration control of the axially moving string in the S-domain. J. Appl. Mech. Trans. ASME 58(1), 189–196 (1991)
Fung, R.F., Huang, J.S., Wang, Y.C., Yang, R.T.: Vibration reduction of the nonlinearly traveling string by a modified variable structure control with proportional and integral compensations. Int. J. Mech. Sci. 40(6), 493–506 (1998)
Fung, R.F., Liao, C.C.: Application of variable-structure control in the nonlinear string system. Int. J. Mech. Sci. 37(9), 985–993 (1995)
De Queiroz, M.S., Dawson, D.M., Rahn, C.D., Zhang, F.: Adaptive vibration control of an axially moving string. J. Vib. Acoust. Trans. ASME 121(1), 41–49 (1999)
Li, Y.G., Rahn, C.D.: Adaptive vibration isolation for axially moving beams. IEEE ASME Trans. Mechatron. 5(4), 419–428 (2000)
Ngo, Q.H., Hong, K.-S., Jung, I.H.: Adaptive control of an axially moving system. J. Mech. Sci. Technol. 23(11), 3071–3078 (2009)
Kim, C.W., Hong, K.-S., Park, H.: Boundary control of an axially moving string: actuator dynamics included. J. Mech. Sci. Technol. 19(1), 40–50 (2005)
Nguyen, Q.C., Hong, K.-S.: Asymptotic stabilization of a nonlinear axially moving string by adaptive boundary control. J. Sound Vib. 329(22), 4588–4603 (2010)
Nguyen, Q.C., Piao, M., Hong, K.-S.: Multivariable adaptive control of the rewinding process of a roll-to-roll system governed by hyperbolic partial differential equations. Int. J. Control Autom. Syst. 16(5), 2177–2186 (2018)
Yang, K.J., Hong, K.-S., Matsuno, F.: Robust adaptive boundary control of an axially moving string under a spatio temporally varying tension. J. Sound Vib. 273(4–5), 1007–1029 (2004)
Hong, K.-S., Pham, P.-T.: Control of axially moving systems: a review. Int. J. Control Autom. Syst. 17(12), 2983–3008 (2019)
Pakdemirli, M., Ulsoy, A.G., Ceranoglu, A.: Transverse vibration of an axially accelerating string. J. Sound Vib. 169(2), 179–196 (1994)
Zhu, W.D., Ni, J.: Energetics and stability of translating media with an arbitrarily varying length. J. Vib. Acoust. Trans. ASME 122(3), 295–304 (2000)
Bhat, R.B., Xistris, G.D., Sankar, T.S.: Dynamic behavior of a moving belt supported on elastic-foundation. J. Mech. Des. 104(1), 143–147 (1982)
Zhang, H.J., Chen, L.Q.: Vibration of an axially moving string supported by a viscoelastic foundation. Acta Mech. Solida Sin. 29(3), 221–231 (2016)
Ghayesh, M.H.: Parametric vibrations and stability of an axially accelerating string guided by a non-linear elastic foundation. J. Nonlinear Mech. 45(4), 382–394 (2010)
Ghayesh, M.H., Moradian, N.: Nonlinear dynamic response of axially moving, stretched viscoelastic strings. Arch. Appl. Mech. 81(6), 781–799 (2011)
Zhang, N.H., Wang, J.J., Cheng, C.J.: Complex-mode Galerkin approach in transverse vibration of an axially accelerating viscoelastic string. Appl. Math. Mech. Engl. Ed. 28(1), 1–9 (2007)
Zhao, W.J., Chen, L.Q.: A numerical algorithm for non-linear parametric vibration analysis of a viscoelastic moving belt. Int. J. Nonlinear Sci. Numer. Simul. 3(2), 139–144 (2002)
Malkin, A.Y., Isayev, A.I.: Rheology: Concepts, Methods, and Applications. ChemTec Publishing, Toronto (2006)
Mote, C.D.: A study of band saw vibrations. J. Frankl. Inst. Eng. Appl. Math. 279(6), 430–444 (1965)
Wickert, J.A., Mote, C.D.: On the energetics of axially moving continua. J. Acoust. Soc. Am. 85(3), 1365–1368 (1989)
Öz, H.R., Pakdemirli, M.: Vibrations of an axially moving beam with time-dependent velocity. J. Sound Vib. 227(2), 239–257 (1999)
Özkaya, E., Öz, H.R.: Determination of natural frequencies and stability regions of axially moving beams using artificial neural networks method. J. Sound Vib. 252(4), 782–789 (2002)
Chen, S.H., Huang, J.L., Sze, K.Y.: Multidimensional Lindstedt–Poincare method for nonlinear vibration of axially moving beams. J. Sound Vib. 306(1–2), 1–11 (2007)
Chen, L.Q., Yang, X.D.: Steady-state response of axially moving viscoelastic beams with pulsating speed: comparison of two nonlinear models. Int. J. Solids Struct. 42(1), 37–50 (2005)
Pellicano, F., Vestroni, F.: Complex dynamics of high-speed axially moving systems. J. Sound Vib. 258(1), 31–44 (2002)
Ravindra, B., Zhu, W.D.: Low-dimensional chaotic response of axially accelerating continuum in the supercritical regime. Arch. Appl. Mech. 68(3–4), 195–205 (1998)
Wang, L.H., Hu, Z.D., Zhong, Z., Ju, J.W.: Hamiltonian dynamic analysis of an axially translating beam featuring time-variant velocity. Acta Mech. 206(3–4), 149–161 (2009)
Duan, Y.C., Wang, J.P., Wang, J.Q., Liu, Y.W., Shao, F.: Theoretical and experimental study on the transverse vibration properties of an axially moving nested cantilever beam. J. Sound Vib. 333(13), 2885–2897 (2014)
Chen, L.Q., Yang, X.D.: Stability in parametric resonance of axially moving viscoelastic beams with time-dependent speed. J. Sound Vib. 284(3–5), 879–891 (2005)
Mockensturm, E.M., Guo, J.P.: Nonlinear vibration of parametrically excited, viscoelastic, axially moving strings. J. Appl. Mech. Trans. ASME 72(3), 374–380 (2005)
Ding, H., Chen, L.Q.: Stability of axially accelerating viscoelastic beams: multi-scale analysis with numerical confirmations. Eur. J. Mech. A Solids 27(6), 1108–1120 (2008)
Ghayesh, M.H., Amabili, M.: Parametric stability and bifurcations of axially moving viscoelastic beams with time-dependent axial speed. Mech. Based Des. Struct. Mech. 41(3), 359–381 (2013)
Ding, H., Yan, Q.Y., Zu, J.W.: Chaotic dynamics of an axially accelerating viscoelastic beam in the supercritical regime. Int. J. Bifurc. Chaos 24(5), 1450062 (2014)
Ding, H., Zu, J.W.: Periodic and chaotic responses of an axially accelerating viscoelastic beam under two-frequency excitations. Int. J. Appl. Mech. 5(2), 1350019 (2013)
Marynowski, K., Kapitaniak, T.: Zener internal damping in modelling of axially moving viscoelastic beam with time-dependent tension. J. Nonlinear Mech. 42(1), 118–131 (2007)
Kazemirad, S., Ghayesh, M.H., Amabili, M.: Thermal effects on nonlinear vibrations of an axially moving beam with an intermediate spring–mass support. Shock Vib. 20(3), 385–399 (2013)
Gosselin, F., Païdoussis, M.P., Misra, A.K.: Stability of a deploying/extruding beam in dense fluid. J. Sound Vib. 299(1–2), 123–142 (2007)
Ni, Q., Li, M.W., Tang, M., Wang, L.: Free vibration and stability of a cantilever beam attached to an axially moving base immersed in fluid. J. Sound Vib. 333(9), 2543–2555 (2014)
Païdoussis, M.P., Interactions, F.S.: Slender Structures and Axial Flows I. Academic Press, London (1998)
Païdoussis, M.P., Issid, N.T.: Dynamic stability of pipes conveying fluid. J. Sound Vib. 33(3), 267–294 (1974)
Sugiyama, Y., Tanaka, Y., Kishi, T., Kawagoe, H.: Effect of a spring support on the stability of pipes conveying fluid. J. Sound Vib. 100(2), 257–270 (1985)
Wang, L.: Size-dependent vibration characteristics of fluid-conveying microtubes. J. Fluids Struct. 26(4), 675–684 (2010)
Ni, Q., Zhang, Z.L., Wang, L.: Application of the differential transformation method to vibration analysis of pipes conveying fluid. Appl. Math. Comput. 217(16), 7028–7038 (2011)
Lundgren, T.S., Sethna, P.R., Bajaj, A.K.: Stability boundaries for flow induced motions of tubes with an inclined terminal nozzle. J. Sound Vib. 64(4), 553–571 (1979)
Bajaj, A.K., Sethna, P.T., Lundgren, T.S.: Hopf bifurcation phenomena in tubes carrying a fluid. SIAM J. Appl. Math. 39(2), 213–230 (1980)
Rousselet, J., Herrmann, G.: Dynamic behavior of continuous cantilevered pipes conveying fluid near critical velocities. J. Appl. Mech. 48(4), 943–947 (1981)
Modarres-Sadeghi, Y., Païdoussis, M.P.: Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends. J. Fluids Struct. 25(3), 535–543 (2009)
Lim, C.W., Li, C., Yu, J.L.: Dynamic behaviour of axially moving nanobeams based on nonlocal elasticity approach. Acta. Mech. Sin. 26(5), 755–765 (2010)
Li, C.: On vibration responses of axially travelling carbon nanotubes considering nonlocal weakening effect. J. Vib. Eng. Technol. 4(2), 175–181 (2016)
Li, C., Liu, J.J., Cheng, M., Fan, X.L.: Nonlocal vibrations and stabilities in parametric resonance of axially moving viscoelastic piezoelectric nanoplate subjected to thermo-electro-mechanical forces. Compos. Part B Eng. 116, 153–169 (2017)
Wang, J., Shen, H.M., Zhang, B., Liu, J.: Studies on the dynamic stability of an axially moving nanobeam based on the nonlocal strain gradient theory. Mod. Phys. Lett. B 32(16), 1850167 (2018)
Eringen, A.C.: On differential-equations of nonlocal elasticity and solutions of screw dislocation and surface-waves. J. Appl. Phys. 54(9), 4703–4710 (1983)
Sarigul, M.: Parametric vibrations of axially moving beams with multiple edge cracks. Int. J. Acoust. Vib. 24(2), 241–252 (2019)
Lee, U., Kim, J.H., Oh, H.M.: Spectral analysis for the transverse vibration of an axially moving Timoshenko beam. J. Sound Vib. 271(3–5), 685–703 (2004)
An, C., Su, J.: Dynamic response of axially moving Timoshenko beams: integral transform solution. Appl. Math. Mech. Engl. Ed. 35(11), 1421–1436 (2014)
Yan, Q.Y., Ding, H., Chen, L.Q.: Periodic responses and chaotic behaviors of an axially accelerating viscoelastic Timoshenko beam. Nonlinear Dyn. 78(2), 1577–1591 (2014)
Ding, H., Tan, X., Zhang, G.C., Chen, L.Q.: Equilibrium bifurcation of high-speed axially moving Timoshenko beams. Acta Mech. 227(10), 3001–3014 (2016)
Mokhtari, A., Mirdamadi, H.R.: Study on vibration and stability of an axially translating viscoelastic Timoshenko beam: non-transforming spectral element analysis. Appl. Math. Model. 56, 342–358 (2018)
Huang, C.C.: Vibrations of pipes containing flowing fluids according to Timoshenko theory. ASME J. Appl. Mech. 41(3), 814–817 (1974)
Laithier, B.E., Païdoussis, M.P.: The equations of motion of initially stressed Timoshenko tubular beams conveying fluid. J. Sound Vib. 79(2), 175–195 (1981)
Lin, Y.H., Tsai, Y.K.: Nonlinear vibrations of Timoshenko pipes conveying fluid. Int. J. Solids Struct. 34(23), 2945–2956 (1997)
Yu, D., Wen, J., Zhao, H.: Flexural vibration band gap in a periodic fluid-conveying pipe system based on the Timoshenko beam theory. J. Vib. Acoust. Trans. ASME 133(1), 014502 (2011)
Xia, W., Wang, L.: Microfluid-induced vibration and stability of structures modeled as microscale pipes conveying fluid based on non-classical Timoshenko beam theory. Microfluid. Nanofluid. 9(4–5), 955–962 (2010)
Tan, X., Mao, X.-Y., Ding, H., Chen, L.-Q.: Vibration around non-trivial equilibrium of a supercritical Timoshenko pipe conveying fluid. J. Sound Vib. 428, 104–118 (2018)
Ding, H., Tan, X., Dowell, E.H.: Natural frequencies of a super-critical transporting Timoshenko beam. Eur. J. Mech. A Solids 66, 79–93 (2017)
Rezaee, M., Lotfan, S.: Non-linear nonlocal vibration and stability analysis of axially moving nanoscale beams with time-dependent velocity. Int. J. Mech. Sci. 96–97, 36–46 (2015)
Mase, G.T.: Continuum Mechanics for Engineers. CRC Press, Boca Raton, FL (1999)
Ghayesh, M.H.: On the natural frequencies, complex mode functions, and critical speeds of axially traveling laminated beams: parametric study. Acta Mech. Solida Sin. 24(4), 373–382 (2011)
Li, Y.H., Wang, L., Yang, E.C.: Nonlinear dynamic responses of an axially moving laminated beam subjected to both blast and thermal loads. J. Nonlinear Mech. 101, 56–67 (2018)
Marynowski, K.: Dynamic analysis of an axially moving sandwich beam with viscoelastic core. Compos. Struct. 94(9), 2931–2936 (2012)
Lv, H.W., Li, Y.H., Li, L., Liu, Q.K.: Transverse vibration of viscoelastic sandwich beam with time-dependent axial tension and axially varying moving velocity. Appl. Math. Model. 38(9–10), 2558–2585 (2014)
Yang, X.D., Zhang, W., Chen, L.Q.: Transverse vibrations and stability of axially traveling sandwich beam with soft core. J. Vib. Acoust. Trans. ASME 135(5), 051013 (2013)
Wei, M.H., Sun, L., Hu, G.: Dynamic properties of an axially moving sandwich beam with magnetorheological fluid core. Adv. Mech. Eng. 9(2), 1687814017693182 (2017)
Hao, Y., Gao, M.L.: Traverse vibration of axially moving laminated SMA beam considering random perturbation. Shock Vib. 2019, 1–10 (2019)
Lv, H.W., Li, L., Li, Y.H.: Non-linearly parametric resonances of an axially moving viscoelastic sandwich beam with time-dependent velocity. Appl. Math. Model. 53, 83–105 (2018)
Marynowski, K.: Vibration analysis of an axially moving sandwich beam with multiscale composite facings in thermal environment. Int. J. Mech. Sci. 146, 116–124 (2018)
Sahebkar, S.M., Ghazavi, M.R., Khadem, S.E., Ghayesh, M.H.: Nonlinear vibration analysis of an axially moving drillstring system with time dependent axial load and axial velocity in inclined well. Mech. Mach. Theory 46(5), 743–760 (2011)
Ding, H., Zhang, G.C., Chen, L.Q.: Supercritical vibration of nonlinear coupled moving beams based on discrete Fourier transform. J. Nonlinear Mech. 47(10), 1095–1104 (2012)
Ding, H., Chen, L.Q.: Galerkin methods for natural frequencies of high-speed axially moving beams. J. Sound Vib. 329(17), 3484–3494 (2010)
Riedel, C.H., Tan, C.A.: Coupled, forced response of an axially moving strip with internal resonance. J. Nonlinear Mech. 37(1), 101–116 (2002)
Ghayesh, M.H.: Coupled longitudinal-transverse dynamics of an axially accelerating beam. J. Sound Vib. 331(23), 5107–5124 (2012)
Ghayesh, M.H., Amabili, M.: Nonlinear dynamics of an axially moving Timoshenko beam with an internal resonance. Nonlinear Dyn. 73(1–2), 39–52 (2013)
Ghayesh, M.H., Amabili, M.: Nonlinear vibrations and stability of an axially moving Timoshenko beam with an intermediate spring support. Mech. Mach. Theory 67, 1–16 (2013)
Chen, L.H., Zhang, W., Yang, F.H.: Nonlinear dynamics of higher-dimensional system for an axially accelerating viscoelastic beam with in-plane and out-of-plane vibrations. J. Sound Vib. 329(25), 5321–5345 (2010)
Farokhi, H., Ghayesh, M.H., Hussain, S.: Three-dimensional nonlinear global dynamics of axially moving viscoelastic beams. J. Vib. Acoust. Trans. ASME 138(1), 011007 (2016)
Ghayesh, M.H., Farokhi, H.: Nonlinear dynamical behavior of axially accelerating beams: three-dimensional analysis. J. Comput. Nonlinear Dyn. 11(1), 011010 (2016)
Ghayesh, M.H., Amabili, M.: Three-dimensional nonlinear planar dynamics of an axially moving Timoshenko beam. Arch. Appl. Mech. 83(4), 591–604 (2013)
Ding, H., Chen, L.Q.: Natural frequencies of nonlinear vibration of axially moving beams. Nonlinear Dyn. 63(1–2), 125–134 (2011)
Ding, H., Zhang, G.C., Chen, L.Q.: Supercritical equilibrium solutions of axially moving beams with hybrid boundary conditions. Mech. Res. Commun. 38(1), 52–56 (2011)
Ulsoy, A.G., Mote, C.D.: Vibration of wide band-saw blades. J. Eng. Ind. Trans. ASME 104(1), 71–78 (1982)
Shin, C.H., Kim, W.S., Chung, J.T.: Free in-plane vibration of an axially moving membrane. J. Sound Vib. 272(1–2), 137–154 (2004)
Lin, C.C., Mote, C.D.: Equilibrium displacement and stress distribution in a two-dimensional, axially moving web under transverse loading. J. Appl. Mech. Trans. ASME 62(3), 772–779 (1995)
Liu, J.T., Yang, X.D., Chen, L.Q.: Bifurcations and chaos of an axially moving plate under external and parametric excitations. Int. J. Struct. Stab. Dyn. 12(4), 1250023 (2012)
Marynowski, K.: Two-dimensional rheological element in modelling of axially moving viscoelastic web. Eur. J. Mech. A Solids 25(5), 729–744 (2006)
Hatami, S., Azhari, M., Saadatpour, M.M.: Free vibration of moving laminated composite plates. Compos. Struct. 80(4), 609–620 (2007)
Zhang, W., Lu, S.F., Yang, X.D.: Analysis on nonlinear dynamics of a deploying composite laminated cantilever plate. Nonlinear Dyn. 76(1), 69–93 (2014)
Arani, A.G., Haghparast, E.: Vibration analysis of axially moving carbon nanotube-reinforced composite plate under initial tension. Polym. Compos. 38(4), 814–822 (2017)
Arani, A.G., Haghparast, E., Zarei, H.B.: Vibration analysis of functionally graded nanocomposite plate moving in two directions. Steel Compos. Struct. 23(5), 529–541 (2017)
Liu, J.J., Li, C., Fan, X.L., Tong, L.H.: Transverse free vibration and stability of axially moving nanoplates based on nonlocal elasticity theory. Appl. Math. Model. 45, 65–84 (2017)
Eringen, A.C., Edelen, D.G.B.: On nonlocal elasticity. Int. J. Eng. Sci. 10(3), 233–248 (1972)
Yao, G., Zhang, Y.M.: Dynamics and stability of an axially moving plate interacting with surrounding airflow. Meccanica 51(9), 2111–2119 (2016)
Wang, Y.Q., Xue, S.W., Huang, X.B., Du, W.: Vibrations of axially moving vertical rectangular plates in contact with fluid. Int. J. Struct. Stab. Dyn. 16(2), 1450092 (2016)
Bagdatli, S.M., Uslu, B.: Free vibration analysis of axially moving beam under non-ideal conditions. Struct. Eng. Mech. 54(3), 597–605 (2015)
Wang, K.W., Mote, C.D.: Vibration coupling analysis of band-wheel mechanical systems. J. Sound Vib. 109(2), 237–258 (1986)
Yue, M.G.: Belt vibration considering moving contact and parametric-excitation. J. Mech. Des. 115(4), 1024–1030 (1993)
Hwang, S.J., Perkins, N.C.: High-speed stability of coupled band/wheel systems—theory and experiment. J. Sound Vib. 169(4), 459–483 (1994)
Kong, L.Y., Parker, R.G.: Vibration of an axially moving beam wrapping on fixed pulleys. J. Sound Vib. 280(3–5), 1066–1074 (2005)
Orloske, K., Leamy, M.J., Parker, R.G.: Flexural-torsional buckling of misaligned axially moving beams. I. Three-dimensional modeling, equilibria, and bifurcations. Int. J. Solids Struct. 43(14–15), 4297–4322 (2006)
Orloske, K., Parker, R.G.: Flexural-torsional buckling of misaligned axially moving beams-II. Vibration and stability analysis. Int. J. Solids Struct. 43(14–15), 4323–4341 (2006)
Ding, H., Li, D.P.: Static and dynamic behaviors of belt-drive dynamic systems with a one-way clutch. Nonlinear Dyn. 78(2), 1553–1575 (2014)
Ding, H., Zu, J.W.: Steady-state responses of pulley–belt systems with a one-way clutch and belt bending stiffness. J. Vib. Acoust. Trans. ASME 136(4), 041006 (2014)
Ding, H.: Periodic responses of a pulley–belt system with one-way clutch under inertia excitation. J. Sound Vib. 353, 308–326 (2015)
Ding, H.: Steady-state responses of a belt-drive dynamical system under dual excitations. Acta Mech. Sin. 32(1), 156–169 (2016)
Ding, H., Zhang, Z., Chen, L.Q.: Vibration reduction effect of one-way clutch on belt-drive systems. Eur. J. Mech. A Solids 71, 378–385 (2018)
Ding, H., Wang, S., Zhang, Y.W.: Free and forced nonlinear vibration of a transporting belt with pulley support ends. Nonlinear Dyn. 92(4), 2037–2048 (2018)
Ding, H., Lim, C.W., Chen, L.Q.: Nonlinear vibration of a traveling belt with non-homogeneous boundaries. J. Sound Vib. 424, 78–93 (2018)
Van Horssen, W.T.: On the influence of lateral vibrations of supports for an axially moving string. J. Sound Vib. 268(2), 323–330 (2003)
Yurddas, A., Özkaya, E., Boyaci, H.: Nonlinear vibrations of axially moving multi-supported strings having non-ideal support conditions. Nonlinear Dyn. 73(3), 1223–1244 (2013)
Pellicano, F., Vestroni, F.: Nonlinear dynamics and bifurcations of an axially moving beam. J. Vib. Acoust. Trans. ASME 122(1), 21–30 (2000)
Wang, L.H., Hu, Z.D., Zhong, Z.: Dynamic analysis of an axially translating plate with time-variant length. Acta Mech. 215(1–4), 9–23 (2010)
Shin, C.H., Chung, J.T., Yoo, H.H.: Dynamic responses of the in-plane and out-of-plane vibrations for an axially moving membrane. J. Sound Vib. 297(3–5), 794–809 (2006)
Stylianou, M., Tabarrok, B.: Finite-element analysis of an axially moving beam. 1. Time integration. J. Sound Vib. 178(4), 433–453 (1994)
Stylianou, M., Tabarrok, B.: Finite-element analysis of an axially moving beam. 2. Stability analysis. J. Sound Vib. 178(4), 455–481 (1994)
Hua, H.L., Qiu, M., Liao, Z.Q.: Dynamic analysis of an axially moving beam subject to inner pressure using finite element method. J. Mech. Sci. Technol. 31(6), 2663–2670 (2017)
Hatami, S., Azhari, M., Saadatpour, M.M.: Nonlinear analysis of axially moving plates using FEM. Int. J. Struct. Stab. Dyn. 7(4), 589–607 (2007)
Yang, X.D., Zhang, W., Chen, L.Q., Yao, M.H.: Dynamical analysis of axially moving plate by finite difference method. Nonlinear Dyn. 67(2), 997–1006 (2012)
Ni, Q., Huang, Y.Y.: Differential quadrature: method to stability analysis of pipes conveying fluid with spring support. Acta Mech. Solida Sin. 13(4), 320–327 (2000)
Robinson, M.T.A.: Analysis of the vibration of axially moving viscoelastic plate with free edges using differential quadrature method. J. Vib. Control 24(17), 3908–3919 (2018)
Ding, H., Tang, Y.Q., Chen, L.Q.: Frequencies of transverse vibration of an axially moving viscoelastic beam. J. Vib. Control 23(20), 3504–3514 (2017)
Cepon, G., Boltezar, M.: Computing the dynamic response of an axially moving continuum. J. Sound Vib. 300(1–2), 316–329 (2007)
Ghayesh, M.H.: Stability and bifurcations of an axially moving beam with an intermediate spring support. Nonlinear Dyn. 69(1–2), 193–210 (2012)
An, C., Su, J.: Dynamic response of clamped axially moving beams: integral transform solution. Appl. Math. Comput. 218(2), 249–259 (2011)
An, C., Su, J.: Dynamic analysis of axially moving orthotropic plates: integral transform solution. Appl. Math. Comput. 228, 489–507 (2014)
Ponomareva, S.V., van Horssen, W.T.: On transversal vibrations of an axially moving string with a time-varying velocity. Nonlinear Dyn. 50(1–2), 315–323 (2007)
Fung, R.F., Huang, J.S., Chu, J.J.: Dynamic stability of an axially travelling string/slider coupling system with moving boundary. J. Sound Vib. 211(4), 689–701 (1998)
Ghayesh, M.H.: Nonlinear transversal vibration and stability of an axially moving viscoelastic string supported by a partial viscoelastic guide. J. Sound Vib. 314(3–5), 757–774 (2008)
Pakdemirli, M., Ulsoy, A.G.: Stability analysis of an axially accelerating string. J. Sound Vib. 203(5), 815–832 (1997)
Öz, H.R., Pakdemirli, M., Boyaci, H.: Non-linear vibrations and stability of an axially moving beam with time-dependent velocity. J. Nonlinear Mech. 36(1), 107–115 (2001)
Chen, L.Q., Yang, X.D.: Vibration and stability of an axially moving viscoelastic beam with hybrid supports. Eur. J. Mech. A Solids 25(6), 996–1008 (2006)
Malookani, R.A., van Horssen, W.T.: On the asymptotic approximation of the solution of an equation for a non-constant axially moving string. J. Sound Vib. 367, 203–218 (2016)
Moon, J., Wickert, J.A.: Non-linear vibration of power transmission belts. J. Sound Vib. 200(4), 419–431 (1997)
Pellicano, F., Zirilli, F.: Boundary layers and non-linear vibrations in an axially moving beam. J. Nonlinear Mech. 33(4), 691–711 (1998)
Cheung, Y.K., Chen, S.H., Lau, S.L.: Application of the incremental harmonic balance method to cubic non-linearity systems. J. Sound Vib. 140(2), 273–286 (1990)
Meirovitch, L.: A modal analysis for the response of linear gyroscopic systems. J. Appl. Mech. 42(2), 446–450 (1975)
Yang, X.D., Liu, M., Qian, Y.J., Yang, S., Zhang, W.: Linear and nonlinear modal analysis of the axially moving continua based on the invariant manifold method. Acta Mech. 228(2), 465–474 (2017)
Zhang, H.J., Ma, J., Ding, H., Chen, L.Q.: Vibration of axially moving beam supported by viscoelastic foundation. Appl. Math. Mech. Engl. Ed. 38(2), 161–172 (2017)
Wang, K.W.: Dynamic stability analysis of high-speed axially moving bands with end curvatures. J. Vib. Acoust. Trans. ASME 113(1), 62–68 (1991)
Özhan, B.B.: Vibration and stability analysis of axially moving beams with variable speed and axial force. Int. J. Struct. Stab. Dyn. 14(06), 1450015 (2014)
Parker, R.G.: Supercritical speed stability of the trivial equilibrium of an axially-moving string on an elastic foundation. J. Sound Vib. 221(2), 205–219 (1999)
Ghayesh, M.H., Amabili, M.: Nonlinear stability and bifurcations of an axially moving beam in thermal environment. J. Vib. Control 21(15), 2981–2994 (2015)
Ghayesh, M.H.: Nonlinear forced dynamics of an axially moving viscoelastic beam with an internal resonance. Int. J. Mech. Sci. 53(11), 1022–1037 (2011)
Ghayesh, M.H., Kafiabad, H.A., Reid, T.: Sub- and super-critical nonlinear dynamics of a harmonically excited axially moving beam. Int. J. Solids Struct. 49(1), 227–243 (2012)
Ghayesh, M.H., Amabili, M., Farokhi, H.: Global dynamics of an axially moving buckled beam. J. Vib. Control 21(1), 195–208 (2015)
Mao, X.Y., Ding, H., Chen, L.Q.: Forced vibration of axially moving beam with internal resonance in the supercritical regime. Int. J. Mech. Sci. 131, 81–94 (2017)
Ding, H., Li, Y., Chen, L.Q.: Effects of rotary inertia on sub- and super-critical free vibration of an axially moving beam. Meccanica 53(13), 3233–3249 (2018)
Liu, P.C., Yu, H.N., Cang, S.: Trajectory synthesis and optimization of an underactuated microrobotic system with dynamic constraints and couplings. Int. J. Control Autom. Syst. 16(5), 2373–2383 (2018)
Mao, X.Y., Ding, H., Chen, L.Q.: Internal resonance of a supercritically axially moving beam subjected to the pulsating speed. Nonlinear Dyn. 95(1), 631–651 (2019)
Marynowski, K., Kapitaniak, T.: Kelvin–Voigt versus Burgers internal damping in modeling of axially moving viscoelastic web. J. Nonlinear Mech. 37(7), 1147–1161 (2002)
Sahoo, B., Panda, L.N., Pohit, G.: Parametric and internal resonances of an axially moving beam with time-dependent velocity. Model. Simul. Eng. 2013, 919517 (2013)
Sahoo, B., Panda, L.N., Pohit, G.: Stability, bifurcation and chaos of a traveling viscoelastic beam tuned to 3: 1 internal resonance and subjected to parametric excitation. Int. J. Bifurc. Chaos 27(2), 1750017-1–1750017-20 (2017)
Sahoo, B., Panda, L.N., Pohit, G.: Two-frequency parametric excitation and internal resonance of a moving viscoelastic beam. Nonlinear Dyn. 82(4), 1721–1742 (2015)
Sahoo, B., Panda, L.N., Pohit, G.: Combination, principal parametric and internal resonances of an accelerating beam under two frequency parametric excitation. Int. J. Nonlinear Mech. 78, 35–44 (2016)
Sahoo, B.: Nonlinear dynamics of a viscoelastic beam traveling with pulsating speed, variable axial tension under two-frequency parametric excitations and internal resonance. Nonlinear Dyn. 27, 1–35 (2019)
Huang, J.L., Su, R.K.L., Li, W.H., Chen, S.H.: Stability and bifurcation of an axially moving beam tuned to three-to-one internal resonances. J. Sound Vib. 330(3), 471–485 (2011)
Ding, H., Huang, L.L., Dowell, E., Chen, L.Q.: Stress distribution and fatigue life of nonlinear vibration of an axially moving beam. Sci. China Technol. Sci. 62(7), 1123–1133 (2019)
Li, Y.H., Dong, Y.H., Qin, Y., Lv, H.W.: Nonlinear forced vibration and stability of an axially moving viscoelastic sandwich beam. Int. J. Mech. Sci. 138, 131–145 (2018)
Zhu, B., Dong, Y.H., Li, Y.H.: Nonlinear dynamics of a viscoelastic sandwich beam with parametric excitations and internal resonance. Nonlinear Dyn. 94(4), 2575–2612 (2018)
Sarigul, M.: Internal resonance of axially moving beams with masses. Iran. J. Sci. Technol. Trans. Mech. Eng. 43(1), 1–16 (2019)
Ghayesh, M.H., Kazemirad, S., Amabili, M.: Coupled longitudinal-transverse dynamics of an axially moving beam with an internal resonance. Mech. Mach. Theory 52, 18–34 (2012)
Farokhi, H., Ghayesh, M.H., Hussain, S.: Dynamic stability in parametric resonance of axially excited Timoshenko microbeams. Meccanica 51(10), 2459–2472 (2016)
Shao, M.Y., Wu, J.M., Wang, Y., Wu, Q.M.: Nonlinear parametric vibration and chaotic behaviors of an axially accelerating moving membrane. Shock Vib. 2019, 1–11 (2019)
Zhou, Y.F., Wang, Z.M.: Dynamic instability of axially moving viscoelastic plate. Eur. J. Mech. A Solids 73, 1–10 (2019)
Duan, J.B., Zhang, D.P., Wang, W.J.: Flutter and divergence instability of axially-moving nanoplates resting on a viscoelastic foundation. Appl. Sci. Basel 9(6), 1097 (2019)
Yang, X.D., Chen, L.Q., Zu, J.W.: Vibrations and stability of an axially moving rectangular composite plate. J. Appl. Mech. 78(1), 011018 (2011)
Ghayesh, M.H., Amabili, M.: Non-linear global dynamics of an axially moving plate. J. Nonlinear Mech. 57, 16–30 (2013)
Li, H.Y., Li, J., Lang, T.Y., Zhu, X.: Dynamics of an axially moving unidirectional plate partially immersed in fluid under two frequency parametric excitation. J. Nonlinear Mech. 99, 31–39 (2018)
Wang, Y.Q., Guo, X.H., Sun, Z., Li, J.: Stability and dynamics of axially moving unidirectional plates partially immersed in a liquid. Int. J. Struct. Stab. Dyn. 14(4), 1450010 (2014)
Li, H.Y., Li, J., Liu, Y.J.: Internal resonance of an axially moving unidirectional plate partially immersed in fluid under foundation displacement excitation. J. Sound Vib. 358, 124–141 (2015)
Wang, Y.Q., Zu, J.W.: Instability of viscoelastic plates with longitudinally variable speed and immersed in ideal liquid. Int. J. Appl. Mech. 9(1), 1750005 (2017)
Acknowledgements
This study was funded by the National Research Foundation (NRF) of Korea under the auspices of the Ministry of Science and ICT, Korea (Grant Number NRF-2017R1A2A1A17069430).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pham, PT., Hong, KS. Dynamic models of axially moving systems: A review. Nonlinear Dyn 100, 315–349 (2020). https://doi.org/10.1007/s11071-020-05491-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-020-05491-z