Review and perspectives in applied mechanics of axially moving flexible structures

Abstract

This comprehensive review primarily concerns axially moving flexible structures in problems involving distributed structure-to-solid contact. The distinguishing features of axially moving structures are presented in terms of prevalent studies regarding models with simplified support conditions. Subsequent sections focus on the particular difficulties of treating contact problems with classical structural theories, on the appropriate non-material kinematic description for travelling structures, on the proper formulation of established mechanical principles for open systems and on the category of Arbitrary Lagrangian–Eulerian (ALE) approaches, which are frequently applied for the development of application-oriented finite element schemes. Novel analytical and numerical transient solutions for the benchmark problem of an axially moving beam, which is travelling across a rough surface between two misaligned joints, are presented to illustrate particular challenges as well as to highlight perspectives for future research activities. There are 177 references cited in this paper.

1 Introduction

Axially moving structures, also known as travelling structures, are slender bodies with a predominant motion in direction of their longitudinal axis. In technical applications, they appear as transmission or conveyor belts, ropeway cables, band saw blades, paper webs, steel slabs or metal sheets moving across a rolling mill and so forth. The surrounding parts of such machinery keep the structure running and guide it along the desired path of motion, which is typically achieved by means of an interaction through some kind of solid contact. For example, the frictional contact between belt and pulleys permits power transmission in flat belt drive systems.

In operation, travelling structures exhibit various kinds of mechanical phenomena, like: divergence buckling, self-excited vibrations or parametric resonance at critical axial transport rates. Moreover, intrinsic imperfections or changes of the environmental conditions can induce undesirable deformations or cause the structure to leave its designated path of motion. In view of this mechanical richness, the ongoing development of such systems cannot do without a thorough scientific investigation that helps to avoid potentially catastrophic incidents beforehand and serves as the basis for improved control designs.

It is generally a difficult task to account for the interaction of an axially moving structure with the surrounding parts of machinery. This inherent complexity often necessitates simplification. Hence, idealised approaches regarding the boundary conditions prevail in the literature and few researchers have considered unified models that incorporate those parts of the mechanism that drive, guide or in some other manner directly interact with the axially moving structure, see, for example: contributions of the authors’ research group [1,2,3,4] as well as Rubin [5], Kong and Parker [6] or Raeymaekers and Talke [7], among others. In view of this knowledge gap, the present review article aims to present a selective, yet sufficiently comprehensive overview of past research on axially moving structures and, moreover, to point out promising strategies to bridge the gap as well as to bolster the research activity in this field with great practical relevance.

The paper focuses on the modelling and the analytical or numerical treatment of problems of travelling structures in the framework of the classical structural theories of strings, beams, rods or membranes, plates and shells. Owing to their reduced kinematic capabilities in contrast to the 3D-continuum, these theories are computationally efficient but generally difficult to handle in problems of distributed contact. Except for some simple cases, numerical solution techniques are required based on either strong or weak mathematical formulations. We shall refer to these methods along the way, elaborate on some and, in particular, on the finite element method (FEM) in the general context of the Arbitrary Lagrangian–Eulerian (ALE) kinematic approach.

In the upcoming Sect. 2, emanating from a brief recap of a few seminal works, the discussion continues with a survey on the research concerned with dynamic vibration, stability and bifurcation as well as large deflection problems that, however, lack an explicit account for distributed contact. Afterwards, we highlight the implications of distributed frictionless and frictional contact in problems of structural mechanics and proceed with a review of past attempts to incorporate contact in unified models of axially moving structures. In preparation of the discussion on finite element schemes in the ALE-framework, we meticulously distinguish the different variants of kinematic parametrisation. Regarding non-material kinematics, further emphasis is put on the proper formulation of the governing equations for open systems, which, often times, is not remarked explicitly.

In writing this review, we aim to acknowledge researchers, who have contributed significantly to the topics at hand. At the same time, we explicitly apologize to those, who were mistakenly overlooked or disregarded in the survey.

In Sect. 3, we revisit the seemingly simple, geometrically linear example of a partially slipping Euler–Bernoulli beam on a moving rough surface, most recently considered in [1]. Novel transient solutions are produced both semi-analytically and with beam finite elements in the Mixed Eulerian–Lagrangian (MEL) framework. This prototype example illustrates the inherent complexity of frictional contact problems of axially moving structures, which, nonetheless, can be tackled by means of properly designed solution techniques.

2 General lines of past research in the mechanics of axially moving structures

The study of transverse vibrations of axially moving structures dates back to Skutsch [8], who considered the problem of small transverse vibrations of an axially moving string, see Fig. 1, that was later, for the first time in English, revisited by Sack [9] as well as by Archibald and Emslie [10].

Fig. 1

Motion of transverse waves in an axially moving string captured at two time instances: the string is transported at constant rate v through the control domain; material particles are marked with red dots

This simple problem of a slender structure moving at a certain material transport rate between two supports constitutes a prototype example for studies on stability and transverse vibrations. We shall later consider different extensions of the above setting and, for now, utilize the basic setup to highlight some of the distinct features of axially moving structures: The small-deflection problem of an ideal string with no flexural stiffness is governed by the wave equation

$$\begin{aligned} \ddot{w} = c^2 w'', \quad \dot{w} = \left. \frac{\partial w}{\partial t}\right| _{s=\text {const}}, \quad w' = \frac{\partial w}{\partial s}, \end{aligned}$$

(1)

with the wave speed c and the transverse deflection w, which, in the context of the usual Lagrangian kinematic description of solid mechanics, is understood as a function of the material (particle) coordinate s and time t. This description is, however, inappropriate, because the particles are constantly travelling across the boundaries of the spatial control domain $0 \le x \le L$, where the kinematic constraints must be enforced. A simple coordinate transformation suffices to avoid this inconvenience of time-variable constraints in the parametrisation with the material coordinate s:

$$\begin{aligned} s = x - v t, \quad \dot{w} = \partial _t w + v \, \partial _x w, \quad \partial _x w= \frac{\partial w}{\partial x}, \quad \partial _t w = \left. \frac{\partial w}{\partial t}\right| _{x = \text {const}} \end{aligned}$$

(2)

where the deflection is regarded as a function of the Eulerian coordinate x and time t, i.e. $w = w(x,t)$; the operators $\partial _t$ and $\partial _x$ to account for the spatial and convective derivative are introduced accordingly. The above transformation step is well established and, thus, frequently taken in a tacit manner, although it involves the systematically important transition from the Lagrangian to the Eulerian perspective.

We compute the second-order material derivative of w to proceed with the transformation of the wave equation (1):

$$\begin{aligned} \ddot{w} = \partial _t^2 w + 2 v \, \partial _t\partial _xw + v^2 \, \partial _x^2 w, \quad w'' = \partial _x^2 w. \end{aligned}$$

(3)

The derivatives with respect to s and x are interchangeable in the present case due to $s' = 1 = x'$. Substitution yields the transformed boundary value problem:

$$\begin{aligned} \partial _t^2 w + 2 v \, \partial _t\partial _x w = \left( c^2 - v^2\right) \partial _x^2 w, \quad w(0,t) = 0, \quad w(L,t) = 0. \end{aligned}$$

(4)

Though the coordinate change somewhat complicates the governing PDE, it allows to state the boundary conditions at fixed points in space and helps to work out the physics of the problem more clearly: The type of PDE changes as the particle transport rate v approaches the wave speed c and a gyroscopic term appears that is of critical importance when it comes to stability and buckling of axially moving structures, see Renshaw and Mote [11]. Furthermore, transverse waves, as visualised by the two separating fronts in Fig. 1, are observed to propagate with velocity $c + v$ in direction of axial motion (downstream) and with $c-v$ upstream, see [9].

2.1 Axially moving structures in problems with idealised support conditions

The simple setup depicted in Fig. 1 already exhibits many characteristics of axially moving structures. However, the idealised support conditions imposed at the boundaries of the control domain present a rather rough approximation of the actual circumstances, which in reality assume the form of eyelets, channels, guide and chain wheels or are realised as rollers, pulleys or cylindrical drums. In the following survey, we peruse the open literature for studies that share this deliberate neglect of the complicated interactions with the surrounding parts.

A vast number of these publications are concerned with the dynamics of initially straight axially moving structures in terms of modal analysis, transverse vibrations or stability and buckling. In this regard, the recently published book by Banichuk [12] is devoted to the stability analysis of axially moving strings, beams or plates; for a general discussion on the evolved methods of nonlinear stability and bifurcation theory, we further refer to Troger and Steindl [13]. In addition, the review papers by Chen [14] with respect to axially moving strings as well as the one by Marynowski and Kapitaniak [15] with respect to plate-like systems present rich sources of information. In view of these extensive repositories, we shall provide only a modest number of references on exhaustively covered topics and instead highlight less recognised works on large deflection problems, boundary layers and the effects of a small flexural stiffness or axially moving structures of variable length.

2.1.1 Vibrations and stability of axially moving rods and strings

The prototype example of Fig. 1 is revisited by Wickert and Mote [16] for string and beam models of the structure. Based on the differential operator representation of the governing partial differential equation (4), the Green’s function method and a modal analysis are employed to conclude on the system’s response on arbitrary excitations and the limiting speed for divergence instability of the gyroscopic system. Though limited to small deflections, the authors even considered a kinematic excitation in form of the harmonic transverse motion of one of the supports. The conclusion in [16] that the string model runs into a critical state as the transport speed approaches wave speed was later revised by Renshaw and Mote [11] and, more recently, by Wang et al. [17], who, with the help of Hamiltonian mechanics, found that the string does not possess a divergence instability due to a weak interaction of the imaginary eigenvalue pairs. However, the equivalent beam model exhibits both divergence and flutter instabilities in the supercritical range.

These characteristic differences between the beam and string models arise due to the governing PDE for the beam being of forth order:

$$\begin{aligned} \partial _t^2 w + 2v \, \partial _t\partial _x w + a \, \partial _x^4 w = (c^2 - v^2) \partial _x^2 w, \end{aligned}$$

(5)

where a is proportional to the bending stiffness of the beam, again see [16]. Kong and Parker [18], motivated by the fact that many applications feature slender structures with small flexural stiffness, employed the phase closure principle, see Mead [19], to study the transition between the beam and string model. Indeed, at small bending stiffness the problem (5) may be approached with methods of singular perturbation theory, see Pellicano and Zirilli [20], and is also suitable for the application of the method of matched asymptotic expansions, see Schneider [21] in the context of transverse vibrations of a rectangular plate as well as Özkaya and Pakdemirili [22] for the vibration analysis of an axially accelerating beam. In this context, Seitzberger et al. [23] consider a simplified static problem of a conveyor system with emphasis on the importance of local bending effects in proximity to the support positions.

As established in a brief note by Mote [24] for the nonlinear vibration of an axially moving string, the applicability of geometrically linear dynamic analysis is limited to high-tension and low-velocity levels, because the geometrically nonlinear effect of tensioning due to transverse deflections is not negligible at higher transport rates. In an effort to cover the complete range of sub- and supercritical velocities, Wickert [25] deduces an extended integro-differential equation that accounts for the stretching due to transverse vibrations by means of a cubic nonlinearity and utilizes the asymptotic method of Krylov and Bogoliubov to solve this augmented problem. Pellicano and Vestroni [26] apply the Galerkin method to cast the coupled equations of transverse and longitudinal vibrations presented in [25] into a set of ordinary differential equations. Simplifications of this coupled system frequently serve as the basis of studies on transverse vibrations, see for example: Ghayesh and Amabili [27], who make use of the Galerkin method to study post-buckling bifurcation and forced vibrations of a simply supported beam moving at high speed, or Yang et al. [28], who apply the invariant manifold method to perform a nonlinear modal analysis in a similar setting.

Shear deformations and rotary inertia are typically neglected in traditional studies that rely on the Bernoulli–Euler beam theory, but may become essential in cases of less slender structures as well as in dynamic problems that feature higher frequencies. Thus, Timoshenko beam theory is adopted by, among others, Ding et al. [29] for a study on equilibrium bifurcations at supercritical speeds and Yan et al. [30] for the numerical analysis of the nonlinear dynamics of a viscoelastic beam. Kim and Chung [31] use Galerkin’s method to study coupled transverse vibrations of an elastically supported belt drive system under significant simplifying assumptions regarding the contact interaction between belt and pulleys, see also Pan et al. [32] for a similar analysis of an automotive serpentine belt drive. Concerning different material models of the moving structure, Marynowski [33] considers both the Kelvin-Voigt and the Maxwell rheological model to investigate the effect of internal damping on the nonlinear dynamics of an axially moving viscoelastic beam; Mockensturm and Gua [34] study the nonlinear vibrations of a viscoelastic, parametrically excited string. The effects of an external damping on the stability of axially moving structures are covered in the extensively cited papers on band saw vibrations by Mote and Ulsoy [35, 36].

2.1.2 Vibrations and stability of axially moving membranes, plates and shells

The just referenced article by Ulsoy and Mote [36] is one of the first to cover dynamics of an axially moving two-dimensional structure. Transverse vibrations and stability of an axially moving Reissner–Mindlin plate are investigated using global Ritz approximations as well as the finite element method, which, since then, has evolved to become one of the primary tools to treat sophisticated problems in solid mechanics in general and of axially moving structures in particular, see Sect. 2.4 related thereto.

Having said that, a great variety of different solution techniques remains applicable for the typically considered simplified model setup, which comprises a material surface (membrane, plate, shell) with rectangular reference configuration that travels at constant speed between two ideal support edges, see Fig. 2.

Fig. 2

Extended prototype setup to study transverse deformations of travelling membranes, plates or shells: the structure moves across a fixed spatial domain with constant transport rate v, idealised support conditions are imposed at the boundaries $x = 0,L$

Aside from the early studies on band saw vibrations like the one cited above, a significant number of publications featuring this configuration are concerned with moving paper webs. In their papers [37,38,39] published in close succession, Lin and Mote investigate the mechanics of such webs with regard to stationary deflection and stress distribution, static wrinkling due to a distributed edge loading as well as free vibrations and stability, respectively. In account for the smallness of the flexural stiffness, the methods of asymptotic matching between inner and outer expansions are employed in [37] to obtain the solution for an axially moving von Kármán plate under transverse loading; the comparison against results with membrane or linear plate theory shows the impact of bending rigidity and geometric nonlinearity. In [39], the author determines the critical speeds for divergence buckling and supercritical flutter instabilities of an axially moving plate in the geometrically linear range. Both dynamic and static buckling analyses, the latter determining the critical state by seeking a non-trivial equilibrium, yield the same critical speed of divergence buckling, which is identified as the propagation speed of transverse waves; the results are further compared to string and beam solutions of the reduced one-dimensional problem. Banichuk et al. [40] revisit this problem and deduce an analytic formula for the first critical speed, which in [39] was established as the root of a transcendental equation. In addition, [40] features extensive parameter studies and it is remarked that the transverse deflections of the first symmetric buckling mode are localised at the free side edges. The latter conclusion is also reflected by the results presented in Shin et al. [41], wherein transverse vibrations of an axially moving membrane are treated with the Galerkin method for two different cases of kinematic boundary conditions. Likewise, Luo and Hamidzadeh [42] apply the same solution strategy in combination with perturbation expansions to study buckling of an axially moving plate with special account for in-plane Coriolis terms and shear.

Further topics on axially moving two-dimensional structures like: internal resonances of transverse vibrating axially moving plates [43], alternative material models and internal damping [44, 45] or control design for axially moving webs [17, 46], are covered in the aforementioned review paper authored by Marynowski and Kapitaniak [15].

2.1.3 Parametric resonance and self-excited vibrations

Axially moving structures are susceptible to parametric resonance, as demonstrated in an early paper by Elmaraghy and Tabarrok [47]. Moreover, sources of parametric excitation appear frequently in technical applications, for example: in the form of torque ripple in electric motors, see Arrasate et al. [48], as the result of the interaction between camshaft and timing belt in a combustion engine, see Hirmann and Belyaev [49], or as crankshaft oscillations that cause tension fluctuations in an automotive serpentine belt drive.

The latter case motivated the study by Mockensturm et al. [50]: The authors extend the aforementioned integro-differential equation for the axially moving extensible string, see [25, 26], with a harmonic excitation term in account for a time variation of the axial tension. The complex-valued eigenfunctions of the geometrically linear free vibration problem of an axially moving string serve as ansatz functions for the Galerkin procedure that is used to compute the stability boundaries of the linear parametrically excited problem. Furthermore, a weakly nonlinear system based on a series expansion of the original nonlinear problem is investigated to derive analytic expressions for the amplitudes of the limit cycles about the instabilities. Pellicano et al. [51] reconsider this problem and apply a single mode Galerkin expansion based on the same class of ansatz functions considered in [50]. The stability analysis of the derived nonlinear ordinary differential equations in the complex amplitude and its conjugate complex counterpart is carried out with normal form theory; a physical test setup is devised to validate the analytic results. In conformity with the experimentally investigated two-pulley belt drive setup, the computational model is further extended with respect to the elastic tensioning of the opposite span, see Pellicano et al. [52].

Certain practical applications (e.g. crankshaft oscillations) feature parametric excitations with a rich frequency content. In such cases, the consideration of a single harmonic excitation, as done in the above references, does not suffice to capture the dynamics of the mechanical system. Hence, Parker and Lin [53] extend the just considered benchmark problem by inclusion of multi-frequency fluctuations of the belt tension and of the transport speed. It is found that the typical primary instability at the 2:1 frequency ratio ceases to exist in the case with multiple sources of parametric excitation. Secondary resonances are obtained with the linear model, and the limit cycle amplitude of the primary instability is derived by means of the multiple scales method. Recently, Zhang et al. [54] have considered a similar problem of an axially moving viscoelastic beam subject to a two-frequency tension fluctuation and tuned to a 1:3 internal resonance. A viscoelastic string model with parametric variation of the tension level is considered by Mockensturm and Guo [34]. The authors emphasize the importance of a physically accurate modelling of viscoelasticity for the axially moving structure, which amounts to a discussion on the differences between material and spatial time derivatives in travelling systems. The related discrepancies to earlier works are highlighted, and the nonlinear stability analysis is performed with the method of multiple scales.

An interesting case of self-excited instability of an axially moving structure is investigated by Spelsberg-Korspeter et al. [55]. The model comprises an Euler–Bernoulli beam that moves across a spatial domain with linear guides at the boundaries and is in point-contact with frictional pads in the middle; the setup serves as a prototype problem for break squeal. The beam thickness is consistently taken into account through a careful modelling of the contact kinematics. Divergence and flutter instabilities are investigated by means of a stability analysis with perturbation techniques.

Owing to the small flexural stiffness and low specific mass, paper webs are particularly susceptible to self-excited vibrations caused by a fluid–structure interaction with the surrounding medium. In related studies, the governing equations of the travelling web are typically augmented with prescribed excitation terms in account of the aerodynamic response, see Niemi and Pramila [56], Banichuk et al. [57] or Yao et al. [58]. Problems of fluid–structure interaction, as discussed in detail by Païdoussis [59, 60], are closely related to those of axially moving structures in general. The most prominent example to demonstrate this similarity is the fluid conveying circular tube with supported ends, which is governed by (5) just like the transverse vibrations of the travelling beam, see Païdoussis [61]. This equivalence is well illustrated by Pieber et al. [62] who address extended versions of these problems with a single finite element scheme. The flow induced bifurcation of the cantilevered fluid conveying tube (garden hose) is addressed by several authors, see [63] for a comprehensive overview. Stangl et al. [64] employ an alternative approach based on the Lagrangian equations of motion for non-material volumes as presented by Irschik and Holl [65] and compare the numerical results against solutions found in the literature.

2.1.4 Large deflection problems of axially moving cables and beams

Having focussed on the dynamics of taut structures with straight reference configuration, we now turn our attention to large deflection problems of travelling structures. The prominent example of axially moving cables for ropeways was studied in the thesis by Renezeder supervised by Steindl [66]. The author investigated dynamics of the sagged catenary of a single rope field between two ideal eyelets or two circular rollers, employed perturbation techniques in account for a small flexural stiffness of the cable and applied a standard material finite element procedure to conclude on the resonance phenomenon of sag-oscillations in a multi-field ropeway system. A promising multi-body ALE alternative that should resolve most of the inherent difficulties encountered with classic Lagrangian finite element approaches in this context, is proposed by Pieber et al. in their recent publication [62] on the stability of fluid conveying pipes and axially moving beams. The study on transverse vibrations of axially moving strings and beams by Vetyukov [67] further emphasises the advantages of a mixed kinematic description in the numerical treatment of problems with large support motions.

An analytic model to study three-dimensional vibrations of elastic sagged axially moving cables in the field of gravity is established and experimentally validated in two papers by Perkins and Mote [68, 69]. The equations of motion linearised about stationary catenary configurations of the travelling cable are solved with the Galerkin method, previously reported effects of curve veering and mode crossing of eigenvalues are ascertained and the speed tensioning phenomenon to stabilise the standing (arched) equilibrium configuration of the rope is verified experimentally. Wolfe’s treatise on the same problem in [70] is based on an alternative mathematical formulation that allows to derive the exact analytical solution. The results agree to those reported in the above cited earlier works; special attention is paid to the stabilisation of the arched equilibrium configuration due to speed tensioning.

The observation that, under certain operation conditions, a cable moving between two eyelets possesses multiple steady-state configurations is studied by O’Reilly [71]. A closed-form solution for an arbitrarily sagged elastic cable under uniform loading is reported by Luo and Mote [72], see also Miroshnik [73] for a study on the phenomenon of steady-state contour motion of axially moving strings under gravity in a viscous medium.

Cable dynamics in absence of a steady-state equilibrium configuration are studied by Wang and Luo [74]. The authors investigate the periodic large amplitude oscillation of an inextensible axially moving cable and present an extended system that allows a superposition of elastic vibrations. The stability of the in-plane vibration of the inextensible model is established, and it is shown that at ever increasing speed the vibration amplitude diminishes and that the configuration approaches a stationary configuration at the limiting case of infinite speed.

2.1.5 Axially moving structures of variable length

Axially moving structures of time-varying length are encountered in numerous technical applications, such as: wire drawing, plastic extrusion, industrial robots, sheet paper printing, hoist and elevator systems. The prototype example of a string or beam of finite length that is retracted through an orifice was dubbed “the spaghetti problem” by Carrier [75] in allusion to the rather embarrassing culinary experience of sucking in a spaghetti noodle too quickly. For the similar setup of a cantilevered beam with harmonically varying length, Zajaczkowski and J. Lipiński [76] employ Galerkin’s method to analyse the parametric instability. In the reverse spaghetti problem, on the other hand, the direction of motion is flipped such that the structure is now pushed out of the guide. Mansfield and Simmonds [77] study this inverse problem for a horizontal setup with relation to paper printing. Approximate analytic solutions are obtained as a series expansion and numerical results are obtained by means of the finite element method; see also Wang et al. [78] for the use of Galerkin’s method to perform the vibration analysis of an unshearable plate with variable length.

In the above provided references, the authors acknowledge the usefulness of a coordinate switch to transform the system of variable length to a problem in a domain of constant size in a stretched coordinate. This change of variable allows to formulate the kinematic boundary conditions at fixed points in the new coordinate, which proves particularly beneficial for the application of numerical schemes like the Galerkin projection or the finite element method. In their elaborate article, Vu-Quoc and Li [79] extend the so-called sliding beam formulation to the geometrically nonlinear regime. The aforementioned switch to a stretched coordinate is performed twofold: directly from the usual material description and, secondly, via the introduction of an intermediate configuration. In addition to the traditional spaghetti and reverse spaghetti problems, a superimposed rigid body rotatory motion of the sliding beam is considered in resemblance of a robotic system. This seminal work presents a primary reference for the continued development of the sliding beam formulation in the articles by Humer [80, 81], Steinbrecher et al. [82] and Humer et al. [83]. In [80], an elliptic integral solution is presented for the large transverse deflection problem of a beam that is clamped on its left and clamped but free to move axially on the right (linear guide). As bending of the structure through an external transverse force progresses, additional material enters the control volume through the linear guide owing to the coupling of axial and bending deflections in the geometrically nonlinear range. A limiting force level is found at which the static equilibrium ceases to exist, which amounts to the onset of and infinite sliding motion of the beam. A slightly modified version of the sliding spaghetti problem is revisited in [81] as a benchmark example to validate a beam finite element model, whose advantages in comparison with more traditional schemes for beams and solids are further highlighted in [82]. The primary feature of this model in the absolute nodal coordinate formulation and of its generalisation presented in [83] is the switch to a set of stretched coordinates that represent different segments of the complete material volume. In particular cases, where the axial transport of material across the spatial boundaries is not kinematically prescribed but solution dependent, the coordinate transformation becomes solution dependent as well.

Recently, Boyer et al. [84] proposed a different kinematic description to model sliding beams that is based on a co-deforming non-material envelope; the rod coincides with this surrounding tube at all times such that its relative motions are limited to sliding in axial direction and rotations about the axis. Concerning numerics, the authors employ a Ritz reduction of strains, see Boyer et al. [85], from which displacements are recovered by means of a spatial integration.

Zhu and Ni [86] employ energy criteria to conclude on the stability of small transverse vibrations of a sliding beam with an attached tip mass. Additional effects considered are: external and material damping as well as a non-constant transport rate, which dynamically impacts the axial tension. The two analysed examples resemble a flexible robot arm and a hoist cable in a high-rise elevator. The latter is modelled as vertical string in the field of gravity; see also Wang [87] for the impact of gravity on the vibrations of an axially moving heavy string. Reeving systems, see Escalona and Mohammadi [88] for a numerical treatment, are a prominent research topic in general. In particular, high-rise elevator systems, encountered in skyscrapers or deep mine shafts, receive much attention as they exhibit a rich dynamical behaviour and are frequently subjected to external excitations like building sway. A significantly simplified model of a vertically translating string with an attached rigid mass is analysed analytically by Sandilo and Horssen [89]. Perturbation methods are used to obtain approximate solutions for the cases of linearly and of harmonically varying hoist cable length. Different kinds of stochastic excitations of a vertical cable due to the sway of the host structure are analysed Kaczmarczyk and Iwankiewicz [90]. Arrasate et al. [48] develop a computational model for axial vibrations induced through torque ripple of the drive system of an elevator and put it to the test against a physical experiment. A comprehensive multi-body elevator model is considered by Crespo et al. [91] to investigate the interaction of the mechanical hoist and guide system in the event of a low frequency building sway; a quasistatic analysis is performed with the Galerkin method and frequency veering as well as internal resonances are obtained as the position of the elevator cabin changes.

2.2 Axially moving structures in problems involving distributed contact

The following discussion on problems of axially moving structures that involve distributed contact is focussed on “unified approaches”, that is, attempts to model the axially moving structure of the complete system with a single structural theory. In particular, we do not focus on discrete multi-body models of the axially moving structures, see for example Kubas and Harlecki [92]. In terms of the physical contact model, we restrict our attention to the most familiar case of Coulomb dry friction and refer to the extensive review paper by Berger [93] for a presentation of alternative models as well as to Yastrebov [94] for methods of implementation of frictional contact in numerical frameworks. The general aspects of frictional contact problems of axially moving continua are examined by Hetzler [95]. Originating from Hamilton’s principle, which presents a convenient starting point for weak formulations, the author considers exact and penalty methods of contact enforcement and elaborates on the different approaches of kinematic modelling based on either a material reference configuration or an intermediate spatial frame.

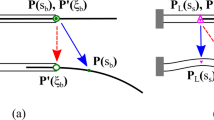
Since the invention of belt creep theory by Reynolds [96] problems related to belt drive mechanics stand in focus of most literature sources concerning the treatment of distributed contact problems with structural theories. In particular, belt creep theory states that, as the belt passes through the contact zone with a pulley, it first adheres to the pulley surface and at some point begins to slip, see Fig. 3.

Fig. 3

Prototype example of a flat belt transmission system with a single pulley; the solution is reminiscent of belt creep theory: at a constant material transport rate v (steady state), the velocity of the pulley surface $\omega R$ determines the position of the transition point between stick zone and slip zone; the contact forces depend on the modelling decisions regarding the contact interaction and the structural theory for the belt

The occurrence of slip is referred to as “belt creep”, which relates to a shortening or lengthening of the belt in account for the tension adjustment between the slack and the tight span.

The applicability of belt creep theory relies on the axial extensibility of the belt, a prerequisite that is not met by modern V-belt designs that feature rubber-embedded, virtually inextensible tension cords. For this kind of setup, Firbank [97] developed “belt shear” theory, to be later extended by Gerber [98]; see also the papers by Frendo and Bucchi [99, 100] with respect to the similar “brush” contact model usually utilized for pneumatic tires. As the name implies, power transmission is achieved by means of shear deformation of the rubber envelope that deforms according to the velocity difference between pulley surface and inextensible cords. Contrary to belt creep theory, the arc of adhesion contributes to the transmission and a slip zone is not required, but still occurs if the frictional tractions reach their limiting value along the way. Alciatore and Traver [101] compare both theories, discuss their applicability and remark on the correct formulation of compatibility conditions needed to extend the procedures to multi-pulley belt drives.

After this brief recap of classic ways of contact modelling for axially moving structures, we shall survey the available literature and highlight issues and deficiencies encountered when applying classic structural theories to problems of distributed frictionless or frictional contact. In this regard, the prototype example of a one-pulley belt drive, depicted in Fig. 3 and recently considered by Scheidl and Vetyukov [102], shall serve as reference case that already captures most of theses challenges.

2.2.1 Axially moving structures at contour motion

The term “contour motion” designates a particular solution that is identified by a spatially fixed deformed configuration of the axially moving structure; all material particles follow the same trajectory (contour) that determines the outer appearance of this seemingly statically deflected state.

Provided transverse vibrations are disregarded, transmission belt drive systems operate at contour motion. Bechtel et al. [103] considered this kind of model for the analysis of a two-pulley belt drive at steady-state operation. In contrast to preceding studies, the proposed model includes inertia effects due to an accelerated stretching of particles in axial direction, which is of particular importance in drawing processes of textile or polymer fibres. A Newtonian approach is taken to derive the governing system based on the application of balance laws to free-body diagrams of the belt in the contact zone and the free span. In contrast, the related analysis of a multi-pulley belt drive by Rubin [5] emanates from the governing equations of the nonlinear theory of extensible strings, see Antman [104] or Eliseev [105]. Particular attention is paid to the correct formulation of the “compatibility condition” required to close the system of equations. In essence, this algebraic constraint ensures that the computed total length of the belt equals the prescribed one, a corresponding remark can be found in [101] as well. The effects of linear viscoelasticity and large axial strains on the transmission characteristics of a flat belt drive are examined by Morimoto and Iizuka [106].

Eliseev and Vetyukov [107] adopt a fully Eulerian kinematic parametrisation to describe the steady-state operation of a two-pulley belt drive. The assumption of perfect adherence between belt and pulley throughout the contact zones leads to a contradiction that is resolved by the account for concentrated interactions (jump of the axial force) at the run-off points, where the belt disengages from the pulleys. This presents a limiting case for belt creep theory kind of solutions (e.g. Rubin [5]), where the sliding zone degenerates to a single point; in practice steel conveyor belts may exhibit this behaviour owing to their high membrane stiffness, see Scheidl et al. [2]. The model considered in [107] is extended by Vetyukov et al. [108] with respect to transient dynamics (belt drive start-up) and, in continuation, by Oborin et al. [109] with respect to distributed dry friction contact. In the latter reference, solutions for the transient start-up of the drive are obtained threefold by means of: a semi-analytical integration of a delay differential equation, simulations with a non-material finite element scheme as well as computations with conventional Lagrangian finite elements, whose weaknesses become apparent in comparison.

With regard to the kinematics of the contact interaction, the taut string model considered in the above cited references is convenient, because the free segments connect the pulleys in the form of straight lines and, thus, the contact zones are fully determined by the geometric setup. The inclusion of the flexural stiffness of the belt, see Kong and Parker [6], or of large transverse deflections due to gravity, see Scheidl [110], further complicates the problem, since the positions of the contact zone boundaries become solution dependent. In particular, the account for bending deflections of the belt in the single-pulley problem, considered in [102] and depicted in Fig. 3, implies that the start and end of the contact zone are unknown at first and are to be determined as part of the solution. Consequently a boundary value problem with variable domain is obtained for the individual segments (free spans, stick zone, slip zone). An appropriate coordinate transformation then allows to formulate the problem in standard form with fixed domains; the positions of the transition points belong to the general set of the unknowns with respective equations that complete the system. The extension of the prototype problem depicted in Fig. 3 to the usual two-pulley belt drive setup, as considered by Belyaev et al. [111] as well as by Scheidl and Vetyukov [112], is not trivial owing to additional continuity requirements for the closed loop structure. The semi-analytical and mixed finite element procedures proposed in [112] facilitate the search for belt creep theory type of solutions that may only exist in a narrow parameter range.

2.2.2 Constrained theories of rods in frictionless contact problems

Contrary to contact problems in general solid mechanics (see Yastrebov [94]), the contact detection between the axially moving structure and the surrounding parts is usually a fairly straightforward task, owing to typically considered simple geometric setups. However, what proves challenging is the accurate resolution of the contact response of the employed structural theories that does not always comply with the behaviour of the underlying continuum. Consider, for example, the small-deflection problem (second-order theory) for the transverse deflections w of a beam with flexural stiffness a that is tensioned by an axial force F and pressed against a rigid stamp as depicted in Fig. 4. Assuming frictionless contact and a shear-deformable Timoshenko beam, it is governed by:

$$\begin{aligned} a \left( w'''' - \psi ''' \right) - F w'' + Q' = 0, \quad Q' + q = 0, \quad Q = \psi /b, \end{aligned}$$

(6)

where q denotes the distributed contact pressure. The constitutive relation, which connects the transverse force Q to shear angle $\psi$ and shear compliance b, is meaningless for the corresponding Bernoulli–Euler problem (unshearable theory), which due to $\psi = 0$ reduces to $q = -F w''$; i.e.: the constant contact pressure equals tensile force divided by the curvature radius of the rigid stamp, see Denoël [113].

Fig. 4

Normal contact responses of a beam pressed against a rigid stamp and subjected to axial tension with a force F (second-order theory): a unshearable Euler-Bernoulli theory—constant interior pressure level q and concentrated interactions at the boundaries P; b Timoshenko theory—the pressure q reaches its maximum values at the boundaries, as the shear compliance mitigates the concentrated boundary effects of the unshearable theory

The corresponding contact force distributions for the entire structure are depicted in Fig. 4a for the Euler–Bernoulli beam and in Fig. 4b for the Timoshenko theory. In (a), the constant pressure level in the interior is complemented by two concentrated contributions at the ends of the contact zone, whereas the pressure distribution for the shear-deformable beam remains finite throughout the contact zone with its maxima at the boundaries. These maxima degenerate to Dirac-impulses in the limiting case of vanishing shear compliance, thus yielding the result of Fig. 4a. However, owing to their kinematic limitations, none of the two theories reproduce the result of the continuum solution, which predicts the contact pressure to vanish at the contact zone boundaries. A very similar problem of a straight beam pressed against a circular surface is considered by Gasmi et al. [114], who compare the results obtained for different structural theories based on a polynomial expansion with respect to the transverse coordinate against reference computations obtained with continuum finite elements. A common strategy to avoid these peculiarities of the structure to rigid body interaction is to either replace the rigid counterpart by a prescribed pressure distribution, see e.g. Lorenz and Ams [115] or the related thesis by Lorenz supervised by Ams [116] on wire-sawing of silicium ingots, or to utilize a compliant counterpart, see e.g. Hetzler and Willner [117], who model friction pads as viscoelastic winkler foundations in a study on break squeal. As concluded by Essenburg [118] as well as by Naghdi and Rubin [119], the structural theory needs to account for transverse normal strains, i.e. thickness compression of the cross-section, in order to comply with the continuum solution. In [119], the authors consider different constrained theories based on Naghdi’s generalised director formulation to compare their response in a distributed contact problem and to emphasize that, as seen from Fig. 4b, the account for transverse shear does not suffice to obtain a physically meaningful pressure distribution.

The classic theories of rods, beams as well as plates and shells exhibit these deficiencies, which arise as localised effects at the transitions between contact zones and the free regions. Like in singular perturbed problems, the accurate resolution of the mechanics in this “edge layer” requires a different asymptotic expansion. However, despite their local inaccuracies, these theories remain applicable for problems of distributed contact as long as the analysis is focussed on the global picture, e.g.: Batista [120] and Belyaev et al. [121] analytically consider the static frictionless contact problem of a circular belt being stretched by a relative displacement of two pulleys for the belt modelled with unshearable and shear-deformable extensible rod theory, respectively. Vetyukov et al. [122] develop a semi-analytic and a non-material finite element procedure to solve the large deflection problem of a weakly-tensioned belt hanging on two pulleys. The same problem setup and solution strategy are reconsidered by Scheidl and Vetyukov [112] for the steady-state motion of the belt modelled as a Cosserat rod. As depicted in Fig. 4, the limiting case of vanishing shear compliance is studied numerically to conclude on the formulation of appropriate boundary conditions for the unshearable theory. In this regard, the shear compliance may be viewed as a numerical regularisation parameter: As it tends to zero, the problem becomes numerically stiff and increasingly harder to solve. Evidently, though localised and negligible in many cases, the particular contact effects of the structural theories possess the potential to deteriorate numerical solutions.

2.2.3 Problems of distributed contact involving friction

A typical simplification in the modelling of contact problems is the neglect of the thickness of the axially moving structure: As a matter of fact, in Fig. 3, not the middle line but the lower fibre of the belt is in contact with the rotating pulley. As pointed out by Belyaev et al. [111], the offset action of the frictional force requires transverse shear to be incorporated in the structural theory. This is due to the fact that an unshearable Kirchhoff type of theory, owing to its kinematic coupling of cross-sectional rotation with the bending deflections, cannot adjust to the geometry of the pulley and, at the same time, account for the distributed moment at the centre line induced by the frictional tractions. Oborin and Vetyukov [123] studied the effect of this offset action of frictional forces in the simplified setting of a straight beam in contact with a travelling surface. In continuation, Oborin [124] treated the geometrically linearised problem of a one-pulley belt drive analytically and compared the results against [102], where the geometrically nonlinear setup of Fig. 3 is considered but the contact is applied at the centre line. In conclusion, the account for an eccentric action of frictional forces is found to have a significant impact on the contact response.

Nordenholz and O’Reilly [125] apply the generalised director formulation, see Naghdi and Rubin [126], to steady-state contact problems of axially moving rods; transverse normal strains and the eccentric action of contact forces are accounted for. Another reference worth mentioning with respect to the latter aspect is the analysis of divergence buckling of an edge-loaded axially moving beam by Mote [127]. The considered problem of flexural-torsional buckling of band saw blades is exceptional owing to the three-dimensional nature of the buckling mechanism. On a side note, the coupling of torsional rigidity and axial tension known as Wagner effect, see Schmidrathner et al. [3] or Manta and Gonçalves [128], is important to consider for coupled deformations of thin-walled structures of open profile at high-tension levels.

As reflected by the references provided so far, studies on planar, two-dimensional problems of axially moving structures prevail in the literature. However, moving flat structures exhibit the phenomenon of lateral motion, that is, an undesirable movement in direction of the pulley or drum axes, which is sometimes called “run-off”. Corresponding three-dimensional models relate to, for example, moving webs, see Shelton and Reid [129] or Benson [130], magnetic tapes, see Raeymaekers and Talke [7, 131], or steel conveyor belts, see Schulmeister [132], Scheidl et al. [2] or Schmidrathner et al. [3]. The importance of an accurate account for the frictional contact interaction depends on the process under investigation. Distributed frictional contact may be disregarded, like in the above cited articles concerning webs, replaced with approximate models for the sake of computational efficiency, as done in [2, 3] for steel belts with high membrane stiffness, or become particularly important, as pointed out in an experimental study by Taylor and Talke [133] concerning flexible magnetic tapes.

Moreover, the classic structural theories are known to exhibit unexpected behaviour in frictional contact problems with rough surfaces. The cooling of railway rails after hot rolling was analysed by Nikitin et al. [134], who adopted the model of a semi-infinite Euler–Bernoulli beam resting on a rough surface (Coulomb friction) and loaded by a thermally induced distributed bending moment. The derived analytic solution shows that the transition between the deflected free end and the undeformed rest of the structure happens in the form of an infinite series of self-similar solutions with ever flipping signs of the friction forces between subsequent regions. This peculiar result is a consequence of the struggle of the kinematically limited theory to accommodate to the boundary conditions at the transition to the undeformed rest of the structure. Stupkiewicz and Mróz [135] treated the similar case of monotonic and cyclic loading of the tip of a semi-infinite beam supported by a rough surface. We shall refer back to this article for the analytic treatment of the example considered in Sect. 3, where novel transient solutions for a beam travelling over a rough surface between two laterally offset prismatic joints are presented. As recently established by Vetyukov [1], self-similar sliding segments constitute the steady-state solution of this problem much like in the above references. The simplicity of the setup facilitates its use as a prototype example to study different structural theories in combination with various contact models in the future. In addition, the accurate resolution of the frictional contact response proves particularly difficult with established finite element schemes, which highlights their weaknesses and leaves room for a further advancement of these methods.

2.3 Kinematic description and governing equations for axially moving structures

At the beginning, we considered the problem of transverse wave propagation in an axially moving string from the Lagrangian and the Eulerian perspectives, see Fig. 1. Owing to the geometric linearity, the axial and transverse deflections decoupled and the switching between the different descriptions given in (2) was particularly easy. This simplicity is lost if large deformations are considered and one must carefully distinguish between the variants of material, spatial and mixed kinematic parametrisations. In addition, the preferred way to account for the material transport at constant rate v through a change of variable in analogy to (2) is limited to steady operation of the axially moving structure, see Nordenholz and O’Reilly [136].

In contrast to the usual setup of solid mechanics with a closed material volume of particles, problems of axially moving structures are formulated for spatial control domains with fluxes of material and energy across the boundaries. These quantities balance out at steady-state motion, but not in general. Thus, the familiar variational principles and derivatives thereof (Hamilton’s principle, Lagrangian equations) must be augmented accordingly.

In view of these aspects, we shall first consider a variety of established methods of kinematic parametrisation for travelling structures based on the geometrically nonlinear problem of an extensible string and, secondly, elaborate on the proper formulation of the governing equations for systems with spatial control domains.

2.3.1 Kinematic description of axially moving structures

The position vector to a material particle of an axially moving, extensible string in the total Lagrangian formulation may be written as

$$\begin{aligned} \varvec{r} = \varvec{r}(s,t), \end{aligned}$$

(7)

where s denotes the material arc coordinate of the undeformed reference configuration. Now, suppose the structure is moving across a spatial control domain at a constant material transport rate v, which determines the “amount” of material particles entering and leaving the domain per time unit. Then, we can identify the particles of the structure currently contained in this confined space (these particles comprise the active material volume) by means of the transformation

$$\begin{aligned} s = \sigma - v t. \end{aligned}$$

(8)

This time-variable transformation maps the active material volume onto a fixed intermediate coordinate $\sigma$. We call the corresponding description “updated Lagrangian”, which is equivalent to (2) in the geometrically linear setting, where the spatial coordinate x and material coordinate $\sigma$ are indistinguishable. It is important to note that this simple explicit transformation relies on the operation at constant transport rate v and is to be replaced with the implicit form $s = s(\sigma ,t)$ in general. Since the arrangement of particles in axial direction is usually unknown even in the stationary case, only an implicit formula can be provided for the transformations to a truly Eulerian coordinate x:

$$\begin{aligned} s = s(x,t), \end{aligned}$$

(9)

which poses no restrictions on the actual provenance of the spatial coordinate. For example, x may denote a simple Cartesian coordinate or represent a curvilinear one if the path of the axial motion is not straight, as it is the case for looped belt drives. Evidently, in contrast to (2), the Eulerian coordinate x and the intermediate one $\sigma$ are to be distinguished in general.

Table 1 Different variants of kinematic parametrisation for the position vector $\varvec{r}$ of an extensible string; stretch and material time derivatives are related to the Lagrangian coordinate s of the undeformed reference state

At a given constant transport rate v, the just introduced different kinematic descriptions are contrasted in Table 1 with respect to the axial stretch and the material time derivatives both defined with respect to the arc coordinate of the reference configuration s. Corresponding position vectors $\varvec{R}$ are introduced for each row to denote the representation of $\varvec{r}$ in the particular kinematic descriptions. At steady-state motion, the updated Lagrangian description $\varvec{R}(\sigma ,t)$ is preferred over the Eulerian one by many authors, see the analytical studies [5, 6, 106] as well as Laukkanen [137] for a corresponding plate finite element implementation to simulate axially moving paper webs. However, a fully spatial parametrisation becomes advantageous for the treatment of transient dynamics, see [108, 109] as well as Huynen et al. [138] for an alternative application in the static problem of an elastic rod constrained by a surrounding tube.

Koivurova and Salonen [139] discuss a mixed kinematic approach for geometrically nonlinear problems that constructs the actual deformed state via the deflection from an intermediate stationary configuration. Naturally, the use of this special intermediate state poses certain restrictions on the applicability of this scheme with regard to the flow of material particles through the control domain. Such advanced parametrisation strategies are efficient in the development of finite element schemes in the general framework of ALE methods, which shall be topic of Sect. 2.4.

2.3.2 Governing equations for open systems

The second determining factor that, apart from the particular choice of kinematic parametrisation, affects the mathematical expression of the basic principles of mechanics is the choice of the control volume. The use of a material control volume that contains an invariable set of material particles is typical for solid mechanics in general, and the standard forms of the Lagrangian equations of motion as well as of D’Alembert’s and Hamilton’s principle reflect that. However, it is usually more efficient to study problems of axially moving structures in spatial control domains, that feature a flux of particles, momentum and energy across the domain boundaries, which has to be accounted for by means of a consistent augmentation of the principles.

It turns out that Hamilton’s principle and Lagrangian equations require special attention, while the balance of momentum and D’Alembert’s principle, i.e. the principle of virtual work, remain mostly unaffected by the change of perspective. This preservation of the latter two relates to the fact that both can be applied for the material currently contained in the control domain (active material volume) at a given instant and then merely need to be, with the words of Renshaw et al. [140], “continuously re-applied at every instant”. To put it differently, these formalisms hold for open domains in unchanged form, because they may be applied to the active material volume at any time, which is not impeded by a variable material contents. The cited remark from [140] refers to the balance of momentum; the paper itself is concerned with the formulation of conserved quantities for axially moving strings and beams, for which it is concluded that only the Eulerian functionals qualify as Lyapunov functions for stability analysis. Chen et al. [141] demonstrate that the (formally unchanged) principle of virtual work for non-material control volumes is equivalent to the appropriately extended version of Lagrange’s equations, as stated by Irschik and Holl [65]. The study in [141] also features a corresponding implementation of an ALE cable finite element and an instructive numerical example.

The discussion of the appropriate extension of Hamilton’s principle and of the Lagrangian equations for open systems dates back to McIver [142] and, since the publication of the aforementioned article by Irschik and Holl [65], has been carried forward primarily in the journal Acta Mechanica. Casetta and Pesce [143] derive the augmented Hamilton’s principle with the help of Reynold’s transport theorem, establish correspondence with the extended Lagrangian equations proposed in [65], and mention that the version presented in [142] lacks a term that relates to the flux of kinetic energy across the boundaries of the spatial domain. Remarkably, in relying on [142], Hetzler [95] disregards this term as well. In continuation of their earlier work, Irschik and Holl [144] again employ the method of fictitious particles to derive the extended version of Lagrangian equations, but this time based on the Lagrangian kinematic description, in contrast to the Eulerian perspective adopted in [65]. In addition, Casetta [145] considers the inverse Lagrangian problem for a spatial control volume, i.e. the task of deriving a Lagrangian functional based on a given system of equations of motion; the analysis is limited to systems with one degree of freedom.

The primary results of the above given references concerning Hamilton’s principle are collected, unified and extended further in the recently published paper by Steinböck et al. [146]. The authors formulate the principle for all possible combinations of Lagrangian or Eulerian kinematic descriptions with material or spatial control volumes. The simple example of an axially moving elastic bar is used to verify the equivalence of these formulations and to emphasize their importance for practical applications. Here, we present the standard expressions of Hamilton’s principle for the Lagrangian description in a closed material volume:

$$\begin{aligned} \int _{t_1}^{t_2} \left( -\delta T + \delta E_V + \delta E_S - \delta W_{nc} \right) \,\textrm{d}t = 0, \end{aligned}$$

(10)

as well as the one for the Eulerian description in an open volume, owing to its significance for axially moving structures:

$$\begin{aligned}{} & {} \int _{t_1}^{t_2}\left[ -\delta _c T + \delta _c E_V + \delta _c E_S - \delta _c W_{nc} \right. \nonumber \\{} & {} \quad + \,\int _{\partial V_c} \rho \left( \delta \bar{\varvec{u}} \cdot \bar{\varvec{\nu }}\right) \left( \bar{\varvec{\nu }} - \varvec{\nu }_c\right) \cdot \varvec{n}_c \,\textrm{d}A \nonumber \\{} & {} \quad \left. - \,\int _{\partial V_c} \rho \left( \frac{1}{2} \bar{\varvec{\nu }} \cdot \bar{\varvec{\nu }} - e_V \right) \left( \delta \bar{\varvec{u}} - \delta _c \varvec{u}_c\right) \cdot \varvec{n}_c \,\textrm{d}A \right] \,\textrm{d}t = 0. \end{aligned}$$

(11)

For an application of (11), we refer to the aforementioned article by Boyer et al. [84]. Both versions are taken directly from Steinboeck et al. [146], where the corresponding mixed formulations can be looked up as well. The uppercase letters denote integral quantities, namely: the kinetic energy T, potential energy of strains and volumetric forces $E_V$, potential energy of surface tractions $E_S$ and the work of non-conservative forces $W_{nc}$. The first line of (11) replicates (10) with the variational operator $\delta _c$ that corresponds to the fixed spatial control volume $V_c$ in contrast to the material variational operator $\delta$, which implies holding the material volume constant. Additional surface integrals arise in (11) owing to the net flux of momentum and to the net virtual shift of the kinetic energy minus potential energy $e_V$ across the control volume, respectively; $\rho$ denotes the mass density. Apart from the particle motions in Eulerian description (deflection $\bar{\varvec{u}}$, particle velocity $\bar{\varvec{\nu }}$) this general formulation also accounts for a potential motion of the spatial boundary (deflection $\varvec{u}_c$, velocity $\varvec{\nu }_c$, normal vector $\varvec{n}_c$). Naturally, in case of a stationary state the additional fluxes must balance out and the extended principle reduces to the standard form.

In case of a system with a finite number of degrees of freedom, which typically results from a discretisation of the continuous system by means of a Ritz or a finite element approximation, an extended version of the Lagrangian equations can be formulated that is equivalent to (11), see [65, 143]:

$$\begin{aligned} Q_k= & {} \frac{d}{dt} \frac{\partial _c T}{\partial \dot{q}_k} - \frac{\partial _c T}{\partial q_k} \nonumber \\{} & {} -\, \int _{V_c} \frac{1}{2} \rho v^2 \left( \frac{\partial \bar{\varvec{\nu }}}{\partial \dot{q}_k} - \frac{\partial \varvec{\nu }_c}{\partial \dot{q}_k}\right) \cdot \varvec{n}_c \,\textrm{d}A \nonumber \\{} & {} +\, \int _{V_c} \rho \bar{\varvec{\nu }} \cdot \frac{\partial \bar{\varvec{\nu }}}{\partial \dot{q}_k} \left( \bar{\varvec{\nu }} - \varvec{\nu }_c \right) \cdot \varvec{n}_c \,\textrm{d}A, \end{aligned}$$

(12)

which specifies the equation for the generalised coordinate $q_k$ and is taken from Casetta and Pesce [143] with an appropriately adapted notation; in this regard $\textrm{d}/\textrm{d}t$ denotes a total material time derivative and, like $\delta _c$ above, the operator $\partial _c$ is introduced to indicate that the differentiated quantity is computed for the fixed control volume $V_c$. As remarked in [146], the contributions of conservative and non-conservative forces are not distinguished in [143] and, thus, are merged into a single virtual work component that enters (12) by means of the generalised force $Q_k$. Recent contributions that feature (12) as the basis of ALE finite element implementations for axially moving structures are authored by, for example, Pechstein and Gerstmayr [147] or Pieber et al. [62].

2.4 Arbitrary Lagrangian–Eulerian FEM for axially moving structures

The major issue in the computational analysis of axially moving flexible structures is that the traditional material (Lagrangian) kinematic description of structural mechanics becomes inefficient because material particles enter and leave the control domain. Finite elements that are strictly tied to material particles must continuously pass through the boundaries of the domain, at which kinematic conditions need to be applied. Even when the structure is looped like a belt drive (e.g. Duvfa et al. [148]), the finite elements are moving between qualitatively different domains all the time: from the free spans to the contact zones and back. This results in numerically induced oscillations, such that obtaining a stationary solution becomes impossible, see Oborin et al. [109], where the deficiencies of the traditional Lagrangian description are highlighted in comparison to a Eulerian alternative. A less obvious, but still important issue is that one cannot refine the mesh locally near the contact zones to better resolve the complicated friction processes developing there: Because of the axial motion, the finer part of the mesh would move along and coarser elements would eventually arrive in the contact zone. Attempts to treat mentioned issues with the existing methods of computational mechanics like mortar approach or re-meshing techniques result into cumbersome and potentially non-robust formulations.

An effective alternative is the application of the Eulerian kinematical description, which traditionally belongs to the field of computational fluid mechanics. Evidently, the mentioned difficulties can be resolved by writing the mechanical fields such as displacements, strains or stresses as functions of the spatial coordinate in the direction of the axial motion. The overwhelming advantage is that the stationary contour motion, at which the structure retains its shape from the viewpoint of a spatially fixed observer, can be described as time-independent with no numerically induced oscillations.

Historically, the development of respective Arbitrary Lagrangian–Eulerian formulations for structural mechanics was motivated by problems like automobile crash tests and high strain rate metal forming operations, which pose the risk of an excessive distortion of the Lagrangian element mesh and are thus capable of pushing the conventional finite element approach beyond its limit, see Benson [149] for one of the early works and Davey and Ward [150] for an application to the metal forming process of ring rolling. One of the initial intentions of ALE was to evade mesh distortion by detaching the finite elements from the material particles and to thereby enable a time evolution of the finite element mesh to the advantage of the problem at hand. The basic idea of the classical form of ALE, summarized later by Donea et al. [151], is to split the operator of the problem. The partial differential equations disintegrate into two systems that are solved sequentially within a time increment. In terms of the implementation in the finite element procedure, it means that each time increment is performed in two steps: The first one is the conventional Lagrangian step, in which the equations of motion are integrated implicitly or the new equilibrium is sought if the problem is quasistatic, but with the account for the distributions of stress, mass density and possibly inelastic variables, accumulated from the previous time increments. The second step is the Eulerian one, at which the solution is projected back to the spatially fixed non-material mesh according to the small displacement increments obtained during the Lagrangian step, which means performing a single step of time integration of an advection equation. Recently, this formalism has been applied to modelling the roll forming process by Crutzen et al. [152]: both the contact and the material nonlinearities need to be accurately resolved for the elastoplastic analysis of a metal strip that is incrementally bent to a final cross-sectional profile as it passes through a succession of roll stands.

The main drawback of this very general approach is that the re-mapping of the field variables during the Eulerian step degrades the solution quality as the advection equation is difficult to integrate accurately over time. Certain problem-specific variants of the method are suggested in the literature, which make the Eulerian step obsolete or at least less important. For example, Askes, Kuhl and Steinmann [153, 154] propose a “monolithic” version of ALE for hyperelastic continua that gets rid of the Eulerian convective update altogether. Others employ an appropriate variable transformation, like Nackenhorst [155], who adapts the ALE formalism for the problem of rolling with contact and friction: The deformations are superimposed upon the rotation of the wheel, and the differential relations of the theory are determined by the relative kinematic description. The underlying motion of material particles because of the rotation is pre-defined, and a stream-line-upwind technique is only needed for the integration of the evolution law for inelastic internal variables. A rare example of the use of isogeometric approximation technique in the context of non-material kinematic description is provided by Garcia and Kaliske [156], also in the context of the rolling contact.

For thin structures, such as beams and cables, variants of the approach with redundant nodal coordinates were suggested by several authors. The field of application comprises: petroleum drilling operations [157], pipe reeling [158, 159], sliding joints that appear in ropeways [160] or arresting cable systems of marine aircraft carriers [161] as well as reeving systems [88, 162, 163]. See also Hyldahl et al. [164] for an extension to plate finite elements. Featuring both the spatial and the material coordinates among the nodal degrees of freedom such models impose additional constraints, which complete the system of equations and provide a possibility to control, whether a specific node behaves as a Eulerian one, a Lagrangian one or as a hybrid thereof. Special methods of numerical time integration, typical for simulations in the field of multi-body system dynamics, are required to accommodate the high number of constraint conditions. The increased number of unknowns and the need to integrate differential-algebraic equations may impact the numerical efficiency of this otherwise highly flexible technique.

As a “light” version of ALE, we can classify various models, in which the axial material flow takes place in the background, in the spirit of $\varvec{R}(\sigma ,t)$, see Table 1. It does not affect the elastic response of the flexible structure and manifests itself just in the form of several possibly nonlinear additional terms in the kinetic energy, which are either postulated or derived under certain kinematic assumptions. On occasion, the Ritz method is applied to either the extended version of Hamilton’s principle (11), see Stangl et al. [64], or the Lagrangian equations of motion, see Ghayesh et al. [165], who study the dynamics of an axially moving von Kármán plate. The inherent difficulty to satisfy the $C^1$ continuity condition for unshearable theories of Kirchhoff or von Kármán plates complicates the formulation of related finite element schemes, see Vetyukov [166]. Hence, many authors resort to the Reissner–Mindlin theory, which features additional degrees of freedom in account for transverse shear, to formulate finite elements for travelling plates, see Wang [167] or Laukkanen [137]. These elements are susceptible to shear locking, which is alleviated using the method of “mixed interpolated tensorial components” (MITC) in the above cited papers. Alternatively, shear deformations may be restrained artificially to mimic the kinematics of the unshearable Kirchhoff theory, see Luo and Hutton [42] for the development of triangular finite elements for axially moving discrete Kirchhoff plates. The spectral element formulation presents a viable alternative for the modal analysis of axially moving plates as long as the considered domain remains geometrically simple, see Kim et al. [168]. The framework of “light” ALE, employed in the above references, allows to investigate specific dynamical effects, but is generally restricted to moderately small deformations and does not fully address the question of the interaction between the parts of the structure within the control domain and outside of it.

The Mixed Eulerian–Lagrangian (MEL) kinematic description is actively promoted by the authors’ research group. The MEL formalism is based on the variable transformation to a mixed set of Eulerian and Lagrangian coordinates in the spirit of Sect. 2.3.1. Thus, large vibrations of an axially moving beam or string with coupled longitudinal and transverse deformations are captured by two functions of space and time, namely the material coordinate s and the finite transverse deflection w [67]:

$$\begin{aligned} s=s(x,t),\quad w=w(x,t). \end{aligned}$$

(13)

In each spatial point in the axial direction $x=\textrm{const}$, the relations (13) identify a specific material particle and its transverse deflection. Consequenlty, the position vector $\varvec{r}$ in the planar Cartesian basis $\{\varvec{i}, \varvec{j}\}$ features the spatial coordinate x to mark the axial position of a point and the material one w to grasp its deflection:

$$\begin{aligned} \varvec{r} = x \varvec{i} + w(x,t) \varvec{j}, \end{aligned}$$

(14)

which emphasises the mixed Eulerian and Lagrangian nature of the formulation. In the special case of a constant transport rate v, the kinematics of this description are governed by the last line in Table 1 for the position vector given as $\varvec{R}(x,t)$.

In recent years, the authors’ group and related researchers have published a substantial number of articles in conjunction with the MEL kinematic approach: In [67], it is demonstrated how the semi-implicit variable transformation (13) gives rise to an efficient non-material finite element scheme both by means of the variational equation of the principle of virtual work and with the help of Lagrange’s equations of motion. Large vibrations of axially moving beams and strings are accurately described with just a few finite elements in the control domain $0\le x\le L$. An extension to multi-dimensional continua like plates and shells builds upon a two-stage mapping from the material reference configuration to the deformed actual one: all mechanical fields are considered functions of coordinates in an abstract intermediate configuration, and a geometrically exact formulation is achieved with the multiplicative decomposition of the deformation gradient tensor [169].

Featuring the minimal set of unknowns, the approach is very convenient for elastic problems and allows treating variable distributions of the material influx and outflux rates at the boundaries of the control domain. The practical application to the hot rolling process in [170] required the transport conditions of the inelastic variables to be treated within the Eulerian step of each time increment; see also [171] for the simulation of the roll forming process. In continuation of Vetyukov et al. [122], the frictional contact with a rotating pulley as the source of the axial motion of the belt stand in focus of the research in [102]. A compound coordinate system, consisting of Cartesian and polar domains, allows to generalize MEL to looped structures like belt drives by introducing the Eulerian coordinate in the circumferential direction of the machine. The possibility to refine the mesh in the important domain of contact of the moving belt with a rotating drum makes it possible to investigate the stick and slip behaviour, which is important for estimating the efficiency of power transmission [110, 112]. For the practically relevant study of the phenomenon of lateral run-off of flat belt drives because of geometric imperfections in the 3D setting, see [2, 3, 172] for rod and shell models of the travelling structure.

Other authors pursue kinematic approaches in the framework of ALE that are closely related to MEL: Synka and Kainz [173] adopt the MEL concept for the development of continuum finite elements to simulate steady-state hot rolling. The aforementioned formulation proposed by Koivurova and Salonen [139] and put to use by Kulachenko et al. [174] utilises a stationary configuration for the purpose of parametrising the actual state. Gerstmayr and co-workers [62, 147] employ an explicit variant of (13) that is closely related to what we called “updated Lagrangian” in terms of Sect. 2.3.1, see also Grundl et al. [175] for an extension of this formalism with respect to continuous variable transmission belt drive systems.

3 Benchmark problem: partially sliding beam travelling across a rough surface

As a representative example of an axially moving flexible structure, we consider an endless beam, travelling in contact with a rough surface, moving with the velocity v, see Fig. 5.

Fig. 5

Flexible beam travelling in frictional contact with a moving rough surface

We focus the consideration on a control domain, bounded by two guides seen as prismatic joints. The beam enters the domain through the entry guide such that the axis of the beam coincides with the direction of the surface velocity v, and it leaves the domain through the exit guide in the same direction. The relative lateral misfit between the guides $w_0$, which can be seen as a (possibly time dependent) geometric imperfection, triggers sliding of the beam in at least part of the control domain because the particles of the beam must acquire a lateral velocity component to reach the exit guide. The transverse deflections decouple from the axial motion of the beam in the geometrically linear setting, such that the axial transport rate of particles always equals the surface velocity v. This mechanical system can be considered a prototype for various technical processes like the motion of a metal strip on a roller table of a rolling mill or as a “flattened” version of the problem of contact of a flat belt with a cylindrical rotating drum of a belt drive.

The essentially nonlinear character of the dry friction contact law results into a non-trivial transient dynamic behaviour of the system even at very slow motion, when the inertia effects are negligible and the beam is in equilibrium at each time instant. Complicated patterns of sliding zones develop in time. The existence of the zone of sticking contact over longer time intervals depends on the parameters of the model. In this example problem, we consider a Bernoulli–Euler beam, ignore inertia and remain under the assumptions of geometric linearity (small deformations) and Coulomb’s dry friction law. The discussion begins with a brief recap of the analytical solution for the stationary motion, recently presented by Vetyukov in [1]. Transient solutions as well as a numerical approach featuring the Mixed Eulerian–Lagrangian formulation are considered later on.

3.1 Stationary solution for the boundary value problem

At stationary contour motion, the lateral positions of the guides are fixed and the deformed axis of the beam retains its outer appearance, i.e.: each particle of the beam follows the same trajectory across the control domain over time. The deflection is a function of the spatial axial coordinate, $w=w(x)$ with $\dot{x}=v$ and $\partial _t w=0$, and the direction of the sliding friction force $q_0$ depends on the sign of the lateral velocity of a particle $\dot{w}=vw'$, see Fig. 6.

Fig. 6

Stationary contour motion of an endless beam travelling across the control domain $0\le x\le \ell$ between two misaligned prismatic joints

The material velocity of a particle $\dot{w}$ again follows from the variable transformation (2) with $\partial _tw=0$ for the stationary case. We use $w'=\partial _xw$, as the material coordinate s no longer appears in the present context.

The deformed line of the beam, which is in equilibrium at each time instant, follows as a solution of the essentially nonlinear boundary value problem

$$\begin{aligned} \begin{array}{l} \displaystyle aw''''=q,\quad q=\left\{ \begin{array}{ll} -q_0,&{}w'>0\\ 0,&{}w'=0\\ q_0,&{}w'<0 \end{array} \right. , \\ w(0)=0,\quad w'(0)=0,\quad w(\ell )=w_0,\quad w'(\ell )=0 \end{array} \end{aligned}$$

(15)

with $\ell$ being the length of the control domain, a the bending stiffness of the beam and q the distributed friction force, whose sign depends on the sign of the slope $w'$. If there exists a continuous zone of stick with $w'=0$, then the sticking friction force must vanish there as a consequence of the beam equation. Isolated points, in which the slope changes the sign and $w'$ turns to zero, can be ignored in the definition of q.

As long as the sliding friction force $q_0$ is small, the deformed line of the beam shall look similar to the one, depicted in Fig. 6 with $w'>0$ and $q=-q_0$ everywhere; an analytical solution of (15) is easy to find. At growing $q_0$ the beam would bend downwards more and more, until $w'$ becomes zero at some point, specifically at the left end $x=0$. A naive expectation is that at higher values of $q_0$ a zone of stick with $w=0$ would emerge from the entry to the right, followed by a zone of sliding upwards in obedience to the boundary condition $w(\ell )=w_0$. It is, however, easy to realize that this kind of solution is impossible. Indeed, there shall act no concentrated forces nor moments at the boundary between the zones of sticking and sliding, which means that the deflection w, the slope $w'$, the bending moment $aw''$ and the transverse shear force $-aw'''$ shall be continuous there—and they all vanish in the zone of stick. This results into 6 boundary conditions for the zone of sliding, as two more need to be imposed at $x=\ell$, which cannot be fulfilled because the differential equation is of the 4th order.

The contradiction is resolved in [1]: As soon as $q_0$ exceeds the first critical value $q_{0,1}=72aw_0/\ell ^4$, $w'$ changes sign in the vicinity of the entry point and the solution features two segments of sliding: in the first one, the particles are sliding downwards and $q>0$, and in the subsequent one the situation is the opposite with $q<0$. The coordinate of the switching point in dependence on $q_0$ follows from a system of nonlinear algebraic equations. Further growth above the second critical value $q_{0,2}\approx 219.177aw_0/\ell ^4$ leads to the solution comprising three segments of sliding, and so on. The sequence converges to the ultimate critical value,

$$\begin{aligned} \lim _{n\rightarrow \infty }q_{0,n}=q_{0,\infty }=168\sqrt{5}\,aw_0/\ell ^4. \end{aligned}$$

(16)

At $q>q_{0,\infty }$, the deformed beam comprises a zone of sticking contact, followed by infinitely many segments of sliding with alternating directions of friction. These segments of sliding form a self-similar structure, where each segment is a copy of the neighbouring one, scaled in both directions; for details, we again refer to Vetyukov [1]. Such self-similar solutions were previously known for static beam problems with friction [134, 135], now we observe this situation for an axially moving structure. Questions remain open, how the account for the finite thickness of the beam (which additionally features frictional moment interaction between the beam and the moving surface and requires higher-order beam theory or 2D modelling) or the inertia terms would affect the obtained solution. We, however, remain with the idealization of the Bernoulli–Euler beam theory and with the assumption of quasistatics in the following and focus on the transient behaviour of the structure.

3.2 Analytical solution for the initial stage of transient motion

The transient setup of the problem considered in the following is depicted in Fig. 7.

Fig. 7

Structure of the initial stage of the transient solution for the beam travelling at constant rate v subjected to an upward motion of the left entry joint; we introduce local segment-wise coordinates $x_i$ for the sequence of N sliding segments with lengths $l_i$ and transition points $X_i$

The beam is again transported across the domain at constant rate v, but the lateral misfit of the entry and exit joints grows linearly over time owing to a transverse motion of the left boundary with velocity c:

$$\begin{aligned} w|_{x=0} = c t, \end{aligned}$$

(17)

such that the beam is straight initially at $t = 0$. Stupkiewicz and Mróz [135] analysed the related case of a semi-infinite beam resting on a rough surface and loaded by a time-variable concentrated force or bending moment at its tip. In fact, we follow a similar solution procedure, because the governing ODE is equivalent and the account for axial transport and the kinematic loading at the entry joint amounts to a modification of the boundary and transition conditions. In doing so, we assume the region of non-trivial transverse deflections to always remain smaller than the length of the control domain l. This guarantees that no complicated interactions at the exit joint can occur and that the boundary conditions there can be ignored, which renders the problem analogous to one of a semi-infinite beam.

As a consequence, the distance between the joints l is no longer a characteristic length and we instead introduce alternative scales:

$$\begin{aligned} L = \left( a/q_0\right) ^{1/3}, \quad T = L/c, \quad V = L/T, \end{aligned}$$

(18)

to normalise the variables and parameters accordingly:

$$\begin{aligned} \hat{w} = w/L, \quad \hat{x} = x/L, \quad \hat{t} = t/T, \quad \hat{v} = v/V, \quad \hat{q} = q/q_0. \end{aligned}$$

(19)

For the sake of simplicity, we suspend with the explicit designation of dimensionless quantities and reuse the usual operators to denote derivatives with respect to the new variables.

The transformed nonlinear transient boundary value problem reads:

$$\begin{aligned} \begin{aligned}&w''''=q,\quad w|_{x=0}=t,\quad w'|_{x=0}=0 \\&\dot{w}=\partial _t w+vw',\quad q=\left\{ \begin{array}{ll}-1,&{}\dot{w}>0\\ (-1,1),&{}\dot{w}=0\\ 1,&{}\dot{w}<0\end{array}, \right. \end{aligned} \end{aligned}$$

(20)

where the frictional state with corresponding traction q is determined by the sign of the transverse particle velocity $\dot{w}$, which in the previously considered stationary case was related to the slope $w'$, see (15).

In accordance with the conclusions drawn in [1, 135], the attempt at a solution with one sliding region on the left that somewhere transitions to a trivial stick zone is in vain. Instead, as Fig. 7 already insinuates, we seek the transverse deflection in a continuous zone of sliding as a piecewise sequence $w_i$ of $0\le i < N$ segments with alternating directions of the friction force, which is reminiscent of the self-similar stationary solution above. To this end, we define local coordinates $x_i$ for each segment to allow a uniform description of the individual solutions:

$$\begin{aligned} w_i = w_i (x_i, t), \quad x_i = x - X_i,\quad 0 \le x_i \le X_{i+1}-X_i \equiv l_i, \end{aligned}$$

(21)

where $X_i = X_i(t)$ and $l_i =l_i(t)$ denote the time-variable positions of the transition points and the corresponding segment lengths, respectively, see Fig. 7; derivatives with respect to x and $x_i$ are exchangeable. Since the entry joint is moving upwards with $w|_{x=0}=t$, the frictional traction q must act downwards in the segment $i = 0$, i.e. $\dot{w}_1 >0$ and $q = -1$, which sets the starting direction for the sequence of ODEs in the sliding zone:

$$\begin{aligned} w_i'''' = \left( -1\right) ^{i+1}, \end{aligned}$$

(22)

with the general solution

$$\begin{aligned} w_i = \left( -1\right) ^{i+1} \frac{x_i^4}{24} + Q_i \frac{x_i^3}{6} + M_i \frac{x_i^2}{2} + \Phi _i x_i + W_i. \end{aligned}$$

(23)

The uppercase letters denote the unknown constants obtained in the course of sequential integration. They equal $w_i$ and its derivatives up to third order at $x_i = 0$ and are named according to their physical counterparts, namely, in order of appearance in (23): transverse force, bending moment, slope and deflection.

In absence of concentrated forces and moments, the solution must remain $C^3$-continuous within the sliding zone:

$$\begin{aligned} \begin{aligned}&w_i(l_i,t) = w_{i+1}(0,t), \quad w'_i(l_i,t) = w'_{i+1}(0,t), \\&w''_i(l_i,t) = w''_{i+1}(0,t), \quad w'''_i(l_i,t) = w'''_{i+1}(0,t). \end{aligned} \end{aligned}$$

(24)

Moreover, the corresponding smooth transition to the trivial stick zone at the rightmost point $X_N$ requires w and its derivatives to vanish identically:

$$\begin{aligned} \begin{aligned}&w_{N-1} (l_{N-1},t) = 0,\quad w'_{N-1} (l_{N-1},t) = 0,\\&w''_{N-1} (l_{N-1},t) = 0,\quad w'''_{N-1} (l_{N-1},t) = 0. \end{aligned} \end{aligned}$$

(25)

By evaluation of these continuity conditions with (23), we first determine the unknown integration constants in the rightmost segment and, in sequence, work our way back from right to left until we finally arrive at a unified series representation:

$$\begin{aligned}{} & {} Q_i = \sum _{k=i}^{N-1}\left[ (-1)^k l_{k}\right] \nonumber \\{} & {} M_i = \sum _{k=i}^{N-1}\left[ (-1)^k \frac{l_{k}^2}{2} - Q_k l_{k}\right] \nonumber \\{} & {} \Phi _i = \sum _{k=i}^{N-1}\left[ (-1)^k \frac{l_{k}^3}{6} - Q_k \frac{l_{k}^2}{2} - M_k l_{k}\right] \nonumber \\{} & {} W_i = \sum _{k=i}^{N-1} \left[ (-1)^k \frac{l_{k}^4}{24} - Q_k \frac{l_{k}^3}{6} - M_k \frac{l_{k}^2}{2} - \Phi _k l_{k}\right] . \end{aligned}$$

(26)

The same result, albeit for a slightly modified notation, is found in [135], where the derivation is also covered in greater detail. The main advancement of (26) is that it determines the solution (23) up to the unknown, time-variable lengths of the individual segments $l_i(t)$. These are to be determine such that the kinematic conditions at the entry joint and at the intermediate transition points are fulfilled:

$$\begin{aligned}{} & {} \left. w\right| _{x=0} = t, \quad \left. w'\right| _{x=0} = 0, \nonumber \\{} & {} \left. \dot{w}\right| _{x=X_i} = \left. \partial _tw\right| _{x=X_i} + v \left. w'\right| _{x=X_i} = 0, \quad 1\le i \le N-1. \end{aligned}$$

(27)

The constraints collected in the second line require the sliding velocity of the particles instantly residing in transition points $X_i$ to vanish. In other words: If a particle is currently sliding upwards or downwards, it cannot be situated at a boundary between two segments with opposite sliding direction. In total, (27) constitutes $N+1$ constraints for only N lengths $l_i$, i.e. we lack one unknown. Hence, the system is overdetermined, which gives us a hint that the actual analytic solution requires an infinite number of segments $N \rightarrow \infty$, see [1, 134, 135].

In order to write (27) in terms of the solutions at the transition points, we need to expand the partial time derivative $\partial _t w$, which, in contrast to uppercase quantities specified in (26), relates to the global Cartesian coordinate x. With $\partial _t x = 0$ and (21), we obtain

$$\begin{aligned} \partial _t x_i = - \dot{X}_i, \end{aligned}$$

(28)

for the local coordinate, where $\dot{X}_i$ is just the time derivative of the function $X_i(t)$. Now, we can rewrite the corresponding derivative of the deflection at a transition point ($x = X_i$ or $x_i = 0$) in a form suitable for substitution by means of (26):

$$\begin{aligned} \left. \partial _tw\right| _{x=X_i} = - w_i'(0,t) \, \dot{X}_i + \left. \frac{\partial w_i(0,t)}{\partial t}\right| _{x_i = \textrm{const}}. \end{aligned}$$

(29)

The transformed system (27) reads:

$$\begin{aligned}{} & {} \dot{W}_0 = 1, \quad \dot{\Phi }_0 = 0, \nonumber \\{} & {} \Phi _i \left( v - \dot{X}_i\right) + \dot{W}_i = 0, \quad 1\le i \le N-1, \end{aligned}$$

(30)

where the algebraic equations of the first line in (27) have been differentiated to obtain a system of ODEs. Again, the time derivatives of the uppercase quantities simply relate to the differentiation of time-variable functions. Recalling that the segment lengths were introduced in (21) as a mere abbreviation, i.e. $l_i = X_{i+1}-X_i$, we see that (30) presents an (overdetermined) system of nonlinear ODEs for the evolution of the transition points $X_i$.

The initial conditions for the reference state of the straight undistorted beam are trivial, but, at the same time, the transition points adopt an infinite velocity as soon as the entry prismatic joint starts moving in transverse direction:

$$\begin{aligned} \left. X_i\right| _{t \rightarrow 0} = 0, \quad \dot{X}_i|_{t = 0} \rightarrow \infty , \quad 1 \le i \le N, \end{aligned}$$

(31)

which poses a problem for the numerical integration. In fact, the analytic investigation under the assumption of a self-similar solution along the lines of Stupkiewicz [135] shows that $\dot{X}_i|_{t\rightarrow 0} \propto t^{-3/4}$ holds asymptotically. Understandably, the finite rate of axial transport v has no impact on this result. Thus, the static self-similar solution for $v = 0$, which is easy to construct by analogy to Stupkiewicz [135], holds initially regardless of the chosen value for v. We thus begin the time integration at a small but positive time instant with non-trivial initial values of $X_i$, set up accordingly to the analytically known solution of the static case.

To facilitate a simple numerical solution of the initial value problem, we merely truncate the sequence at a finite number N and regard the last constraint of (30) for $i = N-1$ as a residual error to judge the accuracy of the approximation. For all practical purposes and in view of the later comparison against finite element simulations, the choice $N = 4$ is sufficiently accurate. The corresponding time evolutions of $X_i$ and $\dot{X}_i$ for a specified transport rate $v = 100$ (i.e. the joint moves in transverse direction 100 times slower than the underlying surface to the right) are computed with the help of Wolfram Mathematica¹ and depicted in Fig. 8.

Fig. 8

Time evolution of transition point positions $X_i$ and their velocities $\dot{X}_i$ as obtained from the semi-analytic solution for $N = 4$ sliding segments; the lengths of subsequent sliding segments diminish rapidly; the initially infinite velocities decrease monotonously and become equal to the axial transport rate v at characteristic time instances

As can be seen from the left picture, every additional segment added by increasing N decreases in length significantly and its impact on the solution diminishes accordingly. This contributes to the rapid convergence of the approximate solution with respect to N, which is verified by the decay of the residual error in the numerical experiments. The initially infinite extension rates $\dot{X}_i$, presented in the plot on the right with a logarithmic ordinate, decrease monotonously and hit the transport rate v at the marked points. According to (30), these time instances are potentially critical and may cause a characteristic change of the solution. Though the extension rate of the first point $\dot{X}_1$ crosses the line first, this occurrence has no significant impact: What happens is that material particles begin to cross the boundary $X_1$ of two adjacent slip segments and, in the process, switch their sliding direction. This does not impede the sustainability of the solution.

However, a truly critical state is reached once previously sliding particles start to cross the boundary $X_N$ to the stick zone, which amounts to the establishment of a non-trivial zone of stick. In the present case, this occurs at $t_*= 1.58446\times 10^{-3}$. To further analyse this state, we take a look at the expanded version of the last transition condition of (30) for the rightmost segment:

$$\begin{aligned} \left. \dot{w}\right| _{x = X_{N-1}} =\frac{1}{6} (-1)^{N-1} \, l_{N-1}^3 \, \left( v - \dot{X}_{N}\right) = 0. \end{aligned}$$

(32)

This constraint is regarded as residual error of the numerical solution, which tries to approximate the analytic result $l_{N-1}\rightarrow 0$ in the limiting case of $N\rightarrow \infty$. At the critical instant $t_*$ the root $\dot{X}_N = v$ is reached. With this result in hand, we proceed to evaluate the remaining transition conditions sequentially in descending order from $i = N-1$ downwards. In doing so, we always substitute the preceding steps to simplify the expressions; the findings may be conveniently summarised in the following sequence:

$$\begin{aligned}{} & {} \left. \dot{w}\right| _{x = X_{i-1}} = \frac{1}{3} (-1)^{i-1} \, l_{i-1}^3 \, \left( v - \dot{X}_{i}\right) = 0, \quad N-1 \ge i \ge 2, \nonumber \\{} & {} \left. \dot{w}\right| _{x = 0} = \frac{1}{3} \, l_0^3 \, \left( v - \dot{X}_{1}\right) = 1. \end{aligned}$$

(33)

The last expression must not vanish owing to the prescribed motion of the entry prismatic joint ($\dot{w}|_{x = 0} = 1$); it yields $\dot{X}_1 = v - 3 l^{-3}_0 < v$ in accordance with Fig. 8. However, owing to the first line of (33), $\dot{X}_i = v$ holds for all $i\ge 2$. Reinserting this result in the expression for the particle velocities, we find that $\dot{w}_i$ must vanish at $t_*$ not only at the transition points but throughout all sliding segments except for the first one. The intriguing observation that only the first segment must necessarily remain in sliding state motivates us to attempt a continuation beyond $t_*$, see Sect. 3.4.

3.3 Finite element analysis

It is an easy task to develop an explicit numerical solution scheme for the transient boundary value problem (20) based on the finite differences discretization with a regularized dry friction law that enables a small “drift" in the zone of stick. Experience shows, however, that while the solutions appear physical at the first glance, the algorithm does not possess sufficient accuracy and robustness even at very fine grids and time integration with very small steps. The non-material finite element scheme presented in the following behaves significantly better. It features an implicit time integration and the technique of augmented Lagrange multipliers, see Simo and Laursen [176], for the dry friction law. The aim of the finite element simulation is to validate the above analytical solution and to draw conclusions regarding further stages, when a non-trivial zone of stick appears or the kinematic condition at the exit prismatic joint starts playing a role. Moreover, the academic example at hand allows to optimize the numerical algorithm and to better understand its strong and weak points, which is crucial for practically relevant, more complicated cases.

We divide the dimensionless control domain $0\le x\le 1$ into n equally long finite elements, each bounded by two nodes. Choosing the non-dimensional deflection w and the slope $w'$ as nodal degrees of freedom, we use cubic approximation within an element, see Vetyukov [177], and obtain the necessary $C^1$ interelement continuity. Along with the time evolution of the displacement field w(x), we also consider the distribution of the transverse friction force q(x) as part of solution; $q=-1$ in the segments currently sliding upwards and $q=1$ in the segments sliding downwards. The field q(x) is determined by the values in the two Gaussian integration points of each finite element. In the zones of sticking contact, q plays the role of a Lagrange multiplier for the imposed kinematic constraint $\dot{w}=0$ and assumes values in the range $-1<q<1$.

The Lagrangian step of each time increment $t\rightarrow t+\Delta t$ features a fixed-point iterations loop for obtaining a new equilibrium state, which is the substantial difference from the numerical scheme presented in [1]. In the spirit of the technique of augmented Lagrange multipliers, we first solve the linear equilibrium problem

$$\begin{aligned} \int _0^1\left( \frac{1}{2} w''^2-qw+\frac{1}{2} P(q)(w-w_\textrm{prev})^2\right) \,\textrm{d}x\rightarrow \min . \end{aligned}$$

(34)

The minimization is performed with respect to w(x), i.e. the nodal degrees of freedom are updated. The first term under the integral corresponds to the strain energy of the beam, which we integrate analytically. The second term answers to the potential of the current distribution of the friction forces, which we integrate according to the Gaussian quadrature rule for the current distribution of q(x). The third term penalizes the violation of the sticking condition $w=w_\textrm{prev}$. Here

$$\begin{aligned} P(q)=\left\{ \begin{array}{ll}P_0,&{}-1<q<1\\ 0,&{}q=-1\text { or }q=1\end{array} \right. \end{aligned}$$

(35)

is the artificial penalty stiffness, which takes on the large value $P_0$ in the zones with current sticking behaviour. The values $w_\textrm{prev}$ are relevant only in the domains of sticking and are computed at the end of the previous time increment. The second part of the step features the augmentation of the Lagrange multipliers according to

$$\begin{aligned}{} & {} q_\textrm{trial}=q-P_0(w-w_\textrm{prev}),\nonumber \\{} & {} q=\left\{ \begin{array}{ll}-1,&{}q_\textrm{trial}<-1\\ q_\textrm{trial},&{}-1\le q_\textrm{trial}\le 1\\ 1,&{} q_\textrm{trial}>1\end{array} \right. . \end{aligned}$$

(36)

Note that this update rule fully covers the conditions of switching from the sliding state to stick and back. Sequentially updating w(x) and q(x), we eventually obtain a converged state.

The Eulerian step of the time increment consists of the projection of the deformed state after the Lagrangian step back to the spatially fixed finite element mesh, which provides us with the reference values $w_\textrm{prev}$ for the condition of stick during the subsequent time increment. Approximating $\partial _t w$ locally using a simple finite difference, we perform a single step of the advection equation $\dot{w}=\partial _t w+vw'=0$ and store the results in the integration points:

$$\begin{aligned} w_\textrm{prev}=w-vw'\Delta t. \end{aligned}$$

(37)

Note that the slope $w'$ is directly available from the finite element approximation.

The simulation was implemented within the Wolfram Mathematica environment. An equidistant, fine mesh with 400 elements covers the spatial domain of unit length to guarantee a smooth resolution of the contact zone evolution. Simulations are carried out with the time step $\Delta t = 10^{-6}$ and the contact penalty $P_0 = 10^6$. Numerical ill-conditioning prevents the use of even higher penalties, which, in turn, would benefit the convergence of the iterative update of the contact forces (36). Owing to this limitation, the fixed-point iterations for the integration point tractions q proceeds slowly; in particular, a total of $N_q = 200$ steps are performed for each time step.

Finite element results for the particular choice $v = 100$ of the axial transport rate are compared against the semi-analytic reference solution of Sect. 3.2 in Fig. 9.

Fig. 9

Comparison of finite element and semi-analytic results: time evolution of the transition points $X_i$ (left); distribution of contact tractions q at $t = t_*$ (right)

We depict the evolution of the sliding zone boundaries $X_i(t)$ on the left and the distribution of the contact tractions at the critical time instant $q(x, t_*)$ on the right. Regions of stick or sliding are shaded in grey and white, respectively. Evidently, the finite element solution reproduces the assumed solution shape of a finite number of sliding segments with alternating sliding direction followed by a single (trivial) stick zone. It captures the first three sliding segments with good accuracy, while those with diminishing length towards the transition to the stick zone become increasingly harder to resolve. In contrast to the analytic solution, where $q=0$ must hold identically in the trivial stick zone, the finite element solution retains some compliance there owing to the penalty approximation of the contact response. A more accurate resolution of the transition may be obtained with excessive computational effort regarding mesh refinement and contact iteration steps $N_q$.

Regardless of these local effects, the global results remain in good agreement up to the critical instant $t_*$. The analytical solution of Sect. 3.2 ceases at this point, but the finite element simulation can be carried further, and thus provides a basis for a continuation of the analytical solution past $t_*$.

3.4 Analytical solution for a non-trivial segment of sticking contact

Both the analytical solution in Sect. 3.2 and the finite element simulations convince us that the transient behaviour qualitatively changes after the critical time instant $t_*$, when the velocity of the switching point between the segments of sliding and the “pre-historic” zone of sticking contact $\dot{X}_N(t)$ drops below the velocity of the moving surface v. Figure 9 demonstrates that during this supercritical stage $t>t_*$ the remaining segment of sliding $0\le x\le X_1(t)$ is immediately followed by a zone of sticking contact $x>X_1(t)$, in which the deformed beam is merely transported by the surface. While complicated scenarios with growth and shrinking of secondary sliding segments far behind $X_1(t)$ as well as the interaction with the exit prismatic joint at the right end of the control domain are possible, we focus at the time evolution of the size of the initial sliding zone under the stated assumption: sticking contact at $x>X_1(t)$.

Seeking an analytical solution for the coordinate of the switching point, we denote by $w_1(x,t)$ the deflection in the initial segment of sliding at $x\le X_1(t)$, where the unit friction force is acting downwards. Accounting for the boundary conditions at $x=0$, we solve $w_1'''' = -1$ and write:

$$\begin{aligned} w_1(x,t)=t - \frac{x^4}{24} + c_1(t) \frac{x^3}{6} + c_2(t)\frac{x^2}{2}; \end{aligned}$$

(38)

the integration constants $c_1$ and $c_2$ change in time. The deflection in the segment of stick $w_2(x,t)$ must fulfil $\dot{w}_2=\partial _t w_2+vw_2'=0$ at $x>X_1$, which immediately implies

$$\begin{aligned} w_2(x,t)=f(x-vt), \end{aligned}$$

(39)

with some yet unknown function f. Continuity conditions in the switching point result into:

$$\begin{aligned}{} & {} w_1(X_1(t),t)=w_2(X_1(t),t)=f(X_1(t)-vt),\quad w_1'(X_1(t),t)=f'(X_1(t)-vt), \nonumber \\{} & {} w_1''(X_1(t),t)=f''(X_1(t)-vt),\quad w_1'''(X_1(t),t)=f'''(X_1(t)-vt), \end{aligned}$$

(40)

because computing derivatives of $w_2$ with respect to x means differentiating f with respect to its single argument. Now we address the time derivative of the deflection in the switching point (note that it is neither the material time derivative $\dot{w}$ nor the local one $\partial _tw$, as the switching point is moving on its own and is not bound to any material point):

$$\begin{aligned} \frac{\,\textrm{d}}{\,\textrm{d}t}w_1(X_1(t),t)=\frac{\,\textrm{d}}{\,\textrm{d}t}f(X_1(t)-vt)=f'(X_1-vt)(\dot{X}_1-v)=w_1'(X_1,t)(\dot{X}_1-v). \end{aligned}$$

(41)

Computing the same time rate using (38) with $x=X_1(t)$ and equating both expressions, we find the first differential equation for the unknown functions of time $X_1$, $c_1$ and $c_2$:

$$\begin{aligned} 6 + 6 v c_2 X_1 + (3 v c_1 + (\dot{c}_1-v) X_1 + 3 \dot{c}_2) X_1^2 = 0. \end{aligned}$$

(42)

The second equation makes use of the second time derivative of the deflection in the switching point, in which we again utilize the continuity conditions (40):

$$\begin{aligned} \frac{\,\textrm{d}^2}{\,\textrm{d}t^2}w_1(X_1,t)= & {} \frac{\,\textrm{d}}{\,\textrm{d}t}\left( f'(X_1-vt)(\dot{X}_1-v)\right) \nonumber \\= & {} f''(X_1-vt)(\dot{X}_1-v)^2+f'(X_1-vt)\ddot{X}_1\nonumber \\= & {} w_1''(X_1,t)(\dot{X}_1-v)^2+w_1'(X_1,t)\ddot{X}_1. \end{aligned}$$

(43)

We compute the second time derivative once more using (38), compare the two expressions and obtain the second differential equation, which we do not present here because of its lengthiness. The third, even more lengthy differential equation follows after repeating the procedure for the third time derivative of the deflection at the switching point and making use of the continuity of the third spatial derivative in (40).

Further simplifications with the help of Wolfram Mathematica allow bringing the equations to a concise form:

$$\begin{aligned} \dot{c}_1=v+\frac{2vc_2}{X_1^2},\quad \dot{c}_2=-vc_1-\frac{2vc_2}{X_1},\quad vc_2X_1=3. \end{aligned}$$

(44)

In the following, we eliminate the integration constants and remain with the sought for single differential equation:

$$\begin{aligned} 3X_1\ddot{X}_1-6(v-\dot{X}_1)^2+v^3X_1^3=0. \end{aligned}$$

(45)

Interestingly, this equation allows for a stationary solution:

(46)

If the control domain is long enough, the initial sliding segment will eventually retain a constant length.

Regarding the initial conditions at the time $t=t_*$, we know $X_1(t_*)$ from the semi-analytical solution for the initial stage, while $\dot{X}_1(t_*)$ is easy to obtain through a transformation of (44):

$$\begin{aligned} \dot{X}_1=\frac{1}{3}(6v-v^2c_1X_1^2). \end{aligned}$$

(47)

The related values for the integration constants $c_1$ and $c_2$ can be taken from the initial stage as well:

$$\begin{aligned} \lim _{t\rightarrow t_*^{-}} \left. w''' \right| _{x=0} = c_1(t_*), \quad \lim _{t\rightarrow t_*^{-}} \left. w'' \right| _{x=0} = c_2(t_*), \end{aligned}$$

(48)

where the left-sided limits indicate an approaching from the past ($t\le t_*$). According to the last algebraic condition in (44), the constant $c_2$, which relates to the bending moment at the entry prismatic joint, and the current length $X_1$ remain inverse proportional throughout. As verified numerically, the semi-analytic solution of the initial stage also satisfies this condition at $t_*$.

Integrating the nonlinear initial value problem numerically over time, we compare with the results of the finite element analysis over a longer time period in Fig. 10.

Fig. 10

Extension of simulation results and continuation of $X_1(t)$ past $t_*$: Evolution of sliding regions and non-trivial regions of stick for the complete time span (left); detail picture in proximity to $t_*$ to conclude on the convergence of finite element simulations with respect to the number of fixed-point iterations $N_q$ for the contact state

The finite element contact resolution becomes increasingly fragile in the secondary regions of sliding and sticking. In addition, complicated interactions with the exit prismatic joint at $x = 1$ appear once the trivial stick zone has vanished. These effects, however, do not impact the solution in the first sliding segment due to the decoupling quality of the intermediate non-trivial segment of stick. Consequently, the solution retains correspondence to the case of a semi-infinite beam and, thus, is in agreement with the just constructed analytic result. The detail picture on the right of Fig. 10 visualises the transition process from the initial solution stage to the late stage for two finite element solutions with different number of fixed-point iterations $N_q$ in comparison with the analytic result. The numerically induced steep dip at $t_*$ observed for $N_q = 25$ slowly diminishes as the number of iterations is increased. Moreover, the time instant of this occurrence gradually shifts towards the semi-analytically determined limit of $t_*$ as well. Both observations indicate convergence of the finite element scheme towards the analytic reference solution, albeit at an undesirable slow rate that clearly demonstrates the limitations of the standard update procedure (36) for the contact states.

4 Conclusion and perspectives

The main objective of the present review paper is to summarize the state of knowledge on the modelling and simulation of axially moving structures with special focus on problems involving distributed contact that are frequently encountered in all kinds of technical applications. We present an extensive survey on the available literature and emphasize particularly challenging topics to highlight unresolved issues and conclude on future perspectives of the research in this lively field with great practical relevance.

Mechanical models of axially moving structures typically comprise a travelling slender body that is moving across a spatially fixed domain at some axial transport rate v with particles continuously entering and exiting through the domain boundaries. As such, these problems constitute open systems, which is unusual in the general context of solid mechanics and needs to be addressed with care and approached with appropriately modified mechanical principles. In the latter regard, we devote an entire section to the proper formulation of Hamilton’s principle, the principle of virtual work and the Lagrangian equations of motion for open systems.

Owing to the unusual characteristics of axially moving structures, it has long been recognised that the Lagrangian point of view is inferior compared to an at least partially Eulerian perspective when it comes to the kinematic parametrisation. This is due to the strict attachment of Lagrangian (material) coordinates to material particles, which does not allow to decouple the axial motion from the kinematic description and has significant drawbacks that become particularly severe in connection with numerical simulation models. In response, different variants of the nowadays well-established Arbitrary Lagrangian–Eulerian (ALE) approach have been developed, which typically finds use in application-oriented finite element codes. Traditional forms of ALE rely on an operator split of the governing partial differential equations that allows for a sequential solution in terms of a Lagrangian and a Eulerian step. The re-mapping of field variables onto the spatially fixed mesh at the second stage, which amounts to the numerical integration of an advection problem, is potentially destabilising and may degrade the solution quality. Modern approaches, like the Mixed Eulerian–Lagrangian description put to use in the benchmark problem of Sect. 3, resolve these numerical issues successfully. Nowadays, the category of ALE approaches has matured to a sizeable degree such that scientists may adapt or simply pick a suitable variant from the pool of established formalisms and related solution algorithms.

Even with these evolved techniques at hand, the consistent account for distributed frictional contact in problems of axially moving structures remains a difficult task. While the typically employed numerical models are generally appropriate to resolve contact for a continuum bodies, the classic structural theories of strings and rods or membranes, plates and shells exhibit some peculiar effects that require special attention. Despite their deficiencies and additional numerical challenges in contact problems, discussed in the respective sections, the classic structural theories remain attractive due to their computational efficiency and thus are sometimes without alternative for the development of complicated application-oriented simulation schemes.

In view of the state of knowledge, it is evident that there is still significant potential to improve the numerical methods of contact treatment in simulation models of axially moving structures. The results presented in Sect. 3 for the prototype example of a partially sliding Bernoulli–Euler beam highlight the limitations of the state-of-the-art finite element scheme with respect to accuracy, convergence rate and numerical efficiency. In the authors’ opinion, these issues may in future be approached from two distinct vantage points: First, one could pursue a continued development of the established contact algorithms. In this regard, it is particularly important that the physical contact model, its numerical implementation and the adopted structural theory are properly matched. Secondly, one could strive for an improved, more consistent modelling of the contact kinematics. In doing so, it is important to be aware of the potential drawbacks of kinematically enriched structural theories, namely: increased number of unknowns and the potential risk of additional numerical issues like shear locking. In addition, the accurate geometric representation of the structure-to-solid contact, for example by means of the isogeometric analysis, could alleviate some of the problems related to the kinematic limitations of standard finite elements with polynomial shape functions.

In conclusion, it is our firm belief that the continued research on axially moving structures shall rest upon a proper combination of established methods in the general framework of computational solid mechanics. In this respect, we sincerely hope that the present review paper provides a substantial knowledge base to aid scientists in their research endeavour.