Skip to main content
SpringerLink
Log in

Chaotic and multifractal characteristic analysis of noise of thermal variables from rotary kiln

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

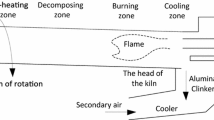
In numbers of industrial fields, many filtering algorithms of industrial signals, mechanism-based modeling methods and control strategies are based on the hypothesis of white noise. However, some researchers propose that the colored noise is closer to the real noise than the white noise. Then, whether the noise is the white noise, the colored noise or other else? And what is the intrinsic dynamic characteristics of the noise? In this paper, noise signals of thermal variables from rotary kiln are extracted and their chaotic, statistical and multifractal characteristics are analyzed to answer the two questions. Based on the experimental results, it is the first time to discover that they are not the white noise or the monofractal colored noise but have the high-dimensional chaotic characteristic, that is, they are determinate and predictable for short term theoretically. However, some models are failed to predict them. Then, further experimental results imply those noise signals have both persistent and anti-persistent multifractal characteristics. In particular, the latter is a reason to failed predictions of noise signals. Moreover, it is firstly discovered that the multifractality of each noise signal is generated mainly by the long-term temporal correlation. Finally, two ideas about modeling multifractality of noise from rotary kiln are proposed as the future work.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Xu, Y., Jia, Y., Wang, H., Liu, Y., Wang, P., Zhao, Y.: Spiking activities in chain neural network driven by channel noise with field coupling. Nonlinear Dyn. 95(4), 3237–3247 (2019). https://doi.org/10.1007/s11071-018-04752-2

    Article  Google Scholar 

  2. Davies, H.G.: Slow sinusoidal modulation through bifurcations: the effect of additive noise. Nonlinear Dyn. 36(2), 217–228 (2004)

    MathSciNet  MATH  Google Scholar 

  3. Montillet, J., Tregoning, P., McClusky, S., Yu, K.: Extracting white noise statistics in gps coordinate time series. IEEE Geosci. Remote Sens. Lett. 10(3), 563–567 (2013)

    Google Scholar 

  4. Yang, Y., Wei, X., Jia, W., Han, Q.: Stationary response of nonlinear system with caputo-type fractional derivative damping under Gaussian white noise excitation. Nonlinear Dyn. 79(1), 139–146 (2015)

    MathSciNet  Google Scholar 

  5. Qi, L., Cai, G.Q.: Dynamics of nonlinear ecosystems under colored noise disturbances. Nonlinear Dyn. 73(1), 463–474 (2013)

    MathSciNet  MATH  Google Scholar 

  6. Lei, Y., Hua, M., Lin, D.: Onset of colored-noise-induced chaos in the generalized duffing system. Nonlinear Dyn. 89(2), 1371–1383 (2017)

    MathSciNet  Google Scholar 

  7. Fokou, I.S.M., Buckjohn, C.N.D., Siewe, M.S., Tchawoua, C.: Probabilistic distribution and stochastic p-bifurcation of a hybrid energy harvester under colored noise. Commun. Nonlinear Sci. Numer. Simul. 56, 177–197 (2018)

    MathSciNet  Google Scholar 

  8. Yang, C., Gao, Z., Liu, F.: Kalman filters for linear continuous-time fractional-order systems involving coloured noises using fractional-order average derivative. IET Control Theory Appl. 12(4), 456–465 (2018)

    MathSciNet  Google Scholar 

  9. Tang, T., Jia, L., Lou, J., Tao, R., Wang, Y.: Adaptive eiv-fir filtering against coloured output noise by using linear prediction technique. IET Signal Proc. 12(1), 104–112 (2018)

    Google Scholar 

  10. Vasseur, D., Yodzis, P.: The color of environmental noise. Ecology 85, 1146–1152 (2004)

    Google Scholar 

  11. Grinsted, A., Moore, J.C., Jevrejeva, S.: Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 11(5/6), 561–566 (2004)

    Google Scholar 

  12. Schulz, M., Mudelsee, M.: Redfit: estimating red-noise spectra directly from unevenly spaced paleoclimatic time series. Comput. Geosci. 28(3), 421–426 (2002)

    Google Scholar 

  13. Koscielny-Bunde, E., Bunde, A., Havlin, S., Roman, H.E., Goldreich, Y., Schellnhuber, H.-J.: Indication of a universal persistence law governing atmospheric variability. Phys. Rev. Lett. 81, 729–732 (1998)

    Google Scholar 

  14. Kasdin, N.J.: Discrete simulation of colored noise and stochastic processes and 1/f/sup /spl alpha// power law noise generation. Proc. IEEE 83(5), 802–827 (1995)

    Google Scholar 

  15. Viswanathan, R.: On the autocorrelation of complex envelope of white noise. IEEE Trans. Inf. Theory 52(9), 4298–4299 (2006)

    MathSciNet  MATH  Google Scholar 

  16. Ostry, D.I.: Synthesis of accurate fractional Gaussian noise by filtering. IEEE Trans. Inf. Theory 52(4), 1609–1623 (2006)

    MathSciNet  MATH  Google Scholar 

  17. Kaulakys, B.: On the intrinsic origin of 1/f noise. Microelectron. Reliab. 40(11), 1787–1790 (2000)

    Google Scholar 

  18. Hung, Y.-C., Struzik, Z.R., Chin-Kun, H.: Noise as a potential controller in antagonist inter-reacting systems. Physica A 512, 500–506 (2018)

    MathSciNet  Google Scholar 

  19. Poxon, J., Jennings, P., Allman-Ward, M.: Development of a hybrid electric vehicle (HEV) model for interactive customer assessment of sound quality. In: IET HEVC 2008—Hybrid and Eco-Friendly Vehicle Conference, pp. 1–4 (2008)

  20. Garmendia, N., Portilla, J.: Investigations of AM, PM noise, and noise figure in an SiGe-HBT amplifier operating in linear and nonlinear regimes. IEEE Trans. Microw. Theory Tech. 58(4), 807–813 (2010)

    Google Scholar 

  21. Revoredo, T., Mora-Camino, F., Slama, J.: A two-step approach for the prediction of dynamic aircraft noise impact. Aerosp. Sci. Technol. 59, 122–131 (2016)

    Google Scholar 

  22. Filippone, A.: Aircraft noise prediction. Prog. Aerosp. Sci. 68, 27–63 (2014)

    Google Scholar 

  23. Hao, W., Li, K., Shi, W., Clarke, K.C., Zhang, J., Li, H.: A wavelet-based hybrid approach to remove the flicker noise and the white noise from GPS coordinate time series. GPS Solut. 19(4), 511–523 (2015)

    Google Scholar 

  24. Muhammad, N., Bibi, N., Jahangir, A., Mahmood, Z.: Image denoising with norm weighted fusion estimators. Pattern Anal. Appl. 21(4), 1013–1022 (2018)

    MathSciNet  Google Scholar 

  25. Muhammad, N., Bibi, N., Wahab, A., Mahmood, Z., Akram, T., Naqvi, S.R., Oh, H.S., Kim, D.-G.: Image de-noising with subband replacement and fusion process using Bayes estimators. Comput. Electr. Eng. 70, 413–427 (2018)

    Google Scholar 

  26. Mughal, B., Muhammad, N., Sharif, M., Rehman, A., Saba, T.: Removal of pectoral muscle based on topographic map and shape-shifting silhouette. BMC Cancer 18(1), 778 (2018)

    Google Scholar 

  27. Khalid, S., Muhammad, N., Sharif, M.: Automatic measurement of the traffic sign with digital segmentation and recognition. IET Intell. Transp. Syst. 13, 269–279 (2019)

    Google Scholar 

  28. Casalino, D., Diozzi, F., Sannino, R., Paonessa, A.: Aircraft noise reduction technologies: a bibliographic review. Aerosp. Sci. Technol. 12(1), 1–17 (2008). (Aircraft noise reduction)

    MATH  Google Scholar 

  29. Crupi, F., Giusi, G., Ciofi, C., Pace, C.: Enhanced sensitivity cross-correlation method for voltage noise measurements. IEEE Trans. Instrum. Meas. 55(4), 1143–1147 (2006)

    Google Scholar 

  30. Thompson, J.R., Wilson, J.R.: Multifractal detrended fluctuation analysis: practical applications to financial time series. Math. Comput. Simul. 126, 63–88 (2016)

    MathSciNet  Google Scholar 

  31. Gao, C., Qian, J.: Evidence of chaotic behavior in noise from industrial process. IEEE Trans. Signal Process. 55(6), 2877–2884 (2007)

    MathSciNet  MATH  Google Scholar 

  32. Packard, N.H., Crutchfield, J.P., Farmer, J.D., Shaw, R.S.: Geometry from a time series. Phys. Rev. Lett. 45, 712–716 (1980)

    Google Scholar 

  33. Takens, F.: Detecting strange attractors in turbulence. In: Rand, D., Young, L.-S. (eds.) Dynamical Systems and Turbulence, Warwick 1980, pp. 366–381. Springer, Berlin (1981)

    Google Scholar 

  34. Theiler, J., Eubank, S., Longtin, A., Galdrikian, B., Farmer, J.D.: Testing for nonlinearity in time series: the method of surrogate data. Physica D Nonlinear Phenom. 58(1), 77–94 (1992)

    MATH  Google Scholar 

  35. Theiler, J., Eubank, S.: Don’t bleach chaotic data. Chaos 3(4), 771–782 (1993)

    Google Scholar 

  36. Small, M., Dejin, Y., Harrison, R.G.: Surrogate test for pseudoperiodic time series data. Phys. Rev. Lett. 87, 188101 (2001)

    Google Scholar 

  37. Schreiber, T., Schmitz, A.: Surrogate time series. Physica D 142(3), 346–382 (2000)

    MathSciNet  MATH  Google Scholar 

  38. Thiel, M., Romano, M.C., Kurths, J., Rolfs, M., Kliegl, R.: Twin surrogates to test for complex synchronisation. Europhys. Lett. (EPL) 75(4), 535–541 (2006)

    Google Scholar 

  39. Lancaster, G., Iatsenko, D., Pidde, A., Ticcinelli, V., Stefanovska, A.: Surrogate data for hypothesis testing of physical systems. Phys. Rep. 748, 1–60 (2018)

    MathSciNet  MATH  Google Scholar 

  40. Theiler, J.: On the evidence for low-dimensional chaos in an epileptic electroencephalogram. Phys. Lett. A 196(5), 335–341 (1995)

    Google Scholar 

  41. Schreiber, T., Schmitz, A.: Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 77, 635–638 (1996)

    Google Scholar 

  42. Calvet, L.E., Fisher, A.J.: How to forecast long-run volatility: regime switching and the estimation of multifractal processes. J. Financ. Econom. 2(1), 49–83 (2004)

    Google Scholar 

  43. Mandelbrot, B., Fisher, A., Calvet, L.: A multifractal model of asset returns. Cowles Foundation Discussion Papers 1164, Cowles Foundation for Research in Economics, Yale University (1997)

  44. Lux, T.: The Markov-switching multifractal model of asset returns. J. Bus. Econ. Stat. 26(2), 194–210 (2008)

    Google Scholar 

  45. Schreiber, T.: Extremely simple nonlinear noise-reduction method. Phys. Rev. E 47, 2401–2404 (1993)

    Google Scholar 

  46. Walczak, B., Massart, D.L.: Noise suppression and signal compression using the wavelet packet transform. Chemometr. Intell. Lab. Syst. 36(2), 81–94 (1997)

    Google Scholar 

  47. Donoho, D.L.: De-noising by soft-thresholding. IEEE Trans. Inf. Theory 41(3), 613–627 (1995)

    MathSciNet  MATH  Google Scholar 

  48. Xia, C., Song, P., Shi, T., Yan, Y.: Chaotic dynamics characteristic analysis for matrix converter. IEEE Trans. Industr. Electron. 60(1), 78–87 (2013)

    Google Scholar 

  49. Rao, X.-B., Chu, Y.-D., Lu-Xu, Chang, Y.-X., Zhang, J.-G.: Fractal structures in centrifugal flywheel governor system. Commun. Nonlinear Sci. Numer. Simul. 50, 330–339 (2017)

    MathSciNet  Google Scholar 

  50. Kennel, M.B., Brown, R., Abarbanel, H.D.I.: Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 45, 3403–3411 (1992)

    Google Scholar 

  51. Fraser, A.M., Swinney, H.L.: Independent coordinates for strange attractors from mutual information. Phys. Rev. A 33, 1134–1140 (1986)

    MathSciNet  MATH  Google Scholar 

  52. Wolf, A., Swift, J.B., Swinney, H.L., Vastano, J.A.: Determining Lyapunov exponents from a time series. Physica D 16(3), 285–317 (1985)

    MathSciNet  MATH  Google Scholar 

  53. Bolotin, Y., Tur, A., Yanovsky, V.: Chaos: Concepts, Control and Constructive Use. Springer, Berlin (2017)

    MATH  Google Scholar 

  54. Nakamura, T., Small, M.: Applying the method of small-shuffle surrogate data: testing for dynamics in fluctuating data with trends. Int. J. Bifurc. Chaos 16(12), 3581–3603 (2006)

    MATH  Google Scholar 

  55. Parlitz, U., Kocarev, L.: Using surrogate data analysis for unmasking chaotic communication systems. Int. J. Bifurc. Chaos 07(02), 407–413 (1997)

    MATH  Google Scholar 

  56. Kantelhardt, J.W., Zschiegner, S.A., Koscielny-Bunde, E., Havlin, S., Bunde, A., Stanley, H.E.: Multifractal detrended fluctuation analysis of nonstationary time series. Physica A Stat. Mech. Appl. 316(1), 87–114 (2002)

    MATH  Google Scholar 

  57. Feder, J.: Fractals. Springer, Boston, MA (1988)

    MATH  Google Scholar 

  58. Peitgen, H.O., Jürgens, H., Saupe, D.: Chaos and Fractals. Springer, New York, NY (2004)

    MATH  Google Scholar 

  59. Ihlen, E.A.F.: Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. 3, 141 (2012)

    Google Scholar 

  60. Beran, S.G.R.K.J., Feng, Y.: Long-Memory Processes: Probabilistic Properties and Statistical Methods. Springer, Berlin (2013)

    MATH  Google Scholar 

  61. Tang, J., Wang, D., Fan, L., Zhuo, R., Zhang, X.: Feature parameters extraction of GIS partial discharge signal with multifractal detrended fluctuation analysis. IEEE Trans. Dielectr. Electr. Insul. 22(5), 3037–3045 (2015)

    Google Scholar 

  62. Livi, L., Sadeghian, A., Sadeghian, H.: Discrimination and characterization of Parkinsonian rest tremors by analyzing long-term correlations and multifractal signatures. IEEE Trans. Biomed. Eng. 63(11), 2243–2249 (2016)

    Google Scholar 

  63. Cao, G., He, L.Y., Cao, J.: Multifractal Detrended Analysis Method and Its Application in Financial Markets. Springer, Singapore (2018)

    Google Scholar 

  64. Matia, K., Ashkenazy, Y., Stanley, H.E.: Multifractal properties of price fluctuations of stocks and commodities. EPL (Europhys. Lett.) 61(3), 422 (2003)

    Google Scholar 

  65. Gao, C., Qian, J.: Evidence of chaotic behavior in noise from industrial process. IEEE Trans. Signal Process. 55(6), 2877–2884 (2007)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Natural Sciences Foundation of China (Nos. 61672216, 61673162), in part by the Natural Science Foundation of Hunan Province (No. 2018JJ2056), in part by the Research Committee at University of Macau (No. MYRG2018-00136-FST) and in part by the Macau Science and Technology Development Fund (No. FDCT/189/2017/A3). We thank the editor and anonymous reviewers for valuable comments that improved this article. We also thank Professor Charles L. Webber, Professor Herwig Wendt and Post-Doctor Tim Ziemer for, respectively, providing profound insights about chaotic theory, multifractal theory and noise signal. In particular, we thank to Professor Michael Small for discussing with us about the surrogate analysis.

Author information

Authors and Affiliations

  1. College of Electrical and Information Engineering, Hunan University, Changsha, 410082, China

    Mingyang Lv & Xiaogang Zhang

  2. College of Computer Science and Electronic Engineering, Hunan University, Changsha, 410082, People’s Republic of China

    Hua Chen

  3. Department of Computer and Information Science, University of Macau, Macau, China

    Yicong Zhou

  4. College of Engineering and Design, Hunan Normal University, Changsha, 410081, China

    Jianmin Li

Authors
  1. Mingyang Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaogang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hua Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yicong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jianmin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaogang Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

1.1 The wavelet packet decomposition method

The steps of noise extraction based the wavelet packet decomposition (WPD) method are introduced as follows. Moreover, please see Ref. [46, 47] for the more details.

Step 1.:

The wavelet packet decomposition (WPD) and the confirmation of the best basis. In the point of view of compression, the standard wavelet transform may not produce the best result, since it is limited to wavelet bases that increase by a power of two toward the low frequencies, that is, the best basis of the WPD should be found out after the WPD. Moreover, the best basis corresponds to the minimum entropy or maximum information for the distribution of coefficients [46]. In this paper, the first step can be realized using the command “wpdec” in MATLAB.

Step 2.:

The confirmation of the thresholding value. Generally, small coefficients are mostly noises and large coefficients contain the actual signal. Then, a thresholding value should be proposed to distinguish small coefficients and large coefficients. The penalization method is proposed to calculate the universal thresholding value and can be realized using the command “wpbmpen” in MATLAB.

Step 3.:

The reconstruction of the signal based on wavelet transform. Donoho [47] pointed out that only coefficients whose absolute value is higher than the predefined threshold value is retained. Then, in this paper, the soft thresholding method [47] is used to replace wavelet transform coefficients as follows:

$$\begin{aligned} Rw_i^p =\left\{ \begin{array}{ll} 0, &{}\quad \mathrm{if} \quad |w_i^p|<\mathrm{thr} \\ \mathrm{sign}(w_i^p)(|w_i^p|-thr), &{}\quad \mathrm{if}\quad |w_i^p|>\mathrm{thr} \end{array} \right. \end{aligned}$$
(22)

where the \(w_i^p\) is the wavelet transform coefficient of the ith sub-signal in the pth level, the \(Rw_i^p\) is the replace wavelet transform coefficient of the ith sub-signal in the pth level and the thr is the universal threshold which is calculated by the penalization method [47]. After replacing wavelet transform coefficients, the retained coefficients are used to reconstruct the useful signal. And the denoise procedure is realized using the command “wpdencmp” in Matlab.

Step 4.:

The noise signal is extracted through subtracting the useful signal from the original signal.

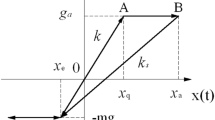
1.2 The Gao method

The Gao method [65] is a moving average method in nature, and the illustration of noise extraction using the Gao method is shown in Fig. 13. Moreover, the procedure is introduced as follows.

Step 1.:

From the head to the end, l signal points are selected as a segment in turn.

Step 2.:

The average value of each segment is calculated.

Step 3.:

The average value of each segment is subtracted by the l signal values of relative segment. Then, l noise values in each segment are extracted.

Step 4.:

The whole noise time series are extracted.

Fig. 13
figure 13

Illustration of noise extraction using the Gao method. The \(s_i\) is the value of the thermal signal of rotary kiln, \(\overline{s}_i\) and \(\overline{s}_j\) are the mean value, and \(x_i\) is the value of the extracted noise signal

Full size image

The higher frequency of noise, the smaller the value of the l is selected [65]. In our paper, we set \(l=2\), that is, two points of signals are selected as a segment in turn and the average value \(\overline{s}_i=(s_i+s_{i+1})/2\) is calculated. Then, each value of noise is calculated through \(x_{i+1}=s_{i+1}- \overline{s}_i\).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lv, M., Zhang, X., Chen, H. et al. Chaotic and multifractal characteristic analysis of noise of thermal variables from rotary kiln. Nonlinear Dyn 99, 3089–3111 (2020). https://doi.org/10.1007/s11071-020-05466-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05466-0

Keywords

Search

Navigation