Dynamical analysis and control strategies of an SIVS epidemic model with imperfect vaccination on scale-free networks

Abstract

Vaccination is an effective method to prevent the spread of infectious diseases. In this paper, we develop an SIVS epidemic model with degree-related transmission rates and imperfect vaccination on scale-free networks. Firstly, we derive two threshold parameters and existence conditions of multiple endemic equilibria. Secondly, not only the global asymptotical stability of disease-free equilibrium and the persistence of the disease are derived, but also the global attractivity of the unique endemic equilibrium is proved using the monotone iterative technique. Thirdly, the effects of various immunization schemes including uniform immunization, targeted immunization and acquaintance immunization are studied, and the optimal vaccination strategy is analyzed by Pontryagin’s maximum principle. Finally, we perform numerical simulations to verify these theoretical results.

1 Introduction

The new and reemerging infectious diseases have posed considerable challenges to modern life [1,2,3]. Notable viral emergence events include the 2009 pandemic of H1N1 influenza, the emergence of Middle East Respiratory Syndrome-associated coronavirus (MERS-CoV) in the Arabian peninsula, the West African Ebola outbreak, and ZIKV’s invasion of the Americas [4]. In the largest recorded outbreak of Ebola virus in humans, 28625 cases were confirmed and 11325 died [5]. As of February 28, 2018, 2182 cases of MERS-CoV infection (with 779 deaths) in 27 countries were reported to WHO worldwide, with most being reported in Saudi Arabia (1807 cases with 705 deaths) [6]. Therefore, it is very important to prevent and control the occurrence and spread of infectious diseases.

Vaccination is one of the most effective public policies to prevent the transmission of infectious diseases [7, 8]. Since Kermack and Mckendrick established the Susceptible Infected Removed (SIR) model of plague in 1927 [9] and Susceptible Infected Susceptible (SIS) model in 1932 [10], respectively, more and more epidemic models of infectious diseases with vaccination have largely focused on the standard SIS model. In 2000, Kribs-Zaleta and Velasco-Hernández [11] put forward an SIVS model with multiple endemic states which exhibited a backward bifurcation for some parameter values and presented a complete analysis of its behavior. Thereafter, many researchers considered various cases based on this model, such as nonlinear incidence rate [12], age of vaccination [13], spatial dispersal of individuals [14], and state-dependent pulse vaccination [15]. However, the basic assumption for the above works is that individuals in each compartment are homogeneously mixed. There are a few developments on the case of heterogeneously mixed. In 2013, Peng et al. extended the SIVS model to Watts–Strogatz small world, Barabási–Albert scale-free, and random scale-free networks and made numerical analysis in detail [16]. In 2016, Peng et al. studied the combination of human behavior and demographics and put forward adaptive SIVS models on networks [17]. But the dynamic analysis and control strategy were excluded from these works. Recently, Chen et al. added the quarantined compartment to the SIVS model on scale-free networks and presented the global dynamics [18].

In this paper, we develop the SIVS epidemic model [16] on BA network to general scale-free networks, which includes two degree-related infectious contact rates and a degree-related vaccination rate. Different to Refs. [16,17,18], we derive two threshold parameters, discuss the existence conditions of multiple endemic equilibria, prove the global attractivity of the unique endemic equilibrium, compare the effects of the uniform immunization, the targeted immunization and the acquaintance immunization schemes, and present an optimal control strategy of vaccination by Pontryagin’s maximum principle. In particular, we provide the numerical bounds for the weight ratios of densities of infected individuals and control expenses in the optimal control scheme. All the theoretical predictions are verified by numerical simulations.

The remainder of the paper is organized as follows. In Sect. 2, the new SIVS epidemic model on scale-free networks is constructed. Section 3 presents the existence conditions of equilibria and dynamical analysis. Three immunization schemes and the optimal control strategy are carried out in Sect. 4. The numerical simulations are performed to illustrate the theoretical results in Sect. 5. Section 6 concludes the paper finally.

2 Model formulation

In this section, we will give the new network-based model in the absence of demographic effects based on Ref. [16]. Suppose a scale-free network with N nodes is established and all individuals are spatially distributed on this network, each node is occupied by one individual. The connectivities of nodes in network at each time are assumed to be uncorrelated. In an epidemic spreading process, every node has three optional states: susceptible, infected and vaccinated. In order to account for the heterogeneity of contact patterns, it is needed to consider the difference of node degrees. Let $S_{k}(t),I_{k}(t),$ and $V_{k}(t)$ denote the densities of susceptible, infected, and vaccinated individuals with degree k at time t, respectively. For any k and t, $S_{k}(t)+I_{k}(t)+V_{k}(t)=1.$ Therefore, the evolution processes of $S_{k}(t), I_{k}(t)$, and $V_{k}(t)$ are governed by the following differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} S'_{k}(t){=}\gamma I_{k}(t) {-}\beta _{S}(k) S_{k}(t)\Theta (t){+}\phi V_{k}(t){-}\varphi _{k}S_{k}(t),\\ I'_{k}(t){=}[\beta _{S}(k)S_{k}(t){+}\beta _{V}(k) V_{k}(t)]\Theta (t){-}\gamma I_{k}(t),\\ V'_{k}(t){=} \varphi _{k} S_{k}(t){-}\beta _{V}(k) V_{k}(t)\Theta (t){-}\phi V_{k}(t), \end{array}\right. }\nonumber \\ \end{aligned}$$

(1)

with initial conditions

$$\begin{aligned}&\Big \{(S_{k}(0),I_{k}(0),V_{k}(0))|0\\&\quad \le S_{k}(0),I_{k}(0),V_{k}(0)\le 1, k=1,2,\ldots ,n\Big \}. \end{aligned}$$

The meanings of the parameters and variables in system (1) are as follows:

• $\beta _{S}(k)$ represents the transmission rate that each susceptible individual with degree k can be infected through contact if it is connected to k infected nodes, $\beta _{V}(k)$ is the reduced transmission rate that each vaccinated individual with degree k directly gets infected. For any k,  $0<\beta _{V}(k)<\beta _{S}(k).$

• $\Theta (t)=\frac{1}{\langle k\rangle }\sum _{k=1}^{n}k P(k)I_{k}(t)$ describes the probability of a link pointing to an infected individual, $\langle k\rangle$ is the average degree of the network, P(k) is the probability of a node with degree k, n is the maximal degree.

• $\varphi _{k}$ is the vaccination rate that each susceptible individual with degree k can be vaccinated, $\varphi _{k}\ge 0.$$\phi$ is the rate that each vaccinated individual with degree k can return to the susceptible class as the vaccine wears off, $\gamma$ is the recovery rate, $\phi ,\gamma >0.$

• Let $S(t)=\sum _{k=1}^{n}P(k)S_{k}(t),$$I(t)=\sum _{k=1}^{n}P(k)I_{k}(t)$, $V(t)=\sum _{k=1}^{n}P(k)V_{k}(t)$ be the average densities of susceptible, infected, and vaccinated individuals, respectively.

Remark 1

In system (1), the transmission rates $\beta _{S}(k)$ and $\beta _{V}(k)$ are more general than those of Ref. [16]. $\frac{\beta _{V}(k)}{\beta _{S}(k)}$ measures the efficiency of the vaccine. Two special cases $\beta _{V}(k)=0$ and $\beta _{V}(k)=\beta _{S}(k)$ indicate that the vaccination is completely effective and utterly useless, respectively. Moreover, we extend the constant vaccination rate to be degree-related $\varphi _{k}$, which is more realistic than that of Ref. [16]. If we take $\beta _{S}(k) =\beta k,$$\beta _{V}(k) =\sigma \beta k$ and $\varphi _{k}=\varphi$, then system (1) is turned into model (10) of Ref. [16], where $\sigma$ shows the efficiency of the vaccine as a multiplier to the infection rate, $\sigma =0$ and $\sigma =1$ represent completely effective and utterly ineffective vaccination.

Remark 2

The condition $\phi >0$ means the vaccination is imperfect; that is, the vaccination can only cover a fraction of susceptible individuals.

3 Dynamic analysis

In this section, we will consider the dynamic behavior of system (1). Firstly, we derive the two threshold parameters and present the existence conditions of the equilibria. Secondly, the global stability of the disease-free equilibrium is proved. Finally, the uniform persistence and global attractivity of the unique endemic equilibrium are analyzed.

3.1 Equilibria and threshold parameters

The basic reproduction number $R_{0}$ is the most common of threshold parameters [19]. Next, we will derive two important threshold parameters containing $R_{0}$ and present the existence conditions of the equilibria.

It is easy to see that

$$\begin{aligned} \Omega= & {} \{(S_{k},I_{k},V_{k})\in \mathbb {R}^{3n}_{{+}}|0{\le } S_{k},I_{k},V_{k}{\le }1, k=1,\ldots ,n\} \end{aligned}$$

is a positively invariant set for system (1). To get the equilibria, set

$$\begin{aligned} {\left\{ \begin{array}{ll} \gamma I_{k} -\beta _{S}(k) S_{k}\Theta +\phi V_{k}-\varphi _{k}S_{k}=0,\\ \big [\beta _{S}(k)S_{k}(t)+\beta _{V}(k) V_{k}(t)\big ]\Theta -\gamma I_{k}=0,\\ \varphi _{k} S_{k}-\beta _{V}(k) V_{k}\Theta -\phi V_{k}=0. \end{array}\right. } \end{aligned}$$

It is clear that system (1) admits a unique disease-free equilibrium $P^{0}(S^{0}_{k},I^{0}_{k},V^{0}_{k})$ with

$$\begin{aligned} S^{0}_{k}= & {} \frac{\phi }{\varphi _{k}+\phi }, \quad I^{0}_{k}=0, \quad \\ V^{0}_{k}= & {} \frac{\varphi _{k}}{\varphi _{k}+\phi }, \quad k=1,\ldots ,n. \end{aligned}$$

The basic reproduction number of system (1) is calculated according to Ref. [19]:

$$\begin{aligned} R_{0}=\frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{ kP(k)\left[ \phi \beta _{S}(k)+\varphi _{k}\beta _{V}(k)\right] }{\gamma (\varphi _{k}+\phi )}. \end{aligned}$$

(2)

Note that

$$\begin{aligned} \widetilde{R}_{0}\triangleq R_{0}|_{\varphi _{k}=0}=\sum _{k=1}^{n}\frac{ k\beta _{S}(k)P(k)}{\gamma \langle k\rangle }. \end{aligned}$$

(3)

Remark 3

$R_{0}$ and $\widetilde{R}_{0}$ are important threshold parameters for the following dynamic analysis. It is obvious that $R_{0}\le \widetilde{R}_{0}$ for all $\varphi _{k}\ge 0(k=1,2,\ldots ,n),$ which indicates the influence of vaccination on $R_{0}.$

Any positive equilibrium satisfies that

$$\begin{aligned} S_{k}&{=}&\frac{\gamma \left[ \beta _{V}(k)\Theta {+}\phi \right] }{\big [\beta _{S}(k)\Theta {+}\gamma \big ]\big [\beta _{V}(k)\Theta {+}\phi \big ]{+}\varphi _{k}\big [\beta _{V}(k)\Theta {+}\gamma \big ]}, \end{aligned}$$

(4)

$$\begin{aligned} I_{k}&{=}&\frac{\Theta \big [\beta _{S}(k)(\beta _{V}(k)\Theta {+}\phi ){+}\varphi _{k}\beta _{V}(k)\big ]}{\big [\beta _{S}(k)\Theta {+}\gamma \big ]\big [\beta _{V}(k)\Theta {+}\phi \big ]{+}\varphi _{k}\big [\beta _{V}(k)\Theta {+}\gamma \big ]},\end{aligned}$$

(5)

$$\begin{aligned} V_{k}&{=}&\frac{\gamma \varphi _{k}}{\big [\beta _{S}(k)\Theta {+}\gamma \big ]\big [\beta _{V}(k)\Theta {+}\phi \big ]{+}\varphi _{k}\big [\beta _{V}(k)\Theta {+}\gamma \big ]},\end{aligned}$$

(6)

$$\begin{aligned} \Theta&{=}&\frac{1}{\langle k\rangle }\sum _{k{=}1}^{n}k P(k)I_{k}. \end{aligned}$$

(7)

Substituting (5) into (7), we obtain the self-consistency equation:

$$\begin{aligned} \Theta =\frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{kP(k)\Theta \big \{\beta _{S}(k)\big [\beta _{V}(k)\Theta {+}\phi \big ]{+}\varphi _{k}\beta _{V}(k)\big \}}{\big [\beta _{S}(k)\Theta {+}\gamma \big ]\big [\beta _{V}(k)\Theta {+}\phi \big ]{+}\varphi _{k}\big [\beta _{V}(k)\Theta {+}\gamma \big ]}. \end{aligned}$$

It is equivalent to $\Theta f(\Theta )=0(0\le \Theta \le 1)$, where

$$\begin{aligned} f(\Theta )=\frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{kP(k)\big \{\beta _{S}(k)\big [\beta _{V}(k)\Theta {{+}}\phi \big ]{+}\varphi _{k}\beta _{V}(k)\big \}}{\big [\beta _{S}(k)\Theta {+}\gamma \big ]\big [\beta _{V}(k)\Theta {+}\phi ]{+}\varphi _{k}\big [\beta _{V}(k)\Theta {+}\gamma \big ]}{-}1. \end{aligned}$$

It is obvious that

$$\begin{aligned} f(0)= & {} R_{0}{-}1,\\ f(1)= & {} {-}\frac{\gamma }{\langle k\rangle }\sum _{k=1}^{n}\frac{kP(k)\big [\beta _{V}(k){+}\varphi _{k}{+}\phi \big ]}{\big [\beta _{S}(k)\Theta {+}\gamma \big ]\big [\beta _{V}(k)\Theta {+}\phi \big ]{+}\varphi _{k}\big [\beta _{V}(k)\Theta {+}\gamma \big ]}<0. \end{aligned}$$

For $0<\Theta <1,$ we have

$$\begin{aligned} f'(\Theta )=\frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{kP(k)h(\Theta )}{\left\{ \big [\beta _{S}(k)\Theta {+}\gamma \big ]\big [\beta _{V}(k)\Theta {+}\phi \big ]{+}\varphi _{k}\big [\beta _{V}(k)\Theta {+}\gamma \big ]\right\} ^{2}}, \end{aligned}$$

where $h(\Theta )=-[\beta _{S}(k)\beta _{V}(k)]^{2}\Theta ^{2}-2\beta _{S}(k)\beta _{V}(k)[\phi \beta _{S}(k)+\varphi _{k}\beta _{V}(k)]\Theta +g_{k},$$g_{k}=\gamma \beta _{S}(k)\beta _{V}(k)(\varphi _{k}+\phi )-[\phi \beta _{S}(k)+\beta _{V}(k)(\varphi _{k}+\gamma )][\phi \beta _{S}(k)+\varphi _{k}\beta _{V}(k)].$

We consider the special cases to study the behavior of $f(\Theta )=0$:

Case 1 When $g_{k}\le 0$, which is equivalent to

$$\begin{aligned} R_{1}\triangleq \frac{ \gamma \varphi _{k}\beta _{V}(k)[\beta _{S}(k)-\beta _{V}(k)]}{[\phi \beta _{S}(k)+\varphi _{k}\beta _{V}(k)]^{2}}\le 1. \end{aligned}$$

(8)

And $f'(\Theta )\le 0$ for $\Theta >0.$ Obviously, the equation $f(\Theta )=0$ has a unique positive solution only if $R_{0}>1$.

Case 2 When $g_{k}>0$, we can get that the discriminant $4\beta ^{2}_{S}(k)\beta ^{2}_{V}(k)\{[\phi \beta _{S}(k)+\varphi _{k}\beta _{V}(k)]^{2}+g_{k}\}>0.$ Thus, the equation $h(\Theta )=0$ has two unequal solutions:

$$\begin{aligned} \Theta _{1}= & {} \frac{{-}\sqrt{\gamma \varphi _{k}\beta _{V}(k)[\beta _{S}(k){-}\beta _{V}(k)]}{-}[\phi \beta _{S}(k){+}\varphi _{k}\beta _{V}(k)]}{\beta _{S}(k)\beta _{V}(k)}<0,\\ \Theta _{2}= & {} \frac{\sqrt{\gamma \varphi _{k}\beta _{V}(k)[\beta _{S}(k){-}\beta _{V}(k)]}{-}[\phi \beta _{S}(k){+}\varphi _{k}\beta _{V}(k)]}{\beta _{S}(k)\beta _{V}(k)}>0. \end{aligned}$$

Then, we have $h(\Theta )>0, f'(\Theta )>0$ for $\Theta \in (0,\Theta _{2})$ and $h(\Theta )<0, f'(\Theta )<0$ for $\Theta \in (\Theta _{2},+\infty ).$ Define

$$\begin{aligned} R_{2}\triangleq & {} \frac{ \gamma \varphi _{k}\beta _{V}(k)\big [\beta _{S}(k)-\beta _{V}(k)\big ]}{\big [\phi \beta _{S}(k)+\varphi _{k}\beta _{V}(k)+\beta _{S}(k)\beta _{V}(k)\big ]^{2}}, \end{aligned}$$

(9)

$$\begin{aligned} R_{3}\triangleq & {} f(\Theta _{2})+1. \end{aligned}$$

(10)

For $R_{1}>1>R_{2},$ we get the following results:

If $R_{0}>1$ or $R_{0}=1$ or $R_{0}<1=R_{3}$, the equation $f(\Theta )=0$ has a positive solution in (0, 1) and system (1) has a unique endemic equilibrium.

If $R_{0}<1$ and $R_{3}>1,$ the equation $f(\Theta )=0$ has two positive solutions in (0, 1) and system (1) has multiple endemic equilibria.

From the above analysis, we conclude these results:

Theorem 1

For system (1), there always exists the disease-free equilibrium $P^{0}$, and the following statements are true:

• (1) If $R_{0}>1$, there exists a unique endemic equilibrium $P^{*}(S^{*}_{k},I^{*}_{k},V^{*}_{k}).$

• (2) If $R_{0}=1$ and $R_{1}>1>R_{2},$ there exists an endemic equilibrium $P_{1}^{*}(S^{*}_{1k},I^{*}_{1k},$$V^{*}_{1k}).$

• (3) If $R_{0}<1$ and $R_{1}>1=R_{3}>R_{2},$ there exists an endemic equilibrium $P_{2}^{*}(S^{*}_{2k},I^{*}_{2k},V^{*}_{2k}).$

• (4) If $R_{0}<1$, $R_{1}>1>R_{2}$ and $R_{3}>1$, there exist two endemic equilibria $P_{3}^{*}(S^{*}_{3k},I^{*}_{3k},V^{*}_{3k})$ and $P_{4}^{*}(S^{*}_{4k},I^{*}_{4k},V^{*}_{4k}).$

• (5) There is no endemic equilibrium except the above four cases.

Where $R_{0}$ and $R_{i}(i=1,2,3)$ are defined by (2),(8)–(9), $P^{*}$ and $P_{j}^{*}(j=1,2,3,4)$ satisfy Eqs. (4)–(7).

Remark 4

Theorem 1 indicates the possibility of multiple endemic equilibria for $R_{0}<1$ and the occurrence of a backward bifurcation in system (1). Under $R_{1}\le 1,$ there is no endemic equilibrium for $R_{0}<1$ under which system (1) only exhibits forward bifurcation.

3.2 Global stability of disease-free equilibrium

It is important to analyze the stability of the disease-free equilibrium $P^{0},$ as it indicates whether the disease dies out eventually. Next, we will show that the disease-free equilibrium $P^{0}$ is locally asymptotically stable by analyzing the Jacobian matrix of system (1) at $P^{0}$ for $R_{0}<1$. Moreover, the global stability of $P^{0}$ will be obtained for $\widetilde{R}_{0}<1$.

Theorem 2

If $R_{0}<1$, then the disease-free equilibrium $P^{0}$ is locally asymptotically stable in $\Omega$, where $R_{0}$ is defined as Eq. (2).

Proof

See “Appendix A”. $\square$

Theorem 3

If $\widetilde{R}_{0}<1$, then the disease-free equilibrium $P^{0}$ is globally asymptotically stable in $\Omega$, where $\widetilde{R}_{0}$ is defined as Eq. (3).

Proof

See “Appendix B”. $\square$

Remark 5

Theorem 3 does not include the stability of endemic equilibria which may exist for $R_{0}<1.$ Theorems 2 and  3 indicate that the vaccination extends the local stability of the disease-free equilibrium. Since there is no endemic equilibrium for $R_{0}<1$ and $R_{1}\le 1$, the disease-free equilibrium of system (1) is globally asymptotically stable under these conditions.

3.3 Global attractivity of endemic equilibrium

As mentioned in Theorem 1, there exists a unique endemic equilibrium $P^{*}$ for $R_{0}>1$. In this section, we will analyze the uniform persistence and global attractivity of the endemic equilibrium $P^{*}$ of system (1).

Theorem 4

When $R_{0}>1$, system (1) is permanent, i.e., there exists a $\xi >0$ which is independent on the initial condition $I(0)>0$, such that

$$\begin{aligned} \lim _{t\rightarrow \infty }\inf I(t)=\lim _{t\rightarrow \infty }\inf \sum \limits _{k=1}^{n}P(k)I_{k}(t)\ge \xi . \end{aligned}$$

where $I(0)=\sum \limits _{k=1}^{n}P(k)I_{k}(0).$

Proof

See “Appendix C”. $\square$

Theorem 5

Suppose that $(S_{k}(t),I_{k}(t),V_{k}(t))$ is a solution of system (1) satisfying $I(0)>0$. If $R_{0}>1$ and $R_{1}\le ~1$, then

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }(S_{k}(t),I_{k}(t),V_{k}(t))=(S_{k}^{*},I_{k}^{*},V_{k}^{*}). \end{aligned}$$

where $P^{*}(S_{k}^{*},I_{k}^{*},V_{k}^{*})$ satisfies Eqs.  (4)–(7) for $k=1,2,\ldots ,n.$

Proof

See “Appendix D”. $\square$

Remark 6

According to Theorem 4, for $R_{0}>1,$ the infection will always exist. Theorem 5 shows that the unique equilibrium $P^{*}$ is globally attractive under its conditions.

4 Control strategy

In this section, we will put forward three immunization control schemes containing the uniform immunization, the targeted immunization, the acquaintance immunization, and an optimal control strategy to control the spread and diffusion of the disease. The effectiveness of the first three immunization strategies will be compared. The optimal control method will be presented.

4.1 Uniform immunization control

Uniform immunization control is to immunize the susceptible individuals with the same probability randomly. Let $\tilde{\delta }\in [0,1)$ be the proportion of immune nodes, then the density of the susceptible individuals who are not immunized is $(1-\tilde{\delta })S_{k}.$ Thus, we acquire a uniform immunization system as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} S'_{k}(t)=\gamma I_{k}(t) -\beta _{S}(k) (1-\tilde{\delta })S_{k}(t)\Theta (t)\\ \quad + \phi V_{k}(t)-\varphi _{k}S_{k}(t),\\ I'_{k}(t)=[\beta _{S}(k)(1-\tilde{\delta })S_{k}(t)+\beta _{V}(k) V_{k}(t)]\\ \Theta (t)-\gamma I_{k}(t),\\ V'_{k}(t)= \varphi _{k} S_{k}(t)-\beta _{V}(k) V_{k}(t)\Theta (t)-\phi V_{k}(t). \end{array}\right. } \end{aligned}$$

(11)

With the same discussion in Sect. 3, we calculate the basic reproduction number of system (11)

$$\begin{aligned} R^{U}_{0}=\frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{ kP(k)\left[ \phi (1-\tilde{\delta })\beta _{S}(k)+\varphi _{k}\beta _{V}(k)\right] }{\gamma (\varphi _{k}+\phi )}, \end{aligned}$$

and

$$\begin{aligned} \widetilde{R}^{U}_{0}=\sum _{k=1}^{n}\frac{ kP(k)(1-\tilde{\delta })\beta _{S}(k)}{\gamma \langle k\rangle }. \end{aligned}$$

Remark 7

When $\tilde{\delta }=0,$ the immunization is not taken into effect and $R^{U}_{0}=R_{0},\widetilde{R}_{0}^{U}=\widetilde{R}_{0}$. When $\tilde{\delta }\in (0,1),$$R^{U}_{0}<R_{0}$ and $\widetilde{R}_{0}^{U}<\widetilde{R}_{0}.$ This means that the harm will be decreased to some extent. When $\tilde{\delta }\rightarrow 1,$$\widetilde{R}^{U}_{0}\rightarrow 0,$ that is, in the case of a full immunization, it would be impossible for the epidemic to spread in the network.

4.2 Targeted immunization control

Targeted immunization control is to immunize the susceptible nodes with large degree. Let $k_{c}$ denote an upper threshold which is larger than the minimum degree, then the nodes with degree $k>k_{c}$ are immunized. The immunization rate $\mu _{k}$ can be defined by

$$\begin{aligned} \mu _{k}= {\left\{ \begin{array}{ll} 1,~~k>k_{c},\\ \mu ,~~k=k_{c},\\ 0,~~k<k_{c}, \end{array}\right. } \end{aligned}$$

where $0<\mu \le 1.$ Then, we get a targeted immunization system as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} S'_{k}(t)=\gamma I_{k}(t) -\beta _{S}(k) (1-\mu _{k})S_{k}(t)\Theta (t)\\ \quad + \phi V_{k}(t)-\varphi _{k}S_{k}(t),\\ I'_{k}(t)=[\beta _{S}(k)(1-\mu _{k})S_{k}(t)+\beta _{V}(k) V_{k}(t)]\\ \Theta (t)-\gamma I_{k}(t),\\ V'_{k}(t)= \varphi _{k} S_{k}(t)-\beta _{V}(k) V_{k}(t)\Theta (t)-\phi V_{k}(t). \end{array}\right. } \end{aligned}$$

(12)

The basic reproduction number of system (12) is

$$\begin{aligned} R^{T}_{0}=\frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{ kP(k)\left[ \phi (1-\mu _{k})\beta _{S}(k)+\varphi _{k}\beta _{V}(k)\right] }{\gamma (\varphi _{k}+\phi )}, \end{aligned}$$

and

$$\begin{aligned} \widetilde{R}^{T}_{0}=\sum _{k=1}^{n}\frac{ kP(k)(1-\mu _{k})\beta _{S}(k)}{\gamma \langle k\rangle }. \end{aligned}$$

Remark 8

For $\mu \in (0,1],$ we have $R^{T}_{0}<R_{0}$ and $\widetilde{R}^{T}_{0}<\widetilde{R}_{0},$ which indicates that the targeted immunization scheme is effective. For $0<\langle \mu _{k}\rangle =\tilde{\delta }<1,$ we can get that $R^{T}_{0}<R^{U}_{0}$ and $\widetilde{R}^{T}_{0}<\widetilde{R}^{U}_{0},$ which means that the targeted immunization control is more effective than the uniform scheme when adopting the same average immunization proportion.

Remark 9

From the expression of $\mu _{k},$ the fewer $k_{c}$ is, the higher the densities of the vaccinated individuals and the consequential costs are, and the better the control effects are, vice versa. The value of $k_{c}$ should keep balance between control effects and control costs. Moreover, we can take the upper threshold $k_{c}$ as control variable, $k_{c}\in [1,n]$ as main control constraints, the control effects and costs as objective functions and put forward a biobjective optimal control problem to maximize control effects and minimize control costs. It is a feasible method to obtain the optimal value of $k_{c}.$

4.3 Acquaintance immunization control

It is difficult to provide the upper threshold $k_{c}$ for the targeted immunization scheme [20]. To overcome this problem, we consider the acquaintance immunization control. We choose $\nu N$ individuals from the total N individuals by the proportion $\nu$ randomly. Thus, the individuals with degree k are immunized by the probability $\nu _{k}=\frac{k\nu P(k)}{\langle k\rangle }.$ Then, we obtain an acquaintance immunization system as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} S'_{k}(t)=\gamma I_{k}(t) -\beta _{S}(k) (1-\nu _{k})S_{k}(t)\Theta (t)\\ \quad + \phi V_{k}(t)-\varphi _{k}S_{k}(t),\\ I'_{k}(t)=[\beta _{S}(k)(1-\nu _{k})S_{k}(t)+\beta _{V}(k) V_{k}(t)]\\ \Theta (t)-\gamma I_{k}(t),\\ V'_{k}(t)= \varphi _{k} S_{k}(t)-\beta _{V}(k) V_{k}(t)\Theta (t)-\phi V_{k}(t). \end{array}\right. } \end{aligned}$$

(13)

The basic reproduction number of system (13) is

$$\begin{aligned} R^{A}_{0}= & {} \frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{ kP(k)\left[ \phi (1-\nu _{k})\beta _{S}(k)+\varphi _{k}\beta _{V}(k)\right] }{\gamma (\varphi _{k}+\phi )}\\= & {} \frac{\langle \overline{X}_{k}+\overline{Y}_{k}\rangle -\langle \nu _{k}\overline{X}_{k}\rangle }{\langle \overline{X}_{k}+\overline{Y}_{k}\rangle -\langle \mu _{k}\overline{X}_{k}\rangle }R^{T}_{0}, \end{aligned}$$

and

$$\begin{aligned} \widetilde{R}^{A}_{0}= & {} \frac{1}{\langle k\rangle }\sum _{k=1}^{n}\frac{ kP(k)\left[ \phi (1-\nu _{k})\beta _{S}(k)+\varphi _{k}\beta _{V}(k)\right] }{\gamma (\varphi _{k}+\phi )}\\= & {} \frac{\langle k\beta _{S}(k)\rangle -\langle \nu _{k} k\beta _{S}(k)\rangle }{\langle k\beta _{S}(k)\rangle -\langle \mu _{k} k\beta _{S}(k)\rangle }\widetilde{R}^{T}_{0}. \end{aligned}$$

where $\overline{X}_{k}=\frac{k\phi \beta _{S}(k)}{\varphi _{k}+\phi }$ and $\overline{Y}_{k}=\frac{k\varphi _{k}\beta _{V}(k)}{\varphi _{k}+\phi }.$ It is obvious to get that $\langle k\beta _{S}(k)\rangle -\langle \nu _{k} k\beta _{S}(k)\rangle >0$ and $\langle \overline{X}_{k}+\overline{Y}_{k}\rangle -\langle \nu _{k}\overline{X}_{k}\rangle >0$ for $\nu <\frac{\langle k\rangle }{2m(m+1)}.$

Remark 10

When $\nu <\frac{\langle k\rangle }{2m(m+1)},$$R^{A}_{0}=AR^{T}_{0}$ and $\widetilde{R}^{A}_{0}=B\widetilde{R}^{T}_{0},$ where $A=\frac{\langle \overline{X}_{k}+\overline{Y}_{k}\rangle -\langle \nu _{k}\overline{X}_{k}\rangle }{\langle \overline{X}_{k}+\overline{Y}_{k}\rangle -\langle \mu _{k}\overline{X}_{k}\rangle }$ and $B=\frac{\langle k\beta _{S}(k)\rangle -\langle \nu _{k} k\beta _{S}(k)\rangle }{\langle k\beta _{S}(k)\rangle -\langle \mu _{k} k\beta _{S}(k)\rangle }$ are positive constants. This means the acquaintance immunization scheme is comparable in effectiveness to the targeted immunization scheme.

4.4 Optimal control

Adopting immunization strategies to control diseases may bring inevitable expenses in the actual situation [21]. Apparently, vaccinating a node can generate a cost, such as economic costs of vaccines, transportation charges, and so on. Therefore, we have to take the controlling costs into consideration. In this section, we will perform an optimal control strategy.

To choose the control variables, we perform sensitivity analysis of the basic reproduction number $R_{0}$ by calculating

$$\begin{aligned} \Upsilon _{\mathfrak {p}}=\frac{\partial R_{0}}{\partial \mathfrak {p}}\times \frac{\mathfrak {p}}{R_{0}}, \end{aligned}$$

where $\mathfrak {p}$ is the parameter determining $R_{0}$. After calculations, we can get that the vaccinated rate $\varphi _{k}$ and the recovery rate $\gamma$ have negative impact on the basic reproductive number $R_{0}$. Among parameters which have negative effects on disease, the most practicable one is vaccination. By introducing time-dependent control functions to measure the effectiveness of vaccination strategies, system (1) can be extended to

$$\begin{aligned} {\left\{ \begin{array}{ll} S'_{k}(t)=\gamma I_{k}(t) -\beta _{S}(k) S_{k}(t)\Theta (t)\\ \quad + \phi V_{k}(t)-\varphi _{k}(t)S_{k}(t),\\ I'_{k}(t)=[\beta _{S}(k)S_{k}(t)+\beta _{V}(k) V_{k}(t)]\Theta (t)-\gamma I_{k}(t),\\ V'_{k}(t)= \varphi _{k}(t) S_{k}(t)-\beta _{V}(k) V_{k}(t)\Theta (t)-\phi V_{k}(t). \end{array}\right. } \end{aligned}$$

To minimize the density of infected individuals and the cost of control measures, an objective functional $\mathcal {J}$ over a finite time interval [0, T] is given by

$$\begin{aligned} \mathcal {J}(\varphi _{k}(t))=\int _{0}^{T}\sum _{k=1}^{n}\left[ D_{k}I_{k}(t)+\frac{W_{k}}{2}\varphi _{k}^{2}(t)\right] \mathrm{d}t, \end{aligned}$$

(14)

where $D_{k}$ and $W_{k}$ are weighted constants for infected population and relative costs of intervention, respectively. The optimal control problem is to find optimal functions $\varphi _{k}^{*}(t)$ for $k=1,\ldots ,n$ such that

$$\begin{aligned} \mathcal {J}(\varphi _{k}^{*}(t))=\min _{\varphi _{k}(t)\in \Lambda }\mathcal {J}(\varphi _{k}(t)) \end{aligned}$$

with $\Lambda =\{\varphi _{k}(t)\in L^{1}[0,T]|0\le \varphi _{k}(t)\le 1, k=1,\ldots ,n\}.$

To achieve that, we construct the Hamilton function

$$\begin{aligned} \mathcal {H}= & {} \sum \limits _{k=1}^{n}\left[ D_{k}I_{k}(t)+\frac{W_{k}}{2}\varphi _{k}^{2}(t)+\lambda _{k}(t)S'_{k}(t)\right. \\&\left. +\,\lambda _{k+n}(t)I'_{k}(t)+\lambda _{k+2n}(t)V'_{k}(t)\right] \\= & {} \sum \limits _{k=1}^{n}\left\{ D_{k}I_{k}(t)+\frac{W_{k}}{2}\varphi _{k}^{2}(t)\right\} \\&+\sum \limits _{k=1}^{n}\lambda _{k}(t)\left[ \gamma I_{k}(t) -\beta _{S}(k) S_{k}(t)\Theta (t)\right. \\&\left. +\,\phi V_{k}(t)-\varphi _{k}(t)S_{k}(t)\right] \\&+\sum \limits _{k=1}^{n}\lambda _{k+n}(t)\left\{ [\beta _{S}(k)S_{k}(t)\right. \\&\left. +\,\beta _{V}(k) V_{k}(t)]\Theta (t)-\gamma I_{k}(t)\right\} \\&+\sum \limits _{k=1}^{n}\lambda _{k+2n}(t)\left[ \varphi _{k}(t) S_{k}(t)\right. \\&\left. -\,\beta _{V}(k) V_{k}(t)\Theta (t)-\phi V_{k}(t)\right] . \end{aligned}$$

Applying Pontryagin’s maximum principle, one obtains the following theorem.

Theorem 6

There exist optimal controls

$$\begin{aligned} \varphi _{k}^{*}(t)= & {} \min \left\{ \max \left\{ 0,\frac{S_{k}(t)}{W_{k}}[\lambda _{k}(t)\right. \right. \nonumber \\&\left. \left. -\lambda _{k+2n}(t)]\right\} ,1\right\} , \end{aligned}$$

(15)

that minimize $\mathcal {J}(\varphi _{k}(t))$ over $\Lambda$. And it is necessary that there exist continuous functions $\lambda _{k}(t)(k=1,\ldots ,n)$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda '_{k}(t)=[\lambda _{k}(t)-\lambda _{k+n}(t)]\beta _{S}(k) \Theta (t)\\ ~~~~~~~~~~~~~~~~+[\lambda _{k}(t)-\lambda _{k+2n}(t)]\varphi _{k}(t),\\ \lambda '_{k+n}(t)=-D_{k}+\gamma [\lambda _{k+n}(t)-\lambda _{k}(t)]\\ ~~~~~~~~~~~~~~~~+[\lambda _{k}(t)-\lambda _{k+n}(t)]k\beta _{S}(k) S_{k}(t)\frac{P(k)}{\langle k\rangle }\\ ~~~~~~~~~~~~~~~~+[\lambda _{k+2n}(t)-\lambda _{k+n}(t)]k\beta _{V}(k) V_{k}(t)\frac{P(k)}{\langle k\rangle },\\ \lambda '_{k+2n}(t)=\phi [\lambda _{k+2n}(t)-\lambda _{k}(t)]\\ ~~~~~~~~~~~~~~~~+[\lambda _{k+2n}(t)-\lambda _{k+n}(t)]\beta _{V}(k) \Theta (t), \end{array}\right. } \end{aligned}$$

with transversality conditions

$$\begin{aligned} \lambda _{k}(T)=\lambda _{k+n}(T)=\lambda _{k+2n}(T)=0,~k=1,\ldots ,n. \end{aligned}$$

Proof

See “Appendix E”. $\square$

Remark 11

Theorem 6 focuses on the necessary conditions of the optimal control problem. In the objective functional (14), it is difficult to evaluate the weights $D_{k}$ and $W_{k}$ for $k=1,\ldots ,n$. In the next section, we will discuss the numerical bounds for these weight ratios.

5 Numerical simulations

In this section, we will perform numerical simulations to illustrate the theoretical results in Sects. 3 and 4.

All the simulations are based on BA networks with size $N=5000$, which evolves from the initial network with $m_{0}=4$ and adds new node with $m=3$ new edges. The average degree of the generated network is $\langle k\rangle =5.9976 ,$ the minimum degree is 3 and the maximum is $n=198.$ We set the infection rates as $\beta _{S}(k)=\beta k$ and $\beta _{V}(k)=\sigma \beta k$, and the vaccinated rate as $\varphi _{k}=\varphi .$ We set the time interval as [0, T], where $T(>0)$ is the terminal time; the time t can be taken as different unit if system (1) is applied to different epidemic based on different actual situations, including day, week, and so on. In Table 1, all parameters of system (1) are fixed except the infected rate $\beta$ and the initial values $S_{k}(0),V_{k}(0),I_{k}(0).$ To observe the influence of different infected rates and initial values on the infected individuals, we take two values for $\beta$ and the initial values shown in Table 1.

Table 1 Values of parameters and initial conditions of system (1)

Fig. 1

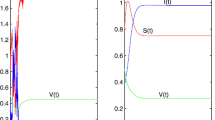
Comparison of Monte Carlo stochastic simulation (red circle) and the mean-field approach (black curve) of system (1), where $R_{0}=8.8508$ in (a, b) and $\widetilde{R}_{0}=0.9625$ in (c, d),  $\varphi _{k}=0.04,k=3,4,\ldots ,198$

5.1 Uniformity of two simulations

We will show the comparisons of the mean-field approach and Monte Carlo simulations for the prediction of the average densities of the susceptible, the infected, and the vaccinated individuals at the time interval [0, T]. To minimize the random fluctuation, we make 100 time average. Given two kinds of different initial conditions and infected rates (as shown in Table 1), we plot the average densities S(t), V(t) and I(t) for the mean-field approach and Monte Carlo simulations in Fig. 1, where the red circles denote the Monte Carlo stochastic simulation and the black curves denote the mean-field approach simulation. $\beta$ is taken as 0.015 for Fig. 1a, b and 0.0007 for Fig. 1c, d; I(0) is taken as 0.1 for Fig. 1a, c and 0.05 for Fig. 1b, d. The threshold parameters $R_{0}=8.8508>1$ for Fig. 1a, b and $\widetilde{R}_{0}=0.9625<1$ for Fig. 1c, d. From Fig. 1, we can observe that the numerical results for the two approaches are in agreement, which implies that the analysis based on the mean-field approach is effective.

Fig. 2

Comparison of the uniform immunization, the targeted immunization and the acquaintance immunization schemes, where $\tilde{\delta }=0.1, \mu =0.185, k_{c}=10,\nu =0.18$

In all figures below, the numerical results are obtained from the mean-field approach.

5.2 Dynamical properties of equilibria

We will verify Theorems 2–5. In Fig. 1c, d, the basic reproduction number $R_{0}=0.4310<1$. Based on Theorem 2, the disease-free equilibrium $P^{0}$ is locally asymptotically stable, which is shown in Fig. 1c, d. Furthermore, we calculate the threshold number $\widetilde{R}_{0}=0.9625<1.$ It depicts that the disease-free equilibrium $P^{0}$ is globally asymptotically stable, which corresponds to the results of Theorem 3.

The condition $R_{1}\doteq 4.9867 \times 10^{-6}<1$ of Theorem 5 is satisfied. From the above, the basic reproduction number $R_{0}=8.8508>1.$ We discover that the densities of the susceptible, the infected and the vaccinated individuals converge to a positive constant, respectively. It is clear that the endemic equilibrium $P^{*}$ is uniformly persistent and globally attractive in Fig. 1a, b, which coincides with Theorems 4 and 5.

In addition, from Fig. 1, we can observe that the initial conditions have almost no influence on the stationary fraction of infected individuals for $R_{0}>1$ or $\widetilde{R}_{0}<1$.

5.3 Effects of three immunization schemes on disease diffusion

We present the numerical results investigating the effectiveness of the uniform, targeted and acquaintance immunization schemes. We set $\tilde{\delta }=0.1,\mu =0.185, k_{c}=10.$ The average rate $\langle \mu _{k}\rangle$ for the targeted immunization control is the same with the immunization rate $\tilde{\delta }$ for the uniform one. The numerical results are summarized in Fig. 2. We can see that the three immunization methods reduce the final densities of the infected individuals and make the size of any epidemic smaller. Two threshold parameters of three immunization methods are shown for $\beta =0.015$ and $\beta =0.0007$ in Table 2.

Table 2 Values of $R_{0}$ and $\widetilde{R}_{0}$ corresponding to different $\beta$

Fig. 3

Optimal control $\varphi _{k}^{*}(t)$ for different k and comparison of the average infected density I(t) for $\varphi _{k}(t)=\varphi ^{*}_{k}(t),0.04,0$ with $R_{0}>1$, where $\beta =0.015$

Fig. 4

Optimal control $\varphi _{k}^{*}(t)$ for different k and comparison of the average infected density I(t) for $\varphi _{k}(t)=\varphi ^{*}_{k}(t),0.04,0$ with $\widetilde{R}_{0}<1$, where $\beta =0.0007$

From Table 2, we can conclude that $R_{0}>R^{A}_{0}>R^{U}_{0}>R^{T}_{0}>1$ for Fig. 2a, b and $\widetilde{R}^{T}_{0}<\widetilde{R}^{U}_{0}<\widetilde{R}^{A}_{0}<\widetilde{R}_{0}<1$ for Fig. 2c, d. It is obvious that the targeted immunization control has the absolute advantage to control the disease over the uniform and acquaintance immunization schemes. However, the targeted immunization control requires global information about the degrees of the nodes on the network, i.e., the upper threshold $k_{c}.$ For the acquaintance immunization scheme, we choose $\nu =0.18<\frac{\langle k\rangle }{2m(m+1)}=0.2499;$ then, it is comparable to the targeted immunization scheme in effectiveness. It can also be seen from Fig. 2 that the acquaintance immunization method shows a higher average density of the infected individuals than the targeted immunization method. Clearly, the targeted immunization scheme is the most effective among the three schemes.

5.4 Effects of optimal control on disease diffusion

For the optimal control scheme, we solve system (1) by the fourth-order Runge–Kutta scheme and employ forward–backward sweep method [22] to find optimal solutions. The stop condition is relative error $\epsilon =0.001.$ Besides parameter values and initial conditions set in Table 1, $D_{k}=10$ and $W_{k}=0.01$ are adopted, $k=3,4,\ldots ,198.$

Figures 3a, b and 4c, d show the optimal control $\varphi ^{*}_{k}(t)$ for different degrees k in the cases of $R_{0}>1$ and $\widetilde{R}_{0}<1$, where k is taken as $3, 20, 35, 50, 75, 97, 118, 146, 163, 198.$ From the four subfigures, it can be observed that the optimal control $\varphi ^{*}_{k}(t)$ increases with the degree k increasing in most of the interval. Figures 3$\text {a}_{1}, \text {b}_{1}$ and 4$\text {c}_{1},\text {d}_{1}$ indicate the comparison of the average infected density I(t) with optimal controls $(\varphi _{k}(t)=\varphi ^{*}_{k}(t))$, with $\varphi _{k}(t)=0.04$, and without optimal controls $(\varphi _{k}(t)=0)$, where $\beta =0.015$ for Fig. 3 and $\beta =0.0007$ for Fig. 4. In Fig. 3$\text {a}_{1}, \text {b}_{1}$, $R_{0}=20.6244$ and 8.8508 correspond to $\varphi _{k}(t)=0$ and 0.04; hence, the infection persists. Nevertheless, once effective vaccination is applied, the disease will be controlled and die out ultimately. In the face of global prevalence, great efforts must be made to control propagation during a given period. To minimize both the infected density and control cost, the optimal controls $\varphi ^{*}_{k}(t)$ decrease with fixed degree k during almost entire evolution and increase with the degree k increasing at fixed time. It is well understood that if a large fraction of susceptible are vaccinated, the possibility of the outbreak of an infectious disease will be reduced apparently. On the other hand, the infection will fade out gradually without any containment, as demonstrated in Fig. 4$\text {c}_{1},\text {d}_{1}$, where $\widetilde{R}_{0}=0.9625<1$. So long as the vaccination is performed, the survival of the disease will be greatly reduced.

Fig. 5

Effect of $D_{k}:W_{k}$ on the average densities of the infected individuals with optimal control, $k=3,4,\ldots ,198$

At last, we will discuss how the value $D_{k}:W_{k}$ has effect on the average densities of the infected individuals with optimal control. Here, we only consider the value of $D_{k}:W_{k}$ does not change with the degree k. Figure 5 provides the effect of the value change of $D_{k}:W_{k}$ on I(t) with $\varphi _{k}^{*}(t).$ In Fig. 5a, b, the infected rate $\beta =0.015$ and the basic production number $R_{0}>1.$ The pink and red lines are demarcations. In Fig. 5a, for $D_{k}:W_{k}\ge 1:0.011,$ the average density I(t) of the infected individuals decreases progressively in the interval [0, T];  that is, the disease can be controlled effectively; for $1:0.011<D_{k}:W_{k}< 1:2.65,$ the disease can be controlled in a period of time first and become increasingly prevalent finally; for $D_{k}:W_{k}\le 1:2.65,$ the average density I(t) always increases in [0, T]; that is, the disease is out of control. In Fig. 5b, the analysis is analogous with Fig. 5a. Figure 5c, d shows the effect of the value $D_{k}:W_{k}$ on the average density I(t) for $\widetilde{R}_{0}<1$, where $\beta =0.0007.$ We present the ratios of $D_{k}:W_{k}$ to control the disease till 0.2T, 0.25T, 0.4T, 0.5T. In Fig. 5c, those ratios are 1 : 0.02, 1 : 0.45, 1 : 3.7, 1 : 9.6 corresponding to 0.2T, 0.25T, 0.4T, 0.5T,  respectively. In Fig. 5d, those ratios are 1 : 0.01, 1 : 0.24, 1 : 1.8, 1 : 4.7 corresponding to 0.2T, 0.25T, 0.4T, 0.5T,  respectively. We can conclude that the fewer the ratios are, the longer the spent time to control the disease is for $\widetilde{R}_{0}<1$.

6 Conclusions

The purpose of this paper is to study the global dynamics and control strategies of a newly proposed SIVS epidemic model on scale-free networks. We analytically derive the expressions of the epidemic threshold parameters $R_{0}$ and $\widetilde{R}_{0}$. And we show that when $\widetilde{R}_{0}<1,$ the disease-free equilibrium of system (1) is globally asymptotically stable, i.e., the disease will die out; when $R_{0}>1,$ there is a unique endemic equilibrium and the disease will persist on networks. For the four control schemes, we conclude that the targeted immunization method is the most effective among the first three schemes under some condition and present the numerical bounds of $D_{k}:W_{k}$ for different cases.

In the current work, we only discuss the global dynamics of the endemic equilibrium $P^{*}$ for $R_{0}>1$. However, there exist other endemic equilibria $P^{*}_{i}(i=1,2,3,4)$ for $R_{0}\le 1.$ In addition, we only consider the density of infected individuals and the control expenses in the optimal control strategy. The spent time to control the spread of the disease is not taken into account. These limitations will be overcome in the further work.

Appendices

Appendix A: Proof of Theorem 2

Since $S_{k}+I_{k}+V_{k}=1$ for any k,  we can reduce the size of system (1) by $S_{k}=1-I_{k}-V_{k}.$ Now system (1) is turned to

$$\begin{aligned} {\left\{ \begin{array}{ll} I'_{k}=\{\beta _{S}(k)(1-I_{k})-[\beta _{S}(k)-\beta _{V}(k)] V_{k}\}\Theta -\gamma I_{k},\\ V'_{k}= \varphi _{k} (1-I_{k})-\beta _{V}(k) V_{k}\Theta -(\varphi _{k}+\phi ) V_{k}. \end{array}\right. } \end{aligned}$$

(16)

The Jacobian matrix of system (16) at $P^{0}$ is

$$\begin{aligned} \mathfrak {J}(P^{0})= & {} \left( \begin{array}{lll} \mathbf {J}&{}\quad \mathbf {0}\\ \mathbf {K}&{}\quad \mathbf {M} \end{array} \right) _{2n\times 2n}, \end{aligned}$$

where

$$\begin{aligned} \mathbf {J}= & {} \left( \begin{array}{cccccc} \frac{ P(1)\{\beta _{S}(1)-[\beta _{S}(1)-\beta _{V}(1)] V^{0}_{1}\} }{\langle k\rangle }-\gamma &{}\ldots &{}\frac{n P(n)\{\beta _{S}(1)-[\beta _{S}(1)-\beta _{V}(1)] V^{0}_{1}\}}{\langle k\rangle } \\ \vdots &{}\vdots &{}\vdots \\ \frac{ P(1)\{\beta _{S}(n)-[\beta _{S}(n)-\beta _{V}(n)] V^{0}_{n}\}}{\langle k\rangle }&{}\cdots &{}\frac{nP(n)\{\beta _{S}(n)-[\beta _{S}(n)-\beta _{V}(n)] V^{0}_{n}\}}{\langle k\rangle }-\gamma \\ \end{array} \right) ,\\ \mathbf {K}= & {} \left( \begin{array}{cccccc} -\frac{\beta _{V}(1) V^{0}_{1}P(1)}{\langle k\rangle } -\varphi _{1} &{}-\frac{2\beta _{V}(1) V^{0}_{1}P(2)}{\langle k\rangle }&{} \cdots &{}- \frac{n\beta _{V}(1) V^{0}_{1}P(n)}{\langle k\rangle } \\ -\frac{\beta _{V}(2) V^{0}_{2}P(1)}{\langle k\rangle } &{}-\frac{2\beta _{V}(2) V^{0}_{2}P(2)}{\langle k\rangle } -\varphi _{2}&{} \cdots &{}- \frac{n\beta _{V}(2) V^{0}_{2}P(n)}{\langle k\rangle } \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ - \frac{\beta _{V}(n) V^{0}_{n}P(1)}{\langle k\rangle } &{}-\frac{2\beta _{V}(n) V^{0}_{n}P(2)}{\langle k\rangle }&{}\cdots &{} -\frac{n \beta _{V}(n) V^{0}_{n}P(n)}{\langle k\rangle } -\varphi _{n} \\ \end{array} \right) ,\\ \mathbf {M}= & {} \left( \begin{array}{cccccc} -\,(\varphi _{1}+\phi )&{}0 &{} \cdots &{}0\\ 0&{} -\,(\varphi _{2}+\phi )&{}\cdots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0&{}0 &{}\cdots &{} -(\varphi _{n}+\phi )\\ \end{array} \right) . \end{aligned}$$

A direct calculation leads to the characteristic polynomial of the disease-free equilibrium in the following form:

$$\begin{aligned} (\lambda +\gamma )^{n-1}\left[ \lambda -\gamma (R_{0}-1)\right] \prod _{k=1}^{n}(\lambda +\varphi _{k}+\phi )=0. \end{aligned}$$

Since $R_{0}<1$, all eigenvalues of $\mathfrak {J}(P^{0})$ are all negative, which completes the proof.

Appendix B: Proof of Theorem 3

First, we will show $\lim _{t\rightarrow +\infty }I_{k}(t)=0$ for any $k=1,\ldots ,n$. The derivative of $\Theta (t)$ is

$$\begin{aligned} \frac{\mathrm{d}\Theta }{\mathrm{d}t}= & {} \frac{1}{\langle k\rangle }\sum _{k=1}^{n}kP(k)I'_{k}\\= & {} \frac{1}{\langle k\rangle }\sum _{k=1}^{n}kP(k)\{[\beta _{S}(k)(1-I_{k})\\&-\,(\beta _{S}(k)-\beta _{V}(k)) V_{k}]\Theta -\gamma I_{k}\}\\\le & {} \frac{1}{\langle k\rangle }\sum _{k=1}^{n}k\beta _{S}(k)P(k)\Theta -\gamma \Theta , \end{aligned}$$

then

$$\begin{aligned} \Theta (t)\le & {} \Theta (0)\exp \{\gamma (\widetilde{R}_{0}-1)t\}. \end{aligned}$$

Since $\widetilde{R}_{0}<1$, we have $\lim _{t\rightarrow +\infty }\Theta (t)=0$ and $\lim _{t\rightarrow +\infty }I_{k}(t)=0$ for any k. Moreover, for any $\varepsilon >0,$ there exists a $t_{\varepsilon }>0$; we have $0\le I_{k}(t)\le \varepsilon$ for $t>t_{\varepsilon }.$ Next, we will claim that $\lim _{t\rightarrow +\infty }V_{k}(t)=V_{k}^{0}$ for any k. For the third equation of system (1), we get

$$\begin{aligned} V'_{k}= & {} \varphi _{k} S_{k}-\beta _{V}(k) V_{k}\Theta -\phi V_{k}\\\le & {} \varphi _{k} -(\varphi _{k}+\phi ) V_{k}; \end{aligned}$$

thus,

$$\begin{aligned} \lim _{t\rightarrow +\infty }\sup V_{k}(t)\le \frac{\varphi _{k}}{\varphi _{k}+\phi }=V_{k}^{0}. \end{aligned}$$

On the other hand, considering $0\le I_{k}(t)\le \varepsilon$, we have

$$\begin{aligned} V'_{k}\ge & {} \varphi _{k}-[\beta _{V}(k)+\varphi _{k}]\varepsilon -(\varphi _{k}+\phi )V_{k}. \end{aligned}$$

Setting $\varepsilon \rightarrow 0$, we get that

$$\begin{aligned} \lim _{t\rightarrow +\infty }\inf V_{k}(t)\ge \frac{\varphi _{k}}{\varphi _{k}+\phi }=V_{k}^{0}. \end{aligned}$$

Therefore, $\lim _{t\rightarrow +\infty } V_{k}(t)=V_{k}^{0}$ for any $k=1,2,\ldots ,n.$ Because $S_{k}(t)=1-I_{k}(t)-V_{k}(t)$, it follows that $\lim _{t\rightarrow +\infty } S_{k}(t)=S_{k}^{0}$ for any k. These prove that $P^{0}$ is globally attractive for $\widetilde{R}_{0}<1.$ Combining with Theorem 2, $P^{0}$ is globally asymptotically stable in $\Omega$.

Appendix C: Proof of Theorem 4

The result follows from an application of Theorem 4.6 in Ref. [23]. Define

$$\begin{aligned} X_{1}= & {} \{(S_{k}(t),I_{k}(t),V_{k}(t))\in \Omega |I(t)\\= & {} \sum \limits _{k=1}^{n}P(k)I_{k}(t)>0\},~X_{2}=\Omega \setminus X_{1}. \end{aligned}$$

First, we will show $X_{1}$ is positive invariant with respect to system (1). For $(S_{k}(0),I_{k}(0),V_{k}(0))\in X_{1}$, $I(0)>0,$ which is equivalent to $\Theta (0)>0.$ Then, we have

$$\begin{aligned} \frac{\mathrm{d}\Theta }{\mathrm{d}t}= & {} \frac{1}{\langle k\rangle }\sum _{k=1}^{n}kP(k)\{\beta _{S}(k)(1-I_{k})\\&-\,[\beta _{S}(k)-\beta _{V}(k)] V_{k}\}\Theta -\gamma \Theta . \end{aligned}$$

Thus,

$$\begin{aligned} \Theta (t)= & {} \Theta (0)\exp \left\{ \frac{1}{\langle k\rangle }\int _{0}^{t}\sum _{k=1}^{n}kP(k)[\beta _{S}(k)(1-I_{k}(\tau ))\right. \\&\left. -\,(\beta _{S}(k)-\beta _{V}(k)) V_{k}(\tau )]d\tau -\gamma t\right\} , \end{aligned}$$

which implies that $\Theta (t)>0$ for $t>0.$ Therefore, we can obtain

$$\begin{aligned} I'(t)= & {} \sum \limits _{k=1}^{n}P(k)I'_{k}(t)\\= & {} \sum _{k=1}^{n}P(k)\{\beta _{S}(k)(1-I_{k}(t))\\&-\,[\beta _{S}(k)-\beta _{V}(k)] V_{k}(t)\}\Theta (t)-\gamma I(t)\\> & {} -\,\gamma I(t); \end{aligned}$$

then, $I(t)> I(0)\exp \{-\gamma t\}>0$ for $t>0$. Thus, $X_{1}$ is positive invariant. Furthermore, the compactness condition ($\hbox {C}_{4.2})$ of Theorem 4.6 in Ref. [23] is easily verified.

Denote

$$\begin{aligned} Y_{1}= & {} \bigcup _{x_{0} \in Y_{2}}\{\omega (x_{0}) \},\\ Y_{2}= & {} \{x_{0}=(S_{k}(0),I_{k}(0),V_{k}(0))\\&\in X_{2} |x(t,x_{0}) \in X_{2}, t\ge 0\}, \end{aligned}$$

where $x(t,x_{0})$ is the solution of system (1) with the initial value $x_{0}$. $\omega (x_{0})$ is the omega limit set of the solution of system (1) starting in $x_{0}\in \Omega$. Restricting system (1) on $M_{1}=\{x_{0}|I(t)=0, t\ge 0\}$ gives

$$\begin{aligned} {\left\{ \begin{array}{ll} S'_{k}= \phi V_{k}-\varphi _{k} S_{k},\\ I'_{k}=-\gamma I_{k},\\ V'_{k}=\varphi _{k} S_{k}-\phi V_{k}. \end{array}\right. } \end{aligned}$$

(17)

It is easy to verify that system (17) has a unique equilibrium $P^{0}(S_{k}^{0},0,V_{k}^{0})$ in $M_{1}$. We can also get that $P^{0}$ is locally asymptotically stable in $M_{1}$, and it is also globally asymptotically stable since system (17) is a linear system. Therefore, $Y_{1}=\{P^{0}\}$. And $P^{0}$ is a covering of $Y_{1}$, which is isolated and acyclic.

Finally, the proof will be done if we show $P^{0}$ is a weak repeller for $X_{1}$, i.e.,

$$\begin{aligned} \lim _{t\rightarrow \infty }\sup d(x(t,x_{0}),P^{0})>0 ~\text {for}~ \text {any}~ x_{0}\in X_{1}. \end{aligned}$$

We only prove

$$\begin{aligned} W^{s}(P^{0})\cap X_{1}=\emptyset , \end{aligned}$$

(18)

where $W^{s}(P^{0})$ denotes the stable manifold of $P^{0}.$ Suppose (18) is not valid, that is for the initial value $(\overline{S}_{k}(0),\overline{I}_{k}(0),\overline{V}_{k}(0))\in X_{1},$ such that

$$\begin{aligned}&\overline{S}_{k}(t)\rightarrow S_{k}^{0},~\overline{I}_{k}(t)\rightarrow I_{k}^{0},~\overline{V}_{k}(t)\\&\quad \rightarrow V_{k}^{0},~\text {as}~t\rightarrow \infty ,~k=1,\ldots ,n. \end{aligned}$$

Since $R_{0}>1,$ we can choose a $\delta >0$ small enough such that

$$\begin{aligned}&m_{\delta }\triangleq \frac{1}{\gamma \langle k\rangle }\sum _{k=1}^{n}kP(k)\left\{ \frac{\phi \beta _{S}(k)+\varphi _{k}\beta _{V}(k)}{\varphi _{k}+\phi }\right. \\&\quad \left. -\,[\beta _{S}(k)+\beta _{V}(k)]\delta \right\} >1. \end{aligned}$$

On the other side, for the above $\delta >0,$ there exists a $t_{\delta }>0$ such that

$$\begin{aligned}&S_{k}^{0}-\delta \le S_{k}(t)\le S_{k}^{0}+\delta ,~0\le I_{k}(t)\le \delta ,~V_{k}^{0}\nonumber \\&\quad -\delta \le V_{k}(t)\le V_{k}^{0}+\delta , \nonumber \\&\qquad ~\text {for}~t\ge t_{\delta },~k=1,\ldots ,n. \end{aligned}$$

(19)

Denoting $\Phi (t)=\frac{1}{\gamma }\Theta (t),$ then for $t\ge t_{\delta }$ we have

$$\begin{aligned} \frac{\mathrm{d}\Phi (t)}{\mathrm{d}t}= & {} \frac{1}{\gamma }\Theta '(t)\\= & {} \frac{1}{\gamma \langle k\rangle }\sum \limits _{k=1}^{n}kP(k)\left\{ \phi \beta _{S}(k)\right. \\&\left. +\,\varphi _{k}\beta _{V}(k)\Theta (t)-\gamma I_{k}\right\} \\\ge & {} \frac{1}{\gamma \langle k\rangle }\sum \limits _{k=1}^{n}kP(k)\left\{ [\beta _{S}(k)S_{k}^{0}+\beta _{V}(k)V_{k}^{0}]\right. \\&\left. -\,[\beta _{S}(k)+\beta _{V}(k)]\delta \right\} \Theta (t)-\Theta (t)\\= & {} \gamma (m_{\delta }-1)\Phi (t). \end{aligned}$$

Hence $\Phi (t)\ge \Phi (t_{\delta })\exp \{\gamma (m_{\delta }-1)t\}$, we have $\lim _{t\rightarrow \infty }\Phi (t)=\infty ,$ which contradicts to (19). Thus, (18) holds, which completes the proof.

Appendix D: Proof of Theorem 5

From Theorem 4, there exist a constant $0<\xi <\frac{1}{3}$ and a large enough constant $\bar{t}>0$ such that $I(t)\ge \xi \langle k\rangle$ for $t>\bar{t}$. For the second equation of system (1), we can get that

$$\begin{aligned} I'_{k}\le \beta _{S}(k)(1-I_{k})-\gamma I_{k},~t>\bar{t}. \end{aligned}$$

Hence, for $0<\xi _{1}<\min \{\xi ,\frac{\gamma }{2[\beta _{S}(k)+\gamma ]}\}$, there exists a $t_{1}>\bar{t}$, such that $I_{k}(t)\le X_{k}^{(1)}-\xi _{1}$ for $t>t_{1}$, where

$$\begin{aligned} X_{k}^{(1)}=\frac{\beta _{S}(k)}{\beta _{S}(k)+\gamma }+2\xi _{1}<1. \end{aligned}$$

From the third equation of system (1), we can get

$$\begin{aligned} V'_{k}\le \varphi _{k} - \beta _{V}(k) V_{k}\xi -(\varphi _{k}+\phi )V_{k},~t>t_{1}. \end{aligned}$$

Then, for $0<\xi _{2}<\min \left\{ \frac{1}{2},\xi _{1},\frac{\beta _{V}(k)\xi +\phi }{2[\beta _{V}(k)\xi +\varphi _{k}+\phi ]}\right\}$, there exists a $t_{2}>t_{1}$, such that $V_{k}(t)\le Y_{k}^{(1)}-\xi _{2}$ for $t>t_{2}$, where

$$\begin{aligned} Y_{k}^{(1)}=\frac{\varphi _{k}}{\beta _{V}(k)\xi +\varphi _{k}+\phi }+2\xi _{2}<1. \end{aligned}$$

On the other hand, substituting $\Theta (t) \ge \xi$ into the second equation of system (1), we get

$$\begin{aligned} I'_{k}\ge & {} \xi \left[ \beta _{S}(k)(1-I_{k})-( \beta _{S}(k)- \beta _{V}(k)) Y_{k}^{(1)}\right] \\&-\,\gamma I_{k},~t>t_{2}. \end{aligned}$$

Hence, for $0<\xi _{3}<\min \left\{ \frac{1}{3},\xi _{2},\right. \left. \frac{\xi \left\{ \beta _{S}(k)-[\beta _{S}(k)- \beta _{V}(k)] Y_{k}^{(1)}\right\} }{2[\beta _{S}(k)\xi +\gamma ]}\right\}$, there exists a $t_{3}>t_{2}$, such that $I_{k}(t)\ge x_{k}^{(1)}+\xi _{3}$ for $t>t_{3}$, where

$$\begin{aligned} x_{k}^{(1)}=\frac{\xi \left\{ \beta _{S}(k)-[\beta _{S}(k)- \beta _{V}(k)] Y_{k}^{(1)}\right\} }{\beta _{S}(k)\xi +\gamma }-2\xi _{3}>0. \end{aligned}$$

And

$$\begin{aligned} V'_{k}\ge & {} \varphi _{k}\left( 1- X_{k}^{(1)}\right) -\beta _{V}(k)\xi V_{k}\\&-\,(\varphi _{k}+\phi )V_{k},~t>t_{3}. \end{aligned}$$

Then for $0<\xi _{4}<\min \left\{ \frac{1}{4},\xi _{3},\frac{\varphi _{k}\left( 1- X_{k}^{(1)}\right) }{2[\beta _{V}(k)\xi +\varphi _{k} +\phi ]}\right\}$, there exists a $t_{4}>t_{3}$, such that $V_{k}(t)\ge y_{k}^{(1)}+\xi _{4}$ for $t>t_{4}$, where

$$\begin{aligned} y_{k}^{(1)}=\frac{\varphi _{k}\left( 1- X_{k}^{(1)}\right) }{ \beta _{V}(k)\xi +\varphi _{k} +\phi }-2\xi _{4}>0. \end{aligned}$$

Since $\xi$ is a small constant, it holds that $0<x_{k}^{(1)}<X_{k}^{(1)}<1$ and $0<y_{k}^{(1)}<Y_{k}^{(1)}<1$ .

Denote

$$\begin{aligned} H^{(j)}= & {} \frac{1}{\langle k\rangle }\sum \limits _{k=1}^{n}kP(k)X_{k}^{(j)}, \end{aligned}$$

(20)

$$\begin{aligned} h^{(j)}= & {} \frac{1}{\langle k\rangle }\sum \limits _{k=1}^{n}kP(k)x_{k}^{(j)},~j=1,2,\ldots . \end{aligned}$$

(21)

It is easy to get that $0<h^{(1)}\le \Theta (t)\le H^{(1)},~t>t_{4}.$

Once again, we have

$$\begin{aligned} I'_{k}\le & {} H^{(1)}\left\{ \beta _{S}(k)(1-I_{k})-[\beta _{S}(k)-\beta _{V}(k)]y_{k}^{(1)}\right\} \\&-\,\gamma I_{k},~t>t_{4}. \end{aligned}$$

Thus, for $0<\xi _{5}<\min \left\{ \frac{1}{5},\xi _{4}\right\}$, there exists a $t_{5}>t_{4}$, such that

$$\begin{aligned}&I_{k}(t)\le X_{k}^{(2)}\triangleq \min \left\{ X_{k}^{(1)}\right. \\&\quad -\,\xi _{1},\frac{H^{(1)}\left\{ \beta _{S}(k)-[\beta _{S}(k)-\beta _{V}(k)]y_{k}^{(1)}\right\} }{\beta _{S}(k)H^{(1)}+\gamma }\\&\quad \left. +\,\xi _{5}\right\} ,~t>t_{5}. \end{aligned}$$

And

$$\begin{aligned} V'_{k}\le & {} \varphi _{k}\left( 1- x_{k}^{(1)}\right) \\&-\,\beta _{V}(k) V_{k}h^{(1)}-(\varphi _{k}+\phi )V_{k},~t>t_{5}. \end{aligned}$$

Then, for $0<\xi _{6}<\min \left\{ \frac{1}{6},\xi _{5}\right\}$, there exists a $t_{6}>t_{5}$, such that

$$\begin{aligned}&V_{k}(t)\le Y_{k}^{(2)}\triangleq \min \left\{ Y_{k}^{(1)}\right. \\&\quad \left. -\,\xi _{2},\frac{\varphi _{k}\left( 1- x_{k}^{(1)}\right) }{ \beta _{V}(k)h^{(1)}+\varphi _{k}+ \phi }+\xi _{6}\right\} ,~t>t_{6}. \end{aligned}$$

On the other side, one has

$$\begin{aligned} I'_{k}\ge & {} h^{(1)}\left\{ \beta _{S}(k)(1-I_{k})-[\beta _{S}(k)- \beta _{V}(k)]Y_{k}^{(2)}\right\} \\&-\,\gamma I_{k},~t>t_{6}. \end{aligned}$$

Then, for $0<\xi _{7}<\min \left\{ \frac{1}{7},\xi _{6},\right. \left. \frac{h^{(1)}\left\{ \beta _{S}(k)-[\beta _{S}(k)- \beta _{V}(k)]Y_{k}^{(2)}\right\} }{2[\beta _{S}(k)h^{(1)}+\gamma ]}\right\}$, there exists a $t_{7}>t_{6}$, such that $I_{k}(t)\ge x_{k}^{(2)}+\xi _{7}$ for $t>t_{7}$, where

$$\begin{aligned}&x_{k}^{(2)}=\max \left\{ x_{k}^{(1)}\right. \\&\quad \left. +\,\xi _{3},\frac{h^{(1)}\left\{ \beta _{S}(k)-[\beta _{S}(k)- \beta _{V}(k)]Y_{k}^{(2)}\right\} }{\beta _{S}(k)h^{(1)}{+}\gamma }{-}2\xi _{7}\right\} . \end{aligned}$$

And

$$\begin{aligned} V'_{k}\ge & {} \varphi _{k}\left( 1- X_{k}^{(2)}\right) \\&-\,\beta _{V}(k) V_{k}H^{(2)}-(\varphi _{k}+\phi )V_{k},~t>t_{7}. \end{aligned}$$

Then, for $0<\xi _{8}<\min \left\{ \frac{1}{8},\xi _{7},\frac{\varphi _{k}\left( 1- X_{k}^{(2)}\right) }{2[ \beta _{V}(k)H^{(2)}+\varphi _{k}+\phi ]}\right\}$, there exists a $t_{8}>t_{7}$, such that $V_{k}(t)\ge y_{k}^{(2)}+\xi _{8}$ for $t>t_{8}$, where

$$\begin{aligned} y_{k}^{(2)}=\max \left\{ y_{k}^{(1)}+\xi _{5},\frac{\varphi _{k}\left( 1- X_{k}^{(2)}\right) }{ \beta _{V}(k)H^{(2)}+\varphi _{k}+\phi }-2\xi _{8}\right\} . \end{aligned}$$

Similarly, the l-th step can be performed and four sequences are obtained: $\{X_{k}^{(l)}\},\{Y_{k}^{(l)}\},\{x_{k}^{(l)}\}$ and $\{y_{k}^{(l)}\}$. Since the first two are monotone increasing and the last two are strictly decreasing, there exists a large positive integer K such that for $l\ge K$:

$$\begin{aligned} X_{k}^{(l)}= & {} \frac{ H^{(l-1)}\left\{ \beta _{S}(k)-[\beta _{S}(k)- \beta _{V}(k)]y_{k}^{(l-1)}\right\} }{\beta _{S}(k)H^{(l-1)}+\gamma }\nonumber \\&+\,\xi _{4l-3}, \end{aligned}$$

(22)

$$\begin{aligned} x_{k}^{(l)}= & {} \frac{ h^{(l-1)}\left\{ \beta _{S}(k)-[\beta _{S}(k)- \beta _{V}(k)]Y_{k}^{(l)}\right\} }{\beta _{S}(k)h^{(l-1)}+\gamma }\nonumber \\&-\,2\xi _{4l-1},\end{aligned}$$

(23)

$$\begin{aligned} Y_{k}^{(l)}= & {} \frac{\varphi _{k}\left( 1- x_{k}^{(l-1)}\right) }{\beta _{V}(k)h^{(l-1)}+\varphi _{k}+\phi }+\xi _{4l-2},\end{aligned}$$

(24)

$$\begin{aligned} y_{k}^{(l)}= & {} \frac{\varphi _{k}\left( 1- X_{k}^{(l)}\right) }{ \beta _{V}(k)H^{(l)}+\varphi _{k} +\phi }-2\xi _{4l} . \end{aligned}$$

(25)

It is clear that

$$\begin{aligned} x_{k}^{(l)}\le I_{k}(t)\le X_{k}^{(l)},y_{k}^{(l)}\le V_{k}(t)\le Y_{k}^{(l)},~t>t_{4l}. \end{aligned}$$

(26)

Noting that $0<\xi _{l}<\frac{1}{l}$, one has $\xi _{l}\rightarrow 0$ as $l\rightarrow \infty$. For the six sequences of (20)–(25), direct computations as $j\rightarrow \infty$ and $l\rightarrow \infty$ lead to

$$\begin{aligned}&\lim _{j\rightarrow \infty }H^{(j)}=\frac{1}{\langle k\rangle }\sum \limits _{k=1}^{n}kP(k)X_{k}\triangleq H,\end{aligned}$$

(27)

$$\begin{aligned}&\lim _{j\rightarrow \infty }h^{(j)}=\frac{1}{\langle k\rangle }\sum \limits _{k=1}^{n}kP(k)x_{k}\triangleq h,\end{aligned}$$

(28)

$$\begin{aligned}&\lim _{l\rightarrow \infty }X^{(l)}_{k}\nonumber \\&\quad =\frac{H\left\{ \beta _{S}(k)[\beta _{V} (k)H+\phi ]+\varphi _{k}\beta _{V}(k)\right\} }{[\beta _{V}(k)H+\phi ][\beta _{S} (k)H+\gamma ]+\varphi _{k}[\beta _{V}(k)H+\gamma ]}\triangleq X_{k},\nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned}&\lim _{l\rightarrow \infty }x^{(l)}_{k}\nonumber \\&\quad =\frac{h\left\{ \beta _{S}(k)[\beta _{V} (k)h+\phi ]+\varphi _{k}\beta _{V}(k)\right\} }{[\beta _{V}(k)h+\phi ][\beta _{S} (k)h+\gamma ]+\varphi _{k}[\beta _{V}(k)h+\gamma ]}\triangleq x_{k},\nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned}&\lim _{l\rightarrow \infty }Y^{(l)}_{k}\nonumber \\&\quad =\frac{\gamma \varphi _{k}}{[\beta _{V}(k)h+\phi ][\beta _{S} (k)h+\gamma ]+\varphi _{k}[\beta _{V}(k)h+\gamma ]}\triangleq Y_{k},\nonumber \\\end{aligned}$$

(31)

$$\begin{aligned}&\lim _{l\rightarrow \infty }y^{(l)}_{k}\nonumber \\&\quad =\frac{\gamma \varphi _{k}}{[\beta _{V}(k)H+\phi ][\beta _{S} (k)H+\gamma ]+\varphi _{k}[\beta _{V}(k)H+\gamma ]}\triangleq y_{k}.\nonumber \\ \end{aligned}$$

(32)

Substituting (29) into (27) and (30) into (28), respectively, one obtains

$$\begin{aligned}&\frac{1}{\langle k \rangle }\sum \limits _{k=1}^{n}\frac{kP(k)\{\beta _{S}(k)[\beta _{V} (k)H+\phi ]+\varphi _{k}\beta _{V} (k)\}}{[\beta _{V}(k)H+\phi ][\beta _{S} (k)H+\gamma ]+\varphi _{k}[\beta _{V}(k)H+\gamma ]}=1,\\&\frac{1 }{\langle k\rangle }\sum \limits _{k=1}^{n}\frac{kP(k)\{\beta _{S}(k)[\beta _{V} (k)h+\phi ]+\varphi _{k}\beta _{V} (k)\}}{[\beta _{V}(k)h+\phi ][\beta _{S} (k)h+\gamma ]+\varphi _{k}[\beta _{V}(k)h+\gamma ]}=1. \end{aligned}$$

Subtracting the above two equations, we can get

$$\begin{aligned} \frac{1}{\langle k\rangle }\sum \limits _{k=1}^{n}\frac{kP(k)F(k)(h-H)}{ G(k)}=0, \end{aligned}$$

where

$$\begin{aligned} F(k)= & {} \beta ^{2}_{S} (k)[\beta _{V}(k)h+\phi ] [\beta _{V}(k)H+\phi ]\\&+\,\varphi _{k}\beta _{S}(k)\beta _{V}(k)(\phi -\gamma )\\&+\,\varphi _{k}\beta _{V}(k)\{\beta _{S}(k) \beta _{V}(k)(H+h)\\&+\,[\phi \beta _{S}(k)+\gamma \beta _{V}(k)]+\varphi _{k}\beta _{V}(k)\},\\ G(k)= & {} \{[\beta _{V}(k)h+\phi ][\beta _{S}(k)h+\gamma ]\\&+\,\varphi _{k}[\beta _{V}(k)h+\gamma ]\}\\&\cdot \{[\beta _{V}(k)H+\phi ][\beta _{S}(k)H+\gamma ]\\&+\,\varphi _{k}[\beta _{V}(k)H+\gamma ]\}. \end{aligned}$$

The condition $R_{1}\le 1$ implies that $H=h,$ which is equivalent to $X_{k}=x_{k}$ and $Y_{k}=y_{k}$ for $k=1,\ldots ,n.$ Therefore, from (26), it follows that

$$\begin{aligned}&\lim \limits _{t\rightarrow \infty }I_{k}(t)=X_{k}=x_{k},~\\&\quad \lim \limits _{t\rightarrow \infty }V_{k}(t)=Y_{k}=y_{k},~k=1,\ldots ,n. \end{aligned}$$

In view of (4)–(7) and (27)–(32), it is found that $X_{k}=I_{k}^{*}$, $Y_{k}=V_{k}^{*}$, and $H=h=\Theta ^{*}.$ Since $S_{k}=1-I_{k}-V_{k}$ for any k, $\lim _{t\rightarrow \infty }S_{k}=1-I^{*}_{k}-V^{*}_{k}=S^{*}_{k}.$ This completes the proof.

Appendix E: Proof of Theorem 6

The existence of optimal controls is easy to be proved according to Ref. [24]. Applying Pontryagin’s maximum principle, one obtains

$$\begin{aligned} \lambda '_{k}(t)= & {} -\frac{\partial \mathcal {H}}{\partial S_{k}}=[\lambda _{k}(t)-\lambda _{k+n}(t)]\beta _{S}(k) \Theta (t)\\&+\,[\lambda _{k}(t)-\lambda _{k+2n}(t)]\varphi _{k}(t),\\ \lambda '_{k+n}(t)= & {} -\frac{\partial \mathcal {H}}{\partial I_{k}}=-D_{k}+\gamma [\lambda _{k+n}(t)-\lambda _{k}(t)]\\&+\,[\lambda _{k}(t)-\lambda _{k+n}(t)]\beta _{S} (k)S_{k}(t)\frac{kP(k)}{\langle k\rangle }\\&+\,[\lambda _{k+2n}(t)-\lambda _{k+n}(t)]\beta _{V}(k) V_{k}(t)\frac{kP(k)}{\langle k\rangle },\\ \lambda '_{k+2n}(t)= & {} -\frac{\partial \mathcal {H}}{\partial V_{k}}=\phi [\lambda _{k+2n}(t)-\lambda _{k}(t)]\\&+\,[\lambda _{k+2n}(t)-\lambda _{k+n}(t)]\beta _{V}(k)\Theta (t), \end{aligned}$$

and

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial \varphi _{k}}= & {} \varphi _{k}(t) W_{k}-\lambda _{k}(t)S_{k}(t) +\lambda _{k+2n}(t)S_{k}(t). \end{aligned}$$

Solving for $\varphi _{k}(t)$ yields

$$\begin{aligned} \varphi _{k}(t)= & {} \frac{S_{k}(t)}{W_{k}}[\lambda _{k}(t)-\lambda _{k+2n}(t)]. \end{aligned}$$

Using standard argument for bounds $0\le \varphi _{k}(t)\le 1$ for $k=1,\ldots ,n$, one gets (15).