Skip to main content
SpringerLink
Log in

Application of the Riemann–Hilbert method to the vector modified Korteweg-de Vries equation

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

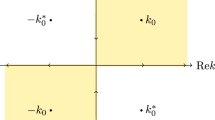
Under investigation in this paper is the inverse scattering transform of the vector modified Korteweg-de Vries (vmKdV) equation, which can be reduced to several integrable systems. For the direct scattering problem, the spectral analysis is performed for the equation, from which a Riemann–Hilbert problem is well constructed. For the inverse scattering problem, the Riemann–Hilbert problem corresponding to the reflection-less case is solved. Furthermore, as applications, three types of multi-soliton solutions are found. Finally, some figures are presented to discuss the soliton behaviors of the vmKdV equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Wazwaz, A.M., El-Tantawy, S.A.: A new integrable (3+1)-dimensional KdV-like model with its multiple-soliton solutions. Nonlinear Dyn. 83, 1529–1534 (2016)

    MathSciNet  MATH  Google Scholar 

  2. Wazwaz, A.M., El-Tantawy, S.A.: A new (3+1)-dimensional generalized Kadomtsev–Petviashvili equation. Nonlinear Dyn. 84, 1107–1112 (2016)

    MathSciNet  Google Scholar 

  3. Wazwaz, A.M.: Two new integrable fourth-order nonlinear equations: multiple soliton solutions and multiple complex soliton solutions. Nonlinear Dyn. 94, 2655–2663 (2018)

    Google Scholar 

  4. Zhang, H.Q., Ma, W.X.: Lump solutions to the (2+1)-dimensional Sawada–Kotera equation. Nonlinear Dyn. 87, 2305–2310 (2017)

    MathSciNet  Google Scholar 

  5. Guo, D., Tian, S.F., Zhang, T.T., Li, J.: Modulation instability analysis and soliton solutions of an integrable coupled nonlinear Schrödinger system. Nonlinear Dyn. 94, 2749–2761 (2018)

    Google Scholar 

  6. Xie, X.Y., Tian, B., Chai, J., Wu, X.Y., Jiang, Y.: Dark soliton collisions for a fourth-order variable-coefficient nonlinear Schrödinger equation in an inhomogeneous Heisenberg ferromagnetic spin chain or alpha helical protein. Nonlinear Dyn. 86, 131–135 (2016)

    Google Scholar 

  7. Dai, C.Q., Wang, Y., Liu, J.: Spatiotemporal Hermite-Gaussian solitons of a (3+1)-dimensional partially nonlocal nonlinear Schrödinger equation. Nonlinear Dyn. 84, 1157–1161 (2016)

    MATH  Google Scholar 

  8. Liu, Y., Li, B., An, H.L.: General high-order breathers, lumps in the (2+1)-dimensional Boussinesq equation. Nonlinear Dyn. 92, 2061–2076 (2018)

    Google Scholar 

  9. Lan, Z.Z., Su, J.J.: Solitary and rogue waves with controllable backgrounds for the non-autonomous generalized AB system. Nonlinear Dyn. 96, 2535–2546 (2019)

    Google Scholar 

  10. Yang, B., Chen, Y.: Dynamics of high-order solitons in the nonlocal nonlinear Schrödinger equations. Nonlinear Dyn. 94, 489–502 (2018)

    MATH  Google Scholar 

  11. Zhao, Z., Han, B.: The Riemann–Bäcklund method to a quasiperiodic wave solvable generalized variable coefficient (2+1)-dimensional KdV equation. Nonlinear Dyn. 87, 2661–2676 (2017)

    MATH  Google Scholar 

  12. Zhao, Z., Han, B.: Residual symmetry, Bäcklund transformation and CRE solvability of a (2+1)-dimensional nonlinear system. Nonlinear Dyn. 94, 461–474 (2018)

    MATH  Google Scholar 

  13. Wazwaz, A.M., Kaur, L.: Optical solitons for nonlinear Schrödinger (NLS) equation in normal dispersive regimes. Optik 184, 428–435 (2019)

    Google Scholar 

  14. Kaur, L., Wazwaz, A.M.: Lump, breather and solitary wave solutions to new reduced form of the generalized BKP equation. Int. J. Numer. Meth. Heat Fluid Flow 29(2), 569–579 (2019)

    Google Scholar 

  15. Kaur, L., Wazwaz, A.M.: Bright-dark optical solitons for Schrödinger-Hirota equation with variable coefficients. Optik 179, 479–484 (2019)

    Google Scholar 

  16. Wazwaz, A.M., Kaur, L.: Complex simplified Hirota’s forms and Lie symmetry analysis for multiple real and complex soliton solutions of the modified KdV-Sine-Gordon equation. Nonlinear Dyn. 95(3), 2209–221 (2019)

    Google Scholar 

  17. Wang, X.B., Han, B.: The three-component coupled nonlinear Schrödinger equation: Rogue waves on a multi-soliton background and dynamics. Europhys. Lett. 126, 15001 (2019)

    Google Scholar 

  18. Wang, X.B., Han, B.: Novel rogue waves and dynamics in the integrable pair-transition-coupled nonlinear Schrödinger equation. Appl. Math. Lett. 99, 105987 (2020)

    MathSciNet  MATH  Google Scholar 

  19. Peng, W.Q., Tian, S.F., Zou, L., Zhang, T.T.: Characteristics of the solitary waves and lump waves with interaction phenomena in a (2+1)-dimensional generalized Caudrey–Dodd–Gibbon–Kotera–Sawada equation. Nonlinear Dyn. 93, 1841–1851 (2018)

    MATH  Google Scholar 

  20. Ablowitz, M.J., Segur, H.: Solitons and the Inverse Scattering Transform. SIAM, Philadelphia (1981)

    MATH  Google Scholar 

  21. Zakharov, V.E., Manakov, S.V., Novikov, S.P., Pitaevskii, L.P.: The Theory of Solitons: The Inverse Scattering Method. Consultants Bureau, New York (1984)

    MATH  Google Scholar 

  22. Yang, J.K.: Nonlinear Waves in Integrable and Nonintegrable Systems. SIAM, Philadelphia (2010)

    MATH  Google Scholar 

  23. Wang, D.S., Zhang, D.J., Yang, J.: Integrable properties of the general coupled nonlinear Schrodinger equations. J. Math. Phys. 51, 023510 (2010)

    MathSciNet  MATH  Google Scholar 

  24. Wang, D.S., Yin, S., Tian, Y., Liu, Y.: Integrability and bright soliton solutions to the coupled nonlinear Schrödinger equation with higher-order effects. Appl. Math. Comput. 229, 296–309 (2014)

    MathSciNet  MATH  Google Scholar 

  25. Ma, W.X.: Riemann-Hilbert problems and \(N\)-soliton solutions for a coupled mKdV system. J. Geom. Phys. 132, 45–54 (2018)

    MathSciNet  MATH  Google Scholar 

  26. Ma, W.X.: Application of the Riemann–Hilbert approach to the multicomponent AKNS integrable hierarchies. Nonlinear Anal. RWA. 47, 1–17 (2018)

    MathSciNet  MATH  Google Scholar 

  27. Ma, W.X.: Riemann–Hilbert problems of a six-component mKdV system and its soliton solutions act. Math. Sci. 39, 509–523 (2019)

    Google Scholar 

  28. Wang, X.B., Han, B.: Riemann-Hilbert problem and multi-soliton solutions of the integrable spin-1 gross-Pitaevskii equations. Z. Naturforsch. A 74(2), 139–145 (2019)

    Google Scholar 

  29. Wang, X.B., Han, B.: The pair-transition-coupled nonlinear Schrödinger equation: The Riemann–Hilbert problem and N-soliton solutions. Eur. Phys. J. Plus 134, 78 (2019)

    Google Scholar 

  30. Kaup, D., Yang, J.: The inverse scattering transform and squared eigenfunctions for a degenerate \(3\times 3\) operator. Inverse Probl. 25, 105010–105021 (2009)

    MATH  Google Scholar 

  31. Guo, B., Ling, L.: Riemann-Hilbert approach and \(N\)-soliton formula for coupled derivative Schrödinger equation. J. Math. Phys. 53, 133–3966 (2012)

    MATH  Google Scholar 

  32. Zhang, Y.S., Cheng, Y., He, J.S.: Riemann–Hilbert method and \(N\)-soliton for two-component Gerdjikov–Ivanov equation. J. Nonlinear Math. Phys. 24(2), 210–223 (2017)

    MathSciNet  MATH  Google Scholar 

  33. Geng, X.G., Wu, J.P.: Riemann–Hilbert approach and N-soliton solutions for a generalized Sasa–Satsuma equation. Wave Motion 60, 62–72 (2016)

    MathSciNet  MATH  Google Scholar 

  34. Tian, S.F.: Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method. J. Differ. Equ. 262, 506–558 (2017)

    MATH  Google Scholar 

  35. Tian, S.F.: Initial-boundary value problems of the coupled modified Korteweg-de Vries equation on the half-line via the Fokas method. J. Phys. A: Math. Theor. 50, 395204 (2017)

    MathSciNet  MATH  Google Scholar 

  36. Tian, S.F.: The mixed coupled nonlinear Schrödinger equation on the half-line via the Fokas method. Proc. R. Soc. Lond. A 472, 20160588 (2016)

    MATH  Google Scholar 

  37. Fokas, A.S., Lenells, J.: The unified method: I Nonlinearizable problems on the half-line. J. Phys. A 45, 195201 (2012)

    MathSciNet  MATH  Google Scholar 

  38. Tian, S.F., Zhang, T.T.: Long-time asymptotic behavior for the Gerdjikov–Ivanov type of derivative nonlinear Schrödinger equation with time-periodic boundary condition. Proc. Am. Math. Soc. 146, 1713–1729 (2018)

    MATH  Google Scholar 

  39. Wang, D.S., Wang, X.L.: Long-time asymptotics and the bright N-soliton solutions of the Kundu–Eckhaus equation via the Riemann–Hilbert approach. Nonlinear Anal. RWA 41, 334–361 (2018)

    MathSciNet  MATH  Google Scholar 

  40. Xu, J., Fan, E.G.: The unified transform method for the Sasa–Satsuma equation on the half-line. Proc. R. Soc. A 469, 20130068 (2013)

    MathSciNet  MATH  Google Scholar 

  41. Xu, J., Fan, E.G.: Long-time asymptotics for the Fokas–Lenells equation with decaying initial value problem: without solitons. J. Differ. Equ. 259, 1098–1148 (2015)

    MathSciNet  MATH  Google Scholar 

  42. Lenells, J.: Initial-boundary value problems for integrable evolution equations with \(3 \times 3\) Lax pairs. Phys. D 241, 857–875 (2012)

    MathSciNet  MATH  Google Scholar 

  43. Liu, H., Geng, X.G.: Initial-boundary problems for the vector modified Korteweg-de Vries equation via Fokas unified transform method. J. Math. Anal. Appl. 440, 578–596 (2016)

    MathSciNet  MATH  Google Scholar 

  44. Matveev, V.B., Salle, M.A.: Darboux Transformation and Solitons. Springer, Berlin (1991)

    MATH  Google Scholar 

  45. Hirota, R.: Direct Methods in Soliton Theory. Springer, Berlin (2004)

    MATH  Google Scholar 

  46. Wazwaz, A.M., El-Tantawy, S.A.: Solving the (3+1)-dimensional KP-Boussinesq and BKP-Boussinesq equations by the simplified Hirota’s method. Nonlinear Dyn. 88, 3017–3021 (2017)

    MathSciNet  Google Scholar 

  47. Lenells, L.: Dressing for a novel integrable generalization of the nonlinear Schrödinger equation. J. Nonliner Sci. 20, 709–722 (2010)

    MathSciNet  MATH  Google Scholar 

  48. Zhang, H.Q., Tian, B., Xu, T., Li, H., Zhang, C., Zhang, H.: Lax pair and Darboux transformation for multi-component modified Korteweg-de Vries equations. J. Phys. A: Math. Theor. 41, 355210 (2008)

    MathSciNet  MATH  Google Scholar 

  49. Hirota, R.: Exact solution of the modified korteweg-de vries equation for multiple collisions of solitons. J. Phys. Soc. Jpn. 33, 1456–1458 (1972)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China

    Xiu-Bin Wang & Bo Han

Authors
  1. Xiu-Bin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Han
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiu-Bin Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work is supported by the National Natural Science Foundation of China (NNSFC) under Grant No. 11871180.

Appendices

Appendix A

The \({\mathcal {N}}_{1}\)-soliton solution for the vmKdV equation (1) yields

$$\begin{aligned} \left\{ \begin{aligned}&q_{1}=2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha ^{(1)}_{k}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=1}^{2{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha ^{(1)}_{k}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha ^{(1)*}_{k-{\mathcal {N}}_{1}}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha ^{(1)*}_{k-{\mathcal {N}}_{1}}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj},\\&q_{2}=2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha ^{(2)}_{k}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha ^{(2)}_{k}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha ^{(2)*}_{k-{\mathcal {N}}_{1}}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha ^{(2)*}_{k-{\mathcal {N}}_{1}}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj},\\&\vdots \\&q_{n}=2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha ^{(n)}_{k}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha ^{(n)}_{k}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha ^{(n)*}_{k-{\mathcal {N}}_{1}}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha ^{(n)*}_{k-{\mathcal {N}}_{1}}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}, \end{aligned} \right. \end{aligned}$$
(62)

in which \(M=(m_{kj})_{2{\mathcal {N}}_{1}\times 2{\mathcal {N}}_{1}}\) with

$$\begin{aligned} m_{kj}=\left\{ \begin{aligned}&\frac{\left( \alpha ^{(1)*}_{k}\alpha ^{(1)}_{j}+\alpha ^{(2)*}_{k}\alpha ^{(2)}_{j}+\ldots +\alpha ^{(n)*}_{k}\alpha ^{(n)}_{j}\right) e^{\varTheta _{k}^{*}+\varTheta _{j}}+e^{-\varTheta _{k}^{*}-\varTheta _{j}}}{\lambda _{j}-\lambda _{k}^{*}},~~1\le k,j\le {\mathcal {N}}_{1};\\&\frac{\left( \alpha ^{(1)*}_{k}\alpha ^{(1)*}_{j-{\mathcal {N}}_{1}}+\alpha ^{(2)*}_{k}\alpha ^{(2)*}_{j-{\mathcal {N}}_{1}} +\ldots +\alpha ^{(n)*}_{k}\alpha ^{(n)*}_{j-{\mathcal {N}}_{1}}\right) e^{\varTheta _{k}^{*}+\varTheta _{j-{\mathcal {N}}_{1}}^{*}}+e^{-\varTheta _{k}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}^{*}}}{-\lambda _{j-{\mathcal {N}}_{1}}^{*}-\lambda _{k}^{*}},\\&~~1\le k\le {\mathcal {N}}_{1},~{\mathcal {N}}_{1}+1\le j\le 2{\mathcal {N}}_{1};\\&\frac{\left( \alpha ^{(1)}_{k-{\mathcal {N}}_{1}}\alpha ^{(1)}_{j}+\alpha ^{(2)}_{k-{\mathcal {N}}_{1}}\alpha ^{(2)}_{j} +\ldots +\alpha ^{(n)}_{k-{\mathcal {N}}_{1}}\alpha ^{(n)}_{j}\right) e^{\varTheta _{k-{\mathcal {N}}_{1}}+\varTheta _{j}}+e^{-\varTheta _{k-{\mathcal {N}}_{1}}-\varTheta _{j}}}{\lambda _{j}+\lambda _{k-{\mathcal {N}}_{1}}},\\&~~{\mathcal {N}}_{1}+1\le k\le 2{\mathcal {N}}_{1},~1\le j\le {\mathcal {N}}_{1};\\&\frac{\left( \alpha ^{(1)}_{k-{\mathcal {N}}_{1}}\alpha ^{(1)*}_{j-{\mathcal {N}}_{1}}+\alpha ^{(2)}_{k-{\mathcal {N}}_{1}}\alpha ^{(2)*}_{j-{\mathcal {N}}_{1}}+\ldots +\alpha ^{(n)}_{k-{\mathcal {N}}_{1}} \alpha ^{(n)*}_{j-{\mathcal {N}}_{1}}\right) e^{\varTheta _{k-{\mathcal {N}}_{1}}+\varTheta _{j-{\mathcal {N}}_{1}}^{*}}+e^{-\varTheta _{k-{\mathcal {N}}_{1}}-\varTheta _{j-{\mathcal {N}}_{1}}^{*}}}{\lambda _{j-{\mathcal {N}}_{1}}^{*}-\lambda _{k-{\mathcal {N}}_{1}}}.\\&~~{\mathcal {N}}_{1}+1\le k,j\le 2{\mathcal {N}}_{1}. \end{aligned} \right. \end{aligned}$$
(63)

Appendix B

Then an \({\mathcal {N}}_{2}\)-soliton solution for the vmKdV equation (1) reads

$$\begin{aligned} \left\{ \begin{aligned}&q_{1}=2i\sum _{k=1}^{{\mathcal {N}}_{2}}\sum _{j=1}^{{\mathcal {N}}_{2}}\alpha ^{(1)}_{k}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj},\\&q_{2}=2i\sum _{k=1}^{{\mathcal {N}}_{2}}\sum _{j=1}^{{\mathcal {N}}_{2}}\alpha ^{(2)}_{k}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj},\\&\vdots \\&q_{n}=2i\sum _{k=1}^{{\mathcal {N}}_{2}}\sum _{j=1}^{{\mathcal {N}}_{2}}\alpha ^{(n)}_{k}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj}, \end{aligned} \right. \end{aligned}$$
(64)

in which \(M=(m_{kj})_{{\mathcal {N}}_{2}\times {\mathcal {N}}_{2}}\) is defined by

$$\begin{aligned} m_{kj}=\frac{\left( \alpha ^{(1)}_{k}\alpha ^{(1)}_{j}{+}\alpha ^{(2)}_{k} \alpha ^{(2)}_{j}{+}\ldots {+}\alpha ^{(n)}_{k}\alpha ^{(n)}_{j}\right) e^{ \varTheta _{k}{+}\varTheta _{j}} {+}e^{{-}\varTheta _{k}{-}\varTheta _{j}}}{\lambda _{j}{-}\lambda _{k}^{*}}. \end{aligned}$$
(65)

Appendix C

The \(({\mathcal {N}}_{1}+{\mathcal {N}}_{2})\)-soliton solution for the vmKdV equation (1) arrives at

$$\begin{aligned} \left\{ \begin{aligned}&q_{1}=2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k}^{(1)}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k}^{(1)}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k-{\mathcal {N}}_{1}}^{(1)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k-{\mathcal {N}}_{1}}^{(1)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\alpha _{k}^{(1)}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\alpha _{k-{\mathcal {N}}_{1}}^{(1)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k}^{(1)}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k}^{(1)}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=2{\mathcal {N}}_{1}+11}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\alpha _{k}^{(1)}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj},\\&q_{2}=2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k}^{(2)}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k}^{(2)}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k-{\mathcal {N}}_{1}}^{(2)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k-N_{2}}^{(1)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+N_{2}}\alpha _{k}^{(2)}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}+1}^{2{\mathcal {N}}_{1}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\alpha _{k-{\mathcal {N}}_{1}}^{(2)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k}^{(2)}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k}^{(2)}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\alpha _{k}^{(2)}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj},\\&\vdots \\&q_{n}=2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k}^{(n)}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k}^{(n)}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k-{\mathcal {N}}_{1}}^{(n)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k-{\mathcal {N}}_{1}}^{(1)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=1}^{{\mathcal {N}}_{1}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+N_{2}}\alpha _{k}^{(n)}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj} +2i\sum _{k={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\alpha _{k-{\mathcal {N}}_{1}}^{(n)*}e^{\varTheta _{k-{\mathcal {N}}_{1}}^{*}-\varTheta _{j}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j=1}^{{\mathcal {N}}_{1}}\alpha _{k}^{(n)}e^{\varTheta _{k}-\varTheta _{j}^{*}}\left( M^{-1}\right) _{kj} +2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j={\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}}\alpha _{k}^{(n)}e^{\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}}\left( M^{-1}\right) _{kj}\\&+2i\sum _{k=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\sum _{j=2{\mathcal {N}}_{1}+1}^{2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}}\alpha _{k}^{(n)}e^{\varTheta _{k}-\varTheta _{j}}\left( M^{-1}\right) _{kj}, \end{aligned} \right. \end{aligned}$$
(66)

where \(M=(m_{kj})_{(2{\mathcal {N}}_{1}+{\mathcal {N}}_{2})\times (2{\mathcal {N}}_{1}+{\mathcal {N}}_{2})}\) is given by

$$\begin{aligned} m_{kj}=\left\{ \begin{aligned}&\frac{\left( \alpha ^{(1)*}_{k}\alpha ^{(1)}_{j}+\alpha ^{(2)*}_{k}\alpha ^{(2)}_{j}+\ldots +\alpha ^{(n)*}_{k}\alpha ^{(n)}_{j}\right) e^{\varTheta _{k}^{*}+\varTheta _{j}}+e^{-\varTheta _{k}^{*}-\varTheta _{j}}}{\lambda _{j}-\lambda _{k}^{*}},~~1\le k,j\le {\mathcal {N}}_{1};\\&\frac{\left( \alpha ^{(1)*}_{k}\alpha ^{(1)*}_{j-{\mathcal {N}}_{1}}+\alpha ^{(2)*}_{k}\alpha ^{(2)*}_{j-{\mathcal {N}}_{1}} +\ldots +\alpha ^{(n)*}_{k}\alpha ^{(n)*}_{j-{\mathcal {N}}_{1}}\right) e^{\varTheta _{k}^{*}+\varTheta _{j-{\mathcal {N}}_{1}}^{*}}+e^{-\varTheta _{k}^{*}-\varTheta _{j-{\mathcal {N}}_{1}}^{*}}}{-\lambda _{j-{\mathcal {N}}_{1}}^{*}-\lambda _{k}^{*}},\\&~~1\le k\le {\mathcal {N}}_{1},~{\mathcal {N}}_{1}+1\le j\le 2{\mathcal {N}}_{1};\\&\frac{\left( \alpha ^{(1)}_{k-{\mathcal {N}}_{1}}\alpha ^{(1)}_{j}+\alpha ^{(2)}_{k-{\mathcal {N}}_{1}}\alpha ^{(2)}_{j} +\ldots +\alpha ^{(n)}_{k-{\mathcal {N}}_{1}}\alpha ^{(n)}_{j}\right) e^{\varTheta _{k-{\mathcal {N}}_{1}}+\varTheta _{j}}+e^{-\varTheta _{k-{\mathcal {N}}_{1}}-\varTheta _{j}}}{\lambda _{j}+\lambda _{k-{\mathcal {N}}_{1}}},\\&~~{\mathcal {N}}_{1}+1\le k\le 2{\mathcal {N}}_{1},~1\le j\le {\mathcal {N}}_{1};\\&\frac{\left( \alpha ^{(1)}_{k-{\mathcal {N}}_{1}}\alpha ^{(1)*}_{j-{\mathcal {N}}_{1}}+\alpha ^{(2)}_{k-{\mathcal {N}}_{1}}\alpha ^{(2)*}_{j-{\mathcal {N}}_{1}}+\ldots +\alpha ^{(n)}_{k-{\mathcal {N}}_{1}} \alpha ^{(n)*}_{j-{\mathcal {N}}_{1}}\right) e^{\varTheta _{k-{\mathcal {N}}_{1}}+\varTheta _{j-{\mathcal {N}}_{1}}^{*}}+e^{-\varTheta _{k-{\mathcal {N}}_{1}}-\varTheta _{j-{\mathcal {N}}_{1}}^{*}}}{\lambda _{j-{\mathcal {N}}_{1}}^{*}-\lambda _{k-{\mathcal {N}}_{1}}},\\&~~{\mathcal {N}}_{1}+1\le k,j\le 2{\mathcal {N}}_{1};\\&\frac{\left( \alpha _{k-{\mathcal {N}}_{1}}^{(1)}\alpha _{j}^{(1)}+\alpha _{k-{\mathcal {N}}_{1}^{(2)}}\alpha _{j}^{(2)}+\ldots +\alpha _{k-{\mathcal {N}}_{1}}^{(n)}\alpha _{j}^{(n)}\right) e^{\varTheta _{k-{\mathcal {N}}_{1}}+\varTheta _{j}} +e^{-\varTheta _{k-{\mathcal {N}}_{1}}-\varTheta _{j}}}{\lambda _{j}+\lambda _{k-{\mathcal {N}}_{1}}},\\&~~{\mathcal {N}}_{1}+1\le k\le 2{\mathcal {N}}_{1},~2{\mathcal {N}}_{1}+1\le j\le 2{\mathcal {N}}_{1}+{\mathcal {N}}_{2};\\&\frac{\left( \alpha _{k}^{(1)}\alpha _{j}^{(1)}+\alpha _{k}^{(2)}\alpha _{j}^{(2)}+\ldots +\alpha _{k}^{(n)}\alpha _{j}^{(n)}\right) e^{\varTheta _{k}+\varTheta _{j}} +e^{-\varTheta _{k}-\varTheta _{j}}}{\lambda _{j}-\lambda _{k}^{*}},\\&~~2{\mathcal {N}}_{1}+1\le k\le 2{\mathcal {N}}_{1}+{\mathcal {N}}_{2},~1\le j\le {\mathcal {N}}_{1};\\&\frac{\left( \alpha _{k}^{(1)}\alpha _{j-{\mathcal {N}}_{1}}^{(1)*}+\alpha _{k}^{(2)}\alpha _{j-{\mathcal {N}}_{1}}^{(2)*}+\ldots +\alpha _{k}^{(n)}\alpha _{j-{\mathcal {N}}_{1}}^{(n)*}\right) e^{\varTheta _{k}+\varTheta _{j-{\mathcal {N}}_{1}}^{*}}+e^{-\varTheta _{k}-\varTheta _{j-{\mathcal {N}}_{1}}^{*}}}{-\lambda _{j-{\mathcal {N}}_{1}}^{*}-\lambda _{k}^{*}},\\&~~2{\mathcal {N}}_{1}+1\le k\le 2{\mathcal {N}}_{1}+N_{2},~~{\mathcal {N}}_{1}+1\le j\le 2{\mathcal {N}}_{1};\\&\frac{\left( \alpha _{k}^{(1)}\alpha _{j}^{(1)}+\alpha _{k}^{(2)}\alpha _{j}^{(2)}+\ldots +\alpha _{k}^{(n)}\alpha _{j}^{(n)}\right) e^{\varTheta _{j}+\varTheta _{k}} +e^{-\varTheta _{j}-\varTheta _{k}}}{\lambda _{j}-\lambda _{k}^{*}},\\&~~2{\mathcal {N}}_{1}+1\le k,j\le 2{\mathcal {N}}_{1}+{\mathcal {N}}_{2}. \end{aligned} \right. \end{aligned}$$
(67)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, XB., Han, B. Application of the Riemann–Hilbert method to the vector modified Korteweg-de Vries equation. Nonlinear Dyn 99, 1363–1377 (2020). https://doi.org/10.1007/s11071-019-05359-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05359-x

Keywords

Search

Navigation