Abstract
This paper reveals some new and rich dynamics of a two-dimensional prey–predator system and to anticontrol the extinction of one of the species. For a particular value of the bifurcation parameter, one of the system variable dynamics is going to extinct, while another remains chaotic. To prevent the extinction, a simple anticontrol algorithm is applied so that the system or bits can escape from the vanishing trap. As the bifurcation parameter increases, the system presents quasiperiodic, stable, chaotic and also hyperchaotic orbits. Some of the chaotic attractors are Kaplan–Yorke type, in the sense that the sum of its Lyapunov exponents is positive. Also, atypically for undriven discrete systems, it is numerically found that, for some small parameter ranges, the system seemingly presents strange nonchaotic attractors. It is shown both analytically and by numerical simulations that the original system and the anticontrolled system undergo several Neimark–Sacker bifurcations. Beside the classical numerical tools for analyzing chaotic systems, such as phase portraits, time series and power spectral density, the ‘0–1’ test is used to differentiate regular attractors from chaotic attractors.


















Similar content being viewed by others
Notes
The formula for the first Lyapunov coefficient (genericity condition), which indicates the type of N–S bifurcation, is not considered here.
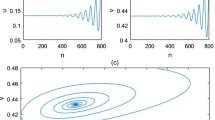
It is known that a physical mark of the N–S bifurcation is the apparition of a new additional frequency in the time series.
For simplicity, the proof is not presented here.
Anticontrol, or chaoticization, represents a concept that one can make a given system chaotic or enhance the existing chaos of a chaotic system (see, e.g., [17]).
“We conjecture that, in general, continuous-time systems (“flows”) which are not externally driven at two incommensurate frequencies should not be expected to have SNAs except possibly on a set of measure zero in the parameter space.”
References
Liu, X., Xiao, D.: Complex dynamic behaviors of a discrete-time predator–prey system. Chaos Solitons Fractals 32(1), 80–94 (2007)
Debaldev, J.: Chaotic dynamics of a discrete predator–prey system with prey refuge. Appl. Math. Comput. 224(1), 848–865 (2013)
Zhang, H., Cong, X., Huang, T., Ma, S., Pan, G.: Neimark–Sacker–Turing instability and pattern formation in a spatiotemporal discrete predator–prey system with Allee effect. Discrete Dyn. Nat. Soc. 8713651, 1–17 (2018)
Fan, M., Wang, K.: Periodic solutions of a discrete time non-autonomous ratio-dependent predator–prey system. Math. Comput. Model. 35(–10), 951–61 (2002)
Agiza, H.N., ELabbasy, E.M., EL-Metwally, H., Elsadany, A.A.: Chaotic dynamics of a discrete prey–predator model with Holling type II. Nonlinear Anal. Real 10(1), 116–129 (2009)
Huo, H.F., Li, W.T.: Stable periodic solution of the discrete periodic Leslie–Gower predator–prey model. Math. Comput. Model. 40(3–4), 261–9 (2004)
Danca, M.-F., Codreanu, S., Bako, B.: Detailed analysis of a nonlinear prey–predator model. J. Biol. Phys. 23(1), 11–20 (1997)
Maynard, S.J.: Mathematical Ideas in Biology. Cambridge University Press, London (1968)
Ghaziani, R.K., Govaerts, W., Sonck, C.: Resonance and bifurcation in a discrete-time predator–prey system with Holling functional response. Nonlinear Anal. Real 13(3), 1451–1465 (2012)
He, Z., Lai, X.: Bifurcation and chaotic behavior of a discrete-time predator–prey system. Nonlinear Anal. Real 12(1), 403–417 (2011)
Khan, A.Q.: Neimark–Sacker bifurcation of a two-dimensional discrete-time predator–prey model. SpringerPlus 5, 126 (2016)
Grebogi, C., Ott, E., Pelikan, S., Yorke, J.: Strange attractors that are not chaotic. Phys. D 13(1–2), 261 (1984)
Argyris, J., Faust, G., Haase, M.: Die Erforschung des Chaos. Vieweg Verlag, Braunschweig (1994)
Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)
Grebogi, C., Ott, E., Yorke, J.A.: Crises, sudden changes in chaotic attractors and transient chaos. Phys. D 7(1–3), 181–200 (1983)
Kapitaniak, T., Wojewoda, J.: Chaos in a limit-cycle system with almost periodic excitation. Phys. A Math. Gen. 21, L843–L847 (1988)
Chen, G., Lai, D.: Feedback control of Lyapunov exponents for discrete-time dynamical systems. Int. J. Bifurc. Chaos 6, 1341–1349 (1996)
Matìas, M.A., Güémez, J.: Stabilization of chaos by proportional pulses in system variables. Phys. Rev. Lett. 72, 1455–1458 (1994)
Güémez, J., Matìas, M.A.: Control of chaos in unidimensional maps. Phys. Lett. A 181, 29–32 (1993)
Yang, W., Ding, M., Mandell, A.J., Ott, E.: Preserving chaos: control strategies to preserve complex dynamics with potential relevance to biological disorders. Phys. Rev. E 51, 102–110 (1995)
Loyd, A.: The coupled logistic map: a simple model for the effects of spatial heterogeneity on population dynamics. J. Theor. Biol. 173(3), 106–129 (1995)
Prasad, A., Negi, S.S., Ramaswamy, R.: Strange nonchaotic attractors. Int. J. Bifurc. Chaos 11(02), 291–309 (2001)
Venkatesan, A., Lakshmanan, M.: Different routes to chaos via strange nonchaotic attractors in a quasiperiodically forced system. Phys. Rev. E 58, 3008 (1998)
Sherratt, J.A.: How does nonlocal dispersal affect the selection and stability of periodic traveling waves? SIAM J. Appl. Math. 78(6), 3087–3102 (2018)
Brandt, M.J., Lambin, X.: Movement patterns of a specialist predator, the weasel Mustela nivalis exploiting asynchronous cyclic field vole Microtus agrestis populations. Acta Theriol. 52, 13–25 (2007)
Wieters, E.A., Gaines, S.D., Navarrete, S.A., Blanchette, C.A., Menge, B.A.: Scales of dispersal and the biogeography of marine predator–prey interactions. Am. Nat. 171, 405–417 (2008)
Malchow, H.: Motional instabilities in prey–predator systems. J. Theor. Biol. 204(4), 639–647 (2000)
Sun, G.-Q., Wu, Z.-Y., Wang, Z., Jin, Z.: Influence of isolation degree of spatial patterns on persistence of populations. Nonlinear Dyn. 83(1–2), 811–819 (2016)
Gottwald, G.A., Melbourne, I.: A new test for chaos in deterministic systems. Proc. R. Soc. London. Ser. A 460, 603 (2004)
Nicol, M., Melbourne, I., Ashwin, P.: Euclidean extensions of dynamical systems. Nonlinearity 14(2), 275 (2001)
Gopal, R., Venkatesan, A., Lakshmanan, M.: Applicability of 0–1 test for strange nonchaotic attractors. Chaos 23, 023123 (2013)
Acknowledgements
This study was partially funded by Russian Science Foundation Project 19-41-02002.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
A. Stability of \(X_{1,23}^*\)
Denote by e the eigenvalues. As is well known, a fixed point \(X^*\) of a discrete system is stable if and only if its eigenvalues, e, satisfy the condition of \(|e|<1\).
(i) For \(X_1^*\), eigenvalues are \(e_1=0\) and \(e_2(a)=a\). Therefore, \(X_1^*\) is stable for \(a<1\).
(ii) For \(X_2^*\), eigenvalues are \(e_1(a)=2-a\) and \(e_2(a,d)=(a-1)d/a\). Therefore, for \(a\in (1,3)\) and \(d<a/(a-1)\), the fixed point \(X_2^*\) is stable.
(iii) For \(X_3^*\) with \(a>1\), the graphs considered next are obtained by representing d as a function of a: \(d=d(a)\) (Fig. 1b). Denote \(\Delta (a,d)=(a/d+2)^2-4a\) (see the graph \(\textcircled {4}\) in Fig. 1b). If \(\Delta (a,b)\ge 0\) (regions \(\textcircled {3}\), \(\textcircled {5}\) and \(\textcircled {8}\), including the blue region), the eigenvalues are real: \(e_{1,2}^r(a,d)=\Big (1-\frac{a}{2d}\Big )\pm \frac{1}{2}\sqrt{\Delta (a,d)}\). If \(\Delta (a,d)< 0\) (regions \(\textcircled {2}\), \(\textcircled {1}\) and \(\textcircled {6}\)), the eigenvalues \(e_{1,2}^c\) are complex conjugated, \(e_1^c=\overline{e_2^c}\): \(e_{1,2}^c(a,d)=\Big (1-\frac{a}{2d}\Big )\pm \imath \frac{1}{2}\sqrt{-\Delta (a,d)}\). Modulus of the complex (and also of the real) eigenvalue is
Finally, after some simple calculations, omitted here, the stability parametric domain is found (regions \(\textcircled {2}\), \(\textcircled {3}\) and \(\textcircled {4}\), with boarders \(\textcircled {1}\) and \(\textcircled {5}\), respectively):
In the remaining regions, \(\textcircled {6}\) and \(\textcircled {8}\), fixed points are unstable.
B. Proof of Theorem 1
(i) The bifurcation condition, \(|e_{1,2}^c(a,d)|=1\), i.e., \(A(a,d)=1\) [see (A.1)], leads to \(d-2a/(a-1)=0\);
(ii) The derivative of \(e_{1,2}^c\) with respect to d, determined along AB, is
(iii) On the curve AB, the equation \((e_{1,2}^c(a,d))^j=1\), for \(d=2a/(a-1)\), has the following solutions: for \(j=1\), \(a=1\); for \(j=2\), \(a\in \{1,9\}\); for \(j=3\), \(a\in \{1,7\}\), and for \(j=4\), \(a\in \{1,5,9\}\). Therefore, on the considered domain \(a\in (1,4]\) and \(d=2a/(a-1)\) (see Fig. 1a), the condition (iii) is satisfied.
C. Neimark–Sacker (\(\hbox {N}-\hbox {S}\)) bifurcation of the anticontrolled system
(i) \(A(\gamma )=1\) if and only if
The graph of \(\gamma \) in the space \((a,d,\gamma )\), \({\mathcal {S}}\), is the N–S surface (Fig. 1d).
Note that the intersection with the plane \(\gamma =0\) (Fig. 1d) represents the N–S curve for the uncontrolled system (1), at the fixed point \(X_3^*\).
(ii) Next, one has
(iii) To ensure \(\gamma \in (0,1)\), suppose \(d>2a/(a-1)\). For \(a\in (1,9)\), the eigenvalues \(e_{1,2}^c(\gamma )\) are: \(e_{1,2}^c(\gamma )=\frac{5-a}{4}\pm \imath \frac{1}{4}\sqrt{(9-a)(a-1)}\). Note that the image of the fixed point \(e_{1}^c(\gamma )=\frac{5-a}{4}+\imath \frac{1}{4} \sqrt{(9-a)(a-1)}\) is in the half upper complex-plane, hence [compare with (3)]
Since \(\arccos \frac{5-a}{4}\) is increasing from 0 to \(\pi \) for \(a\in (1,9)\), the equation \((e_{1,2}(\gamma ))^{j}=1\) has only the following solutions: \(j=3\), \(a=7\), \(j=4\), \(a=5\).
D. The ‘0–1’ test
The ‘0–1’ test, proposed in [29], is designed to distinguish chaotic behavior from regular behavior in deterministic systems. Consider a discrete or continuous-time dynamical system and a one-dimensional observable data set \(\phi (j)\), \(j=1,2,\ldots ,N\), of the underlying system, constructed from time series. The 0–1 test has a theorem [30], which states that a nonchaotic motion is bounded, while a chaotic dynamic behaves like a Brownian motion.
(1) First, compute the translation variables (for some \(c\in (0,\pi )\), [29])
for \(n=1,2,\ldots ,N\).
(2) To determine the growths of p and q, the mean-square displacement is determined:
where \(n\ll N\) (in practice, \(n=N/10\) gives good results).
(3) The asymptotic growth rate is defined as
Because of occurrence of resonances for isolated values of c (where K is larger), the median of the computed values of K is used, since the median is robust against outliers associated with resonances [29]. If the underlying dynamics is regular (i.e., periodic or quasiperiodic), then \(K = 0\); if the underlying dynamics is chaotic, then \(K = 1\). Improved variants can be found in [29, 31].
In Fig. 18, the GOPY model are presented. Figure 18a represents the plot of q versus p and in Fig. 18b the mean-square displacement M as a function of n. Figure 18(i) represents the regular orbit of the logistic map \(x_{n+1}=rx_n(1-x_n)\) for \(r=3.55\); Fig. 18(ii) presents the chaotic orbit of the logistic map for \(r=4\), while Fig. 18(iii) the SNA of the GOPY map \(x_{n+1}=2a\tanh (x_n)\cos (2\pi \theta _n)\), \(\theta _{n+1}=\theta _n+\omega \), with \(a=1.5\), and \(\omega =(\sqrt{5}-1)/2\) [12].
Rights and permissions
About this article
Cite this article
Danca, MF., Fečkan, M., Kuznetsov, N. et al. Rich dynamics and anticontrol of extinction in a prey–predator system. Nonlinear Dyn 98, 1421–1445 (2019). https://doi.org/10.1007/s11071-019-05272-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-019-05272-3