1 Introduction

In the present study, we analyse the oscillation of towed wheels. This phenomenon, often referred to as wheel-shimmy, is one of the most common stability problems in vehicle dynamics [5, 11]. The oscillation of the rolling/sliding wheels can occur in various vehicle systems, such as motorcycles [13], trailers [20], cars, aircraft landing gears [17, 18, 21] or even baby strollers and shopping trolleys. In the past, large effort was made to understand and to avoid these oscillations, since they can be the source of accidents, reduced driving comfort, higher tyre wear and fuel consumption.

As several former studies showed, these oscillations have very rich dynamics and the associated vibrations are essentially nonlinear [17, 18]. In experiments, so-called bistable parameters were identified [1] where although the rectilinear motion is stable, it has a finite domain of attraction. This means that depending on the initial conditions, the system can converge either to the straight-line motion or to a large-amplitude periodic solution (shimmy) at the same towing speed. This behaviour can be explained by a subcritical Hopf bifurcation [8] of the rectilinear motion at the critical towing speed, corresponding to the linear stability boundary. Using the simplest, one-degree-of-freedom model of a towed wheel, the standard quasi-steady-state tyre models do not provide such parameter domains. In the meantime, the existence of bistable parameter regions can be shown if the so-called memory effect in the tyre-ground contact and the contact friction is considered simultaneously [1, 4].

In our study, we capture these effects with the help of the brush tyre model (see in [12]) which enables us to describe the dynamically varying lateral tyre deformation with relatively few tyre parameters. The lateral slip of the tyre in the contact region is considered by parabolic deformation limits, resulting a piecewise-smooth continuous system with its specific bifurcation problems (see [9, 14]) while the local bifurcation of the rectilinear motion also can be studied by performing the centre manifold reduction and analysing the non-smooth normal form [3]; in this paper, we concentrate on the numerical calculation of the periodic solutions exploring the global structure of the limit cycles in the system.

The rest of the paper is organised as follows: In Sect. 2, we introduce our mechanical model and the equations of motion. Then, in Sect. 3, we discretise the governing equations using the method of collocation and we present the algorithm calculating the Floquet multipliers to determine the stability of the periodic solutions. In Sect. 4, we give an overview of the analytical study of the non-smooth Hopf bifurcation of the rectilinear motion. In Sect. 5, we present the results of the bifurcation continuation which are compared to measurements in Sect. 6. We summarise our results and give our conclusions in Sect. 7.

2 Governing equations

Fig. 1
figure 1

The mechanical model of the caster wheel system with elastic tyre. (Colour figure online)

Full size image
Fig. 2
figure 2

Lateral deformation and the different domains in the \(x \in [-a,a]\) contact patch. The green section corresponds to sticking while the red to sliding region. The dashed curves indicate the parabolic deformation boundaries. (Colour figure online)

Full size image

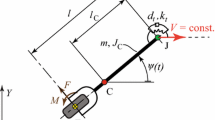
The mechanical model of the towed wheel is shown in Fig. 1. We consider an elastic tyre with a rigid wheel rim in a rigid caster. The caster is towed with a constant speed V in the X direction at the rotational joint A. In the joint, a torsional damping \(b_\mathrm {t}\) is assumed. As a result of the tyre deformation, a lateral force \(F_y\) and a self-aligning moment \(M_z\) is generated, which are acting on the wheel. Using the yaw angle \(\psi \) as generalised coordinate, one can apply Lagrange’s equation of the second kind to derive the equation of motion of the system

$$\begin{aligned} J_\text {A} \ddot{\psi }(t)+b_{\text {t}} {{\dot{\psi }}} (t) = M_z-F_y l, \end{aligned}$$
(1)

where the yaw mass moment of inertia \(J_\text {A}\) with respect to the joint A can be given as

$$\begin{aligned} J_\text {A} = J_\mathrm{C} + m l_{\mathrm{C}}^2, \end{aligned}$$
(2)

where \(l_{\mathrm{C}}\) is the distance of the centre of gravity C from the joint, m is the mass of the caster and the wheel while \(J_\mathrm{C}\) is the yaw mass moment of inertia with respect to the centre of gravity.

We use the brush tyre model (see Fig. 2) to calculate the lateral tyre force \(F_y\) and self-aligning moment \(M_z\). By means of this model, the elastic tyre is modelled as massless particles with linearly distributed lateral stiffness k. We assume that the effect of longitudinal deformation is negligible. Thus, we can calculate the tyre force and self-aligning moment using the lateral tyre deformation q(x, t). By means of the brush model, it is assumed that the tyre deforms in the \(x \in [-a,a]\) contact region only. Consequently, introducing the angular velocity \(\Omega \) the equation of motion (1) can be expressed as

$$\begin{aligned}&J_\text {A} {\dot{\Omega }}(t)+b_{\text {t}} \Omega (t) = k \int _{-a}^a (x-l)q(x,t) \text {d} x, \end{aligned}$$
(3)
$$\begin{aligned}&{\dot{\psi }} (t) = \Omega (t). \end{aligned}$$
(4)

While we calculate the lateral deformation, we distinguish between two cases: when the tyre particles stick to or when they slide on the ground. In general, sticking and sliding may occur simultaneously in different parts of the contact region. In the sticking region(s), the lateral tyre deformation is described by the nonlinear partial differential equation

$$\begin{aligned} \begin{aligned} \dot{q}(x,t) =&V \sin \psi (t)-(x-l) {\dot{\psi }} (t) \\&- q'(x,t) \left( q(x,t) {\dot{\psi }}(t) - V \cos \psi (t)\right) , \\ \end{aligned} \end{aligned}$$
(5)

with the boundary condition \(q(a,t) = 0\) [4, 15, 16]. This condition implies that the tyre particles enter the contact region with zero deformation. For this problem, a travelling wave solution can be provided, introducing time delay \(\tau (x)\), distributed along the x-axis. The source of the time delay in the contact can be explained by studying the tyre deformation in a caster-fixed frame of reference. While the tyre particles have zero velocity in the ground-fixed frame of reference, they appear to travel ‘backwards’, i.e. in the direction of the rear edge \(x = -a\) with respect to the caster. In this context, the time delay \(\tau (x)\) gives the time that is needed for a tyre particle to travel to its actual position x from \(x_0\) where it stuck to the ground. Considering these, the lateral displacement in the sticking part of the contact can be given by

$$\begin{aligned} q(x,t) =&V \tau (x) \sin \psi (t) - (x_0-l)\nonumber \\&\times \sin \left( \psi (t) - \psi (t-\tau (x)) \right) \nonumber \\&{+}\, q(x_0, t{-}\tau (x)) \sin \left( \psi (t) {-} \psi (t{-}\tau (x)) \right) , \end{aligned}$$
(6)

while we can also derive a formula for the longitudinal position:

$$\begin{aligned} \begin{aligned} x(\tau ) =&V \tau \cos \psi (t) + l + (x_0-l)\\&\cos \left( \psi (t) - \psi (t-\tau ) \right) \\&+\, q_0 \sin \left( \psi (t) - \psi (t-\tau ) \right) , \\ \end{aligned} \end{aligned}$$
(7)

where \(q_0\) and \(x_0\) denote the lateral deformation and longitudinal position at the instant when the tyre particle in question stuck to the ground. Using the travelling wave solution has a clear advantage over the semi-discretisation of the PDE (5) into a system of ODEs as it does not introduce new state variables. Thus, the dimension of the nonlinear zero problem, which we obtain by applying numerical collocation in time, can be kept relatively low.

The effect of partial sliding is considered assuming parabolic vertical force distribution in the \(x \in [-a, a]\) contact region. Since by means of the brush tyre model it is assumed that the tyre particles can deform independently from each other, we consider parabolic limits for the lateral deformation, too. Depending on the sliding direction, the lateral deformation in the sliding regions can be given as

$$\begin{aligned} s^\pm (x) = N^{\pm } (a^2-x^2), \end{aligned}$$
(8)

where \(N^{\pm }\) defines the magnitude of the limiting parabolae. These can be given as a function of the vertical load \(F_z\), the lateral tyre stiffness k, the contact-patch half length a and the friction coefficient \(\mu \) characteristic to the tyre-ground contact:

$$\begin{aligned} N^{\pm } = \pm \frac{3 F_z \mu }{4 a^3 k} \end{aligned}$$
(9)

where the positive sign corresponds to the upper and the negative to the lower deformation limit. The derivation of the time-delayed formulae (6) and (7) is given in [15, 16], whereas the detailed explanation and the analytical study of the brush tyre model with time delay and side slip can be found in [4].

The main challenge in handling this non-smooth delay differential equation is that unfortunately, there is no closed-form expression available for the position of the sticking/sliding boundary which is otherwise a function of the time-delayed state variables \(\varPsi (t+s)\), \(\Omega (t+s)\) for \(s \in [-\tau _\mathrm{max},0]\) with \(\tau _\mathrm{max}\) being the largest time delay in the system. This issue is overcome by finding the sticking/sliding boundary numerically in the course of calculating the lateral deformation.

3 Discretisation and periodic solutions

First, a collocation method is developed to identify the approximate periodic solutions in the discretised mechanical model. Then, the stability of each periodic solutions is determined by means of the calculation of the corresponding Floquet multipliers.

3.1 Numerical collocation

We calculate numerically the periodic solutions of the dynamical system Eqs. (3) and (4) as a two-point boundary value problem over a time period with the help of the method of collocation [19]. Accordingly, the solutions are approximated by m piecewise Lagrange polynomials of degree n [10]. Thus, the time \(t \in [0, T]\) is discretised by using \(nm+1\) equidistant representation points:

$$\begin{aligned} 0=t_0< t_1< \cdots< t_i< \cdots< t_{nm} < t_{nm+1} = T. \end{aligned}$$
(10)

Note that alternatively, one could apply an equidistant, periodic grid by using a finite segment of Fourier series for the discretisation [2]. In this case, the periodicity of the solutions would be assumed by definition; hence, no additional periodicity condition is needed. However, if a periodic grid is used for the discretisation, the numerical stability analysis of the periodic orbits cannot be performed.

We introduce the dimensionless time \(\vartheta : = t/T\) to project the time period onto the \(\vartheta \in [0, 1]\) interval. The collocation points in the dimensionless time are introduced as

$$\begin{aligned} \vartheta _{i,j} = \frac{1}{T}t_{(i-1)n+j}, \; \mathrm {for} \; i=1,...,m, \; j=0,...,n \, . \end{aligned}$$
(11)

Then, in the \(i\mathrm {th}\) interval \(t \in [t_{(i-1)n},t_{in}]\), a function \(u(t): \; [t_{(i-1)n},t_{in}] \rightarrow {\mathcal {R}}\) is approximated as

$$\begin{aligned} u(t) \approx \sum \limits _{j = 0}^n u \left( T \vartheta _{i,j} \right) p_{i,j} (\vartheta ), \end{aligned}$$
(12)

with the coefficients \(p_{i,j}\) defined by

$$\begin{aligned} p_{i,j} (\vartheta ) = \prod \limits _{k = 1, j \ne k}^n \frac{\vartheta - \vartheta _{i,k}}{\vartheta _{i,j} - \vartheta _{i,k}}. \end{aligned}$$
(13)

Based on this, the time derivative \({\dot{u}}(t)\) can be calculated:

$$\begin{aligned} {\dot{u}} (t) \approx \frac{1}{T} \sum \limits _{j = 0}^n u \left( T \vartheta _{ij} \right) p'_{ij} (\vartheta ), \end{aligned}$$
(14)

where prime denotes derivation with respect to the dimensionless time \(\vartheta \). Evaluating this equation in the representation points given in (10), one can introduce the differentiation matrix \({\mathbf {D}}_{{L}_{m,n}}\) corresponding to the piecewise discretisation relying on m Lagrange polynomials of degree n. This procedure provides a regular \((mn+1) \times (mn+1)\) matrix which has a block-diagonal-like structure (see Fig. 3) where the nonzero blocks are obtained from Lagrange differential matrices \({\mathbf {D}}_{{L}_n}\) relying on n intervals. Introducing the solution vector \({\mathbf {u}}\) contains the function values \(u_i = u(t_i)\) at the representation points \(t_i\) for \(i = 0, ..., mn+1\)). The vector of the time derivatives can be given as

$$\begin{aligned} \dot{{\mathbf {u}}} \approx \frac{1}{T} {\mathbf {D}}_{{L}_{m,n}} {\mathbf {u}} \end{aligned}$$
(15)

where the elements of the derivative vector \(\dot{{\mathbf {u}}}\) are defined as \(\dot{u}_i = \dot{u}(t_i)\). Based on this, the angular velocity function \(\Omega (t)\) and the yaw angle function \(\psi (t)\) are represented in the solution vectors \(\varvec{{\Omega }}\) and \(\varvec{{\psi }}\) and their derivatives are calculated as

$$\begin{aligned}&\dot{\mathbf {\varvec{{\Omega }}}} \approx \frac{1}{T} {\mathbf {D}}_{{L}_{m,n}} \mathbf {\varvec{{\Omega }}}, \end{aligned}$$
(16)
$$\begin{aligned}&\dot{\mathbf {\varvec{{\psi }}}} \approx \frac{1}{T} {\mathbf {D}}_{{L}_{m,n}} \mathbf {\varvec{{\psi }}}. \end{aligned}$$
(17)
Fig. 3
figure 3

The structure of the differentiation matrix with piecewise Lagrange polynomials. (In this example 4 sub-intervals are assumed). The shaded segments belong to differentiation matrices for Lagrange polynomials of degree n. In the overlapping parts the matrix elements are added together

Full size image
Fig. 4
figure 4

Discretisation of the lateral tyre deformation q(x, t) over the time period \(t \in [0,T]\) for a periodic solution of (3) and (4) with (6) and (7), i.e. when wheel-shimmy occurs. The green curves belong to sticking while the red ones to sliding parts of the tyre-ground contact. The thick blue curve shows how a given point travels towards the rear edge \(x = -a\). The application of Lagrange polynomials provides an equidistant mesh in the time domain while the spatial discretisation along the \(x \in [-a,a]\) contact patch is a result of the travelling wave solution (7). (Colour figure online)

Full size image

Assuming that the function values \(\Omega _i\) and \(\psi _i\) for \(i = 0, ..., nm+1\) are available, we can provide the corresponding lateral deformation in the contact region using the travelling wave solution (6), (7) and the limiting parabolae (8). This procedure is performed starting from the leading edge \(x = a\) because \(q(a,t_i) = 0\) is given by the boundary condition attached to the PDE (5). Then, we follow the path of each tyre particles in the wheel-fixed frame of reference (see Fig. 4) in time steps defined by the discretisation of the time period. In each step, we assume rolling to calculate the longitudinal position with the travelling wave solution

$$\begin{aligned} q_{i,j}^\mathrm{r} =&V \tau _{i,j} \sin \psi _i - (x_{0_{i,j}}-l) \sin \left( \psi _i - \psi _{0_{i,j}} \right) \nonumber \\&+ q_{0_{i,j}} \sin \left( \psi _i - \psi _{0_{i,j}} \right) \end{aligned}$$
(18)

and

$$\begin{aligned} x_{i,j}^\mathrm{r} =&V \tau _{i,j} \cos \psi _i + l + (x_{0_{i,j}}-l) \cos \left( \psi _i - \psi _{0_{i,j}} \right) \nonumber \\&+ q_{0_{i,j}} \sin \left( \psi _i - \psi _{0_{i,j}} \right) . \end{aligned}$$
(19)

where \(\tau _{i,j}\) is the time delay needed for the tyre particle in question after it sticks to the ground. The longitudinal position and lateral deformation corresponding to this delay are denoted by \(x_{0_{i,j}}\) and \(q_{0_{i,j}}\), respectively. The time-delayed yaw angle can be given as \(\psi _{0_{i,j}} = \psi (t-\tau _{i,j})\). Using the periodicity of the solution, this can be obtained by the modulo operation as

$$\begin{aligned} \psi _{0_{i,j}} = \psi _{\mathrm {mod} \left( i-\frac{\tau _{i,j}}{T}, mn \right) }. \end{aligned}$$
(20)

Then, the calculated deformation is compared with the parabolic limits (8). Namely, if the deformation is between these parabolic boundaries, then the travelling wave solution is accepted. Otherwise, considering equal friction coefficients for sticking and sliding, the deformation is equal to the corresponding sliding limit, that is,

$$\begin{aligned} q_{i,j} = {\left\{ \begin{array}{ll} s^+(x_{i,j}), &{} s^+(x_{i,j}) \le q_{i,j}^\mathrm{r} \\ q_{i,j}^\mathrm{r}, &{} s^-(x_{i,j})<q_{i,j}^\mathrm{r}<s^+(x_{i,j}) \\ s^-(x_{i,j}), &{} q_{i,j}^\mathrm{r} \le s^-(x_{i,j}) \\ \end{array}\right. }. \end{aligned}$$
(21)

This procedure is repeated until all the tyre particles leave the \(x \in [-a,a]\) contact region at the rear end \(x = -a\) of the contact line. As a result of this calculation, the deformed shape is available at each time instant \(t_i\). We use these values to calculate the integrals \(I_i : = I(t_i)\) at the right-hand side in (3):

$$\begin{aligned} I(t_i) := k \int _{-a}^a (x-l) q (x, t_i) \mathrm {d}x. \end{aligned}$$
(22)

We approximate this integral by means of the trapezoid rule:

$$\begin{aligned} I(t_i) \approx k \sum _{j=1}^{\nu } w_{i,j}(x_j-l) q (x_j, t_i), \end{aligned}$$
(23)

where the weights are calculated as

$$\begin{aligned} w_{i,j}= {\left\{ \begin{array}{ll} (x_{i,1}-x_{i,2})/2 &{} j=1\\ (x_{i,j-1}-x_{i,j+1})/2 &{} j=1,...,\nu _i-1,\\ (x_{i, \nu -1}-x_{i, \nu })/2 &{} j=\nu _i\\ \end{array}\right. } \end{aligned}$$
(24)

with \(\nu _i\) denoting the number of discretisation points in the contact region \(x \in [-a,a]\) corresponding to the representation point \(t_i\). Thus, the discretised system of the equation of motions (3), (4) can be given as

$$\begin{aligned}&\dfrac{1}{T} \sum _{j=1}^{N} D_{\mathrm {L_{mn}}}^{i,j}\Omega _j +\dfrac{b_\mathrm {t}}{J_{\text {A}}} \Omega _i \nonumber \\&\quad -\dfrac{k}{J_{\text {A}}} \sum _{k=1}^{\nu _i} w_{i,k}(x_{i,k}-l)q_{i,k} = 0, \end{aligned}$$
(25)
$$\begin{aligned}&\dfrac{1}{T} \sum _{j=1}^{N} D_{\mathrm {L_{mn}}}^{i,j}\psi _j-\Omega _i = 0. \end{aligned}$$
(26)

To ensure the periodicity of the solution, we attach the following conditions to the discretised system:

$$\begin{aligned}&\Omega _0 - \Omega _{(mn+1)} = 0, \end{aligned}$$
(27)
$$\begin{aligned}&\psi _0 - \psi _{(mn+1)} = 0, \end{aligned}$$
(28)

while in order to fix the phase of the periodic solutions, we also add the condition

$$\begin{aligned} \psi _0 = 0. \end{aligned}$$
(29)

Using equations (25)–(29), we define the nonlinear zero problem

$$\begin{aligned} \varvec{{\phi }}({\mathbf {x}}, \varvec{{\lambda }}) = {\mathbf {0}}, \end{aligned}$$
(30)

where the solution vector \({\mathbf {x}}\) can be expressed as

$$\begin{aligned} {\mathbf {x}} = \left( \begin{matrix} \Omega _0 \\ \Omega _1 \\ \vdots \\ \Omega _{(mn+1)} \\ \psi _0 \\ \psi _1 \\ \vdots \\ \psi _{(mn+1)} \\ T \\ \end{matrix} \right) \end{aligned}$$
(31)

while the vector \(\varvec{{\lambda }}\) contains the bifurcation parameters. We carry out the continuation of the periodic solutions by means of two bifurcation parameters: the towing speed V and the caster length l. This two-dimensional continuation is realised by the Continuation Core and Toolboxes (COCO) in MATLAB relying on the 2D atlas algorithm [6].

3.2 Stability of the periodic solutions

The stability of the numerically calculated periodic solutions can be decided with the help of the corresponding Floquet multipliers that are the eigenvalues of the monodromy matrix [10]. Let us consider our governing equations (3) and (4) in a delay differential equation form as

$$\begin{aligned} \dot{{\mathbf {y}}}(t) = {\mathbf {f}} \big ( {\mathbf {y}}(t+s) \big ) \; \mathrm {for} \; s \in [-\tau _{\mathrm {max}},0], \end{aligned}$$
(32)

with a periodic solution

$$\begin{aligned} {\mathbf {y}}_\mathrm {p}(t) = {\mathbf {y}}_\mathrm {p}(t+T), \end{aligned}$$
(33)

where \(\tau _{\mathrm {max}}\) stands for the largest time delay, while the vector of state variables is defined as

$$\begin{aligned} {\mathbf {y}}(t):= \left( \begin{matrix} \Omega (t) \\ \psi (t) \\ \end{matrix} \right) . \end{aligned}$$
(34)

Let us consider a solution \({\mathbf {y}}\) as a sum of the periodic solution \({\mathbf {y}}_\mathrm {p}\) and a perturbation \({\mathbf {v}}\):

$$\begin{aligned} {\mathbf {y}}(t) = {\mathbf {y}}_{\mathrm {p}}(t)+{\mathbf {v}}(t). \end{aligned}$$
(35)

Substituting the expression above in the delay differential equation (32), we obtain

$$\begin{aligned}&\dot{{\mathbf {y}}}_{\mathrm {p}}(t)+ \dot{{\mathbf {v}}}(t) \nonumber \\&\quad = {\mathbf {f}} \big ( {\mathbf {y}}_{\mathrm {p}}(t+s) + {\mathbf {v}}(t+s) \big ) \; \mathrm {for} \; s \in [-\tau _{\mathrm {max}},0]. \end{aligned}$$
(36)

Linearisation of the system around the periodic solution provides

$$\begin{aligned} \begin{aligned}&\dot{{\mathbf {y}}}_{\mathrm {p}} (t)+ \dot{{\mathbf {v}}}(t) \approx {\mathbf {f}} \big ( {\mathbf {y}}_{\mathrm {p}}(t+s) \big )\\&\quad + D {\mathbf {f}} \big ( {\mathbf {y}}_{\mathrm {p}}(t+s) \big ){\mathbf {v}}(t+s) \; \mathrm {for} \; s \in [-\tau _{\mathrm {max}},0] \end{aligned} \end{aligned}$$
(37)

where \(D {\mathbf {f}}(.)\) is the Fréchet derivative of the right-hand side. Since the periodic solution \({\mathbf {y}}_{\mathrm {p}}\) satisfies the equation of motion (32) by definition, this equation can be simplified as

$$\begin{aligned} \dot{{\mathbf {v}}}(t) \approx D {\mathbf {f}} \big ( {\mathbf {y}}_{\mathrm {p}}(t+s) \big ){\mathbf {v}}(t+s) \; \mathrm {for} \; s \in [-\tau _{\mathrm {max}},0].\nonumber \\ \end{aligned}$$
(38)

Discretising this equation with the help of piecewise Lagrange polynomials as described in Sect. 3.1, the following equation is obtained:

$$\begin{aligned} {\mathbf {D}} {\mathbf {w}} = \mathrm {grad}_{{\mathbf {w}}} {\mathbf {F}} {\mathbf {w}}, \end{aligned}$$
(39)

where the vector \({\mathbf {F}}\) contains the right-hand-side \({\mathbf {f}}\) evaluated at the representation points given in (10), while \({\mathbf {w}}\) contains the state variables at the representation points

$$\begin{aligned} {\mathbf {F}} = \left( \begin{matrix} f_1 (t_0) \\ f_1 (t_1) \\ \vdots \\ f_1 (t_{mn+1}) \\ f_2 (t_0) \\ f_2 (t_1) \\ \vdots \\ f_2 (t_{mn+1}) \\ \end{matrix} \right) \qquad \mathrm {and} \qquad {\mathbf {w}} = \left( \begin{matrix} \Omega (t_{-r}) \\ \vdots \\ \Omega (t_0) \\ \Omega (t_1) \\ \vdots \\ \Omega (t_{mn+1}) \\ \psi (t_{-r}) \\ \vdots \\ \psi (t_0) \\ \psi (t_1) \\ \vdots \\ \psi (t_{mn+1}) \\ \end{matrix} \right) , \end{aligned}$$
(40)

where the time instant \(t_{-r}\) corresponds to the maximal delay \(\tau _{\mathrm {max}}\) and the differentiation matrix \({\mathbf {D}}\) can be given in a block-diagonal form

$$\begin{aligned} {\mathbf {D}} = \left( \begin{matrix} {\mathbf {D}}_{{L}_{m,n}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {D}}_{{L}_{m,n}} \end{matrix} \right) . \end{aligned}$$
(41)

The discretised variational equations (39) can be expressed also in the form

$$\begin{aligned} {\mathbf {J}} {\mathbf {w}} = {\mathbf {0}}. \end{aligned}$$
(42)

The coefficient matrix \({\mathbf {J}} = {\mathbf {D}}-\mathrm {grad}_{{\mathbf {w}}} {\mathbf {F}}\) can be obtained from the Jacobian of the zero problem (30) without considering the phase and periodicity conditions and the modulo operation in the time-delayed variables [10].

The Jacobian \({\mathbf {J}}_{\mathrm {mod}}\) of the zero problem (30) has a block matrix structure as shown in Fig. 5 where we already omitted the periodicity and the phase conditions, as well as the derivations with respect to the period T. Based on equations (25) and (26), three of the four blocks can be given analytically. However, we cannot calculate the top-right block (shaded in light grey in Fig. 5) directly since this corresponds to the derivatives of (25) with respect to the yaw angle \(\psi \). Accordingly, these derivatives depend on the lateral deformation and the consideration of sliding makes it impossible to provide a formula that links the deformation to the time-delayed state variables in a straightforward way. This is why we calculate this block by finite differences. Nevertheless, we still know that due to the distributed contact delay, matrix \({\mathbf {J}}_{\mathrm {mod}}\) is expected to have a band-like structure, which, as a result of the modulo operation, appears also in the upper-right triangle of the block.

Fig. 5
figure 5

The structure of the Jacobian matrix with and without the modulo operation for the time-delayed terms. The light grey shading indicates the part of the matrix which has to be calculated by finite differences. The dark grey bands show the structure of the nonzero derivatives from the terms with distributed delay

Full size image

In order to omit the modulo operation, one can reorganise this matrix resulting the extended Jacobian \({\mathbf {J}}\) in case the largest delay is smaller than the period: \(\tau _{\mathrm {max}}<T\). However, this cannot be performed directly for \(\tau _{\mathrm {max}}>T\) since in this case the periodic band in the top-right block overlaps itself. Thus, one has to calculate the top-right block of the extended Jacobian by finite differences evaluating the zero problem (30) without the modulo operation.

The monodromy matrix can be calculated by defining a map between the initial and the final solution segments \({\mathbf {v}}(t_0+s)\) and \({\mathbf {v}}(t_0+T+s), \; s \in [-\tau _{\mathrm {max}},0]\), respectively. In the discretised system (39), this can be provided by the extended Jacobian \({\mathbf {J}}\). Reorganising the columns of matrix \({\mathbf {J}}\) (see Fig. 6), Eq. (42) can be expressed in a block matrix form

$$\begin{aligned} \left( \begin{matrix} {\mathbf {A}} &{} {\mathbf {B}} \\ \end{matrix} \right) \tilde{{\mathbf {w}}} = {\mathbf {0}}. \end{aligned}$$
(43)
Fig. 6
figure 6

The structure of the coefficient matrices before and after reorganisation in equations (42) and (43). The numbers under the braces indicate the dimension in the corresponding blocks

Full size image

This equation is underdetermined, with a \(2(r+1)\)-dimensional solution space. Thus, the final solution segment \({\mathbf {w}}_1\) can be given as a function of the initial solution segment \({\mathbf {w}}_0\)

$$\begin{aligned} {\mathbf {w}}_1 = {\mathbf {M}} {\mathbf {w}}_0, \end{aligned}$$
(44)

where

$$\begin{aligned} {\mathbf {w}}_1 = \left( \begin{matrix} \Omega _{mn-r+1} \\ \vdots \\ \Omega _{mn} \\ \psi _{mn-r+1} \\ \vdots \\ \psi _{mn} \\ \end{matrix} \right) , \qquad {\mathbf {w}}_0 = \left( \begin{matrix} \Omega _{0-r} \\ \vdots \\ \Omega _{0} \\ \psi _{0-r} \\ \vdots \\ \psi _{0} \\ \end{matrix} \right) , \end{aligned}$$
(45)

and the coefficient matrix \({\mathbf {M}}\) is the monodromy matrix. Note that if \(\tau _{\mathrm {max}}>T\), the solution segments \({\mathbf {w}}_1\) and \({\mathbf {w}}_0\) overlap and one part of the monodromy matrix is the identity.

The stability of the periodic solutions can be decided with the help of the eigenvalues of the monodromy matrix \({\mathbf {M}}\). A periodic solution is stable, if the spectral radius of the mondoromy matrix satisfies \(\rho ({\mathbf {M}}) \le 1\), where \(\rho ({\mathbf {M}}) = \mathrm {max} \big ( \mathrm {abs} ( \lambda ) \big ) \), for any \( {\mathbf {M}} {\mathbf {s}} = \lambda {\mathbf {s}}\). Note that for a periodic solution, 1 is always a trivial eigenvalue of the monodromy matrix. Asymptotic stability is ensured if the eigenvalue \(\lambda = 1\) is multiplicity one while for the non-trivial eigenvalues \({\tilde{\rho }}({\mathbf {M}}) < 1\) holds, where \({\tilde{\rho }}({\mathbf {M}}) = \mathrm {max} \big ( \mathrm {abs} ( {\tilde{\lambda }} ) \big ) \), for any \( {\mathbf {M}} {\mathbf {s}} = {\tilde{\lambda }} {\mathbf {s}}\), \(\tilde{\lambda } \ne 1\).

Theoretically, the boundary of the bistable domain(s) could be determined by the continuation of the saddle-node bifurcation (fold) of the periodic solutions. However, the calculation of the monodromy matrix is computationally expensive while determining its critical eigenvalue is also an ill-conditioned problem due to the non-smooth nature of the system. Therefore, in our analysis, we determined the stability of the periodic solutions after the solution manifold is calculated.

4 Analytical study of the non-smooth Hopf bifurcation

One can also get an image of the stability of the periodic solutions by topologically extrapolating the properties of the local non-smooth Hopf bifurcation of the rectilinear motion \(\psi (t) \equiv 0, \, \Omega (t) \equiv 0\) at the linear stability boundaries. This bifurcation can be studied analytically as described in detail in [3, 4]. For this purpose, we consider only one sliding region in the \(x \in [-a,a]\) contact range at the vicinity of the rear edge \(x = -a\). Thus, it is assumed that in the interval \(x \in [-x^*, a]\) all particles stick to the ground, while the in \(x \in [-a, x^*]\) all points are sliding. It can be shown that this assumption is sufficient for studying small oscillations around the rectilinear motion. Consequently, the equation of motion (3) can be expressed in the following form:

$$\begin{aligned} \begin{aligned} J_\text {A} \ddot{\psi }(t)+b_{\text {t}} {{\dot{\psi }}} (t)&= k \underbrace{\int _{\tau ^*}^0 (x (\tau )-l)q(x(\tau ),t) \dfrac{\text {d} x}{\text {d} \tau } \text {d} \tau }_{=:I_1} \\&\quad + k \underbrace{\int _{-a}^{x^*}(x-l)N^{\pm } (a^2-x^2) \text {d}x}_{=:I_2}, \\ \end{aligned} \end{aligned}$$
(46)
Table 1 The list of the parameters used for numerical collocation
Full size table
Fig. 7
figure 7

Periodic solutions of the undamped system. The blue markers correspond to stable and the red ones to unstable solutions, respectively. (Colour figure online)

Full size image

where the integral \(I_1\) refers to the sticking region, where the travelling wave solution (6), (7) applies, while \(I_2\) gives the effect of the sliding region, where the deformation is given by the limiting parabolae (8). Note that the boundary \(x^*\) and the corresponding time delay \(\tau ^*\) are state dependent, i.e. they are varying as the tyre oscillates. It is shown in [4] that, by performing centre manifold reduction in the non-smooth delay differential equation, (46) can be transformed to a normal form with smooth linear and piecewise-smooth second-order terms

$$\begin{aligned} \left( \begin{matrix} {\dot{u}}_1 \\ {\dot{u}}_2 \\ \end{matrix} \right) = \left( \begin{matrix} \mu &{} \omega \\ -\omega &{} \mu \\ \end{matrix} \right) \left( \begin{matrix} u_1 \\ u_2 \\ \end{matrix} \right) + {\mathbf {h}}_2 (u_1,u_2;\mu ), \end{aligned}$$
(47)

where \(\mu \) and \(\omega \) are the real and imaginary parts of the critical characteristic exponent, while \({\mathbf {h}}_2 (.)\) contains the non-smooth second-order terms. Analysing the normal form, one can determine the sub- or supercritical nature of the bifurcation, while it also provides the tangent lines of the arising branches of limit cycles at the non-hyperbolic equilibrium. The amplitude of the limit cycles around the critical equilibrium can be given as a function of the towing speed V by the formula

$$\begin{aligned} r_0 (V) \approx - \frac{\mu ' \left( V_{\text {cr}}\right) }{\delta } \left( V-V_{\text {cr}}\right) , \end{aligned}$$
(48)

where the parameter \(\delta \) is equivalent to the Poincare–Lyapunov constant in smooth systems. That is, if \(\delta < 0\) the non-hyperbolic equilibrium is asymptotically stable due to the nonlinear terms, and the non-smooth Hopf bifurcation is supercritical and the emerging periodic solutions are orbitally asymptotically stable, and similarly, if \(\delta > 0\) the non-hyperbolic equilibrium is unstable, the bifurcation is subcritical and the limit cycles are unstable. This formula also shows that the periodic orbits emerge in a conical structure rather than in a paraboloid one that is characteristic in Hopf bifurcations of smooth systems [9].

5 Results

Before the nonlinear analysis, we divided the (V, l) parameter plane into linearly stable and unstable domains. Studying Eqs. (3) and (4), one can establish that lateral sliding does not contribute to the linear part of the equation. Thus, the linear stability of the rectilinear motion can be decided by semi-discretisation [7] of the delay differential equations and by the eigenvalues of the resultant coefficient matrix.

We carried out the two parameter continuation of the periodic solutions, emerging from the linear stability boundaries by means of the towing speed V and the caster length l. For this analysis, we used the parameters given in Table 1. Figure 7 shows the vibration amplitudes \(\psi _{\mathrm {max}}\) of the periodic solutions in the undamped system (\(b_{\mathrm {t}} = 0 \)). We also plotted the linear stability boundaries of the rectilinear motion in the (V, l) plane. One can show analytically that, as common in time-delay systems, an infinite number of stable and unstable domains exist, appearing in a chessboard-like structure. In our analysis, however, we only focus on the periodic solutions above the rightmost unstable domains. The nonlinear analysis reveals that the subsequent critical speeds correspond to sub- and supercritical bifurcations of the rectilinear motion in an alternating fashion. The critical nature of the stability boundary at \(l = a\) also becomes apparent. This line is found to be ‘neutral’, that is, neither sub- or supercritical by analysing the non-smooth second-order terms. In a sense, this boundary behaves similarly to a coincident Hopf bifurcation of the rectilinear motion and the fold bifurcation of the periodic solutions since it separates both stable and unstable equilibria and limit cycles. It can be seen that each surface of periodic solutions has a generic ‘fold’ line as well, corresponding to the fold of the periodic orbits. Accordingly, bistable parameter domains appear which correspond to the subcritical bifurcation of the rectilinear motion.

Fig. 8
figure 8

Bifurcation diagrams (upper panels) and nonlinear stability chart (bottom panel) of the undamped system. The bifurcation diagrams in panels (a) and (b) correspond to the sections A and B, respectively. The continuous blue lines indicate stable, while the dashed red lines unstable solutions. (Colour figure online)

Full size image

Thus, we can distinguish four types of parameter domains as shown if Fig. 8. In the white ‘stable’ regions, the rectilinear motion is linearly stable and has an infinitely large domain of attraction. In the ‘unstable’ regions (shaded in medium red), the rectilinear motion is unstable, whereas in the ‘bistable’ domains (shaded in light red) the rectilinear motion is stable but has a finite domain of attraction. That is, the system converges to a stable limit cycle for large enough perturbation. This structure is also visible in the one-parameter bifurcation diagrams (panels (a) and (b) of Fig. 8) where only the towing speed V is varied while the caster length l is kept fixed. In panel (b), it is also apparent that there exist a parameter range where the rectilinear motion is unstable, but the system has two stable limit cycles. This type of parameter domain is marked by dark red shading in panel (c).

Fig. 9
figure 9

Panel (a): periodic solutions of the damped (\(b_{\mathrm {t}} = 0.61 \mathrm {N ms} \)) system. The blue markers correspond to stable, the red ones to unstable solutions, respectively. Panel (b): bifurcation diagram corresponding to section C. Panel (c). nonlinear stability chart. (Colour figure online)

Full size image

Figure 9 shows that if damping is considered in the rotational joint A, the chessboard-like structure of the linearly stable and unstable domains collapses into one D-shaped unstable parameter region. Our analysis revealed that the structure of periodic orbits is largely preserved even in this case; namely, a bistable domain occurs beside the stability boundary corresponding to subcritical bifurcation of the rectilinear motion. It is also visible that all the calculated branches of limit cycles emerge in a conical structure from the linear stability as predicted by the analytical calculations.

Unfortunately, when compared to numerical simulations, the calculation of the Floquet multipliers turned out to be unreliable as indicators of stability in certain cases. While they turned out to be robust at the solution surface at the highest speed, they tend to provide contradictory results at lower speeds, especially at the solutions close to linear stability boundaries. The suspected reason of this behaviour is that due to the non-smooth nature of the system, the continuation of the periodic solutions can only be carried out with relaxed error tolerances of the solution algorithm while, among others, the boundary between the sticking and sliding regions is found only approximately. Although these approximations are tolerable for calculating the periodic solutions, the Jacobian matrix will be effected by these inaccuracies as it is partly calculated by finite differences, involving the evaluation of the zero problem (30) with the variation of each state variable. As a conclusion, the periodic solutions are marked as stable/unstable based on the topology of the manifold using the fold line.

6 Measurements

Fig. 10
figure 10

Shimmying wheel running on a conveyor belt. (Colour figure online)

Full size image

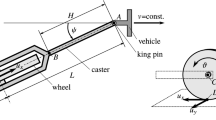
Measurements were carried out on a towed bicycle wheel running on a treadmill. The experimental rig is shown in Fig. 10. The wheel is rotating in the fork which is mounted to the caster, such that the caster length l can be modified by a slider. The caster is mounted to the rack by a rotational joint. The deflection angle \(\psi (t)\) is measured by an angle sensor built on the joint. By means of the Galilean transformation, it can be showed that the scenario when the conveyor belt has a speed V is identical to the configuration when the caster wheel system is towed with speed V with respect to the ground. By varying the speed of the conveyor belt, we explore the linear stability boundary where the system spontaneously diverges from the rectilinear motion. Then, after the system converged to large-amplitude oscillation, we decrease the treadmill speed until the oscillations spontaneously decay. This speed corresponds to the fold of the periodic solutions which defines the boundary of a bistable parameter domain. This procedure is repeated for different caster lengths. Thus, the linear stability boundary and the bistable parameter range can be explored in the (V, l) parameter plane. In Fig. 11, the measurement results are compared to our calculations. It can be seen that our mechanical model and the measurements provided qualitatively identical diagrams and that the bistable parameter domains appear in a similar structure in the two nonlinear stability charts. Nevertheless, there are quantitative differences related to a known error of the brush tyre model: since this model neglects tyre deformation outside the contact region, the unstable and bistable domains appear at a somewhat lower speed domain than in the experiment. This error could be adjusted via the stretched string tyre model [12]. As shown in [1], this model provides qualitatively similar, but quantitatively better results for the critical towing speed. However, by means of the stretched string model, sliding can be considered only with differential equations instead of pre-defined sliding limits. As a result, one may find it challenging to perform a similar theoretical study with the stretched string model.

Fig. 11
figure 11

Experimental and theoretical bifurcation diagrams (upper panels) and nonlinear stability charts (lower panels). The crosses show the measured data while the blue curves correspond to stable, the red ones to unstable solutions, respectively. (Colour figure online)

Full size image

7 Conclusions

In our study, we investigated the nonlinear dynamics of wheel-shimmy. By performing the continuation of the periodic solutions in two bifurcation parameters, the towing speed and the caster length, beside the linearly stable and unstable regions, we were able to identify bistable parameter domains which are undetectable by using the standard quasi-steady-state tyre models with the one-degree-of freedom model of the caster wheel system. The local bifurcation of the rectilinear motion can also be investigated analytically. This reveals that, at the stability boundaries corresponding to the bistable domains, the straight-line motion undergoes a subcritical Hopf bifurcation. Additionally, it is also proven that the limit cycles emerge in a conical structure due to the non-smooth nature of the system. These results were also corroborated by numerical analysis.

By conducting experiments on a treadmill, we showed that the structure of the periodic solutions is qualitatively similar in the real-life system as it is predicted by the theoretical results. Nevertheless, there are quantitative differences between the theoretical and experimental results due to the neglected tyre relaxation (deformation outside the contact region). Moreover, obtaining the periodic solutions numerically has its own limitations, too. The continuation of the solution manifold, as well as determining their stability, requires the Jacobian matrix of the system equations. However, the calculation of the Jacobian is ill-conditioned due to the non-smooth nature of the system. Therefore, besides the Floquet multipliers, we also relied on the topology of the periodic solution surfaces and results of analytical calculations when we determined the stability of the solutions.

The part of the parameter domain where two nearby stability boundaries with different critical frequencies intersect each other is still relatively rarely identified. One can encounter quasi-periodic vibrations in those parameter domains where two complex conjugate pairs of roots of the characteristic equation have a positive real part. The analysis corresponding Hopf–Hopf bifurcations and the continuation of the quasi-periodic solutions is subject of future research.