Transition radiation in a piecewise-linear and infinite one-dimensional structure–a Laplace transform method

Abstract

Transition zones in railway tracks are areas with considerable variation of track properties (i.e., foundation stiffness), encountered near structures such as bridges and tunnels. Due to strong amplification of the response, transition zones require frequent maintenance. To better understand the underlying degradation mechanisms, a one-dimensional model is formulated, consisting of an infinite Euler–Bernoulli beam resting on a locally inhomogeneous and nonlinear Winkler foundation, subjected to a moving load. The nonlinearity is characterized by a piecewise-linear stiffness, and the system thus behaves piecewise linearly. Therefore, the solution can be obtained by sequentially applying the Laplace transform combined with the Finite Difference Method for the spatial discretization and derived non-reflective boundary conditions. Results show that the plastic deformation is a consequence of constructive interference of the excited waves and the response to the load’s deadweight, particularly for the soft-to-stiff transition. The plastic deformation area decreases quasi-monotonically with increasing transition length, and for super-critical velocities, small transition lengths and/or large stiffness dissimilarities, parts of the foundation experience plastic deformation even in the second loading–unloading cycle. Furthermore, the nonlinearity causes the maximum energy associated with the waves radiated forward and the maximum energy input not to occur for the smallest transition length, contrary to findings in corresponding linear systems. Moreover, the energy input drastically increases for the second passage of the moving load, making it a possible indicator of the damage in the supporting structure. The novelty of the current work lies in the computationally efficient solution method for an infinite system which locally exhibits nonlinear behaviour and in the study into the influence of the foundation’s nonlinear behaviour on the generated waves (i.e., transition radiation), and on the resulting plastic deformation. The model presented here can be used for the preliminary design of transition zones in railway tracks.

1 Introduction

Transition radiation is emitted when a source moves along a straight line with constant velocity and acts on or near an inhomogeneous medium [1, 2]. It occurs, for example, when a train crosses an inhomogeneity in a railway track, such as a variation in foundation stiffness. The velocity of high-speed trains or conventional trains running on soft soils may approach the critical velocity in the supporting structure leading to strong transition radiation. Apart from potentially giving rise to vehicle instability and passenger discomfort, transition radiation has been addressed as one of the causes of track and foundation degradation due to the often strong amplification of the stress and strain fields [3,4,5,6]. This leads to a high frequency of maintenance required for transition zones in areas with soft soils, which can be 3–8 times higher than for the regular parts of the railway track [7, 8]. Frequent maintenance leads to high costs and reduced availability of the track.

The first study on transition radiation of elastic waves was published by Vesnitskii and Metrikin [9]. It considered an infinite string on a piecewise-homogeneous Winkler foundation subjected to a moving point force and a moving point mass, respectively. To also account for the flexural rigidity of the system, Vesnitskii and Metrikin [10] analysed transition radiation in a semi-infinite beam on elastic springs clamped at one end. This system is equivalent to an infinite one where part of the foundation has infinitely high stiffness. Later on, the problem of a beam resting on a piecewise-homogeneous Winkler foundation was also addressed by others using different solution methods: modal expansion techniques [11, 12] and the moving element method [13]. To study wave propagation in the ground due to transition radiation, 2-D models of a continuum acted upon by a moving load were analysed. The continuum was modelled as a piecewise-homogeneous half-space [14, 15] and as a piecewise-homogeneous finite-depth layer [16, 17].

The geometry of the transition zone has a strong influence on the transition radiation, and modelling it as piecewise homogeneous usually does not suffice for design purposes. The detailed geometry of the transition zone has been more accurately modelled using 2-D and 3-D finite-element models or combined boundary-element models and finite-element models [e.g., 1; a good review of models for transition zones can be found in [7]. Such models are necessary at the final stage of designing a transition zone, but they are computationally demanding. A simplified way to model a transition zone in a 1-D model, but more accurately than assuming a piecewise-homogeneous foundation, is to incorporate a smooth transition between domains with constant support stiffness. This has been introduced by Metrikine et al. [25] for the model of an infinite string-foundation system. Incorporating a smooth transition in a 1-D model opens the possibility of studying the performance of different transition-zone geometries in earlier design stages.

Many studies about the dynamic response of railway tracks assume linear behaviour of the supporting structure. However, the influence of the foundations nonlinearity on a railway track is significant, as shown experimentally by Dahlberg [26], and should not be overlooked. A study of the steady-state response of an infinite string supported by nonlinear elastic springs subjected to two moving point loads can be found in [27]. To also account for the flexural rigidity, the steady-state response of a beam on a homogeneous and nonlinear elastic foundation subjected to a moving load has been analysed, considering a finite system [28,29,30] and an infinite one [31,32,33]. In addition, Hoang et al. [34] studied the steady-state response of an infinite beam with periodic nonlinear elastic supports.

Fig. 1

Schematization of the model: infinite Euler–Bernoulli beam supported by an inhomogeneous and nonlinear Winkler foundation, subjected to a moving load

Transition radiation has also been addressed in systems with nonlinear elastic behaviour of the supporting structure. Castro Jorge et al. [35] used a nonlinear elastic foundation to analyse the effect of the nonlinearity on the maximum displacements in a finite and piecewise-homogeneous system. In addition, Varandas et al. [36, 37] considered nonlinear elastic behaviour of the supporting structure in a 3-D finite-element model of a transition zone. However, to study the degradation in a transition zone, the employed model should incorporate plastic behaviour of the foundation. To this end, Varandas et al. [38] developed a finite 1-D model describing the accumulated permanent deformation in a transition zone using a phenomenological model for the cyclic degradation of the supports. Moreover, Gallego Giner et al. [39] used an elastic-perfectly plastic model (i.e., Drucker–Prager) for the supporting structure in his study of a transition zone using a 3-D finite element model.

Detailed 3-D models of finite and inhomogeneous systems that incorporate nonlinear behaviour of the foundation are available in the literature, as shown previously. However, simplified models of transition zones in infinite systems with nonlinear elasto-plastic foundation behaviour are not available in the literature. This motivates the aim of the current work, which is to formulate a 1-D model of an infinite Euler–Bernoulli beam on a smoothly inhomogeneous and nonlinear elasto-plastic Winkler foundation, subjected to a moving load, and to study the effect of the nonlinear behaviour on the transition radiation and the degradation in the transition zone. The novelty of the current work is twofold. Firstly, a computationally efficient solution method for an infinite system which locally exhibits nonlinear behaviour is presented. Secondly, the influence of the foundation’s nonlinear behaviour on the generated waves (i.e., transition radiation), and the resulting plastic deformation are studied. The model presented here can be used for preliminary designs of transition zones in railway tracks by assessing the potential damage (i.e., plastic deformation) occurring in the transition zone as a function of the smoothness of the transition (i.e., length of the transition), of the moving load velocity, of the system’s damping and of the stiffness dissimilarity. Furthermore, the results presented here offer insight into the physical mechanisms leading to degradation in the supporting structure.

This paper is structured as follows. In Sect. 2, the problem statement is presented and the solution is derived. Section 3 introduces the constitutive relation of the foundation stiffness and the assumptions considered. In Sect. 4, the results are presented and discussed, while Sect. 5 presents the drawn conclusions.

2 Model and solution

2.1 Problem statement

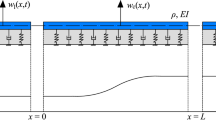
In this section, a 1-D model is formulated, consisting of an infinite Euler–Bernoulli beam resting on a smoothly inhomogeneous and nonlinear Winkler foundation, subjected to a constant moving load (Fig. 1). In view of practical relevance (degradation is often encountered inside or close to the transition zone), the nonlinear behaviour of the supporting structure is restricted to the transition zone and its vicinity; this domain is referred to as the computational domain. The computational domain is connected at the boundaries to two linear and homogeneous semi-infinite domains to accommodate the infinite extent of the railway track. The equations of motion for the three domains read

$$\begin{aligned}&w''''_\mathrm {l} + \rho \, \ddot{w}_\mathrm {l} + c_\mathrm {d,l}\, \dot{w}_\mathrm {l} + k_\mathrm {d,l}\, w_\mathrm {l} \nonumber \\&\quad \,\,=-F_\mathrm {0}\,\delta (x-vt) \, H(-t), \quad \, -\mathrm {\infty }<x <\mathrm {0}, \end{aligned}$$

(1)

$$\begin{aligned}&w'''' + \rho \, \ddot{w} + c_\mathrm {d}(x)\, \dot{w} + F_{\mathrm {k,W}}(x,w) \nonumber \\&\quad =-F_\mathrm {0}\delta (x-vt)\bigg (H(t) - H \bigg (t-\frac{L}{v}\bigg )\bigg ), \, 0<x < L, \end{aligned}$$

(2)

$$\begin{aligned}&w''''_\mathrm {r} + \rho \, \ddot{w}_\mathrm {r} + c_\mathrm {d,r}\, \dot{w}_\mathrm {r} + k_\mathrm {d,r}\, w_\mathrm {r} \nonumber \\&\quad =-F_\mathrm {0}\,\delta (x-vt) \, H \bigg (t-\frac{L}{v}\bigg ), \,\,\,\,\,\, L<x <\mathrm {\infty }, \end{aligned}$$

(3)

where primes denote partial derivatives with respect to x, overdots denote partial derivatives with respect to t, and all parameters have been scaled by the beam’s bending stiffness EI; $\rho$ represents the scaled mass per unit length of the beam; $k_\mathrm {d,l}$ and $c_\mathrm {d,l}$ are the scaled (homogeneous) foundation stiffness and damping of the left semi-infinite domain, respectively; $k_\mathrm {d,r}$ and $c_\mathrm {d,r}$ represent the same quantities for the right semi-infinite domain; $F_{\mathrm {k,W}}(x,w)$ and $c_\mathrm {d}(x)$ are the scaled force exerted by the foundation and the scaled foundation damping of the computational domain, respectively; $F_\mathrm {0}$ and v represent the scaled magnitude and the velocity of the moving load; $\delta (\ldots )$ denotes the Dirac delta function, and $H(\ldots )$ the Heaviside function; $\mathrm {0}$ and L represent the positions of the left and right boundaries of the computational domain, respectively. Finally, $w_\mathrm {l}$, $w_\mathrm {r}$ and w are the unknown displacements of the left and right semi-infinite domains, and of the computational domain, respectively. The space and time dependency of the unknown displacements is omitted from the expressions for brevity.

As interface conditions between the domains, continuity in displacement and slope, as well as in shear force and bending moment, is imposed. The set of boundary conditions is completed by imposing that, due to the presence of damping, the displacements of the left and right domains are zero as x tends to negative and positive infinity, respectively:

$$\begin{aligned}&w_\mathrm {l}(0,t) = w(0,t),&w_\mathrm {r}(L,t) = w(L,t), \end{aligned}$$

(4)

$$\begin{aligned}&w'_\mathrm {l}(0,t) = w'(0,t),&w'_\mathrm {r}(L,t) = w'(L,t), \end{aligned}$$

(5)

$$\begin{aligned}&w''(0,t) = w''_\mathrm {l}(0,t),&w''(L,t) = w''_\mathrm {r}(L,t), \end{aligned}$$

(6)

$$\begin{aligned}&w'''(0,t) = w'''_\mathrm {l}(0,t),&w'''(L,t) = w'''_\mathrm {r}(L,t), \end{aligned}$$

(7)

$$\begin{aligned}&\lim _{(x-vt)\rightarrow -\infty } w_\mathrm {l}(x,t)= 0,&\lim _{(x-vt)\rightarrow \infty } w_\mathrm {r}(x,t) = 0. \end{aligned}$$

(8)

For computational efficiency, the simulation is performed for the time interval when the moving load is close to and inside the transition zone. Therefore, the choice of initial conditions is crucial for ensuring that the infinite extent of the model is respected. In reality, before reaching a transition zone, the displacement field caused by a train can be considered to be in the steady state. Consequently, the initial conditions have to be chosen such that they represent the steady state at the beginning of the simulation. These initial conditions are referred to (in this paper) as the input initial conditions. The input initial conditions read

$$\begin{aligned}&w_\mathrm {l}(x,t=0) = w_\mathrm {l}^\mathrm {in}(x),&\dot{w}_\mathrm {l}(x,t=0) = \dot{w}_\mathrm {l}^\mathrm {in}(x), \end{aligned}$$

(9)

$$\begin{aligned}&w(x,t=0) = w\mathrm {^{in}}(x),&\dot{w}(x,t=0) = \dot{w}^\mathrm {{in}}(x), \end{aligned}$$

(10)

$$\begin{aligned}&w_\mathrm {r}(x,t=0) = w_\mathrm {r}^\mathrm {in}(x),&\dot{w}_\mathrm {r}(x,t=0) = \dot{w}_\mathrm {r}^\mathrm {in}(x), \end{aligned}$$

(11)

where superscript “in” stands for the input initial conditions, which are derived in Sect. 2.3.1.

Equations (1) to (11) constitute a complete description of the problem. In the next section, the solution method is presented.

2.2 Locally inhomogeneous and nonlinear system

Several time-domain methods are available for obtaining the solution to a system representing a railway track with nonlinear behaviour of the foundation [e.g., 2. These methods are suitable for systems that exhibit nonlinear behaviour continuously throughout the simulation. An alternative method is using the Laplace transform sequentially, as shown by Hoving and Metrikine [41]. The main condition for this method to be applicable is that the system’s behaviour is piecewise linear, implying that the system behaves linearly between the moments at which its parameters, being functions of the field variables (displacements, velocities, etc.), change abruptly (i.e., nonlinear events). This method has the potential of being computationally efficient for systems that have a limited number of nonlinear events.

For simplicity of the derivation in this section, the foundation’s constitutive law is assumed to be bilinearly elastic. A more realistic constitutive relation, discussed in Sect. 3, is adopted for the results presented in this paper. Here, the force provided by the Winkler foundation springs is given by

$$\begin{aligned} F_{\mathrm {k,W}}(x,w) = {\left\{ \begin{array}{ll} k_\mathrm {d}^\mathrm {A}(x) \, w, &{} w \le w_\mathrm {el}, \\ k_\mathrm {d}^\mathrm {B}(x) \, w - \Delta k_\mathrm {d}(x) \, w_\mathrm {el}, &{} w > w_\mathrm {el}, \end{array}\right. }\nonumber \\ \end{aligned}$$

(12)

where $k_\mathrm {d}^\mathrm {A}(x)$ and $k_\mathrm {d}^\mathrm {B}(x)$ represent the foundation stiffness related to the first and second branches of the bilinear constitutive law (see Fig. 6, considering just branches A and B for loading and unloading), $\Delta k_\mathrm {d}(x) = k_\mathrm {d}^\mathrm {B}(x) - k_\mathrm {d}^\mathrm {A}(x)$ is the stiffness difference between the two branches, and $w_\mathrm {el}$ represents the elastic displacement limit at which the stiffness changes from branch A to branch B. Note that, due to the inhomogeneity, both stiffness parameters $k_\mathrm {d}^\mathrm {A}(x)$ and $k_\mathrm {d}^\mathrm {B}(x)$ are functions of space; however, the elastic displacement limit $w_\mathrm {el}$ is independent of the spatial coordinate. The choice of the parameters is discussed in Sect. 3.

Assuming that the system is in the linear regime at the start of the simulation and applying the Laplace transform over time to Eq. (2), the Laplace-domain equation of motion valid in the computational domain reads

$$\begin{aligned} \hat{w}_1'''' + [\rho \, s^2 + c_\mathrm {d}(x)\, s + k_\mathrm {d}^\mathrm {A}(x)]\,\hat{w}_1 = \hat{F}_\mathrm {1}^\mathrm {IC} + \hat{F}_\mathrm {1}^\mathrm {ML}, \nonumber \\ \end{aligned}$$

(13)

where $\hat{w}_\mathrm {1}$ represents the unknown displacement in the Laplace domain; $s=\sigma + \mathrm {i}\omega$ is the Laplace variable, where $\sigma$ is a small and positive real number and $\omega$ represents the angular frequency; subscript 1 represents that the analysis is performed for the system before the elastic displacement limit $w_\mathrm {el}$ is exceeded for the first time. Furthermore, $\hat{F}_\mathrm {1}^\mathrm {ML}$ represents the Laplace-domain force exerted by the moving load and $\hat{F}_{1}^\mathrm {IC}$ represents the forcing induced by the input initial conditions:

$$\begin{aligned} \hat{F}_\mathrm {1}^\mathrm {ML}&= -\frac{F_0}{v}\, \mathrm {e}^{-s \frac{x}{v}}, \end{aligned}$$

(14)

$$\begin{aligned} \hat{F}_{1}^\mathrm {IC}&= \rho (s\, w^\mathrm {in} + \dot{w}^\mathrm {in}) + c_\mathrm {{d}}(x)\, w^\mathrm {{in}}. \end{aligned}$$

(15)

It must be noted that the Dirac delta function which describes the moving load in the time domain becomes a spatially distributed load in the Laplace domain, as can be seen in Eq. 14.

Because of the spatial variation of the foundation stiffness and damping, Eq. (13) cannot be solved analytically for all stiffness and damping profiles. Therefore, the fourth-order spatial derivative is approximated using the Finite Difference Method. A central difference scheme of order $O(\Delta x^6)$ is used inside the domain, and a hybrid between a central and a forward/backward scheme is used at the boundaries. The coefficients used for the finite difference discretization are given in Appendix A. As boundary conditions for the computational domain, the reaction forces delivered by the semi-infinite domains, namely the bending moment Eq. (6) and the shear force Eq. (7), are employed. These reaction forces are derived in Sect. 2.3.2 by imposing the displacement Eq. (4) and slope Eq. (5) of the computational domain as boundary conditions for the semi-infinite domains. Note that for the non-reflective boundaries derived in Sect. 2.3.2 to be correct, the computational domain must behave linearly at the boundaries. Therefore, the length of the computational domain must be chosen such that the expected nonlinear behaviour is located between its boundaries. After applying the Finite Difference Method to discretize the computational domain, the Laplace-domain equation of motion reads

$$\begin{aligned}&[K_{ij} + (\rho \, s^2 + c_{\mathrm {d,}i} \, s + k_{\mathrm {d},1,i}) I_{ij}]\, \hat{w}_{1,j} \nonumber \\&\quad = \hat{F}_{1,i}^\mathrm {IC} + \hat{F}_{1,i}^\mathrm {ML} + \hat{F}_{1,i}^\mathrm {D} \, , \end{aligned}$$

(16)

where $K_{ij}$ represents the bending stiffness matrix of the beam incorporating the contribution of the boundary conditions which is proportional to the unknown displacement, while $\hat{F}_{1,i}^\mathrm {D}$ represents the contribution of the boundary conditions independent of the unknown displacement, which is regarded as an external forcing (see Sect. 2.3.2); $I_{ij}$ is the identity matrix. The Laplace-domain displacement $\hat{w}_{1,j}$ is obtained by left-multiplying Eq. (16) by the inverse of the dynamic stiffness matrix (i.e., the term in the square brackets). Then, the inverse Laplace transform is numerically evaluated to obtain the solution in the time domain. Making use of the symmetry properties of the imaginary and real parts of the Laplace-domain spectrum, only positive frequencies are considered. For the results presented in this paper, the Trapezoidal Rule is used to evaluate the integral numerically.

Fig. 2

Definition of the time intervals and the local and global (overbar) nonlinear events

The obtained time-domain solution is correct until the first nonlinear event, defined as the moment in time at which the solution exceeds the elastic limit $w_\mathrm {el}$ at a certain location inside the computational domain. To obtain the correct solution after the first nonlinear event (i.e., time moment $\tau _1$), the equation of motion of the computational domain, Eq. (2), is changed as follows:

• The Winkler stiffness profile is modified by assigning the adequate stiffness to the nodes where the elastic limit has been exceeded.

• A new time variable is introduced, namely $t_\mathrm {2} = t - \overline{\tau }_1$ for $t \ge \overline{\tau }_1$. Note that time t represents the global time. Furthermore, for clarity, the time moment of a nonlinear event in the global time axis t is represented with an overbar ($\overline{\tau }_n$), while in the local time axes $t_n$, this moment is indicated without the overbar ($\tau _n$). Figure 2 offers a graphical representation of the different time axes and nonlinear events.

• To ensure continuity, the displacement and velocity of the previous system at $\tau _1$ are prescribed as initial conditions for the new system:

  $$\begin{aligned}&w_2(x,t_2=0) = w_1(x,t=\tau _1), \end{aligned}$$

  (17)
  $$\begin{aligned}&\dot{w}_2(x,t_2=0) = \dot{w}_1(x,t=\tau _1). \end{aligned}$$

  (18)

  Note that these initial conditions differ from the input initial conditions defined in Sect. 2.3.1.

• The boundary conditions are updated, as shown in Sect. 2.3.2.

• The position of the moving load is updated accordingly.

The updated system behaves again linearly until the next nonlinear event. Therefore, the forward Laplace transform is applied with respect to the new time variable $t_\mathrm {2}$. The Laplace-domain equation of motion of the new system reads

$$\begin{aligned}&[K_{ij} + (\rho \, s_2^2 + c_\mathrm {{d,\textit{i}}} s_2 + k_\mathrm {{d,2,\textit{i}}}) I_{ij}]\, \hat{w}_{2,j} \nonumber \\&\quad =\hat{F}_{2,i}^\mathrm {IC} + \hat{F}_{2,i}^\mathrm {ML} + \hat{F}_{2,i}^\mathrm {NL} + \hat{F}_{2,i}^\mathrm {D} , \end{aligned}$$

(19)

where $s_\mathrm {2}$ represents the Laplace variable associated with the new time variable $t_\mathrm {2}$, $\hat{w}_{2}$ is the unknown Laplace-domain displacement of the new system, and subscript 2 represents that the analysis is performed for the system in the second time interval. The term $\hat{F}_{2,i}^\mathrm {ML}$ is associated with the moving load acting on the new system, while the initial conditions for the new time interval are accounted for through $\hat{F}_{2,i}^\mathrm {IC}$:

$$\begin{aligned} \hat{F}_{2,i}^\mathrm {ML}= & {} -\frac{F_0}{v}\, \mathrm {e}^{-s_2 \big (\frac{x_i}{v} - \overline{\tau }_1 \big )} \, H\bigg (\frac{x_i}{v}-\overline{\tau }_1\bigg ), \end{aligned}$$

(20)

$$\begin{aligned} \hat{F}_{2,i}^\mathrm {IC}= & {} \rho (s_2\, w_{1,i}(\tau _1) + \dot{w}_{1,i}(\tau _1)) + c_\mathrm {{d,\textit{i}}}\,w_{1,i}(\tau _1).\nonumber \\ \end{aligned}$$

(21)

The Laplace-domain force exerted by the foundation is split into its contribution proportional to the unknown displacement, $k_{\mathrm {d,2},i} \, \hat{w}_2$, and the one independent of the unknown displacement, which is accounted for through the external force $\hat{F}_\mathrm {2}^\mathrm {NL}$, with superscript NL standing for nonlinear:

$$\begin{aligned} k_{\mathrm {d,2},i} \, \hat{w}_{2,i}&= {\left\{ \begin{array}{ll} k_{\mathrm {d},i}^\mathrm {A} \, \hat{w}_{2,i}, &{} w_{2,i}(t_2=0) \le w_\mathrm {el}, \\ k_{\mathrm {d},i}^\mathrm {B} \, \hat{w}_{2,i}, &{} w_{2,i}(t_2=0) > w_\mathrm {el}, \end{array}\right. } \end{aligned}$$

(22)

$$\begin{aligned} \hat{F}_{2,i}^\mathrm {NL}&= {\left\{ \begin{array}{ll} 0, &{} w_{2,i}(t_2=0) \le w_\mathrm {el},\\ \frac{\Delta k_{\mathrm {d},i} w_\mathrm {el}}{s_2}, &{} w_{2,i}(t_2=0) > w_\mathrm {el}. \end{array}\right. } \end{aligned}$$

(23)

The solution of the new system is obtained in the same manner as for the previous one. Moreover, the procedure of searching for the next nonlinear event, modifying the system and then solving it using the Laplace transform, is repeated. To this end, the procedure is generalized. The Laplace-domain equation of motion for the nth time interval reads

$$\begin{aligned}&[K_{ij} + (\rho \, s_n^2 + c_{\mathrm {d},i} s_n + k_{\mathrm {d},n,i}) I_{ij}]\, \hat{w}_{n,j}\nonumber \\&\quad =\hat{F}_{n,i}^\mathrm {IC} + \hat{F}_{n,i}^\mathrm {ML} + \hat{F}_{n,i}^\mathrm {NL} + \hat{F}_{n,i}^\mathrm {D} \, , \end{aligned}$$

(24)

where the generalized moving load and initial condition forces are given as

$$\begin{aligned} \hat{F}_{n,i}^\mathrm {ML}&= -\frac{F_0}{v}\, \mathrm {e}^{-s_n \big (\frac{x_i}{v} - \overline{\tau }_{n-1} \big )} \, H\bigg (\frac{x_i}{v} - \overline{\tau }_{n-1} \bigg ), \end{aligned}$$

(25)

$$\begin{aligned} \hat{F}_{n,i}^\mathrm {IC}&= \rho \big (s_n\, w_{n-1,i}(\tau _{n-1}) + \dot{w}_{n-1,i}(\tau _{n-1}) \big )\nonumber \\&\quad +c_{\mathrm {d},i}\,w_{n-1,i}(\tau _{n-1}). \end{aligned}$$

(26)

The described procedure is repeated until the whole solution is obtained in the time domain. The discretized displacement of the computational domain thus becomes

$$\begin{aligned} w_j(t)= & {} [w_{1,j}(0, \ldots ,\tau _1-\Delta t), \,\, w_{2,j}(0, \ldots ,\tau _2-\Delta t),\nonumber \\&\ldots \, , w_{N,j}(0, \ldots ,t_\mathrm {max}-\overline{\tau }_{N-1})], \end{aligned}$$

(27)

where $\Delta t$ is the time spacing, N is the index of the last time interval, and $t_\mathrm {max}$ is the final moment in time of the simulation.

To obtain correct results, the continuity of displacements and velocities at the nonlinear events is of crucial importance. However, the Laplace-domain spectra of the two quantities exhibit a poor decay due to the applied initial conditions. Consequently, the numerical integration must be performed up to very high frequencies leading to a significant computational effort. In the following section, a method of incorporating the high frequencies without increasing the computational effort is presented.

2.2.1 Improvement of the frequency-spectra decay

The high-frequency regime of the Laplace-domain displacement, obtained from Eq. (24), is dominated by the initial conditions as follows:

$$\begin{aligned} \hat{w}_{n,j} \sim \frac{w_{n-1,j}(\tau _{n-1})}{\sigma +\mathrm {i}\omega _n} + \frac{\dot{w}_{n-1,j}(\tau _{n-1})}{(\sigma +\mathrm {i}\omega _n)^2}, \quad \omega _n \xrightarrow {} \infty . \nonumber \\ \end{aligned}$$

(28)

Similarly, the Laplace-domain velocity $\hat{v}_{n,j}$ in the high-frequency regime reads

$$\begin{aligned} \hat{v}_{n,j} \sim \frac{\dot{w}_{n-1,j}(\tau _{n-1})}{\sigma +\mathrm {i}\omega _n} + \frac{\ddot{w}_{n-1,j}(\tau _{n-1})}{(\sigma +\mathrm {i}\omega _n)^2}, \quad \omega _n \xrightarrow {} \infty . \nonumber \\ \end{aligned}$$

(29)

The initial displacement, velocity and acceleration in the numerators of Eqs. (28) and (29) are clearly independent of frequency. Therefore, the Laplace-domain spectra are dominated by the expressions in the denominator, exhibiting the slow decay proportional to $1/\omega _n$.

To incorporate the high frequencies without the need to integrate numerically up to very high frequencies, the high-frequency approximations, Eqs. (28) and (29), could be subtracted from $\hat{w}_{n,j}$ and $\hat{v}_{n,j}$, respectively. However, in doing so, a high peak is introduced in the remaining frequency spectra close to $\omega _n = 0$, which would require a very small step in frequency for obtaining accurate results. To overcome this issue, the high-frequency approximations are only subtracted over part of the frequency axis $\omega _n \ge \omega _\mathrm {A}$. The only criterion for choosing $\omega _\mathrm {A}$ is that it is sufficiently distant from the origin $\omega _n = 0$ to ensure that the resulting spectrum does not exhibit a high peak. The Laplace-domain displacement and velocity can now be expressed as

$$\begin{aligned} \hat{w}_{n,j}= & {} \hat{w}_{n,j}^\mathrm {imp} + \frac{w_{n-1,j}(\tau _{n-1})}{\sigma +\mathrm {i}\omega _n} H(\omega _n - \omega _\mathrm {A}) \nonumber \\&+ \frac{\dot{w}_{n-1,j}(\tau _{n-1})}{(\sigma +\mathrm {i}\omega _n)^2} H(\omega _n - \omega _\mathrm {A}), \end{aligned}$$

(30)

$$\begin{aligned} \hat{v}_{n,j}= & {} \hat{v}_{n,j}^\mathrm {imp} + \frac{\dot{w}_{n-1,j}(\tau _{n-1})}{\sigma +\mathrm {i}\omega _n} H(\omega _n - \omega _\mathrm {A}) \nonumber \\&+ \frac{\ddot{w}_{n-1,j}(\tau _{n-1})}{(\sigma +\mathrm {i}\omega _n)^2} H(\omega _n - \omega _\mathrm {A}), \end{aligned}$$

(31)

where $\hat{w}_{n,j}^\mathrm {imp}$ and $\hat{v}_{n,j}^\mathrm {imp}$ represent the improved (i.e., with strong decay) Laplace-domain expressions of the displacement and velocity, respectively. To obtain the time-domain response, the inverse Laplace transform is evaluated numerically for the improved expressions, and analytically for the high-frequency approximations, as follows:

$$\begin{aligned} w_{n,j}&= \frac{1}{\uppi }\int _{0}^{\omega _\mathrm {max}}\mathrm {Re}(\hat{w}_{n,j}^\mathrm {imp} \, \mathrm {e}^{s_n t_n}) \mathrm {d}\omega _n \nonumber \\&\quad + w_{n-1,j}(\tau _{n-1}) \, I_\mathrm {a}(t_n)+ \dot{w}_{n-1,j}(\tau _{n-1}) \, I_\mathrm {b}(t_n), \end{aligned}$$

(32)

$$\begin{aligned} \dot{w}_{n,j}&= \frac{1}{\uppi }\int _{0}^{\omega _\mathrm {max}}\mathrm {Re}(\hat{v}_{n,j}^\mathrm {imp} \, \mathrm {e}^{s_n t_n}) \mathrm {d}\omega _n \nonumber \\&\quad +\dot{w}_{n-1,j}(\tau _{n-1}) \, I_\mathrm {a}(t_n) + \ddot{w}_{n-1,j}(\tau _{n-1}) \, I_\mathrm {b}(t_n), \end{aligned}$$

(33)

where $\omega _\mathrm {max}$ represents the maximum frequency of integration, while $I_\mathrm {a}(t_n)$ and $I_\mathrm {b}(t_n)$ represent the time-domain images of the high-frequency approximations divided by the corresponding initial condition terms. Their expressions are not presented here for brevity; however, they can be easily computed using a symbolic mathematics tool (e.g., Maple).

By evaluating the inverse Laplace transform analytically for the high-frequency approximations, frequencies up to infinity are actually included, which represents an improvement not just in computational time, but also in accuracy (although the results are still approximations since $\hat{w}_{n,j}^\mathrm {imp}$ and $\hat{v}_{n,j}^\mathrm {imp}$ are not completely zero at $\omega _\mathrm {max}$). Using the improvement presented in this section, the solution obeys the continuity conditions (i.e., displacement and velocity) imposed at nonlinear events. The input initial conditions and the non-reflective boundary conditions are derived in the next section.

2.3 Infinite extent of the model

2.3.1 Moving-load entry of the computational domain

At the start of the computation, the position of the moving load is at $x=0$. For computational efficiency, this point must be as close as possible to the transition zone. To correctly represent the behaviour as described by Eqs. (1) to (3), which assume that the load has been active for a long time, the input initial conditions must be chosen such that the system is in the steady-state regime. Assuming that the system is initially in the linear regime ($w(x,t=0) < w_\mathrm {el}$), the input initial conditions are based on the steady-state field of the approaching load, also referred to as the eigenfield$w^\mathrm {e}(x,t)$. The steady-state response of an infinite Euler–Bernoulli beam resting on a homogeneous and linear Winkler foundation to a moving constant load was derived using different methods (e.g., time-domain method, transform method) in, for example, [42]. Accounting also for the viscous damping of the supporting structure, the eigenfield reads

$$\begin{aligned} w^\mathrm {e}(x,t) = {\left\{ \begin{array}{ll} A_1 \mathrm {e}^{-\mathrm {i}k_{2}^\mathrm {e}(x-vt)} + B_1 \mathrm {e}^{-\mathrm {i}k_{3}^\mathrm {e}(x-vt)}, &{} x < vt, \\ A_2 \mathrm {e}^{-\mathrm {i}k_{1}^\mathrm {e}(x-vt)} + B_2 \mathrm {e}^{-\mathrm {i}k_{4}^\mathrm {e}(x-vt)}, &{} x \ge vt, \end{array}\right. } \nonumber \\ \end{aligned}$$

(34)

where $A_1$, $A_2$, $B_1$ and $B_2$ represent the complex-valued amplitudes and $k_{1}^\mathrm {e}$, $k_{2}^\mathrm {e}$, $k_{3}^\mathrm {e}$ and $k_{4}^\mathrm {e}$ represent the complex wavenumbers of the eigenfield. Their expressions are given in Appendix B. It must be noted that $w^\mathrm {e}(x,t)$ in Eq. (34) is real-valued.

The eigenfield is derived assuming a homogeneous Winkler foundation. Consequently, choosing the input initial conditions based on the eigenfield is correct only if the field is not disturbed by the inhomogeneity (transition zone). The length of the computational domain and the position of the transition zone should thus be chosen such that the input initial state (i.e., displacement field, velocity field) based on the eigenfield has decayed before the inhomogeneity. Therefore, the part of the computational domain to the left of the transition zone has as input initial conditions the eigenfield part in front of the load, while the left semi-infinite domain has as input initial conditions the eigenfield part behind the load. Moreover, the input initial conditions at the inhomogeneity and to the right of it, including the right semi-infinite domain, are trivial. Equating t to 0 in Eq. (34) and in its time derivative, the input initial conditions, Eqs. (9) to (11), become

$$\begin{aligned}&w_\mathrm {l}^\mathrm {in}(x) = w^\mathrm {e}(x,t=0), \qquad \qquad \mathrm {-\infty }<x<\mathrm {0}, \nonumber \\&\dot{w}_\mathrm {l}^\mathrm {in}(x)= \dot{w}^\mathrm {e}(x,t=0), \qquad \qquad \mathrm {-\infty }<x <\mathrm {0}, \end{aligned}$$

(35)

$$\begin{aligned}&w\mathrm {^{in}}(x) = w^\mathrm {e}(x,t=0), \qquad \qquad \quad \,\, \mathrm {0}<x< L,\nonumber \\&\dot{w}^\mathrm {{in}}(x) = \dot{w}^\mathrm {e}(x,t=0),\qquad \qquad \quad \,\, \mathrm {0}<x < L, \end{aligned}$$

(36)

$$\begin{aligned}&w_\mathrm {r}^\mathrm {in}(x) = 0, \qquad \qquad \qquad \qquad \quad \,\,\,\,\, L<x<\mathrm {\infty }, \nonumber \\&\dot{w}_\mathrm {r}^\mathrm {in}(x) = 0, \qquad \qquad \qquad \qquad \quad \,\,\,\,\, L<x <\mathrm {\infty }. \end{aligned}$$

(37)

With these input initial conditions, the system reaches the steady-state regime instantly at the start of the computation. Next, boundary conditions are derived such that the waves generated inside the computational domain are not reflected at the boundaries.

2.3.2 Derivation of the non-reflective boundary conditions

In Sect. 2.2, the boundary conditions for the computational domain, imposed bending moment Eq. (6) and shear force Eq. (7), were kept general. In this section, the reaction forces of the semi-infinite domains at the interfaces with the computational domain are derived. When these forces are prescribed as boundary conditions of the computational domain, the finite system will behave exactly as the infinite one. Therefore, these interface reaction forces constitute non-reflective boundary conditions for the computational domain. The goal is to express the interface reaction forces (bending moment and shear force) of the left and right domains as functions of the unknown displacement and slope of the computational domain at the corresponding interfaces. To this end, the forward Laplace transform is applied over time $t_n$ to the equations of motion of the two semi-infinite domains, Eqs. (1) and (3):

$$\begin{aligned} \hat{w}_{\mathrm{l},n}'''' - k_\mathrm{l}^4 \, \hat{w}_{\mathrm{l},n}&= \hat{F}_{\mathrm{l},n}^\mathrm {IC}, \end{aligned}$$

(38)

$$\begin{aligned} \hat{w}_{\mathrm{r},n}'''' - k_\mathrm{r}^4 \, \hat{w}_{\mathrm{r},n}&= \hat{F}_{\mathrm{r},n}^\mathrm {IC} + \hat{F}_{\mathrm {r},n}^\mathrm {ML}, \end{aligned}$$

(39)

where $\hat{w}_{\mathrm {l},n}$ and $\hat{w}_{\mathrm {r},n}$ represent the unknown Laplace-domain displacements of the left and right semi-infinite domains, respectively, for the nth time interval, and $\hat{F}_{\mathrm {r},n}^\mathrm {ML}$ represents the Laplace-domain moving load acting on the right domain, given by Eq. 26, but with a continuous spatial coordinate x. $k_\mathrm {l}$ and $k_\mathrm {r}$ represent the wavenumbers of the two semi-infinite domains and read

$$\begin{aligned} k_h = \root 4 \of {-\rho \, s_n^2 - c_{\mathrm {d},h}\, s_n - k_{\mathrm {d},h}}, \qquad h=\{\mathrm {l,r}\}, \end{aligned}$$

(40)

where the branches of the complex wavenumbers are chosen such that $\mathrm {Im}{(k_h)}<0$ and $\mathrm {Re}{(k_{h})}>0$. Furthermore, $\hat{F}_{\mathrm {l},n}^\mathrm {IC}$ and $\hat{F}_{\mathrm {r},n}^\mathrm {IC}$ represent the Laplace-domain initial condition forces given by

$$\begin{aligned} \begin{aligned} \hat{F}_{h,n}^\mathrm {IC}(x,s_n)&= (\rho s_n + c_{\mathrm {d},h}) \, w_{h}(x,\overline{\tau }_{n-1}) \\&\quad + \rho \, \dot{w}_{h}(x,\overline{\tau }_{n-1}), \quad h=\{\mathrm {l,r}\}. \end{aligned} \end{aligned}$$

(41)

At infinity, the condition of zero displacements is imposed, Eq. (8), while at the interfaces the unknown Laplace-domain displacement and slope of the computational domain are prescribed:

$$\begin{aligned} \hat{w}_{\mathrm {l},n}(0,s_n)&= \hat{w}_n(0,s_n),&\hat{w}_{\mathrm {r},n}(L,s_n)&= \hat{w}(L,s_n), \end{aligned}$$

(42)

$$\begin{aligned} \hat{w}'_{\mathrm {l},n}(0,s_n)&= \hat{w}'_n(0,s_n),&\hat{w}'_{\mathrm {r},n}(L,s_n)&=\hat{w}'_n (L,s_n). \end{aligned}$$

(43)

The Laplace-domain displacement of the two semi-infinite domains can be obtained by solving Eqs. (38) and (39) with the above-discussed boundary conditions. By taking the second- and third-order derivatives with respect to space and evaluating them at the interfaces, the reaction forces of the two semi-infinite domains are expressed as functions of the displacement and slope of the computational domain prescribed at the corresponding interfaces:

$$\begin{aligned} \begin{pmatrix} \hat{w}'''_{\mathrm {l},n} (0,s_n) \\ \hat{w}''_{\mathrm {l},n} (0,s_n) \end{pmatrix}= & {} \begin{pmatrix} k_\mathrm {l,V\upupsilon } &{} k_\mathrm {l,V\upphi } \\ k_\mathrm {l,M\upupsilon } &{} k_\mathrm {l,M\upphi } \end{pmatrix} \begin{pmatrix} \hat{w}_n (0,s_n) \\ \hat{w}'_n (0,s_n) \end{pmatrix}\nonumber \\&\quad - \mathbf D _{\mathrm {l},n}, \end{aligned}$$

(44)

$$\begin{aligned} \begin{pmatrix} \hat{w}'''_{\mathrm {r},n} (L,s_n) \\ \hat{w}''_{\mathrm {r},n} (L,s_n) \end{pmatrix}= & {} \begin{pmatrix} k_\mathrm {r,V\upupsilon } &{} k_\mathrm {r,V\upphi } \\ k_\mathrm {r,M\upupsilon } &{} k_\mathrm {r,M\upphi } \end{pmatrix} \begin{pmatrix} \hat{w}_n (L,s_n) \\ \hat{w}'_n (L,s_n) \end{pmatrix} \nonumber \\&-\, \mathbf D _{\mathrm {r},n} - \begin{pmatrix} \hat{V}_{\mathrm {L},n}(s_n) \\ \hat{M}_{\mathrm {L},n}(s_n) \end{pmatrix}, \end{aligned}$$

(45)

where the entries of the matrices represent the dynamic stiffness coefficients giving rise to the boundary forces proportional to the unknown displacement and slope at the boundary; subscript V stands for shear force, M for bending moment, $\upupsilon$ for translation, and $\upphi$ for rotation. The coefficients read

$$\begin{aligned} k_{h,\mathrm {V\upupsilon }}&= (-1+\mathrm {i})k_h^3,&k_{h,\mathrm {V\upphi }}&= \mathrm {i}k_h^2, \end{aligned}$$

(46)

$$\begin{aligned} k_{h,\mathrm {M\upphi }}&= (1+\mathrm {i})k_h ,&k_{h,\mathrm {M\upupsilon }}&= \mathrm {i} k_h^2, \quad h=\{\mathrm {l,r}\}. \end{aligned}$$

(47)

In addition, $\mathbf D _\mathrm {l,\textit{n}}$ and $\mathbf D _\mathrm {r,\textit{n}}$ are vectors containing the influence of the initial conditions Eq. (41) on the reaction forces, giving rise to boundary forces independent of the unknown displacement and slope of the computational domain. The two vectors are given by the following expressions:

$$\begin{aligned} \mathbf D _{\mathrm {l},n}= & {} \begin{pmatrix} \hat{w}'''_{\mathrm {l},n,\mathrm {p}} (0,s_n) \\ \hat{w}''_{\mathrm {l},n,\mathrm {p}} (0,s_n) \end{pmatrix} + \begin{pmatrix} k_\mathrm {l,V\upupsilon } &{} k_\mathrm {l,V\upphi } \\ k_\mathrm {l,M\upupsilon } &{} k_\mathrm {l,M\upphi } \end{pmatrix} \begin{pmatrix} \hat{w}_{\mathrm {l},n,\mathrm {p}} (0,s_n) \\ \hat{w}'_{\mathrm {l},n,\mathrm {p}} (0,s_n) \end{pmatrix}, \end{aligned}$$

(48)

$$\begin{aligned} \mathbf D _{\mathrm {r},n}= & {} \begin{pmatrix} \hat{w}'''_{\mathrm {r},n,\mathrm {p}} (L,s_n) \\ \hat{w}''_{\mathrm {r},n,\mathrm {p}} (L,s_n) \end{pmatrix} + \begin{pmatrix} k_\mathrm {r,V\upupsilon } &{} k_\mathrm {r,V\upphi } \\ k_\mathrm {r,M\upupsilon } &{} k_\mathrm {r,M\upphi } \end{pmatrix} \begin{pmatrix} \hat{w}_{\mathrm {r},n,\mathrm {p}} (L,s_n) \\ \hat{w}'_{\mathrm {r},n,\mathrm {p}} (L,s_n) \end{pmatrix},\nonumber \\&\quad \overline{\tau }_{n-1} \le \frac{L}{v}, \nonumber \\ \end{aligned}$$

(49)

where $\hat{w}_{\mathrm {l},n,\mathrm {p}}(0,s_n)$ and $\hat{w}_{\mathrm {r},n,\mathrm {p}} (L,s_n)$ are the particular solutions that account for the initial condition forcing in Eqs. (38) and (39). Furthermore, $\hat{V}_{\mathrm {L},n}$ and $\hat{M}_{\mathrm {L},n}$ are the shear force and bending moment, respectively, exerted by the moving load on the right boundary after it has entered the right semi-infinite domain:

$$\begin{aligned} \hat{V}_{\mathrm {L},n}(s_n)&= \frac{\mathrm {i}F_0 \big (s_n + (1+\mathrm {i}) k_\mathrm {r} v \big )}{(k_\mathrm {r}v + s_n)(k_\mathrm {r} v - \mathrm {i} s_n)} \,\mathrm {e}^{-s_n\big (\frac{L}{v} - \overline{\tau }_{n-1}\big )},\nonumber \\&\qquad \overline{\tau }_{n-1} \le \frac{L}{v}, \end{aligned}$$

(50)

$$\begin{aligned} \hat{M}_{\mathrm {L},n}(s_n)&= \frac{-\mathrm {i}F_0 v}{(k_\mathrm {r}v + s_n)(k_\mathrm {r} v - \mathrm {i} s_n)}\,\mathrm {e}^{-s_n\big ( \frac{L}{v} - \overline{\tau }_{n-1} \big )}, \nonumber \\&\qquad \overline{\tau }_{n-1} \le \frac{L}{v}. \end{aligned}$$

(51)

Note that $\mathbf D _{\mathrm {r},n}$, $\hat{V}_{\mathrm {L},n}$ and $\hat{M}_{\mathrm {L},n}$ as given in Equations (49) to (51), respectively, are valid for $\overline{\tau }_{n-1} \le \frac{L}{v}$, meaning that the nonlinear events occur while the moving load is inside the computational domain. They still correctly describe the dynamics when the load is in the right domain, up to the moment a nonlinear event occurs. When nonlinear events occur while the moving load is in the right domain, this is divided into two domains, one behind the load and one in front, rendering the expressions for $\mathbf D _{\mathrm {r},n}$, $\hat{V}_{\mathrm {L},n}$ and $\hat{M}_{\mathrm {L},n}$ lengthy for $\overline{\tau }_{n-1}> \frac{L}{v}$. Therefore, these expressions are given in Appendix C.

To obtain the particular solutions in Eqs. (48) and (49), the Green’s-function approach is used as follows:

$$\begin{aligned} \hat{w}_{\mathrm {l},n,\mathrm {p}}(x,s_n)&= \int _{-\infty }^{0} \hat{g}_\mathrm {l}(x-\xi ,s_n) \, \hat{F}_{\mathrm {l},n}^\mathrm {IC}(\xi ,s_n) \, \mathrm {d}\xi , \end{aligned}$$

(52)

$$\begin{aligned} \hat{w}_{\mathrm {r},n,\mathrm {p}} (x,s_n)&= \int _{L}^{\infty } \hat{g}_\mathrm {r}(x-\xi ,s_n) \hat{F}_{\mathrm {r},n}^\mathrm {IC}(\xi ,s_n) \, \mathrm {d}\xi , \end{aligned}$$

(53)

where $\hat{g}_\mathrm {l}(x-\xi ,s_n)$ and $\hat{g}_\mathrm {r}(x-\xi ,s_n)$ are the Laplace-domain Green’s functions of two infinite domains having the same properties as the corresponding semi-infinite ones. The particular solutions are needed only at the interfaces, as seen in Eqs. (48) and (49). Therefore, excitation variable $\xi$ is smaller than or equal to the observation point $x=0$ for the left domain and $\xi$ is larger than or equal to $x=L$ for the right domain. Consequently, the Green’s functions are given by [43]

$$\begin{aligned}&\hat{g}_\mathrm {l}(x-\xi ,s_n) = -\frac{1}{k_\mathrm {l}^3} (\mathrm {ie}^{-\mathrm {i}k_\mathrm {l}(x-\xi )} + \mathrm {e}^{-k_\mathrm {l}(x-\xi )}), \end{aligned}$$

(54)

$$\begin{aligned}&\hat{g}_\mathrm {r}(x-\xi ,s_n) = -\frac{1}{k_\mathrm {r}^3} (\mathrm {ie}^{-\mathrm {i}k_\mathrm {r}(\xi -x)} + \mathrm {e}^{-k_\mathrm {r}(\xi -x)}). \end{aligned}$$

(55)

Now, the only unknowns left for deriving the non-reflective boundary conditions are the initial conditions of the two semi-infinite domains in Eq. (41). The state (i.e., displacement field, velocity field) of the two domains at time moment $\overline{\tau }_{n-1}$ consists of a superposition of the eigenfield and the waves generated inside the computational domain which have propagated to the two semi-infinite domains, referred to as the free field$w^\mathrm {f}$. The eigenfield’s contribution can be evaluated analytically by equating global time t to $\overline{\tau }_{n-1}$ in Eq. (34) and in its time derivative, and inserting the relevant medium parameters. The state of the two domains as induced by the free field can be obtained by solving two boundary value problems for the two domains with the time history of the free-field displacement and slope of the computational domain observed at the boundaries prescribed as boundary conditions (Fig. 3). The free-field displacement at the boundaries is obtained by subtracting the eigenfield from the displacement of the computational domain Eq. (27), which is known until time moment $\overline{\tau }_{n-1}$:

$$\begin{aligned} w^\mathrm {f} (0;t=0, \ldots ,\overline{\tau }_{n-1})&= w (0; t=0, \ldots ,\overline{\tau }_{n-1})\nonumber \\&\quad - w^\mathrm {e} (0; t=0, \ldots ,\overline{\tau }_{n-1}), \end{aligned}$$

(56)

$$\begin{aligned} w^\mathrm {f} (L;t=0, \ldots ,\overline{\tau }_{n-1})&=w (L; t=0, \ldots ,\overline{\tau }_{n-1})\nonumber \\&\quad - w^\mathrm {e} (L; t=0, \ldots ,\overline{\tau }_{n-1}). \end{aligned}$$

(57)

After computing the free-field slopes numerically, the boundary value problems needed to determine the state of the left and right domains (Fig. 3) are solved using the Laplace transform over global time t. Note that $w^\mathrm {f}(0,t>\overline{\tau }_{n-1})$ and $w^\mathrm {f}(L,t>\overline{\tau }_{n-1})$ are still unknown and by default equal to zero. Consequently, the discontinuity in the free-field displacements and slopes at $\overline{\tau }_{n-1}$ introduces high-frequency content in its Laplace-domain counterparts.

Fig. 3

Time-domain boundary value problems to be solved for obtaining the initial states of the left and right domains due to the free field at time moment $t = \overline{\tau }_{n-1}$

To avoid this, an artificial smooth continuation is imposed on the free-field displacements and slopes for $t > \overline{\tau }_{n-1}$, which does not affect the response for $t \le \overline{\tau }_{n-1}$. Then, the Laplace-domain free-field displacements are given as follows:

$$\begin{aligned} \hat{w}_\mathrm {l}^\mathrm {f} (x,s)&= C_{\mathrm {l}} \, \mathrm {e}^{\mathrm {i}k_\mathrm {l}x} + D_{\mathrm {l}} \, \mathrm {e}^{k_\mathrm {l}x}, \end{aligned}$$

(58)

$$\begin{aligned} \hat{w}_\mathrm {r}^\mathrm {f} (x,s)&= C_{\mathrm {r}} \, \mathrm {e}^{-\mathrm {i}k_\mathrm {r}x} + D_{\mathrm {r}} \, \mathrm {e}^{-k_\mathrm {r}x}, \end{aligned}$$

(59)

where $C_{\mathrm {l}}$, $D_{\mathrm {l}}$, $C_{\mathrm {r}}$ and $D_{\mathrm {r}}$ represent complex-valued amplitudes which read

$$\begin{aligned} C_{\mathrm {l}}&= \frac{1+\mathrm {i}}{2k_\mathrm {l}}[k_\mathrm {l} \, \hat{w}^{\mathrm {f}} (0,s) - \hat{w}^{\mathrm {f} \prime } (0,s)], \end{aligned}$$

(60)

$$\begin{aligned} D_{\mathrm {l}}&= \frac{1-\mathrm {i}}{2k_\mathrm {l}}[k_\mathrm {l} \, \hat{w}^{\mathrm {f}} (0,s) + \mathrm {i}\hat{w}^{\mathrm {f} \prime }(0,s)], \end{aligned}$$

(61)

$$\begin{aligned} C_{\mathrm {r}}&= \frac{1+\mathrm {i}}{2k_\mathrm {r}}[k_\mathrm {r} \, \hat{w}^\mathrm {f} (L,s) - \hat{w}^{\mathrm {f} \prime } (L,s)] \, \mathrm {e}^{\mathrm {i}k_\mathrm {r} L}, \end{aligned}$$

(62)

$$\begin{aligned} D_{\mathrm {r}}&= \frac{1-\mathrm {i}}{2k_\mathrm {r}}[k_\mathrm {r} \, \hat{w}^\mathrm {f} (L,s) - \mathrm {i}\hat{w}^{\mathrm {f} \prime } (L,s)] \, \mathrm {e}^{k_\mathrm {r} L}. \end{aligned}$$

(63)

Note that the forward Laplace transform is applied with respect to the time variable t because the displacement and slope imposed as boundary conditions act from the time moment $t = 0$ until $t = \overline{\tau }_{n-1}$. Therefore, $\hat{w}^\mathrm {f}(0,s)$ and $\hat{w}^\mathrm {f}(L,s)$ represent Laplace-domain history contributions for the new system and need to be computed for each nonlinear event.

Fig. 4

Synoptic chart describing the algorithm; n denotes the time interval and indices i and j represent the node number

To obtain the time-domain displacement and velocity of the two semi-infinite domains needed in Eq. (41) and thus for the derivation of the non-reflective boundary conditions, the inverse Laplace transform is applied to Eqs. (58), (59) and the corresponding velocities and is evaluated at $\overline{\tau }_{n-1}$:

$$\begin{aligned} w_{\mathrm {l}} (x,\overline{\tau }_{n-1})&= \frac{1}{2\uppi \mathrm {i}}\int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty }\hat{w}_\mathrm {l}^\mathrm {f} (x,s) \, \mathrm {e}^{s \overline{\tau }_{n-1}} \mathrm {d}s \nonumber \\&\qquad + w^\mathrm {e}(x,\overline{\tau }_{n-1}), \end{aligned}$$

(64)

$$\begin{aligned} \dot{w}_{\mathrm {l}} (x,\overline{\tau }_{n-1})&= \frac{1}{2\uppi \mathrm {i}}\int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty }s \, \hat{w}_\mathrm {l}^\mathrm {f} (x,s) \, \mathrm {e}^{s \overline{\tau }_{n-1}} \mathrm {d}s \nonumber \\&\qquad + \dot{w}^\mathrm {e}(x, \overline{\tau }_{n-1}), \end{aligned}$$

(65)

$$\begin{aligned} w_{\mathrm {r}} (x,\overline{\tau }_{n-1})&= \frac{1}{2\uppi \mathrm {i}}\int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty }\hat{w}_\mathrm {r}^\mathrm {f} (x,s) \, \mathrm {e}^{s \overline{\tau }_{n-1}} \mathrm {d}s \nonumber \\&\qquad + w^\mathrm {e}(x, \overline{\tau }_{n-1}), \end{aligned}$$

(66)

$$\begin{aligned} \dot{w}_{\mathrm {r}} (x,\overline{\tau }_{n-1})&= \frac{1}{2\uppi \mathrm {i}}\int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty }s \, \hat{w}_\mathrm {r}^\mathrm {f} (x,s) \, \mathrm {e}^{s \overline{\tau }_{n-1}} \mathrm {d}s \nonumber \\&\qquad + \dot{w}^\mathrm {e}(x, \overline{\tau }_{n-1}). \end{aligned}$$

(67)

The particular solutions are now obtained by substituting Eqs. (64) to (67) in Eqs. (41), and (41) in Eqs. (52) and (53), and then changing the order of integration:

$$\begin{aligned} \hat{w}_{\mathrm {l},n,\mathrm {p}}(x,s_n)&= \frac{1}{2\uppi \mathrm {i}}\int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty } (\rho s_n + c_\mathrm {d,l} + \rho s) \, \mathrm {e}^{s \overline{\tau }_{n-1}} \nonumber \\&\quad \cdot {}\int _{-\infty }^{0} \hat{g}_\mathrm {l}(x - \xi ,s_n) \hat{w}_\mathrm {l}^\mathrm {f} (\xi ,s) \, \mathrm {d}\xi \mathrm {d}s \nonumber \\&\quad +\hat{w}_\mathrm {l,\textit{n},p}^\mathrm {e} (x,s_n), \end{aligned}$$

(68)

$$\begin{aligned} \hat{w}_{\mathrm {r},n,\mathrm {p}} (x,s_n)&= \frac{1}{2\uppi \mathrm {i}} \int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty } (\rho s_n +c_{\mathrm {d,r}}+ \rho s) \, \mathrm {e}^{s \overline{\tau }_{n-1}} \nonumber \\&\quad \cdot {} \int _{L}^{\infty } \hat{g}_\mathrm {r}(x - \xi ,s_n) \hat{w}_\mathrm {r}^\mathrm {f} (\xi ,s) \, \mathrm {d}\xi \, \mathrm {d}s \nonumber \\&\quad +\hat{w}_\mathrm {r,\textit{n},p}^\mathrm {e} (x,s_n), \end{aligned}$$

(69)

where $\hat{w}_\mathrm {l,\textit{n},p}^\mathrm {e} (x,s_n)$ and $\hat{w}_\mathrm {r,\textit{n},p}^\mathrm {e} (x,s_n)$ represent the particular solutions accounting for the parts of the eigenfield in the left and right domains, respectively, at $\overline{\tau }_{n-1}$. The integration over $\xi$ can be performed analytically, while the inverse Laplace transform evaluated at $\overline{\tau }_{n-1}$ should be performed numerically. Moreover, the spatial derivatives needed in Eqs. (48) and (49) can be evaluated analytically.

The non-reflective boundary conditions for the computational domain are now fully determined. The Laplace-domain boundary conditions are given by the following expressions:

$$\begin{aligned} \begin{pmatrix} \hat{w}'''_{n} (0,s_n) \\ \hat{w}''_{n} (0,s_n) \end{pmatrix}&= \begin{pmatrix} k_\mathrm {l,V\upupsilon } &{} k_{\mathrm {l,V\upphi }} \\ k_\mathrm {l,M\upupsilon } &{} k_{\mathrm {l,M\upphi }} \end{pmatrix} \begin{pmatrix} \hat{w}_n (0,s_n) \\ \hat{w}'_n (0,s_n) \end{pmatrix}\nonumber \\&\quad - \mathbf D _{\mathrm {l},n},&\end{aligned}$$

(70)

$$\begin{aligned} \begin{pmatrix} \hat{w}'''_{n} (L,s_n) \\ \hat{w}''_{n} (L,s_n) \end{pmatrix}&= \begin{pmatrix} k_\mathrm {r,V\upupsilon } &{} k_\mathrm {r,V\upphi } \\ k_\mathrm {r,M\upupsilon } &{} k_\mathrm {r,M\upphi } \end{pmatrix} \begin{pmatrix} \hat{w}_n (L,s_n) \\ \hat{w}'_n (L,s_n) \end{pmatrix} \nonumber \\&\quad - \mathbf D _{\mathrm {r},n} - \, \begin{pmatrix} \hat{V}_{\mathrm {L},n}(s_n) \\ \hat{M}_{\mathrm {L},n}(s_n) \end{pmatrix} . \end{aligned}$$

(71)

The contribution of the boundary conditions which is proportional to the yet unknown displacement and slope is incorporated into the beam’s bending stiffness matrix $K_{ij}$ (see Eq. (24)), while the contribution which is independent of the unknown displacement and slope is accounted for through the boundary-forcing vector $\tilde{F}_{n,i}^\mathrm {D}$. As can be seen, the beam’s bending stiffness matrix does not change from one system to the other; however, the boundary-forcing vector needs to be updated at each system change. A synoptic chart of the developed algorithm is presented in Fig. 4.

Although the obtained non-reflective boundary conditions have been derived for the moving load problem, the same procedure can be applied for any arbitrary loading. Next, the Winkler foundation model used for the results presented in this paper is described.

3 Winkler foundation

A variety of models have been used to represent the supporting structure in 1-D systems for railway applications (e.g., linear elastic, bilinear elastic, cubic super-linear, etc.); a good overview of models for the foundations in 1-D systems can be found in [44]. One of the most used nonlinear elastic models is the cubic super-linear one [e.g., 3. It assumes that the foundation springs exert a reaction force (visualized in Fig. 5) proportional to the displacement, through a linear stiffness term $k_\mathrm {l}$, and one proportional to the displacement cubed, through a nonlinear stiffness term $k_\mathrm {nl}$. In this paper, the constitutive relation of the Winkler foundation is based on the cubic super-linear model, but also incorporates the possibility of plastic deformation by selecting a different unloading path than that of the loading, as seen in Fig. 6.

Fig. 5

Piecewise-linear approximation (solid line) of the cubic super-linear constitutive model (dashed line); $F_\mathrm {k,W} = - k_\mathrm {l}\,w - k_\mathrm {nl}\,w^3$ for the cubic super-linear model with $k_\mathrm {l} = 35.03 \times 10^6 [\mathrm {N/m^2}]$ and $k_\mathrm {nl} = 1.74 \times 10^{13} [\mathrm {N/m^4}]$ [31, 32]

Fig. 6

Piecewise-linear constitutive law of the foundation; the loading/unloading path for the linear parts of the computational domain (1) and the first loading/unloading cycle for the nonlinear parts of the computational domain (2)

The loading path of the chosen constitutive relation approximates the cubic super-linear model through a piecewise-linear profile (Fig. 5) to accommodate the solution method presented in Sect. 2.2. Firstly, $k_\mathrm {d}^\mathrm {A}$ is assumed to be equal to the stiffness of the equivalent linear model [45]. This assumption is based on the ballast being relatively well compacted at the start of the simulation, represented in Fig. 5 through the nonzero displacement at zero force in the piecewise-linear approximation. This implies that the initial soft response of the foundation, as sometimes encountered, is excluded. Furthermore, assuming that the compaction is uniform along the track, the compacted configuration is taken as reference (zero displacement for zero force in Fig. 6). Secondly, the steady-state eigenfield is assumed to be in the linear regime. This assumption is based on the fact that in the homogeneous parts of the railway track, the steady-state displacement field induced by a train does not lead to significant degradation of the supporting structure. Thirdly, the elastic displacement limit $w_\mathrm {el}$ is chosen relative to the eigenfield’s maximum displacement $w^\mathrm {e}_\mathrm {max}$ in the soft part of the computational domain, where the ratio $q = w_\mathrm {el}/w^\mathrm {e}_\mathrm {max}$ is larger than 1. If $w_\mathrm {el}$ is not exceeded during the simulation, the system remains in the linear regime (branch (1) in Fig. 6). At locations where $w_\mathrm {el}$ is exceeded, the corresponding part of the foundation enters the second loading branch $k_\mathrm {d}^\mathrm {B}$. The value of $k_\mathrm {d}^\mathrm {B}$ is chosen such that it approximates the cubic super-linear model (Fig. 5).

The parameters of the cubic super-linear model which is approximated are chosen as similar to the ones used in other publications [i.e., 4, 5. However, the parameters for the unloading path, $k_\mathrm {d}^\mathrm {C}$ and $k_\mathrm {d}^\mathrm {D}$, are not well known. For the moment, the parameters are chosen such that the overall constitutive relation resembles the results of cyclic loading experiments on granular material [i.e., 6, but specific additional experiments or 3-D modelling might be needed in order to choose these parameters realistically. The model developed in this paper can even incorporate cyclic behaviour, and the parameters of the constitutive relation can be modified for each cycle to accommodate the behaviour as observed in the literature: changing stiffness with increasing cycle number, as well as a changing area (energy dissipation). However, the computational time required for the simulation of thousands of trains passages will be high. Nonetheless, valuable observations can be made from the short-term cyclic behaviour which have relevant implications for the long-term behaviour.

The constitutive model incorporates the possibility of separation between the rail and the supporting structure (Fig. 6). When the displacement of the beam is larger than the plastic deformation ($w>w_\mathrm {pl}$), the separation of the beam and foundation occurs. This results in a zero foundation force $F_\mathrm {k,W}$ as depicted in Fig. 6. However, this is only allowed at the location where the plastic deformation has been activated; in the parts of the computational domain with no plastic deformation, the beam is in permanent contact with the supporting structure. In case of separation, besides the foundation stiffness, also the foundation damping is modified. Consequently, the foundation damping is given by

$$\begin{aligned} c_{\mathrm {d}}(x,w) = {\left\{ \begin{array}{ll} c_\mathrm {d}(x), &{} w \le w_\mathrm {pl} \,\,\,\, \mathrm {or} \,\,\,\, w_\mathrm {pl} = 0 , \\ c_\mathrm {d}^\mathrm {S}, &{} w > w_\mathrm {pl} \,\,\,\, \mathrm {and} \,\,\,\, w_\mathrm {pl} \ne 0, \end{array}\right. } \end{aligned}$$

(72)

where $w_\mathrm {pl}$ represents the plastic deformation which has a negative value and $c_\mathrm {d}^\mathrm {S}$ is the remaining damping coefficient in case of separation which, in fact, could represent part of the internal damping of the beam.

The parameters of the constitutive relation are not only functions of the displacement, but also functions of space, due to the inhomogeneity of the modelled system. To study the influence of the transition smoothness on the plastic deformation in the transition zone and on the radiated wave field, the spatial profile of the foundation stiffness is chosen based on a sine squared as follows:

$$\begin{aligned} k_{\mathrm {d}}^h(x) = {\left\{ \begin{array}{ll} k_\mathrm {d,l}^h, \qquad \qquad \qquad \qquad \quad \,\,\, 0 \le x< x_\mathrm {tc}-\frac{l_\mathrm {t}}{2},\\ \begin{aligned} k_\mathrm {d,l}^h \bigg (1 + &{}\sin ^2\bigg [\Big (\frac{x-x_\mathrm {tc}}{l_\mathrm {t}}+\frac{1}{2}\Big ) \, \frac{\pi }{2}\bigg ] \, (p-1) \bigg ),\\ &{}\qquad \qquad \quad \, x_\mathrm {tc}-\frac{l_\mathrm {t}}{2} \le x \le x_\mathrm {tc}+\frac{l_\mathrm {t}}{2}, \end{aligned}\\ k_\mathrm {d,r}^h, \qquad \qquad \qquad \qquad \quad \,\,\, x_\mathrm {tc}+\frac{l_\mathrm {t}}{2}< x < L, \end{array}\right. } \end{aligned}$$

(73)

where $h=\{\mathrm {A, B, C, D}\}$; $x_\mathrm {tc}$ represents the transition centre, $l_\mathrm {t}$ the transition length, and p the stiffness ratio between the stiff and soft domains. The location of the transition zone inside the computational domain is dictated by the spatial extent of the input initial conditions, as discussed in Sect. 2.3.1. In addition, a similar spatial variation is chosen for the foundation damping. In the rest of the paper, the damping is expressed through the ratio $\zeta$ which is defined similar to that of a single-degree-of-freedom system:

$$\begin{aligned} \zeta = \frac{c_\mathrm {d}(x)}{2 \sqrt{\rho \, k_\mathrm {d}^\mathrm {A}(x)}}. \end{aligned}$$

(74)

Therefore, by maintaining a constant damping ratio $\zeta$ throughout the system, the spatial variation of the foundation damping is proportional to the square root of that of the stiffness (branch A), except for the parts of the beam which have lost contact with the foundation.

Table 1 System parameters (the overbar represents that the coefficient has not been scaled by the beam’s bending stiffness)

4 Results and discussion

Here, the proposed model is first validated by considering a limit case and comparing the obtained results to a semi-analytical solution. Then, the time-domain displacement field is presented for two specific cases and the influence of the nonlinear foundation on the transition radiation is highlighted. Afterwards, the influence of the transition length, load velocity and stiffness dissimilarity on the plastic deformation is assessed through a parametric study. Finally, the influence of the nonlinear foundation on the radiated energy and on the energy input is discussed. The parameters which are kept constant throughout the presented results are given in Table 1, while the ones which are varied are mentioned for each case individually.

4.1 Validation and convergence

Fig. 7

Error versus space for the linear limit case with imposed artificial nonlinear events (left panel) and without them (right panel); the abrupt transition is at $x = 25 \, \mathrm {m}$, $v = 0.95\,c_\mathrm {l,ph,min}$, $\zeta = 0.05$

To validate the solution derived in Sect. 2, a limit case is considered, in which the foundation is piecewise homogeneous and behaves linearly, but for which artificial nonlinear events are introduced in the solution. To this end, a soft-to-stiff case is considered where the foundation stiffness coefficients $\overline{k}_\mathrm {d,l}^\mathrm {B}$, $\overline{k}_\mathrm {d,l}^\mathrm {C}$, $\overline{k}_\mathrm {d,l}^\mathrm {D}$ (described in Sect. 3) are set equal to $\overline{k}_\mathrm {d,l}^\mathrm {A}$. The same is done for the stiff domain, the stiffness coefficients being equal to $\overline{k}_\mathrm {d,r}^\mathrm {A}$. To validate the solution, 100 artificial nonlinear events are introduced in the solution, which is comparable to the total number of nonlinear events in the most intensive computations encountered.

Fig. 8

Time-domain displacement field for the nonlinear system (solid line), for the linear system (dashed line), the plastic deformation (dash-dot line) and the elastic displacement limit (light grey; given in Table 1) for the soft-to-stiff case; $l_\mathrm {t}=0.1 \, \mathrm {m}$, $x_\mathrm {tc} = 35 \, \mathrm {m}$, $v=0.95\, c_\mathrm {l,ph,min}$, $\zeta = 0.05$; the arrow indicates the position of the load. Note that panels (g) and (h) have a different vertical axis scale for clarity

The limit-case solution is compared to the semi-analytical solution of a piecewise-homogeneous and linear system. This semi-analytical benchmark solution can be obtained by solving a system of two semi-infinite domains with different foundation stiffnesses by using the Fourier transform over time. In the Fourier domain, after imposing interface conditions and the condition of zero displacements at infinity, the displacements of the two domains can be obtained analytically [i.e., 7, 8. To obtain the time-domain solution, the inverse Fourier integral can be applied numerically.

The error e(x) presented in Fig. 7 is defined as the summed-over-time absolute value of the difference between the limit-case solution $w_\mathrm {lin}$ and the benchmark solution $w_\mathrm {bench}$, divided by the summation of the absolute value of the benchmark solution over time:

$$\begin{aligned} e(x) = \frac{\sum _{t=0}^{t_\mathrm {max}} |w_\mathrm {bench}(x,t) - w_\mathrm {lin}(x,t)|}{\sum _{t=0}^{t_\mathrm {max}} |w_\mathrm {bench}(x,t)|}. \end{aligned}$$

(75)

This error is caused by two main factors: the sequential application of the Laplace transform and the finite difference discretization. The left panel of Fig. 7 presents the total error. To isolate the error caused by the finite difference discretization, the case with no artificial nonlinear events is presented in the right panel of Fig. 7. To test the convergence of the derived solution, the maximum frequency has been varied (also done in the numerical integration for the benchmark solution). Note that by changing the maximum frequency, according to the Nyquist sampling rule, the time stepping also changes.

Figure 7 shows that the solution derived in Sect. 2 converges to the correct one as the maximum frequency increases. The higher relative error in the stiffer part of the computational domain can be explained by the smaller displacements. A higher maximum frequency leads to smaller error; however, the computational effort increases significantly. For the rest of the results presented in this section, the maximum frequency was chosen as 1000 Hz.

Fig. 9

Time-domain displacement field for the nonlinear system (solid line), the plastic deformation (dash-dot line) and the elastic displacement limit (light grey; given in Table 1) for the stiff-to-soft case; $l_\mathrm {t}=0.1 \, \mathrm {m}$, $x_\mathrm {tc} = 10 \, \mathrm {m}$, $v=0.95\, c_\mathrm {r,ph,min}$, $\zeta = 0.05$; the arrow indicates the position of the load

4.2 Displacement field in the time domain

To study the effect of the nonlinear foundation on the wave field excited during the transition radiation process, a relatively severe case is presented. The load velocity is chosen as 95% of the minimum phase velocity in the soft part of the computational domain ($c_\mathrm {l,ph,min}$), and the transition length $l_\mathrm {t}$ is chosen as 0.1 m, which is close to the piecewise-homogeneous case. To ensure that the initial displacement and velocity fields do not interact with the inhomogeneity, the centre of the transition zone $x_\mathrm {tc}$ is positioned at $35 \, \mathrm {m}$. The influence of the nonlinearity is highlighted by comparing the response to the linear case, as shown in Fig. 8.

The plastic deformation close to the transition zone is a result of constructive interference of the approaching eigenfield and the waves generated in the transition zone. As in the linear case, the eigenfield interacts with the transition zone, generating waves which mostly propagate towards the softer medium. By constructively interfering, the displacement under the load exceeds the elastic displacement limit (indicated by the grey line in Fig. 8) giving rise to permanent deformation in the foundation to the left of the transition zone.

In the nonlinear system, the free field has both larger amplitude and is sustained for a much longer period of time when compared to the linear one. This can clearly be seen in Fig. 8. Both the larger amplitude and longer duration are consequences of the beam’s separation from the foundation. The loss of contact leads to larger upward displacement which in turn affects the wave field in areas without loss of contact. The loss of contact also causes the loss of external damping which results in the longer duration of the vibration. Moreover, the shape of the radiated waves is also changed. In the nonlinear case, the contact loss leads to a slight increase in the wavelength of the free field (Fig. 8 panels (d), (e) and (f)). This is in accordance with the findings in Sect. 4.4.

Fig. 10

Plastic deformation area versus transition length for different load velocities; $\zeta = 0.05$ (left panel), $\zeta = 0.20$ (right panel) and $p=5$

When the moving load travels from a stiff medium to a soft one, the displacement field does not exceed the elastic displacement limit (at all), meaning that plastic deformation does not develop, as seen in Fig. 9. As in the previous case (Fig. 8), the large-amplitude free waves propagate into the softer medium, which in this case is in the forward direction. This leads to much less constructive interference between the eigenfield and the free field and thus to no plastic deformation. Therefore, in the remainder of the paper, only the soft-to-stiff case is presented. However, if the load travelled super-critically (in the soft medium or in both media) for the stiff-to-soft case, it would move faster than the minimum phase velocity of the free waves, probably leading to more pronounced constructive interference, which could induce plastic deformation to the right of the transition zone.

4.3 Parametric study

In this section, the damage occurring in the supporting structure is addressed as a function of the load velocity, the transition length and the stiffness dissimilarity p through a parametric study. The area of the plastic deformation, $A_\mathrm {pl} = \int w_\mathrm {pl}(x) \, \mathrm {d}x$, is chosen as the quantifier for the damage in the supporting structure. The three parameters chosen to be varied influence the transition radiation phenomenon most. Furthermore, these parameters can be adjusted in the design stage of railway tracks to minimize damage in the supporting structure.

The plastic deformation area versus varying transition length is presented in Fig. 10 for different load velocities and damping ratios. The plastic deformation area decreases as the transition length increases, as could be expected, and the decreasing trend is quasi-monotonic for all load velocities and damping ratios. For the damping ratio $\zeta = 0.05$ (left panel in Fig. 10), the transition-length range in which plastic deformation occurs increases with increasing velocity until the minimum phase velocity, beyond which it decreases. However, for the super-critical case ($v=1.05\, c_\mathrm {l,ph,min}$) and small transition lengths ($l_\mathrm {t}=0, \ldots ,3$ m), the plastic deformation is still larger than for the critical case ($v=1.00\, c_\mathrm {l,ph,min}$), which makes the two lines intersect. This larger plastic deformation is caused by the fact that parts of the foundation experience additional plastic deformation produced in the second loading–unloading cycle. This is not the case for larger transition lengths ($l_\mathrm {t}=4, \ldots ,6$ m), and because the displacement of the eigenfield under the load is smaller in the super-critical case than in the critical case, a smaller plastic deformation area results, which explains the intersection of the two lines. Furthermore, for $\zeta = 0.20$ (right panel in Fig. 10), additional plastic deformation is not produced in the second loading–unloading cycle for any of the transition lengths due to the higher damping ratio, and the range as well as the plastic deformation area just decrease as the velocity increases beyond the minimum phase velocity.

Furthermore, the analysis shows that it is not just the duration of passage$t_\mathrm {p} = \frac{l_\mathrm {t}}{v}$ that governs the resulting plastic deformation (which could be intuited), but also the absolute values of the transition length $l_\mathrm {t}$ and load velocity v separately. It can clearly be seen in Fig. 10 that for the same duration of passage, significantly different plastic deformation values are observed for different load velocities.

In Fig. 11, the plastic deformation area is presented as a function of the velocity of the moving load for different transition lengths and damping ratios. The plastic deformation area increases with increasing velocity until close to the minimum phase velocity, beyond which it decreases. For $\zeta = 0.05$ (left panel in Fig. 11), the critical velocity appears to be around 1.05 $c_\mathrm {l,ph,min}$ for $l_\mathrm {t} = 0.1$ m, and its value decreases with increasing transition length reaching 1.00 $c_\mathrm {l,ph,min}$ for $l_\mathrm {t} = 4$ m. This shows that the critical velocity for the plastic deformation area is dependent on the transition length. Moreover, the increasing trend (sub-critical velocities) and the decreasing trend (super-critical velocities) have different slopes, which is explained by the fact that in the super-critical cases parts of the foundation experience additional plastic deformation caused in the second loading–unloading cycle. For $\zeta = 0.20$ (right panel in Fig. 11), a similar behaviour to the case of $\zeta = 0.05$ is observed. However, the magnitude of the plastic deformation area is smaller and the slopes of the increasing and decreasing trends (left and right of the critical velocity) are almost identical because the foundation does not experience additional plastic deformation caused in the second loading–unloading cycle.

Fig. 11

Plastic deformation area versus velocity of the moving load for different transition lengths; $\zeta = 0.05$ (left panel), $\zeta = 0.20$ (right panel) and $p=5$

Fig. 12

Plastic deformation area versus stiffness dissimilarity for different velocities and transition lengths; $\zeta = 0.05$

The plastic deformation area as a function of the stiffness dissimilarity p is presented in Fig. 12 for different load velocities and transition lengths. The plastic deformation area increases with increasing stiffness dissimilarity for all velocities and transition lengths presented, as could be expected. The increasing trends tend to constant values, which could be obtained in the limit case of the stiff domain being infinitely stiff. It is clear from the trends that the maximum sensitivity of the plastic deformation area occurs at small stiffness dissimilarities. Therefore, the maximum gain in decreasing the damage of the supporting structure can be obtained at small stiffness dissimilarities. For small stiffness dissimilarity, the maximum plastic deformation area is observed for a load velocity $v=1.00\,c_\mathrm {l,ph,min}$, but for larger stiffness dissimilarity the maximum plastic deformation area is obtained for a load velocity $v=1.05\,c_\mathrm {l,ph,min}$. This shows that the critical velocity, when it comes to the plastic deformation area, is dependent also on the stiffness dissimilarity (next to transition length).

To conclude, studying the influence of the transition length, load velocity and stiffness dissimilarity on the plastic deformation area provides valuable information about the value ranges of these parameters where the initial design of transition zones should aim at so as to minimize the damage in the supporting structure. Next, the transition radiation phenomenon is studied from an energy point of view.

4.4 Energy radiation

In this section, the influence of the nonlinearity on the transition radiation is studied from the energy point of view, which gives additional insight into the properties of the radiated field. To investigate the energy radiation solely due to the transition radiation phenomenon, the study is restricted to sub-critical load velocities. Based on the solution derived in Sect. 2.2, the energy flux through cross sections of the beam to the left and right of the transition zone can be computed as seen in [10, 16, 42]. To study the energy associated with the radiated waves induced by the load passing the transition zone, the power flux corresponding with the free field $S^\mathrm {f}(x,t)$ through a certain cross-section x of the Euler–Bernoulli beam is considered [42]:

$$\begin{aligned} S^\mathrm {f}(x,t) = EI (w^\mathrm {f \prime \prime \prime }\dot{w}^\mathrm {f} - w^\mathrm {f \prime \prime }\dot{w}^\mathrm {f \prime }), \end{aligned}$$

(76)

where $w^\mathrm {f} = w - w^\mathrm {e}$ represents the free-field displacement; w is the displacement given by Eq. 27, and $w^\mathrm {e}$ is the eigenfield displacement given by Eq. 34. It must be noted that in Eq. (76) the power flux propagating in positive x-direction is considered; to obtain the power flux in negative x-direction, a minus sign needs to be added. The total free-field energy flux $E^\mathrm {f}(x)$ through a cross section is found by integrating the power flux over time. Moreover, to visualize the spectral energy density corresponding to the free field, $E^\mathrm {f}(x)$ can be rewritten in terms of the Fourier-domain counterparts of the time-domain quantities, as shown in [15, 16]:

$$\begin{aligned} \begin{aligned} E^\mathrm {f}(x)&= EI \int _{-\infty }^{\infty } (w^\mathrm {f \prime \prime \prime }\dot{w}^\mathrm {f} - w^\mathrm {f \prime \prime }\dot{w}^\mathrm {f \prime }) \mathrm {d}t \\&= \frac{EI}{\pi } \int _{0}^{\infty } \mathrm {Re}(\tilde{w}^\mathrm {f \prime \prime \prime } \tilde{v}^\mathrm {f*} - \tilde{w}^\mathrm {f \prime \prime } \tilde{v}^\mathrm {f*\prime }) \mathrm {d}\omega , \end{aligned} \end{aligned}$$

(77)

where the integrand in the last expression represents the spectral energy density $E^\mathrm {s} (x,\omega )$, $\omega$ represents the Fourier-domain angular frequency (rather than that in the Laplace domain as introduced in Sect. 2.2), the tilde represents the Fourier-domain quantities, $\tilde{v}$ represents the Fourier-domain velocity, and the asterisk represents complex conjugation.

It must be noted that Eq. (77) does not capture the entire transition radiation energy; it only covers the energy carried by the isolated free field. The total energy flux through a certain cross section contains the eigenfield contribution, the free-field contribution, as well as an interference term; the last two both contribute to the radiation energy, while only the free-field contribution is considered here. Furthermore, the computed energy does not represent the total free-field energy because part of it is absorbed by the foundation before reaching the considered cross sections left and right of the transition. Moreover, due to the spatial variation of the foundation damping, the energy propagating in the stiff domain is damped more than that propagating in the soft domain. To avoid the last issue, for the computations performed in this section, the spatial damping profile is maintained constant throughout the computational domain (where $\zeta$ is defined with respect to the soft domain), except for the parts where the beam–foundation separation occurs Eq. (72).

The influence of the transition length on the free-field energy is now addressed through a parametric study. The energy associated with the leftward-propagating free field $E^\mathrm {f}_\mathrm {left}$, presented in the left panels of Fig. 13, decreases with increasing transition length, as could be intuited. However, for small transition lengths, $E^\mathrm {f}_\mathrm {left}$ in the lightly damped case (panel a in Fig. 13) is smaller in the nonlinear system as compared to that in the linear one. This can be explained by the fact that part of the energy is consumed to plastically deform the foundation, but also by stronger radiation in the rightward direction (panel b in Fig. 13). Furthermore, although $E^\mathrm {f}_\mathrm {left}$ decreases with increasing transition length, the decrease rate is smaller in the nonlinear case as compared to that in the linear one. Consequently, for some values of the transition length ($l_\mathrm {t} \approx 3, \ldots ,7 \, \mathrm {m}$ in panel a of Fig. 13), $E^\mathrm {f}_\mathrm {left}$ is larger in the nonlinear case. However, the behaviour described above is not general. The bottom-left panel in Fig. 13 shows that in the system with higher damping ratio ($\zeta = 0.20$), $E^\mathrm {f}_\mathrm {left}$ is higher in the nonlinear system than in the linear one for all transition lengths.

Fig. 13

Total energy flux leftward $E^\mathrm {f}_\mathrm {left}$ (left panels) and rightward $E^\mathrm {f}_\mathrm {right}$ (right panels) for the nonlinear system (solid line) and linear system (dashed line) versus transition length; the cross sections were chosen 10 m left and right of the transition centre; $\zeta = 0.05$ (top panels) and $\zeta = 0.20$ (bottom panels)

Fig. 14

Spectral energy density leftward $E^\mathrm {s}_\mathrm {left}$ (left panel) and rightward $E^\mathrm {s}_\mathrm {right}$ (right panel) for the nonlinear system (solid line) and linear system (dashed line); the cross sections were chosen 10 m left and right of the transition centre; $v = 0.95 \, c_\mathrm {l,ph,min}$, $l_\mathrm {t} = 0.1 \, \mathrm {m}$ and $\zeta = 0.05$

Furthermore, the energy associated with the rightward-propagating free field $E^\mathrm {f}_\mathrm {right}$ (presented in the right panels of Fig. 13) is significantly higher in the nonlinear case as compared to that in the linear one. Moreover, $E^\mathrm {f}_\mathrm {right}$ is not largest for the shortest transition length, but for a transition length $l_\mathrm {t} \approx 0.5, \ldots ,2.5 \, \mathrm {m}$ (depends on the load velocity). This is specific to the nonlinear case since for all the linear cases considered, the free-field energy decreases with increasing transition length. In addition, for the considered cases, $E^\mathrm {f}_\mathrm {right}$ is clearly smaller than $E^\mathrm {f}_\mathrm {left}$, implying that the free field radiated into the soft part of the system carries most energy, although this is not a necessity as shown in [16].

Fig. 15

Difference in energy input between the linear and nonlinear cases for varying transition length; $\zeta = 0.05$ (left panel) and $\zeta = 0.20$ (right panel)

The spectral energy density $E^\mathrm {s}$ for the same system as in Fig. 8 ($l_\mathrm {t} = 0.1 \, \mathrm {m}$, $v = 0.95 \, c_\mathrm {l,ph,min}$ and $\zeta = 0.05$) is presented in Fig. 14. The leftward-propagating energy $E^\mathrm {s}_\mathrm {left}$ for the nonlinear system exhibits a small shift towards the lower frequencies as well as a decrease in energy in the nonlinear case, when compared to the linear system. The lower frequencies of the radiated waves in the nonlinear system can also be observed in the time-domain response (Fig. 8, panels d), e) and f)) through the larger wavelengths of the left-propagating waves. Furthermore, the energy propagating rightward $E^\mathrm {s}_\mathrm {right}$ in the nonlinear system has, next to a higher magnitude (as already observed in the right panel of Fig. 14), also higher-frequency content as compared to the linear system.

Fig. 16

Maximum power input for the linear case (dashed line) and nonlinear case (solid line) against varying transition length; $\zeta = 0.05$ (left panel) and $\zeta = 0.20$ (right panel)

4.5 Energy input

Besides the influence of the nonlinear foundation on the energy radiation, presented in the previous subsection, its influence on the energy input from the moving load could also offer valuable insight. While the energy radiation refers to the far field, the energy input offers information about the near field, as it relates to the contact point between the moving load and the beam. More energy input leads to more energy radiated and/or more energy dissipated into the foundation, the latter leading to damage. Therefore, the energy input or the maximum power input could represent a good indicator of the potential damage occurring in the foundation. To investigate the energy input solely due to the transition radiation phenomenon, the study is restricted to sub-critical load velocities.

The energy input is defined as the power input integrated over time. Due to the damping present in the structure, the power input $P^\mathrm {in}$ is nonzero over the whole time axis (i.e., even when the load is not in the vicinity of the transition zone), and therefore, the energy input is infinite. Consequently, the difference in energy input between the linear and nonlinear cases is presented instead. The difference in energy input $\Delta E^\mathrm {in}$ is given by the following expression:

$$\begin{aligned} \begin{aligned} \Delta E^\mathrm {in}&= \int _{-\infty }^{\infty } \big (P^\mathrm {in}(t) - P^\mathrm {in}_\mathrm {lin}(t)\big ) \mathrm {d}t \\&= \overline{F}_0 \int _{-\infty }^{\infty } \Bigg (\dot{w} \Bigr |_{\begin{array}{c} x=vt \end{array}} - \dot{w}_\mathrm {lin} \Bigr |_{\begin{array}{c} x=vt \end{array}} \Bigg ) \mathrm {d}t, \end{aligned} \end{aligned}$$

(78)

where $P^\mathrm {in}_\mathrm {lin}$ and $\dot{w}_\mathrm {lin}$ represent the power input and velocity at the contact point, respectively, of the linear case.

Fig. 17

Maximum power input (left panel) and difference of energy input between the linear and nonlinear cases (right panel) for the first load passage (triangle) and for the second load passage (asterisk) against transition length; $v=0.95\,c_\mathrm {l,ph,min}$ and $\zeta = 0.05$

Figure 15 presents the difference in energy input $\Delta E^\mathrm {in}$ as a function of the transition length for different velocities and damping ratios. It can be observed that the maximum difference in energy input does not occur at the smallest transition zone, reinforcing the findings in the energy radiation study (right panels in Fig. 13). Furthermore, the difference in energy input increases with increasing velocity, but the difference is smaller in the higher-damping case (right panel in Fig. 15).

The normalized maximum power input $P^\mathrm {in}_\mathrm {max}$ is presented in Fig. 16 as a function of the transition length for different velocities and damping ratios. The maximum power input is normalized by the steady-state power input in the soft domain $P^\mathrm {in}_\mathrm {soft}$. It can be observed that the maximum power input decreases with increasing transition length and decreasing velocity of the moving load. Moreover, the maximum power input in the transition zone can be a factor 1.8 larger than the one in the steady state. Part of this additional power input could cause damage in the supporting structure.

The difference between the linear and the nonlinear cases (for the first passage of the moving load) is small and cannot be seen in Fig. 16, even though the difference in total energy input can be significant (Fig. 15). However, the increase is much more drastic for the second passage of the moving load (i.e., of the system that has already been deformed plastically) as can be seen in Fig.  17. Both the maximum power input (left panel in Fig. 17) and the difference in energy input (right panel in Fig. 17) exhibit a considerable increase compared to the first load passage. The maximum power input and the energy input have the potential to be good indicators of the damage occurring in the foundation of the railway track. However, more extensive research into these two indicators needs to be performed in order to justify this.

5 Conclusions

In this paper, the influence of the foundation’s nonlinear behaviour on the waves generated by a moving load crossing an inhomogeneity in the foundation as well as the resulting plastic deformation have been studied. To this end, a one-dimensional model has been formulated, consisting of an infinite Euler–Bernoulli beam resting on a locally inhomogeneous and nonlinear Winkler foundation, subjected to a moving load. The reaction of the Winkler foundation has been characterized by a piecewise-linear (in displacements) constitutive relation which accounts for permanent deformations. The foundation’s piecewise-linear behaviour allows to obtain the solution by sequentially applying the Laplace transform over time, while the Finite Difference Method has been used for the spatial discretization. The infinite extent of the system has been accounted for through a set of non-reflective boundary conditions, derived by replacing the semi-infinite domains by their response at the interfaces, and through the input initial conditions based on the steady-state response of a beam with homogeneous foundation subject to the moving load. The solution has been validated for the limit case of a linear and piecewise-homogeneous foundation against a semi-analytical benchmark solution.

Results have shown that the plastic deformation originates from constructive interference between the waves excited at the transition and the response to the load’s deadweight. Furthermore, through a parametric study conducted for the soft-to-stiff transition, it has been found that the plastic deformation decreases quasi-monotonically with increasing transition length, and that the decrease rate depends on the velocity of the load and on the magnitude of the foundation damping. Moreover, for super-critical velocities, additional plastic deformation is generated in the second loading–unloading cycle of the foundation for small transition lengths and/or large stiffness dissimilarities. The critical velocity related to the plastic deformation area, which was chosen to quantify the damage in the supporting structure, was observed to be dependent on the transition length and on the stiffness dissimilarity. In addition, the resulting plastic deformation area has been observed to be influenced not only by the time of passage of the transition zone, defined as the transition zone length divided by the load’s velocity, but also by these quantities individually. Finally, when the load travels from a stiff medium to a soft one, no plastic deformation has been observed, which is due to less pronounced constructive interference.

The influence of the foundation’s nonlinear behaviour on the radiated field has also been studied from the energy point of view, by considering the energy flux associated with the free field through cross sections left and right of the transition zone. Results have shown that in the nonlinear system, the maximum rightward-propagating energy flux does not occur at the smallest transition length, but at a larger one, a finding which is reinforced by the difference in energy input between the linear and nonlinear case. This feature is specific to the nonlinear system since in the linear case, the energy flux has been observed to always decrease with increasing transition length. Furthermore, the spectral energy densities have not only shown that the nonlinearity redistributes the energy between frequencies, but have also highlighted the redistribution between the soft and stiff media. Moreover, it has been observed that the maximum power input and the difference in energy input between the linear and nonlinear case drastically increases for the second passage of the moving load (i.e., of the system that has already been deformed plastically). This suggests the use of these energy quantities as possible indicators of the damage in the supporting structure.

Although one-dimensional models are not able to model all phenomena, they are useful for initial assessments. The model presented here can be used for preliminary designs of transition zones in railway tracks. Given the stiffness dissimilarity and/or the magnitude of the initial plastic deformation, the optimum length of the transition zone and the maximum velocity of the train can be obtained such that the damage in the railway track is minimized.

Appendices

Appendix A: Finite difference coefficients

Here, the finite difference coefficients used to discretize the beam in Sect. 2.2 are provided. The finite difference scheme with 9 nodes is used. The fourth-order derivative reads

$$\begin{aligned} \begin{aligned} \hat{w}_m''''&\approx \frac{1}{\mathrm {\Delta } x^4} \bigg (\frac{7}{240} \, \hat{w}_{m-4} - \frac{2}{5} \, \hat{w}_{m-3} + \frac{169}{60} \, \hat{w}_{m-2} \\&\quad - \frac{122}{15} \, \hat{w}_{m-1} + \frac{91}{8} \, \hat{w}_{m} - \frac{122}{15} \, \hat{w}_{m+1} + \frac{169}{60} \, \hat{w}_{m+2} \\&\quad - \frac{2}{5} \, \hat{w}_{m+3} + \frac{7}{240} \, \hat{w}_{m+4} \bigg ), \quad \quad m = 3 \ldots M-2, \end{aligned} \end{aligned}$$

(79)

where M represents the number of nodes of the computational domain. As can be seen from Eq. 79, this approximation is applied only from node 3 to node $M-2$. This is because there are only two boundary conditions at each boundary, and thus, only two ghost nodes can be used. The fourth-order derivative approximations for nodes 1, 2, $M-1$ and M are obtained by using a hybrid between the central scheme and the forward scheme (for nodes 1 and 2) or the backward scheme (for nodes $M-1$ and M). The expressions are given in the following:

$$\begin{aligned} \hat{w}_1''''&\approx \frac{1}{\mathrm {\Delta } x^4} \bigg (\frac{127}{240} \, \hat{w}_{-1} - \frac{11}{15} \, \hat{w}_{0} - \frac{77}{20} \, \hat{w}_{1} \nonumber \\&\quad + \frac{193}{15} \, \hat{w}_{2} - \frac{407}{24} \, \hat{w}_{3} + \frac{61}{5} \, \hat{w}_{4} \nonumber \\&\quad - \frac{311}{60} \, \hat{w}_{5} + \frac{19}{15} \, \hat{w}_{6} - \frac{11}{80} \, \hat{w}_{7} \bigg ), \end{aligned}$$

(80)

$$\begin{aligned} \hat{w}_2''''&\approx \frac{1}{\mathrm {\Delta } x^4} \bigg (-\frac{11}{80} \, \hat{w}_{-1} + \frac{53}{30} \, \hat{w}_{0} - \frac{341}{60} \, \hat{w}_{1} \nonumber \\&\quad + \frac{77}{10} \, \hat{w}_{2} - \frac{107}{24} \, \hat{w}_{3} + \frac{11}{30} \, \hat{w}_{4} \nonumber \\&\quad + \frac{13}{20} \, \hat{w}_{5} - \frac{7}{30} \, \hat{w}_{6} + \frac{7}{240} \, \hat{w}_{7} \bigg ), \end{aligned}$$

(81)

$$\begin{aligned} \hat{w}_{M-1}''''&\approx \frac{1}{\mathrm {\Delta } x^4} \bigg (\frac{7}{240} \, \hat{w}_{M-6} - \frac{7}{30} \, \hat{w}_{M-5} + \frac{13}{20} \, \hat{w}_{M-4} \nonumber \\&\quad + \frac{11}{30} \, \hat{w}_{M-3} - \frac{107}{24} \, \hat{w}_{M-2} + \frac{77}{10} \, \hat{w}_{M-1} \nonumber \\&\quad - \frac{341}{60} \, \hat{w}_{M} + \frac{53}{30} \, \hat{w}_{M+1} - \frac{11}{80} \, \hat{w}_{M+2} \bigg ), \end{aligned}$$

(82)

$$\begin{aligned} \hat{w}_{M}''''&\approx \frac{1}{\mathrm {\Delta } x^4} \bigg (-\frac{11}{80} \, \hat{w}_{M-6} + \frac{19}{15} \, \hat{w}_{M-5} - \frac{311}{60} \, \hat{w}_{M-4} \nonumber \\&\quad + \frac{61}{5} \, \hat{w}_{M-3} - \frac{407}{24} \, \hat{w}_{M-2} + \frac{193}{15} \, \hat{w}_{M-1} \nonumber \\&\quad - \frac{77}{20} \, \hat{w}_{M} - \frac{11}{15} \, \hat{w}_{M+1} + \frac{127}{240} \, \hat{w}_{M+2} \bigg ), \end{aligned}$$

(83)

where the nodes $-1$, 0, $M+1$ and $M+2$ represent the so-called ghost nodes. These nodes are not part of the computational domain; therefore, the displacements of these nodes ($\hat{w}_{-1}$, $\hat{w}_{0}$, $\hat{w}_{M+1}$, $\hat{w}_{M+2}$) are expressed in terms of the displacements of the nodes inside the computational domain by using the four non-reflective boundary conditions. The resulting equations are included in Eq. (24).

Appendix B: Coefficients of the eigenfield

Here, the coefficients needed to fully determine the eigenfield in Eq. (34) are listed:

$$\begin{aligned} A_1&= \frac{\mathrm {i} {F_0}}{(k_{2}^\mathrm {e}-k_{1}^\mathrm {e})(k_{2}^\mathrm {e}-k_{3}^\mathrm {e})(k_{2}^\mathrm {e}-k_{4}^\mathrm {e})} , \end{aligned}$$

(84)

$$\begin{aligned} B_1&= \frac{\mathrm {i} {F_0}}{(k_{3}^\mathrm {e}-k_{1}^\mathrm {e})(k_{3}^\mathrm {e}-k_{2}^\mathrm {e})(k_{3}^\mathrm {e}-k_{4}^\mathrm {e})}, \end{aligned}$$

(85)

$$\begin{aligned} A_2&= \frac{\mathrm {i} {F_0}}{(k_{1}^\mathrm {e}-k_{2}^\mathrm {e})(k_{1}^\mathrm {e}-k_{3}^\mathrm {e})(k_{1}^\mathrm {e}-k_{4}^\mathrm {e})} , \end{aligned}$$

(86)

$$\begin{aligned} B_2&= \frac{\mathrm {i} {F_0}}{(k_{4}^\mathrm {e}-k_{1}^\mathrm {e})(k_{4}^\mathrm {e}-k_{2}^\mathrm {e})(k_{4}^\mathrm {e}-k_{3}^\mathrm {e})}, \end{aligned}$$

(87)

where $k_\mathrm {1}^\mathrm {e}$, $k_\mathrm {2}^\mathrm {e}$, $k_\mathrm {3}^\mathrm {e}$ and $k_\mathrm {4}^\mathrm {e}$ are the eigenfield’s complex wavenumbers. These are found by solving the following equation:

$$\begin{aligned} k^4 - \rho k^2 v^2 + \mathrm {i}kvc_\mathrm {d,l}+k_\mathrm {d,l}=0. \end{aligned}$$

(88)

The expressions of the wavenumber are not presented due to brevity; however, they can straightforwardly be obtained by solving Eq. (88) using a symbolic mathematics tool (e.g., Maple). The choice of the sign of the wavenumbers is as follows:

$$\begin{aligned} \mathrm {Re}(k_\mathrm {1}^\mathrm {e}) > 0, \quad&\mathrm {Im}(k_\mathrm {1}^\mathrm {e}) < 0, \end{aligned}$$

(89)

$$\begin{aligned} \mathrm {Re}(k_\mathrm {2}^\mathrm {e})> 0, \quad&\mathrm {Im}(k_\mathrm {2}^\mathrm {e}) > 0, \end{aligned}$$

(90)

$$\begin{aligned} \mathrm {Re}(k_\mathrm {3}^\mathrm {e}) < 0, \quad&\mathrm {Im}(k_\mathrm {3}^\mathrm {e}) > 0, \end{aligned}$$

(91)

$$\begin{aligned} \mathrm {Re}(k_\mathrm {4}^\mathrm {e})< 0, \quad&\mathrm {Im}(k_\mathrm {4}^\mathrm {e}) < 0. \end{aligned}$$

(92)

Appendix C: Non-reflective boundary conditions at the right

In Sect. 2.3.2, the expressions for the non-reflective boundary conditions have been derived for the situation in which the nonlinear events occur while the moving load is inside the computational domain. Due to the rail losing and regaining contact with the supporting structure, nonlinear events can still occur while the moving load is in the right domain. In this section, the expressions for the non-reflective boundary conditions at the right are derived for that situation. The aim is to express the reaction forces of the right domain, at the interface with the computational domain, as functions of the displacement and slope of the computational domain at the right boundary. The procedure is similar to the one explained in Sect. 2.3.2. It must be noted that the non-reflective boundary conditions at the left, derived in Sect. 2.3.2, remain valid through the simulation.

If a nonlinear event occurs when $\overline{\tau }_{n-1} > \frac{L}{v}$, the right semi-infinite domain must be divided in two sub-domains, one sub-domain behind the load (sub-domain A) and the second one in front of it (sub-domain B). The forward Laplace transform is applied to the governing equations, and the solution of the sub-domain behind the moving load $\hat{w}_{r}^\mathrm {A}$ and that in front $\hat{w}_{r}^\mathrm {B}$, already accounting for the condition of vanishing displacement at infinity, are obtained as follows:

$$\begin{aligned} \hat{w}_{\mathrm {r},n}^\mathrm {A}(x,s_n)&= C_1^\mathrm {A} \, \mathrm {e}^{-\mathrm {i}k_\mathrm {r}x} + C_2^\mathrm {A} \, \mathrm {e}^{+\mathrm {i}k_\mathrm {r}x} + C_3^\mathrm {A} \, \mathrm {e}^{+k_\mathrm {r}x}\nonumber \\&\quad + C_4^\mathrm {A} \, \mathrm {e}^{-k_\mathrm {r}x} \,\,\, + \hat{w}_{\mathrm {r},n,\mathrm {p}}^\mathrm {A}, \quad \,\,\, L< x < x_\mathrm {P}, \end{aligned}$$

(93)

$$\begin{aligned} \hat{w}_{\mathrm {r},n}^\mathrm {B}(x,s_n)&= C_1^\mathrm {B} \, \mathrm {e}^{-\mathrm {i}k_\mathrm {r}x} + C_4^\mathrm {B} \, \mathrm {e}^{-k_\mathrm {r}x} + \hat{w}_{n,\mathrm {p}}^\mathrm {ML}\nonumber \\&\quad +\hat{w}_{\mathrm {r},n,\mathrm {p}}^\mathrm {B}, \quad \,\,\, x > x_\mathrm {P}, \end{aligned}$$

(94)

where $x_\mathrm {P} = v \, \overline{\tau }_{n-1}$ is the position of the load at the moment of the nonlinear event, $C_1^\mathrm {A}, C_2^\mathrm {A}, C_3^\mathrm {A}, C_4^\mathrm {A}, C_1^\mathrm {B}$ and $C_4^\mathrm {B}$ represent yet unknown complex amplitudes, $\hat{w}_{\mathrm {r},n,\mathrm {p}}^\mathrm {A}$ and $\hat{w}_{\mathrm {r},n,\mathrm {p}}^\mathrm {B}$ represent the particular solutions accounting for the initial state of the two sub-domains, and $\hat{w}_{n,\mathrm {p}}^\mathrm {ML}$ represents the particular solution accounting for the moving load which reads:

$$\begin{aligned} \hat{w}_{n,\mathrm {p}}^\mathrm {ML} = - \frac{F_0\,v^3}{s_n^4-k_\mathrm {r}^4\,v^4} \, \mathrm {e}^{-s_n \, \frac{x-x_\mathrm {P}}{v}}. \end{aligned}$$

(95)

The six unknown complex amplitudes are obtained by employing the two boundary conditions at $x=L$ given by Eqs. (42) and (43), and four interface conditions at $x=x_\mathrm {P}$, namely the continuity of displacement and slope, and the equilibrium of bending moment and shear force. To find the reaction forces of the right domain at the interface with the computational domain, the second and third derivatives of $\hat{w}_{\mathrm {r},n}^\mathrm {A}$ with respect to space are taken and are evaluated at $x=L$:

$$\begin{aligned} \begin{pmatrix} \hat{w}^{\mathrm {A} \prime \prime \prime }_{\mathrm {r},n} (L,s_n) \\ \hat{w}^{\mathrm {A} \prime \prime }_{\mathrm {r},n} (L,s_n) \end{pmatrix}= & {} \begin{pmatrix} k_\mathrm {r,V\upupsilon } &{} k_\mathrm {r,V\upphi } \\ k_\mathrm {r,M\upupsilon } &{} k_\mathrm {r,M\upphi } \end{pmatrix} \begin{pmatrix} \hat{w}_n (L,s_n) \\ \hat{w}'_n (L,s_n) \end{pmatrix} \nonumber \\&-\, \mathbf D _{\mathrm {r},n} - \begin{pmatrix} \hat{V}_{\mathrm {L},n}(s_n) \\ \hat{M}_{\mathrm {L},n}(s_n) \end{pmatrix}. \end{aligned}$$

(96)

Vector $\mathbf D _{\mathrm {r},n}$ now reads

$$\begin{aligned} \mathbf D _{\mathrm {r},n}= & {} \begin{pmatrix} \hat{w}^{\mathrm {A} \prime \prime \prime }_{\mathrm {r},n,\mathrm {p}} (L,s_n) \\ \hat{w}^{\mathrm {A} \prime \prime }_{\mathrm {r},n,\mathrm {p}} (L,s_n) \end{pmatrix} +\begin{pmatrix} k_\mathrm {r,V\upupsilon } &{} k_\mathrm {r,V\upphi } \\ k_\mathrm {r,M\upupsilon } &{} k_\mathrm {r,M\upphi } \end{pmatrix} \begin{pmatrix} \hat{w}^{\mathrm {A}}_{\mathrm {r},n,\mathrm {p}} (L,s_n) \\ \hat{w}^{\mathrm {A} \prime }_{\mathrm {r},n,\mathrm {p}} (L,s_n) \end{pmatrix}\nonumber \\&+\begin{pmatrix} a_{\mathrm {V}} &{} b_{\mathrm {V}} &{} c_{\mathrm {V}} &{} d_{\mathrm {V}}\\ a_{\mathrm {M}} &{} b_{\mathrm {M}} &{} c_{\mathrm {M}} &{} d_{\mathrm {M}} \end{pmatrix} \begin{pmatrix} \mathrm {\Delta }\hat{w}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n) \\ \mathrm {\Delta }\hat{w}'_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n) \\ \mathrm {\Delta }\hat{w}''_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n) \\ \mathrm {\Delta }\hat{w}'''_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n) \end{pmatrix}, \quad \overline{\tau }_{n-1} > \frac{L}{v}, \nonumber \\ \end{aligned}$$

(97)

where $\mathrm {\Delta }\hat{w}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n) = \hat{w}^\mathrm {B}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n) - \hat{w}^\mathrm {A}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n)$ represents the difference of the particular solutions of the two sub-domains evaluated at $x = x_\mathrm {P}$; $a_{\mathrm {V}}$, $b_{\mathrm {V}}$, $c_{\mathrm {V}}$, $d_{\mathrm {V}}$, $a_{\mathrm {M}}$, $b_{\mathrm {M}}$, $c_{\mathrm {M}}$ and $d_{\mathrm {M}}$ represent complex coefficients which read

$$\begin{aligned} \begin{aligned}&a_{\mathrm {V}} = \frac{-1+\mathrm {i}}{2} \, k_\mathrm {r}^3 \big ( \mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ), \\&b_{\mathrm {V}} = \frac{1+\mathrm {i}}{2} \, k_\mathrm {r}^2 \big ( \mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {i}\mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ), \\&c_{\mathrm {V}} = \frac{-1+\mathrm {i}}{2} \, k_\mathrm {r} \big ( -\mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ), \\&d_{\mathrm {V}} = \frac{1+\mathrm {i}}{2} \big ( -\mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {i}\mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ), \\&a_{\mathrm {M}} = \frac{-1-\mathrm {i}}{2} \, k_\mathrm {r}^2 \big ( \mathrm {i}\mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ), \\&b_{\mathrm {M}} = \frac{-1-\mathrm {i}}{2} \, k_\mathrm {r} \big ( \mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ), \\&c_{\mathrm {M}} = \frac{-1-\mathrm {i}}{2} \big ( -\mathrm {i}\mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ), \\&d_{\mathrm {M}} = \frac{-1-\mathrm {i}}{2 \, k_\mathrm {r} } \big ( -\mathrm {e}^{\mathrm {i}k_\mathrm {r}(L-x_\mathrm {P})} + \mathrm {e}^{k_\mathrm {r}(L-x_\mathrm {P})} \big ). \end{aligned} \end{aligned}$$

(98)

The particular solutions $\hat{w}^\mathrm {A}_{\mathrm {r},n,\mathrm {p}} (L,s_n)$, $\hat{w}^\mathrm {A}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n)$ and $\hat{w}^\mathrm {B}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n)$ that account for the non-trivial initial state are obtained as explained in Sect. 2.3.2 and read

$$\begin{aligned} \hat{w}^\mathrm {A}_{\mathrm {r},n,\mathrm {p}} (L,s_n)&= \frac{1}{2\uppi \mathrm {i}} \int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty } (\rho s_n +c_{\mathrm {d,r}}+ \rho s) \, \mathrm {e}^{s\overline{\tau }_{n-1}}\nonumber \\&\quad \cdot {}\int _{L}^{x_\mathrm {P}} \hat{g}_\mathrm {r}(x - \xi ,s_n) \hat{w}_\mathrm {r}^\mathrm {f} (\xi ,s) \, \mathrm {d}\xi \, \mathrm {d}s \nonumber \\&\quad +\hat{w}_\mathrm {r,\textit{n},p}^\mathrm {e} (L,s_n), \end{aligned}$$

(99)

$$\begin{aligned} \hat{w}^\mathrm {A}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n)&= \frac{1}{2\uppi \mathrm {i}} \int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty } (\rho s_n +c_{\mathrm {d,r}}+ \rho s) \, \mathrm {e}^{s\overline{\tau }_{n-1}}\nonumber \\&\quad \cdot {}\int _{L}^{x_\mathrm {P}} \hat{g}_\mathrm {l}(x - \xi ,s_n) \hat{w}_\mathrm {r}^\mathrm {f} (\xi ,s) \, \mathrm {d}\xi \, \mathrm {d}s \nonumber \\&\quad +\hat{w}_\mathrm {r,\textit{n},p}^\mathrm {e} (x_\mathrm {P},s_n), \end{aligned}$$

(100)

$$\begin{aligned} \hat{w}^\mathrm {B}_{\mathrm {r},n,\mathrm {p}} (x_\mathrm {P},s_n)&= \frac{1}{2\uppi \mathrm {i}} \int _{\sigma -\mathrm {i}\infty }^{\sigma +\mathrm {i}\infty } (\rho s_n +c_{\mathrm {d,r}}+ \rho s) \, \mathrm {e}^{s \overline{\tau }_{n-1}} \nonumber \\&\quad \cdot {}\int _{x_\mathrm {P}}^{\infty } \hat{g}_\mathrm {r}(x - \xi ,s_n) \hat{w}_\mathrm {r}^\mathrm {f} (\xi ,s) \, \mathrm {d}\xi \, \mathrm {d}s \nonumber \\&\quad +\hat{w}_\mathrm {r,\textit{n},p}^\mathrm {e} (x_\mathrm {P},s_n). \end{aligned}$$

(101)

The integration over $\xi$ in Eqs. (99) to (101) can be performed analytically, while the integration over s needs to be performed numerically. Furthermore, the contribution from the moving load in the right domain on the reaction forces at $x=L$, namely $\hat{V}_{\mathrm {L},n}(s_n)$ and $\hat{M}_{\mathrm {L},n}(s_n)$, also change compared to Eqs. (50) and (51) and are given by the following expressions:

$$\begin{aligned} \hat{V}_{\mathrm {L},n}(s_n)&= \frac{(1-\mathrm {i})\,F_0}{2} \, \Bigg (\frac{\mathrm {e}^{-\mathrm {i}k_\mathrm {r}(x_\mathrm {P}-L)}}{k_\mathrm {r}v-\mathrm {i}s_n} + \frac{\mathrm {e}^{-k_\mathrm {r}(x_\mathrm {P}-L)}}{k_\mathrm {r}v+s_n} \Bigg ), \nonumber \\&\qquad \overline{\tau }_{n-1} > \frac{L}{v}, \end{aligned}$$

(102)

$$\begin{aligned} \hat{M}_{\mathrm {L},n}(s_n)&= \frac{(1-\mathrm {i})\,F_0}{2\,k_\mathrm {r}} \, \Bigg (\frac{-\mathrm {e}^{-\mathrm {i}k_\mathrm {r}(x_\mathrm {P}-L)}}{k_\mathrm {r}v-\mathrm {i}s_n} + \mathrm {i}\frac{\mathrm {e}^{-k_\mathrm {r}(x_\mathrm {P}-L)}}{k_\mathrm {r}v+s_n} \Bigg ), \nonumber \\&\qquad \overline{\tau }_{n-1} > \frac{L}{v}. \end{aligned}$$

(103)

Together with the expressions in Sect. 2.3.2, Eqs. (49), (50) and (51), the non-reflective boundary conditions at the right boundary are now complete.