A comprehensive model for transient behavior of tapping mode atomic force microscope

Abstract

Many investigations have focused on steady-state nonlinear dynamics of cantilevers in tapping mode atomic force microscopy (TM-AFM). However, a transient dynamic model—which is essential for a model-based control design—is still missing. In this paper, we derive a mathematical model which covers both the transient and steady-state behavior. The steady-state response of the proposed model has been validated with existing theories. Its transient response, however, which is not covered with existing theories, has been successfully verified with experiments. Besides enabling model-based control design for TM-AFM, this model can explain the high-end aspects of AFM such as speed limitation, image quality, and eventual chaotic behavior.

1 Introduction

Atomic force microscopy (AFM) is a powerful tool for imaging the surface of samples with a sub-nanometer resolution which has many different applications in experimental sciences such as physics and biology [1,2,3,4]. Nowadays, AFM is also attracting more and more attention in the semiconductor industry as an inspection and metrology tool. The latter applications demand much stricter requirements regarding throughput, accuracy, reliability, and nondestructiveness [5,6,7,8]. To improve the imaging throughput and reliability of AFM, it is essential to understand its physics and optimize its mechanical parts and controllers.

A popular and promising AFM-based measurement technique, both for research and industrial applications, is the amplitude modulation (AM-AFM) or the tapping mode AFM (TM-AFM). TM-AFM is mainly popular because it applies very small forces on the sample surface and, consequently, has lower probability of damaging the sample. The nondestructiveness of TM-AFM can be so important that, e.g., researchers in the field of biology refer to it as a blessing [9].

Fig. 1

Schematic representation of relationship between amplitude and distance, depicting the reasoning for parachuting effect, coexistence of attractive–repulsive regimes, snap-in phenomenon and transient behavior

The TM-AFM works as follows: A cantilever with a sharp tip attached to its free end is excited at a frequency around its fundamental resonance frequency, and brought close to the surface of the sample. At a certain distance from the sample surface, the tip starts to interact with the sample via different forces such as van der Waals (vdW) interaction, Pauli repulsion, squeezed film damping, hydro-capillarity, electrostatic forces, etc [10]. As a result of the tip–sample interaction (TSI) forces, the amplitude of the motion of the cantilever reduces [11, 12]. A feedback control loop adjusts the distance between the cantilever and the sample surface using a piezoelectric (z-stage) actuator, such that the amplitude of the cantilever is kept constant at a user-defined fraction of its free air amplitude. While raster scanning the sample surface, and keeping the amplitude constant, the output signal of the controller is recorded and interpreted as the height profile of the sample.

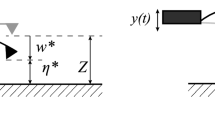
In case the amplitude of the cantilever has a one-to-one relationship with its distance to the surface, keeping the amplitude constant would mean keeping the distance constant. Therefore, any fluctuation in the height profile of the sample is compensated with the z-stage control unit, and the height profile of the sample can be measured via the control signal. However, as schematically shown in Fig. 1, the relationship between the amplitude and the distance is not always one-to-one, and consequently, the height measurement is not always trivial. For example, at the far right-hand side of Fig. 1, where the sample is far from the cantilever, obviously there is no interaction and the amplitude is independent of the distance. If this situation happens during imaging, the error signal saturates and the so-called parachuting-type artifacts appear on the image [4, 13]. Similarly, at the far left-hand side of the curve in Fig. 1, where the attractive forces exceed a certain value, the tip snaps onto the surface and sticks to it, the so-called snap-in phenomena. Thus, independent of small variations of the distance, the amplitude remains zero [14]. Another situation where amplitude and height do not have a one-to-one relationship is the coexistence of the attractive and repulsive regimes [15]. At two different distances from the surface, the TSI force can reduce the amplitude of the cantilever to the same value. In one regime, the average force is attractive, and in the other, it is repulsive. In Fig. 1, if the distance between the cantilever and the sample is $h_1$, the vibration amplitude could be either $A_1$ or $A_2$. Similarly, if the measured amplitude is equal to $A_2$, the distance could be either $h_1$ or $h_2$. In this case, a certain amplitude may correspond to two different height values and vice versa. Hence the controller fluctuates between the two height values, which causes artifacts on the image. Researchers have studied these nonlinear effects, their consequences, and the related problems, extensively [15,16,17]. However, all these studies consider a steady-state condition and the transient response of the cantilever is neglected.

The nonlinearities are not the only cause for distortion of the amplitude–distance relationship, also transient behavior of the cantilever can distort this one-to-one relationship. The amplitude–distance relationship in Fig. 1 is only valid for steady-state situations, i.e., where the amplitude signal is settled to a constant value. For example, suppose that the system is initially settled to Point A in Fig. 1, then, suddenly, the surface is retracted up to a distance corresponding to Point B. Obviously, the amplitude of the cantilever cannot adapt suddenly. Therefore, it might follow a different trajectory than the linear steady-state one. How fast the amplitude can adjust itself to the variations in the height totally depends on its dynamic trajectory. This problem is crucial for high-speed AFM, where the changes of the distance happen in time intervals that are comparable or shorter than the cantilevers response time. Note that, the transient response of the cantilever is not taken into account in control design for AFM. Hence, such a transient behavior of the cantilever may cause a closed-loop chaotic behavior in presences of nonlinear tip–sample interactions [18]. It has been previously reported that this chaotic behavior strictly limits the speed of the TM-AFM and can only be avoided by reducing the control gains and imaging speed [18].

To understand and improve the speed limit of AFM, an in-depth investigation of the transient response of the cantilever is crucial. However, the transient dynamics of the cantilever, which governs the overall performance of AFM, is often ignored or purely discussed from a tip–sample interactions point of view [19]. Therefore, here we try to answer the following research question: how does the amplitude (and phase) of the motion of the cantilever evolve in transient situations? For this, we derive a set of governing differential equations based on Fourier components of the force and displacement. Different aspects of the proposed model are verified with experiments and compared with existing steady-state models. The proposed model is generic in a sense that it does not contain a certain tip–sample interaction model and enables graphical interpretations. A graphical interpretation is helpful for understanding the effects of cantilever dynamics on high-end aspects such as image quality and speed limit. Moreover, the proposed model can be a first step toward designing model-based controllers for high-speed nondestructive TM-AFM.

This paper is further organized as follows: In Sect. 2, we present a detailed derivation of the proposed mathematical model based on an averaging approach. In Sect. 3, we present analytic, numerical, and experimental results based on the proposed model. This is divided into four different subsections. The first subsection shows that the linear steady-state response of the proposed model is exactly equal to a steady-state response of a one-degree-of-freedom (DOF) resonator. The second subsection compares the nonlinear steady-state response of the proposed method with the existing theories for TM-AFM. In the third subsection, we introduce the transient response in time domain and verify it with experiments. Finally, in the fourth subsection, we use a specific experiment to verify the transient response in frequency domain and try to explain some of the existing experimental results. Section 4 is devoted to practical implications of the transient behavior for high-speed TM-AFM. This section consists of two subsections. The first subsection explains the effect of cantilever dynamics on image quality based on closed-loop nonlinear simulation. The second subsection graphically explains the reason behind the chaotic behavior of TM-AFM as a consequence of high control gains as previously reported in [18].

2 Mathematical modeling

According to experiments and previously achieved numerical results, despite the strong nonlinearities of the tip–sample interactions, the motion of the cantilever in conventional TM-AFM is harmonic up to a large extent [20]. The reason behind this harmonic motion is the extreme contrast between the sensitivity of the cantilever to different forces. The cantilever is highly sensitive to the forces that correspond to its resonance frequency, and almost not responsive to any other forces. Therefore, the Fourier component of the forces which correspond to the fundamental resonance frequency of the cantilever generates a measurable displacement, while the effects of the other forces are likely to be obscured by the noise [20]. When this contrast is low [low quality (Q)-factor [21] or multi-harmonic cantilevers [22, 23]] or if the TSI force is so strong that it compensates for the low sensitivity, the motion of the cantilever can contain some higher frequency components. However, for conventional TM-AFM, and in the presence of measurement noises, it is almost impossible to measure the higher frequency content of the motion.

Considering only a single harmonic motion, it is a legitimate choice to model the AFM cantilever as a one-DOF mass–spring–damper system. For brevity, we start with a non-dimensional form of a one-DOF model of the AFM cantilever as:

$$\begin{aligned} \ddot{x}+\xi {\dot{x}}+x=F_\mathrm{d} \hbox {cos}(\omega t) + f_\mathrm{ts}, \end{aligned}$$

(1)

where x is the non-dimensional displacement of the tip, with over-dot representing the time derivative. $\xi =\frac{1}{Q}$ is the damping ratio, with Q being the Q-factor of the cantilever. $F_\mathrm{d}, f_\mathrm{ts}$ and $\omega$ represent the normalized driving force, TSI force, and excitation frequency, respectively.

Although Eq. (1) represents the dynamics of the cantilever up to a reasonably high precision, it is not very useful for control design purposes. As mentioned before, the motion of the cantilever only contains one harmonic component and the controller observes its amplitude, which by definition varies much slower than the motion of the cantilever. In practice, a lock-in amplifier (LIA) demodulates the motion of the cantilever into its amplitude and phase and feeds them to the controller. The details of the LIA are outside the scope of this paper, however, it is essential to note that there does not exist any transfer function or linear approximation for the LIA. Hence, to incorporate the functionality of the LIA, one should either solve for the strongly nonlinear multiple-time-scale dynamics of the cantilever which is coupled with the LIA, or derive a demodulated model, directly. Obviously, the first would not be efficient for applications such as control design or long time-horizon simulations. Moreover, the TSI force ($f_\mathrm{ts}$) in Eq. (1) is normally a continuous, but non-differentiable function. Theoretically, such functions do not have any Taylor series approximation, which makes it even more elusive for stability analysis in control design. To overcome these problems, we opt for deriving a demodulated model for the cantilever.

Defining $s_1 \triangleq {\dot{x}}$ and $s_2\triangleq x$, Eq. (1) reads in state-space format:

$$\begin{aligned} \begin{Bmatrix} \dot{s_1}\\ \dot{s_2} \end{Bmatrix}= \begin{Bmatrix} -\xi s_1 - s_2 +f_\mathrm{ts}+F_\mathrm{d} \hbox {cos}(\omega t)\\ s_1 \end{Bmatrix}. \end{aligned}$$

(2)

Since the amplitude and the phase evolve with a much slower time scale, it is useful to define a new time coordinate $\tau$, assuming that the signals in $\tau$ domain are constant during one cycle of vibration of the cantilever. Thus, $\tau$ shall be used to describe any slowly varying function. A function $f(\tau )$ is called “slow” in contrast to a rapidly varying periodic function g(t) with the periodicity of T, if it has the following property:

$$\begin{aligned} \int \limits _0^{T} f(\tau )g(t)\hbox {d}t \approx f(\tau ) \int \limits _0^{T} g(t)\hbox {d}t \end{aligned}$$

(3)

Note that, $\tau$ by itself does not differ from t, it is only a notation which is introduced to explicitly separate the slowly varying functions from quickly changing ones.

Assuming that each of the state variables are harmonic functions with slowly varying amplitude and phase (hereafter referred to as semi-harmonic), one can write:

$$\begin{aligned} \begin{matrix} s_{i}(t){\approx } A_{i}(\tau )\hbox {cos}(\omega t {+} \varphi _{i}(\tau )){=} \mathfrak {R}[A_{i}(\tau ) \hbox {e}^{j(\omega t+\varphi _{i}(\tau ))}] \end{matrix}. \end{aligned}$$

where $i=1,2$, $j=\sqrt{-1}$, and $\mathfrak {R}$ indicates the real operator ($\mathfrak {I}$ will be used for the Imaginary operator). Note that the static component and all the higher harmonics of the s signal is filtered by LIA, and bandwidth of the A and $\varphi$ is limited to that of the LIA. By defining $X_{i}(\tau )\triangleq A_{i}(\tau ) \hbox {e}^{j \varphi _{i}(\tau )} \in {\mathbb {C}}$, the state variables can be written as the following explicit multiplication of a slowly varying complex function and a pure harmonic function:

$$\begin{aligned} s_{i}(t)=\mathfrak {R}\left[ \underbrace{X_{i}(\tau )}_{\text {slow}} \, \underbrace{\hbox {e}^{j \omega t}}_{\text {harmonic}}\right] . \end{aligned}$$

(4)

Hence, the complex variable $X_{i}(\tau )$ represents the amplitude and phase of $s_{i}(t)$ corresponding to frequency $\omega$. Using the chain rule of differentiation, and since differentiation is distributive for the $\mathfrak {R}$ operator, we have:

$$\begin{aligned} \dot{s_{i}}= & {} \frac{\hbox {d}}{\hbox {d}t}\mathfrak {R}\left( X_{i}(\tau )\hbox {e}^{j\omega t}\right) =\mathfrak {R}\left( \frac{\hbox {d}X_{i}}{\hbox {d}\tau } \hbox {e}^{j\omega t}+X_{i} \frac{\hbox {d}\hbox {e}^{j\omega t}}{\hbox {d}t}\right) \nonumber \\= & {} \mathfrak {R}\left( \dot{X_{i}}\hbox {e}^{j\omega t}+j\omega X_{i} \hbox {e}^{j\omega t}\right) . \end{aligned}$$

(5)

In the same manner, the TSI force is a semi-periodic signal. Thus, it can be decomposed into its semi-harmonic components as:

$$\begin{aligned} f_\mathrm{ts}(t)=\mathfrak {R}\left( \sum \limits _{n=0}^{\infty } F_\mathrm{ts}^{(n)}(\tau ) \hbox {e}^{j n\omega t}\right) \end{aligned}$$

(6)

where $F_\mathrm{ts}^{(n)}(\tau ) \in {\mathbb {C}}$ represents the amplitude and phase of the $n^{th}$ harmonic component of the tip–sample interaction force. Note that Eq. (6) differs from the standard complex Fourier transform only in a way that the amplitude values are not necessarily constant, but represent slowly varying functions in time domain $\tau$.

Substituting Eqs. (4) to (6) in Eq. (2) yields:

$$\begin{aligned}&\mathfrak {R}\Big [(\dot{X_1}(\tau )+j\omega X_1(\tau ) +\xi X_1(\tau ) + X_2(\tau ) )\hbox {e}^{j \omega t} \nonumber \\&\quad - \sum \limits _{n=0}^{\infty } F_\mathrm{ts}^{(n)}(\tau ) \hbox {e}^{j n \omega t} -F_\mathrm{d} \hbox {e}^{j \omega t}\Big ]=0 \end{aligned}$$

(7a)

$$\begin{aligned}&\mathfrak {R}[(\dot{X_2}(\tau )+j\omega X_2 (\tau )- X_1(\tau ))\hbox {e}^{j\omega t}]=0 \end{aligned}$$

(7b)

Multiplying both sides of Eq. (7) with $\hbox {e}^{j \omega t}$ and integrating through a vibration cycle $\left( \int \nolimits _{0}^{\frac{2\pi }{\omega }}(\cdot )\hbox {e}^{j \omega t}\hbox {d}t\right)$, one can project the equations onto the space of the first harmonic component as:

$$\begin{aligned}&\underbrace{\int \limits _0^{\frac{2\pi }{\omega }} \mathfrak {R}\left[ (\dot{X_1}+j\omega X_1 +\xi X_1(\tau ) + X_2(\tau ) -F_\mathrm{d} - F_\mathrm{ts}^{(1)}(\tau ))\hbox {e}^{j \omega t}\right] \hbox {e}^{j \omega t} \hbox {d}t}_{\varGamma _1} \nonumber \\&\quad -\underbrace{\int \limits _0^{\frac{2\pi }{\omega }} \mathfrak {R}\left[ F_\mathrm{ts}^{(0)}(\tau )\right] \hbox {e}^{j \omega t} \hbox {d}t }_{\varGamma _0}- \underbrace{\int \limits _0^{\frac{2\pi }{\omega }} \sum \limits _{n=2}^{\infty } \mathfrak {R}\left[ F_\mathrm{ts}^{(n)}(\tau ) \hbox {e}^{j n \omega t}\right] \hbox {e}^{j \omega t} \hbox {d}t}_{\varGamma _n}=0\nonumber \\ \end{aligned}$$

(8a)

$$\begin{aligned}&\int \limits _0^{\frac{2\pi }{\omega }} \mathfrak {R}\left[ (\dot{X_2}+j\omega X_2 - X_1)\hbox {e}^{j\omega t}\right] \hbox {e}^{j \omega t} \hbox {d}t=0 \end{aligned}$$

(8b)

Notice that we deliberately expanded the zeroth and first harmonics of the TSI force ($\varGamma _0$, and $F_\mathrm{ts}^{(1)}$ in $\varGamma _1$) out of the $\sum$ (sum) operator. In this way, the equations are rearranged in frequency order where $\varGamma _0, \varGamma _1$, and $\varGamma _n$ represent the terms with zero frequency, first harmonic, and higher harmonics, respectively.

Moreover, from the orthogonality of harmonic functions, it is easy to check that, for $\forall \ n \in {\mathbb {N}}, c \in {\mathbb {C}}$ we have:

• 1. If $n \ne 1, \Rightarrow \int \limits _0^{2\pi } \hbox {e}^{ j \theta } \mathfrak {R}[c \hbox {e}^{j n \theta }] \hbox {d}\theta =0$.

• 2. If $\int \limits _0^{2\pi } \hbox {e}^{j \theta } \mathfrak {R}[c \hbox {e}^{j \theta }]\hbox {d}\theta =0, \Rightarrow c=0$.

Considering the first statement of the orthogonality above, and the definition in Eq. (3), the last term in Eq. (8a) vanishes ($\varGamma _n=0$). Applying the second statement of orthogonality to the remaining terms in Eq. (8), the $\mathfrak {R}$ operator drops and the following differential equations are obtained:

$$\begin{aligned} \dot{X_1}= & {} -j\omega X_1 -\xi X_1 -X_2 +F_\mathrm{ts}^{(1)} +F_\mathrm{d} \end{aligned}$$

(9a)

$$\begin{aligned} \dot{X_2}= & {} -j\omega X_2 + X_1 \end{aligned}$$

(9b)

Equation (9) is an ordinary differential equation with complex variables and coefficients. By defining new state parameters as $\mathbf{q } \triangleq [q_1, q_2,q_3,q_4]^{\mathrm{T}}=[\mathfrak {R}(X_1), \mathfrak {I}(X_1),\mathfrak {R}(X_2), \mathfrak {I}(X_2)]^{\mathrm{T}}\in {\mathbb {R}}^4$ and separating the real and imaginary parts of Eq. (9), the governing differential equations for the modulated system can be written in the standard real valued state-space form as:

$$\begin{aligned} \begin{Bmatrix} \dot{q_1}\\\dot{q_2}\\\dot{q_3}\\\dot{q_4} \end{Bmatrix}= & {} \underbrace{ \begin{bmatrix} -\xi&\omega&-1&0 \\ -\omega&-\xi&0&-1 \\ 1&0&0&\omega \\ 0&1&-\omega&0 \end{bmatrix}}_{\varLambda } \begin{Bmatrix} q_1\\q_2\\q_3\\q_4 \end{Bmatrix} \nonumber \\&+ \begin{Bmatrix} F_\mathrm{d}+ \mathfrak {R}(F_\mathrm{ts}^{(1)}) \\ \mathfrak {I}(F_\mathrm{ts}^{(1)}) \\0\\0 \end{Bmatrix}, \end{aligned}$$

(10a)

$$\begin{aligned} \begin{aligned} A_2(\tau )&=\sqrt{q_3^2+q_4^2}, \\ \varphi _2(\tau )&=\tan ^{-1}\left( \frac{q_3}{q_4}\right) , \end{aligned} \end{aligned}$$

(10b)

where

$$\begin{aligned} F_\mathrm{ts}^{(1)}(\tau )=\mathfrak {R}(F_\mathrm{ts}^{(1)})+j\mathfrak {I}(F_\mathrm{ts}^{(1)}) =\int \limits _0^{\frac{2\pi }{\omega }} f_\mathrm{ts}(t) \hbox {e}^{j \omega t} \hbox {d}t, \end{aligned}$$

is the slowly varying first Fourier component of the TSI force, $A_2(\tau )$ represents the amplitude of the motion, and $\varphi _2(\tau )$ is the phase.

It might be counterintuitive to observe that the second-order system in Eq. (1) is converted to a fourth-order system in Eq. (10). However, it is straightforward to check that Eq. (10) is a minimal realization, meaning that, four is the minimum dimensionality of the state-space that can accurately represent the modulated system.

It is useful to summarize the physical meaning of the equations and the derivation steps. We started with a single-DOF mass–spring model of the cantilever in Eqs. (1) and (2). Then, assumed that the amplitude and phase of the cantilever change significantly slower than the motion of the cantilever in Eqs. (3) and (4). Furthermore, by projecting the equations onto the Fourier kernel in Eq. (8), the differential equations for amplitude and phase at the slow timescale Eq. (10a) have been achieved. According to Eq. (10a), the amplitude modulated cantilever is a fourth-order linear dynamic system, with a nonlinear sensing (amplitude and phase). The dynamic properties of this system depend on its Q-factor and excitation frequency. The input of the modulated system only consists of the dither force and the first harmonic of the tip–sample interaction force.

The first harmonic of the force ($F_\mathrm{ts}^{(1)}$) has a nonlinear relationship with the state variables ($q_{i}$) and the distance of the cantilever from the sample surface. “Appendix A” presents the derivation of $F_\mathrm{ts}^{(1)}$ as a function of the distance and the state parameters for the well-known Derjaguin–Muller–Toporov (DMT) force model.

3 Numerical and experimental results

In this section, the proposed formulation is used to study the dynamic behavior of AFM cantilevers. First, the steady-state response of the proposed model is verified with existing models. Next, the transient behavior of the cantilever is studied in time and frequency domains and verified with experiments.

3.1 Linear steady-state response

The most simple test to check the proposed model is to evaluate it for linear steady-state case. For this, the steady solution of Eq. (10) can be calculated by putting the TSI force and the left-hand side of Eq. (10a) equal to zero ($F_\mathrm{ts}^{(1)}=0$, $\dot{\mathbf{q }}_{\mathrm{ss}}=O$), thus:

$$\begin{aligned} \begin{bmatrix} -\xi&\omega&-1&0 \\ -\omega&-\xi&0&-1 \\ 1&0&0&\omega \\ 0&1&-\omega&0 \end{bmatrix} \begin{Bmatrix} q_1\\q_2\\q_3\\q_4 \end{Bmatrix}_{\mathrm{ss}}=- \begin{Bmatrix} F_\mathrm{d}\\0\\0\\0 \end{Bmatrix}. \end{aligned}$$

(11)

The subscript ss stands for steady state. This algebraic set of equations can be solved analytically as follows. The last two equations in Eq. (11) can be solved separately as: $q_{1}=-\omega q_4$ and $q_2=\omega q_3$. Substituting this results in the first two equations of the Eq. (11) gives:

$$\begin{aligned} \begin{bmatrix} 1- \omega ^2&-\xi \omega \\ \xi \omega&1- \omega ^2 \end{bmatrix} \begin{Bmatrix} q_3\\q_4 \end{Bmatrix}_{\mathrm{ss}}= \begin{Bmatrix} F_\mathrm{d}\\0 \end{Bmatrix}. \end{aligned}$$

(12)

Solving the above equation analytically, the stationary state variables become:

$$\begin{aligned} q_3= & {} \frac{F_\mathrm{d}(1-\omega ^2)}{(1-\omega ^2)^2+\xi ^2 \omega ^2}, \\ q_4= & {} \frac{-F_\mathrm{d}\xi \omega }{(1-\omega ^2)^2+\xi ^2 \omega ^2}. \end{aligned}$$

Substituting the static solution for state variables into Eq. (10b), the following well-known relations are obtained:

$$\begin{aligned} A_{\mathrm{ss}}= & {} \frac{F_\mathrm{d}}{\sqrt{(1-\omega ^2)^2+\xi ^2 \omega ^2}}, \end{aligned}$$

(13a)

$$\begin{aligned} \varphi _{\mathrm{ss}}= & {} \tan ^{-1} \frac{\xi \omega }{(1-\omega ^2)}. \end{aligned}$$

(13b)

This shows that the static response of the proposed model in linear case indeed leads to the steady-state response of a one-DOF linear resonator [24].

3.2 Nonlinear steady-state response

The proposed model eliminates the fast timescale and represents the dynamics of AFM cantilever in slow timescale. Therefore, its static response corresponds to the steady-state response of the AFM cantilever, whereas its dynamic response represents the transient behavior. In this subsection, the steady response of the proposed model is compared to the existing theories presented in [12, 17, 25]. Similar to the previous subsection, by putting the left-hand side of Eq. (10a) equal to zero, the steady-state response of the AFM cantilever can be obtained. However, in contrast to the previous section, the TSI force is not equal to zero, but its relationship with state parameters has to be calculated via a so-called force model. For this, we used the Derjaguin–Muller–Toporov (DMT) model which consists of the attractive van der Waals (vdW), repulsive Hertz, and dissipative viscoelastic forces. For details on this model please refer to “Appendix A” and the references [26,27,28].

Fig. 2

Nonlinear frequency response curves of cantilever in TM-AFM for different cantilever-sample separations; red represents the smallest and blue represent the largest distance. The green-dashed curve schematically represents the amplitude–distance relationship as shown in Fig. 1. Simulation parameters are the same as reference [25], and the results in this figure are in good agreement with literature, for example see reference [25]. (Color figure online)

Using this model, the first harmonic component of the TSI force can be written as:

$$\begin{aligned} \mathfrak {R}(F_\mathrm{ts}^{(1)})= & {} \left( \beta A_2^{\frac{1}{2}} I_2\left( \frac{h}{A_2},\frac{\sigma }{A_2}\right) -\frac{\alpha }{A_2^3} I_1\left( \frac{h}{A_2},\frac{\sigma }{A_2}\right) \right) q_3 \nonumber \\&+\gamma A_2^{-\frac{1}{2}} I_3\left( \frac{h}{A_2},\frac{\sigma }{A_2}\right) q_1, \end{aligned}$$

(14a)

$$\begin{aligned} \mathfrak {I}(F_\mathrm{ts}^{(1)})= & {} \left( \beta A_2^{\frac{1}{2}} I_2\left( \frac{h}{A_2},\frac{\sigma }{A_2}\right) - \frac{\alpha }{A_2^3} I_1\left( \frac{h}{A_2},\frac{\sigma }{A_2}\right) \right) q_4 \nonumber \\&+\gamma A_2^{-\frac{1}{2}} I_3\left( \frac{h}{A_2},\frac{\sigma }{A_2}\right) q_2, \end{aligned}$$

(14b)

where, $\alpha =\frac{HR}{6kA_0^3}$, $\beta =\frac{4E_\mathrm{Eff}\sqrt{RA_0}}{3k}$, and $\gamma =\omega \eta \sqrt{RA_0^3}$, are the coefficients of the vdW, Hertz and viscoelastic forces, respectively. $H, R, E_\mathrm{Eff}, h, A_0, A_2$, and $\sigma$ are Hammaker constant, tip radius, effective stiffness of tip–sample contact, separation of the sample surface and the cantilever in its undeflected configuration, free air amplitude, actual amplitude at any time [as described in Eq. (10b)], and the intermolecular distance, respectively. The integral functions ($I_1$, $I_2$ and $I_3$) as a function of their arguments ($\zeta _1, \zeta _2$) are defined as:

$$\begin{aligned} I_1(\zeta _1,\zeta _2)= & {} \int \limits _0^{2\pi } \frac{\hbox {cos}(\theta )\hbox {d}\theta }{(\zeta _1-\hbox {cos}(\theta ))^2_{D_{\zeta _2}}}, \end{aligned}$$

(15a)

$$\begin{aligned} I_2(\zeta _1,\zeta _2)= & {} \int \limits _0^{2\pi }(\hbox {cos}(\theta )-\zeta _1+\zeta _2)^{\frac{3}{2}}_{D_0}\hbox {cos}(\theta )\hbox {d}\theta , \end{aligned}$$

(15b)

$$\begin{aligned} I_3(\zeta _1,\zeta _2)= & {} \int \limits _0^{2\pi }(\hbox {cos}(\theta )-\zeta _1+\zeta _2)^{\frac{1}{2}}_{D_0}\hbox {cos}(\theta )\hbox {d}\theta . \end{aligned}$$

(15c)

where the discontinuity function $(a)_{D_{b}}$ is defined to impose the discontinuity of the forces during the contact as: $(a)_{D_b}={\left\{ \begin{array}{ll} a &{} \text {if } a \ge b\\ b &{} \text {if } a < b \end{array}\right. }$. A detailed derivation of the force model for slow timescale and the details of DMT model is presented in “Appendix A”.

Typically, an arc-length continuation method is used to calculate the nonlinear frequency response of a nonlinear system. However, the frequency response of the system represented by Eq. (10) can always be transformed to a quadratic algebraic problem in terms of excitation frequency squared ($\omega ^2$), irrespective of the type of the nonlinearity. Hence, its nonlinear frequency response can also be calculated analytically as well. The details of calculating the nonlinear frequency response of the cantilever using the proposed model are presented in “Appendix B”.

Figure 2 shows the steady-state nonlinear frequency response of the cantilever considering different cantilever-sample separations. These results were calculated with the same parameters as in [25] (spring constant 2 N/m, resonance frequency 52.4 kHz, quality factor 66.7, tip radius 20nm Hammaker constant $2.96 \times 10^-19$ J, intermolecular distance 2.0 Å, and free air amplitude 100 nm). The nonlinear frequency responses in Fig. 2 are in good agreement with the results presented by Lee et al. [25], whereas the dashed green curve represents the amplitude–distance relationship depicted in Fig. 1.

These results show that the static response of the proposed model agrees with the existing models for steady-state response of the AFM cantilever. The next sections will study the transient behavior of the AFM cantilever which captures the dynamic transition between each of the lines in Fig. 2.

Fig. 3

Step response of the amplitude and phase in polar and Cartesian coordinates. In the phasor plot, the distance from the center of coordinates shows the amplitude and the angle shows the phase delay. The reasoning behind overshoot of amplitude and the trajectory of phase is stem from the spiral trajectory shown in the phasor plot

3.3 Transient response in the time domain

To investigate the evolution of the amplitude and phase in the time domain, here the step response of the modulated system is studied. The assumption is that the cantilever is initially at rest (zero amplitude). Suddenly, a harmonic force with a constant amplitude and frequency is applied (i.e., dither piezo turned on). Figure 3 shows the dynamic trajectory of the amplitude and phase from rest to its steady-state.

Fig. 4

Dynamic trajectories of amplitude–phase pair with different excitation frequency. a Experimental: a cantilever with the Q factor $\approx 300$, stiffness $\approx 1~\hbox {N/m}$ and fundamental resonance frequency $\approx 45$ kHz) has been used in a commercial AFM system. While the cantilever was far from any sample surface, the excitation power has been suddenly increased from 3 to 6 V. b Numerical: step responses of Eq. (10). If the excitation frequency is less than the resonance frequency of the cantilever, the dynamic trajectory is a clockwise spiral and vice versa

Note that the dynamic trajectory of the cantilever is a spiral of which the direction is determined by the ratio between the excitation frequency and the resonance frequency of the cantilever. If the excitation frequency is lower than the resonance frequency, the cantilever follows a counterclockwise spiral, and vice versa. This is illustrated via numerical and experimental results in Fig. 4. Here, the numerical results show the step response of linear part of Eq. (10) and experimental results are captured using a commercially available AFM and LIA , i.e., Bruker Fast-Scan and Zurich Instruments UHFLI 1.8 GSa/s 600 MHz. In the experiments, first the cantilever was settled to a certain amplitude and phase, then suddenly, we increase the excitation power to twice its steady value. Note that the initial point in experiments start from different phase values, with approximately identical amplitudes, because the excitation frequency was different for the three cases. Moreover, we did not start the experiment from rest condition, because the phase signal is defined based on the dither signal and cannot be defined while the cantilever is at rest.

The spiral shape of the trajectory is more relevant when high-speed AFM controllers are concerned. The spiral-shaped trajectory in Fig. 4 shows that there can be an initial response in the wrong direction, similar to the non-minimum-phase (MNP) behavior in linear systems [29]. Meaning that, if for any reason one expects the amplitude to drop, it might first increase and then drop, or vice versa. This wrong direction of the initial response makes it very challenging for high-speed controllers. If the time constant of the controller is shorter than the settling time of the cantilever, the controller might take wrong actions based on the wrong directional response of the cantilever.

Fig. 5

Schematic of the experimental setup for frequency domain analysis. LIA 1 modulates and demodulates the motion of the cantilever, and the LIA 2 modulates and demodulates the amplitude signals that are provided to and received from the LIA 1. The output amplitude and phase of LIA 2 represents the dynamic behavior of the modulated cantilever in frequency domain

3.4 Nonlinear transient response in the frequency domain

This subsection investigates the frequency domain response of the demodulated system. In order to understand the model represented by Eq. (10) in frequency domain, it is assumed that the excitation force is modulated with another harmonic signal which has a much lower frequency than the resonance frequency of the cantilever. Considering the linear dynamics of the modulated system, i.e., Eq. (10a), one observes that the system has two pairs of complex conjugate poles [eigenvalues of matrix $\varLambda$ in Eq. (10)] at:

$$\begin{aligned} \begin{matrix} P_{1-4}=-\frac{\xi \pm j |\sqrt{4-\xi ^2} \pm 2\omega |}{2}\approx -\frac{\xi }{2} \pm j \frac{2\pm 2\omega +\frac{\xi ^2}{2}+\cdots }{2} \end{matrix} \nonumber \\ \end{aligned}$$

(16)

Normally, an AFM cantilever in ambient conditions is a highly underdamped system. Therefore one can simplify Eq. (16) further considering that $\omega \approx 1$ and $\xi \approx 0$, and $\xi ^2 \ll (1-\omega )$.¹ In that case, one observes that the system has one pair of dominant and one pair of non-dominant poles at:

$$\begin{aligned} \begin{aligned} P_{1,2}&\approx -\frac{\xi }{2} \pm 2j \\ P_{3,4}&\approx -\frac{\xi }{2} \pm (1-\omega )j \end{aligned} \end{aligned}$$

(17)

The non-dominant pair of poles, with complex part 2 ($P_{1,2}$), represent the up-modulation of the resonator and are not relevant for the TM-AFM problem because, besides being non-dominant, their response would be filtered by the LIA. The other two poles ($P_{3,4}$), which are dominant, actually determine the transient behavior of the AFM cantilever. Eq. (17) suggests that the imaginary part of the dominant poles of the modulated system ($P_{3,4}$) are approximately equal to the difference between the excitation frequency and the resonance frequency of the cantilever, i.e., $|\omega _\mathrm{e}-\omega _\mathrm{r}|$ (or in non-dimensional form $|\omega -1|$), and their real part ($\frac{\xi }{2}=\frac{1}{2Q}$) represent the settling time of the system. In fact, the real part of the dominant poles which determine the relaxation time of the system is already known by AFM experts as it is a common knowledge that lower the Q-factor higher the speed of AFM. However, the imaginary part is not well understood.

Recently, the relationship between the real part of the poles (quality factor of the cantilever) has been experimentally confirmed by Adams et al. [30] They used different custom-made cantilevers with various Q-factors and showed the dependency of the settling time to the Q-factor. In their experiments, they used a piezoelectric actuator to modulate the surface height, artificially. In this way they measured the frequency response of the amplitude due to height variations. A very interesting and counterintuitive detail in their experiments is that the magnitude of the amplitude signal could go beyond zero decibel at certain frequencies. This effect which was not explained, is an evidence of the resonance in the modulated system (see Figure 4.b in [30]). Note that the presence of a resonance can only be explained with complex conjugate poles.

To systematically investigate the resonance of the amplitude signal, we repeated the experiment presented by Adams et al. [30]. However, with the difference that, instead of modulating the surface, we modulated the amplitude of the excitation signal. In this way the nonlinearities regarding the TSI force are out of the equation, and the pure dynamics of the cantilever is measured. For this experiment, two lock-in amplifiers were used as shown in Fig. 5. One of the LIAs provides the modulation/demodulation of the cantilever with the so-called carrier frequency, i.e., the excitation frequency of the dither ($\omega _\mathrm{e}$), whereas the second LIA modulates the amplitude of the carrier signal and extracts the amplitude and phase of the amplitude of the cantilever. In this way, effects of the fluctuation of harmonic force are measured depending on the frequency content of the fluctuation.

Fig. 6

Measured (dashed lines) and calculated (solid lines) response of the amplitude of the cantilever to the fluctuations in magnitude of the total harmonic force with five different carrier frequencies. These figures show the input–output relationship of the modulated system, where the input is amplitude of the total harmonic force and the out put is the amplitude of the cantilever. Magnitude and phase are directly measured via the second LIA shown in Fig. 5

Figure 6 shows both the measured and calculated frequency response of the amplitude to these fluctuations. The numerical results were achieved as follows:

The transfer function matrix for the linear part of the system [from $F(\omega _M)$ to $\mathbf{q }(\omega _M)$] is calculated as the first column of $(sI-\varLambda )^{-1}$ where s is the Laplace variable and I is a ($4\times 4$) unit matrix. Therefore, substituting a probe function as $F_\mathrm{d}=\sin (\omega _M\tau )$, the amplitude and phase signals ($A_2$ and $\varphi _2$) can be calculated analytically. Then, the functionality of the second LIA can be implemented by multiplying the amplitude signal ($A_2$) by the probe signal and integrating as:

$$\begin{aligned} A_A= & {} \sqrt{\left( \int _0^{2\pi } A_2 \sin (\omega _M\tau )\hbox {d}\tau \right) ^2 + \left( \int _0^{2\pi } A_2 \cos (\omega _M\tau )\hbox {d}\tau \right) ^2} \end{aligned}$$

(18a)

$$\begin{aligned} \varphi _A= & {} \tan ^{-1}\frac{\int _0^{2\pi } A_2 \sin (\omega _M\tau )\hbox {d}\tau }{\int _0^{2\pi } A_2 \cos (\omega _M\tau )\hbox {d}\tau } \end{aligned}$$

(18b)

In this way amplitude and phase ($A_A, \varphi _A$) of the amplitude signal ($A_2$) due to disturbance in total harmonic force ($F_\mathrm{d}$) were calculated.

Fig. 7

Time domain simulation results of TM-AFM while approaching the surface. In this simulation, the distance between the cantilever and the sample surface starts at 1.5 time the free air amplitude, while the cantilever is at rest. At time 0, the dither force and the PI controller are turned on. See the supplementary material for an animated version

In Fig. 6, five different carrier frequencies were chosen around the resonance frequency with an interval of 500 Hz. As it can be seen, there is a good agreement between the experimental and numerical results. Both experimental and numerical results demonstrate that the peak of the amplitude occurs at a frequency equal to the difference between the carrier and the resonance frequencies ($|\omega _\mathrm{e}-\omega _\mathrm{r}|$), which confirms Eq. (16). The experiments were done using a commercial AFM and LIAs (Bruker Fast-Scan and Zurich Instruments UHFLI 1.8 GSa/s 600 MHz) with a standard cantilever which has a resonance frequency of $\omega _\mathrm{r}=319.015$ kHz and Q-factor $Q\approx 520$. Simulations consider the same cantilever.

An other important observation from the frequency domain analysis is the slope of the decay line after resonance. The linear part of Eq. (10) suggests that the system has one pair of dominant complex conjugate poles. Hence, the system should behave like a second-order system, and have a decay line with a slope of $-40~\hbox {dB}$ per decade after the resonance. However, due to the output nonlinearity [see Eq. (10b)], the slope of the decay line can differ from $-20$ till $-40$ dB per decade, depending on the carrier frequency. This observation suggests that it would be very challenging for any system identification method to find any reliable integer-order fit for the system. This hinders the design of model-based controllers. Obviously, this problem would not appear without the output nonlinearity related to A and $\varphi$. Therefore, to design a model-based controller, one has to either design fractional-order controllers [31, 32] or use the $q_3$ and $q_4$ as the control input instead of the amplitude.

4 Implications of transient behavior of cantilevers in TM-AFM experiments

In this section, the nonlinear closed-loop behavior of the system is studied. The results show the practical implications of the transient behavior of the TM-AFM on the final image quality. Also the origin for previously reported chaotic behavior of the TM-AFM [18] can be explained.

4.1 Nonlinear closed-loop behavior of the TM-AFM

To investigate the nonlinear behavior of AFM in a closed-loop setting, a force model and a model for the controller are needed, besides the model of the cantilever. For the force, we use the slow time domain DMT model as presented in previous subsections (Eq. 14). A detailed derivation of the slow time model is presented in “Appendix A”. As the controller, an ideal proportional–integral (PI) controller is considered which assumes that the z-stage actuator is fast enough not to have any effect on the closed-loop dynamics of the system. In this way the distance between the cantilever and the sample (h) is defined as:

$$\begin{aligned} h(\tau )=k_\mathrm{p} (A(\tau )-A_\mathrm{set})+k_{i} \int ^{\tau }_0(A(s)-A_\mathrm{set}) \hbox {d}s, \nonumber \\ \end{aligned}$$

(19)

where $k_\mathrm{p}, k_{i},$ and $A_\mathrm{set}$ are proportional gain, integral gain and set-point amplitude, respectively. Equations (10), (14) and (19) representing the cantilever (and LIA), the tip–sample interactions, and the controller are coupled with each other through shared signals A, h, and $F_\mathrm{ts}^{(1)}$. Figure 7 shows the simulated amplitude, phase, and the magnitude of the harmonic component of the TSI forces during an approach process.

Fig. 8

Phasor plot representation of the amplitude and phase for three different excitation frequencies. The vectors show the steady-state forces vectors. See [11] for the explanation of the steady-state situation and Supplementary Material for an animated version

Fig. 9

Height image of a calibration sample (UMG02B from Anfatec Instruments) with three different excitation frequencies, corresponding to Fig. 8. All three images are taken from the same spot on the sample, using a standard tapping mode cantilever with a resonance frequency of 72 kHz, Q factor of 200, and spring constant of 2.5 N/m. The free air amplitude, set-point amplitude, and scan rate for all three cases are 100 nm, 75 nm, and 1 Hz, respectively. The color masks are applied to exaggerate the imaging artifacts. Imaging with a lower excitation frequency adds fewer artifacts

As it can be seen from Fig. 7, every time that the cantilever engages the surface (i.e., the distance becomes equal to the amplitude of the cantilever) the TSI force emerges and affects the cantilever and changes its amplitude and phase. It is important to notice that during the engagement time, the TSI force causes always a considerable phase lead, while the amplitude mildly changes. However, after disengaging the surface, the amplitude value keeps reducing with a larger rate and then increases again. To further investigate the transient behavior of the amplitude and the phase, Fig. 8 shows the dynamic trajectory of the system in phasor plane for three different excitation frequencies. Using these graphs, we can study the following three questions: (i) Why do the tip–sample interactions always induce a phase lead? (ii) Why does the amplitude keep reducing and then increasing when disengaged from the surface? (iii) Why is the image quality better when we choose an excitation frequency slightly lower than the resonance frequency of the cantilever?

Fig. 10

Cross section of one of the holes in Fig. 9. The profiles measured with an excitation frequency less than the resonance frequency of the cantilever show a less noisy, more stable profile

Fig. 11

Closed-loop behavior of TM-AFM in polar coordinates. a Chaotic. b Stable. The aggressive control action causes more than $2\pi$ radians phase lead in each engage–disengage cycle and prevents the system from reaching a stable center point which generates a chaotic motion

Before the cantilever engages to the surface, the motion of the cantilever has a phase delay with respect to the dither force. Since the TSI force is opposite to the displacement, the direction of the total harmonic force at the first moment of the contact is upwards (a positive phase). Also because the TSI force in first engagement is much stronger than the dither force, the total harmonic force is mainly dominated by the TSI force. In this situation, the phase increases and amplitude tries to increase by indenting the tip more and more into the sample surface. Hence, the cantilever follows the circular arc in Fig. 8 in counterclockwise. At the moment that the phase lead does not need to increase anymore, the cantilever looses contact with the surface and only the dither force is acting on the cantilever. After losing the connection, the cantilever follows its free trajectory which first reduces the amplitude and then increases. As explained in Fig. 4, the free trajectory of the motion can be either a straight line or a spiral trajectory, depending on the excitation frequency. Repeating this engaging–disengaging process for few times, the cantilever reaches its steady-state situation. The damping needed for this process is provided by all three elements: the cantilever, the non-conservative part of TSI force, and the control action.

Fig. 12

Height image of the calibration sample (UMG02B from Anfatec Instruments) with parameters corresponding to Fig. 11. When the cantilever is in chaotic regime (the control gains are too high), the images do not provide any useful information

Comparing the three different cases in Fig. 8, for the lower excitation frequency, the cantilever has a lower phase delay before the contact. Thus, it needs to follow a shorter trajectory on the circular arc to lose contact. On the other hand, after losing contact, it follows a counterclockwise spiral to reach the surface again which is shorter than a clockwise trajectory to the surface. Therefore, in total the cantilever has a shorter path to the stable steady-state situation, when it is excited with a lower frequency. That is why the images captured with a lower excitation frequency have higher image quality, which is intuitively known by experienced AFM users and is experimentally demonstrated in Fig. 9. For this example, a calibration sample is measured with three different excitation frequencies where all other parameters are exactly the same for all the three cases. The difference in image quality can be observed more clearly in Fig. 10 which illustrates the added imaging artifacts on the cross section of one of the holes in Fig. 9.

4.2 Chaotic behavior

It has been reported that if the controller is tuned to be faster than a certain threshold, the closed-loop system shows a chaotic behavior [18]. Although the presence of chaos was confirmed by studying the Poincaré sections and Lyapunov exponents, the origin of the chaos was not explained. Figure 11 shows the difference between a stable and a chaotic trajectory, and Fig. 12 shows the images captured with conditions corresponding to Fig. 11. In the scenario as explained in the previous subsection, if the controller acts more aggressive than a certain limit, the cantilever experiences more than $2\pi$ radian phase lead before losing the surface and re-engaging. Therefore, the next attempt to re-engage does not start from a better initial point. Thus, the new initial condition is not closer to the stable point comparing the previous engaging point. Hence, the “engage/disengage” process repeats forever in a periodic or non-periodic manner, depending on the control gains. While the periodic “engage/disengage” generates a quasi-periodic regime, the non-periodic one represents the chaotic trajectory. Both these regimes have been reported in [18]. All in all, the chaotic behavior can be attributed to the wrong direction response of the amplitude signal.

5 Conclusions

In this paper, we presented a dynamic model for amplitude modulation (tapping mode) AFM as the first step toward a model-based control design. The model graphically explains the behavior of the AFM cantilever in a slow timescale, i.e., the changes in the amplitude, phase and the control signals. The proposed model has been verified with experiments and shows that the behavior of the AFM cantilever in slow timescale is profoundly affected by the excitation frequency and Q-factor of the cantilever. According to the presented model the amplitude per sé is not the best indication of the distance, and should not be used as the error signal in the control loop. Instead, to design high-performance controllers and avoid chaos, one should consider a modulated transient model of the cantilever as a multi-input–multi-output system.

Appendices

Appendix A: Calculation of the tip–sample interaction force

To derive a relationship between the modulated TSI force and the state variables of the resonating cantilever, we use a generalized form of the well-known Derjaguin–Muller–Toporov (DMT) model which consist of the attractive van der Waals (vdW) force, repulsive Hertz, and a dissipative viscoelastic terms [26,27,28]. According to this model, the physical force $f_\mathrm{ts}^\mathrm{ph}$ can be written as:

$$\begin{aligned} \begin{matrix} f_\mathrm{ts}^\mathrm{ph}=\frac{HR}{6(Z-x)^2_{D_\sigma }} - \frac{4}{3}E_\mathrm{Eff}R^{\frac{1}{2}}(x+\sigma -Z)^{\frac{3}{2}}_{D_0} \\ -\eta R^{\frac{1}{2}}(x+\sigma -Z)^{\frac{1}{2}}_{D_0} \frac{\hbox {d}x}{\hbox {d}t}, \end{matrix} \end{aligned}$$

(20)

where H, R, Z, and $\sigma$ are Hammaker constant, tip radius, separation of the sample surface and the cantilever in its undeflected configuration, and the intermolecular distance, respectively. $E_\mathrm{Eff}= \left( \frac{1-\nu _\mathrm{tip}^2}{E_\mathrm{tip}}+\frac{1-\nu _\mathrm{sample}^2}{E_\mathrm{sample}} \right) ^{-1}$ is the effective elasticity of the contact which is calculated from the elasticity (E) and Poisson ratio ($\nu$) of the tip and the sample. $\eta$ is the effective viscoelasticity of the contact area. The discontinuity function $(a)_{D_{b}}$ is defined to impose the discontinuity of the forces during the contact as: $(a)_{D_b}={\left\{ \begin{array}{ll} a &{} \text {if } a \ge b\\ b &{} \text {if } a < b \end{array}\right. }.$

Normalizing the model in Eq. (20) according to the same scales as in Eq. (1), the non-dimensional form of the TSI force $\left( f_\mathrm{ts}=\frac{f_\mathrm{ts}^\mathrm{ph}}{kA_0}\right)$ can be written as:

$$\begin{aligned} f_\mathrm{ts}&=\frac{\alpha }{(h-x)^2_{D_\sigma }} - \beta (x+\sigma -h)^{\frac{3}{2}}_{D_0}\nonumber \\&\quad -\gamma (x+\sigma -h)^{\frac{1}{2}}_{D_0} \frac{\hbox {d}x}{\hbox {d}t}, \end{aligned}$$

(21)

where $h=\frac{Z}{A_0}$, $\alpha =\frac{HR}{6kA_0^3}$, $\beta =\frac{4E_\mathrm{Eff}\sqrt{RA_0}}{3k}$, and $\gamma =\omega \eta \sqrt{RA_0^3}$, are the coefficients of the vdW, Hertz and viscoelastic forces, respectively. $A_0$, and k represent the free air amplitude and the spring constant of the cantilever. Applying the Fourier operation as explained in Sect. 2 , we obtain:

$$\begin{aligned} F_\mathrm{ts}^{(1)}=F_\mathrm{vdW}^{(1)}-F_\mathrm{H}^{(1)}-F_{\mathrm{vis}}^{(1)}, \end{aligned}$$

(22)

where the first harmonic of the van der Waals force ($F_\mathrm{vdW}^{(1)}$), Hertzian contact force ($F_\mathrm{H}^{(1)}$), and viscoelastic damping ($F_{\mathrm{vis}}^{(1)}$) are defined as:

$$\begin{aligned}&F_\mathrm{vdW}^{(1)}=\alpha \int \limits _0^{\frac{2\pi }{\omega }} \frac{ \hbox {e}^{j\omega t} \hbox {d}t}{(h-\mathfrak {R}[X_2 \hbox {e}^{j\omega t}])^2_{D_\sigma }}, \end{aligned}$$

(23a)

$$\begin{aligned}&F_\mathrm{H}^{(1)}=\beta \int \limits _0^{\frac{2\pi }{\omega }} (\mathfrak {R}[X_2 \hbox {e}^{j\omega t}]+\sigma -h)^{\frac{3}{2}}_{D_0} \hbox {e}^{j\omega t} \hbox {d}t, \end{aligned}$$

(23b)

$$\begin{aligned}&F_{\mathrm{vis}}^{(1)}=\gamma \int \limits _0^{\frac{2\pi }{\omega }} (\mathfrak {R}[X_2 \hbox {e}^{j\omega t}]+\sigma -h)^{\frac{1}{2}}_{D_0}\nonumber \\&\qquad \qquad {\times } \mathfrak {R}[X_1 \hbox {e}^{j\omega t}]\hbox {e}^{j\omega t} \hbox {d}t. \end{aligned}$$

(23c)

Considering the definition of $X_{i}=A_{i} \hbox {e}^{\varphi _{i}},i=1,2$, and defining variables $\theta _{i}=\omega t+\varphi _{i}$, $i=1,2$, $\zeta _1=\frac{h}{A_2}$, and $\zeta _2=\frac{\sigma }{A_2}$, the integral in Eq. (23a) can be simplified as:

$$\begin{aligned}&\int \limits _{0}^{\frac{2\pi }{\omega }} \frac{ \hbox {e}^{j\omega t} \hbox {d}t}{(h-\mathfrak {R}[X_2 \hbox {e}^{j\omega t}])^2_{D_\sigma }}= \int \limits _{\varphi _2}^{2\pi +\varphi _2} \frac{ \hbox {e}^{(\theta -\varphi _2)} \hbox {d}\theta }{(h-A_2\mathfrak {R}[ \hbox {e}^{j(\theta )}])^2_{D_\sigma }} \\&\qquad =\frac{\hbox {e}^{-\varphi _2}}{A_2^2} \int \limits _{0}^{2\pi } \frac{[\cos (\theta )+j \sin (\theta )]\hbox {d}\theta }{\left( \frac{h}{A_2}-\cos (\theta )\right) ^2_{D_{\left( \frac{\sigma }{A_2}\right) }}}\\&\qquad = \frac{-X_2}{A_2^3} \int \limits _{0}^{2\pi } \frac{\cos (\theta ) \hbox {d}\theta }{(\zeta _1-\cos (\theta ))^2_{D_{(\zeta _2)}}}. \end{aligned}$$

Note that:

$$\begin{aligned} \int \limits _{0}^{2\pi } \frac{ \sin (\theta )\hbox {d}\theta }{\left( \frac{h}{A_2}-\cos (\theta )\right) ^2_{D_{\left( \frac{\sigma }{A_2}\right) }}} =0 \end{aligned}$$

because it is an odd periodic function of $\theta$.

Fig. 13

Integral functions $I_1$ till $I_3$ as a function their arguments

Repeating the same procedure for Eqs. (23b) and (23c), we obtain:

$$\begin{aligned} \mathfrak {R}(F_\mathrm{ts}^{(1)})= & {} (K_\mathrm{H}-K_\mathrm{vdW} ) q_3 +C_{\mathrm{vis}} q_1, \end{aligned}$$

(24a)

$$\begin{aligned} \mathfrak {I}(F_\mathrm{ts}^{(1)})= & {} (K_\mathrm{H} - K_\mathrm{vdW} ) q_4 +C_{\mathrm{vis}} q_2, \end{aligned}$$

(24b)

where $K_\mathrm{vdW}$, $K_\mathrm{H}$, and $C_{\mathrm{vis}}$ are defined as:

$$\begin{aligned}&K_\mathrm{vdW}=\frac{\alpha }{A^3} I_1\left( \frac{h}{A},\frac{\sigma }{A}\right) , \end{aligned}$$

(25a)

$$\begin{aligned}&K_\mathrm{H}=\beta A^{\frac{1}{2}} I_2\left( \frac{h}{A},\frac{\sigma }{A}\right) , \end{aligned}$$

(25b)

$$\begin{aligned}&C_{\mathrm{vis}}= \gamma A^{-\frac{1}{2}} I_3\left( \frac{h}{A},\frac{\sigma }{A}\right) , \end{aligned}$$

(25c)

and can be considered as added negative stiffness due to the vdW force, added stiffness by the Hertz force, and the added damping of the viscoelastic force, respectively. The integral functions in Eq. (25) are defined as:

$$\begin{aligned} I_1(\zeta _1,\zeta _2)= & {} \int \limits _0^{2\pi } \frac{\hbox {cos}(\theta )\hbox {d}\theta }{(\zeta _1-\hbox {cos}(\theta ))^2_{D_{\zeta _2}}}, \end{aligned}$$

(26a)

$$\begin{aligned} I_2(\zeta _1,\zeta _2)= & {} \int \limits _0^{2\pi }(\hbox {cos}(\theta )-\zeta _1+\zeta _2)^{\frac{3}{2}}_{D_0}\hbox {cos}(\theta )\hbox {d}\theta , \end{aligned}$$

(26b)

$$\begin{aligned} I_3(\zeta _1,\zeta _2)= & {} \int \limits _0^{2\pi }(\hbox {cos}(\theta )-\zeta _1+\zeta _2)^{\frac{1}{2}}_{D_0}\hbox {cos}(\theta )\hbox {d}\theta , \end{aligned}$$

(26c)

and are illustrated in Fig. 13. Note that, the conservative part of the force ($(K_\mathrm{H} - K_\mathrm{vdW})X_2$) is in the opposite direction of the modulated displacement ($X_2$), and the dissipative force ($C_\mathrm{vis} X_1$) is in the opposite direction of the modulated tip velocity ($X_1$). Therefore,$(K_\mathrm{H} - K_\mathrm{vdW})$, and $C_\mathrm{vis}$ can be considered as the added stiffness and the damping of the TSI force, respectively.

Appendix B: Calculation of the nonlinear frequency response curve

The steady-state frequency response of the cantilever can be calculated by substituting Eq. (24) into Eq. (10) and putting ${\dot{q}}_{i}=0$ yields:

$$\begin{aligned} \underbrace{ \begin{bmatrix} \begin{bmatrix} 1- \omega ^2&-\xi \omega \\ \xi \omega&1-\omega ^2 \end{bmatrix}+ \\ \\ \begin{bmatrix} K_\mathrm{H}-K_\mathrm{vdW}&-C_\mathrm{vis}\omega \\C_\mathrm{vis}\omega&K_\mathrm{H}-K_\mathrm{vdW} \end{bmatrix} \end{bmatrix}}_{\varXi } \underbrace{ \begin{Bmatrix} q_3\\q_4 \end{Bmatrix}}_{X_2} =\underbrace{ \begin{Bmatrix} F_\mathrm{d}\\0 \end{Bmatrix}}_{\varUpsilon }. \nonumber \\ \end{aligned}$$

(27)

As it can be seen from Eq. (25), the added nonlinear stiffness and damping values do not depend on the phase or frequency, instead they are only a function of amplitude. It is easy to check that this is the case for any time-invariant nonlinearity.

To avoid solving the nonlinear equation (27) for amplitude and phase, we suggest instead to scan the amplitude, and solve for frequency. Therefore, we defined $\varXi$ and $\varUpsilon$ in Eq. (27) such that $\varXi X_2=\varUpsilon$. Considering Eq. (10b) ($q_3^2+q_4^2=A^2$), one can eliminate the phase by multiplying Eq. (27) by $\varXi ^{-1}$, and left-multiply the transpose of the resultant by itself:

$$\begin{aligned} A^2=X_2^TX_2=\varUpsilon ^{\mathrm{T}} \varXi ^{-\mathrm{T}}\varXi ^{-1} \varUpsilon . \end{aligned}$$

(28)

Independent of the type of the nonlinearity (only if the nonlinearity is time independent), $\varXi$ can always be written as a summation of a skew symmetric matrix and a scaled unit matrix. Therefore, $\varXi \varXi ^{\mathrm{T}}$ will always be diagonal, with both of the elements equal to each other which leads to the single algebraic equation:

$$\begin{aligned} \frac{F_\mathrm{d}^2}{A^2}=(1+K_\mathrm{H}-K_\mathrm{vdW} - \omega ^2 )^2+(\xi +C_\mathrm{vis})^2 \omega ^2. \end{aligned}$$

(29)

For one-DOF resonators, Eq. (29) is always quadratic in terms of $\omega ^2$ and has an analytic solution for any value of the amplitude. The square root of the real and positive solutions of the Eq. (29) show the frequency for each amplitude. After calculating the amplitude–frequency pair, the phase can be calculated simply by solving the Eq. (27) for $X_2$, which is linear. The main advantage of this method as compared to arc-length methods is that in this way the computational time can be significantly reduced without compromising the accuracy. However, this method, in its present form, can only deal with one-DOF resonators with nonlinearities that are not explicitly time dependent.