1 Introduction

Drilling is used for the exploration of oil, gas, minerals and increasingly for geothermal energy. Current drilling operations are challenging as often complex, deviated wells need to be drilled, for oil and gas exploration, while, for geothermal applications, drilling into hard rock is required. Improving the efficiency of these drilling operations will significantly reduce the costs. Particularly in geothermal drilling operations, where 30–50% of the total development costs are from drilling [4, 6, 14]. Therefore, the development of new technologies to improve drilling performance is key to increase the economic feasibility of geothermal drilling operations.

Fig. 1
figure 1

(Adapted from Marck [26])

Schematic overview of a drilling system in an inclined well.

Full size image

Rotary drilling with polycrystalline diamond compact (PDC) bits is widely accepted as most efficient for exploration and production drilling operations. Figure 1 depicts the major components of a rotary drilling system: rig, drill-string, bottom hole assembly (BHA), including stabilizers and down-hole tools, and drill-bit. In a rotary drilling system, a key indicator of its efficiency is the rate-of-penetration (ROP), which is the speed at which the bit is drilling into the sub-surface formation. In order to optimize the ROP, suitable values of the hook-load, which translates into an axial force on the bit referred to as weight-on-bit (WOB), and rotation speed (RPM) imposed at the surface (rig) must be set by drilling operators. For this ROP optimization purpose, the Bourgoyne and Young ROP model is widely used in industry [8, 30]. This model takes into account different aspects, such as formation strength, WOB, angular velocity and bit wear, which influence the ROP. Based on the optimal operational parameters, the ROP is then optimized by using various controllers [7]. However, the dynamics of the drill-string, the bit–rock interaction and the (frictional) contact along the drill-string in a deviated well are not taken into account in this modelling approach. A different approach for ROP improvement is the selection of drill-string components, such as drill-bits or down-hole tools located at the BHA of the drill-string [4, 5, 15]. Down-hole tools can be either active [5, 15] or passive [4, 31, 37]. Active tools typically provide axial excitation during drilling, which can alter the effect of axial friction and consequently improve the drilling efficiency. The current paper aims to model and analyse the effect of a passive down-hole tool on the drilling efficiency in presence of friction between the drill-string and borehole wall. This work is motivated by field data that show evidence that the AST can increase the drilling efficiency in terms of ROP, also in deviated wells [31, 33].

In particular, this paper focuses on the modelling and analysis of the coupling of axial and torsional vibrations in drill-string dynamics, and studies how a down-hole tool, called the anti-stall tool (AST) [31], affects the drilling performance (in terms of ROP) in a deviated borehole. Previous works, e.g., [9, 10, 32] have shown that a rate-independent bit–rock interaction model [11], including both cutting and frictional contact processes, is essential in the coupling between the axial and torsional dynamics. In the current paper, we also pursue such type of modelling approach, further motivated by the fact that the AST also operates by coupling the axial and torsional dynamics [31, 37]. The dynamics of drill-string systems, including such rate-independent bit–rock interaction model, has been described by a variety of dynamical models. In [9, 10, 17, 19, 20, 23,24,25, 28, 29, 32] lumped-parameter models for the axial-torsional drill-string dynamics have been proposed, while in [2, 3, 13, 16] both finite-element based and distributed models have been developed. These models have been employed to study instabilities and axial and torsional vibrations of drill-string systems, and recently to investigate the effect of the AST on the ROP [37]. However, the effect of friction between the drill-string and the borehole due to deviated well scenarios has not yet been taken into account.

The modelling of the frictional contact along the drill-string has been considered extensively in the scope of so-called torque and drag models [1, 21, 34]. The magnitude of the frictional forces mainly depends on the normal force acting between the drill-string and the borehole wall. Hence, in highly deviated wells the effects of this friction indeed becomes more prominent, because the drill-string is resting under its own weight on the borehole wall. However, in these models no vibrational dynamics and down-hole tooling have been taken into account, while it has been shown that the functioning of the AST is intrinsically related to the drill-string dynamics [37].

This work builds on and extends the developments in [37] by modelling and analysis of the (frictional) contact between the BHA and the borehole wall, thereby broadening its applicability to deviated well scenarios. The main contributions of this paper are as follows:

  • Firstly, a benchmark model of the drill-string dynamics (without AST) and a drill-string model including AST, both with spatial friction between the borehole and drill-string, are developed. Herein, both unilateral contact and frictional characteristics of the bit–rock interaction and the spatial friction between the borehole and drill-string have been modelled by set-valued force laws. This allows for a unified treatment of these nonlinear model features in a time-stepping-based simulation tool for the resulting delay differential inclusion model;

  • Secondly, a model-based analysis of the effect of frictional contact between BHA and borehole wall on the drilling performance (in terms of ROP and drilling efficiency) is performed;

  • Finally, a parametric performance study on the AST design is performed leading to an optimal design to maintain a high drilling efficiency, which is robust for a wide range of deviated wells.

The outline of this paper is as follows. In Sect. 2, the dynamic models of a drill-string system without and with AST for drilling in a deviated well are derived. In Sect. 3, a dynamic analysis is performed with a focus on the effect of the spatial frictional contact on drilling performance (ROP and drilling efficiency; for both cases without and with AST). Subsequently, a parametric design study on the AST design is presented in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 Dynamic modelling

In this section, two models of a drill-string including spatial friction between the BHA and the borehole are presented. In Sect. 2.1, two drill-string models, with and without AST, are introduced, enabling the comparative analysis of systems with and without the AST. In Sect. 2.2, the bit–rock interaction model is discussed. In Sect. 2.3, the model that describes the frictional contact between the borehole and the BHA is presented. Finally, in Sect. 2.4 the two dynamic models, with and without AST, are expressed in dimensionless perturbation coordinates around their nominal solutions in order to identify a minimum set of parameters characterizing the dynamics.

A total overview of a drilling system in a deviated well is depicted in Fig. 1. A typical drilling system is operated from the rig located at the surface, where the top-drive equipment sets the angular speed and adjusts the weight by regulating the hook-load. These operational conditions are transmitted via slender drill-pipes and a BHA to the drill-bit. The BHA is specifically designed to fulfil a particular drilling objective(s) based on the sub-surface geological conditions and can be composed by several down-hole components, such as stabilizer(s), rotary steerable system (RSS), logging tools, mud motor(s), etc. Due to the larger diameter of the stabilizers compared to the rest of the BHA components, the stabilizers are in contact with the borehole wall, which consequently results in additional friction affecting the drill-string dynamics. The physical aspects to be considered in the modelling are the boundary conditions at the rig, the drill-string dynamics including the AST, the bit–rock interaction as the down-hole boundary conditions and the frictional contact between the stabilizers and the borehole.

2.1 Drill-string dynamics

In this section, the dynamic models of the drill-string systems are presented. First the benchmark model, excluding AST, is discussed. Thereafter, the model including AST is discussed.

2.1.1 Benchmark drill-string dynamics

In Fig. 2, the lumped-parameter benchmark model (i.e., without AST) is schematically depicted. The axial and torsional dynamics are described by this model, which consists of two degrees-of-freedom (DOFs), namely the axial displacement of the bit \(U_b\) and the angular displacement of the bit \(\varPhi _b\).

Fig. 2
figure 2

Schematic representation of the benchmark model

Full size image

At the rig, the boundary conditions are given by an imposed constant angular velocity \(\varOmega _0\) and a constant upward force \(H_0\), the so-called hook-load. The total mass and inertia of the drill-string including the BHA are lumped in the discrete mass M and inertia I. The torsional stiffness of the drill-pipes is modelled as a torsional spring with stiffness \(C_p\). The viscous friction along the drill-string and BHA in axial and angular directions are characterized by the parameters D and \(D_{\varPhi }\), respectively. The parameters \(\lambda _{T_a}\) and \(\lambda _{T_t}\) are associated with the spatial Coulomb friction between the stabilizers and the borehole in axial and torsional direction, respectively, which is discussed in more detail in Sect. 2.3. The weight acting on the bit is denoted by W and the torque acting on the bit is denoted by T.

The bit–rock interaction model, which is discussed in more detail in Sect. 2.2, relates the weight-on-bit (WOB) W and the torque-on-bit (TOB) T to the axial and angular motion of the bit. This bit–rock law considers two independent processes, namely a pure cutting process and a frictional contact. Hence, the force and torque can be decomposed in a cutting and frictional component, denoted by the superscripts c and f, respectively, i.e., for the total WOB \(W=W^c+W^f\), and for the total TOB \(T=T^c+T^f\). The force and torque contributions associated with the wearflat will from now on be denoted as follows

$$\begin{aligned} W^f=-\lambda _{b_a}, \quad T^f=-\lambda _{b_t}. \end{aligned}$$
(1)

By using a Lagrangian approach, the equations of motion (EOMs) for this model are obtained. In general, these can be written in the following form:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {q}} - \mathbf {h}(t,\mathbf {q},\dot{\mathbf {q}}) = \mathbf {W}\varvec{\lambda }, \end{aligned}$$
(2)

where \(\mathbf {q}\) represent the column with generalized coordinates. \(\mathbf {M}\) is the mass matrix and the column \(\mathbf {h}(t,\mathbf {q},\dot{\mathbf {q}})\) contains all generalized forces except the friction forces (both due to frictional contacts at the bit and between the borehole and the stabilizers at the BHA). The vector \(\varvec{\lambda }\) contains the generalized forces associated with the set-valued force laws, characterizing both due to frictional contacts at the bit and between the borehole and the stabilizers at the BHA, see Sects. 2.2 and 2.3, and the matrix \(\mathbf {W}\) contains the associated generalized force directions. In case of the benchmark model with the generalized coordinates \(\mathbf {q}=[U_b \; \varPhi _b ]^{\mathsf {T}}\), this results in the following matrices and columns in (2):

$$\begin{aligned}& \mathbf {M} = \begin{bmatrix} M&\quad 0\\ 0&\quad I \end{bmatrix} \nonumber \\& \mathbf {h}(t,\mathbf {q},\dot{\mathbf {q}}) = \begin{bmatrix} -\,D \dot{U}_b - H_0 + W_{s} - W^c\\ -\,D_{\varPhi } \dot{\varPhi }_b + C_p(\varOmega _0 t-\varPhi _b) - T^c \end{bmatrix}\\& \mathbf {W} = \begin{bmatrix} 1&\quad 0&\quad 1&\quad 0\\ 0&\quad 1&\quad 0&\quad R \end{bmatrix}\nonumber \\& \varvec{\lambda } = \begin{bmatrix} \lambda _{b_a}&\quad \lambda _{b_t}&\quad \lambda _{T_a}&\quad \lambda _{T_t} \end{bmatrix}^{\mathsf {T}}\nonumber \end{aligned}$$
(3)

where \(W^c\) and \(T^c\) satisfying (6), (7) and (8) and \(\varvec{\lambda }\) satisfying (9), (12) and (25) and \(W_{s}\) represents the submerged weight of the drill-string. A detailed derivation of the equations of motion can be found in [38].

2.1.2 Drill-string dynamics including AST

Fig. 3
figure 3

The working principle of the anti-stall tool (AST): an increase in torque \(\left( M_{2}\right) \) will cause a contraction \(\left( S\right) \) to off-load the weight from the cutters \(\left( F_{2}\right) \) [4]

Full size image

The AST is designed to influence the coupling between the axial and torsional displacement. The AST consists of two tool bodies connected by a helical spline and an axial internal spring, as viewed in Fig. 3. According to Selnes et al. [33], the working principle of the tool is that a torsional load with sufficient magnitude to overcome the compressed spring will make the upper tool body, with the internal helical spline, rotate on the mating lower body. When the upper and lower part screw together in this manner, the tool telescopically contracts. Consequently, this results in an adjustment of the axial and torsional loading acting on the bit. Hence, the tool prevents dynamic forces from reaching destructive levels.

Fig. 4
figure 4

Schematic representation of the drill-string model including AST

Full size image

In Fig. 4, the lumped-parameter model including AST is schematically depicted. The AST separates the drill-string in two parts, where the coordinates U and \(\varPhi \) are related to the displacement of the top part and \(U_b\) and \(\varPhi _b\) to displacement of the part below the tool. The mass and inertia of the drill-string including the part of the BHA above the tool are lumped into a discrete mass \(M_{a}\) and inertia \(I_{a}\), while the mass and inertia of the part of the BHA below the tool are lumped into a discrete mass \(M_{b}\) and inertia \(I_{b}\). The torsional stiffness of the drill-pipes and the viscous friction components are identical to the benchmark model. However, the axial viscous friction only acts on the part above the tool. The viscous friction in the angular direction is modelled by two dampers characterized by \(D_{\varPhi }\) and \(D_{\varPhi _b}\). The spatial friction acts both on the DOFs above the tool and on the DOF at the bit, and the distribution of the friction between the two parts of the drill-string is denoted by \(\varDelta \in [0, 1 ]\), as introduced in (22) and (23). The radius of the stabilizer below the tool is assumed to be the same as above the tool. Let us now introduce the model of the AST, which introduces an additional axial spring \(K_b\) and damper \(D_b\), see Fig. 4. Furthermore, the helical spline in the tool introduces a kinematic constraint, which is characterized by the lead p, lead angle \(\beta \) and the radius \(r_{spline}\) of the helical spline, and can be written as

$$\begin{aligned} \begin{aligned} U-U_b&= \frac{p}{2\pi r_{spline}}(\varPhi r_{spline} -\varPhi _b r_{spline})\\&= \frac{p}{2\pi }(\varPhi - \varPhi _b) =: \alpha (\varPhi -\varPhi _b). \end{aligned} \end{aligned}$$
(4)

Herein U (\(\varPhi \)) and \(U_b\) (\(\varPhi _b\)) represent the axial (angular) positions above the tool and at the bit, respectively (see Fig. 4). The lead is given by \(p = 2\pi r_{spline} \tan \beta \).

The generalized coordinates of the model including AST are given by \(\mathbf {q}^c=[U \; \varPhi \; U_b \; \varPhi _b ]^{\mathsf {T}}\). However, due to the kinematic, holonomic constraint of the AST, this model can be alternatively formulated in terms of three independent generalized coordinates \(\mathbf {q}=[U \; U_b \; \varPhi _b]^{\mathsf {T}}\). This coordinate transformation is discussed in detail in “Appendix A”. Using a Lagrangian approach for systems with constraints and after eliminating the DOF \(\varPhi \), the obtained EOMs can be written in the general form of (2), with the following matrices and columns:

$$\begin{aligned}& \mathbf {M} =\begin{bmatrix} M_{a} + \frac{1}{\alpha ^2}I_{a}&\quad -\frac{1}{\alpha ^2}I_{a}&\quad \frac{1}{\alpha }I_{a}\\ -\,\frac{1}{\alpha ^2}I_{a}&\quad \frac{1}{\alpha ^2}I_{a} +M_{b}&\quad -\,\frac{1}{\alpha }I_{a}\\ \frac{1}{\alpha }I_{a}&\quad -\,\frac{1}{\alpha }I_{a}&\quad I_{a} + I_{b} \end{bmatrix} \nonumber \\& \mathbf {h}(t,\mathbf {q},\dot{\mathbf {q}}) = \left[ \begin{matrix} -\,K_b(U-U_b) -\frac{1}{\alpha }C_p Y -\frac{1}{\alpha }D_{\varPhi } \dot{Y} -D\dot{U} \\ K_b(U-U_b) + \frac{1}{\alpha }C_p Y + \frac{1}{\alpha }D_{\varPhi } \dot{Y} \\ -\,C_p Y - D_{\varPhi } \dot{Y} - D_{\varPhi _b}\dot{\varPhi }_b \end{matrix}\right. \nonumber \\&\qquad \qquad \quad \left. \begin{matrix} -\,D_b(\dot{U}-\dot{U}_b) + \frac{1}{\alpha }C_p\varOmega _0 t + W_{s} - H_0\\ +\,D_b(\dot{U}-\dot{U}_b) - W^c - \frac{1}{\alpha }C_p\varOmega _0 t + W_{bs}\\ -\, T^c + C_p \varOmega _0 t \end{matrix}\right] \\& \mathbf {W} =\begin{bmatrix} 0&\quad 0&\quad 1&\quad \frac{R}{\alpha }&\quad 0&\quad 0\\ 1&\quad 0&\quad 0&\quad -\,\frac{R}{\alpha }&\quad 1&\quad 0\\ 0&\quad 1&\quad 0&\quad R&\quad 0&\quad R \end{bmatrix}\nonumber \\& \varvec{\lambda } = \begin{bmatrix} \lambda _{b_a}&\quad \lambda _{b_t}&\quad \lambda _{T_a}&\quad \lambda _{T_t}&\quad \lambda _{T_{ba}}&\quad \lambda _{T_{bt}} \end{bmatrix}^{\mathsf {T}}\nonumber \end{aligned}$$
(5)

with the auxiliary variables \(Y=\varPhi _b+\frac{1}{\alpha }(U-U_b)\) and \(\dot{Y}=\dot{\varPhi }_b+\frac{1}{\alpha }(\dot{U}-\dot{U}_b)\) in the expression for \(\mathbf {h}(t,\mathbf {q},\dot{\mathbf {q}})\), while \(W^c\) and \(T^c\) satisfy (6), (7) and (8), \(\varvec{\lambda }\) satisfies (9), (12) and (25). The parameters \(W_{s}\) and \(W_{bs}\) denote the submerged weights of the drill-string parts above and below the tool, respectively. A detailed derivation of the equations of motion can be found in [38].

2.2 Bit–rock interaction model

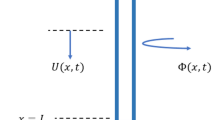
In this paper, the rate-independent bit–rock interaction law as introduced in [11, 12] is adopted, which relates the WOB and the TOB to the axial and angular motions of the bit. The bit–rock interaction involves two independent processes: a pure cutting process taking place at the front of the cutters and a frictional contact between the rock and the so-called wearflat underneath the cutters. According to Detournay et al. [11, 12], the cutting contributions for a bit consisting of n identical and symmetrically distributed blades of cutters around the axis of revolution and a bit radius of a, can be written as

$$\begin{aligned} W^c = na\varepsilon \zeta d_n, \quad T^c = \frac{1}{2}na^2\varepsilon d_n, \end{aligned}$$
(6)

where \(\varepsilon \) is the intrinsic specific energy related to the rock strength and \(\zeta \) is related to the orientation of the cutting face. The cutting force and torque are proportional to the depth-of-cut (DOC) \(d_n\) produced by a single blade, which is in general not constant. The DOC depends on the axial position of the bit and the rock surface generated by the previous blade according to

$$\begin{aligned} d_n = U_b(t) - U_b(t-t_n(t)), \end{aligned}$$
(7)

where \(U_b(t)\) is the axial bit position and t denotes time, see Fig. 5. Furthermore, \(t_n(t)\) is the time required for the bit to rotate by an angle of \(2\pi /n\), which is the angle between two successive blades. This time-dependent delay \(t_n(t)\) (actually state-dependent) is characterized by the implicit equation:

$$\begin{aligned} \int _{t-t_n(t)}^{t} \frac{\mathrm {d}\varPhi _b(s)}{\mathrm {d}s} \mathrm{d}s= & {} \varPhi _b(t)-\,\varPhi _b \nonumber \\ (t-t_n(t))= & {} \frac{2\pi }{n}, \end{aligned}$$
(8)

where \(\varPhi _b(t)\) denotes the angular position of the bit at time t.

In the contributions associated with the wearflat as introduced in (1), the wearflat reaction force \(\lambda _{b_a}\) is essentially discontinuous in terms of the bit axial velocity. When the bit moves downwards, the contact between the wearflat and the rock is fully mobilized. However, when the bit moves upwards, the contact is lost and consequently the reaction force vanishes. Hence, the wearflat reaction force can be described in a set-valued force law by the following inclusion:

$$\begin{aligned} \lambda _{b_a} \in -na\bar{\sigma }l_n \frac{1+\text {Sign}(\dot{U}_b)}{2}, \end{aligned}$$
(9)

where \(\bar{\sigma }\) is the maximum contact stress and \(l_n\) is the wearflat length per blade. The axial velocity of the bit is denoted by \(\dot{U}_b\) and the set-valued sign-function in (9) is defined as

$$\begin{aligned} \text {Sign}(y)= {\left\{ \begin{array}{ll} 1, &{}\quad y>0,\\ \text {[}-1,1\text {]}, &{}\quad y = 0,\\ -\,1, &{}\quad y < 0. \end{array}\right. } \end{aligned}$$
(10)

As a consequence of the set-valued nature of the law in (9), the admissible values of the wearflat reaction force form a convex set \(C_a\) given by

$$\begin{aligned} C_a = \{\lambda _{b_a}\, |-\,na\bar{\sigma } l_n \le \lambda _{b_a} \le 0 \}. \end{aligned}$$
(11)
Fig. 5
figure 5

Bottom hole profile between two successive blades [9]

Full size image

The force acting on the wearflat also induces a frictional torque \(\lambda _{b_t}\). Since the friction always acts in opposite direction compared to the bit rotational velocity, this frictional torque is discontinuous with respect to the rotational velocity and can be modelled by the following inclusion:

$$\begin{aligned} \lambda _{b_t} \in \frac{1}{2}a\mu \xi \lambda _{b_a}\text {Sign}(\dot{\varPhi }_b). \end{aligned}$$
(12)

Herein, \(\mu \) is a rate-independent friction coefficient and \(\xi \) characterizes the orientation and spatial distribution of the frictional contact of the surfaces along the bit blade(s). The angular velocity of the bit is denoted by \(\dot{\varPhi }_b\). The admissible values of the frictional torque forms a convex set \(C_t\), which depends on the wearflat (normal) reaction force \(\lambda _{b_a}\). This set is given by

$$\begin{aligned} C_t(\lambda _{b_a}) = \left\{ \lambda _{b_t}\, |\, \frac{1}{2}a\mu \xi \lambda _{b_a} \le \lambda _{b_t} \le -\frac{1}{2}a\mu \xi \lambda _{b_a} \right\} . \nonumber \\ \end{aligned}$$
(13)

The set-valued force laws for reaction force \(\lambda _{b_a}\) and frictional torque \(\lambda _{b_t}\) can be formulated by using normal cones of the convex sets (11) and (13), respectively [18, 22]:

$$\begin{aligned} -\,\dot{U}_b&\in N_{C_a}(\lambda _{b_a}), \end{aligned}$$
(14)
$$\begin{aligned} -\,\dot{\varPhi }_b&\in N_{C_t}(\lambda _{b_t}). \end{aligned}$$
(15)

From convex analysis, these inclusions are equivalent to implicit proximal point formulations [22]. Hence, these formulations transform the associated inclusions into nonlinear implicit equations, which are ultimately used in the (time-stepping-based) numerical solver which is developed in this work. These read as

$$\begin{aligned} \lambda _{b_a}&= \text {prox}_{C_a} (\lambda _{b_a} - r_1\dot{U}_b), \end{aligned}$$
(16)
$$\begin{aligned} \lambda _{b_t}&= \text {prox}_{C_t} (\lambda _{b_t} - r_2\dot{\varPhi }_b), \end{aligned}$$
(17)

for \(r_1,r_2>0\) arbitrary, positive constants.

Remark

During a torsional slip phase, the cutting edge is in full contact with the rock. However, during torsional stick, this contact is not necessarily fully mobilized, which results in an unknown distribution between torque associated with cutting and friction in this case. To include torsional stick in the model, it is assumed that during torsional stick the contact between the cutting edge of the bit blade and the rock remains fully mobilized. Therefore, this assumption has conditioned that the cutting component of the model in (6) is only valid under the conditions of a nonnegative angular motion of the bit (\(\dot{\varPhi }_b\ge 0\)) and with nonnegative DOC (\(d_n \ge 0\)). Furthermore, a negative DOC is associated with bouncing of the bit, which indicates total loss of contact between the bit and the rock. Hence, bit-bouncing is not analysed in this work.

Fig. 6
figure 6

The BHA resting on its own weight in an inclined well with the axial (\(\lambda _{T_a}\), \(\lambda _{T_{ba}}\)) and tangential (\(\lambda _{T_t}\), \(\lambda _{T_{bt}}\), pointing out the plane) components of the spatial friction acting on the stabilizers and the distributed normal force \(F_{N}\) with distribution \(\varDelta \)

Full size image

2.3 Spatial Coulomb friction model

In drilling operations in inclined wells, the drill-string rests on the borehole wall with its own weight, resulting in additional frictional contact between the drill-string and borehole. This contact is mainly generated by a specific BHA component, the stabilizers, due to their larger diameter compared to the rest of the BHA components (see Fig. 6). The frictional contact between the drill-string and borehole has been modelled by torque and drag models [21, 34]. In these models, the frictional contact forces depend on the normal force and the frictional coefficient between contact surfaces. In a drilling operation, the drill-string rotates and translates in axial direction. Hence, the sliding velocity of the contact point has two components, both in axial and tangential direction. Due to this spatial contact, the spatial Coulomb’s friction law involves a two-dimensional force \(\varvec{\lambda }_T=[\lambda _{T_a} \; \lambda _{T_t}]^{\mathsf {T}}\). In Fig. 6 a schematic representation of the forces acting on the BHA is depicted. Figure 6 also depicts the AST located in between the top and bottom stabilizer of the BHA. In this case, the normal force \(F_{N}\) is distributed over the two stabilizers. In the benchmark model (excluding AST), all friction force acts on a single stabilizer, because in the benchmark model both stabilizers related to the same DOF. Furthermore, homogeneous rock formations are considered in this study, such that the spatial friction law is assumed to be isotropic and its force reservoir is represented by a disc. The admissible values of the spatial Coulomb friction force for a single frictional contact point (i.e., as in the benchmark model) are given by the convex set \(C_T\):

$$\begin{aligned} C_T = \left\{ \varvec{\lambda }_T \in \mathbb {R}^2 \; | \; ||\varvec{\lambda }_T|| \le \mu _{w} F_{N} \right\} , \end{aligned}$$
(18)

where \(\mu _{w}\) is the friction coefficient and \(F_{N}\) denotes the normal force between the stabilizer in the BHA and the borehole wall.

Low-order lumped-parameter models for the drill-string dynamics are used in this study, such that only the gravitational effect (represented by the drill-string weight) is considered to contribute to the normal force. Thus, the possible force contributions due to the curvature of the borehole are neglected. Furthermore, it is assumed that the stabilizers are always in contact with the borehole wall. However, when the geometrical structure of the borehole is perfectly vertical (\(\varTheta =0^{\circ }\)), the spatial friction force vanishes. As the normal force presumptively depends on the buoyed weight of the BHA and the inclination of the borehole structure \(\varTheta \), as depicted in Fig. 6, this normal force is defined as

$$\begin{aligned} F_{N} = B_{F} M_{BHA}g\sin {\varTheta }, \end{aligned}$$
(19)

where \(M_{BHA}\) denotes the total mass of the BHA, g the gravitational acceleration and \(B_{F}\) is the buoyancy factor given by

$$\begin{aligned} B_{F} = \frac{\rho -\rho _m}{\rho }. \end{aligned}$$
(20)

Herein, \(\rho \) is the density of the BHA and \(\rho _m\) is the density of the mud in which the BHA is submerged below the surface. Hence, the magnitude of the normal force increases as the borehole inclination (\(\varTheta \)) increases.

In the benchmark model without the tool, the sliding velocity \(\varvec{\gamma }_T\) at the frictional contact between borehole and BHA is given by

$$\begin{aligned} \varvec{\gamma }_T = \begin{bmatrix} \dot{U}_b\\ \dot{\varPhi }_b R \end{bmatrix}, \end{aligned}$$
(21)

where the first component is associated with the axial and the second with the tangential velocity component. In this definition, R is the outer radius of the stabilizers.

In the drill-string model with the tool, the BHA is separated in two parts, such that the spatial friction can act partly above and partly below the tool as shown in Fig. 6. Essentially, the normal force \(F_{N}\) is distributed between the two locations, namely above and below the AST. As a consequence, the force reservoir \(C_T\) can be segregated into two smaller isotropic reservoirs. In order to enable the analysis of the cases where all the friction acts only above or below the tool, a linear distribution parameter \(\varDelta \in [0 \; 1 ]\) is introduced. The admissible friction force reservoirs associated to the friction forces above and below the tool are, respectively, given by the following convex sets:

$$\begin{aligned} C_T&= \left\{ \varvec{\lambda }_T \in \mathbb {R}^2 \; | \; ||\varvec{\lambda }_T|| \le \varDelta \mu _{w} F_{N} \right\} , \end{aligned}$$
(22)
$$\begin{aligned} C_{T_b}&= \left\{ \varvec{\lambda }_{T_b} \in \mathbb {R}^2 \; | \; ||\varvec{\lambda }_{T_b}|| \le (1-\varDelta )\mu _{w} F_{N}\right\} . \end{aligned}$$
(23)

The index b denotes the contributions, which are lumped at the bit. Note that for a straightforward comparison between the model with and without the tool, the sum of maximal allowable friction forces are equal. When \(\varDelta =1\) holds, the spatial friction only acts above the AST; when \(\varDelta =0\) holds, all spatial friction acts below the tool. The corresponding sliding velocities are given by

$$\begin{aligned} \varvec{\gamma }_T = \begin{bmatrix} \dot{U}\\ \dot{\varPhi }R \end{bmatrix} \qquad \text {and} \quad \varvec{\gamma }_{T_b} = \begin{bmatrix} \dot{U}_b\\ \dot{\varPhi }_bR \end{bmatrix}. \end{aligned}$$
(24)

The relation between the sliding velocity and the spatial friction force can be expressed by the following inclusion, using the normal cone formulation of the set-valued spatial Coulomb friction law [22]

$$\begin{aligned} -\,\varvec{\gamma }_T \in N_{C_T}(\varvec{\lambda }_T). \end{aligned}$$
(25)

This inclusion can equivalently be written as an implicit proximal point formulation:

$$\begin{aligned} \varvec{\lambda }_T = \text {prox}_{C_T}(\varvec{\lambda }_T - r \varvec{\gamma }_T), \end{aligned}$$
(26)

where \(r>0\) is an arbitrary positive constant.

2.4 Dimensionless perturbation models

The EOMs, given by (2), are scaled in order to reduce the number of parameters. Furthermore, the dynamics are expressed around its nominal solution (reflected by a constant angular velocity and ROP) by introducing perturbation coordinates. Following [32], a timescale \(t_*\) and a characteristic length \(L_*\) are introduced, which are defined by

$$\begin{aligned} t_* = \sqrt{\frac{I_{tot}}{C_p}} \quad \text {and} \quad L_* = \frac{2C_p}{\varepsilon a^2}, \end{aligned}$$
(27)

with the total inertia in the benchmark model \(I_{tot}=I\) and in the model including AST \(I_{tot}=I_{a}+I_{b}\). Since the total inertia is equal in both models, the timescale is the same in both models. By using these scaling parameters, the following dimensionless perturbation coordinates are introduced

$$\begin{aligned} \begin{aligned} u(\tau )&=\frac{U-U_0}{L_*}, \quad u_b(\tau ) = \frac{U_b-U_{b0}}{L_*},\\ \phi _b(\tau )&=\varPhi _b-\varPhi _{b0}, \end{aligned} \end{aligned}$$
(28)

which are functions of the dimensionless time

$$\begin{aligned} \tau =\frac{t}{t_*}. \end{aligned}$$
(29)

These coordinates represent the dimensionless axial and torsional perturbations with respect to its nominal responses, where the coordinates denoted with subscript b are associated with the bit. Explicit expressions for the nominal displacements \(U_0\), \(U_{b0}\) and \(\varPhi _{b0}\) in both models are given in the subsequent sections.

The generalized forces associated with set-valued force laws are scaled by a characteristic cutting force corresponding to a DOC equal to the characteristic length \(L_*\). This results in the following dimensionless perturbation forces and torque associated to the set-valued force laws introduced in Sects. 2.2 and 2.3:

$$\begin{aligned} \begin{aligned} \hat{\lambda }_{b_a}&= \frac{a}{2\zeta C_p}(\lambda _{b_a}-\lambda _{b_{a0}}), \quad \hat{\lambda }_{b_t} = \frac{1}{C_p}(\lambda _{b_t}-\lambda _{b_{t0}}),\\ \hat{\varvec{\lambda }}_T&= \frac{a}{2\zeta C_p}(\varvec{\lambda }_T-\varvec{\lambda }_{T_0}). \end{aligned} \end{aligned}$$
(30)

Note that \(\hat{\varvec{\lambda }}_T\) is a column containing the dimensionless axial and tangential components of the spatial Coulomb friction. Furthermore, in the model including the tool, the spatial Coulomb friction acting above and below the tool both satisfy the same dimensionless perturbed form as above for \(\hat{\varvec{\lambda }}_T\). However, the values of each associated friction forces can be different as these are scaled by the parameter \(\varDelta \) in (22) and (23). Furthermore, the nominal values of the frictional contact component in the bit–rock interaction law are \(\lambda _{b_{a0}}=-na\bar{\sigma }l_n\) and \(\lambda _{b_{t0}}=-\frac{1}{2}na^2\mu \xi \bar{\sigma }l_n\). Expressions for \(\varvec{\lambda }_{T_0}\) for both models are given in the subsequent sections.

The dimensionless form of the time delay, depth-of-cut and axial and torsional nominal velocities are given by

$$\begin{aligned} \tau _n= & {} \frac{t_n}{t_*}, \quad \delta =\frac{d}{L_*}, \nonumber \\ v_0= & {} \frac{V_0 t_*}{L_*}, \quad \omega _0 =\varOmega _0 t_*. \end{aligned}$$
(31)

The nominal axial velocity \(V_0\) (in original coordinates) in both models is given by

$$\begin{aligned} V_0 = \frac{1}{D}\left( -\,H_0 +M_sg - a\varepsilon \zeta d_{0} + \lambda _{b_{a0}} + \lambda _{T_{a0}} \right) . \end{aligned}$$
(32)

The nominal DOC \(d_0\) and the axial component of the nominal spatial friction \(\lambda _{T_{a0}}\) are both functions of the nominal velocity \(V_0\) and given by

$$\begin{aligned}& d_0 = V_0t_{n0}\end{aligned}$$
(33)
$$\begin{aligned}& \lambda _{T_{a0}} = -\frac{V_0}{\varOmega _0 R} \sqrt{\frac{\mu _w^2 F_{N}^2}{1 + \left( \frac{V_0}{\varOmega _0 R}\right) ^2}}, \end{aligned}$$
(34)

with \(t_{n0}=2\pi /(n\varOmega _0)\). Substitution of these expressions results in a fourth-order polynomial in \(V_0\), which is monotone for positive values of \(V_0\). Hence, (32) exhibits a unique solution for normal drilling operations (reflected by a positive nominal axial velocity \(V_0\)).

Moreover, the dimensionless nominal time delay is defined as \(\tau _{n0}=t_{n0}/t_* = 2\pi /(n\omega _0)\). The dimensionless depth-of-cut (\(\delta \)) can be expressed in terms of a perturbation \(\hat{\delta }\) from the nominal depth-of-cut per revolution (\(\delta _0 = 2\pi v_0/ \omega _0\)):

$$\begin{aligned} \delta = \hat{\delta } + \delta _0. \end{aligned}$$
(35)

The dimensionless perturbed DOC \(\hat{\delta }\) is given by

$$\begin{aligned} \hat{\delta } = n\left( u_b(\tau )-u_b(\tau -\tau _n)\right) + nv_0 \hat{\tau }_n. \end{aligned}$$
(36)

Herein, \(\tau _n\) is the dimensionless time delay \(\tau _n = \hat{\tau }_n + \tau _{n0}\), where \(\hat{\tau }_n\) is its perturbation from the nominal time delay \(\tau _{n0}\). This time delay is obtained with the implicit delay equation, given in (8), which reads in a dimensionless formulation:

$$\begin{aligned} \phi _b(\tau ) - \phi _b(\tau -\tau _n) + \omega _0 \hat{\tau }_n = 0. \end{aligned}$$
(37)

2.4.1 Benchmark drill-string model

The column with the dimensionless perturbation coordinates in the benchmark model is given by \(\mathbf {z}=[u_b \; \phi _b ]^{\mathsf {T}}\). In the case of a nominal drilling operation, there are no vibrations; thus, the axial and torsional velocities are constant and positive. Due to the constant velocities, the accelerations are equal to zero. By substitution of the constant velocities and zero accelerations in the dynamic models, expressions for the nominal values of the displacements, velocities and forces are obtained. The nominal values of the axial and angular bit displacement, \(U_{b0}\) and \(\varPhi _{b0}\) (see (28)), are given by

$$\begin{aligned} U_{b0}&= V_0t, \end{aligned}$$
(38)
$$\begin{aligned} \varPhi _{b0}&= \varOmega _0t + \frac{1}{C_p}\left( -D_{\varPhi }\varOmega _0 - \frac{1}{2}na^2\varepsilon d_0 \right. \nonumber \\&\quad \left. + \,\lambda _{b_{t0}} + R\lambda _{T_{t0}} \right) . \end{aligned}$$
(39)

The nominal values of the spatial Coulomb friction (\(\varvec{\lambda }_{T_0}=[\lambda _{T_{a0}} \; \lambda _{T_{t0}}]^{\mathsf {T}}\)) are given by

$$\begin{aligned} \lambda _{T_{a0}}&= -\frac{V_0}{\varOmega _0 R} \sqrt{\frac{\mu _{w}^2 F_{N}^2}{1+ \left( \frac{V_0}{\varOmega _0 R}\right) ^2}}, \end{aligned}$$
(40)
$$\begin{aligned} \lambda _{T_{t0}}&= - \sqrt{\frac{\mu _{w}^2 F_{N}^2}{1+ \left( \frac{V_0}{\varOmega _0 R}\right) ^2}}. \end{aligned}$$
(41)

The scaling and introduction of the perturbation coordinates leads to the dimensionless EOMs in general form:

$$\begin{aligned} \varvec{\mathscr {M}}\mathbf {z}'' - \varvec{\mathscr {H}}(\tau ,\mathbf {z},\mathbf {z}') = \varvec{\mathscr {W}} \hat{\varvec{\lambda }}. \end{aligned}$$
(42)

Then, the corresponding matrices and columns in the benchmark are given by

$$\begin{aligned} \begin{aligned}& \varvec{\mathscr {M}} = \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} \quad \mathscr {H}(\tau , \mathbf {z}, \mathbf {z}') = \begin{bmatrix} -\,\gamma u_b' - \psi \hat{\delta }\\ -\,\gamma _{\phi } \phi _b' -\phi _b - \hat{\delta } \end{bmatrix}\\& \mathscr {W} = \begin{bmatrix} \psi&\quad 0&\quad \psi&\quad 0\\ 0&\quad 1&\quad 0&\quad \chi \end{bmatrix} \quad \hat{\varvec{\lambda }} = \begin{bmatrix} \hat{\lambda }_{b_a}&\quad \hat{\lambda }_{b_t}&\quad \hat{\lambda }_{T_a}&\quad \hat{\lambda }_{T_t} \end{bmatrix}^{\mathsf {T}} \end{aligned} \end{aligned}$$
(43)

2.4.2 Drill-string model including AST

The column with the dimensionless perturbation coordinates in the model including AST is given by \(\mathbf {z}=[u \; u_b\; \phi _b]^{\mathsf {T}}\). The nominal values of the axial and angular displacements, \(U_0\), \(U_{b0}\) and \(\varPhi _{b0}\), are given by

$$\begin{aligned} U_0&= V_0 t + \frac{1}{\alpha K_b}\left( \frac{1}{2}na^2\varepsilon d_{n0} + \alpha na\varepsilon \zeta d_{n0} + D_{\varPhi _b}\varOmega _0 \right. \nonumber \\&\quad \left. -\, \alpha M_{bs}g -\alpha \lambda _{b_{a0}} - \lambda _{b_{t0}} - \alpha \lambda _{T_{ba0}} - R\lambda _{T_{bt0}} \right) , \end{aligned}$$
(44)
$$\begin{aligned} U_{b0}&= V_0 t, \end{aligned}$$
(45)
$$\begin{aligned} \varPhi _{b0}&= \frac{1}{\alpha K_b}\Big (-na\varepsilon \zeta d_{n0} +M_{bs}g + \frac{1}{\alpha }D_{\varPhi }\varOmega _0 \nonumber \\&\quad +\, \lambda _{b_{a0}} + \lambda _{T_{ba0}} \Big )\nonumber \\&\quad +\, \left( \frac{1}{C_p}+\frac{1}{\alpha ^2 K_b} \right) \left( -\frac{1}{2}na^2\varepsilon d_{n0} -\,(D_{\varPhi }+D_{\varPhi _b})\varOmega _0 \right. \nonumber \\&\quad \left. +\,\lambda _{b_{t0}}+R\lambda _{T_{bt0}} \right) + \frac{R}{C_p}\lambda _{T_{t0}} + \varOmega _0 t. \end{aligned}$$
(46)

The nominal values of the spatial Coulomb friction located above and below the AST (\(\varvec{\lambda }_{T_0} =[\lambda _{T_{a0}} \; \lambda _{T_{t0}} \; \lambda _{T_{ba0}} \; \lambda _{T_{bt0}}]^{\mathsf {T}}\)) are given by

$$\begin{aligned} \lambda _{T_{a0}}&= -\frac{V_0}{\varOmega _0 R}\sqrt{\frac{\varDelta ^2 \mu _{w}^2 F_{N}^2}{1+ \left( \frac{V_0}{\varOmega _0 R}\right) ^2}}, \end{aligned}$$
(47)
$$\begin{aligned} \lambda _{T_{t0}}&= - \sqrt{\frac{\varDelta ^2 \mu _{w}^2 F_{N}^2}{1+ \left( \frac{V_0}{\varOmega _0 R}\right) ^2}}, \end{aligned}$$
(48)
$$\begin{aligned} \lambda _{T_{ba0}}&= -\frac{V_0}{\varOmega _0 R}\sqrt{\frac{(1-\varDelta )^2 \mu _{w}^2 F_{N}^2}{1+ \left( \frac{V_0}{\varOmega _0 R}\right) ^2}}, \end{aligned}$$
(49)
$$\begin{aligned} \lambda _{T_{bt0}}&= - \sqrt{\frac{(1-\varDelta )^2 \mu _{w}^2 F_{N}^2}{1+ \left( \frac{V_0}{\varOmega _0 R}\right) ^2}}. \end{aligned}$$
(50)

Then, the scaled EOMs in dimensionless perturbation coordinates for the model including AST can be written in the general form of (42). The corresponding matrices and columns are given by

$$\begin{aligned} \begin{aligned}& \varvec{\mathscr {M}} = \begin{bmatrix} m_*+\kappa \iota&\quad -\, \kappa \iota&\quad \nu \iota \\ -\,\kappa \iota&\quad -\,m_* + \kappa \iota + 1&\quad -\,\nu \iota \\ \frac{\kappa }{\nu }\iota&\quad -\,\frac{\kappa }{\nu }\iota&\quad 1 \end{bmatrix}\\& \varvec{\mathscr {H}}(\tau , \mathbf {z}, \mathbf {z}') = \left[ \begin{matrix} -\,\eta _b^2(u-u_b) - \gamma u' - \gamma _b(u'-u_b') - \nu \phi _b\\ \nu \phi _b + \kappa (u-u_b) + \nu \gamma _{\phi _1} \phi _b' + \kappa \gamma _{\phi _1}(u'-u_b')\\ -\,\phi _b -\frac{\kappa }{\nu }(u-u_b) -\gamma _{\phi _1}\phi _b' \end{matrix}\right. \\&\qquad \qquad \qquad \quad \left. \begin{matrix} -\, \kappa (u-u_b) - \nu \gamma _{\phi _1} \phi _b' - \kappa \gamma _{\phi _1}(u'-u_b')\\ +\, \eta _b^2 (u-u_b) + \gamma _b(u'-u_b') -\psi \hat{\delta }\\ -\, \gamma _{\phi _1} \frac{\kappa }{\nu }(u'-u_b') -\gamma _{\phi _2} \phi _b' -\hat{\delta } \end{matrix}\right] \\& \varvec{\mathscr {W}} = \begin{bmatrix} 0&\quad 0&\quad \psi&\quad \nu \chi&\quad 0&\quad 0\\ \psi&\quad 0&\quad 0&\quad -\,\nu \chi&\quad \psi&\quad 0\\ 0&\quad 1&\quad 0&\quad \chi&\quad 0&\quad \chi \end{bmatrix}\\& \hat{\varvec{\lambda }} = \begin{bmatrix} \hat{\lambda }_{b_a}&\quad \hat{\lambda }_{b_t}&\quad \hat{\lambda }_{T_a}&\quad \hat{\lambda }_{T_t}&\quad \hat{\lambda }_{T_{ba}}&\quad \hat{\lambda }_{T_{bt}} \end{bmatrix}^{\mathsf {T}}. \end{aligned} \end{aligned}$$
(51)

The definitions of the characterizing dimensionless parameters in (43) and (51) are given in Table 1, along with their values used in Sect. 3. The models presented in this section will now be used to analyse their dynamics, in particular to study the effect of the AST and spatial frictional on the drilling performance.

Table 1 Characteristic system parameters
Full size table

3 Drilling performance analysis

In this section, the effect of spatial Coulomb friction on the drilling performance is investigated. The drilling performance is characterized by the drilling efficiency and ROP. This paper focuses on the effect of friction on the drilling performance under different operational conditions, namely the prescribed angular speed and the hook-load at the surface. The characterizing parameters are introduced in Sect. 3.1. Next, in Sect. 3.2 the drilling performance of the benchmark model is investigated. In Sect. 3.3, the drilling performance of the model including AST is investigated and these results are compared to the benchmark model in order to investigate the effectiveness of the AST.

3.1 Drilling performance variables

From stability analyses of the benchmark model in the absence of spatial Coulomb friction, it is observed that the nominal solution is typically unstable for realistic operating conditions [10, 32, 36]. As a consequence, solutions diverge away from the unstable nominal response and result in a time-varying steady-state response from the nonlinear dynamics, where the nonlinearities are related to the set-valued nonlinearities in the bit–rock interaction law, the set-valued spatial friction law and the state-dependent delay effect. The drill-string system exhibits both axial and torsional vibrations, where the torsional vibrations typically evolve over a significantly slower timescale compared to the axial vibrations. Since the torsional vibrations typically converge to a steady-state torsional limit cycle, in this section, the performance characterization variables are averaged over a torsional limit cycle.

The performance of a drilling operation is mainly characterized by the drilling efficiency [27]. The drilling efficiency reflects how much of the total torque provided to the bit is used for cutting.

Remark

Note that the torque provided at the bit is in general not equal to the torque applied at the surface due to frictional losses along the drill-string.

In line with previous studies [32, 37], this efficiency is defined as the ratio between the energy devoted to the cutting process and the total energy dissipated at the bit (i.e., by cutting and frictional forces). The average drilling efficiency \(\eta \) is given by

$$\begin{aligned} \eta = \frac{\langle T^c \rangle }{\langle T^c \rangle + \langle T^f \rangle }. \end{aligned}$$
(52)

Herein \(T^c\) represents the cutting torque and \(T^f\) denotes the frictional torque at the bit. The brackets \(\langle . \rangle \) denote the average over a torsional limit cycle. However, the averaged frictional torque at the bit, \(\langle T^f \rangle \), is not directly obtained from the numerical simulation, since the frictional torque at the wearflat, \(T^f\), acts on the same DOF as the tangential component of the set-valued Coulomb friction force below the AST, \(\lambda _{T_{bt}}\) (see (3) and Fig. 2 for the benchmark model and (5) and Fig. 4 for the model including AST). Besides, both torques are governed by a similar set-valued force law, see (15) and (25). As a consequence, it is not possible to distinguish between the wearflat torque and the set-valued frictional torque below the AST in numerical simulations with the model.

Let us now explain how we obtain an accurate measure for the frictional losses acting at the bit in order to assess the efficiency in (52). According to (12), the frictional torque at the bit is proportional to the wearflat reaction force \(W^f\) with a factor \(1/2a\mu \xi \). From the model including the tool, as depicted in Fig. 4, the average of the sum of the wearflat force and the axial set-valued friction force below the AST, \(\langle W^f + \lambda _{T_{ba}} \rangle \), can directly be computed. Since the averaged axial velocity is much smaller compared to the averaged tangential velocity (i.e., \(\langle \dot{U}_b \rangle / \langle R \dot{\varPhi }_b \rangle =\mathscr {O}(10^{-4}-10^{-2})\)), the frictional contact basically only produces a frictional torque and thus the axial component \(\lambda _{T_{ba}}\) is negligible. Hence, the average wearflat force \(\langle W^f \rangle \) is approximated by \(\langle W^f + \lambda _{T_{ba}} \rangle \) and can be used to calculate the average frictional torque at the bit \(\langle T^f \rangle \).

Fig. 7
figure 7

a The axial bit velocity for the benchmark model without friction between the BHA and borehole wall (\(\varTheta =0\)) and b with Coulomb friction (\(\varTheta =90^{\circ }\)) (\(W_0=171\) kN and \(\varOmega _0=80\) RPM)

Full size image

A higher drilling efficiency will result in more efficient drilling and consequently in saving drilling costs. Moreover, a higher drilling efficiency, as defined in (52), implies less frictional dissipation at the bit, which is generally favourable from a bit wear perspective (i.e., longer bit life-time or maintaining bit sharpness).

A control parameter in both models is the hook-load \(H_0\) at the surface (an upward force). It can be deduced that an increase in the hook-load is causing a decrease in the total weight applied to the bit, and this consequently will decrease the ROP. However, the total weight applied on the bit is not only defined by the hook-load, but also by the gravitational forces acting on the submerged drill-string. Therefore, instead of varying the hook-load, the total nominal weight applied on the bit \(W_0\) is varied as a control parameter in the simulations. The total weight applied on the bit is defined as

$$\begin{aligned} W_0=W_{s} - H_0, \end{aligned}$$
(53)

with \(W_{s}\) the submerged weight of the drill-string.

Remark

In general, the WOB depends on the inclination of the well, since the submerged weight of a drill-string decreases when the inclination increases. However, it is beyond the scope of this paper to study how all individual force components vary with the inclination. Therefore, it is assumed that the hook-load is adjusted when the inclination changes such that the WOB remains constant.

3.2 Drilling performance of the benchmark model

The performance analysis pursued in this section focuses on the axial bit velocity, because this ultimately determines the ROP. The dynamic models as presented in Sect. 2 are simulated with a time-stepping-based numerical simulator. The structure of the numerical simulator is based on [35].

Time-domain responses of the axial bit velocity of the benchmark model with and without spatial friction between the BHA and the borehole wall are depicted in Fig. 7. In both simulations, the same boundary conditions are applied (the total weight applied on the bit \(W_0=171\) kN and the angular velocity at the top-drive \(\varOmega _0=80\) RPM). The initial conditions in both simulations are chosen close to the desired nominal operating conditions (\(u_b(0)=\phi _b(0)=1\times 10^{-4}\) and \(\dot{u}_b(0)=\dot{\phi }_b(0)=0\)), such that the initial perturbations are small with respect to the nominal solution. Figure 7a, b shows the axial bit velocity without and with spatial friction, respectively. Both cases show unstable transient behaviour where the oscillations grow until the bit experiences an axial (and a torsional) stick-slip limit cycle. Furthermore, the transient phase in the case with friction is longer, i.e., it requires more time to reach the axial (and torsional) limit cycle. This implies that the friction has a stabilizing effect on the drill-string dynamics, which reduces the growth rate of the axial (and torsional) vibrations. The spatial Coulomb friction does not qualitatively change the drill-string system response of the benchmark model for this specific set of operation conditions.

Next, the effect of the spatial friction is investigated for a broad range of operation conditions. The range of the nominal WOB (\(W_0\)) corresponds with the range of hook-load forces of \(H_0=370-440\) kN. This range is chosen such that lower values result in bit-bouncing and higher values in a negative nominal axial velocity (see (32) for the relation between \(H_0\) and \(V_0\)). The range of angular velocities corresponds with \(\varOmega _0 = 30-150\) RPM. The drilling efficiency \(\eta \) and averaged ROP for this range of operation conditions are depicted in Figs. 8, 9 and 10 for different inclined scenarios with \(\varTheta =0^{\circ }\), \(\varTheta =45^{\circ }\) and \(\varTheta =90^{\circ }\), respectively.

In Figs. 8a, b, 9a, b and 10a, b, it can be observed that the ROP increases with increasing nominal WOB and prescribed angular velocity. An increase in \(W_0\), under a prescribed constant angular velocity, results in an increased ratio between the cutting and frictional forces. Also with faster rotation (higher values of \(\varOmega _0\)) more volume of rock is cut in a given time window. Furthermore, the spatial Coulomb friction has a small effect on the ROP, implying that the portion of the total force used for the cutting process is not affected significantly by the spatial friction between the BHA and borehole.

The drilling efficiency for different operation conditions is shown in Figs. 8c, d, 9c, d and 10c, d. An increase in the nominal WOB results in a higher drilling efficiency. This indicates that for a higher \(W_0\) more energy is used for the cutting process, which is in line with the results in Figs. 8a, 9a and 10a. However, an increasing prescribed angular velocity results in a decreasing drilling efficiency, which indicates that less energy is used for cutting. This implies a decrease in DOC. Even with the decrease in DOC, an increased ROP is still maintained. This consequently happens since with a higher angular velocity more volume of rock is removed by cutting in a given amount of time. From these results, it can be concluded that the spatial Coulomb friction mainly acts in tangential direction. This is a direct consequence of the large angular velocity compared to the axial velocity of the drill-string, which results in a sliding velocity (between stabilizer and borehole) with a relative small axial component compared to the tangential component. Consequently, this is reflected by the ratio between the axial and tangential components of the spatial Coulomb friction (\(\varvec{\lambda }_T=\lambda _{T_a}/\lambda _{T_t}\)), which is of \(\mathscr {O}(10^{-4}-10^{-2}\)). This observation indicates that the spatial Coulomb friction basically only produces a torsional friction and consequently hardly influences the axial motion of the bit, as reflected in the ROP observations.

Fig. 8
figure 8

Drilling performance without and with AST in a vertical well with inclination angle \(\varTheta =0^{\circ }\). The rate-of-penetration as function of a applied WOB \(W_0\) and b rotational velocity \(\varOmega _0\) and drilling efficiency as a function of c applied WOB \(W_0\) and d rotational velocity \(\varOmega _0\) (\(W_0=184\) kN and \(\varOmega _0=80\) RPM, unless parameter is varied)

Full size image
Fig. 9
figure 9

Drilling performance without and with AST in an inclined well with inclination angle \(\varTheta =45^{\circ }\). The rate-of-penetration as function of a applied WOB \(W_0\) and b rotational velocity \(\varOmega _0\) and drilling efficiency as a function of c applied WOB \(W_0\) and d rotational velocity \(\varOmega _0\) (\(W_0=184\) kN and \(\varOmega _0=80\) RPM, unless parameter is varied)

Full size image
Fig. 10
figure 10

Drilling performance without and with AST in an inclined well with inclination angle \(\varTheta =90^{\circ }\). The rate-of-penetration as function of a applied WOB \(W_0\) and b rotational velocity \(\varOmega _0\) and drilling efficiency as a function of c applied WOB \(W_0\) and d rotational velocity \(\varOmega _0\) (\(W_0=184\) kN and \(\varOmega _0=80\) RPM, unless parameter is varied)

Full size image

3.3 Drilling performance of the model including AST

In this section, we analyse the drilling performance of the system with AST in the presence of spatial friction between borehole and stabilizers.

Steady-state time-domain responses of the axial bit velocity for the drill-string model including the AST with and without spatial friction are depicted in Fig. 11. These responses are obtained with the same boundary conditions as used in benchmark model (\(W_0=171\) kN and \(\varOmega _0=80\) RPM). The initial conditions are chosen close to the nominal operating conditions (\(u(0)=u_b(0)=\phi _b(0)=1 \times 10^{-4}\) and \(\dot{u}(0)=\dot{u}_b(0)=\dot{\phi }_b(0)=0\)). In the absence of spatial Coulomb friction, the axial vibrations have a larger amplitude compared to the cases with spatial Coulomb friction. Furthermore, the axial bit velocity exhibits stick-slip transitions in case with and without spatial friction. Comparing the response of the model including AST with response of the benchmark shows a significant difference between the axial responses. In particular, the amplitude of the axial bit velocity (\(\dot{U}_b\)) increases by including the AST up to two times the amplitude of the axial bit velocity obtained with the benchmark model.

Fig. 11
figure 11

a The steady-state axial bit velocity for the model including AST without friction between the BHA and borehole wall (\(\varTheta =0\)), b with Coulomb friction (\(\varTheta =90^{\circ }\)) acting fully above the tool \(\varDelta =1\) and c with Coulomb friction (\(\varTheta =90^{\circ }\)) acting fully below the tool \(\varDelta =0\) (\(W_0=171\) kN and \(\varOmega _0=80\) RPM)

Full size image

The drilling performance for a range of operational conditions is depicted in Figs. 8, 9 and 10 for different inclined scenarios with \(\varTheta =0^{\circ }\), \(\varTheta =45^{\circ }\) and \(\varTheta =90^{\circ }\), respectively. The trends are comparable with the benchmark model, since the increase of the nominal WOB and prescribed angular velocity result in an increasing ROP, while the drilling efficiency increases with \(W_0\) and decreases with increasing \(\varOmega _0\). These figures also indicate that the spatial friction hardly affects the ROP. However, Fig. 10 shows that it makes a difference if the spatial Coulomb friction fully acts below (\(\varDelta =0\)) or above (\(\varDelta =1\)) the AST. In the simulations, it is observed that the axial vibrations above the tool (\(\dot{U}\)) decreases when the spatial friction acts fully above the tool (\(\varDelta =1\)). This indicates that smaller vibrations above the AST have a positive effect on the effectiveness of the tool, since it results in a slight improvement of ROP. When the friction fully acts below the tool (\(\varDelta =0\)), the ROP is slightly lower compared to the case without spatial friction. Furthermore, the influence of the location where the spatial friction acts is also observed in the drilling efficiency, which is lower in the case when all spatial friction acts below the tool. Hence, it can be concluded that the effect of the spatial friction on the axial vibrations, which are related to the improved drilling performance, depends on the location where the spatial friction acts. For various operational conditions (\(W_0\) and \(\varOmega _0\)), the drilling performance is higher for the case where all the additional friction acts above the tool. This insight reveals that it is more beneficial in practice to place the AST closer to the bit, such that the friction acts mainly above the tool.

A comparison between the ROP and drilling efficiency obtained with the benchmark model and with the model including AST shows that incorporating the AST significantly improves the ROP and the drilling efficiency for a broad range of spatial friction levels. For example, in the case of a prescribed angular velocity \(\varOmega _0=80\) RPM and a nominal WOB of \(W_0=192\) kN, the benchmark model results in the absence of spatial friction in a ROP of \(\langle \dot{U}_b \rangle =3.94 \times 10^{-3}\) m/s and a drilling efficiency \(\eta =0.28\), see Fig. 8. Under the same operational condition, a ROP of \(\langle \dot{U}_b \rangle =6.08\times 10^{-3}\) m/s and a drilling efficiency \(\eta =0.37\) is obtained with the model including AST. In this specific case, an increase of more than \(50\%\) in ROP and more than \(30\%\) in drilling efficiency is achieved by incorporating the AST. In the presence of spatial friction, the increase in ROP and drilling efficiency are comparable.

3.4 Discussion

From the performance analysis, it is concluded that the spatial friction hardly affects the ROP, since the axial component of the friction is relatively small compared to the tangential component. Furthermore, simulation results have revealed that incorporating the AST in the drill-string results in an improved drilling efficiency and ROP for a broad range of deviated wells. In case when the spatial friction acts fully above the AST, a slight improvement of drilling performance is observed compared to the case without spatial friction and when all friction acts below the tool.

4 Parametric design study AST

Based on the analysis performed in the previous section, incorporating the AST can provide a solution to improve the drilling efficiency, also in inclined drilling scenarios with increased frictional contact. From this point of view, the question arises how to find the optimal tool settings that provide the highest drilling efficiency. A parametric design study is performed in order to investigate the optimal tool design and to understand whether the optimality of this design is influenced by the frictional contacts between the BHA and the borehole wall (i.e., whether optimal tool settings can be found that robustly optimize performance for a broad range of deviated wells).

In practical field cases, the tool is placed in the bottom part of the BHA [33], which results in more mass of the BHA above the tool than below the tool. Since the largest contribution to the spatial friction comes from the heaviest part of the BHA, all simulations in this section are performed under the assumption that all spatial Coulomb friction forces fully act above the tool (\(\varDelta =1\)).

The tool design is mainly reflected by two parameters, namely the lead of the helical spline \(\beta \) and the spring stiffness \(K_b\). In the current design of the AST, a lead angle of \(\beta =45^{\circ }\) and a spring stiffness \(K_b=1522.5\) kN/m are used. The investigated range of the lead angle is in between \(\beta =10-70^{\circ }\) and the spring stiffness range is in between \(50-11133\) kN/m. Higher values of spring stiffness results in bit-bouncing in absence of spatial friction. Two different operational scenarios are investigated, namely with a low angular velocity, where \(\varOmega _0=50\) RPM, and a high angular velocity, where \(\varOmega _0=120\) RPM. By considering these two operation scenarios, it can be investigated if the tool design is robust for different operational conditions. In all simulations \(W_0=171\) kN.

Fig. 12
figure 12

Drilling efficiency for different tool settings at a\(\varTheta =0\), b\(\varTheta =45^{\circ }\) and c\(\varTheta =90^{\circ }\) with \(\varOmega _0=50\) RPM and \(W_0=201\) kN. The highest drilling efficiency is denoted by the red dots. (Color figure online)

Full size image
Fig. 13
figure 13

Drilling efficiency for different tool settings at a\(\varTheta =0\), b\(\varTheta =45^{\circ }\) and c\(\varTheta =90^{\circ }\) with \(\varOmega _0=120\) RPM and \(W_0=201\) kN. The highest drilling efficiency is denoted by the red dots. (Color figure online)

Full size image

From the resulting parametric study, it is observed that a higher spring stiffness results in a higher frequency of the vibrations induced by the tool contraction. Furthermore, a smaller value of the lead will result in less contraction at a certain torsional displacement.

In Fig. 12, the drilling efficiency is plotted against the lead angle and the spring stiffness for different well inclination angles, and for the low angular velocity case (\(\varOmega _0=50\) RPM). The shape of the surfaces characterizing the drilling efficiency have similar trends for different values of \(\varTheta \), indicating that the influence of the spring stiffness and the lead on the drilling efficiency is comparable under various levels of spatial Coulomb friction. Figure 12 shows that for various spatial Coulomb frictions, the optimal value for the lead angle is around \(30^{\circ }\). Since in the current designs a lead angle of \(45^{\circ }\) is used, between 2 and 7\(\%\) in drilling efficiency can be gained by changing the lead angle to \(30^{\circ }\) in this specific case with the above-mentioned operational conditions. Furthermore, it is observed that for lower values of the spring stiffness, the tool provides a higher drilling efficiency. However, the influence of the spring stiffness is relatively small compared to the influence of the lead angle.

In Fig. 13, the drilling efficiency for the high angular velocity case (\(\varOmega _0=120\) RPM) is depicted for various values of the lead angle and spring stiffness and for different values of \(\varTheta \). The shapes in these figures are slightly different compared to the low angular velocity case. The dependency of the drilling efficiency \(\eta \) on the spring stiffness \(K_b\) reveals a less clear trend compared to the low angular velocity case. The optimal lead angle in this case is also around \(\beta =30^{\circ }\), which is equal to the low angular velocity case. However, it is observed that in the high angular velocity case the drilling efficiency is less sensitive for an increase in lead angle compared to the low angular velocity case.

Based on these results, the general conclusion is that the optimal values of the tool design are robust for different friction levels and a range of angular velocities imposed at the surface (rig). Hence, an optimal design for the AST that gives optimal drilling efficiency over a broad range of inclined scenarios is feasible.

5 Conclusions

In this paper, the effect of a passive down-hole anti-stall tool on the drilling performance of rotary drilling systems has been investigated for deviated well scenarios. A model including the coupled axial-torsional drill-string dynamics, the bit–rock interaction, the tool and the frictional effects of the stabilizers, due to borehole inclination, has been developed. A set-valued modelling approach for all contact and frictional effects has been pursued leading to a model in terms of a delay differential inclusion for which a time-stepping method is employed for simulation purposes. Numerical analysis results revealed that the down-hole tool significantly improves drilling efficiency and ROP for a broad range of deviated wells. Moreover, based on a parametric design study it is concluded that an optimal tool design, in terms of drilling efficiency, can be found that is robust for a large range of borehole inclinations and operational conditions.